- 1Research Center for Wind Engineering and Engineering Vibration, Guangzhou University, Guangzhou, China
- 2College of Urban and Rural Construction, Zhongkai University of Agriculture and Engineering, Guangzhou, China
This paper investigates the nonlinear behavior and buckling of shallow arches under gradient thermal and mechanical loading. The gradient temperature varies continuously along the thickness of the cross section of the arch but uniformly distributes over the entire length of the arch. The principle of virtual work and mid-plane plane formulations are employed to derive analytical solutions for the structural responses, internal force and critical buckling loads of the arch. Subsequently, the phenomenon of the buckling mode switching are also identified and discussed. It is found that the fixed arch under gradient thermo-mechanical loading can buckle in a symmetric instability mode or an anti-symmetric instability mode, namely limit point buckling or bifurcation buckling, which depend on its geometric parameter and the gradient temperature. The effects of the gradient temperature change on the radial displacement, axial displacement, axial compressive force and bending moment as well as critical buckling loads of the arch are investigated through parametric studies comprehensively.
Introduction
Arches have been used extensively in civil and ocean engineering load-bearing structures. The stability of arch structures has attracted considerable attention from both research and engineering communities, and numerous studies on the nonlinear instability behavior of arches can be found in the open literature (Pi and Bradford, 2004a; Pi and Bradford, 2004b; Pi et al., 2011; Liu et al., 2018a; Liu et al., 2018b; He et al., 2020; Liu et al., 2020). In practical engineering, a steel arch may be subjected to thermo-mechanical load that leads to instability of the arch. It is well known that the material property of the steel is dependent on the temperature (Standard Australia, 1998; Heidarpour et al., 2010a; Maruschak et al., 2012; Moghaddasie and Stanciulescu, 2013; Yasniy et al., 2013; Heidarpour et al., 2014; Wang et al., 2020). When the applied temperature is uniformly distributed over the whole arch, the variations of the material property of steels caused by the temperature is uniform, and the steel arch is still isotropic structure. So the classical analysis method can be used to determine the structural behavior of the arch. A considerable amount of literature has been published on the linear or nonlinear behavior of arches subjected to uniform thermal load. Bradford et al. (Bradford, 2006a; Bradford, 2006b; Bradford, 2010) studied nonlinear instability behavior of a pinned arch under uniform thermal loading only. They found that the axial force in the arch produced by temperature is uniform along the arch axis. Pi et al. (Pi and Bradford, 2010a; Pi and Bradford, 2010b; Pi and Bradford, 2014) conducted a series of studies regarding the nonlinear in-plane thermo-elastic behavior of the crown-pinned, pin-ended and fixed steel arch. Heidarpour et al. (2010b) proposed a generic model to investigate the nonlinear elastic behavior of steel-concrete arches subjected to sustained loading at elevated temperatures. Lu et al. (2019) derived the exact solutions for the out-of-plane buckling load of the steel arch in a thermal environment incorporating shear deformations. The dynamic buckling of an arch subjected to transient thermal loading is studied by Keibolahi et al. (2018), from which they verified that the dynamic snap through buckling of the arch may occur when under rapid surface heating. Virgin et al. (2014) considered the influence of temperature and proved that temperature had a great influence on the extreme point of instability of arch. Malekzadeh et al. (2009) investigated the in-plane free vibrations of FGM arches under thermal environment by adopting two-dimensional elasticity theory and first-order shear deformation theory (FSDT). Yang and Huang (Yang et al., 2019a; Yang et al., 2019b; Yang et al., 2020a; Yang et al., 2020b; Yang et al., 2020c). presented an analytical solution of nonlinear in-plane buckling for a novel graphene reinforced composite arch/beam under mechanical/thermal loading, and determined the special parameter switching the buckling mode of the arch.
However, when the applied temperature is gradient distributed along one or two direction of the arch, the variations of the material property of steels caused by the temperature is non-uniform, and so the arch becomes anisotropic structure. The existence of anisotropy and involvement of geometric nonlinearity makes the problem of structural stability of the steel arch more complicated. So far, there has been very limit research investigating the nonlinear instability behavior of arches under gradient thermo-mechanical loadings. Cai et al. (2012) studied the elastic buckling of parabolic arches with rotational constraint under a vertical uniform load and uniform/gradient temperature changes. Pi et al. (Pi and Bradford, 2010c) developed a research on the nonlinear thermo-elastic buckling of pinned arches under temperature gradient field, and they also studied the out-of-plane buckling of fixed and rotationally restrained slender beam under linear gradient thermal action (Pi and Bradford, 2008; Pi and Bradford, 2010a; Pi and Bradford, 2015). Bateni and Eslami. (2014) discussed the effects of temperature gradient on the buckling of FGM arches and concluded that the temperature gradient enhances the buckling resistance of arches under a lateral mechanical load. Similar researches were also observed from Babaei’s report for the Thermo-mechanical nonlinear in-plane analysis of fix-ended FMG shallow arches (Babaei et al., 2018a; Babaei et al., 2018b). Song et al. (2019) carried out a linear analysis on the instability of steel arch under linear temperature gradient field and uniformly distributed radial load according to the effective centroid method and the principle of virtual work. To the best of authors knowledge, no work has been done on the nonlinear behavior and buckling of steel arches under gradient thermal and uniform radial loading.
Therefore, an analytical study is carried out in this paper to investigate the structural responses and specifically the buckling behavior of arches under gradient thermo-mechanical loadings. The principle of virtual work and mid-plane plane formulations are employed to derive the nonlinear equilibrium paths and critical buckling loads. The temperature-dependent geometric parameters determining the buckling modes of the arch are also obtained. The effects of gradient on the structural response, such as radial and axial displacement, internal force and critical buckling loads are discussed.
Nonlinear Equilibrium
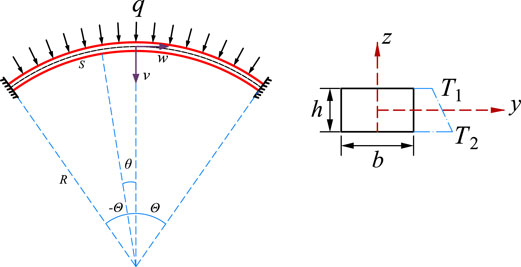
As shown in Figure 1, a fixed arch with center angle
Before the structural analysis, the following assumptions are adopted as: 1) deformations of the arch satisfy the Euler-Bernoulli hypothesis; 2) expansions of the cross section are ignored; 3) the states of temperature is treated as time-independent; 4) the coefficient of thermal expansion
According to classic shallow arch theory, the nonlinear strain-displacement relation of the arch is given as
where
Therefore, the nonlinear stress of the arch under gradient temperature T(z) is
where the reference temperature is 20°C, the linear gradient temperature T(z) is formulated as
where T1 and T2 are the temperature at the top and bottom of cross section. E(z) is the temperature-dependent elasticity modulus of steel according to the Australian Code AS4100 (Heidarpour et al., 2010a) which is given as
where E20 is the elastic modulus of steel at 20°C.
According to the principle of virtual work and mid-plane plane formulations, the nonlinear equilibrium equation of the arch is stated as
in which, axial compressive force N and bending moment M are formulated as
where A11, B11 and D11 are the stiffness components defined as
By substituting Eq. 6 into Eq. 7 leads to a new expression of Eq. 7 as
Integrating Eq. 5 by parts obtains the equilibrium equation as
and also obtains the boundary conditions of the fixed arch as
By substituting Eqs 9, 10 into Eq. 11, the equilibrium equation of arches is rewritten as
where μ is defined as
By solving Eq. 12 and considering the fixed-end boundary conditions, obtains
By substituting Eq. 14 into Eq. 10, the axial displacement
Substituting Eqs 14, 15 into Eqss 6, 7, the exact expression of the axial compressive force N and bending moment M of the arch are determined as
Eqs 10, 16 shows that the axial compressive force of the arch is constant through the arch when the gradient temperature is given.
By substituting Eq. 14 into Eq. 6 and integrating it over the entire length of the arch, the nonlinear equilibrium equation is obtained as
where
where
By combining Eqs 14, 18, the solutions of the nonlinear equilibrium conditions of the fixed arch under gradient thermo-mechanical loadings.
Buckling Analysis
Typical symmetric limit point buckling may occur when the arch is subjected to a gradient thermal and uniform radial load. When this happens, the arch reaches a limit point load and buckle in a limit point instability mode. The limit point loads are located at the local extrema of the nonlinear equilibrium path defined in Eq. 18, and the equation of equilibrium between limit point loads and axial force parameter
where
Solving Eqs 18, 23 simultaneously, the critical axial force parameter
Beyond symmetric limit point buckling, the anti-symmetric bifurcation buckling may also occur to the arch under gradient thermal and uniform radial load. The differential equation for bifurcation equilibrium of the arch is determined by the author previous research as (Heidarpour et al., 2010b)
where
When
Substituting
and substituting
which is a mono basic quadratic equation, and the existence of real solutions for Eq. 29 requires that
from which a critical parameter
When
Substituting
When the axial force parameter
Similarly, a critical parameter
When the arch having
Parametric Study
Comparisons
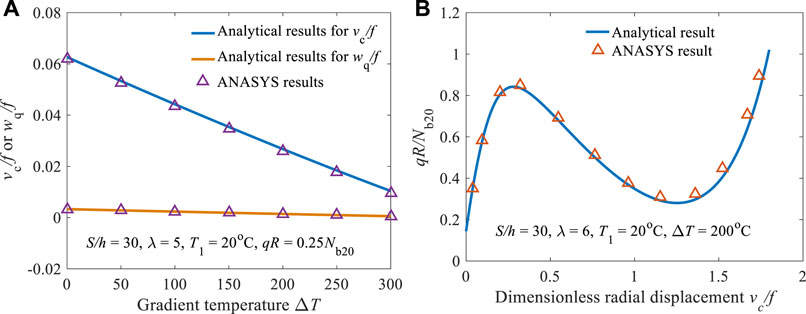
The finite element (FE) results are presented in this section to validate the proposed method. For conveniently and accurately, the FE analyses are performed by ANSYS 14.0 (Pi and Bradford, 2015) with using SHELL181 elements. In the ANSYS modeling, the dimension of cross section is b× h = 0.03 m × 0.025 m, and the cross section is subdivided into multiple layers in the thickness direction for simulating the material variation where the material properties of each layers are determined by Eq. 4. According to the convergence study, the difference between the results with 10 layers and 1,000 layers is less than 0.3%, which means that 10 layers adopted in the finite element model is sufficiently accurate to model a beam with continuous gradient varying material properties. Thus, 10 layers are adopted in the following FE analyses.
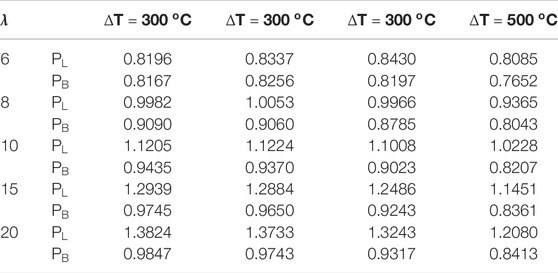
The result verification of the radial displacement at arch crown (vc/f,
Nonlinear Structural Responses and Buckling Loads
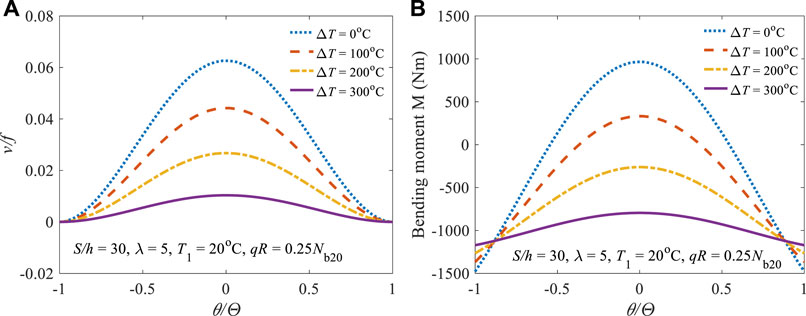
Figure 3 displays the variations of the structural responses (Figures 3A,B) and internal actions (Figures 3C,D) due to the gradient temperature change
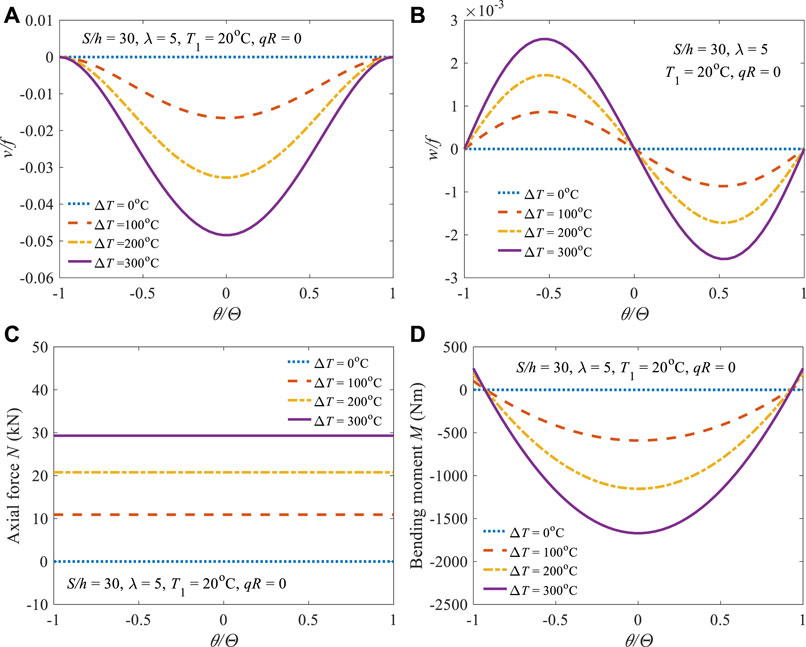
FIGURE 3. Structural responses of (A) dimensionless radial displacement, (B) dimensionless axial displacement, and internal actions of (C) axial force, (D) bending moment.
The combining effects of the gradient temperature change and uniform radial load on the dimensionless radial displacement and bending moment are shown in Figures 4A,B, respectively with qR = 0.25Nb20. From the observation, the directions of the force-induced radial displacement and bending moment are opposite to that of temperature-induced, and the increasing temperature-induced structural responses are counteracting the responses produced by the applied uniform radial load as the gradient temperature change increasing.
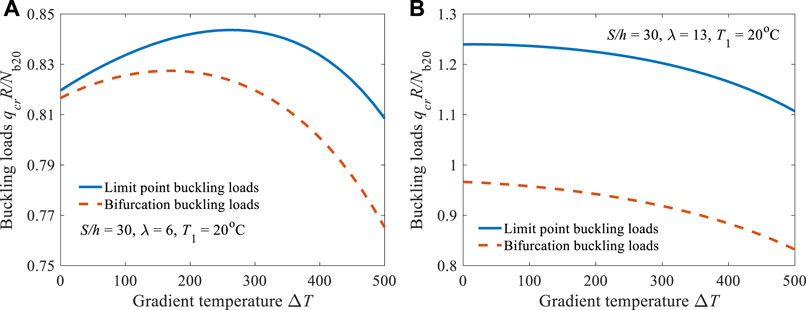
Figure 5 illustrates the influence of gradient temperature on the limit point buckling load (PL) and bifurcation buckling load (PB) of the arch. As can be seen from Figure 5 that the effects are related significantly to the geometrical parameter
Nonlinear Equilibrium Paths and Buckling Mode Switching
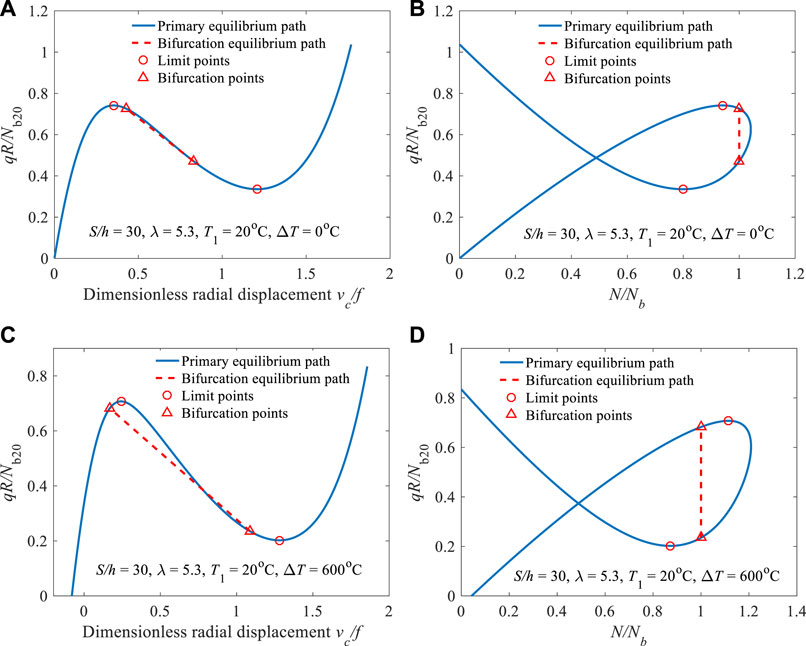
In addition to the investigation on the nonlinear structural responses and buckling loads, the nonlinear equilibrium paths and the buckling mode of the arch under gradient thermal and uniform radial load are explored in this section. Figure 6 depicts the nonlinear equilibrium paths of the arch with
Noted from Figures 6A,B, when the gradient temperature change is equal to zero, the limit point buckling occur to the arch because the bifurcation point is located behind the limit point. However, as shown in Figures 6C,D, when the temperature applied to the arch is higher than a certain value (i.e.
As previously discussed, there are critical parameters
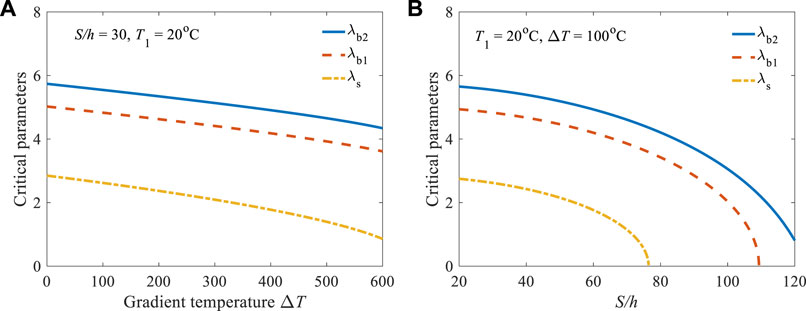
FIGURE 7. Variations of critical parameters
Conclusion
The nonlinear elastic behavior and buckling of shallow arch under gradient thermal and uniform radial loading has been studied in this paper. Exact solutions for the structural responses, internal force and critical buckling loads of the arch have been derived by adopting the principle of virtual work and mid-plane plane formulations. The effects of gradient temperature on the radial displacement, axial displacement, internal force and critical buckling loads have been discussed comprehensively. From the numerical discussion, the effects of the gradient temperature are quite significantly on the structural behavior of the arch. The arch deflects in its concave direction and buckles when a critical temperature gradient and external load are reached. It is also found that the arch under gradient thermal and uniform radial loadings can buckle in a limit point instability mode or a bifurcation mode. The critical gradient temperature change
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
RR: Conceptualization, writing—review and editing, funding acquisition, Software, methodology ZY: Data curation, writing—original draft preparation JL: Software, methodology YH: Validation, supervision AL: Conceptualization, Funding acquisition, validation.
Funding
This work was financially supported by the 111 Project (Grant No. D21021), Municipal Science and Technology Planning Project of Guangzhou (Grant No. 20212200004).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
This research is financially supported by the National Natural Science Foundation of China (No. 51925802, 11972123 and 51878188), Technology Planning Project of Guangzhou City (No. 201807010021), China-Australia Joint Research Centre for Resilient Material and Structures (No. 2020A050519002). The authors are grateful for these supports.
References
Babaei, H., Kiani, Y., and Eslami, M. R. (2018b). Geometrically Nonlinear Analysis of Functionally Graded Shallow Curved Tubes in Thermal Environment. Thin-Walled Struct. 132, 48–57. doi:10.1016/j.tws.2018.08.008
Babaei, H., Kiani, Y., and Eslami, M. R. (2018a). Thermomechanical Nonlinear In-Plane Analysis of Fix-Ended FGM Shallow Arches on Nonlinear Elastic Foundation Using Two-step Perturbation Technique. Int. J. Mech. Mat. Des. 15, 225–244. doi:10.1007/s10999-018-9420-y
Bateni, M., and Eslami, M. R. (2014). “Effect of Temperature Gradient on the Mechanical Buckling Resistance of FGM Shallow Arches,” in ASME 2014 12th Biennial Conference on Engineering Systems Design and Analysis (New York, United States: American Society of Mechanical Engineers (ASME)). doi:10.1115/esda2014-20363
Bradford, M. A. (2006). Elastic Analysis of Straight Members at Elevated Temperatures. Adv. Struct. Eng. 9, 611–618. doi:10.1260/136943306778827484
Bradford, M. A. (2006). In-plane Nonlinear Behaviour of Circular Pinned Arches with Elastic Restraints under Thermal Loading. Int. J. Str. Stab. Dyn. 06, 163–177. doi:10.1142/s0219455406001897
Bradford, M. A. (2010). Long-span Shallow Steel Arches Subjected to Fire Loading. Adv. Struct. Eng. 13, 501–511. doi:10.1260/1369-4332.13.3.501
Cai, J., Xu, Y., Feng, J., and Zhang, J. (2012). In-plane Elastic Buckling of Shallow Parabolic Arches under an External Load and Temperature Changes. J. Struct. Eng. 138, 1300–1309. doi:10.1061/(asce)st.1943-541x.0000570
He, H., Yuan, B., Chen, H., and Wei, Y. (2020). In-plane Failure Mechanism and Stability Bearing Capacity Design of Planar Plate-Tube-Connected Circular Steel Arches. Mech. Based Des. Struc., 1–16. doi:10.1080/15397734.2020.1713157
Heidarpour, A., Abdullah, A. A., and Bradford, M. A. (2010). Non-linear Inelastic Analysis of Steel Arches at Elevated Temperatures. J. Constr. Steel Res. 66, 512–519. doi:10.1016/j.jcsr.2009.10.003
Heidarpour, A., Cevro, S., Song, Q. Y., and Zhao, X. L. (2014). Behaviour of Stub Columns Utilising Mild-Steel Plates and VHS Tubes under Fire. J. Constr. Steel Res. 95, 220–229. doi:10.1016/j.jcsr.2013.12.007
Heidarpour, A., Pham, T. H., and Bradford, M. A. (2010). Nonlinear Thermoelastic Analysis of Composite Steel-Concrete Arches Including Partial Interaction and Elevated Temperature Loading. Eng. Struct. 32, 3248–3257. doi:10.1016/j.engstruct.2010.06.014
Keibolahi, A., Kiani, Y., and Eslami, M. R. (2018). Dynamic Snap-Through of Shallow Arches under Thermal Shock. Aerosp. Sci. Technol. 77, 545–554. doi:10.1016/j.ast.2018.04.003
Liu, A., Yang, Z., Bradford, M. A., and Pi, Y. L. (2018). Nonlinear Dynamic Buckling of Fixed Shallow Arches under an Arbitrary Step Radial Point Load. J. Eng. Mech. 144, 04018012. doi:10.1061/(asce)em.1943-7889.0001425
Liu, A., Yang, Z., Lu, H., Fu, J., and Pi, Y.-L. (2018). Experimental and Analytical Investigation on the In-Plane Dynamic Instability of Arches Owing to Parametric Resonance. J. Vib. Control 24, 4419–4432. doi:10.1177/1077546317726210
Liu, D., Sun, J., and Lan, L. (2020). Elasticity Solutions for In-Plane Free Vibration of FG-GPLRC Circular Arches with Various End Conditions. Appl. Sci. 10, 4695. doi:10.3390/app10144695
Lu, H., Liu, A., Pi, Y.-L., Bradford, M. A., and Fu, J. (2019). Lateral-torsional Buckling of Arches under an Arbitrary Radial Point Load in a Thermal Environment Incorporating Shear Deformations. Eng. Struct. 179, 189–203. doi:10.1016/j.engstruct.2018.10.071
Malekzadeh, P., Atashi, M. M., and Karami, G. (2009). In-plane Free Vibration of Functionally Graded Circular Arches with Temperature-dependent Properties under Thermal Environment. J. Sound Vib. 326, 837–851. doi:10.1016/j.jsv.2009.05.016
Malekzadeh, P. (2009). Two-dimensional In-Plane Free Vibrations of Functionally Graded Circular Arches with Temperature-dependent Properties. Compos. Struct. 91, 38–47. doi:10.1016/j.compstruct.2009.04.034
Maruschak, P. O., Konovalenko, I. V., and Bishchak, R. T. (2012). Effect of Thermal Fatigue Cracks on Brittle-Ductile Deformation and Failure of Cbcm Roller Surface Layers. Metallurgist 56 (1-2), 30–36. doi:10.1007/s11015-012-9532-9
Moghaddasie, B., and Stanciulescu, I. (2013). Equilibria and Stability Boundaries of Shallow Arches under Static Loading in a Thermal Environment. Int. J. Non-Linear Mech. 51, 132–144. doi:10.1016/j.ijnonlinmec.2013.01.001
Pi, Y. L., Andrew Bradford, M., and Qu, W. (2011). Long-term Non-linear Behaviour and Buckling of Shallow Concrete-Filled Steel Tubular Arches. Int. J. Non-Linear Mech. 46, 1155–1166. doi:10.1016/j.ijnonlinmec.2011.05.003
Pi, Y. L., and Bradford, M. A. (2014). Effects of Nonlinearity and Temperature Field on In-Plane Behaviour and Buckling of Crown-Pinned Steel Arches. Eng. Struct. 74, 1–12. doi:10.1016/j.engstruct.2014.05.006
Pi, Y. L., and Bradford, M. A. (2004). Effects of Prebuckling Deformations on the Elastic Flexural-Torsional Buckling of Laterally Fixed Arches. Int. J. Mech. Sci. 46, 321–342. doi:10.1016/j.ijmecsci.2004.02.012
Pi, Y. L., and Bradford, M. A. (2010). In-plane Thermoelastic Behaviour and Buckling of Pin-Ended and Fixed Circular Arches. Eng. Struct. 32, 250–260. doi:10.1016/j.engstruct.2009.09.012
Pi, Y. L., and Bradford, M. A. (2010). Nonlinear In-Plane Elastic Buckling of Shallow Circular Arches under Uniform Radial and Thermal Loading. Int. J. Mech. Sci. 52, 75–88. doi:10.1016/j.ijmecsci.2009.10.011
Pi, Y. L., and Bradford, M. A. (2010). Nonlinear Thermoelastic Buckling of Pin-Ended Shallow Arches under Temperature Gradient. J. Eng. Mech. 136, 960–968. doi:10.1061/(asce)em.1943-7889.0000134
Pi, Y. L., and Bradford, M. A. (2008). Thermoelastic Lateral-Torsional Buckling of Fixed Slender Beams under Linear Temperature Gradient. Int. J. Mech. Sci. 50, 1183–1193. doi:10.1016/j.ijmecsci.2008.04.004
Pi, Y. L., and Bradford, M. A. (2004). Experimental and Analytical Modal Analysis of Steel Arch Bridge. J. Struct. Eng. 130, 1022–1031. doi:10.1061/(ASCE)0733-9445(2004)130:7(1022)
Pi, Y. L., and Bradford, M. A. (2015). Out-of-plane Buckling of Beams Having In-Plane Elastic Restraints under Gradient Thermal Action. J. Eng. Mech. 142, 04015080.
Song, X., Lu, H., Liu, A., and Huang, Y. (2019). In-plane Instability of Fixed Arches under Linear Temperature Gradient Field and Uniformly Distributed Radial Load. Math. Probl. Eng.2019, 1–12. doi:10.1155/2019/5938030
Virgin, L. N., Wiebe, R., Spottswood, S. M., and Eason, T. G. (2014). Sensitivity in the Structural Behavior of Shallow Arches. Int. J. Non-Linear Mech. 58, 212–221. doi:10.1016/j.ijnonlinmec.2013.10.003
Wang, Q., Ji, B., Fu, Z., and Wang, H. (2020). Effect of High-Temperature Pavement Paving on Fatigue Durability of Bearing-Supported Steel Decks. Appl. Sci. 10, 7196. doi:10.3390/app10207196
Yang, Z., Feng, C., Yang, J., Wang, Y., Lv, J., Liu, A., et al. (2020b). Geometrically Nonlinear Buckling of Graphene Platelets Reinforced Dielectric Composite (GPLRDC) Arches with Rotational End Restraints. Aerosp. Sci. Technol. 107, 106326. doi:10.1016/j.ast.2020.106326
Yang, Z., Huang, Y., Liu, A., Fu, J., and Wu, D. (2019a). Nonlinear In-Plane Buckling of Fixed Shallow Functionally Graded Graphene Reinforced Composite Arches Subjected to Mechanical and Thermal Loading. Appl. Math. Model. 70, 315–327. doi:10.1016/j.apm.2019.01.024
Yang, Z., Liu, A., Yang, J., Fu, J., and Yang, B. (2019b). Dynamic Buckling of Functionally Graded Graphene Nanoplatelets Reinforced Composite Shallow Arches under a Step Central Point Load. J. Sound. Vib. 465, 115019. doi:10.1016/j.jsv.2019.115019
Yang, Z., Tam, M., Zhang, Y., Kitipornchai, S., Lv, J., and Yang, J. (2020a). Nonlinear Dynamic Response of FG Graphene Platelets Reinforced Composite Beam with Edge Cracks in Thermal Environment. Int. J. Str. Stab. Dyn. 20, 2043005. doi:10.1142/s0219455420430051
Yang, Z., Zhao, S., Yang, J., Lv, J., Liu, A., and Fu, J. (2020c). In-plane and Out-Of-Plane Free Vibrations of Functionally Graded Composite Arches with Graphene Reinforcements. Mech. Adv. Mat. Struc., 1–11. doi:10.1080/15376494.2020.1716420
Keywords: nonlinear, limit point buckling, bifurcation buckling, lowest buckling, gradient temperature, shallow arches
Citation: Rao R, Ye Z, Lv J, Huang Y and Liu A (2022) Nonlinear Instability Behavior and Buckling of Shallow Arches Under Gradient Thermo-Mechanical Loads. Front. Mater. 9:894260. doi: 10.3389/fmats.2022.894260
Received: 11 March 2022; Accepted: 09 May 2022;
Published: 02 June 2022.
Edited by:
Yunchao Tang, Guangxi University, ChinaReviewed by:
Pavlo Maruschak, Ternopil Ivan Pului National Technical University, UkraineReza Kolahchi, Zhejiang University, China
Zhuangpeng Yi, Changsha University of Science and Technology, China
Copyright © 2022 Rao, Ye, Lv, Huang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Airong Liu, bGl1YXJAZ3podS5lZHUuY24=
 Rui Rao
Rui Rao Zijie Ye1
Zijie Ye1 Yonghui Huang
Yonghui Huang Airong Liu
Airong Liu