Influence of Quartz Fiber on Electromagnetic Wave Transmission Properties of High-Alumina Cement Paste

In this paper, the effects of quartz fibers on the resistivity, complex permittivity, complex permeability, and S-parameters of high-alumina cement pastes are investigated. Meanwhile, the change of microstructure after adding quartz fibers were analyzed by mercury intrusion porosimetry (MIP) and scanning electron microscope (SEM). The results show that with the increase the content of quartz fiber, the real part of complex permittivity decreases, while the imaginary part of complex permittivity, dielectric loss tangent, and resistivity increased. At the same time, there are more small pores, and the interface situation is more complicated after adding quartz fiber. Therefore, the reflectivity decreases and the absorptivity increases, but the scope of increase in the absorptivity is smaller than the decrease in the reflectivity, resulting in an increase in the transmittivity. When the content of quartz fiber is 0.15, 0.30, 0.45, and 0.60%, the average transmittance of high-alumina cement paste is increased by 3.69, 6.18, 15.51, and 21.03% respectively. It is indicated that the quartz fibers can improve the wave transmission properties of the high-alumina cement paste.

1 Introduction

With the fast development of communication technology, 5G signals are known as having the advantages of high energy efficiency, low latency, and large capacity (Khalfi et al., 2017; Esmail et al., 2018). However, the wavelength of 5G signals is shorter, which leads to a weak ability to diffract obstacles. In the process of signal transmission, electromagnetic wave signal will be continuously attenuated by various buildings, which greatly affects the transmission efficiency of electromagnetic wave signal. Therefore, reducing the loss of electromagnetic wave signals in buildings is an urgent problem to be solved (Ishii et al., 2005; Ding et al., 2021). Portland cement is the most widely used architecture ingredient, but the C-S-H gel in its product of hydration reaction has great hindrance to the transmission of electromagnetic waves (Hay et al., 2020; Shen et al., 2021).

High-alumina cement hydration reaction products are mainly calcium aluminate hydrate crystal, calcium silicate hydrate gel is very few, so it has the potential to be used as electromagnetic wave transmission material. At present, the research on high-alumina cement mainly focuses on heat resistance (Antonovich et al., 2010), adsorption properties (Studart et al., 2003), mechanical properties (Kumar et al., 2012; Jing et al., 2018), and admixture control (Fu et al., 1995; Ding et al., 1996). The main problem of high-alumina cement is strength shrinkage at later stage, but studies have shown that the later strength shrinkage can be improved by adding silica fume (Monosi et al., 1996).

This paper studied the possibility of high-alumina cement as a new type of wave-transmitting cement-based material. If it has good wave-transmitting properties, it is expected to apply this type of material in constructing building envelopes as well as other fields in the future. At present, there were little research on the electromagnetic properties of high-alumina cement-based materials. In addition, Zhang’s (Zhang et al., 2009) research showed that silica fume had little effect on the electromagnetic wave transmission properties of materials. Therefore, in this study adding silica fume to high-alumina cement to improve its strength was not considered. Only the electromagnetic properties of high-alumina cement itself would be discussed.

At the same time, the electromagnetic properties of composite materials are determined by the synergistic effect of the matrix material and the reinforcing material. And the electromagnetic properties are related to resistivity, dielectric constant, and magnetic permeability (Moukwa et al., 1991; Ma et al., 2020). Wiltshire et al. (2003) studied the propagation characteristics of two different types of electromagnetic waves propagating in the horizontal and vertical directions, established the electromagnetic wave propagation model, and proved that the transmission and loss of electromagnetic waves are related to frequency through theory and experiment. Alqadi et al. (1995) proposed a non-destructive testing method for ordinary concrete materials using electromagnetic waves. The complex permittivity of six groups of different batches of concrete at the frequency of 0.1–40 MHz was measured. It is found that the permittivity would change significantly with the different curing time, and the electromagnetic properties were also significantly different. Rhim and Buyukozturk (1998) tested the electromagnetic properties of concrete test samples in the frequency range of 0.1–20 GHz. It was found that the electromagnetic properties are related to the moisture content of materials. Quartz fiber was widely used as insulating and wave-transmitting material based on its low thermal conductivity and low dielectric loss. Cui et al. (2020) and Liu et al. (2015) researched in the use of quartz fiber as reinforcing material to improve the electromagnetic properties of the material. They found that both dielectric constant and loss tangent were small after adding quartz fiber, and it had good wave transmission properties.

Based on the above analysis, this paper took high-alumina cement paste as the matrix while quartz fiber was chosen to be the material adjusting the wave transmission properties of the cement paste. The influence of different content of quartz fiber on the electromagnetic properties of high-alumina cement paste was researched, meanwhile the mechanism of how quartz fiber affected the wave transmission properties of high-alumina cement paste was analyzed.

2 Raw Material

The test adopted CA50-A600 high-alumina cement. The chemical composition of the high-alumina cement is shown in Table 1, and the basic physical properties of the high-alumina cement are shown in Table 2. The quartz fiber adopts SJ104-6 type quartz fiber, the length is 6mm, the diameter is 7 $\mu m$. The main chemical composition of quartz fiber is SiO₂, SiO₂ mass fraction is 99.95%. The basic properties of the quartz fiber are shown in Table 3.

TABLE 1

TABLE 1. Chemical composition of high-alumina cement (by mass)/%.

TABLE 2

TABLE 2. Basic physical properties of high-alumina cement.

TABLE 3

TABLE 3. Basic properties of quartz fiber.

3 Design of Mix Ratio and Test Methods

3.1 Mix Ratio

Five groups of cement paste test samples were prepared. The water binder ratio was 0.3, and the volume content of quartz fiber was 0, 0.15, 0.30, 0.45, and 0.60% respectively. Three samples were prepared for each group to test the resistivity and strength for 28 days.

First, weigh the raw materials required by each group. Then stir the high-alumina cement with a cement paste mixer at low speed and gradually add quartz fibers. Stir at low speed for 60 s to make the fibers evenly dispersed, after which add water and stir at low speed for 60 s. Stop mixing for 15 s, then stir at high speed 120 s. In the end, the stirred paste was put into the three-joint mold for vibration molding.

3.2 Test Methods

3.2.1 Resistivity Test

The resistivity test used APS-4000C multi-frequency power supply as the power supply, while the resistivity was measured by the four-probe method. A copper sheet with a thickness of 0.2 mm and a width of 20 mm was inserted into the formed sample. The distance between copper sheets was 32 mm, and the distance between copper sheets and the outermost side was 32 mm. Two outer copper sheets were used to measure the electrical current. Meanwhile, two inner copper sheets were used to measure the voltage, as shown in Figure 1. The resistivity of the high-alumina cement paste could be calculated according to Eq. 1.

$\rho =2\pi \text{a}\frac{U}{I}(1)$

where: ρ is the resistivity (Ω $\cdot$ m) of high-alumina cement paste; a is the distance (m) between the inner probes; U is the potential difference (V) between the inner probes; I is the electrical current (A) between the outer probes.

FIGURE 1

FIGURE 1. The device for testing resistivity.

3.2.2 Electromagnetic Parameter Test

The electromagnetic parameters were tested using the E5071C Series Network analyzer through the waveguide measurements. The frequency of the sample detected was 3.94–5.99 GHz. It is in the medium frequency band of 5G system, which means that it can achieve a better balance between 5G signal coverage and capacity (Wang et al., 2015). The complex permittivity, complex permeability and S-parameters in this range could be measured. The sample had been completely dried before the electromagnetic parameter test, so as to avoid the influence of water in the material on the test results. The drying method was to place the demoulded sample in a vacuum drying oven for at least 3 days, and the drying temperature was 40°C. The drying was completed after the sample was dried to constant weight.

3.2.3 Mechanical Property Test

The samples tested for strength were cured in a standard curing box with a temperature of $20\pm 1\mathrm{°}$C and a humidity of more than 90% for 28 days. The compressive strength and flexural strength of the samples were measured by DYE-300S automatic cement compressive and flexural testing machine. The maximum test force was 300KN, the loading speed of compressive strength was 2.4 kN/s, and the loading speed of flexural strength was 50 N/s.

3.2.4 Mercury Intrusion Porosimetry

The sample for pore structure analysis was under identical curing conditions as the strength test. After being fully dried, 2∼3 g of sample was taken for mercury intrusion porosimetry test. The drying method of mercury injection test was the same as that in Electromagnetic Parameter Test. The test equipment was AutoPore IV 9510 with a working pressure was $6.90\times {10}^{-4}$ ∼413.70 MPa.

3.2.5 Scanning Electron Microscope Test

The equipment model tested by scanning electron microscope was Zeiss sigma 300. The sample was also under the same curing conditions as the strength test. After being fully dried, 3∼5 g sample was sprayed with gold. The diameter and thickness of the sample should be both less than 5 mm.

4 Results and Discussion

4.1 Strength

Figure 2 shows the 28 days strength of high-alumina cement with different volume of fiber content. With the increase of quartz fiber content, the compressive and flexural strength gradually increased. When the fiber content was 0.6%, the compressive strength was 74.3 MPa and the flexural strength was 12.6 MPa. It was increased by 29.22 and 18.87% respectively compared to the group without any fiber addition. Due to the addition of quartz fibers, the development of cracks in the matrix is limited, which improves the crack resistance and toughening that leads to the improvement of strength (Avilagalhano et al., 2005; Li et al., 2017).

FIGURE 2

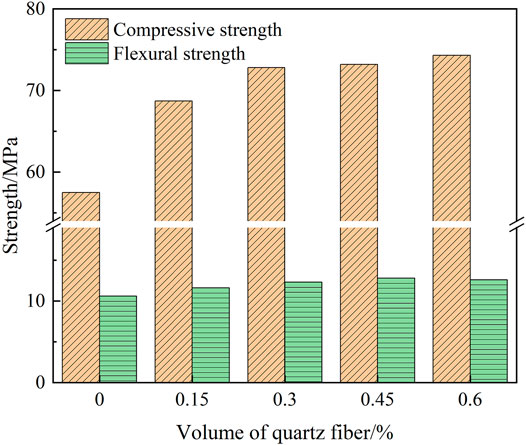
FIGURE 2. Compressive strength and flexural strength of high-alumina cement of different fiber content.

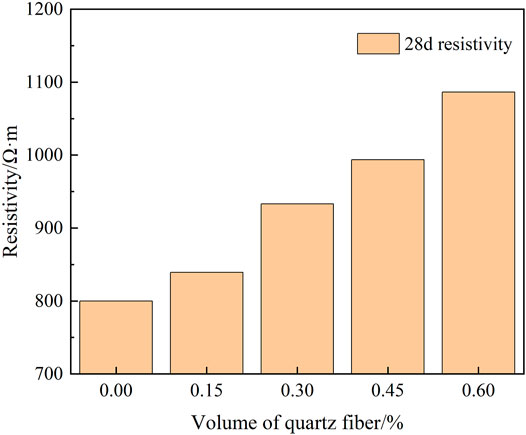
4.2 Resistivity

Studies have shown that resistivity is an important factor affecting microwave absorption and transmission properties. Resistivity is related to the dielectric constant and loss tangent of the material (Ishikawa, 1994; Cao and Chung, 2004). The 28 days resistivity of high-alumina cement paste with different fiber content is shown in Figure 3. With the increase of quartz fiber content, the resistivity gradually increases. When the content of quartz fiber is 0.15, 0.30, 0.45, and 0.60%, the resistivity was increased by 4.92, 16.66, 24.23, and 35.81%, respectively. This can be explained by the fact that conductive phase of the cement-based material is mainly the liquid phase and the conductive medium in the pores of the cement paste (El-Enein et al., 1995). The quartz fiber as a non-conductive fiber has a much higher resistivity than the cement paste. With the addition of quartz fiber, the interface between fiber and high-alumina cement becomes more complex (Tayeh et al., 2012), resulting in the inhibition of ion transport, so the resistivity increases gradually.

FIGURE 3

FIGURE 3. Resistivity of high-alumina cement with different fiber content.

4.3 Dielectric Constant

Dielectric constant is an important parameter to measure the electromagnetic properties of materials. It is divided into real part and imaginary part ($\epsilon ={\epsilon }^{\prime }-i{\epsilon }^{″}$). The real part is used to measure the properties of the medium to store and release electromagnetic energy, and the imaginary part is used to measure the properties of the medium to loss electromagnetic energy. The relationship between the dielectric constant and frequency of the test samples with different fiber contents is shown in Figure 4.

FIGURE 4

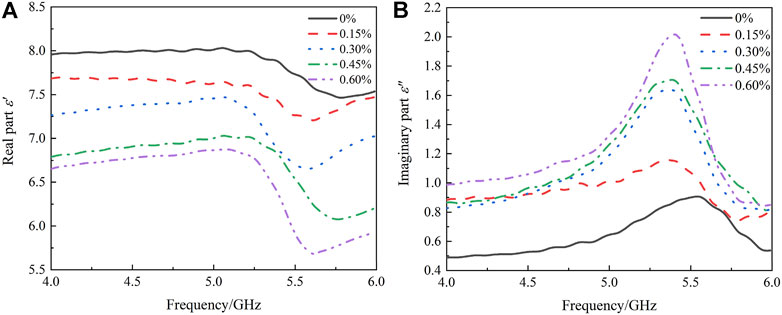
FIGURE 4. Dielectric constant curve with frequency. (A) Real part of dielectric constant (B) Imaginary part of dielectric constant.

As can be seen from Figure 4, the real part of dielectric constant decreases significantly after adding quartz fiber. Because the dielectric constant of quartz fiber is 3.74, which is lower than that of ordinary cement-based materials, and the addition of quartz fiber makes the interface more complex, resulting in more interface polarization, resulting in the reduction of the properties of the overall stored electromagnetic energy of the sample. Therefore, with the increase of the content of quartz fiber, the real part of the dielectric constant is lower. Furthermore, it was found that the real part of the permittivity of the composites decreases with increasing resistivity (Aono and Nitta, 2002), which is consistent with the results in Test Methods. According to the transmission line theory, the lower the real part of the dielectric constant, the better the impedance matching effect, so it is easier for electromagnetic waves to enter the material, thereby reducing the reflection of electromagnetic waves. For lossy transmission lines in practice, the amplitudes of incident and reflected waves decay exponentially with their respective propagation directions. When the impedance of the material is equal to that of the free space, the transmission line is called matching. At this time, the electromagnetic wave is zero reflected on the surface of the material, which is the ideal working state of the transmission line. Therefore, in order to improve the wave transmission properties of high-alumina cement paste, it is necessary to improve the matching degree between the material and the free space, so as to make more electromagnetic wave signals enter the interior of the material.

However, with the increase of the quartz fiber content, the imaginary part of the dielectric constant increases significantly. This is because that the polarization strength of the material needs to reach the corresponding value after a period of time under the action of the alternating electromagnetic field (Yuri, 2002). However, by adding quartz fiber, the post-fiber relaxation time becomes longer. The polarization strength of the high-alumina cement is not able to keep up with the change of the alternating electromagnetic field. This phenomenon causes dielectric loss, resulting in a sharp drop in the real part of the dielectric constant and a peak in the imaginary part.

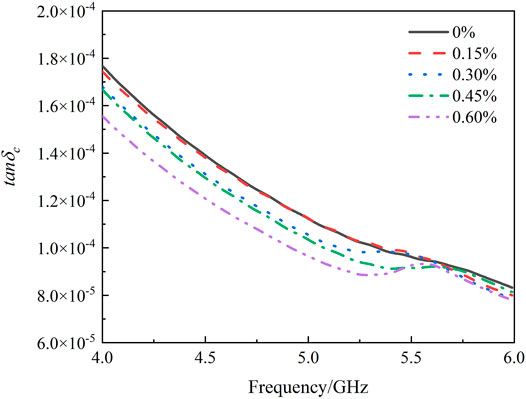
It can be seen from Figure 5 that the image of the dielectric loss is basically the same as the image of the imaginary part of the dielectric constant, which means that the imaginary part of the dielectric constant can reflect the properties of the material loss of electromagnetic energy (Guo et al., 2011). In addition, after adding quartz fiber, a dielectric loss peak appeared in the range of 3.94–5.99 GHz. The peak overall shifted to the left, indicating that a group of dielectric relaxations occurred in this frequency range.

FIGURE 5

FIGURE 5. Dielectric loss tangent curve with frequency.

The dielectric loss mainly contains conductance loss and polarization relaxation loss (Yuri, 2002). The tangent value of the dielectric loss angle is usually used to measure the size of the dielectric loss, as it is shown in Eq. 2.

$\tan {\delta }_{\epsilon }=\frac{\epsilon \mathrm{″}}{\epsilon \mathrm{\prime }}(2)$

where: $\tan {\delta }_{\epsilon }$ is the tangent of the dielectric loss angle, ${\epsilon }^{\prime }$ is the real part of the dielectric constant, and ${\epsilon }^{″}$ is the imaginary part of the dielectric constant.

1) Conductivity loss

The conductivity loss is due to the electric current generated in the cement paste under the action of the electromagnetic field, which converts electrical energy into heat energy that results in the loss of electromagnetic wave energy (Jia et al., 2009). The conductance loss tangent is usually used to measure the conductance loss, as it is shown in Eq. 3.

$\tan {\delta }_c=\frac{1.8\times {10}^{10}}{{\epsilon }^{\prime }f\rho }(3)$

where: $\tan {\delta }_c$ is the tangent value of the conduction loss angle, and f is the frequency.

According to the measured resistivity and the real part of the dielectric constant, a curve of conductance loss versus frequency can be drawn as shown in Figure 6. After adding quartz fiber, the real part of the permittivity decreases, the resistivity increases, while the total conductance loss decreases. But the total dielectric loss has an order of 10⁻¹ and the conductance loss has an order of 10⁻⁴, which means that the conductance loss has less effect on the dielectric loss.

2) Polarization relaxation loss

FIGURE 6

FIGURE 6. Conductivity loss tangent curve with frequency.

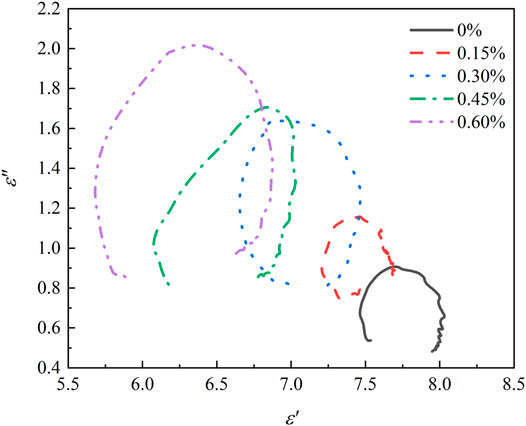
The mechanism of polarization relaxation loss can be explained by Debye relaxation theory (Wu et al., 2018). Taking the real part of the dielectric constant as the x-axis and the imaginary part as y-axis. Produce the Colo-Colo diagram as shown in Figure 7. Each arc represents a Debye polarization relaxation process, and these relaxation effects are mainly caused by interfacial polarization from electron aggregation and dipole polarization caused by uneven charge distribution at the defects of the cement paste (Biswas, 2010). After adding quartz fiber, the Debye arc increases, indicating that the introduction of quartz fiber adds more heterogeneous interfaces, and defects to the cement paste. As a stronger polarization relaxation process is performed, the absorbing properties of high-alumina cement pastes is improved.

FIGURE 7

FIGURE 7. Colo-colo graph.

4.4 Magnetic Permeability

Magnetic permeability is also an important parameter to measure the electromagnetic properties of materials, which is made of a real part and an imaginary part, as it is shown in Eq. 4.

$\tan {\delta }_{\mu }=\frac{\mu \mathrm{″}}{\mu \mathrm{\prime }}(4)$

where: $\tan {\delta }_{\mu }$ is the tangent of the magnetic loss angle, ${\mu }^{\prime }$ is the real part of the permeability, and ${\mu }^{″}$ is the imaginary part of the permeability.

Figure 8 is the magnetic permeability curve with frequency of different fiber content samples. It can be seen that the real part of the permeability is approximately 1, while the imaginary part of the permeability and the tangent of the magnetic loss angle are both approximately 0. This means that the high-alumina cement paste is a non-magnetic material and the addition of quartz fibers Magnetic permeability has very little effect on that. Part of the imaginary part of permeability is negative, which can be explained theoretically by Maxwell’s equations (Yan et al., 2018). Since magnetic field can be induced by electromagnetic radiation from alternating electric field, when the induced magnetic field exceeds the loss capacity of the material, the excess magnetic field will be radiated out, and then the imaginary part of negative permeability will be generated.

FIGURE 8

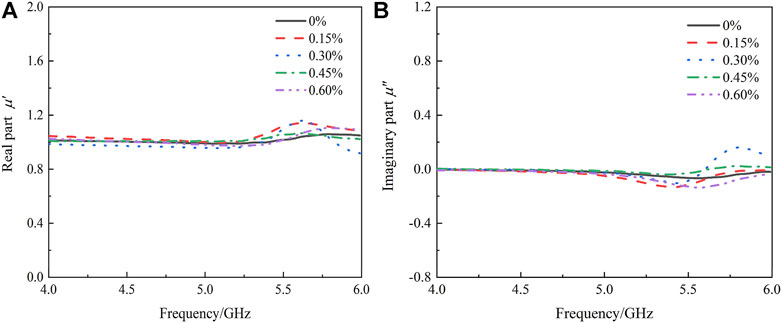
FIGURE 8. The Permeability curve with frequency. (A) Real part of permeability (B) Imaginary part of permeability.

4.5 Scattering Parameter

S-parameter, also known as scattering parameter, is an important parameter in microwave transmission. It can be classified into S₁₁, S₁₂, S₂₁, and S₂₂, which represent input reflection coefficient, reverse transmission coefficient, forward transmission coefficient and output reflection coefficient, respectively. The reflectivity, transmittivity and absorptivity can be obtained by calculation. The calculation formulas are shown below as Eqs. 5–7. The calculation results are shown in Figure 9.

$R={\left|S_{11}\right|}^2(5)$

$T={\left|S_{21}\right|}^2(6)$

$A=1-R-T(7)$

where: R is the reflectivity; T is the transmittivity; A is the absorptivity.

FIGURE 9

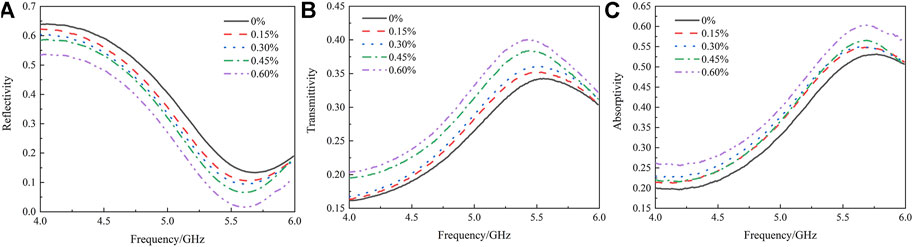
FIGURE 9. Relationship curve between reflectivity, transmittivity, absorptivity, and frequency. (A) Reflectivity (B) Transmittivity (C) Absorptivity.

It can be seen from Figure 9 that the reflectivity of the sample decreases with the addition of quartz fiber, while the transmittance and absorption rate increase. With the content of quartz fiber of 0.15, 0.30, 0.45, and 0.60%, the average transmittivity increases by 3.69, 6.18, 15.51, and 21.03%, respectively. This indicates that adding quartz fiber can significantly improve the transmittivity of high-alumina cement, and the higher the content, the better the improvement effect.

According to the conservation of energy, the sum of reflectivity, transmittivity, and absorptivity is 1. After adding quartz fiber, the dielectric loss increases, resulting in an increase in the absorptivity. Meanwhile, the real part of the dielectric constant is significantly reduced, resulting in better impedance matching effect, so that the reflection of electromagnetic wave is reduced and the incidence is increased. In summary, with the addition of quartz fiber, incidence, and loss increase. However, the results show that transmittivity increases, indicating that the increase of electromagnetic wave incidence is greater than that of absorption loss, so the total transmittivity increases.

5 Microanalysis

5.1 Mercury Intrusion Porosimetry

In order to explore the effect of quartz fibers on the pore structure of high-alumina cement pastes, pore characteristics of high-alumina cement pastes with fiber content of 0 and 0.6% were measured by mercury intrusion, as shown in Figure 10.

FIGURE 10

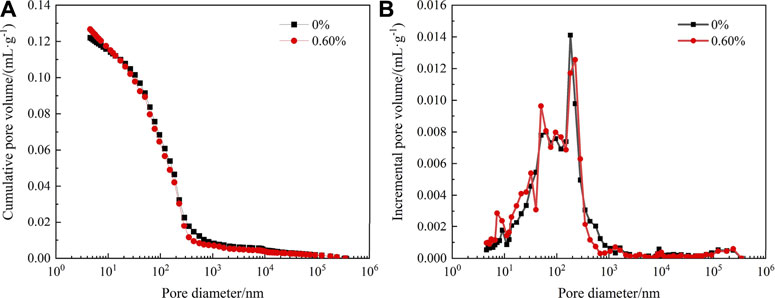
FIGURE 10. Pore characteristics of high-alumina cement paste with different fiber content. (A) Cumulative pore volume distribution (B) Pore size distribution.

After adding quartz fiber, the porosity percentage with fiber content 0 and 0.60% are 22.0 and 24.9%, respectively, indicating that the addition of quartz fiber makes the interface pore structure more complicated, thus increasing the porosity. Since the dielectric constant of air is approximately 1, the higher the porosity, the lower the overall dielectric constant of the high-alumina cement. It gives a better impedance matching, thereby reducing the reflection of electromagnetic waves and increasing the transmission of electromagnetic waves.

The pores related to electromagnetic wave absorption in the cement paste are divided into two categories: mesopores (pore diameter <50 nm) and macropores (pore diameter >50 nm). According to this classification standard, after sorting out the data from Figure 10, the pores with 0 and 0.60% fibre content occupy a percentage of 25.04 and 29.49%, respectively. There are more mesopores after adding fibers. According to existing studies, more pores smaller than 50 nm there are, more significant the interface polarization effect will be. This will lead to the loss of electromagnetic wave energy and increase the absorptivity.

5.2 Scanning Electron Microscopy

In order to observe the effect of quartz fiber addition on high-alumina cement paste in detail, the samples with quartz fiber content of 0 and 0.60% were analyzed under SEM, as shown in Figure 11.

FIGURE 11

FIGURE 11. SEM image of high-alumina cement paste with different fiber content. (A) Fiber content of 0% (B) Fiber content of 0.60%.

It can be seen from Figure 11 that the matrix is dense and smooth without quartz fiber, which is easy to reflect electromagnetic wave, indicating that the impedance matching effect of the whole material is poor at this time. After adding quartz fiber, the interface becomes more uneven. This multi-level nested structure makes the ion transmission more difficult (Hou et al., 2019), thus improving the resistivity. This is consistent with the resistivity test results. At the same time, the rougher interface will cause more interface polarization when the electromagnetic wave penetrates, resulting in dielectric loss, and the improvement of microwave absorption properties. However, since the reflected electromagnetic wave is reduced more after adding quartz fiber, the impedance matching effect is also improved, which indirectly improves the transmission properties. See Scattering Parameter for specific analysis and test results.

In conclusion, according to mercury injection test and scanning electron microscope test, the reasons for the increase of transmission properties of high-alumina cement paste are further analyzed from the microscopic point of view. After adding quartz fiber, the porosity increases and the interface becomes more complex. When the porosity increases, the real part of the dielectric constant of the whole material decreases, and the impedance matching effect is better, which is the main reason for the improvement of electromagnetic wave transmission properties.

6 Conclusion

1) With the increase of quartz fiber content, the real part of dielectric constant decreases, and the imaginary part of dielectric constant, the tangent of dielectric loss angle and resistivity increase. At the same time, the small holes in the paste increase and the interface becomes more complex.

2) After adding quartz fiber, the reflectivity decreases more than the absorptivity increases, so the transmittivity increases.

3) When the content of quartz fiber is 0.15, 0.30, 0.45, and 0.60%, the average transmittivity of high-alumina cement paste is increased by 3.69, 6.18, 15.51, and 21.03%, respectively. The results show that adding quartz fiber can improve the wave transmission properties of high-alumina cement paste.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LY and JC contributed to conception and design of the study. YB and LJ organized the database. YB and LYN performed the statistical analysis. YB, LY, and JC wrote the first draft of the manuscript. LH, LJ, and LYN wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors would like to acknowledge the financial support provided by National Natural Science Foundation of China (52078015), Beijing Millions of Talents Project (2018A37), Beijing Natural Science Foundation (8202005).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Qadi, I. L., Hazim, O. A., Su, W., and Riad, S. M. (1995). Dielectric Properties of Portland Cement Concrete at Low Radio Frequencies. J. Mater. Civil Eng. 7 (3), 192–198. doi:10.1061/(asce)0899-1561(1995)7:3(192)

CrossRef Full Text | Google Scholar

Antonovich, V., Pundene, I., Stonis, R., and Pyren’kin, O. (2010). Study of the Effect of Type of High-Alumina Cement on the Properties of Heat-Resistant Concrete with a Composite Deflocculant. Refract Ind. Ceram. 51 (4), 279–282. doi:10.1007/s11148-010-9307-4

CrossRef Full Text | Google Scholar

Aono, M., and Nitta, S. (2002). High Resistivity and Low Dielectric Constant Amorphous Carbon Nitride Films: Application to Low-K Materials for ULSI. Diamond Relat. Mater. 11 (3-6), 1219–1222. doi:10.1016/s0925-9635(01)00718-x

CrossRef Full Text | Google Scholar

Avilagalhano, G., Felipevalandro, L., Marquesdemelo, R., Scotti, R., and Antoniobottino, M. (2005). Evaluation of the Flexural Strength of Carbon Fiber-, Quartz Fiber-, and Glass Fiber-Based Posts. J. Endodontics. 31 (3), 209–211. doi:10.1097/01.don.0000137652.49748.0c

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, M. (2010). Debye-type Relaxation in Yittria Stabilized Zirconia. J. Alloys Compounds. 491 (1-2), 30–35. doi:10.1016/j.jallcom.2009.10.233

CrossRef Full Text | Google Scholar

Cao, J., and Chung, D. D. L. (2004). Use of Fly Ash as an Admixture for Electromagnetic Interference Shielding. Cement Concrete Res. 34 (10), 1889–1892. doi:10.1016/j.cemconres.2004.02.003

CrossRef Full Text | Google Scholar

Cui, G., Cheng, Y., Liu, C., Huang, K., Li, J., Wang, P., et al. (2020). Massive Growth of Graphene Quartz Fiber as a Multifunctional Electrode. Acs Nano. 14 (5), 5938–5945. doi:10.1021/acsnano.0c01298

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, J., Fu, Y., and Beaudoin, J. J. (1996). Study of Hydration Mechanisms in the High Alumina Cement - Sodium Silicate System. Cement Concrete Res. 26 (5), 799–804. doi:10.1016/s0008-8846(96)85017-4

CrossRef Full Text | Google Scholar

Ding, Y., Zhao, X., Li, Q., Zhang, Z., Kang, Z., Liao, Q., et al. (2021). Broadband Electromagnetic Wave Absorption Properties and Mechanism of MoS2/rGO Nanocomposites. Mater. Chem. Front. 5 (13), 5063–5070. doi:10.1039/d1qm00364j

CrossRef Full Text | Google Scholar

El-Enein, S. A. A., Kotkata, M. F., Hanna, G. B., Saad, M., and El Razek, M. M. A. (1995). Electrical Conductivity of concrete Containing Silica Fume. Cement Concrete Res. 25 (8), 1615–1620. doi:10.1016/0008-8846(95)00156-5

CrossRef Full Text | Google Scholar

Esmail, M. A., Ragheb, A., Fathallah, H., and Alshebeili, S. (2018). Demonstration of Photonics-Based Switching of 5G Signal over Hybrid All-Optical Network. IEEE Photon. Technol. Lett. 30 (13), 1250–1253. doi:10.1109/lpt.2018.2841974

CrossRef Full Text | Google Scholar

Fu, Y., Ding, J., and Beaudoin, J. J. (1995). Expansion Characteristics of a Compounded-Expansive Additive and Pre-hydrated High Alumina Cement Based Expansive Additive. Cement Concrete Res. 25 (6), 1295–1304. doi:10.1016/0008-8846(95)00122-s

CrossRef Full Text | Google Scholar

Guo, A. L., Gao, R., and Ba, H. J. (2011). “Electromagnetic Properties of Bearing Cement-Based Materials,” in International Conference on Civil Engineering and Building Materials (CEBM), 663–668. doi:10.4028/www.scientific.net/amr.261-263.663

CrossRef Full Text | Google Scholar

Hay, R., Li, J., and Celik, K. (2020). Influencing Factors on Micromechanical Properties of Calcium (Alumino) Silicate Hydrate C-(A-)S-H under Nanoindentation experiment. Cement Concrete Res. 134, 106088. doi:10.1016/j.cemconres.2020.106088

CrossRef Full Text | Google Scholar

Hou, D., Yu, J., and Wang, P. (2019). Molecular Dynamics Modeling of the Structure, Dynamics, Energetics and Mechanical Properties of Cement-Polymer Nanocomposite. Composites B: Eng. 162, 433–444. doi:10.1016/j.compositesb.2018.12.142

CrossRef Full Text | Google Scholar

Huo, J., Wang, L., and Yu, H. (2009). Polymeric Nanocomposites for Electromagnetic Wave Absorption. J. Mater. Sci. 44 (15), 3917–3927. doi:10.1007/s10853-009-3561-1

CrossRef Full Text | Google Scholar

Ishii, N., Miyakawa, M., and Sakai, K. (2005). A Method for Achieving Electromagnetic Wave Absorption by Low-Loss Stratified Construction Materials. IEEE Trans. Electromagn. Compat. 47 (1), 105–111. doi:10.1109/temc.2004.842105

CrossRef Full Text | Google Scholar

Ishikawa, T. (1994). Recent Developments of the Sic Fiber Nicalon and its Composites, Including Properties of the Sic Fiber Hi-Nicalon for Ultra-high Temperature. Composites Sci. Technology. 51 (2), 135–144. doi:10.1016/0266-3538(94)90184-8

CrossRef Full Text | Google Scholar

Jing, R., Chang, M., Jin, H., and Xue, X. (2018). Effects of Nano-SiO₂ on Properties of Spinel-Containing High-Alumina Cement. Key Eng. Mater. 768, 314–319. doi:10.4028/www.scientific.net/KEM.768.314

CrossRef Full Text | Google Scholar

Khalfi, B., Hamdaoui, B., and Guizani, M. (2017). Extracting and Exploiting Inherent Sparsity for Efficient Iot Support in 5g: Challenges and Potential Solutions. IEEE Wireless Commun. 24 (5), 68–73. doi:10.1109/mwc.2017.1700067

CrossRef Full Text | Google Scholar

Kumar, V., Singh, V. K., Srivastava, A., and Agrawal, G. N. (2012). Low Temperature Synthesis of High Alumina Cements by Gel-Trapped Co-precipitation Process and Their Implementation as Castables. J. Am. Ceram. Soc. 95 (12), 3769–3775. doi:10.1111/j.1551-2916.2012.05453.x

CrossRef Full Text | Google Scholar

Li, Y., Liu, X. F., and Li, J. Q. (2017). Experimental Study of Retrofitted Cracked concrete with FRP and Nanomodified Epoxy Resin. J. Mater. Civil Eng. 29 (5), 04016275. doi:10.1061/(asce)mt.1943-5533.0001810

CrossRef Full Text | Google Scholar

Liu, H. Y., Zhao, W. D., and Pan, L. Y. (2015). Study on Structure, Heat Resistence Property and Electromagnetic Property of Quartz Fiber Rein-Forced Polyimide Composite. J. Aeronaut. Mater. 35 (4), 34–38. doi:10.11868/j.issn.1005-5053.2015.4.006

CrossRef Full Text | Google Scholar

Ma, G., Zhang, Y., and Liu, X. (2020). Electromagnetic Wave Absorption Performance of Magnesium Phosphate Cement Functionalized by Nano-Fe3O4 Magnetic Fluid and Hollow Glass Microspheres. Construction Building Mater. 265, 120771. doi:10.1016/j.conbuildmat.2020.120771

CrossRef Full Text | Google Scholar

Monosi, S., Troli, R., Coppola, L., and Collepardi, M. (1996). Water Reducers for the High Alumina Cement-Silica Fume System. Mat. Struct. 29 (194), 639–644. doi:10.1007/bf02485972

CrossRef Full Text | Google Scholar

Moukwa, M., Brodwin, M., Christo, S., Chang, J., and Shah, S. P. (1991). The Influence of the Hydration Process upon Microwave Properties of Cements. Cement Concrete Res. 21 (5), 863–872. doi:10.1016/0008-8846(91)90181-g

CrossRef Full Text | Google Scholar

Rhim, H. C., and Buyukozturk, O. (1998). Electromagnetic Properties of concrete at Microwave Frequency Range. Aci Mater. J. 95 (3), 262–271. doi:10.14395/370

CrossRef Full Text | Google Scholar

Shen, Y., Li, Q., Xu, S., and Liu, X. (2021). Electromagnetic Wave Absorption of Multifunctional Cementitious Composites Incorporating Polyvinyl Alcohol (PVA) Fibers and Fly Ash: Effects of Microstructure and Hydration. Cement Concrete Res. 143, 106389. doi:10.1016/j.cemconres.2021.106389

CrossRef Full Text | Google Scholar

Studart, A. R., Pandolfelli, V. C., Tervoort, E., and Gauckler, L. J. (2003). Selection of Dispersants for High-Alumina Zero-Cement Refractory Castables. J. Eur. Ceram. Soc. 23 (7), 997–1004. doi:10.1016/s0955-2219(02)00275-3

CrossRef Full Text | Google Scholar

Tayeh, B. A., Abu Bakar, B. H., Megat Johari, M. A., and Voo, Y. L. (2012). Mechanical and Permeability Properties of the Interface between normal concrete Substrate and Ultra High Performance Fiber concrete Overlay. Construction Building Mater. 36, 538–548. doi:10.1016/j.conbuildmat.2012.06.013

CrossRef Full Text | Google Scholar

Wang, T., Li, G., Ding, J., Miao, Q., Li, J., and Wang, Y. (2015). 5G Spectrum: Is China Ready? IEEE Commun. Mag. 53 (7), 58–65. doi:10.1109/mcom.2015.7158266

CrossRef Full Text | Google Scholar

Wiltshire, M. C. K., Shamonina, E., Young, I. R., and Solymar, L. (2003). Dispersion Characteristics of Magneto-Inductive Waves: Comparison between Theory and experiment. Electron. Lett. 39 (2), 215–217. doi:10.1049/el:20030138

CrossRef Full Text | Google Scholar

Wu, Z., Tian, K., Huang, T., Hu, W., Xie, F., Wang, J., et al. (2018). Hierarchically Porous Carbons Derived from Biomasses with Excellent Microwave Absorption Performance. ACS Appl. Mater. Inter. 10 (13), 11108–11115. doi:10.1021/acsami.7b17264

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, F., Zhang, S., Zhang, X., Li, C., Zhu, C., Zhang, X., et al. (2018). Growth of CoFe2O4 Hollow Nanoparticles on Graphene Sheets for High-Performance Electromagnetic Wave Absorbers. J. Mater. Chem. C 6 (47), 12781–12787. doi:10.1039/c8tc04222e

CrossRef Full Text | Google Scholar

Yuri, F. (2002). Non-Debye Dielectric Relaxation in Complex Materials. Chem. Phys. 284 (1-2), 139–168. doi:10.1016/S0301-0104(02)00545-1

CrossRef Full Text | Google Scholar

Zhang, X., Sun, W., and Zhao, J. (2009). Microwave Absorbing Properties of Single-Layer and Double-Layer Cementitious Plates. Kuei Suan Jen Hsueh Pao/J. Chin. Ceram. Soc. 37 (7), 1218–1223. doi:10.1007/978-0-387-74660-9_12

CrossRef Full Text | Google Scholar