Designing Magnetic Semiconductors From a Ferromagnetic Metallic Glass

Utilizing both charge and spin degrees of freedom of electrons simultaneously in magnetic semiconductors promises new device concepts by creating an opportunity to realize data processing, transportation and storage in one single spintronic device. Unlike most of the traditional diluted magnetic semiconductors, which obtain intrinsic ferromagnetism by adding magnetic elements to non-magnetic semiconductors, we attempt to develop new magnetic semiconductors via a metal-semiconductor transition by introducing oxygen into a ferromagnetic Co-Fe-B metallic glass. The atomic structure and electronic structure of the Co-Fe-B-O sample are explored by using first-principles calculations. The total pair correlation functions of both the Co-Fe-B and Co-Fe-B-O samples evidence their glass structures. The bond pair and coordination number analysis together demonstrate that the oxygen addition enables the bond types to change from the dominant metallic bonding in the Co-Fe-B metallic glass to the mixture of metallic, ionic and covalent bonding in the Co-Fe-B-O oxide glass. This results in the localization of electron charge density and the opening of the band gap in the Co-Fe-B-O oxide glass. The density of states suggests the Co-Fe-B-O oxide glass is semiconducting with a band gap of about 1.7 eV, but there are intermediate energy levels in the band gap. Meanwhile, the Co-Fe-B-O oxide glass remains to be ferromagnetic. These results indicate that the Co-Fe-B-O oxide glass is a magnetic semiconductor transferred from a ferromagnetic Co-Fe-B metallic glass, which is further verified by the experimental realization of a Co-Fe-B-O magnetic semiconductor. Furthermore, our calculation results reveal that a hybridization of the 4s/4p, 3d electrons of ferromagnetic Co and Fe atoms and O 2p electrons exists. Such s, p-d exchange interaction is essential to bridge the mutual interaction between the electrical conduction arising from s-like electrons and ferromagnetism supported by 3d electrons in magnetic semiconductors, thereby enabling the control of ferromagnetism by electrical means. Our calculation results represent an important step to gain a deeper understanding of the oxygen addition induced metal-semiconductor transition in an amorphous alloy Co-Fe-B system. We anticipate that our calculation results provide theoretical fundamentals for experimentally transferring many other ferromagnetic amorphous alloys into ferromagnetic semiconductors with attractive magnetoelectric coupling properties.

1 Introduction

Generally, semiconductor devices offer irreplaceable advantages in information processing, while the information storage is widely based on metal-based magnetic devices (Awschalom and Flatté 2007). They are two separate components and have their own respectively independent development in the field of information technology. Emerging as advanced materials with multi functions, magnetic semiconductors (MSs) combine the characteristics of both semiconductor and ferromagnet, in which both charge and spin degrees of freedom of electrons can be manipulated simultaneously to fullfill the requirement for realizing logic computing function and information storage in one single device (Munekata et al., 1989; Dietl and Ohno 2014). This may provide an effective way to greatly reduce the energy consumption, increase the integration density, and improve the data operation speed (Ohno et al., 1999; Ohno et al., 2000). Currently, the research activity on MSs is mainly devoted to the dilute magnetic semiconductors (DMSs), that is, adding magnetic elements to conventional semiconductor materials to obtain magnetic properties, especially III-V semiconductors doped with magnetic elements (Ohno et al., 1992; Ohno et al., 1996; Matsukura et al., 1998). However, almost all DMSs prepared by this method have Curie temperatures far below room temperature (Schallenberg and Munekata 2006). For example, the highest Curie temperature recorded for (Ga, Mn)As is 200 K (Chen et al., 2011), based on which the devices cannot work at room temperature for practical applications.

The basic reason for the low Curie temperatures of these DMSs mentioned above is that the solid solubility of the magnetic elements in the non-magnetic semiconductor matrix is normally low. Additions of these magnetic elements beyond their solid solubility may lead to the introduction of a magnetic second phase (Zhang et al., 2012), which could disrupt the interaction of charge carriers and local magnetic moments. In contrast to these crystalline DMSs, metallic glasses (MGs) are characterized by long-range disordered atomic structures with uniform free volume distributions (Greer 1995). Additionally, the atomic bonding type dominated in MGs is metallic, which is non-directional and non-saturating. Therefore, MGs can be used as hosts to bring in a large amount of additional elements without altering the glass formation over a wide range of compositions, which makes it possible to realize room-temperature MSs (Liu et al., 2016). In this study, we select a Co-Fe-B metallic system because this system has been widely studied in the field of spintronics. This Co-Fe-B system not only shows strong ferromagnetism, but also has a Curie temperature higher than 500 K. In addition, it has high spin polarization and exhibits an unusual correlation between its spin-dependent transport and ferromagnetism (Paluskar et al., 2009). As a result, the amorphous Co-Fe-B system has been used as ferromagnetic electrodes in magnetic tunnel junction-based spintronic devices for data storage (Feng and Childress 1999; Wang et al., 2004; Djayaprawira et al., 2005; Wang et al., 2005; Fuji et al., 2018). Transferring this system into MSs may enable good compatability of this material with the existing semiconductor materials. Taken together, we attempt to design new room temperature MSs by introducing a large amount of oxygen into a ferromagnetic Co-Fe-B MG.

Currently, relatively few studies have been made to explore the electronic structure and exchange interactions of oxide glass (OG) ferromagnets (Wang et al., 2006; Hu et al., 2014). Apparently, the main obstacle to be solved relies on their unclear atomic structure. Experimentally, only average structural information is available, such as the coordination numbers and the bond length of the first nearest-neighbor shell mainly through synchrotron X-ray measurements. Moreover, these experiments generally could not provide sufficient structural information for gaining a deep understanding of the physics behind the oxygen effects on their unique properties, particularly in multivariate complex glass systems (Hirata et al., 2010). Recent progress in computational simulations offers an opportunity to resolve the atomic-level structure of glass materials and extend the local atomic packing schemes from short-range order to medium-range order (Ding et al., 2014; Ding et al., 2015). Meanwhile, it is possible to correlate the properties mainly focused on mechanical properties with the structures simulated by using computational techniques (Ding et al., 2012; Xu et al., 2015; Ding et al., 2016). In comparison, the details of how the atomic-level structure and electronic band structure affect the ferromagnetism, electricity and their coupling effects as well as exchange interactions in OG ferromagnets remain poorly understood from both experimental and theoretical aspects. Therefore, first-principles computational simulations are quite useful to uncover the underlying mechanisms that govern the oxygen-induced metal-semiconductor transitions in the OGs. In this paper, a melt-and-quench scheme implemented by first-principles molecular dynamics simulations has been employed to construct the structure models of Co-Fe-B and Co-Fe-B-O glass systems. These two systems are designed to explore the effects of oxygen addition on the structural, magnetic and electronic properties of the ferromagnetic Co-Fe-B system. Corresponding to the oxygen-induced changes in both the atomic structure and electronic structure, the magnetic and electronic properties of the Co-Fe-B-O system differ significantly from those of the Co-Fe-B MG system. The simulation results show that the developed Co-Fe-B-O material from the ferromagnetic Co-Fe-B system becomes a room-temperature MS and may hold potential for spintronic application. To verify the prediction of our computational simulations, a Co-Fe-B-O MS has been successfully prepared by magnetron sputter deposition. Our results provide a theoretical basis for demonstrating the effects of the oxygen addition on the metal-semiconductor transition in MGs and create a new avenue for experimentally designing and preparing new type of MSs transferred from ferromagnetic MGs.

2 Materials and Methods

2.1 First-Principles Calculations

First-principles simulations were carried out by employing generalized gradient approximation (GGA)/GGA + U with Perdew–Burke–Ernzerhof (PBE) formalism (Blöchl 1994; Perdew et al., 1996) on the basis of density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP) (Kresse and Hafner 1993). The supercell models of Co-Fe-B/Co-Fe-B-O system with a total of 200 atoms were adopted as initial structures. Automatic k-point mesh of 1 × 1 × 1 containing Gamma was used for geometry optimization. The convergence criterion used in the electronic self-consistent was set to 10^–5 eV and the magnitude of force on each atom fell below 0.005 eV Å⁻¹. For the Co-Fe-B/Co-Fe-B-O system, isothermal process was simulated at 300 K with 1,000 steps being collected for structural analysis. Electron spins were taken into account throughout the simulation.

The melt-and-quench approach (Kresse and Hafner 1994) has been used to theoretically obtain the structural model for amorphous transition metal oxides (ATMOs). Previously, it has been verified that such approach can successfully generate the structural models for amorphous semiconductors (Kresse and Hafner 1994) and MGs (Guan et al., 2012).

2.2 Experiments

Thin films were deposited on different substrates such as quartz glass, single-crystal silicon and silica by radio frequency (RF) magnetron sputtering. The base pressure was lower than 6 × 10^–5 Pa while the working pressure was 0.3 Pa under a gas mixture of high purity argon and oxygen. The composition of thin film was measured by auger electron spectroscopy (AES). The structure of the thin film was investigated by using a high resolution transmission electron microscope (HRTEM). The magnetic properties were measured by a superconducting quantum interference device-vibrating sample magnetometer (SQUID-VSM). The electrical properties were examined by a physical property measurement system (PPMS-9T).

3 Results and Discussion

3.1 Oxygen Enabled the Transformation From a Single-Phase Co-Fe-B MG to a Single-Phase Co-Fe-B-O OG

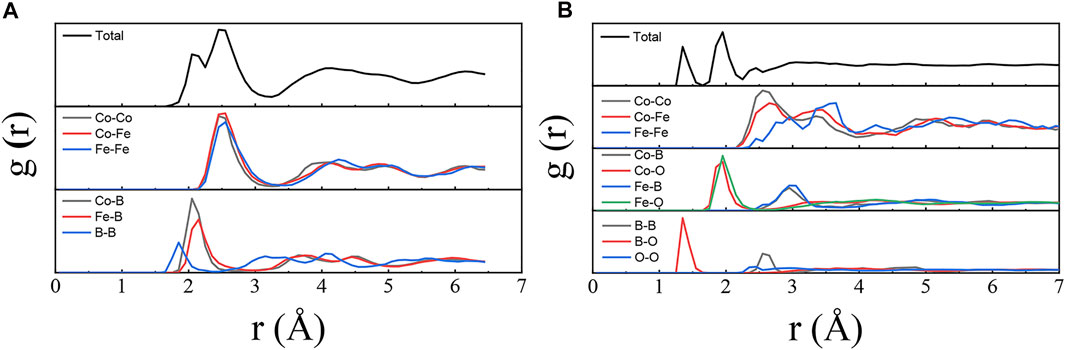
We select Co₄₀Fe₄₀B₂₀ and Co₂₃Fe₁₄B₁₀O₅₃ for first-principles calculations to study the effects of oxygen addition on both structure and properties of the Co-Fe-B system. Firstly, the difference in the atomic structures of the two systems are analyzed. The partial and total pair correlation functions (PCFs) for the Co-Fe-B and Co-Fe-B-O samples are plotted in the g(r) curves of Figure 1. The total PCFs of the two systems show broad peaks characteristic of their glass structures. Two obvious peaks arising from the first-nearest-neighbor shells are observed in the total PCF of the Co-Fe-B system as shown in Figure 1A. Compared with the partial PCFs of the elements involved in the Co-Fe-B system, one peak at around 2.1 Å mainly corresponds to the bonding pairs between the ferromagnetic (Co, Fe) atoms and metalloid (B) atom. The other peak at ∼2.55 Å is caused by the bonding pairs of transition metal (TM) elements Co-Co, Co-Fe and Fe-Fe. With the oxygen addition, the number and position of the first-nearest-neighbor peaks in the PCFs of the Co-Fe-B-O system differ from those of the Co-Fe-B system as shown in Figure 1B.

FIGURE 1

FIGURE 1. PCFs of (A) Co-Fe-B, (B) Co-Fe-B-O systems at 300 K.

Three obvious first-nearest-neighbor peaks are observed in the total PCF of the Co-Fe-B-O system in Figure 1B. Compared with its partial PCFs, the first peak is mainly attributed to the first-nearest-neighbor pairs of oxygen and boron atoms with an average atomic distance of about 1.35 Å between them. The second peak at around 1.95 Å is mainly due to the contributions from the atomic pairs between the TM atoms and non-metallic (O) atom. Owing to the high affinity of both Co and Fe to oxygen, there exists strong interaction between the Co, Fe atoms and O atoms, resulting in their intense first-nearest-neighbor peaks in the g(r) curves. Therefore, unlike the first-nearest-neighbor binding of TM-B at 2.1 Å in the Co-Fe-B system, no B as first nearest neighbors around the TM atoms can be observed due to the addition of oxygen. But B exists as the second nearest neighbors at about 3 Å around the TM atoms. In comparison, the third peak stems primarily from the first-nearest-neighbor atomic pairs of Co-Co, Co-Fe and Fe-Fe. Besides, the second-nearest-neighbor atomic pair of B-B also contributes to the third peak. At the same time, due to the addition of oxygen, the first-nearest-neighbor distances of TM-TM pairs increase as a whole. And all the first peaks of the partial PCFs of Co-Co, Co-Fe and Fe-Fe split as shown in Figure 1B. Such splitting suggests that ferromagnetic Co and Fe atoms may exist in different environments and thus form atomic bonds with different bond lengths.

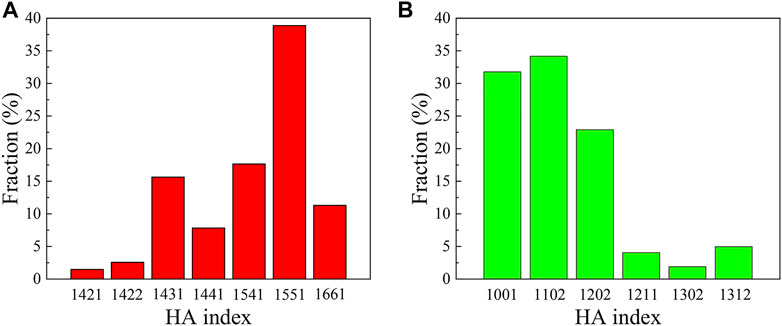
In order to further understand the local atomic structure of the Co-Fe-B MG and the Co-Fe-B-O OG, the bond pair index method of Honeycutt and Andersen (HA) is used. The type distributions of characteristic bond pairs with more than 1% in the amorphous Co-Fe-B and Co-Fe-B-O systems are shown in Figure 2. Among them, the 1,551 characteristic bond pairs representing the icosahedral clusters have the highest fraction, followed by 1,541 and 1,431 bond pairs representing the deformed icosahedra in the Co-Fe-B system (Figure 2A). These three bond pairs account for 72% of the total bond pairs, which is a typical feature for MGs. Figure 2B shows the statistical results of characteristic bond pairs in the Co-Fe-B-O system, which are very different from those of the Co-Fe-B system. The cluster structures characterized by 1,001, 1,102 and 1,202 bond pairs are the most popular, accounting for 88% of the total architecture. According to the definition of HA index, the 1,001 bond pair represents the B-O covalent bond, because its directivity and saturation determine the absence of its common first-nearest-neighbor atoms shared by B and O. And 1,102 and 1,202 bond pairs are more inclined to correspond to the mixture of ionic and metallic bonds. It shows that the number of atoms around the bond pair studied reduces.

FIGURE 2

FIGURE 2. Fractions of typical HA index of (A) Co-Fe-B, (B) Co-Fe-B-O systems.

The investigation of coordination number is based on the PCF analysis, taking the distance at the first trough as the cutoff value for the first nearest neighbors of the center atoms in the PCF curves. The average coordination numbers in M (Co, Fe, B, O)-centered clusters are listed in Table 1. Due to the oxygen addition, the average coordination numbers of Co and Fe elements become 7.6 and 6.9, respectively, which are much lower than 13.6 and 14.4 in the Co-Fe-B MG. The average coordination number around the B atom also decreases sharply from 9.0 to 3.1 after the oxygen addition. In the Co-Fe-B MG, these B-centered local structures with the coordination number of 9.0 are related to the tricapped trigonal prisms (TTP) at normal conditions, similar to the local configurations such as BFe₉ and B₂Fe₈ in Fe-B amorphous alloys (Tian et al., 2012). But the B-centered polyhedra have changed to the determined local BO₃ structural units in the Co-Fe-B-O OG as shown in Figure 3, similar to those in boron oxide. The average coordination number of O is 3.4, which further verifies the results of the HA index analysis. Therefore, the addition of oxygen causes dramatic structural changes, including the difference in the coordination environments of magnetic atoms and the emergence of oxide structural units, which may bring special magnetic and electrical properties.

TABLE 1

TABLE 1. Average coordination number of the elements.

FIGURE 3

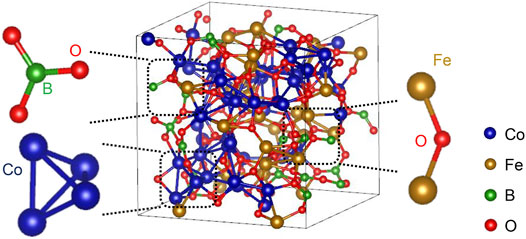
FIGURE 3. The atomic structure model of the Co-Fe-B-O system, in which the enlarged parts are the BO₃ structural unit, the tetrahedral structural unit consisting of four Co atoms and oxygen-mediated Fe-O-Fe structure.

3.2 Oxygen Induced Changes in the Ferromagnetism of the Amorphous Co-Fe-B-O System

In order to study the magnetic properties of the materials, the electrons’ spins were considered during the simulation. Firstly, according to the relationship between saturation magnetic induction (B_S) and magnetic moment (M_S) of $B_{\text{S}} = {\mu }_0(M_{\text{S}}/V_{\text{S}})$, where V_S is the involved supercell volume, μ₀ is vacuum permeability (4π × 10^–7 TmA⁻¹), the calculated B_S value of the Co-Fe-B amorphous system is 1.62 T. Meanwhile, the partial and average magnetic moments of different electron orbits of M (Co, Fe, B) atoms are listed in Table 2, which are similar to the calculation results of conventional CoFe-based amorphous alloys (Li et al., 2019).

TABLE 2

TABLE 2. Magnetic moments of s, p, d, and Total orbitals for the atoms in the Co-Fe-B system.

However, magnetic calculation of ATMOs is more complicated and less studied. This is because the magnetic super-exchange interactions mediated by oxygen atoms depend on their structures, whereas the amorphous short-range ordered structure is different from the unit cell structure of crystals. Therefore, it is difficult to determine the spin direction of each atom in the system. In this paper, we discuss the spin order of the Co-Fe-B-O system from its microstructure, and use a concise and effective theoretical method to determine the magnetic ground state of the involved ferromagnetic atoms combined with first-principles calculation.

From the structural analysis in the previous section, it is known that, unlike the atomic structure of the Co-Fe-B system, two different coordination environments exist for the magnetic Co and Fe within the Co-Fe-B-O system. According to the partial PCFs, the first peaks of Co-Co and Fe-Fe split into two sub-peaks (Figure 1B). The location of the first sub-peak is close to the first nearest-neighbor distance between the magnetic atoms in the Co-Fe-B system, while the second sub-peak locates at an average distance corresponding to the M-O-M groups connected by oxygen atoms. Therefore, the location of the splitting valley can be taken as a critical cutoff distance to distinguish the M-M and M-O-M groups, which experience the direct and indirect exchange interactions, respectively (Hu et al., 2014). According to the M-M bond lengths, the area consisting of magnetic atoms can be thus classified into two regions. One has short-range ordering clusters with direct exchange interaction via ferromagnetic coupling (D-region), while the other possesses local clusters with indirect exchange interaction via antiferromagnetic coupling (I-region). From the relative sizes of the two sub-peaks in the partial PCF diagrams (Figure 1B), almost all Co atoms are direct neighbors. Based on the Co-Fe-B-O atomic structure model in Figure 3, most of these directly neighbored Co atoms form tetrahedral structural units. In comparison, only a small number of Fe atoms are directly connected and experience direct exchange interaction, whereas most of Fe atoms form the oxygen-mediated Fe-O-Fe structural units with indirect exchange interaction (Figure 3). The bonding ability of the involved TMs of Co and Fe with oxygen depends on their affinities to oxygen. Fe has higher affinity to oxygen than Co, thus bonding with oxygen more easily. Hence, most local structural units of TM-O-TM are Fe-O-Fe, which may contribute to the decreased saturation magnetization.

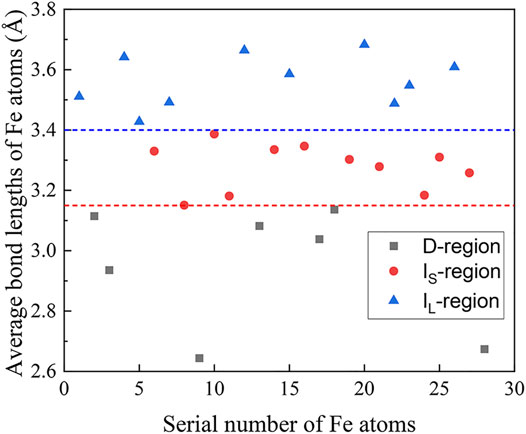
In order to better understand the correlation between local cluster structure and magnetic exchange interaction, the average Fe coordination numbers of Fe atoms involved in the two regions are counted to be 1.5 for D-region and 0.6 for I-region, respectively. At the same time, the Voronoi polyhedron analysis is used to probe the local atomic configurations via short-range order of the simulated amorphous structure (Medvedev 1986). The major types of the Fe-centered clusters are differentiated with the corresponding Voronoi polyhedral indices as shown in Figure 4A (Co-Fe-B MG) and Figure 4B (Co-Fe-B-O OG), respectively. From the statistical histogram of Voronoi polyhedral indices in Figure 4A, the Fe-centered clusters in the Co-Fe-B system are mainly characterized by two types of polyhedra indexed as < 0, 2, 8, x > and <0, 1, 10, x >. These two types of polyhedra are generally grouped as icosahedral-like clusters, indicating that the short-range ordering mainly exists in terms of icosahedral-like clusters (Zhang et al., 2015). Compared with the Fe-centered clusters in the Co-Fe-B system, the atomic configurations are quite different in the Co-Fe-B-O system (Figure 4B). All the typical coordination polyhedra are almost completely different from those in the Co-Fe-B system. Meanwhile, the percentages of these polyhedron types generally decrease and the distribution is more uniform in the Co-Fe-B-O system. To correlate the local structure and the ferromagnetism of this Co-Fe-B-O system, the Voronoi index type distributions of Fe-contained clusters in the D-region and I-region are statistically analyzed, respectively. As shown in Figure 4C and Figure 4D, the Fe-contained Voronoi polyhedron types are different in these two regions. The distribution of the Voronoi polyhedron indices in the I-region is almost identical to that of the overall Fe-contained Voronoi polyhedron indices of the system (Figure 4B). This indicates that the Fe atoms are mainly distributed in the I-region. In addition, in the statistical analysis of the Fe-O-Fe structural units, it is found that the average bond lengths of the two Fe atoms in the indirect exchange interaction are in the first and the second half of the posterior sub-peak, respectively. Figure 5 shows the average bond length distribution of Fe atoms in the system. Therefore, considering the combining influence of the coordination environment of Fe atoms and oxygen atoms on their spin directions, the Fe atoms in the I-region can be divided into two zones. One includes Fe atoms with large bond lengths (I_L-region) and the other consists of Fe atoms with small bond lengths (I_S-region). Different spin directions can be assigned to Fe atoms in these two zones, respectively. Thus, based on this method, we set up four spin ground states comprising the non-ferromagnetic (NM) state, the ferromagnetic coupling in all regions (FM), the negative magnetic moments of magnetic atoms in the I_S-region (AFM-Ⅰ) and the negative magnetic moments of magnetic atoms in the I_L-region (AFM-Ⅱ). Then, the total energy for each type of spin ordering can be calculated using the first-principles calculations. The calculated results are summarized in Table 3.

FIGURE 4

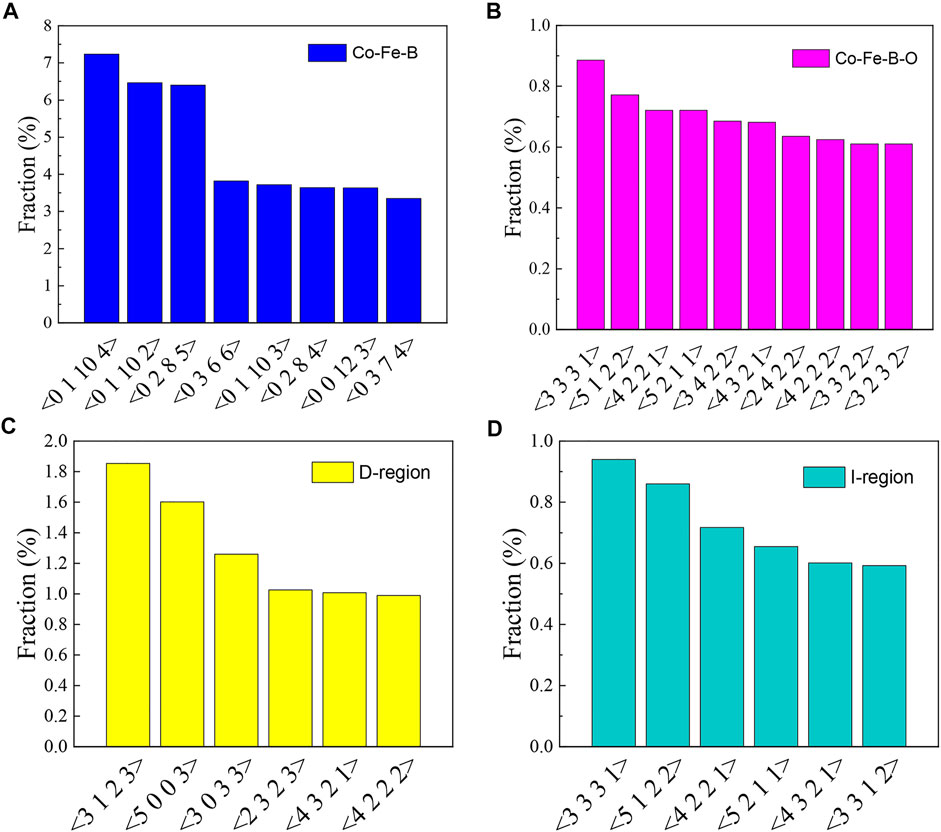
FIGURE 4. Distributions of typical Voronoi polyhedral indices of Fe-centered clusters in the (A) Co-Fe-B, (B) Co-Fe-B-O systems, (C) D-region and (D) I-region of the Co-Fe-B-O system.

FIGURE 5

FIGURE 5. Distribution of the average bond length of Fe atoms.

TABLE 3

TABLE 3. The total energies for each type of spin ordering and relative energies with respect to spin ordering NM.

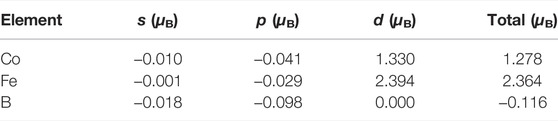
From Table 3, the AFM-Ⅱ type spin ordering is the lowest in energy. Based on this magnetic moment setting of the ground state, the partial and average magnetic moments of different electron orbits of M (Co, Fe, B, O) atoms are calculated. Compared with the Co-Fe-B MG, the average magnetic moment of Co atoms does not decrease, but slightly increases as shown in Table 4. This can be explained from two aspects. First, the oxygen addition appropriately increases the bond lengths between Co atoms, which enhances the direct magnetic exchange effect and therefore strengthens the ferromagnetism. Second, although there are fewer Co atoms in the I-region, the charge transfer between oxygen and Co atoms also contributes to the improvement of atomic magnetic moment. In contrast, Fe has a higher affinity to oxygen than Co, thus bonding with oxygen more easily. Most of Fe form the oxygen-mediated Fe-O-Fe structural units with indirect exchange interaction, whereas most of Co are direct neighbors with direct magnetic interaction. The average magnetic moment of Fe atoms decreases from 2.364 µ_B in the Co-Fe-B system to 0.879 µ_B in the Co-Fe-B-O system, which is mainly due to the presence of negative magnetic moments induced by oxygen-mediated indirect exchange interaction. Eventually, the B_S value decreases from 1.62 T in the Co-Fe-B system to 0.44 T in the Co-Fe-B-O system. Meanwhile, the Co-Fe-B-O OG becomes ferrimagnetic because of the presence of the negative magnetic moments.

TABLE 4

TABLE 4. Magnetic moments of s, p, d, and Total orbitals for the atoms in the Co-Fe-B-O system.

3.3 Oxygen Induced Changes in the Electronic Structure of the Co-Fe-B-O System

The DFT is an exact theory for reproducing and predicting ground state properties of an electronic system. Nevertheless, the usual LDA and GGA approximations cannot describe correctly the strongly correlated systems with partially filled d or f shells (Terakura et al., 1984). Therefore, the strong electronic correlations between 3d electrons in the transition metal atoms suggest the necessity to use a DFT + U approximation with correlation energy correction (Anisimov et al., 1991). We employed a GGA + U approach to characterize the electronic structure of the Co-Fe-B-O amorphous oxide, using a 3 × 3 × 3 Gamma centered k-point mesh and U_eff = 6.9 and 5.9 eV for d electrons of Co and Fe atoms, respectively (Anisimov et al., 1991).

In order to understand the difference in the electronic structures of the Co-Fe-B and Co-Fe-B-O systems, we calculated the charge density distribution and density of states (DOS) for the two systems. Their two-dimension (2d) charge density diagrams are shown in Figure 6. Compared with the Co-Fe-B-O system, the overall charge density of the Co-Fe-B MG is higher and more uniformly distributed, which conforms to the free-electron gas model of metals. The much more localized electron charge distribution of the Co-Fe-B-O OG indicates that this system tends to become insulating due to the oxygen addition.

FIGURE 6

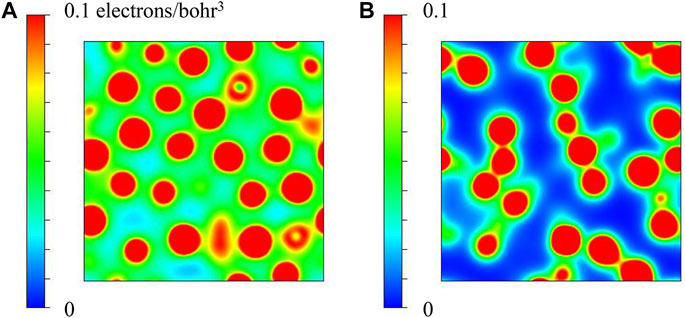
FIGURE 6. 2d charge density diagrams of (A) Co-Fe-B and (B) Co-Fe-B-O systems (intercepted parallel to the X-Y plane at 1/2 of the Z-axis direction of the supercell).

Figure 7 shows the total and partial DOS of the Co-Fe-B MG, characterizing metallic conductivity. The Fermi level (E_F) located in the gap of the spin-down bands, indicating that the system presents strong ferromagnetism (Malozemoff et al., 1984; Wang et al., 2013). The bands near E_F are mainly attributed to Fe-3d states with a small contribution from the 2p states of B, manifesting evidently the hybridization between 2p and 3d orbitals.

FIGURE 7

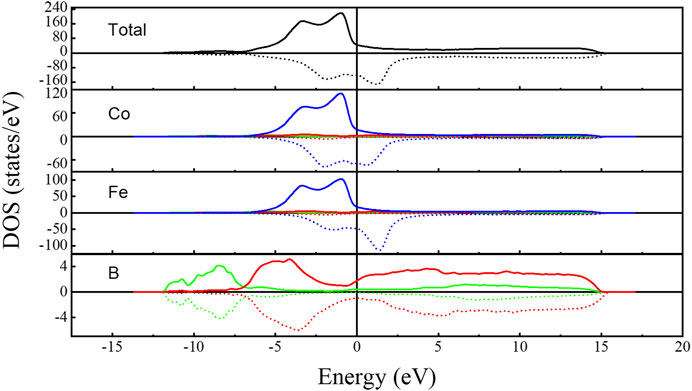
FIGURE 7. Total (the black curves) and partial DOS of Co-Fe-B metallic glass. The green, red, and blue curves represent the s, p, and d orbitals, respectively. Solid lines and dotted lines represent the spin-up and spin-down. The vertical line indicates the Fermi level.

The total and partial DOS of the Co-Fe-B-O OG are shown in Figure 8. According to the analysis of the total DOS, its E_F is in the band gap. The calculated band gap of the Co-Fe-B-O OG is about 1.7 eV, characterizing its semiconducting transport properties. At the same time, the asymmetry of the spin density of states demonstrates that the Co-Fe-B-O OG is still ferromagnetic. It is noted that there exist intermediate energy levels at around -1 eV in the spin-down band gap and near E_F in the spin-up band gap as enlarged in Figure 8B. Compared with the partial DOS diagrams, it is found that these intermediate energy levels are mainly attributed to the Co-3d, Fe-3d and O-2p states. This indicates that the TM (Co, Fe)-O bonding is dominated by the electron hybridization of the 2p states from O and the 3d states from TM. The density of states of Co atoms at the intermediate energy levels is higher than that of Fe atoms. But near the top of the valence band and the bottom of the conduction band, the Fe atoms contribute more electrons, indicating that the bonding of Fe-O may have an important role in the metal-semiconductor transition of the system. Therefore, Co-O and Fe-O jointly regulate the magnetic and semiconducting electrical properties of the system. There are also small amounts of s and p electrons of TM in the intermediate energy levels, suggesting the hybridization of non-local conductive s, p electrons and the 3d electrons of the TM atoms. Similar electron distribution also exists in the bands between −17.5 eV and −20.5 eV. Such hybridization-induced s-d exchange interaction between the carrier spins and the localized magnetic moments leads to the spin polarization of the s-like conduction electrons. The mutual interaction of the electrical conduction from spin-polarized s-like electrons and ferromagnetism from 3d electrons paves the way for controlling the intrinsic ferromagnetism externally by electrical means in MSs (Meng et al., 2007; Walsh et al., 2008; Dietl, 2010; Tian et al., 2010; Hu et al., 2014).

FIGURE 8

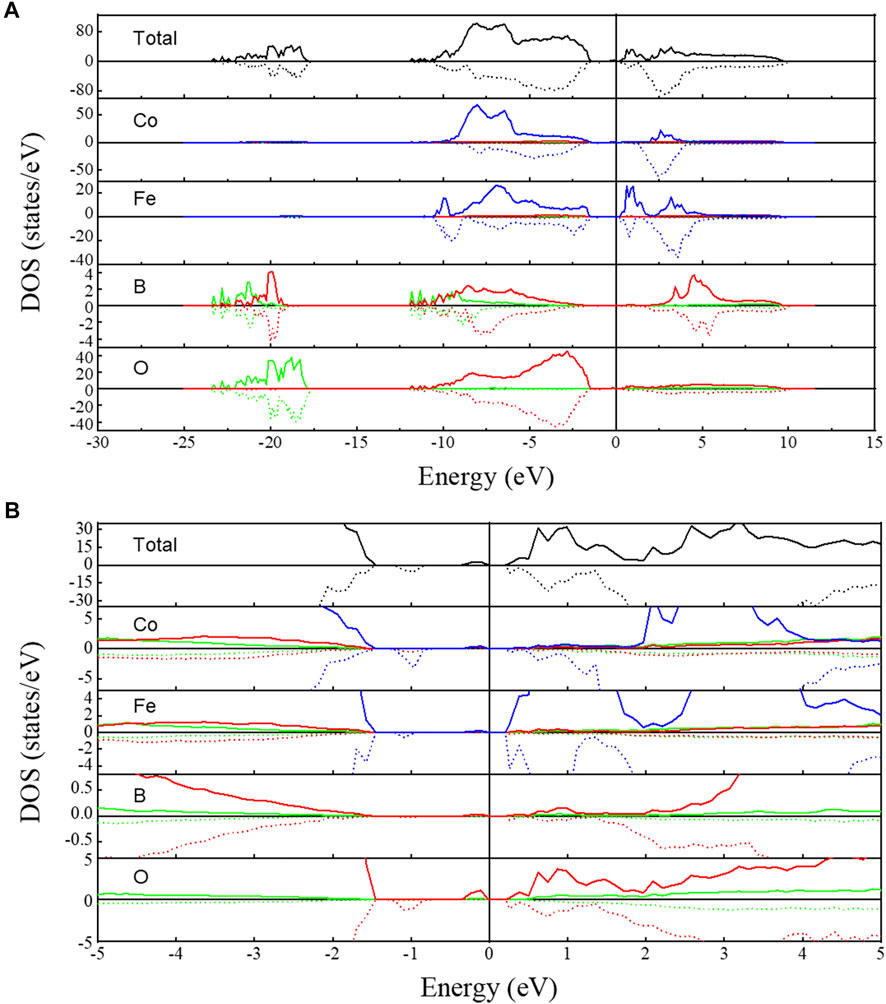
FIGURE 8. (A) Total (the black curves) and partial DOS of Co-Fe-B-O amorphous oxide. (B) Enlarged image of DOS near Fermi level. The green, red, and blue curves represent the s, p, and d orbitals, respectively. Solid lines and dotted lines represent the spin-up and spin-down. The vertical line indicates the Fermi level.

3.4 Experimental Verification

To verify our computer calculation results, we further conducted the corresponding experiments. The Co_22.6Fe_14.4B_9.9O_53.1 thin film was deposited by magnetron sputtering. The HRTEM image of the thin film shows maze-like atomic arrangements, characterizing disordered amorphous structure (Figure 9A). The corresponding selected area electron diffraction (SAED) pattern inserted in Figure 9A contains one obvious diffuse halo ring, further confirming the formation of single-phase OG in the Co-Fe-B-O thin film.

FIGURE 9

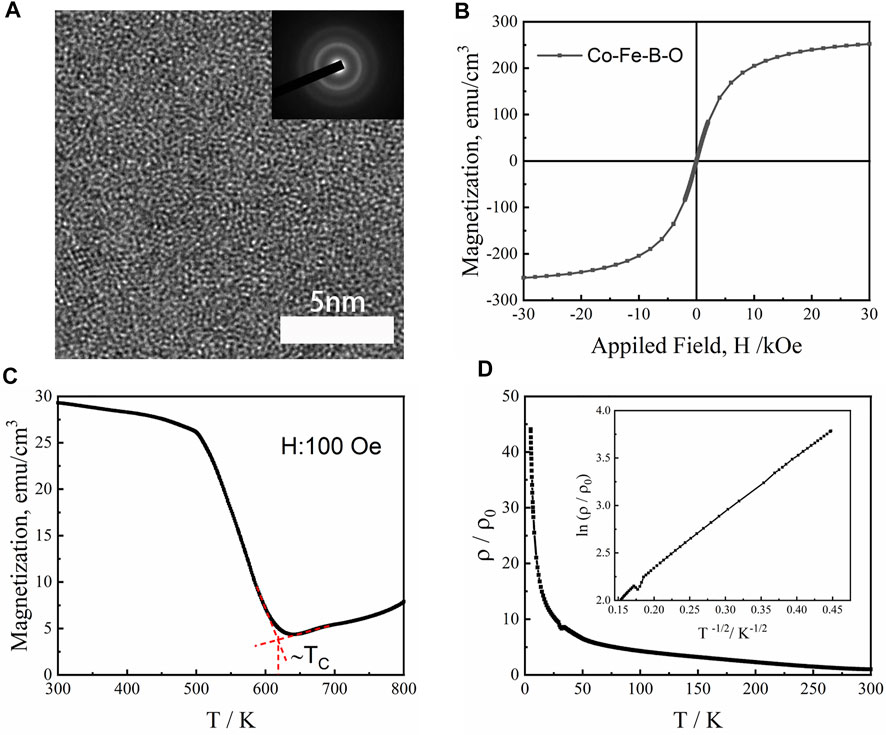
FIGURE 9. (A) HRTEM image of Co-Fe-B-O thin films. The inset is the SAED patterns. (B) Magnetic behavior of the Co-Fe-B-O: Magnetic field dependence of the magnetization (M–H) curves measured at room temperature. (C) High-temperature magnetization-temperature (M–T) curve measured at an external field of 100 Oe. (D) The normalized resistivity ρ/ρ₀ as a function of temperature (ρ₀ is the room temperature resistivity) for the thin film. Inset is the plot of ln (ρ/ρ₀) versus T^−1/2 based on the experimental data.

The magnetic properties of the Co-Fe-B-O OG are shown in Figure 9B. Its B_S at room temperature is 252 emu/cm³ (0.32 T), confirming its room-temperature ferromagnetism. The experimental B_S is lower than the calculated B_S value (0.44 T). In fact, thin film ferromagnets usually show lower B_S values than their bulk counterparts because both the free surfaces of the thin films and the interfaces between the substrate and the thin films could decrease B_S (Poulopoulos and Baberschke 1999). As shown in Figure 9C, the M-T curve of the sample indicates that the Co-Fe-B-O sample has a Curie temperature higher than 620 K. At first, the magnetization decreases with increasing temperature from 300 to 640 K, which is consistent with the temperature dependence of spontaneous magnetization for traditional magnetic metals. When the temperature is higher than 640 K, the magnetization of the sample begins to increase likely due to the crystallization of the thin film. Similar results were also reported for the Co-Fe-Ta-B-O thin films (Liu et al., 2016).

As shown in Figure 9D, the room-temperature resistivity of the Co-Fe-B-O film is of order of 1 Ω cm (in the range of 10⁻³–10¹² Ω cm for semiconductors). In addition, the Co-Fe-B-O sample shows a negative temperature dependence of resistivity in terms of $ln(\rho /{\rho }_0) \propto T^{-1/2}$ (inset of Figure 9D), typically observed for semiconductors. In the amorphous semiconductors, the presence of structural disorder induces the localization of electrons. Éfros suggested that the conduction mechanism underlying this correlation was electron hopping between the localized states, which occurred at low temperature by taking into account the Coulomb interaction in disordered systems (Anderson 1958; Éfros and Shklovskii 1975). In comparison with the non-magnetic semiconductors, the transport mechanism for ATMOs is supposed to be spin-dependent due to the presence of doped TM atoms (Yan et al., 2006). Our calculation results show that the 3d electrons of TM atoms in the Co-Fe-B-O MS are hybridized with those s electrons on the one hand and interact with 2p electrons of O on the other hand. These two interactions together could make our Co-Fe-B-O OG possess the intrinsic magnetoelectric coupling effects modulated by the spin-polarized carriers. Therefore, we anticipate that such Co-Fe-B-O MS could show intriguing magnetoelectrical transport properties, which is out of the scope of the present study and needs to be further investigated in our future work.

4 Conclusion

In conclusion, we performed first-principles calculations to gain a deep understanding of the mechanism for the metal-semiconductor transition via oxygen manipulation in a ferromagnetic MG Co-Fe-B system. The structure analysis shows that a single-phase Co-Fe-B MG transforms into a single-phase Co-Fe-B-O OG. Both the Co-Fe-B MG and Co-Fe-B-O OG show homogeneous glass structures. The structural analysis in details documents significant difference in their local structural configurations. The Co-Fe-B MG is mainly characterized by the icosahedron-like clusters, similar to most other MGs reported so far. With the oxygen addition, the Co-Fe-B-O OG contains more polyhedron types with lower cluster coordination numbers compared with the Co-Fe-B MG. The basic reason is that the atomic bonds change from the dominant metallic bonding in the Co-Fe-B MG to the coexistence of metallic, ionic and covalent bonding in the Co-Fe-B-O OG. That is to say, the oxygen addition affects the local atomic configurations and thus leads to different electronic and magnetic structures. It is found that there are two different coordination environments for ferromagnetic Co and Fe atoms. The ferromagnetism contributed by Co element is dominated by direct exchange interaction among these Co atoms, while Fe element contributes to the ferromagnetism mainly by indirect exchange interaction. As a result, the Co-Fe-B-O system is determined to be ferrimagnetic by means of an average bond length parameter of magnetic atoms combined with first-principles calculation, which provides an effective way for the magnetic calculation of ATMOs in ferromagnetic systems. The DOS results indicate that the 3d electrons of TM atoms are hybridized with their s electrons on the one hand and interact with 2p electrons of O on the other hand, making it possible for our Co-Fe-B-O OG to possess the intrinsic magnetoelectric coupling effects modulated by the spin-polarized carriers. The theoretical results obtained from the first-principles calculations, including the room-temperature ferromagnetism and semiconductor transport properties of the Co-Fe-B-O system, are further verified by the experiments. Our results reveal that the Co-Fe-B-O OG is a new type of room-temperature MS and a promising spintronic material, and provide a theoretical basis for possibly transferring many other ferromagnetic MGs into MSs with excellent magnetoelectric coupling characteristics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is sponsored by the National Science Fund for Excellent Young Scholars (Grant No. 51922053).

Conflict of Interest

Author XL is employed by China Electronics Technology Group Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This simulation work was carried out in the National Supercomputer Center in Zhengzhou University (Zhengzhou).

References

Anderson, P. W. (1958). Absence of Diffusion in Certain Random Lattices. Phys. Rev. 109 (5), 1492–1505. doi:10.1103/PhysRev.109.1492

CrossRef Full Text | Google Scholar

Anisimov, V. I., Zaanen, J., and Andersen, O. K. (1991). Band Theory and Mott Insulators: HubbardUinstead of StonerI. Phys. Rev. B 44 (3), 943–954. doi:10.1103/PhysRevB.44.943

PubMed Abstract | CrossRef Full Text | Google Scholar

Awschalom, D. D., and Flatté, M. E. (2007). Challenges for Semiconductor Spintronics. Nat. Phys 3 (3), 153–159. doi:10.1038/nphys551

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector Augmented-Wave Method. Phys. Rev. B 50 (24), 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Chen, L., Yang, X., Yang, F., Zhao, J., Misuraca, J., Xiong, P., et al. (2011). Enhancing the Curie Temperature of Ferromagnetic Semiconductor (Ga,Mn)As to 200 K via Nanostructure Engineering. Nano Lett. 11 (7), 2584–2589. doi:10.1021/nl201187m

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietl, T. (2010). A Ten-Year Perspective on Dilute Magnetic Semiconductors and Oxides. Nat. Mater 9 (12), 965–974. doi:10.1038/nmat2898

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietl, T., and Ohno, H. (2014). Dilute Ferromagnetic Semiconductors: Physics and Spintronic Structures. Rev. Mod. Phys. 86 (1), 187–251. doi:10.1103/RevModPhys.86.187

CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y.-Q., and Ma, E. (2014). Full Icosahedra Dominate Local Order in Cu64Zr34 Metallic Glass and Supercooled Liquid. Acta Materialia 69, 343–354. doi:10.1016/j.actamat.2014.02.005

CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y.-Q., Sheng, H., Asta, M., Ritchie, R. O., and Ma, E. (2016). Universal Structural Parameter to Quantitatively Predict Metallic Glass Properties. Nat. Commun. 7 (1), 13733. doi:10.1038/ncomms13733

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, J., Cheng, Y. Q., and Ma, E. (2012). Correlating Local Structure with Inhomogeneous Elastic Deformation in a Metallic Glass. Appl. Phys. Lett. 101 (12), 121917. doi:10.1063/1.4754121

CrossRef Full Text | Google Scholar

Ding, J., Ma, E., Asta, M., and Ritchie, R. O. (2015). Second-Nearest-Neighbor Correlations from Connection of Atomic Packing Motifs in Metallic Glasses and Liquids. Sci. Rep. 5 (1), 17429. doi:10.1038/srep17429

PubMed Abstract | CrossRef Full Text | Google Scholar

Djayaprawira, D. D., Tsunekawa, K., Nagai, M., Maehara, H., Yamagata, S., Watanabe, N., et al. (2005). 230% Room-Temperature Magnetoresistance in CoFeB/MgO/CoFeB Magnetic Tunnel Junctions. Appl. Phys. Lett. 86 (9), 092502. doi:10.1063/1.1871344

CrossRef Full Text | Google Scholar

Efros, A. L., and Shklovskii, B. I. (1975). Coulomb gap and Low Temperature Conductivity of Disordered Systems. J. Phys. C: Solid State. Phys. 8 (4), L49–L51. doi:10.1088/0022-3719/8/4/003

CrossRef Full Text | Google Scholar

Feng, T., and Childress, J. R. (1999). Fabrication of Exchange-Biased Spin Valves with CoFeB Amorphous Layers. J. Appl. Phys. 85 (8), 4937–4939. doi:10.1063/1.370051

CrossRef Full Text | Google Scholar

Fuji, Y., Kaji, S., Hara, M., Higashi, Y., Hori, A., Okamoto, K., et al. (2018). Highly Sensitive Spintronic Strain-Gauge Sensor Based on a MgO Magnetic Tunnel junction with an Amorphous CoFeB Sensing Layer. Appl. Phys. Lett. 112 (6), 062405. doi:10.1063/1.5017287

CrossRef Full Text | Google Scholar

Greer, A. L. (1995). Metallic Glasses. Science 267 (5206), 1947–1953. doi:10.1126/science.267.5206.1947

PubMed Abstract | CrossRef Full Text | Google Scholar

Guan, P. F., Fujita, T., Hirata, A., Liu, Y. H., and Chen, M. W. (2012). Structural Origins of the Excellent Glass Forming Ability ofPd40Ni40P20. Phys. Rev. Lett. 108 (17), 175501. doi:10.1103/PhysRevLett.108.175501

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirata, A., Guan, P., Fujita, T., Hirotsu, Y., Inoue, A., Yavari, A. R., et al. (2010). Direct Observation of Local Atomic Order in a Metallic Glass. Nat. Mater 10 (1), 28–33. doi:10.1038/nmat2897

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S.-j., Yan, S.-s., Zhang, Y.-p., Zhao, M.-w., Kang, S.-s., and Mei, L.-m. (2014). Stoichiometry Determined Exchange Interactions in Amorphous Ternary Transition Metal Oxides: Theory and experiment. J. Appl. Phys. 116 (4), 043711. doi:10.1063/1.4891474

CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab Initiomolecular Dynamics for Liquid Metals. Phys. Rev. B 47 (1), 558–561. doi:10.1103/PhysRevB.47.558

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1994). Ab Initiomolecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 49 (20), 14251–14269. doi:10.1103/PhysRevB.49.14251

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Shi, Z., and Zhang, T. (2019). Effect of Similar Element Substitution on Fe-B-Si-Mo Bulk Metallic Glasses Studied by experiment and Ab Initio Molecular Dynamics Simulation. J. Alloys Comp. 784, 1139–1144. doi:10.1016/j.jallcom.2019.01.122

CrossRef Full Text | Google Scholar

Liu, W., Zhang, H., Shi, J.-a., Wang, Z., Song, C., Wang, X., et al. (2016). A Room-Temperature Magnetic Semiconductor from a Ferromagnetic Metallic Glass. Nat. Commun. 7 (1), 13497. doi:10.1038/ncomms13497

PubMed Abstract | CrossRef Full Text | Google Scholar

Malozemoff, A. P., Williams, A. R., and Moruzzi, V. L. (1984). "Band-gap Theory" of strong Ferromagnetism: Application to Concentrated Crystalline and Amorphous Fe- and Co-metalloid Alloys. Phys. Rev. B 29, 1620–1632. doi:10.1103/PhysRevB.29.1620

CrossRef Full Text | Google Scholar

Matsukura, F., Ohno, H., Shen, A., and Sugawara, Y. (1998). Transport Properties and Origin of Ferromagnetism in (Ga,Mn)As. Phys. Rev. B 57 (4), R2037–R2040. doi:10.1103/PhysRevB.57.R2037

CrossRef Full Text | Google Scholar

Medvedev, N. N. (1986). The Algorithm for Three-Dimensional Voronoi Polyhedra. J. Comput. Phys. 67 (1), 223–229. doi:10.1016/0021-9991(86)90123-3

CrossRef Full Text | Google Scholar

Meng, H. J., Hou, D. L., Jia, L. Y., Ye, X. J., Zhou, H. J., and Li, X. L. (2007). Role of Oxygen Vacancies on Ferromagnetism in Fe-Doped TiO2 Thin Films. J. Appl. Phys. 102 (7), 073905. doi:10.1063/1.2786115

CrossRef Full Text | Google Scholar

Munekata, H., Ohno, H., von Molnar, S., Segmüller, A., Chang, L. L., and Esaki, L. (1989). Diluted Magnetic III-V Semiconductors. Phys. Rev. Lett. 63 (17), 1849–1852. doi:10.1103/PhysRevLett.63.1849

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohno, H., Chiba, D., Matsukura, F., Omiya, T., Abe, E., Dietl, T., et al. (2000). Electric-field Control of Ferromagnetism. Nature 408 (6815), 944–946. doi:10.1038/35050040

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohno, H., Munekata, H., Penney, T., von Molnár, S., and Chang, L. L. (1992). Magnetotransport Properties Ofp-type (In,Mn)As Diluted Magnetic III-V Semiconductors. Phys. Rev. Lett. 68 (17), 2664–2667. doi:10.1103/PhysRevLett.68.2664

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohno, H., Shen, A., Matsukura, F., Oiwa, A., Endo, A., Katsumoto, S., et al. (1996). (Ga,Mn)As: A New Diluted Magnetic Semiconductor Based on GaAs. Appl. Phys. Lett. 69 (3), 363–365. doi:10.1063/1.118061

CrossRef Full Text | Google Scholar

Ohno, Y., Young, D. K., Beschoten, B., Matsukura, F., Ohno, H., and Awschalom, D. D. (1999). Electrical Spin Injection in a Ferromagnetic Semiconductor Heterostructure. Nature 402 (6763), 790–792. doi:10.1038/45509

CrossRef Full Text | Google Scholar

Paluskar, P. V., Lavrijsen, R., Sicot, M., Kohlhepp, J. T., Swagten, H. J. M., and Koopmans, B. (2009). Correlation between Magnetism and Spin-dependent Transport in CoFeB Alloys. Phys. Rev. Lett. 102 (1), 016602. doi:10.1103/PhysRevLett.102.016602

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulopoulos, P., and Baberschke, K. (1999). Magnetism in Thin Films. J. Phys. Condens. Matter 11 (48), 9495–9515. doi:10.1088/0953-8984/11/48/310

CrossRef Full Text | Google Scholar

Schallenberg, T., and Munekata, H. (2006). Preparation of Ferromagnetic (In,Mn)As with a High Curie Temperature of 90K. Appl. Phys. Lett. 89 (4), 042507. doi:10.1063/1.2236210

CrossRef Full Text | Google Scholar

Terakura, K., Oguchi, T., Williams, A. R., and Kübler, J. (1984). Band Theory of Insulating Transition-Metal Monoxides: Band-Structure Calculations. Phys. Rev. B 30 (8), 4734–4747. doi:10.1103/PhysRevB.30.4734

CrossRef Full Text | Google Scholar

Tian, H., Zhang, C., Zhao, J., Dong, C., Wen, B., and Wang, Q. (2012). First-principle Study of the Structural, Electronic, and Magnetic Properties of Amorphous Fe-B Alloys. Physica B: Condensed Matter 407 (2), 250–257. doi:10.1016/j.physb.2011.10.042

CrossRef Full Text | Google Scholar

Tian, Y. F., Yan, S.-s., Zhao, M. W., Dai, Y. Y., Zhang, Y. P., Qiao, R. M., et al. (2010). Controllable Spin-Polarized Electrical Transport in Wide-Band-gap Oxide Ferromagnetic Semiconductors. J. Appl. Phys. 107 (3), 033713. doi:10.1063/1.3305457

CrossRef Full Text | Google Scholar

Walsh, A., Da Silva, J. L. F., and Wei, S.-H. (2008). Theoretical Description of Carrier Mediated Magnetism in Cobalt Doped ZnO. Phys. Rev. Lett. 100 (25), 256401. doi:10.1103/PhysRevLett.100.256401

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., Nordman, C., Daughton, J. M., Qian, Z., Fink, J., Wang, D., et al. (2004). 70% TMR at Room Temperature for SDT sandwich Junctions with CoFeB as Free and Reference Layers. IEEE Trans. Magn. 40 (4), 2269–2271. doi:10.1109/tmag.2004.830219

CrossRef Full Text | Google Scholar

Wang, D., Nordman, C., Qian, Z., Daughton, J. M., and Myers, J. (2005). Magnetostriction Effect of Amorphous CoFeB Thin Films and Application in Spin-dependent Tunnel Junctions. J. Appl. Phys. 97 (10), 10C906. doi:10.1063/1.1848355

CrossRef Full Text | Google Scholar

Wang, H., Hu, T., and Zhang, T. (2013). Atomic, Electronic and Magnetic Properties of Fe80P11C9 Amorphous alloy: A First-Principles Study. Physica B: Condensed Matter 411, 161–165. doi:10.1016/j.physb.2012.11.044

CrossRef Full Text | Google Scholar

Wang, Y. X., Liu, H., Li, Z. Q., Zhang, X. X., Zheng, R. K., and Ringer, S. P. (2006). Role of Structural Defects on Ferromagnetism in Amorphous Cr-Doped TiO2 Films. Appl. Phys. Lett. 89 (4), 042511. doi:10.1063/1.2240139

CrossRef Full Text | Google Scholar

Xu, T., Li, R., Xiao, R., Liu, G., Wang, J., and Zhang, T. (2015). Tuning Glass Formation and Brittle Behaviors by Similar Solvent Element Substitution in (Mn,Fe)-Based Bulk Metallic Glasses. Mater. Sci. Eng. A 626, 16–26. doi:10.1016/j.msea.2014.12.048

CrossRef Full Text | Google Scholar

Yan, S.-s., Liu, J. P., Mei, L. M., Tian, Y. F., Song, H. Q., Chen, Y. X., et al. (2006). Spin-dependent Variable Range Hopping and Magnetoresistance in Ti1−xCoxO2and Zn1−xCoxO Magnetic Semiconductor Films. J. Phys. Condens. Matter 18 (46), 10469–10480. doi:10.1088/0953-8984/18/46/014

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L.-J., Wang, J.-Q., Li, J., Zhou, J., Cai, W.-P., Cheng, J., et al. (2012). High-Tcferromagnetism in a Co-doped ZnO System Dominated by the Formation of a Zinc-Blende Type Co-rich ZnCoO Phase. Chem. Commun. 48 (1), 91–93. doi:10.1039/c1cc15622e

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W., Li, Q., and Duan, H. (2015). Study of the Effects of Metalloid Elements (P, C, B) on Fe-Based Amorphous Alloys by Ab Initio Molecular Dynamics Simulations. J. Appl. Phys. 117 (10), 104901. doi:10.1063/1.4914303

CrossRef Full Text | Google Scholar