- 1College of Materials and Fujian Provincial Key Laboratory of Materials Genome, Xiamen University, Xiamen, China
- 2Xiamen Key Laboratory of High Performance Metals and Materials, Xiamen University, Xiamen, China
- 3Institute of Materials Genome and Big Data, Harbin Institute of Technology, Shenzhen, China
In order to improve the thermal stability and mechanical properties of W-free light-weight Co–V–Ta-based superalloys, the effects of alloying elements including Sc, Ti, Cr, Mn, Fe, Ni, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Hf, W, Re, Os, Ir, and Pt on γ′-Co3(V, Ta) stability and elastic properties were studied. The results from the reaction energy indicate that Sc, Ti, Y, Zr, Nb, Mo, Hf, and W tend to occupy the V site, whereas Cr, Mn, Fe, Ni, Tc, Ru, Rh, Pd, Re, Os, Ir, and Pt prefer to occupy the Co site. It was found that Sc, Ti, Y, Zr, Fe, and Mn stabilize the γ′-Co3(V, Ta) phase by raising the phase-transfer energy. The addition of Mo and W increases the bulk modulus, shear modulus, and Young’s modulus. According to Pugh’s classical criterion, the γ′-Co3(V, Ta) phase is an intrinsically brittle material, and the addition of elements such as Tc and Re significantly enhances the ductility. At finite temperature, the doping of Sc, Ti, Mn, Fe, and Hf enhances the relative stability of the γ′-Co3(V, Ta) phase in the whole temperature range from 0 to 1200 K and are candidates for improving the stability of the γ′-Co3(V, Ta) phase.
1 Introduction
Since the discovery of the γ′ phase in the Co–Al–W ternary system (Sato et al., 2006), extensive attention has been attracted to the γ′-strengthened Co-based superalloys. The coherent γ/γ′ structure makes this new class of Co-based superalloy possess good high temperature strength and creep resistance, and its solidus and liquidus temperatures are 100°C–150°C higher than those of advanced Ni-based alloys (Pollock et al., 2010). Therefore, the development of γʹ-strengthened Co-based superalloys has become a significant subject for research. It has been reported that W can effectively stabilize the γ′ phase and elevate the γ′ solvus temperature in Co-based superalloys (Pyczak et al., 2015). However, the heavy element W significantly increases the density of Co–Al–W-based superalloys (Shi et al., 2015), which is unfavorable for industrial applications, such as turbine blades. Recently, a considerable amount of literature work has been focused on the development of W-free Co-based high-temperature superalloys, aiming at reducing the mass density while maintaining the microstructure stability and high-temperature properties (Bantounas et al., 2019; Reyes Tirado et al., 2019; Migas et al., 2020; Reyes Tirado et al., 2020; Ruan et al., 2020; Davydov et al., 2021). Recently, Ruan et al. (2020) used machine learning algorithms and CALPHAD methods to successfully design a Co–V–Ta alloy with a wide γ/γ′ two-phase region, lower density than that of the Co–9Al–9.8W alloy (8.86 vs. 9.82 g/cm3), and higher yield strength. These advantages make the Co–V–Ta system a promising base alloy for further development.
However, the stability of the γ′ phase in the Co–V–Ta system is relatively low, and the volume fraction of the γ′ phase is not high enough. To improve the γ′ phase stability and volume fraction, an understanding of effects of alloying elements on the γ′ phase stability is required. Ruan et al. (2020) found that Ti effectively increases the γ′ solvus temperature by 70°C. Reyes Tirado et al. (2019) studied the alloying effects of Al, Ti, and Cr additions on the γ/γ′ microstructure and discovered that Al can stabilize the γ′ phase, and the addition of Ti and Ni has no significant effects on γ′ stability. Cr can slightly increase the γ′ volume. However, compared to the commercial Ni-based alloys, which contain upward of ten additional alloying elements, the research studies on alloying effects in the Co–V–Ta system are quite insufficient. The traditional experimental methods are quite expensive and time-consuming. Alternatively, the first-principle method provides an efficient way to explore the alloying effects and can give a deeper insight into the electronical interactions, which is hard to obtain by experiments.
To deeply understand the alloying effects of TM elements (including Sc, Ti, Cr, Mn, Fe, Ni, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Hf, W, Re, Os, Ir, and Pt) on the γ′-Co3(V, Ta) phase, the first-principle calculations were performed to systematically investigate the phase stabilities and mechanical and thermodynamic properties of alloying effects of TM elements on the γ′-Co3(V, Ta) phase. First, the site preference of TM elements in the γ′-Co3(V, Ta) phase was calculated. On this basis, the stability and mechanical properties of γ′-Co3(V, Ta) were evaluated. Further studies on the electronic structure explain the alloying effects of TM elements. Our research could be highly valuable for the interpretation of the experimental results in the Co-based superalloy, which provides very useful guidelines for the design and preparation of W-free Co–V–Ta-based superalloys.
2 Computational Methods
2.1 Structural Model
The γ′-Co3(V, Ta) phase is built as a 2 × 2 × 2 supercell with Co at the cubic corner sites and V/Ta at the face center sites, as shown in Figure 1A. The supercell has 24 Co atoms, six V atoms, and two Ta atoms, which is consistent with experimental results (Ruan et al., 2020). There are six non-equivalent substitutional sites, namely, Co1, Co2, Co3, V1, V2, and Ta in Figure 1A. Since the D019 phase is preferred in both Co–V and Co–Ta binary systems (Drapier and Coutsouradis, 1968; Wang et al., 2018), it is rational to consider the D019 phase as the main competing phase in the Co–V–Ta ternary system. The D019-Co3(V, Ta) phase is built as a 2 × 2 × 1 supercell, and 10 non-equivalent substitutional sites, marked as Co1, Co2, Co3, Co4, Co5, Co6, Co7, V1, and V2, Ta are shown in Figure 1B.
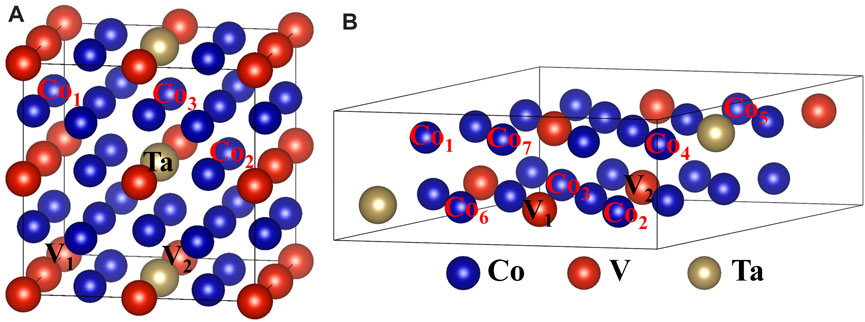
FIGURE 1. (A) Crystal structure of L12-ordered Co3(V, Ta) with six nonequivalent sites (Co1, Co2, Co3, V1, V2, and Ta) for the substitution by TM elements. (B) Crystal structure of D019-ordered Co3(V, Ta) with 10 nonequivalent sites (Co1, Co2, Co3, Co4, Co5, Co6, Co7, V1, V2, and Ta) for the substitution by TM elements.
2.2 Reaction Energy
To reveal the preferred substitutional sites of TM elements, the following reaction process is considered:
The reaction energy is defined as follows:
where
2.3 Phase Stability
Once the preferred sites are determined, the phase stability can be decided by its formation enthalpy,
where
2.4 Mechanical Properties
To understand the effects of TM elements on mechanical properties, the elastic constants are calculated using the stress–strain method (Shang et al., 2007). Based on Hooke’s law, the relationship between strain and stress is defined as follows:
where
According to the symmetry of the L12 structure, only
where
Based on the calculated results, the aggregate properties can be calculated by
where
2.5 Calculation Details
All calculations were performed using the Vienna ab initio simulation package (VASP) (Kresse and Furthmüller, 1996) based on the density functional theory using the projector augmented wave (PAW) pseudopotential method (Kresse and Joubert, 1999). The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) was used to calculate the exchange–correlation functional. The cut-off energy of the plane-wave basis was set to 450 eV. After careful testing, the Brillouin zone was sampled by 7 × 7 × 7 and 3 × 3 × 7 k-meshes for L12 and D019 structures using the Monkhort–Pack scheme (Monkhorst and Pack, 1976). In the ionic relaxation, the Methfessel–Paxton method (Methfessel and Paxton, 1989) was used for reciprocal integration, and the smearing width was set to 0.12 eV. The energy and force convergence criteria were 10−5 eV/atom and 10−2 eV/Å, respectively. Spin polarization was considered.
3 Results and Discussion
3.1 Site Preference and Phase Stability
The reaction energy
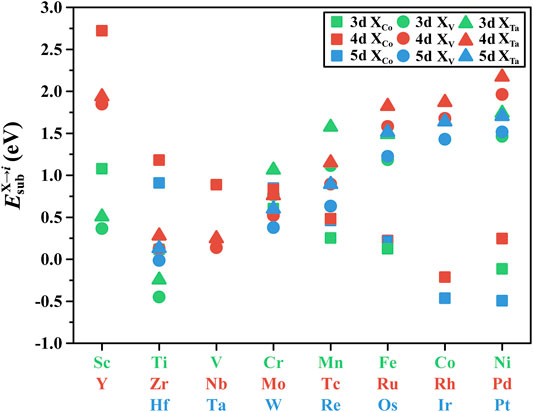
FIGURE 2. Reaction energy for the TM-substituted γ′-Co3(V, Ta). The square, round, and triangle markers denote TM elements occupying the Co, V, and Ta sites, respectively.
The formation enthalpies
Other than
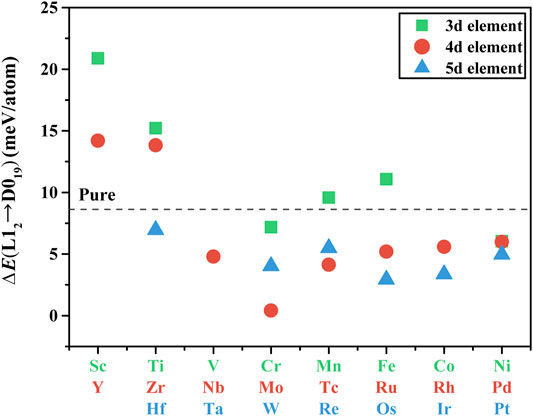
FIGURE 3. Calculated structure transition energy of X-substituted γ′-Co3(V, Ta), where 3d-, 4d-, and 5d-elements are denoted by square, round, and triangle, respectively.
3.2 Effect of TM Elements on Mechanical Properties
To investigate the alloying effects of TM elements on the mechanical properties, the elastic constants
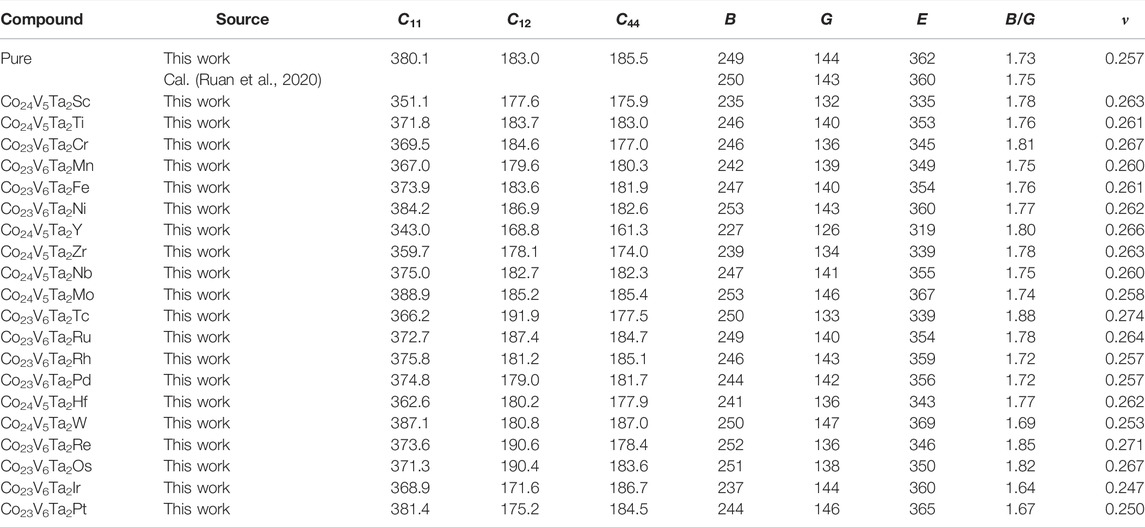
TABLE 2. Elastic properties of γ′-Co3(V, Ta), including elastic constants
As seen, the elastic constants are remarkably changed by TM elements. We evaluated the mechanical stability of the TM-substituted γ′-Co3(V, Ta) phase using the Born criterion (Born, 1939):
To reveal the changing pattern of elastic properties induced by TM elements, the volume change concerning elastic properties is plotted in Figure 4. The doped TM elements cause the volume to expand despite the different substitutional sites (Co and Ta), which can be explained by a larger atomic radius of TM elements than that of their substituted atom. For 3d and 4d elements, the bulk/shear modulus change with respect to the volume change exhibits negative correlation, namely, expansion in volume and reduction in the bulk/shear modulus. However, for 5d elements, this relationship no longer holds. It is believed that mechanical properties have a strong correlation with the electron density in pure metals and binary alloys (Miedema et al., 1973). Figure 5 plots the relationship between the electron density
where
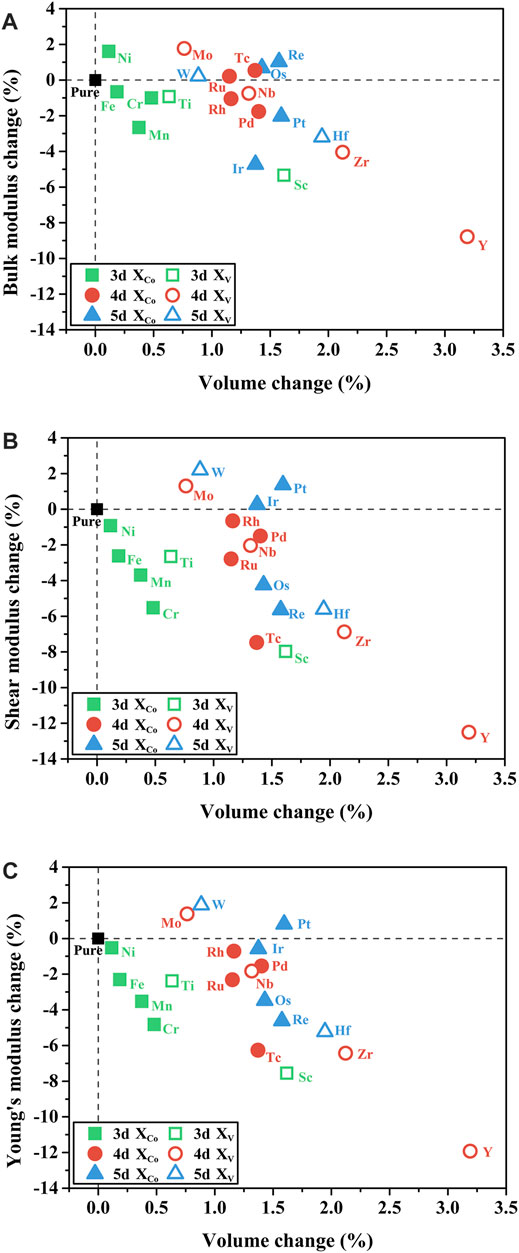
FIGURE 4. Relationship between the elastic modulus changes and volume changes of X-substituted γ′-Co3(V, Ta): (A) bulk modulus
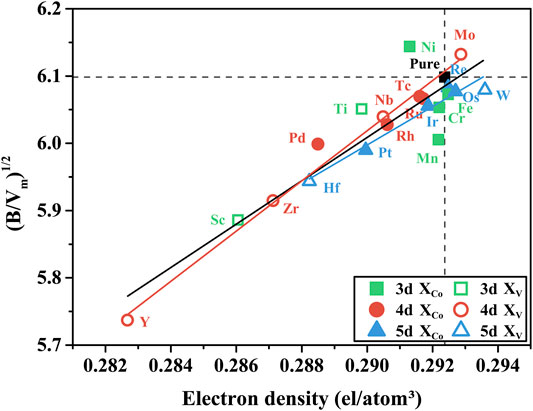
FIGURE 5. Relationship between the electron density and
It can be seen that
To further investigate the mechanism that how TM elements affect the elastic modulus of the γ′-Co3(V, Ta) phase, their charge density difference (CDD) on the (100) plane is plotted in Figure 6. Here, we selected two elements W and Y that significantly changed the shear modulus
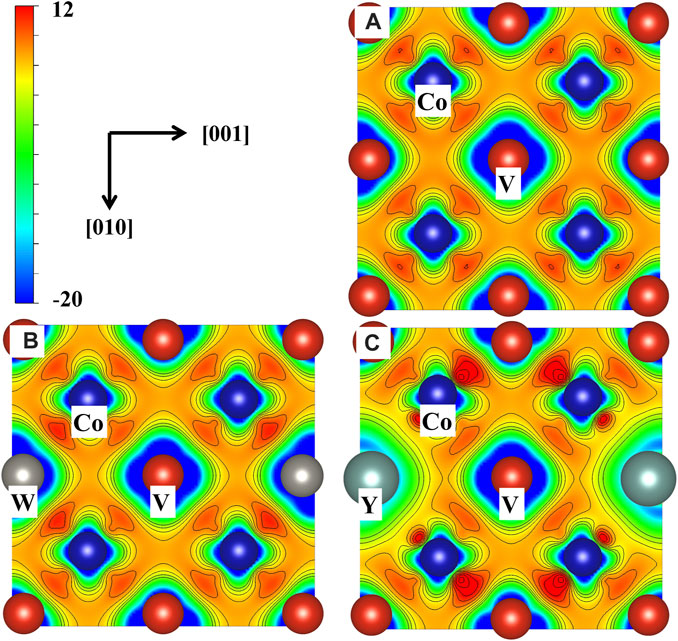
FIGURE 6. Charge density differences (CDD) of the γ′-Co3(V, Ta) phase on the (100) plane of (A) pure, (B) W occupying the V site, and (C) Y occupying the V site.
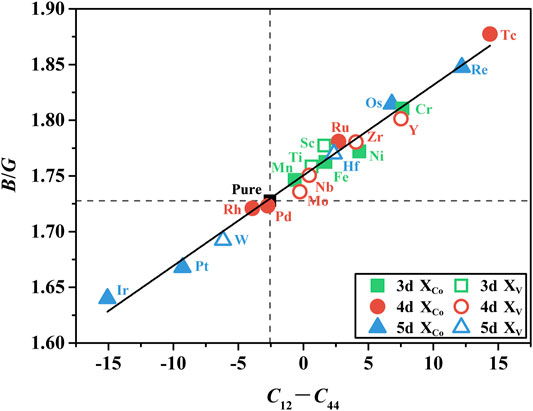
The ductility of the γ′-Co3(V, Ta) phase after doping with TM elements was further evaluated using the Pugh’s classical criterion and Cauchy pressure. According to Pugh’s theory (Pugh, 1954), the value of B/G represents the ductility of materials. The critical value to distinguish the material ductility from brittleness is 1.75, and the higher the ratio, the more tough the material is, and conversely, the lower the ratio, the more brittle the material tends to be. On the other hand, Pettifor (1992) suggested that the Cauchy pressure (C12–C44) is a sign of atomic bonding within crystals, and systems with positive values of Cauchy pressure are dominated by metallic bonds, while systems with negative values are dominated by covalent bonds. For metallic systems, higher Cauchy pressure means that the system is more ductile. To clarify the intrinsic relationship between atomic bonding and ductility, Figure 7 plots the B/G value versus the Cauchy pressure. It is clear that there is a linear relationship between the B/G value and the Cauchy pressure, which indicates that the ductility of the γ′-Co3(V, Ta) phase doped with X is mainly due to the influence of the metallic bonding within the structure. As shown in Figure 7, the undoped γ′-Co3(V, Ta) phase exhibits intrinsic brittleness, and doping of TM elements changes the ductility of the γ′-Co3(V, Ta) phase, for example, the addition of Tc, Re, and Os increases the Corsi pressure of the γ′-Co3(V, Ta) phase, which enhances its internal metallicity and thus significantly improves the ductility of the γ′-Co3(V, Ta) phase, which means that these elements can improve the mechanical properties of the γ′-Co3(V, Ta) phase. In contrast, doping of Ir, Pt, W, Rh, and Pd causes the brittleness of the γ′-Co3(V, Ta) phase, which reduces the mechanical properties.
3.3 Effect of TM Elements on the Thermodynamic Properties of the γ′-Co3(V, Ta) Phase
Based on the Debye model of quasi-harmonic approximation (Francisco et al., 2001; Blanco et al., 2004), we investigated the thermodynamic properties of the γ′-Co3(V, Ta) phase at elevated temperature using the Gibbs2 program (Otero-de-la- Roza et al., 2011). First, we discussed the relative stability of the γ′-Co3(V, Ta) phase by analyzing the Gibbs free energy difference between the L12 structure and the D019 structure. The definition of the Gibbs free energy difference is as follows:
where
1) Sc, Ti, Mn, Fe, and Hf can improve the relative stability of the γ′-Co3(V, Ta) phase in the entire temperature range of 0–1200 K. The calculated results are compared with experimental results. According to Ruan et al. (2020), the γ′ phase decomposition was observed in the Co–12V–2Ta alloy that annealed at 800°C for 720 hours. When doped with Ti, the γ′ phase is maintained under the same anneal condition, which is in good agreement with the prediction in this study.
2) Elements that increase the relative stability of the γ′-Co3(V, Ta) phase in some temperature ranges, namely, Cr, Y, Zr, and Tc. Although the doping of Cr and Tc will reduce the relative stability of the γ′-Co3(V, Ta) phase at low temperatures, the relative stability of the γ′-Co3(V, Ta) phase will increase as the temperature rises from about 700 K.
3) Ni, Nb, Mo, Ru, Rh, Pd, W, Re, Os, Ir, and Pt reduced the relative stability of the γ′-Co3(V, Ta) phase in the entire temperature range of 0–1200 K. Among them, the doping of the TM Mo will make it negative in the entire temperature range, which means that the Mo-doped L12-Co3(V, Ta) is always in a metastable state. Ruan et al. (2020) showed that the decomposition of the γ′ phase is observed after annealing at 800°C for 48 hours in the Co–12V–2Ta alloy doped with Nb, Ni, Mo, and W, which agrees well with our calculation results.
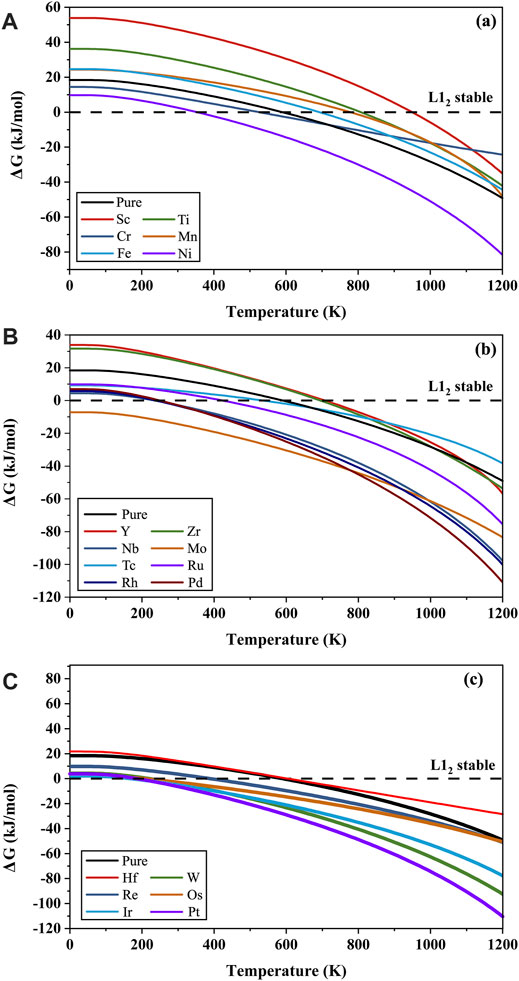
FIGURE 8. Gibbs free energy difference
Then, the change of isochoric heat capacity
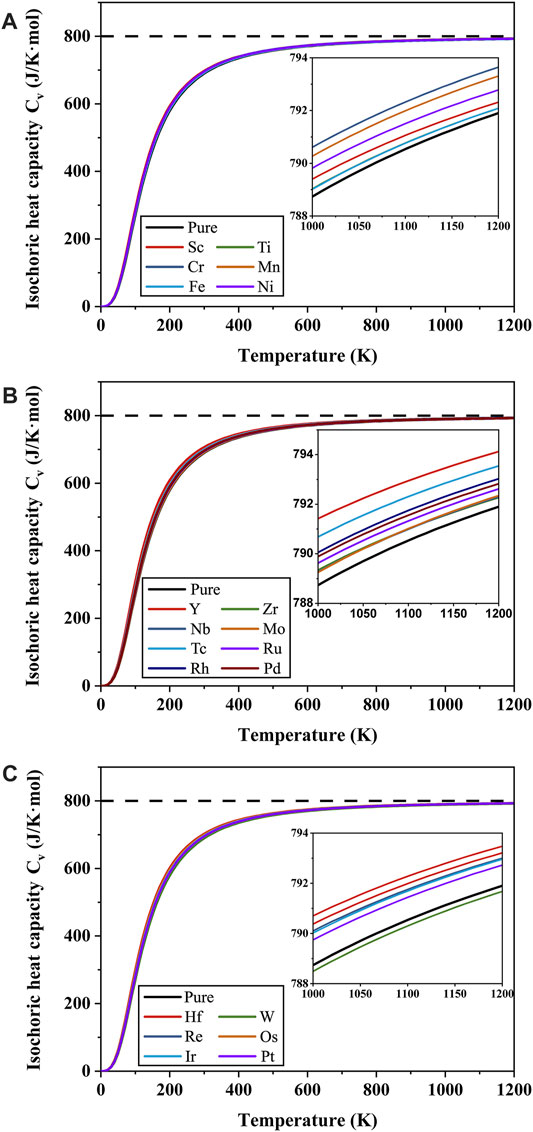
FIGURE 9. Isochoric heat capacity
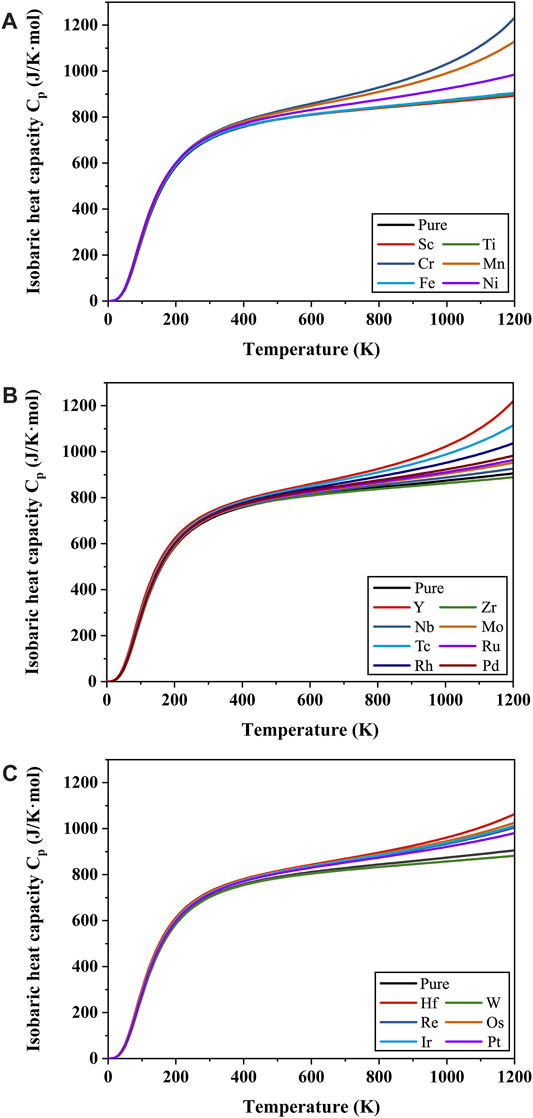
FIGURE 10. Isobaric heat capacity
Finally, the effect of TM elements on the volume thermal expansion coefficient α of the γ′-Co3(V, Ta) phase at a finite temperature is calculated, and the results are shown in Figure 11. The
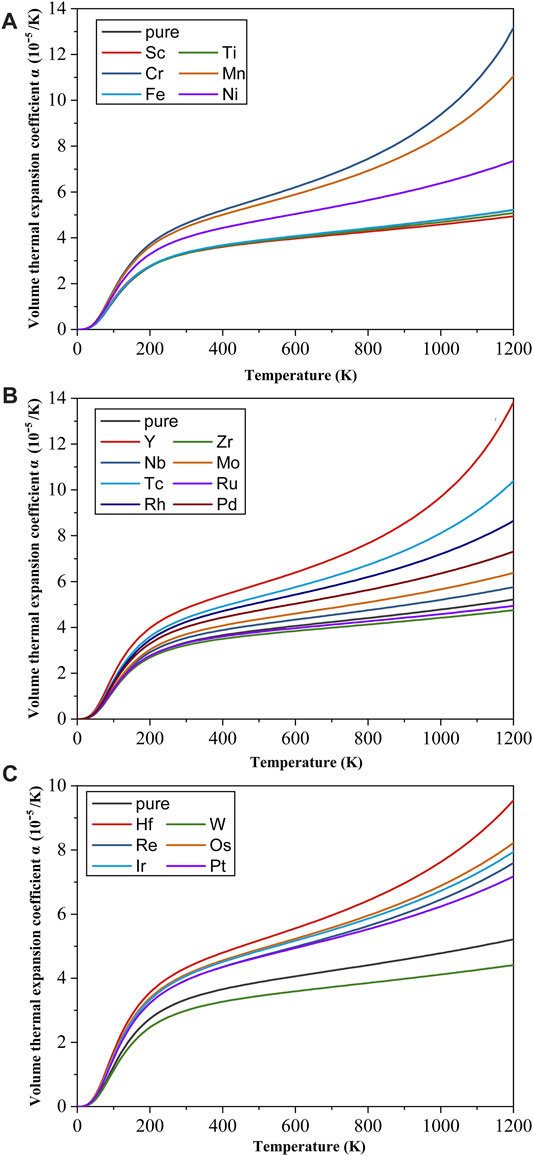
FIGURE 11. Volume thermal expansion coefficient
4 Conclusion
In this study, the first-principle–based density function theory (DFT) is used to investigate the effect of TM elements X (X = Sc, Ti, Cr, Mn, Fe, Ni, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Hf, W, Re, Os, Ir, and Pt) on the structural stability, mechanical properties, and thermodynamic properties of the γ′-Co3(V, Ta) phase. The main results are as follows:
(1) The occupancy tendency of TM elements in the γ′-Co3(V, Ta) phase was obtained by comparing the substitutional reaction energies of each non-equivalent site in the ground state: Sc, Ti, Y, Zr, Nb, Mo, Hf, and W atoms occupied the V atomic site; Cr, Mn, Fe, Ni, Tc, Ru, Rh, Pd, Re, Os, Ir, and Pt atoms occupied the Co atomic site. The structural transition energy showed that X-doped Co3(V, Ta) phases are all more stable in the L12 structure than that the in D010 structure in the ground state, and some of the TM elements can enhance the relative stability of the γ′ phase, such as Sc, Ti, Y, Zr, Fe, and Mn.
(2) In the ground state, the γ′-Co3(V, Ta) phases are all mechanically stable after the doping of TM elements. The addition of Mo and W increases the bulk modulus, shear modulus, and Young’s modulus. When doped with 3d elements, the volume change is an important factor affecting its elastic modulus. When doped with 4d elements, the volume change and electron density affect its elastic modulus simultaneously. When doped with 5d elements, the effect of electron density on its elastic modulus is more important than the volume change. According to Pugh’s classical criterion, the γ′-Co3(V, Ta) phase is an intrinsically brittle material, and the addition of elements such as Tc and Re can significantly enhance the ductility.
(3) The L12 structure of Co3(V, Ta) is more stable than the D019 structure in the temperature range from 0 to 600 K, and the D019 structure is more stable in the temperature range from 600 to 1200 K. The doping of Sc, Ti, Mn, Fe, and Hf enhances the relative stability of the γ′-Co3(V, Ta) phase in the whole temperature range from 0 to 1200 K. The doping of TM elements does not significantly change the isovolumetric heat capacity
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
Conceptualization: XL and CW. Formal analysis: YC and JH. Investigation: YC, CZ, and CY. Original draft preparation: YC and JH. Writing—review and editing: YC and JH. Visualization: YC and JH. Supervision: XL and CW.
Funding
This work was supported by the Key-Area Research and Development Program of Guangdong Province (No. 2019B010943001) and the National Natural Science Foundation of China (Grant No. 51831007).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bantounas, I., Gwalani, B., Alam, T., Banerjee, R., and Dye, D. (2019). Elemental Partitioning, Mechanical and Oxidation Behaviour of Two High-γ′ W-free γ/γ′ Polycrystalline Co/Ni Superalloys. Scr. Mater. 163, 44–50. doi:10.1016/j.scriptamat.2018.12.025
Blanco, M. A., Francisco, E., and Luaña, V. (2004). GIBBS: Isothermal-Isobaric Thermodynamics of Solids from Energy Curves Using a Quasi-Harmonic Debye Model. Comput. Phys. Commun. 158 (1), 57–72. doi:10.1016/j.comphy.2003.12.001
Born, M. (1939). Thermodynamics of Crystals and Melting. J. Chem. Phys. 7 (8), 591–603. doi:10.1063/1.1750497
Davydov, D., Kazantseva, N., Ezhov, I., and Popova, E. (2021). Effect of Alloying on the γ-γ′ Microstructure of W-free Co-based Superalloys. Mater. Today Proc. 38, 1971–1973. doi:10.1016/j.matpr.2020.09.131
Drapier, J. M., and Coutsouradis, D. (1968). Precipitation Hardening of Co‐Cr‐Ta Alloys. Cobalt 39, 63–74.
Francisco, E., Blanco, M. A., and Sanjurjo, G. (2001). Atomistic Simulation of SrF2 Polymorphs. Phys. Rev. B 63 (9), 094107. doi:10.1103/physrevb.63.094107
Kittel, C., and Hellwarth, R. W. (1957). Introduction to Solid State Physics. Phys. Today 10 (6), 43–44. doi:10.1063/1.3060399
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758
Methfessel, M., and Paxton, A. T. (1989). High-precision Sampling for Brillouin-Zone Integration in Metals. Phys. Rev. B 40 (6), 3616–3621. doi:10.1103/physrevb.40.3616
Miedema, A. R., Boer, F. R. d., and Chatel, P. F. d. (1973). Empirical Description of the Role of Electronegativity in Alloy Formation. J. Phys. F. Metall. Phys. 3 (8), 1558–1576. doi:10.1088/0305-4608/3/8/012
Migas, D., Moskal, G., and Maciąg, T. (2020). Thermal Analysis of W-free Co-(Ni)-al-mo-nb Superalloys. J. Therm. Anal. Calorim. 142 (1), 149–156. doi:10.1007/s10973-020-09375-7
Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/physrevb.13.5188
Otero-de-la-Roza, A., Abbasi-Pérez, D., and Luaña, V. (2011). Gibbs2: A New Version of the Quasiharmonic Model Code. II. Models for Solid-State Thermodynamics, Features and Implementation. Comput. Phys. Commun. 182 (10), 2232–2248. doi:10.1016/j.cpc.2011.05.009
Pettifor, D. G. (1992). Theoretical Predictions of Structure and Related Properties of Intermetallics. Mater. Sci. Technol. 8 (4), 345–349. doi:10.1179/mst.1992.8.4.345
Pollock, T. M., Dibbern, J., Tsunekane, M., Zhu, J., and Suzuki, A. (2010). New Co-based γ-γ′ High-Temperature Alloys. JOM 62 (1), 58–63. doi:10.1007/s11837-010-0013-y
Pugh, S. F. (1954). XCII. Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 45 (367), 823–843. doi:10.1080/14786440808520496
Pyczak, F., Bauer, A., Göken, M., Lorenz, U., Neumeier, S., Oehring, M., et al. (2015). The Effect of Tungsten Content on the Properties of L12-Hardened Co–al–W. J. Alloys Compd. 632, 110–115. doi:10.1016/j.jallcom.2015.01.031
Reyes Tirado, F. L., Taylor, S., and Dunand, D. C. (2019). Effect of Al, Ti and Cr Additions on the γ-γ' Microstructure of W-free Co-ta-V-based Superalloys. Acta Mater. 172, 44–54. doi:10.1016/j.actamat.2019.04.031
Reyes Tirado, F. L., Taylor, S. V., and Dunand, D. C. (2020). Low-density, W-free Co-nb-V-al-based Superalloys with γ/γ' Microstructure. Mater. Sci. Eng. A 796, 139977. doi:10.1016/j.msea.2020.139977
Ruan, J., Xu, W., Yang, T., Yu, J., Yang, S., Luan, J., et al. (2020). Accelerated Design of Novel W-free High-Strength Co-base Superalloys with Extremely Wide γ/γʹ Region by Machine Learning and CALPHAD Methods. Acta Mater. 186, 425–433. doi:10.1016/j.actamat.2020.01.004
Sato, J., Omori, T., Oikawa, K., Ohnuma, I., Kainuma, R., and Ishida, K. (2006). Cobalt-Base High-Temperature Alloys. Science 312 (5770), 90–91. doi:10.1126/science.1121738
Shang, S., Wang, Y., and Liu, Z.-K. (2007). First-principles Elastic Constants of α- and θ-Al2O3. Appl. Phys. Lett. 90 (10), 101909. doi:10.1063/1.2711762
Shi, L., Yu, J. J., Cui, C. Y., and Sun, X. F. (2015). Microstructural Stability and Tensile Properties of a Ti-Containing Single-Crystal Co-ni-al-W-base Alloy. Mater. Sci. Eng. A 646, 45–51. doi:10.1016/j.msea.2015.08.044
Keywords: first-principle calculations, Co–V–Ta-based superalloys, mechanical properties, thermodynamic properties, phase stability
Citation: Chen Y, Wang C, Zhang C, Yang C, Han J and Liu X (2022) Theoretical Investigation of Effects of Transition Elements on Phase Stabilities and Elastic Properties of the γ′ Phase in Co–V–Ta Superalloys. Front. Mater. 9:885608. doi: 10.3389/fmats.2022.885608
Received: 28 February 2022; Accepted: 21 April 2022;
Published: 25 May 2022.
Edited by:
Yong A. Zhang, University of Science and Technology Beijing, ChinaReviewed by:
Souraya Goumri-Said, Alfaisal University, Saudi ArabiaXiaotian Wang, Southwest University, China
Copyright © 2022 Chen, Wang, Zhang, Yang, Han and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiajia Han, amlhamlhaGFuQHhtdS5lZHUuY24=; Xingjun Liu, eGpsaXVAaGl0LmVkdS5jbg==
 Youheng Chen1
Youheng Chen1 Cuiping Wang
Cuiping Wang Jiajia Han
Jiajia Han Xingjun Liu
Xingjun Liu