Accelerated Design of High γ′ Solvus Temperature and Yield Strength Cobalt-Based Superalloy Based on Machine Learning and Phase Diagram

This study combines machine learning and a phase diagram to accelerate the design of a cobalt-based superalloy with a composition of Co-30Ni-10Al-6Ta (at%). The results show that Co-30Ni-10Al-6Ta alloy exhibits high γ′ solvus temperature (1,215 °C) and high yield strength (1,220 Mpa at 25 °C), which is comparable with commercial nickel-based polycrystalline superalloy M-Mar-247. Moreover, the wide processing window and excellent γ′ phase stability make it lucrative for further applications at high temperatures. Meanwhile, the alloy design method also provides a new idea for efficiently realizing the preparation of high-performance alloys.

1 Introduction

In 2006, Professor Ishida from Japan successfully prepared a Co-Al-W-based superalloy with γ/γ′ two-phase microstructure, making the γ′ phase-strengthened cobalt-based superalloy expected to develop into the next generation of high-temperature structural materials (Sato et al., 2006). In recent years, researchers have developed new types of cobalt-based superalloys, other than Co-Al-W/Mo/V bases (Sato et al., 2006; Makineni et al., 2015a; Yuechao Chen et al., 2019), as well as Co-Ti-based, Co-V-Nb/Ta, Co-W-Ga/Ge, and many other cobalt-based superalloys (Chinen et al., 2007; Chinen et al., 2009; Zenk et al., 2017; Reyes Tirado et al., 2018; Ruan et al., 2020), which greatly enriched the research and development of new cobalt-based superalloy systems. However, the superalloys of these systems often have defects such as a narrow γ/γ′ two-phase composition region, low γ′ solvus temperature, and low yield strength, which greatly limit the high-temperature application potential of this type of alloy. Therefore, it is of great significance to develop a new type of cobalt-based superalloy with higher γ′ solvus temperature and yield strength. It is worth noting that the Co-Al-Ta-based superalloy was successfully designed and prepared by Chen et al. (2020), which gave fresh vitality to the development of new cobalt-based superalloys (Chen et al., 2020). However, the Co-30Ni-12Al-4Ta-12Cr alloy designed by Chen suffers the defects of low γ′ solvus temperature and yield strength. We consider that in the Co-Ni-Al-Ta quaternary alloy with the γ/γ′ two-phase structure, there may be a better quaternary master alloy. The master alloy has the characteristics of high γ′ solvus temperature and yield strength, which can provide another quaternary alloy system with application potential for the subsequent multi-component composition design of Co-Al-Ta-based superalloys. However, the design of these alloys is based on a large number of complex experiments, and the workload and the experimental period are long. Therefore, how to speed up the development of high-performance alloys efficiently is a major challenge we need to solve.

People can rationally design the alloy composition according to the phase diagram, reducing the generation of harmful phases in the design process. Therefore, the phase equilibrium diagram of metal alloys has important guiding significance for the design and development of new superalloys (WhIttenberger et al., 1992). With the rapid development of artificial intelligence, machine learning has also played an irreplaceable role in the material design process. Ruan and Zhuang have successfully designed a new type of cobalt-based superalloy that meets experimental expectations with the help of machine learning (Liu et al., 2020; Ruan et al., 2020). The solvus temperature, volume fraction, and hardness of the γ′ phase in the new cobalt-based superalloy are important performance indicators that affect the application prospects of the alloy. For example, γ′ solvus temperature is one of the key parameters of alloy service temperature, and γ′-phase volume fraction and hardness can affect alloy mechanical properties. Guo studied the relationship between various strengthening mechanisms of the superalloy and the volume fraction of the γ′ -phase; the statistical data showed that the number of precipitation strengthening phases is the fundamental guarantee for the strengthening of superalloys (Guo, 2008). This research combines the advantages of experimental-phase diagrams and machine learning to quickly design a high-strength quaternary Co-Ni-Al-Ta-based superalloy with high γ′-phase solvus temperature and γ′-phase volume fraction in line with expectations.

2 Experimental Procedure

The alloy Co-30Ni-10Al-6Ta (at%) was flipped and remelted many times to obtain homogeneous ingots. The purity of all raw materials used in this study exceeded 99.9%. The specimens for heat treatment were sealed in a vacuum quartz tube. After homogenizing at 1,290 C for 24 h and then annealing at 800 C for 24–240 h (the standard heat treatment), some ingots were cut into columns of Φ 4 mm × 6 mm to conduct compression tests (1.0 × 10^–4 s⁻¹ strain rate). Flake alloy samples were homogenized at 1,290 C for 24 h and annealed at 800 C for different times, then quenched in cold water and embedded in bakelite powder for microstructural observation. The alloy surface was corroded by a corrosion solution with a ratio of nitric acid (50 vol%) + hydrochloric acid (30 vol%) + water (20 vol%). The alloy microstructural observation was carried out using a scanning electron microscope (FE-SEM, SU-70) and transmission electron microscope (TEM, Talos-F200). The transmission electron microscope (TEM, Talos-F200) was utilized to determine the crystal structure of γ′-phase precipitates and composition partition. ImageJ software was used to evaluate the γ′-phase area fractions and sizes. The phase transformation temperatures were examined by differential scanning calorimetry (DSC) at a heating rate of 20 C/min, and by the Archimedes law, we determined the mass density. By X-ray diffraction (XRD), the lattice constants of phases were measured. In order to obtain the lattice constants of the γ and γ′ phases, material researchers usually use data processing software to distinguish the diffraction sub-peaks of the γ and γ′ phases. Therefore, the Voigt Amp equation in PeakFit software was used to fit the 111) crystal plane of the alloy. XRD peaked to the γ and γ′ phase splitting to obtain the lattice constants of the γ and γ′ phases. The composition of the studied alloys was measured by a field-emission electron probe microanalyzer (FE-EPMA, JXA-8530F). A hardness tester (load 0.5 kg) and high-temperature testing machine (indenter feed rate 10⁻⁴ mm/s) were used to test the mechanical properties of the alloy.

3 Results and Discussion

3.1 Alloy Design

In 2020, Yu used a variety of machine learning regression algorithms to establish a prediction model for the γ′-phase area fraction and solvus temperature of the cobalt-based superalloy (Yu et al., 2020). The algorithms include random forest, support regression, K-approaching, and gradient boosting, and through the adjustment of the key parameters of each algorithm, the optimal parameters of each algorithm were obtained. This research finally used the best performing random forest algorithm as the final algorithm model to predict the γ′ area fraction, Vickers hardness, γ′ solvus temperature, solidus, and mass density. The model database was derived from the published literature on the Internet and some unpublished alloy components of our groups. In addition, Chen of our group carried out experimental research on the phase equilibrium of Co-(10, 20, 30) Ni-Al-Ta alloy and drew the pseudo-ternary phase diagram of this series of alloys at 800 C (Chen et al., 2020). In this study, the pseudo-ternary phase diagram of Co-30Ni-Al-Ta, which has the widest γ/γ′ two-phase region, was used as the basic object.

In this study, using the machine learning model obtained by Yu (Yu et al., 2020), combined with the experimental phase diagram information obtained by Chen (Chen et al., 2020), the γ′ area fractions, Vickers hardness, γ′ solvus temperatures, solidus, and mass density of the Co-30Ni-Al-Ta quaternary alloy (annealed at 800°C for 48 h) were calculated. The trend chart of properties and composition are shown in Figures 1A–D, where red represents higher properties including γ′ area fraction, Vickers hardness, γ′ solvus temperature, and mass density, while blue represents the opposite. In this trend chart, we need to select appropriate component points in the γ/γ′ two-phase region to prevent the precipitation of miscellaneous phases. At the same time, we found that alloys with an Al element content in the range of 8–11 (at%) have a higher γ′ area fraction, while the Ta element content is above 5 (at%), the alloy hardness reached its peak. From Figures 1C, D, we find that γ′ solvus temperature and alloy mass density will increase with the addition of Ta. Therefore, considering that the designed alloy should have characteristics of higher γ′ area fraction, hardness, and γ′ solvus temperature but lower density. This study finally designed a Co-30Ni-10Al-6Ta (at%) component alloy as the target master alloy, which is represented by a black five-pointed star in Figure 1, and our previous component Co-30Ni-12Al-4Ta (at%) is represented by a pink five-pointed star. Figure 1E is the calculations of Co-30Ni-(16-x)Al-xTa (at %) about solidus and γ′ solvus temperature by machine learning, and we utilize this trend graph to determine 1,290°C as the homogenized temperature.

FIGURE 1

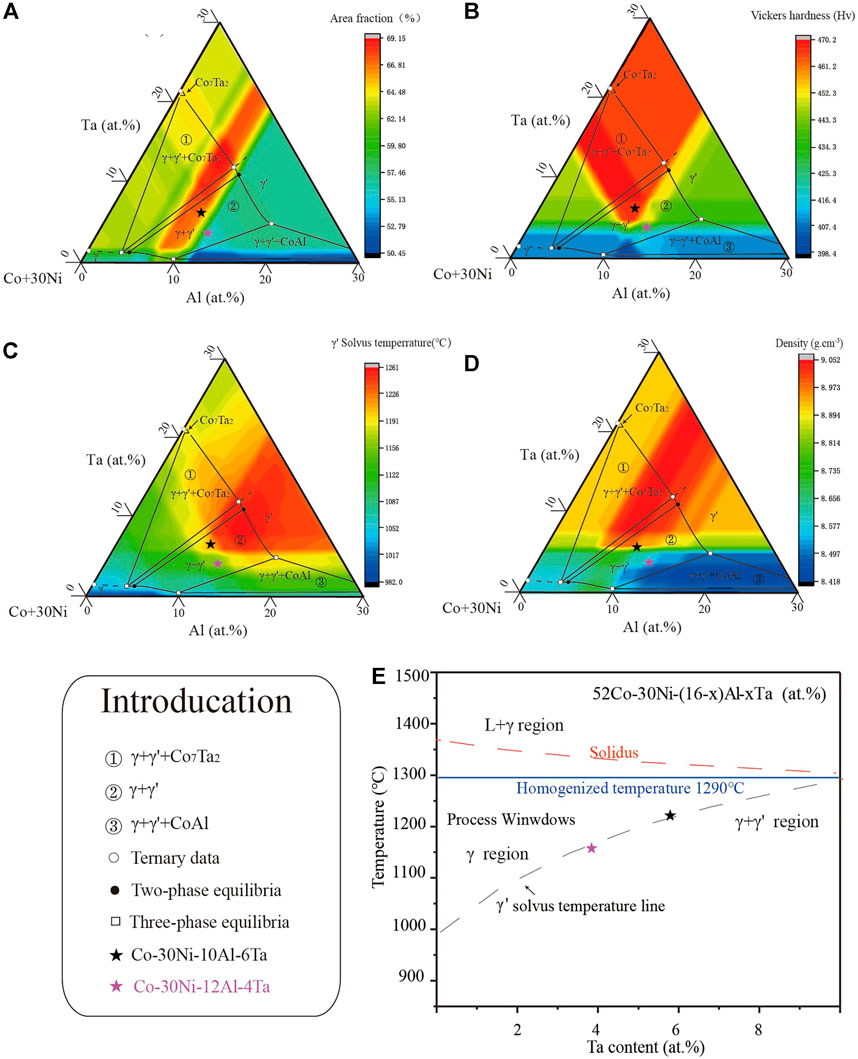
FIGURE 1. Relation image between (A) γ′ area fraction, (B) Vickers hardness, (C) γ′ solvus temperature, (D) density, and (E) phase transformation temperature line and pseudo-ternary isothermal section diagram of the Co-30Ni-Al-Ta quaternary system at 800°C based on machine-learning method calculation.

3.2 Experimental Results

3.2.1 L1₂-Ordered γ′ Phase

The TEM images obtained from the composition of Co-30Ni-10Al-6Ta (at%) alloy, annealed at 800°C for 48 h after solution treatment at 1,290°C for 24 h, are shown in Figure 2A. Fine γ/γ′ two-phase microstructures are observed in it, and Figure 2B is the diffraction pattern along the [001] zone axis and reveals that the cuboidal γ′ precipitates are L1₂-ordered structures. The fine L1₂-ordered γ′ phase is 120 ± 30 nm in size in Figure 2C, distributing throughout the γ matrix homogeneously, which is analogous to the γ/γ′ two-phase microstructure found in Ni-based and Co-based superalloys. Figure 2D shows the EDS mapping of Co-30Ni-10Al-6Ta alloys annealed at 800 °C for 48 h. We can clearly observe that Co tends to partition into the γ matrix, while Ta and Al tend to partition into the γ′ phase as strong γ′-forming elements.

FIGURE 2

FIGURE 2. (A) Dark-field TEM, (B) selected diffraction pattern, (C)TEM-HADDF, and (D) EDS mapping of Co-30Ni-10Al-6Ta alloys annealed at 800°C for 48 h.

3.2.2 Experiments and Calculations

Figure 3A shows the area fraction and Vickers hardness of the Co-30Ni-10Al-6Ta (at %) alloy with the change of aging time from 24 to 240 h. The factor of their decline after a long time of aging may be attributed to changes in the radius of γ′ precipitates and grain sizes under the constant diffusion of elements. We noticed that when the heat treatment time is 30–70h, the alloy has both higher hardness and area fraction. Figure 3B is the result of the lattice misfit study of the alloy after 48 h aging. The γ′ phase lattice constant is 0.3619 nm, the γ phase lattice constant is 0.3579 nm, and the calculation method of the γ/γ′ two-phase lattice misfit is according to the formula $\delta =2\left(\frac{a_{{\gamma }^{\text{'}}}-a_{\gamma }}{a_{{\gamma }^{\text{'}}}+a_{\gamma }}\right)$, showing that the calculation result is, respectively, +1.11%. Figure 3C is the DSC heating curve of the Co-30Ni-10Al-6Ta (at %) alloy after aging at 800 °C for 48 h. The solvus temperature of the γ′ phase is 1, 215°C, and the melting point of the γ phase is 1, 340 °C. The processing window of more than 120 °C means that the alloy has a huge alloying potential to improve alloy defects. Figure 3D shows the fit between the experimental results and the machine learning calculation results. We can find that the prediction has very high accuracy in terms of γ′ solvus temperature and density up to E_r≈0.01%. However, because the γ′ area fraction and alloy hardness will vary greatly with the aging time and temperature, the improvement of prediction accuracy may require more basic data.

FIGURE 3

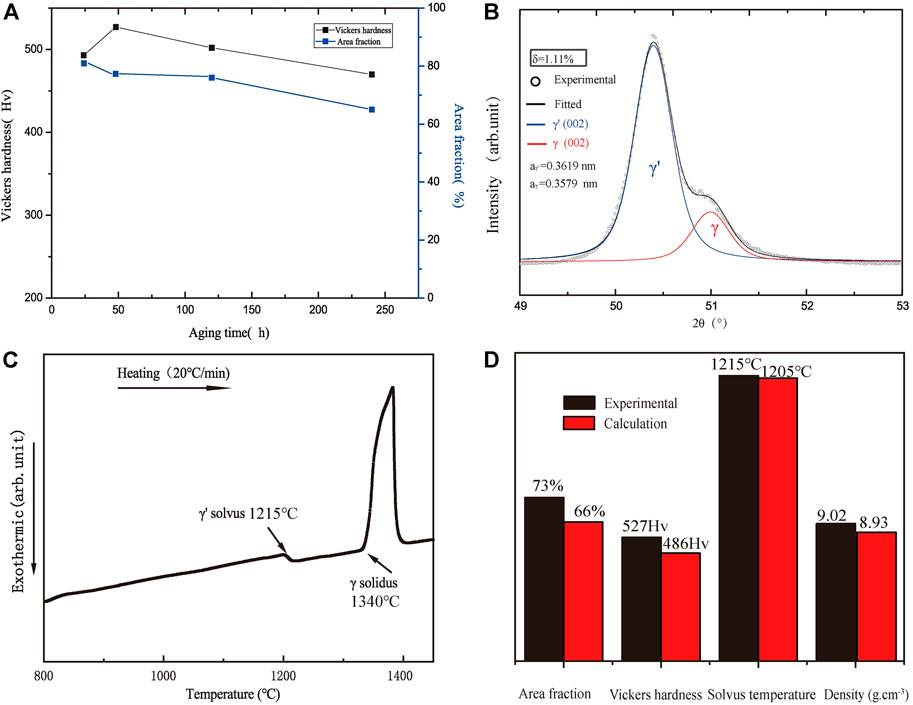
FIGURE 3. (A) Room-temperature hardness and γ′ area fraction of Co-30Ni-10Al-6Ta (at%) alloy annealed at 800°C for different times, (B) XRD images, and (C) DSC curve of Co-30Ni-10Al-6Ta (at%) alloy annealed at 800°C for 48 h. (D) Comparison of alloy characteristics between the experimental and calculated results.

3.2.3 Microstructure and Stability of γ′ Phase

The grain boundary and the change of γ′ phase size and shape with aging time are shown in Figure 4, where it is found that no secondary phases emerge in the matrix and grain boundary regions, and γ′ phase size increased with the extension of the aging time, whose shape remains cubic although the lattice misfit is slightly high. It should be noted that cold-rolling is conducted prior to the heat treatment in order to observe the stability of the γ′ phase. This pretreatment seems to shorten the annealing time of the studied alloy, which is required to obtain the thermal equilibrium stage. This cold rolling treatment method is also applied in Co-Al-W-based alloy (Tsukamoto et al., 2010) to obtain the phase equilibrium composition. Figure 5 shows the typical γ/γ′ two-phase microstructure obtained in the cold-rolled Co-30Ni-10Al-6Ta (at%) quaternary alloy, respectively, annealed at 800–1100 °C for 300 h. It can be seen that after the aging treatment, the alloy Co-30Ni-10Al-6Ta (at %) maintain stable γ/γ′ two-phase structure and no harmful impurities such as HCP, TCP, B2, and μ phase are found in the matrix. The composition of γ/γ′ and the partition coefficient are displayed in Table 1. Usually, the partitioning tendency of alloying elements between the γ and γ′ phases can be ascertained by the partition coefficient K_X, where K_X > 1 indicates that X is partitioned to the γ′ phase, while K_X < 1 means that X distributes to the γ phase (Yuechao Chen et al., 2019). Thus, it is clear that the Ta strongly partitions to the γ′ phase, especially at 800°C (K_Ta = 8.45), and the similar effect elements are Ti, W, Nb, etc. (Omori et al., 2013), and the Co partitions to the γ phase, which accords with the reported Co-based superalloys. The effective design of high-performance Co-based superalloys can be achieved by elucidating the role of alloying elements. In Table 1, we found that the Ta element is a strong γ′ phase forming element, its addition may be the key factor for the excellent γ′ phase thermal stability of the alloy. A similar action rule was also found in the study of Suzuki A et al. (Suzuki et al., 2007). We find K_Ta, K_Ni, and K_Al (particularly is K_Ta) change from high to low with increasing temperature, while K_Co is the opposite. The distribution behavior of all elements approaches K_X = 1 with increasing annealing temperature and this trend is also was found in other Co-Al-W-based (Omori et al., 2013) and Ni-Al-based superalloys (Jia et al., 1994).

FIGURE 4

FIGURE 4. SEM microstructure of Co-30Ni-10Al-6Ta (at %) alloy was annealed at 800°C at different times (24–240 h).

FIGURE 5

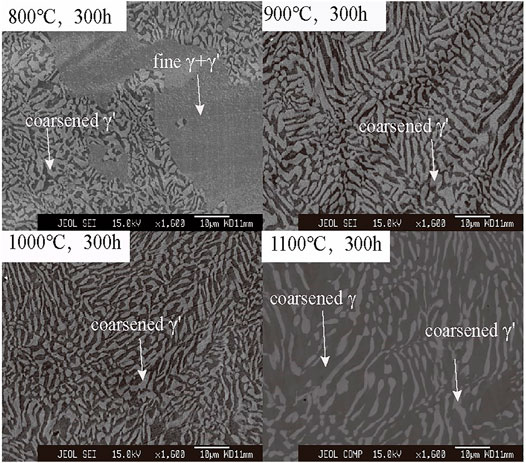
FIGURE 5. Phase equilibrium microstructure of Co-30Ni-10Al-6Ta (at %) alloy annealed at different temperatures for 300 h after cold-rolling with 50% reduction.

TABLE 1

TABLE 1. Composition of γ'/γ phases of alloys at various temperatures.

3.3 Property Comparisons and Discussions

3.3.1 γ′ Solvus Temperature and Density Comparisons

Figure 6 shows the γ′ solvus temperature and density comparisons of Co-30Ni-10Al-6Ta (at%) alloy, Co-Ni-Al-V-based (Yuechao Chen et al., 2019), Co-Ni-Al-Mo-based (Makineni et al., 2015b), Co-Ni-Al-W-based (Qu et al., 2019), Co-Ti-based (Zenk et al., 2017), and Ni-based (Baldan et al., 2013) superalloy. It is obvious from the figure that the γ′ solvus temperature of this alloy is much higher than that of the aforementioned Cobalt-based alloys and comparable to commercial nickel-based superalloy M-Mar-247. The reason may be that Ta is a strong γ′-phase former element, and the addition of this element can increase the solvus temperature of the γ′ phase. However, we should also note that Ta as a heavy element can also sharply increase the alloy density, which is consistent with the calculation results in Figures 1C, D. When considering the lightweight design of the alloy, the addition of Ta or W element should be appropriate.

FIGURE 6

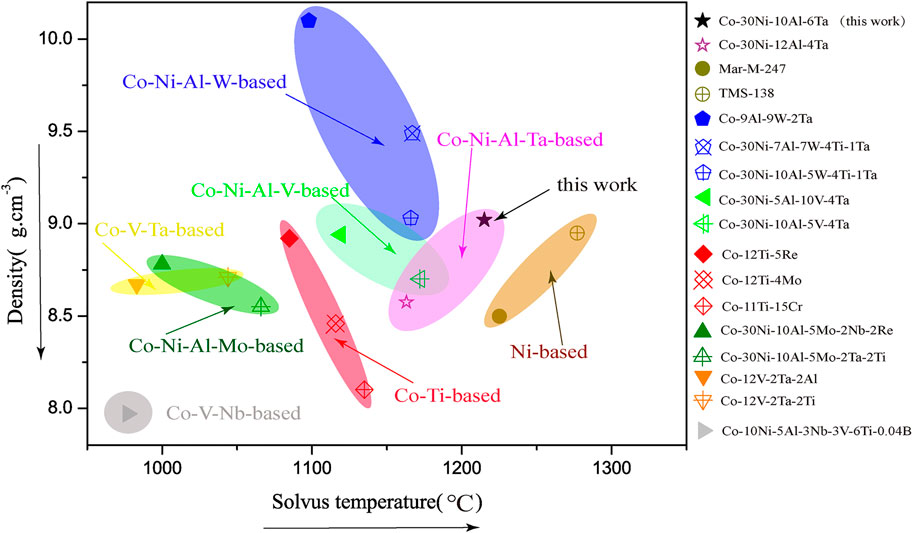
FIGURE 6. γ′ solvus temperature and density comparisons of Co-30Ni-10Al-6Ta (at %) alloy and various Co-based and Ni-based superalloys.

3.3.2 Lattice Misfit Comparison

Figure 7 shows the lattice misfit comparisons of Co-30Ni-10Al-6Ta (at%) alloy with other Co-based superalloys; it is found that this alloy has a high lattice misfit (+1.11%) compared to Co-12Ti alloy and Co-12Ti-4Mo alloy, and Co-Ni-Al-W-based alloys exhibit a suitable lattice misfit around 0.5% (Zenk et al., 2017). The morphology of the γ′ phase in new Co-based superalloys is closely related to the lattice misfit of the two γ/γ′ phases: when the lattice misfit is 0–0.2%, 0.5–1.0%, and higher than 1.25%, the shape of the γ′ precipitates is spherical, cubic, and plate. A too high lattice misfit may cause the precipitated γ′ phase of the alloy to be unstable at high temperatures, the alloy rafting phenomenon is a good proof in Co-12Ti alloy (Zenk et al., 2017), and it can affect the mechanical properties. Therefore, a suitable lattice misfit is critical for subsequent alloy designers. Compared to Co-30Ni-12Al-4Ta (at%) alloys, we found that an increase in the Ta/Al ratio leads to an increase in the γ/γ′ lattice constants. However, as a strong γ′ phase forming element, the Ta element is more inclined to be distributed in the γ′ phase (Table 1), which causes a sharp increase in the γ′ phase lattice constant, and leads to an increase in the γ/γ′ lattice misfit. But it is worth noting that the Cr element, as a γ phase forming element, can effectively increase the lattice constant of the γ phase. The addition of the Cr element maybe is an effective way to improve the defect for alloys with excessive lattice misfit. This method is a good embodiment of the Co-Ti-based alloy (Zenk et al., 2017).

FIGURE 7

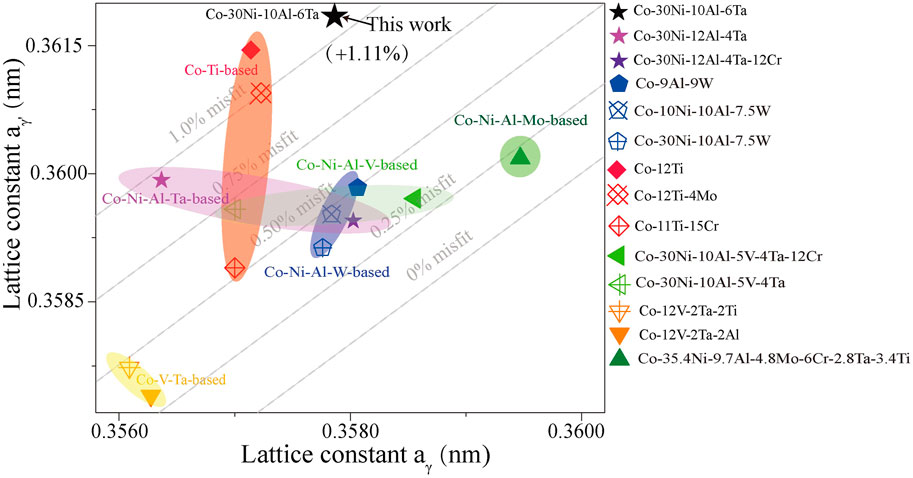
FIGURE 7. Comparison of lattice misfit among Co-Ni-Al-Ta-based, Co-Ni-Al-W-based, Co-Ti-based, Co-Ni-Al-V-based, Co-Ni-Al-Mo-based, and Co-V-Ta-based superalloys.

3.3.3 Mechanical Properties

Figure 8 is a graph showing the relationship between yield strength and temperature of this alloy. In this study, part of Co-Ni-Al-V-based (Yuechao Chen et al., 2019), Co-Ni-Al-Mo-based (Makineni et al., 2015c), Co-Al-W-based (Suzuki et al., 2007), Co-Ti-based (Zenk et al., 2017), and Ni-based (Sims et al., 1987) polycrystalline superalloys are listed as comparative alloys. What can be seen from Figure 7 is that the alloy in this study exhibit excellent yield strength (950–1220Mpa) in the low and medium temperature range (20–700 C), which far exceeds other new Co-based superalloys and Ni-based polycrystalline superalloy M-Mar-247. However, the yield strength of this alloy in the middle and high-temperature range (700–900 C) has a relatively obvious and rapid decline, and it is equivalent to the comparison alloys of various series above 800 C. Gerold (Gerold and Haberkorn, 2010) pointed out in the study of the relationship between alloy strengthening and dislocations, elastic stress fields that when the dislocations pass through the precipitation phase particles by cutting, the mathematical formula for the increase in yield strength due to coherent strain strengthening is Δτ = AGε^3/2 (r₀f/b)^1/2, where A is a constant, G is the shear modulus, ε is the degree of lattice misfit, r₀ is the average radius of the precipitated phase particles, f is the volume fraction of the precipitated phase, and b is the primary Gus vector. This mathematical formula clearly shows that the increase in yield strength due to precipitation strengthening increases with the increase in ε, r₀, and f at room temperature. The alloys that use this mechanism for strengthening include GH4169, GH2706, and Inconel718.

FIGURE 8

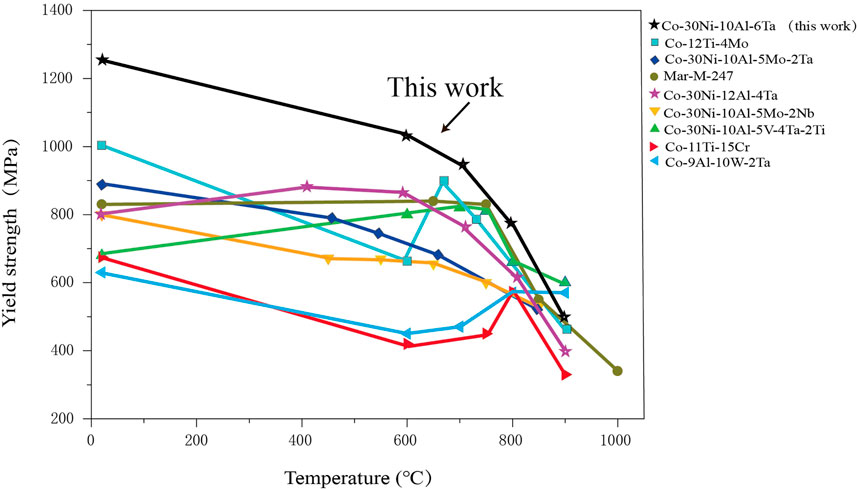
FIGURE 8. Yield strength vs. temperature curves for Co-30Ni-10Al-6Ta, Ni-based polycrystalline Mar-M-247, Co-30Ni-10Al-5Mo-2Nb, Co-30Ni-10Al-5V-4Ta-2Ti, Co-11Ti-15Cr, and Co-9Al-10W-2Ta superalloys.

Under high-temperature conditions, the grain boundary strength decreases rapidly as the temperature rises, especially the lateral grain boundary becomes a weak link. Above the isothermal strength, the superalloys that do not strengthen the grain boundary are prone to fracture along the grain under high-temperature stress conditions. Therefore, a small amount of grain boundaries strengthening elements such as C and B can be added to improve the high-temperature creep performance of polycrystalline alloys (Reed, 2008). On the other hand, the reason that yield strength decreases rapidly under high temperature may be that the slip on the octahedral plane is activated, the interaction mechanism between the 1/3 [112] partial dislocations and the γ′ phase particles changes from the “cut-through” mechanism to “bypass” mechanism (Suzuki et al., 2007).

4 Conclusion

In summary, the alloy Co-30Ni-10Al-6Ta (at%) obtained by the material design method that combines machine learning and phase diagram displays good characteristics in this work. The following conclusions are drawn:

(1) The material design method combining machine learning and phase diagram can effectively design cobalt-based superalloys with multiple desired properties and shorten the experimental period.

(2) The existence of the L1₂-ordered γ′ phase was experimentally confirmed, and Co tends to partition into the γ matrix, while Ta, Ni, and Al tend to partition into the γ′ phase.

(3) After the experimental verification, the γ′ solvus temperature (1,215 °C), γ′ volume fraction (73%), hardness (527 Hv), and density (9.02 g cm⁻³) can perfectly consistent with the calculated results.

(4) The studied alloy was subjected to equilibrium heat treatment at 800–1, 100°C for 300 h, and the obtained γ′ phases were proved thermodynamically stable.

(5) The increase in the Ta/Al ratio can significantly increase the γ′ solvus temperature, density, lattice misfit, and yield strength of the alloy.

(6) The Co-30Ni-10Al-6Ta (at %) alloy has a high γ′ solvus temperature (1, 215 °C) and high yield strength (1, 220 Mpa/25 °C). Moreover, the wide processing window (125 °C) and excellent γ′ phase stability make it lucrative for further applications at high temperatures.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author Contributions

CW: conceptualization, supervision, project administration, and financial support. XC: experimental, data curation, and writing—original draft. YC: formal analysis, supervision, and writing—review and editing. JY: writing—review and editing. WC: investigation. ZC: supervision and investigation. XY: supervision and investigation. YL: supervision and resources. YY: supervision and resources. XL: conceptualization, supervision, project administration, and financial support.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 51831007), the Ministry of Science and Technology of China (Grant No. 2014DFA53040), and the Key-Area Research and Development Program of GuangDong Province (No. 2019B010943001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baldan, R., da Rocha, R. L. P., Tomasiello, R. B., Nunes, C. A., da Silva Costa, A. M., Barboza, M. J. R., et al. (2013). Solutioning and Aging of MAR-M247 Nickel-Based Superalloy. J. Materi Eng. Perform. 22 (9), 2574–2579. doi:10.1007/s11665-013-0565-4

CrossRef Full Text | Google Scholar

Chen, Y., Wang, C., Ruan, J., Yang, S., Omori, T., Kainuma, R., et al. (2020). Development of Low-Density γ/γ′ Co-al-ta-based Superalloys with High Solvus Temperature. Acta Materialia 188, 652–664. doi:10.1016/j.actamat.2020.02.049

CrossRef Full Text | Google Scholar

Chinen, H., Omori, T., Oikawa, K., Ohnuma, I., Kainuma, R., and Ishida, K. (2009). Phase Equilibria and Ternary Intermetallic Compound with L12 Structure in Co-W-Ga System. J. Phase Equilib. Diffus. 30 (6), 587–594. doi:10.1007/s11669-009-9580-4

CrossRef Full Text | Google Scholar

Chinen, H., Sato, J., Omori, T., Oikawa, K., Ohnuma, I., Kainuma, R., et al. (2007). New Ternary Compound Co3(Ge, W) with L12 Structure. Scripta Materialia 56 (2), 141–143. doi:10.1016/j.scriptamat.2006.09.007

CrossRef Full Text | Google Scholar

C. T. Sims, N. S. Stoloff, and W. C. Hagel (Editors) (1987). Superalloys II: High-Temperature Materials for Aerospace and Industrial Power (J. Wiley & Sons).

Google Scholar

Gerold, V., and Haberkorn, H. (2010). “On the Critical Resolved Shear Stress of Solid Solutions Containing Coherent Precipitates,” in Physica Status Solidi, 16, 675–684.2

Google Scholar

Guo, J.-T. (2008). Materials Science and Engineering for Superalloys. Beijing: Science Press.

Google Scholar

Jia, C. C., Ishida, K., and Nishizawa, T. (1994). Partition of Alloying Elements between γ (A1), γ′ (L12), and β (B2) Phases in Ni-Al Base Systems. Mmta 25 (3), 473–485. doi:10.1007/bf02651589

CrossRef Full Text | Google Scholar

Liu, P., Huang, H., Antonov, S., Wen, C., Xue, D., Chen, H., et al. (2020). Machine Learning Assisted Design of γ′-strengthened Co-based Superalloys with Multi-Performance Optimization. npj Comput. Mater. 6 (1), 1–9. doi:10.1038/s41524-020-0334-5

CrossRef Full Text | Google Scholar

Makineni, S. K., Nithin, B., and Chattopadhyay, K. (2015). A New Tungsten-free γ-γ' Co-al-mo-nb-based Superalloy. Scripta Materialia 98, 36–39. doi:10.1016/j.scriptamat.2014.11.009

CrossRef Full Text | Google Scholar

Makineni, S. K., Nithin, B., and Chattopadhyay, K. (2015). Synthesis of a New Tungsten-free γ-γ′ Cobalt-Based Superalloy by Tuning Alloying Additions. Acta Materialia 85, 85–94. doi:10.1016/j.actamat.2014.11.016

CrossRef Full Text | Google Scholar

Makineni, S. K., Samanta, A., Rojhirunsakool, T., Alam, T., Nithin, B., Singh, A. K., et al. (2015). A New Class of High Strength High Temperature Cobalt Based γ-γ′ Co-mo-al Alloys Stabilized with Ta Addition. Acta Materialia 97, 29–40. doi:10.1016/j.actamat.2015.06.034

CrossRef Full Text | Google Scholar

Omori, T., Oikawa, K., Sato, J., Ohnuma, I., Kattner, U. R., Kainuma, R., et al. (2013). Partition Behavior of Alloying Elements and Phase Transformation Temperatures in Co-al-W-base Quaternary Systems. Intermetallics 32, 274–283. doi:10.1016/j.intermet.2012.07.033

CrossRef Full Text | Google Scholar

Qu, S., Li, Y., He, X., Wang, C., Liu, X., Chen, Y., et al. (2019). Microstructural Evolution and Compression Property of a Novel γʹ-strengthened Directionally Solidified CoNi-Base Superalloy. Mater. Sci. Eng. A 761, 138034. doi:10.1016/j.msea.2019.138034(

CrossRef Full Text | Google Scholar

Reed, R. C. (2008). The Superalloys: Fundamentals and Applications-Introduction. Cambridge University Press.

Google Scholar

Reyes Tirado, F. L., Perrin Toinin, J., and Dunand, D. C. (2018). γ+γ′ Microstructures in the Co-ta-V and Co-nb-V Ternary Systems. Acta Materialia 151, 137–148. doi:10.1016/j.actamat.2018.03.057

CrossRef Full Text | Google Scholar

Ruan, J., Xu, W., Yang, S., Yu, J., Yang, S., Luan, J., et al. (2020). Accelerated Design of Novel W-free High-Strength Co-based Superalloys with Extremely Wide γ/γʹ Region by Machine Learning and CALPHAD Methods. Acta Materialia 186, 425–433. doi:10.1016/j.actamat.2020.01.004

CrossRef Full Text | Google Scholar

Sato, J., Omori, T., Oikawa, K., Ohnuma, I., Kainuma, R., and Ishida, K. (2006). Cobalt-base High-Temperature Alloys. Science 312 (5770), 90–91. doi:10.1126/science.1121738

PubMed Abstract | CrossRef Full Text | Google Scholar

Suzuki, A., DeNolf, G. C., and Pollock, T. M. (2007). Flow Stress Anomalies in γ/γ′ Two-phase Co-al-W-base Alloys. Scripta Materialia 56 (5), 385–388. doi:10.1016/j.scriptamat.2006.10.039

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Kobayashi, S., and Takasugi, T. (2010). “The Stability of γ '-Co3(Al, W) Phase in Co-al-W Ternary System,” in Materials Science Forum (Trans Tech Publ), 448–451. doi:10.4028/www.scientific.net/msf.654-656.448

CrossRef Full Text | Google Scholar

WhIttenberger, J. D. (1992). “A Review of “SUPERALLOYS II”,” in Materials and Manufacturing Processes. Editors C. T. Sims, N. S. Stoloff, and W. C. Hagel (New York, NY: A Wiley-Interscience Publication John Wiley & Sons), 7, 463–468. 615 pages, hardcover, 1987.

CrossRef Full Text | Google Scholar

Yu, J., Wang, C., Chen, Y., Wang, C., and Liu, X. (2020). Accelerated Design of L12-Strengthened Co-based Superalloys Based on Machine Learning of Experimental Data. Mater. Des. 195. doi:10.1016/j.matdes.2020.108996

CrossRef Full Text | Google Scholar

Yuechao Chen, C. W., Ruan, J., Omori, T., Kainuma, R., Kiyohito, X., and Ishida, L. (2019). High-strength Co-al-V-base Superalloys Strengthened by γ′-Co3 (Al, V) with High Solvus Temperature. Acta Materialia. 170, 62-74. doi:10.1016/j.actamat.2019.03.013

CrossRef Full Text | Google Scholar

Zenk, C. H., Povstugar, I., Li, R., Rinaldi, F., Neumeier, S., Raabe, D., et al. (2017). A Novel Type of Co-ti-cr-base γ/γ′ Superalloys with Low Mass Density. Acta Materialia 135, 244–251. doi:10.1016/j.actamat.2017.06.024

CrossRef Full Text | Google Scholar