Meta-Structure Surface Based on Dielectric Tensor Rotation Induced by AC Electric Field for Insulation Improvement

Electric field distribution along gas–solid interfaces determines the reliability of insulating components. However, the dielectric gradient insulating component prepared by the conventional method is considered to only control the internal electric field, but is not beneficial to the surface insulation, especially when the electrode is at an acute angle from the dielectric surface. The aim of this study is to clarify that the meta-structure surface based on dielectric tensor rotation constructed by the electric field-induced assembly (EIA) method could improve surface insulation. The self-assembly and orientation axis rotation of filler particles near the interface were observed by in-situ optical observation, and the relationship between the dielectric tensor rotation and electric field refraction was revealed. Simulation of meta-structure surface induced by the EIA method on the basin insulator was conducted. The meta-structure surface exhibits negative and high reduced permittivity, confining electric field path and transferring the electrical stress from gas to insulator, which offers theoretical support to optimize the surface electric field. Flashover tests on the basin insulator proved the insulation improvement by meta-structure surface.

Introduction

How to withstand the higher voltage using the same insulation distance is a focus throughout the era of electrical energy. There was general agreement that homogenizing the electric field to take full advantage of the insulation distance can avoid the “barrel effect" (Cigré 2014; Cigré 2020; Li et al., 2020). The conventional insulation design aims to optimize the topology of electrodes, which increases the complexity of the structure and has a limited effect on electric field mitigation. In recent years, researchers have focused on dielectric functional gradient materials (d-FGM), which use the gradient distribution of dielectric parameters to mitigate the spatial electric field and have a widespread application prospect. In Cigre’s report of 2017, the effectiveness of d-FGM in modulating electric fields was fully recognized. The fabrication methods that have been developed can be divided into two main categories: (1) “building block” methods, including lamination (Brealey et al., 1982), magnetron sputtering (Du et al., 2020), flexible casting (Hayakawa et al., 2018), and 3D printing (Li et al., 2019), and (2) energy field assisted methods, which use an external energy field to manipulate the filler particle distribution during the casting of insulating components, including centrifugation (J. Ishiguro et al., 2014), electrophoresis (Diaham et al., 2021; Diaham et al., 2021; Diaham et al., 2021), magnetophoresis (Tommaso Nardi et al., 2016), and electric field-induced assembly (EIA) method (Shen et al., 2020; Shen et al., 2021; Shen et al. 2022). The first type of methods cannot deal with more complex space electric fields, and the second type of methods’ applicability depends on the similarity of the applied energy field to the operating electric field.

Maxwell–Wagner polarization occurs at the interface due to differences in the dielectric parameters of the filler and the matrix. Polarized fillers interact with each other in the electric field and assemble in chains along the direction of the electric field, resulting in the increased effective permittivity of the composite in the electric field direction (Singh et al., 2019; Shen et al., 2021), i.e., the electric field-induced self-assembly effect. The higher the applied field strength, the faster the alignment of the chains and the faster the corresponding increase of the permittivity. If an assistant AC electric field similar to the spatial distribution of the actual working electric field is applied to the prepolymer state during the casting of the insulator to induce self-assembly of the internal filler of high permittivity, due to the inhomogeneity of the electric field, the self-assembly speed and the corresponding growth rate of the effective permittivity vary with space. By controlling the action time of the assistant electric field, the obtained permittivity gradient satisfies the stronger the electric field, the higher the permittivity, which helps to mitigate the electric field. This is the principle of the EIA method (Shen et al., 2021).

However, the dielectric gradient is generally considered to control the internal electric field of the components, but not beneficial to the surface insulation, especially when the electrode is at an acute angle with the insulating components, the dielectric gradient will enhance the electric field on the gas side, which is prone to trigger the flashover. As a key insulating component of high voltage transmission, more than half of the failure of basin insulators are caused by flashover on the concave surface. Thus it is urgent to regulate the surface electric field. In this paper, a method was proposed to construct a meta-structure surface based on the rotation of the dielectric tensor induced by the AC electric field, to confine the electric field path and improve the surface insulation. This method is expected to broaden the application of the EIA method.

Theoretical Background

In the electric field, the suspended spherical dielectric particle is polarized and the dipole moment is (Thomas 1995)

$p_s=4\pi {\epsilon }_m{R}^3\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_p+2{\epsilon }_m}\right)E_0,(1)$

For 1D rod-like particles, the dipole moment can be calculated approximately based on the ellipsoidal particles (a>b = c). Decomposing the electric field $E_0$ in the parallel and perpendicular long axis, the induced dipole moments are (Thomas 1995)

${\stackrel{\rightharpoonup }{p}}_{\parallel }=\frac{4\pi a{b}^2}{3}\frac{{\epsilon }_p-{\epsilon }_m}{1+\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_m}\right)L_{\left|\right|}}{E}_0\mathit{cos}\theta ,(2)$

${\stackrel{\rightharpoonup }{p}}_{\perp }=\frac{4\pi a{b}^2}{3}\frac{{\epsilon }_p-{\epsilon }_m}{1+\left(\frac{{\epsilon }_p-{\epsilon }_m}{{\epsilon }_m}\right)L_{\perp }}{E}_0\mathit{sin}\theta ,(3)$

where ${\epsilon }_p$ and ${\epsilon }_m$ are the permittivities of the particle and matrix, respectively, $\theta$ is the angle between the major axis and electric field, $L_{\left|\right|}=\frac{b^2}{2a^2{e}^3}\left[\ln \left(\frac{1+e}{1-e}\right)-2e\right]$, $e=\sqrt{1-b^2/a^2}$, and $L_{\perp }=\left(1-L_{\parallel }\right)/2$. If the dipole moment is not parallel to the electric field, an electric torque $\left(\stackrel{\rightharpoonup }{T}=\stackrel{\rightharpoonup }{p}\times \stackrel{\rightharpoonup }{E}\right)$ is generated to drive the nonspherical particles to orient along the electric field direction. At the same time, the particles are subjected to viscous drag from the matrix, and the angular velocity of rotation depends on the balance of the two forces. In the scope of this study, the liquid polymer has a low Reynolds number relative to the particles (Re < 1), and is a creep flow. The viscous drag is proportional to the relative velocity of motion and is insensitive to the shape details of the particles. Therefore, the rotational friction coefficients of the ellipsoid and the cylinder can be approximated to each other (Bruce and Young, 2009).

$\omega =T/f_{\theta },(4)$

$f_{\theta }=\frac{16}{3}\pi \eta \frac{\left(a^2+b^2\right)a}{2\ln \left(\frac{2a}{b}\right)-1},(5)$

where $f_{\theta }$ is the rotational friction coefficient of the ellipsoidal particle, and $\eta$ is the viscosity coefficient of the matrix, a and b are the semi-long and semi-short axes of the ellipsoid, respectively.

The polarized particles will be subjected to dielectrophoretic force due to the electric field gradient, for transmission and substation insulation systems, where the electric field is slightly inhomogeneous, the dielectrophoretic force generated by the applied electric field can be neglected. However, neighboring fillers (as shown in the figure) will interact with each other and the electrostatic force expression is

${\stackrel{\rightharpoonup }{F}}_{21}=\frac{3p^2}{4\pi {\epsilon }_{\mathrm{m}}{r}^4}\left(\left(1-3{\cos }^2\theta \right){\widehat{r}}_{21}-\sin \theta \cos \theta \widehat{\theta }\right),(6)$

Figure 1shows the relationship between the electrostatic force and the angle. When $\theta =0$, the attractive force is along with the dipole linkage with the magnitude of $3p^2/\left(2\pi {\epsilon }_m{r}^4\right)$; when $\theta =90°$, the repulsive force is along with the dipole linkage with the magnitude of $3p^2/\left(4\pi {\epsilon }_m{r}^4\right)$. It can be further found that when $0<\theta <54.7°$, dipoles attract each other; when $\theta >54.7°$, dipoles repel each other. This means that the fillers in the liquid polymer will self-assemble driven by the electric field and eventually arranged in chains along the electric field direction. The viscous drag forces on the spherical and ellipsoidal particles during the translational motion are (Verrelli 2014)

$F_{drag}=6\pi \eta r_{eff}v{f}_{corr,\parallel },(7)$

where $r_{eff}={\left(abc\right)}^{1/3}$ is the equivalent radius of the particle, $f_{corr,\parallel }={\left(0.8+\lambda /5\right)/\lambda }^{1/3}$, $1<\text{λ}<6$ or $f_{corr,\parallel }=0.67{\lambda }^{2/3}/\left(\ln \left(2\lambda \right)-0.5\right)$, $\lambda >6$ is the correction coefficient, $\lambda =a/b$.

FIGURE 1

FIGURE 1. Spatial position of parallel isotropic dipole and variation of force with angle.

Fillers go from disorder to fully self-assembly in a time-domain process, due to electrostatic force and viscous drag. Figure 2 shows the schematic diagram of particle orientation as well as complete self-assembly. The change of microstructure is inevitably mapped to macroscopic properties, and the previous work found that the effective permittivity of liquid composites will first increase and then stabilize in a uniform AC electric field. The transient process of the effective permittivity of the liquid prepolymer composites in a uniform AC electric field satisfies (Shen et al., 2021)

${\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}\left(t\right)=a_0-b_0{e}^{- \frac{t}{\tau }},(8)$

$\tau =k{E}^{-2},(9)$

where $a_0-b_0$ and $a_0$ are the initial and steady-state permittivity, respectively, depending on the composite material, $t$ is the duration of the applied electric field action, $\tau$ is the time constant of the transient process, $k$ is a constant related to the composite material, and $E$ is the applied electric field strength. The higher the applied field strength, the smaller the time constant and the quicker the transient process of the permittivity.

FIGURE 2

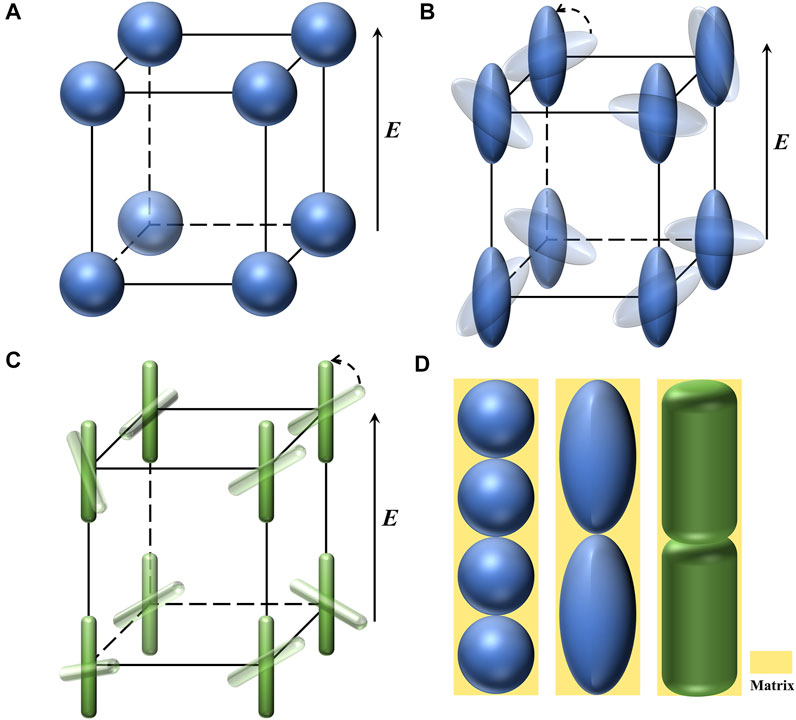
FIGURE 2. Orientation and self-assembly of fillers (A), spheres (B), ellipsoid (C), and rod-like particle (D) fully aligned along the electric field.

The fabrication steps for typical composite insulating components, such as basin insulators, can be summarized as (1) pouring the liquid prepolymer composite into a casting mold with electrodes embedded and (2) curing the material. If in the first step, an alternative (AC or bipolar repetitive pulse) voltage is applied through the embedded electrodes, then a nonuniform electric field will be generated inside the liquid prepolymer composites. According to the above theory, the speed of transient process of permittivity varies in different areas, and the permittivity changes faster in high field strength areas and slower in other areas. According to Maxwell’s equations, the space electric field satisfies

$\nabla \cdot \left({\epsilon }_0{\epsilon }_r\nabla \varnothing \right)=\mathrm{0,}(10)$

The kinetic equation for the evolution of the permittivity here is (Shen et al., 2021)

$\frac{d{\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}}{dt}=\frac{\left(a-{\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)}{\tau },(11)$

The dielectric gradient built by the EIA method is adaptive to the real electric field. In (Shen et al., 2021), it is confirmed by simulation that, if a suitable operating time is chosen, the gradient permittivity constructed by the EIA method can significantly mitigate the internal electric field, regardless of the number and distribution of high field strength regions.

Conventional dielectric gradient components are locally isotropic, while components prepared by the EIA method are locally anisotropic with a second-order dielectric tensor, as shown in thefollowing equation:

$\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{\epsilon }}\left(t\right)=\left[\begin{array}{ccc}{\epsilon }_{11}\left(t\right)& 0& 0\\ 0& {\epsilon }_{22}& 0\\ 0& 0& {\epsilon }_{33}\end{array}\right],(12)$

where ${\epsilon }_{11}\left(t\right)$ represents the permittivity along the orientation axis, which is also the value of transient permittivity measured in (Shen et al., 2021) and Eq. 8, ${\epsilon }_{22}$ and ${\epsilon }_{33}$ are the permittivities along with any two orthogonal directions in the plane orthogonal to the orientation axis, as illustrated in Figure 3A. The non-diagonal elements are all zero because we choose the filler orientation axis as one of the main axes of the dielectric tensor (of course, the choice of the main axes is free and does not affect the properties of the material). In general, ${\epsilon }_{11}>{\epsilon }_{22}={\epsilon }_{33}$. ${\epsilon }_{22}$ and ${\epsilon }_{33}$ can be approximated by the permittivity of the matrix, because of the series and randomly dispersed structure (Luo et al., 2017).

FIGURE 3

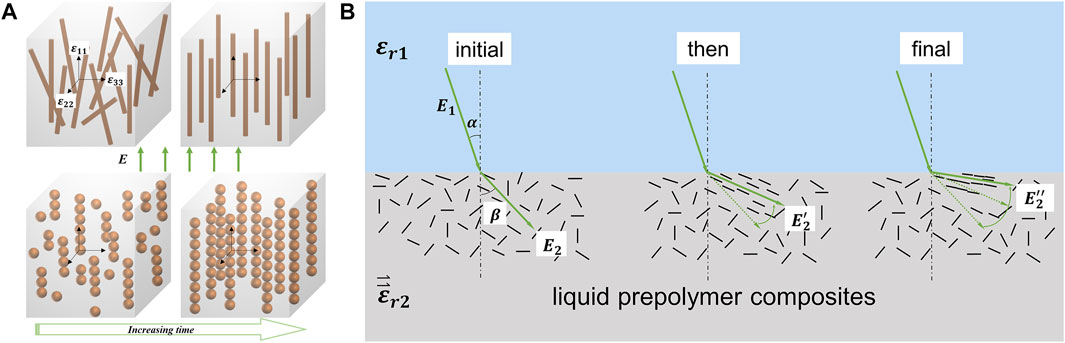
FIGURE 3. Changes in magnitude and direction of the dielectric tensor: (A) self-assembly process of fillers in an electric field; (B) rotation of orientation axis of fillers near the interface.

The polarization of the medium is

$\stackrel{\rightharpoonup }{P}=\left[\begin{array}{c}{\epsilon }_{11}{E}_1\\ {\epsilon }_{22}{E}_2\\ {\epsilon }_{33}{E}_3\end{array}\right]-{\epsilon }_0\stackrel{\rightharpoonup }{E},(13)$

where $E_i$ represents the electric field component in each tensor axis. The refraction of the electric field at the interface meets the requirement of the conservative field and the potential displacement continuity. Due to the electric field, the permittivity ${\epsilon }_{11}$ in the orientation axis gradually increases, and the angle of refraction changes accordingly, this process may be considered quasi-static. The angle $\delta$ between the refractive electric field and the filler orientation axis is small, and the resulting electric torque is

$\stackrel{\rightharpoonup }{T}=\stackrel{\rightharpoonup }{P}\times \stackrel{\rightharpoonup }{E}\approx -\left(-\widehat{j}\right)\left({\epsilon }_{11}-{\epsilon }_{33}\right)E_3^2 \delta ,(14)$

Electric torque drives the dielectric tensor to rotate to reduce $\delta$ as shown in Figure 3B.

Materials and Methods

Materials

TiO₂w with an average diameter of 300 nm and an average length of 5 μm, was purchased from Shanghai Haoxi Nano Technology Co., Ltd.; α-Al₂O₃ with an average diameter of 20 μm was purchased from Guangzhou Nanuo Chemistry Co., Ltd. Dimethyl silicone oil with a viscosity of 1000 mPa.s at room temperature, was purchased from Dow Corning. The EP (E39) and methyl-hexahydrophthalic anhydride (MeHHPA) were purchased from Jining Huakai Co., Ltd. Benzyldimethylamine (BDMA) was used as the catalytic agent.

Online Observation of Tensor Rotation

To investigate the typical process of dielectric tensor rotation, an online optical observation system was developed. Figure 4 shows the schematic diagram of the experimental setup. A square transparent glass plate surface was attached with 1 mm thick copper electrodes at both ends and a 1 mm thick biaxially oriented polypropylene (BOPP) film on the rest area (a 1 mm wide gap was left diagonally, filling with 1vol% TiO₂w/silicone oil mixture). Briefly, a 10 kHz AC voltage (RMS of 1kV) is applied through the electrodes for 1 min while the filler distribution near the interface is observed using an optical microscope.

FIGURE 4

FIGURE 4. Experimental setup for online observation of tensor rotation.

Simulation Method

All simulations are based on the Electrostatic module and the Domain Ordinary Differential Equation (DODE) module in COMSOL Multiphysics.

First step: we simulate the spatiotemporal evolution of the permittivity due to electric field-induced self-assembly of fillers for liquid prepolymer composite components in the mold. Since the principal axis of the dielectric tensor wherever in this process are isotropic with the electric field, there is no need to consider the effect of the tensor, just enter the scalar function ${\epsilon }_{eff}\left(x,y,z,t\right)$ in the material properties of the liquid components. Then, we enter the time-domain differential form of ${\epsilon }_{eff}\left(x,y,z,t\right)$ in the DODE module, i.e., Eq. (11), with an initial value of ${\epsilon }_m$. Next, we study the time-dependent electric field and permittivity distribution. In particular, the introduction of the nojac () function avoids circular calls between the electric field and the permittivity in the same time step, reducing the memory required for the operation. Finally, we export the data of a given moment from COMSOL as text file (.txt). The data include the direction of the electric field inside the liquid component (e.g., the angle γ with the x-axis in two dimensions) and the scalar permittivity ${\epsilon }_{eff}$. The text files contain the coordinates of each grid node and the corresponding data.

Second step: we simulate the effect of the cured polymeric component on the operating electric field. In practical application, the mold material is replaced with other dielectrics such as air. Due to the curing reaction, the permittivity of the composite component drops. This effect is isotropic and a constant for the same matrix $\left(-\Delta \epsilon \right)$. We import the text files from the previous step into a new project, and define the dielectric tensor of the cured component based on the data therein in the material properties. Then, we transform the dielectric tensor in Eq. (12) by first considering the effect of the permittivity drop and then rotating the coordinate system (around z-axis), as shown in Eqs (15), (16), where $A_z$ is the transformation matrix. Finally, we study the stationary electric field in the insulation system.

$A_z=\left[\begin{array}{ccc}\cos \gamma & \sin \gamma & 0\\ -\sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right],(15)$

${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{\epsilon }}}^{\prime }=A_z^T\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{\epsilon }}{A}_z=\left[\begin{array}{ccc}{\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}{\cos }^2\gamma +{\epsilon }_{\mathrm{m}}{\sin }^2\gamma -\mathrm{\Delta }\epsilon & {\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}\sin \gamma \cos \gamma -{\epsilon }_{\mathrm{m}}\sin \gamma \cos \gamma & 0\\ {\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}\sin \gamma \cos \gamma -{\epsilon }_{\mathrm{m}}\sin \gamma \cos \gamma & {\epsilon }_{\mathrm{e}\mathrm{f}\mathrm{f}}{\sin }^2\gamma +{\epsilon }_{\mathrm{m}}{\cos }^2\gamma -\mathrm{\Delta }\epsilon & 0\\ 0& 0& {\epsilon }_{\mathrm{m}}-\mathrm{\Delta }\epsilon \end{array}\right],(16)$

Fabrication of Basin Insulator by the EIA Method

To investigate the improvement of the insulation performance by the meta-structured surface based on the dielectric tensor rotation, we prepared scaled-down basin insulators by the EIA method. In the EIA method, high-frequency AC assistant voltage is preferred because it both reduces Joule heating and suppresses filler electrophoresis (Liu et al., 2018). One-dimensional (1D) high permittivity fillers (except carbon) are preferred because of their high self-assembly efficiency and the large improvement in the effective permittivity of the composite after self-assembly (Shen et al., 2022). The low filler content is also preferred to reduce the effect on the dielectric loss and breakdown field strength of the composite insulation material.

The cross section of the basin insulator is shown in the figure. In the factory, liquid epoxy composites are poured into the mold with embedded electrodes and then cured to form basin insulators. In the EIA method, the material of the mold is replaced from metal to PTFE, and a 10 kHz AC voltage is applied during the liquid state through the embedded electrodes to induce filler self-assembly and construct the bulk dielectric gradient as well as the meta-structure surface, as shown in Figure 5A. Compared to the preparation process, the permittivity changes on both sides of the interface when used. On one side, $\Delta {\epsilon }_1$ is due to air replacing the mold material; on the other side, $\Delta {\epsilon }_2$ is due to epoxy resin curing.

FIGURE 5

FIGURE 5. Experimental setup for fabrication of basin insulators by EIA method: (A) cross-sectional schematic; (B) optical image of the setup.

The above process was simulated using COMSOL Multiphysics, as described in (Shen et al., 2021). Casting composition is E39/Al₂O₃/TiO₂w (mass ratio of 100:300:15), according to a previous experimental study (Shen et al., 2022), $a$ is set to 39.6, $b$ is set to 27.2, $\alpha$ is set to 2.16 × 10¹² sV²·m², in corresponding Eqs (8), (9). The applied voltage is set to 10 kV (f = 10 kHz) for 6 min $\Delta {\epsilon }_1$ is set to -1.2, and $\Delta {\epsilon }_2$ is set to -7.6 for the dielectric tensor.

The fabrication setup of the insulator is shown in Figure 5B. The TiO₂w/Al₂O₃/E39/MeHHPA (mass ratio of 15:300:100:66) was stirred for 10 min using a machine and then put into a vacuum oven to defoam three times, each time lasting 5 min. Added 2 phr of BDMA (relative to E39) to the mixture, stirred well, and then poured into the PTFE mold with electrodes from the pouring port; left it at room temperature 2 h, then applied 1.5 kV/10 kHz AC voltage on the inner electrode for 200 s and next to the voltage was reduced to 40 V for 6 h; after that, turned off the voltage and left the setup at room temperature for 16 h; finally, the mold was placed in an oven to cure (35°C for 2 h and 120°C for 2 h). Control samples without assisted voltage were prepared according to the same procedure.

Flashover Testing of Basin Insulator

According to IEC 60243–1:2013, we performed the short-time 50 Hz flashover test with a rate of increase of 500 V/s. The voltage waveform collected by the oscilloscope and the arc are used to determine whether a flashover has occurred. Eight replicate experiments were performed for each sample, with two flashover intervals of 5 min.

Results and Discussion

Figure 6A shows the typical image of the filler distribution at the initial moment. As the voltage action time increases, the fillers near the interface gradually self-assemble and the orientation axis rotates. We used FibrilTool, an ImageJ plug-in to quantify fibrillar structures in microscopy images (Boudaoud et al., 2014), including the anisotropy and average direction of the region of interest, as shown in Figures 6B,C. The anisotropy score follows the convention: 0 for no order and 1 for perfectly ordered (see Boudaoud et al. (2014) for detailed image processing algorithms).

FIGURE 6

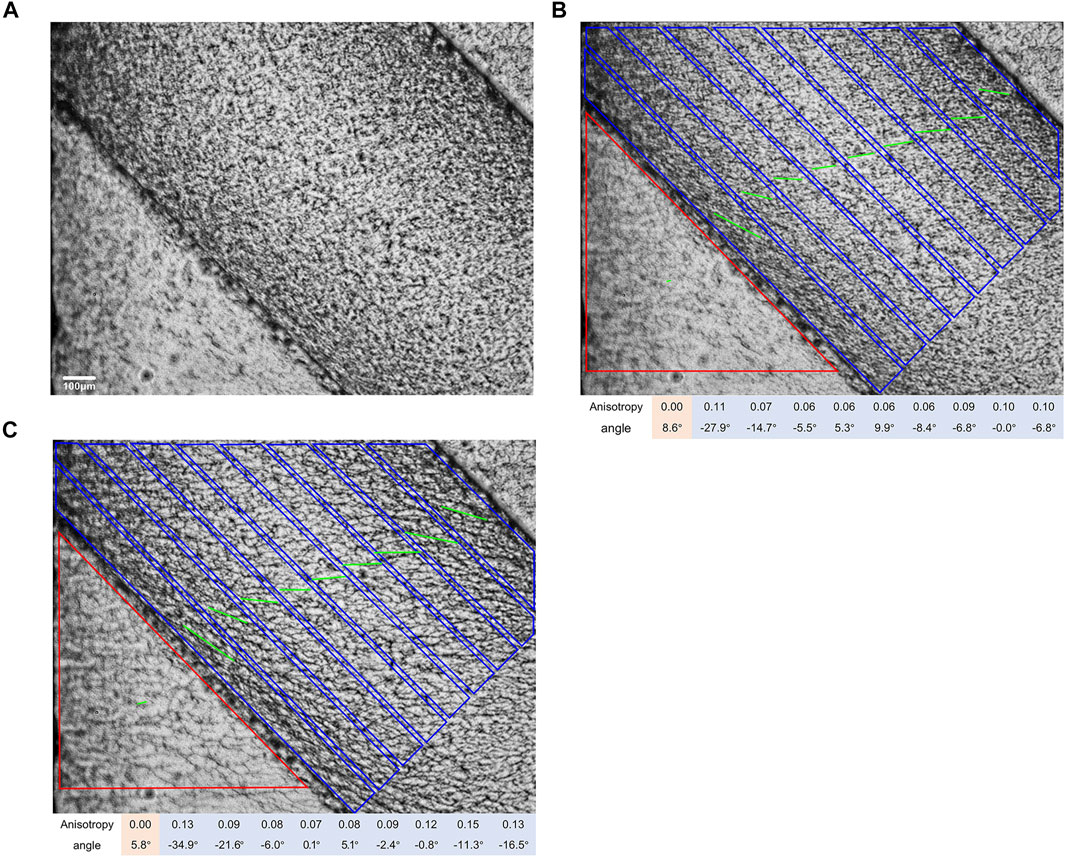
FIGURE 6. Optical image near the interface of the setup in Figure 4. (A) Initial time, (B) middle time, and (C) final time. (B,C) are output from FibrilTool: a line segment (green) is drawn, the angle of which represents the average orientation of the array and the length of which is proportional to the array anisotropy, the polygon represents the region of interest.

Figures 6B,C show the filler orientation and anisotropy at different distances from the interface, which is a visualization of the electric field lines. There is a little mixture on the BOPP on the left side of the interface that cannot be completely erased, which does not affect the permittivity of the BOPP, but helps us to determine the direction of incidence of the electric field. In Figure 6B, the incidence angle and the refraction angle between the interface are 36.4° and 72.9°, respectively. As time goes by, these two angles become 39.2° and 79.9°, respectively, as shown in Figure 6C.

When the electric field is along the tensor axis or the medium is isotropic, the electric field refraction at the interface satisfies

$\frac{{\epsilon }_1}{{\epsilon }_2}=\frac{\mathit{tan}\alpha }{\mathit{tan}\beta },(17)$

where $\alpha$ is the incidence angle in medium 1 $\left({\epsilon }_1\right)$, $\beta$ is the refraction angle in medium 2 $\left({\epsilon }_2\right)$. The permittivity of BOPP is 2.2; thus, it can be inferred that the local permittivities on the right side of the interface are 9.7 (Figure 6B) and 15.2 (Figure 6C), respectively. The change in electric field incidence direction indicates that the dielectric tensor rotation at the interface affects the electric field on the other side.

When ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{\epsilon }}}_2$ is kept constant (e.g., cured) and ${\epsilon }_1$ is changed, the two mediums do not match, the behavior of the electric field at the interface will be very interesting. Figures 7A,B show the direction of local filler orientation (angle to horizontal axis) and composite’s effective permittivity in the direction of local filler orientation of the basin insulator induced by the EIA method. Figure 7C shows the trend of the electric field lines and the refraction at the interface of the original basin insulator. Figure 7D shows the trend of the electric field lines and the refraction at the interface of the basin insulator induced by the EIA method. Compared to the original insulator, the electric field lines are limited at the interface after refraction and pass through a longer path inside the insulator (may share a higher voltage). This will result in decreased electric field strength at the triple junction point (electrode, gas, and dielectrics). Figure 7E shows the electric field distribution along the concave surface of the gas side. In particular, it reduces the tangential electric field (up to 25%) and has a little effect on the normal electric field.

FIGURE 7

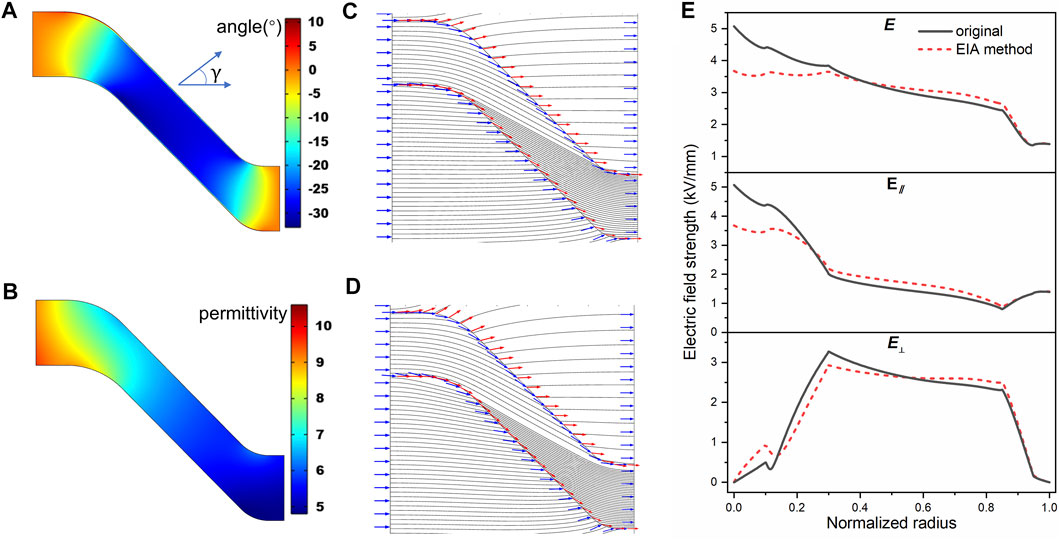
FIGURE 7. Results of simulation. (A) The direction of local filler orientation (angle to horizontal axis), (B) composite’s effective permittivity in the direction of local filler orientation, (C) electric field in the original insulator, (D) electric field in the insulator fabricated by the EIA method, and (E) electric field along the concave surface of the basin insulator.

Figure 8A presents the incidence and refraction angles along the concave interface for two kinds of basin insulators. The incidence and refraction angles of the insulator with super-structure surface are higher than those of homogenous insulators, i.e., the angle between the electric field and the surface decreases on the gas side (the blue area). The reduced permittivity of the interface dielectric tensor is calculated according to Eq. (17), as shown in Figure 8B. The closer to the inner electrode, the higher the reduced permittivity (up to 9). It exhibits negative and high values near the normalized radius of 0.2. In general, the negative permittivity is achieved by filling the metal (Wang et al., 2020). The negative reduced permittivity here may be generated due to the overall microstructure. The high permittivity means that the refractive electric field is approximately parallel to the interface, and the negative means that the normal electric field after refraction is reversed. By regulating the incidence and refraction angles of the electric field at the gas–solid interface, the meta-structure surface confines the electric field path and transfers the electric field stress from the gas to the insulator.

FIGURE 8

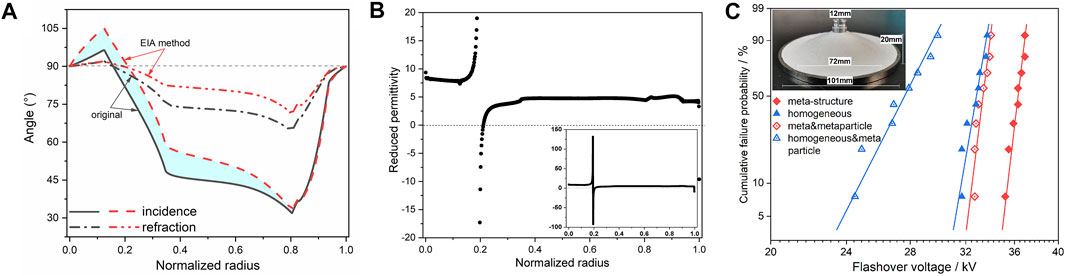
FIGURE 8. Effect of meta-structure surface on electric field and flashover voltage: (A) incidence and refraction angles (relative to the normal direction) along the concave interface, (B) reduced permittivity of the interface dielectric tensor, and (C) Weibull plot of the flashover voltage of the basin insulators.

Researchers employed the support vector regression (SVR) method based on mass experimental data to predict the flashover voltage, indicating that flashover voltage is affected not only by the maximum electric field but also by multiple features of the surface electric field (Liu et al., 2019). Flexible modulation of the electric field (including incidence angle) by the meta-structure surface, combined with the data-driven predicting models, can help reduce test work during acceptance testing, which could substantially reduce the economic cost. Improved insulation of the meta-structure surface induced by EIA method was experimentally verified by (Shen et al., 2022), as shown in Figure 8C, with a 12.7% increase in flashover voltage on clean surfaces and a 20.8% increase while there is a metal particle near the ground electrode.

Conclusion

The meta-structure surface of insulating components based on dielectric tensor rotation induced by the EIA method can achieve high or negative reduced permittivities to constrain the electric field paths and transfer the electric field stresses from the triple junction point. The meta-structure surface can also affect the angle between the electric field and surface on both sides of the interface, improving the surface insulation. With the help of the above analysis and the modeling of the EIA method, researchers can easily formulate a scheme to optimize the electric field of the specific insulating component (including filler selection, assistant voltage magnitude, and action time). Further developments of the proposed idea of the meta-structure surface would potentially transform the insulating components in high-voltage applications and expand the frontiers of dielectrics for the power industry.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

ZS: data curation and writing the original draft; YH: supervision; ZX: data curation and formal analysis; XW: investigation, methodology, and project administration; and ZJ: project administration and supervision. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52177021) and Shenzhen fundamental research and discipline layout project (No. JCYJ20180508152044145).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boudaoud, A., Burian, A., Borowska-Wykręt, D., Uyttewaal, M., Wrzalik, R., Kwiatkowska, D., et al. (2014). FibrilTool, an ImageJ Plug-In to Quantify Fibrillar Structures in Raw Microscopy Images. Nat. Protoc. 9 (2), 457–463. doi:10.1038/nprot.2014.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Brealey, R. H., Juneau, P. W., and Zlupko, J. E. (1982). Fabrication Design and Electrical Evaluation of Bulk-Graded Filled Polymer post Insulators, in 1982 IEEE International Conference on Electrical Insulation, Philadelphia, PA, USA, June 7-9, 1982. (Piscataway, New Jersey, United States: IEEE), 225–228. doi:10.1109/EIC.1982.7464475Available at: http://ieeexplore.ieee.org/document/7464475/

CrossRef Full Text | Google Scholar

Bruce, M., and Young, D. F. (2009). Fundamentals of Fluid Mechanics. New York: John Wiley & Sons.

Google Scholar

Cigré (2020). Field Grading in Electrical Insulation Systems. Paris: CIGRÉ.

Google Scholar

Cigré (2014). Optimized Gas-Insulated Systems by Advanced Insulation Techniques. Paris: CIGRÉ.

Google Scholar

Diaham, S., Valdez-Nava, Z., Le, T. T., Leveque, L., Laudebat, L., and Lebey, T. (2021). Field Grading Composites Tailored by Electrophoresis-Part 2: Permittivity Gradient in Non-uniform Electric Field. IEEE Trans. Dielect. Electr. Insul. 28 (2), 341–347. doi:10.1109/TDEI.2020.009031

CrossRef Full Text | Google Scholar

Diaham, S., Valdez-Nava, Z., Le, T. T., Leveque, L., Laudebat, L., and Lebey, T. (2021). Field Grading Composites Tailored by Electrophoresis-Part 3: Application to Power Electronics Modules Encapsulation. IEEE Trans. Dielect. Electr. Insul. 28 (2), 348–354. doi:10.1109/TDEI.2020.009032

CrossRef Full Text | Google Scholar

Diaham, S., Valdez-Nava, Z., Leveque, L., Le, T. T., Laudebat, L., and Lebey, T. (2021). Field Grading Composites Tailored by Electrophoresis - Part 1: Principle and Permittivity Gradient in Uniform Electric Field. IEEE Trans. Dielect. Electr. Insul. 28 (2), 333–340. doi:10.1109/TDEI.2020.009030

CrossRef Full Text | Google Scholar

Du, B. X., Wang, Z. H., Li, J., Liang, H. C., and Li, Z. H. (2020). Epoxy Insulator with Surface Graded-Permittivity by Magnetron Sputtering for Gas-Insulated Line. IEEE Trans. Dielect. Electr. Insul. 27 (1), 197–205. doi:10.1109/TDEI.2019.008385

CrossRef Full Text | Google Scholar

Ishiguro, J., Kurimoto, M., Kojima, H., Kato, K., Okubo, H., and Hayakawa, N. (2014). “Electric Field Control in Coaxial Disk-type Solid Insulator by Functionally Graded Materials (FGM).” in Proceedings of the 2014 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Des Moines, IA, USA, October 2014.

CrossRef Full Text | Google Scholar

Li, J., Liang, H., Chen, Y., and Du, B. (2020). Promising Functional Graded Materials for Compact Gaseous Insulated Switchgears/pipelines. High Voltage 5 (3), 231–240. doi:10.1049/hve.2019.0327

CrossRef Full Text | Google Scholar

Li, X.-R., Liu, Z., Li, W.-D., Sun, G.-Y., Xue, J.-Y., Wang, C., et al. (2019). 3D Printing Fabrication of Conductivity Non-uniform Insulator for Surface Flashover Mitigation. IEEE Trans. Dielect. Electr. Insul. 26 (4), 1172–1180. doi:10.1109/TDEI.2019.007938

CrossRef Full Text | Google Scholar

Liu, L., Chen, K., Xiang, N., and Ni, Z. (2018). Dielectrophoretic Manipulation of Nanomaterials: A Review. Electrophoresis 40 (6), 873–889. doi:10.1002/elps.201800342

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Li, X., Wen, T., Zhang, R., Wu, Z., Zhao, J., et al. (2019). Investigation on Surface Electric Field Distribution Features Related to Insulator Flashover in SF6 Gas. IEEE Trans. Dielect. Electr. Insul. 26 (5), 1588–1595. doi:10.1109/TDEI.2019.008194

CrossRef Full Text | Google Scholar

Luo, S., Shen, Y., Yu, S., Wan, Y., Liao, W.-H., Sun, R., et al. (2017). Construction of a 3D-BaTiO3 Network Leading to Significantly Enhanced Dielectric Permittivity and Energy Storage Density of Polymer Composites. Energy Environ. Sci. 10 (1), 137–144. doi:10.1039/c6ee03190k

CrossRef Full Text | Google Scholar

Hayakawa, N., Miyaji, Y., Kojima, H., and Kato, K. (2018). Simulation on Discharge Inception Voltage Improvement of GIS Spacer with Permittivity Graded Materials (ε-FGM) using Flexible Mixture Casting Method. IEEE Trans. Dielect. Electr. Insul. 25 (4), 1318–1323. doi:10.1109/TDEI.2018.007236

CrossRef Full Text | Google Scholar

Nardi, T., Mora, N., Rachidi, F., and Leterrier, Y. (2016). Graded-permittivity Polymer Nanocomposites as superior Dielectrics. Composites Sci. Tech. 129 (6), 1–9. doi:10.1016/j.compscitech.2016.04.010

CrossRef Full Text | Google Scholar

Shen, Z., Jia, Z., Hao, Y., Xin, Z., and Wang, X. (2022).A Fabrication Method for Adaptive Dielectric Gradient Insulating Components. High Voltage. In press. doi:10.48550/arXiv.2112.00896

CrossRef Full Text | Google Scholar

Shen, Z., Wang, X., Xin, Z., Zhang, T., Xu, C., and Jia, Z. (2021). Analytical Model for the Spatiotemporal Permittivity of uncured-Composite Devices in an AC Electric Field. J. Phys. D: Appl. Phys. 54 (15), 155302. doi:10.1088/1361-6463/abd9a7

CrossRef Full Text | Google Scholar

Shen, Z., Wang, X., Zhang, T., and Jia, Z. (2020). In Situ electric Field Driven Assembly to Construct Adaptive Graded Permittivity BaTiO3/epoxy Resin Composites for Improved Insulation Performance. Appl. Mater. Today 20, 100647. doi:10.1016/j.apmt.2020.100647

CrossRef Full Text | Google Scholar

Shen, Z., Xin, Z., Wang, X., Wei, X., and Jia, Z. (2021). Analytical Model for the Transient Permittivity of uncured TiO 2 Whisker/liquid Silicone Rubber Composites under an AC Electric Field. High Voltage 6 (3), 470–479. doi:10.1049/hve2.12060

CrossRef Full Text | Google Scholar

Singh, S. K., Aryaan, N., Shikder, M. R. A., Byles, B. W., Pomerantseva, E., and Subramanian, A. (2019). A 3D Nanoelectrokinetic Model for Predictive Assembly of Nanowire Arrays using Floating Electrode Dielectrophoresis. Nanotechnology 30 (2), 025301. doi:10.1088/1361-6528/aae9a4

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, J. (1995). Electromechanics of Particles. Cambridge: Cambridge Uniersity Press.

Google Scholar

Verrelli, D. I. (2014). Convenient Formulæ for the Drag on a Prolate Ellipsoid Moving along its axis of Symmetry Perpendicular to a Plane Surface. Int. J. Multiphase Flow 65, 138–142. doi:10.1016/j.ijmultiphaseflow.2014.05.010

CrossRef Full Text | Google Scholar

Wang, Z., Sun, K., Wu, H., Xie, P., Wang, Z., Li, X., et al. (2020). Compressible Sliver Nanowires/polyurethane Sponge Metacomposites with Weakly Negative Permittivity Controlled by Elastic Deformation. J. Mater. Sci. 55 (32), 15481–15492. doi:10.1007/s10853-020-05126-z

CrossRef Full Text | Google Scholar