Static Behavior of Circular Section CFRP Concrete-Filled Steel Tubes Under Compressive–Torsional Load

Introduction

In recent years, with the reduction of cost, carbon fiber has also been widely used in the construction engineering industry (Chen et al., 2018). As a derivative of carbon fiber, carbon fiber polymer reinforcement (CFRP) is often used in the reinforcement of building structures (Liang et al., 2021). Concrete-filled steel tubes (CFSTs) have the advantages of high bearing capacity and convenient construction. At present, it is widely used in the field of construction engineering (Hu and Han, 2016; Ye et al., 2016), but its own defects cannot be ignored, especially local buckling under load and corrosion in the marine environment (Hua et al., 2015). Based on this, a new composite structure of CFRP concrete-filled steel tubes is proposed; it fully combines the advantages of concrete-filled steel tubes and CFRP so that compared with the traditional CFST structure, it has the advantages of delaying structural buckling and improving the synergy between concrete and steel tubes (Li et al., 2018; Zhang et al., 2020).

Nie et al. (2013) conducted a study on the flexural–shear–torsion coupling bearing capacity of concrete-filled steel tubular short columns and concluded that the failure mechanism of concrete-filled steel tubular short columns was significantly affected by the bending moment–torque ratio. Zhang et al. (2019) carried out axial compression test research on eight concrete-filled steel tubular short columns strengthened with CFRP with spherical crown void defects. Chen et al. (2018) carried out the axial compression test of square concrete-filled steel tubular short columns after CFRP restraint heating. Based on the regression of test data, a simplified formula for the ultimate strength of concrete-filled square steel tubular short columns after CFRP confined heating is proposed. Tang et al. (2020) studied the axial compressive bearing capacity of CFRP concrete-filled steel tubes, with a total of 24 short columns. Sundarraja and Ganesh Prabhu (2011) studied the strengthening effect of CFRP on concrete-filled steel tubular flexural members. Romero et al. (2020) carried out experimental research and finite element theoretical analysis on the fire performance of concrete-filled steel tubular members. The results show that the steel tube and CFRP can work together, and the deformation of the component approximately conforms to the plane section assumption. Han and Zhong (2004) deduced the axial force–torque correlation equation of concrete-filled steel tubular members, described the moment torque correlation equation, and analyzed the whole process of such specimens. Nie et al. (2014a) conducted an experimental study on the torsional hysteretic behavior of concrete-filled steel tubes with circular sections and rectangular sections. The results show that the hysteretic curve is very full, the unloading stiffness and the initial loading stiffness of the specimen are almost the same, and the specimen shows good energy dissipation performance; the torsion resistance of the specimen with too large axial compression ratio is weakened due to too serious deformation. Zhou et al. (2017) carried out the pure torsional hysteretic behavior test of hollow sandwich concrete-filled steel tubular specimens with section form and void ratio as the main parameters. The experimental results show that the initial elastic stiffness is close to the unloading stiffness, the specimens show good energy dissipation capacity, and the hysteretic behavior of circular section hollow sandwich concrete-filled steel tubes is better than that of square section (Nie, 2005; Nie et al., 2014b). Sundarraja and Ganesh (Park, 2010) found that the steel ratio and the number of CFRP layers have great influence on the bearing capacity of square CFRP-CFST specimens and proposed a finite element simulation method to reproduce the mechanical behavior of square CFRP-CFST effectively. Tao et al. (2007a; Sundarraja and Ganesh, 2011) indicated that the bearing capacity of CFRP-CFST specimens was significantly reduced after the fire, but the fire resistance ability of concrete-filled CFRP-steel tubular specimens was better than that of ordinary concrete-filled steel tubular specimens. Wang and Shao (Tao et al., 2007b) studied the influence of various materials on the bearing capacity of square concrete-filled CFRP-steel tubes under axial compression.

However, most of these were mainly focused on the compressive and flexural performances of the composite members. In practice, CF-CFRP-ST often also bears coupling loads, such as fans and other building structures. In view of this, eight specimens were designed. During the loading of the test, the effects of the axial compression ratio and a number of longitudinal CFRP layers were studied under compression torsion load. Based on experimental research, a finite element method for establishing CF-CFRP-ST compression–torsion member is proposed by finite element simulation. The influence of main parameters on performance is studied by this method so as to provide a bearing capacity correlation equation for engineering practice.

Experimental Study of CF-CFRP-ST Under Compression–Torsion Load

Design of Specimens and Performance of Material

Design of Specimens

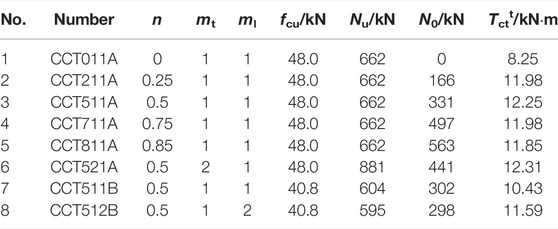
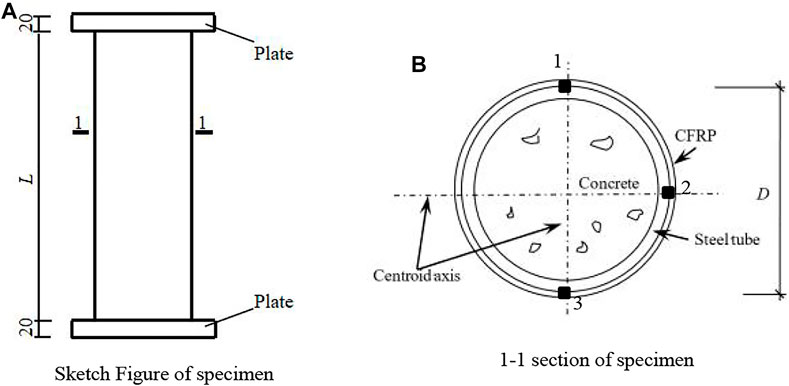
A total of eight compression-torsional static performance tests of circular concrete-filled CFRP steel tubes were designed, and the main parameters include n, m_t, m_l, and f_cu. L of all specimens is 342 mm, the wall thickness (t_s) is 1.6 mm, and D_s is 114 mm. N_u is the axial compression bearing capacity of the C-CF-CFRP-ST specimen. N₀ is the axial force under specimens in the test. T_ct^t is the torque applied during the test. All parameters are shown in Table 1. A schematic diagram of the C-CF-CFRP-ST specimen is shown in Figure 1.

TABLE 1

TABLE 1. Specific indexes of specimens.

FIGURE 1

FIGURE 1. Schematic diagram of the C-CF-CFRP-ST specimen.

Performance of Material

The measured material properties of steel tubes are shown in Table 2, and the performance of concrete in the test is shown in Table 3.

TABLE 2

TABLE 2. Measured material properties of the steel tube.

TABLE 3

TABLE 3. Performance of concrete in test.

Carbon fiber fabric is a unidirectional fabric woven by Toray T700 12 K carbon fiber in Japan. The thickness of the single layer and the weight of CFRP are 0.111 mm and 200 g/m³, respectively. The elongation at break of CFRP is 2.1%, and the tensile strength of monofilament is 4.9 GPA. ε_cftr and ε_cflr are the fracture strains of CFRP in the transverse and longitudinal directions, respectively, Mechanical property of CFRP is shown in Table 4.

TABLE 4

TABLE 4. Mechanical property of CFRP.

Loading and Measurement

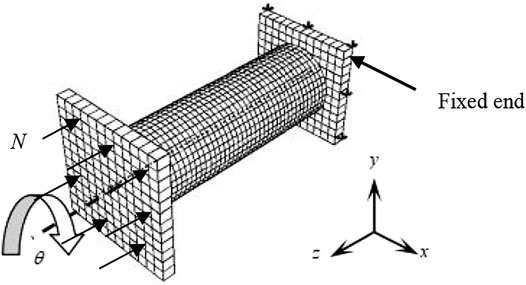
The loading equipment of CFRP concrete-filled steel tubes under compression–torsion specimens is shown in Figure 2. The end plate fixing device is connected at one end to avoid the relative displacement between the end plate and the reaction wall or the force arm, and the force arm is connected at the other end to apply torque. In addition, a jack is added to apply axial force. The graded loading system is adopted in the test. Within the elastic range, the loading amount of each level is 1/10 of the estimated bearing capacity, and the next level of loading is carried out after holding the load for 2 min. When the torque reaches about 60% of the estimated bearing capacity, the continuous slow loading mode shall be adopted until the jack range is reached, and the test shall be stopped. The estimation method of bearing capacity is as follows: according to the principle of equal strength, all CFRPs are quantified as steel tubes, and then the bearing capacity is calculated according to the relevant calculation formula (Hou et al., 2016) of torsional bearing capacity of concrete-filled steel tubes. Figure 3 shows all compression torsion test pieces before loading.

FIGURE 2

FIGURE 2. Test loading device.

FIGURE 3

FIGURE 3. All specimens before the test.

Experimental Phenomenon

Partial circular compression torsion specimen after loading is shown in Figure 4. At the beginning of loading, the torque and rotation angle are linear, and the appearance of the specimen has no obvious change. As the torque increases, a slight adhesive cracking sound can be heard, and the axial compression ratio has a significant impact on the test phenomenon. For the specimen with n = 0, CFRP breaks continuously with the continuous increase of torque. For specimens with n > 0, CFRP begins to fracture when the torque reaches about 70% of the peak torque. When the torque reaches about 80–90% of the peak torque, local convex bending appears in the middle section and its nearby position of the specimen. With the continuous increase of torque, a large number of CFRPs in the middle section fracture. After reaching the peak torque, the specimens continue to deform and the bearing capacity decreases. During the loading process, the longitudinal CFRP does not break.

FIGURE 4

FIGURE 4. Partial circular compression torsion specimen after loading. (A–F) Different axial compression ratio for those specimen.

When the steel tube loaded with the test piece is cut open, it can be seen that when the axial compression ratio is small, a large number of inclined cracks in the direction of 30°–45° appear on the surface of the concrete [Figure 5A]. When the axial compression ratio is large, the cracks are more obvious and the concrete is crushed. Since CFRP steel tubes provide good constraints on concrete, the convex of concrete is consistent with that of steel tubes [Figure 5B], and the concrete shows good plastic filling performance.

FIGURE 5

FIGURE 5. Failure characteristics of concrete. (A,B) Crack location of concrete.

Experimental Results

T–θ Curves

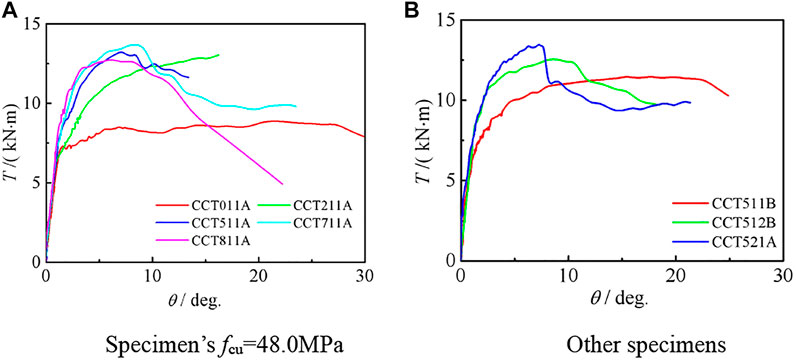
Figure 6 shows the T–θ curve of the circular compression torsion specimen. It can be seen that at the initial stage of loading, the curve is in the elastic stage, and the torque has a linear relationship with the rotation angle. When the angle is about 8°, the growth rate of the angle exceeds the torque, and the curve enters the strengthening stage. As loading continues, the axial compression ratio has a significant impact on the curve. When n = 0, there is no steep drop section in the curve. When 0.25 ≤ n ≤ 0.75, the peak torque increases with the increase of the axial compression ratio, and in the falling section, the speed of torque increases with the increase of the axial compression ratio; when n = 0.85, the peak torque decreases compared with n = 0.75, and the torque decreases faster in the descending section. Since concrete is the main component of the specimen, improving the strength of concrete can significantly improve the bearing capacity of the specimen.

FIGURE 6

FIGURE 6. T–θ curve of the C-CF-CFRP-ST specimen. (A,B) Different specimens.

τ–γ Curves

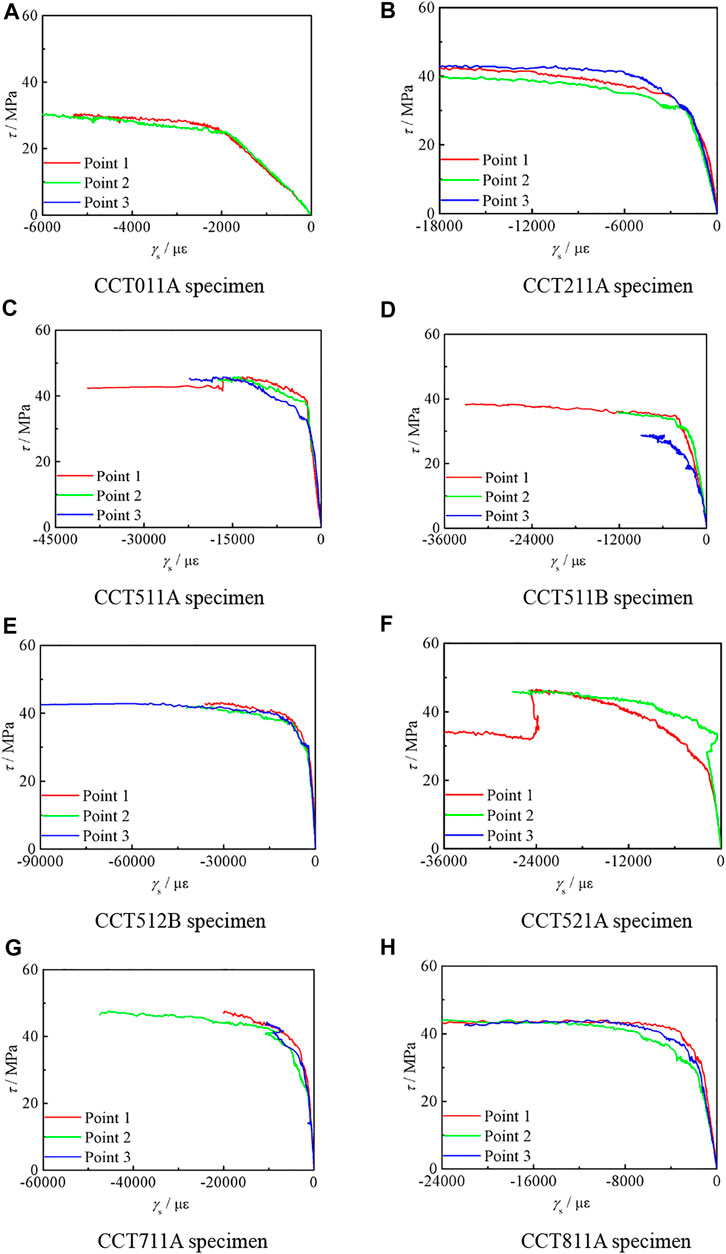
Figure 7 shows the τ–γ curve of circular compression torsion specimens, where γ = 2ε_s45−(ε_st+ε_sl).

FIGURE 7

FIGURE 7. τ–γ curve of the C-CF-CFRP-ST specimen. (A–H) Strain gauges at different locations.

It can be seen that at the initial stage of loading, the curve develops linearly, belonging to the elastic stage. With the increase of torque, the shear stress increases, and the shear strain increases slowly. It is indicated that the shear capacity of the specimen is good. When the torque reaches about 70–80% of the peak torque, the shear strain continues to increase and the torque remains basically unchanged. In the later stage of loading, the curve has no descending section and gradually tends to be gentle. The shear stress increases slightly, and the shear strain increases significantly.

Cooperation Between Steel Tube and CFRP

Figures 8–10,, are the T-ε_t, T-ε_l, and T-ε₄₅ curves of compression torsion specimens, respectively. It can be seen that ε_st and ε_cft are basically the same, and steel pipe and CFRP can work together. Also, ε_s45 is always negative and ε_st is always positive. For ε_sl, when n ≤ 0.25, ε_sl is positive. When n ≥ 0.75, ε_sl is negative. When n = 0.5, ε_sl is either positive or negative.

FIGURE 8

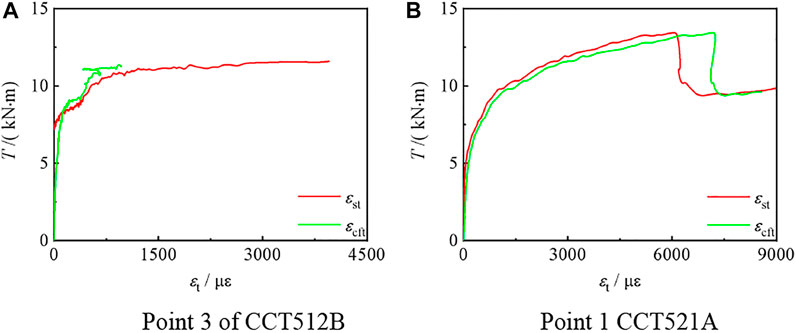
FIGURE 8. T–ε_t curve of the partial C-CF-CFRP-ST specimen. (A) Transverse strain of steel tube and (B) CFRP.

FIGURE 9

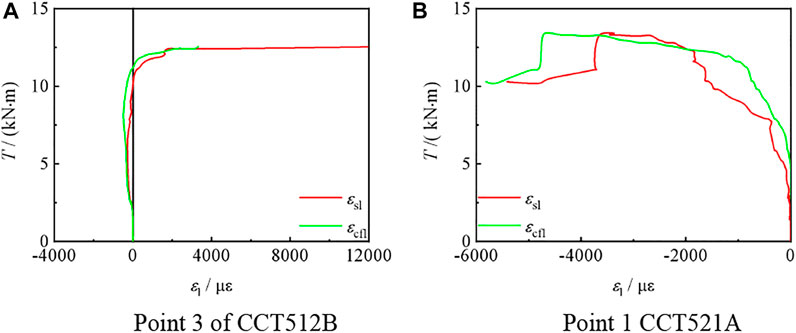
FIGURE 9. T–ε_l curve of the partial C-CF-CFRP-ST specimen. (A) Longitudinal strain of steel tube and (B) CFRP.

FIGURE 10

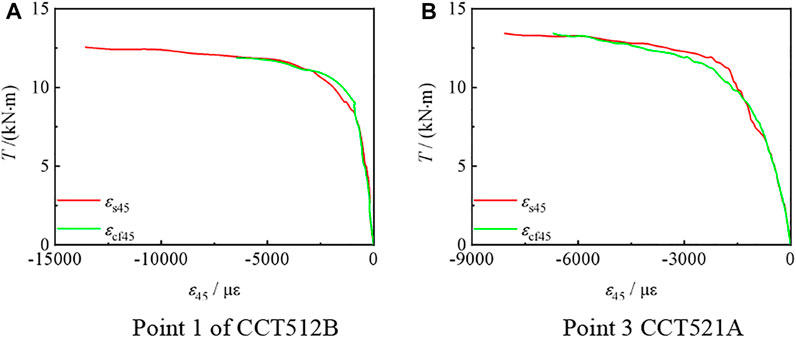
FIGURE 10. T–ε₄₅ curve of the partial C-CF-CFRP-ST specimen. (A) 45° strain of steel tube and (B) CFRP.

Finite Element Study of CF-CFRP-ST Under Compression–Torsion Load

Stress–Strain Relationship of Materials

In the process of using ABAQUS finite element modeling, the steel tube adopts the mixed hardening model provided by ABAQUS software and concrete adopts the plastic damage model provided by ABAQUS finite element software. To further analyze the mechanical behavior of C-CF-CFRP-ST specimens under eccentric load comprehensively, finite element models are established and analyzed in this study. The details of the stress–strain relationships of the steel are used according to the constitutive model suggested by Wang et al. (Wang and Shao, 2014).

The confinement of transverse CFRP is quantified by the confinement factor of transverse CFRP (ξ_cf) (Wang et al., 2015). The reinforcement efficiency of longitudinal CFRP is defined as a strengthening coefficient (η) (Tao et al., 2008; Wang et al., 2017). All influence factors are given from Eqs 1–3.

$\mathit{\eta =}\frac{A_{cfl}{f}_{cfl}}{A_s{f}_y},(1)$

$f_{\mathrm{cft}}=E_{\mathrm{cf}}{\epsilon }_{\mathrm{cftr}},(2)$

$f_{\mathrm{cfl}}=E_{\mathrm{cf}}{\epsilon }_{\mathrm{cflr}},(3)$

where A_cft and f_cft are the cross-sectional area and the ultimate tensile strength of the transverse CFRP, respectively. A_cfl and f_cfl are the cross-sectional area and the ultimate tensile strength of the longitudinal CFRP, respectively (.

When the strain of transverse CFRP reaches its fracture strain ε_cftr (5500 με) or the strain of longitudinal CFRP reaches its fracture strain ε_cflr (7000 με), the transverse restraint effect or longitudinal reinforcement effect on the steel pipe will be lost.

Element Selection and Boundary Conditions

In the finite element simulation, the three-dimensional solid element C3D8R is used to simulate steel pipe, concrete, and end plate, and the M3D4R element is used to simulate CFRP. The full model calculation is adopted, one end adopts completely fixed boundary conditions, and the other end applies rotation angle on the reference point. One side is used as the fixed end to restrict the displacement and rotation angle in x, y, and z directions; as the loading end, first apply the same axial force N on the end plate as in the test, and N is always constant during the whole loading process. Then set a reference point in the center of the end plate and connect it with the loading end plate, and then apply a rotation angle θ on the reference point. Figure 11 is Boundary conditions for finite element simulation of specimens. Figure 12 is Grid generation of all materials.

FIGURE 11

FIGURE 11. Boundary conditions for finite element simulation of specimens.

FIGURE 12

FIGURE 12. Grid generation of all materials. (A) Grid generation of concrete and steel tube(B) Grid generation of CFRP.

Comparison Between Simulation Results and Test Results

Figure 13 shows the comparison between the simulation results of the T–θ curve of the circular compression–torsion specimen and the test results. It can be seen that the simulation results are basically consistent with the experimental results.

FIGURE 13

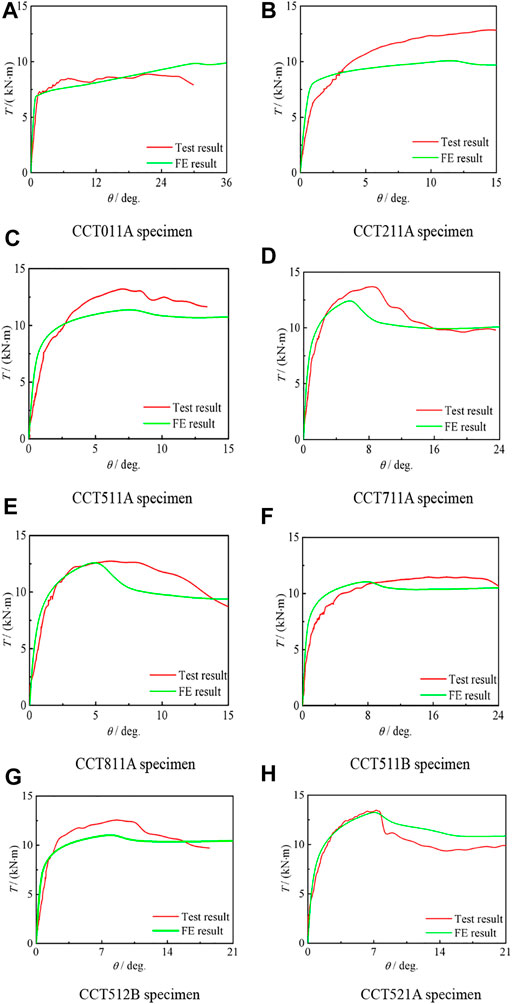
FIGURE 13. Comparison between T–θ curve simulation results and test results of compression torsion specimens. (A–H)Different curves between Test and FE result.

Figure 14 shows the comparison between the simulation results of the τ–γ curve of the circular compression–torsion specimen and the test results. It can be seen that the simulation results are basically consistent with the experimental results.

FIGURE 14

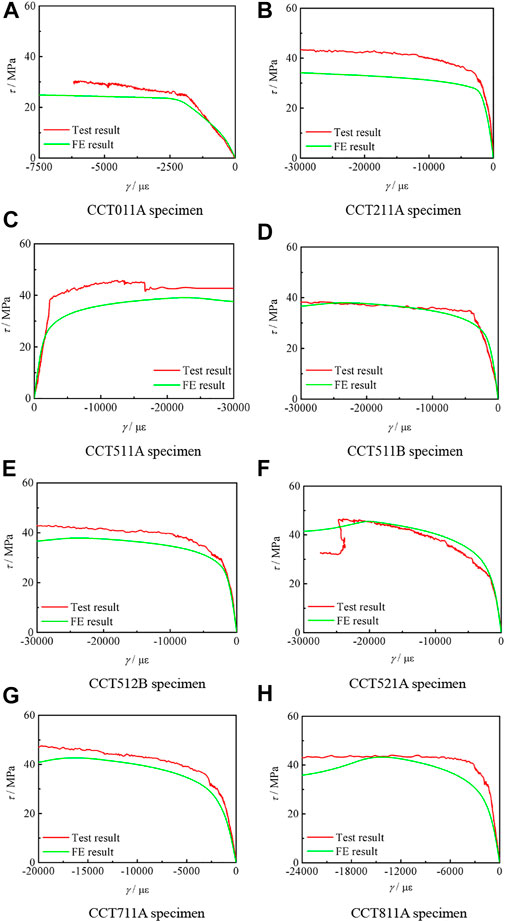
FIGURE 14. Comparison between τ–γ curve simulation results and test results of compression torsion specimens. (A–H) Different curves between Test and FE result.

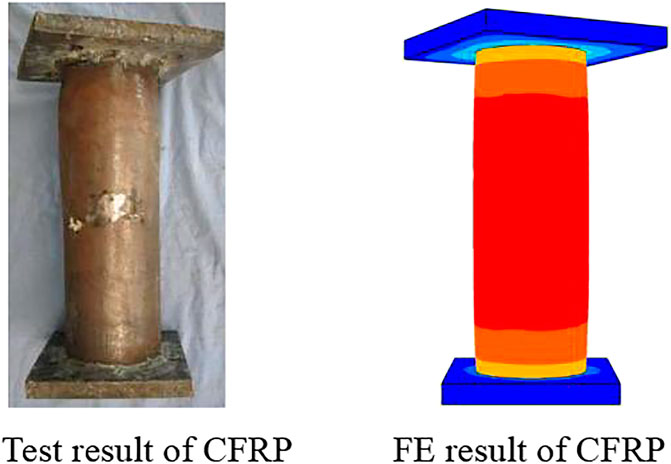
Figure 15 shows the failure mode of CFRP. It can be seen that the fracture of transverse CFRP in the test results and simulation results are basically the same.

FIGURE 15

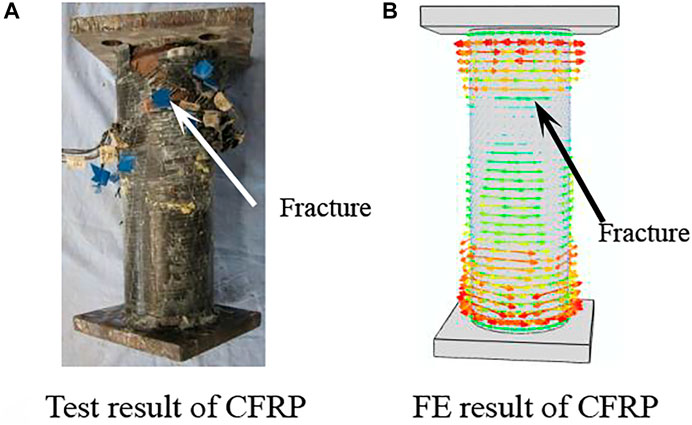
FIGURE 15. Failure mode of CFRP of the compression torsion specimen. (A) Test results of CFRP, (B) FE results of CFRP.

Figure 16 shows the failure mode of the steel tube. It can be seen that the specimen is twisted, and the stress is mainly concentrated in the middle.

FIGURE 16

FIGURE 16. Failure mode of the steel tube of the compression torsion specimen.

Figure 17 shows the failure mode of concrete. The results of finite element simulation show that the crack mainly extends from the middle of the specimen, which is basically consistent with the test results. In conclusion, the failure modes of CFRP, steel tube, and concrete are compared, respectively, and the finite element is basically consistent with the test results.

FIGURE 17

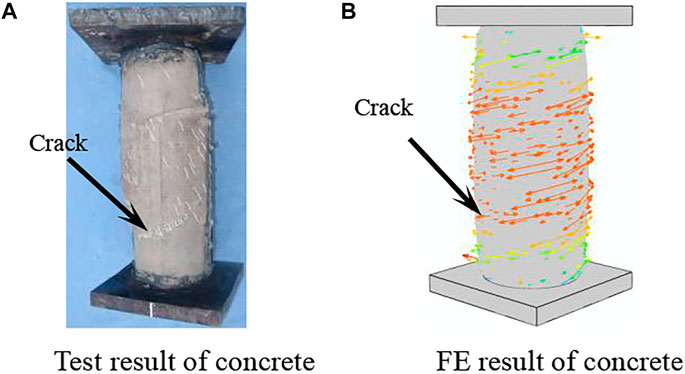
FIGURE 17. Failure mode of concrete of the compression torsion specimen. (A) Test results of concrete, (B) FE results of concrete.

Analysis of the Whole Process of Stress

Typical Torque Angle Curve

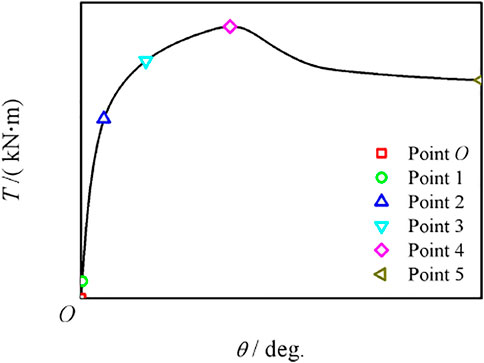
Figure 18 shows the typical T–θ curve of CFRP concrete-filled steel tubular compression torsion members. The curve is divided into three stages and five feature points are selected. In the elastic stage (point O ∼ point 2), the torque is basically linear with the rotation angle. Due to the action of axial force, point 1 corresponds to the steel entering the yield state, and point 2 corresponds to the cracks in the concrete; in the elastic–plastic stage (2–3 points), with the gradual increase of torque, the steel pipe and concrete are in a two-way shear state and produce an interaction force, and the three points correspond to the transverse CFRP fracture; in the plastic strengthening stage (3–5 points), the cracks in the concrete continue to develop, and some of the concrete quit work. However, due to the constraint of the outer pipe on the concrete, the bearing capacity continues to increase, and the torsional bearing capacity is reached at four points. After four points, the curve enters the descending section first, and the bearing capacity gradually decreases. In the later stage of loading, the bearing capacity increases slightly, and the corresponding rotation angle at five points reaches 15°. During the loading process, the longitudinal CFRP was not fractured.

FIGURE 18

FIGURE 18. Typical T–θ curve of C-CF-CFRP-ST compression torsion members.

Through three stages are Elastic stage, elastoplastic stage and plastic stage and five characteristic points to analyze its working mechanism in the whole stress process. Calculation parameters include L = 342 mm, D_s = 114 mm, t_s = 1.6 mm, f_cu = 48 mpa, E_c = 4700 f '_c^0.5(f '_c = 42 MPa), f_y = 290.8 MPa, ξ_s = 0.530, ξ_cf = 0.162, and n = 0.75.

Interaction Between Steel Tube and Concrete

Figure 19 shows the distribution of interaction force between the steel tube and concrete in compression torsion member. It can be seen that at point O, the member deformation is small. With the gradual increase of member deformation, the interaction force of members increases. During the loading process, the interaction force of members is evenly distributed on the concrete surface. Due to the action of axial force, the interaction force between the end plate and concrete end is greater than that between the steel tube and concrete.

FIGURE 19

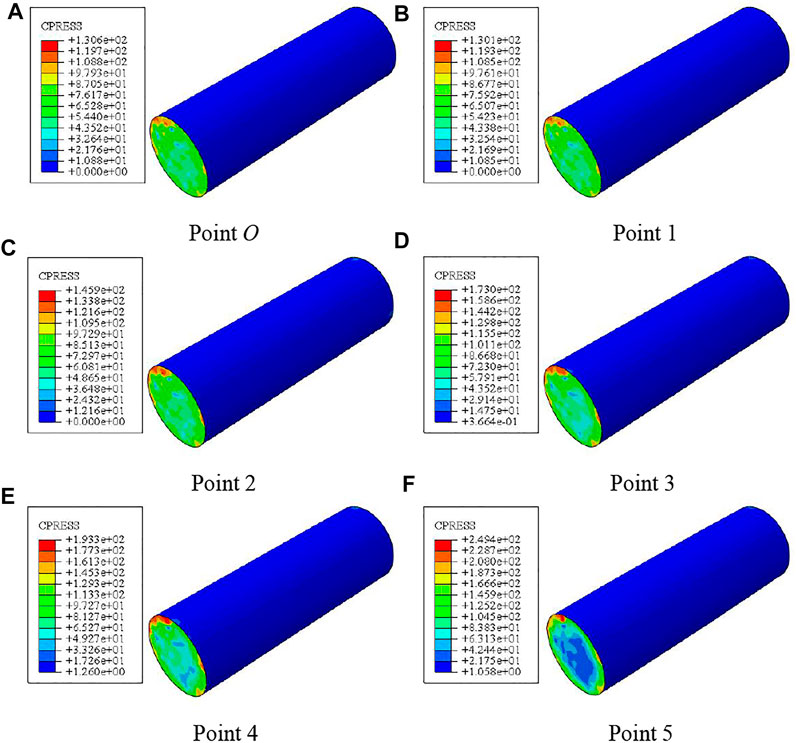
FIGURE 19. Distribution of interaction force between the steel tube and concrete. (A–F) Crack of Distribution of interaction force between the steel tube and concrete at different 0–5 points.

Shear Stress Distribution of Concrete

Figure 20 shows the shear stress distribution of the section concrete in the compression torsion member. It can be seen that the shear stress of the member first increases and then decreases. At point four, the shear stress reaches its peak, about 26 MPa. During the loading process, the shear stress is roughly antisymmetric distribution on the section, and the stress contour always follows “U”-shaped distribution.

FIGURE 20

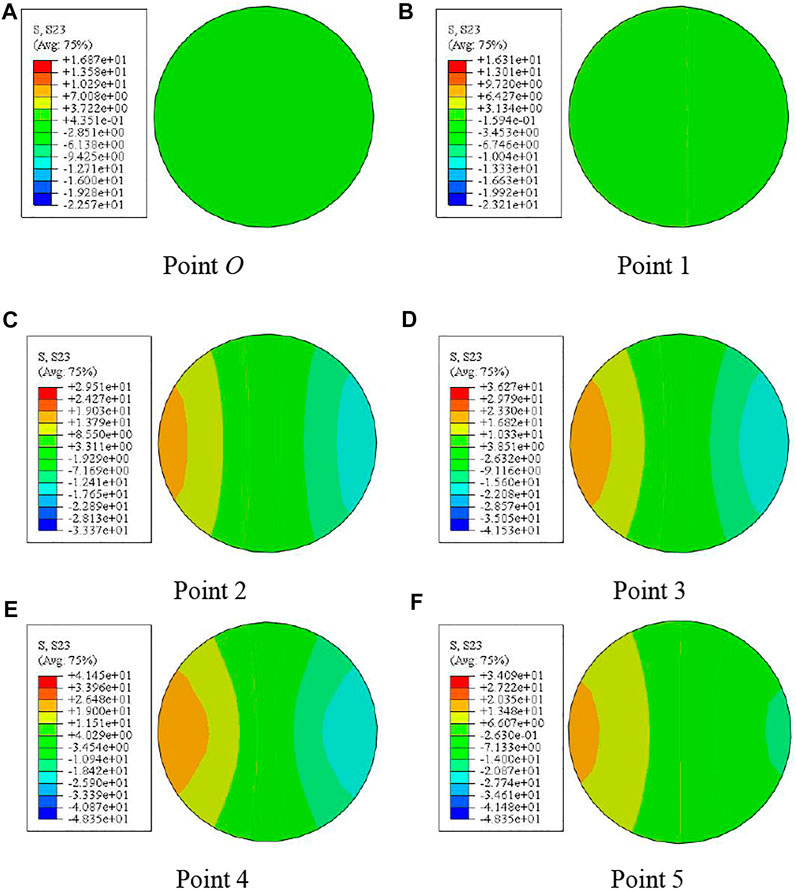
FIGURE 20. Shear stress distribution of the section concrete. (A–F) crack of Shear stress distribution of the section concrete at different 0–5 points.

Mises Stress of Steel Tube

Figure 21 shows the Mises stress distribution of the compression torsion member steel tube. In the loading process, the steel tube quickly reaches the yield strength; that is, at pointone, the Mises stress of the steel pipe is about 291 MPa, and the steel enters the yield state. Under the action of torque, the Mises stress of the section in the steel changes little.

FIGURE 21

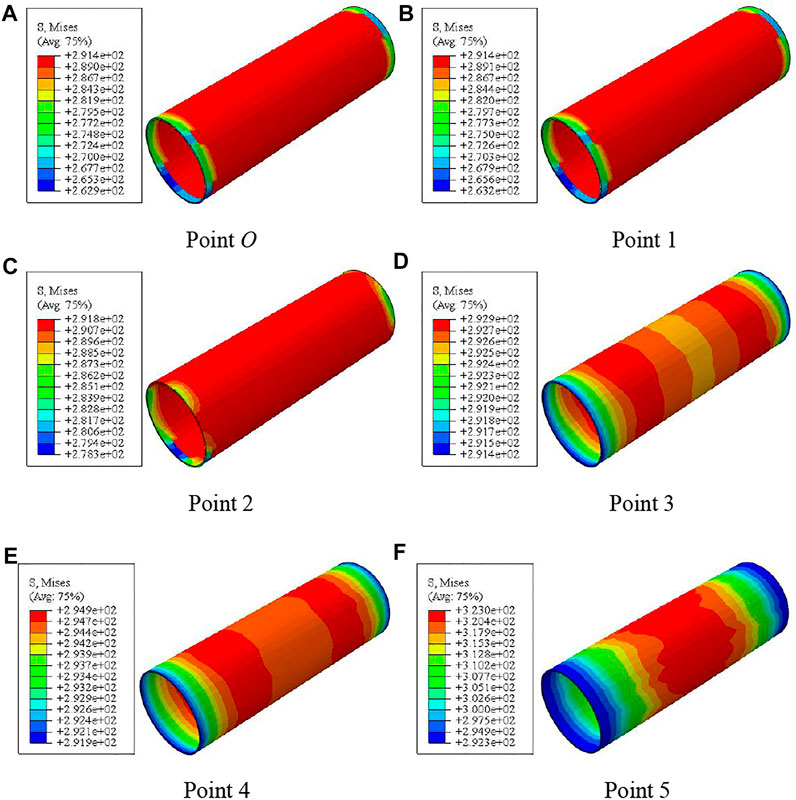
FIGURE 21. Mises distribution of the steel tube. (A–F) Mises distribution of the steel tube at different 0–5 points.

Stress of CFRP

Figure 22 shows the stress distribution of transverse CFRP of compression torsion members. It can be seen that at the initial stage of loading, the stress growth rate of transverse CFRP is slow. In the process of loading to point two, the stress of transverse CFRP increases gradually; at point three, the transverse CFRP stress of the member is about 1265 MPa and the corresponding strain is about 5500 με, at this time, the transverse CFRP is broken. After loading to point four, the fracture area of transverse CFRP gradually increases from the middle section to the end.

FIGURE 22

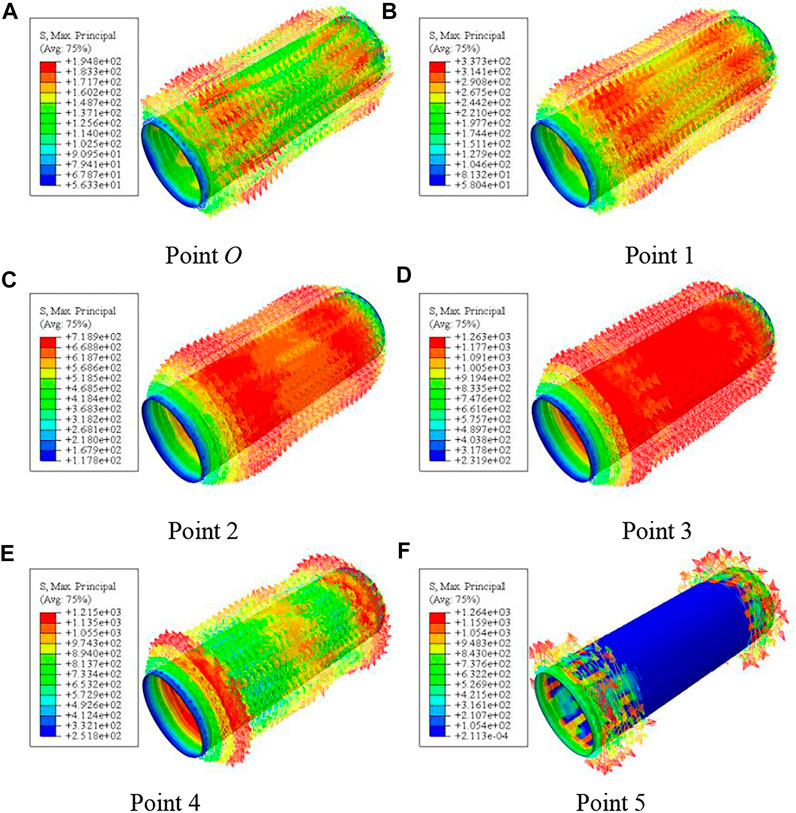
FIGURE 22. Stress distribution of transverse CFRP. (A–F) Stress distribution of transverse CFRP at different 0–5 points.

Parameter Analysis

The possible parameters affecting the Tθ curve of compression torsion members include the number of transverse CFRP layers, material strength, steel ratio, and axial compression ratio. Therefore, this is a typical example to analyze the influence of the above parameters on the T–θ curve of CFRP concrete-filled steel tubular compression torsion members.

Influence of Transverse CFRP

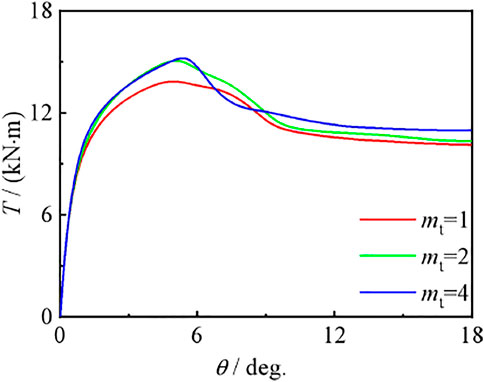
Figure 23 shows the effect of the number of transverse CFRP layers on the torque angle (T–θ) curve of compression torsion members. It can be seen that with the increase of m_t, the bearing capacity of members increases gradually, and the stiffness in the curve elastic stage has no obvious change. The main reason for this phenomenon is that the carbon fiber cloth has the restraint ability on the specimen, so the change in the number of layers will affect the bearing capacity.

FIGURE 23

FIGURE 23. m_t effect on the T–θ curve of the compression torsion member.

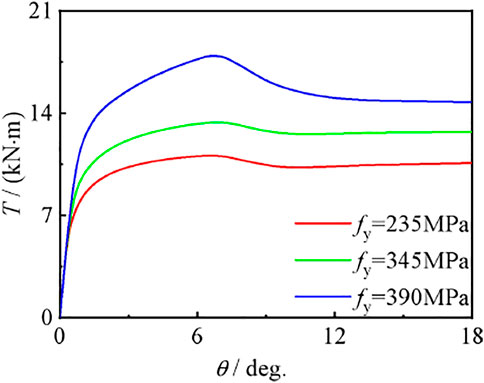
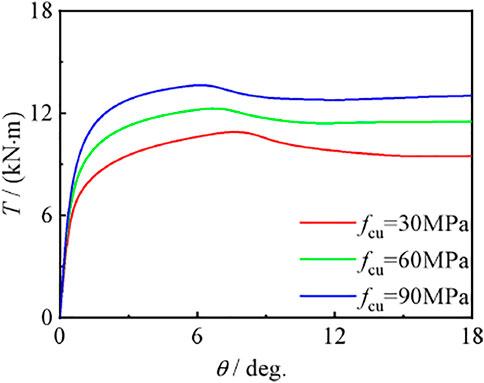
Effect of Material Strength

Figures 24, 25 show the effects of steel yield strength and concrete strength on the torque angle (T–θ) curve of compression torsion members, respectively. It can be seen that with the improvement of material strength, the bearing capacity of members increases, and the curve shape and initial stiffness do not change significantly, but the bearing capacity is improved, and the role of steel is more obvious. Because steel tubes and concrete are the main components of CF-CFRP-ST, the change in their strength plays a decisive role in the bearing capacity of specimens. Macroscopically, the bearing capacity of members is proportional to f_y and f_cu.

FIGURE 24

FIGURE 24. f_y effect on the T–θ curve of the compression torsion member.

FIGURE 25

FIGURE 25. f_cu effect on the T–θ curve of the compression torsion member.

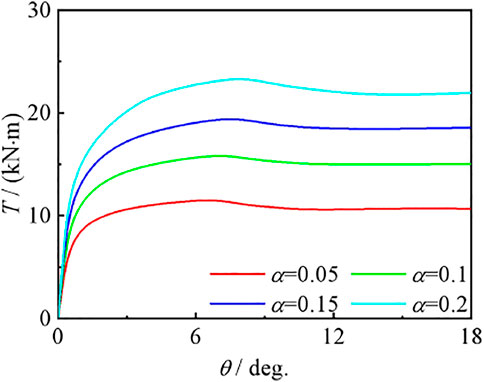
Effect of Steel Ratio

Figure 26 shows the effect of steel content on the torque angle (T–θ) curve of compression torsion members. It can be seen that with the improvement of α, the bearing capacity of the member is significantly improved, and the stiffness in the curve elastic stage is also significantly increased.

FIGURE 26

FIGURE 26. α effect on the T–θ curve of the compression torsion member.

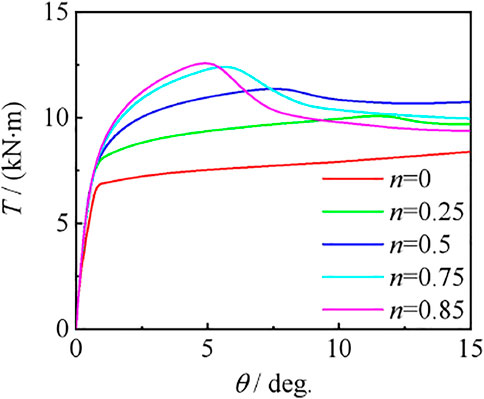
Influence of Axial Compression Ratio

Figure 27 shows the effect of the axial compression ratio on the torque angle (T–θ) curve of compression torsion members. It can be seen that the axial compression ratio has a significant impact on the shape and bearing capacity of the curve, but has no significant impact on the stiffness of the initial stage of the curve. The reason is that the torque moment increases with the increase of n so that the load borne by the specimen increases significantly, the energy loss of the member increases, and the macroscopic performance is that the bearing capacity decreases.

FIGURE 27

FIGURE 27. n effect on the T–θ curve of the compression torsion member.

Calculation Equation of Bearing Capacity of CF-CFRP-ST Under Compression–Torsion Load

Strength Definition

According to the whole process analysis results of the CF-CFRP-ST compression torsion specimen, through a large number of calculations and the analysis of T–γ relationship curve, it is defined that when the shear strain reaches Eq. 4, the specimen reaches its torsional bearing capacity:

$\gamma =9498n-15000.(4)$

Calculation Equation of Bearing Capacity

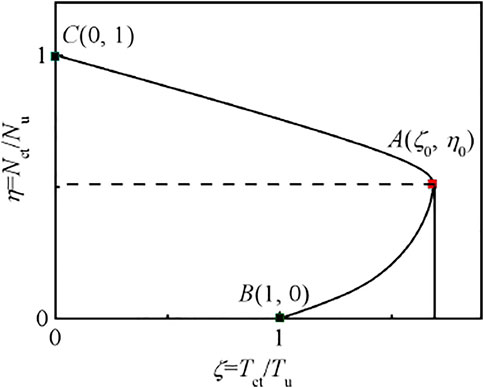
Figure 28 shows the typical N_ct/N_u-T_ct/T_u relationship curve of CF-CFRP-ST compression torsion members. A large number of parameters are calculated for the T–θ curve, and the calculation parameters (scope of application) are as follows: f_y = 235–390MPa, f_cu = 30–90MPa, α = 0.05–0.2, ξ_s = 0.238–0.951, and ξ_cf = 0.162–0.649.

FIGURE 28

FIGURE 28. Typical N_ct/N_u-T_ct/T_u curve of specimens.

The results of parameter calculation show that ζ₀ and η₀ of equilibrium point A can be approximately expressed as a function of the total constraint coefficient ξ. Through the regression analysis of the calculation results, the expressions of ζ₀ and η₀ can be deduced as follows:

${\varsigma }_0=1.29\xi -0.47,(5)$

${\eta }_{\text{0}}=\{\begin{array}{cc}0.65-0.104\xi & \left(\xi \le 0.9\right)\\ 0.49+0.043{\xi }^{-3.2}& \left(\xi >0.9\right)\end{array}.(6)$

The typical N_ct/N_u-T_ct/T_u curve of components can be roughly divided into two parts, and the expressions are as follows:

Part A-C (Nct/Nu>η0)

$N_{\mathrm{ct}}/N_{\mathrm{u}}+a{T}_{\mathrm{ct}}/T_{\mathrm{u}}=1,(7)$

Part B-A (Nct/Nu≤η0)

$-b{\left(N_{\mathrm{ct}}/N_{\mathrm{u}}\right)}^2-c{N}_{\mathrm{ct}}/N_{\mathrm{u}}+T_{\mathrm{ct}}/T_{\mathrm{u}}=1,(8)$

where a = (1-η₀)/ζ₀, and b=(1-ζ₀)/η₀², and c = 2(ζ₀-1)/η₀。.

Correlation Equation Verification

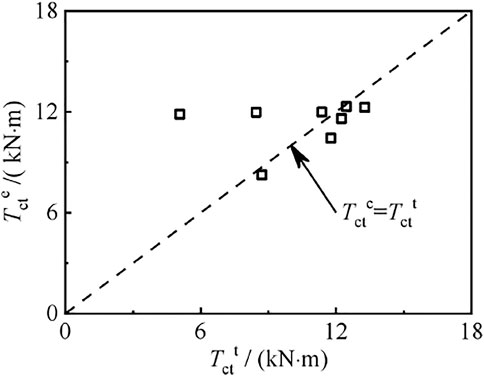
Figure 29 shows the comparison between calculated torsional bearing capacity T_ct^c and test value T_ct^t of specimens. The average value of T_ct^c/T_ct^t of the member is 0.94 and the mean square deviation is 0.18. It can be seen that the calculated results are in good agreement with the test results.

FIGURE 29

FIGURE 29. Comparison of T_ct^c and T_ct^t of specimens under compressive torsional load.

Conclusion

(1) The T–θ curves of the CF-CFRP-ST specimen can be divided into the elastic stage, the elastic–plastic stage, and the plastic strengthening stage. After reaching the bearing capacity, the specimen can still maintain a considerable bearing capacity after experiencing a large corner, which belongs to ductile failure. The deformation of the specimen basically conforms to the assumption of the plane section.

(2) The T–θ curves and deformation mode of the CF-CFRP-ST specimen can be well simulated by ABAQUS. The stress distribution of each component material of the CF-CFRP-ST specimen under compressive torsional load is analyzed, and the simulation results are in good agreement with the experimental results.

(3) The results of parameter analysis show that the increase of transverse CFRP layers, material strength, and steel ratio can improve the bearing capacity of members. With the increase of axial compression ratio, the bearing capacity of members first increases and then decreases slightly.

(4) The bearing capacity equation of the CF-CFRP-ST specimen under compressive torsional load is proposed. The calculation results of this equation are in good agreement with the experimental results.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

QW conducted experimental research, JZ conducted finite element simulation, and KP translated and contributed the article.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The research reported in the study is supported by the Project for Talent of Liaoning Province of China (No. XLYC1902009), and the authors thank Shenyang jianzhu University for its support in experimental equipment.

References

Chen, Y., Wang, K., He, K., Wei, J., and Wan, J. (2018). Compressive Behavior of CFRP-Confined Post Heated Square CFST Stub Columns. Thin-Walled Struct. 127, 434–445. doi:10.1016/j.tws.2018.02.012

CrossRef Full Text | Google Scholar

Han, L. H., and Zhong, S. T. (2004). Bearing Capacity Correlation Equations of Concrete Filled Steel Tubular Members under Compression Torsion and Bending Torsion. J. of Harbin Inst. of Archit. Eng. 27 (2), 32–37. (in Chinese). doi:10.15951/j.tmgcxb.2016.10.004

CrossRef Full Text | Google Scholar

Hou, C. C., Han, L. H., Wang, Q. L., and Hou, C. (2016). Flexural Behavior of Circular Concrete Filled Steel Tubes (CFST) under Sustained Load and Chloride Corrosion. Thin-Walled Struct. 107 (1), 182–196. doi:10.1016/j.tws.2016.02.020

CrossRef Full Text | Google Scholar

Hu, C. M., and Han, L. H. (2016). Experimental Study on Impact Resistance of Circular Concrete Filled Steel Tubular Composite Members. J. of Civ. Eng. 49 (10), 11–17.

Google Scholar

Hua, Y. X., Hou, C., and Han, L. H. (2015). Study on Mechanical Properties of Concrete Filled Steel Tubular Flexural and Torsional Members under Chloride Ion Corrosion Environment. Eng. Mech. 32 (S1), 149–152.

Google Scholar

Li, N., Lu, Y. Y., Li, S., and Liu, L. (2018). Slenderness Effects on Concrete-Filled Steel Tube Columns Confined with CFRP. J. of Constr. Steel Res. 143, 110–118. doi:10.1016/j.jcsr.2017.12.014

CrossRef Full Text | Google Scholar

Liang, J., Lin, S., Li, W., and Liu, D. (2021). Axial Compressive Behavior of Recycled Aggregate Concrete-Filled Square Steel Tube Stub Columns Strengthened by CFRP. Structures 29, 1874–1881. doi:10.1016/j.istruc.2020.12.084

CrossRef Full Text | Google Scholar

Nie, J.-g., Wang, Y.-h., and Fan, J-S. (2013). Experimental Research on Concrete Filled Steel Tube Columns under Combined Compression-Bending-Torsion Cyclic Load. Thin-Walled Struct. 67, 1–14.doi:10.1016/j.tws.2013.01.013

CrossRef Full Text | Google Scholar

Nie, J. G. (2005). Stiffness and Capacity of Steel-Concrete Composite Beams with Profiled Sheeting. Eng. Struct. 27 (7), 1074–1085. doi:10.1016/j.engstruct.2005.02.016

CrossRef Full Text | Google Scholar

Nie, J. G., Wang, Y. H., and Fan, J. S. (2014a). Study on Seismic Behavior of Concrete Filled Steel Tube under Pure Torsion and Compression Torsion Load. Ocean. Eng. 47 (1), 47–58. doi:10.15951/j.tmgcxb.2014.01.008

CrossRef Full Text | Google Scholar

Nie, J. G., Wang, Y. H., and Fan, J. S. (2014). Study on Seismic Behavior of Concrete Filled Steel Tubular Columns under Pure Torsion and Compression Torsion Load. Steel Compos. Struct. 47 (1), 47–58.

Google Scholar

Park, J. W. (2010). Behavior of Concrete Filled Circular Steel Tubes Confined by Carbon Fiber Sheets under Compression and Cyclic Loads. Steel Compos. Struct. 10 (2), 187–205. doi:10.12989/scs.2010.10.2.187

CrossRef Full Text | Google Scholar

Romero, M. L., Espinos, A., Lapuebla-Ferri, A., Albero, V., and Hospitaler, A. (2020). Recent Developments and Fire Design Provisions for CFST Columns and Slim-Floor Beams. J. of Constr. Steel Res. 172, 106159. doi:10.1016/j.jcsr.2020.106159

CrossRef Full Text | Google Scholar

Sundarraja, M. C., and Ganesh Prabhu, G. (2011). Finite Element Modeling of CFRP Jacketed CFST Members under Flexural Loading. Thin-Walled Struct. 49 (12), 1483–1491. doi:10.1016/j.tws.2011.07.008

CrossRef Full Text | Google Scholar

Sundarraja, M. C., and Ganesh, P. G. (2011). Investigation on Strengthening of CFST Members under Compression Using CFRP Composites. J. of Reinf. Plastics Compos. 30 (15), 1251–1264. doi:10.1177/0731684411418018

CrossRef Full Text | Google Scholar

Tang, H. Y., Chen, J. L., Fan, L. Y., Sun, X. J., and Peng, C. M. (2020). Experimental Investigation of FRP-Confined Concrete-Filled Stainless Steel Tube Stub Columns under Axial Compression. Thin-Walled Struct. 146, 1–14. doi:10.1016/j.tws.2019.106483

CrossRef Full Text | Google Scholar

Tao, Z., Han, L. H., and Zhuang, J. P. (2008). Cyclic Performance of Fire-Damaged Concrete-Filled Steel Tubular Beam-Columns Repaired with CFRP Wraps. J. of Constr. Steel Res. 64 (1), 37–50. doi:10.1016/j.jcsr.2007.02.004

CrossRef Full Text | Google Scholar

Tao, Z., Han, L. H., and Wang, L. L. (2007). Compressive and Flexural Behaviour of CFRP Repaired Concrete-Filled Steel Tubes after Exposure to Fire. J. of Constr. Steel Res. 63 (8), 1116–1126. doi:10.1016/j.jcsr.2006.09.007

CrossRef Full Text | Google Scholar

Tao, Z., Han, L. H., and Zhuang, J. P. (2007). Axial Loading Behavior of CFRP Strengthened Concrete-Filled Steel Tubular Stub Columns. Adv. Struct. Eng. 10 (1), 37–46. doi:10.1260/136943307780150814

CrossRef Full Text | Google Scholar

Wang, Q. L., Li, J., Shao, Y. B., and Zhao, W. J. (2015). Flexural Performances of Concrete Filled CFRP-Steel Tubes. Adv. Struct. Eng. 18 (8), 1319–1344. doi:10.1260/1369-4332.18.8.1319

CrossRef Full Text | Google Scholar

Wang, Q. L., and Shao, Y. B. (2014). Compressive Performances of Concrete Filled Square CFRP-Steel Tubes (S-CFRP-CFST). Steel Compos. Struct. 16 (5), 455–480. doi:10.12989/scs.2014.16.5.455

CrossRef Full Text | Google Scholar

Wang, Q. L., Zhao, Z., Shao, Y. B., and Li, Q. L. (2017). Static Behavior of Axially Compressed Square Concrete Filled CFRP-Steel Tubular (S-CF-CFRP-ST) Columns with Moderate Slenderness. Thin-Walled Struct. 110 (1), 106–122. doi:10.1016/j.tws.2016.10.019

CrossRef Full Text | Google Scholar

Ye, Y., Han, L. H., and Tao, Z. (2016). Analysis of Influence of Void on Shear Behavior of Concrete Filled Circular Steel Tubular. Eng. Mech. 33 (S1), 62–66.

Google Scholar

Zhang, K., Liao, F. Y., and Huang, Z. W. (2019). Study on Axial Compression Behavior of Concrete Filled Steel Tubular Short Columns with Spherical Crown Void Strengthened with CFRP. J. of Build. Struct. 40 (1), 220–225.

Google Scholar

Zhang, Y. R., Wei, Y., Zhao, K., Ding, M. M., and Wang, L. B. (2020). Analytical Model of Concrete-Filled FRP-Steel Composite Tube Columns under Cyclic Axial Compression. Soil Dyn. Earthq. Eng. 139, 1–11. doi:10.1016/j.soildyn.2020.106414

CrossRef Full Text | Google Scholar

Zhou, X. H., Wang, Y. H., and Lu, G. B. (2017). Research on Mechanical Behavior of Hollow Sandwich Concrete Filled Steel Tubular Columns under Reciprocating Pure Torsion. J. of Build. Struct. 38 (S1), 266–271. doi:10.14006/j.jzjgxb.2017.S1.036

CrossRef Full Text | Google Scholar