- Center for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, TN, United States
Machine learning and artificial intelligence (AI/ML) methods are beginning to have significant impact in chemistry and condensed matter physics. For example, deep learning methods have demonstrated new capabilities for high-throughput virtual screening, and global optimization approaches for inverse design of materials. Recently, a relatively new branch of AI/ML, deep generative models (GMs), provide additional promise as they encode material structure and/or properties into a latent space, and through exploration and manipulation of the latent space can generate new materials. These approaches learn representations of a material structure and its corresponding chemistry or physics to accelerate materials discovery, which differs from traditional AI/ML methods that use statistical and combinatorial screening of existing materials via distinct structure-property relationships. However, application of GMs to inorganic materials has been notably harder than organic molecules because inorganic structure is often more complex to encode. In this work we review recent innovations that have enabled GMs to accelerate inorganic materials discovery. We focus on different representations of material structure, their impact on inverse design strategies using variational autoencoders or generative adversarial networks, and highlight the potential of these approaches for discovering materials with targeted properties needed for technological innovation.
Introduction
The ability to discover new materials or manipulate matter to alter the properties of existing materials has long driven technological innovation. However, the traditional Edisonian trial-and-error approach to materials discovery is characteristically slow. Commercialization of blue light-emitting diodes (LEDs) and lasers provides an illustrative example of how this sluggish approach to materials discovery negatively impacts technological innovation (Nakamura, 1998). Despite existing knowledge of GaN, blue LEDs and laser diodes did not have a significant commercial impact on energy-saving lighting or data storage until nearly 30 years after the first LED (20 years after the first blue LED) patents when Nakamura et al. discovered a route to efficiently alloy In with GaN to form InxGa1-xN heterostructures (Nakamura, 1998). Hence, it would greatly benefit many applications of chemistry and condensed matter physics research to accelerate materials discovery. Examples of such applications include multiferroics (Spaldin and Ramesh, 2019), quantum technology (e.g., superconductors) (Keimer et al., 2015; Duan et al., 2016; Basov et al., 2017), solar energy (Giustino and Snaith, 2016), or batteries (Zhao et al., 2020).
Recent years have seen an explosion of studies using machine learning and artificial intelligence (AI/ML) (Jordan and Mitchell, 2015) as a methodology to better use modern computational power to understand data and facilitate technological innovation. Early proposals of ML use in materials science included genetic algorithms with fuzzy logic in the loop and local neural network experts for predicting structure-property relationships for design of materials with desired properties (Sumpter and Noid, 1996). Growing interest in AI/ML has influenced materials science regarding accelerating the materials discovery process by developing large libraries and databases and creating algorithms to discover structure-property relationships. These efforts include large-scale collaborative projects such as the Materials Genome Initiative (MGI) (de Pablo et al., 2014), Automatic Flow for Materials Discovery (AFLOWLIB) (Curtarolo et al., 2012), Joint Automated Repository for Various Integrated Simulations (JARVIS) (Choudhary et al., 2020), and many individual studies and reviews (Sumpter et al., 2015; Hill et al., 2016; Mueller et al., 2016; Vasudevan et al., 2019). To date, most efforts to integrate AI/ML methods with materials science research have focused on high-throughput virtual screening (HTVS) of known materials for the discovery of new functions, or discovering new materials through combinatorial screening (Pilania et al., 2013; Pyzer-Knapp et al., 2015; Ramprasad et al., 2017; Ward and Wolverton, 2017; Butler et al., 2018). The modus operandi for HTVS is fairly similar across many of these studies: train a predictor model that maps a composition to a property (e.g., thermodynamic stability), combinatorial screening of different compositions, and prediction of new material candidates. For example, Jha et al. (Jha et al., 2018) developed the EleNet framework for using a materials elemental composition to predict its enthalpy of formation. Models based on global optimization approaches using genetic-algorithms or particle swarm have also become popular (Glass et al., 2006; Wang et al., 2012; Avery et al., 2019). The popularity of these methods can be attributed to the significant improvement in computationally efficiency compared to density functional theory (DFT) or other first principles computational chemistry methods.
As successful as these approaches have been, they suffer from two key limitations. The first limitation is that their efficiency is “data hungry,” and improvements in accuracy require not only better algorithms, but larger datasets where scaling can become an issue (e.g., it is more difficult to sample data in larger phase spaces). Another limitation is that candidate generation is biased by the screening process (e.g., screening binary materials for specific properties will inevitably be biased against quaternary materials that may, in reality, yield better properties for the target application). An alternative approach, would be for AI to leverage chemistry or physics-based knowledge of the phase space to generate new materials from, in a non-traditional meaning of the words, “first principles,” but on a timescale faster than would be required with computational chemistry methods such as DFT.
One strategy to achieve these goals would be to use generative models (GM) (Sanchez-Lengeling and Aspuru-Guzik, 2018), which encode materials information into a continuous vector (or latent) space, and manipulates the latent space to generate new material data points. Growing interest in GMs for materials discovery can be partitioned into three main categories: autoencoder variations (e.g., variational autoencoders or VAEs), recurrent neural networks (RNNs), and generative adversarial networks (GANs) (Ferguson, 2017; Sanchez-Lengeling and Aspuru-Guzik, 2018; Elton et al., 2019; Xu et al., 2019). Early emergence of generative chemistry and physics has been somewhat limited though to organic or “soft” materials due to their smaller, less complicated phase-space than inorganic materials. For example, GMs applied to molecules can use simple molecular representations (e.g., SMILES) (Gómez-Bombarelli et al., 2018; Kim et al., 2018) to represent material structure. ML can therefore be trained on a simple user-defined representation of data, generate new data points, and post-processing can invert the new data points back into a physically interpretable structure. On the other hand, “fingerprinting” for inverse design is much more difficult for “hard” inorganic materials where typical approaches (e.g., crystal graphs) (Xie and Grossman, 2018) are difficult to decode back into a physically interpretable structure. In this review, we describe efforts to overcome these challenges and advance the use of GMs for inorganic materials discovery. We focus our discussion on VAEs and GANs (the two most commonly used methods), efforts to circumvent the need for a detailed structure representation (e.g., using simple compositions), efforts and strategies to better represent inorganic structure, and efforts to connect either approach to the discovery of materials with a specific set of properties.
Generative Adversarial Networks and Variational Autoencoders: Strategies for Materials Design
A reoccurring challenge for materials discovery using GMs (and many other ML models) is the choice of structure representation, or feature selection (often referred to as descriptors) (Jha et al., 2018). Regardless of model type, there is usually a trade-off between simplicity (e.g., a representation of structure that only uses composition or possibly composition with a few physical property labels) and specificity (e.g., near full capture of atomic structure such as atomic coordinates and lattice constants). Models that use simplistic structural descriptors tend to be the most robust and capable of applying to a broad range of materials within a database, but at the cost of limited predictive capabilities (e.g., pure compositional predictions often cannot account well for polymorphism). On the other hand, as structural descriptors become more complex, models may become more descriptive, but overfitting becomes an increasing concern, memory requirements generally increase (limiting the size of training data), and it becomes more difficult to make predictions outside of a specific, small system (e.g., having to choose a very specific compositional phase space within a database).
For the purposes of this review, we will focus on three general representations of structure: 1) Phase-fields (defined here as elemental combinations that lead to distinct chemistries), 2) composition (specific combinations of atoms), and 3) coordinate or image-based structure (representations that account for more complex aspects of structure than just composition such as lattice parameters or atomic coordinates). While each of these representations of structure will be discussed in more depth in subsequent sections (in the context of specific studies), issues surrounding them have also been summarized in related studies (Chen et al., 2020; Keith et al., 2021; Zhao et al., 2021). In addition to data representation, a generative model must be selected. While a thorough review of all GAN and VAE architectures is beyond the scope of our discussion, we will briefly describe several architectures that are commonly used, and note that more complete reviews of these architectures and their use for molecule generation can be found elsewhere (Jørgensen et al., 2018; Sanchez-Lengeling and Aspuru-Guzik, 2018; Vanhaelen et al., 2020).
Deep-learning pipelines using VAEs or GANs are designed to learn representations of a data distribution, and then through exploration and manipulation of the latent space generate new samples (Figure 1) (Karthikeyan and Priyakumar, 2021). This general methodology applies to all of the VAE and GAN approaches we describe in this review; variations in methodology and architectures therefore only reflect differences in the way a GM learns the representation of a data distribution. A typical VAE architecture includes two deep learning neural networks (Kingma and Welling, 2013). One of these networks (the encoder) encodes high dimensional data (here, materials structure, phase-field, or composition) into a lower dimensional latent space. The second of these networks (the decoder) generates new data points (here, material structures) by inverse mapping of the latent space. The optimization process of this approach approximates a posterior distribution of the data to generate new materials (Kingma and Welling, 2013). Traditional autoencoders (AEs) follow a similar process but merely decode the original input, and therefore can be used in materials discovery for pre- or post-processing of structure.
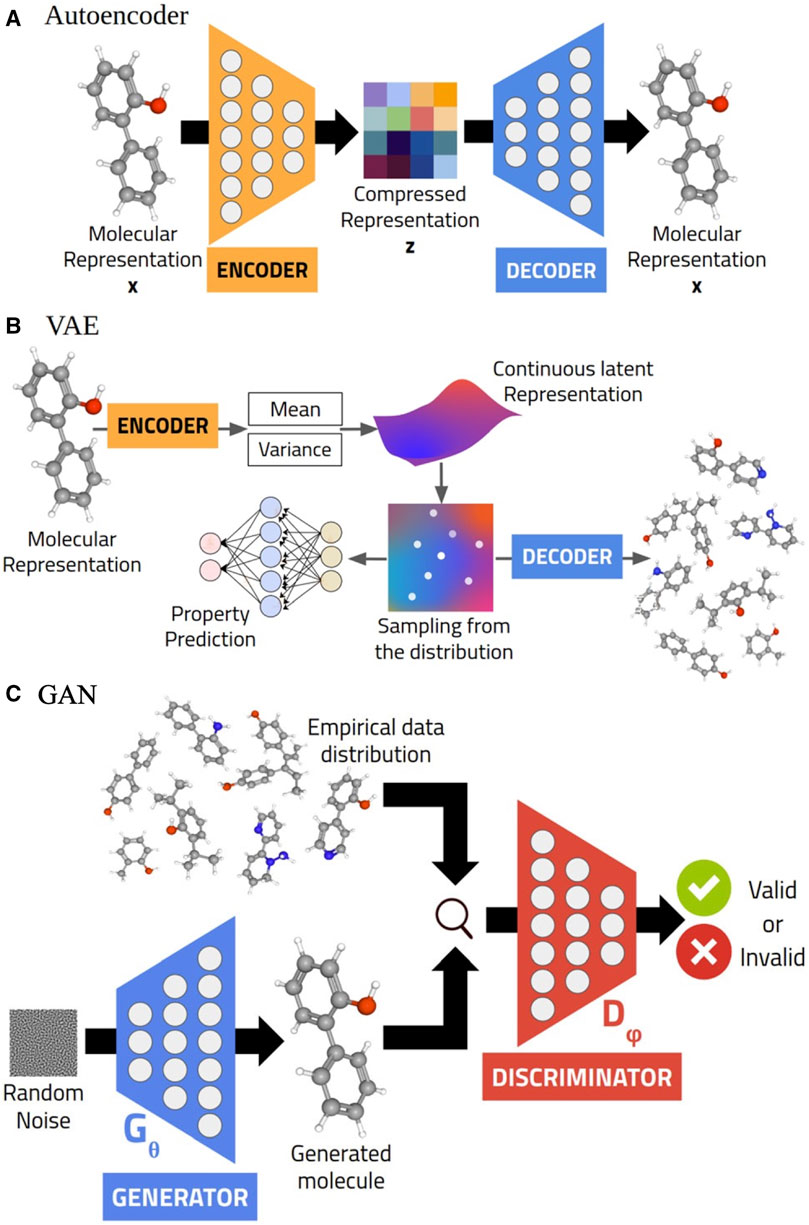
FIGURE 1. Generative models typically used in molecular generation: AE (A), VAE (B), and GAN (C). Reprinted with permission from Karthikeyan et al. (2021).
GANs, on the other hand, learn data distribution for materials implicitly. Specifically, instead of approximating the likelihood of a data distribution, two neural networks (generator and discriminator) simultaneously compete and cooperate with each other in a zero-sum game, or minimax problem (Goodfellow et al., 2014). The generator takes an input noise vector and tries to generate fake data (e.g., an image), which is given to the discriminator along with real data. Throughout the process the discriminator parameters will be updated to better distinguish between real and fake data, and the generator parameters will be updated to better generate fake data and attempt to “fool” the discriminator. We say “compete and cooperate” because each neural network is improved directly by its competition with the other: the generator improves by trying to “fool” the discriminator, and the discriminator improves by trying to “catch” the generator. Much like a VAE, a GAN builds latent space representations of material structures. However, unlike VAEs, it does not assume a model distribution and directly use discrepancies within the data from that model distribution to generate new data points. Both GANs and VAEs can be extended as conditional VAEs (CVAEs) or conditional GANs (CGANs) by adding a condition vector input (e.g., formation energies for predicting synthesizability) to learn multimodal probability distributions (Mirza and Osindero, 2014; Simonovsky and Komodakis, 2017; Bianchi et al., 2019). In addition, these approaches can be extended for cross-domain learning such as CycleGANs, which can learn how to translate latent spaces (e.g., style transfer in images) (Zhu et al., 2017).
Materials Discovery Using Generative Models
Generative Models for Phase-Fields and Composition
The simplest representation for structure are composition (e.g., simple stoichiometry) or phase-fields (defined here as elemental substitutions that lead to distinct chemistries or physics), which makes them logical starting points for material discovery GMs. As described earlier, simpler representations of structure—representations that do not include the specific arrangement of atoms (e.g., full atomic coordinates)—tend to produce GMs that are more robust, generalizable, and often can use clearer evaluation metrics (e.g., it is easier to determine if a crystal composition is charge neutral than if each atom in a large-scale structure has the correct coordinates). There are, however, several common challenges for GMs that use either representation. For example, it is conceptually well-known that exploration of different elemental combinations (phase-fields) can lead to the discovery of new chemistries or physics [e.g., even though kesterites (Giraldo et al., 2019) and halide perovskites (Jena et al., 2019) can both be used in solar cells, their chemistry and physics are notably different], but doing this at scale has been difficult. Traditional HTVS screens individual materials for specific chemistry or physics. Generative phase-field models, alternatively, learn the chemistry or physics of different elemental combinations, and generates new ones to explore experimentally via a VAE or GAN. This distinction is where the problem of scaling occurs, because each phase-field will inevitably include large variations of chemistry/physics within the phase-field and finding clear generalizable parameters for multiple phase-spaces is challenging. In addition, AI needs to generate a human-interpretable prioritization system within reasonable resource commitment constraints to aid materials discovery.
Vasylenko et al. (Vasylenko et al., 2021) described a neural network approach where they overcame this issue and explored phase-fields found in the Inorganic Crystal Structure (ICSD) database which provided a route to generate new phase-fields for experimental materials discovery by training the neural network on existing, synthesized materials. ML exploration of ICSD phase-fields using a VAE identified distinctive sets of chemistries via complex correlations, which would normally be difficult for humans to process. However, they made it processable for humans by numerically ranking the likelihood of each phase-space to find a target material. In particular, they focused on Li materials with multiple anions for potential Li fast-ion conductors, a relatively unexplored but important chemistry (Harada et al., 2019; Bates et al., 1992; Kraft et al., 2017; Kageyama et al., 2018). In step 1 of their approach (Figure 2) they extract 2021 MxM’yAzA’t phases from ICSD (where M and M’ represent cations, A and A’ anions, and x, y, z, t their concentrations). Then in step 2, they associated unexplored phase-fields with known phases to determine their similarity using 37 individual feature descriptors (e.g., first ionization radius, number of unfilled p-orbitals, etc.) (Glawe et al., 2016; Jha et al., 2018; Vasylenko et al., 2021) using a VAE. Their VAE model was trained to minimize the Euclidean distances (described as reconstruction errors) between the encoded and decoded 148-dimensional (37 features x 4 elements) vector feature space.
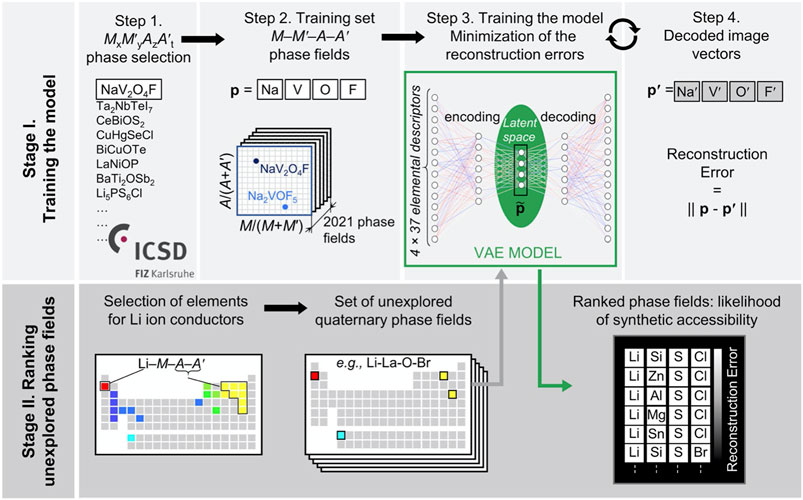
FIGURE 2. GM approach using phase-fields. Stage I: Phase fields are gathered for two anion quartenary materials in ICSD and represented as 148-dimension (4 elements x 37 features) vector. VAE encodes/decodes each field and optimizes by minimizing the reconstruction error (Euclidean distance between encoded and decoded vectors). Stage II: Exploration of new phase-fields for Li fast-ion conductors using the trained VAE, and corresponding ranking based on reconstruction error. Similarity of unexplored phase field to explored phase field dictates how ideal it is for experimental exploration. Reprinted with permission from Vasylenko et al. (2021).
A general challenge of VAEs compared with GANs is their bias towards predictions near the distribution of the data, which is to be expected given that VAEs model the distribution explicitly whereas GANs model them implicitly via adversarial training. However, in this case, the bias of VAEs is a strength because the training data in ICSD represents materials that have already been synthesized (as compared with theoretical structures), which means generated phase-spaces will be biased towards synthesizable structures. The reconstruction error, which captures deviation from the learned model, therefore can be interpreted to represent deviation from trends in the data, which are trends in synthesizable phase-fields, and the degree of deviation can be used as a metric to prioritize different phase spaces to explore experimentally (generated candidates versus known phase-fields) (Amarbayasgalan et al., 2018; Gong et al., 2019; Vasylenko et al., 2021). This is an example of a positive bias model (searches the likelihood of positive outcomes instead of the absence of negative outcomes), which can be advantageous for materials discovery because negative outcomes (here, no known material) may merely be a reflection of an undiscovered material.
In step 2, quaternary dual anion phase fields are quantified for their likelihood to contain stable compounds based on their similarity to known phase-fields. This of course, requires some user-defined limitations (e.g., removing elements that are particularly scarce, toxic, or have undesired redox properties). After narrowing such desired chemistries, 303 unexplored phase fields were ranked in regard to their attractiveness for experimental exploration. The reconstruction errors for the validation dataset were below 0.5 for ∼80% of the explored phase fields, and the VAE was able to generate experimentally known phase-fields not included in the training data (e.g., the Li-P-S-O field) (Suzuki et al., 2016). They eventually experimentally explored the Li-Sn-S-Cl field (ranked 5th) leading to the experimental discovery of a specific Li-conductor (Li3.3SnS3.3Cl0.7).
Dan et al. (Dan et al., 2020) took a different approach, and used generative modeling to predict a large number of distinct compositions. They used a Wasserstein GAN (MatGAN) to generate hypothetical compounds (instead of phase spaces for exploration), and combined data from a broader range of data sources (OQMD (Kirklin et al., 2015), Materials Project (Jain et al., 2013), and ICSD (ICSD)). For data preprocessing, they used a simple statistical calculation of materials in the OQMD dataset (Saal et al., 2013) and found 85 reoccurring elements, and noted that most compounds had <8 atoms. Each material could therefore be represented as a sparse matrix of 0/1 integer values where the column vectors represent the one-hot-encoded matrix for each of the 85 elements. This implies that real chemical rules such as charge neutrality and electronegativity are indirectly captured by the one-hot-encoded matrix where combinations of different atom numbers would be expected to obey these rules. After applying additional filters to eliminate compositions that do not obey charge neutrality rules or lead to reasonable electronegativities, MatGAN generated an impressive 1.69 million compositions (Dan et al., 2020). Accuracy of structure predictions were tested by performing electronegativity and charge neutrality checks using the t-SNE method (Maaten and Hinton, 2008), and found similar distributions in both the training and test sets. Impressively, ∼84–92% of the generated materials (depending on the dataset) obeyed charge neutrality rules and were electronegativity balanced despite the lack of inclusion of concrete chemistry or physics rules in the GAN, which indicates that the adversarial process learned these rules implicitly by modeling the latent space (Davies et al., 2016).
Generative Models for Coordinate and Image-Based Structure
One disadvantage of GMs that use simplistic descriptions of structure (e.g., composition or phase-fields) is their limited predictive capabilities for individual materials or smaller phase spaces (e.g., pure compositional predictions often cannot account well for polymorphism). Noh et al. found a way to incorporate structure, or computationally generated fingerprints for materials discovery with an invertible encoding/decoding scheme coupled with a VAE called iMatGen (Image-based Materials Generator). (Noh et al., 2019). The encoder/decoder scheme allowed them to use invertible 3D grid-based images as a representation of structure (Kajita et al., 2017; Ryczko et al., 2017; Noh et al., 2019). Specifically, they decomposed crystal structures of inorganic materials into an image of the unit cell that incorporates the length of cell edges, angles between cell edges, and atomic positions (Figure 3 for a 2D slice of a 3D unit cell shown for simplicity). The logic behind this approach is centered on the idea that many deep learning methods (especially generative methods) were designed for images and developing methodologies for defining crystal structures as images (here, a 3D-voxel image grid), will have facile coupling with neural networks for materials discovery.
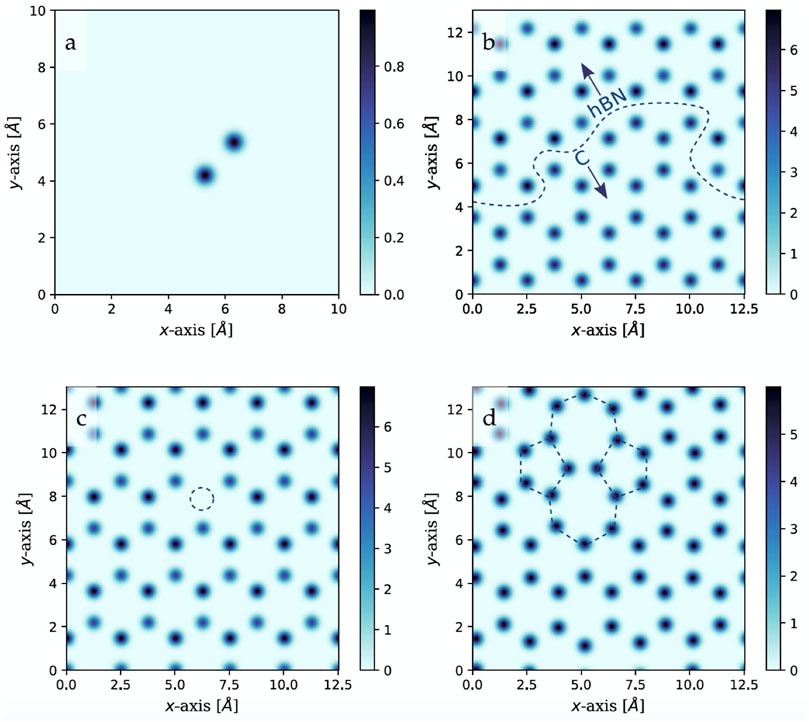
FIGURE 3. Simplified 2D representation of 3D voxelized image representations of materials: (A) Represents a dimer, (B) a graphene-hBN heterostructure, (C) hBN with a N vacancy, and (D) graphene with a Stone-Wales defect. Reprinted with permission from Ryczko et al. (2017).
After determining a proper way to represent structure, iMatGen generates materials by first compressing the image of the structure with an AE, and then encoding it with a VAE into smaller intermediate vectors as “fingerprints” in the materials generator using element information from the AE step (Figure 4). The VAE constructed materials space can potentially be used for materials discovery for various systems, but here they focused on the V-O materials system due to both the large availability of training data, and structural complexity (multiple polymorphs and large variation in V oxidation states). Their model was able to both reproduce known experimental structures and generate new materials (both new compositions and new polymorphs of known compositions) using the MP dataset (Jain et al., 2013). They evaluated autoencoder and materials discovery performance using several metrics. First, they analyzed the inverse transformed cell information (lattice parameters and atomic positions) focusing on the accuracy of the AE to back convert their materials representation to human-interpretable structures. This approach, in essence, is evaluating the accuracy of “fingerprint” generation, and they found that they were able to recover most structures within 0.1 Å edge lengths, 2° between edges, and atomic positions within 0.2 Å for most known structures and were able to generate more than 10,000 new structures in total using this approach. Further validation with DFT found that many of these structures were stable. Moreover, while this study focused specifically on one material space (VxOy), this 3D voxel image approach has also found success in other studies such as by Hoffman et al. where they included a UNet segmentation to allow for the architecture to produce multiple material classes (Hoffmann et al., 2019).
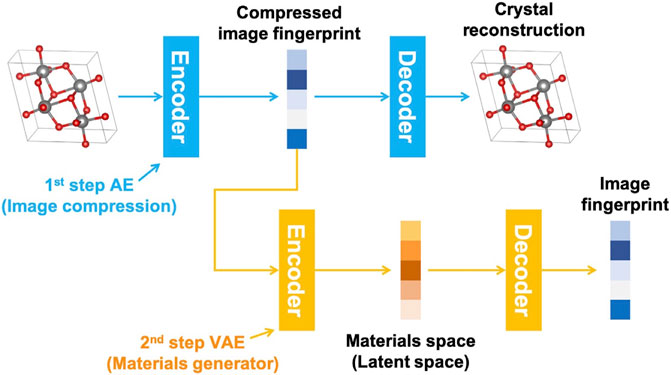
FIGURE 4. AE compression of material structure image, followed by VAE generation of new materials. Reprinted with permission from Noh et al. (2019).
While the 3D voxel image representation has already shown significant success in GMs for materials discovery, several issues persist. For example, while the extension by Hoffman et al. was able to generate multiple classes of structures, they had a difficult time producing crystal structures that were stable (Hoffmann et al., 2019). Long training times are also required due to the memory-intensive material representation, and the development of user-friendly post-processing is required for inversion of the material representation. In addition, unit-cell sizing is limited due to cubic scaling of 3D grids. Kim et al. (2020) sought to overcome these issues by developing a representation with lower memory requirements (a factor of 400 compared to iMatGen) and is inversion-free (Figure 5). (Kim et al., 2020) They were able to do this using a “point cloud” approach in which objects are represented as a set of points with 3D vector coordinates (here, crystal structures with cell parameters and a set of atomic coordinates) (Qi et al., 2016; Zhou and Tuzel, 2017; Lang et al., 2018; Li et al., 2018; Nouira et al., 2018; Wu et al., 2018). This representation, unlike the Voxel image, is essentially the material itself, which removes the requirement of inversion entirely and does not require as much memory due to the lack of grid data.
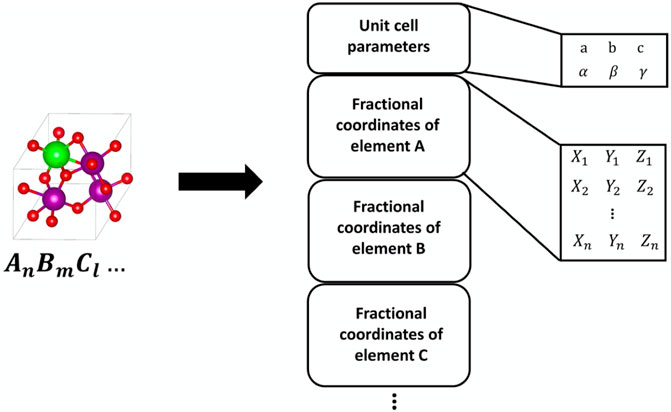
FIGURE 5. Example of point cloud approach to structure representation. Reprinted with permission from Kim et al. (2020).
In this case, the generative model of choice was a CGAN instead of a VAE. Similar to GANs described earlier for generating compositions, they used one-hot encoding of MP (Jain et al., 2013) data for each structure as representation of its composition. However, unlike compositional generating GANs, they used this one-hot encoded composition vector as the conditional input for the GAN instead of the target structure. In other words, the GAN generator uses input from the typical random Gaussian noise vector and the compositional conditional vector and generates point cloud representations of structure paired to a specific composition using the typical CGAN competition between generator and discriminator (here, using the Wasserstein distance to represent the dissimilarity between fake data and the ground truth). Much like VAEs for coordinate or image-based generation, this work focused on a particular material system (ternary Mg-Mn-O compositions).
This approach for capturing full inorganic structure has found additional uses. Specifically, a similar representation of structure was used by Nouira et al. (2018) in a CycleGAN for cross-domain modeling (CrystalGAN). In this case, they were able to generate complex ternary hydride structures from simpler starting binary hydrides. This difficult task for materials discovery (generating data of increasing complexity from simpler reference data) has been a notable limitation for GMs that attempt to use coordinate or image-based structure (e.g., limiting GMs to a small phase space of materials within a larger database). CrystalGAN impressively generates ternary structures with reasonable interatomic distances. However, as noted directly by the authors, further work is required to verify the stability of their generated materials (e.g., by DFT).
GMs for Inverse Design of Materials With Targeted Properties
Thus far we have focused our discussion on methodologies for generating different types of structures with GMs. However, many of these approaches have been employed for inverse design schemes wherein a material with targeted properties can be generated for a specific application. The conventional route for inverse design has traditionally been computational chemistry approaches such as DFT, which predict structure-property relationships, but are compute and time-intensive. Indeed, much of the motivation for using ML for materials discovery is driven by the desire to circumvent cumbersome ab initio calculations. ML methods for predicting structure-property relationships and aiding in inverse design have therefore been extensively reviewed (Pilania et al., 2013; Pyzer-Knapp et al., 2015; Sumpter et al., 2015; Hill et al., 2016; Mueller et al., 2016; Ramprasad et al., 2017; Ward and Wolverton, 2017; Butler et al., 2018; Vasudevan et al., 2019). In this section, we focus on how these approaches can be integrated with GMs for inverse design of materials with specific properties.
There are two key general approaches that have been explored for inverse design using GMs. The first approach uses a GM purely for structure or composition discovery, and then applies an additional ML model to search GM discovered materials for ideal structures, or materials that have a specific set of properties for a targeted application. The alternative, or second approach is to use a CVAE or CGAN that directly incorporates properties in the GMs—CVAEs and CGANs are described in more detail in the section titled “GANs and VAEs: Strategies for Materials Design.” An important distinction from our earlier examples of CVAEs and CGANs is that the conditional vector must be correlated to a property and not to structure (e.g., a conditional vector of band gaps could be understood as a property conditional input versus a conditional vector based on composition would be understood as a structure conditional input). Properties in this case could be distinct physical properties (e.g., band gap), or synthesizability (e.g., formation energy), and the GM can still use any of the structure representations we described earlier (e.g., composition, point cloud, or voxel image).
Song et al.(Song et al., 2021) demonstrated that a composition generating GAN can be combined with additional ML for predicting synthesizability. They used MatGAN (Dan et al., 2020) (see section “Generative Models for Phase-Fields and Composition” for more details) to generate 2.65 million hypothetical 2D compositions, trained a composition-processing materials classifier on known structures, and then applied the trained classifier on the GAN produced compositions to predict 2D materials that are synthesizable (e.g., have favorable formation energies, Figure 6). In this case, the classifier was a random forest model trained on verified 2D and non-2D materials, which enabled them to make it a simple binary classification problem using the Magpie feature set (calculates several important statistical measures such as the mean, range, etc., for different elemental properties such as atomic radii) calculated by the matminer library (Liaw and Wiener, 2002; Ward et al., 2016; Ward et al., 2018). They compared the Magpie features on their training and test data of known 2D materials, non-2D materials, and materials generated by MatGAN (where known 2D and non-2D materials are used as positive and negative samples for the classifier, respectively). After probability scores are determined for each material, further validation is achieved via DFT to calculate the formation energies, phonon thermostability, and exfoliation energies. They generated an impressive 1,485 2D materials with probability scores that surpassed 95%, and further verified that 92 materials had negative DFT calculated formation energies. They proposed 31 possible monolayer materials (structures that also had exfoliation energies <200 meV, which could lead to stable exfoliated nanosheets from thin-layered materials).
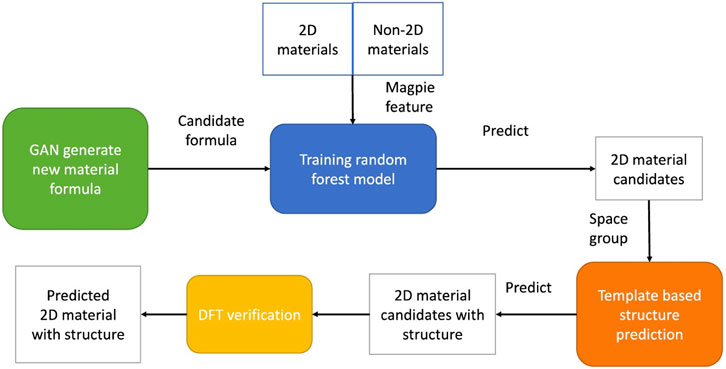
FIGURE 6. Four components of 2D material generation using MatGAN. The green box represents MatGAN generation of new materials, and the blue box represents the random forest classifier. The orange box (template-based element substitution) and yellow box (DFT) are validation steps. Reprinted with permission from Song et al. (2021).
This general strategy has found success in other studies using a coordinate or image representation instead of composition (e.g., Kim et al. (Kim et al., 2020) where HTVS screening of GAN generated materials using the point cloud structure representation found stable Mg-Mn-O materials). As can be expected though, design or training of multiple models in an AI pipeline can be complicated and it may be desirable to find a single model that can achieve similar results. Pathak et al. developed a CVAE approach to generate new material compositions named the Deep Inorganic material Generator (DING, Figure 7). (Pathak et al., 2020) Here, they use a condition vector of material properties related to synthesizability (formation enthalpy, energy per atom, volume per atom) in the OQMD (Saal et al., 2013; Kirklin et al., 2015), and the generator network of the CVAE generates materials with properties close to those desired by the user (e.g., formation energy). A second predictor network is further used to assess whether the generated materials match those desired properties, and in this case is used to filter/evaluate discovered materials. This is markedly different than the earlier described AI pipelines where physical properties are not used in the generative step and are only later applied in non-generative AI to screen generated materials. Their approach generated material compositions with small errors in the enthalpy of formation (∼50 meV), energy per atom (∼70 meV), and volume per atom (∼0.4 Å3). Similarly, iMatGen has also been extended to include a conditional vector and has been proven capable of distinguishing between stable and unstable (or, synthesizable versus not synthesizable) structures using a CVAE (Noh et al., 2019).
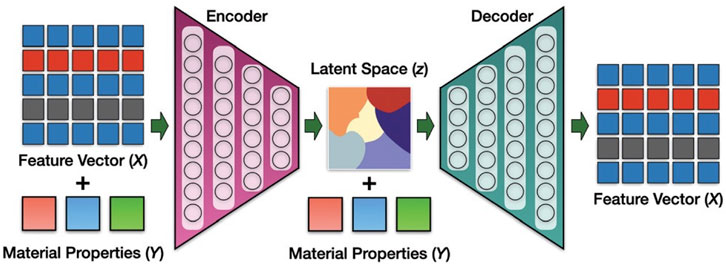
FIGURE 7. DING architecture. CVAE is used to generate materials with specific properties (formation enthalpy, energy per atom, and volume per atom). Reprinted with permission from Pathak et al. (2020).
Each of the methods outlined here have shown tremendous progress in the use of GMs for materials discovery. However, many still have the limitation of requiring user-provided a priori information (e.g., iMatGen needs a user to choose a specific composition space such as V-O within a broader database). Moreover, the only set of properties we have described thus far have been focused on synthesizability and stability. While generally it is accepted that other properties could be substituted, an explicit demonstration would be valuable. To this end, Cole et al. (Court et al., 2020) presented a VAE-driven AI pipeline that used the 3D image voxel approach to generate materials while also predicting eight properties for discovered materials: formation energy, energy per atom, bandgap, bulk modulus, shear modulus, Poisson ratio, polycrystalline dielectric constant (electronic contribution), and refractive index (Figure 8).
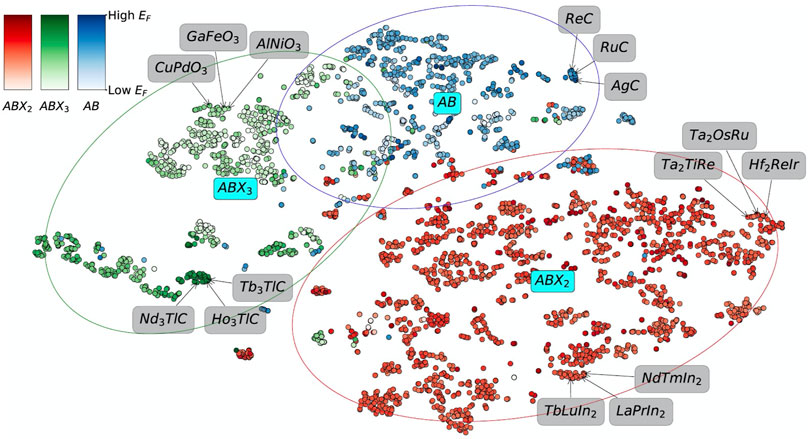
FIGURE 8. Latent space for CVAE generated materials where colors represent the formation energy per atom of each structure (high intensity indicates high formation energy and low intensity indicates low formation energy). Reprinted with permission from Cole et al. (Court et al., 2020).
They achieved these impressive results via a three step AI pipeline. First, they use a voxelized electron density map representation of cubic binary alloys, perovskites, and Heusler materials from MP (Jain et al., 2013) to train the CVAE to encode/decode known materials and create a material structure-property latent space. The latent space can then be sampled for generation of new materials with a specific property. In this case, they used formation energy per atom as the conditional to insure that generated materials are stable. Considering this is an invertible process, they used a combination of morphological transformations and UNet semantic segmentation to convert generated materials back into a normal atomic site representation. Lastly, a crystal-graph convolutional neural network (CGNN) was used to predict the 8 associated properties of new materials (e.g., band gap or refractive index).
Outlook
Generative models have been explored more extensively in organic systems than inorganic, but the approaches described in this review show their potential to accelerate inorganic materials discovery. Representation of structure remains a key issue due to the complexity of inorganic material structures. The simplest depiction described here are phase spaces, which merely reflect elemental combinations that are expected to yield desirable chemistry or physics. This approach shows the power of simplicity by making large phase spaces easily interpretable for researchers (e.g., capturing nearly 40 different physical features of known systems, and generating new ones ranked by their desirability for experimental exploration), and has already lead to the experimental discovery of new materials (Giraldo et al., 2019).
Generation of specific compositions adds complexity to the representation of structure, but it is still simpler than other methods. A virtue of this approach that is similar to phase space generation is the facile application across broad sets of chemistry and physics (e.g., a GAN can learn chemical rules such as charge neutrality across a broad range of different material classes at the same time) (Gong et al., 2019). Inclusion of full atomic coordinates (e.g., by voxel image or point cloud) is the highest level of complexity, and yields predictions of the most specific, realistic descriptions of structure. The greatest virtue of this approach for inverse design is that coordinate or image-based structures are best suited for further work with other traditional computational chemistry approaches, or other methods to search structure-property relationships with ML (e.g., graph neural networks) (Fung et al., 2021).
There is a trade-off though in adding complexity to structural representations. Phase space generation is easily interpretable by experimental researchers, but the recommendations (e.g., “search the Li-Sn-S-Cl field for the chemistry or physics you desire”) are incredibly broad. On the other hand, while it is impressive that GANs can generate millions of specific compositions that may find many uses, it is not always apparent to an experimental researcher what do with such a large set of information. Representations that include atomic coordinates are best suited for coupling with additional AI or computational chemistry because they yield the most detailed structures. However, overfitting can become more of a problem, and most methods still require a priori information provided by the user and training on smaller more specific datasets than other approaches. In addition, as recommendations become more specific experiments can arguably become more complicated because it is difficult for synthetic chemists to develop “recipes” for very specific structures. Challenges aside, each approach exhibits good potential for materials discover. GMs are still relatively new to materials discovery in general, and specifically for inorganic systems. With many practical tutorials available (Doersch, 2016; Goodfellow, 2016), use of GMs are expected to grow. Ongoing work indicates that a bright future is likely ahead for generative models to accelerate materials discovery and innovation for a broad range of technical applications.
Author Contributions
BS conceived the general idea of reviewing deep generative models for materials design/discovery. AF performed the literature review and drafted the manuscript.
Funding
Center for Nanophase Materials Sciences (CNMS) and the Alvin M. Weinberg Fellowship at Oak Ridge National Laboratory.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
AF acknowledges support from the Alvin M. Weinberg Fellowship at Oak Ridge National Laboratory. This work was carried out at Oak Ridge National Laboratory’s Center for Nanophase Materials Sciences, a US Department of Energy Office of Science User Facility.
References
Amarbayasgalan, T., Jargalsaikhan, B., and Ryu, K. (2018). Unsupervised Novelty Detection Using Deep Autoencoders with Density Based Clustering. Appl. Sci. 8 (9), 1468. doi:10.3390/app8091468
Avery, P., Toher, C., Curtarolo, S., and Zurek, E. (2019). XtalOpt Version R12: An Open-Source Evolutionary Algorithm for crystal Structure Prediction. Comput. Phys. Commun. 237, 274–275. doi:10.1016/j.cpc.2018.11.016
Basov, D. N., Averitt, R. D., and Hsieh, D. (2017). Towards Properties on Demand in Quantum Materials. Nat. Mater 16 (11), 1077–1088. doi:10.1038/nmat5017
Bates, J., Dudney, N. J., Gruzalski, G. R., Zuhr, R. A., Choudhury, A., Luck, C. F., et al. (1992). Electrical Properties of Amorphous Lithium Electrolyte Thin Films. Solid State Ionics 53-56, 647–654. doi:10.1016/0167-2738(92)90442-r
Bianchi, F. M., Grattarola, D., Livi, L., and Alippi, C. (2019). Graph Neural Networks with Convolutional ARMA Filters. IEEE Trans. Pattern Anal. Machine Intelligence. arXiv:1901.01343. doi:10.48550/arXiv.1901.01343
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O., and Walsh, A. (2018). Machine Learning for Molecular and Materials Science. Nature 559 (7715), 547–555. doi:10.1038/s41586-018-0337-2
Chen, C., Zuo, Y., Ye, W., Li, X., Deng, Z., and Ong, S. P. (2020). A Critical Review of Machine Learning of Energy Materials. Adv. Energ. Mater. 10 (8), 1903242. doi:10.1002/aenm.201903242
Choudhary, K., Garrity, K. F., Reid, A. C. E., DeCost, B., Biacchi, A. J., Hight Walker, A. R., et al. (2020). The Joint Automated Repository for Various Integrated Simulations (JARVIS) for Data-Driven Materials Design. Npj Comput. Mater. 6 (1), 173. doi:10.1038/s41524-020-00440-1
Court, C. J., Yildirim, B., Jain, A., and Cole, J. M. (2020). 3-D Inorganic Crystal Structure Generation and Property Prediction via Representation Learning. J. Chem. Inf. Model. 60 (10), 4518–4535. doi:10.1021/acs.jcim.0c00464
Curtarolo, S., Setyawan, W., Wang, S., Xue, J., Yang, K., Taylor, R. H., et al. (2012). AFLOWLIB.ORG: A Distributed Materials Properties Repository from High-Throughput Ab Initio Calculations. Comput. Mater. Sci. 58, 227–235. doi:10.1016/j.commatsci.2012.02.002
Dan, Y., Zhao, Y., Li, X., Li, S., Hu, M., and Hu, J. (2020). Generative Adversarial Networks (GAN) Based Efficient Sampling of Chemical Composition Space for Inverse Design of Inorganic Materials. Npj Comput. Mater. 6 (1), 84. doi:10.1038/s41524-020-00352-0
Davies, D. W., Butler, K. T., Jackson, A. J., Morris, A., Frost, J. M., Skelton, J. M., et al. (2016). Computational Screening of All Stoichiometric Inorganic Materials. Chem 1 (4), 617–627. doi:10.1016/j.chempr.2016.09.010
de Pablo, J. J., Jones, B., Kovacs, C. L., Ozolins, V., and Ramirez, A. P. (2014). The Materials Genome Initiative, the Interplay of experiment, Theory and Computation. Curr. Opin. Solid State. Mater. Sci. 18 (2), 99–117. doi:10.1016/j.cossms.2014.02.003
Duan, X., Wang, C., Fan, Z., Hao, G., Kou, L., Halim, U., et al. (2016). Synthesis of WS2xSe2-2x Alloy Nanosheets with Composition-Tunable Electronic Properties. Nano Lett. 16 (1), 264–269. doi:10.1021/acs.nanolett.5b03662
Elton, D. C., Boukouvalas, Z., Fuge, M. D., and Chung, P. W. (2019). Deep Learning for Molecular Design-A Review of the State of the Art. Mol. Syst. Des. Eng. 4 (4), 828–849. doi:10.1039/c9me00039a
Ferguson, A. L. (2017). Machine Learning and Data Science in Soft Materials Engineering. J. Phys. Condens. Matter 30 (4), 043002. doi:10.1088/1361-648x/aa98bd
Fung, V., Zhang, J., Juarez, E., and Sumpter, B. G. (2021). Benchmarking Graph Neural Networks for Materials Chemistry. Npj Comput. Mater. 7 (1), 84. doi:10.1038/s41524-021-00554-0
Giraldo, S., Jehl, Z., Placidi, M., Izquierdo‐Roca, V., Pérez‐Rodríguez, A., and Saucedo, E. (2019). Progress and Perspectives of Thin Film Kesterite Photovoltaic Technology: A Critical Review. Adv. Mater. 31 (16), 1806692. doi:10.1002/adma.201806692
Giustino, F., and Snaith, H. J. (2016). Toward Lead-Free Perovskite Solar Cells. ACS Energ. Lett. 1 (6), 1233–1240. doi:10.1021/acsenergylett.6b00499
Glass, C. W., Oganov, A. R., and Hansen, N. (2006). USPEX—Evolutionary crystal Structure Prediction. Comput. Phys. Commun. 175 (11), 713–720. doi:10.1016/j.cpc.2006.07.020
Glawe, H., Sanna, A., Gross, E. K. U., and Marques, M. A. L. (2016). The Optimal One Dimensional Periodic Table: a Modified Pettifor Chemical Scale from Data Mining. New J. Phys. 18 (9), 093011. doi:10.1088/1367-2630/18/9/093011
Gómez-Bombarelli, R., Wei, J. N., Duvenaud, D., Hernández-Lobato, J. M., Sánchez-Lengeling, B., Sheberla, D., et al. (2018). Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules. ACS Cent. Sci. 4 (2), 268–276. doi:10.1021/acscentsci.7b00572
Gong, D., Liu, L., Le, V., Saha, B., Mansour, M. R., Venkatesh, S., et al. (2019) “Memorizing Normality to Detect Anomaly: Memory-Augmented Deep Autoencoder for Unsupervised Anomaly Detection.” in Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea (South), 27 October-2 November 2019. doi:10.1109/iccv.2019.00179
Goodfellow, I. (2016). NIPS 2016 Tutorial: Generative Adversarial Networks. arxiv. arXiv:1701.00160.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative Adversarial Nets,” in Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal Canada, December 2014 (Cambridge, MA: MIT Press), 2672–2680.
Harada, J. K., Charles, N., Poeppelmeier, K. R., and Rondinelli, J. M. (2019). Heteroanionic Materials by Design: Progress toward Targeted Properties. Adv. Mater. 31 (19), 1805295. doi:10.1002/adma.201805295
Hill, J., Mulholland, G., Persson, K., Seshadri, R., Wolverton, C., and Meredig, B. (2016). Materials Science with Large-Scale Data and Informatics: Unlocking New Opportunities. MRS Bull. 41 (5), 399–409. doi:10.1557/mrs.2016.93
Hoffmann, J., Maestrati, L., Sawada, Y., Tang, J., Sellier, J. M., and Bengio, Y. (2019). Data-Driven Approach to Encoding and Decoding 3-D Crystal Structures. arXiv. arXiv:1909.00949.
ICSD. Inorganic crystal Structure Database. Available at: http://icsd.fiz-karlsruhe.de.
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 1 (1), 011002. doi:10.1063/1.4812323
Jena, A. K., Kulkarni, A., and Miyasaka, T. (2019). Halide Perovskite Photovoltaics: Background, Status, and Future Prospects. Chem. Rev. 119 (5), 3036–3103. doi:10.1021/acs.chemrev.8b00539
Jha, D., Ward, L., Paul, A., Liao, W.-k., Choudhary, A., Wolverton, C., et al. (2018). ElemNet: Deep Learning the Chemistry of Materials from Only Elemental Composition. Sci. Rep. 8 (1), 17593. doi:10.1038/s41598-018-35934-y
Jordan, M. I., and Mitchell, T. M. (2015). Machine Learning: Trends, Perspectives, and Prospects. Science 349 (6245), 255–260. doi:10.1126/science.aaa8415
Jørgensen, P. B., Schmidt, M. N., and Winther, O. (2018). Deep Generative Models for Molecular Science. Mol. Inform. 37 (1-2). doi:10.1002/minf.201700133
Kageyama, H., Hayashi, K., Maeda, K., Attfield, J. P., Hiroi, Z., Rondinelli, J. M., et al. (2018). Expanding Frontiers in Materials Chemistry and Physics with Multiple Anions. Nat. Commun. 9 (1), 772. doi:10.1038/s41467-018-02838-4
Kajita, S., Ohba, N., Jinnouchi, R., and Asahi, R. (2017). A Universal 3D Voxel Descriptor for Solid-State Material Informatics with Deep Convolutional Neural Networks. Sci. Rep. 7 (1), 16991. doi:10.1038/s41598-017-17299-w
Karthikeyan, A., and Priyakumar, U. D. (2021). Artificial Intelligence: Machine Learning for Chemical Sciences. J. Chem. Sci. 134 (1), 2. doi:10.1007/s12039-021-01995-2
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S., and Zaanen, J. (2015). From Quantum Matter to High-Temperature Superconductivity in Copper Oxides. Nature 518 (7538), 179–186. doi:10.1038/nature14165
Keith, J. A., Vassilev-Galindo, V., Cheng, B., Chmiela, S., Gastegger, M., Müller, K.-R., et al. (2021). Combining Machine Learning and Computational Chemistry for Predictive Insights into Chemical Systems. Chem. Rev. 121 (16), 9816–9872. doi:10.1021/acs.chemrev.1c00107
Kim, K., Kang, S., Yoo, J., Kwon, Y., Nam, Y., Lee, D., et al. (2018). Deep-learning-based Inverse Design Model for Intelligent Discovery of Organic Molecules. Npj Comput. Mater. 4 (1), 67. doi:10.1038/s41524-018-0128-1
Kim, S., Noh, J., Gu, G. H., Aspuru-Guzik, A., and Jung, Y. (2020). Generative Adversarial Networks for Crystal Structure Prediction. ACS Cent. Sci. 6 (8), 1412–1420. doi:10.1021/acscentsci.0c00426
Kirklin, S., Saal, J. E., Meredig, B., Thompson, A., Doak, J. W., Aykol, M., et al. (2015). The Open Quantum Materials Database (OQMD): Assessing the Accuracy of DFT Formation Energies. Npj Comput. Mater. 1 (1), 15010. doi:10.1038/npjcompumats.2015.10
Kraft, M. A., Culver, S. P., Calderon, M., Böcher, F., Krauskopf, T., Senyshyn, A., et al. (2017). Influence of Lattice Polarizability on the Ionic Conductivity in the Lithium Superionic Argyrodites Li6PS5X (X = Cl, Br, I). J. Am. Chem. Soc. 139 (31), 10909–10918. doi:10.1021/jacs.7b06327
Lang, A. H., Vora, S., Caesar, H., Zhou, L., Yang, J., and Beijbom, O. (2018). “PointPillars: Fast Encoders for Object Detection from Point Clouds,” in Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, June 2019. arXiv:1812.05784.
Li, J., Chen, B. M., and Lee, G. H. (2018). “SO-net: Self-Organizing Network for Point Cloud Analysis,” in Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, June 2018. arXiv:1803.04249.
Maaten, L. V. D., and Hinton, G. (2008). Visualizing Data Using T-SNE. J. Mach. Learn. Res. 9, 2579–2605.
Mirza, M., and Osindero, S. (2014). Conditional Generative Adversarial Nets. arXiv. arXiv:1411.1784.
Mueller, T., Kusne, A. G., and Ramprasad, R. (2016). “Machine Learning in Materials Science,” in Reviews in Computational Chemistry. Editors K. B. Lipkowitz, T. R. Cundari, and V. J. Gillet (Hoboken, New Jersey, United States: Wiley), 186–273. doi:10.1002/9781119148739.ch4
Nakamura, S. (1998). The Roles of Structural Imperfections in InGaN-Based Blue Light-Emitting Diodes and Laser Diodes. Science 281 (5379), 955–961. doi:10.1126/science.281.5379.956
Noh, J., Kim, J., Stein, H. S., Sanchez-Lengeling, B., Gregoire, J. M., Aspuru-Guzik, A., et al. (2019). Inverse Design of Solid-State Materials via a Continuous Representation. Matter 1 (5), 1370–1384. doi:10.1016/j.matt.2019.08.017
Nouira, A., Sokolovska, N., and Crivello, J.-C. (2018). CrystalGAN: Learning to Discover Crystallographic Structures with Generative Adversarial Networks. arXiv. arXiv:1810.11203.
Pathak, Y., Juneja, K. S., Varma, G., Ehara, M., and Priyakumar, U. D. (2020). Deep Learning Enabled Inorganic Material Generator. Phys. Chem. Chem. Phys. 22 (46), 26935–26943. doi:10.1039/d0cp03508d
Pilania, G., Wang, C., Jiang, X., Rajasekaran, S., and Ramprasad, R. (2013). Accelerating Materials Property Predictions Using Machine Learning. Sci. Rep. 3 (1), 2810. doi:10.1038/srep02810
Pyzer-Knapp, E. O., Suh, C., Gómez-Bombarelli, R., Aguilera-Iparraguirre, J., and Aspuru-Guzik, A. (2015). What Is High-Throughput Virtual Screening? A Perspective from Organic Materials Discovery. Annu. Rev. Mater. Res. 45 (1), 195–216. doi:10.1146/annurev-matsci-070214-020823
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2016). PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. arXiv. arXiv:1612.00593.
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A., and Kim, C. (2017). Machine Learning in Materials Informatics: Recent Applications and Prospects. Npj Comput. Mater. 3 (1), 54. doi:10.1038/s41524-017-0056-5
Ryczko, K., Mills, K., Luchak, I., Homenick, C., and Tamblyn, I. (2017). Convolutional Neural Networks for Atomistic Systems. Comput. Mater. Sci. 149, 134–142. arXiv:1706.09496. doi:10.1016/j.commatsci.2018.03.005
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. (2013). Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). JOM 65 (11), 1501–1509. doi:10.1007/s11837-013-0755-4
Sanchez-Lengeling, B., and Aspuru-Guzik, A. (2018). Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering. Science 361 (6400), 360–365. doi:10.1126/science.aat2663
Simonovsky, M., and Komodakis, N. (2017). “Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs,” in Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, July 2017. arXiv:1704.02901.
Song, Y., Siriwardane, E. M. D., Zhao, Y., and Hu, J. (2021). Computational Discovery of New 2D Materials Using Deep Learning Generative Models. ACS Appl. Mater. Inter. 13 (45), 53303–53313. doi:10.1021/acsami.1c01044
Spaldin, N. A., and Ramesh, R. (2019). Advances in Magnetoelectric Multiferroics. Nat. Mater 18 (3), 203–212. doi:10.1038/s41563-018-0275-2
Sumpter, B. G. a., and Noid, D. W. (1996). On the Design, Analysis, and Characterization of Materials Using Computational Neural Networks. Annu. Rev. Mater. Sci. 26 (1), 223–277. doi:10.1146/annurev.ms.26.080196.001255
Sumpter, B. G., Vasudevan, R. K., Potok, T., and Kalinin, S. V. (2015). A Bridge for Accelerating Materials by Design. Npj Comput. Mater. 1 (1), 15008. doi:10.1038/npjcompumats.2015.8
Suzuki, K., Sakuma, M., Hori, S., Nakazawa, T., Nagao, M., Yonemura, M., et al. (2016). Synthesis, Structure, and Electrochemical Properties of Crystalline Li-P-S-O Solid Electrolytes: Novel Lithium-Conducting Oxysulfides of Li10GeP2S12 Family. Solid State Ionics 288, 229–234. doi:10.1016/j.ssi.2016.02.002
Vanhaelen, Q., Lin, Y.-C., and Zhavoronkov, A. (2020). The Advent of Generative Chemistry. ACS Med. Chem. Lett. 11 (8), 1496–1505. doi:10.1021/acsmedchemlett.0c00088
Vasudevan, R. K., Choudhary, K., Mehta, A., Smith, R., Kusne, G., Tavazza, F., et al. (2019). Materials Science in the Artificial Intelligence Age: High-Throughput Library Generation, Machine Learning, and a Pathway from Correlations to the Underpinning Physics. MRS Commun. 9 (3), 821–838. doi:10.1557/mrc.2019.95
Vasylenko, A., Gamon, J., Duff, B. B., Gusev, V. V., Daniels, L. M., Zanella, M., et al. (2021). Element Selection for Crystalline Inorganic Solid Discovery Guided by Unsupervised Machine Learning of Experimentally Explored Chemistry. Nat. Commun. 12 (1), 5561. doi:10.1038/s41467-021-25343-7
Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2012). CALYPSO: A Method for crystal Structure Prediction. Comput. Phys. Commun. 183 (10), 2063–2070. doi:10.1016/j.cpc.2012.05.008
Ward, L., Agrawal, A., Choudhary, A., and Wolverton, C. (2016). A General-Purpose Machine Learning Framework for Predicting Properties of Inorganic Materials. Npj Comput. Mater. 2 (1), 16028. doi:10.1038/npjcompumats.2016.28
Ward, L., Dunn, A., Faghaninia, A., Zimmermann, N. E. R., Bajaj, S., Wang, Q., et al. (2018). Matminer: An Open Source Toolkit for Materials Data Mining. Comput. Mater. Sci. 152, 60–69. doi:10.1016/j.commatsci.2018.05.018
Ward, L., and Wolverton, C. (2017). Atomistic Calculations and Materials Informatics: A Review. Curr. Opin. Solid State. Mater. Sci. 21 (3), 167–176. doi:10.1016/j.cossms.2016.07.002
Wu, W., Qi, Z., and Fuxin, L. (2018). “PointConv: Deep Convolutional Networks on 3D Point Clouds,” in Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, June 2018. arXiv:1811.07246.
Xie, T., and Grossman, J. C. (2018). Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/physrevlett.120.145301
Xu, Y., Lin, K., Wang, S., Wang, L., Cai, C., Song, C., et al. (2019). Deep Learning for Molecular Generation. Future Med. Chem. 11 (6), 567–597. doi:10.4155/fmc-2018-0358
Zhao, Q., Stalin, S., Zhao, C.-Z., and Archer, L. A. (2020). Designing Solid-State Electrolytes for Safe, Energy-Dense Batteries. Nat. Rev. Mater. 5 (3), 229–252. doi:10.1038/s41578-019-0165-5
Zhao, Q., Zhang, L., He, B., Ye, A., Avdeev, M., Chen, L., et al. (2021). Identifying Descriptors for Li+ Conduction in Cubic Li-Argyrodites via Hierarchically Encoding crystal Structure and Inferring Causality. Energ. Storage Mater. 40, 386–393. doi:10.1016/j.ensm.2021.05.033
Zhou, Y., and Tuzel, O. (2017). “VoxelNet: End-To-End Learning for Point Cloud Based 3D Object Detection,” in Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, June 2018. arXiv:1711.06396.
Keywords: machine learning, materials discovery, inverse design, generative adversarial networks, variational autoencoders, generative models, deep learning, artificial intelligence
Citation: Fuhr AS and Sumpter BG (2022) Deep Generative Models for Materials Discovery and Machine Learning-Accelerated Innovation. Front. Mater. 9:865270. doi: 10.3389/fmats.2022.865270
Received: 29 January 2022; Accepted: 07 March 2022;
Published: 22 March 2022.
Edited by:
Peter Fischer, Lawrence Berkeley National Laboratory, United StatesReviewed by:
Paolo Emilio Trevisanutto, National University of Singapore, SingaporeAdama Tandia, Corning Inc., United States
Copyright © 2022 Fuhr and Sumpter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Addis S. Fuhr, ZnVocmFzQG9ybmwuZ292
 Addis S. Fuhr
Addis S. Fuhr Bobby G. Sumpter
Bobby G. Sumpter