- Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, Faculty of Materials and Manufacturing, Beijing University of Technology, Beijing, China
Piezoelectric materials possess excellent electromechanical coupling characteristics, which are functional and suitable in structural vibration control. This study investigates the active control of free and forced vibration for piezoelectric-integrated functionally graded carbon nanotube reinforced composite (FG-CNTRC) plate using the finite element method (FEM). Based on the first-order shear deformation theory (FSDT), the governing equations of the motion of a piezoelectric-integrated FG-CNTRC plate are derived by Hamilton’s principle. The convergence and accuracy of the numerical method is verified through the results of natural frequencies. The influences of CNT volume fraction, CNT distribution type, piezoelectric layer thickness-to-plate thickness ratio, and boundary condition on the natural frequencies are investigated. A constant gain velocity feedback algorithm is used to achieve the dynamic response control of the piezoelectric-integrated FG-CNTRC plate. In addition, the effects of dynamic load, feedback control gain, and boundary condition on the dynamic response of the plate are studied. Numerical results indicate that active control is promising for practical applications in civil and mechanical engineering.
Introduction
The carbon nanotube (CNT) is a remarkable reinforcement for composite materials with excellent mechanical, electrical, absorbance, and thermal conduction properties (Chen et al., 2018; Li et al., 2020; Wang et al., 2021a; Wang et al., 2022), including light weight, superior stiffness, and strength, and is commonly used in aerospace, automotive, and civil engineering fields (Zhang et al., 2022). The functionally graded materials (FGMs) are inhomogenous composites, and the material properties change smoothly and continuously along one or more directions (Li et al., 2019; Tam et al., 2020; Yang et al., 2021a). Compared with laminated materials, FGMs are able to reduce thermal stresses, residual stresses, and stress concentration factors (Datta, 2021). Inspired by the concept of FGMs, the functionally graded (FG) distribution of reinforcement has been successfully applied for various structures (Wang et al., 2021b; Yang et al., 2021b; Yang et al., 2022a; Yang et al., 2022b).
Plates are primary structural components in numerous engineering fields (Wang et al., 2021c), which are very vulnerable to vibration under complex mechanical load and severe environmental condition. The undesirable vibration affects the accuracy of the precision instrument, accelerates the fatigue failure of the equipment, and even leads to serious safety incidents and enormous property damage (Zhang et al., 2017). Consequently, the investigation of civil and mechanical engineering aims at suppressing the vibration of plate structures such as trim panel, glazing window, and separating wall (Okina et al., 2019). Piezoelectric materials have excellent electromechanical coupling characteristics, which are able to realize the mutual conversion of electrical energy and mechanical energy. In addition, piezoelectric materials are usually used to achieve the vibration control of flying-wing, helicopter blade, space station hull, solar panel, reflector, and large sophisticated antenna owing to the high sensitivity and quick response (Tzou et al., 2004). Zhang et al. (2019a) reviewed the modeling techniques of piezoelectric structures. Nguyen-Quang et al. (2018) proposed an isogeometric approach to study the dynamic response of a laminated CNTRC plate integrated with piezoelectric layers.
Currently, the vibration control methods generally include passive control (Chen et al., 2020), semi-active control (Gardonio et al., 2021), and active control (Niu et al., 2018). Passive control is easy to implement and does not require an external power source (Thenozhi and Yu, 2013). However, due to the inevitable changes of structural properties and the stochastic nature of external excitations, passive control performance is not that excellent (Casciati and Yildirim, 2012). Semi-active control generates a pleasurable control force with low energy consumption (Das et al., 2012). Owing to outstanding control effect and excellent environmental adaptability, active control is effective to suppress low-frequency structural vibration and becomes the main method to realize the static deflection control and dynamic response control of structures (Qureshi et al., 2014; Ali et al., 2021). Nguyen et al. (2019) investigated the free vibration and dynamic response of smart FG metal foam plate structures reinforced by graphene platelets and analyzed the active control of the plates with piezoelectric sensor and actuator layers. Song et al. (2016) derived the discrete ordinary differential equations using Hamilton’s principle and assumed mode method, and studied the active vibration control of the FG-CNTRC plate using piezoelectric actuator/sensor pairs. Zhang et al. (2016b) studied the optimal shape control of FG-CNTRC plates and performed the shape control by optimizing the open-loop control voltages and the closed-loop displacement feedback control gain. Li et al. (2018) used the velocity feedback and LQR control algorithm to design the controller and indicated that the controller is very effective in suppressing the vibration of a composite pyramidal truss core sandwich plate. He et al. (2002) analyzed the static and dynamic responses of the FG plate based on the displacement and velocity feedback control algorithm.
The FEM has been successfully applied to the active vibration control of smart structures in civil engineering, control engineering, and computer science. He et al. (2001) applied the FEM to investigate the active shape and vibration control of the FGM plate. Based on the first-order shear deformation theory (FSDT), Liew et al. (2004) developed a generic FEM model to study the static deflection and dynamic vibration control of FGM shells. Parandvar and Farid (2016) established a nonlinear FEM model for the FGM plate under thermal, static, and harmonic loads and studied the effects of initial conditions and static pressure on the dynamic response of the system. Tian et al. (2020) presented an accurate two-noded laminated piezoelectric beam element to study the dynamic response and active vibration control of the laminated composite beam. Zhang et al. (2019b) developed a geometrically nonlinear FEM model to study the static and dynamic response of the piezoelectric integrated FG-CNTRC plate.
Various active control methods have been proposed to analyze the FGM and FG-CNTRC plate with piezoelectric layers. The velocity feedback control enhances the system damping and controls the oscillation amplitude effectively to achieve vibration control (Amezquita-Sanchez et al., 2014). In this study, an efficient and reliable control system is developed by the velocity feedback control algorithm and FEM to protect structures from natural or man-made hazards, which provides important theoretical significance and practical value for the dynamic response analysis of civil structures with complex external environmental factors and electromechanical coupling effect. The active control of free and forced vibration for the piezoelectric-integrated FG-CNTRC plate is investigated with four distribution types of CNTs. Based on the FSDT and Hamilton’s principle, the governing equations of motion are derived, and the velocity feedback control algorithm is adopted to achieve the dynamic response control. The control effect of the piezoelectric-integrated FG-CNTRC plate is analyzed under step load and sine excitation, and the effect of CNT volume fraction and feedback control gain is investigated on the vibration amplitude. In addition, the variation of natural frequency for the FG-CNTRC plate with piezoelectric layer thickness and boundary condition is studied in detail.
Formulations of the FG-CNTRC Plate With Piezoelectric Layers
Material Properties
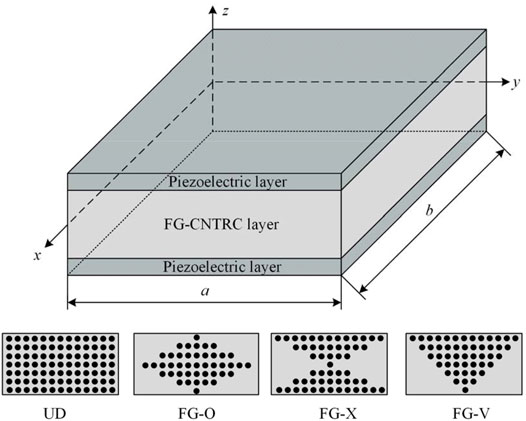
In this section, the plate structure comprises piezoelectric materials for the top and bottom layers and FG-CNTRC for the middle layer, as shown in Figure 1. Four CNT distributions along the thickness direction of the FG-CNTRC layer are considered including uniformly distributed (UD) and functionally graded-V (FG-V), FG-O, and FG-X. In the UD pattern, the CNT is uniformly distributed along the thickness direction. In the FG-V distribution type, CNT is found in abundance on the top of the plate while poorly distributed in the bottom. Moreover, the CNT is abundant in the middle of the plate while poorly distributed in the top and bottom in the FG-O distribution type. In contrast, the CNT is abundant in both the top and the bottom of the plate while poorly distributed in the middle in the FG-X distribution type. The CNT volume fraction of each layer is expressed as
where
According to the rule of mixtures (Shen, 2009), Young’s modulus and the shear modulus of the CNTRC plate are expressed as
where
Governing Equation
In the piezoelectric-integrated FG-CNTRC plate with four distribution types of CNT, the core layer is made of FG-CNTRC material. The schematic sketch of the piezoelectric-integrated FG-CNTRC plate is illustrated in Figure 1. The length and width of the plate are denoted by
According to the FSDT, the displacement fields are defined as
where
The stress components of the kth layer in the FG-CNTRC plate are calculated by the constitutive relation as
where
Axial forces and bending moments are expressed by the following equations
where
The stress and moment resultants are obtained as follows:
The in-plane stiffness matrix, coupled bending–stretching matrix, and bending–stiffness matrix are expressed as
The linear constitutive relations of the piezoelectric-integrated plate are expressed as
where
The electric variables need to satisfy Maxwell’s static electricity equation, where the divergence for electric displacements vanishes at any arbitrary point through the piezoelectric actuator and sensor layer thickness, that is,
The electric potential is approximately assumed as a combination of cosine and linear variation (Wang, 2002)
where
The piezoelectric and dielectric constant matrices are defined as
The strain energy of the plate is obtained as
The kinetic energy is obtained as
where
where fs represents the external mechanical surface load and qs represents the external surface charge. The total energy function of the piezoelectric-integrated FG-CNTRC plate is expressed as
Finite Element Formulation
In terms of the active control analysis for the CNTRC plate, the FEM is an efficient numerical technique among the community of laminated composite beams, plates, and shells due to its robustness in handling engineering practical problems with complex geometry and complicated condition (Steiger and Mokrý, 2015). The calculation amount of the FEM increases with the increase of element number, and an appropriate element number is needed to satisfy the requirements of computational accuracy and efficiency. The plate is discretized into a certain number of quadrilateral elements, and the approximate displacement functions of arbitrary quadrilateral elements are expressed as
The membrane strain, bending strain, and shear strain matrix of the plate are presented as
where
Substituting Eqs 36–39, 41, 47 into Eq. 40, the governing equations of motion are obtained as
where the detailed expressions of matrices are shown in Appendix A.
The FEM is used to analyze the free and forced vibration control of the piezoelectric-integrated FG-CNTRC plate. Three boundary conditions are considered including simply supported (S), fully clamped (C), and free (F) edge. The simply supported boundary condition is expressed as
The fully clamped boundary condition is expressed as
Since the electric field intensities
Substituting Eq. 55 into Eq. 51, the governing equations of motion are obtained as follows:
Velocity Feedback Control
When the external charge
where the sensor charge is determined by
The actuator voltage
where the constant
where
where
Results and Discussion
In this section, the FEM is used to analyze the free and forced vibration control of the piezoelectric-integrated FG-CNTRC plate.
Convergence and Comparison Study
The convergence and comparison study of the piezoelectric-integrated plate under three different boundary conditions is studied. The length and width of the piezoelectric-integrated plate are
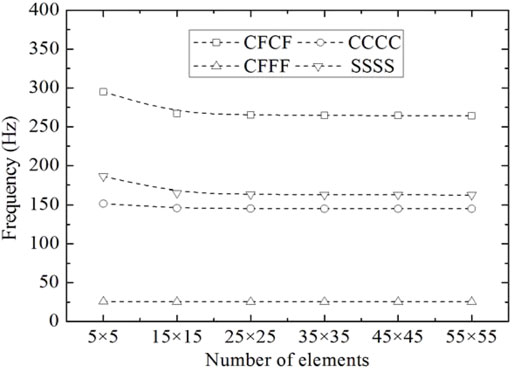
FIGURE 2. Convergence study of the piezoelectric-integrated plate under different boundary conditions.
The first six natural frequencies of the piezoelectric-integrated plate under the CCCC boundary condition are presented in Table 1 and are compared with those obtained based on the CLPT (He et al., 2001), FSDT (Kiani, 2016a), and HSDT (Selim et al., 2016). It is observed that the maximum relative errors with the FSDT and HSDT are 1.28 and 0.22%, respectively, and the CLPT is less than 2.5%, which is possibly because the element number in He et al. (2001) is 8 × 8 and did not give a completely converged value of the frequency (Askari Farsangi et al., 2013). In Table 2, the maximum relative error of the first six frequencies for the piezoelectric-integrated plate is about 0.28% under the SSSS boundary condition, which proves the accuracy of the numerical method and the applicability of different boundary conditions. Figures 3, 4 depict the first six vibration modes of CFFF and SSSS piezoelectric-integrated plates.
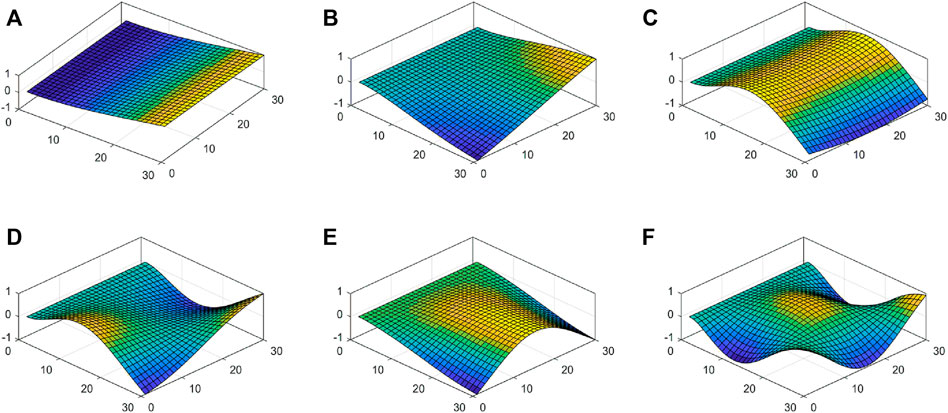
FIGURE 3. First six modes of the piezoelectric-integrated FG plate (CFFF): (A) first mode; (B) second mode; (C) third mode; (D) fourth mode; (E) fifth mode; and (F) sixth mode.
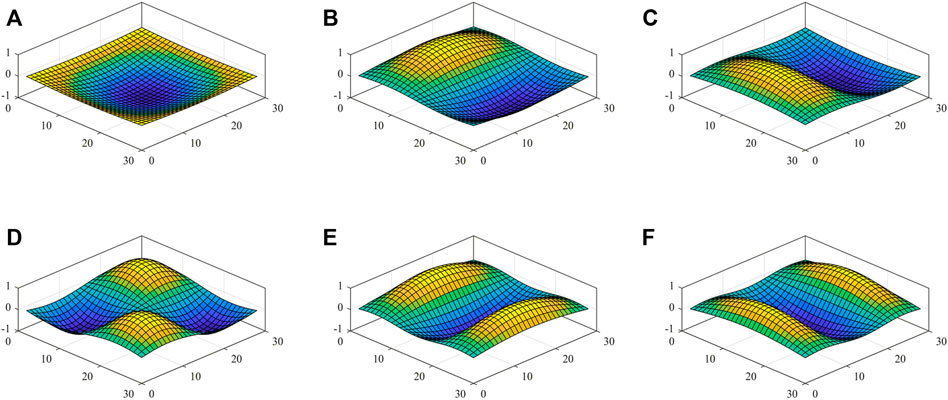
FIGURE 4. First six modes of the piezoelectric-integrated FG plate (SSSS): (A) first mode; (B) second mode; (C) third mode; (D) fourth mode; (E) fifth mode; and (F) sixth mode.
Free Vibration
In this section, CNT and poly methyl methacrylate (PMMA) are used as the reinforcement and matrix materials of the core layer. Unless otherwise stated, the geometrical and material parameters of the piezoelectric-integrated FG-CNTRC plate are listed as follows: Young’s modulus, Poisson’s ratio, and density of PMMA are
Tables 3, 4 indicate the effects of CNT volume fraction and distribution type on the first three frequencies for the piezoelectric-integrated FG-CNTRC plate under CCCC and SSSS boundary conditions, respectively. In these two cases, the numerical result of natural frequency increases as the CNT volume fraction increases. In addition, FG-X has the highest natural frequency among the four CNT distributions of FG-CNTRC plates, and the FG-O CNTRC plate has the lowest one, which matches the data from the existing literature consistently (Thanh et al., 2018). This phenomenon indicates that the volume fraction and distribution type of CNTs affect the stiffness of the piezoelectric-integrated FG-CNTRC plate significantly.
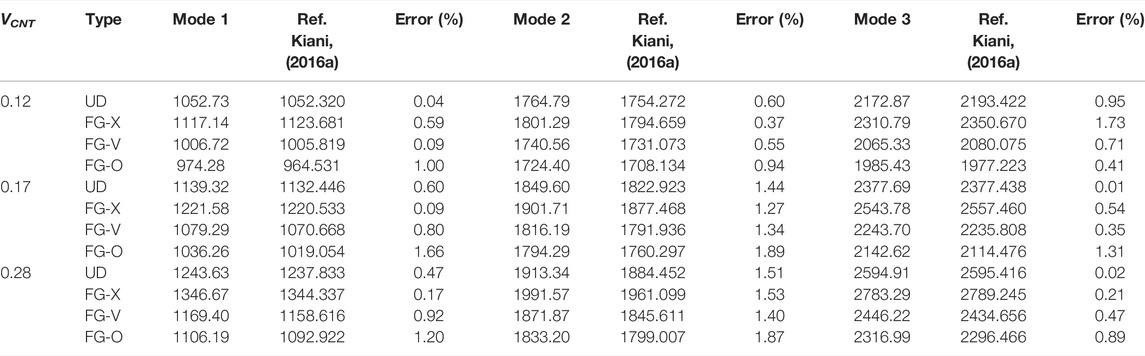
TABLE 3. Effects of CNT volume fraction and distribution type on the first three frequencies (CCCC).
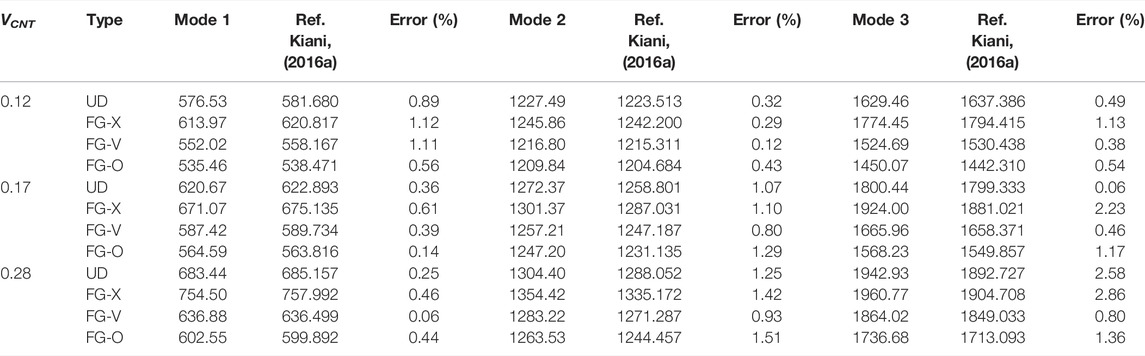
TABLE 4. Effects of CNT volume fraction and distribution type on the first three frequencies (SSSS).
The frequency difference ratio between the piezoelectric-integrated FG-CNTRC plate and core plate is generally adopted to quantify the effect of the piezoelectric layer thickness on fundamental frequency. Figure 5 demonstrates the effect of the piezoelectric layer thickness on the fundamental frequency for the piezoelectric-integrated FG-CNTRC plate. The frequency difference ratio is positive when
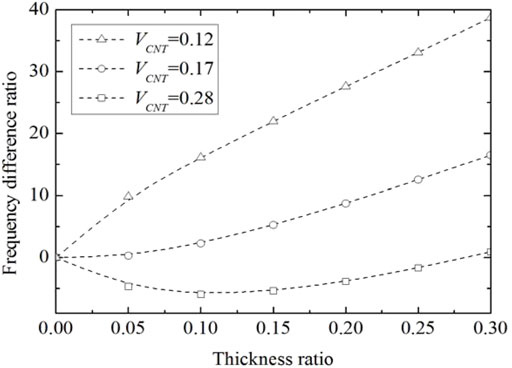
FIGURE 5. Variation of frequency difference ratio with the thickness ratio under SSSS boundary conditions.
Active Vibration Control
The active control of dynamic vibration is studied for the piezoelectric-integrated FG-CNTRC plate with two PZT-5A piezoelectric layers. The velocity feedback control algorithm is used to control the vibration of the piezoelectric-integrated FG-CNTRC plate. Figure 6 illustrates the results under SSSS boundary condition with different velocity feedback gains. When the feedback gain is equal to 0.001, the deflection of plate midpoint converges to zero after a time period of 0.25 s, and the period is shortened to 0.1 s when the feedback gain is 0.005. The vibration response of the piezoelectric-integrated FG-CNTRC plate attenuates rapidly while the velocity feedback gain increases. In addition, it should be emphasized that the feedback control gain is restricted because of the failure voltage of the piezoelectric material.
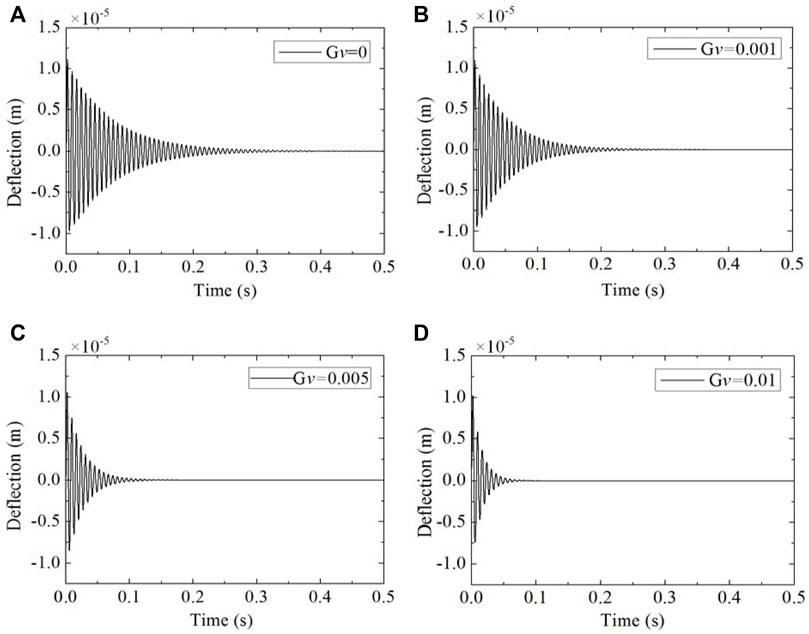
FIGURE 6. Active vibration control of the piezoelectric-integrated FG plate under SSSS boundary conditions with different velocity feedback gains: (A) Gv = 0; (B) Gv = 0.001; (C) Gv = 0.005; (D) Gv = 0.01.
The effects of boundary condition and dynamic load on the vibration response are investigated for the piezoelectric-integrated FG-CNTRC plate. Figures 7, 8 present the deflection response of the piezoelectric-integrated plate subject to step load and sine excitation under the CFCF boundary condition. In the time period
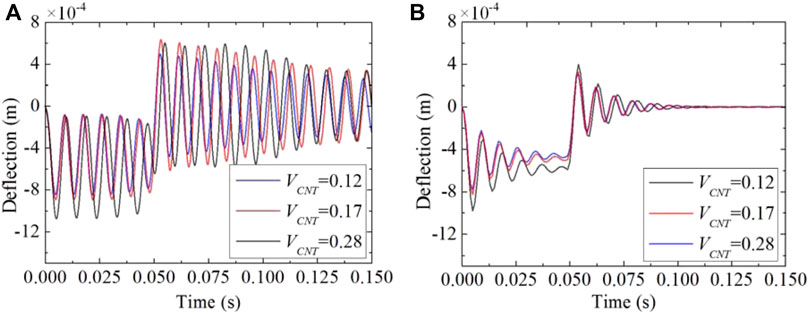
FIGURE 7. Central deflection response control under CFCF boundary conditions subjected to step load with different velocity feedback gains: (A) Gv = 0.001; (B) Gv = 0.01.
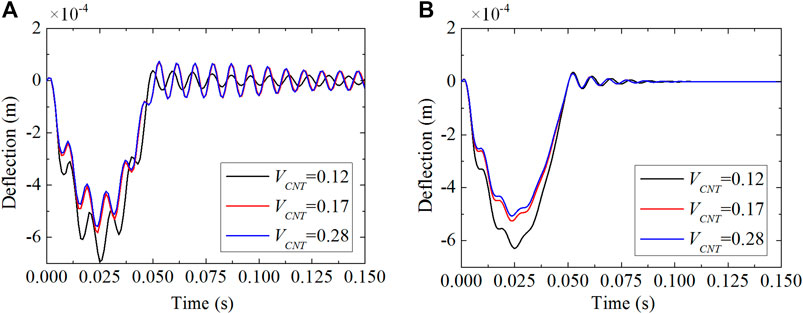
FIGURE 8. Central deflection response control under CFCF boundary conditions subjected to sine excitation with different velocity feedback gains: (A) Gv = 0.001; (B) Gv = 0.01.
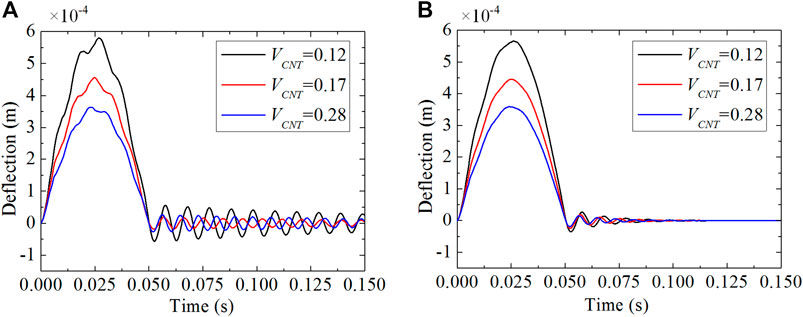
FIGURE 9. Central deflection response control under SSSS boundary conditions subjected to sine excitation with different velocity feedback gains: (A) Gv = 0.001; (B) Gv = 0.01.
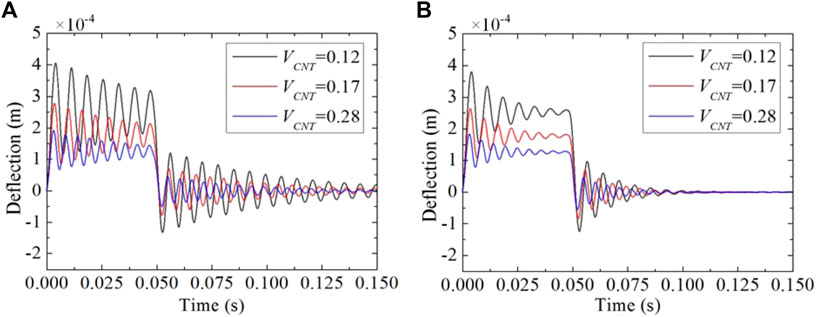
FIGURE 10. Central deflection response control under SSSS boundary conditions subjected to step load with different velocity feedback gains: (A) Gv = 0.001; (B) Gv = 0.01.
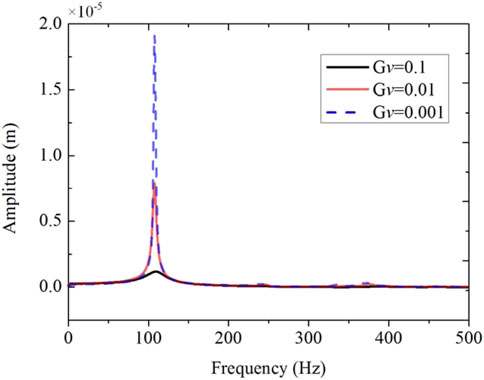
The amplitude–frequency response curve for the piezoelectric FG-CNTRC plate is shown in Figure 11. The vibration responses in the frequency domain are investigated for various feedback gains. With the increase of velocity feedback control gain, the active damping of the piezoelectric FG-CNTRC plate increases and the resonant amplitude decreases, which depicts that the velocity feedback control gain plays a major role in the process of vibration attenuation.
Conclusion
Based on the FSDT, the governing equations of the motion of the piezoelectric-integrated FG-CNTRC plate are derived by Hamilton’s principle. The active control of free and forced vibration for the piezoelectric-integrated FG-CNTRC plate under different boundary conditions is investigated using the FEM. The main conclusions are summarized as follows:
(1) The volume fraction and distribution type of the CNT affect the stiffness of the piezoelectric-integrated FG-CNTRC plate significantly. The natural frequency of the piezoelectric-integrated FG-CNTRC plate increases with the increase in CNT volume fraction, and the natural frequency of the piezoelectric FG-X CNTRC plate is relatively large compared with those of the other CNT distribution types including UD, FG-O, and FG-V.
(2) The fundamental frequency of the piezoelectric-integrated plate is related to the combined effect of mass density, elastic modulus, and electromechanical coupling. The increase of piezoelectric layer thickness leads to the increase of fundamental frequency for the piezoelectric-integrated plate owing to electromechanical coupling.
(3) The vibration response control of the piezoelectric-integrated FG-CNTRC plate is investigated under the step load and sinusoidal excitation. The velocity feedback control method is able to achieve the dynamic response control of the piezoelectric FG-CNTRC plate with excellent control effect on both forced vibration and free vibration.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
XY: methodology, investigation, and writing—original draft. XZ: conceptualization and writing—review and editing. JW: writing—review and editing, supervision, project administration, and funding acquisition.
Funding
The authors gratefully acknowledge the support of the National Natural Science Foundation of China (Grant No. 12072003) and the Beijing Natural Science Foundation (Grant No. 1222001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abad, F., and Rouzegar, J. (2019). Exact Wave Propagation Analysis of Moderately Thick Levy-type Plate with Piezoelectric Layers Using Spectral Element Method. Thin-Walled Struct. 141, 319–331. doi:10.1016/j.tws.2019.04.007
Ali, S., Gavgani, M., Hojat, H., and Fahimi, M. (2021). Semi-Active Control of Jacket Platforms under Wave Loads Considering. fluid-structure interaction 117, 1–11.
Amezquita-Sanchez, J. P., Dominguez-Gonzalez, A., Sedaghati, R., De Jesus Romero-Troncoso, R., and Osornio-Rios, R. A. (2014). Vibration Control on Smart Civil Structures: A Review. Mech. Adv. Mater. Struct. 21, 23–38. doi:10.1080/15376494.2012.677103
Askari Farsangi, M. A., and Saidi, A. R. (2012). Levy Type Solution for Free Vibration Analysis of Functionally Graded Rectangular Plates with Piezoelectric Layers. Smart Mater. Struct. 21, 094017. doi:10.1088/0964-1726/21/9/094017
Askari Farsangi, M. A., Saidi, A. R., and Batra, R. C. (2013). Analytical Solution for Free Vibrations of Moderately Thick Hybrid Piezoelectric Laminated Plates. J. Sound Vib. 332, 5981–5998. doi:10.1016/j.jsv.2013.05.010
Barati, M. R., and Zenkour, A. M. (2016). Electro-Thermoelastic Vibration of Plates Made of Porous Functionally Graded Piezoelectric Materials under Various Boundary Conditions. J. Vib Control. 24 (10), 319–331. doi:10.1177/1077546316672788
Casciati, F., and Yildirim, U. (2012). Active and Semi-Active Control of Structures Theory and Applications: A Review of Recent Advances. Jour Ntell Materl Syst. Struct. 23 (11), 1181-1195. doi:10.1177/1045389x12445029
Chen, Y., Song, Z., and Li, F. (2020). Generating Mechanism of Mode Localization for the Beams and its Application in the Passive Vibration Control. J. Sound Vib. 485, 115531. doi:10.1016/j.jsv.2020.115531
Chen, Z., Wu, Y., Yang, Y., Li, J., Xie, B., Li, X., et al. (2018). Multilayered Carbon Nanotube Yarn Based Optoacoustic Transducer with High Energy Conversion Efficiency for Ultrasound Application. Nano Energy 46, 314–321. doi:10.1016/j.nanoen.2018.02.006
Das, D., Datta, T. K., and Madan, A. (2012). Semiactive Fuzzy Control of the Seismic Response of Building Frames with MR Dampers. Earthquake Engng. Struct. Dyn. 41, 99–118. doi:10.1002/eqe.1120
Datta, P. (2021). Active Vibration Control of Axially Functionally Graded Cantilever Beams by Finite Element Method. Mater. Today Proc. 44, 2543–2550. doi:10.1016/j.matpr.2020.12.628
Gardonio, P., Turco, E., Kras, A., Bo, L. D., and Casagrande, D. (2021). Semi-active Vibration Control Unit Tuned to Maximise Electric Power Dissipation. J. Sound Vibr. 499, 116000. doi:10.1016/j.jsv.2021.116000
He, X. Q., Liew, K. M., Ng, T. Y., and Sivashanker, S. (2002). A FEM Model for the Active Control of Curved FGM Shells Using Piezoelectric Sensor/actuator Layers. Int. J. Numer. Meth. Engng. 54, 853–870. doi:10.1002/nme.451
He, X. Q., Ng, T. Y., Sivashanker, S., and Liew, K. M. (2001). Active Control of FGM Plates with Integrated Piezoelectric Sensors and Actuators. Int. J. Sol. Struct. 38, 1641–1655. doi:10.1016/s0020-7683(00)00050-0
Ke, L.-L., Liu, C., and Wang, Y.-S. (2015). Free Vibration of Nonlocal Piezoelectric Nanoplates under Various Boundary Conditions. Physica E: Low-Dimensional Syst. Nanostruct. 66, 93–106. doi:10.1016/j.physe.2014.10.002
Kiani, Y. (2016). Free Vibration of Functionally Graded Carbon Nanotube Reinforced Composite Plates Integrated with Piezoelectric Layers. Comput. Maths. Appl. 72, 2433–2449. doi:10.1016/j.camwa.2016.09.007
Kiani, Y. (2016). Thermal Postbuckling of Temperature-dependent sandwich Beams with Carbon Nanotube-Reinforced Face Sheets. J. Therm. Stresses 39, 1098–1110. doi:10.1080/01495739.2016.1192856
Li, J., Xue, Y., Li, F., and Narita, Y. (2019). Active Vibration Control of Functionally Graded Piezoelectric Material Plate. Compos. Struct. 207, 509–518. doi:10.1016/j.compstruct.2018.09.053
Li, J., Yang, Y., Chen, Z., Lei, S., Shen, M., Zhang, T., et al. (2020). Self-healing: A New Skill Unlocked for Ultrasound Transducer. Nano Energy 68, 104348. doi:10.1016/j.nanoen.2019.104348
Li, M., Li, F., and Jing, X. (2018). Active Vibration Control of Composite Pyramidal Lattice Truss Core Sandwich Plates. J. Aerosp. Eng. 31, 04017097. doi:10.1061/(asce)as.1943-5525.0000817
Liew, K. M., He, X. Q., and Kitipornchai, S. (2004). Finite Element Method for the Feedback Control of FGM Shells in the Frequency Domain via Piezoelectric Sensors and Actuators. Comput. Methods Appl. Mech. Eng. 193, 257–273. doi:10.1016/j.cma.2003.09.009
Nguyen, N. V., Lee, J., and Nguyen-Xuan, H. (2019). Active Vibration Control of GPLs-Reinforced FG Metal Foam Plates with Piezoelectric Sensor and Actuator Layers. Composites B: Eng. 172, 769–784. doi:10.1016/j.compositesb.2019.05.060
Nguyen-Quang, K., Vo-Duy, T., Dang-Trung, H., and Nguyen-Thoi, T. (2018). An Isogeometric Approach for Dynamic Response of Laminated FG-CNT Reinforced Composite Plates Integrated with Piezoelectric Layers. Comput. Methods Appl. Mech. Eng. 332, 25–46. doi:10.1016/j.cma.2017.12.010
Niu, W., Li, B., Xin, T., and Wang, W. (2018). Vibration Active Control of Structure with Parameter Perturbation Using Fractional Order Positive Position Feedback Controller. J. Sound Vibr. 430, 101–114. doi:10.1016/j.jsv.2018.05.038
Okina, F. T. A., Baro, S., Ripamonti, F., and Buiochi, F. (2019). Modelling and Active Control Aiming at Enhancing the Sound Transmission Loss of Thin Partition Panels. Smart Struct. Mater. Nondestruct Evalua Hea Monit. 10967.
Parandvar, H., and Farid, M. (2016). Large Amplitude Vibration of FGM Plates in thermal Environment Subjected to Simultaneously Static Pressure and Harmonic Force Using Multimodal FEM. Compos. Struct. 141, 163–171. doi:10.1016/j.compstruct.2016.01.044
Qureshi, E. M., Shen, X., and Chen, J. (2014). Vibration Control Laws via Shunted Piezoelectric Transducers: A Review. Int. J. Aeronaut. Space Sci. 15, 1–19. doi:10.5139/ijass.2014.15.1.1
Selim, B. A., Zhang, L. W., and Liew, K. M. (2017). Active Vibration Control of CNT-Reinforced Composite Plates with Piezoelectric Layers Based on Reddy's Higher-Order Shear Deformation Theory. Compos. Struct. 163, 350–364. doi:10.1016/j.compstruct.2016.11.011
Selim, B. A., Zhang, L. W., and Liew, K. M. (2016). Active Vibration Control of FGM Plates with Piezoelectric Layers Based on Reddy's Higher-Order Shear Deformation Theory. Compos. Struct. 155, 118–134. doi:10.1016/j.compstruct.2016.07.059
Shen, H.-S. (2009). Nonlinear Bending of Functionally Graded Carbon Nanotube-Reinforced Composite Plates in thermal Environments. Compos. Struct. 91, 9–19. doi:10.1016/j.compstruct.2009.04.026
Shen, H.-S. (2011). Postbuckling of Nanotube-Reinforced Composite Cylindrical Shells in thermal Environments, Part I: Axially-Loaded Shells. Compos. Struct. 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011
Shen, H.-S. (2014). Torsional Postbuckling of Nanotube-Reinforced Composite Cylindrical Shells in thermal Environments. Compos. Struct. 116, 477–488. doi:10.1016/j.compstruct.2014.05.039
Shen, H.-S., and Zhang, C.-L. (2010). Thermal Buckling and Postbuckling Behavior of Functionally Graded Carbon Nanotube-Reinforced Composite Plates. Mater. Des. 31, 3403–3411. doi:10.1016/j.matdes.2010.01.048
Song, Z. G., Zhang, L. W., and Liew, K. M. (2016). Active Vibration Control of CNT Reinforced Functionally Graded Plates Based on a Higher-Order Shear Deformation Theory. Int. J. Mech. Sci. 105, 90–101. doi:10.1016/j.ijmecsci.2015.11.019
Steiger, K., and Mokrý, P. (2015). Finite Element Analysis of the Macro Fiber Composite Actuator: Macroscopic Elastic and Piezoelectric Properties and Active Control Thereof by Means of Negative Capacitance Shunt Circuit. Smart Mater. Struct. 24, 025026. doi:10.1088/0964-1726/24/2/025026
Tam, M., Yang, Z., Zhao, S., Zhang, H., Zhang, Y., and Yang, J. (2020). Nonlinear Bending of Elastically Restrained Functionally Graded Graphene Nanoplatelet Reinforced Beams with an Open Edge Crack. Thin-Walled Struct. 156, 106972. doi:10.1016/j.tws.2020.106972
Thanh, C.-L., Phung-Van, P., Thai, C. H., Nguyen-Xuan, H., and Abdel Wahab, M. (2018). Isogeometric Analysis of Functionally Graded Carbon Nanotube Reinforced Composite Nanoplates Using Modified Couple Stress Theory. Compos. Struct. 184, 633–649. doi:10.1016/j.compstruct.2017.10.025
Thenozhi, S., and Yu, W. (2013). Advances in Modeling and Vibration Control of Building Structures. Annu. Rev. Control. 37, 346–364. doi:10.1016/j.arcontrol.2013.09.012
Tian, J., Guo, Q., and Shi, G. (2020). Laminated Piezoelectric Beam Element for Dynamic Analysis of Piezolaminated Smart Beams and GA-based LQR Active Vibration Control. Compos. Struct. 252, 112480. doi:10.1016/j.compstruct.2020.112480
Tzou, H. S., Lee, H.-J., and Arnold, S. M. (2004). Smart Materials, Precision Sensors/actuators, Smart Structures, and Structronic Systems. Mech. Adv. Mater. Struct. 11, 367–393. doi:10.1080/15376490490451552
Wang, J. F., Cao, S. H., and Zhang, W. (2021). Thermal Vibration and Buckling Analysis of Functionally Graded Carbon Nanotube Reinforced Composite Quadrilateral Plate. Eur. J. Mech. - A/Solids 85, 104105. doi:10.1016/j.euromechsol.2020.104105
Wang, J. F., Shi, S. Q., Yang, J. P., and Zhang, W. (2021). Multiscale Analysis on Free Vibration of Functionally Graded Graphene Reinforced PMMA Composite Plates. Appl. Math. Model. 98, 38–58. doi:10.1016/j.apm.2021.04.023
Wang, J. F., Yang, J. P., Tam, L.-h., and Zhang, W. (2022). Effect of CNT Volume Fractions on Nonlinear Vibrations of PMMA/CNT Composite Plates: A Multiscale Simulation. Thin-Walled Struct. 170, 108513. doi:10.1016/j.tws.2021.108513
Wang, J. F., Yang, J. P., Tam, L.-h., and Zhang, W. (2021). Molecular Dynamics-Based Multiscale Nonlinear Vibrations of PMMA/CNT Composite Plates. Mech. Syst. Signal Process. 153, 107530. doi:10.1016/j.ymssp.2020.107530
Wang, Q. (2002). Axi-symmetric Wave Propagation in a cylinder Coated with a Piezoelectric Layer. Int. J. Sol. Struct. 39, 3023–3037. doi:10.1016/s0020-7683(02)00233-0
Yang, Z., Lu, H., Sahmani, S., and Safaei, B. (2021a). Isogeometric Couple Stress Continuum-Based Linear and Nonlinear Flexural Responses of Functionally Graded Composite Microplates with Variable Thickness. Arch. Civ Mechl Eng. 21, 1–19. doi:10.1007/s43452-021-00264-w
Yang, Z., Wu, D., Yang, J., Lai, S., Lv, J., Liu, A., et al. (2021b). Thin-Walled Structures Dynamic Buckling of Rotationally Restrained FG Porous Arches Reinforced with Graphene Nanoplatelets under a Uniform Step LoadThin-Walled Struct.. 166, 1–11. doi:10.1016/j.tws.2021.108103
Yang, Z., Liu, A., Lai, S.-K., Safaei, B., Lv, J., Huang, Y., et al. (2022). Thermally Induced Instability on Asymmetric Buckling Analysis of Pinned-Fixed FG-GPLRC Arches. Eng. Struct. 250, 113243. doi:10.1016/j.engstruct.2021.113243
Yang, Z., Safaei, B., Sahmani, S., and Zhang, Y. (2022). A Couple-Stress-Based Moving Kriging Meshfree Shell Model for Axial Postbuckling Analysis of Random Checkerboard Composite Cylindrical Microshells. Thin-Walled Struct. 170, 108631. doi:10.1016/j.tws.2021.108631
Zhang, B.-L., Han, Q.-L., and Zhang, X.-M. (2017). Recent Advances in Vibration Control of Offshore Platforms. Nonlinear Dyn. 89, 755–771. doi:10.1007/s11071-017-3503-4
Zhang, L. W., Song, Z. G., and Liew, K. M. (2016). Optimal Shape Control of CNT Reinforced Functionally Graded Composite Plates Using Piezoelectric Patches. Composites Part B: Eng. 85, 140–149. doi:10.1016/j.compositesb.2015.09.044
Zhang, S.-Q., Zhao, G.-Z., Rao, M. N., Schmidt, R., and Yu, Y.-J. (2019). A Review on Modeling Techniques of Piezoelectric Integrated Plates and Shells. J. Intell. Mater. Syst. Struct. 30, 1133–1147. doi:10.1177/1045389x19836169
Zhang, S. Q., Gao, Y. S., Zhao, G. Z., Yu, Y. J., Chen, M., and Wang, X. F. (2019). Geometrically Nonlinear Analysis of CNT-Reinforced Functionally Graded Composite Plates Integrated with Piezoelectric Layers. Compos. Struct. 234 (6348), 111694. doi:10.1016/j.compstruct.2019.111694
Zhang, W., He, L. J., and Wang, J. F. (2022). Content-Dependent Nonlinear Vibration of Composite Plates Reinforced with Carbon Nanotubes. J. Vib Eng. Technol. 10, 1–12. doi:10.1007/s42417-022-00441-y
Appendix A
Keywords: first-order shear deformation theory, Hamilton’s principle, velocity feedback control, functionally graded materials, active vibration control
Citation: Yu XL, Zhang XH and Wang JF (2022) Active Vibration Control of Functionally Graded Carbon Nanotube Reinforced Composite Plate with Coupled Electromechanical Actuation. Front. Mater. 9:861388. doi: 10.3389/fmats.2022.861388
Received: 24 January 2022; Accepted: 15 March 2022;
Published: 26 April 2022.
Edited by:
Zhicheng Yang, Zhongkai University of Agriculture and Engineering, ChinaReviewed by:
Kim Meow Liew, City University of Hong Kong, Hong Kong SAR, ChinaYouheng Dong, Nanjing University of Aeronautics and Astronautics, China
Jinqiang Li, Harbin Engineering University, China
Copyright © 2022 Yu, Zhang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. F. Wang, amYud2FuZ0BianV0LmVkdS5jbg==
 X. L. Yu
X. L. Yu X. H. Zhang
X. H. Zhang J. F. Wang
J. F. Wang