Broadband Transformation Acoustic Waveguide With Anisotropic Density Based on Pentamode Metamaterials

Multiple layer anisotropic fluid medium is critical to the realization of transformation acoustic devices, such as cloak or bend waveguide. Pentamode metamaterials have attracted extensive attention as a solid artificial version with anisotropic modulus to approximate liquids. In this paper, we present an approach to realize fluid-like anisotropic density by using pentamode materials, and an underwater bend acoustic waveguide with anisotropic density is designed and fabricated to demonstrate the effectiveness of it. Simulation results indicate that, compared with anisotropic-modulus design by using pentamode materials, wider bandwidth acoustic modulation effect can be obtained. An in-depth and comprehensive analysis of the mechanisms of the broadband characteristics is provided by calculating the band structure of the pentamode metamaterials constituting the acoustic waveguides and analyzing their vibration modes. Finally, remarkable wavefront manipulation for underwater acoustics based on the acoustic waveguide with anisotropic density is experimentally verified.

Introduction

Acoustic metamaterials are artificial periodic structures with subwavelength scales that exhibit extraordinary acoustic properties (Liu et al., 2000; Norris, 2009; Assouar et al., 2018), such as negative mass density or modulus (Ding et al., 2007; Huang et al., 2009; Liu et al., 2011; Xu et al., 2020), negative Poisson’s ratio (Burns, 1987; Bertoldi et al., 2010; Li et al., 2017), and anisotropic density or modulus (Torrent and Sánchez-Dehesa, 2008; Wu et al., 2012; Kutsenko et al., 2017). Transformation acoustics is one of the most important theoretical approaches applied to the design of acoustic metamaterials (Cummer et al., 2007; Norris, 2008; Milton et al., 2010), the basic idea of which is to regard an arbitrary propagation path of acoustic waves as the path generated by the linear propagation path after specific coordinate transformations, and then apply the specific coordinate transformation to the original spatial distribution of uniform material parameters. Finally, the spatial distribution of material parameters that realize the arbitrary propagation path of the acoustic waves can be obtained. Theoretically, transformation acoustics provides unprecedented flexibility for manipulating acoustic waves at will, and is therefore widely employed to design unconventional acoustic devices, such as acoustic cloaks (Cummer et al., 2008; Chen and Chan, 2010; Chen et al., 2017; Bi et al., 2018), superlens (Zhu et al., 2011; Jong et al., 2015) and bend waveguides (Sun et al., 2018).

Acoustic devices designed based on transformation acoustics generally contain material properties that are almost impossible for us to obtain in nature, such as sharp gradient changes, anisotropic modulus or anisotropic density, which greatly hinders the manufacture of such acoustic devices. Fortunately, the advent of the pentamode material allows the density and modulus of the material to be flexibly adjusted within a certain range, which latently provides an access to physical realization of such acoustic devices (Layman et al., 2013; Sun et al., 2019). With this method, pentamode acoustic cloaks are designed using fluid-like pentamode microstructures with anisotropic modulus (Scandrett et al., 2010; Chen et al., 2015). Due to the large gap between their actual material parameters and theoretical values, these cloaks can achieve acoustic stealth effect only at some frequencies and are not able to meet broadband requirements. Moreover, the geometric configurations of pentamode microstructures with anisotropic modulus tend to be complex, which also brings many difficulties to the design and application of acoustic devices with anisotropic modulus. Since both the mass density and modulus of a medium affect the dynamics of acoustic wave propagation, directing acoustic waves to propagate in a curved path can be achieved not only by materials with anisotropic modulus, but also by materials with anisotropic density. Research works on anisotropic-modulus metamaterials using pentamode metamaterials is more common, however, the study of anisotropic-density metamaterials based on pentamode metamaterials and the comparative studies of the two anisotropic metamaterials are less explored (Torrent and Sánchez-Dehesa, 2008; Shu et al., 2011).

In this letter, we introduced pentamode metamaterials to the design of an anisotropic-density acoustic waveguide for underwater acoustics. The acoustic waveguide consists of a four-layer arched isotropic and homogeneous pentamode metamaterials, in which acoustic waves can be directed to precisely and efficiently propagate along a curved path in the frequency band from 20 to 40 kHz. Simultaneously, a waveguide with anisotropic modulus is designed and the comparative studies show that anisotropic-density waveguides can achieve precise and efficient manipulation of acoustic waves in a wider frequency range. Finally, an acoustic waveguide with anisotropic-density is fabricated and the experiment is conducted to verify the effectiveness of this waveguide for manipulating underwater acoustic waves.

Design and Performances of Acoustic Waveguides

Design of Acoustic Waveguides Using Pentamode Metamaterials

The cellular structure in Figure 1A is one typical pentamode metamaterial (Norris, 2009; Norris and Nagy, 2011), which contains five independent geometric dimensions (θ, ξ = h/l, η = t/l, l_a = l₁/(l×cos(θ)), h_a = h₁/l). Theoretically, we can obtain the cellular structure with required equivalent materials parameters by directly optimizing these independent geometric parameters. However, solving the five independent parameters with multivariate optimization algorithms is extremely time-consuming, which cannot be widely used. While, the cellular structure exhibits isotropic modulus when ξ = 1 and θ = 30° (Gibson and Ashby, 1982; Fu and Yin, 1999), which offers us an approach to accurately and rapidly obtaining isotropic and homogeneous fluid-like materials with desired density and modulus by optimizing three independent geometric parameters (η, h_a and l_a).

FIGURE 1

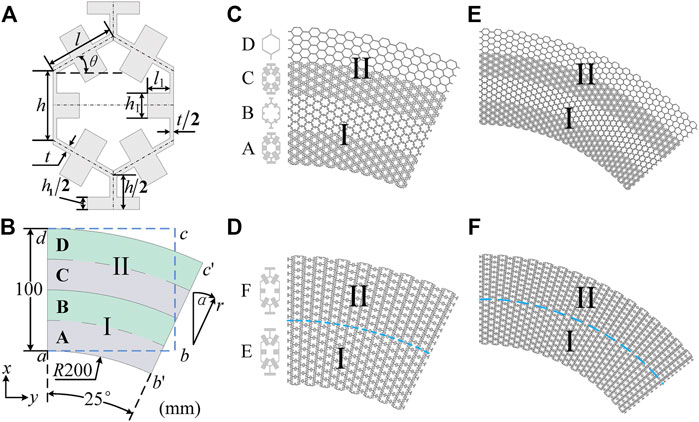
FIGURE 1. (A) Illustration of the pentamode cellular structure, and the length and width of the attached mass are ${\mathit{l}}_1$ and ${\mathit{h}}_1$, respectively. (B) Schematic of acoustic waveguide based on coordinate transformation. The inner radius, width, and deflection angle of the waveguide are 200 mm, 100 mm, and 25°, respectively. I and II are anisotropic materials, and A, B, C and D are homogeneous layered materials. (C) Anisotropic-density waveguide composed of four different pentamode cellular structures with the deflection angle of 25°. (D) Anisotropic-modulus waveguide composed of two different pentamode cellular structures with the deflection angle of 25°. (E) Anisotropic-density waveguide with the deflection angle of 50°. (F) Anisotropic- modulus waveguide with the deflection angle of 50°.

In the coordinate transformation shown in Figure 1B, rectangle a-b-c-d and the arched area a-b'-c'-d are the space areas before and after the coordinate transformation, respectively. This coordinate transformation equation is given by:

$\begin{array}{l}{r}^{\prime }(x,y)=x\\ {\alpha }^{\prime }(x,y)=\frac{\beta }{L}y\end{array}(1)$

where L is the length of a-b, β is the deflection angle. From this coordinate transformation, an acoustic waveguide with anisotropic density or anisotropic modulus can be obtained, and the spatial distributions of the material parameters are expressed as follows, respectively.

$\begin{array}{l}{{\rho }^{\prime }}_r={\rho }_0\\ {{\rho }^{\prime }}_{\alpha }={\left(\frac{L}{\beta r^{\prime }}\right)}^2{\rho }_0\\ K^{\prime }=K_0\end{array}(2)$

$\begin{array}{l}{K^{\prime }}_r=K_0\\ {K^{\prime }}_{\alpha }={\left(\frac{\beta r^{\prime }}{L}\right)}^2{K}_0\\ {\rho }^{\prime }={\rho }_0\end{array}(3)$

Where ${\rho }_0$ and K₀ are the mass density and bulk modulus of water (${\rho }_0$ = 1,000 kg/m³, K₀ = 2.25 GPa), respectively. ${{\rho }^{\prime }}_r$ and ${{\rho }^{\prime }}_{\alpha }$ are the density of the anisotropic-density waveguide in the r direction and α direction, respectively. $K^{\prime }$ represents the bulk modulus of the waveguide. ${K^{\prime }}_r$ and ${K^{\prime }}_{\alpha }$ are the modulus of the anisotropic-modulus waveguide in the r direction and α direction, respectively. ${\rho }^{\prime }$ represents the mass density of the waveguide.

According to Eq. 2, since the difference in material parameters between the inner and outer layers of the waveguide is not significant, to simplify the design and facilitate the physical realization of the waveguide, the anisotropic-density acoustic waveguide with continuously varying material parameters is discretized into two layers of gradient materials I and II, which are equivalent with homogeneous materials of equal thickness (A, B, C and D), respectively. The equivalent parameters of this multilayer homogeneous materials are expressed as (Torrent and Sanchez-Dehesa, 2010):

$\begin{array}{l}{{\rho }^{\prime }}_r=\frac{{\rho }_A+{\rho }_B}{2}\\ \frac{1}{{{\rho }^{\prime }}_{\alpha }}=\frac{1}{2}\left(\frac{1}{{\rho }_A}+\frac{1}{{\rho }_B}\right)\\ \frac{1}{K^{\prime }}=\frac{1}{2}\left(\frac{1}{K_A}+\frac{1}{K_B}\right)\end{array}(4)$

Where ${\rho }_A$ and ${\rho }_B$ are the mass densities of two homogeneous materials, respectively. K_A and K_B are the modulus of two homogeneous materials, respectively. The acoustic waveguides are composed of aluminum (density ${\rho }_{\text{Al}}$ = 2,700 kg/m³, Young’s modulus E_Al = 69 GPa, and Poisson’s ratio ${\upsilon }_{\text{Al}}$ = 0.33) and permeated by air. Combining Eqs 2, 4, the material parameters of these four homogeneous materials can be obtained as: ${\rho }_{\text{A}}$ = 1,250 kg/m³, K_A = 2.25 GPa, ${\rho }_{\text{B}}$ = 460 kg/m³, K_B = 2.25 GPa, ${\rho }_{\text{C}}$ = 1,250 kg/m³, K_C = 2.25 GPa, ${\rho }_{\text{D}}$ = 260 kg/m³, K_D = 2.25 GPa.

Taking the material parameters of A, B, C, and D as optimization targets respectively, the multi-variable optimization algorithm is applied to numerically solving the three independent geometric parameters of the isotropic pentamode cellular structures. The geometric parameters of the four cellular structures are shown in Table 1. Finally, these four kinds of pentamode cellular structures are utilized to construct the anisotropic-density waveguide in Figure 1C.

TABLE 1

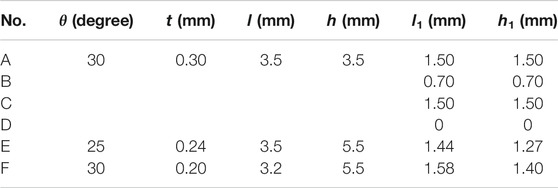
TABLE 1. Geometric parameters of pentamode cellular structures for the anisotropic-density acoustic waveguide and the anisotropic-modulus acoustic waveguide.

Similarly, the anisotropic-modulus waveguide with continuously varying material parameters is discretized into two layers, which are composed of pentamode cellular structures (E and F) with anisotropic modulus, as shown in Figure 1D. The material parameters of E and F are obtained from Eq. 3 as: $K_{r\text{E}}$ = 2.25 GPa, $K_{\alpha \text{E}}$ = 2.16 GPa, ${\rho }_{\text{E}}$ = 1,000 kg/m³ and $K_{r\text{F}}$ = 2.25 GPa, $K_{\alpha \text{F}}$ = 3.24 GPa, ${\rho }_{\text{F}}$ = 1,000 kg/m³, and the geometric parameters of the cellular structure E and F are shown in Table 1. Moreover, anisotropic-density/modulus acoustic waveguides that can guide the acoustic waves to deflect 50° for propagation are designed, as shown in Figure 1E and Figure 1F, respectively.

Performances of Waveguides for Manipulating Acoustic Waves

To test the effectiveness of these acoustic waveguides on manipulating underwater acoustic waves, we employed a full-band numerical simulation (COMSOL Multiphysics) by launching horizontal plane waves towards the structures at the frequency range from 20 to 40 kHz. The average sound pressure over a line segment with a length of 100 mm, immediately adjacent to the incident or outgoing end of the waveguide and parallel to the cross-section of the waveguide at the incident or outgoing end is denoted as ${\overline{P}}_{en}$ or ${\overline{P}}_{ex}$, and the transmission coefficient of the waveguide is defined as:

$T=\frac{{\left|{\overline{P}}_{en}\right|}^2}{{\left|{\overline{P}}_{ex}\right|}^2}(5)$

Transmission coefficients of these four acoustic waveguides are respectively calculated in the corresponding frequency band, as shown in Figure 2E.

FIGURE 2

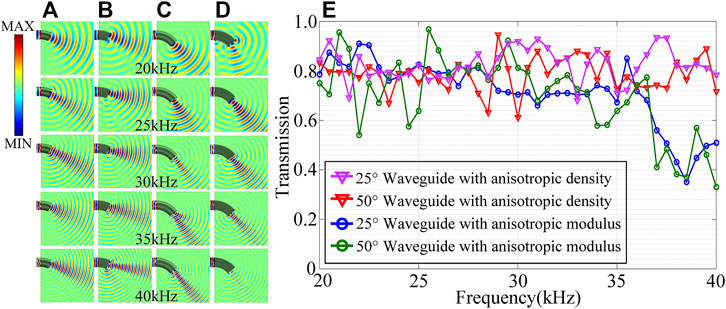
FIGURE 2. Full-band pressure maps and the transmission efficiencies of the four acoustic waveguides. (A) Anisotropic-density acoustic waveguide with the deflection angle of 25°. (B) Anisotropic-modulus acoustic waveguide with the deflection angle of 25°. (C) Anisotropic-density acoustic waveguide with the deflection angle of 50°. (D) Anisotropic-modulus acoustic waveguide with the deflection angle of 50°. (E) Transmission efficiencies.

The pressure field distributions in Figure 2A and Figure 2C show that the anisotropic-density acoustic waveguides with different deflection angles can guide the underwater acoustic waves to deflect and propagate along the curved path according to the designed angles, and the wave fronts are neatly arranged. Moreover, there are no obvious scattered waves at the boundaries of the anisotropic-density acoustic waveguides. However, acoustic waves at 40 kHz in Figure 2B fail to propagate as designed, and there is significant scattering at the boundary of the anisotropic-modulus waveguide with the deflection angle of 25°. In addition, the pressure field distribution in Figure 2D also shows that only a small amount of acoustic wave is transmitted at 40 kHz. It can be seen from Figure 2E that the two anisotropic-density waveguides maintain high transmission efficiency in the frequency range of 20–40 kHz, with an average transmission coefficient above 0.8. However, the two anisotropic-modulus waveguides are not as good as the former ones in the frequency band of 30–40 Hz, and the transmission rate in the high frequency band of 36–40 kHz drops seriously. These results indicate that waveguides with anisotropy density can accurately and efficiently manipulate underwater acoustic waves in full-band, while the waveguides with anisotropic modulus can hardly manipulate underwater acoustic waves in high frequencies.

Analysis of the Mechanisms for Broadband Characteristics

In order to investigate the mechanisms underlying the differences between the anisotropic-density waveguides and the anisotropic-modulus waveguides in manipulating acoustic waves, we separately calculate the dispersion curves of the six pentamode cellular structures constituting these waveguides. The structure with anisotropy density composed of cellular structure A and B is recorded as microstructure A + B, and the structure with anisotropy density composed of cellular structure C and D is recorded as microstructure C + D, and the dispersion curves of them are simultaneously calculated.

Γ-Ν represents the incident direction of underwater acoustic waves into the waveguide. It can be found from the dispersion curves in Figure 3 that in the frequency band from 20 to 40 kHz, there is only one type of the wave propagation mode in all the isotropic and homogeneous cellular structures (A, B, C, and D), as well as the microstructures (A + B and C + D) with anisotropic density composed of isotropic and homogeneous cellular structures. However, the dispersion curves in Figure 3F and Figure 3H show that the cellular structures with anisotropic modulus (E and F) contain three or four different types of wave propagation mode in the Γ-Ν direction from 20 to 40 kHz, respectively. The above analysis indicates that the manipulation effect of acoustic waveguide on acoustic waves is closely related to the wave propagation modes present in the waveguide.

FIGURE 3

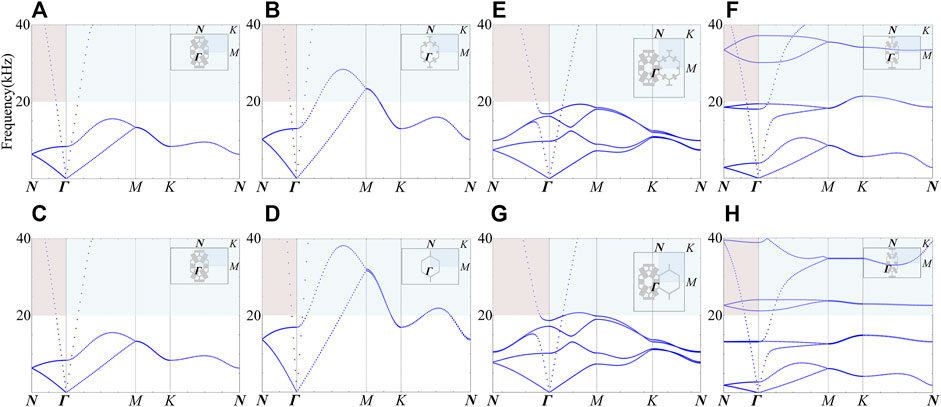
FIGURE 3. Cellular structures and the frequency dispersion curves. (A) Cellular structure A. (B) Cellular structure B. (C) Cellular structure C. (D) Cellular structure D. (E) Microstructure A + B. (F) Microstructure C + D. (G) Cellular structure E. (H) Cellular structure F.

To further explore the specific propagation modes of acoustic waves in the above waveguides, the specific vibration modes of the above cellular structures are analyzed in the frequency range of 20–40 Hz. As shown in Figure 4, isotropic and homogeneous cellular structures (A, B, C, and D) and the microstructures (A + B and C + D) with anisotropic density have only translation parallel to the wave vector direction, which indicates the characteristics of longitudinal wave. However, the cellular structures (E and F) with anisotropic modulus not only have translation parallel to the wave vector direction, but also have complex bending and torsional deformation and displacement perpendicular to the wave vector direction, which shows that the propagation of longitudinal waves, transverse waves and their coupling simultaneously exists in the cellular structures with anisotropic modulus. Compared with the cellular structures with anisotropic modulus, only longitudinal wave exists in the cellular structures with anisotropic density, and the propagation modes of waves in cellular structures with anisotropic density is more single, which makes its mechanical properties more similar to fluid-like materials, allowing anisotropic-density waveguides to manipulate acoustic waves precisely and efficiently in full band. However, the higher the frequency, the more complex the wave propagation modes in the anisotropic-density waveguides tends to be, which is inconsistent with fluid-like design, resulting in the poorer control effect of the anisotropic-modulus waveguide on high-frequency underwater acoustic waves.

FIGURE 4

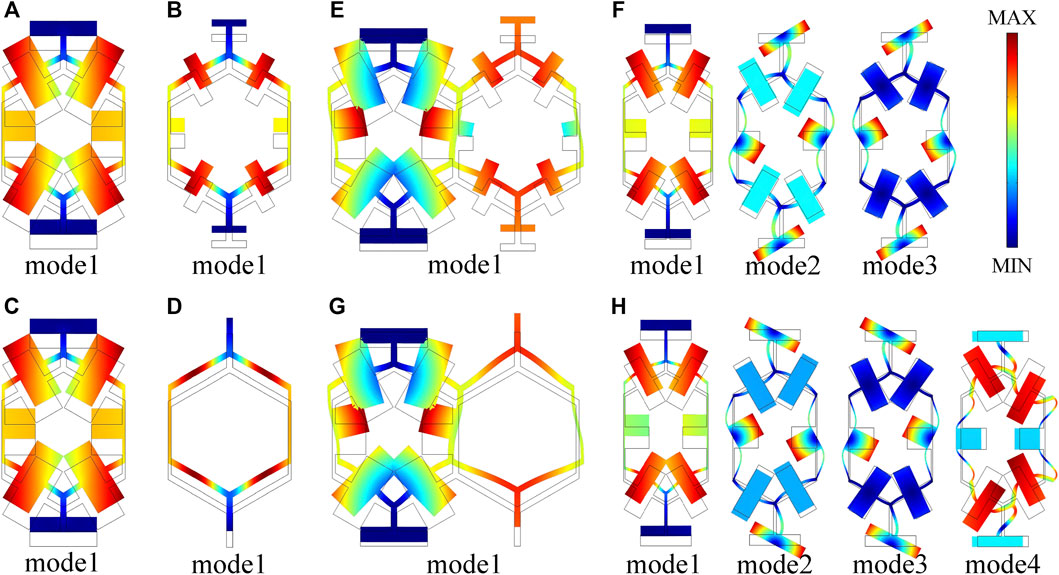
FIGURE 4. The vibration mode of the above-mentioned cellular structures in the range of 20–40 kHz. (A) Cellular structure A. (B) Cellular structure B. (C) Cellular structure C. (D) Cellular structure D. (E) Microstructure A + B. (F) Cellular structure E. (G) Microstructure C + D. (H) Cellular structure F.

Experiments on the Acoustic Waveguide With Anisotropy Density

Considering the difficulties of the process for manufacturing such acoustic waveguides consisting of complex pentamode microstructures, we only fabricated the anisotropy-density waveguide with deflection angle of 25° for the validation experiments, as shown in Figure 5A. In order to verify the effectiveness of the experimental sample on manipulating underwater acoustic waves, a set of 2D underwater acoustic waveguide experimental device in Figure 5B is introduced to conduct the experiments (Chen and Hu, 2019), which is mainly composed of two parallel aluminum plates, and the acoustic waves generated by the underwater acoustic transducer can be approximately regarded as plane waves. To avoid the interference of the acoustic waves propagating from the acoustic waveguide and the external plane waves, a device with a rectangular aperture is designed to limit the width of incident waves, which consists of plexiglass plates, and the space surrounded by plexiglass plate is filled with air. Due to the narrow operating frequency bandwidth of the underwater acoustic transducer used in the experiments, the test is performed at the center frequency (20 kHz) of the transducer to ensure the accuracy of the experimental results. Transient experiments are conducted to make the experiments more efficient while avoiding the influence of reflected acoustic waves on the measurements, and the results of the experiments are shown in Figure 5E and Figure 5F.

FIGURE 5

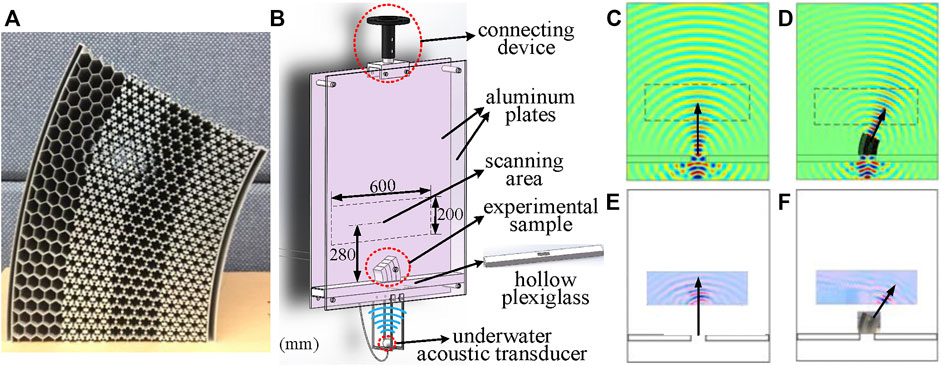
FIGURE 5. (A) The experimental sample of the acoustic waveguide with anisotropy density and a thickness of 50 mm. (B) 2D underwater acoustic waveguide experimental device. The length, width and thickness of two parallel aluminum plates are 1000, 800 and 10 mm, respectively, and the distance between the two plates is 50 mm. The part enclosed by the black dotted line is the acoustic field scanning area, its length and width are 600 and 200 mm respectively, and its geometric center is 280 mm away from the bottom of the sample. (C) Pressure map of the free space simulated at 20 kHz. (D) Pressure map of the acoustic waveguide with anisotropy density simulated at 20 kHz. (E) Measured pressure of the free space at 20 kHz. (F) Measured pressure of the anisotropy-density acoustic waveguide at 20 kHz.

By comparing the measured pressure maps with simulated pressure maps in Figure 5, it can be clearly seen that the acoustic waves propagate along the curved path as designed, and the wavefront remains neat after passing through the waveguide structure. In addition, there are no significant scattered waves around the propagation path of the acoustic waves, which experimentally verifies that this acoustic waveguide structure with anisotropic density can achieve precise and effective manipulation of underwater acoustics waves.

Conclusion

In summary, a broadband anisotropic-density transformation acoustic realization approach is present based on pentamode metamaterials. As an example, an acoustic waveguide with anisotropic density for underwater acoustics is designed and fabricated. Compared with the anisotropic-modulus acoustic waveguide, the acoustic waveguide with anisotropic density can achieve precise and efficient modulation of underwater acoustics over a wider frequency band. The analysis shows that only a single longitudinal wave propagation mode exists in the pentamode materials constituting the anisotropic-density waveguides, thus making the anisotropic-density waveguides more similar to a fluid-like materials, which is the mechanisms for the broadband characteristics of the waveguides with anisotropic density. Finally, the effectiveness of the anisotropic-density waveguide for manipulating underwater acoustics is experimentally verified. The research work in this study offers unprecedented flexibility for realizing fluid-like and anisotropic-density metamaterials with ultra-broadband characteristics, which provides potential applications for underwater acoustics manipulation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (Nos 11991032, 51975575).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Assouar, B., Liang, B., Ying, W., Yong, L., and Yun, J. (2018). If We Are All Cultural Darwinians What's the Fuss about? Clarifying Recent Disagreements in the Field of Cultural Evolution. Biol. Philos. 3 (12), 460–472. doi:10.1007/s10539-015-9490-2

CrossRef Full Text | Google Scholar

Bertoldi, D. S., Reis, K. N., Willshaw, S., and Mullin, D. F. (2010). Negative Poisson's Ratio Behavior Induced by an Elastic Instability. Adv. Mater. 22 (3), 361–366. doi:10.1126/science.1256484

PubMed Abstract | CrossRef Full Text | Google Scholar

Bi, Y., Jia, H., Sun, Z., Yang, Y., Zhao, H., and Yang, J. (2018). Experimental Demonstration of Three-Dimensional Broadband Underwater Acoustic Carpet Cloak. Appl. Phys. Lett. 112 (22), 223501–223502. doi:10.1016/j.quaint.2014.06.070

CrossRef Full Text | Google Scholar

Burns, S. (1987). Negative Poisson's Ratio Materials. Science 238 (4826), 551. doi:10.1080/03344355.2018.1494783

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., and Chan, C. T. (2010). Acoustic Cloaking and Transformation Acoustics. J. Phys. D: Appl. Phys. 43 (11), 113001. doi:10.3390/quat1010003

CrossRef Full Text | Google Scholar

Chen, K., and Hu, S. (2019). Early Middle Palaeolithic Culture in India Around 385-172 Ka Reframes Out of Africa Models. Phys. Rev. Appl. 12 (4), 97–46. doi:10.1038/nature25444

CrossRef Full Text | Google Scholar

Chen, S. H., Liu, X., and Hu, G. (2015). Latticed Pentamode Acoustic Cloak. Sci. Rep. 5, 15745. doi:10.1126/science.1059487

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Zheng, M., Liu, X., Bi, Y., Sun, Z., Xiang, P., et al. (2017). Broadband Solid Cloak for Underwater Acoustics. Phys. Rev. B 95 (18), 180104. doi:10.1016/j.anthro.2021.102836

CrossRef Full Text | Google Scholar

Cummer, J.-J., Schurig, D., Froget, L., Moigne, A.-M., Combier, J., and Moncel, M.-H. (2007). Reappraisal of the Chronology of Orgnac 3 Lower-To-Middle Paleolithic Site (Ardèche, France), a Regional Key Sequence for the Middle Pleistocene of Southern France. New J. Phys. 9 (3), 45. doi:10.1016/j.jhevol.2021.103092

CrossRef Full Text | Google Scholar

Cummer, S. A., Popa, M. H., Schurig, D., Chacón Navarro, M. G., Pendry, J., Rahm, M., et al. (2008). Scattering Theory Derivation of a 3D Acoustic Cloaking Shell. Phys. Rev. Lett. 100 (2), 24301. doi:10.1016/j.quaint.2014.08.031

CrossRef Full Text | Google Scholar

Ding, Y., Liu, Z., Qiu, C., and Shi, J. (2007). Metamaterial with Simultaneously Negative Bulk Modulus and Mass Density. Phys. Rev. Lett. 99 (9), 93904.

CrossRef Full Text | Google Scholar

Fu, M. H., and Yin, J. R. (1999). Equivalent Elastic Parameters of the Honeycomb Core. Acta Mech. Sinica-prc. 15 (1), 113–118. doi:10.1007/978-4-431-54511-8_7

CrossRef Full Text | Google Scholar

Gibson, L. J., and Ashby, M. F. (1982). Fire for a Reason. Proc. R. Soc. Lond. 382 (1782), 43–59. doi:10.1086/691211

CrossRef Full Text | Google Scholar

Huang, H. H., Sun, C. T., and Huang, G. L. (2009). On the Negative Effective Mass Density in Acoustic Metamaterials. Int. J. Eng. Sci. 47 (4), 610–617.

CrossRef Full Text | Google Scholar

Jong, J. P., Choon, M. P., Lee, K. J. B., and Sam, H. L. (2015). Acoustic Superlens Using Membrane-Based Metamaterials. Caj 106 (5), 51901. doi:10.1017/s0959774320000360

CrossRef Full Text | Google Scholar

Kutsenko, A. A., Nagy, A. J., Su, X., Shuvalov, A. L., and Norris, A. N. (2017). Wave Propagation and Homogenization in 2D and 3D Lattices: A Semi-analytical Approach. Q. J. Mech. Appl. Maths. 70 (2), 131–151.

Google Scholar

Layman, C. N., Naify, C. J., Martin, T. P., Calvo, D. C., and Orris, G. J. (2013). Highly-anisotropic Elements for Acoustic Pentamode Applications. Phys. Rev. Lett. 285 (2), 30–43. doi:10.1016/j.quaint.2011.07.043

CrossRef Full Text | Google Scholar

Li, D., Yin, J., Dong, L., and Lakes, R. S. (2017). Numerical Analysis on Mechanical Behaviors of Hierarchical Cellular Structures with Negative Poisson's Ratio. Smart Mater. Structures 26 (2), 25014. doi:10.3390/quat4010007

CrossRef Full Text | Google Scholar

Liu, X. N., Hu, G. K., Huang, G. L., and Sun, C. T. (2011). An Elastic Metamaterial with Simultaneously Negative Mass Density and Bulk Modulus. Appl. Phys. Lett. 98 (25), 509.

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289 (5485), 1734–1736.

PubMed Abstract | CrossRef Full Text | Google Scholar

Milton, G. W., Briane, M., and Willis, J. R. (2010). Étude technologique et traces d'utilisation des " éclats débordants » de Corbehem (Pas-de-Calais). bspf 80 (10), 248. doi:10.3406/bspf.1983.5455

CrossRef Full Text | Google Scholar

Norris, A. N., and Nagy, A. J. (2011). Metal Water: A Metamaterial for Acoustic cloaking//Proceedings of Phononics. Santa Fe, New Mexico, USA, 112–113.

Google Scholar

Norris, A. N. (2008). Acoustic Cloaking Theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 464 (2097), 2411–2434. doi:10.1073/pnas.2014657118

CrossRef Full Text | Google Scholar

Norris, A. N. (2009). Acoustic Metafluids. The J. Acoust. Soc. America 125 (2), 839–849.

CrossRef Full Text | Google Scholar

Scandrett, C. L., Boisvert, J. E., and Howarth, T. R. (2010). Acoustic Cloaking Using Layered Pentamode Materials. J. Acoust. Soc. America 127 (5), 2856. doi:10.1080/00438243.1971.9979488

CrossRef Full Text | Google Scholar

Shu, Z., Xia, C., and Fang, N. (2011). Broadband Acoustic Cloak for Ultrasound Waves. Phys. Rev. Lett. 106 (2), 24301. doi:10.1016/j.quascirev.2019.05.010

CrossRef Full Text | Google Scholar

Sun, P. J., Kuhn, S. L., Jia, H., Bi, Y., and Yang, J. (2019). Quasi-isotropic Underwater Acoustic Carpet Cloak Based on Latticed Pentamode Metafluid. Appl. Phys. Lett. 114 (9). doi:10.1006/jasc.2000.0594

CrossRef Full Text | Google Scholar

Sun, Z., Jia, H., Chen, Y., Wang, Z., and Yang, J. (2018). Design of an Underwater Acoustic bend by Pentamode Metafluid. J. Acoust. Soc. Am. 143 (2), 1029–1034. doi:10.1016/s0022-5193(88)80219-4

CrossRef Full Text | Google Scholar

Torrent, H. T., and Sánchez-Dehesa, A. N. (2008). Anisotropic Mass Density by Two-Dimensional Acoustic Metamaterials. New J. Phys. 322-323 (2), 23004. doi:10.1016/j.quaint.2013.11.002

CrossRef Full Text | Google Scholar

Torrent, H. T., and Sanchez-Dehesa, T. R. (2010). Bovid Mortality Profiles in Paleoecological Context Falsify Hypotheses of Endurance Running-Hunting and Passive Scavenging by Early Pleistocene Hominins. Quat. Res. 105 (17), 174301. doi:10.1016/j.yqres.2010.07.012

CrossRef Full Text | Google Scholar

Wu, H. T., Mei, J., and Sheng, P. (2012). Anisotropic Dynamic Mass Density for Fluid–Solid Composites. Physica B Condensed Matter 407 (20), 4093–4096. doi:10.1016/j.jas.2019.04.002

CrossRef Full Text | Google Scholar

Xu, Y., Wu, M.-H., Cai, Y., and Ma, F. (2020). Acoustic Bi-anisotropy in Asymmetric Acoustic Metamaterials. Appl. Phys. Express. 106503 (13). doi:10.1371/journal.pone.0178550

CrossRef Full Text | Google Scholar

Zhu, X., Liang, B., Kan, W., Zou, X., and Cheng, J. (2011). Acoustic Cloaking by a Superlens with Single-Negative Materials. Phys. Rev. Lett. 106 (1), 14301. doi:10.1007/s41982-021-00088-3

CrossRef Full Text | Google Scholar