Spin Properties and Metal-Semiconductor Transition of Nitrogen-Containing Zigzag Graphyne Nanoribbon Caused by Magnetic Atom Doping

In this study, the density function theory (DFT) was used to study the influence of the magnetic atoms (Fe, Co, Ni) doping on the electrical properties of nitrogen-containing zigzag graphyne-like nanoribbon (N-ZGyNR). The results show that, by doping different atoms into the natural “holes” of N-ZGyNR, the changes in the structure, magnetic moment distribution and electrical properties of N-ZGyNR are different. Due to the incomplete saturation of the edge C atoms, the initial N-ZGyNR presents metallicity and spin degeneracy. The doping of Fe atoms will cause the C-C bond in N-ZGyNR to be completely broken, resulting in structural distortion, and about 0.8e- will transfer from Fe to N-ZGyNR. Compared with Fe doping, Co/Ni doping has a smaller effect on the N-ZGyNR and will not cause structural distortion, but will redistribute the spin charge in N-ZGyNR, thereby forming a band gap of 60 meV near the Fermi level to realize the transition of metal-semiconductor. The above results show that the electrical properties of N-ZGyNR can be controlled by magnetic atom doping, and the metal-semiconductor transition can be realized by Co/Ni doping, which provides a new alternative for spintronic devices.

Introduction

In recent years, the research on graphene and graphyne has become the focus of attention in the new carbon isomorphic nanostructures. Graphyne is a new kind of carbon nanostructure material, which contains a large number of carbon chemical bonds. Its structure has the characteristics of large conjugated system, wide surface spacing, and stable chemical properties and semiconductor properties. In the 1980s, Baughman et al. (1987) proposed the concept of graphyne for the first time, predicting that graphyne has high temperature dynamic stability and high synthesis probability. Unlike graphene with sp2-hybridized carbon atoms, there are sp- and sp2-hybridized carbon atoms in graphynes, which make it completely different from graphene in geometry and physical properties (Li et al., 2014a; Bhattacharya et al., 2015). For example, four known graphyne lattice structures have been widely reported, namely, α, β, γ and 6,6,12-Graphyne (Baughman et al., 1987; Narita et al., 1998; Malko et al., 2012; Wu et al., 2013; Puigdollers et al., 2016).

Like graphene nanoribbons (GNRs), graphynes nanoribbons (GyNRs) are also realized by cutting graphyne sheets along the zigzag or armchair edges. GyNRs can have unusual magnetic, electronic properties such as magnetic/nonmagnetic or edge-dependent metal/semiconductor behavior (Zhang and Ma, 2011; Yue et al., 2012; Sarma et al., 2014; Sevinçli and Sevik, 2014; Wang et al., 2015; Li et al., 2020). Wu et al. (2013) studied the magnetic, electronic and transport properties of all types of GyNRs devices. They found that there was negative differential resistance effect (NDR) appeared in all other types of GyNRs except for α- and 6,6,12-GyNRs. Xi et al. (2014) used Wannier interpolation technique to study the electron-phonon coupling and charge transport properties of α and γ graphyne nanoribbons, and speculated that the electron mobility of α and γ graphynes reached ∼10⁴cm²V⁻¹s⁻¹ at room temperature. Through the above studies, it is shown that the graphyne system may have more amazing electrical properties than graphene, so graphyne is often regarded as a material for the production of carbon-based electronic devices.

One-dimensional/two-dimensional doped carbon materials have attracted more and more attention due to their structural diversity and unique electronic properties (Nayebi and Shamshirsaz, 2020; Chang et al., 2021). Haji-Nasiri and Fotoohi (Haji-Nasiri and Fotoohi, 2018) studied the transport properties of α-Armchair GyNRs (α-AGyNRs) devices doped with B and N atoms. They found that rectifying properties strongly depend on the location of defects (doped atoms). Qi et al. (2019) proposed a new two-dimensional carbonitride structure. The structure is composed of sp- and sp2-hybrid carbon atoms and nitrogen atoms, with kagome, rhombus and hexagonal lattice. The first-principles calculations of these structures show that these two-dimensional nitrogen-containing graphynes are direct band gap semiconductors. At the same time, it is also found that in the two-dimensional diamond-shaped graphyne structure, the carrier mobility is the same as that of graphene, and the tensile strength is higher than that of graphene.

The study of magnetic properties of materials plays an important role in spintronics, which can contribute to the study of electronic transport in spin filters. In graphene or graphynes nanoribbons, the magnetic changes of nanoribbons can be realized by applying the applied transverse electric field (Son et al., 2006; Yue et al., 2012), boundary modification (Kan et al., 2008; Dutta et al., 2009; Deng et al., 2014; Krause et al., 2021), interface effect (Li et al., 2015; Wang et al., 2016; Zakharov, 2021) or adding various defects (Wang et al., 2009; Lin and Ni, 2011; Li and Zhang, 2013; Li et al., 2014b; Zhao et al., 2017; Jing et al., 2020; Liu et al., 2021). These methods effectively offset the local state energy of carbon atoms at the boundary to realize the magnetic transformation, and the most commonly used and efficient methods are doping and adsorption (Cocchi et al., 2010; Li and Zhang, 2013; Donati et al., 2014; Lin et al., 2014; Lazić and Crljen, 2015; Pan et al., 2015; Zhao et al., 2017; Jing et al., 2020; Liu et al., 2021). The doping method is used to study the electromagnetic changes of graphene and graphyne systems.

In this paper, inspired by the above research work, the effects of magnetic atoms (Fe, Co and Ni) doped in the structure of one-dimensional nitrogen-containing zigzag graphene-like nanoribbon (N-ZGyNR) on their electrical and magnetic properties are studied. The emphasis is on the magnetic interaction between the doped atoms and the boundary state, which will bring possibilities for the study of electronic devices of graphyne-like nanoribbon (GyNR).

Simulation Model and Calculation Method

There are many large natural “holes” in the N-ZGyNR, which can be doped with magnetic atoms to adjust the electromagnetic properties. The geometric structure of M-N-ZGyNR is given in Figures 1A–D, where the M atoms represent the doped magnetic atoms (M = Fe, Co, Ni). We know that for graphene or graphyne compound nanoribbons, the electron occupation at the edge of the carbon atom controls the spin polarized transmission. In our study, the initial spin of the N-ZGyNR is in the antiferromagnetic state, that is, the upper two C atoms (C₁ and C₁₇) are set to spin-up, and the lower two C atoms (C₁₆ and C₃₂) are set to spin-down. In order to study the effect of embedded magnetic atoms on the boundary states near the Fermi level, we choose the natural “hole” near the edge carbon atom as the doping object. Due to symmetry (Supplementary Figure S1), the case that the initial spin of the magnetic atom is set to spin-up is only discussed. The repetitive unit cell structure has been enclosed by a rectangular dotted line. Each edge C atoms is passivated by a single hydrogen atom, and a large enough vacuum region in the x and y directions is given to prevent any interaction between the studied structure and its mirror image. The formation energies of the structures (ΔE_M-N-ZGyNR) involved in this study are as follows:

$\Delta {\text{E}}_{\text{M}-\text{N}-\text{ZGyNR}}={\text{E}}_{\text{M}-\text{N}-\text{ZGyNR}}-{\text{E}}_{\text{N}-\text{ZGyNR}}-{\text{E}}_{\text{M}}(1)$

FIGURE 1

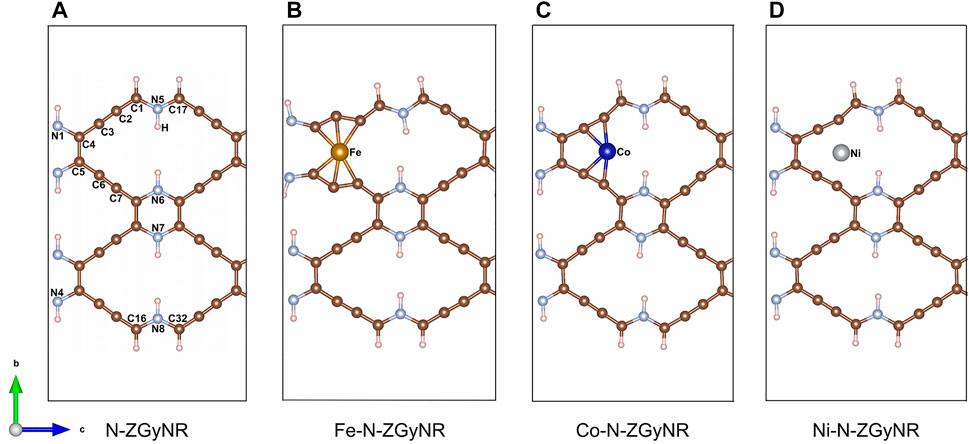
FIGURE 1. (A–D) Structure diagram of nitrogen-containing zigzag graphynes-like nanoribbons doped with magnetic atoms (M-N-ZGyNR, M = Fe,Co,Ni). The edge C atom is passivated by a single H atom and the repetitive unit cell structure of M-N-ZGyNR has been marked by the gray imaginary rectangle region.

E_M-N-ZGyNR, E_N-ZGyNR and E_M represent the total energy of N-ZGyNR doped with magnetic atoms M, pure N-ZGyNR structure without magnetic atoms and the isolated atoms M, respectively. In Table 1, we show the formation energies of M-N-ZGyNR ΔE_M-N-ZGyNR. It can be found from Table 1 that all the formation energies of M-N-ZGyNR are negative and much larger than room temperature disturbances (∼25 meV/atom), which means that the M-N-ZGyNR are stable at room temperature.

TABLE 1

TABLE 1. The formation energies of M-N-ZGyNR.

The spin electron density (SED) of M-N-ZGyNR, which can determine the type and size of the spin charge on each atom, can be calculated from the spin-up/spin-down charge density ${\rho }_{\uparrow \text{/}\downarrow }$

$\Delta {\text{ρ}}^{\text{SED}}={\text{ρ}}_{\uparrow }-{\text{ρ}}_{\downarrow }(2)$

and the spin electron density difference (SEDD) of M-N-ZGyNR, which can get the total charge transfer before and after magnetic atom doping, is defined as

$\Delta {\text{ρ}}_{\text{M}-\text{N}-\text{ZGyNR}}^{\text{SEDD}}={\text{ρ}}_{\text{M}-\text{N}-\text{ZGyNR}}-{\text{ρ}}_{\text{N}-\text{ZGyNR}}-{\text{ρ}}_{\text{M}}(3)$

Here the ${\rho }_{\text{M}-\text{N}-\text{ZGyNR}}$, ${\rho }_{\text{N}-\text{ZGyNR}}$ and ${\rho }_{\text{M}}$ represent the total electron density of M-N-ZGyNR, N-ZGyNR and the doped atom M, respectively.

In this work, all the first-principles calculations are performed by the Vienna Ab Initio Simulation Package (VASP) (Kresse and Furthmüller, 1996; Ren et al., 2019) with PAW potentials (Kresse and Joubert, 1999) and Strongly Constrained and Appropriately Normed Semilocal Density Functional (SCAN) (Young and Kane, 2015). The cutoff energy is set to 500eV in all calculations. The convergence criterion of force adopts quasi-Newton method for structural relaxation until the force tolerance reaches 0.02 eV/Å. The K grid sampling used in optimization and static calculations is 1*1*11. In the energy band calculation, 30 K-points were taken along the z direction, and in the Co/Ni doping, an additional 20 K-points were taken near the band gap to confirm the existence of the band gap. The spin electron density distribution and spin electron distribution difference diagram are processed by VESTA (Momma and Izumi, 2011).

Results and Discussion

Band Structure Analysis

The band structures of M-N-ZGyNR (M = Fe, Co and Ni) are shown in Figure 2 (the red dotted lines represent the spin-up bands, and the black solid lines represent the spin-down bands). The band structure of the N-ZGyNR is given in Figure 2A for comparison. The lengths of C₁(sp)-C₂(sp), C₂(sp)≡C₃(sp), C₃(sp)-C₄(sp), C₄(sp2) = C₅(sp2) bonds in N-ZGyNR (The atomic label is shown in Figure 1A) are 1.35, 1.24, 1.36, 1.42 Å, respectively, which is in good agreement with those reported in the previous literature (Sevinçli and Sevik, 2014). All the atoms in N-ZGyNR are saturated and bonded, except for the C atoms on the edge. Take the C₁ as an example, it only has C₁(sp)-C₂(sp), C₁-H, C₁-N bonds. Combined with the inversion symmetry of the entire structure, N-ZGyNR exhibits spin-degenerate metallicity (in Figure 2A).

FIGURE 2

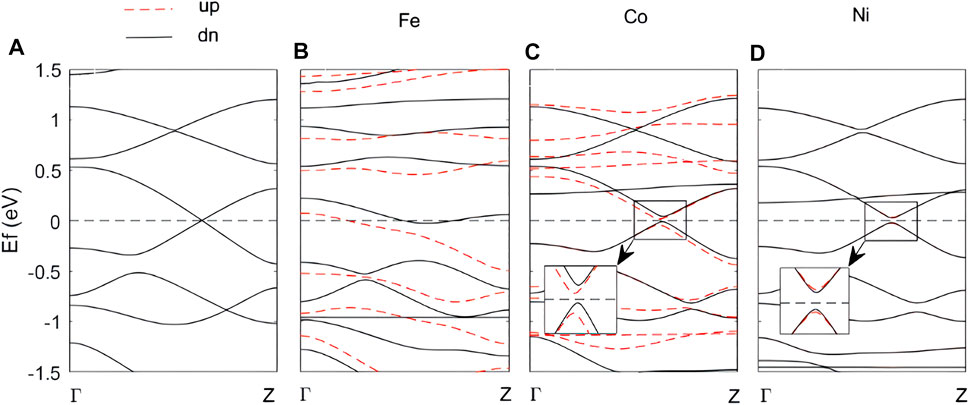
FIGURE 2. The band structure of the original N-ZGyNR (A) and that of the M-N-ZGyNR (M = Fe, Co or Ni) when the spin direction of the doped atom M is set to spin-up (B–D). The band structure of spin-up (spin-down) electrons is represented by red dotted lines (black real lines). The Fermi level is set to zero, which is represented by the horizontal dotted line.

During the Fe doping process, the interaction between Fe and C atoms will cause significant structural distortions in N-ZGyNR (in Figure 1B). For example, the C₃ and C₆ will be pushed away (The atomic label is the same as N-ZGyNR in Figure 1A). The distance between C₄ and C₅ will increase from 1.42 Å to 2.59 Å, indicating that the C₄(sp2) = C₅(sp2) bond is completely broken. The bond lengths of C₂(sp)≡C₃(sp) and C₆(sp)≡C₇(sp) will increase from ∼1.24 Å to ∼1.34 Å and becomes a C(sp)-C(sp) bond. With the larger structural relaxation changes in Fe-N-ZGyNR, the electronic band structure will also change significantly (in Figure 2B). When the doping atoms change from Fe to Co and Ni, the structural distortion is only limited to C₂-C₃ and C₆-C₇, which are very close to the dopant atoms. Similar to Fe-N-ZGyNR, the bond lengths of C₂-C₃ and C₆-C₇ in Co/Ni-N-ZGyNR changed from triple bonds (1.24 Å) to single bonds (1.30 Å). With the destruction of the triple bond, an electronic band gap of 60 meV appears in Co-N-ZGyNR and Ni-N-ZGyNR (in Figures 2C,D), indicating that the electrical properties of the original N-ZGyNR changed from metal to semiconductor. The existence of the band gap value in Co/Ni-N-ZGyNR also can be confirmed from the dense density of states curves (Supplementary Figure S2). These results indicate that the electrical properties of N-ZGyNR can be effectively controlled and designed for the metal-semiconductor transition through magnetic atom doping.

Spin Electron Density Analysis

To study the influence of doped magnetic atoms on the spin properties of N-ZGyNR, we calculated the spin electron density distribution of M-N-ZGyNR. The spin electron density distribution $\Delta {\rho }^{\text{SED}}$ by Eq. 2 is used to intuitively describe the distribution of magnetic moment in the structure, as shown in Figure 3. The spin electron density distribution of the original N-ZGyNR structure is given in Figure 3A as a comparison. Here the yellow (light blue) part represents the spin-up (spin-down) magnetic moment, respectively. It should be note that the isosurface levels from large to small are Fe-N-ZGyNR(2 × 10⁻³ e/ų), Co-N-ZGyNR(2 × 10⁻⁴ e/ų), Ni-N-ZGyNR (2 × 10⁻⁵ e/ų) and N-ZGyNR(2 × 10⁻⁶e/ų) to make the comparison clear. It can be seen from Figure 3A that for N-ZGyNR, the magnetic moments are mainly distributed on the atomic chains at the edges, the magnetic moments on the edge atomic chain presents an up-down staggered distribution, and the magnetic moments between the two edge chains are inverted symmetry. Therefore, as shown in Figure 2A, there will be spin degeneracy in N-ZGyNR.

FIGURE 3

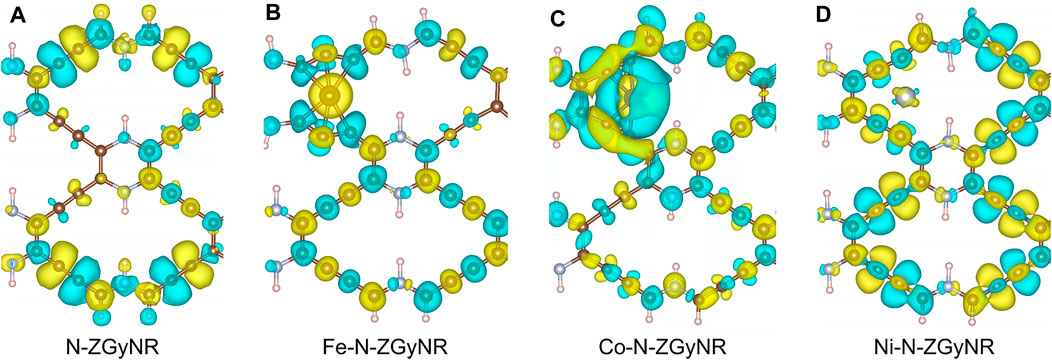
FIGURE 3. (A–D) The spin electron density of (M-)N-ZGyNR (M = Fe,Co,Ni) respectively. The electronic magnetic moment of spin up (spin down) is represented by the yellow (light blue) region. To make the comparison clear, the isosurface level of N-ZGyNR, Fe-N-ZGyNR, Co-N-ZGyNR and Ni-N-ZGyNR are set to 2 × 10⁻⁶ e/ų, 2 × 10⁻³ e/ų, 2 × 10⁻⁴ e/ų and 2 × 10⁻⁵ e/ų, respectively.

When the Fe is doped into N-ZGyNR, it can be found from Figure 3B that, the spin distribution on the entire N-ZGyNR will be greatly affected. It can be seen that the magnetic moments on the middle C atom and N atom of the Fe-N-ZGyNR are significantly increased compared with the N-ZGyNR. The doped Fe atom breaks the original magnetic moment balance and changes the left-right symmetrical spin distribution of N-ZGyNR into an antisymmetrical distribution, and at the same time enhances the spin polarization. For example, the spin magnetic moment of C₁-C₇ in N-ZGyNR will increase from ∼0 μ_B to 0.043, −0.063, 0.021, −0.035, −0.065, 0.038, −0.095 μ_B, respectively. In addition, there is a residual spin magnetic moment of about 1.69 μ_B on the doped Fe atoms.

When the Co atom is doped into N-ZGyNR, similar to the case in the Fe-N-ZGyNR structure, the original magnetic moment balance is broken and the magnetic moment of the original N-ZGyNR structure is affected. Different from Fe-N-ZGyNR, the influence of Co on the spin distribution of the N-ZGyNR is mainly limited to the C atoms adjacent to Co, such as C₂, C₃, C₆, C₇ (in Figure 3C). The spin-up electrons are mainly concentrated in the Co atoms, while the spin-down electrons are mainly concentrated in the C₂, C₃, C₆, C₇ atoms. The spin magnetic moments of C₂, C₃, C₆, C₇ and Co are −0.027, −0.035, −0.014, −0.021, 1.16 μ_B, respectively, which are smaller than the spin magnetic moment of Fe-N-ZGyNR but higher than that of N-ZGyNR. In addition, the spin magnetic moments on N₄ and C₃₂ will change from the reverse to the same direction, which will hinder the spin charge transfer near the Fermi level, resulting in a band gap at the Fermi level, as shown in Figure 2C.

It is obvious from Figure 3D that when the Ni atom is doped into N-ZGyNR structure, the interaction between Ni and N-ZGyNR is weak (in Figure 3D). Compared with N-ZGyNR, the spin distribution in Ni-N-ZGyNR has changed but the intensity has not changed significantly (The isosurface level of Figure 3D is only an order of magnitude higher than Figure 3A), which is different from Fe and Co doping. Similar to Co-N-ZGyNR, the spin magnetic moments on C₁₅ and C₁₆, C₁₇ and C₁₈, C₃₁ and C₃₂ change from the reverse to the same direction. The overall result is that the electrical properties of Ni-N-ZGyNR are basically the same as those of N-ZGyNR, maintaining the basic characteristics of the energy band, but opening the band gap near the Fermi level, as shown in Figure 2D.

Spin Electron Density Difference Analysis

Through the distribution of spin charge, we can find that the Fe doping has the greatest influence on the N-ZGyNR spin distribution, followed by Co doping and the Ni doping has the weakest influence. In order to study the spin charge transfer caused by the doping of magnetic atoms, the spin electron density difference $\Delta {\rho }^{\text{SEDD}}$ calculated by Eq. 3 is shown in Figure 4. As a reference, the spin magnetic moments on isolated Fe, Co, and Ni atoms are 4, 3, 2 μ_B, respectively.

FIGURE 4

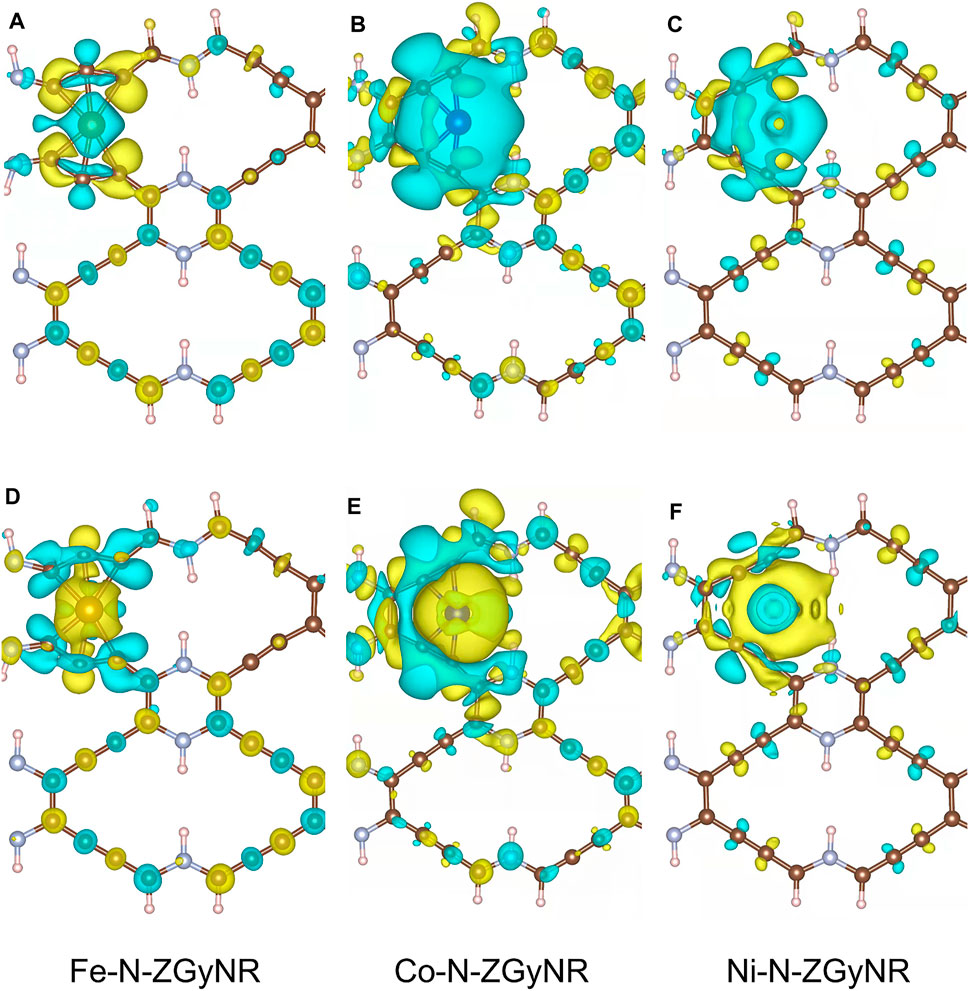
FIGURE 4. The spin-up (A–C)/spin-down (D–F) electron density difference of M-N-ZGyNR (M = Fe,Co,Ni). The increase (decrease) of the spin electron magnetic moment is represented by the yellow (light blue) region. To make the comparison clear, the isosurface levels of Fe-N-ZGyNR, Co-N-ZGyNR and Ni-N-ZGyNR are set to 2 × 10⁻³ e/ų, 2 × 10⁻⁴ e/ų and 8 × 10⁻⁴ e/ų respectively.

It can be found from Figures 4A,D that, when Fe atoms with 4 μB magnetic moment are doped into N-ZGyNR, the number of spin-up electrons on Fe atoms will decrease, and the number of spin-down electrons will increase. In addition, through bader charge analysis (Supplementary Figure S3B), it is found that about 0.8e- will be transferred from Fe atoms to the N-ZGyNR structure. This will reduce the residual magnetic moment on the Fe atom to 1.69 μ_B, as shown in Figure 3B. The 0.8e- transferred to N-ZGyNR are mainly captured by C₄ and C₅, which breaks the C₄(sp2) = C₅(sp2) bond. The secondary effect of charge transfer will change the spin distribution in the N-ZGyNR structure. For example, the spin-up charge on the C₁₆ atom located on the lower edge increases, and the spin-down charge decreases, which will strengthen the residual magnetic moment of the C₁₆ atom from 0.003 to 0.07 μ_B. The spin-up charge on the C₃₂ atom that is also located on the lower edge decreases, and the spin-down charge increases, which makes the residual magnetic moment of the C₃₂ atom reversely strengthened from 0.003 μ_B to −0.086 μ_B. Similar to Fe doping, when Co with a 3 μ_B magnetic moment is doped into N-ZGyNR, the spin-up charge of the Co atom itself will decrease, and the spin-down charge will increase (in Figures 4B,E). But only 0.6e- are transferred from the Co atom to the N-ZGyNR (in Supplementary Figure S3C), which causes the magnetic moment of the Co atom to weaken from 3 to 1.16 μ_B. The 0.6e- transferred to N-ZGyNR have significantly less influence on the original structure than Fe doping. For example, breaking C₂(sp)≡C₃(sp) into a C(sp)-C(sp) bond, increases the magnetic moment of N₈ at the lower edge from ∼0 to 0.008 μ_B, which is the same as the direction of the magnetic moment of C₃₂. The effect of Ni doping on N-ZGyNR is minimal. The spin charge reversal of Ni atoms is limited to Ni atoms themselves, thereby eliminating the magnetic moment of Ni atoms (in Figures 4C,F), and there will be no charge transfer from Ni atoms to N-ZGyNR (in Supplementary Figure S3D). But the weak interaction between Ni and N-ZGyNR will also redistribute the spin on N-ZGyNR, such as flipping the magnetic moment on C16 from 0.003 μ_B to −0.001 μ_B, which is the same as the direction of the magnetic moment on C₇.

Conclusion

In this work, the first-principles theory is used to study the effect of magnetic atom doping on the electrical properties of nitrogen-containing graphyne nanoribbon (N-ZGyNR). The results show that different magnetic doping atoms have different effects on the structure and electrical properties of N-ZGyNR. When Fe atoms are doped, one of the C-C bonds will be completely broken, and the entire structure will undergo great structural distortion. With the transfer of about 0.8e- from Fe atoms to the N-ZGyNR, the electrical properties of Fe-N-ZGyNR will change significantly. When Co atoms are doped, the influence on the N-ZGyNR is smaller than that of Fe doping. With the transfer of 0.6e- electrons from the Co atom to the N-ZGyNR, the spin up-down alternating magnetic moment distribution at the N-ZGyNR edge will be broken, and a band gap of ∼60 meV near the Fermi level in Co-N-ZGyNR will appear, thereby realizing the metal-semiconductor transition. The effect of Ni doping on the N-ZGyNR is the smallest among these three types of magnetic atom doping. There is no charge transfer from Ni to the N-ZGyNR, but the Van der Waals interaction between Ni and N-ZGyNR will also cause the magnetic moment redistribution in N-ZGyNR. Similar to the Co doping, an electronic band gap of about 60 meV is also generated near the Fermi level, which can also achieve a metal-semiconductor transition. The above results show that the electrical properties of N-ZGyNR can be controlled by magnetic atom doping, and the metal-semiconductor transition can be realized by Co/Ni doping, which provides a new alternative for spintronic devices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

X-FP and S-HT organized the project, Z-CM completed the calculation and analysis of the results, and wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 11704417), by Hunan Provincial Natural Science Foundation of China (Grant No. 2019JJ40532), by Hunan Provincial Education Department research project, China (No. 17C1640), by the key projects of Hunan Provincial Department of Education (Grant No. 21A0167).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.854656/full#supplementary-material

References

Baughman, R. H., Eckhardt, H., and Kertesz, M. (1987). Structure-property Predictions for New Planar Forms of Carbon: Layered Phases Containing Sp2 and Sp Atoms. J. Chem. Phys. 87 (11), 6687–6699. doi:10.1063/1.453405

CrossRef Full Text | Google Scholar

Bhattacharya, B., Singh, N. B., and Sarkar, U. (2015). Tuning the Magnetic Property of Vacancy-Defected Graphyne by Transition Metal Absorption. Struct. Chem. 25, 1695. doi:10.1063/1.4917707

CrossRef Full Text | Google Scholar

Chang, C., Chen, W., Chen, Y., Chen, Y. H., Chen, Y., Ding, F., et al. (2021). Recent Progress on Two-Dimensional Materials. Acta Phys. -Chim. Sin 37 (12), 1–151. doi:10.3866/PKU.WHXB202108017

CrossRef Full Text | Google Scholar

Cocchi, C., Prezzi, D., Calzolari, A., and Molinari, E. (2010). Spin-transport Selectivity upon Co Adsorption on Antiferromagnetic Graphene Nanoribbons. J. Chem. Phys. 133, 124703–124705. doi:10.1063/1.3478317

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, X. Q., Zhang, Z. H., Tang, G. P., Fan, Z. Q., and Yang, C. H. (2014). Spin Filter Effects in Zigzag-Edge Graphene Nanoribbons with Symmetric and Asymmetric Edge Hydrogenations. Carbon 66, 646–653. doi:10.1016/j.carbon.2013.09.061

CrossRef Full Text | Google Scholar

Donati, F., Gragnaniello, L., Cavallin, A., Natterer, F. D., Dubout, Q., Pivetta, M., et al. (2014). Tailoring the Magnetism of Co Atoms on Graphene through Substrate Hybridization. Phys. Rev. Lett. 113, 177201–177206. doi:10.1103/PhysRevLett.113.177201

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutta, S., Manna, A. K., and Pati, S. K. (2009). Intrinsic Half-Metallicity in Modified Graphene Nanoribbons. Phys. Rev. Lett. 102, 096601–096604. doi:10.1103/PhysRevLett.102.096601

PubMed Abstract | CrossRef Full Text | Google Scholar

Haji-Nasiri, S., and Fotoohi, S. (2018). Doping Induced Diode Behavior with Large Rectifying Ratio in Graphyne Nanoribbons Device. Phys. Lett. A 382, 2894–2899. doi:10.1016/j.physleta.2018.08.007

CrossRef Full Text | Google Scholar

Jing, M., Wu, T., Zhou, Y., Li, X., and Liu, Y. (2020). Nitrogen-Doped Graphene via Iin-Ssitu Alternating Voltage Electrochemical Exfoliation for Supercapacitor Application. Front. Chem. 8, 428. doi:10.3389/fchem.2020.00428

PubMed Abstract | CrossRef Full Text | Google Scholar

Kan, E.-j., Li, Z., Yang, J., and Hou, J. G. (2008). Half-Metallicity in Edge-Modified Zigzag Graphene Nanoribbons. J. Am. Chem. Soc. 130, 4224–4225. doi:10.1021/ja710407t

PubMed Abstract | CrossRef Full Text | Google Scholar

Krause, R., Chávez-Cervantes, M., Aeschlimann, S., Forti, S., Fabbri, F., Rossi, A., et al. (2021). Ultrafast Charge Separation in Bilayer WS2/Graphene Heterostructure Revealed by Time- and Angle-Resolved Photoemission Spectroscopy. Front. Phys. 9, 668149. doi:10.3389/fphy.2021.668149

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Lazić, P., and Crljen, Ž. (2015). Graphyne on Metallic Surfaces: A Density Functional Theory Study. Phys. Rev. B 91, 125423–125425. doi:10.1103/PhysRevB.91.125423

CrossRef Full Text | Google Scholar

Li, X., and Zhang, G. (2013). Enhancing the Extremely High thermal Conduction of Graphene Nanoribbons. Front. Phys. 1, 19. doi:10.3389/fphy.2013.00019

CrossRef Full Text | Google Scholar

Li, Y., Xu, L., Liu, H., and Li, Y. (2014). Graphdiyne and Graphyne: from Theoretical Predictions to Practical Construction. Chem. Soc. Rev. 43, 2572. doi:10.1039/c3cs60388a

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Zhang, Z. H., Wang, D., Zhu, Z., Fan, Z. Q., Tang, G. P., et al. (2014). Electronic Structures, Field Effect Transistor and Bipolar Field-Effect Spin Filtering Behaviors of Functionalized Hexagonal Graphene Nanoflakes. Carbon 69, 142–150. doi:10.1016/j.carbon.2013.11.076

CrossRef Full Text | Google Scholar

Li, Z., Xie, W., Liu, X., and Wu, Y. (2015). Magnetic Property and Possible Half-Metal Behavior in Co-doped Graphene. J. Appl. Phys. 117, 084311–084315. doi:10.1063/1.4913387

CrossRef Full Text | Google Scholar

Li, H., Chen, T., Zhu, Y., Yan, S., and Zhou, G. (2020). Spin Multiple Functional Devices in Zigzag-Edged Graphyne Nanoribbons Based Molecular Nanojunctions. J. Magnetism Magn. Mater. 498, 166223. doi:10.1016/j.jmmm.2019.166223

CrossRef Full Text | Google Scholar

Lin, X., and Ni, J. (2011). Half-metallicity in Graphene Nanoribbons with Topological Line Defects. Phys. Rev. B 84, 075461–075464. doi:10.1103/PhysRevB.84.075461

CrossRef Full Text | Google Scholar

Lin, Z.-Z., Wei, Q., and Zhu, X. (2014). Modulating the Electronic Properties of Graphdiyne Nanoribbons. Carbon 66, 504–510. doi:10.1016/j.carbon.2013.09.027

CrossRef Full Text | Google Scholar

Liu, W., Cao, T., Dai, X., Bai, Y., Lu, X., Li, F., et al. (2021). Nitrogen-Doped Graphene Monolith Catalysts for Oxidative Dehydrogenation of Propane. Front. Chem. 9, 835. doi:10.3389/fchem.2021.759936

CrossRef Full Text | Google Scholar

Malko, D., Neiss, C., Viñes, F., and Görling, A. (2012). Competition for Graphene: Graphynes with Direction-dependent Dirac Cones. Phys. Rev. Lett. 108, 086804. doi:10.1103/PhysRevLett.108.086804

PubMed Abstract | CrossRef Full Text | Google Scholar

Momma, K., and Izumi, F. (2011). VESTA 3for Three-Dimensional Visualization of crystal, Volumetric and Morphology Data. J. Appl. Cryst. 44, 1272–1276. doi:10.1107/S0021889811038970

CrossRef Full Text | Google Scholar

Narita, N., Nagai, S., Suzuki, S., and Nakao, K. (1998). Optimized Geometries and Electronic Structures of Graphyne and its Family. Phys. Rev. B 58, 11009–11014. doi:10.1103/physrevb.58.11009

CrossRef Full Text | Google Scholar

Nayebi, P., and Shamshirsaz, M. (2020). Effect of Vacancy Defects on Transport Properties of α-armchair Graphyne Nanoribbons. Eur. Phys. J. B 93, 170. doi:10.1140/epjb/e2020-10183-5

CrossRef Full Text | Google Scholar

Pan, J., Du, S., Zhang, Y., Pan, L., Zhang, Y., Gao, H.-J., et al. (2015). Ferromagnetism and Perfect Spin Filtering in Transition-Metal-Doped Graphyne Nanoribbons. Phys. Rev. B 92, 205429. doi:10.1103/PhysRevB.92.205429

CrossRef Full Text | Google Scholar

Puigdollers, A. R., Alonso, G., and Gamallo, P. (2016). First-principles Study of Structural, Elastic and Electronic Properties of α-, β- and γ-graphyne. Carbon 96, 879–887. doi:10.1016/j.carbon.2015.10.043

CrossRef Full Text | Google Scholar

Qi, S., Ma, X., Yang, B., Sun, L., Li, W., and Zhao, M. (2019). Two-dimensional Graphyne-like Carbon Nitrides: Moderate Band Gaps, High Carrier Mobility, High Flexibility and Type-II Band Alignment. Carbon 149, 234–241. doi:10.1016/j.carbon.2019.04.024

CrossRef Full Text | Google Scholar

Ren, K., Ren, C., Luo, Y., Xu, Y., Yu, J., Tang, W., et al. (2019). Using van der Waals heterostructures based on two-dimensional blue phosphorus and XC (X = Ge, Si) for water-splitting photocatalysis: a first-principles study. Phys. Chem. Chem. Phys. 21, 9949–9956. doi:10.1039/C8CP07680D

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarma, J. V. N., Chowdhury, R., and Jayaganthan, R. (2014). Graphyne-based Single Electron Transistor: Ab Initio Analysis. Nano 09, 1450032. doi:10.1142/S1793292014500325

CrossRef Full Text | Google Scholar

Sevinçli, H., and Sevik, C. (2014). Electronic, Phononic, and Thermoelectric Properties of Graphyne Sheets. Appl. Phys. Lett. 105, 223108. doi:10.1063/1.4902920

CrossRef Full Text | Google Scholar

Son, Y.-W., Cohen, M. L., and Louie, S. G. (2006). Half-metallic Graphene Nanoribbons. Nature 444, 347–349. doi:10.1038/nature05180

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Ouyang, T., Chen, Y., and Zhong, J. (2015). Enhancement of Thermoelectric Properties of Gamma-Graphyne Nanoribbons with Edge Modulation. Eur. Phys. J. B 88, 130. doi:10.1140/epjb/e2015-60153-y

CrossRef Full Text | Google Scholar

Wang, D., Zhang, Z. H., Deng, X. Q., Fan, Z. Q., and Tang, G. P. (2016). Magnetism and Magnetic Transport Properties of the Polycrystalline Graphene Nanoribbon Heterojunctions. Carbon 98, 204–212. doi:10.1016/j.carbon.2015.10.090

CrossRef Full Text | Google Scholar

Wang, Y., Huang, Y., Song, Y., Zhang, X., Ma, Y., Liang, J., et al. (2009). Room-Temperature Ferromagnetism of Graphene. Nano Lett. 9 (1), 220–224. doi:10.1021/nl802810g

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W., Guo, W., and Zeng, X. C. (2013). Intrinsic Electronic and Transport Properties of Graphyne Sheets and Nanoribbons. Nanoscale 5, 9264. doi:10.1039/c3nr03167e

PubMed Abstract | CrossRef Full Text | Google Scholar

Xi, J., Wang, D., Yi, Y., and Shuai, Z. (2014). Electron-phonon Couplings and Carrier Mobility in Graphynes Sheet Calculated Using the Wannier-Interpolation Approach. J. Chem. Phys. 141, 034704–034711. doi:10.1063/1.4887538

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, S. M., and Kane, C. L. (2015). Dirac Semimetals in Two Dimensions. Phys. Rev. Lett. 115, 126803. doi:10.1103/PhysRevLett.115.126803

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue, Q., Chang, S., Kang, J., Tan, J., Qin, S., and Li, J. (2012). Magnetic and Electronic Properties of α-graphyne Nanoribbons. J. Chem. Phys. 136, 244702. doi:10.1063/1.4730325

PubMed Abstract | CrossRef Full Text | Google Scholar

Zakharov, A. A. (2021). Ambipolar Behavior of Ge-Intercalated Graphene: Interfacial Dynamics and Possible Applications. Front. Phys. 9, 101. doi:10.3389/fphy.2021.641168

CrossRef Full Text | Google Scholar

Zhang, S., and Ma, J. (2011). Width- and Edge-dependent Stability, Electronic Structures, and Magnetic Properties of Graphene-like and Wurtzite ZnS Nanoribbons. J. Phys. Chem. C 115, 4466–4475. doi:10.1016/j.physe.2014.01.00310.1021/jp110148m

CrossRef Full Text | Google Scholar

Zhao, C.-C., Tan, S.-H., Zhou, Y.-H., Wang, R.-J., Wang, X.-J., and Chen, K.-Q. (2017). Half-metallicity and High Spin-Filtering Effect of Magnetic Atoms Embedded Zigzag 6, 6, 12-graphyne Nanoribbon. Carbon 113, 170–175. doi:10.1016/j.carbon.2016.11.022

CrossRef Full Text | Google Scholar