Characterization of Mechanical Property Degradation of Ion-Irradiated Materials

Evaluating the degradation of mechanical properties under irradiation is crucial for nuclear structural materials. Although ion irradiations have been commonly used for fundamental research on irradiation effects and fast screening of potential materials, the mechanical property tests on ion-irradiated materials are challenging due to the shallow irradiation depth. The research progress on utilizing small-scale mechanical property tests to characterize the ion-irradiation induced mechanical property degradation is the focus of this review. While the current techniques can access the mechanical properties at the nano- to micro-scale from various perspectives, the rationality and accuracy of the existing data analysis models, e.g., for the size-dependence, remain unclear or debating, especially for the ion-irradiated materials, resulting in the lack of consistency and reliability of the evaluation of the irradiation effects of materials. Establishing a standardized method is highly demanded to quantitatively bridge the gap between micro- and macro-scale mechanical properties of ion irradiated materials.

Introduction

The structural materials in nuclear reactors suffer from severe irradiation environments. The irradiation-induced defects cause or accelerate the degradation of mechanical properties, such as embrittlement (usually accompanied by hardening), creep, fatigue, etc., which strongly threatens the safe operation of reactors (Zinkle and Busby, 2009; Was, 2016). Therefore, the mechanical properties of materials after irradiation deserve careful evaluation and prediction, and are major concerns during the screening of nuclear structural materials.

Although neutron irradiation experiments are necessary to the final test of candidate materials, they suffer from the issues of long duration, high cost, radioactivity, and, practically, insufficient neutron sources (Was et al., 2002; Was et al., 2014). Ion irradiations have been commonly used for both fundamental research on the irradiation effects of materials and rapid screening the novel materials, due to the high availability, efficiency, and easy control of irradiation parameters. However, ion irradiations have inherently shallow penetration depth within a few microns (Xiao and Yu, 2020a), which disables most conventional mechanical property test methods. Therefore, small-scale mechanical property tests are necessary for ion-irradiated materials to enable the characterization of their mechanical properties.

Overall, the key mechanical properties concerned for structural materials under operation in nuclear reactors include strength and ductility, fracture toughness, creep, and fatigue resistance. Most of these properties can be measured, directly or indirectly, by the commonly used small-scale mechanical property tests, such as nanoindentation, micro-compression, micro-tensile, and micro-cantilever tests (Hosemann et al., 2008; Armstrong et al., 2015; Vo et al., 2017; Jawaharram et al., 2018). However, they face various challenges regarding sample preparation, irradiation condition control (dose/damage depth profile), data analyses, etc. The size-effect, i.e., the impact of sample sizes on the measured mechanical properties, is the key scientific challenge to correlate the results from the micro/nanoscale to the macro-scale conventional mechanical tests. Over the past decades, extensive research efforts, both theoretical and experimental, have been made on this issue (Nix and Gao, 1998; Hosemann et al., 2015; Ajantiwalay et al., 2019; Jawaharram et al., 2020; Lavenstein et al., 2020). Nonetheless, many of the existing models remain empirical or semi-empirical, and their rationality and reliability remain questionable, especially when taking irradiation-induced defect clusters and their inhomogeneous depth distribution into consideration (Kiener et al., 2011a; Wharry et al., 2019).

This review focuses on the research progress on the application of small-scale mechanical property tests on investigating the mechanical property degradation of ion-irradiated materials, i.e., radiation-induced strengthening/hardening, and embrittlement, as well as creep and fatigue, as shown in Figure 1. The advantages and shortcomings of the currently used techniques, as well as the data analysis models, are discussed, and the consistency and reliability of them are overviewed.

FIGURE 1

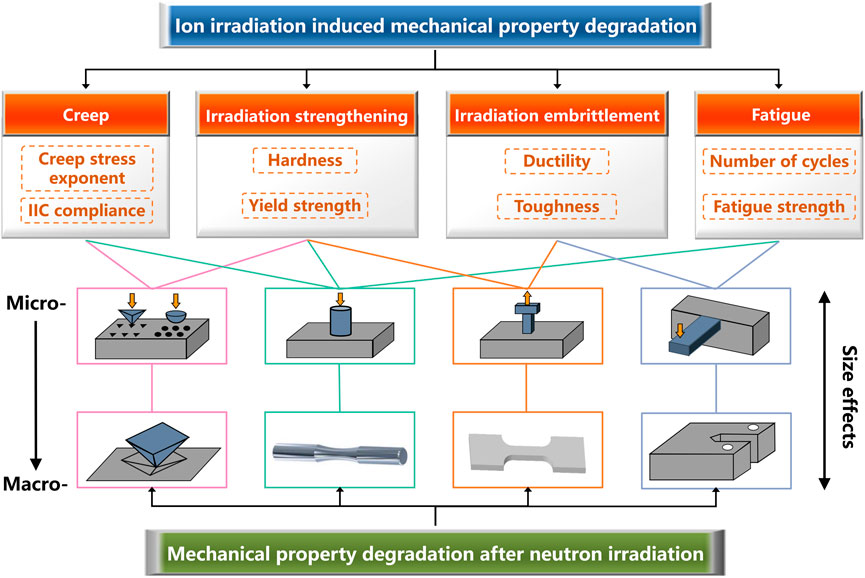
FIGURE 1. The small-scale and macroscale mechanical property tests to evaluate the irradiation induced mechanical property degradation.

Irradiation Strengthening

The irradiation induced defect clusters often act as obstacles to dislocation motion, causing the increase in the strength and hardness of materials (Zinkle and Steven, 2012). Although irradiation strengthening itself is not necessarily detrimental to materials performance, it is usually accompanied by the irradiation embrittlement, which is one of the most important concerns of the materials used under irradiation environments. Considering that the evaluation of strengthening is much more straightforward and convenient compared with that of embrittlement, especially for ion irradiated materials, the majority of the studies about ion irradiation induced mechanical property degradation target on the strengthening.

Strengthening effects can be evaluated through indirect hardness measurements (Liu et al., 2010; Kasada et al., 2011; Xu et al., 2017) or direct yield strength measurements (Grieveson et al., 2012; Shin et al., 2014; Prasitthipayong et al., 2018a) at small scales. Owing to the experimental simplicity and efficiency, nanoindentation is the most used method to measure the nanohardness of materials, which could be converted to the yield strength based on several empirical relationships (Hosemann et al., 2008). The yield strength values can also be directly measured using this technique, if a spherical indenter was used (Weaver et al., 2018). Nevertheless, the test results from nanoindentation are extremely sensitive to the surface quality of the samples and require complex data analyses. Therefore, the recently developed focused ion beam (FIB) milling-based micro-mechanical property test techniques, including micro-compression (Kiener et al., 2011b; Lupinacci et al., 2014; Yano et al., 2017), micro-tensile (Reichardt et al., 2015; Ding et al., 2016; Xu et al., 2020a), and micro-cantilever bending (Gibson et al., 2014; Armstrong et al., 2015) have been increasingly used to directly evaluate the yield strength, of which the data analyses are more straightforward but the experimental complexity is much increased.

Hardness

The early microhardness tests on ion-irradiated materials can be dated back to at least the 1980s on the Cu and Cu-Zr alloys (Zinkle and Oliver, 1986). Nowadays, the nanohardness and elastic modulus could be easily obtained using nanoindentation, based on the Oliver-Pharr method (Oliver and Pharr, 1992; Oliver and Pharr, 2004). However, some issues on the data analyses remained (Oliver and Pharr, 2004; Hosemann et al., 2012; Hardie et al., 2015; Xiao and Yu, 2020a), e.g., pile-up effects, damage gradient effects (DGE), implantation and surface effects, and soft substrate effects (SSE), especially the indentation size effect (ISE).

The Pile-Up Effects

The key parameter to calculate hardness is the indentation area. Rather than imaging the hardness impression, the Oliver-Pharr method allows us to obtain the contact area based on the area function. The basic assumption of the method is that the contact periphery sinks in, which does not account for the pile-up around the contact impression in many elastic-plastic materials (Oliver and Pharr, 2004). When pile-up occurs, the predicted contact area by the method is less than the actual area, consequently overestimating the hardness values.

It has been reported that the ratio of the elastic modulus to yield strength ($E/{\sigma }_y$) and the work hardening coefficient (n) are the fundamental material properties affecting the pile-up behavior (Bolshakov and Pharr, 1998; McElhaney et al., 1998). In general, the pile-up is greatest in materials with large $E/{\sigma }_y$ and small n. In addition, the pile-up can be more prominent during indenting the thin coating/substrate systems (Pharr and Oliver, 1992), like the structure of ion-irradiated materials, i.e., the thin damaged layers on the underlying unirradiated soft substrate. Hardie et al. investigated the role of pile-up effect on the mechanical property evaluation of self-irradiated Fe12%Cr alloys (Hardie et al., 2015), and found that the pile-up behavior between unirradiated and irradiated materials was significantly different using a cube-corner indenter, producing large errors in the irradiation hardening evaluation based on the area function. They attributed the pile-up to the restricted growth of the plastic zone in the damaged layer and the direct evaluation using the uncorrected indentation data that involve the combined effects of both irradiation hardening and irradiation-induced indentation pile-up.

Hence, the differences in the pile-up effects between the unirradiated and irradiated materials need to be considered when evaluating the irradiation strengthening, to obtain the actual hardness or modulus changes of irradiated materials.

The DGE and SSE

The limited ion penetration depth and the inhomogeneous dose profile are inevitable for ion irradiation. As could be conveniently estimated using the Monte-Carlo codes such as The Stopping and Range of Ions in Matter (SRIM) (Ziegler et al., 2010), the dose and dose rate dramatically vary with irradiation depth, and the maximum dose is, in general, many times or even orders greater than that in the platform region. On the other hand, the plastic zone is usually much greater than the indentation depth (Johnson, 1970; Kiener et al., 2006) [this review focuses on the metals and alloys, and this fact is also applicable for ceramics (Hockey et al., 1978; Lankford and Davidson, 1979)]. Thus, a wide dose depth range is sampled within the plastic zone under the sample surface during indentation, likely involving the unirradiated soft substrate. Such damage gradient effects and soft substrate effects strongly challenge the data analyses.

The surface nanoindentation (see Figures 2A–C) is the most widely applied method to evaluate nanohardness (Gao et al., 2019; Cui et al., 2017; Zhang et al., 2016), due to the simple sample preparation procedure. But the DGE, SSE, ISE, and surface effects are inevitable, as shown in Figure 2B. Regarding the SSE, Hosemann et al. proposed a “simple law of mixture” (Hosemann et al., 2012; Kiener et al., 2012), in which the plastic zone is semi-spherically assumed with a radius of five times to indentation depth for simplicity, to calculate the “fictive” hardness of irradiated materials. By calculating the volume fraction of the unirradiated materials sampled in the total sampling plastic zone, the measured hardness data at the specific indentation depth can be converted to the “fictive hardness” as if the plastic zone is performed exactly as the entire irradiation zone, as illustrated with the blue dotted line in Figure 2C. This simplified approach only gives a semi-quantitative estimate for the true hardness of irradiated materials. Compared with the “simple law of mixture,” the precise plastic zone of the indention on irradiated materials can be obtained by transmission electron microscope (TEM) observation and finite element simulation, as reported in (Kiener et al., 2006; Dolph et al., 2016; Saleh et al., 2016), and thus the more accurate “fictive hardness” can be calculated.

FIGURE 2

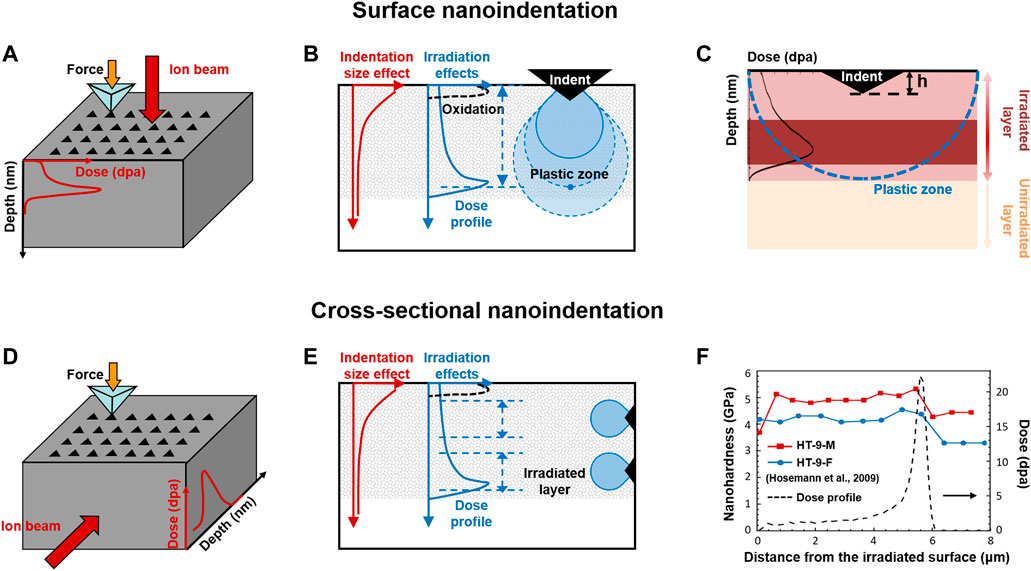
FIGURE 2. Schematic diagrams for (A) surface nanoindentation and (D) cross-sectional nanoindentation, respectively; The issues on data analyses for (B) surface nanoindentation and (E) cross-sectional nanoindentation; (C) Schematic drawing for the “simple law of mixture”; (F) The damage-dependent hardness for proton-irradiated steels using cross-sectional nanoindentation. Data adapted from Hosemann et al. (2009).

In contrast to the surface indentation, the cross-sectional nanoindentation (see Figures 2D–F) may “deconvolute” the indentation hardness to a specific depth (actually a depth range) to allow the correlation between the hardness and dose, as shown in Figure 2F. Thus, it could ignore the irradiation-induced surface contamination effects (although additional cross-sectional surface is made), and eliminate the DGE and SSE, as illustrated with Figure 2E. Over the past decades, the cross-sectional nanoindentation has gained increasing popularity for ion-irradiated materials (Hosemann et al., 2009; M. Rice and Stoller, 1997; Snead et al., 1992). However, the preparation of cross-sectional samples is tedious and difficult, especially to obtain a sharp and clean edge. Moreover, it needs to note that the lateral size of the plastic zone should not be ignored either, which could also cover hundreds of nanometers to blur the corresponding dose of certain indents. Therefore, the cross-sectional method usually contains quite few numbers of indents across the damage depth especially for the shallow irradiation.

The Indentation Size Effect

The size-dependent behavior can be observed in indentation tests. At small scales, the apparent hardness changes with the indentation sizes, bringing challenges for the actual hardness evaluation, so-called ISE. Over the past decades, two types of effects have been reported (Bückle, 1959; Upit and Varchenya, 1973; Ma and Clarke, 1995; Sangwal, 2000; Pharr et al., 2010; Renjo et al., 2014). The normal ISE, i.e., the hardness increases at small indentation depths, is the more frequently seen effect. The reverse type of ISE, where the hardness increases with the increasing indentation sizes, has also been observed (Sangwal, 2000), but is usually ascribed to testing artifacts (Pharr et al., 2010). Here we focus on the frequently observed normal ISE, called ISE for simplicity in the following.

Several models have been built to understand the ISE, of which the most widely accepted one is the Nix-Gao model (Nix and Gao, 1998). The model separates the effects caused by geometrically necessary dislocations (GNDs) (Ashby, 1970) and statistically stored dislocations (SSDs), to describe the depth dependence of hardness for crystalline, as shown in Eq. 1. The linear relationship between the square of nanoindentation hardness (H²) and the reciprocal of indentation depth (1/h) has been widely used to fit the experimental data.

$\begin{array}{c}\frac{H}{H_{\mathbf{0}}}=\sqrt{\mathit{1}\mathbf{+}\frac{h^{\mathbf{\ast }}}{h}}\end{array}(1)$

where H is the hardness of a given depth h; H₀ is the hardness at infinite depth, i.e., macroscopic hardness, as described with the following Eq. 2; h* is a characteristic length that depends on the materials (the shear modulus $\mu$ and H₀) and the shape of the indenter, described with Eq. 3.

$\begin{array}{c}{H}_0=3\sqrt{3}\alpha \mu b\sqrt{{\rho }_s}\end{array}(2)$

$\begin{array}{c}{h}^{\ast }=\frac{81}{2}b{\alpha }^2{\mathit{tan}}^2\theta {\left(\frac{\mu }{H_0}\right)}^2\end{array}(3)$

where α is a constant; b is the length of the Burgers vector; ${\rho }_s$ is the SSD density; and $\theta$ is the angle between the surface of the indenter and the plane of the surface.

Nonetheless, such a simple linear relationship may not hold for irradiated materials. For example, the bi-linear behavior has been reported in the irradiated ferritic alloys, stainless steels, and F82H steels, and the underlying mechanism is believed to be related to the SSE (Kasada et al., 2011; Yabuuchi et al., 2014; Takayama et al., 2013). Moreover, the ISE could be weaker in the irradiated materials. For example, Jin et al. found that the ISE of ion irradiated Mo became weaker with increasing irradiation doses, as shown in Figure 3A (Jin et al., 2018). They believed that the increased density of SSDs induced by ion irradiation weakens the role of the depth-dependent GNDs, and so the ISE is less pronounced for irradiated materials. Similarly, the weaker ISE was discovered in the proton-irradiated single crystal copper after correcting the nanohardness data, based on the "simple law of mixture" (Hosemann et al., 2012). Other than the conventional room temperature tests, Prasitthipayong et al. also found that the ISE-dependent length h* decreased with the increasing temperatures for both unirradiated and irradiated 800H steels (Prasitthipayong et al., 2018b), which can be explained by the decreasing GND density at elevated temperatures, as shown in Figure 3B.

FIGURE 3

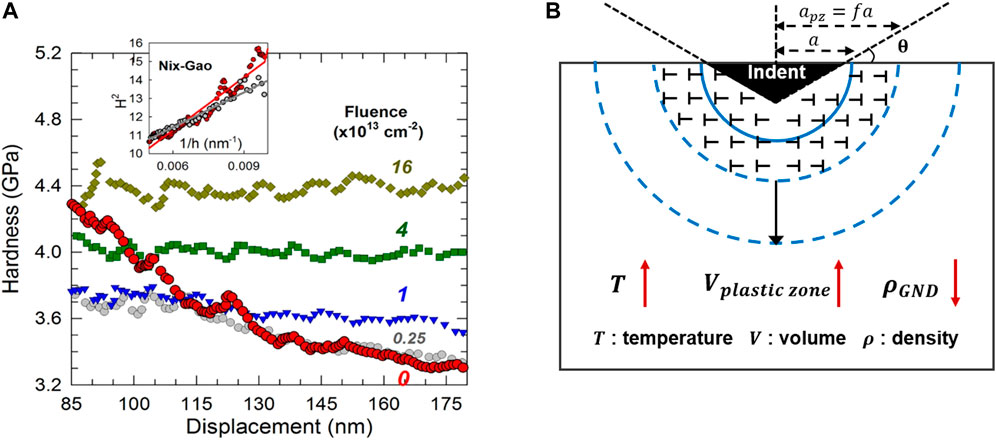
FIGURE 3. (A) Nanoindentation hardness as a function of displacement at a variety of irradiation influence. Insert shows the Nix-Gao model fitted line [Reprinted with permission from Jin et al. (2018). Copyright 2018 by Elsevier]. (B) Schematic drawing for the plastic zone evolution (the GNDs stored volume) with the change of temperatures.

In addition to the irradiated materials, poor fitting also occurs when indentation depth is below 100 nm. To address this issue, Huang et al. modified the Nix-Gao model by introducing the concept of “maximum allowable GND density (${\rho }_G^{\max }$),” i.e., the upper limit of GND density, and found that the model agreed reasonably with the nanohardness data even below 100 nm of MgO and iridium (Huang et al., 2006). The feasibility of the model on ion-irradiated materials has recently been supported by Yang et al. (2020), when fitting the nanohardness data effectively in different ferritic steels. However, the modified model based on the ${\rho }_G^{\max }$ also faces some challenges such as the more complex parameters.

Yield Strength

Yield strength is one of the key parameters to evaluate the irradiation strengthening, which could be obtained using nanoindentation, micro-compression, and micro-tensile tests.

Nanoindentation

The yield strength of ion irradiated materials could be evaluated in nanoindentation tests using either the Berkovich indenter, through a so-called “three-step approach” (Lupinacci et al., 2015; Hosemann, 2018) to convert the nanohardness to the yield strength, or the spherical indenter to directly obtain the stress-strain curves (Herbert et al., 2001; Basu et al., 2006; Kalidindi and Pathak, 2008; Pathak and Kalidindi, 2015).

Three-Step Approach

Estimating the size-effect difference between the nanohardness and micro-hardness measurements by making indents on both irradiated and unirradiated materials is the “first-step.” The two steps after that are mainly based on the nanohardness-microhardness relationship and the microhardness-yield strength relationship.

The former has been identified to be linear according to experimental data, and the most widely used correlation is Eq. 4 (Lupinacci et al., 2015; Prasitthipayong et al., 2018a; Krumwiede et al., 2018). Nonetheless, different values of the linear coefficients have been reported depending on the test materials and irradiation conditions, such as 0.937 for a series of model ferritic alloys and two commercial steels (Rice and Stoller, 2000), 0.76 for the irradiated stainless steel (Yabuuchi et al., 2014), 0.73 for the unirradiated stainless steel (Qian et al., 2005), etc.

$\begin{array}{c}{H}_{micro}\left[\mathrm{G}\mathrm{P}\mathrm{a}\right]=0.945H_{nano}\left[\mathrm{G}\mathrm{P}\mathrm{a}\right]\end{array}(4)$

The correlation between microhardness and yield strength is also linear. As proposed by Tabor (1956), for the materials with an ideal plastic behavior, YS (MPa) ≈ 3*HV (kgf/mm²). Nowadays, the commonly used empirical formula includes those proposed by Busby et al. (2005) and Milot (2012), both collecting extensive standard Vickers hardness and tensile test data for irradiated and unirradiated materials. Busby compared the changes in Vickers hardness and in yield strength, see Eq. 5, while Milot correlated the absolute values of yield strength to Vickers hardness, as shown in Eq. 6.

$\begin{array}{c}\Delta {\sigma }_y\left[\mathrm{M}\mathrm{P}\mathrm{a}\right]=3.06\mathrm{\Delta }HV\left[\mathrm{k}\mathrm{g}\mathrm{f}/\mathrm{m}{\mathrm{m}}^{\mathbf{2}}\right]\end{array}(5)$

$\begin{array}{c}{\sigma }_y\left[\mathrm{M}\mathrm{P}\mathrm{a}\right]=2.82HV\left[\mathrm{k}\mathrm{g}\mathrm{f}/\mathrm{m}{\mathrm{m}}^2\right]-114\end{array}(6)$

Krumwiede et al. studied the accuracy of those correlations by comparing the macro-tensile test data and nano-hardness on eight alloys before and after neutron irradiation. They concluded that Eq. 6 was preferred in their study due to the smaller uncertainties and it had the benefit of not requiring the prior tensile tests on the unirradiated materials to calculate the changes in yield strength (Krumwiede et al., 2018).

It is important to note that, although the reliable relations between nanohardness and yield strength could be established based on these empirical correlations, the linear coefficients vary significantly for different materials. Further experimental and theoretical efforts need to be made, to obtain accurate and reliable correlations, especially for novel materials after irradiation.

Spherical Indentation Stress-Strain Curves

While the Berkovich indenter is widely used to obtain the nanohardness and modulus during nanoindentation tests based on the Oliver-Pharr methods, it has been reported that the indentation strain-stress curves could be obtained using the spherical indenter (Field and Swain, 1993; Angker and Swain, 2006). The key step for converting the load-depth data to the strain-stress curve is to define properly the indentation stress (${\mathit{\sigma }}_{\mathit{ind}}$) and indentation strain (${\mathit{\epsilon }}_{\mathit{ind}}$). Two definitions have been commonly used thus far, both based on Hertz’s theory, as shown in Eqs 7 and 8.

$\begin{array}{c}{\sigma }_{ind}=\frac{P}{\pi a^2} , {\epsilon }_{ind}=\frac{a}{R_{eff}} , {\sigma }_{ind}=\frac{4E_{eff}}{3\pi }{\epsilon }_{ind}\end{array}(7)$

$\begin{array}{c}{\sigma }_{ind}=\frac{P}{\pi a^2} , {\epsilon }_{ind}=\frac{4}{3\pi }\frac{h}{a}\approx \frac{h}{2.4a} , {\sigma }_{ind}=E_{eff}{\epsilon }_{ind}\end{array}(8)$

where P is the load; a is the contact radius; h is the indentation depth; $R_{eff}$ and $E_{eff}$ refer to the effective radius and the elastic modulus of the indenter and sample system.

Equation 7 has been widely used due to the simple form, in which the $R_{eff}$ could be modified as $R$ for simplicity (Field and Swain, 1993; Herbert et al., 2001; Murugaiah et al., 2004; Basu et al., 2006), but the simplified equation lacks physical interpretation. Kalidindi and Pathak proposed another definition of indentation strain (Eq. 8) and demonstrated it to be rational and meaningful based on finite elements modeling and experimental studies (Kalidindi and Pathak, 2008).

Equation 8 has also been widely used to characterize the mechanical behavior of both unirradiated and irradiated materials (Pathak and Kalidindi, 2015; Weaver et al., 2017a; Weaver et al., 2017b; Pathak et al., 2017). For example, Pathak et al. demonstrated that the spherical nanoindentation tests with different indenter sizes could provide insights to heterogeneous characteristic of irradiation damage zone (Pathak et al., 2017). Weave et al. found that the extracted yield strength of unirradiated nanostructure ferritic alloys (1100–1400 MPa) was consistent with the available tensile data (1100 MPa) (Weaver et al., 2017a).

Micro-Compression

Compared with nanoindentation, the micro-compression technique is more direct to evaluate the irradiation strengthening (Yu et al., 2010; Lupinacci et al., 2014; Shin et al., 2014; Yano et al., 2017). The accuracy is affected by the geometric factors of pillars, such as the taper of pillars, fillet radius (the curvature at the bottom of pillars connecting to the base), and the aspect ratio of the pillars (the height/diameter ratio). Using two-dimensional (2D) and three-dimensional (3D) finite element modeling, Zhang et al. recommend minimal taper, fillet radius of 0.2–0.5, and pillars aspect ratios of 2-3 to provide sufficient testing accuracy (Zhang et al., 2006). These suggestions have been adopted to fabricate defined micro-pillars in unirradiated and ion-irradiated materials (Jin et al., 2016; Reichardt et al., 2017; Heo et al., 2018; Fan et al., 2019; Paccou et al., 2019).

The key challenge to correlate the small-scale yield strength values with those at the macro-scales is also the size effects. In the micro-size regime, the “smaller is stronger” phenomenon has been discovered for abundant metallic materials, as expressed with a generic form (Eq. 9) (Dehm, 2009; Greer and De Hosson, 2011). Some researchers have established dislocation-based models to explain the scaling behavior, such as the dislocation-starvation (Greer et al., 2005) and the single-ended dislocation source model (Parthasarathy et al., 2007).

$\begin{array}{c}\sigma =A{D}^m\end{array}(9)$

where $\sigma$ is the compressive flow strength; D refers to the pillar diameter; m is the size-effect exponent; and A is a constant.

When more grains are sampled with increasing sample sizes, the strength may increase toward the bulk strength due to the “grain boundary strengthening.” Combining the two conditions in the micro- and meso-scales leads to the black curve in Figure 4A (Hosemann et al., 2015; Hosemann, 2018), which indicates the size-effect behavior of the materials with low defect density. The size effect of irradiated materials (red curve) is significantly different from that of the unirradiated materials, i.e., the weaker size effects and the missing region “B” (Figure 4A), as well as the smaller specimen dimension to arrive at the size-independent strength (Figure 4B) (Kiener et al., 2011a). These differences may be related to the interaction between dislocations and irradiation induced defects, but the underlying mechanism and quantitative relationships of size effects remain unclear.

FIGURE 4

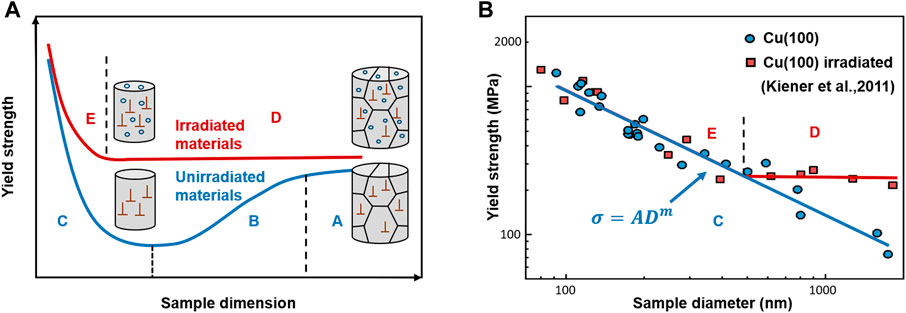
FIGURE 4. (A) Proposed size effects of irradiated and unirradiated polycrystalline materials; (B) The different size effects for unirradiated and irradiated (100) single-crystal Cu. Data adapted from Kiener et al. (2011b).

Micro-Tensile

The most direct quantification method of strength and critical resolved shear stress (CRSS) for ion-irradiated materials could be the micro-tensile tests (Vo et al., 2017; Ajantiwalay et al., 2019). For example, using this method, Vo et al. (2017) found significant increase in the yield strength in 304SS after irradiation. The yield strength and CRSS values were in good agreements with the macroscopic tensile test results of neutron-irradiated stainless steels in the literature. Ajantiwalay et al. (2019) also discovered that the yield strength and CRSS of 304SS matches well with the macro-tensile test values in the literature. These findings demonstrated that the reliable CRSS values can be estimated locally using the micro-tensile tests.

Ajantiwalay et al. have investigated the applicability of the proposed size scaling behavior [Figure 4A (Hosemann et al., 2015)] for unirradiated 304SS based on micro-tensile tests, as illustrated in Figure 5 (Ajantiwalay et al., 2019). The yield strength values follow the overall trend of the proposed curve. Further studies are required for the irradiated materials to verify the feasibility of the proposed size scaling behavior.

FIGURE 5

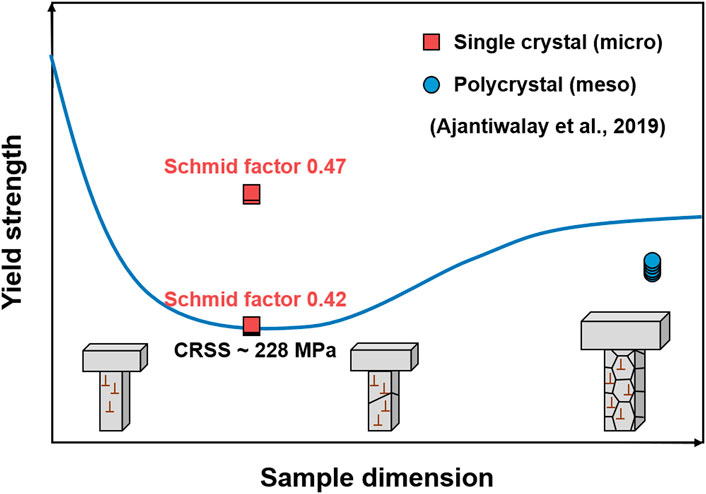
FIGURE 5. Proposed size effects for unirradiated 304SS, based on micro-tensile tests data adapted from Ajantiwalay et al. (2019).

Comparison of Different Small-Scale Techniques

Over the past decades, some works have combined or compared different small-scale mechanical property tests to study the irradiation strengthening (Hosemann et al., 2008; Vo et al., 2015; Weaver et al., 2017b; Prasitthipayong et al., 2018a).

Hosemann et al. found that the yield strength values of unirradiated and irradiated stainless steels using micro-compression tests were in relatively good agreements with nanoindentation data using the “three-step” method with the Busby’s pre-factor (Hosemann et al., 2008). Prasitthipayong et al. also found that the yield strength values of irradiated 800H and T91 converted from nanohardness are comparable with the micro-compression measurements (Prasitthipayong et al., 2018a). These results demonstrate the consistency of the yield strength values obtained from different small-scale tests. However, some studies reported the discrepancies on the irradiation strengthening using different evaluation methods (Moschetti et al., 2020; Sadeghilaridjani et al., 2020). For example, Sadeghilaridjani et al. found that the irradiation hardening effects evaluated by micro-compression (28%) were more significant than nanoindentation (13%) for HfTaTiVZr (Sadeghilaridjani et al., 2020).

Weaver et al. conducted a direct comparison between spherical nanoindentation, micro-compression, and micro-tensile tests, by converting the indentation strain-stress curves to uniaxial responses, as shown in Figure 6 (Weaver et al., 2017b). The main finding was that the work hardening behaviors of these techniques were basically alike for unirradiated materials (Figures 6A,B) while strong disagreements existed for the irradiated materials (Figures 6C,D). They believed that the little to no hardening behaviors of the irradiated pillars or tensile bars may be explained by the dislocation channeling mechanism.

FIGURE 6

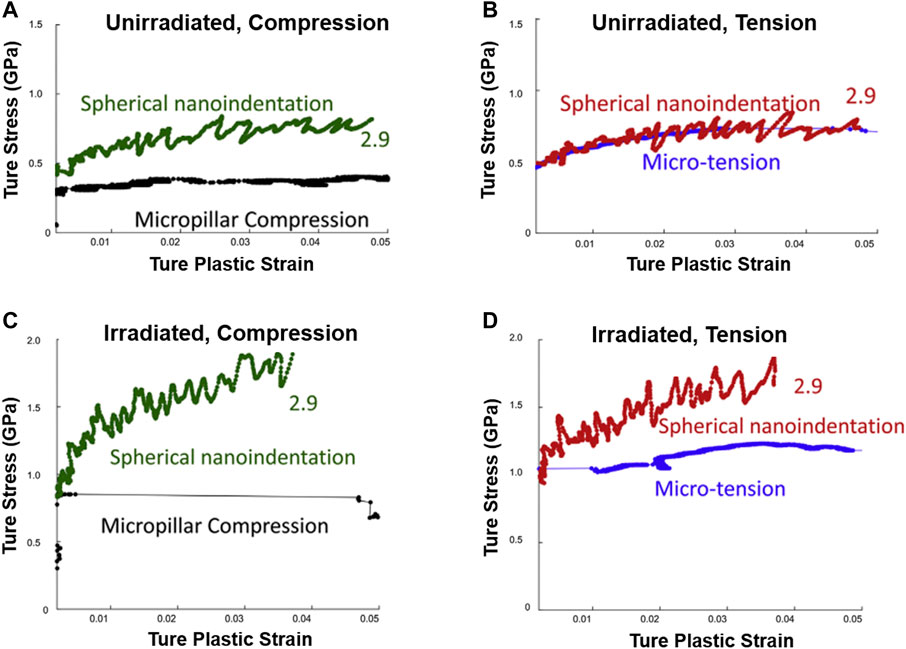
FIGURE 6. The comparison of the uniaxial engineering stress-strain curves and indentation stress-strain of unirradiated (A,B) and irradiated 304 stainless steels (C,D), obtained from micro-compression, micro-tension, and spherical nanoindentation tests. Adapted from Weaver et al. (2017). Reproduced with the permission of the copyright holder (Elsevier).

Irradiation Embrittlement

Reactor structural materials undergo embrittlement due to the harsh irradiation environment, affecting the plant reliability (Was, 2016). Thus, assessing the irradiation-induced embrittlement is critical to screen the candidate materials. The ductile to brittle transition temperatures (DBTT) evaluation has been conducted in neutron irradiated materials (Kayano et al., 1988; Byun et al., 2008), but the DBTT is extremely difficult to obtain for ion-irradiated specimens due to shallow and gradient damage profile. Therefore, other parameters related to the ductility and toughness assessment need to be considered.

The embrittlement of materials can be evaluated through fracture strength/strain (Vo et al., 2017; Howard et al., 2019) and fracture toughness measurements (Park et al., 2002; Leide et al., 2021) at the small-scales, reflecting the ductility and toughness, respectively. Micro-tensile tests have been commonly used to assess the fracture strength/strain because it permits straining the sample to failure and gets the entire strain-stress curves. The fracture toughness is the major considered parameter, which is usually obtained by the classical indentation-based methods for fragile materials, the pillar splitting method for thin ceramic films, and the notched cantilever bending method for both brittle and ductile materials, as the most commonly used method.

Fracture Strain

Based on the various tensile-test setups, as illustrate with Figure 7 (reference [6,7] in the "Figure and caption revision" file), the evolution of stress and strain can be easily characterized by the recording load-displacement data. Many studies have reported ductility loss of ion-irradiated materials using the micro-tensile tests. For example, Vo et al. found that the total elongation of 304SS is greatly reduced after proton irradiation (from 47% to 11% approximately), showing radiation induced embrittlement significantly. Reichardt et al. reported that the fracture strength of single-crystal Ni foils increases roughly proportional to the damage dose and the ductility (fracture strain) decreases with increasing dose, showing embrittlement accompanied with strengthening (Reichardt et al., 2015).

FIGURE 7

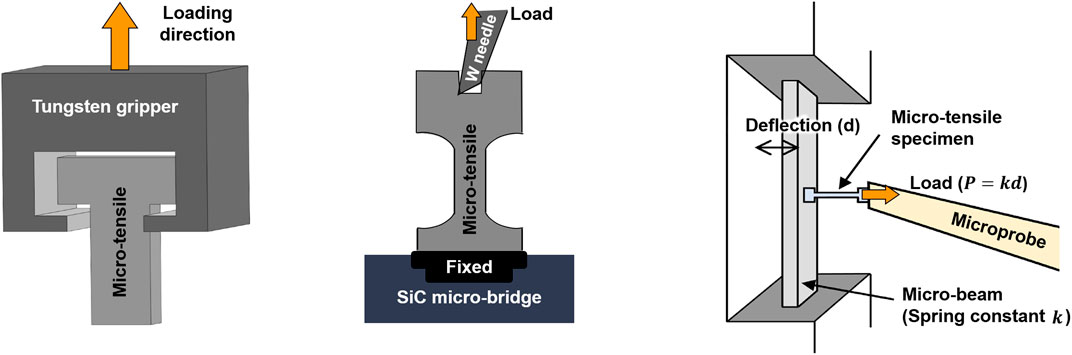
FIGURE 7. Schematic drawings of the various micro-tensile test setups. Reproduced from Yu et al. (2022) and Miura et al. (2018), under the Creative Commons CC-BY-NC-ND license.

During investigating the mechanical properties evolution of 304 stainless steels (Vo et al., 2017), it is worth noting that the failure strain values measured by micro-tensile tests (single-crystal) correlated well to the macro-scale tensile tests (polycrystal) on irradiated materials. They believed that the differences between single-crystal and polycrystal irradiated materials can be mitigated by the nanoscale nature of the radiation damage. However, the general comparability of micro- and macro-fracture strain is still unclear.

Fracture Toughness

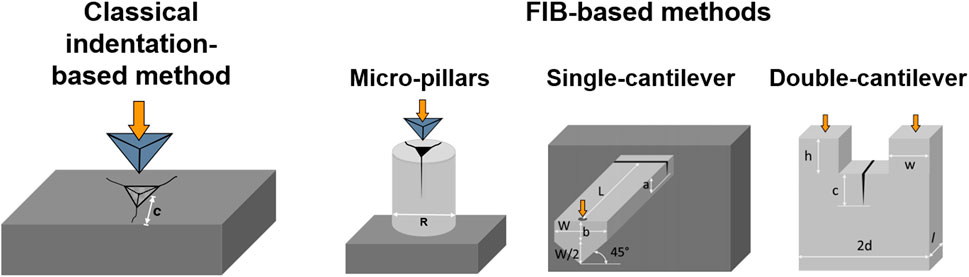
There are two primary classes of methods to measure the fracture toughness at small scales: the classical indentation-based method and FIB-based methods, as illustrated in Figure 8. The specimen geometries for the latter methods include the single and double-cantilever (Liu et al., 2013; Sernicola et al., 2017), pillars, clamped beams (Jaya B et al., 2012; Hintsala et al., 2017), membranes (Merle and Göken, 2011; Preiß et al., 2017), and micro-tension (Schwiedrzik et al., 2018). Up to now, some works have assessed fracture toughness of irradiated materials using these methods (Park et al., 2002; Armstrong et al., 2015; Henry et al., 2020a; Henry et al., 2020b; Leide et al., 2021).

FIGURE 8

FIGURE 8. The schematic diagrams of the methods to evaluate fracture toughness at small scales.

Classical Indentation-Based Method

Indentation technique is a simple, rapid, and inexpensive method to evaluate the fracture toughness. Based on the Lawn, Evans, and Marshall (LEM) model and its modified expressions proposed in the 1980s (Lawn et al., 1980; Anstis et al., 1981; Laugier, 1987), the fracture toughness (K_Ic) can be measured with the crack lengths (c) for the Vickers indentation cracks, as shown in Eq. 10. The geometry-dependent constant $\mathit{\alpha }$ in Eq. 10 must be revised for nanoindentation tests because the indenters are standard Berkovich and cube-corner rather than Vickers, such as 0.036 for cube-corner indenters while 0.016 for Vickers indenters (Harding et al., 1994; Cuadrado et al., 2012).

$\begin{array}{c}{K}_{Ic}=\alpha {\left(\frac{E}{H}\right)}^{1/2}\left(\frac{P}{c^{3/2}}\right)\end{array}(10)$

where E is the elastic modulus; H is the hardness; P is the peak indentation load; and $\alpha$ refers to an empirical constant which depends on the indenter geometry and the crack morphology.

Many researchers have used the nanoindentation to evaluate the fracture toughness of ion-irradiated SiC (Park et al., 2002; Yang et al., 2015; Leide et al., 2021), and obtained similar results that the radiation damage seems to improve the fracture toughness. Yang et al. explained such unusual phenomenon by the compressive stress and the deflection, pinning, and branching of cracks induced by irradiation defects (Yang et al., 2015). By means of high-resolution electron backscatter diffraction (HR-EBSD) and Raman spectroscopy, Leide et al. concluded that no crack in irradiated SiC is an artificial consequence of compressive residual stress, caused by constrained radiation swelling (Leide et al., 2021).

It is regrettable that the true fracture toughness values of ion-irradiated materials are difficult to assess using the classical indentation-based method and the method cannot be utilized on semi-brittle and ductile materials because of the high cracking thresholds.

Pillar Splitting Method

The fracture toughness values could be calculated based on a simple correlation between the critical load at failure (P_c), and the pillar radius (R), as shown in Eq. 11 (Sebastiani et al., 2015a). For the pillar splitting method, there is no need to image and measure the indentation crack lengths accurately; the residual stress can be eliminated by making the pillar diameter approximately equal to its length; the substrate effects are also minimized.

$\begin{array}{c}{K}_c=\gamma \cdot \frac{P_c}{R^{3/2}}\end{array}(11)$

where the dimensionless coefficient γ is calibrated with the cohesive finite element simulation, not related to the LEM coefficient α in Eq. 10.

The micro-pillar splitting method has been successfully performed on various materials, such as thin ceramic films and coating (Sebastiani et al., 2015a; Sebastiani et al., 2015b; Bolelli et al., 2019), silicon (Jaya et al., 2015; Ghidelli et al., 2017; Lauener et al., 2018), battery (Mughal et al., 2016; Mughal et al., 2017; Wang et al., 2018a), and composite materials (Liu et al., 2017). In addition, this method could be applied at high temperatures on silicon and ceramic hard coatings (Lauener et al., 2018; Best et al., 2019). Nevertheless, it is impractical for most metals because their high toughness prevents splitting.

Cantilever Bending Method

Single-Cantilever Geometry

Based on the linear elastic fracture mechanics (LEFM), the fracture toughness can be assessed accurately using the micro-cantilever bending method. For example, Di Maio and Roberts found that the fracture toughness values of reference brittle silicon coatings were in great agreement with the expected values, based on Eq. 12 (Di Maio and Roberts, 2005). When the material responses are no longer elastic-brittle, fracture toughness can be obtained based on the elastic-plastic fracture mechanics (EPFM). For example, Wurster et al. (2012) concluded that the LEFM gives a lower limit for critical fracture toughness of semi-brittle tungsten while the J-values give the largest values. The fracture toughness values from the crack tip opening displacement (CTOD) agree best with the values of macro-specimens.

$\begin{array}{c}{K}_{Ic}={\sigma }_c\cdot \sqrt{\pi a}\cdot F\left(\frac{a}{b}\right)\end{array}(12)$

where ${\sigma }_c$ is the fracture strength; a is the pre-crack length; b is the depth of the cantilever; and F(a/b) is a dimensionless shape factor that depends on sample geometry.

By means of the micro-cantilever bending method, some studies have characterized the fracture toughness of ion-irradiated materials, and most of them targeted on the irradiated pressurized water reactors (PWR) refractory ceramic UO₂ fuel. For example, Henry et al. found that both notched and un-notched micro-cantilevers could be used to characterize the local fracture properties of irradiated nuclear fuel (Henry et al., 2020a). They also found that irradiation has a limited effect on the fracture properties inside grains, while a huge difference occurs at grain boundaries (Henry et al., 2020b). Besides the experimental studies, the irradiation embrittlement phenomenon of the UO₂ micro-cantilevers fuel (10 J/m² to 5 J/m²) was discovered using the finite element simulation (Doitrand et al., 2020).

Except the studies for irradiated fuel, Armstrong et al. have performed the micro-cantilever bending method on the ion-irradiated tungsten, to study and quantify the fracture behavior of irradiation embrittled layers (Armstrong et al., 2015).

Double-Cantilever Geometry

The double-cantilever bending method can also evaluate the fracture toughness of materials. In contrast to the traditional single-cantilever geometry, the cracks in double-cantilever bending tests are much more stable and the loading points do not need to be determined. The fracture toughness values of the SiC and GaAs crystals were found to be reproducible, quantitative, and reliable using the double-cantilever bending method (Liu et al., 2013).

In brief, the cantilever bending method is a valuable tool to evaluate the fracture properties of brittle and semi-brittle materials.

Comparison of Various Geometries

Researchers have reported that the fracture toughness values vary significantly with the different testing methods. For example, Jaya et al. reviewed that the fracture toughness of pure single crystal silicon scattered from 0.7 to 2.1 MPa m^1/2 due to the different sample dimensions, sample geometries, and preparation techniques (Jaya et al., 2015).

However, the consistency of fracture toughness evaluated using different methods has also been found. For example, the average fracture toughness values of silicon, deduced by four sample geometries, i.e., single-cantilever, double-cantilever, clamped beams, and pillars, are nearly constants (∼0.80 MPa m^1/2) (Jaya et al., 2015). Besides, the fracture toughness values of CrN coating show great agreements between the single-cantilever bending and pillar splitting methods, while the values obtained by double-cantilever and pillar splitting method show reasonable agreements (within 25%) (Sebastiani et al., 2015b).

Some researchers believed that the discrepancies on the fracture toughness values may be caused by the systematic errors in calibration procedures (Sebastiani et al., 2015b), and the multiple microstructural complexities in materials cannot be captured using some testing methods (Jaya et al., 2015).

Size Effects on Fracture Behaviors

Understanding the size effects and further correlating the micro- to macro-fracture behaviors of various materials have attracted scholars’ interest (Iqbal et al., 2012; Ast et al., 2014; Sumigawa et al., 2015; Ast et al., 2017; Henry et al., 2020b). Both size-independent and size-dependent fracture toughness have been reported.

The bending tests of the notched intermetallic compound NiAl micro-cantilevers show that the fracture toughness is size independent even down to the micro-scale, close to the macroscopic values (Iqbal et al., 2012; Ast et al., 2014). The fracture toughness values are roughly 1 MPa m^1/2 in different singular stress field sizes of single-crystal silicon, and are in good agreement with the values of macro-scale silicon (Sumigawa et al., 2015). Henry et al. (2020b) also found the size-independent fracture toughness of fresh UO₂ fuel by comparing the measured values (∼1.65 ± 0.29 MPa m^1/2) to those of bulk samples (1.4 ± 0.15 MPa m^1/2 to 1.8 ± 0.2 MPa m^1/2).

Although the size-independent fracture toughness has been reported in many materials, the reliability and universality remain unclear. As illustrated in Ast et al.’s work (Ast et al., 2017), the size-affected fracture toughness of single crystal tungsten has been discovered using the micro-cantilever bending method. The samples with intermediate size show the highest fracture toughness values due to the pronounced plastic strain gradients and the rather large plastic zone.

Thus far, the size effects of fracture toughness have remained debatable and few models have been established. Further studies on the size effects of fracture behaviors need to be conducted for materials before and after irradiation.

Creep and Fatigue

The structural materials in the nuclear reactors suffer from high temperatures, high neutron flux, cyclic stress, etc., that may induce or accelerate the creep and fatigue failures (Was, 2016). The evaluation for the creep and fatigue properties is indispensable for irradiated materials.

Creep

The creep properties of ion-irradiated materials can be characterized by ex-situ creep tests and in-situ irradiation induced creep (IIC) tests. The in-situ creep tests are straightforward because they give real-time insights for the effects of radiation-induced defects on the creep performance. Nonetheless, the great technical challenge for the in-situ creep tests requires the ex-situ creep tests as a complemental method to compare the creep performance before and after radiation.

Ex-Situ Nanoindentation Creep

The early indentation creep experiments can be dated back to at least the 1960s (Mulhearn and Tabor, 1960). With the development of the load and depth sensing indentation techniques, nanoindentation creep tests have been used to investigate the creep response of materials at small scales. The basic parameters of indentation creep experiments are stress $\sigma$ and strain rate $\dot{\epsilon }$, as shown in Eq. 13. The projected contact area (A) could be calculated by $A=r\times h^2$ for simplicity, in which r is 24.5 for the Berkovich indenter. The displacement rate ($\dot{h}$) is measured by $\dot{h}=dh/dt$. $h=h_0+a{t}^b+ct$ is one of the empirical equations to fit the h-t curves (Choi et al., 2012).

$\begin{array}{c}\sigma =\frac{F}{A} \dot{\epsilon }=\frac{\dot{h}}{h}\end{array}(13)$

$\sigma$ is taken as the applied load (F) divided by the projected contact area (A); while $\dot{\epsilon }$ is taken as the displacement rate ($\dot{h}$) divided by the instantaneous indent displacement (h).

The conventional uniaxial creep power-law equation is suitable for the stress $\sigma$ and steady state strain rate $\dot{\epsilon }$ data of the steady indentation creep, and the key parameter, creep stress exponent (n), can be yielded using Eq. 14. The creep stress exponent (n) is not only a valuable indicator for creep mechanism, but also corresponds closely to the maximum total elongation (k) during tension creep tests. Frost and Ashby, who integrated the numerical results of Burke and Nix (1975), proposed an empirical correlation between n and k (Eq. 15) (Lund and Nix, 1976), in which k ≈ 2-3.

$\begin{array}{c}\dot{\epsilon }=C{\sigma }^n=B{\sigma }^n\exp \left(-\frac{Q}{RT}\right)\end{array}(14)$

where C is a fitting parameter associated with temperatures and materials; B is a material constant; Q refers to the activation energy; R is the universal gas constant; and T is the absolute temperatures.

$\begin{array}{c}Elongation(\%)=\frac{k}{n-1}\times 100\%\end{array}(15)$

Using the ex-situ nanoindentation creep tests, some works have studied the evolution of creep parameters (n, Q, k, etc.) for various ion-irradiated materials (Huang et al., 2014; Liu et al., 2020; Zhu et al., 2020). Huang et al. evaluated the changes of creep properties after high-temperature irradiation (up to 600°C) (Huang et al., 2014), while Zhu et al. compared the creep resistance of different materials at room-temperature irradiation (Zhu et al., 2020). Zhu et al. also found that the creep plasticity degrades with increasing ion dose for all samples and thought that the irradiation defects perform as the barriers to hinder the dislocation gilding, consequently degrading the creep plasticity. The nanoindentation creep tests show the capability to qualitatively compare the creep properties by comparing the obtained creep parameters (n, k) of different materials. However, the “true” creep parameters from conventional tensile creep tests can hardly be comparable quantitatively with those from the nanoindentation creep tests (Zhu et al., 2020).

In recent years, simple models for indentation creep have been developed to correlate the indentation creep parameters with those obtained in uniaxial creep tests (Ginder et al., 2018; Xiao and Yu, 2020b), but the applicability of the models on ion-irradiated materials has not be proven. Further efforts need to be made to obtain reliable creep parameters for ion-irradiated materials.

In-Situ Irradiation Induced Creep

The stress states of micro-pillars uniaxial creep tests are similar to those of conventional creep tests, making it more reliable to assess the creep properties. Hence, the micro-pillars uniaxial creep tests have emerged on the study of small-scale creep behaviors at room temperature or high temperature (Wang et al., 2010; Choi et al., 2013; Mayer et al., 2015; Kim et al., 2016).

Based on the conventional power-law equation (Eq. 14), the important creep parameters n of micro-pillars uniaxial creep can be extracted by fitting the $\log \dot{\epsilon }-\log \sigma$ data. The steady state strain rate $\dot{\epsilon }$ can be measured from the $\mathit{\epsilon }$-t curves and Garofalo’s mathematical fitted equation, ${\epsilon }_{creep}={\epsilon }_0+\alpha \left(1-e^{-rt}\right)+\omega t$, which was originally suggested for conventional tensile creep analysis, can be adapted for the micro-pillars creep curves (Choi et al., 2013; Kim et al., 2016).

An in-situ micro-pillars compression creep apparatus was developed by Özerinç et al., which consists of an accelerator and a custom designed spring loaded device, and allows them to perform in-situ IIC experiments during heavy ion irradiation (Özerinç et al., 2014). They later upgraded the apparatus for elevated temperatures (Özerinç et al., 2016), and verified the apparatus suitable for accurate creep properties evaluation due to the thermal and mechanical stability.

The real time observation of IIC can be achieved by an in-situ ion irradiation-TEM at Sandia National Laboratories (Hattar et al., 2014). The TEM observation ensures that the samples align with the loading apparatus, enables direct verification for the measured strain values (Dillon et al., 2017), and allows for the IIC compliance (B) measurements, as shown with Eq. 16 (Jawaharram et al., 2020).

$\begin{array}{c}B=\frac{1}{{\sigma }_0}\frac{d\epsilon }{d\varphi }\end{array}(16)$

where ${\sigma }_0$ is the applied stress; $\varphi$ refers to the ion dose (dpa); and $d\epsilon /d\varphi$ is the normalized creep rate.

Many reports have confirmed that the in-situ experiments are capable of quantifying the IIC for various materials, with the pillar geometry or three-point beam geometry (Dillon et al., 2017; Jawaharram et al., 2018; Jawaharram et al., 2020). During the in-situ TEM observation on the ion-irradiated nanocrystalline high entropy alloys (HEAs), Jawaharram et al. found that the IIC compliance values of the HEAs are similar to the values of nanocrystalline Cu alloys at the same irradiation conditions in the literature. The results suggested that the point defect concentrations are comparable for the two alloys and indicated that the recombination is not significantly enhanced in HEAs (Jawaharram et al., 2020).

Size Effects on Irradiation-Induced Creep

Jawaharram et al. have investigated the size effects on IIC of different materials, using the in-situ ion irradiation TEM observation (Jawaharram et al., 2018; Jawaharram et al., 2020). Different size effects were discovered between single crystalline Ag pillars and nanocrystalline HEA. For single-crystal Ag, the creep compliance increases parabolically with the increasing pillar sizes, as a result of the competition between dislocation loops and surfaces acting as sinks (Jawaharram et al., 2018). But the IIC compliance scaled inversely with grain sizes of nanocrystalline HEA in the sink-limited regime because the creep behaviors are controlled by the grain boundary mechanism (Jawaharram et al., 2020).

The different hypothesized regimes of IIC responses as a function of grain sizes are illustrated in Figure 9 (Jawaharram et al., 2020). Specifically, in the nanocrystalline regime, the grain boundary mechanism controls the creep behaviors and the IIC compliance decreases with increasing grain sizes. When the grain size is above the critical sizes, in which the loop nucleation occurs, the dislocation-based mechanism begins to dominate the creep process and the IIC compliance increases with increasing grain sizes.

FIGURE 9

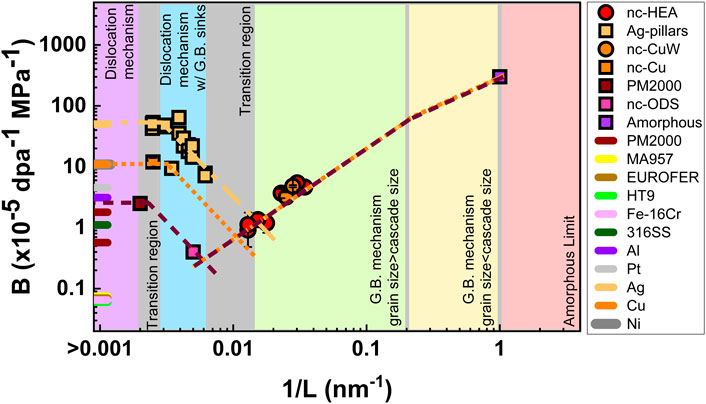
FIGURE 9. The schematic diagram for IIC compliance (B) as a function of inverse grain sizes (1/L). The figure is divided into different parts, representing different control mechanisms during the creep process [Reprinted with permission from Jawaharram et al. (2020) Copyright 2020 by Elsevier].

Fatigue

Nanoindentation is poorly suitable for evaluating the local cyclic behaviors, presumably due to the complex stress state below the indenter (Li and Bhushan, 2002), while the micropillar compression (Jang et al., 2013; Ghassemi-Armaki et al., 2017; Merle and Höppel, 2018) and micro-cantilever bending tests (Fang et al., 2014; Uematsu et al., 2016; Lavenstein et al., 2018; Gabel and Merle, 2020) are preferred owing to the defined stress states.

The micro-compression method has better flexibility for sample fabrication (Merle and Höppel, 2018), while the advantages of the microcantilever bending method include the available tensile loading and the more realistic failure criterion (Gabel and Merle, 2020). Both of them have previously been limited to the low-circle fatigue (LCT) tests due to the conventional quasi-static load mode, which has been solved by using the continuous stiffness method (CSM) to extend the fatigue tests to the high-circle fatigue (HCF) range (Lavenstein et al., 2018; Merle and Höppel, 2018).

Recently, the local HCF behaviors of nanocrystalline copper have been characterized based on ex-situ micro-cantilever bending (Gabel and Merle, 2020). Compared with the in-situ SEM fatigue tests of Lavenstein et al. (2018), that method was faster and not limited to the vacuum conditions. The stress amplitude-number of cycles to failure (S-N) curves were compared with those obtained by micro-compression (Merle and Höppel, 2018). The slopes of both curves showed a similar fatigue strength exponent of ∼ −0.1, but the micro-cantilever data showed higher scatter and longer fatigue lives, which can be explained by the different testing geometries, R ratios, and the definitions of failure criterion. It is important to note that both fatigue behaviors were consistent with the macroscopic fatigue properties of pure equal channel angular pressing (ECAP) Cu (Merle and Höppel, 2018; Gabel and Merle, 2020).

Strong size-dependent fatigue behaviors have been discovered in various materials using micro-cantilever bending methods (Fang et al., 2014; Uematsu et al., 2016; Lavenstein et al., 2018). For example, Fang et al. found that the width of fatigue damage (extrusion/intrusion) decreases with increasing sizes of the single crystal gold cantilevers, and the CRSS to form the damage is much higher in the smaller samples (Fang et al., 2014). They attributed the results to the dislocation starvation mechanism. Besides, the fatigue strength values of single crystal AZ31 magnesium alloy microcantilevers are much higher than those of bulk samples (Uematsu et al., 2016), while the fatigue life of single crystal nickel-based superalloys is much longer than bulk samples (Lavenstein et al., 2018). These results indicate that the fatigue resistance may be better at the small scale.

Recently, a size-dependent probabilistic model for the persistent slip bands (PSBs) nucleation, i.e., the onset of fatigue damage, has been proposed for single-crystal Ni by the in-situ fatigue behaviors observation (Lavenstein et al., 2020). This model allows us to predict the number of cycles required for the PSB nucleation event (E_cyc) in various sizes (D) of single crystal samples, and connects the micro-scale fatigue properties with those of bulk samples, as shown in Eq. 17 and Figure 10.

$\begin{array}{c}{E}_{cyc}=1+\frac{1}{\exp \left\{{\lambda }_0\left[1-\exp \left(-D^2/D_0^2\right)\right]\right\}-1}\end{array}(17)$

where D is the edge length of the slip area, i.e., the crystal size; D₀ refers to the critical size at which the fatigue responses change from bulk responses to size-dependent responses; and the material constant λ₀ is dependent on the grain orientation and strain amplitude.

FIGURE 10

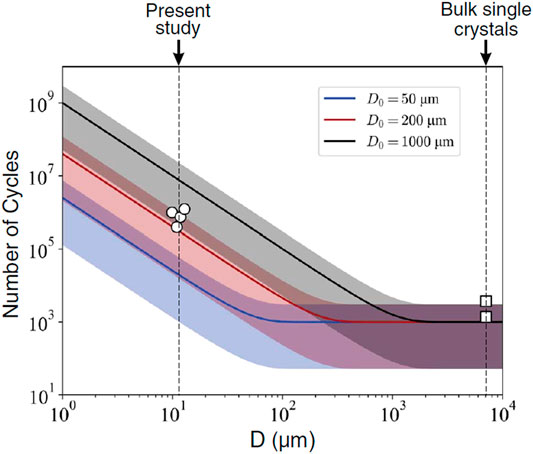
FIGURE 10. Probabilistic model for PSB nucleation (λ₀ = 10⁻³) (Reprinted with permission from Lavenstein et al. (2020) Copyright 2020 by American Association for the Advancement of Science.).

In brief, for ion-irradiated materials, the creep parameters (creep stress exponent) obtained by ex-situ nanoindentation creep tests are difficult to compare with uniaxial creep tests. Although the in-situ micro-compression creep tests could provide useful information for the IIC, this method is restricted by the shortage of in-situ facilities. For small-scale fatigue properties evaluation, few studies focus on the ion-irradiated materials. More relevant studies need to be integrated to further understand the effects of ion irradiation on fatigue properties.

Numerical Simulations

Over the last decades, significant computational efforts have been made to understand and predict the mechanical property degradation of irradiated materials (Marian et al., 2009a; Matsukawa et al., 2009; Shin et al., 2009; Wang et al., 2018b; Xiao et al., 2019). These numerical simulations include finite element methods (FEM), dislocation dynamics (DD), molecular dynamics (MD) simulations, etc., that cover various temporal and spatial scales.

Finite Element Method

FEMs are the most widely used numerical simulation methods for studying the indentation behavior (Xiao and Yu, 2020a). Many studies have combined the FEM and nanoindentation tests to evaluate the mechanical properties of ion-irradiated materials (Shin et al., 2009; Saleh et al., 2016; Wang et al., 2018b). However, the FEMs based on the classical plasticity theory of the continuum do not include the intrinsic length scale of materials, so the simulated hardness-depth curves may deviate from the actual curves (Shui, 2021). Thus, the crystal plasticity finite element method (CPFEM), based on the strain-gradient crystal plasticity theory, has emerged on evaluating the irradiation-mechanics responses (Chen et al., 2018; Xiao and Yu, 2019; Xiao et al., 2021). The previous review (Xiao and Yu, 2020a) has summarized that the FEM and CPFEM are valid for characterizing the inhomogeneous distributed defects, macroscopic mechanical responses of ion-irradiated materials, and the deformation mechanisms at the micro-scale, giving effective simulation for nanoindentation tests of ion-irradiated materials. Over the last decade, an easy-to-use multi-physics software tool “Düsseldorf Advanced Material Simulation Kit” (DAMASK) has been developed to study the crystal plasticity using an FE-based or a spectral numerical solver (Roters et al., 2012; Roters et al., 2019), and has been successfully utilized to evaluate the mechanical structure-property relations in crystalline materials (Liu and Shin, 2021).

Besides simulating the indentation behavior, FEM can also be utilized to study the stress-strain response of micro-compression pillars, micro-tensile bars, and micro-bending beams. For micro-compression, FEM can compute the stress states of the compressed pillars, to find an appropriate specimen geometry for evaluating the mechanical response of a pillar (Zhang et al., 2006; Shin et al., 2013). The visualized plastic deformation occurring in the pillars and their base material can also be calculated using FEM, to normalize the measured displacement by the fraction of the base displacement relative to the pillar displacement (Imrich et al., 2015; Yano et al., 2017), so that the adjusted experimental elastic modulus values could be comparable to the bulk values. Moreover, CPFEM could analyze the dominant deformation mechanisms in the micro-compression tests (Soler et al., 2012), and capture the strain rate effects on the plastic deformation of single crystalline metals (Khan et al., 2015). For the micro-tensile tests, FEM has also been performed to optimize the sample geometry design (Malhaire et al., 2007; Neves et al., 2008), and elucidate the mechanical behaviors (Xu et al., 2020b). As for the micro-bending tests, the yield strength of ion-irradiated materials can be predicted using FEM (Gibson et al., 2014; Armstrong et al., 2015).

Dislocation Dynamics

Based on the linear elasticity dislocation theory (Suzuki et al., 2013), DD eliminates the sample size limitation of MD, and reduces the computational overhead by discretizing dislocation lines into segments. The literature on DD simulations of micro-compression tests has been examined by Uchic et al. (2009), in which they discovered that the flow strength and strain hardening rate are size-dependent and the simulation results are all consistent with the experimental results. Later, Kiener et al. concluded that the increasing stored GND density in smaller pillars is attributed to the size-affected hardening by combining experiments and DD simulations (Kiener et al., 2011c).

DD simulations have been widely used in studying the irradiation effects (Arsenlis et al., 2012; Li et al., 2014; Sobie et al., 2015; Cui et al., 2018a; Cui et al., 2018b; Cui et al., 2018c). The fundamental mechanisms of irradiation hardening, the hardening contributions from different defect types and sizes, the mechanisms of plastic flow localization, as well as the dislocation-defect/barrier interactions process can all be studied based on this dislocation-scale simulation method.

Molecular Dynamics

As a fully discrete atomic-level method, MD simulations could be used to understand the deformation behavior at the nanoscale. The MD simulations of nanopillar compression have been conducted in various materials to study the size effect on the yield strength and plastic deformation (Horstemeyer et al., 2001; Zuo et al., 2005; Xu et al., 2013). As for the irradiated materials, the interactions between the dislocations and irradiation-induced staking-fault-tetrahedra (SFT) have been observed in the MD simulations (Marian et al., 2009b; Zepeda-Ruiz et al., 2013); moreover, the irradiation effects on the incipient plastic deformation and the defect evolution process have been studied for the indentation tests (Ruestes et al., 2018; Singh et al., 2019). However, owing to the limitation of computation ability, the temporal scale (nanosecond to microsecond scale) and spatial scale (nanometer to micron scale) of MD simulation are relatively small. Therefore, the loading rate of tensile, compression, and bending processes may be extremely different from the actual situation, which could cause quantitative or even qualitative discrepancies with experimental results.

In a word, numerical simulations are highly useful to interpret, understand, or even predict the experimental results on mechanical behavior of irradiated materials, from detailed observations of the atomistic and dislocation processes (Kiener et al., 2011a; Xiao and Yu, 2020a). Multi-scale simulations need to be further developed in the future to offer more accurate information at various spatial and temporal scales, to help bridge the understanding gap between micro- and macroscopic deformation behaviors.

Perspective

In general, the quantitative evaluation of ion-irradiation induced mechanical property degradation requires reasonable selection of the characterization techniques, proper experimental parameters, careful sample preparation, and reliable data analyses. Although many efforts have been made to evaluate the ion-irradiation induced strengthening and embrittlement, the results from different small-scale mechanical property techniques show, sometimes, great discrepancies. Hence, further studies about the mechanical property evaluation using different small-scale tests are urgently needed to establish the standardized reliable testing methods. Overall consideration regarding the reliability, capabilities, and efficiency of these small-scale testing techniques needs to be taken into account to find the best solution. To provide convincing evaluation to guide the materials selection for the various potential engineering purposes, different techniques could be utilized complementally to provide more comprehensive perspectives, and well-organized round robin studies may also be necessary.

Author Contributions

LM, XG, and KJ together finished this review, including analyzing, writing, and figures.

Funding

This work was financially supported by the National Natural Science Foundation of China (Grant No. 11905008).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajantiwalay, T., Vo, H., Finkelstein, R., Hosemann, P., and Aitkaliyeva, A. (2019). Towards Bridging the Experimental Length-Scale Gap for Tensile Tests on Structural Materials: Lessons Learned from an Initial Assessment of Microtensile Tests and the Path Forward. Jom 72 (1), 113–122. doi:10.1007/s11837-019-03897-8

CrossRef Full Text | Google Scholar

Angker, L., and Swain, M. V. (2006). Nanoindentation: Application to Dental Hard Tissue Investigations. J. Mater. Res. 21 (8), 1893–1905. doi:10.1557/jmr.2006.0257

CrossRef Full Text | Google Scholar

Anstis, G. R., Chantikul, P., Lawn, B. R., and Marshall, D. B. (1981). A Critical Evaluation of Indentation Techniques for Measuring Fracture Toughness: I, Direct Crack Measurements. J. Am. Ceram. Soc. 64 (9), 533–538. doi:10.1111/j.1151-2916.1981.tb10320.x

CrossRef Full Text | Google Scholar

Armstrong, D. E. J., Hardie, C. D., Gibson, J. S. K. L., Bushby, A. J., Edmondson, P. D., and Roberts, S. G. (2015). Small-scale Characterisation of Irradiated Nuclear Materials: Part II Nanoindentation and Micro-cantilever Testing of Ion Irradiated Nuclear Materials. J. Nucl. Mater. 462, 374–381. doi:10.1016/j.jnucmat.2015.01.053

CrossRef Full Text | Google Scholar

Arsenlis, A., Rhee, M., Hommes, G., Cook, R., and Marian, J. (2012). A Dislocation Dynamics Study of the Transition from Homogeneous to Heterogeneous Deformation in Irradiated Body-Centered Cubic Iron. Acta Materialia 60 (9), 3748–3757. doi:10.1016/j.actamat.2012.03.041

CrossRef Full Text | Google Scholar

Ashby, M. F. (1970). The Deformation of Plastically Non-homogeneous Materials. Philos. Mag. A J. Theor. Exp. Appl. Phys. 21 (170), 399–424. doi:10.1080/14786437008238426

CrossRef Full Text | Google Scholar

Ast, J., Göken, M., and Durst, K. (2017). Size-dependent Fracture Toughness of Tungsten. Acta Materialia 138, 198–211. doi:10.1016/j.actamat.2017.07.030

CrossRef Full Text | Google Scholar

Ast, J., Przybilla, T., Maier, V., Durst, K., and Göken, M. (2014). Microcantilever Bending Experiments in NiAl — Evaluation, Size Effects, and Crack Tip Plasticity. J. Mater. Res. 29 (18), 2129–2140. doi:10.1557/jmr.2014.240

CrossRef Full Text | Google Scholar

Basu, S., Moseson, A., and Barsoum, M. W. (2006). On the Determination of Spherical Nanoindentation Stress-Strain Curves. J. Mater. Res. 21 (10), 2628–2637. doi:10.1557/jmr.2006.0324

CrossRef Full Text | Google Scholar

Best, J. P., Wehrs, J., Polyakov, M., Morstein, M., and Michler, J. (2019). High Temperature Fracture Toughness of Ceramic Coatings Evaluated Using Micro-pillar Splitting. Scripta Materialia 162, 190–194. doi:10.1016/j.scriptamat.2018.11.013

CrossRef Full Text | Google Scholar

Bolelli, G., Righi, M. G., Mughal, M. Z., Moscatelli, R., Ligabue, O., Antolotti, N., et al. (2019). Damage Progression in thermal Barrier Coating Systems during thermal Cycling: A Nano-Mechanical Assessment. Mater. Des. 166, 107615. doi:10.1016/j.matdes.2019.107615

CrossRef Full Text | Google Scholar

Bolshakov, A., and Pharr, G. M. (1998). Influences of Pileup on the Measurement of Mechanical Properties by Load and Depth Sensing Indentation Techniques. J. Mater. Res. 13 (4), 1049–1058. doi:10.1557/jmr.1998.0146

CrossRef Full Text | Google Scholar

Bückle, H. (1959). Progress in Micro-indentation Hardness Testing. Metallurgical Rev. 4 (1), 49–100.

Google Scholar

Burke, M. A., and Nix, W. D. (1975). Plastic Instabilities in Tension Creep. Acta Metallurgica 23 (7), 793–798. doi:10.1016/0001-6160(75)90195-9

CrossRef Full Text | Google Scholar

Busby, J. T., Hash, M. C., and Was, G. S. (2005). The Relationship between Hardness and Yield Stress in Irradiated Austenitic and Ferritic Steels. J. Nucl. Mater. 336 (2-3), 267–278. doi:10.1016/j.jnucmat.2004.09.024

CrossRef Full Text | Google Scholar

Byun, T. S., Li, M., Cockeram, B. V., and Snead, L. L. (2008). Deformation and Fracture Properties in Neutron Irradiated Pure Mo and Mo Alloys. J. Nucl. Mater. 376 (2), 240–246. doi:10.1016/j.jnucmat.2008.03.004

CrossRef Full Text | Google Scholar

Fan, C., Li, Q., Ding, J., Liang, Y., Shang, Z., Li, J., et al. (2019). Helium Irradiation Induced Ultra-high Strength Nanotwinned Cu with Nanovoids, Acta Materialia 177, 107–120.doi:10.1016/j.actamat.2019.07.003

CrossRef Full Text | Google Scholar

Chen, L. R., Xiao, X. Z., Yu, L., Chu, H. J., and Duan, H. L. (2018). Texture Evolution and Mechanical Behaviour of Irradiated Face-Centred Cubic Metals. Proc. R. Soc. A: Math. Phys. Eng. Sci. 474 (2210), 20170604. doi:10.1098/rspa.2017.0604

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, I.-C., Kim, Y.-J., Seok, M.-Y., Yoo, B.-G., Kim, J.-Y., Wang, Y., et al. (2013). Nanoscale Room Temperature Creep of Nanocrystalline Nickel Pillars at Low Stresses. Int. J. Plasticity 41, 53–64. doi:10.1016/j.ijplas.2012.08.008

CrossRef Full Text | Google Scholar

Choi, I.-C., Yoo, B.-G., Kim, Y.-J., and Jang, J.-i. (2012). Indentation Creep Revisited. J. Mater. Res. 27 (1), 3–11. doi:10.1557/jmr.2011.213

CrossRef Full Text | Google Scholar

Cuadrado, N., Casellas, D., Anglada, M., and Jiménez-Piqué, E. (2012). Evaluation of Fracture Toughness of Small Volumes by Means of Cube-Corner Nanoindentation. Scripta Materialia 66 (9), 670–673. doi:10.1016/j.scriptamat.2012.01.033

CrossRef Full Text | Google Scholar

Cui, M. H., Shen, T. L., Zhu, H. P., Wang, J., Cao, X. Z., Zhang, P., et al. (2017). Vacancy like Defects and Hardening of Tungsten under Irradiation with He Ions at 800 °C. Fusion Eng. Des. 121, 313–318. doi:10.1016/j.fusengdes.2017.05.043

CrossRef Full Text | Google Scholar

Cui, Y., Po, G., and Ghoniem, N. M. (2018). A Coupled Dislocation Dynamics-Continuum Barrier Field Model with Application to Irradiated Materials. Int. J. Plasticity 104, 54–67. doi:10.1016/j.ijplas.2018.01.015

CrossRef Full Text | Google Scholar

Cui, Y., Po, G., and Ghoniem, N. (2018). Size-Tuned Plastic Flow Localization in Irradiated Materials at the Submicron Scale. Phys. Rev. Lett. 120 (21), 215501. doi:10.1103/physrevlett.120.215501

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, Y., Po, G., and Ghoniem, N. (2018). Suppression of Localized Plastic Flow in Irradiated Materials. Scripta Materialia 154, 34–39. doi:10.1016/j.scriptamat.2018.04.046

CrossRef Full Text | Google Scholar

Dehm, G. (2009). Miniaturized Single-Crystalline Fcc Metals Deformed in Tension: New Insights in Size-dependent Plasticity. Prog. Mater. Sci. 54 (6), 664–688. doi:10.1016/j.pmatsci.2009.03.005

CrossRef Full Text | Google Scholar

Di Maio, D., and Roberts, S. G. (2005). Measuring Fracture Toughness of Coatings Using Focused-Ion-Beam-Machined Microbeams. J. Mater. Res. 20 (2), 299–302. doi:10.1557/jmr.2005.0048

CrossRef Full Text | Google Scholar

Dillon, S. J., Bufford, D. C., Jawaharram, G. S., Liu, X., Lear, C., Hattar, K., et al. (2017). Irradiation-induced Creep in Metallic Nanolaminates Characterized by In Situ TEM Pillar Nanocompression. J. Nucl. Mater. 490, 59–65. doi:10.1016/j.jnucmat.2017.04.008

CrossRef Full Text | Google Scholar

Ding, M.-S., Du, J.-P., Wan, L., Ogata, S., Tian, L., Ma, E., et al. (2016). Radiation-Induced Helium Nanobubbles Enhance Ductility in Submicron-Sized Single-Crystalline Copper. Nano Lett. 16 (7), 4118–4124. doi:10.1021/acs.nanolett.6b00864

PubMed Abstract | CrossRef Full Text | Google Scholar

Doitrand, A., Henry, R., Zacharie-Aubrun, I., Gatt, J.-M., and Meille, S. (2020). UO2 Micron Scale Specimen Fracture: Parameter Identification and Influence of Porosities. Theor. Appl. Fracture Mech. 108, 102665. doi:10.1016/j.tafmec.2020.102665

CrossRef Full Text | Google Scholar

Dolph, C. K., da Silva, D. J., Swenson, M. J., and Wharry, J. P. (2016). Plastic Zone Size for Nanoindentation of Irradiated Fe–9%Cr ODS. J. Nucl. Mater. 481, 33–45.

Google Scholar

Fang, H., Shiohara, R., Sumigawa, T., and Kitamura, T. (2014). Size Dependence of Fatigue Damage in Sub-micrometer Single crystal Gold. Mater. Sci. Eng. A 618, 416–423. doi:10.1016/j.msea.2014.09.017

CrossRef Full Text | Google Scholar

Field, J. S., and Swain, M. V. (1993). A Simple Predictive Model for Spherical Indentation. J. Mater. Res. 8 (2), 297–306. doi:10.1557/jmr.1993.0297

CrossRef Full Text | Google Scholar

Gabel, S., and Merle, B. (2020). Small-scale High-Cycle Fatigue Testing by Dynamic Microcantilever Bending. MRS Commun. 10 (2), 332–337. doi:10.1557/mrc.2020.31

CrossRef Full Text | Google Scholar

Gao, J., Yabuuchi, K., and Kimura, A. (2019). Ion-irradiation Hardening and Microstructural Evolution in F82H and Ferritic Alloys. J. Nucl. Mater. 515, 294–302. doi:10.1016/j.jnucmat.2018.12.047

CrossRef Full Text | Google Scholar

Ghassemi-Armaki, H., Leff, A. C., Taheri, M. L., Dahal, J., Kamarajugadda, M., and Kumar, K. S. (2017). Cyclic Compression Response of Micropillars Extracted from Textured Nanocrystalline NiTi Thin-Walled Tubes. Acta Materialia 136, 134–147. doi:10.1016/j.actamat.2017.06.043

CrossRef Full Text | Google Scholar

Ghidelli, M., Sebastiani, M., Johanns, K. E., and Pharr, G. M. (2017). Effects of Indenter Angle on Micro-scale Fracture Toughness Measurement by Pillar Splitting. J. Am. Ceram. Soc. 100 (12), 5731–5738. doi:10.1111/jace.15093

CrossRef Full Text | Google Scholar

Gibson, J., Armstrong, D., and Roberts, S. (2014). The Micro-mechanical Properties of Ion Irradiated Tungsten. Phys. Scr. T159, 014056. doi:10.1088/0031-8949/2014/t159/014056

CrossRef Full Text | Google Scholar

Ginder, R. S., Nix, W. D., and Pharr, G. M. (2018). A Simple Model for Indentation Creep. J. Mech. Phys. Sol. 112, 552–562. doi:10.1016/j.jmps.2018.01.001

CrossRef Full Text | Google Scholar

Greer, J. R., and De Hosson, J. T. M. (2011). Plasticity in Small-Sized Metallic Systems: Intrinsic versus Extrinsic Size Effect. Prog. Mater. Sci. 56 (6), 654–724. doi:10.1016/j.pmatsci.2011.01.005

CrossRef Full Text | Google Scholar

Greer, J. R., Oliver, W. C., and Nix, W. D. (2005). Size Dependence of Mechanical Properties of Gold at the Micron Scale in the Absence of Strain Gradients. Acta Materialia 53 (6), 1821–1830. doi:10.1016/j.actamat.2004.12.031

CrossRef Full Text | Google Scholar

Grieveson, E. M., Armstrong, D. E. J., Xu, S., and Roberts, S. G. (2012). Compression of Self-Ion Implanted Iron Micropillars. J. Nucl. Mater. 430 (1-3), 119–124. doi:10.1016/j.jnucmat.2012.06.014

CrossRef Full Text | Google Scholar

Hardie, C. D., Roberts, S. G., and Bushby, A. J. (2015). Understanding the Effects of Ion Irradiation Using Nanoindentation Techniques. J. Nucl. Mater. 462, 391–401. doi:10.1016/j.jnucmat.2014.11.066

CrossRef Full Text | Google Scholar

Harding, D. S., Oliver, W. C., and Pharr, G. M. (1994). Cracking during Nanoindentation and its Use in the Measurement of Fracture Toughness. MRS Proc. 356, 663. doi:10.1557/proc-356-663

CrossRef Full Text | Google Scholar

Hattar, K., Bufford, D. C., and Buller, D. L. (2014). Concurrent In Situ Ion Irradiation Transmission Electron Microscope. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 338, 56–65. doi:10.1016/j.nimb.2014.08.002

CrossRef Full Text | Google Scholar

Henry, R., Zacharie-Aubrun, I., Blay, T., Chalal, S., Gatt, J.-M., Langlois, C., et al. (2020). Fracture Properties of an Irradiated PWR UO2 Fuel Evaluated by Micro-cantilever Bending Tests. J. Nucl. Mater. 538, 152209. doi:10.1016/j.jnucmat.2020.152209

CrossRef Full Text | Google Scholar

Henry, R., Zacharie-Aubrun, I., Blay, T., Tarisien, N., Chalal, S., Iltis, X., et al. (2020). Irradiation Effects on the Fracture Properties of UO2 Fuels Studied by Micro-mechanical Testing. J. Nucl. Mater. 536, 152179. doi:10.1016/j.jnucmat.2020.152179

CrossRef Full Text | Google Scholar

Heo, J., Kim, S., Guim, H., Jin, H.-H., Moon, J., Lee, C.-H., et al. (2018). Ion-irradiation Hardening of Ti/Ta-Added Reduced Activation Ferritic-Martensitic Steel Evaluated with a New Nanopillar Fabrication Technique. J. Nucl. Mater. 512, 184–192. doi:10.1016/j.jnucmat.2018.10.004

CrossRef Full Text | Google Scholar

Herbert, E. G., Pharr, G. M., Oliver, W. C., Lucas, B. N., and Hay, J. L. (2001). On the Measurement of Stress-Strain Curves by Spherical Indentation. Thin Solid Films 398-399, 331–335. doi:10.1016/s0040-6090(01)01439-0

CrossRef Full Text | Google Scholar

Hintsala, E. D., Bhowmick, S., Yueyue, X., Ballarini, R., Asif, S. A. S., and Gerberich, W. W. (2017). Temperature Dependent Fracture Initiation in Microscale Silicon. Scripta Materialia 130, 78–82. doi:10.1016/j.scriptamat.2016.11.016

CrossRef Full Text | Google Scholar

Hockey, B., Wiederhorn, S., and Johnson, H. (1978). Fracture Mechanics of Ceramics, Vol. 3, Flaws and Testing. New York: Plenum Press.

Google Scholar

Horstemeyer, M., Baskes, M., and Plimpton, S. (2001). Length Scale and Time Scale Effects on the Plastic Flow of Fcc Metals. Acta Materialia 49 (20), 4363–4374. doi:10.1016/s1359-6454(01)00149-5

CrossRef Full Text | Google Scholar

Hosemann, P., Kiener, D., Wang, Y., and Maloy, S. A. (2012). Issues to Consider Using Nano Indentation on Shallow Ion Beam Irradiated Materials. J. Nucl. Mater. 425 (1), 136–139. doi:10.1016/j.jnucmat.2011.11.070

CrossRef Full Text | Google Scholar

Hosemann, P., Shin, C., and Kiener, D. (2015). Small Scale Mechanical Testing of Irradiated Materials. J. Mater. Res. 30 (9), 1231–1245. doi:10.1557/jmr.2015.26

CrossRef Full Text | Google Scholar

Hosemann, P. (2018). Small-scale Mechanical Testing on Nuclear Materials: Bridging the Experimental Length-Scale gap. Scripta Materialia 143, 161–168. doi:10.1016/j.scriptamat.2017.04.026

CrossRef Full Text | Google Scholar

Hosemann, P., Swadener, J. G., Kiener, D., Was, G. S., Maloy, S. A., and Li, N. (2008). An Exploratory Study to Determine Applicability of Nano-Hardness and Micro-compression Measurements for Yield Stress Estimation. J. Nucl. Mater. 375 (1), 135–143. doi:10.1016/j.jnucmat.2007.11.004

CrossRef Full Text | Google Scholar

Hosemann, P., Vieh, C., Greco, R. R., Kabra, S., Valdez, J. A., Cappiello, M. J., et al. (2009). Nanoindentation on Ion Irradiated Steels. J. Nucl. Mater. 389 (2), 239–247. doi:10.1016/j.jnucmat.2009.02.026

CrossRef Full Text | Google Scholar

Howard, C., Judge, C. D., and Hosemann, P. (2019). Applying a New Push-To-Pull Micro-tensile Testing Technique to Evaluate the Mechanical Properties of High Dose Inconel X-750. Mater. Sci. Eng. A 748, 396–406. doi:10.1016/j.msea.2019.01.113

CrossRef Full Text | Google Scholar

Huang, Y., Zhang, F., Hwang, K., Nix, W., Pharr, G., and Feng, G. (2006). A Model of Size Effects in Nano-Indentation. J. Mech. Phys. Sol. 54 (8), 1668–1686. doi:10.1016/j.jmps.2006.02.002

CrossRef Full Text | Google Scholar

Huang, Z., Harris, A., Maloy, S. A., and Hosemann, P. (2014). Nanoindentation Creep Study on an Ion Beam Irradiated Oxide Dispersion Strengthened alloy. J. Nucl. Mater. 451 (1-3), 162–167. doi:10.1016/j.jnucmat.2014.03.036

CrossRef Full Text | Google Scholar

Imrich, P. J., Kirchlechner, C., Kiener, D., and Dehm, G. (2015). In Situ TEM Microcompression of Single and Bicrystalline Samples: Insights and Limitations. JOM 67 (8), 1704–1712. doi:10.1007/s11837-015-1440-6

CrossRef Full Text | Google Scholar

Iqbal, F., Ast, J., Göken, M., and Durst, K. (2012). In Situ micro-cantilever Tests to Study Fracture Properties of NiAl Single Crystals. Acta Materialia 60 (3), 1193–1200. doi:10.1016/j.actamat.2011.10.060

CrossRef Full Text | Google Scholar

Jang, D., Maaß, R., Wang, G., Liaw, P. K., and Greer, J. R. (2013). Fatigue Deformation of Microsized Metallic Glasses. Scripta Materialia 68 (10), 773–776. doi:10.1016/j.scriptamat.2012.12.011

CrossRef Full Text | Google Scholar

Jawaharram, G. S., Barr, C. M., Monterrosa, A. M., Hattar, K., Averback, R. S., and Dillon, S. J. (2020). Irradiation Induced Creep in Nanocrystalline High Entropy Alloys. Acta Materialia 182, 68–76. doi:10.1016/j.actamat.2019.10.022

CrossRef Full Text | Google Scholar

Jawaharram, G. S., Price, P. M., Barr, C. M., Hattar, K., Averback, R. S., and Dillon, S. J. (2018). High Temperature Irradiation Induced Creep in Ag Nanopillars Measured via In Situ Transmission Electron Microscopy. Scripta Materialia 148, 1–4. doi:10.1016/j.scriptamat.2018.01.007

CrossRef Full Text | Google Scholar

Jaya B, N., Jayaram, V., and Biswas, S. K. (2012). A New Method for Fracture Toughness Determination of Graded (Pt,Ni)Al Bond coats by Microbeam bend Tests. Philos. Mag. 92 (25-27), 3326–3345. doi:10.1080/14786435.2012.669068

CrossRef Full Text | Google Scholar

Jaya, B. N., Kirchlechner, C., and Dehm, G. (2015). Can Microscale Fracture Tests Provide Reliable Fracture Toughness Values? A Case Study in Silicon. J. Mater. Res. 30 (5), 686–698. doi:10.1557/jmr.2015.2

CrossRef Full Text | Google Scholar

Jin, H.-H., Ko, E., Kwon, J., Hwang, S. S., and Shin, C. (2016). Evaluation of Critical Resolved Shear Strength and Deformation Mode in Proton-Irradiated Austenitic Stainless Steel Using Micro-compression Tests. J. Nucl. Mater. 470, 155–163. doi:10.1016/j.jnucmat.2015.12.029

CrossRef Full Text | Google Scholar

Jin, K., Xia, Y., Crespillo, M., Xue, H., Zhang, Y., Gao, Y. F., et al. (2018). Quantifying Early Stage Irradiation Damage from Nanoindentation Pop-In Tests. Scripta Materialia 157, 49–53. doi:10.1016/j.scriptamat.2018.07.035

CrossRef Full Text | Google Scholar

Johnson, K. L. (1970). The Correlation of Indentation Experiments. J. Mech. Phys. Sol. 18 (2), 115–126. doi:10.1016/0022-5096(70)90029-3

CrossRef Full Text | Google Scholar

Kalidindi, S. R., and Pathak, S. (2008). Determination of the Effective Zero-point and the Extraction of Spherical Nanoindentation Stress-Strain Curves. Acta Materialia 56 (14), 3523–3532. doi:10.1016/j.actamat.2008.03.036

CrossRef Full Text | Google Scholar

Kasada, R., Takayama, Y., Yabuuchi, K., and Kimura, A. (2011). A New Approach to Evaluate Irradiation Hardening of Ion-Irradiated Ferritic Alloys by Nano-Indentation Techniques. Fusion Eng. Des. 86 (9), 2658–2661. doi:10.1016/j.fusengdes.2011.03.073

CrossRef Full Text | Google Scholar

Kayano, H., Kimura, A., Narui, M., Sasaki, Y., Suzuki, Y., and Ohta, S. (1988). Irradiation Embrittlement of Neutron-Irradiated Low Activation Ferritic Steels. J. Nucl. Mater. 155-157, 978–981. doi:10.1016/0022-3115(88)90452-7

CrossRef Full Text | Google Scholar

Khan, A. S., Liu, J., Yoon, J. W., and Nambori, R. (2015). Strain Rate Effect of High Purity Aluminum Single Crystals: Experiments and Simulations. Int. J. Plasticity 67, 39–52. doi:10.1016/j.ijplas.2014.10.002

CrossRef Full Text | Google Scholar

Kiener, D., Guruprasad, P. J., Keralavarma, S. M., Dehm, G., and Benzerga, A. A. (2011). Work Hardening in Micropillar Compression: In Situ Experiments and Modeling. Acta Materialia 59 (10), 3825–3840. doi:10.1016/j.actamat.2011.03.003

CrossRef Full Text | Google Scholar

Kiener, D., Hosemann, P., Maloy, S. A., and Minor, A. M. (2011). In Situ nanocompression Testing of Irradiated Copper. Nat. Mater 10 (8), 608–613. doi:10.1038/nmat3055

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiener, D., Hosemann, P., Maloy, S. A., and Minor, A. M. (2011). In Situ nanocompression Testing of Irradiated Copper. Nat. Mater 10 (8), 608–613. doi:10.1038/nmat3055

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiener, D., Minor, A. M., Anderoglu, O., Wang, Y., Maloy, S. A., and Hosemann, P. (2012). Application of Small-Scale Testing for Investigation of Ion-Beam-Irradiated Materials. J. Mater. Res. 27 (21), 2724–2736. doi:10.1557/jmr.2012.303

CrossRef Full Text | Google Scholar

Kiener, D., Pippan, R., Motz, C., and Kreuzer, H. (2006). Microstructural Evolution of the Deformed Volume beneath Microindents in Tungsten and Copper. Acta Materialia 54 (10), 2801–2811. doi:10.1016/j.actamat.2006.02.024

CrossRef Full Text | Google Scholar

Kim, Y.-J., Qaiser, N., and Han, S. M. (2016). Time-dependent Deformation of Sn Micropillars. Mater. Des. 102, 168–173. doi:10.1016/j.matdes.2016.04.039

CrossRef Full Text | Google Scholar

Krumwiede, D. L., Yamamoto, T., Saleh, T. A., Maloy, S. A., Odette, G. R., and Hosemann, P. (2018). Direct Comparison of Nanoindentation and Tensile Test Results on Reactor-Irradiated Materials. J. Nucl. Mater. 504, 135–143. doi:10.1016/j.jnucmat.2018.03.021

CrossRef Full Text | Google Scholar

Lankford, J., and Davidson, D. L. (1979). The Crack-Initiation Threshold in Ceramic Materials Subject to Elastic/plastic Indentation. J. Mater. Sci. 14 (7), 1662–1668. doi:10.1007/bf00569288

CrossRef Full Text | Google Scholar

Lauener, C. M., Petho, L., Chen, M., Xiao, Y., Michler, J., and Wheeler, J. M. (2018). Fracture of Silicon: Influence of Rate, Positioning Accuracy, FIB Machining, and Elevated Temperatures on Toughness Measured by Pillar Indentation Splitting. Mater. Des. 142, 340–349. doi:10.1016/j.matdes.2018.01.015

CrossRef Full Text | Google Scholar

Laugier, M. T. (1987). Palmqvist Indentation Toughness in WC-Co Composites. J. Mater. Sci. Lett. 6 (8), 897–900. doi:10.1007/bf01729862

CrossRef Full Text | Google Scholar

Lavenstein, S., Gu, Y., Madisetti, D., and El-Awady, J. A. (2020). The Heterogeneity of Persistent Slip Band Nucleation and Evolution in Metals at the Micrometer Scale. Science 370 (6513). doi:10.1126/science.abb2690

CrossRef Full Text | Google Scholar

Lavenstein, S., Crawford, B., Sim, G.-D., Shade, P. A., Woodward, C., and El-Awady, J. A. (2018). High Frequency In Situ Fatigue Response of Ni-Base Superalloy René-N5 Microcrystals. Acta Materialia 144, 154–163. doi:10.1016/j.actamat.2017.10.049

CrossRef Full Text | Google Scholar

Lawn, B. R., Evans, A. G., and Marshall, D. B. (1980). Elastic/Plastic Indentation Damage in Ceramics: The Median/Radial Crack System. J. Am. Ceram. Soc. 63 (9-10), 574–581. doi:10.1111/j.1151-2916.1980.tb10768.x

CrossRef Full Text | Google Scholar

Leide, A. J., Todd, R. I., and Armstrong, D. E. J. (2021). Effect of Ion Irradiation on Nanoindentation Fracture and Deformation in Silicon Carbide. Jom 73 (6), 1617–1628. doi:10.1007/s11837-021-04636-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, D., Zbib, H., Sun, X., and Khaleel, M. (2014). Predicting Plastic Flow and Irradiation Hardening of Iron Single crystal with Mechanism-Based Continuum Dislocation Dynamics. Int. J. Plasticity 52, 3–17. doi:10.1016/j.ijplas.2013.01.015

CrossRef Full Text | Google Scholar

Li, X., and Bhushan, B. (2002). Development of a Nanoscale Fatigue Measurement Technique and its Application to Ultrathin Amorphous Carbon Coatings. Scripta Materialia 47 (7), 473–479. doi:10.1016/s1359-6462(02)00181-1

CrossRef Full Text | Google Scholar

Liu, H., and Shin, Y. C. (2021). A crystal Plasticity Finite Element-Based Approach to Model the Constitutive Behavior of Multi-phase Steels. Arch. Civil Mech. Eng. 21 (2), 83. doi:10.1007/s43452-021-00226-2

CrossRef Full Text | Google Scholar

Liu, H. T., Yang, L. W., Han, S., Cheng, H. F., Mao, W. G., and Molina-Aldareguía, J. M. (2017). Interface Controlled Micro- and Macro- Mechanical Properties of Aluminosilicate Fiber Reinforced SiC Matrix Composites. J. Eur. Ceram. Soc. 37 (3), 883–890. doi:10.1016/j.jeurceramsoc.2016.10.003

CrossRef Full Text | Google Scholar

Liu, S., Wheeler, J. M., Howie, P. R., Zeng, X. T., Michler, J., and Clegg, W. J. (2013). Measuring the Fracture Resistance of Hard Coatings. Appl. Phys. Lett. 102 (17), 171907. doi:10.1063/1.4803928

CrossRef Full Text | Google Scholar

Liu, X. M., Le Flem, M., Béchade, J. L., and Monnet, I. (2010). Nanoindentation Investigation of Heavy Ion Irradiated Ti3(Si,Al)C2. J. Nucl. Mater. 401 (1), 149–153. doi:10.1016/j.jnucmat.2010.04.015

CrossRef Full Text | Google Scholar

Liu, Y., Liu, W., Yu, L., Chen, L., Sui, H., and Duan, H. (2020). Hardening and Creep of Ion Irradiated CLAM Steel by Nanoindentation. Crystals 10 (1). doi:10.3390/cryst10010044

CrossRef Full Text | Google Scholar

Lund, R. W., and Nix, W. D. (1976). High Temperature Creep of Ni-20Cr-2ThO2 Single Crystals. Acta Metallurgica 24 (5), 469–481. doi:10.1016/0001-6160(76)90068-7

CrossRef Full Text | Google Scholar

Lupinacci, A., Chen, K., Li, Y., Kunz, M., Jiao, Z., Was, G. S., et al. (2015). Characterization of Ion Beam Irradiated 304 Stainless Steel Utilizing Nanoindentation and Laue Microdiffraction. J. Nucl. Mater. 458, 70–76. doi:10.1016/j.jnucmat.2014.11.050

CrossRef Full Text | Google Scholar

Lupinacci, A., Kacher, J., Eilenberg, A., Shapiro, A. A., Hosemann, P., and Minor, A. M. (2014). Cryogenic In Situ Microcompression Testing of Sn. Acta Materialia 78, 56–64. doi:10.1016/j.actamat.2014.06.026

CrossRef Full Text | Google Scholar

Ma, Q., and Clarke, D. R. (1995). Size Dependent Hardness of Silver Single Crystals. J. Mater. Res. 10 (4), 853–863. doi:10.1557/jmr.1995.0853

CrossRef Full Text | Google Scholar

Malhaire, C., Ignat, M., Dogheche, K., Brida, S., Josserond, C., and Debove, L. (2007). Realization of Thin Film Specimens for Micro Tensile Tests, TRANSDUCERS 2007 - 2007 International Solid-State Sensors. Actuators and Microsystems Conference. New York: IEEE, 623–626.

Google Scholar

Marian, J., Martinez, E., Lee, H.-J., and Wirth, B. D. (2009). Micro/meso-scale Computational Study of Dislocation-Stacking-Fault Tetrahedron Interactions in Copper. J. Mater. Res. 24 (12), 3628–3635. doi:10.1557/jmr.2009.0424

CrossRef Full Text | Google Scholar

Marian, J., Martínez, E., Lee, H.-J., and Wirth, B. D. (2009). Micro/meso-scale Computational Study of Dislocation-Stacking-Fault Tetrahedron Interactions in Copper. J. Mater. Res. 24 (12), 3628–3635. doi:10.1557/jmr.2009.0424

CrossRef Full Text | Google Scholar

Matsukawa, Y., Briceno, M., and Robertson, I. M. (2009). Combining In Situ Transmission Electron Microscopy and Molecular Dynamics Computer Simulations to Reveal the Interaction Mechanisms of Dislocations with Stacking-Fault Tetrahedron in Nuclear Materials. Microsc. Res. Tech. 72 (3), 284–292. doi:10.1002/jemt.20681

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayer, C. R., Lotfian, S., Molina-Aldareguia, J., and Chawla, N. (2015). High-Temperature Micropillar Compression Creep Testing of Constituent Phases in Lead-Free Solder. Adv. Eng. Mater. 17 (8), 1168–1174. doi:10.1002/adem.201500089

CrossRef Full Text | Google Scholar

McElhaney, K. W., Vlassak, J. J., and Nix, W. D. (1998). Determination of Indenter Tip Geometry and Indentation Contact Area for Depth-Sensing Indentation Experiments. J. Mater. Res. 13 (5), 1300–1306. doi:10.1557/jmr.1998.0185

CrossRef Full Text | Google Scholar

Merle, B., and Göken, M. (2011). Fracture Toughness of Silicon Nitride Thin Films of Different Thicknesses as Measured by Bulge Tests. Acta Materialia 59 (4), 1772–1779. doi:10.1016/j.actamat.2010.11.043

CrossRef Full Text | Google Scholar

Merle, B., and Höppel, H. W. (2018). Microscale High-Cycle Fatigue Testing by Dynamic Micropillar Compression Using Continuous Stiffness Measurement. Exp. Mech. 58 (3), 465–474. doi:10.1007/s11340-017-0362-3

CrossRef Full Text | Google Scholar

Milot, T. S. (2012). Establishing Correlations for Predicting Tensile Properties Based on the Shear Punch Test and Vickers Microhardness Data. Santa Barbara, Ann Arbor: University of California, 196.

Google Scholar

Miura, T., Fujii, K., Fukuya, K., Ando, M., and Tanigawa, H. (2018). Micro-Tensile Testing of Reduced-Activation Ferritic Steel F82H Irradiated with Fe and He Ions. Nucl. Mater. Energy 17, 24-28.

CrossRef Full Text | Google Scholar

Moschetti, M., Xu, A., Schuh, B., Hohenwarter, A., Couzinié, J.-P., Kruzic, J. J., et al. (2020). On the Room-Temperature Mechanical Properties of an Ion-Irradiated TiZrNbHfTa Refractory High Entropy Alloy. JOM 72 (1), 130–138. doi:10.1007/s11837-019-03861-6

CrossRef Full Text | Google Scholar

M. Rice, P., and Stoller, R. E. (1997). The Effect of Solutes on Defect Distributions and Hardening in Ion-Irradiated Model Ferritic Alloys. J. Nucl. Mater. 244 (3), 219–226. doi:10.1016/s0022-3115(96)00753-2

CrossRef Full Text | Google Scholar

Mughal, M. Z., Amanieu, H.-Y., Moscatelli, R., and Sebastiani, M. (2017). A Comparison of Microscale Techniques for Determining Fracture Toughness of LiMn2O4 Particles. Materials 10 (4). doi:10.3390/ma10040403

PubMed Abstract | CrossRef Full Text | Google Scholar

Mughal, M. Z., Moscatelli, R., Amanieu, H.-Y., and Sebastiani, M. (2016). Effect of Lithiation on Micro-scale Fracture Toughness of LixMn2O4 Cathode. Scripta Materialia 116, 62–66. doi:10.1016/j.scriptamat.2016.01.023

CrossRef Full Text | Google Scholar

Mulhearn, T., and Tabor, D. (1960). Creep and Hardness of Metals-A Physical Study. J. Inst. Met. 89 (1), 7–12.

Google Scholar

Murugaiah, A., Barsoum, M. W., Kalidindi, S. R., and Zhen, T. (2004). Spherical Nanoindentations and Kink Bands in Ti3SiC2. J. Mater. Res. 19 (4), 1139–1148. doi:10.1557/jmr.2004.0148

CrossRef Full Text | Google Scholar

Neves, A. d. A., Coutinho, E., Cardoso, M. V., Jaecques, S., Lambrechts, P., Sloten, J. V., et al. (2008). Influence of Notch Geometry and Interface on Stress Concentration and Distribution in Micro-tensile Bond Strength Specimens. J. Dentistry 36 (10), 808–815. doi:10.1016/j.jdent.2008.05.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Nix, W. D., and Gao, H. (1998). Indentation Size Effects in Crystalline Materials: A Law for Strain Gradient Plasticity. J. Mech. Phys. Sol. 46 (3), 411–425. doi:10.1016/s0022-5096(97)00086-0

CrossRef Full Text | Google Scholar

Oliver, W. C., and Pharr, G. M. (1992). An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 7 (6), 1564–1583. doi:10.1557/jmr.1992.1564

CrossRef Full Text | Google Scholar

Oliver, W. C., and Pharr, G. M. (2004). Measurement of Hardness and Elastic Modulus by Instrumented Indentation: Advances in Understanding and Refinements to Methodology. J. Mater. Res. 19 (1), 3–20. doi:10.1557/jmr.2004.19.1.3

CrossRef Full Text | Google Scholar

Özerinç, S., Averback, R. S., and King, W. P. (2014). In Situ creep Measurements on Micropillar Samples during Heavy Ion Irradiation. J. Nucl. Mater. 451 (1-3), 104–110.

Google Scholar

Özerinç, S., Averback, R. S., and King, W. P. (2016). In Situ Measurements of Irradiation-Induced Creep of Nanocrystalline Copper at Elevated Temperatures. JOM 68 (11), 2737–2741.

Google Scholar

Paccou, E., Tanguy, B., and Legros, M. (2019). Micropillar Compression Study of Fe-Irradiated 304L Steel. Scripta Materialia 172, 56–60. doi:10.1016/j.scriptamat.2019.07.007

CrossRef Full Text | Google Scholar

Park, K. H., Katoh, Y., Kishimoto, H., and Kohyama, A. (2002). Evaluation of Dual-Ion Irradiated β-SiC by Means of Indentation Methods. J. Nucl. Mater. 307-311, 1187–1190. doi:10.1016/s0022-3115(02)00955-8

CrossRef Full Text | Google Scholar

Parthasarathy, T. A., Rao, S. I., Dimiduk, D. M., Uchic, M. D., and Trinkle, D. R. (2007). Contribution to Size Effect of Yield Strength from the Stochastics of Dislocation Source Lengths in Finite Samples. Scripta Materialia 56 (4), 313–316. doi:10.1016/j.scriptamat.2006.09.016

CrossRef Full Text | Google Scholar

Pathak, S., and Kalidindi, S. R. (2015). Spherical Nanoindentation Stress-Strain Curves. Mater. Sci. Eng. R: Rep. 91, 1–36. doi:10.1016/j.mser.2015.02.001

CrossRef Full Text | Google Scholar

Pathak, S., Kalidindi, S. R., Weaver, J. S., Wang, Y., Doerner, R. P., and Mara, N. A. (2017). Probing Nanoscale Damage Gradients in Ion-Irradiated Metals Using Spherical Nanoindentation. Sci. Rep. 7 (1), 11918. doi:10.1038/s41598-017-12071-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Pharr, G. M., Herbert, E. G., and Gao, Y. (2010). The Indentation Size Effect: a Critical Examination of Experimental Observations and Mechanistic Interpretations. Annu. Rev. Mater. Res. 40, 271–292. doi:10.1146/annurev-matsci-070909-104456

CrossRef Full Text | Google Scholar

Pharr, G. M., and Oliver, W. C. (1992). Measurement of Thin Film Mechanical Properties Using Nanoindentation. MRS Bull. 17 (7), 28–33. doi:10.1557/s0883769400041634

CrossRef Full Text | Google Scholar

Prasitthipayong, A., Frazer, D., Kareer, A., Abad, M. D., Garner, A., Joni, B., et al. (2018). Micro Mechanical Testing of Candidate Structural Alloys for Gen-IV Nuclear Reactors. Nucl. Mater. Energ. 16, 34–45. doi:10.1016/j.nme.2018.05.018

CrossRef Full Text | Google Scholar

Prasitthipayong, A., Vachhani, S. J., Tumey, S. J., Minor, A. M., and Hosemann, P. (2018). Indentation Size Effect in Unirradiated and Ion-Irradiated 800H Steel at High Temperatures. Acta Materialia 144, 896–904. doi:10.1016/j.actamat.2017.11.001

CrossRef Full Text | Google Scholar

Preiß, E. I., Merle, B., and Göken, M. (2017). Understanding the Extremely Low Fracture Toughness of Freestanding Gold Thin Films by In-Situ Bulge Testing in an AFM. Mater. Sci. Eng. A 691, 218–225.

Google Scholar

Qian, L., Li, M., Zhou, Z., Yang, H., and Shi, X. (2005). Comparison of Nano-Indentation Hardness to Microhardness. Surf. Coat. Tech. 195 (2), 264–271. doi:10.1016/j.surfcoat.2004.07.108

CrossRef Full Text | Google Scholar

Reichardt, A., Ionescu, M., Davis, J., Edwards, L., Harrison, R. P., Hosemann, P., et al. (2015). In Situ micro Tensile Testing of He+2 Ion Irradiated and Implanted Single crystal Nickel Film. Acta Materialia 100, 147–154. doi:10.1016/j.actamat.2015.08.028

CrossRef Full Text | Google Scholar

Reichardt, A., Lupinacci, A., Frazer, D., Bailey, N., Vo, H., Howard, C., et al. (2017). Nanoindentation and In Situ Microcompression in Different Dose Regimes of Proton Beam Irradiated 304 SS. J. Nucl. Mater. 486, 323–331. doi:10.1016/j.jnucmat.2017.01.036

CrossRef Full Text | Google Scholar

Renjo, M. M., Rede, V., and Curkovic, L. (2014). Reverse Indentation Size Effect of a Duplex Steel. Kovove Mater. 52, 299–304.

Google Scholar

Rice, P. M., and Stoller, R. E. (2000). Correlation of Nanoindentation and Conventional Mechanical Property Measurements. MRS Proc. 649. Q7.11. doi:10.1557/proc-649-q7.11

CrossRef Full Text | Google Scholar

Roters, F., Diehl, M., Shanthraj, P., Eisenlohr, P., Reuber, C., Wong, S. L., et al. (2019). DAMASK – the Düsseldorf Advanced Material Simulation Kit for Modeling Multi-Physics crystal Plasticity, thermal, and Damage Phenomena from the Single crystal up to the Component Scale. Comput. Mater. Sci. 158, 420–478. doi:10.1016/j.commatsci.2018.04.030

CrossRef Full Text | Google Scholar

Roters, F., Eisenlohr, P., Kords, C., Tjahjanto, D. D., Diehl, M., and Raabe, D. (2012). DAMASK: the Düsseldorf Advanced MAterial Simulation Kit for Studying crystal Plasticity Using an FE Based or a Spectral Numerical Solver. Proced. IUTAM 3, 3–10. doi:10.1016/j.piutam.2012.03.001

CrossRef Full Text | Google Scholar

Ruestes, C. J., Anders, C., Bringa, E. M., and Urbassek, H. M. (2018). Nanoindentation Tests of Heavy-Ion-Irradiated Au Foams—Molecular Dynamics Simulation. J. Appl. Phys. 123 (22), 225903. doi:10.1063/1.5027191

CrossRef Full Text | Google Scholar

Sadeghilaridjani, M., Ayyagari, A., Muskeri, S., Hasannaeimi, V., Salloom, R., Chen, W.-Y., et al. (2020). Ion Irradiation Response and Mechanical Behavior of Reduced Activity High Entropy alloy. J. Nucl. Mater. 529, 151955. doi:10.1016/j.jnucmat.2019.151955

CrossRef Full Text | Google Scholar

Saleh, M., Zaidi, Z., Ionescu, M., Hurt, C., Short, K., Daniels, J., et al. (2016). Relationship between Damage and Hardness Profiles in Ion Irradiated SS316 Using Nanoindentation - Experiments and Modelling. Int. J. Plasticity 86, 151–169. doi:10.1016/j.ijplas.2016.08.006

CrossRef Full Text | Google Scholar

Sangwal, K. (2000). On the Reverse Indentation Size Effect and Microhardness Measurement of Solids. Mater. Chem. Phys. 63 (2), 145–152. doi:10.1016/s0254-0584(99)00216-3

CrossRef Full Text | Google Scholar

Schwiedrzik, J. J., Ast, J., Pethö, L., Maeder, X., and Michler, J. (2018). A New Push-Pull Sample Design for Microscale Mode 1 Fracture Toughness Measurements under Uniaxial Tension. Fatigue Fracture Eng. Mater. Structures 41 (5), 991–1001. doi:10.1111/ffe.12741

CrossRef Full Text | Google Scholar

Sebastiani, M., Johanns, K. E., Herbert, E. G., Carassiti, F., and Pharr, G. M. (2015). A Novel Pillar Indentation Splitting Test for Measuring Fracture Toughness of Thin Ceramic Coatings. Philos. Mag. 95 (16-18), 1928–1944. doi:10.1080/14786435.2014.913110

CrossRef Full Text | Google Scholar

Sebastiani, M., Johanns, K. E., Herbert, E. G., and Pharr, G. M. (2015). Measurement of Fracture Toughness by Nanoindentation Methods: Recent Advances and Future Challenges. Curr. Opin. Solid State. Mater. Sci. 19 (6), 324–333. doi:10.1016/j.cossms.2015.04.003

CrossRef Full Text | Google Scholar

Sernicola, G., Giovannini, T., Patel, P., Kermode, J. R., Balint, D. S., Britton, T. B., et al. (2017). In Situ stable Crack Growth at the Micron Scale. Nat. Commun. 8 (1), 108. doi:10.1038/s41467-017-00139-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Shin, C., Jin, H.-h., and Kim, M.-W. (2009). Evaluation of the Depth-dependent Yield Strength of a Nanoindented Ion-Irradiated Fe–Cr Model alloy by Using a Finite Element Modeling. J. Nucl. Mater. 392 (3), 476–481. doi:10.1016/j.jnucmat.2009.04.011

CrossRef Full Text | Google Scholar

Shin, C., Jin, H. h., Sung, H., Kim, D. J., Choi, Y. S., and Oh, K. (2013). Evaluation of Irradiation Effects on Fracture Strength of Silicon Carbide Using Micropillar Compression Tests. Exp. Mech. 53 (4), 687–697. doi:10.1007/s11340-012-9678-1

CrossRef Full Text | Google Scholar

Shin, C., Lim, S., Jin, H.-h., Hosemann, P., and Kwon, J. (2014). Development and Testing of Microcompression for post Irradiation Characterization of ODS Steels. J. Nucl. Mater. 444 (1), 43–48. doi:10.1016/j.jnucmat.2013.09.025

CrossRef Full Text | Google Scholar

Shui, S. (2021). Progress and Challenges in Finite Element Simulation of Nanoindentation of Ion-Irradiated Materials. J. Phys. Conf. Ser. 1885 (3), 032039. doi:10.1088/1742-6596/1885/3/032039

CrossRef Full Text | Google Scholar

Singh, V., Kumar, N. N., Krishna, K. V. M., Sharma, G., Tewari, R., and Dey, G. K. (2019). Role of Irradiation Induced Defects in Altering the Micro-mechanical Response of Zr Domains during Nano Indentation: A Molecular Dynamics Study. Comput. Mater. Sci. 161, 151–162. doi:10.1016/j.commatsci.2019.01.036

CrossRef Full Text | Google Scholar

Snead, L. L., Zinkle, S. J., and Steiner, D. (1992). Radiation Induced Microstructure and Mechanical Property Evolution of SiC/C/SiC Composite Materials. J. Nucl. Mater. 191-194, 560–565. doi:10.1016/s0022-3115(09)80108-6

CrossRef Full Text | Google Scholar

Sobie, C., Bertin, N., and Capolungo, L. (2015). Analysis of Obstacle Hardening Models Using Dislocation Dynamics: Application to Irradiation-Induced Defects. Metallurgical Mater. Trans. A 46 (8), 3761–3772. doi:10.1007/s11661-015-2935-z

CrossRef Full Text | Google Scholar

Soler, R., Molina-Aldareguia, J. M., Segurado, J., Llorca, J., Merino, R. I., and Orera, V. M. (2012). Micropillar Compression of LiF [111] Single Crystals: Effect of Size, Ion Irradiation and Misorientation. Int. J. Plasticity 36, 50–63. doi:10.1016/j.ijplas.2012.03.005

CrossRef Full Text | Google Scholar

Sumigawa, T., Ashida, S., Tanaka, S., Sanada, K., and Kitamura, T. (2015). Fracture Toughness of Silicon in Nanometer-Scale Singular Stress Field. Eng. Fracture Mech. 150, 161–167. doi:10.1016/j.engfracmech.2015.05.054

CrossRef Full Text | Google Scholar

Suzuki, T., Takeuchi, S., and Yoshinaga, H. (2013). Dislocation Dynamics and Plasticity. Springer Science & Business Media.

Google Scholar

Tabor, D. (1956). The Physical Meaning of Indentation and Scratch Hardness. Br. J. Appl. Phys. 7 (5), 159–166. doi:10.1088/0508-3443/7/5/301

CrossRef Full Text | Google Scholar

Takayama, Y., Kasada, R., Sakamoto, Y., Yabuuchi, K., Kimura, A., Ando, M., et al. (2013). Nanoindentation Hardness and its Extrapolation to Bulk-Equivalent Hardness of F82H Steels after Single- and Dual-Ion Beam Irradiation. J. Nucl. Mater. 442 (1Suppl. 1), S23–S27. doi:10.1016/j.jnucmat.2012.12.033

CrossRef Full Text | Google Scholar

Uchic, M. D., Shade, P. A., and Dimiduk, D. M. (2009). Plasticity of Micrometer-Scale Single Crystals in Compression. Annu. Rev. Mater. Res. 39 (1), 361–386. doi:10.1146/annurev-matsci-082908-145422

CrossRef Full Text | Google Scholar

Uematsu, Y., Kakiuchi, T., Tamano, S., Mizuno, S., and Tamada, K. (2016). Fatigue Behavior of AZ31 Magnesium alloy Evaluated Using Single crystal Micro Cantilever Specimen. Int. J. Fatigue 93, 30–37. doi:10.1016/j.ijfatigue.2016.08.008

CrossRef Full Text | Google Scholar

Upit, G., and Varchenya, S. (1973). “The Size Effect in the Hardness of Single Crystals, Paper from,” in The Science of Hardness Testing and its Research Applications (Metals Park: ASM), 135–146.

Google Scholar

Vo, H., Reichardt, A., Howard, C., Abad, M. D., Kaoumi, D., Chou, P., et al. (2015). Small-Scale Mechanical Testing on Proton Beam-Irradiated 304 SS from Room Temperature to Reactor Operation Temperature. Jom 67 (12), 2959–2964. doi:10.1007/s11837-015-1596-0

CrossRef Full Text | Google Scholar

Vo, H. T., Reichardt, A., Frazer, D., Bailey, N., Chou, P., and Hosemann, P. (2017). In Situ micro-tensile Testing on Proton Beam-Irradiated Stainless Steel. J. Nucl. Mater. 493, 336–342. doi:10.1016/j.jnucmat.2017.06.026

CrossRef Full Text | Google Scholar

Wang, A.-N., Nonemacher, J. F., Yan, G., Finsterbusch, M., Malzbender, J., and Krüger, M. (2018). Mechanical Properties of the Solid Electrolyte Al-Substituted Li7La3Zr2O12 (LLZO) by Utilizing Micro-pillar Indentation Splitting Test. J. Eur. Ceram. Soc. 38 (9), 3201–3209. doi:10.1016/j.jeurceramsoc.2018.02.032

CrossRef Full Text | Google Scholar

Wang, C. L., Lai, Y. H., Huang, J. C., and Nieh, T. G. (2010). Creep of Nanocrystalline Nickel: A Direct Comparison between Uniaxial and Nanoindentation Creep. Scripta Materialia 62 (4), 175–178. doi:10.1016/j.scriptamat.2009.10.021

CrossRef Full Text | Google Scholar

Wang, Q., Long, F., Wang, Z., Guo, N., and Daymond, M. R. (2018). Orientation Dependent Evolution of Plasticity of Irradiated Zr-2.5 Nb Pressure Tube alloy Studied by Nanoindentation and Finite Element Modeling. J. Nucl. Mater. 512, 371–384. doi:10.1016/j.jnucmat.2018.10.033

CrossRef Full Text | Google Scholar

Was, G. S., Busby, J. T., Allen, T., Kenik, E. A., Jensson, A., Bruemmer, S. M., et al. (2002). Emulation of Neutron Irradiation Effects with Protons: Validation of Principle. J. Nucl. Mater. 300 (2), 198–216. doi:10.1016/s0022-3115(01)00751-6

CrossRef Full Text | Google Scholar

Was, G. S. (2016). Fundamentals of Radiation Materials Science: Metals and Alloys. Springer.

Google Scholar

Was, G. S., Jiao, Z., Getto, E., Sun, K., Monterrosa, A. M., Maloy, S. A., et al. (2014). Emulation of Reactor Irradiation Damage Using Ion Beams. Scripta Materialia 88, 33–36. doi:10.1016/j.scriptamat.2014.06.003

CrossRef Full Text | Google Scholar

Weaver, J., Carvajal Nunez, U., Krumwiede, D., Saleh, T. A., Hosemann, P., Nelson, A. T., et al. (2017). Spherical Nanoindentation Stress-Strain Measurements of BOR-60 14YWT-NFA1 Irradiated Tubes. United States.

Google Scholar

Weaver, J. S., Pathak, S., Reichardt, A., Vo, H. T., Maloy, S. A., Hosemann, P., et al. (2017). Spherical Nanoindentation of Proton Irradiated 304 Stainless Steel: A Comparison of Small Scale Mechanical Test Techniques for Measuring Irradiation Hardening. J. Nucl. Mater. 493, 368–379. doi:10.1016/j.jnucmat.2017.06.031

CrossRef Full Text | Google Scholar

Weaver, J. S., Sun, C., Wang, Y., Kalidindi, S. R., Doerner, R. P., Mara, N. A., et al. (2018). Quantifying the Mechanical Effects of He, W and He + W Ion Irradiation on Tungsten with Spherical Nanoindentation. J. Mater. Sci. 53 (7), 5296–5316. doi:10.1007/s10853-017-1833-8

CrossRef Full Text | Google Scholar

Wharry, J. P., Yano, K. H., and Patki, P. V. (2019). Intrinsic-extrinsic Size Effect Relationship for Micromechanical Tests. Scripta Materialia 162, 63–67. doi:10.1016/j.scriptamat.2018.10.045

CrossRef Full Text | Google Scholar

Wurster, S., Motz, C., and Pippan, R. (2012). Characterization of the Fracture Toughness of Micro-sized Tungsten Single crystal Notched Specimens. Philos. Mag. 92 (14), 1803–1825. doi:10.1080/14786435.2012.658449

CrossRef Full Text | Google Scholar

Xiao, X., Chen, L., Yu, L., and Duan, H. (2019). Modelling Nano-Indentation of Ion-Irradiated FCC Single Crystals by Strain-Gradient crystal Plasticity Theory. Int. J. Plasticity 116, 216–231. doi:10.1016/j.ijplas.2019.01.005

CrossRef Full Text | Google Scholar

Xiao, X., Li, S., and Yu, L. (2021). Effect of Irradiation Damage and Indenter Radius on Pop-In and Indentation Stress-Strain Relations: Crystal Plasticity Finite Element Simulation. Int. J. Mech. Sci. 199, 106430. doi:10.1016/j.ijmecsci.2021.106430

CrossRef Full Text | Google Scholar

Xiao, X., and Yu, L. (2019). Cross-sectional Nano-Indentation of Ion-Irradiated Steels: Finite Element Simulations Based on the Strain-Gradient crystal Plasticity Theory. Int. J. Eng. Sci. 143, 56–72. doi:10.1016/j.ijengsci.2019.06.015

CrossRef Full Text | Google Scholar

Xiao, X., and Yu, L. (2020). Effect of Primary Creep on the Relationship between Indentation and Uniaxial Creep: A Theoretical Model. Int. J. Sol. Structures 206, 114–123. doi:10.1016/j.ijsolstr.2020.09.017

CrossRef Full Text | Google Scholar

Xiao, X., and Yu, L. (2020). Nano-indentation of Ion-Irradiated Nuclear Structural Materials: A Review. Nucl. Mater. Energ. 22, 100721. doi:10.1016/j.nme.2019.100721

CrossRef Full Text | Google Scholar

Xu, A., Armstrong, D. E. J., Beck, C., Moody, M. P., Smith, G. D. W., Bagot, P. A. J., et al. (2017). Ion-irradiation Induced Clustering in W-Re-Ta, W-Re and W-Ta Alloys: An Atom Probe Tomography and Nanoindentation Study. Acta Materialia 124, 71–78. doi:10.1016/j.actamat.2016.10.050

CrossRef Full Text | Google Scholar

Xu, A., Saleh, M., and Bhattacharyya, D. (2020). Experimental and Computational Analysis of the In Situ Tensile Deformation of 2D Honeycomb Lattice Structures in Ni Single Crystals. Composites B: Eng. 186, 107823. doi:10.1016/j.compositesb.2020.107823

CrossRef Full Text | Google Scholar

Xu, A., Wei, T., and Bhattacharyya, D. (2020). The Effect of Strain Rate and Orientation on He Ion Irradiated Ni Single Crystals - an In Situ Micro-tensile Study. Int. J. Plasticity 126, 102627. doi:10.1016/j.ijplas.2019.11.006

CrossRef Full Text | Google Scholar

Xu, S., Guo, Y. F., and Ngan, A. H. W. (2013). A Molecular Dynamics Study on the Orientation, Size, and Dislocation Confinement Effects on the Plastic Deformation of Al Nanopillars. Int. J. Plasticity 43, 116–127. doi:10.1016/j.ijplas.2012.11.002

CrossRef Full Text | Google Scholar

Yabuuchi, K., Kuribayashi, Y., Nogami, S., Kasada, R., and Hasegawa, A. (2014). Evaluation of Irradiation Hardening of Proton Irradiated Stainless Steels by Nanoindentation. J. Nucl. Mater. 446 (1), 142–147. doi:10.1016/j.jnucmat.2013.12.009

CrossRef Full Text | Google Scholar

Yang, T., Zang, H., He, C., Guo, D., Zhang, P., Xi, J., et al. (2015). Evaluation of Mechanical Properties Variations for Kr Ion-Irradiated 6H-SiC by Nanoindentation Methods. Int. J. Appl. Ceram. Tech. 12 (2), 390–398. doi:10.1111/ijac.12170

CrossRef Full Text | Google Scholar

Yang, Y., Ma, B., Zhang, C., Han, X., Niu, M., Chen, Y., et al. (2020). Effective Fitting of Nanohardness Data in Two Different Ferritic Steels Irradiated with He Ions. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 475, 84–88. doi:10.1016/j.nimb.2020.05.013

CrossRef Full Text | Google Scholar

Yano, K. H., Swenson, M. J., Wu, Y., and Wharry, J. P. (2017). TEM In Situ Micropillar Compression Tests of Ion Irradiated Oxide Dispersion Strengthened alloy. J. Nucl. Mater. 483, 107–120. doi:10.1016/j.jnucmat.2016.10.049

CrossRef Full Text | Google Scholar

Yu, J. H., Kurotaki, H., Ando, M., and Nozawa, T. (2022). Mechanical Properties of Self-Ion Irradiated Pure Tungsten using Nano-Indentation Test and Micro-Tensile Test. Nucl. Mater. Energy 30, 101145.

CrossRef Full Text | Google Scholar

Yu, Q., Shan, Z.-W., Li, J., Huang, X., Xiao, L., Sun, J., et al. (2010). Strong crystal Size Effect on Deformation Twinning. Nature 463 (7279), 335–338. doi:10.1038/nature08692

PubMed Abstract | CrossRef Full Text | Google Scholar

Zepeda-Ruiz, L. A., Martinez, E., Caro, M., Fu, E. G., and Caro, A. (2013). Deformation Mechanisms of Irradiated Metallic Nanofoams. Appl. Phys. Lett. 103 (3), 031909. doi:10.1063/1.4813863

CrossRef Full Text | Google Scholar

Zhang, H., Schuster, B. E., Wei, Q., and Ramesh, K. T. (2006). The Design of Accurate Micro-compression Experiments. Scripta Materialia 54 (2), 181–186. doi:10.1016/j.scriptamat.2005.06.043

CrossRef Full Text | Google Scholar

Zhang, Z., Hasenhuetl, E., Yabuuchi, K., and Kimura, A. (2016). Evaluation of Helium Effect on Ion-Irradiation Hardening in Pure Tungsten by Nano-Indentation Method. Nucl. Mater. Energ. 9, 539–546. doi:10.1016/j.nme.2016.06.010

CrossRef Full Text | Google Scholar

Zhu, Z., Huang, H., Liu, J., Ye, L., and Zhu, Z. (2020). Nanoindentation Study on the Creep Characteristics and Hardness of Ion-Irradiated Alloys. Materials (Basel) 13 (14). doi:10.3390/ma13143132

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziegler, J. F., Ziegler, M. D., and Biersack, J. P. (2010). SRIM–The Stopping and Range of Ions in Matter. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 268 (11-12), 1818–1823. doi:10.1016/j.nimb.2010.02.091

CrossRef Full Text | Google Scholar

Zinkle, S. J., and Busby, J. T. (2009). Structural Materials for Fission & Fusion Energy. Mater. Today 12 (11), 12–19. doi:10.1016/s1369-7021(09)70294-9

CrossRef Full Text | Google Scholar

Zinkle, S. J., and Oliver, W. C. (1986). Mechanical Property Measurements on Ion-Irradiated Copper and Cu-Zr. J. Nucl. Mater. 141-143, 548–552. doi:10.1016/s0022-3115(86)80100-3

CrossRef Full Text | Google Scholar

Zinkle, S. J., and Steven, J. (2012). Radiation-Induced Effects on Microstructure, 65–98. doi:10.1016/b978-0-08-056033-5.00003-3Radiation-Induced Effects on Microstructure**Prepared for the Oak Ridge National Laboratory under Contract No. DE-AC05-000R22725

CrossRef Full Text | Google Scholar

Zuo, L., Ngan, A., and Zheng, G. (2005). Size Dependence of Incipient Dislocation Plasticity in Ni 3 Al. Phys. Rev. Lett. 94 (9), 095501. doi:10.1103/PhysRevLett.94.095501

PubMed Abstract | CrossRef Full Text | Google Scholar