Band Gaps and Vibration Attenuation Characteristics Analysis in Homogeneous Beam Coupled With Periodic Oscillators Based on the Method of Reverberation-Ray Matrix

A periodic beam-oscillators coupling system is proposed as a physical model in this paper for analyzing the dynamic characteristics of periodic support beams and low-frequency flexural wave vibration of slender stiffened plate structures. The dispersion relation of flexural wave in the infinite long homogeneous beam coupled with periodic oscillators is calculated using the method of reverberation-ray matrix combined with the Bloch theorem. The accuracy and effectiveness of the method of reverberation-ray matrix in analyzing the band gaps and vibration characteristics of the homogeneous beam coupled with periodic oscillators are verified by the numerical results of the finite long homogeneous beam coupled with periodic oscillators. Both the analytical and numerical results show the existences of flexural wave band gaps in the homogeneous beam coupled with periodic oscillators, in which the propagation of the flexural waves is prohibited and flexural wave vibration is significantly suppressed. Furthermore, the effects of structural and material parameters on the flexural wave band gaps characteristics are respectively investigated. The flexural wave band gaps can be adjusted and optimized manually by adjusting structural and material parameters, which can be applied to vibration and noise control design of periodic support beams and slender stiffened plate structures.

1 Introduction

With the development of naval architecture and ocean engineering with high-speed, large-scale and large-tonnage, vibrations in ship and offshore structures owing to various ocean environmental loads and excitations of power systems become increasingly serious, can reduce productivity, endanger safety, affect service life of the structure and even discomfort of crews (Hirdaris et al., 2014; Murawski and Charchalis, 2014; Kandasamy et al., 2016). Therefore, it is necessary to eliminate or reduce vibration and noise of ship and offshore structures and develop low-noise structural design technology.

Many scholars have done a large number of studies to control vibration and noise of ship and offshore structures (Wang et al., 2013; Lan et al., 2014; Wang et al., 2016; Gripp and Rade, 2018). From their studies, there are three main methods to control vibration and noise. The first way is to control the source, design and manufacture power systems with low noise, low vibration or even silence; the second is to control the propagation path through isolation, absorption, and attenuation methods; the third is to protect the receiver (Wu et al., 2014; Liu et al., 2015; Shi et al., 2016; Som and Das, 2018). As the development of naval architecture and ocean engineering with high-speed, large-scale and large-tonnage, it has become increasingly difficult to reduce noise from the source. Furthermore, the techniques to protect the receivers are unreasonable as the receivers are often moving as well as the rapid developments of the underwater acoustic detection technologies. Therefore, trying to reduce the vibration and noise in the propagation path is a more sensible choice (Ibrahim, 2008; Toky et al., 2020; Yaman et al., 2021). The mainly ways to control vibration and noise can be divided into passive control schemes, semi-active control schemes, and active control schemes (Keir et al., 2005; Ou et al., 2007; Liu et al., 2017; Enferadi et al., 2019; Han et al., 2019; Li and Yang, 2020). Although the existing traditional vibration reduction techniques can control the vibration and noise of ships and offshore structures to a certain extent, it also has some limitations, including the equipment mass must be larger and the narrow frequency band in passive control, the damping vibration attenuation only have an impact on the medium and high frequencies, as well as the system complexity and narrow band characteristics of active control. In addition, it is necessary to strengthen the research on low frequency vibration and noise control of ships and offshore structures, as the vibration and noise in the low frequency range has strong penetration and slow dissipation during propagation (Waye, 2011; Kim et al., 2019). Beam is one of the most important basic structures in engineering and are widely used in civil engineering, aerospace as well as naval architecture and ocean engineering. And stiffened plates, especially the bi-directionally orthogonal stiffened plates are widely used in deck, bottom and side structures of ships and offshore structures. The stiffened plates can be simplified to a multi-span beam model with periodic elastic supports and then into an elastic foundation beam model to study their static and dynamic characteristics (Chen and Chen, 1991). In addition, many slender stiffened plate structures in ships and offshore structures can be simplified into beam models for low frequency flexural wave vibration analysis. Thus, studying the dynamic characteristics of beams is of great significance to the dynamic performance and low noise structural design of ships and marine structures. Many scholars have done a lot of studies to investigate the wave band gaps and propagation characteristics in phononic crystals, acoustic metamaterials and other periodic structures in recent decades (He et al., 2017; Lee et al., 2018; Nateghi et al., 2019). Periodic structures have been introduced into the structural vibration reduction design due to the advantage of band gap characteristics.

Periodic structures have band gaps properties, which the propagation of waves in the periodic structures is forbidden in specific frequency ranges. Due to the various unique physical properties, periodic structures are widely used in various engineering practices such as structural strength enhancement, vibration absorption and vibration control, thus, a large number of studies have been carried out on the band gaps and wave propagation and attenuation characteristics of various periodic structures (Dupont et al., 2019; Muhammad and Lim, 2019; Xu et al., 2021). The existing periodic structure studies reveal two kinds of band gap formation theories: local resonance band gap and Bragg scattering band gap. Mead and his team members have conducted a lot of researches on the wave propagation characteristics in periodic beams since the 1960s (Mead, 1970; Mead, 1996). Kushwaha et al. inferred phononic crystals from the studies of photonic crystals and discovered the band gap phenomenon of phononic crystals (Kushwaha et al., 1993). Liu et al. fabricated a local resonant periodic structure by the idea of localized resonant structures, and the theoretical and experimental studies have verified there is a low-frequency local resonance band gap in this type periodic structure which is much lower than the traditional Bragg gap frequency (Liu et al., 2000). It provides a theoretical foundation for the application of low-frequency band gap characteristics of macroscopic periodic structures.

In the past two decades, the elastic wave band gap characteristics and propagation and attenuation characteristics of various periodic structures have been investigated. Guo and Fang (2014) and Li and Guo (2016) analyzed the longitudinal wave dispersion relations and band gap characteristics in periodic quaternary rods and rod-type piezoelectric periodic structures, respectively. The research results promoted the design of rod-type periodic structures for vibration isolation/control applications. Richards and Pines (2003) utilized the property of a periodic drive shaft that generated stop band gap and pass band regions in the frequency spectra, both the analytical and experimental results indicated that the proposed periodic drive shaft can effectively reduce the transmitted vibration generated by gear mesh contact dynamics. Shen et al. (2012) proposed a periodic shell made of functionally graded material and then investigated the mechanism of wave propagation and vibration transmission in the shell by illustrating the pass/stop band frequency ranges of the periodic shell. An et al. (2018) numerically studied the band gap characteristics of radial wave propagating radically from the inner circle of a two-dimensional cylindrical shell structure with radial and circumferential periodicities. Results showed that radial wave has significant attenuation in band gap frequency region. Sharma and Sun (2016) investigated the low frequency wave propagation behaviours of sandwich beams containing periodically embedded internal resonators, and they demonstrated that local resonance and Bragg band gaps coexist in the proposed periodic sandwich beams. Liu and Yang (2017) analyzed the characteristics of acoustic wave transmitting in a metamaterial seawater pipe which consists of a uniform pipe with air-water chamber Helmholtz resonators mounted periodically along its axial direction, the results showed that the proposed metamaterial seawater pipe could generate a wide band gap in the low-frequency range and rendering the propagation of the frequency range acoustic waves in the piping system dampened spatially. Faiz et al. (2020) theoretically and experimentally investigated the waveguiding and filtering properties of a two-dimensional phononic crystal slab. They verified that the proposed device shows a complete band gap and the Lamb wave in the phononic crystal slab can be suppressed significantly. Zhou et al. (2014) studied the flexural wave band gap and attenuation characteristics in a periodic stiffened-thin-plate with the help of center-finite-difference-method. Results showed that the proposed periodic structure can yield complete band gaps and the wave propagation is forbidden. Zuo et al. (2018) investigated the flexural wave propagation and band gaps of a locally resonant phononic crystal to achieve a wider band gap and a lower cut-on frequency. This research provided an approach for the application of locally resonant phononic crystal in vibration and noise control.

As a preliminary study of periodic structure band gaps characteristics and low-noise structural design of ship and offshore structures, a simple physical model is proposed in this paper for analyzing the dynamic characteristics of periodic support beams and low-frequency flexural wave vibration of slender stiffened plate structures in ship and offshore structures. The proposed physical model is an infinite long homogeneous beam coupled with periodic oscillators which is a periodic beam-oscillators coupling system composed of homogeneous beam and periodic local oscillators. Based on the Timoshenko beam theory and its wave form solution, the calculation method for the flexural wave band gaps in the proposed infinite long homogeneous beam coupled with periodic oscillators is established by the method of reverberation-ray matrix combined with Bloch theorem. The method of reverberation-ray matrix is a semi-analytical method and the advantages of the present method lie in its simplicity, clarity, and accuracy (Guo and Fang, 2011). The rest of this article is organized as follows: First of all, the calculation formulation for analyzing the flexural wave band gaps of the homogeneous beam coupled with periodic oscillators is established by using the method of reverberation-ray matrix, as detailed in Section 2. The theoretical calculation results and discussions of the band gap characteristics are given in Section 3, which the flexural wave band gaps calculation method is verified by structural flexural wave vibration transmission characteristics based on finite element method, as shown in Section 3.2. And then the influences of various structural and material parameters of the homogeneous beam coupled with periodic oscillators on the band gap characteristics are respectively investigated in Section 3.3. Conclusions are given in Section 4.

2 Physics Model and Calculation Method

The proposed simple physical model considered in this paper is constituted of an infinitely long homogeneous beam coupled with periodic local oscillators in parallel connection as illustrated in Figure 1A, which is a periodic beam-oscillators coupling system. The area surrounded by a red dashed line in Figure 1A is the unit cell of the proposed infinite long homogeneous beam coupled with periodic oscillators and the schematic diagram is shown in Figure 1B, and the periodic beam-oscillators coupling system in a unit cell is drawn in Figure 1C. By periodically repeating and combining the unit cell along the length direction, the proposed infinite long homogeneous beam coupled with periodic oscillators can be obtained. The structural parameters of the proposed infinite long homogeneous beam coupled with periodic oscillators are listed as follows: the spring stiffness k_s, the mass m_s and the damping c_s of the periodic oscillators, lattice constant a, section moment of inertia I, section area A as well as the support stiffness of the elastic foundation k*, and the material parameters of the homogeneous beam including Young’s modulus E, mass density ρ and Poisson’s ratio ν. In advance of investigating the flexural wave band gaps and vibration attenuation characteristics in the proposed infinite long homogeneous beam coupled with periodic oscillators, the governing wave equations should be introduced. The main equations of the flexural wave band gaps calculation method for the proposed infinite long homogeneous beam coupled with periodic oscillators are as follows.

FIGURE 1

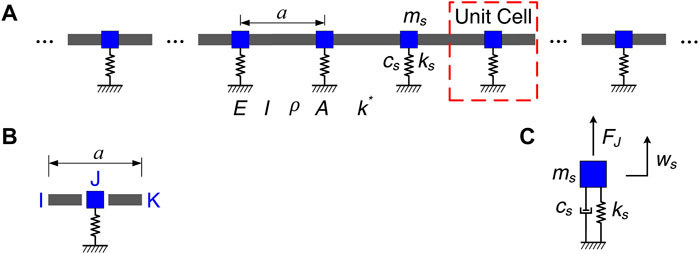
FIGURE 1. The physics model: (A) Schematic diagram of infinite long homogeneous beam coupled with periodic oscillators; (B) Schematic diagram of the unit cell; (C) The beam-oscillators coupling system in a unit cell.

Considering the effects of shear deformation and moment of inertia, the flexural wave vibration governing equations of a homogeneous Timoshenko beam with elastic foundation support can be written as (Li et al., 2014):

$EI\frac{{\partial }^2\phi }{\partial x^2}+\kappa GA\left(\frac{\partial w}{\partial x}-\phi \right)-\rho I\frac{{\partial }^2\phi }{\partial t^2}=0(1)$

$\kappa GA\left(\frac{{\partial }^{2}w}{\partial x^2}-\frac{\partial \phi }{\partial x}\right)-\rho A\frac{{\partial }^{2}w}{\partial t^2}+k^{\ast }w=0(2)$

where G represents the shear elastic modulus, κ denotes the shear correction coefficient, w (x, t) and φ(x, t) are the vertical displacement and rotation angle of the homogeneous beam, respectively.

By eliminating $\partial \phi /\partial x$ after substituting Eq. 1 into Eq. 2, the flexural wave vibration governing equation expressed only by vertical displacement w (x, t) can be obtained as

$\frac{{\partial }^{4}w}{\partial x^4}+\frac{k^{\ast }}{\kappa GA}\frac{{\partial }^{2}w}{\partial x^2}-\left(\frac{\rho }{\kappa G}+\frac{\rho }{E}\right)\frac{{\partial }^{4}w}{\partial x^2\partial t^2}+\left(\frac{\rho A}{EI}-\frac{\rho k^{\ast }}{E\kappa GA}\right)\frac{{\partial }^{2}w}{\partial t^2}+\frac{{\rho }^2}{E\kappa G}\frac{{\partial }^{4}w}{\partial t^4}-\frac{k^{\ast }}{EI}w=0(3)$

The wave form solution for the vertical displacement in the homogeneous beam can be expressed as w = W₀e^i(kx−ωt). Thus, after omitting the simple harmonic time factor e^−iωt, the solution of Eq. 3 in the frequency domain can be expressed as follows:

$w=a_1{e}^{\mathrm{i}{k}_{1}x}+d_1{e}^{-\mathrm{i}{k}_{1}x}+a_2{e}^{\mathrm{i}{k}_{2}x}+d_2{e}^{-\mathrm{i}{k}_{2}x}(4)$

where $k_1=\sqrt{-\alpha /2+\sqrt{{\left(\alpha /2\right)}^2-\beta }}$ and $k_2=\sqrt{-\alpha /2-\sqrt{{\left(\alpha /2\right)}^2-\beta }}$ are wavenumbers, and where

$\alpha =-\frac{k^{\ast }}{\kappa GA}-{\omega }^2\left(\frac{\rho }{\kappa G}+\frac{\rho }{E}\right),\beta =-{\omega }^2\left(\frac{\rho A}{EI}-\frac{\rho k^{\ast }}{E\kappa GA}\right)+\frac{{\rho }^2}{E\kappa G}{\omega }^4-\frac{k^{\ast }}{EI}(5)$

From this, the rotation angle of the homogeneous beam can be written as

$\phi =g_1{a}_1{e}^{\mathrm{i}{k}_{1}x}-g_1{d}_1{e}^{-\mathrm{i}{k}_{1}x}+g_2{a}_2{e}^{\mathrm{i}{k}_{2}x}-g_2{d}_2{e}^{-\mathrm{i}{k}_{2}x}(6)$

where g_j (j = 1, 2) can be expressed as

$g_j=\frac{\mathrm{i}{k}_j\kappa GA}{EI{k}_j^2+\kappa GA-\rho I{\omega }^2}(7)$

According to the relationships between the bending moment with the vertical displacement, $M=EI{\partial }^{2}w/\partial x^2$, and the shear force with the vertical displacement and rotation angle in Timoshenko beam, $V=\kappa GA\left(\phi -\partial w/\partial x\right)$, the expressions of the bending moment and shear force can be obtained as:

$M=-EI\left(k_1^2{a}_1{e}^{\mathrm{i}{k}_{1}x}+k_1^2{d}_1{e}^{-\mathrm{i}{k}_{1}x}+k_2^2{a}_2{e}^{\mathrm{i}{k}_{2}x}+k_2^2{d}_2{e}^{-\mathrm{i}{k}_{2}x}\right)(8)$

$V=\kappa GA\left[\left(g_1-\mathrm{i}{k}_1\right)a_1{e}^{\mathrm{i}{k}_{1}x}-\left(g_1-\mathrm{i}{k}_1\right)d_1{e}^{-\mathrm{i}{k}_{1}x}+\left(g_2-\mathrm{i}{k}_2\right)a_2{e}^{\mathrm{i}{k}_{2}x}-\left(g_2-\mathrm{i}{k}_2\right)d_2{e}^{-\mathrm{i}{k}_{2}x}\right](9)$

The Eqs 4, 5 can be rewritten in matrix form as

${\mathit{W}}_d={\mathit{A}}_d{\mathit{P}}_h\left(-x\right)a+{\mathit{D}}_d{\mathit{P}}_h\left(\mathit{x}\right)\mathit{d}(10)$

and similarly, the Eqs 7, 8 are rewritten in matrix form as

${\mathit{W}}_f={\mathit{A}}_f{\mathit{P}}_h\left(-x\right)a+{\mathit{D}}_f{\mathit{P}}_h\left(\mathit{x}\right)\mathit{d}(11)$

where W_d = {w, φ}^T and W_f = {V, M}^T are the generalized displacement vector and the generalized force vector, a and d respectively stand for the amplitude vectors of arriving wave and leaving wave, A_d and D_d respectively denote the coefficient matrixes of the arriving wave and the leaving wave corresponding to the displacement vector, A_f and D_f are the coefficient matrixes of the arriving wave and leaving wave corresponding to the force vector, and P_h denotes the phase matrix, which the specific expressions are given as follows:

${\mathit{W}}_d={\left\{\begin{array}{cc}w& \phi \end{array}\right\}}^T{\mathit{W}}_f={\left\{\begin{array}{cc}V& M\end{array}\right\}}^T(12)$

$\mathit{a}={\left\{\begin{array}{cc}{a}_1& a_2\end{array}\right\}}^T\mathit{d}={\left\{\begin{array}{cc}{d}_1& d_2\end{array}\right\}}^T(13)$

${\mathit{P}}_h\left(x\right)=\left[\begin{array}{cc}{e}^{-i{k}_{1}x}& 0\\ 0& e^{-i{k}_{2}x}\end{array}\right](14)$

${\mathit{A}}_d=\left[\begin{array}{cc}1& 1\\ g_1& g_2\end{array}\right]{\mathit{D}}_d=\left[\begin{array}{cc}1& 1\\ -g_1& -g_2\end{array}\right](15)$

${\mathit{A}}_f=\left[\begin{array}{cc}\kappa GA& 0\\ 0& -EI\end{array}\right]\left[\begin{array}{cc}{g}_1-i{k}_1& g_2-i{k}_2\\ k_1^2& k_2^2\end{array}\right]{\mathit{D}}_f=\left[\begin{array}{cc}\kappa GA& 0\\ 0& -EI\end{array}\right]\left[\begin{array}{cc}i{k}_1-g_1& i{k}_2-g_2\\ k_1^2& k_2^2\end{array}\right](16)$

As the beam-oscillators coupling system in a unit cell plotted in Figure 1C, the relationships of the generalized displacements continuities and generalized forces equilibriums at the node J of the beam-oscillators coupling system unit cell are expressed as follows:

${\mathit{W}}_d^{JI}={\mathit{T}}_d^J{\mathit{W}}_d^{JK}(17)$

${\mathit{W}}_f^{JI}={\mathit{T}}_f^J{\mathit{W}}_f^{JK}+{\mathit{F}}^J(18)$

where T^J_d=diag {-1, 1} and T_f^J=-T^J_d respectively stand for the transformation matrix of the generalized displacement and generalized force at node j, and F^J denotes the reaction force vector of the local oscillator acting on the beam.

As the beam-oscillators coupling system in a unit cell illustrated in Figure 1C, the coupling vibration equation of the local oscillator coupled with the beam in parallel connection at the connection node can be obtained by

$m_s{\ddot{w}}_s+k_s{w}_s+c_s{\dot{w}}_s=F_J(19)$

Therefore, the reaction force vector of the local oscillator acting on the beam is presented as

${\mathit{F}}^J={\mathit{K}}^J{\mathit{W}}_d^{JK}(20)$

where K^J = diag{k_w k_φ} stand for the dynamic stiffness matrix of the local oscillator acting on the beam at node J, where the k_w = −m_sω²+k_s + ic_sω and k_φ = 0 are the translational stiffness coefficient and rotational stiffness coefficient of the local oscillator acting on the beam, respectively, k_s and m_s respectively represent the spring stiffness and mass of the local oscillator, w_s = w^JK = −w^JI denotes the vertical displacement of the local oscillator and the beam at the node J.

Substituting Eqs 9, 10 and 19 into Eqs 16, 17 obtains the scattering relationship of the beam-oscillators coupling system at node J as follows:

${\mathit{A}}^J{\mathit{a}}^J+{\mathit{D}}^J{\mathit{d}}^J=\mathbf{0}(21)$

where a^J = {(a^JI)^T (a^JK)^T}^T and d^J = {(d^JI)^T (d^JK)^T}^T are the amplitude vectors of the arriving wave and the leaving wave, respectively, A^J and D^J respectively stand for the corresponding coefficient matrixes of a^J and d^J at the node J, respectively, which are expressed as

${\mathit{A}}^J=\left[\begin{array}{cc}{\mathit{A}}_d^{JI}& -{\mathit{T}}_d^J{\mathit{A}}_d^{JK}\\ {\mathit{A}}_f^{JI}& -\left({\mathit{T}}_f^J{\mathit{A}}_f^{JK}+{\mathit{K}}^J{\mathit{A}}_d^{JK}\right)\end{array}\right]{\mathit{D}}^J=\left[\begin{array}{cc}{\mathit{D}}_d^{JI}& -{\mathit{T}}_d^J{\mathit{D}}_d^{JK}\\ {\mathit{D}}_f^{JI}& -\left({\mathit{T}}_f^J{\mathit{D}}_f^{JK}+{\mathit{K}}^J{\mathit{D}}_d^{JK}\right)\end{array}\right](22)$

According to the Bloch theorem of periodic structure, the following equations must be satisfied for the generalized displacement vector and generalized force vector in the unit cell of the proposed infinite long homogeneous beam coupled with periodic oscillators, which are listed as follows:

$e^{iqa}{\mathit{W}}_d^{IJ}={\mathit{T}}_d^J{\mathit{W}}_d^{KJ}(23)$

$e^{iqa}{\mathit{W}}_f^{IJ}={\mathit{T}}_f^J{\mathit{W}}_f^{KJ}(24)$

As the same, substituting Eqs 10, 11 into Eqs 22, 23 obtains

${\mathit{A}}^{\ast J}{\mathit{a}}^{\ast J}+{\mathit{D}}^{\ast J}{\mathit{d}}^{\ast J}=\mathbf{0}(25)$

where a*^J = {(a^IJ)^T (a^KJ)^T}^T and d*^J = {(d^IJ)^T (d^KJ)^T}^T are the amplitude vectors of the arriving wave and the leaving wave, respectively, A*^J and D*^J respectively stand for the corresponding coefficient matrixes of a*^J and d*^J at the node J, which are expressed as

${\mathit{A}}^{\ast J}=\left[\begin{array}{cc}{e}^{iqa}{\mathit{A}}_d^{IJ}& -{\mathit{T}}_d^J{\mathit{A}}_d^{KJ}\\ e^{iqa}{\mathit{A}}_f^{IJ}& -{\mathit{T}}_f^J{\mathit{A}}_f^{KJ}\end{array}\right]{\mathit{D}}^{\ast J}=\left[\begin{array}{cc}{e}^{iqa}{\mathit{D}}_d^{IJ}& -{\mathit{T}}_d^J{\mathit{D}}_d^{KJ}\\ e^{iqa}{\mathit{D}}_f^{IJ}& -{\mathit{T}}_f^J{\mathit{D}}_f^{KJ}\end{array}\right](26)$

By combining Eqs 20, 24, the global scattering relationship in a unit cell of the infinite long homogeneous beam coupled with periodic oscillators can be obtained as follows:

$\mathit{A}\mathit{a}+\mathit{D}\mathit{d}=\mathbf{0}(27)$

where a = {(a^IJ)^T (a^JI)^T (a^JK)^T (a^KJ)^T}^T and d = {(d^IJ)^T (d^JI)^T (d^JK)^T (d^KJ)^T}^T respectively stand for the global amplitude vectors of the arriving wave and the leaving wave of the proposed unit cell, A and D respectively denoted the corresponding coefficient matrixes of a and d at the node J, which the expressions are expressed as follows:

$\begin{array}{l}\mathit{A}=\left[\begin{array}{cccc}{e}^{iqa}{\mathit{A}}_d^{IJ}& \mathbf{0}& \mathbf{0}& -{\mathit{T}}_d^J{\mathit{A}}_d^{KJ}\\ \mathbf{0}& {\mathit{A}}_d^{JI}& -{\mathit{T}}_d^J{\mathit{A}}_d^{JK}& \mathbf{0}\\ \mathbf{0}& {\mathit{A}}_f^{JI}& -({\mathit{T}}_f^J{\mathit{A}}_f^{JK}+{\mathbf{K}}^J{\mathbf{A}}_d^{JK})& \mathbf{0}\\ e^{iqa}{\mathit{A}}_f^{IJ}& \mathbf{0}& \mathbf{0}& -{\mathit{T}}_f^J{\mathit{A}}_f^{KJ}\end{array}\right]\\ \\ \mathit{D}=\left[\begin{array}{cccc}{e}^{iqa}{\mathit{D}}_d^{IJ}& \mathbf{0}& \mathbf{0}& -{\mathbf{T}}_d^J{\mathit{D}}_d^{KJ}\\ \mathbf{0}& {\mathit{D}}_d^{JI}& -{\mathit{T}}_d^J{\mathit{D}}_d^{JK}& \mathbf{0}\\ \mathbf{0}& {\mathit{D}}_f^{JI}& -({\mathit{T}}_f^J{\mathit{D}}_f^{JK}+{\mathit{K}}^J{\mathit{D}}_d^{JK})& \mathbf{0}\\ e^{iqa}{\mathit{D}}_f^{IJ}& \mathbf{0}& \mathbf{0}& -{\mathit{T}}_f^J{\mathit{D}}_f^{KJ}\end{array}\right]\end{array}(28)$

For the flexural wave in any section of the beam, the leaving wave of the left end is exactly the arriving wave of the right node, and vice versa. For any section (e.g., section J) of the beam, the phase relationships can be expressed as follows:

${\mathit{a}}^{JK}={\mathit{P}}^{JK}{\mathit{d}}^{KJ}(29)$

${\mathit{a}}^{KJ}={\mathit{P}}^{JK}{\mathit{d}}^{JK}(30)$

where P^JK = −P_h (L^JK) is the phase matrix of the beam section J.

Thus, according to the phase relationships of each section of the beam, the global phase relationship is obtained as

$\mathit{a}=\mathit{P}{\mathit{d}}^{\ast }(31)$

where d∗ = {(d^JI)^T (d^IJ)^T (d^KJ)^T (d^JK)^T}^T is the rearranged global amplitude vector of the leaving wave in the unit cell of the infinite long homogeneous beam coupled with periodic oscillators, P = diag{P^IJ P^IJ P^JK P^JK} is the global phase matrix.

Comparing the global leaving wave amplitude vectors d∗ and d of the infinite long homogeneous beam coupled with periodic oscillators unit cell, the two vectors have the same elements with different arrangement orders. Thus, the relationship between the amplitude vectors d∗ and d is obtained as follows:

${\mathit{d}}^{\ast }=\mathit{U}\mathit{d}(32)$

$\mathit{U}=\left[\begin{array}{cccc}\mathbf{0}& {\mathit{I}}_2& \mathbf{0}& \mathbf{0}\\ {\mathit{I}}_2& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathit{I}}_2\\ \mathbf{0}& \mathbf{0}& {\mathit{I}}_2& \mathbf{0}\end{array}\right](33)$

where U is the permutation matrix between d∗ and d, in which I₂ stands for the two-order unit matrix.

After substituting Eqs 30, 31 into Eq. 26, the flexural wave dispersion relation in the unit cell of the infinite long homogeneous beam coupled with periodic oscillators can be yielded as follows:

$(\mathit{A}\mathit{P}\mathit{U}+\mathit{D})\mathit{d}=\mathbf{0}(34)$

where R = APU + D denotes the reverberation-ray matrix of the periodic beam-oscillators coupling system.

In order to obtain the non-zero solution of the global leaving wave amplitude vector d, namely, the determinant of the reverberation-ray matrix R must be zero, which is

$\det \left(R\right)=\mathbf{0}(35)$

Thus, the relationship of the flexural wave number q and frequency f in the unit cell of the proposed infinite long homogeneous beam coupled with periodic oscillators can be solved by Eq. 34, which is the flexural wave dispersion relations and vibration band gaps of the proposed periodic beam-oscillators coupling system.

3 Results and Discussions

3.1 Bad Gaps Characteristics in Homogeneous Beam Coupled With Periodic Oscillators

This section calculates and analyses the flexural wave band gaps and vibration attenuation characteristics in the proposed homogeneous beam coupled with periodic oscillators. In order to facilitate the band gaps characteristics study and the effects analysis of the parameters on band gaps characteristics, as a calculation example study, the material parameters of the homogeneous beam are considered as: the Young’s modulus E = 2.1 × 10¹¹ Pa, mass density ρ = 7850 kg/m³ and Poisson’s ratio ν = 0.28. And geometrical parameters of the homogeneous beam and periodic oscillators are presented in Table 1.

TABLE 1

TABLE 1. The parameters of homogeneous beam and periodic oscillators in the calculation example study, in which the subscript 0 is defined to distinguish the calculation example study and parametric study.

According to the flexural wave band gaps calculation method obtained in the previous section, Figure 2A shows the band gaps characteristics calculation results of the proposed infinite long homogeneous beam coupled with periodic oscillators in the calculation example study, in which the left vertical axis and the right vertical axis are the frequency and normalized frequency of the flexural wave. The normalized frequency is defined as $f{a}_0/c_T$ to obtain more general results, in which the $c_T$ is the transversal wave speed in steel which the value is 3140 m/s. It is clear that in the frequency range of 0–1500 Hz, there are two band gaps of 0–198.3 Hz and 522.8–592.3 Hz in the proposed periodic beam-oscillators coupling system, and which the bandwidths are 198.3 Hz and 69.5 Hz, respectively.

FIGURE 2

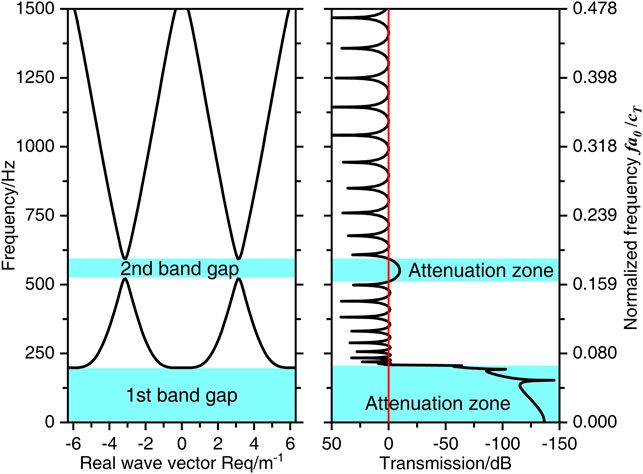
FIGURE 2. (A) The flexural wave band gaps characteristics of the infinite long homogeneous beam coupled with periodic oscillators. (B) The flexural wave vibration transmission spectrum of the finite long homogeneous beam coupled with periodic oscillators with 12 unit cells.

3.2 Numerical Calculation Validation Based on Finite Element Method

To verify the effectiveness of the flexural wave band gaps characteristics calculation method obtained in this paper and demonstrate the existences of the flexural wave band gaps and vibration attenuation characteristics in the proposed periodic beam-oscillators coupling system, a structural dynamic characteristic analysis of a finite long homogeneous beam coupled with periodic oscillators with 12 unit cells based on finite element method is conducted in this section. The flexural wave band gaps and vibration attenuation characteristics of various periodic structures had been analyzed by the numerical calculation of the finite array periodic structures, the numerical calculation method is an effective and efficient calculation method of band gaps and vibration attenuation characteristics and has been widely used to demonstrate the effectiveness of the band gaps calculation methods (Waki et al., 2009; Zhou et al., 2015; Nobrega et al., 2016; Xiang et al., 2020). As shown in Figure 3A, the finite array finite element model with 12 unit cells of the proposed periodic beam-oscillators coupling system is established in Abaqus CAE at the beginning of the numerical calculation, the finite element model is constituted of a homogeneous beam with a rectangular section and coupled with 12 periodic oscillators in parallel connection, which the separation distance is 1.0 m and each unit cell contains 400 beam elements, the vibration direction of the periodic oscillators is vertical direction and the length direction of the homogeneous beam is along X-axis with 12.0 m dimensions. The structural and material parameters of the finite element model are the same with those in the calculation example study in the previous section. The left end of the finite element model is vertically excited by the unit sweep excitation force of 0–1500 Hz with 1 Hz frequency interval during the numerical calculation, the vertical vibration velocity responses of the nodes near the excitation point was used to detect the incident vibration wave signal while those of the nodes near the right end was used to probe the transmitted vibration wave signal, thus the vertical vibration velocity responses of the nodes at both ends of the beam are extracted to detect the vibration transmission spectrum of the flexural wave in the homogeneous beam coupled with periodic oscillators. The sketch map of the excitation force and velocity response are illustrated in Figure 3A. At last, the flexural wave vibration attenuation characteristics at particular frequencies are captured and presented in Figures 3B–D. After the vibration signal processing and spectral analysis, the band gaps and vibration attenuation characteristics of the flexural wave in the periodic beam-oscillators coupling system are represented by the vibration transmission spectrum drawn in Figure 2B.

FIGURE 3

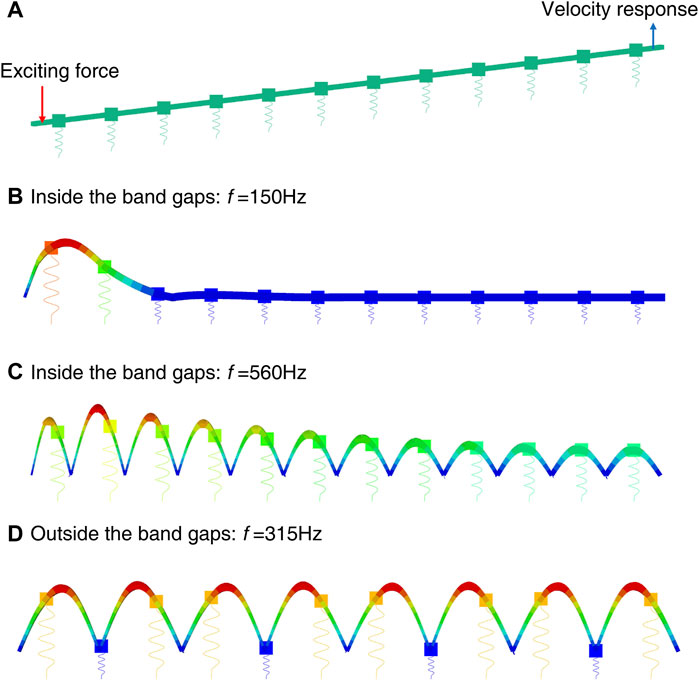
FIGURE 3. (A) Finite element model of the finite long homogeneous beam coupled with periodic oscillators with 12 unit cells; (B–D) The flexural wave vibration attenuation characteristics at particular frequencies.

Calculation results show the existences of two significant vibration attenuation bands in the frequency bands from 0 to 209 Hz and from 511 to 594 Hz respectively in light blue regions as illustrated in Figure 2B, which the bandwidths and locations of the vibration attenuation bands are well consistent with the corresponding flexural wave band gaps, thus the calculation method of flexural wave band gaps characteristics obtained in this paper is validated. The vertical vibration velocity responses at the right part of the beam at 150 and 560 Hz in Figures 3B,C show obvious vibration attenuations, it can be concluded that the propagation of flexural wave in particular frequencies is prohibited, which the effectiveness of the numerical verification method is also further proved. Furthermore, compared the calculation results in Figures 3B–D, the significant reduction of structural vibration in Figures 3B,C indicate that band gaps and vibration attenuations of the flexural wave can appear in the homogeneous beam coupled with periodic oscillators. Different from the vibration attenuations caused by the damping of traditional materials, the vibration attenuation in band gaps frequency ranges of the flexural wave in periodic structures have relatively larger attenuation. The vibration attenuations in band gaps are caused by Bragg reflection and local resonance, which are mainly determined by the periodicity of the periodic structures and the local resonance of the microstructure, respectively. Whereas, as absorbing and consuming the energy of structural vibration is the properties of material damping, the vibration attenuations caused by material damping are appear in all frequency range while the main effective region is medium/high frequency with smaller attenuation amplitudes than those attenuation amplitudes in band gaps frequency ranges.

3.3 Parametric Study

During the parametric studies, the control variable method is used to calculate the flexural wave dispersion relations of the homogeneous beam coupled with periodic oscillators with different parameters values, and then the effects of the parameters on the flexural wave band gaps and vibration attenuation characteristics are studied in this section.

3.3.1 Effect of Spring Stiffness on the Band Gaps Characteristics

In order to study the effects of periodic oscillators spring stiffness k_s on the band gaps characteristics of the flexural wave, the ratio of k_sdim = k_s/k_s0 is defined as dimensionless spring stiffness to realize the dimensionless parameters study, where k_s0 = 5.0 × 10⁷ N/m is the spring stiffness in the calculation example study. During the calculation, the k_sdim gradually increases from 10⁻⁴ to 10⁴ while the material parameters and geometrical parameters of the periodic beam-oscillators coupling system keep constant. The effects of periodic oscillators spring stiffness k_s on the flexural wave band gaps with different k_sdim are illustrated in Figure 4.

FIGURE 4

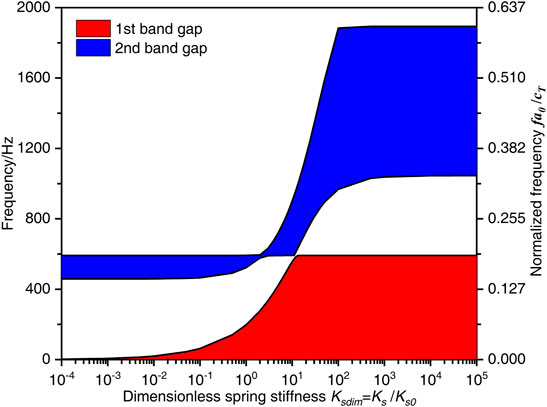
FIGURE 4. The flexural wave band gaps characteristics with different dimensionless spring stiffness k_sdim parameters.

It can be observed from Figure 4 that the spring stiffness k_s has significant influences on the band gaps characteristics of the flexural wave. Which the band gaps increase to a high-frequency region in a multistep manner when the dimensionless spring stiffness k_sdim increases. For the first band gap of the flexural wave in the periodic beam-oscillators coupling system, when the k_sdim increases in the range from 10⁻⁴ to 10⁵, the lower limit frequency remains constant at 0 Hz, while the upper limit frequency accelerated increases to about 592 Hz when the k_sdim = 15, and then keeps constant with the k_sdim in the range from 15 to 10⁵. As the lower limit frequency maintains invariable at 0 Hz, the bandwidth of the first band gap accelerated increases to about 592 Hz and then keeps constant at about 592 Hz when the k_sdim in the range from 15 to 10⁵. This change phenomenon is because the formation mechanism of the first band gap, which is determined by the local resonance of the periodic oscillators, therefore the increase of k_sdim causes the eigenfrequency of the periodic oscillators to increase and resulting in the band gap shifts to a high-frequency region, and there is a critical frequency value f = 590 Hz which is caused by the coupling effects of the periodic oscillators and the homogeneous beam.

The second band gap increase to a high-frequency region in a multistep manner with the dimensionless spring stiffness k_sdim increases from 10⁻⁴ to 10⁵. At the beginning, the lower limit frequency keeps at about 460 Hz unchanged when the k_sdim in the range of 10⁻⁴∼10⁻¹ and gradually increases to 519 Hz when the k_sdim is 3, and then keeps constant when the k_sdim in the range of 3–11, subsequently, the lower limit frequency gradually increases to about 1040 Hz when the k_sdim is 10³ and keeps invariant at last when the k_sdim is in the range from 10³ to 10⁵. The upper limit frequency gradually increases to 1894 Hz from 591 Hz when the k_sdim is in the range of 2∼10², while keeps constant at 591 Hz and about 1894 Hz when the k_sdim are 10⁻⁴∼2 and 10²∼10⁵, respectively. Therefore, the bandwidth of the second band gap maintains invariable at 134 Hz at the beginning, and after that decreases to the minimum value at 42 Hz when the k_sdim = 3, subsequently, the bandwidth gradually increases to 916 Hz when the k_sdim is 100 and then keeps constant at about 850 Hz when the k_sdim in the range of 500∼10⁵. This phenomenon can be explained that the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam. The reaction forces of the periodic oscillators acting on the homogeneous beam increases when the spring stiffness k_s increases, resulting in the increase of the bending stiffness of the homogeneous beam, which leads to an increase in the eigenfrequency of the proposed homogeneous beam coupled with periodic oscillators.

3.3.2 Effect of Periodic Oscillators Mass on the Band Gaps Characteristics

The effects of the periodic oscillators mass m_s on the flexural wave band gaps characteristics in the proposed periodic beam-oscillators coupling system are obtained in Figure 5, in which the dimensionless mass m_sdim = m_s/m_s0 is the ratio of the mass of the periodic oscillators to the one m_s0 defined in the calculation example study and takes the value from 0.1 to 3.0.

FIGURE 5

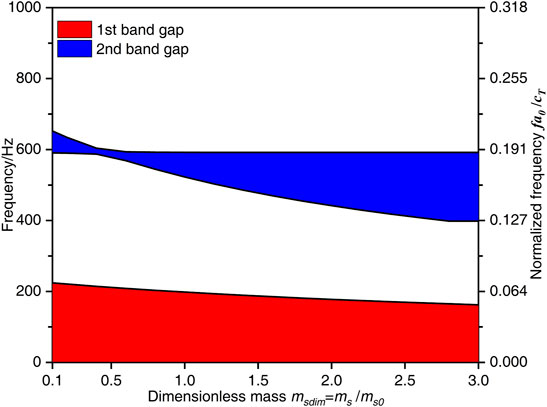
FIGURE 5. The flexural wave band gaps characteristics with different dimensionless mass m_sdim parameters.

It can be seen that, the two band gaps of the flexural wave in the proposed homogeneous beam coupled with periodic oscillators move to the low frequency region in different forms when the dimensionless mass m_sdim increases from 0.1 to 3.0. For the first flexural wave band gap, as the lower limit frequency keeps constant at 0 Hz, and the upper limit frequency gradually decreases from 224 to 162 Hz when the dimensionless mass m_sdim in the range of 0.1–3.0, thus, the bandwidth also gradually decreases from 224 to 162 Hz. This change phenomenon is because the formation mechanism of the first band gap, which is determined by the local resonance of the periodic oscillators, therefore the increase of m_sdim causes the eigenfrequencies of the periodic oscillators to decrease and resulting in the band gap moves to a low-frequency region.

For the second flexural wave band gap, the lower limit frequency keeps constant at 590 and 398 Hz when the dimensionless mass m_sdim increase from 0.1 to 0.4 and 2.8 to 3.0, respectively, while gradually decreases when the m_sdim increases from 0.4 to 2.8. The upper limit frequency gradually decreases from 652 to 592 Hz when the m_sdim increases from 0.1 to 0.8 and then remains unchanged at last. Therefore, the bandwidth of the second flexural wave band gap decreases to the minimum value of 16.9 Hz when the m_sdim = 0.4, and then slowly increases to about 193 Hz when the m_sdim = 2.8 and no longer changes at last. This phenomenon can be explained that the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam. The reaction forces of the periodic oscillators acting on the homogeneous beam decreases when the mass m_s increases, resulting in the decrease of the bending stiffness of the homogeneous beam, which leads to an reduce in the eigenfrequency of the proposed homogeneous beam coupled with periodic oscillators, and there also has a critical frequency value f = 590 Hz.

3.3.3 Effect of Lattice Constant on the Band Gaps Characteristics

Figure 6 demonstrates the effects of the lattice constant a on the flexural wave band gaps characteristics in the infinite long homogeneous beam coupled with periodic oscillators, in which the dimensionless lattice constant a_dim = a/a₀ is the ratio of the lattice constant of the periodic beam-oscillators coupling system to the one a₀ defined in the calculation example study and takes the value from 0.1 to 3.0.

FIGURE 6

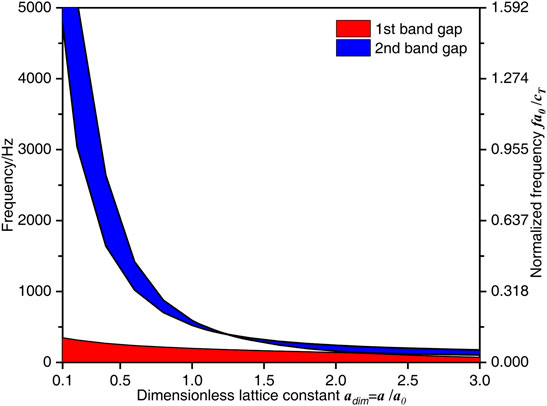
FIGURE 6. The flexural wave band gaps characteristics with different dimensionless lattice constant a_dim parameters.

It can be found from Figure 6 that the increase of the dimensionless lattice constant a_dim moves both the two band gaps of the flexural wave to the low-frequency region by different ways. For the first band gap of the flexural wave in the proposed periodic beam-oscillators coupling system, as the lower limit frequency keeps constant at 0 Hz, the upper limit frequency or the bandwidth reduces from 350 to 73 Hz when the a_dim decreases from 0.1 to 3.0. For the second band gap of the flexural wave, both the lower limit frequency and upper limit frequency rapidly decrease when the a_dim in the range of 0.1–1.25, and then gradually decreases when the a_dim in the range of 1.25–3.0, the bandwidth decreases in the beginning and then gets the local minimum value of 6.5 Hz when the a_dim = 1.25, and then increases to about 80 Hz at last. This phenomenon can be explained that the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam, since the wavelength corresponding to the intermediate frequency of the band gap of the flexural wave in the periodic structure is about twice the lattice constant according to the Bragg scattering theory, the increase of a_dim causes the band gap of the flexural wave to move to a low-frequency region.

3.3.4 Effect of Periodic Oscillators Damping on the Band Gaps Characteristics

Figure 7 shows the effects of periodic oscillators damping c_s on the band gaps characteristics of the flexural wave, in which the dimensionless periodic oscillators damping ratio c_sdim = c_s/c_sc is the ratios of the periodic oscillators damping of the periodic beam-oscillators coupling system to the critical damping c_sc which is defined as $c_{sc}=2\sqrt{k_s{m}_s}=40000N\cdot \raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$m$}\right.$ and takes the value from 0 to 0.2.

FIGURE 7

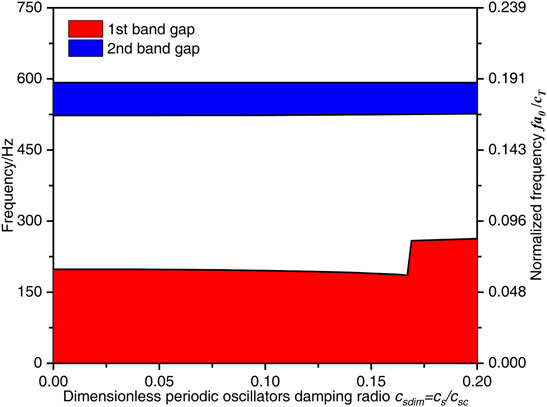
FIGURE 7. The flexural wave band gaps characteristics with different dimensionless periodic oscillators damping ratio c_sdim parameters.

It can be observed from Figure 7 that, the increase of the dimensionless periodic oscillators damping ratio c_sdim has little effect on the second band gap of the flexural wave, whereas the upper limit frequency (the bandwidth) of the first band gap of the flexural wave slowly decreases from 199 to 185Hz when the dimensionless periodic oscillators damping ratio c_sdim in the range of 0–0.168, after that it has a big jump growth to 259 Hz when the c_sdim = 0.17 and then increases to 262 Hz at last. The increase of the c_sdim causes the upper limit frequency of the first band gap to decrease in the beginning is because the formation mechanism of the first band gap, which the increase of c_sdim causes the translational stiffness coefficient of the periodic oscillators acting on the beam to decrease. While the jump growth when the c_sdim in the in the range of 0.17–0.20 is because the larger periodic oscillators damping absorbs and consumes the energy of the flexural wave in specific frequency range.

3.3.5 Effect of Section Moment of Inertia on the Band Gaps Characteristics

The effects of the section moment of inertia I on the flexural wave band gaps characteristics in the proposed periodic beam-oscillators coupling system are illustrated in Figure 8 in which the dimensionless section moment of inertia I_dim = I/I₀ is the ratio of the section moment of inertia of the homogeneous beam to the one I₀ defined in the calculation example study and takes the value from 0.01 to 5.0.

FIGURE 8

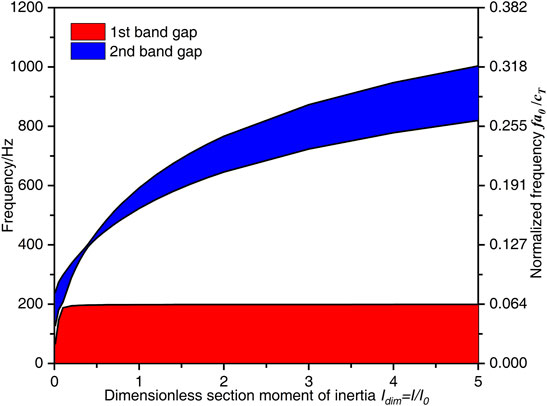
FIGURE 8. The flexural wave band gaps characteristics with different dimensionless section moment of inertia I_dim parameters.

It can be found from Figure 8 that the lower limit frequency and upper limit frequency of the first flexural wave band gap almost keep constant, while the second flexural wave band gap has a significant increase and moves up to the high-frequency region. The lower limit frequency or the bandwidth of the first flexural wave band gap rapidly increases from 66 to 198 Hz when the I_dim increases from 0.01 to 0.4 and then keeps invariant. The lower limit frequency and upper limit frequency of the second flexural wave band gap significantly increase from 128 to 819 Hz and 240–1003 Hz when the I_dim in the range 0.01–5.0, respectively, which the bandwidth of the second band gap gradually decreases to the minimum value of 9.3 Hz when the I_dim = 0.4 and then gradually increases to about 184 Hz. This change phenomenon is because the formation mechanism of the first band gap, which is determined by the local resonance of the periodic oscillators, while the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam. The increase of the I_dim causes bending stiffness of the homogeneous beam to enhance and leads to an increase in the eigenfrequency of the homogeneous beam while can not change the eigenfrequency of the periodic oscillators.

3.3.6 Effect of Section Area on the Band Gaps Characteristics

Figure 9 demonstrates the effects of the section area A on the band gaps characteristics of the flexural wave in the homogeneous beam of the periodic beam-oscillators coupling system, in which the dimensionless section area A_dim = A/A₀ is the ratio of the section area of the homogeneous beam to the one A₀ defined in the calculation example study and takes the value from 0.01 to 5.0.

FIGURE 9

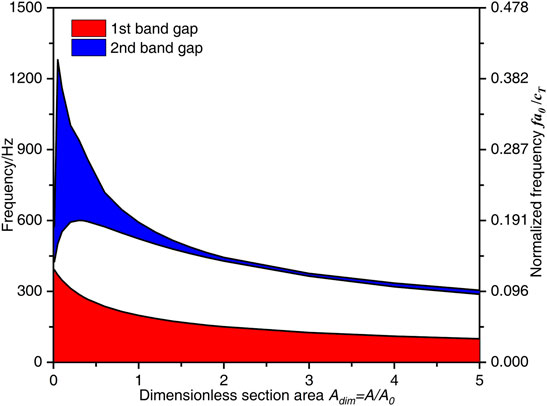
FIGURE 9. The flexural wave band gaps characteristics with different dimensionless section area Adim parameters.

The Figure 9 shows that the lower limit frequency (the bandwidth) of the first band gap of the flexural wave shift to a low-frequency region, whereas the lower limit frequency and the upper limit frequency of the second band gap of the flexural wave increase first and then move to a low-frequency region. To be specific, the lower limit frequency or the bandwidth of the first band gap decreases from 392 to about 100 Hz when the A_dim decreases from 0.01 to 5.0. The lower limit frequency of the second band gap gradually increases from 426 Hz to the maximum value of 600.8 Hz when the A_dim increases from 0.01 to 0.3, and then gradually decreases to 288 Hz at last, as the same, the upper limit frequency rapidly increases from 575 Hz to the maximum value of 1280.3 Hz when the A_dim increases from 0.01 to 0.05 and then gradually decreases to 305 Hz in the end. Therefore, the bandwidth of the second flexural wave band gap increases to the maximum value of 778.3 Hz, and then rapidly decreases to about 12 Hz at last. This change phenomenon is because the formation mechanism of the first band gap, which is determined by the local resonance of the periodic oscillators, while the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam. The increase of the A_dim causes both the mass of the periodic oscillators and the bending stiffness of the homogeneous beam to reduce, which leads to the decrease in the eigenfrequencies of the periodic oscillators and the homogeneous beam, respectively.

3.3.7 Effect of Material Parameters on the Band Gaps Characteristics

To investigate the effect of material parameters of the homogeneous beam on the band gaps characteristics of the flexural wave in the periodic beam-oscillators coupling system, change the material of the homogeneous beam as steel, copper as well as aluminum, which the material parameters of the homogeneous beam are shown in Table 2, and the other geometrical parameters are the same as those defined in the calculation example study and listed in Table 1. Figure 10 respectively obtained the effects of different material parameters on the band gaps characteristics of the flexural wave, in which the normalized frequency $f{a}_0/c_T$ is the ratio of the $f{a}_0$ to the transversal wave speed in steel, copper or aluminum, and the values are 3140, 2260, and 3080 m/s, respectively.

TABLE 2

TABLE 2. The material parameters of the homogeneous beam.

FIGURE 10

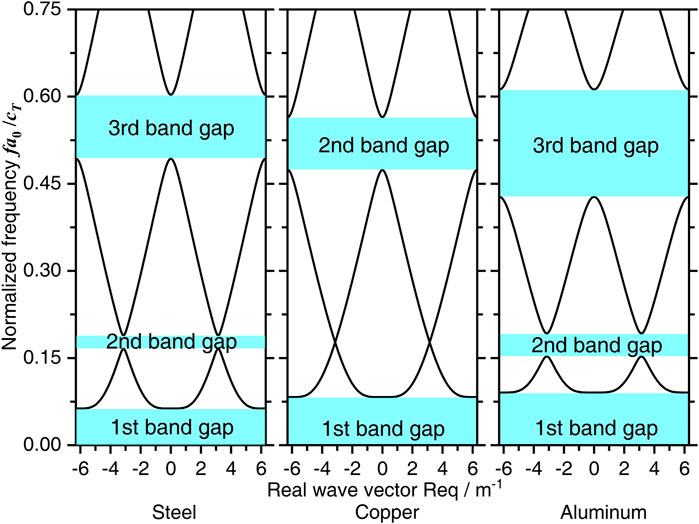
FIGURE 10. The flexural wave band gaps characteristics with different homogeneous beam material properties.

It can be observed from Figure 10 that, when the normalized frequency $f{a}_0/c_T$ in the range of 0–0.75, there are three flexural wave band gaps in the infinite long homogeneous beam coupled with periodic oscillators when the material of the homogeneous beam is steel or aluminum, while it only has two flexural wave band gaps when the homogeneous beam material is copper. The lower limit frequencies or the bandwidths are similar when the material is copper and aluminum, which are higher than that when the material is steel. The locations and bandwidths of the second flexural wave band gap are similar when the material is steel and aluminum, which the normalized band gaps are 0.166–0.189 and 0.153–0.192, respectively. The third flexural wave band gap locations of the steel and aluminum are almost similar to those of the second band gap when the material is copper, which the normalized lower limit frequencies are 0.493, 0.474, 0.428 and the normalized upper limit frequencies are 0.603, 0.565, 0.612 respectively when the material is steel, copper and aluminum.

4 Conclusion

In this paper, we propose a periodic beam-oscillators coupling system as the simple physical model for analyzing the dynamic characteristics of periodic support beams and low-frequency flexural wave vibration of slender stiffened plate structures in ship and offshore structures, the calculation method for the flexural wave band gaps in the proposed infinite long homogeneous beam coupled with periodic oscillators is established by the method of reverberation-ray matrix combined with Bloch theorem. The effectiveness of the flexural wave band gaps theoretical calculation method has been verified by the numerical results expressed by the flexural wave vibration transmission spectrum. Parametric studies show that the flexural wave band gaps can be adjusted and optimized manually by adjusting structural and material parameters. The studies are of great guiding significance for the vibration and noise control design of periodic support beams and slender stiffened plate structures, such as the 1D periodic structures in high-speed railway, building foundations, bridge structures, ships and offshore structures, and the 2D periodic stiffened plates in bridge structures, ships and offshore structures. The main conclusions are as follows:

1) The formation mechanism of the first band gap, which is determined by the local resonance of the periodic oscillators, while the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam. As the lower limit frequency of the first flexural wave band gap keeps constant at 0 Hz, it is conducive to the application of the flexural wave band gap characteristics to the low-frequency vibration and noise control of the periodic structure.

2) As can be seen from the studies of the effects of spring stiffness and mass of the periodic oscillators on the flexural wave band gap characteristics, there is a critical frequency value f = 590 Hz, the lower limit frequency and upper limit frequency of the second band gap remains constant at about 590 Hz when the k_sdim in the range of 10⁻⁴∼2 and 3–11, respectively. Similar to this, the initial frequency and the terminal frequency of the second band gap keep constant at about 590 Hz when the m_sdim in the range of 0.1–0.4 and 0.8–3.0, respectively. This phenomenon can be explained that the second band gap is determined by the coupling effects between the Bragg scattering of periodic oscillators and the propagation of the flexural wave in homogeneous beam.

3) The effects of periodic oscillators damping on the first flexural wave band gap is due to the increase of c_sdim causes the translational stiffness coefficient of the periodic oscillators acting on the beam to decrease.

4) With the dimensionless section moment of inertia I_dim increase, the frequencies of the second band gap have significant gradually increase while those of the first band gap almost keep constant. It is conducive to artificially modulating and optimizing the second band gap characteristic by tuning the section moment of inertia I.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

XY conceived the idea of the manuscript. LT and GW developed the theoretical formulations and the numerical simulation. LT and CW wrote and edited the manuscript. All authors conducted subsequent improvements to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (Nos 51979054 and 51809054).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, S., Shu, H., Liang, S., Shi, X., and Zhao, L. (2018). Band gap Characteristics of Radial Wave in a Two-Dimensional Cylindrical Shell with Radial and Circumferential Periodicities. Aip Adv. 8 (3), 035110. doi:10.1063/1.5023734

CrossRef Full Text | Google Scholar

Chen, T., and Chen, B. (1991). Ship Structural Mechanics. Shanghai Jiaotong University Press.

Google Scholar

Dupont, G., Movchan, A., Enoch, S., and Guenneau, S. (2019). Analysis of Low Frequency Acoustic Stop Bands in Cubic Arrays of Thick Spherical Shells with Holes. Front. Mater. 6 (50). doi:10.3389/fmats.2019.00050

CrossRef Full Text | Google Scholar

Enferadi, M. H., Ghasemi, M. R., and Shabakhty, N. (2019). Wave-induced Vibration Control of Offshore Jacket Platforms through SMA Dampers. Appl. Ocean Res. 90, 101848. doi:10.1016/j.apor.2019.06.005

CrossRef Full Text | Google Scholar

Faiz, M. S., Addouche, M., Zain, A. R. M., Siow, K. S., Chaalane, A., and Khelif, A. (2020). Experimental Demonstration of a Multichannel Elastic Wave Filter in a Phononic Crystal Slab. Appl. Sci. 10 (13), 4594. doi:10.3390/app10134594

CrossRef Full Text | Google Scholar

Gripp, J. A. B., and Rade, D. A. (2018). Vibration and Noise Control Using Shunted Piezoelectric Transducers: A Review. Mech. Syst. Signal Process. 112, 359–383. doi:10.1016/j.ymssp.2018.04.041

CrossRef Full Text | Google Scholar

Guo, Y. Q., and Fang, D. N. (2014). Analysis and Interpretation of Longitudinal Waves in Periodic Multiphase Rods Using the Method of Reverberation-Ray Matrix Combined with the Floquet-Bloch Theorem. J. Vibration Acoustics-Transactions Asme 136 (1). doi:10.1115/1.4025438

CrossRef Full Text | Google Scholar

Guo, Y. Q., and Fang, D. N. (2011). Formation of Longitudinal Wave Band Structures in One-Dimensional Phononic Crystals. J. Appl. Phys. 109 (7), 073515. doi:10.1063/1.3567911

CrossRef Full Text | Google Scholar

Han, J., Kitazawa, D., Kinoshita, T., Maeda, T., and Itakura, H. (2019). Experimental Investigation on a Cabin-Suspended Catamaran in Terms of Motion Reduction and Wave Energy Harvesting by Means of a Semi-active Motion Control System. Appl. Ocean Res. 83, 88–102. doi:10.1016/j.apor.2018.12.003

CrossRef Full Text | Google Scholar

He, Z. C., Xiao, X., and Li, E. (2017). Design for Structural Vibration Suppression in Laminate Acoustic Metamaterials. Composites B: Eng. 131, 237–252. doi:10.1016/j.compositesb.2017.07.076

CrossRef Full Text | Google Scholar

Hirdaris, S. E., Bai, W., Dessi, D., Ergin, A., Gu, X., Hermundstad, O. A., et al. (2014). Loads for Use in the Design of Ships and Offshore Structures. Ocean Eng. 78 (1), 131–174. doi:10.1016/j.oceaneng.2013.09.012

CrossRef Full Text | Google Scholar

Ibrahim, R. A. (2008). Recent Advances in Nonlinear Passive Vibration Isolators. J. Sound Vibration 314 (3), 371–452. doi:10.1016/j.jsv.2008.01.014

CrossRef Full Text | Google Scholar

Kandasamy, R., Cui, F., Townsend, N., Foo, C. C., Guo, J., Shenoi, A., et al. (2016). A Review of Vibration Control Methods for marine Offshore Structures. Ocean Eng. 127 (nov15), 279–297. doi:10.1016/j.oceaneng.2016.10.001

CrossRef Full Text | Google Scholar

Keir, J., Kessissoglou, N. J., and Norwood, C. J. (2005). Active Control of Connected Plates Using Single and Multiple Actuators and Error Sensors. J. Sound Vibration 281 (1-2), 73–97. doi:10.1016/j.jsv.2004.01.007

CrossRef Full Text | Google Scholar

Kim, H.-G., Nerse, C., and Wang, S. (2019). Topography Optimization of an Enclosure Panel for Low-Frequency Noise and Vibration Reduction Using the Equivalent Radiated Power Approach. Mater. Des. 183, 108125. doi:10.1016/j.matdes.2019.108125

CrossRef Full Text | Google Scholar

Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 71 (13), 2022–2025. doi:10.1103/physrevlett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Lan, C.-C., Yang, S.-A., and Wu, Y.-S. (2014). Design and experiment of a Compact Quasi-Zero-Stiffness Isolator Capable of a Wide Range of Loads. J. Sound Vibration 333 (20), 4843–4858. doi:10.1016/j.jsv.2014.05.009

CrossRef Full Text | Google Scholar

Lee, S., Ahn, C. H., and Lee, J. W. (2018). Vibro-acoustic Metamaterial for Longitudinal Vibration Suppression in a Low Frequency Range. Int. J. Mech. Sci. 144, 223–234. doi:10.1016/j.ijmecsci.2018.05.010

CrossRef Full Text | Google Scholar

Li, B., and Yang, H. (2020). Design of Active Vibration Reduction System for Intelligent Ship Mechanical Equipment. J. Coastal Res. 115, 235–237. doi:10.2112/jcr-si115-074.1

CrossRef Full Text | Google Scholar

Li, L., and Guo, Y. (2016). Analysis of Longitudinal Waves in Rod-type Piezoelectric Phononic Crystals. Crystals 6 (4), 45. doi:10.3390/cryst6040045

CrossRef Full Text | Google Scholar

Li, X. Y., Zhao, X., and Li, Y. H. (2014). Green's Functions of the Forced Vibration of Timoshenko Beams with Damping Effect. J. Sound Vibration 333 (6), 1781–1795. doi:10.1016/j.jsv.2013.11.007

CrossRef Full Text | Google Scholar

Liu, B., and Yang, L. (2017). Transmission of Low-Frequency Acoustic Waves in Seawater Piping Systems with Periodical and Adjustable Helmholtz Resonator. Jmse 5 (4), 56. doi:10.3390/jmse5040056

CrossRef Full Text | Google Scholar

Liu, C., Jing, X., and Li, F. (2015). Vibration Isolation Using a Hybrid Lever-type Isolation System with an X-Shape Supporting Structure. Int. J. Mech. Sci. 98, 169–177. doi:10.1016/j.ijmecsci.2015.04.012

CrossRef Full Text | Google Scholar

Liu, G., Lu, K., Zou, D., Xie, Z., Rao, Z., and Ta, N. (2017). Development of a Semi-active Dynamic Vibration Absorber for Longitudinal Vibration of Propulsion Shaft System Based on Magnetorheological Elastomer. Smart Mater. Struct. 26 (7), 075009. doi:10.1088/1361-665X/aa73f3

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289 (5485), 1734–1736. doi:10.1126/science.289.5485.1734.%.J.Science

PubMed Abstract | CrossRef Full Text | Google Scholar

Mead, D. J. (1970). Free Wave Propagation in Periodically Supported, Infinite Beams. J. Sound Vibration 11 (2), 181–197. doi:10.1016/S0022-460X(70)80062-1

CrossRef Full Text | Google Scholar

Mead, D. M. (1996). Wave Propagation in Continuous Periodic Structures: Research Contributions from Southampton, 1964-1995. J. Sound Vibration 190 (3), 495–524. doi:10.1006/jsvi.1996.0076

CrossRef Full Text | Google Scholar

Muhammad, , and Lim, C. W. (2019). Elastic Waves Propagation in Thin Plate Metamaterials and Evidence of Low Frequency Pseudo and Local Resonance Bandgaps. Phys. Lett. A 383 (23), 2789–2796. doi:10.1016/j.physleta.2019.05.039

CrossRef Full Text | Google Scholar

Murawski, L., and Charchalis, A. (2014). Simplified Method of Torsional Vibration Calculation of marine Power Transmission System. Mar. Structures 39, 335–349. doi:10.1016/j.marstruc.2014.10.004

CrossRef Full Text | Google Scholar

Nateghi, A., Sangiuliano, L., Claeys, C., Deckers, E., Pluymers, B., and Desmet, W. (2019). Design and Experimental Validation of a Metamaterial Solution for Improved Noise and Vibration Behavior of Pipes. J. Sound Vibration 455, 96–117. doi:10.1016/j.jsv.2019.05.009

CrossRef Full Text | Google Scholar

Nobrega, E. D., Gautier, F., Pelat, A., and Dos Santos, J. M. C. (2016). Vibration Band Gaps for Elastic Metamaterial Rods Using Wave Finite Element Method. Mech. Syst. Signal Process. 79, 192–202. doi:10.1016/j.ymssp.2016.02.059

CrossRef Full Text | Google Scholar

Ou, J., Long, X., Li, Q. S., and Xiao, Y. Q. (2007). Vibration Control of Steel Jacket Offshore Platform Structures with Damping Isolation Systems. Eng. Structures 29 (7), 1525–1538. doi:10.1016/j.engstruct.2006.08.026

CrossRef Full Text | Google Scholar

Richards, D., and Pines, D. J. (2003). Passive Reduction of Gear Mesh Vibration Using a Periodic Drive Shaft. J. Sound Vibration 264 (2), 317–342. doi:10.1016/S0022-460X(02)01213-0

CrossRef Full Text | Google Scholar

Sharma, B., and Sun, C. T. (2016). Local Resonance and Bragg Bandgaps in sandwich Beams Containing Periodically Inserted Resonators. J. Sound Vibration 364, 133–146. doi:10.1016/j.jsv.2015.11.019

CrossRef Full Text | Google Scholar

Shen, H., Wen, J., Païdoussis, M. P., Yu, D., Asgari, M., and Wen, X. (2012). Control of Sound and Vibration for Cylindrical Shells by Utilizing a Periodic Structure of Functionally Graded Material. Phys. Lett. A 376 (45), 3351–3358. doi:10.1016/j.physleta.2012.08.048

CrossRef Full Text | Google Scholar

Shi, W., Tan, X., Gao, Z., and Moan, T. (2016). Numerical Study of Ice-Induced Loads and Responses of a Monopile-type Offshore Wind Turbine in Parked and Operating Conditions. Cold Regions Sci. Tech. 123, 121–139. doi:10.1016/j.coldregions.2015.12.007

CrossRef Full Text | Google Scholar

Som, A., and Das, D. (2018). Seismic Vibration Control of Offshore Jacket Platforms Using Decentralized Sliding Mode Algorithm. Ocean Eng. 152, 377–390. doi:10.1016/j.oceaneng.2018.01.013

CrossRef Full Text | Google Scholar

Toky, A., Singh, R. P., and Das, S. (2020). Localization Schemes for Underwater Acoustic Sensor Networks - A Review. Comp. Sci. Rev. 37, 100241. doi:10.1016/j.cosrev.2020.100241

CrossRef Full Text | Google Scholar

Waki, Y., Mace, B. R., and Brennan, M. J. (2009). Numerical Issues Concerning the Wave and Finite Element Method for Free and Forced Vibrations of Waveguides. J. Sound Vibration 327 (1-2), 92–108. doi:10.1016/j.jsv.2009.06.005

CrossRef Full Text | Google Scholar

Wang, T., Sheng, M. P., and Guo, H. B. (2016). Multi-large Low-Frequency Band Gaps in a Periodic Hybrid Structure. Mod. Phys. Lett. B 30, 1650116. doi:10.1142/S0217984916501116

CrossRef Full Text | Google Scholar

Wang, W., Chen, L. Y., and Zhang, Y. F. (2013). Study on Vibration Reduction Design of Steel-Composite Material Hybrid Mounting for Ship Based on Material Selection Optimization. Amr 694-697, 415–424. doi:10.4028/www.scientific.net/amr.694-697.415

CrossRef Full Text | Google Scholar

Waye, K. P. (2011). “Effects of Low Frequency Noise and Vibrations: Environmental and Occupational Perspectives,” in Encyclopedia of Environmental Health. Editor J. Nriagu. Second Edition (Oxford: Elsevier), 264–277. doi:10.1016/b978-0-444-63951-6.00245-x

CrossRef Full Text | Google Scholar

Wu, W., Chen, X., and Shan, Y. (2014). Analysis and experiment of a Vibration Isolator Using a Novel Magnetic spring with Negative Stiffness. J. Sound Vibration 333 (13), 2958–2970. doi:10.1016/j.jsv.2014.02.009

CrossRef Full Text | Google Scholar

Xiang, H., Ma, X., and Xiang, J. (2020). Band Gaps and Transmission Characteristics Analysis on a Two-Dimensional Multiple-Scatter Phononic Crystal Structure. Materials 13 (9), 2106. doi:10.3390/ma13092106

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S.-F., Xu, Z.-L., and Chuang, K.-C. (2021). Hybrid Bandgaps in Mass-Coupled Bragg Atomic Chains: Generation and Switching. Front. Mater. 8 (430). doi:10.3389/fmats.2021.774612

CrossRef Full Text | Google Scholar

Yaman, O., Tuncer, T., and Tasar, B. (2021). DES-pat: A Novel DES Pattern-Based Propeller Recognition Method Using Underwater Acoustical Sounds. Appl. Acoust. 175, 107859. doi:10.1016/j.apacoust.2020.107859

CrossRef Full Text | Google Scholar

Zhou, C. W., Lainé, J. P., Ichchou, M. N., and Zine, A. M. (2015). Wave Finite Element Method Based on Reduced Model for One-Dimensional Periodic Structures. Int. J. Appl. Mech. 07 (2), 1550018. doi:10.1142/s1758825115500180

CrossRef Full Text | Google Scholar

Zhou, X. Q., Yu, D. Y., Shao, X., Wang, S., and Tian, Y. H. (2014). Band gap Characteristics of Periodically Stiffened-Thin-Plate Based on center-finite-difference-method. Thin-Walled Structures 82, 115–123. doi:10.1016/j.tws.2014.04.010

CrossRef Full Text | Google Scholar

Zuo, S., Huang, H., Wu, X., Zhang, M., and Ni, T. (2018). Low-frequency Band gap of Locally Resonant Phononic Crystals with a Dual-Base Plate. The J. Acoust. Soc. America 143 (3), 1326–1332. doi:10.1121/1.5025041

CrossRef Full Text | Google Scholar