- 1State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Xuzhou, China
- 2School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou, China
Honeycomb materials have attracted people’s attention because of their light weight, high specific strength, high specific stiffness, and excellent impact resistance and energy absorption. At present, the specific materials have been widely used in aerospace, transportation, mechanical construction, energy, and chemical industry. The mechanical properties of honeycomb steel with special coating under quasi-static and dynamic compression were studied by using the universal strength testing machine (TAWD-2000) and split Hopkinson pressure bar (SHPB) devices. The results showed that the stress–strain curves obtained from the quasi-static compression experiment showed the characteristics of three typical deformation stages of porous materials: the elastic deformation stage, stress platform stage, and densification stage. Due to the fact that the loading time of the dynamic compression experiment is very short and because of the effect of the sample’s height, there was no densification stage in the stress–strain curves under dynamic loading. The dynamic compression deformation process of the samples was captured by the high-speed photography equipment, and its different deformations and failure modes were analyzed in combination with the characteristics of stress–strain curves. The increasing relationship between the peak stress and strain rate showed the strain rate sensitivity of the honeycomb structure. The dynamic energy absorption characteristics of honeycomb materials were described and analyzed by using the dynamic energy absorption capacity and dynamic energy absorption efficiency. By using finite element simulation software, the same structure of the honeycomb steel was modeled and analyzed to explore the causes of dynamic compression failure. Because of its special mechanical properties and failure modes, this honeycomb structure material will have a broader research and application prospect in the future.
Introduction
With the higher requirements of the engineering technology for industrial production in the modern society, more and more attention has been paid to the research of cushioning and energy-absorbing materials. Porous metal has been applied to various fields as a new structural functional material due to its excellent cushioning, energy absorption, thermal conductivity, flow isolation, and silencing properties (Li et al., 2018; Zhou et al., 2018; Wang et al., 2019). Due to the special structural composition of porous materials, they can be divided into two dimensional porous materials (honeycomb structure) and three dimensional porous materials (foam structure). The honeycomb structure has the advantages of low relative density, low stiffness, and large compression deformation capacity and its controllable deformation (Wang et al., 2014; Yan et al., 2014; Zhao et al., 2015). It is an ideal vibration damping and cushioning material and has broad application prospects in various anti-collision and cushioning structures. Its internal hollow part can also be designed and processed according to the actual application to maximize its functional utilization. In recent decades, scholars at home and abroad have focused on different metal materials such as steel and aluminum honeycomb materials as matrix has been studied in many aspects (Mohr and Doyoyo, 2004; Liu et al., 2019; Wang, 2019), including the material failure mode (Xu et al., 2012; Zuhri et al., 2014; Liu et al., 2016), impact velocity effect (Sibeaud et al., 2008; Wang et al., 2014), and size effect (Zhou and Mayer, 2002; Zhou et al., 2015). The shape, size, and composition of the honeycomb structure have a vital impact on the mechanical properties of honeycomb materials (Gibson and Ashby, 1997; Hohe and Becker, 1999; Hohe et al., 1999). Honeycomb structures mainly include regular hexagon, reinforced regular hexagon, flat hexagon, diamond, rectangle, etc. After relevant demonstration by many scholars, it is found that among materials with the same quality, the regular hexagon structure has the largest volume and the best stiffness and is the most material-saving stable structure.
In recent years, the mainly studied honeycomb samples from scholars are two aspects: honeycomb materials and honeycomb structures. The research methods mainly include experiment and numerical simulation (Hazizan and Cantwell, 2003; ZareiMahmoudabadi and Sadighi, 2011; Zhang et al., 2012; Roy et al., 2014). As for honeycomb materials, Tang et al. proposed to use the aluminum honeycomb skeleton and traditional material Al/PTFE to prepare new energetic materials by a special process, and its dynamic properties were tested by using an SHPB loading system. Under the same impact conditions, compared with traditional materials, the compressive strength and release energy of the new material were significantly improved (Tang et al., 2020). Tomas et al. conducted quasi-static and dynamic uniaxial compression experiments on a special honeycomb steel structure and observed the sample optically. Digital image correlation was used to evaluate the in-plane displacement and strain field. The results showed that the strain rate had a significant effect on the denaturation characteristics of the microstructure (Fíla et al., 2019). In terms of honeycomb structures, Shan et al. studied the dynamic compression characteristics of the aromatic hydrocarbon paper honeycomb with different heights using an SHPB device and studied its failure deformation process combined with the numerical simulation method. It is found that there are two deformation modes: in-plane shear fold and out-of-plane wall buckling, and there will be an abnormal size effect for samples with a certain height (Shan et al., 2019). Hong et al. prepared two kinds of numerical honeycomb materials with different horizontal structures by using the PµSL technology. After studying their dynamic and static load mechanical properties, it is concluded that the collapse strength and energy absorption performance of the materials are related to the level of the honeycomb structure. A multi-level honeycomb has higher collapse strength and better energy absorption performance than a single-level honeycomb. It can be improved to improve the level of honeycomb materials Mechanical properties of high materials (query) (Hong et al., 2020). Many scholars choose to observe the compression deformation behavior of honeycomb structures from the customary scale and find that the overall size, cell size, and wall thickness of honeycomb structures have a great influence on the macro deformation of the sample (Mistou et al., 2000; Wilbert et al., 2011; Seemann and Krause, 2017). The research on honeycomb panels is also a research hotspot at present. The research on the impact compression performance of honeycomb panels mainly depends on the SHPB test and drop weight test (Jin et al., 2007; Liu and Zhang, 2008). Yang et al. studied the static and dynamic compression performance of density gradient grid core sandwich panels by combining experimental and numerical simulations and concluded that the gradient grid had an impact on the failure mechanism of the sandwich panel, and the sandwich panel with an ABC gradient structure had a higher impact strength and energy absorption capacity at a higher impact velocity (Yang et al., 2021). Dharmasena et al. analyzed the mechanical properties of five sandwich structures with the same relative density (including the multilayer pyramid lattice, square honeycomb, triangular honeycomb, triangular ripple, and diamond ripple) under underwater explosion load. The results show that the strength of the lattice core is significantly lower than that of other honeycomb sandwich structures (Dharmasena et al., 2010). Zou et al. tested the mechanical properties of a honeycomb plate under dynamic load and static load, respectively, in-plane and out-of-plane, and studied the mechanical properties of the steel honeycomb plate under transverse dynamic impact load. The results show that for the out-of-plane three-point bending test, the mechanical properties in the L direction are better than that in the W direction, in which the deformation of the honeycomb core plays an important role, but it is important for in-plane bending. The effect of the three-point bending experiment is not obvious (Zou et al., 2009).
The objective of this study is to analyze a honeycomb structure with special coating on the surface. Its matrix material is stainless steel. Compared with aluminum alloy, stainless steel has higher hardness, better corrosion resistance, and heat resistance, which can meet the needs of more practical engineering applications. In order to study the mechanical properties and failure forms of the honeycomb material, the quasi-static and dynamic compression experiments are carried out with a pressure testing machine and an SHPB device. The failure deformation process is photographed by high-speed photography, the dynamic energy absorption characteristics are analyzed, and the failure principle of the same honeycomb steel structure is studied by numerical simulation.
Experiment
Experimental Material
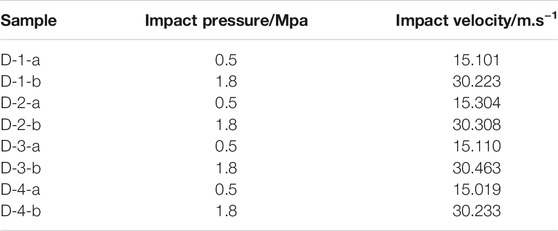
The honeycomb structure used in this experiment is made of stainless steel with specially processed coating materials on the surface. The height of the sample is 48 mm, its thickness is 0.55 mm, its cell length is 7.6 mm, and its weight is 40 g. The specific schematic diagram is shown in Figure 1. Because there are four coating materials used on the sample surface, the sample numbers for the quasi-static compression test are S-1, S-2, S-3, and S-4, and the sample numbers for the dynamic compression test are D-1, D-2, D-3, and D-4. The dynamic load experiment mainly studies the impact velocity of 15 m/s and 30 m/s, and the samples are refined in numbered D-1-a and D-1-b, respectively.
Quasi-Static Compression Tests
The universal strength testing machine (TAWD-2000) was used to conduct the quasi-static compression test on the honeycomb sample. Before the test, the sample was placed between the load application devices, as shown in Figure 2. At the beginning of the test, 1KN prestress is applied to the sample. After the force is stable, the sample was loaded at a displacement loading rate of 5mm/min, and photos were taken to record the test process meanwhile.
Dynamic Compression Tests
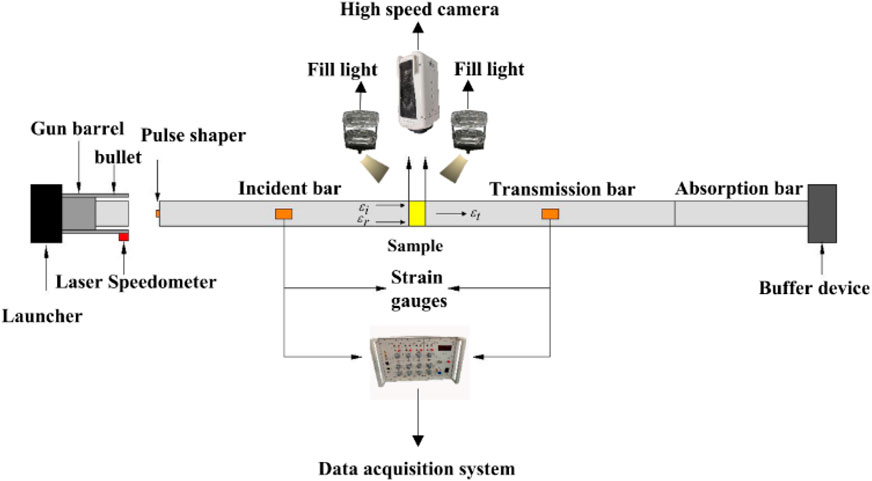
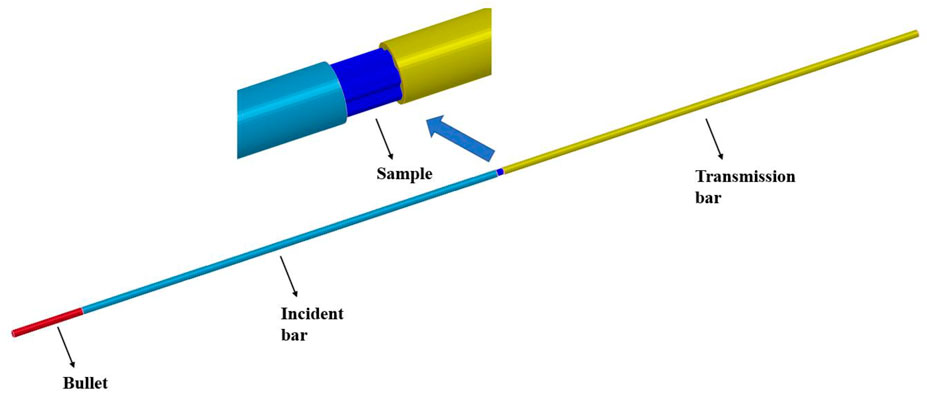
The dynamic compression test of the honeycomb sample is mainly recorded by the dynamic test system composed of the split Hopkinson pressure bar (SHPB) and high-speed photography equipment. The specific schematic diagram of the equipment is shown in Figure 3. The SHPB is the device to characterize the dynamic response of materials deformed at a high strain rate (102–104s−1). It is widely used in the experimental study of dynamic mechanical behavior characteristics of materials under one-dimensional stress state (Mukai et al., 1999; Wang et al., 2015; Deshpande and Fleck, 2020).
The experimental technology of the SHPB is mainly based on two basic assumptions: one is one-dimensional stress wave assumption, which is basically valid when the bar diameter is small, and the other is uniformity assumption, which requires that the stress and strain in the sample are evenly distributed along the length of the sample. The experimental principle is to measure the incident pulse, reflected pulse in the incident bar, and the transmitted pulse in the transmission bar by using strain gauges. Then, the stress–strain relationship of the sample is derived according to the one-dimensional stress wave theory (Marc, 1994). The specific relationship could be given as follows:
where
In this experiment, the SHPB with a diameter of 50 mm is used to carry out the dynamic compression experiment of four honeycomb materials under a high strain rate. The SHPB adopts the dynamic loading mode by releasing the compressed air (nitrogen) stored in the launcher which pushes the bullet to accelerate in the gun of the barrel to impact the incident bar. The bar assembly consists of an incident bar, a transmission bar, an absorption bar, and a buffer device at the end. The corresponding lengths of the 3 bars are 300, 300, and 120 cm, respectively. The bar body is made of silicon manganese spring steel, with an elastic modulus of 210 Gpa, a density of 7.8 g/cm3, and a wave velocity of 5188 m/s. The linear elastic material with high yield strength can ensure the propagation of one-dimensional stress wave in the bar. At the same time, the initial impact velocity of the bullet is recorded by using a laser speedometer, and the experimental data are collected and recorded by the strain gauge symmetrically pasted on the surfaces of the incident bar and the transmission bar and the connected data acquisition system.
During the experiment, the dynamic compression process of the sample was photographed and recorded by high-speed photography equipment. The equipment included high-speed camera and high-intensity fill light. Because the loading time is very short, the shooting mode is set to automatically shoot and record when the high-intensity fill light is turned on, and in order to prevent the test sample from falling off after impact and causing damage to the equipment, the high-speed photography device shall keep a distance of more than 1.5 m from the place where the sample is placed.
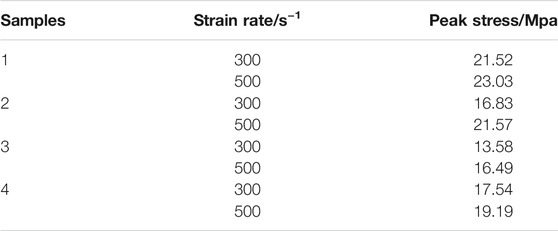
In order to ensure the stress balance and uniform deformation of the sample in the dynamic compression process, the incident wave shaping technology is used before the experiment, and the rubber shaper is pasted at the center of the impact end of the incident bar. The rubber shaper changes the incident waveform by plastic deformation after being impacted by the bullet so as to obtain the incident waveform with long rise time and flat rise front. At the same time, Vaseline is applied on the surface of the bar in contact with the sample to reduce the impact caused by friction. Considering the principle of repetitive experiments, the data with the best experimental effect of each group are selected as the final experimental results for processing. The experimental results are shown in Table 1.
Results and Discussion
Stress–Strain Curve
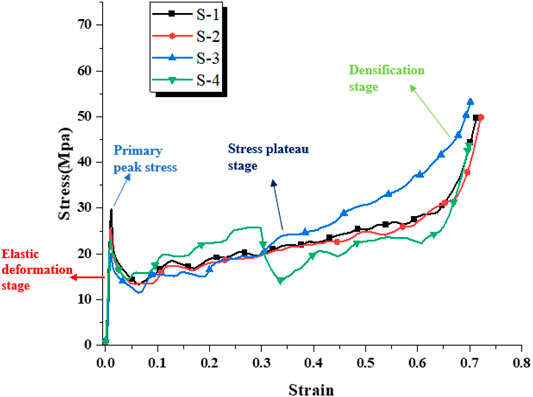
The stress–strain curves of four honeycomb specimens under quasi-static loading are shown in Figure 4. The results in the figure can be obtained that the curves of the four specimens show the characteristics of three stages of typical compression deformation of porous materials: the elastic deformation stage, stress platform stage, and densification stage. In the initial stage of loading, the samples mainly undergo elastic deformation, and the stress increases linearly when reaching the primary peak stress. The stress will decrease rapidly after the peak stress, which is due to the instability and collapse of the cell wall of honeycomb samples, resulting in the reduction of strength. Then, the curve enters the stress platform stage. In the subsequent compression process, the thin-walled structure of the honeycomb sample is continuously folded, resulting in the stress fluctuation up and down. Each peak corresponds to the beginning of a folding process of the cell wall, which is also the main part of the energy absorption of the honeycomb samples. When the cell wall of the whole sample is folded, it begins to enter the densification stage. The folded and buckled honeycomb cell walls contact each other, the internal pores of the sample continue to shrink, and the stress increases rapidly until the pore wall of the sample finally realizes complete densification.
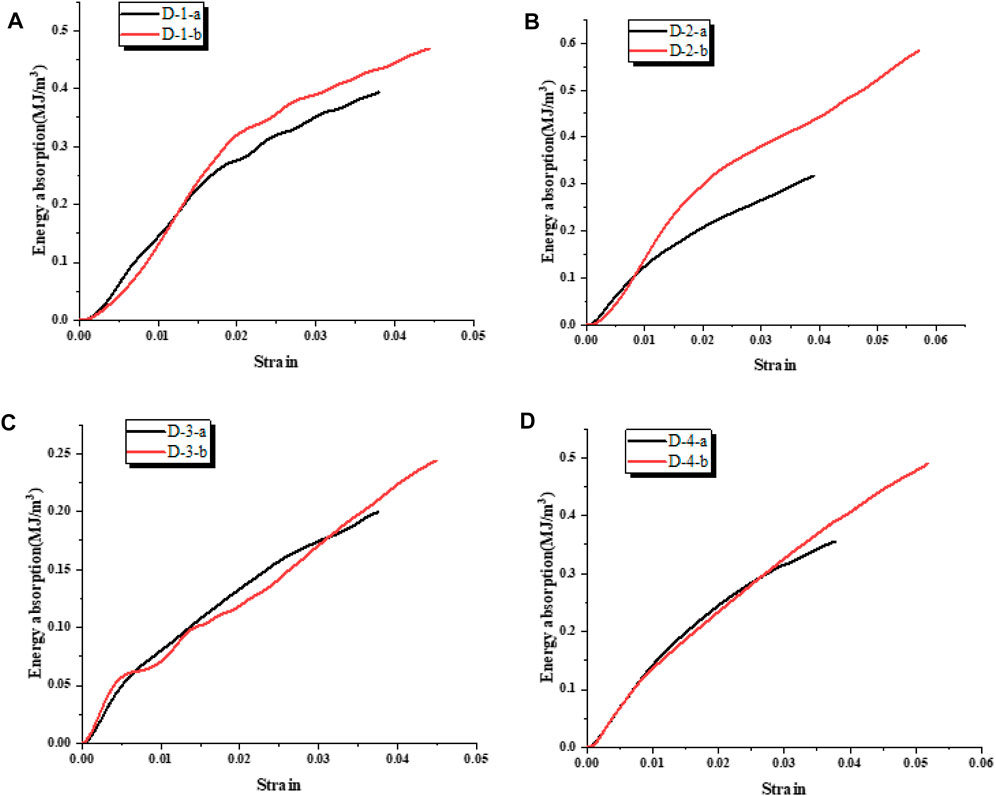
The stress–strain curves of the four samples under dynamic loading are shown in the Figure 5. It can be seen from the figures that the stress–strain curves of the four samples also experienced the elastic deformation stage and stress platform stage, and there was no densification stage in the end. This is mainly because the time of the dynamic compression is very short, the cell wall of samples has not been fully folded and compacted, or the loading has stopped after folding and compaction. Another reason is that it is related to the sample height of honeycomb samples. Liu et al. carried out the impact test with the different heights of the honeycomb samples including 30, 50, and 60 mm and found that there is no densification stage in the stress–strain curve of the sample with the highest height of 60 mm (Liu et al., 2009). It can be seen from the figures that with the increase of impact speed and the strength of dynamic loading, the peak stress of the four samples also increases, and the platform stress stage of the stress–strain curve fluctuates in a higher stress range. Moreover, the peak stress of samples D-1 and D-2 are delayed after the increase of the impact speed, while the peak stress of samples D-3 and D-4 are almost at the same position, and the stress–strain curves of the two samples entering the stress platform stage are advanced compared to samples D-1 and D-2. These phenomena may be related to the different coating materials on the surface of the four honeycomb samples and the compression failure forms. The research on the compression failure forms of honeycomb samples will be described in the next section .
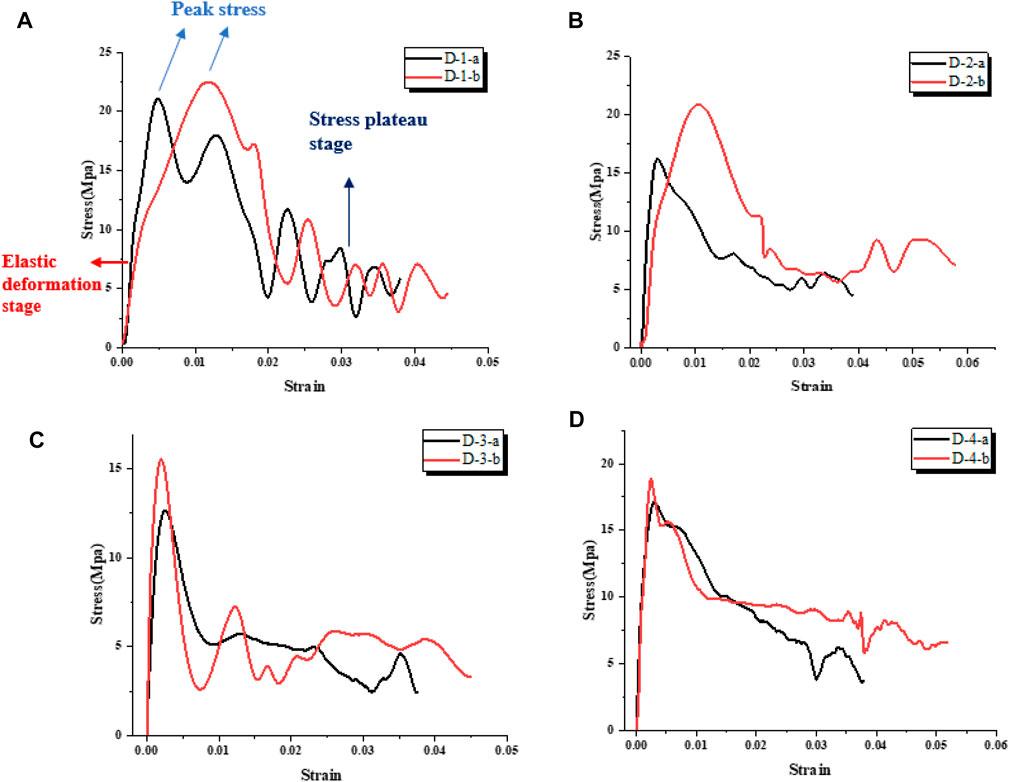
FIGURE 5. Stress–strain curves of dynamic compression experiments. (A) D-1, (B) D-2, (C) D-3, and (D) D-4.
Compression Failure Mode
Figures 6, 7 show the compression failure modes of the quasi-static compression tests and dynamic compression tests, respectively, and this article mainly studies the failure mode under dynamic compression. The failure mode of the honeycomb structures in the process of dynamic compression experiments is studied by using high-speed photography equipment. Figure 7 shows the picture of one frame of the deformation process of four samples taken by high-speed photography in the dynamic compression experiment with an impact speed of 15 m/s. The compression position of D-1 begins from the impact site, that is, the section in contact with the incident bar; the compression position of D-2 begins from the site connected with the transmission bar; D-3 is folded from the middle; the compression position of D-4 begins from both sides, and the compression speed of one side near the transmission bar is faster than that of the other side. The failure modes of the four samples in the quasi-static compression tests are completely consistent with those in the dynamic compression tests according to Figure 7. Considering that the structure and matrix materials of the samples are exactly the same, the root cause of the difference in compression failure modes is the different coating materials on the surface of the four honeycomb samples. Combined with the compression failure modes of the samples and the stress–strain curve of the dynamic compression experiments in the previous section, it can be concluded that for the samples with compression failure only from one side, the strain corresponding to the stress–strain curve reaching the stress platform stage is larger, and the upward and downward trends of stress in the elastic stage are more gentle than the other two samples. Combined with Figures 5, 7, it can be found that during the stress platform stage of No. 4 sample, the stress suddenly decreases and then recovers. Combined with the pictures taken by high-speed photography, it can be concluded that since the compression failure of No. 4 sample begins from both sides, when the cell walls at both sides fold to a certain extent, then the remaining middle cell walls of the sample are unstable and collapse Then, the cell walls of the remaining part begin to repeat the process of yield folding, and the stress platform stage is recovered.
Strain Rate Effect
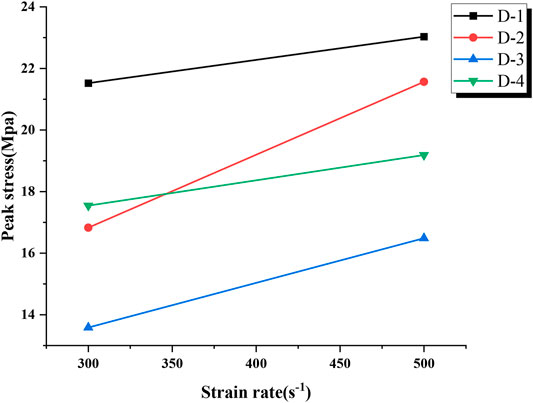
The strain rate sensitivity of porous structural materials is the focus of many scholars. In the mechanical response of the honeycomb structure, the peak stress represents the critical stress that the structure could bear and plays an important role in the design of the buffer energy absorbing structure. The strain rate effect of the honeycomb material is closely related to the structural composition and material composition of the honeycomb sample. In this study, the dynamic response of honeycomb samples under two impact speeds is studied, and the corresponding strain rates are 300s−1 and 500s−1, respectively. Figure 8 shows the relationship between the peak stress and strain rate of four samples in the dynamic compression test. According to the curves in the figure, the peak stress of the four samples increases significantly with the increase of the strain rate, which reflects the strain rate correlation of honeycomb structural materials. The increase of peak stress of the four samples is slightly different. According to the specific data in Table 2, the peak stress of D-2 increases most significantly by 28.16% with the increase of the strain rate, while the amplification of D-1 is the lowest by only 7.02%. Zheng et al. studied the dynamic uniaxial impact behavior of foam metal by using the three-dimensional finite element model. The dynamic stress–strain curve is related to the stratified collapse mode, and the equivalent quasi-static curve is related to the mode of random shear band collapse. (Zheng et al., 2014). The matrix materials of the honeycomb samples used in this study are same, and the micro-collapse mode of the cell wall is also identical. The reason affecting the strain rate sensitivity of the samples may be related to the coating materials.
Dynamic Energy Absorption Characteristics
Honeycomb materials are mainly used as a buffer and energy absorbing materials in practical engineering applications. On the premise of meeting the compressive strength, improving the energy absorbed per unit volume to enhance its cushioning performance is the main research idea of buffer materials at present. Related research is usually divided into two directions: one is to change its materials and study new materials with lighter weight and higher strength. Many honeycomb materials are manufactured under such circumstances (Shin et al., 2008). The other is to design more reasonable structural composition. At present, the former method is more efficient and applicable, and the use of new materials can greatly improve the cushioning and energy absorption characteristics of porous materials.
Honeycomb material has an excellent energy absorption performance in the process of compression. When it is in the process of dynamic compression, the work carried out by the external force is folded through the cell wall continuously and transformed into the plastic properties required for material deformation. The energy (E) absorbed per unit volume of the honeycomb structure can be characterized by the area surrounded by the stress–strain curve. The formula is as follows:
where
As an energy absorption structure, the energy absorption efficiency
where the molecule is the actual absorbed energy at a given compressive strain, and the denominator is the ideal energy absorption obtained by the product of a given compressive strain and the peak stress
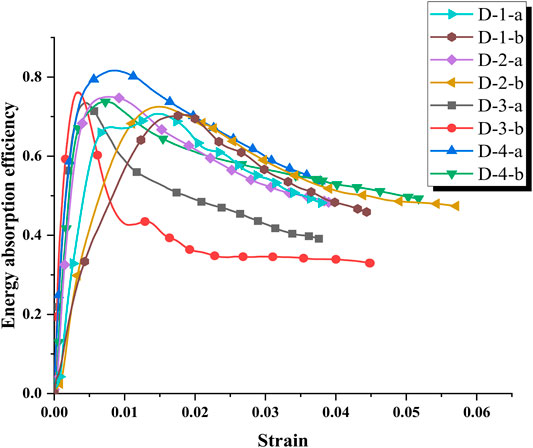
Figure 9 shows the energy absorption curves of four honeycomb structures under dynamic loading. According to the results in the figures, the energy absorption per unit volume of the four samples increases approximately linearly with the increase of the strain. The energy absorbed per unit volume of the sample increases obviously with the increase in impact velocity. In the initial stage of loading, for samples D-1 and D-2, the energy absorption of them under low impact velocity is more, but with the increase of strain, the energy absorption of samples under high impact velocity is more. This is because when D-1 and D-2 are in the elastic stage, the strain of the samples rises faster at a low loading speed and reaches the peak first; they absorb more energy in the initial stage. For D-3 and D-4, the phenomenon of energy absorption curves is that the rising trend of the two samples is almost the same in the elastic stage, and the stress value and peak stress of the samples are larger at a higher impact speed. After the samples pass the peak stress and reach the stress platform stage, the stress value of the samples at the lower impact speed is higher, so they absorb more energy in this part. Then, their energy absorption is exceeded by the samples at a higher impact speed with higher overall platform stress. Figure 10 shows the dynamic energy absorption efficiency of four honeycomb samples under two loading speeds. The regular pattern of the energy absorption efficiency curve is the same as that of porous metal materials studied by Smorygo et al., (2012). In the initial stage of dynamic loading, with the increase of strain, the stress and strength of the samples increase as well, and the energy absorption efficiency also increases. Because of the low toughness of the material under dynamic loading, the honeycomb material decreases significantly after the stress reaches the peak. Therefore, although the stress plateau stage is the main part of the energy absorption of honeycomb samples, the energy absorption efficiency decreases at this stage obviously.
Numerical Simulation Analysis
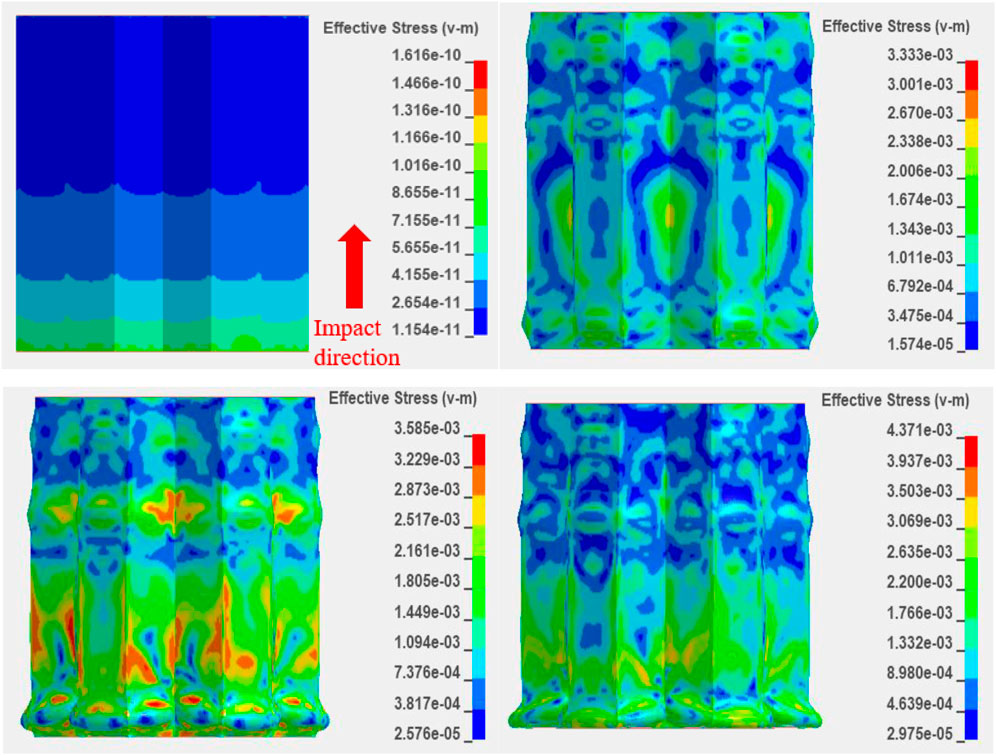
The finite element analysis software (LS-dyna) was used to conduct dynamic simulation to explore the failure process of the honeycomb sample under dynamic load. This is because the composition of the surface coating material of the honeycomb sample studied in this article is too complex, and there are no material constitutive parameters to characterize it. This article just studied the failure form of the same honeycomb structure. Figure 11 shows the built model, and the whole model adopts solid units (solid163) for modeling; the material constitutive models of the bullet, incident bar, and transmission bar are set as the linear elastic model. The constitutive model of the honeycomb sample is set as MAT-plastic-kinematic, which is an elastic–plastic material model related to the strain rate and with failure. Partial material parameters are shown in Table 3. The contact between the four components is set as face-to-face contact. The bullet is given an initial impact velocity at 15 m/s.
Figure 12 shows the effective stress diagrams of honeycomb samples at four different stages. It can be seen from the results in the figures that after the sample is impacted by the incident bar, the decreasing effective stress is generated from the impact surface to the other side of the sample. The compression deformation of the sample occurs from the side in contact with the incident bar initially. When the effective stress at the side in contact with the transmission bar reaches a certain value, the compression deformation also occurs. When the side impacted initially reaches the peak stress, the cell wall close to this side yields and folds and also absorbs more energy. When the impact energy is transmitted to the other side, it has been greatly decreased, so the compression deformation on this side of the sample is reduced. Only the effective stress of the honeycomb material with the same structure is used to study its deformation and failure mode in this study. The honeycomb materials used in this study will be further studied in the subsequent numerical simulation.
Conclusion
In this article, quasi-static compression experiments and dynamic compression experiments were carried out on four kinds of honeycomb steel with special coating materials; their mechanical properties and failure forms were studied by using a pressure testing machine and the split Hopkinson pressure bar (SHPB) device. This special honeycomb structure material will have a broader research and application prospect in the future because of its particular mechanical properties and failure modes. The experimental conclusions are as follows:
1) The quasi-static compressive stress–strain curves of the four honeycomb samples show the characteristics of three typical compression deformation stages of porous materials: the elastic deformation stage, stress platform stage, and densification stage. In the dynamic compressive stress–strain curves, there is no densification stage due to the short loading time and the height of the samples. Furthermore, the relationship between the dynamic peak stress and strain rate is studied, which shows that the honeycomb structure material has a strong correlation with the strain rate.
2) The dynamic compression deformation processes of four kinds of honeycomb samples were recorded by high-speed photography and analyzed combined with their stress–strain curves. The results show that the peak stress of the samples with compression failure from one side is delayed when the loading speed is higher; the stress–strain curves of the samples damaged from both sides will drop instantaneously at the stress platform stage and then restore the phenomenon of stress fluctuation.
3) The relationship between the peak stress under dynamic loading and strain rate is studied. The result showed the conventional phenomenon of the honeycomb structure material: strain rate effect. The strain rate sensitivity of the four honeycomb samples is different, and the reason may be related to the coating materials.
4) The dynamic energy absorption characteristics of honeycomb samples were studied. With the increase of the strain, the dynamic energy absorption curves increased approximately linearly, and the dynamic energy absorption efficiency increases rapidly in the initial stage and then decreases to a steady state. When the impact velocity changes, the energy absorption characteristics of the honeycomb structure also change.
5) The honeycomb steel with the same structure is simulated by the finite element method, and its dynamic failure form is analyzed through the effective stress diagrams. Compression deformation occurs at both sides of the sample. The side first impacted by the incident bar absorbs more energy, and its compression deformation is also prominent. The honeycomb materials used in this article will be further studied in the subsequent numerical simulation.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
YY and NL carried out the design, definition of intellectual content, literature search, data acquisition, data analysis, and manuscript preparation. XF and YS provided assistance for data acquisition, data analysis, and statistical analysis. GM provided assistance for finite element simulation. NL performed manuscript review. All authors have read and approved the content of the manuscript.
Funding
This work was supported by the National Natural Science Foundations of China (No.12072363) and the key R and D plan (Social Development) project of Xuzhou (No.KC21301).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to the advanced analysis and computation center of the China University of Mining and Technology.
References
Deshpande, V. S., and Fleck, N. A. (2020). High Strain Rate Compressive Behavior of Aluminum alloy Foams. Int. J. Impact Eng. 24, 277–298. doi:10.1016/S0734-743X(99)00153-0
Dharmasena, K. P., Queheillalt, D. T., Wadley, H. N. G., Dudt, P., Chen, Y., Knight, D., et al. (2010). Dynamic Compression of Metallic sandwich Structures during Planar Impulsive Loading in Water. Eur. J. Mech. - A/Solids 29 (1), 56–67. doi:10.1016/j.euromechsol.2009.05.003
Fíla, T., Koudelka, P., Zlamal, P., Falta, J., Adorna, M., Neuhauserova, M., et al. (2019). Strain Dependency of Poisson's Ratio of SLS Printed Auxetic Lattices Subjected to Quasi‐Static and Dynamic Compressive Loading. Adv. Eng. Mater. 21 (8), 1900204. doi:10.1002/adem.201900204
Gibson, L. J., and Ashby, M. F. (1997). Cellular Solids, Structure and Properties. UK: Cambridge University Press. ISBN: 0521495601.
Hazizan, M. A., and Cantwell, W. J. (2003). The Low Velocity Impact Response of an Aluminium Honeycomb sandwich Structure. Composites B: Eng. 34, 679–687. doi:10.1016/S1359-8368(03)00089-1
Hohe, J., and Becker, W. (1999). Effective Elastic Properties of Triangular Grid Structures. Compos. Structures 45, 131–145. doi:10.1016/S0263-8223(99)00016-1
Hohe, J., Beschorner, C., and Becker, W. (1999). Effective Elastic Properties of Hexagonal and Quadrilateral Grid Structures. Compos. Structures 46, 73–89. doi:10.1016/S0263-8223(99)00048-3
Hong, H., Hu, M., and Dai, L. (2020). Dynamic Mechanical Behavior of Hierarchical Resin Honeycomb by 3D Printing. Polymers 13 (1), 19. doi:10.3390/polym13010019
Jin, Y., Guo, S., Li, Z., and Han, J. (2007). In-plane Compressive Properties of Mild Steel Honeycomb Sandwich. Mater. Mech. enginnering 31 (8), 19–23. (In chinese). Available from http://en.cnki.com.cn/Article_en/CJFDTOTAL-GXGC200708007.htm.
Li, Z., Wang, T., Jiang, Y., Wang, L., and Liu, D. (2018). Design-oriented Crushing Analysis of Hexagonal Honeycomb Core under In-Plane Compression. Compos. Structures 187, 429–438. doi:10.1016/j.compstruct.2017.12.066
Liu, R., Luo, C., Deng, Z., and Wang, C. (2009). Experimental and Numerical Studies on Aluminum Honeycomb with Various Cell Specifications under Impact Loading. AMSE Int. Mech. Eng. Congress Exposition, 121–126. doi:10.1115/imece2008-67189
Liu, Q., Mo, Z., Wu, Y., Ma, J., Pong Tsui, G. C., and Hui, D. (2016). Crush Response of CFRP Square Tube Filled with Aluminum Honeycomb. Composites Part B: Eng. 98, 406–414. doi:10.1016/j.compositesb.2016.05.048
Liu, J., Chen, W., Hao, H., and Wang, Z. (2019). Numerical Study of Low-Speed Impact Response of sandwich Panel with Tube Filled Honeycomb Core. Compos. Structures 220, 736–748. doi:10.1016/j.compstruct.2019.04.023
Liu, Y., and Zhang, X. (2008). Influence of Cell Micro—topology on the In-Plane Dynamic Properties of Honeycombs. Explosion and shock waves 28, 494–502. (In chinese). Available from http://en.cnki.com.cn/Article_en/CJFDTOTAL-BZCJ200806002.htm.
Marc, A. M. (1994). Dynamic Behavior of Materials. USA: University of California. ISBN: 978-3-319-15220-2.
Mistou, S., Sabarots, M., and Karama, M. (2000). Experimental and Numerical Simulations of the Static and Dynamic Behaviour of sandwich Plates. Barcelona, Spain: European Congress on Computational Methods in Applied Sciences and Engineering.
Mohr, D., and Doyoyo, M. (2004). Deformation-induced Folding Systems in Thin-Walled Monolithic Hexagonal Metallic Honeycomb. Int. J. Sol. Structures 41, 3353–3377. doi:10.1016/j.ijsolstr.2004.01.014
Mukai, T., Kanahashi, H., Miyoshi, T., Mabuchi, M., Nieh, T. G., and Higashi, K. (1999). Experimental Study of Energy Absorption in a Close-Celled Aluminum Foam under Dynamic Loading. Scripta Materialia 40, 921–927. doi:10.1016/s1359-6462(99)00038-x
Roy, R., Nguyen, K. H., Park, Y. B., Kweon, J. H., and Choi, J. H. (2014). Testing and Modeling of Nomex Honeycomb sandwich Panels with Bolt Insert. Composites Part B: Eng. 56, 762–769. doi:10.1016/j.compositesb.2013.09.006
Seemann, R., and Krause, D. (2017). Numerical Modelling of Nomex Honeycomb sandwich Cores at Meso-Scale Level. Compos. Structures 159, 702–718. doi:10.1016/j.compstruct.2016.09.071
Shan, J., Xu, S., Zhou, L., Wang, D., Liu, Y., Zhang, M., et al. (2019). Dynamic Fracture of Aramid Paper Honeycomb Subjected to Impact Loading. Compos. Structures 223, 110962. doi:10.1016/j.compstruct.2019.110962
Shin, K. B., Lee, J. Y., and Cho, S. H. (2008). An Experimental Study of Low-Velocity Impact Responses of sandwich Panels for Korean Low Floor Bus. Compos. Structures 84 (3), 228–240. doi:10.1016/j.compstruct.2007.08.002
Sibeaud, J.-M., Thamié, L., and Puillet, C. (2008). Hypervelocity Impact on Honeycomb Target Structures: Experiments and Modeling. Int. J. Impact Eng. 35, 1799–1807. doi:10.1016/j.ijimpeng.2008.07.037
Smorygo, O., Marukovich, A., Mikutski, V., Gokhale, A. A., Reddy, G. J., and Kumar, J. V. (2012). High-porosity Titanium Foams by Powder Coated Space Holder Compaction Method. Mater. Lett. 83, 17–19. doi:10.1016/j.matlet.2012.05.082
Tang, E., He, Z., Chen, C., and Han, Y. (2020). Characterization of Dynamic Compressive Strength and Impact Release Energy of Al/PTFE Energetic Materials Reinforced by Aluminum Honeycomb Skeleton. Compos. Structures 241, 112063. doi:10.1016/j.compstruct.2020.112063
Wang, Z., Tian, H., Lu, Z., and Zhou, W. (2014). High-speed Axial Impact of Aluminum Honeycomb - Experiments and Simulations. Composites Part B: Eng. 56, 1–8. doi:10.1016/j.compositesb.2013.07.013
Wang, P., Xu, S., Li, Z., Yang, J., Zhang, C., Zheng, H., et al. (2015). Experimental Investigation on the Strain-Rate Effect and Inertia Effect of Closed-Cell Aluminum Foam Subjected to Dynamic Loading. Mater. Sci. Eng. A 620, 253–261. doi:10.1016/j.msea.2014.10.026
Wang, Z., Li, Z., and Xiong, W. (2019). Experimental Investigation on Bending Behavior of Honeycomb sandwich Panel with Ceramic Tile Face-Sheet. Composites Part B: Eng. 164, 280–286. doi:10.1016/j.compositesb.2018.10.077
Wang, Z. (2019). Recent Advances in Novel Metallic Honeycomb Structure. Composites Part B: Eng. 166, 731–741. doi:10.1016/j.compositesb.2019.02.011
Wilbert, A., Jang, W.-Y., Kyriakides, S., and Floccari, J. F. (2011). Buckling and Progressive Crushing of Laterally Loaded Honeycomb. Int. J. Sol. Structures 48 (5), 803–816. doi:10.1016/j.ijsolstr.2010.11.014
Xu, S., Beynon, J. H., Ruan, D., and Lu, G. (2012). Experimental Study of the Out-Of-Plane Dynamic Compression of Hexagonal Honeycombs. Compos. Structures 94, 2326–2336. doi:10.1016/j.compstruct.2012.02.024
Yan, C., Hao, L., Hussein, A., Young, P., and Raymont, D. (2014). Advanced Lightweight 316L Stainless Steel Cellular Lattice Structures Fabricated via Selective Laser Melting. Mater. Des. 55, 533–541. doi:10.1016/j.matdes.2013.10.027
Yang, L., Sui, L., Dong, Y., Li, X., Zi, F., Zhang, Z., et al. (2021). Quasi-static and Dynamic Behavior of sandwich Panels with Multilayer Gradient Lattice Cores. Compos. Structures 255, 112970. doi:10.1016/j.compstruct.2020.112970
Zarei Mahmoudabadi, M., and Sadighi, M. (2011). A Theoretical and Experimental Study on Metal Hexagonal Honeycomb Crushing under Quasi-Static and Low Velocity Impact Loading. Mater. Sci. Eng. A 528, 4958–4966. doi:10.1016/j.msea.2011.03.009
Zhang, X., Zhang, L., and Zhang, P. (2012). Equivalent Constitutive Equations of Honeycomb Material Using Micro-polar Theory to Model Thermo-Mechanical Interaction. Composites Part B: Eng. 43, 3081–3087. doi:10.1016/j.compositesb.2012.04.056
Zhao, M. D., Fan, X., Fang, Q.-Z., and Wang, T. J. (2015). Experimental Investigation of the Fatigue of Closed-Cell Aluminum alloy Foam. Mater. Lett. 160, 68–71. doi:10.1016/j.matlet.2015.07.040
Zheng, Z., Wang, C., Yu, J., Reid, S. R., and Harrigan, J. J. (2014). Dynamic Stress-Strain States for Metal Foams Using a 3D Cellular Model. J. Mech. Phys. Sol. 72, 93–114. doi:10.1016/j.jmps.2014.07.013
Zhou, Q., and Mayer, R. R. (2002). Characterization of Aluminum Honeycomb Material Failure in Large Deformation Compression, Shear, and Tearing. J. Eng. Mater. Technol. 124, 412–420. doi:10.1115/1.1491575
Zhou, X., Zhou, H., Li, X., and Chen, C. (2015). Size Effects on Tensile and Compressive Strengths in Metallic Glass Nanowires. J. Mech. Phys. Sol. 84, 130–144. doi:10.1016/j.jmps.2015.07.018
Zhou, H., Xu, P., Xie, S., Feng, Z., and Wang, D. (2018). Mechanical Performance and Energy Absorption Properties of Structures Combining Two Nomex Honeycombs. Compos. Structures 185, 524–536. doi:10.1016/j.compstruct.2017.11.059
Zou, G., Chang, Z., Xia, X., and Zhang, X. (2009). “Study on Mechanical Properties of Steel Honeycomb Panel Three-point Bending Specimen under In-Plane and Out-Plane Transverse Dynamic Impact Load,”. The Fourth International Conference on Experimental Mechanics (Singapore, 7522, 75220W. doi:10.1117/12.851612
Keywords: honeycomb steel, SHPB, failure modes, energy absorption, numerical simulation
Citation: Luo N, Yuan Y, Fan X, Suo Y and Mou G (2022) Impact Dynamic Behavior and Deformation Mode of a Lightweight-Coated Honeycomb Steel Structure. Front. Mater. 9:848200. doi: 10.3389/fmats.2022.848200
Received: 04 January 2022; Accepted: 27 January 2022;
Published: 18 February 2022.
Edited by:
Jianghua Shen, Northwestern Polytechnical University, ChinaReviewed by:
Yazhou Guo, Northwestern Polytechnic University, United StatesYu Wang, University of Science and Technology of China, China
Pengfei Wang, University of Science and Technology of China, China
Copyright © 2022 Luo, Yuan, Fan, Suo and Mou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ning Luo, bmx1b0BjdW10LmVkdS5jbg==
 Ning Luo
Ning Luo Yishuo Yuan1,2
Yishuo Yuan1,2