Automated Virtual Design of Organic Semiconductors Based on Metal-Organic Frameworks

The arrangement of organic semiconductor molecules in a material can be modulated using different supramolecular approaches, including the metal–organic framework (MOF) approach. These arrangements result in different frameworks topologies and structures. Fabrication of materials comprising optimized assemblies and functional molecules enables efficient tailoring of material properties, including electronic responses. Since semiconducting properties are sensitive to subtle changes in the nanostructure of the material, the exploitation of MOFs has promising potential in the development of new materials with designed structure and function. Based on decade-long method development, virtual design strategies have become ever more important, and such design methods profit from the availability of automated tools. Such tools enable screening of huge libraries of organic molecules in in silico models of the structure of three-dimensional nanoscale assemblies as the prerequisite to predict their functionality. In this report, we present and demonstrate the application of an automated workflow tool developed for MOFs of the primitive cubic (PCU) topology. We use pentacene-based ditopic linkers of a varied chemical composition and pillar linkers of different molecular sizes to automatically generate PCU MOFs, sample their structural dynamics at finite temperature, and predict electronic coupling matrix elements in vibrationally averaged assemblies. We demonstrate the change of the intermolecular ordering in the resulting MOFs and its impact on the semiconducting properties. This development lays the basis of an extendable framework to automatically model a wide variety of MOFs and characterize their function with respect to properties, such as conduction properties, absorption, and interaction with light. The developed workflow protocol and tools are available at https://github.com/KIT-Workflows/PCU-MOF.

1 Introduction

Electronic properties of organic semiconductors (OSCs) and their optoelectronic response highly depend on the structural arrangement of the molecules and their vibrational freedom in the material (Pohl and Pohl, 2020; D’Avino et al., 2016). They determine the electronic coupling between the molecules, which impacts the mechanism and the properties of the electronic conduction (Kera et al., 2009; Mailman et al., 2017; Haldar et al., 2021). The packing geometry of OSC is driven by the subtle intermolecular interactions, which are difficult to control; therefore, crystal engineering remains a significant challenge. The arrangement of molecules depends on the crystallization conditions, which, in most cases, cannot be easily controlled. This limits the fabrication of new OSC with desired orientation of the molecular units and also the optimization of the semiconducting properties, which result from the molecular packing in a material. A precise control over the architecture of the material, which incorporates the OSC components at well-defined positions and orientations, can be realized by a reticular chemistry approach (Freund et al., 2021), applied for the synthesis of metal–organic frameworks (MOFs). This approach has been successfully utilized to obtain materials with a controlled three-dimensional assembly of organic molecules (Alvaro et al., 2007; Liu et al., 2011; Xu et al., 2016; Liu and Wöll, 2017), opening new perspectives in the fabrication of OSC materials with programmable functionality (Garg et al., 2019; Haldar et al., 2019; Xie et al., 2020).

Metal–organic frameworks are materials that consist of organic molecules, i.e., linkers, and inorganic polynuclear clusters (nodes), known as secondary building units (SBUs) (Rowsell and Yaghi, 2004) (Figure 1). Several bipartite nets, known in reticular chemistry (O’Keeffe et al., 2008), represent binary frameworks used for the construction of MOF structures of various topologies (Kalmutzki et al., 2018). By combining different metal ions and organic linkers in diverse topologies, a considerable variety of MOFs can be realized, and around 100,000 different MOF structures have been synthesized so far (Chung et al., 2014; Lyu et al., 2020). They represent a unique variety of structures, and their properties can be tailored through rational design (Freund et al., 2021) and by choosing the appropriate combinations. As one may guess, an unprecedented number of possible combinations occurs, which led also to the creation of huge databases of hypothetical MOF structures and screening of new MOF candidates (Moosavi et al., 2020). MOFs are widely used for gas sorption (Lin et al., 2020; Qiao et al., 2020) and storage (Li et al., 2018; Connolly et al., 2020), sensors (Kreno et al., 2012), or solar cells (Goswami et al., 2016). They are good candidates for establishing new OSC with tailored electronic properties by ordering organic linkers in a network manner with the specific framework topology (Öhrström, 2015; Neumann et al., 2016). However, owing to their porous structure and relatively large distances between neighboring OSC linker molecules, MOFs are typical wide-bandgap semiconductors, but their electronic conduction can be increased by realizing structures that enable efficient charge transfer through-bonds (Narayan et al., 2012) or space (Neumann et al., 2016), as well as by π-stacking (Liu and Wöll, 2017; Haldar et al., 2021; Zojer and Winkler, 2021). The through-bond pathway depends on continuous SBUs comprising metals and ligand moieties; their high charge mobility and small band gap are a result of the proper orbital overlap and well-matched energy levels. Through-space electronic conduction can be enhanced by incorporating guest molecules like TCNQ or fullerenes in MOF pores (Neumann et al., 2016; Liu et al., 2019). It can be also photoswitched by light (Heinke et al., 2014; Kanj et al., 2018; Garg et al., 2019; Haldar et al., 2020). Upscaling of MOF electronic conduction via the incorporation of highly efficient OSC molecules with π-stacking within MOF scaffold, e.g., pentacene, has been also realized (Haldar et al., 2021). Hence, electronic conduction in MOFs is based on several different mechanisms (Xie et al., 2020); therefore, it follows different design strategies. For example, in the last case, due to the localized frustrated rotations of the pentacene cores in the assembled structure, charge carrier mobility is significantly decreased. More rigid linkers (with limited vibrational flexibility) or other types of assemblies with the designed orientation of OSC units in the MOF scaffold are sought after (Haldar et al., 2019).

FIGURE 1

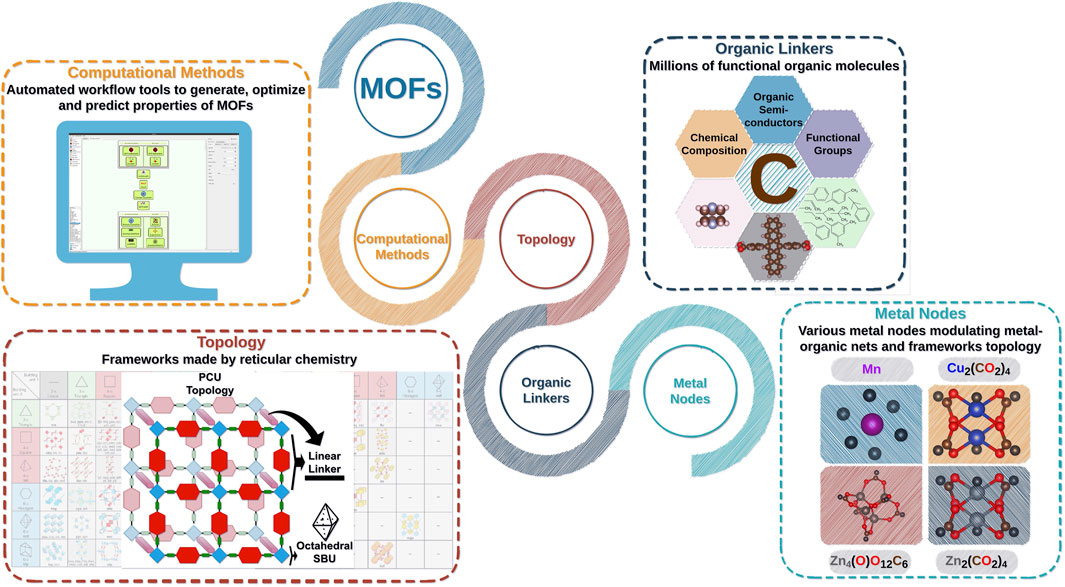
FIGURE 1. Reticular chemistry applied for the fabrication of MOFs with diverse metal–organic networks, components (organic molecules and metal nodes), and properties. Virtual design of new MOF materials by automated workflows investigated in this report.

Considering the enormous chemical space of MOF components, a multitude of new candidates with interesting properties can be realized. Unfortunately, attempting to access them all experimentally via MOF fabrication is expensive, time-consuming, and based on trial and error (Stock and Biswas, 2012). Predictive methods for MOF construction, design, and selection of the most prominent candidates with a desired functionality will significantly accelerate the discovery of new formulations and reduce costs (Mancuso et al., 2020). There are several free and commercial tools or molecular editors for the initial construction of a representative MOF model, e.g., Avogadro (Nefedov et al., 2021) and Materials Studio (Dassault Systèmes, 2020). Often, they require time-consuming manual work and prior knowledge of the topological details and metal–organic interactions in MOF. Advanced algorithms using the reverse topological or top-down approach are implemented, using graph theory, in the tool of Boyd and Woo (2016), and using known nets (topologies) of MOFs that follow a recursive, geometry-based assembly of SBUs and linkers (O’Keeffe et al., 2008), in codes like stk (Turcani et al., 2021), Zeo++ (Martin and Haranczyk, 2014), ToBaCCo (Colón et al., 2017), and AuToGraFS (Addicoat et al., 2014a). All of these tools can be used to prepare a basic MOF model for visualization, whereas subsequent structure optimization and the calculation of electronic and/or optoelectronic properties should be done separately. Some of the tools require programming knowledge, and they have limited automation functionality towards virtual design of new MOFs comprising various components, triggering new interesting phenomena.

In this report, we present an automated, transferable, and user-friendly workflow for the generation, optimization, and structure–property prediction of new MOF materials. We use the SimStack workflow environment (https://www.simstack.de/) to combine several modules, called WaNos (Workflow active Nodes), responsible for the specific tasks or calculation(s) involved in the MOF building protocol and up to the analysis of specific MOF properties, e.g., in the case presented here, electronic coupling elements towards semiconducting MOFs. Each WaNo uses as an input the output from the previous WaNo, enabling an easy transfer of data between compute units and construction of different workflows, as well as a combination of different WaNos aiming at desired purposes. The workflow, introduced here for a MOF design and calculation, is as follows:

• Adaptable: User-friendly graphical user interface (GUI) and automated dataflow between multiple module functions allow easy adaptation of the workflow to specific user requirements;

• Reproducible: Once set up, it will generate the same results independently of the user environment. Automatic flow of data and processes allows an error-free data generation and storage of the work recipes for other investigations;

• Efficient: It significantly reduces the time to prepare and carry out similar calculations that have the same methodological flow, but different starting input data;

• Expandable: By replacing method modules (WaNos), the workflow can be extended to related applications and to diverse MOF topologies. Moreover, it can be used as a part of other workflow(s);

• Transferable: It can be used by users outside the group which has developed it without facing implementation issues.

Considering the variety of MOF materials and possible attained properties, multiple options for such workflow developments are possible. In the present study, we focus on the primitive cubic (PCU) topology of MOFs (O’Keeffe and Yaghi, 2012) (Figure 1) that is a widely used topology found in fabricated MOF materials (Li et al., 2007; Luo et al., 2017; Wei et al., 2019; Xing et al., 2019; Yao et al., 2019). The PCU topology features the network that describes the MOF-2 family, which has paddle-wheel nodes, such as Zn₂(CO₂)₄ and Cu₂(CO₂)₄, connected by linkers (Li et al., 1998; Xing et al., 2019; Goldman et al., 2020; Qiao et al., 2020; Yazdanparast et al., 2020) and the MOF-5 family with octahedral nodes, such as Zn₄(O)O₁₂C₆ (Li et al., 1999; Schoedel et al., 2016). It can be formed also from SBUs based on Mg, Cd, Pb, or rare earth metals (Bhattacharya et al., 2014; Luo et al., 2017; Lin et al., 2018; Yao et al., 2019). In addition, MOF films grown using a layer-by-layer technique on the pre-functionalized surfaces, e.g., surface-anchored MOFs (SURMOFs) (Liu et al., 2012; Zhuang et al., 2016), using Cu₂(CO₂)₄ and Zn₂(CO₂)₄ SBUs are often assembled in PCU-type networks. Owing to the fact that SURMOFs allow us to control the assembly type and the linker order in a material (Heinke et al., 2014; Heinke and Wöll, 2019), crystal structure engineering of such MOFs comprising OSC and chromophore molecules will allow us to investigate new systems systematically and accelerate the selection of the most promising MOF candidates. Virtual screening of various organic linker molecules and their assembly in the MOF allows computation of structure–property relationships that can be accessed by the automated workflows reported here, including the dynamical behavior of the structure at finite temperature.

We demonstrate the architecture of such a workflow and its exemplary usage for the prediction of electronic coupling elements between pentacene cores in a PCU SURMOF structures built from ditopic pentacene layer linkers and DABCO (DABCO = 1,4-diazabicyclo(2.2.2)octane), pyrazine (pyz = 1,4-diazine), and bipyridine (bipy = 4,4′-bipyridine) pillar linkers (Figure 2). Pentacene (Pn) is an organic molecule, which is characterized by high charge mobility in its different crystal forms (Jurchescu et al., 2007; Virkar et al., 2009). It was previously integrated in the SURMOF-2 type of MOF (Haldar et al., 2021), where the stacking of pentacene cores of the linkers, localized at a distance of approximately 5.8 Å, was suggested to be not optimal for efficient charge carrier transport caused by ineffective overlap between the neighboring pentacene cores (Zojer and Winkler, 2021) and weak π–π interactions, which are dynamically changing over time, as observed in MD simulations at 300 K (Haldar et al., 2021). These simulations explained increased vibrational flexibility of molecules in the material and the significant decrease of the effective electronic coupling.

FIGURE 2

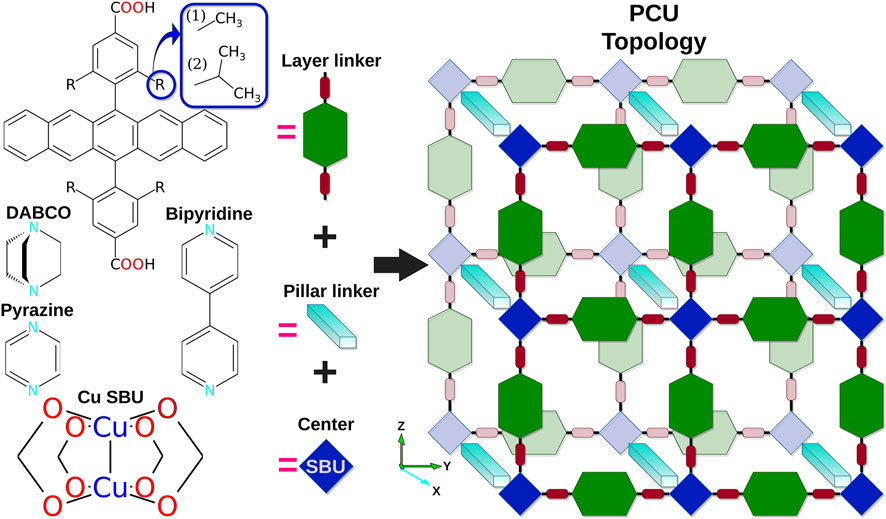
FIGURE 2. Representation of MOF materials of PCU topology investigated in the present report. Layer and pillar linkers are marked in green and cyan, respectively. Copper secondary building units (SBUs) are depicted in blue.

With PCU SURMOF type of assembly, investigated here, we aim to use automated workflows to build and calculate properties of new MOFs and illustrate the change of their semiconducting properties as a function of the controlled separation between the pentacene cores (by different pillar linkers) that change with the stacking type and the dynamics of OSC cores in a material. With this work, we initiate a new approach for further virtual design of versatile MOF assemblies that will enable the upscaling of the functionality of single molecules, such as pentacene, to yield functional solid materials or thin films of macroscopic dimensions in future investigations.

2 Methods and Computational Details

MOFs are modular periodic systems, consisting of metal (oxo)-nodes (SBUs) and organic linker molecules. Depending on the nature of both components, different three-dimensional nets are formed. Virtual design of new MOF constructs requires the combination of several algorithms (methodologies and codes) that are linked together in one workflow, enabling automated data transfer and on-the-fly property prediction. Here, we create an automated methodology to build, optimize, and analyze MOFs of the PCU topology and implement it within SimStack. MOF systems and components used for the protocol demonstration are depicted in Figure 2. Three ditopic linkers, differing by the R-substitution in the linking phenyl group and based on pentacene cores, were used as layer linkers, i.e., connected to the Cu-node by Cu⋯O coordination bonds (on y- and z-axes), while DABCO, pyrazine, and bipyridine were used as pillar linkers with Cu⋯N coordination (x-axis).

In SimStack, each module or WaNo implements a graphical user interface for the backend codes, which performs required calculations. Each WaNo is maximally generalized, therefore can be used to calculate various molecules and types of materials, and can be used for tasks in conceptually different workflows. The PCU-MOF workflow consists of several WaNos for software codes, such as TURBOMOLE (Balasubramani et al., 2020), AuToGraFS (Automatic Topological Generator for Framework Structures) (Addicoat et al., 2014a), GULP (General Utility Lattice Program) (Gale and Rohl, 2003), VASP (Vienna Ab initio Simulation Package) (Kresse and Hafner, 1993), LAMMPS (Large-scale Atomic Molecular Massively Parallel Simulator) (Boyd et al., 2017; Plimpton et al., 2020), and interfaces between codes. We also developed several new codes and algorithms, i.e., LCmaker, Achmol (Assembler of Chemical Molecules), and SuperCeller.

To create an automated workflow for MOF design, we have used several available WaNos, DFT-Turbomole (Schlöder and Rêgo, 2022), DFT-VASP (Ricardo, 2021), QuantumPatch3 (Friederich et al., 2014), and Format-Converter, while all other WaNos (MOF-input, LCmaker, AuToGraFS, GULP, lammps-interface, LAMMPS, Achmol, and SuperCeller) were programmed for the purpose of MOF design and are reported here for the first time. The workflow consists of three central parts, i.e., 1) MOF Builder, 2) MOF Optimizer, and 3) MOF Analyzer (Figure 3). The MOF Builder consists of the general WaNo MOF-input, where the user specifies linker molecules, metal node type, and desired topology; DFT-Turbomole, where optimization of input linkers is done using the TURBOMOLE software; and LCmaker and AuToGraFS used to build the periodic MOF model. To generalize the standard of atomic units in the entire workflow, both in converting formats and in developing the back-end software in different parts of the workflow, we employed the Atomic Simulation Environment (ASE) (Larsen et al., 2017). The MOF Optimizer includes WaNo GULP for the pre-optimization of MOFs with force-field potentials, DFT-VASP for MOF optimization using the quantum mechanical approach (density functional theory, DFT), and Format-Converter designed to convert different file formats between software. The MOF Analyzer is a multifunctional part of a workflow, which is assigned to calculate different properties of MOF based on both 1) optimized structures at 0 K (right branch, including Achmol and SuperCeller WaNos) and 2) sampled MOF structures during molecular dynamics (MD) simulations at finite temperature using LAMMPS. In the present study, we focus on the calculation of the electronic coupling matrix elements, J_if, between the initial state of a donor and the final state of the acceptor, used in the Marcus theory of charge transfer (CT), i.e., in a hopping mechanism (Marcus, 1993) to estimate the semiconducting properties of PCU MOFs. According to this theory (Eq. 1), the charge transfer rate, k_CT, is defined as

$k_{CT}=\frac{2\pi }{\hslash }|J_{if}{|}^2\sqrt{\frac{1}{4\pi k_{B}T\lambda }}\exp \left(\frac{-{(\mathrm{\Delta }{G}^0+\lambda )}^2}{4\lambda k_{B}T}\right).(1)$

FIGURE 3

FIGURE 3. PCU-MOF workflow within the SimStack client to build, optimize, and analyze MOF materials for automated structure–property predictions and design.

Here, λ is the reorganization energy, connected to the change in the equilibrium geometry of both donor and acceptor upon change of the charged state, k_B is the Boltzmann constant, T is the temperature, and ΔG⁰ is the total Gibbs free energy change (i.e., energy difference between frontier molecular orbitals involved in CT). Electronic coupling, J_if, between adjacent OSC cores in a MOF was calculated using the overlap between molecular orbitals obtained from the DFT, as implemented in the WaNo QuantumPatch3. A detailed description of algorithms and computational details is given below.

2.1 Metal-Organic Framework Builder

In this part, the initial model of a MOF is constructed from the user-defined linker molecules and implemented SBU nodes. Here, we describe the PCU topology of MOFs, and we selected as an example Cu metal nodes in the paddlewheel shape (Cu_pw6.inp). The workflow uses the AuToGraFS software; therefore, all SBUs and topologies available in AuToGraFS can be accessed by our tool too, enabling many extensions. Input data, i.e., linker molecules and SBUs, are specified in MOF-input WaNo. Since we have used two linker types, layer and pillar, that have different chemical compositions, two parallel optimization procedures of linker molecules have to be performed in DFT-Turbomole. The choice of different functionals, basis sets, and other DFT parameters is implemented in this WaNo. All linkers studied here were optimized utilizing the B3LYP functional (Lee et al., 1988; Becke, 1993) with the def2-SV(P) basis set (Weigend and Ahlrichs, 2005) and Grimme D3 dispersion correction (Grimme et al., 2010), using default optimization criteria. Optimized structures are then automatically passed to LCmaker.

LCmaker makes a customized “inp” or “xyz” format files for different versions of AuToGraFS and automatically generates the joint points, called dummies, in the places where the organic linker should be linked to the metal node. LCmaker supports two algorithms for dummy selection: (1) for carboxyl group connections, i.e., by removing COOH groups from layer linkers and exchanging them by the dummy points (Figure 4B), and (2) for the nitrogen-terminated pillar linkers by the dummy on the N atom. Moreover, there is also a possibility to define dummies via the user-defined atom indexes. Options available in the LCmaker are depicted in Figure 4 and listed in Supplementary Table S1.

FIGURE 4

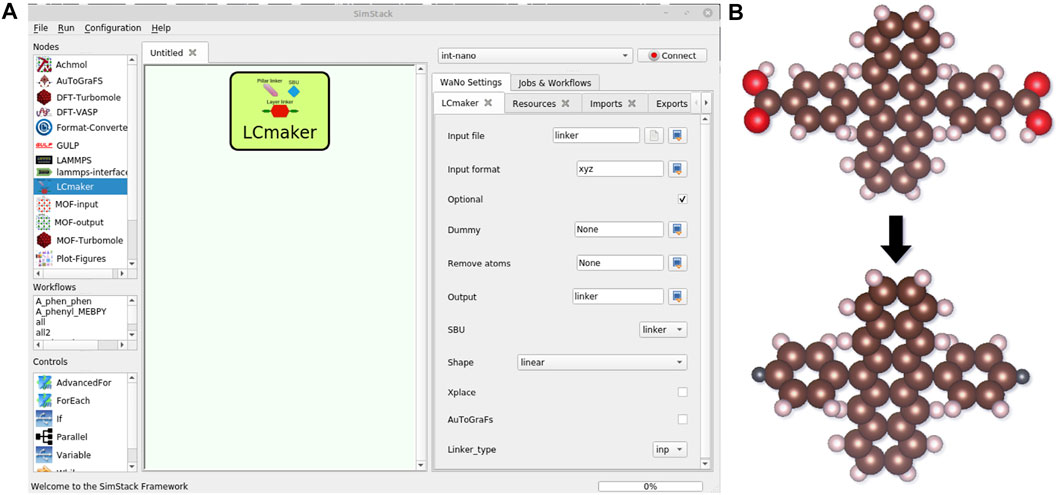
FIGURE 4. LCmaker WaNo window in SimStack (A). Options in the right window are set for the PCU topology. Description of all options available is given in Supplementary Table S1. Main functionality of LCmaker (B).

As mentioned before, there are several algorithms to apply metal center–organic linker connections for the specific MOF topology. We built MOF structures using AuToGraFS (Addicoat et al., 2014a) for three main reasons: 1) the simplicity of MOF construction based on manageable input and output interfaces, 2) its ability to support almost all MOF topologies, 3) its ability to be linked to a fully featured force field UFF4MOF (Universal Force Field for MOF) necessary for further optimization of structures of arbitrary frameworks using, e.g., GULP software (Addicoat et al., 2014b; Coupry et al., 2016). Moreover, UFF4MOF is implemented in LAMMPS package, enabling lots of further investigations of specific MOF properties, including MD simulations. AuToGraFS has also implemented additional atom types found in the Computation-Ready Experimental (CoRE) database (Chung et al., 2014); it shows comparability with experimental results and enables our workflows to be extended to various MOF systems. AuToGraFS was implemented in our workflow in the respective WaNo node called AuToGraFS (Figure 3). This WaNo enables use of the code without any prior programming knowledge and manual preparation of necessary files. Together with LCmaker, AuToGraFS is automatically generating MOF periodic representation that can be processed in the further steps of the workflow.

2.2 Metal–Organic Framework Optimizer

Two consecutive optimization schemes are used to optimize the initially generated MOF model: pre-optimization with the UFF4MOF force field using GULP (Gale and Rohl, 2003; Addicoat et al., 2014b) and later optimization based on DFT using VASP. Such a DFT-optimized MOF structure represents one of the local minima structures necessary for setting up the next steps of the workflow. For the case study presented here, DFT calculations in the DFT-VASP WaNo (Ricardo, 2021) were performed using the PBE functional (Perdew et al., 19961997) with the Tkatchenko-Scheffler method with iterative Hirshfeld partitioning (Bučko et al., 2013) using VASP version 5.4.4. The plane wave energy cutoff was set to 500 eV, and the k-point grid was 3 × 2 × 2. The input–output file formats between codes were handled via Format-Converter WaNo (Figure 3).

2.3 Metal-Organic Framework Analyzer

From this step, functionality of the workflow can be user specific, and different WaNos can be added to the workflow to calculate desired properties of MOF materials. For the semiconducting properties, which can be triggered via different electronic conduction mechanisms, DFT-optimized MOF structures from DFT-VASP may be used:

• To calculate band structure, from which couplings and effective masses of electrons and holes can be derived,

• To calculate electronic couplings between linkers based on molecular orbitals self-consistently converged at the explicit MOF environment, which are used in hopping equations, e.g., Eq. 1,

• To sample temperature-dependent MOF structures with further calculation of couplings from snapshots in MD.

Since our previous studies have proven that the vibrational flexibility of linkers in a MOF impacts charge carrier mobilities measured experimentally (Haldar et al., 2021), in the present study, we focus on the electronic couplings between OSC cores in PCU-type MOF assemblies based on the MD sampled structures at 298 K (left branch in MOF Analyzer in Figure 3). However, in the PCU-MOF workflow, we demonstrate two possible pathways that may be used to estimate electronic couplings in the hopping scenario.

2.3.1 Electronic Coupling in DFT-Optimized Metal-Organic Frameworks

If the electronic conduction of a MOF is based on the charge carrier hopping between OSC linkers in a MOF scaffold with no or negligible impact of the metal atoms linking them (Liu et al., 2019; Haldar et al., 2021), metal atoms can be omitted. To extract optimized MOF in XYZ format from the periodic file formats and provide essential files for the QuantumPatch3 WaNo (cml files with linker molecules in the MOF supercell fragment), where couplings are calculated for each linker separately (Friederich et al., 2014), we developed a python-based code that uses the Open Babel Toolbox within ASE (O’Boyle et al., 2011). It is known that atom positions in periodic calculations are mapped to the unit cell (Figure 5); therefore, direct conversion of files after VASP to Cartesian format, keeping atoms grouped to each linker, is not possible. This is done in our workflow by the Achmol (Assembler of Chemical Molecules) code implemented in Achmol WaNo. It takes the unit cell of the optimized MOF structure and creates a supercell out of it, e.g., 2 × 2 × 2. Then, it removes metal atoms and searches for groups (clusters) of complete linkers (the correct amount of atoms that belong to a specific molecule) based on a condition of volume minimization of the center of mass of the linkers. It finds complete linkers based on the number of atoms of separated linkers after removing metals using a connectivity matrix. The graph of molecules is the main pattern to find complete linkers after optimization (Figure 5B). The main output of Achmol is the Cartesian file with three linkers (on x-, y-, and z-axes, periodically repeated to represent the MOF) with atoms grouped to a specific linker molecule, e.g., atoms 1–49 belong to linker 1, while atoms 50 to 100 to linker 2. All extracted linkers are then automatically hydrogenated to keep neutral charge consistence and can be used to create user-defined clusters, specified in WaNo SuperCeller, necessary for further calculations in QuantumPatch3. Achmol can post-process output files of periodic calculations in CONTCAR, xml and cif formats, e.g., vasprun.xml or sample.cif. Options available in the Achmol WaNo are depicted in Figure 5 and listed in Supplementary Table S2. Functionality of SuperCeller is listed in the Supplementary Material (Supplementary Figure S2; Supplementary Table S3).

FIGURE 5

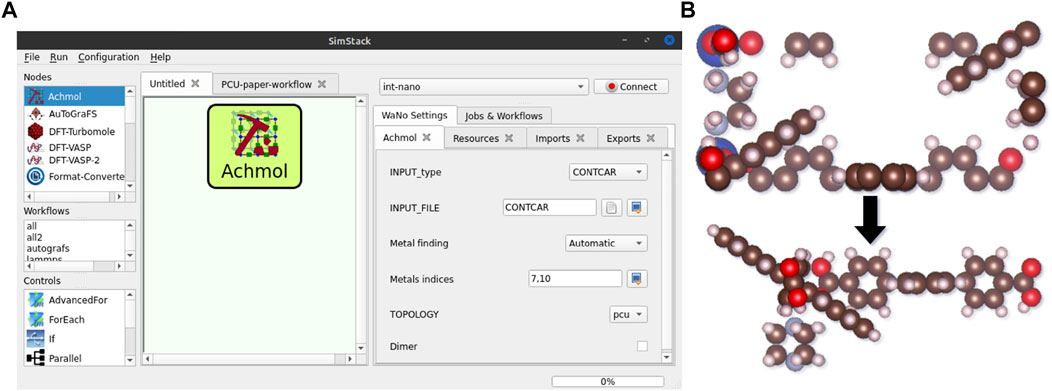
FIGURE 5. Achmol WaNo window in SimStack (A). Options from the right window are described in Supplementary Table S2. Main functionality of Achmol (B).

2.3.2 Electronic Coupling From Molecular Dynamics Sampling

MOF structures obtained after MOF Builder and MOF Optimizer can be used as starting structures in MD simulations at finite temperature in either VASP (ab initio MD) or LAMMPS (force-field-based MD). Considering the high computational cost and limited simulation times of ab initio MD, we performed MOF structure sampling using UFF4MOF as implemented in LAMMPS. For that, two WaNos were created: lammps-interface and LAMMPS (Figure 3). lammps-interface contains a list of options that should be specified by a user to set up automatically input files to run MD. It passes all files to LAMMPS, which performs the actual MD run, including equilibration and production. For the MOF systems studied here, we performed MD simulations of 4 × 4 × 4 supercells for 10 ns (with a timestep of 1 fs) at 298 K. Production runs were preceded with 30 ps equilibration. All simulations were done in a canonical ensemble (NVT).

To calculate electronic couplings between neighboring ditopic linkers structured in a MOF during 10 ns MD, we extracted dimers from 1,000 snapshots (every 10 ps) and performed separate calculations using the Quantum Patch approach (Friederich et al., 2014). Couplings were calculated as an overlap between the highest occupied molecular orbitals, HOMO (hole transport), and the lowest unoccupied molecular orbitals, LUMO (electron transport), in dimers using the B3LYP functional with the def2-SVP basis set.

3 Results and Discussion

The workflow protocol described in Section 2 was applied to automatically generate and optimize five PCU MOF systems with the subsequent structure sampling by MD simulations to collect vibrationally averaged assemblies of pristine and modified (methyl and isopropyl) pentacene ditopic linkers. The cell parameters of optimized structures are listed in Table 1.

TABLE 1

TABLE 1. Unit cell parameters of PCU-type MOF structures studied.

Representative structures are depicted in Figure 6 and Supplementary Figure S3. Due to the similar size of DABCO and pyrazine pillar linkers, the geometrical parameters of both systems are also similar, resulting in center-of-mass (COM) distances between neighboring linkers of approximately 9.2 Å, which is much larger than the distance observed for the previously reported SURMOF-2 structures (Haldar et al., 2021) (around 5.8 Å, Figure 7A). PCU MOF with a bipyrazine pillar has an even larger COM (around 13.6 Å, Figure 6B).

FIGURE 6

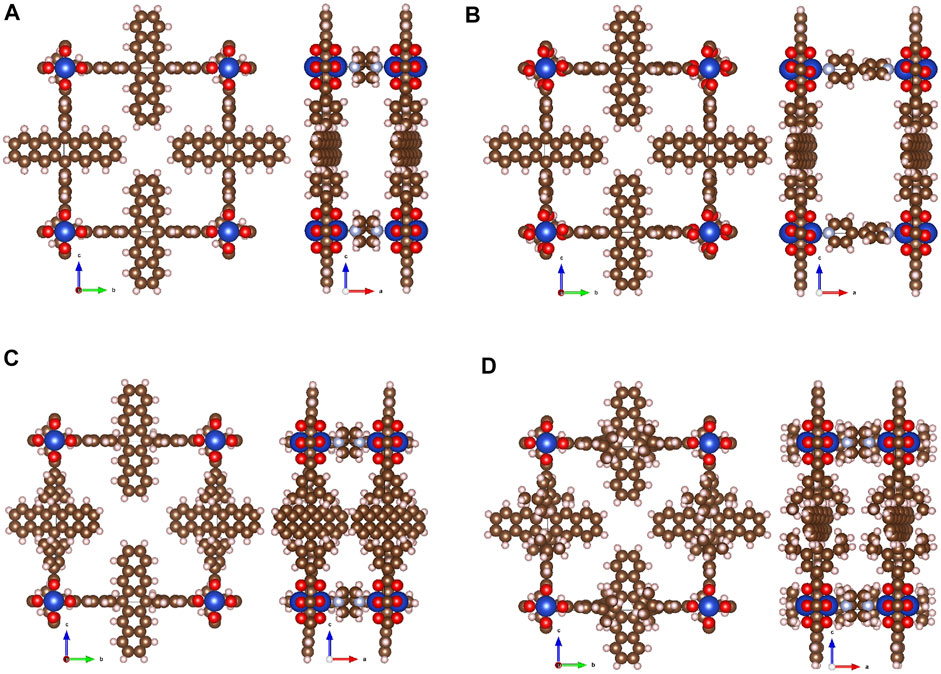
FIGURE 6. Representative structures of MOF of PCU topology obtained automatically after MOF Builder and MOF Optimizer parts of the workflow starting from coordinate files of linkers and specification of SBU type: Cu₂(Pn)₂(DABCO) (A), Cu₂(Pn)₂(bipy) (B), Cu₂(Me-Pn)₂(DABCO) (C), Cu₂(iPr-Pn)₂(DABCO) (D).

FIGURE 7

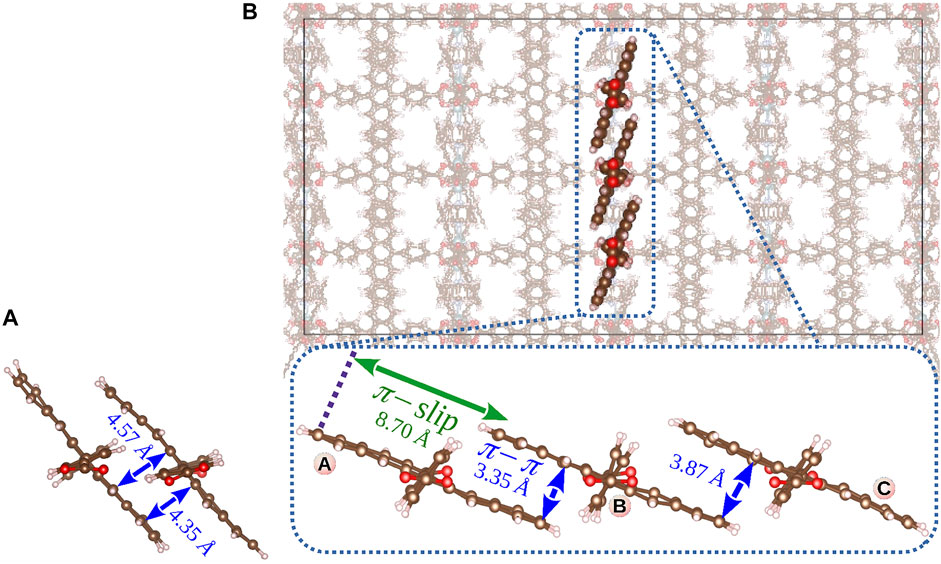
FIGURE 7. Molecular packing of the pentacene cores in a MOF as a function of MOF topology and the COM distance between ditopic linkers: dimer structure from QM/MM MD simulation of Zn paddlewheel SURMOF-2 reported by Haldar et al. (2021) (COM of 5.8 Å) (A). Cu₂(Pn)₂(DABCO) PCU-type MOF simulated in the present study and the trimer of layer linkers formed during MD simulation at 298 K (COM of 9.2 Å) (B).

MD calculations of MOFs with pristine pentacene cores and a DABCO (or pyrazine) pillar revealed system stabilization in a nanosecond scale with the formation of self-assemblies depicted in Figure 7B. Dynamical movements of linkers in these MOFs are decoupled, and after starting an MD production run, some dimers are stabilized faster (within 2 ns) and others slower (within 7 ns), e.g., dimers “A-B” and “B-C” in Figures 8B,C. However, during a 10 ns MD run, all 128 molecules in simulated supercells reached stable assemblies (similar to the ones shown in Figure 7B) without further structural changes in material. Both π–π interaction distances and π-slip are significantly changed in comparison to the dimers formed in SURMOF-2 (Figure 7A); they are also much more stable at room temperature than observed previously (Figure 8).

FIGURE 8

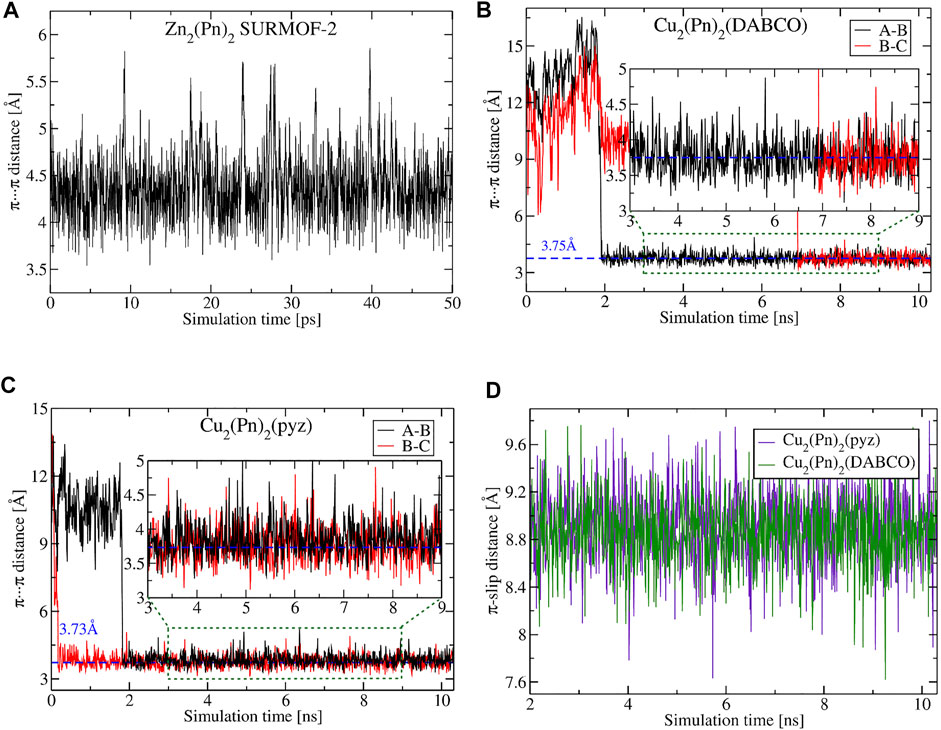
FIGURE 8. Dynamical change of π–π interaction and π-slip distances between pentacene cores in MOF materials of different topologies and COM distances obtained from MD simulations at room temperature. The π–π distance in a dimer from SURMOF-2 reported by Haldar et al. (2021) (A), in a dimer from Cu₂(Pn)₂(DABCO) (B) and Cu₂(Pn)₂(pyz) (C). The comparison of π-slip distances between layer linkers in Cu₂(Pn)₂(DABCO) and Cu₂(Pn)₂(pyz) (D). Plotted structural parameters and “A”-, “B”-, “C”-marked linkers are depicted in Figure 7.

The average values of π–π distances for both Cu₂(Pn)₂(DABCO) and Cu₂(Pn)₂(pyz) are around 3.75 Å (3.74 and 3.77–3.86 Å, respectively), and the dispersity of their change is relatively small with the variance of 0.058–0.066 Å² (for comparison, see plotted π–π distances for SURMOF-2 in Figure 8A). A larger COM distance between metal nodes in the PCU MOF, modulated by pillar linkers, results in different packing of pentacene cores in a material that enables more efficient overlap between orbitals, as was also suggested by Zojer and Winkler (2021) by screening different distances between ditopic pentacene linkers. New structuring of OSC cores impacts electronic couplings between HOMO and LUMO orbitals and, therefore, significantly stabilizes average effective coupling (Figure 9). From 1,000 snapshots collected in MD, the average value of absolute coupling between HOMO and LUMO orbitals of linkers in Cu₂(Pn)₂(DABCO) is 74.5 and 45.2 meV, respectively. The same is also observed for Cu₂(Pn)₂(pyz): J_HOMO of 77.3 meV and J_LUMO of 47.2 meV. The average values of couplings in the last 2 ns of MD are 82.2 and 78.3 meV between HOMO orbitals and 52.0 and 46.7 meV between LUMO orbitals of MOFs with DABCO and pyrazine pillars, respectively. An actual state transition of the electronic coupling is depicted in Supplementary Figures S8, S9.

FIGURE 9

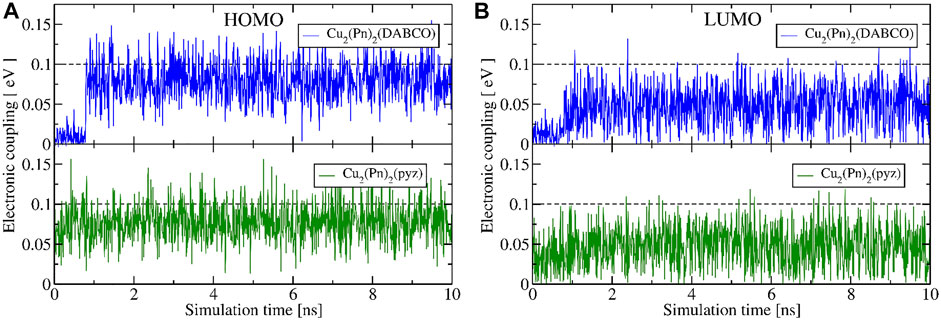
FIGURE 9. Absolute electronic coupling elements (B3LYP/def2-SVP) between HOMO (A) and LUMO (B) orbitals of ditopic pentacene linkers extracted from the force-field MD simulations of Cu₂(Pn)₂(DABCO) (in blue) and Cu₂(Pn)₂(pyz) (in green) PCU-MOFs at 298 K.

Increasing the COM distance further, e.g., by introducing bipyridine (Figure 6B), resulted in the reduction of interactions between the pentacene cores (Supplementary Figure S4). Taking into account the energy barrier for the CCCC dihedral angle rotation between the OSC linked to two phenyl rings (Supplementary Figure S5) and possible barrier-free rotations by 60–120°, large separation of ditopic linkers eliminates any possibility for an overlap between the adjacent molecules (Supplementary Figure S6). Therefore, the Cu₂(Pn)₂(bipy) MOF is not a good candidate for charge transport. For this reason, we were not continuing analysis of electronic coupling matrix elements for this system.

Another approach to modify packing of molecules in a MOF can be realized via introduction of the steric control units (SCU) (Haldar et al., 2019). We investigated two SCUs also in the present study via chemical modification of ditopic pentacene linkers by methyl and isopropyl groups. Hence, we replaced the hydrogen atoms in phenyl rings with methyl groups (Me = CH₃) or isopropyl groups (iPr = CH(CH₃)₂) (Figures 2 and 6C,D). Both systems were automatically structured in a MOF with the DABCO pillars, i.e., structures Cu₂(Me-Pn)₂(DABCO) and Cu₂(iPr-Pn)₂(DABCO). Even if the unit cells of these PCU MOFs are very similar, packing of ditopic linkers in the material and the dynamical behavior of the pentacene cores towards finding stable aggregates differ significantly. Selected snapshots of the neighboring OSC cores are depicted in Supplementary Figure S7. Addition of SCU introduces steric repulsions between neighboring ditopic linkers, disabling the formation of stable assemblies of pentacene OSC cores, as was observed for Cu₂(Pn)₂(DABCO) and Cu₂(Pn)₂(pyz). The COM distance is similar in all four cases, but packing modulated by the SCU allows only for a small coupling between the orbitals (Figure 10). This packing is not stable at room temperature, suggesting worse semiconducting properties of such MOFs. Moreover, the hindrance of efficient packing of pentacene cores depends on the size of the SCU: the addition of isopropyl group in Cu₂(iPr-Pn)₂(DABCO) reduces charge carrier transport in the material (Figure 10B), resulting in average electronic coupling of 1.7 meV (HOMO orbitals) and 3.9 meV (LUMO orbitals).

FIGURE 10

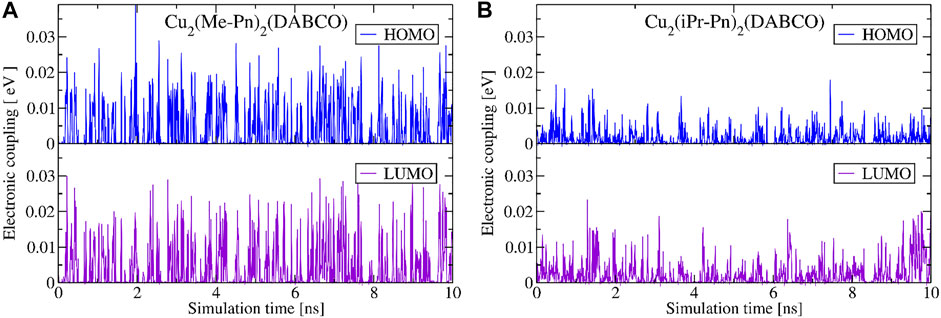
FIGURE 10. Absolute electronic coupling elements (B3LYP/def2-SVP) between HOMO (in blue) and LUMO (in purple) orbitals of functionalized ditopic pentacene linkers (Me-Pn and iPr-Pn, Figure 2) extracted from the force-field MD simulations of Cu₂(Me-Pn)₂(DABCO) (A) and Cu₂(iPr-Pn)₂(pyz) (B) PCU-MOFs at 298 K.

From several examples studied in this report, it is seen that subtle modifications in the chemical composition of MOF components or type of MOF topology result in significant differences in the assemblies of OSC pentacene cores and their dynamically averaged stacking. Introduction of steric control units induces additional steric repulsion, suppressing preferable orientation of pentacene cores (which is observed in the case of pristine ditopic linkers), lowering charge carrier transport. Spatial control of the separation distance between OSC cores via the length of the pillar linker allows us to optimize stacking and increase the average effective couplings for the hole transport up to 75 meV, retaining structural stability at finite temperature. Virtual screening of other linker molecules, their packing in a MOF, and resulting electronic properties is possible using automated workflows reported in this study.

4 Conclusion

We developed an automated workflow tool for virtual design of new MOF materials of the PCU topology with the subsequent prediction of electronic properties. This reproducible, transferable, and adaptable computational protocol (Mostaghimi et al., 2020) allows us to build MOF structures, optimize them using different levels of theory, and analyze electronic coupling matrix elements in dynamically averaged assemblies at finite temperature. We demonstrate the functionality of the developed software by preliminary in silico crystal engineering of molecular assemblies of pentacene OSC. For this, we constructed MOF structures based on pristine and chemically functionalized pentacene ditopic linkers (as layer linkers) and DABCO, pyrazine, and bipyridine (as pillar linkers). Copper paddlewheel nodes were used to keep the three-dimensional order of organic molecules in a material.

All structures were automatically optimized and further investigated using the MD approach. We have shown the change of the stacking type between ditopic linkers with pentacene OSC cores as a function of the intermolecular separation in MOFs controlled by different sizes of MOF pillars. We have proven that stacking of pristine ditopic linkers is more efficient, where the metal node distances are around 9 Å, enabling better overlap of HOMO and LUMO orbitals of OSC cores, increasing both hole and electron conduction, respectively. Moreover, the analysis of the π–π interactions and π-slip changes during 10 ns MD production runs confirmed higher MOF nanostructure stability at room temperature, addressing the concept reported by Haldar et al. (2021) and supporting hypotheses postulated by Zojer and Winkler (2021). The average effective electronic coupling between OSC in Cu₂(Pn)₂(DABCO) and Cu₂(Pn)₂(pyz) was calculated to be 78–82 and 46–52 meV between HOMO and LUMO orbitals, respectively.

Using the developed workflow, we have demonstrated the reduction of the electronic conduction propensity of PCU-type MOF materials fabricated from ditopic pentacene linkers with introduced steric control units (methyl and isopropyl groups). This observation resulted from steric repulsions between neighboring organic linkers in the MOF scaffold, suppressing the formation of the optimal interaction assemblies with high molecular orbital overlap integrals. The exceptional sensitivity of the semiconducting properties of MOFs upon the specific details of the molecular assembly inside a material, modulated by subtle chemical modifications of building components, illustrates the importance of screening protocols for both organic molecules and their structuring in MOFs. The availability of the automated workflow tools reported in this study significantly simplifies the tasks involved in these investigations.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

MM: software and WaNos development (LCmaker, AuToGraFS, GULP, lammps-interface, LAMMPS, Achmol, SuperCeller), investigation, visualization, drafting the paper; CR: SimStack support, WaNos development (DFT-VASP, Format-Converter), paper review; RH: paper review and editing; CW: paper review and editing; WW: conceptualization, resources, funding acquisition, paper review and editing; MK: conceptualization, supervision, investigation, funding acquisition, paper writing, review and editing.

Funding

This research has been funded by Deutsche Forschungsgemeinschaft (DFG) SPP priority program COORNETs “Coordination Networks: Building Blocks for Functional Systems” (SPP1928, grant number WE 1863/37-1). Authors acknowledge funding by the DFG under the Germany Excellence Strategy via the Excellence Cluster 3D Matter Made to Order (Grant No. EXC-2082/1–390761711) and the GRK 2450 “Scale bridging methods of computational nanoscience”, as also the Virtual Materials Design initiative (Virtmat) funded by KIT. WW and CR thank the German Federal Ministry of Education and Research (BMBF) for financial support of the project Innovation-Platform MaterialDigital (www.materialdigital.de) through project funding FKZ no: 13XP5094A. MK acknowledges funding by the Ministry of Science, Research and Art of Baden-Württemberg (Germany) under Brigitte-Schlieben-Lange-Programm.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Authors are grateful to Yohanes Pramudya and Modan Liu for fruitful discussions. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.840644/full#supplementary-material

References

Addicoat, M. A., Coupry, D. E., and Heine, T. (2014). AuToGraFS: Automatic Topological Generator for Framework Structures. The J. Phys. Chem. A 118, 9607–9614. doi:10.1021/jp507643v

CrossRef Full Text | Google Scholar

Addicoat, M. A., Vankova, N., Akter, I. F., and Heine, T. (2014). Extension of the Universal Force Field to Metal–Organic Frameworks. J. Chem. Theor. Comput. 10, 880–891. doi:10.1021/ct400952t

PubMed Abstract | CrossRef Full Text | Google Scholar

Alvaro, M., Carbonell, E., Ferrer, B., Llabrés i Xamena, F. X., and Garcia, H. (2007). Semiconductor Behavior of a Metal-Organic Framework (MOF). Chemistry (Weinheim an Der Bergstrasse, Germany) 13, 5106–5112. doi:10.1002/chem.200601003

PubMed Abstract | CrossRef Full Text | Google Scholar

Balasubramani, S. G., Chen, G. P., Coriani, S., Diedenhofen, M., Frank, M. S., Franzke, Y. J., et al. (2020). TURBOMOLE: Modular Program Suite for Ab Initio Quantum-Chemical and Condensed-Matter Simulations. J. Chem. Phys. 152, 184107. doi:10.1063/5.0004635

CrossRef Full Text | Google Scholar

Becke, A. D. (1993). Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98, 5648–5652. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

Bhattacharya, S., Gnanavel, M., Bhattacharyya, A. J., and Natarajan, S. (2014). Organization of Mn-Clusters in Pcu and Bcu Networks: Synthesis, Structure, and Properties. Cryst. Growth Des. 14, 310–325. doi:10.1021/cg401587r

CrossRef Full Text | Google Scholar

Boyd, P. G., Moosavi, S. M., Witman, M., and Smit, B. (2017). Force-Field Prediction of Materials Properties in Metal-Organic Frameworks. J. Phys. Chem. Lett. 8, 357–363. doi:10.1021/acs.jpclett.6b02532

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyd, P. G., and Woo, T. K. (2016). A Generalized Method for Constructing Hypothetical Nanoporous Materials of Any Net Topology from Graph Theory. CrystEngComm 18, 3777–3792. doi:10.1039/C6CE00407E

CrossRef Full Text | Google Scholar

Bučko, T., Lebègue, S., Hafner, J., and Ángyán, J. G. (2013). Improved Density Dependent Correction for the Description of London Dispersion Forces. J. Chem. Theor. Comput. 9, 4293–4299. doi:10.1021/ct400694h

CrossRef Full Text | Google Scholar

Chung, Y. G., Camp, J., Haranczyk, M., Sikora, B. J., Bury, W., Krungleviciute, V., et al. (2014). Computation-Ready, Experimental Metal–Organic Frameworks: A Tool to Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mater. 26, 6185–6192. doi:10.1021/cm502594j

CrossRef Full Text | Google Scholar

Colón, Y. J., Gómez-Gualdrón, D. A., and Snurr, R. Q. (2017). Topologically Guided, Automated Construction of Metal–Organic Frameworks and Their Evaluation for Energy-Related Applications. Cryst. Growth Des. 17, 5801–5810. doi:10.1021/acs.cgd.7b00848

CrossRef Full Text | Google Scholar

Connolly, B. M., Madden, D. G., Wheatley, A. E. H., and Fairen-Jimenez, D. (2020). Shaping the Future of Fuel: Monolithic Metal–Organic Frameworks for High-Density Gas Storage. J. Am. Chem. Soc. 142, 8541–8549. doi:10.1021/jacs.0c00270

PubMed Abstract | CrossRef Full Text | Google Scholar

Coupry, D. E., Addicoat, M. A., and Heine, T. (2016). Extension of the Universal Force Field for Metal-Organic Frameworks. J. Chem. Theor. Comput. 12, 5215–5225. doi:10.1021/acs.jctc.6b00664

CrossRef Full Text | Google Scholar

Dassault Systèmes (2020). BIOVIA Materials Studio - BIOVIA - Dassault Systèmes®. Available at: https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio/.

Google Scholar

D’Avino, G., Muccioli, L., Castet, F., Poelking, C., Andrienko, D., Soos, Z. G., et al. (2016). Electrostatic Phenomena in Organic Semiconductors: Fundamentals and Implications for Photovoltaics. J. Phys. Condensed Matter 28, 433002. doi:10.1088/0953-8984/28/43/433002

CrossRef Full Text | Google Scholar

Freund, R., Canossa, S., Cohen, S. M., Yan, W., Deng, H., Guillerm, V., et al. (2021). 25 Years of Reticular Chemistry. Angew. Chem. Int. Edition 60, 23946–23974. doi:10.1002/anie.202101644

CrossRef Full Text | Google Scholar

Friederich, P., Symalla, F., Meded, V., Neumann, T., and Wenzel, W. (2014). Ab Initio treatment of Disorder Effects in Amorphous Organic Materials: Toward Parameter Free Materials Simulation. J. Chem. Theor. Comput. 10, 3720–3725. doi:10.1021/ct500418f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gale, J. D., and Rohl, A. L. (2003). The General Utility Lattice Program (GULP). Mol. Simulation 29, 291–341. doi:10.1080/0892702031000104887

CrossRef Full Text | Google Scholar

Garg, S., Schwartz, H., Kozlowska, M., Kanj, A. B., Müller, K., Wenzel, W., et al. (2019). Conductance Photoswitching of Metal–Organic Frameworks with Embedded Spiropyran. Angew. Chem. Int. Edition 58, 1193–1197. doi:10.1002/anie.201811458

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldman, A., Gil-Hernández, B., Millan, S., Gökpinar, S., Heering, C., Boldog, I., et al. (2020). Flexible Bifunctional Monoethylphosphonate/carboxylates of Zn(II) and Co(II) Reinforced with DABCO Co-ligand: Paradigmatic Structural Organization with Pcu Topology. CrystEngComm 22, 2933–2944. doi:10.1039/D0CE00275E

CrossRef Full Text | Google Scholar

Goswami, S., Ma, L., Martinson, A. B. F., Wasielewski, M. R., Farha, O. K., and Hupp, J. T. (2016). Toward Metal–Organic Framework-Based Solar Cells: Enhancing Directional Exciton Transport by Collapsing Three-Dimensional Film Structures. ACS Appl. Mater. Inter. 8, 30863–30870. doi:10.1021/acsami.6b08552

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344

CrossRef Full Text | Google Scholar

Haldar, R., Heinke, L., and Wöll, C. (2020). Advanced Photoresponsive Materials Using the Metal–Organic Framework Approach. Adv. Mater. 32, 1905227. doi:10.1002/adma.201905227

PubMed Abstract | CrossRef Full Text | Google Scholar

Haldar, R., Kozlowska, M., Ganschow, M., Ghosh, S., Jakoby, M., Chen, H., et al. (2021). Interplay of Structural Dynamics and Electronic Effects in an Engineered Assembly of Pentacene in a Metal–Organic Framework. Chem. Sci. 12, 4477–4483. doi:10.1039/D0SC07073D

PubMed Abstract | CrossRef Full Text | Google Scholar

Haldar, R., Mazel, A., Krstic, M., Zhang, Q., Jakoby, M., Howard, I. A., et al. (2019). A De Novo Strategy for Predictive crystal Engineering to Tune Excitonic Coupling. Nat. Commun. 10, 2048. doi:10.1038/s41467-019-10011-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Heinke, L., Cakici, M., Dommaschk, M., Grosjean, S., Herges, R., Bräse, S., et al. (2014). Photoswitching in Two-Component Surface-Mounted Metal–Organic Frameworks: Optically Triggered Release from a Molecular Container. ACS Nano 8, 1463–1467. doi:10.1021/nn405469g

PubMed Abstract | CrossRef Full Text | Google Scholar

Heinke, L., and Wöll, C. (2019). Surface-Mounted Metal–Organic Frameworks: Crystalline and Porous Molecular Assemblies for Fundamental Insights and Advanced Applications. Adv. Mater. 31, 1806324. doi:10.1002/adma.201806324

PubMed Abstract | CrossRef Full Text | Google Scholar

Jurchescu, O. D., Popinciuc, M., van Wees, B. J., and Palstra, T. T. M. (2007). Interface-controlled, High-Mobility Organic Transistors. Adv. Mater. 19, 688–692. doi:10.1002/adma.200600929

CrossRef Full Text | Google Scholar

Kalmutzki, M. J., Hanikel, N., and Yaghi, O. M. (2018). Secondary Building Units as the Turning point in the Development of the Reticular Chemistry of MOFs. Sci. Adv. 4, eaat9180. doi:10.1126/sciadv.aat9180

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanj, A. B., Müller, K., and Heinke, L. (2018). Stimuli-Responsive Metal-Organic Frameworks with Photoswitchable Azobenzene Side Groups. Macromolecular Rapid Commun. 39, 1700239. doi:10.1002/marc.201700239

PubMed Abstract | CrossRef Full Text | Google Scholar

Kera, S., Yamane, H., and Ueno, N. (2009). First-principles Measurements of Charge Mobility in Organic Semiconductors: Valence Hole–Vibration Coupling in Organic Ultrathin Films. Prog. Surf. Sci. 84, 135–154. doi:10.1016/j.progsurf.2009.03.002

CrossRef Full Text | Google Scholar

Kreno, L. E., Leong, K., Farha, O. K., Allendorf, M., Van Duyne, R. P., and Hupp, J. T. (2012). Metal–Organic Framework Materials as Chemical Sensors. Chem. Rev. 112, 1105–1125. doi:10.1021/cr200324t

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab Initio molecular Dynamics for Liquid Metals. Phys. Rev. B 47, 558–561. doi:10.1103/physrevb.47.558

PubMed Abstract | CrossRef Full Text | Google Scholar

Larsen, A. H., Mortensen, J. J., Blomqvist, J., Castelli, I. E., Christensen, R., Du∖lak, M., et al. (2017). The Atomic Simulation Environment—A Python Library for Working with Atoms. J. Phys. Condensed Matter 29, 273002. doi:10.1088/1361-648X/aa680e

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 37, 785–789. doi:10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Eddaoudi, M., Groy, T. L., and Yaghi, O. M. (1998). Establishing Microporosity in Open Metal-Organic Frameworks:Gas Sorption Isotherms for Zn (BDC)( BDC= 1 ,4-Benzenedicarboxylate). J. Am. Chem. Soc. 120, 8571–8572. doi:10.1021/ja981669x

CrossRef Full Text | Google Scholar

Li, H., Eddaoudi, M., O’Keeffe, M., and Yaghi, O. M. (1999). Design and Synthesis of an Exceptionally Stable and Highly Porous Metal-Organic Framework. Nature 402, 276–279. doi:10.1038/46248

CrossRef Full Text | Google Scholar

Li, H., Wang, K., Sun, Y., Lollar, C. T., Li, J., and Zhou, H. C. (2018). Recent Advances in Gas Storage and Separation Using Metal–Organic Frameworks. Mater. Today 21, 108–121. doi:10.1016/j.mattod.2017.07.006

CrossRef Full Text | Google Scholar

Li, J. R., Tao, Y., Yu, Q., and Bu, X. H. (2007). A Pcu-type Metal–Organic Framework with Spindle [Zn 7 (OH) 8 ] 6+ Cluster as Secondary Building Units. Chem. Commun. 0, 1527–1529. doi:10.1039/B615675D

CrossRef Full Text | Google Scholar

Lin, J. D., Rong, C., Lv, R. X., Wang, Z. J., Long, X. F., Guo, G. C., et al. (2018). A 3D Metal-Organic Framework with a Pcu Net Constructed from Lead(II) and Thiophene-2, 5-dicarboxylic Acid: Synthesis, Structure and Ferroelectric Property. J. Solid State. Chem. 257, 34–39. doi:10.1016/j.jssc.2017.09.001

CrossRef Full Text | Google Scholar

Lin, R. B., Xiang, S., Zhou, W., and Chen, B. (2020). Microporous Metal-Organic Framework Materials for Gas Separation. Chem 6, 337–363. doi:10.1016/j.chempr.2019.10.012

CrossRef Full Text | Google Scholar

Liu, B., Ma, M., Zacher, D., Bétard, A., Yusenko, K., Metzler-Nolte, N., et al. (2011). Chemistry of SURMOFs: Layer-Selective Installation of Functional Groups and Post-synthetic Covalent Modification Probed by Fluorescence Microscopy. J. Am. Chem. Soc. 133, 1734–1737. doi:10.1021/ja1109826

CrossRef Full Text | Google Scholar

Liu, B., Shekhah, O., Arslan, H. K., Liu, J., Wöll, C., and Fischer, R. A. (2012). Enantiopure Metal–Organic Framework Thin Films: Oriented SURMOF Growth and Enantioselective Adsorption. Angew. Chem. Int. Edition 51, 807–810. doi:10.1002/anie.201104240

CrossRef Full Text | Google Scholar

Liu, J., and Wöll, C. (2017). Surface-supported Metal–Organic Framework Thin Films: Fabrication Methods, Applications, and Challenges. Chem. Soc. Rev. 46, 5730–5770. doi:10.1039/C7CS00315C

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Kozlowska, M., Okkali, T., Wagner, D., Higashino, T., Brenner-Weifss, G., et al. (2019). Photoconductivity in Metal-Organic Framework (MOF) Thin Films. Angew. Chemie-International Edition 58, 9590–9595. doi:10.1002/anie.201904475

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, T. Y., Liu, C., Eliseeva, S. V., Muldoon, P. F., Petoud, S., and Rosi, N. L. (2017). Rare Earth Pcu Metal–Organic Framework Platform Based on RE4(M3-OH)4(COO)62+ Clusters: Rational Design, Directed Synthesis, and Deliberate Tuning of Excitation Wavelengths. J. Am. Chem. Soc. 139, 9333–9340. doi:10.1021/jacs.7b04532

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyu, H., Ji, Z., Wuttke, S., and Yaghi, O. M. (2020). Digital Reticular Chemistry. Chem 6, 2219–2241. doi:10.1016/j.chempr.2020.08.008

CrossRef Full Text | Google Scholar

Mailman, A., Leitch, A. A., Yong, W., Steven, E., Winter, S. M., Claridge, R. C. M., et al. (2017). The Power of Packing: Metallization of an Organic Semiconductor. J. Am. Chem. Soc. 139, 2180–2183. doi:10.1021/jacs.6b12814

PubMed Abstract | CrossRef Full Text | Google Scholar

Mancuso, J. L., Mroz, A. M., Le, K. N., and Hendon, C. H. (2020). Electronic Structure Modeling of Metal–Organic Frameworks. Chem. Rev. 120, 8641–8715. doi:10.1021/acs.chemrev.0c00148

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcus, R. A. (1993). Electron Transfer Reactions in Chemistry. Theory and experiment. Rev. Mod. Phys. 65, 1111–1121. doi:10.1002/anie.199311113

CrossRef Full Text | Google Scholar

Martin, R. L., and Haranczyk, M. (2014). Construction and Characterization of Structure Models of Crystalline Porous Polymers. Cryst. Growth Des. 14, 2431–2440. doi:10.1021/cg500158c

CrossRef Full Text | Google Scholar

Moosavi, S. M., Nandy, A., Jablonka, K. M., Ongari, D., Janet, J. P., Boyd, P. G., et al. (2020). Understanding the Diversity of the Metal-Organic Framework Ecosystem. Nat. Commun. 11, 4068. doi:10.1038/s41467-020-17755-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Mostaghimi, M., Rêgo, C., Wenzel, W., and Kozlowska, M. (2020). PCU-MOF Workflow. Genève, Switzerland: Zenodo. doi:10.5281/zenodo.5893325

CrossRef Full Text | Google Scholar

Narayan, T. C., Miyakai, T., Seki, S., and Dincă, M. (2012). High Charge Mobility in a Tetrathiafulvalene-Based Microporous Metal–Organic Framework. J. Am. Chem. Soc. 134, 12932–12935. doi:10.1021/ja3059827

CrossRef Full Text | Google Scholar

Nefedov, A., Haldar, R., Xu, Z., Kühner, H., Hofmann, D., Goll, D., et al. (2021). Avoiding the Center-Symmetry Trap: Programmed Assembly of Dipolar Precursors into Porous, Crystalline Molecular Thin Films. Adv. Mater. 33, 2103287. doi:10.1002/adma.202103287

CrossRef Full Text | Google Scholar

Neumann, T., Liu, J., Wächter, T., Friederich, P., Symalla, F., Welle, A., et al. (2016). Superexchange Charge Transport in Loaded Metal Organic Frameworks. ACS Nano 10, 7085–7093. doi:10.1021/acsnano.6b03226

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Boyle, N. M., Banck, M., James, C. A., Morley, C., Vandermeersch, T., and Hutchison, G. R. (2011). Open Babel: An Open Chemical Toolbox. J. Cheminformatics 3, 33. doi:10.1186/1758-2946-3-33

CrossRef Full Text | Google Scholar

Öhrström, L. (2015). Let’s Talk about MOFs—Topology and Terminology of Metal-Organic Frameworks and Why We Need Them. Crystals 5, 154–162. doi:10.3390/cryst5010154

CrossRef Full Text | Google Scholar

O’Keeffe, M., Peskov, M. A., Ramsden, S. J., and Yaghi, O. M. (2008). The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, crystal Nets. Acc. Chem. Res. 41, 1782–1789. doi:10.1021/ar800124u

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Keeffe, M., and Yaghi, O. M. (2012). Deconstructing the Crystal Structures of Metal–Organic Frameworks and Related Materials into Their Underlying Nets. Chem. Rev. 112, 675–702. doi:10.1021/cr200205j

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (19961997). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.Physical Rev. Lett. 7778, 38651396–1396. doi:10.1103/PhysRevLett.78.1396

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S., Kohlmeyer, A., Thompson, A., Moore, S., and Berger, R. (2020). LAMMPS Stable Release 29 October 2020. Genève, Switzerland: Zenodo. doi:10.5281/zenodo.4157471

CrossRef Full Text | Google Scholar

Pohl, U. W. (2020). “Electronic Properties of Organic Semiconductors,” in Epitaxy of Semiconductors: Physics and Fabrication of Heterostructures. Editor U. W. Pohl (Cham, Switzerland: Springer International Publishing), 177–205. Graduate Texts in Physics. doi:10.1007/978-3-030-43869-2_5

CrossRef Full Text | Google Scholar

Qiao, J., Liu, X., Liu, X., Liu, X., Zhang, L., and Liu, Y. (2020). Two Urea-Functionalized Pcu Metal–Organic Frameworks Based on a Pillared-Layer Strategy for Gas Adsorption and Separation. Inorg. Chem. Front. 7, 3500–3508. doi:10.1039/D0QI00641F

CrossRef Full Text | Google Scholar

Ricardo, C. (2021). KIT-Workflows/DFT-VASP: DFT-VASP. Genève, Switzerland: Zenodo. doi:10.5281/zenodo.5501531

CrossRef Full Text | Google Scholar

Rowsell, J. L. C., and Yaghi, O. M. (2004). Metal–organic Frameworks: A New Class of Porous Materials. Microporous Mesoporous Mater. 73, 3–14. doi:10.1016/j.micromeso.2004.03.034

CrossRef Full Text | Google Scholar

Schlöder, T., and Rêgo, C. (2022). Kit-workflows/dft-turbomole. Available at https://github.com/KIT-Workflows (accessed Sept 12, 2021).

Google Scholar

Schoedel, A., and Yaghi, O. M. (2016). “Porosity in Metal-Organic Compounds,” in Macrocyclic and Supramolecular Chemistry. Editor R. M. Izatt (Chichester, UK: John Wiley & Sons), 200–219. doi:10.1002/9781119053859.ch9

CrossRef Full Text | Google Scholar

Stock, N., and Biswas, S. (2012). Synthesis of Metal-Organic Frameworks (MOFs): Routes to Various MOF Topologies, Morphologies, and Composites. Chem. Rev. 112, 933–969. doi:10.1021/cr200304e

PubMed Abstract | CrossRef Full Text | Google Scholar

Turcani, L., Tarzia, A., Szczypiński, F. T., and Jelfs, K. E. (2021). Stk: An Extendable Python Framework for Automated Molecular and Supramolecular Structure Assembly and Discovery. J. Chem. Phys. 154, 214102. doi:10.1063/5.0049708

CrossRef Full Text | Google Scholar

Virkar, A., Mannsfeld, S., Oh, J. H., Toney, M. F., Tan, Y. H., Liu, G. Y., et al. (2009). The Role of OTS Density on Pentacene and C60 Nucleation, Thin Film Growth, and Transistor Performance. Adv. Funct. Mater. 19, 1962–1970. doi:10.1002/adfm.200801727

CrossRef Full Text | Google Scholar

Wei, W., Wang, X., Zhang, K., Tian, C. B., and Du, S. W. (2019). Tuning the Topology from Fcu to Pcu: Synthesis and Magnetocaloric Effect of Metal–Organic Frameworks Based on a Hexanuclear Gd(III)-Hydroxy Cluster. Cryst. Growth Des. 19, 55–59. doi:10.1021/acs.cgd.8b01566

CrossRef Full Text | Google Scholar

Weigend, F., and Ahlrichs, R. (2005). Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 7, 3297. doi:10.1039/b508541a

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, L. S., Skorupskii, G., and Dincă, M. (2020). Electrically Conductive Metal–Organic Frameworks. Chem. Rev. 120, 8536–8580. doi:10.1021/acs.chemrev.9b00766

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, J., Schweighauser, L., Okada, S., Harano, K., and Nakamura, E. (2019). Atomistic Structures and Dynamics of Prenucleation Clusters in MOF-2 and MOF-5 Syntheses. Nat. Commun. 10, 3608. doi:10.1038/s41467-019-11564-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, G., Guo, G. C., Yao, M. S., Fu, Z. H., and Wang, G. E. (2016). The Chemistry of Metal–Organic Frameworks. Hoboken, New Jersey, United States: John Wiley & Sons, 421–462. chap. 14. doi:10.1002/9783527693078.ch14Functional Linkers for Electron-Conducting MOFs

CrossRef Full Text | Google Scholar

Yao, S. L., Tian, X. M., Li, L. Q., Liu, S. J., Zheng, T. F., Chen, Y. Q., et al. (2019). A CdII-Based Metal-Organic Framework with Pcu Topology as Turn-On Fluorescent Sensor for Al3+. Chem. – Asian J. 14, 3648–3654. doi:10.1002/asia.201900739

PubMed Abstract | CrossRef Full Text | Google Scholar

Yazdanparast, M. S., Day, V. W., and Gadzikwa, T. (2020). Hydrogen-Bonding Linkers Yield a Large-Pore, Non-catenated, Metal-Organic Framework with Pcu Topology. Molecules 25, 697. doi:10.3390/molecules25030697

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuang, J. L., Terfort, A., and Wöll, C. (2016). Formation of Oriented and Patterned Films of Metal–Organic Frameworks by Liquid Phase Epitaxy: A Review. Coord. Chem. Rev. 307, 391–424. doi:10.1016/j.ccr.2015.09.013

CrossRef Full Text | Google Scholar

Zojer, E., and Winkler, C. (2021). Maximizing the Carrier Mobilities of Metal–Organic Frameworks Comprising Stacked Pentacene Units. J. Phys. Chem. Lett. 12, 7002–7009. doi:10.1021/acs.jpclett.1c01892

CrossRef Full Text | Google Scholar