Dry Textile Forming Simulations: A Benchmarking Exercise

Sun, Xiaochuan; Belnoue, Jonathan P.-H.; Thompson, Adam; Said, Bassam El; Hallett, Stephen R.

doi:10.3389/fmats.2022.831820

ORIGINAL RESEARCH article

Front. Mater., 16 March 2022

Sec. Polymeric and Composite Materials

Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.831820

This article is part of the Research Topic 2022 Retrospective: Polymeric and Composite Materials View all 7 articles

Dry Textile Forming Simulations: A Benchmarking Exercise

Xiaochuan Sun*

Jonathan P.-H. Belnoue

Adam Thompson

Bassam El Said

Stephen R. Hallett

Bristol Composites Institute, University of Bristol, University Walk, Bristol, United Kingdom

In this study, four representative finite element (FE) based modelling techniques and an analytical solution for the prediction of 2D woven fabrics’ deformation during forming are compared back-to-back. Ordered from high to low fidelity they are: 1/a Multi-Filament (MF) method that sits between micro- and meso-scale that uses multiple beam element chains to represent each fibre yarn; 2/a meso-scale 3D representation (3D-Shell method) that uses 2D structural shell elements to model each fibre yarn; 3/a 2D continuum element approach that uses coincident membrane and shell elements with user defined material properties to capture the deformation response of textiles in an homogenised sense at the macro-scale; 4/pin-jointed net (PJN) models where the reinforcement directions are represented by extendable 1D elements, pin-jointed at the elements’ crossover points. These modelling approaches are systematically compared for identical forming processes with identical process and material parameters such as boundary conditions, weave architecture and tooling geometries. For completeness and to highlight the importance of considering inter-yarn and preform-to-tool interactions, a kinematic drape algorithm (based on geometrical mapping) is also considered. An attempt is made to visualise the overall modelling performance and computational cost of all representative modelling approaches by simplified metrics.

1 Introduction

With the increasing use of carbon fibre reinforced polymers (CFRPs) for structural and non-structural applications in many industries, reduction in manufacturing cost while increasing production volume has become a key driver in both academia and industry. Among all available fibre reinforcement in CFRPs, dry carbon fibre reinforced biaxial woven fabrics have several unique advantages and attractive to many structural applications. They are cost effective, easier to handle, more stable, and they have more balanced mechanical properties and superior formability. 2D woven composites are normally formed into shapes (either on a layer-by-layer basis or as a stack) and then consolidated, infused and finally cured. Among these processes, fabric forming is a key manufacturing step controlling the final quality of parts and requires particular attention. During forming, materials are forced to deform from 2D sheets into 3D shapes and undergo large deformations. At the end of forming, fibre orientations are set on 3D contours. Defects can be induced as the results of the large deformation of the material due to the process constraints and the nature of the material. If defects are not identified early on, they will also affect local material properties after consolidation and/or locally affect resin flow and fabric impregnation, which will ultimately impact parts’ structural performance (Loix et al., 2008; Arbter et al., 2011; Walther et al., 2012; Bloom et al., 2013; Bodaghi et al., 2019; Varkonyi et al., 2020; Rashidi et al., 2021a). Understanding the deformation mechanics of textile and their interactions with tooling during the forming process is key in understanding defect formation and ways to defect-free composites (Liang and Boisse, 2021; Wielhorski et al., 2022).

It has long been thought that robust and efficient numerical process simulations that are able to capture the full response of textile preforms during forming and help reduce material waste and cost associated with the traditional trial-and-error approach and ensure a consistent quality in production of structural composite components. Many efforts have been made to simulate textile composites during forming (or draping) processes by either closed-loop analytical approximations or by finite element analysis (FEA). In the former case, geometric mapping (or kinematic draping analysis) is normally adopted at early design/optimisation process (Krogh et al., 2020). Pin-jointed trellis structures are used to represent the woven fabric in an analytical format (Wang et al., 1999; Cherouat et al., 2005; Skordos et al., 2007; Hearle, 2011). The tensile modulus of the fabric is assumed to be infinite whilst the other moduli are taken as negligible. This method, based on geometrical mapping, is attractive to industry for its low computational cost and allows approximate of fibre re-orientation on complex moulds. However, due to its formulation, it has limited predictive capabilities to reflect the distinct deformation mechanics of fabrics, forming mechanics and the effects of boundary conditions given to the preform. On the other hand, FEA-based models use user-defined material models that are normally validated by material characterisation testing while taking into account the fabrics’ deformation mechanics and preform/tooling interactions. Forming process constraints such as those given by diaphragms in double diaphragm forming (DDF) or by blank holders in punch forming, deep drawn and die (such as that in RTM process) can be easily captured by commercial FEA software with minimum manual interventions (Rashidi et al., 2021b). FEA-based modelling is however more difficult to set-up during pre-processing stage and is often associated with long run-times. Compromise has to be made between the level of fidelity and computational resource available for optimisation purposes (Kärger et al., 2018; Henning et al., 2019).

For multi-ply forming of 2D fabric or compaction/weaving analyses of 3D woven fabrics, their mechanical properties are highly influenced by their compacted or formed geometry and tool geometry, because woven fabrics may experience different level of compaction load and constraint in a single forming case at various locations, and this mesoscale deformation has significant impact on their mechanical performance (Mahadik and Hallett, 2011). Other efforts aiming at explicitly modelling yarn interaction within textiles have also been made. These techniques include the multi-filament methods (1D truss/beam element) (Durville, 2005; Miao et al., 2008; Durville, 2010a; Yousaf et al., 2018) or other 2D elements structured as fibre yarns (El Said et al., 2015; Thompson et al., 2018a) or continuum elements (Boisse et al., 2005; Creech and Pickett, 2006; Charmetant et al., 2011; Gatouillat et al., 2013; Iwata et al., 2019; Wang et al., 2020). They are typically referred to as micro-mesoscale (fibre bundles are modelled) or mesoscale modelling (fibre yarns are modelled), respectively (Wang and Sun, 2001; Sun and Sun, 2004; Wang et al., 2010; Durville, 2010b; Durville, 2021). Due to their high computational cost, these models are normally used for modelling detailed geometry of 2D fabrics or 3D complex woven fabrics at the size of a unit cell and only a few attempts have been made at using them to model an entire preform (Thompson et al., 2018a). However, these models provide the full digital representations of fibre yarns and their outcomes are detailed enough to be post-processed for other manufacturing process modelling or transferred to mechanical virtual testing (Wang et al., 2010).

The present study has conducted a thorough benchmarking exercise of the above-mentioned methods against each other, with the aim of supporting designers and engineers in making choices between required level of accuracy and computational efficiency. Three modelling approaches of different fidelity, developed and implemented at Bristol Composite Institute (BCI), across different modelling platforms are considered. These are supplemented by a kinematic drape model (Krogh et al., 2021; Krogh et al., 2019) and a FEA-based PJN (FE-PJN) model. The FE-PJN model resembles kinematic drape analysis (Skordos et al., 2007); the same assumptions are made but it is implemented in a finite element environment which allows for the interaction between preform and tooling to be taken into account. Therefore, it was expected to have a similar run time but achieve higher predictive capabilities than its analytical counterpart (i.e. kinematic draping). As shown in Figure 1, the three other FEA-based method considered in this study are 1) a 2D shell/membrane elements with user defined material properties (referred as HypoDrape hereafter) which captures the deformation response of textile composites at the macroscale (i.e. in an homogenised sense) (Thompson et al., 2017; Thompson et al., 2018b); 2) the Multi-Filament (MF) method that sits between micro- and meso-scale and uses multiple beam element chains to represent each fibre yarn (El Said et al., 2014; Green and Long, 2014; Thompson et al., 2017); and 3) a meso-scale 3D representation using structured shell elements (referred as 3DShell hereafter) to model each fibre yarn (El Said et al., 2014). It is noted that including forming-induced defects using the selected modelling approaches may lead to additional computational cost and very significantly (unfairly) skew the results of this benchmarking exercise against the method of higher resolution that are more capable of capturing these defects. To counteract these, mould shapes and forming method were designed in such way that the occurrence of manufacturing defects was kept to a minimum. A plain weave fibre architecture forming on simple hemispheric and tetrahedral tool shapes are used in this study.

FIGURE 1

FIGURE 1. Modelling framework and chracteristics of each modelling approach used for comparison.

Attributes of each selected modelling approach is summarised in Table 1. The last column of the table summarises the main assumption behind the models and their ability or not to account for six basic fabric deformation modes that are known to affect the fabric behaviour during forming (Harrison, 2016). The higher the method resolution, the more accurate deformation it can capture. These are complemented by a seventh category indicating whether a modelling method can capture the interaction with tooling, whilst the first category (that every technique scores on) just indicates basic draping capability. Letters on the last column of the table therefore refer to:

a. Draping

b. Tensile properties along the two fibre directions.

c. Shear resistance of the fabric sheet.

d. Out-of-plane flexural modulus of the fabric sheet.

e. In-plane flexural modulus of the fabric sheet.

f. Transverse compressive modulus of the fabric sheet.

g. Integrity/cohesion of the fabric sheet.

h. Interaction with tools.

TABLE 1

TABLE 1. Attributes of all modelling approaches selected for comparison. (letters under “Modelling capabilities” refer to list shown in below).

Over the past few decades, many models of composite forming have been developed with different levels of fidelity and numerical efficiency. Most of them were purpose-built and validated by different experiments (with different measurement techniques) and materials. Hence, a benchmarking exercise with objective measurement of the different model types’ performance is necessary, challenging and novel. This study, with its detailed and quantitative comparison of the numerical methods and their comparison to experiments, helps the modelling selection process for both scientists and engineers working on simulation of woven composites.

The manuscript is organised as follows: in Modelling Strategy, brief background information followed by a brief description of each simulation method selected for this comparative study is presented; Experiments and Modelling Setup reports the experimental work and numerical simulations carried out; finally, Results and Discussions discusses and concludes on the viability and robustness of each modelling technique by comparing the results with experimental observations, quantitative measurements and computational cost. Attempt at visualising the characteristics of each modelling approach for the given forming cases have also been made using radar charts.

2 Modelling Strategy

For completeness, a brief description of each representative modelling method is given in this section with background information and recent developments. Figure 1 illustrates all modelling techniques at the unit-cell level and the reader should return to this when reading the present section. As the initial geometry of the 3DShell and the MF models was processed under the same framework, the MF and 3DShell models are presented together in Micro- and Mesoscale Modelling: MF and Structured Shell (3DShell).

2.1 Kinematic Draping

Kinematic draping initially emerged several decades ago with the purpose of assisting the manual draping process (Mack and Taylor, 1956; Hancock and Potter, 2006), it has been further developed in recent decades and is now available in commercial software and open-source programmes, such as Fibersim (Siemens Industry Software Inc, 2021) (with material deformation capabilities), Interactive Drape (LMAT Ltd, 2021) (with user defined interactive forming path), KinDrape (Krogh et al., 2021) (with application to optimization of manufacturing process parameters) and SteerFab (Xiao and Harrison, 2021a; Xiao and Harrison, 2021b) (for designing steered fibric). Fibre orientations approximated by kinematic draping models are based on composite fabric mechanical features, i.e. warp and weft yarns have high moduli and fabrics normally have limited resistance to shear. A square PJN trellis that has four rigid sides with frictionless pin connector at the four vertices representing yarns and cross-over points, respectively, resembling an ideal structure in FEA representations for this approach. Current developments of kinematic draping are found in combination with optimisation processes, application of preform design and hybridisation with other modelling approaches (Sharma and Sutcliffe, 2003; Hancock and Potter, 2005; Skordos et al., 2007; Cherouat and Borouchaki, 2015; Rashidi and Milani, 2017; Xiao and Harrison, 2021a; Xiao and Harrison, 2021b).

In the current study, an opensource kinematic draping code developed at Aalborg University was adopted (Krogh et al., 2021). The kinematic draping process starts with correlating an origin point on the mould surface and a corresponding origin node from the preform grid (i.e., a “PJN preform sheet”), which sets the first constraint in the algorithm and can be seen as the first contact point between mould and preform during draping. Initial paths following the warp and weft directions from the origin node are computed from an input “initial draping direction” provided by the user. These two paths form a “cross” in the PJN preform and constrain the following draping shape. They generate a unique solution and are therefore referred to as generators. These generators are created on the mould by correlating them with geodesic lines of the mould surface. There are infinite number of paths that can link any two points on an arbitrary surface domain; the path with the shortest length can be defined as a geodesic path of that surface, which can be derived by numerically solving two nonlinear second order differential equations (Ramgulam and Potluri, 2007). Once the generator lines and cell are placed, the remaining PJN grids in all quadrants can be computed subsequently with the constraint of minimising the sum of shear angles in each PJN. The detailed descriptions of an example of kinematic draping model can be found in (Krogh et al., 2021).

As indicated in introduction, in addition to the traditional kinematic draping (i.e., the PJN is analytically formed onto the tool surface) a FEA-PJN forming model, where the textile was modelled by an assembly of PJN grids (see Figure 1) in Abaqus/Explicit, is also considered here. This allows to consider the interaction between fabric and tooling and it was expected to be more accurate than the kinematic draper. For this model, the Automatic General contact was used with a friction coefficient of 0.2 to capture the interactions between the fabric PJN model and tooling. The modelling of the forming tools is described later in Experiments and Modelling Setup.

2.2 Macroscale Model: HypoDrape

As previously mentioned, FE-based numerical models for textile deformation at the macroscale sit between kinematic draping and the micro-mesoscale modelling approaches and reflect some true physical aspect of the fabrics, with affordable computational cost. Several mechanical features of the textile are expected to be captured, including tension/compression, non-linear in-plane shear and out-of-plane bending behaviours. During forming simulation, the orientation of the fabric needs to be locally adapted by the in-plane shear deformation via a material constitutive model. Interactions between the preform and tooling and interply interactions are captured by contact algorithms in commercial finite element packages (Abaqus/Explicit in this study).

Accurate prediction of woven textile in-plane shear deformation during forming has two key aspects. Firstly, the change of fibre directions needs to be adequately tracked in order to ensure that changes in the anisotropy of the textile material are updated with the correct resulting stresses. To ensure this, many studies have been carried out using user-defined material subroutine based on a non-orthogonal constitutive model under hypo-elastic laws. This concept was initially introduced by Peng and Cao (Peng and Cao, 2005) and was then further validated and developed in other studies (Boisse et al., 2005; Badel et al., 2008; Khan et al., 2008; Khan et al., 2010; Peng and Ding, 2011; Chen et al., 2017; Dörr et al., 2017; Thompson et al., 2020) Secondly, the right combination of finite elements needs to be used. Due to the low level of cohesion between different fibres within a yarn and between the yarns themselves (Buet-Gautier and Boisse, 2001), the out-of-plane bending rigidity (low) and the in-plane moduli of the textile in the fibre direction (high) are uncorrelated. This phenomenon cannot be represented by standard 2D shell elements alone. A method using laminated shell elements was implemented in commercial FEA platform to simulate forming of biaxial reinforced knitted fabric in (Döbrich et al., 2014) and non-crimp fabric in (Yu et al., 2020; Yu et al., 2021a). This method requires, two fictitious layers at the outer surfaces of the laminated shell that are used to capture the bending property of the textile; the middle layer of the shell is used to simulate in-plane properties. The desired elastic flexural rigidity can be obtained by changing the thickness of the shell’s layers. Other approaches have used 1D elements (Sharma and Sutcliffe, 2003) in combination of shell or membrane element with shared or offset nodal connectivity to capture basic fabric deformation can be found at (Harrison, 2016; Harrison et al., 2011; d’Agostino et al., 2015).

The method used in the present contribution uses superimposed and mutually constrained membrane and shell elements that share the same nodes. In this way, in-plane behaviour is governed by membrane elements, while the out-of-plane behaviour is controlled by shell elements. Both set of elements use a hypo-elastic material model (HypoDrape) previously implemented in (Thompson et al., 2020) and based on the algorithm presented in (Khan et al., 2008). The non-linear shear behaviour prescribed to the membrane elements was consistent with picture frame shear tests presented in (Hancock and Potter, 2006). The shear modulus in the shell elements was set to zero. The Young’s modulus in the shell elements was back calculated from the flexural rigidity observed in a simple cantilever test, similar to that in (Kärger et al., 2018) from equation $D = \frac{E h^{3}}{12}$ , where D is the flexural rigidity per unit width from experiment; E is the Young’s modulus and h is the thickness of the shell element. A complete model validation and experimental results can be found in (Krogh et al., 2021). The overall set of material input properties for the membrane and shell elements is listed in Table 2. The constitutive behaviour of the textile was implemented in a VUMAT material subroutine in Abaqus/Explicit made freely available on the Bristol Composite Institute (BCI) Github page https://accis.github.io/HypoDrape. Access to the repository can be requested by e-mailing bci-github@bristol.ac.uk. Forming models performed using this approach and based on algorithm presented by Khan et al. (2008) are referred to as “HypoDrape” models in the rest of the manuscript.

TABLE 2

TABLE 2. Material input parameters for the respective elements in plain woven fabric HypoDrape model (Thompson et al., 2020). (γ: shear angle in radians).

2.3 Micro- and Mesoscale Modelling: MF and Structured Shell (3DShell)

Mesoscale models consider the constituent of the textile as sets of interlaced yarns and fully reflect the true yarn architecture and fabric weaving structure. These models usually use 3D solid structural elements arranged in such way that an individual yarn has a lenticular or elliptical shape cross-section (like real physical yarns and tows). Mesoscale models can capture textile yarn-scale deformation such as decohesion and yarn local buckling or nesting effects (in stacked plies forming) as well as typical macroscale deformation. Textile deformation and fibre re-orientation during forming are directly captured by the kinematics of the interlaced yarn that interact through fictional contacts. The model outcomes can be easily processed to predict mechanical properties, permeability of the final part or to simulate other manufacturing processes (Loix et al., 2008; Komeili and Milani, 2012; El Said et al., 2015; Thompson et al., 2017; Bodaghi et al., 2019; Liang et al., 2019). To derive yarn geometrical characteristics, it is common practice to use pre-processing software, such as TexGen (Sherburn, 2007) or WiseTex (Verpoest and Lomov, 2005). Work using fully digitised information directly taken from physical specimens such as micrographs or 3D μCT (computed X-ray microtomography) scans has been presented in (Liu et al., 2017; Wijaya et al., 2020).

Higher resolution modelling whereby fibre bundles are explicitly modelled can also be achieved. The technique is called the digital element method models were originally developed to determine the microscale geometry of textile fabrics (Wang and Sun, 2001; Zhou et al., 2004; Wang et al., 2010). This modelling concept was further developed for capturing deformation of complex textile under compaction and during weaving processes, in which the fibre bundle was modelled by chain of 1D beam elements with shared nodes. Numerical models using this approach sit in between computational micromechanics and meso-mechanics (Múgica et al., 2019) and are referred to as micro-mesoscale modelling or multi-filament (MF) method in the rest of the text. The deformation of the mesoscale and MF models rely heavily on the contact algorithms that control the interactions between yarns (in mesoscale models) and bundles of fibre in yarns (in MF models).

These two modelling approaches are computationally expensive and are, therefore, normally applied at the unit cell level. However, the heterogeneity of complex woven material and non-periodic boundary condition given to the material during complex loading scenarios such as forming are impossible to be captured by unit cell approach without compromising the level of detail in the model. Moreover, tool geometric features (especially whose size is similar to the size of the unit cell) and interactions between tooling and fabrics determine the final geometry of a compacted or formed part and, in turn, the mechanical performance of a component. Therefore, there is need to explore the viability of using these modelling approaches to simulate the forming of an entire fabric sheet and/or a ply stack.

With this in mind, a multiscale modelling framework developed and implemented at Bristol Composite Institute is used in this study. As shown in Figure 2, micro-mesoscale and mesoscale geometric models of 2D textile were generated. A description of the framework (that was originally designed (Mahadik and Hallett, 2010a; Green and Long, 2014) for simulating 3D woven fabrics and nesting effects of multi-ply forming) is concisely restated here, but greater details can be found in the previous publications (Mahadik and Hallett, 2010a; El Said et al., 2014; Green and Long, 2014; Thompson et al., 2017).

FIGURE 2

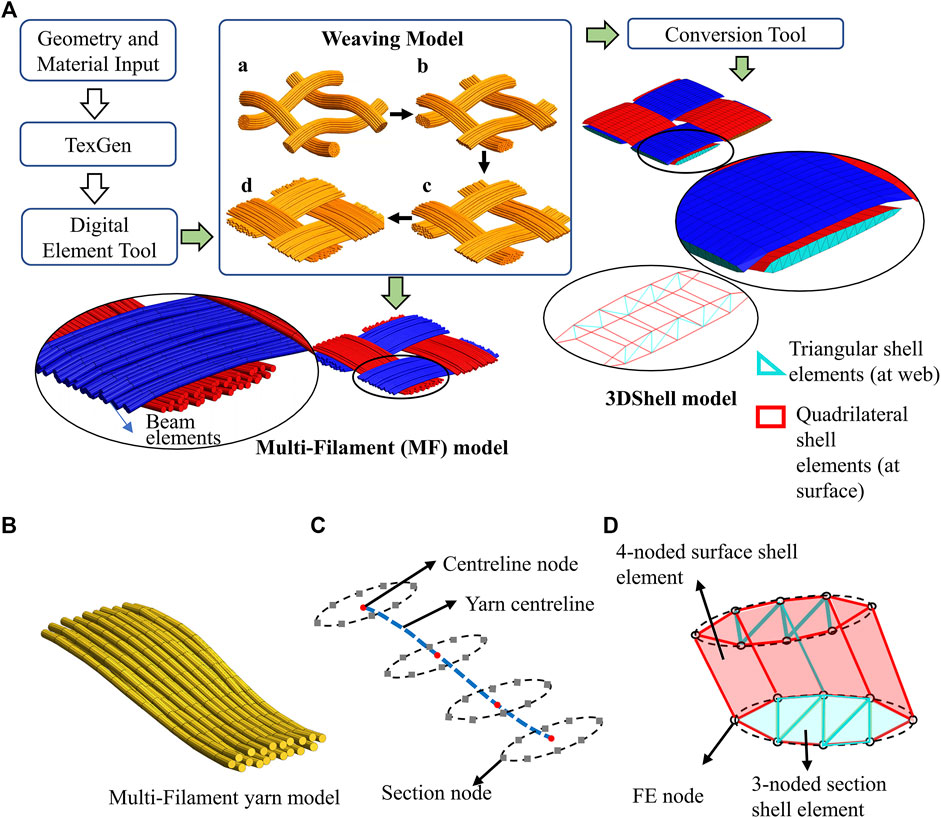
FIGURE 2. (A): Multiscale modelling process of 2D woven fabric geometric modelling from weaving model to multi-filament and 3DShell model (Mahadik and Hallett, 2010a; Green and Long, 2014). (B): The MF model of a single yarn in unit cell size. (C) Yarn geometry representation and (D) yarn cross section FE representation.

As illustrated in Figure 2A, geometric models of a 2D woven fabric are given as an input to the creation of 1D element-based multi-filament models that can be used to build a 3DShell model. This was done using the open-source textile modelling software TexGen (Sherburn) to which a basic description of the textile architecture (e.g., weave style and yarn spacing) was given as input. Essential information in the building block of the textile geometry model, that are the yarn centrelines, can then be extracted from TexGen and imported to an in-house MATLAB code which allows the end-user to define the shape of the yarn cross section and the number of beam elements in it. With this information, the code automatically generates an initial loose geometry of the textile unit cell as an input file for the explicit FE solver LS-Dyna. This is illustrated in Figure 2A (see “a-d” in weaving model). In the Figure, the initial yarn cross section shape is circular, and each fibre yarn is represented by 36 beam element chains; fibre yarns follow the centrelines that are offset from those in TexGen in order to accommodate for the tow cross section. It is worth noting that it is unrealistic to simulate individual fibres even at the unit cell level as the high number of chains would significantly increase the computational cost (without obvious positive effect on simulation quality (Green and Long, 2014)). Once the loose geometry of the textile’s unit cell model is obtained, appropriate boundary conditions are applied, which consider the effect of adjacent cells on periodicity and the variety of unit cells from the same textile (see (Thompson et al., 2017) for more details).

Bending behaviour, as an important deformation mechanism of textile materials during forming, is controlled by the fibre tow/yarn bending and yarns’ interaction. To capture this deformation mechanism a methodology was developed in which beam element in each chain was assigned an elastic, perfectly plastic material model (PLASTIC_KINEMATIC in LS-DYNA) to approximate the tow bending, as well as to simulate the “drawing in” of yarns from beyond the unit cell in real fabric (Mahadik and Hallett, 2010b). The material parameters of the beam elements in MF models are listed in Table 3. This method was proven to be effective in a number of studies (El Said et al., 2014; Green and Long, 2014; El Said et al., 2015; Thompson et al., 2017). Interaction of the yarns is captured by contact between beam element chains within a fibre yarn (intra-yarn) and between fibre yarns (inter-yarn). An AUTOMATIC_GENERAL contact with coulomb friction coefficient prescribed as 0.2 was used in LS-Dyna models to capture the interaction of chains of beam elements.

TABLE 3

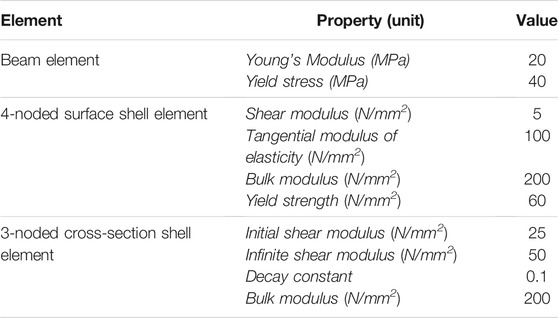
TABLE 3. Material properties of beam elements in the MF model (Green and Long, 2014) and shell elements in the 3DShell model (El Said et al., 2014; LSTC. LS-DYNA, 2021).

An accurate representation of the textile weave geometry is then created, by compacting the loose yarns of the textile unit cell between 2 rigid surfaces (with appropriate periodic boundary conditions). A negative thermal coefficient and a fictive temperature ramp is applied to the models in order to contract the beam element chains simulating yarn tension during weaving, this draws the textile together to achieve a virtual representation of the as-woven textile meso-structure. The actual fibre length of the as-woven textile can be approximated from the knowledge of the textile areal weight, fibre count, fibre radius, density and unit cell size (an assumption that all fibres are perfectly straight and aligned is made). To create MF fabric models (in preform size for forming simulation) from the unit cell, an in-house post-processing code is used to tessellate the unit-cell model.

As illustrated in Figure 2A, a robust post-processing tool that converts the MF unit cell model (in a micro-/meso-scale representation) to a computationally more efficient meso-scale unit-cell has also been developed. The method was validated for a complex forming of a 3D woven orthogonal fabric in (El Said et al., 2014). The relevant parameters in this validation process were expected to be adequate to model punch forming of a single 2D woven fabric, therefore are adopted here. Instead of elaborating a full description of this methodology, key steps are introduced here, and the details of this method can be found in (El Said et al., 2014; Thompson et al., 2018a).

The process of converting a MF unit-cell into a meso-scale model is illustrated in Figures 2B–D. It can be seen that the yarn cross section is defined by section nodes surrounding each centreline node. The conversion process starts from generalising the as-woven geometry in the MF unit cell model (see single yarn MF model in Figure 2B). To reduce resolution in the yarn direction, the number of nodes along the centreline is reduced based on yarn path curvature and beam element length. Then, the number of section nodes representing the yarn cross section at each centreline node is reduced. In the example shown in Figures 2B–D, 8 section points are used at each centreline node. These 8-noded section definitions, with neighbouring sections, can be used to construct structural 4-node shell elements (ELFORM_16 in LS-DYNA), as that shown in Figure 2D, that represent the yarns’ surfaces. By connecting the 8 nodes in each section, 3-node triangular shell elements can be built. The obtained meso-scale models where yarns are modelled by structured shell elements are named “3DShell” in the rest of this study. The 3DShell unit-cell model is further processed to form a complete sheet of textile, ready for forming simulation in LS-Dyna. During forming simulation, the surface shell elements are designed to represent the interaction between yarns and between yarns and the tooling. They also help control the yarn’s flexural behaviour. As described in Macroscale Model: HypoDrape, the internal formulation of standard shell elements prevents the in-plane and bending stiffness to be uncoupled. Hence, using shell elements only at the yarn surface would not allow to correctly capture both the cross-section deformation and the flexural behaviour of the yarns. This limitation is overcome through the use of the triangular elements filling up the cross-sections (see in blue in Figure 2D) that resist excessive deformation and collapse of the cross-sections. Forming is an irreversible process. Hence, by the fibrous nature of textiles, yarns sliding or compaction are not restored by simple removal of the applied force. To account for that and better computational efficiency, the surface shell elements in the 3DShell model are assigned an elastoplastic (MAT 12 in Ls-Dyna) material behaviour (El Said et al., 2014), and a viscoelastic material model (MAT 6 in Ls-Dyna) is used for the cross-sectional support triangular elements (Bickerton et al., 2003). The material parameters used are listed in Table 3.

Both the meso-scale (i.e., 3DShell) and the MF models are derived from the same modelling framework and weaving simulation were compared with other modelling approaches for 2D fabric sheet forming. Their respective computational cost and predictive capabilities were then quantified and assessed.

3 Experiments and Modelling Setup

Throughout this study, a simple 2D plain weave material, the specification of which is listed in Table 4, is used. As discussed in Macroscale Model: HypoDrape and Micro- and Mesoscale Modelling: MF and Structured Shell (3DShell), material properties used in the HypoDrape, MF and 3DShell models have been previously validated at both the unit-cell and the preform (or laminate) levels by comparing model predictions to experimental data.

TABLE 4

TABLE 4. Measured test case material information.

Fabrics were formed onto both a hemispheric and a tetrahedral mould, the dimensions of which are given in Figures 3A,B. The hemisphere is axis-symmetric and provides, during forming, a balanced tension radiating from the centre of the contact region to the rest part of the fabric. Therefore, it was expected that all the modelling approaches will yield similar outcomes. On the other hand, the tetrahedron mould is doubly symmetric and combines some geometrical features of cubic and prism. Forming over tetrahedron might present some challenges to the kinematic draping method and even for some highly-detailed modelling approaches (Allaoui et al., 2014).

FIGURE 3

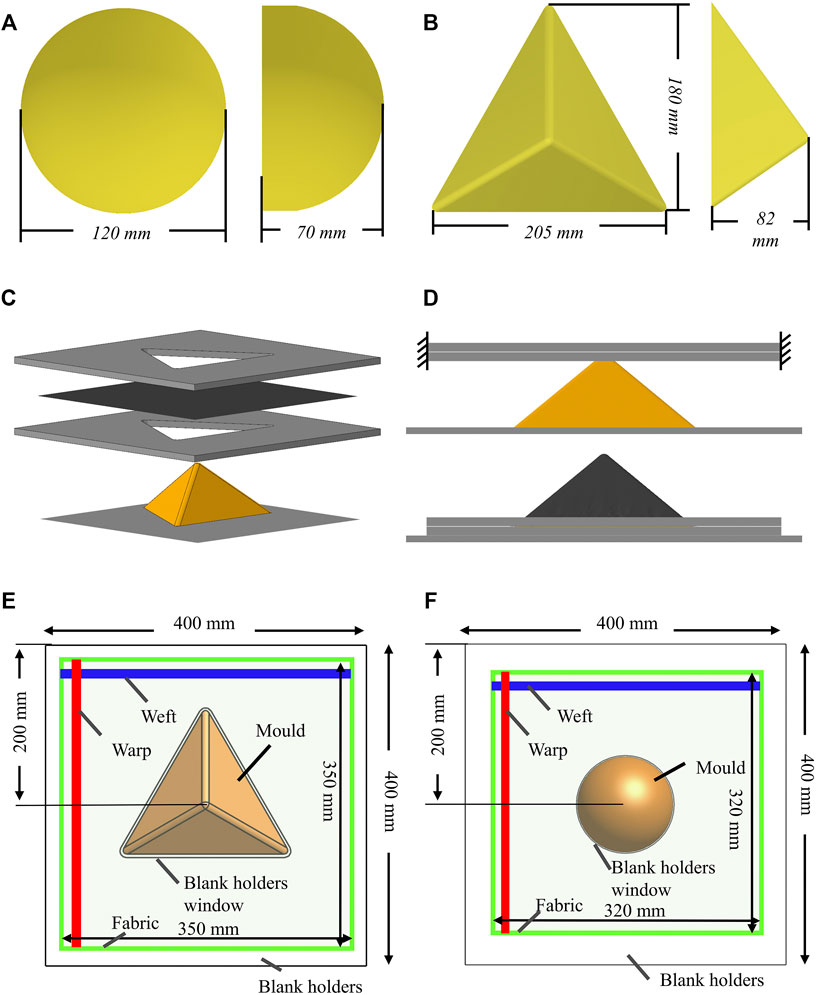
FIGURE 3. Dimensions of (A) hemispheric and (B) tetrehedron mould; (C) Exlpoded view of punch forming setup; (D) Snap shots at the rspective postion of the differrent components of the setup at the beginging and the end of the punch forming process. (E) General dimensions of the hemispheric punch; (F) General dimensions of tetrahedral punch.

The fabric was draped over the selected shapes via punch forming. Punch forming is a forming process whereby a preform is sandwiched between two blank holders and a mould is pushed through holes created in the blank holders in order to form the fabric. Displacement (i.e., a fixed distance of 0.5 mm (textile thickness) was kept between the blank holders) rather than pressure-controlled loading was used. This way, the in-plane movement of the fabric was only restricted by the friction exerted by the blank holders. This relaxed boundary condition was designed so that fabric can only deform through in-plane shear. The blank holders together with the fabric in between can then be displaced onto the mould until the lower blank holder rests on top of the flat supporting surface of the mould.

Figures 3C–F show a schematic representation of the experimental setup and of the boundary conditions applied in the FE models. In the models, a rigid material property was assigned to the blank holders, mould and the supporting surface of the mould. The blank holders were spaced 0.5 mm apart and fully constrained, and the mould (with flat rigid surface) was given a prescribed motion of 1 mm/s displacement rate to move into the blank holders’ windows until the bottom of mould reaches to the gap between the two blank holders. As is common practice for quasi-static analysis in explicit finite element simulations, the material densities of all parts were scaled up (by 1 × e³) to reduce computational cost. An AUTOMATIC_GENERAL contact was used in LS-Dyna models (the MF and the 3DShell models) and general contact was defined for all parts in Abaqus models (the HypoDrape and the FEA-PJN models). In all the models, a static coulomb friction coefficient of 0.2 between fabric and forming tools was applied. This value should be kept low as the amount of friction for the given fixed gap between blank holders should not provide enough force to deform the fabric. In the experiments, blank holders were made from transparent acrylic sheet. White dots were drawn on the fabric so that the general deformation of the fabric could be measured via photographs taken directly above moulds’ centre points.

The FEA-PJN and HypoDrape models were processed using 16 × 2.6 GHz SandyBridge cores with 64GB/node RAM on the University of Bristol’s high performance computer cluster (BlueCrystal phase 3 - https://www.bristol.ac.uk/acrc/high-performance-computing/). The MF and 3DShell models, due to their sizes, required high memory processors (16 × 2.6 GHz SandyBridge cores with 256GB/node RAM). The kinematic draping models were processed on a single processor in a desktop workstation as they do not consume high computational resource.

4 Results and Discussions

4.1 Model Construction

The yarn spacing (2.6 mm) of the textile used in this study can be calculated from Table 4 or from direct measurement on the fabric. This is then used to assign the unit-cell’s size in the MF and 3DShell models, the distance between the points on the grid in kinematic drape models, the FEA-PJN models and the element size in the HypoDrape models.

It has been reported that the number of beam element chains to predict the best possible unit cell geometry of a complex 3D weave without excessive computational cost is 61 (Green and Long, 2014). However, 61 chains, with 13 beam elements, results in nearly 4,800 degrees of freedom per tow to be solved in a unit-cell. Using MF models with 61 beam element chains in each yarn would require too much computational capability. For modelling less complex textile, a fewer number of beam chains was also suggested (Daelemans et al., 2016). Therefore, a more pragmatic approach was adopted. The yarn width of the MF model was, therefore, made slightly less than the 3DShell case. 13 element chains per yarns were used in the present. Negative impacts of this could be reduced accuracy in capturing shear locking and, consequently, a delayed wrinkle formation due to the additional void between yarns. To achieve higher accuracy of tow interaction, the yarn cross section of the 3DShell model used here was generated from a similar MF model but with optimal 61 beam element chains per tows.

4.2 Experimental Measurements

Photographs of the top view of each experiment were taken, and the white dots drawn on the deformed fabric were measured in image processing software (ImageJ (Rasband, 2007)). As the tetrahedron and hemisphere are respectively doubly and quarterly symmetric, only half and quarter of the image was analysed. The marked dots were joined to build grids that contain several textile unit cells (see Figure 4). To avoid distortion on the 3D shapes in the 2D images, shear angles were measured in grids around the flat shape transition region instead of on the 3D surfaces, as shown in Figure 4. This metric on general fabric shear deformation at the shape transition between mould and flat surface as well as the profile of the entire textile (reflecting the overall shear deformation) were used to systematically compare the models with the experiments.

FIGURE 4

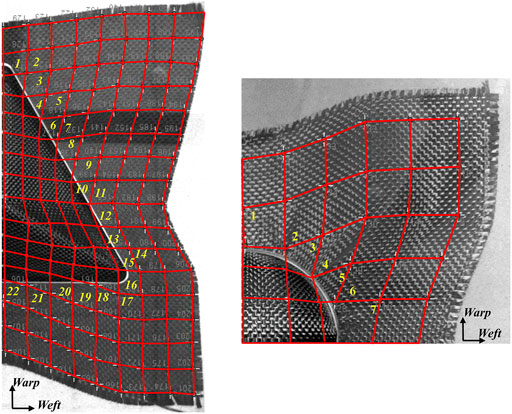
FIGURE 4. Iamges of half view of formed fabric in tetrehedron forming (left) and quarter view of hemisphere forming (right). White dots on fabrics are joint by red lines to form cells contraining a number of fabric unit cells. Measuring cells are mark with numbers.

Variabilities from textile manufacturing processes and forming tests exist and inevitable, which leads to experimental scatter and the formed geometry of the textile specimens not exactly following the symmetry of the mould. This actual specimen and process variability is neglected in general purpose numerical modelling where preform models are designed to be ideal and under perfect boundary conditions and processing constraints. Unless a fully digitised experiment in place, where multiple specimens of the same test case are used and discrete points on specimen are tracked before and after forming with respect to a fixed point in space, it is reasonable to ignore the manufacturing and forming process variabilities in a single specimen test case. Therefore, it is reasonable that experimental results of half of the formed fabric in the tetrahedron forming and a quarter of the formed fabric in the hemisphere forming were considered.

In this later section, modelling results are compared with experimental results in three different aspects: overall deformation of the fabric; fibre orientation and detailed features. An attempt is then made to visualise the overall modelling performance with proposed metrics. Computational efficiency is accounted for in the evaluation.

4.3 Overall Deformation

Figures 5A,B collectively compare the overall deformation between specimens and all modelling results from hemispheric and tetrahedron forming, respectively. Specimen profile and the profile of the top blank holder window of each forming test are marked in red, and these two profiles are overlaid to all modelling results in each forming case. Although the textile was constrained by blank holders (see Experiments and Modelling Setup) in the hemispheric forming experiment, out-of-plane deformation of the textile still happened due to the lack of constraining around the mould. Because shear deformation of the fabric in the tetrahedron forming test was less than the hemispheric case, similar observation was not found in the tetrahedron forming. Nevertheless, these wrinkles seem to be at the early stage and should not significantly affect the model comparison, as shown in Figure 4. In general, all five models captured the overall deformations of the textiles in both forming cases very well, except for the kinematic draping model in the tetrahedron forming. It was a reasonable result as the outcome of the current kinematic draping algorithm is significantly influenced by the selection of the origin point and initial fibre paths. For the hemispheric forming case where initial fibre paths (warp and weft directions) set in kinematic draping were aligned with the axes of symmetry of the hemisphere, the draping result is comparable to the FE-based methods (see Figure 5A). By contrast, the kinematic draping model fell short of capturing the actual forming sequence and forming kinematics in the tetrahedron forming, where the fabric should land on the three faces of the mould at the same rate (see Figure 5B). On the other hand, the FEA-PJN models, using similar assumptions as kinematic draping but implemented in finite element framework and considering interaction with tooling, presented a much better results for the tetrahedron case and produced similar results to the HypoDrape models in both forming cases. This is because the in-plane shear stiffness of the actual textile is insignificant for small shear angles and the modulus of the truss elements in the FEA-PJN models together with node/surface friction contributed some resistant to shear deformation. Predictions of the overall formed textile shape by the HypoDrape models are in good agreement with both experimental results. During tetrahedron forming, it was difficult to control the alignment between textile and the mould centre, and the first contact point between the mould’s apex and fabric may lead to slightly different deformation shapes. Deformation along one direction can be slightly higher if the first contact point lands exactly at a fibre yarn, which was believed to be the reason why all models underestimated the top edge deformation of the textile in tetrahedron forming, as shown in Figure 5B. Among all models, the MF and 3DShell models offered the best results in capturing overall deformation. Prediction of overall deformation of the textile under forming is subsequently used as one of the metric parameters in the modelling performance comparison. It is also noticeable that, except for the mesoscale and micro-mesoscale models, most of the simulations fell short of capturing accurate shear deformation at the corners of the specimens in both forming cases, as shown in Figure 5. This is due to the fact that the material is discontinued and fibre yarns are easily able to slide at the textile boundaries, which can be an important behaviour to simulate for near net-shape preform design and where the MF and 3DShell modelling approaches are needed.

FIGURE 5

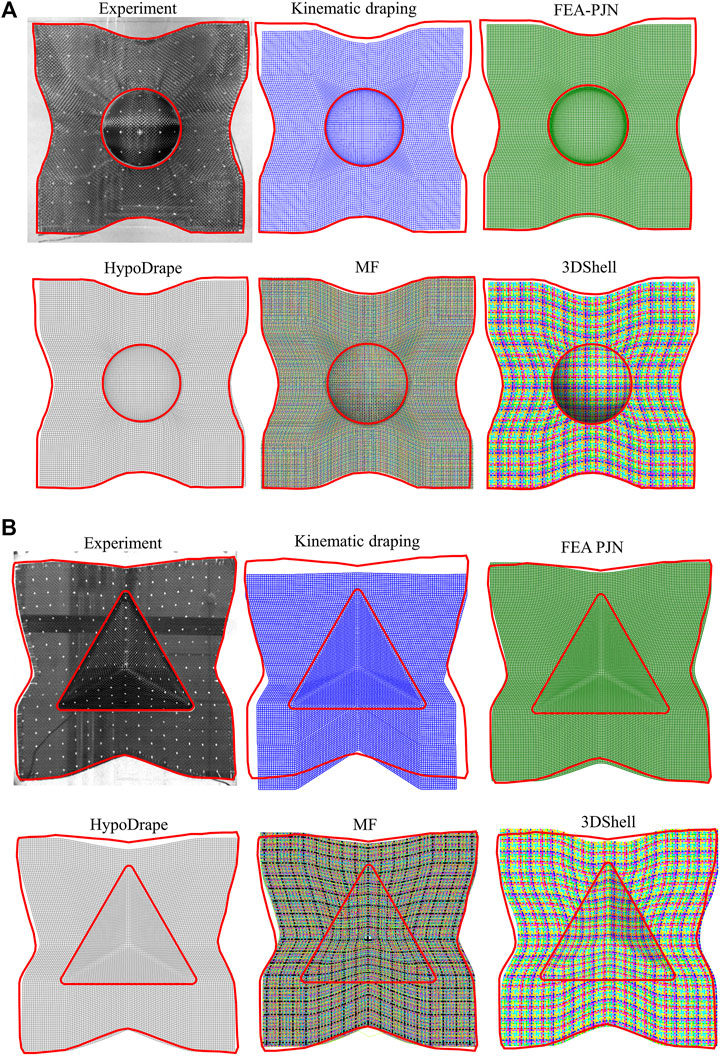
FIGURE 5. Overviews of overall deformation of experimetnal and all modelling resutls in (A) hemispheric forming and (B) Tetrahedron forming. Profiles of the boundary of top blank holder window and deformed fabric are marked in red and are overlaid to all modelling for comparison purpose.

4.4 Fibre Orientation

Nodes were marked in the fabric model in each simulation at similar locations to those points drawn on the specimens before forming, and these nodes were joined by lines in each deformed fabric model to compare with experimental results. Comparison of the grids predicted by each modelling strategy against the experimental results are shown in Figure 6 and Figure 7 for the hemispheric and tetrahedron moulds respectively. As the kinematic drape model was not able to capture the overall deformation of the fabric on the tetrahedron, it was excluded from this comparison.

FIGURE 6

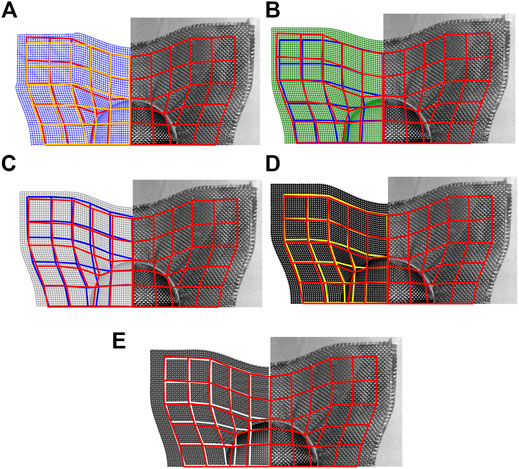
FIGURE 6. Comparison of the predicted formed fabric profiles with experiment resutls in (A) the kinematic draping model (profile marked with yellow lines), (B) the FEA-PJN model (profile marked with blue lines), (C) the HypoDrape model (profile marked with blue lines), (D) the MF model (isolated yarns coloured in yellow), and (E) the 3DShell model (isolated yarns coloured in white) for hemispheric forming. Deformed profile of the specimen (only quarter of which is shown) indicated by red lines at the RHS is overlaid to the deformed profile of fabric model shown at the LHS.

FIGURE 7

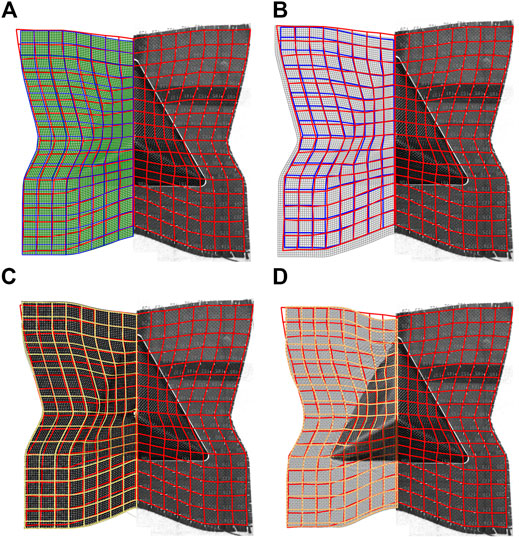
FIGURE 7. Comparison of the predicted formed fabric profiles with experiment resutls in (A) the FEA-PJN model (profile marked with blue lines), (B) the HypoDrape model (profile marked with blue lines), (C) the MF model (isolated yarns coloured in yellow), and (D) the 3DShell model (isolated yarns coloured in white) for tetrehedron forming. Deformed profile of the specimen (only half of which is shown) indicated by red lines at the RHS is overlaid to the deformed profile of fabric model shown at the LHS.

Good correlation of fibre orientation between all model results and test results can be found in the hemisphere forming case (see Figure 6). However, slight mismatches between the experimental and modelling grids were found in the HypoDrape and the FEA-PJN model, as shown in Figures 6A,B. These deformation mismatches are much improved in models with higher fidelity as shown in Figures 6C–E. The measured shear behaviour of the fabric was given as an input to the HypoDrape model (see Table 2) whilst yarns and their interactions are explicitly modelled in the both the MF and 3DShell models. Nevertheless, it is worth noting that the modelling capability of the FEA-PJN models provides fairly good predictions and close to the HypoDrape models in both forming cases, as shown in Figure 6B and Figure 7A. By contrast, the MF and 3DShell models predicted both overall deformation and local fibre orientation very well for both forming cases, as shown in Figures 6D,E and Figures 7C,D. The maximum deviation of local fibre orientation between the models and the test results is always observed at the shape transition region for both the hemispheric and tetrahedron cases. It is believed to be caused by the local interaction between the opening of the upper blank holder and the fabric in testing where the edge of the opening affected the local fibre orientation. The other reason is the wrinkle onset at the hemispheric forming shape transition, due to lock of blank holder pressure (see Experiments and Modelling Setup and Figure 4). These deviations were reduced or even avoided by the MF and the 3DShell models, as shown Figures 6D,E, which may also imply that the interaction between tooling, i.e. mould top and the edge of top blank holder opening, and fibre yarns is an important mechanism to capture for more accurate local fibre orientation predication at abrupt shape transitions.

4.5 Detailed Features

For a given material, detailed features of the deformed fabric can be generated from the incompatibilities of radius of tooling, boundary conditions and key process parameters or in combination, which leads to irregularities in local fibre architectures at surface contours or features of the mould. These detailed features are not normally captured by macroscale modelling and have to be simulated by models with higher fidelity that are capable of capturing yarn/yarn and yarn/tooling kinematics. In the tetrahedron forming case, due to its unique shape, the textile was under shear deformation in different directions at each face of the mould. Figure 8A compares the detailed fibre orientation between experimental and numerical results from the MF and the 3DShell models at the shape transition between the bottom of the tetrahedral shape and the flat surface, this region was considered to be the most complex part and is involved intra-yarn, inter-yarn and textile/tool interactions. It can be found that the re-orientation of fibres in both models is in good agreement with experimental results, as shown in Figure 8A, which further validates the modelling techniques and key parameters used for these interactions.

FIGURE 8

FIGURE 8. Close up image of the formed fabric in experiment, the MF model and the 3DShell model in tetrehefron forming at (A) shape transisiton region and (B) at the apex of the mould.

The effects of mould shape on textile integrity become more significant if the mould’s features are prominent and if their size is in the same order of magnitude as the unit-cell size of the preform. In the tetrahedron forming case, the forming force applied by the apex of the mould to the centre of the weave in a small area (see Figure 3B) and can force yarns just above it to separate. Figure 8B shows close-up image of the experimental results with focus on the textile on top of the tetrahedron mould apex after forming, and it can be found that the yarn spacing increases as a result of yarn sliding along the mould surface due to the high forming pressure. Alongside the experiment results, simulation results at the same location from the MF and the 3DShell models are also presented in Figure 8B. A slightly different scenario was found in the MF model in that the central yarn landed precisely on top of the mould apex throughout the forming simulation and undertook most of the forming force, hence it was under compaction loading. In Figure 8B, it is clear that significant yarn spreading is captured by the MF model. However, the amount of yarn spreading and sliding are overpredicted in this case due to the oversized yarn spacing in the MF model (for computational efficiency purpose) as depicted in the beginning of Results and Discussions. In addition, it is also found that the 3DShell model captured a small amount of yarn sliding, the magnitude of which agrees better with the experimental results.

In macro-scale modelling, continuous finite elements with user defined material properties (HypoDrape model in this work) representing the textile provides informative results. Shear angle is usually assessed against locking angle which indicates the occurrence of out-of-plane deformation and onset of defects. Figures 9A,B present shear angle contour plots of HypoDrape models for the hemispheric and tetrahedron forming. Numerical variabilities from solving the contact process exist in the finite element platforms, and the shear angle contour plots of both forming simulations are not entirely symmetric as their mould geometry. However, the maximum shear angle at each quadrant or side is similar and close to the shear lock angle (45^o found in (Thompson et al., 2020)) in hemispheric forming, which correlates well with experimental observations of wrinkles (see Figure 5). The shear angle predictions from kinematic draping in hemispheric and tetrahedron forming are also presented in Figures 9C,D; and it can be found that the size and magnitude of the high shear regions at each quadrant and shear-free region at textile corners are in very good agreement with the HypoDrape model in hemispheric forming case, despite some localised shear bands around the high shear regions. The kinematic drape model appeared to be capable of approximating high shear regions for axis-symmetric mould shapes but not perfectly suited for irregular shape such as tetrahedron (see Figure 9D).

FIGURE 9

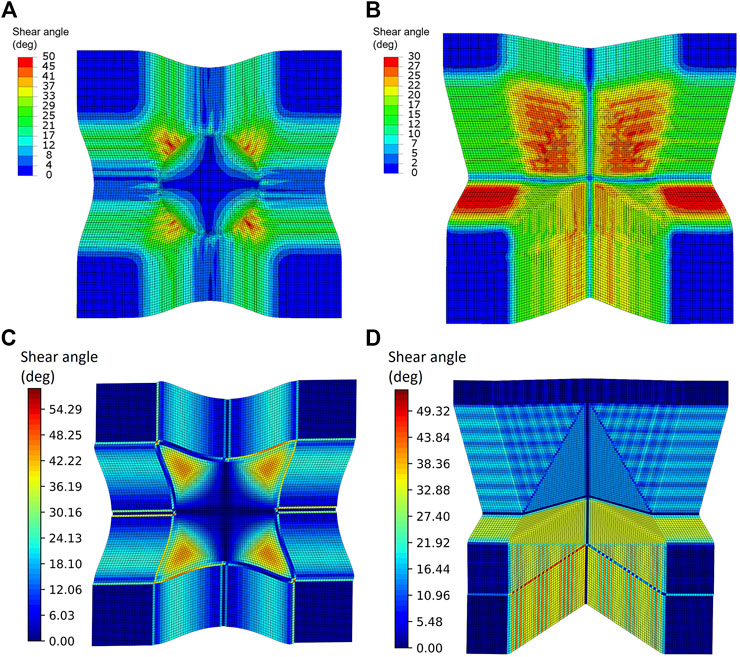
FIGURE 9. Shear angle contour plot from (A) the HypoDrape model in hemispheric forming; (B) tetrehedron forming; (C) the shear angle of the kinematic draping in hemispheric forming and (D) the shear angle of the kinematic draping in tetrahedron forming.

4.6 Quantitative Comparison and Performance Metrics of Modelling

As shown in Figure 6 and Figure 7, textile specimens were partitioned into a number of grids/cells by joining grid points previously marked on them. These continuous cells were then used to quantify the amount of fibre re-orientated during forming, i.e., shear angle, at discrete locations. Image-based measurement of fibre orientation taken from specimens on the 3D contoured surfaces may not be sufficiently reliable for un-instrumented tests. Therefore, for quantitative comparison, shear angles at those cells of specimens on the 3D mould surfaces were not considered. Only the shear angles around the shape transition regions on the flat surface and near the opening of upper blank holder (see Figure 4) were considered and these were then compared with the modelling results. Each cell from which the measurements were taken were numbered as shown in Figure 4. In total 22 measurements on the tetrahedron and 7 on the hemisphere specimen were taken. These grid lines (and measuring cells) in the experimental results, representing fibre orientation (and shear angle) at the shape transition regions, were then compared with modelling results shown in Figure 6 and Figure 7.

Figures 10A,B compares local shear angle of the formed textile between experimental and modelling results from all simulations for the two mould geometries. In general, all models capture the variation of shear angle in the hemisphere forming case. The greatest difference between experiment and modelling is in cells cell 3 to 5 of hemispheric forming where the shear deformation is the highest and where slight out-of-plane deformation was observed experimentally. The slight overestimations from the MF model at cell 3 and 4 may be due to the slightly larger yarn spacing in the MF model reported before (Figure 10A).

FIGURE 10

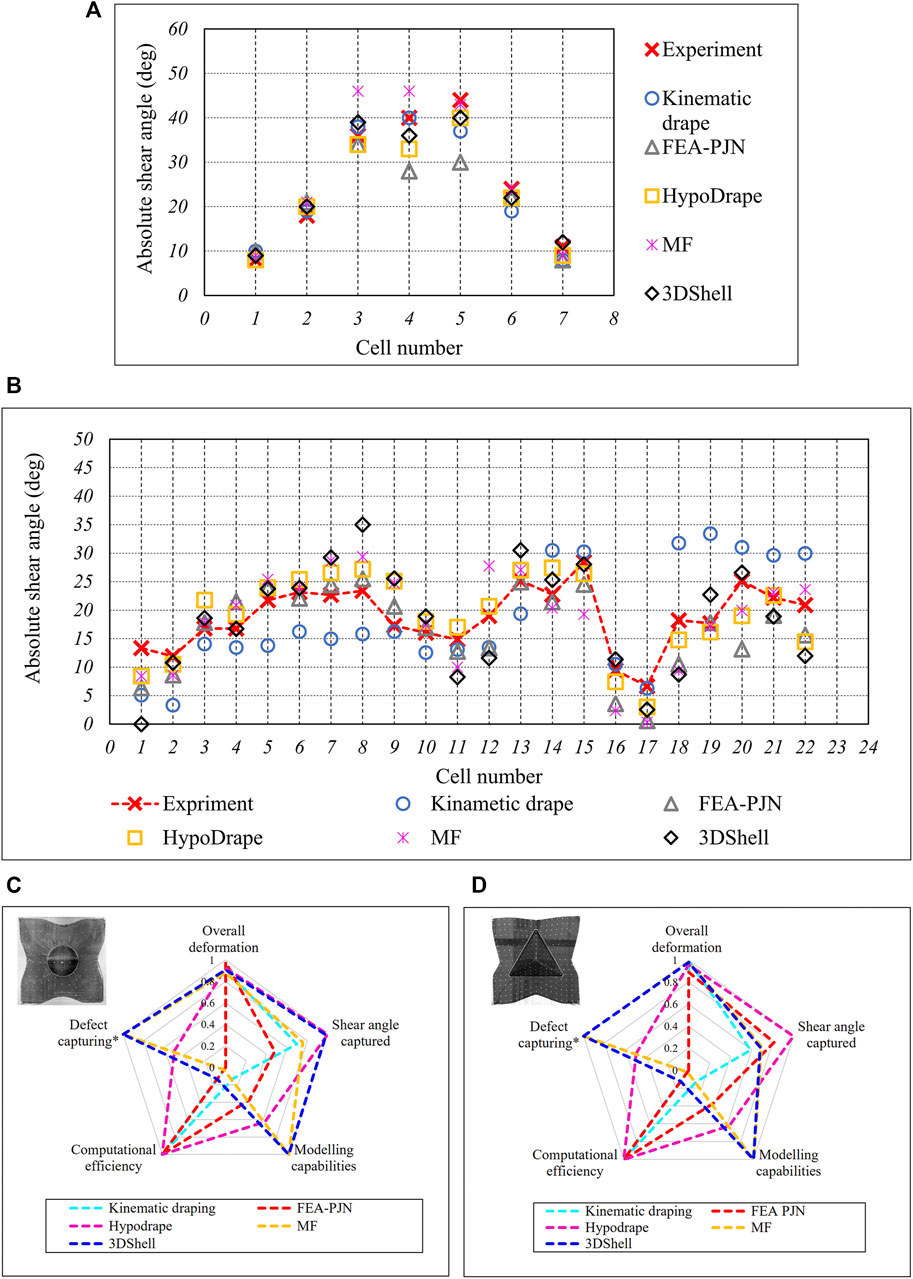
FIGURE 10. Shear angle comparison between experiment and modelling resutls in (A) hemisphere and (B) tetrehedron forming. Note that measuring cell number is specified in Figure 4. Radar charts of modelling performance of all models in (C) hemispheric forming and (D) tetrahedron forming.(*:expectations based on modelling capability).

For the tetrahedron forming case (see Figure 10B), most of the models predicted the overall trend in the variation of the shear angle accurately. This is particularly true at the locations where the shear angle changes direction (see cell 10-12). The most significant overall discrepancy between modelling and experiment is obtained from the kinematic drape model (it is plausible that the initial fibre path in the geometric mapping was not the same as the correct forming sequence). The FEA-PJN model where the correct forming sequence and constraints are applied on the fabric provides significant improvement compared with the kinematic drape model. In general, stronger variations can be found between the modelling and experiment in tetrahedron forming compared with the hemispheric mould. This is because the tetrahedron shape is more complex and larger than the hemispheric mould, which leads to a greater material and process variabilities. Nevertheless, among all modelling approaches and forming case, it is found that the HypoDrape and the MF model predict shear angle better than the rest of the cases.

To quantitatively compare the computational efficiency of the different models, CPU run times of each model for the two different forming cases were recorded and listed in Table 5. It is worth noting that the FEA-PJN models with similar internal constraints as in the kinematic drape but implemented within an FE framework has the shortest run time. This run time was achieved by mass scaling and mass proportional damping to reduce dynamic effects. The greatest run time is from the MF model in tetrahedron forming due to the large number of contact pairs. As the material behaviour is fully represented by the interactions of beam element chains in the MF models, there was limited option to speed up the run time further without any secondary effects. Although the number of degrees of freedom in 3DShell models is of the same order of magnitude as that in the MF model, the number of contacts to solve in the 3DShell models are much less than the MF model as there is no contact definition at intra-yarn level. Hence the run time of the 3DShell models are roughly 6 times lower than the MF cases. In case of other forming techniques, such as double diaphragm forming, or similar forming technique with multiple plies, the run time can be increased significantly due to the increment of the number of contact pairs to be solved. It is also worth noting that the accuracy and stability of FE-based modelling approaches are sensitive to the forming rate or displacement rate of the mould, which may bring dynamic effects and contact instability to the fabric model, especially when the fabric is not very well constrained. This can also cause detrimental effects on computational efficiency, and a mass proportional damping becomes necessary in these cases. For a robust forming simulation, a parametric study of fabric damping should also be performed if the fabric model is highly mass scaled and has a high forming rate.

TABLE 5

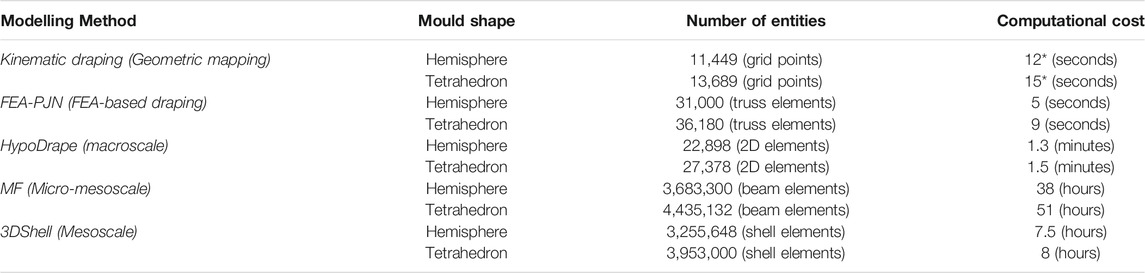
TABLE 5. Summary of number of entities of all preform models (tooling parts are excluded) and computational cost of all simulations. *The kinematic draping models were solved using Python on a desktop workstation with single processor at 3.60 GHz.

Figures 10C,D present radar charts to compare modelling performance of all simulations in both forming cases for: overall deformation prediction, shear angle prediction, modelling capabilities, computational efficiency and the ability to capture defects. Since there are no standard metrics to perform such a comparison study, these five variables were normalised by either the maxima/minima within their own group or by experimental measurement.

Overall predications of deformation of each modelling case was normalised by dividing the area of deformed textile models by the area of the deformed specimens. For comparing shear angle prediction, averaged errors were calculated first and normalised by the minima. Computational efficiencies were normalised by 1 h CPU time, and models with run time lower than 1 h were given a rating value of 1.

Modelling capabilities cannot be quantified. Hence, the rating was derived from the last column of Table 1 by dividing the number of items of each modelling approach is capable of by 8, which is the total number of behaviours of textile to be captured for accurate forming prediction. For example, the modelling capability rating of the HypoDrape model is equal to 0.625 (from 5/8). The assumption of this simplified metric is that all behaviours listed in Section 1 are equally important and have linear relation to the overall modelling capability and quality. For quantifying the modelling performance of the ability to capture defects, a simplified approach was used, i.e. “1” means modelling capabilities for both yarn-level defects and macroscale level defects; and “0.5” means modelling capabilities for only macroscale level defects, and “0” indicate no defects can be captured. The overall performance of a model can then be quantified by the area enclosed in the radar chart.

From Figures 10C,D, it can be found that the overall modelling performances displayed across different modelling approaches in the two forming cases using these user-defined metrics agree with the general expectations and the results presented earlier in this section. The kinematic drape performs reasonably well, except for lacking in modelling capability and capturing accurate shear angle, and its predictive capability of shear angle reduces in tetrahedron forming with a non-symmetric mould shape. The HypoDrape models excel in capturing overall deformation and shear deformation but are lacking in detailed material behaviours such as that shown in Figure 8B due to the perform length scale the model captures. It is found that the 3DShell models offers the best resolution for the two forming cases. However, it failed to capture shear angle accurately enough at some locations in the tetrahedron forming (see Figures 10A,B) and its run time is very significant compared to other faster methods.

The present results provide an overview of the strengths and weaknesses of the various models tested. However, many other factors that can influence the modelling performance have not been considered here. This is the case for example for pre- and post-processing efforts, material characterisation and validation tests required before implementation. It is worth noting for example that the MF and 3DShell methods are associated with substantial pre-processing time whilst the continuum approach necessitates characterisation of the formed material.

5 Conclusion

There are a number of different modelling techniques with different levels of detail that have been developed for predicting textile deformation during forming or other processes involving textile deformation and fibre re-orientation. To understand the advantages and disadvantages of each modelling approach in assisting the composite design process, the best way is to compare all available modelling results against the same set of experimental observations. A systematic comparison of some modelling methods for textile forming has been undertaken here.

Five modelling approaches of different resolution (i.e., scale) and computational efficiency were used to simulate punch forming processes of two moulds with different geometrical complexity (i.e., hemispheric and tetrahedron punch forming). Fibre orientation and overall deformation at the end of forming were experimentally measured to compare with and assess the model accuracy. The modelling results were quantitatively compared and their performance against overall textile deformation, prediction of shear angle at region of interest, computational efficiency and ability to capture defect formation. Radar charts were produced using a simplified metrics system to rapidly compare the different modelling techniques with each other.

It was found that the kinematic drape analysis works well for hemispheric forming. It can capture overall deformation and shear angle with a run time of a few seconds. As geometrical complexity of the mould becomes greater, the model accuracy becomes more and more dependent on the choice of the initial fibre path. The FEA-based PJN models despite using the same basic assumptions as the kinematic drape, allow to account for the interaction between preform and tooling and generate better results for both the forming cases studied here. Higher computational efficiency is also observed. The HypoDrape models appear to offer the best compromise. They are robust in predicting fibre orientation and overall textile deformation without obvious increase in run time compared with other macroscale models. The MF models required the most computational resource but provides the best resolution. They were able to capture defects arising from inter- and intra-yarn interactions. As it was developed previously for geometric modelling of complex 3D weave where the deformation of the entire textile is small and limited, parameters that govern the interactions within the textile and kinematics of textile subject to large deformation may require further characterisation for more accurate predictions. For the best predictive capability in the MF models, more beam element chains per fibre yarn may be required (Green and Long, 2014; Daelemans et al., 2016). Creating preform models from tessellated unit-cells with this level of resolution would require too much computational resources. It appears from the present study that used a “lighter” version of the MF (with only 31 beam element chains per yarn) that the method may be best suited for modelling deformation of highly complex weaves at critical locations and where full descriptions of the fibre architecture is required (e.g., infusion modelling or mechanical performance modelling, etc). The 3DShell models were created based on the parent MF unit cell model. It was found that 3DShell models performed very well on most metrics proposed in this study, but their computational time was very high. An interactive multiscale modelling strategy that allows user to switch between different modelling techniques at region of interest within a single process simulate may be beneficial in future (Yu et al., 2021b). It is worth noting that, in addition to the models’ computational cost, different levels of effort and time is required to prepare the models associated with each modelling strategy. Material characterisation tests that capture fabric deformations under in-plane shear and out-of-plane bending are necessary for macroscale modelling. For models presenting greater detail, additional material characterisation such as yarn level and fabric compaction tests may also be required for reliable deformation and defect predictions. FE Model creation and pre-processing steps for micro- and mesoscale models and their conversion were made automatically via in-house codes in this study. However, they may present some programming challenges and lead to a longer pre-processing time in comparison with the macroscale models.

Capturing interaction between neighbouring plies during multi-ply forming would be necessary in a benchmarking exercise of all modelling strategies that are based on FEA. This is, however, considered to be out of scope for the present study, which concentrates on single ply forming simulated by all available modelling approaches (numerical and analytical). The choice of forming scenarios where wrinkles are not observed was deliberate in order to avoid undervaluing the performance of the studied modelling approaches. A precise, quantitative benchmarking exercise for predicative capability of defects, such as wrinkles, across different models would require capturing the exact wavelength and magnitude of a wrinkle, which currently remains out of reach for many dry textile forming models.

In the forming experiments, it was confirmed that variabilities of material and forming process influence the measurement. To ensure more robust comparison between experimental results and modelling predictions, an instrumented forming test facility where fibre orientation can be measured with respect to a fix coordinate system in space and where material and variabilities during the forming process can be kept to a minimum would be beneficial. In the current experiments, out-of-plane deformation of textile materials during the hemispheric and tetrahedron forming tests was constrained by the blank holders, and the macroscale deformation was limited to in-plane shear. Further testing with less constraint, allowing for out-of-plane deformation, is needed in future work to compare the predicative capability of out-of-plane behaviour of textiles when combined in each of the modelling approaches.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

XS: Conceptualisation, Methodology, Writing—Original draft preparation, Visualization, Investigation, Software Jonathan PB: Methodology, Writing—Reviewing and Editing, Supervision AT: Methodology, Software, Writing- Reviewing and Editing BS: Methodology, Software, Writing—Reviewing and Editing SH: Conceptualisation, Writing—Reviewing and Editing, Supervision.

Funding

The research being submitted is entirely funded by EPSRC with reference number EP/P027350/1. This work was funded by the EPSRC platform grant “SIMulation of new manufacturing PROcesses for Composite Structures (SIMPROCS)”, (EP/P027350/1).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allaoui, S., Hivet, G., Soulat, D., Wendling, A., Ouagne, P., and Chatel, S. (2014). 'Experimental Preforming of Highly Double Curved Shapes with a Case Corner Using an Interlock Reinforcement'. Int. J. Mater. Forming 7, 155–165. doi:10.1007/s12289-012-1116-5