Quantifying the Influence of Out-Time on Prepreg Material Properties and Out-Of-Plane Steering Defects During Automated Fiber Placement

In automated fiber placement (AFP), knowledge about the interaction between material properties and process parameters is essential to achieve cost-efficient manufacturing. Both, lay-up rate and defects are dependent on the properties of the uncured prepreg tapes which are out-time dependent. However, information thereof is not given in data sheets and there are no standardized test methods. To quantify the changes of the material properties, we conducted experiments on mechanical properties and tack with IM7/8552 up to 15 days out-time using previously evaluated test methods. Furthermore, we carried out AFP lay-up trials to quantify the effects on steering defects. The results for the mechanical properties reveal a non-linear increase of the shear modulus and the transverse tensile modulus and a strong correlation to the test temperature. Results from the probe tack tests show a strong dependence on out-time at 20°C and a weak dependence at 40°C. Results from a novel peel tack test method and the lay-up trials revealed a monotonous change as a function of out-time. In both cases, we identified the lay-up rate and the infrared (IR) emitter power as the process parameters with the largest influence. The obtained results present an overall view of the material behavior depending on different test and process parameters as a function of out-time. By this, they help optimize the AFP process parameters and serve as input for material models and AFP defect models.

1 Introduction

Composite materials contribute to a sustainable aviation by means of their high weight-specific mechanical properties which enable a lighter, more fuel-efficient aircraft design (Timmis et al., 2015). The emissions during flight are the largest source of environmental impact (Timmis et al., 2015), however, all stages of an aircraft’s life cycle—from production to end of life—have to be considered to minimize its negative effects. Structural composite aerospace parts are commonly manufactured using pre-impregnated carbon fibers (prepreg) as precursors which comprise carbon fibers impregnated with an uncured epoxy resin (Lengsfeld et al., 2016). Even though resource efficiency has been the goal for aerospace manufacturing for several decades (Argüelles et al., 2001), the two biggest aircraft manufacturers, Airbus and Boeing, and their supply chain generate about 1000 t of cured and uncured carbon fiber prepreg waste each year (Biron and Kidlington, 2020). To maximize the resource efficiency, manufacturing processes with a low scrap rate like automated fiber placement (AFP) should be used preferably (Hagnell and Åkermo 2015). Yet, larger amounts of uncured prepreg might be scrapped as the material properties change during processing due to storage at elevated temperatures (out-time). Because of the ongoing cross-linking process in the resin above its glass transition temperature ($T_g$), the prepreg properties change (Ellis 1993) which might increase lay-up defects or even lead to inapplicability of the material (Heller et al., 2018). Essential prepreg properties with regard to AFP processing are the tack and the mechanical properties in the uncured state as they are input parameters for numerous lay-up defect prediction models (Beakou et al., 2011; Matveev et al., 2016; Bakhshi and Hojjati 2018, 2019; Belhaj and Hojjati 2018; Rajan et al., 2020; Wehbe et al., 2020). The tack—a measure of mechanical resistance which needs to be overcome to separate the prepreg from a substrate (Budelmann et al., 2020)—is influenced by the out-time which affects the flowability and the molecular mobility of the resin (Ahn et al., 1992a; Endruweit et al., 2018). Several authors have investigated out-time effects on tack with various prepregs, test methods, and out-time conditions (Cole et al., 1991; Ahn et al., 1992a; Banks et al., 2004; Dubois et al., 2010; Miller et al., 2010; Grunenfelder and Nutt 2011; Nguyen and Krombholz 2016; Blass et al., 2017; Böckl et al., 2018; Endruweit et al., 2018; Budelmann et al., 2019; Andrade Raponi et al., 2020; Smith et al., 2020). All of these studies observed a change in tack due to out-time with some reporting a monotonic decrease (Cole et al., 1991; Dubois et al., 2010; Miller et al., 2010; Blass et al., 2017) while the others reported non-monotonic changes. In none of the cases did the tack increase monotonically.

The mechanical properties used in AFP defect prediction models include the tensile modulus $E_1$, the in-plane transverse tensile modulus $E_2$, the Poisson’s ratio ${\nu }_{12}$, and the in-plane shear stiffness $G_{12}$ of the uncured prepreg (Beakou et al., 2011; Matveev et al., 2016; Bakhshi and Hojjati 2018, 2019; Belhaj and Hojjati 2018; Rajan et al., 2020; Wehbe et al., 2020). The tensile modulus $E_1$ is almost entirely dependent on the tensile modulus of the fiber and the fiber volume fraction due to the low stiffness of the uncured resin. Therefore, it is not expected to be significantly affected by out-time. The transverse tensile modulus $E_2$ , in turn, is expected to be affected by out-time. Margossian et al. (2016) and Rajan et al. (2020) measured the transverse tensile modulus of a prepreg. However, they did not consider out-time effects nor could we find any other publication on out-time effects on $E_2$. The Poisson’s ratio ${\nu }_{12}$ is, in principle, affected by out-time. O’Brien et al. (2007) and Saseendran et al. (2017) investigated the Poisson’s ratio of neat epoxy resins as a function of degree of cure (DoC). However, their respective range of DoC was higher—above 79% and above 50%—than the DoC due to out-time during AFP processing which is expected to be below 50%. Even though ${\nu }_{12}$ may be affected by out-time, the changes are not likely to influence the lay-up behavior as Rajan et al. (2020) state that the out-of-plane buckling formation mechanism due to steering is unaffected for the relevant Poisson’s ratio range (0.1–1). The in-plane shear modulus $G_{12}$ of uncured prepreg was assessed in several publications (Potter 2002a, 2002b; Harrison et al., 2004; Larberg et al., 2012; Margossian et al., 2015; Wang et al., 2020), however, none of them considered out-time effects. Other mechanical properties like the out-of-plane transverse compression modulus $E_3$ are not considered since the defects mainly evolve after lay-up when the tape is not subjected to a compression load by the compaction roller anymore (Bakhshi and Hojjati 2019).

Maximum material usage and optimized processing during AFP can only be achieved with an extensive knowledge of the out-time effects on the material properties and their implications for lay-up quality. To quantify these effects and to correlate them to the occurrence of lay-up defects, we conducted a series of experiments with varying test and process parameters respectively using previously evaluated test methods. The material we used was HexPly IM7/8552 in several different conditions—1, 5, 10, and 15 days out-time. The experiments include tack measurements with two different principles, $E_2$ measurements, $G_{12}$ measurements, and AFP steering experiments evaluating out-of-plane defects during lay-up which serve as an assessment criterion for the out-time effects on the lay-up quality.

This paper describes the experimental methods we used in the section Materials and Methods. The results for each property and for the steering evaluation are presented in the section Results while the implications for material usage, AFP processing, and defect prediction are covered in the section Discussion.

2 Materials and Methods

2.1 Material

We used aerospace grade unidirectional (UD) HexPly IM7/8552 prepreg in all experiments. According to the data sheet, the tack life—time at room temperature during which prepreg retains enough tack for easy component lay-up—of 8552 is 10 days (Hexcel Corporation 2020). The fiber areal weight was 134 g/m² and the nominal cured ply thickness was 0.131 mm. For the lay-up trials and the peel tests, we used slit-tapes with a width of 1/8” (3.175 mm) as it was predetermined by the AFP machine configuration. For the other experiments, specimens were cut from a wider roll. Wherever we needed multi-layer specimens ($E_2$ and $G_{12}$ measurements), we used a preparation method from previous investigations (Heller et al., 2020a): we compacted large layers applying vacuum at room temperature for 35 min followed by cutting the layers into the specimen size using an NC cutting machine. To measure the influence of controlled out-time conditions on the properties, the material was kept in controlled temperature and humidity conditions at 21°C and 40% RH and tests were conducted at the aforementioned out-times $t_{out}$—1, 5, 10, and 15 days. We chose these times to study the changes within the material’s tack life and to see the effects when it is exceeded.

2.2 Degree of Cure

To correlate the out-time to a measurable material condition, we determined the glass transition temperature $T_g$ according to ASTM E1356-08 [ASTM E1356-08(2014)] on several out-times using a TA Instruments Q200 DSC. We used the midpoint method—midpoint between the heat flow level before the inflection and after the inflection (Ellis 1993)—to determine $T_g$ and calculated the relation between $T_g$ and the DoC $\alpha$ using the modified DiBenedetto equation from (Pascault and Williams 1990):

$\alpha =\frac{T_g-T_{g0}}{T_g\left(1-\lambda \right)+\lambda T_{g\infty }-T_{g0}}(1)$

where $T_{g0}$ is the glass transition temperature of the uncured material, $T_{g\infty }$ is the glass transition temperature of the fully cured material, and $\lambda$ is an adjustable parameter between 0 and 1.

2.3 Probe Tack

The probe tack test has been used by several authors for the determination of prepreg tack either using a universal testing machine (UTM) (Ahn et al., 1992b; Ahn et al., 1992a; Dubois et al., 2010; Grunenfelder and Nutt 2011; Gillanders et al., 1981; Putnam et al., 1995; Hayes et al., 1996; Buehler and Seferis 2000) or a rheometer (Budelmann et al., 2019; Andrade Raponi et al., 2020; Wohl et al., 2017; Forghani et al., 2018; Smith et al., 2019) for force application and measurement and it serves as an input for defect prediction models (Belhaj and Hojjati 2018; Forghani et al., 2018; Bakhshi and Hojjati 2018, 2019). We chose rheometer measurements as it allows for an accurate force and temperature control and expected measured forces are comparably low. All measurements were done using an Anton Parr MCR 302 rheometer. The general experimental procedure was adopted from Budelmann et al.’s publication (Budelmann et al., 2019). The test procedure comprises the compaction phase, where the probe is pressed onto the specimen, the relaxation phase, and the measurement phase, where the probe is pulled away from the specimen and the counteracting force is measured. The test preparation—see Figure 1A — includes placing the specimen (size: 30 mm $\times$ 30 mm) inside the lower plate and covering it with a downholder. We placed all specimens with the tackier side down to avoid a pull up of the whole specimen and took great care to avoid entrapped air between specimen and lower plate surface. We fixed the downholder with adhesive tape serving as another way to avoid a pull up of the whole specimen. The used probe was a flat aluminium probe with a 10 mm diameter replicating the first-ply tack on an aluminium tool—see Figure 1B. The temperature was controlled by a peltier temperature device (PTD) in combination with a hood covering the experimental chamber. We derived test parameters from Budelmann et al.‘s publication (Budelmann et al., 2019) for a full factorial experimental design—see Table 1. The test temperatures 20°C and 40°C cover the relevant range for TS-AFP processing: the lower limit 20 °C represents processing at ambient temperature with no additional heat input while the upper limit 40°C is just above the highest temperature of the AFP investigations and it is the nominal processing temperature for IM7/8552 (Rajan et al., 2021). Figure 2 illustrates the three readings we evaluated from the measurement phase: the maximum force (per probe area $A$) ${\sigma }_{probe}$ ($=F_{max}/A$), the work of adhesion (per probe area) $W_{adh}/A$ which is the integral under the force-displacement curve from the start of the separation to full separation, and the tack stiffness ${\sigma }_{probe}/d$ which corresponds to the force per displacement from the start of separation to the maximum force (per probe area). The maximum force represents the shear resistance during debonding and the work of adhesion accounts for the stress relieve by relaxation. Budelmann et al. proved that both parameters have to be considered for tack characterization. The third, the tack stiffness, is assessed as it is used as input for defect prediction models, e. g. in (Belhaj and Hojjati 2018; Bakhshi and Hojjati 2019).

FIGURE 1

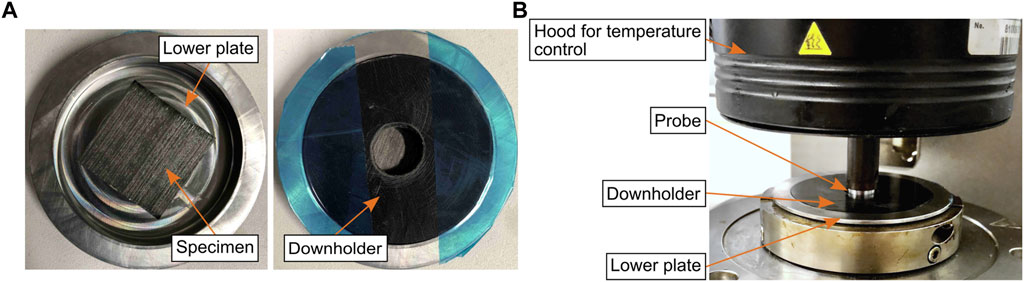
FIGURE 1. Probe tack test—experimental setup. (A): Specimen in lower plate. (B): Setup in rheometer.

TABLE 1

TABLE 1. Probe tack test—test parameters.

FIGURE 2

FIGURE 2. Probe tack test—readings.

2.4 Peel Tack

We considered peel tests as a complementary test method to the probe tack test method since peel tests allow for a better relation to the peel mechanisms in automated lay-up processes (Crossley et al., 2012). In a previous publication (Heller et al., 2020b), we presented a novel peel tack test for prepreg tapes which is incorporated in a standalone test bench—see Figure 3. Since specimen preparation and peel test are decoupled, the influence of the lay-up rate on tack can be measured independently of the peel rate. Furthermore, the specimens can be prepared directly with the AFP machine—see Figure 3B—so that AFP process parameters can be adjusted directly. By this, we were able to use the exact same process parameters for the peel test specimens as for the lay-up trials. The AFP machine we used is a CORIOLIS GROUP SAS (Queven, France) machine which processes up to eight slit-tapes with a width of 1/8” (3.175 mm). Its maximum compaction force is 500 N which is applied onto the compaction roller via the pneumatic system of the lay-up head. The compaction roller is a silicone roller with Perfluoroalkoxy (PFA) coating with a diameter of 40 mm and a width of 30 mm. The deviation in pressure distribution along the width of the roller is ±5%. The heat source is an infrared (IR) emitter with a maximum power of 430 W and a nominal heated area of 40 mm width and 23 mm length ensuring a homogeneous distribution of heat along the width of the tapes. The IR emitter is mounted 60 mm above the substrate and is tilted 20° with respect to the substrate. Based on experiences from preliminary lay-up trials, we defined the parameters listed in Table 2. As the lay-up rate is expected to have a significant influence on the peel tack and the steering defects, we defined three levels. Preliminary experiments showed that defects occur at 0.1 m/s depending on the material properties and the lay-up trajectory. To investigate to which extent a reduction of lay-up rate would reduce defects, we defined 0.06 m/s and 0.03 m/s as the other values. For the compaction force and the IR emitter power, we defined two levels within the general operating range of the used AFP machine. The experimental design was a one-factor-at-a-time design with $v=0.06 m/s$, $F=400 N$, $P_{IR}=350 W$ as the baseline. We used the maximum lay-up width for the specimens consisting of eight tapes with a length of 360 mm. The specimens were deposited on aluminium sample carriers by the AFP machine replicating the first-ply tack on an aluminium tool—see Figure 4. We conducted all peel measurements 1.5 min after material deposition due to the time needed for the transfer of the sample carrier from the lay-up area to the test bench and the clamping of the specimen. We set a constant peel rate of 5 mm/s which is equal to the peel rate in the standard that the peel test is adopted from DIN EN ISO 29862:2019-09 (DIN Deutsches Institut für Normung e. V. 2019).

FIGURE 3

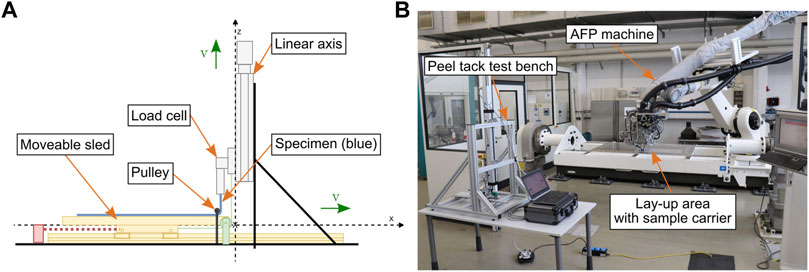
FIGURE 3. TUM peel tack test. (A) Peel test principle (Heller et al. 2020b). (B) Test bench next to AFP machine.

TABLE 2

TABLE 2. AFP process parameters for lay-up trials and peel tests.

FIGURE 4

FIGURE 4. Peel tack test—clamped specimen.

2.5 Transverse Tensile Modulus

Being an input parameter for AFP defect prediction models, we evaluated the influence of transverse tensile modulus changes due to out-time on AFP processing. We conducted transverse tensile measurements in the same manner as Margossian et al. (Margossian et al., 2016) using a TA Instruments Q800 DMA with a constant loading rate. To obtain the desired specimen thickness of 1 mm (length: 23 mm, width: 6.5 mm), we compacted seven layers of the material. The test parameters for the full factorial experimental design are stated in Table 3. We set the test temperatures to 20°C and 40°C covering the relevant range for TS-AFP and applied two different loading rates to investigate their influence on the transverse tensile modulus $E_2$. As proposed by Margossian et al., we determined $E_2$ from the linear part of the stress-strain curves.

TABLE 3

TABLE 3. Transverse tensile modulus—test parameters.

2.6 In-Plane Shear Modulus

The second mechanical property which is an input parameter for AFP defect prediction models and is affected by out-time is the in-plane shear modulus $G_{12}$. Based on a previous comparison of test methods (Heller et al., 2020a), we selected the torsion bar test for the characterization of $G_{12}$. The test principle which is based on the correlation between the torque and the rotation angle for a prismatic bar with the fiber direction parallel to the rotation axis is explained extensively in (Haanappel and Akkerman 2014) and (Heller et al., 2020a). For the experiments, we used the Anton Parr MCR 302 rheometer and prepared 60-layer specimens to obtain the required specimen thickness of 12 mm (length: 60 mm, width: 12 mm). The specimen thickness did not change significantly due to the tests—the thickness difference before and after testing was less than 2.6% at all out-times. Therefore, we used the thickness before testing for the evaluation. The test parameters for the full factorial experimental design are listed in Table 4. We set the test temperatures to 20°C and 40°C covering the relevant range for TS-AFP and used the maximum possible range of the angular frequency to account for different lay-up rates during AFP. In accordance with the test method theory presented by Haanappel and Akkerman (Haanappel and Akkerman 2014), we assessed the shear behavior at different shear rates. We determined the in-plane shear modulus by linearization of the stress-strain curves.

TABLE 4

TABLE 4. In-plane shear modulus—test parameters.

2.7 AFP Lay-Up Trials

We used AFP steering experiments as a quality criterion for the material process interaction. During steering—lay-up along non-geodesic paths, defects like in-plane waviness, out-of-plane buckling, and tape pull-up occur. These defects are affected by the material properties and the process parameters (Lukaszewicz et al., 2012; Hörmann 2015). A previous study (Heller et al., 2018) has demonstrated that steering induced defects change due to out-time. The dependence on out-time in combination with varying process parameters, however, has not yet been investigated. Furthermore, the occurrence of lay-up defects has not yet been correlated to the material changes due to out-time. In the experiments, we kept the steering radius constant (600 mm, arc length: 400 mm) and varied the process parameters in the same one-factor-at-a-time experimental design as the peel tests—see Table 2. We processed single slit-tapes and used an aluminium plate as substrate—see Figure 5A. The out-of-plane buckling is the local separation of the steered tape from the substrate at the inner edge due to excessive compressive forces, the tape pull-up is the local separation of the steered tape from the substrate at the outer edge due to excessive tensile forces, and the in-plane waviness is the in-plane fiber undulation due to compressive forces (Lukaszewicz et al., 2012; Hörmann 2015). Since the latter is considered an initial defect (Hörmann 2015), we only evaluated the former two which are the eventual defects—see Figure 5B. We measured the length of buckles and pull-up 40 min after lay-up since preceding observations as well as studies by other authors (Bakhshi and Hojjati 2019; Rajan et al., 2019) revealed that buckle formation is time-dependent—in this case up to 40 min. The measurement method comprises marking the buckle and pull-up length at the measuring time, taking photographs from above, and digitally measuring the lengths in relation to a reference length (graph paper). As several defects occurred per tape, we cumulated the buckle length and the pull-up length for each tape. For the result presentation, we defined the results in positive expressions: relative buckle-free length $L_{bfree}$ and relative pull-up-free length $L_{pfree}$ which equals the total arc length minus the respective cumulative defect length normalized to the arc length. The definition of $L_{bfree}$ and $L_{pfree}$ is summarized in Eq. 2.

$L_{b/pfree}=\frac{arc length - cumulative buckle/pull-up length}{arc length}(2)$

FIGURE 5

FIGURE 5. Steering experiments. (A) Steered tapes and digital camera. (B) Pull-up and buckles.

During later stages of out-time, several tapes did not adhere at all. To account for these defects, we considered them as both buckle and pull-up.

3 Results

In the presentation of the results, we focus on the mean values of each individual result to increase the readability of the graphs. A considerable scatter was present during most measurements with single-layer specimens—probe tack, peel tack, AFP lay-up trials. Prepreg tapes exhibit a local variability in properties like resin content (Lukaszewicz and Potter 2011) which directly influences the scattering of the aforementioned tack-related measurements. For specimens prepared via AFP, there is a second source of variability: it cannot be controlled which prepreg side is in contact with the substrate since the narrow tapes can be twisted at several locations of the AFP machine’s material feed. As the prepreg side plays a significant role for resin distribution and tack (Endruweit et al., 2018), it will affect the peel tack of AFP specimens as well as the steering results. The additional data mean values, standard deviations, minima, and maxima of the relevant test series are listed in the Appendix.

3.1 Degree of Cure

The results for glass transition temperature $T_g$ and degree of cure $\alpha$ of five measurements each are depicted in Figure 6. For the $T_g$ measurements, we extended the out-time range from 0 to 20 days. The $T_g$ increased from −2.55°C at 0 days out-time to a maximum of 12.63°C at 20 days out-time following a second order polynomial curve progression. The corresponding fit is described as

$T_g=A_{Tg}\cdot t_{out}^2+B_{Tg}\cdot t_{out}+C_{Tg}(3)$

with $A_{Tg}=2.57\cdot {10}^{-2}$°C/d², $B_{Tg}=2.4\cdot {10}^{-1}$°C/d, and $C_{Tg}=-2.55$°C. The fit has a coefficient of determination of $R^2=0.9997$. Similarly, the degree of cure $\text{α}$ increases following a second order polynomial curve progression up to 9% at 20 days out-time. The corresponding fit is described as

$\text{α}=A_{\alpha }\cdot t_{out}^2+B_{\alpha }\cdot t_{out}(4)$

with $A_{\alpha }=1.485\cdot {10}^{-4} d^{-2}$, and $B_{\alpha }=1.5029\cdot {10}^{-3} d^{-1}$. The fit has a coefficient of determination of $R^2=0.9998$. The input values for the calculation of $\alpha$ are $T_{g0}=-2.55 °C$ (own measurement), $T_{g\infty }=209.51 °C$ (own measurement), and $\lambda =0.78$ (van Ee and Poursartip 2009).

FIGURE 6

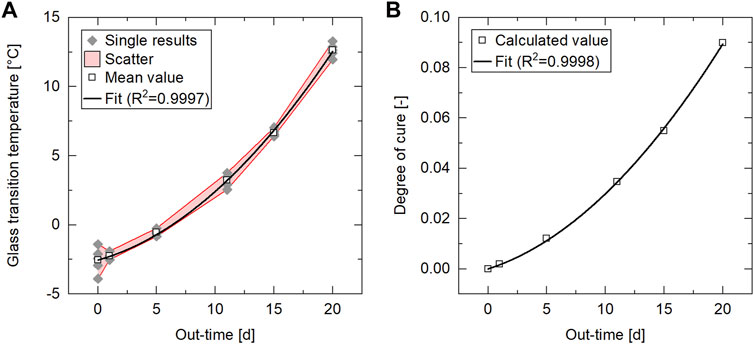
FIGURE 6. Cure-related properties as a function of out-time from DSC runs at 10 K/min (Material: IM7/8552 prepreg; out-time: 1 day 20 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$). (A) Glass transition temperature. (B) Degree of cure.

Using these results, any $T_g$ measurement of 8552 material can be linked to an equivalent out-time. Thus, in combination with the results below, any $T_g$ measurement of 8552 (within the investigated range) can be used as an estimate for the tack, the mechanical properties, and the lay-up behavior of the prepreg.

3.2 Probe Tack

3.2.1 Maximum Force

Figure 7A gives an overview of the mean values of the probe tack results for the maximum force per area ${\sigma }_{probe}$ from six measurements each. Additional data is listed in Supplementary Table SA9. The mean standard deviation was 0.02 N/mm². Several trends can be read off the results. Except for the high temperature and slow rate ($T=40 °C$, $v=0.02 mm/s$) at 1 and 5 days out-time, the maximum force ${\sigma }_{probe}$ is higher at the high test temperature. The increase in temperature generally improves the surface wetting of the substrate due to the decrease in viscosity (Budelmann et al., 2020). However, the decrease in viscosity also leads to a lower shear resistance during debonding, which, after a certain point, outweighs the increase in surface wetting leading to a decrease in tack (Budelmann et al., 2020). This fact may explain the higher maximum force at $T=20 °C$ at out-times 1 day and 5 days where the viscosity is lower than at later out-times.

FIGURE 7

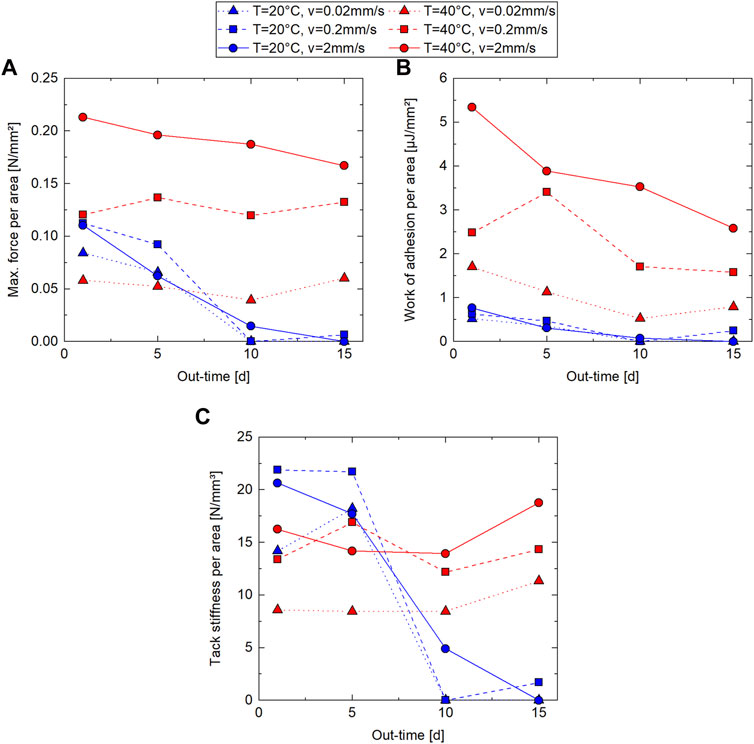
FIGURE 7. Probe tack results as a function of out-time from rheometer probe tack tests (Material: IM7/8552 prepreg; out-time: 1 day–15 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$). (A) Maximum force. (B) Work of adhesion. (C) Tack stiffness.

At the high test temperature, ${\sigma }_{probe}$ is clearly rate dependent with the highest value at the highest test rate ($v=2 mm/s$) and vice versa corresponding to the viscoelastic behavior of the tack. Budelmann et al. (Budelmann et al., 2019) assumed that at higher rates, the short debonding time does not allow the interface to relieve stresses by relaxation. At the low test temperature ($T=20 °C$), the effect of the rate is much smaller and there is no clear trend whether ${\sigma }_{probe}$ increases or decreases with the rate. A clear trend, on the other hand, is evident for the out-time dependence of ${\sigma }_{probe}$ at $T=20 °C$: it decreases by 18% to 44% from 1 to 5 days out-time—depending on the rate—and drops to almost zero at 10 and 15 days out-time which corresponds to the tack life specified by the manufacturer. Due to the increase in viscosity/decrease in molecular mobility at higher out-times, the surface wetting worsens leading to a decrease in tack. At $T=40 °C$, there is no strong dependence on the out-time as the higher temperature decreases the viscosity (Ellis 1993), counteracting the increase due to out-time effects.

3.2.2 Work of Adhesion

Figure 7B shows the probe tack results for the work of adhesion per area $W_{adh}/A$ from six measurements each. Additional data is listed in Supplementary Table SA9. The mean standard deviation was 0.59 µJ/mm². The work of adhesion is higher at the high test temperature at all out-times and rates. At the high temperature, a large amount of separation energy is dissipated during debonding due to the prevailing viscous behavior of the material (Budelmann et al., 2019) leading to a higher work of adhesion. Similar to the maximum force, at $T=40 °C$ the work of adhesion is rate dependent with the highest value at the highest test rate ($v=2 mm/s$) and vice versa while there is no clear trend towards rate dependence at $T=20 °C$. At both temperatures, the out-time dependence is apparent with the same assumed root causes as for the maximum force. Besides some deviations ($T=20 °C$, $v=0.2 mm/s$, $t_{out}=15 d$; $T=40 °C$, $v=0.2 mm/s$, $t_{out}=5 d$; $T=40 °C$, $v=0.02 mm/s$, $t_{out}=15 d$), the work of adhesion generally decreases as a function of out-time as the poorer surface wetting leads to a smaller effective debonding area.

3.2.3 Tack Stiffness

The probe tack results for the tack stiffness ${\sigma }_{probe}/d$ from six measurements each are depicted in Figure 7C. Additional data is listed in Supplementary Table SA10. The mean standard deviation was 2.64 N/mm³. Similar to the maximum force, for the tack stiffness there is no strong out-time dependence at $T=40 °C$. At $T=20 °C$, however, the tack stiffness is generally even higher than at $T=40 °C$ for out-times 1 and 5 days before dropping off sharply from 5 to 10 days. The tack stiffness is assumed to be dependent on the elastic component of the material behavior which may be lower at $T=40 °C$ and low out-times due to the low viscosity. The sharp decrease is attributed to the poor surface wetting at high out-times. Again, there is no clear trend concerning the influence of rate at the low temperature. At the high temperature, a higher rate generally leads to a higher tack stiffness with the exception of $v=0.2 mm/s$ and $v=2 mm/s$ at 5 days out-time with the same assumed reasons as explained for the maximum force.

3.3 Peel Tack

Figure 8 presents the peel tack results from five measurements each. Additional data is listed in Supplementary Table SA11. The mean standard deviation was 1.95 mN/mm. In all process parameter settings, the peel tack decreased monotonously as a function of out-time which, again, is explained by the increase in viscosity leading to a poor surface wetting. The process parameter lay-up rate evidently influences the peel tack: at 1day and 15 days out-time, a lower lay-up rate leads to a higher peel tack. At 5 days and 10 days out-time, the middle rate ($v=0.06 m/s$) leads to a higher peel tack than the low rate ($v=0.03 m/s$). Yet, at all out-times, the high rate ($v=0.1 m/s$) leads to lower peel tack than the other rates. Besides the roller compliance, the lay-up rate is the main input for the compaction time. As a higher compaction time generally leads to a higher tack (Ahn et al., 1992b; Endruweit et al., 2018), the lay-up rate directly affects tack. Except for 1 day out-time, the higher compaction force ($F=400 N$) leads to a higher peel tack as it enhances surface wetting. The higher IR emitter power ($P_{IR}=350 W$) leads to a higher peel tack at 1 and 5 days out-time whereas there is no significant influence of IR emitter power on peel tack at 10 and 15 days out-time. In combination with the lay-up rate, the IR emitter power influences the material temperature. Tack generally increases up to a certain temperature because of the improved surface wetting before dropping off at higher temperatures because of the onset of cohesive failure (Ahn et al., 1992a; Crossley et al., 2012; Budelmann et al., 2019; Budelmann et al., 2020). Therefore, at 1 and 5 days out-time, the increase in IR emitter power leads to an increase in tack while at 10 and 15 days out-time, the temperature influence in the investigated range is not high enough to compensate the out-time effects. All specimens exhibited adhesive failure indicating that the temperature for maximum tack was not exceeded.

FIGURE 8

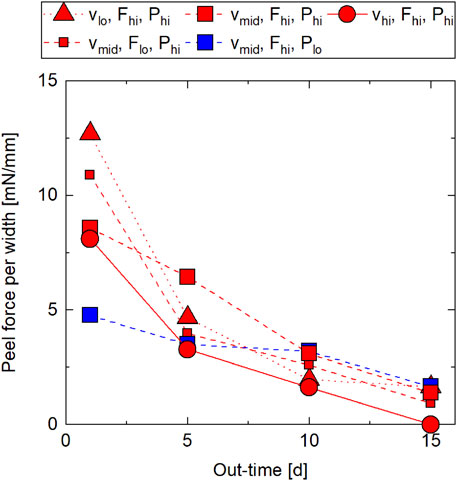
FIGURE 8. Peel tack results as a function of out-time from TUM peel tack tests (Material: IM7/8552 prepreg; out-time: 1 day–15 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$; ${\mathit{v}}_{\mathit{lo}}=0.03\mathit{ m}/\mathit{s}$, ${\mathit{v}}_{\mathit{mid}}=0.06\mathit{ m}/\mathit{s}$, ${\mathit{v}}_{\mathit{hi}}=0.1\mathit{ m}/\mathit{s}$, ${\mathit{F}}_{\mathit{lo}}=200\mathit{ N}$, ${\mathit{F}}_{\mathit{hi}}=400\mathit{ N}$, ${\mathit{P}}_{\mathit{lo}}=150\mathit{ W}$, ${\mathit{P}}_{\mathit{hi}}=350\mathit{ W}$).

3.4 Transverse Tensile Modulus

Figure 9 shows the results for the transverse tensile modulus $E_2$ from five measurements each. Additional data is listed in Supplementary Table SA12. The mean standard deviation was 0.06 MPa. The scatter of the results was a lot less compared to the tack measurements as variabilities in a single layer have less severe effects in multi-layer specimens. Furthermore, $E_2$ is not dependent on the prepreg surface which otherwise might be a source of variability. The transverse tensile modulus is generally higher at the higher loading rate ($\dot{F}=0.1 N/min$) due to the viscoelasticity. Yet, the influence is comparably small—factor 1.0 to 1.6. In comparison, there is a pronounced temperature dependence as the higher temperature ($T=40 °C$) leads to a reduction of $E_2$ of 72 to 90%. This is in agreement with the expected temperature dependence of the viscosity which affects the transverse tensile stiffness (Ellis 1993). $E_2$ generally increases with increasing out-time, as expected, as the viscosity increases due to the increase in molecular size and decrease in molecular mobility (Ellis 1993; Hubert et al., 2001; Endruweit et al., 2018). From 1 day to 15 days out-time, the increase is around factor 3.3 at $T=20 °C$ and around factor 1.2 to 1.7 at $T=40 °C$. The dependence on out-time can be expressed as second order polynomial curve fits as

$E_2\left(T,\dot{F}\right)=A_{E2}\left(T,\dot{F}\right)\cdot t_{out}^2+B_{E2}\left(T,\dot{F}\right)\cdot t_{out}+C_{E2}\left(T,\dot{F}\right)(5)$

FIGURE 9

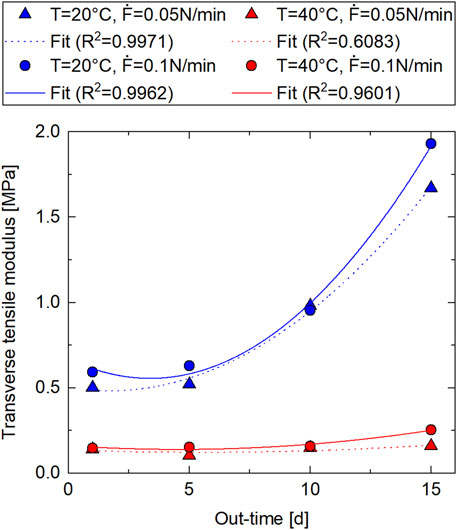
FIGURE 9. Transverse tensile modulus results as a function of out-time from DMA transverse tensile tests (Material: IM7/8552 prepreg; out-time: 1 day–15 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$).

The parameters of the fits and the coefficients of determination are listed in Table 5.

TABLE 5

TABLE 5. Transverse tensile modulus—parameters of fits.

The coefficients of determination are rather high — 0.9971, 0.9962, and 0.9601 — except for E₂(T = 40°C, $\dot{F}=0.05 \mathrm{N}/\min )$ where the coefficient is 0.6083 indicating a lower conformability of the results with second order polynomial curve.

3.5 In-Plane Shear Modulus

The in-plane shear modulus results from five measurements each are depicted in Figure 10. The values were calculated at shear rates of 0.001, 0.005, and 0.01 s⁻¹. The in-plane shear modulus $G_{12}$ obtained from the torsion bar test is a result of several conversion steps based on the mean values of the measured storage and loss modulus. Therefore, the measured values serve as an indicator for the variation of the converted results: the mean coefficient of variation for the storage and loss modulus was 5.3%. Figure 10 demonstrates that the obtained shear modulus is rate dependent since it is affected by the viscous behavior of the resin. At both test temperatures, $G_{12}$ increases with increasing shear rate. At $T=20 °C$, the increase from $\dot{\gamma }=0.001 s^{-1}$ to $\dot{\gamma }=0.01 s^{-1}$ is around factor 1.7 to 2.1 — depending on the out-time—and at $T=40 °C$ the increase is around factor 1.4. The temperature dependence of $G_{12}$ is clearly evident, too. The higher temperature ($T=40 °C$) leads to a reduction of $G_{12}$ of 58 to 86% depending on rate and out-time. Similar to $E_2$, the in-plane shear modulus increases with increasing out-time as the viscosity increases due to the increase in molecular size and decrease in molecular mobility. The dependence on out-time can be expressed as second order polynomial curve fits at $T=20 °C$ as

$G_{12}\left(T,\dot{\gamma }\right)=A_{G12}\left(T,\dot{\gamma }\right)\cdot t_{out}^2+B_{G12}\left(T,\dot{\gamma }\right)\cdot t_{out}+C_{G12}\left(T,\dot{\gamma }\right)(6)$

while at $T=40 °C$, the out-time dependence appeared rather linear so that we set $A_{G12}\left(T=40°C\right)$ to zero. The parameters of the fits and the coefficients of determination are listed in Table 6.

FIGURE 10

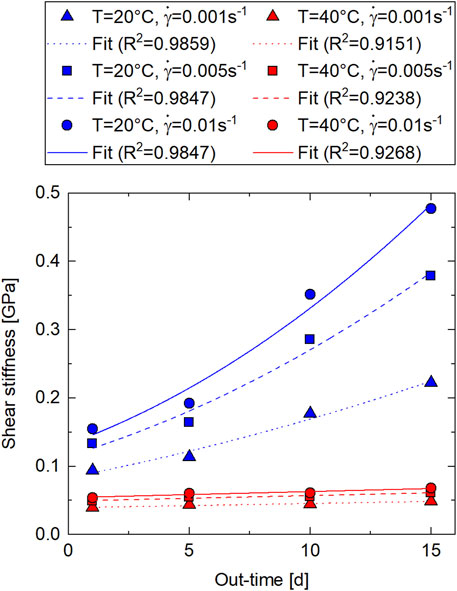
FIGURE 10. In-plane shear modulus results as a function of out-time from rheometer torsion bar tests (Material: IM7/8552 prepreg; out-time: 1 day–15 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$).

TABLE 6

TABLE 6. In-plane shear modulus—parameters of fits.

3.6 AFP Lay-Up Trials

3.6.1 Out-Of-Plane Buckles

Figure 11 gives an overview of the results of the occurrence of buckles during steering from five measurements each. Additional data is listed in Supplementary Table SA13. The mean standard deviation was 0.11. On average, there were buckles in every out-time and process parameter setting. The setting with the least buckling was $v=0.03 m/s$, $F=400 N$, $P_{IR}=350 W$ at 1 day out-time with a relative buckle-free length of 0.968. The buckle-free length is rate-dependent as a lower lay-up rate leads to less buckles at all out-times. While the difference at 1 day out-time is comparably small—$L_{bfree}(v=0.03 m/s)=0.968$ and $L_{bfree}(v=0.1 m/s)=0.919$—the influence increases with increasing out-time—e. g. $L_{bfree}(v=0.03 m/s)=0.833$ and $L_{bfree}(v=0.1 m/s)=0$ at 15 days out-time. On the lines of the peel tack, the compaction time and temperature—both dependent on the lay-up rate—significantly affect the bond between tape and substrate. We observed a similar dependence on the IR emitter power. The low IR emitter power ($P_{IR}=150 W$) led to a smaller buckle-free length at all out-times. Again, the influence was more pronounced at higher out-times. Except for a deviation at 5 days out-time, the higher compaction force ($F=400 N$) led to a higher buckle-free length while the influence was less pronounced than the lay-up rate and IR emitter power influences. The out-time effects are clearly visible, too, in Figure 11. The buckle-free length generally decreases monotonously as out-time increases caused by the decrease in molecular mobility leading to poor surface wetting. While the difference between 1 and 5 days out-time is comparably small, the buckle-free length decreases considerably after 10 days out-time and even more after 15 days out-time. At 15 days out-time, none of the tapes adhered to the substrate at the high rate ($v=0.1 m/s$) and at the low IR emitter power ($P_{IR}=150 W$).

FIGURE 11

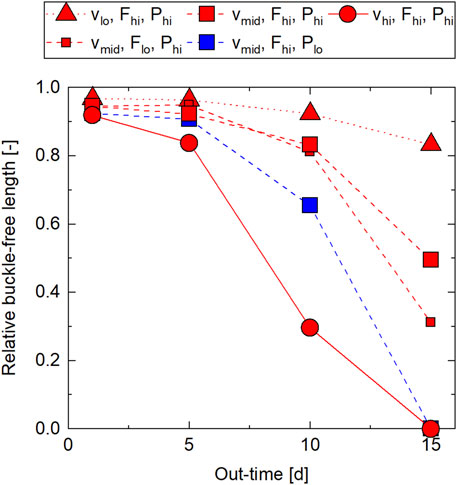
FIGURE 11. Steering results—out-of-plane buckles as a function of out-time from AFP lay-up experiments at steering radius $\mathit{R}=600\mathit{ mm}$ (Material: IM7/8552 prepreg; out-time: 1 day–15 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$; ${\mathit{v}}_{\mathit{lo}}=0.03\mathit{ m}/\mathit{s}$, ${\mathit{v}}_{\mathit{mid}}=0.06\mathit{ m}/\mathit{s}$, ${\mathit{v}}_{\mathit{hi}}=0.1\mathit{ m}/\mathit{s}$, ${\mathit{F}}_{\mathit{lo}}=200\mathit{ N}$, ${\mathit{F}}_{\mathit{hi}}=400\mathit{ N}$, ${\mathit{P}}_{\mathit{lo}}=150\mathit{ W}$, ${\mathit{P}}_{\mathit{hi}}=350\mathit{ W}$).

3.6.2 Tape Pull-Up

Figure 12 shows the results of the occurrence of tape pull-up during steering from the same five measurements each as the out-of-plane buckle measurements. Additional data is listed in Supplementary Table SA13. The mean standard deviation was 0.17. Tape pull-up occurred either once per tape—with varying length—or not at all. The dependence of the relative pull-up-free length on process parameters and out-time is quite similar to the case of the buckle-free length. The pull-up-free length remained almost the same from 1 to 5 days out-time in most setting and even increased at $v=0.06 m/s$, $F=200 N$, $P_{IR}=350 W$ and $v=0.06 m/s$, $F=400 N$, $P_{IR}=150 W$. Apart from that, the observations are comparable to the ones of the buckle-free length.

FIGURE 12

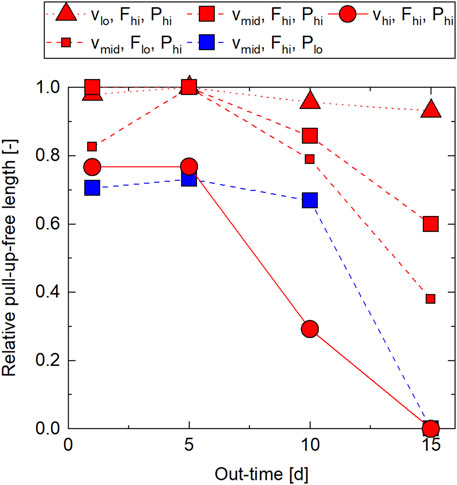
FIGURE 12. Steering results—tape pull-up as a function of out-time from AFP lay-up experiments at steering radius $\mathit{R}=600\mathit{ mm}$ (Material: IM7/8552 prepreg; out-time: 1 day–15 days at $\mathit{T}=21\mathit{ }°\mathit{C}$, $\mathit{RH}=40\mathit{ \%}$; ${\mathit{v}}_{\mathit{lo}}=0.03\mathit{ m}/\mathit{s}$, ${\mathit{v}}_{\mathit{mid}}=0.06\mathit{ m}/\mathit{s}$, ${\mathit{v}}_{\mathit{hi}}=0.1\mathit{ m}/\mathit{s}$, ${\mathit{F}}_{\mathit{lo}}=200\mathit{ N}$, ${\mathit{F}}_{\mathit{hi}}=400\mathit{ N}$, ${\mathit{P}}_{\mathit{lo}}=150\mathit{ W}$, ${\mathit{P}}_{\mathit{hi}}=350\mathit{ W}$).

4 Discussion

To further understand the impacts of the test/process parameters to account for out-time effects, we determined the Pearson correlation coefficient as per (Rousseau et al., 2018) for the presented experiments using the single values of each experiment. The Pearson correlation coefficient $-1\le r_{xy}\le 1$ quantifies the linear correlation between two sets of data. A correlation coefficient close to –1 indicates a strong negative correlation while close to one indicates a strong positive correlation and 0 indicates no correlation (Rousseau et al., 2018). Even though the correlation coefficient only quantifies linear correlation, we considered it valuable to assess the impacts of the test/process parameters.

Figure 13 shows the correlation coefficients for the mechanical properties $E_2$ and $G_{12}$. In both cases, the strongest correlation is between the temperature and the respective mechanical properties which is due to the temperature-dependent viscoelastic behavior of the resin. As discussed in Sections 3.4 and 3.5, an increase in temperature can be used to compensate out-time effects which have the second strongest correlation. The main difference between the correlation coefficients of $E_2$ and $G_{12}$ is the correlation to rate which is higher for $G_{12}$ than for $E_2$. The smaller investigated range of the rate in the $E_2$ measurements compared to the $G_{12}$ measurements and the difference in the type of boundary conditions—constant loading rate vs constant strain rate, however, have to be considered.

FIGURE 13

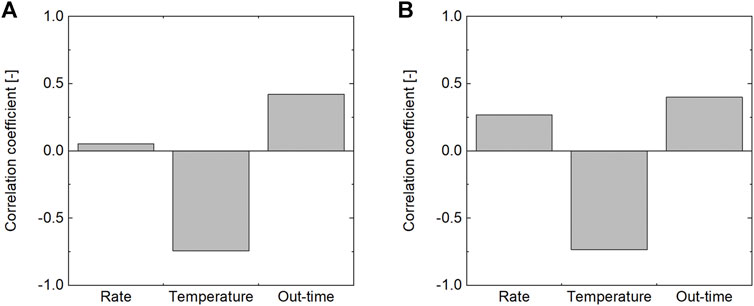
FIGURE 13. Correlation coefficient of mechanical properties of uncured IM7/8552 prepreg. (A) Transverse tensile modulus. (B) In-plane shear modulus.

The correlation coefficients for the probe tack results are depicted in Figure 14A. Here, the correlation coefficients differ for each reading. While the maximum force and the work of adhesion have a similar maximum correlation to the temperature followed by the rate, the tack stiffness has a weaker correlation to the test parameters and a stronger correlation to the out-time. As the tack stiffness is assumed to be influenced by the elastic component of the viscoelastic material behavior, apparent stiffening effects due to out-time may be more significant than for the other readings. The rate dependence of all three readings is a result of the viscoelastic behavior. Implications for AFP processing are, however, difficult to derive, as the debonding rate during AFP lay-up is difficult to estimate and it is highly dependent on the type of defect (Budelmann et al., 2019). In contrast, implications for AFP processing from the temperature dependence observed in probe tack tests are more straightforward. As discussed in Section 3.2, at prolonged out-times, the higher test temperature led to a higher tack implying that a temperature increase—within the investigated range—can be used to increase tack at these out-times.

FIGURE 14

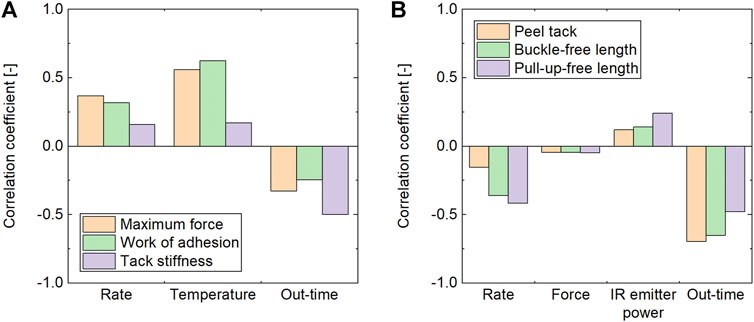
FIGURE 14. Correlation coefficient of tack and lay-up related results of uncured IM7/8552 prepreg. (A) Probe tack. (B) Peel tack, buckles, and pull-up.

Figure 14B combines the correlation coefficients for the lay-up defects with the ones for the peel tack. Since we used the same material, machine, and process parameters in both experiments, we can compare the correlation coefficients directly. The general trend of the correlation coefficients is quite similar for all three results. There is almost no correlation of the compaction force with the lay-up defects and the peel tack. The strongest process parameter correlation for all three results is the lay-up rate followed by the IR emitter power. This demonstrates that the lay-up rate can be used as the main process parameter to reduce the occurrence of steering induced lay-up defects. As implied by the steering defect results—Figures 11, 12, reducing the lay-up rate leads to a lay-up with very little defects even at 10 days out-time while increasing the lay-up rate significantly worsens the lay-up result. Since reducing the lay-up rate decreases the productivity of the manufacturing process, an increase in IR emitter power should be considered, too, as a countermeasure for defect occurrence. The strongest correlation coefficient evident in Figure 14B is between the out-time and the three results—peel tack, buckle, pull-up. This underlines the importance of the consideration of out-time effects on AFP processing. Another aspect that our results unfold, is the direct relation of steering defect results to the peel tack which is possible as the material, the machine, and the process parameters are the same in the AFP lay-up trials and the peel tack test. The comparison is illustrated in Figure 15 where the defect-free lengths are shown as a function of peel tack. The data points demonstrate that there is a correlation between relative buckle-free length and peel tack. In the peel tack range from 12.7 to 3.5 mN/mm, the buckle-free length decreases only slightly from 0.968 to 0.907. Below a peel tack of 3.5 mN/mm, the buckle-free length begins to drop significantly, indicating that this value marks a critical value for the magnitude of buckle occurrence (without considering other material properties) in the investigated case. The relation between relative pull-up-free length and peel tack is less clear—see Figure 15B. In the peel tack range from 12.7 to 1.6 mN/mm, the pull-up-free length ranges from 1 to 0.669 and drops off at lower peel tack values mainly due to the tapes not adhering at all. Yet, the findings from Figure 15 underline that peel tack measurements are a useful indicator to experimentally predict the lay-up behavior during AFP processing with a particular correlation to out-of-plane buckles during steering.

FIGURE 15

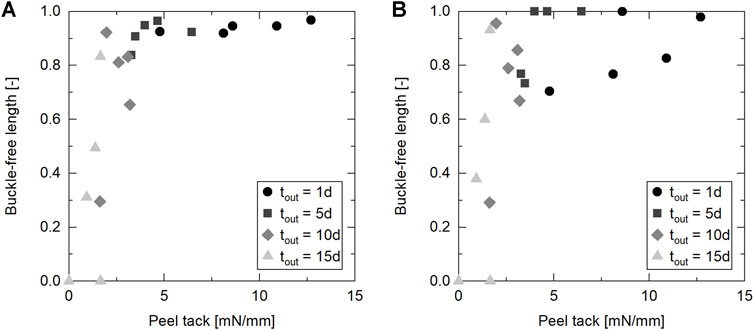
FIGURE 15. Steering induced defects as a function of peel tack of uncured IM7/8552. (A) Out-of-plane buckles. (B) Tape pull-up.

To estimate the impact of mechanical and probe tack properties on the lay-up behavior, we put our material data in an existing analytical model for the prediction of out-of-plane buckles presented by Bakhshi and Hojjati (Bakhshi and Hojjati 2019) which is the latest of a series of analytical model for steering (Beakou et al., 2011; Hörmann 2015; Matveev et al., 2016; Belhaj and Hojjati 2018). For this, we used the minimum and maximum values of each measured property—transverse tensile modulus $E_2$, in-plane shear modulus $G_{12}$, tack stiffness $\sigma /d$ — and calculated the long term critical steering radius using Bakhshi and Hojjati’s model [Eqs. 24, 26 in (Bakhshi and Hojjati 2019)] one by one. Where we did not assess the minimum or maximum of a property we used the mean value of all measurements. The unchanged input parameters are listed in Table 7 and the varied parameters are listed in Table 8. The critical steering radius did not change depending on the transverse tensile modulus. The relative change of critical steering radius from $E_{2,min}$ to $E_{2,max}$ was –0.0001% which indicates that the change in transverse tensile modulus plays a negligible role for the occurrence of out-of-plane buckles. In contrast, the relative change of critical steering radius from ${(\sigma /d)}_{min}$ to ${(\sigma /d)}_{max}$ was –35% and from $G_{12,min}$ to $G_{12,max}$ it was –61%. Expectedly, the tack stiffness significantly affects the occurrence of out-of-plane buckles underlining the importance of tack characterization to predict lay-up behavior. The comparison of calculated critical steering radii indicates a surprisingly high influence of the in-plane shear modulus. The buckling model is formulated as a plate buckling problem. Therefore, a higher in-plane shear modulus leads to a smaller critical steering radius since the load for buckle development has to be higher to overcome the shear modulus. Considering the observation that buckling occurs more frequently at higher out-time, the influence of $G_{12}$ might be overestimated either due to the model assumptions or due to the order of magnitude of our results. In our findings, the in-plane shear modulus at $T=20 °C$ increased strongly due to out-time. Looking only at $T=40 °C$ results, the change of critical steering radius from $G_{\mathrm{12,40}°C,min}$ to $G_{\mathrm{12,40}°C,max}$ was only –10% indicating that the influence of the material properties is also temperature dependent.

TABLE 7

TABLE 7. Buckling model—unchanged input parameters.

TABLE 8

TABLE 8. Buckling model—varied input parameters.

5 Conclusion

AFP-related material properties of uncured prepreg tapes are strongly affected by the material’s out-time. These material changes, in turn, significantly affect the occurrence of lay-up defects during steering. The mechanical properties transverse tensile modulus and in-plane shear modulus increase as a function of out-time following a second order polynomial fit and the most influential test parameter is the temperature. According to calculations with a defect prediction model, the in-plane shear modulus considerably affects the out-of-plane buckling while the transverse tensile modulus’ influence is negligible within the observed range. Furthermore, the model underlines the influence of tack on buckling. Experimental results from probe tack measurements revealed a sharp drop in tack after 10 days out-time (which equals the tack life specified by the manufacturer) at the lower test temperature. Yet, the probe tack at higher out-times may be increased by applying a higher temperature. By means of a novel peel tack test, we were able to correlate the material’s tack directly to AFP process parameters. The peel tack results displayed a strong correlation to defects during AFP lay-up trials underlining that they can be used to predict the lay-up behavior. The variation of AFP process parameters demonstrated that the lay-up rate has the largest influence on both the peel tack and the occurrence of out-of-plane steering defects followed by the IR emitter power. Decreasing the lay-up rate is therefore the first countermeasure to reduce lay-up defects at high out-times and by that increase the material usage. Since we evaluated an easily accessible reference value—the glass transition temperature $T_g$, any $T_g$ measurements of the investigated material IM7/8552 combined with our findings can be used to estimate the material properties and lay-up behavior. Furthermore, the interdependences between material properties, test parameters, and out-time can be transferred to other prepreg materials and the findings can serve as guiding input parameters for defect prediction models.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

KH conducted the investigation, acquired the data, formally analyzed the data, defined the methodology, and wrote the first draft of the manuscript. DC contributed to the formal analysis of data and to the methodology definition. KD supervised the work. All authors contributed to the conceptualization, the manuscript revision, read, and approved the submitted version.

Funding

Part of the present work was funded by the German Federal Ministry for Economic Affairs and Energy under the project “Thermisch-elektrisch optimierte Luftfahrtantriebssysteme (TELOS)” (No. 20Y1516F). The open access publication fee was funded by the TUM Publishing Fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

David de Haes and Juan Ramón Torresano Gómez are recognized for conducting part of the experiments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.825809/full#supplementary-material

References

Ahn, K. J., Peterson, L., Seferis, J. C., Nowacki, D., and Zachmann, H. G. (1992a). Prepreg Aging in Relation to Tack. J. Appl. Polym. Sci. 45 (3), 399–406. doi:10.1002/app.1992.070450304

CrossRef Full Text | Google Scholar

Ahn, K. J., Seferis, J. C., Pelton, T., and Wilhelm, M. (1992b). Analysis and Characterization of Prepreg Tack. Polym. Compos. 13 (3), 197–206. doi:10.1002/pc.750130308

CrossRef Full Text | Google Scholar

Argüelles, P., Bischoff, M., Busquin, P., Droste, B. A. C., Evans, R., Kröll, W., et al. (2001). European Aeronautics: A Vision for 2020, Meeting Society's Needs and Winning Global Leadership. Luxembourg: Office for Official Publications of the European Communities.

Google Scholar

Bakhshi, N., and Hojjati, M. (2018). An Experimental and Simulative Study on the Defects Appeared during Tow Steering in Automated Fiber Placement. Compos. Part A Appl. Sci. Manuf. 113, 122–131. doi:10.1016/j.compositesa.2018.07.031

CrossRef Full Text | Google Scholar

Bakhshi, N., and Hojjati, M. (2019). Time-dependent Wrinkle Formation during Tow Steering in Automated Fiber Placement. Compos. Part B Eng. 165, 586–593. doi:10.1016/j.compositesb.2019.02.034

CrossRef Full Text | Google Scholar

Banks, R., Mouritz, A. P., John, S., Coman, F., and Paton, R. (2004). Development of a New Structural Prepreg: Characterisation of Handling, Drape and Tack Properties. Compos. Struct. 66 (1-4), 169–174. doi:10.1016/j.compstruct.2004.04.034

CrossRef Full Text | Google Scholar

Beakou, A., Cano, M., Le Cam, J.-B., and Verney, V. (2011). Modelling Slit Tape Buckling during Automated Prepreg Manufacturing: A Local Approach. Compos. Struct. 93 (10), 2628–2635. doi:10.1016/j.compstruct.2011.04.030

CrossRef Full Text | Google Scholar

Belhaj, M., and Hojjati, M. (2018). Wrinkle Formation during Steering in Automated Fiber Placement: Modeling and Experimental Verification. J. Reinf. Plastics Compos. 37 (6), 396–409. doi:10.1177/0731684417752872

CrossRef Full Text | Google Scholar

Biron, M. (2020). “A Practical Guide to Plastics Sustainability,” in Concept, Solutions, and Implementation. Editor O. Kidlington (Cambridge, MA: William Andrew, Applied Science Publishers (Plastics design library).

Google Scholar

Blass, D., Kreling, S., and Dilger, K. (2017). The Impact of Prepreg Aging on its Processability and the Postcure Mechanical Properties of Epoxy-Based Carbon-Fiber Reinforced Plastics. Proc. Institution Mech. Eng. Part L J. Mater. Des. Appl. 231 (1-2), 62–72. doi:10.1177/1464420716665413

CrossRef Full Text | Google Scholar

Böckl, B., Jetten, C., Heller, K., Ebel, C., and Drechsler, K. (2018). “Online Monitoring System for the Tack of Prepreg Slit Tapes Used in Automated Fiber Placement,” in ECCM 2018 - 18th European Conference on Composite Materials, 24-28th June 2018, Athens, Greece (Athens, Greece: European Society for Composite Materials: Applied Mechanics Laboratory).

Google Scholar

Budelmann, D., Detampel, H., Schmidt, C., and Meiners, D. (2019). Interaction of Process Parameters and Material Properties with Regard to Prepreg Tack in Automated Lay-Up and Draping Processes. Compos. Part A Appl. Sci. Manuf. 117, 308–316. doi:10.1016/j.compositesa.2018.12.001

CrossRef Full Text | Google Scholar

Budelmann, D., Schmidt, C., and Meiners, D. (2020). Prepreg Tack: A Review of Mechanisms, Measurement, and Manufacturing Implication. Polym. Compos. 41 (9), 3440–3458. doi:10.1002/pc.25642

CrossRef Full Text | Google Scholar

Buehler, F. U., and Seferis, J. C. (2000). Effect of Reinforcement and Solvent Content on Moisture Absorption in Epoxy Composite Materials. Compos. Part A Appl. Sci. Manuf. 31 (7), 741–748. doi:10.1016/S1359-835X(00)00036-1

CrossRef Full Text | Google Scholar

Cole, K. C., Noël, D., Hechler, J.-J., Cielo, P., Krapez, J.-C., Chouliotis, A., et al. (1991). Room-temperature Aging of Narmco 5208 Carbon-Epoxy Prepreg. Part II: Physical, Mechanical, and Nondestructive Characterization. Polym. Compos. 12 (3), 203–212. doi:10.1002/pc.750120311

CrossRef Full Text | Google Scholar

Crossley, R. J., Schubel, P. J., and Warrior, N. A. (2012). The Experimental Determination of Prepreg Tack and Dynamic Stiffness. Compos. Part A Appl. Sci. Manuf. 43 (3), 423–434. doi:10.1016/j.compositesa.2011.10.014

CrossRef Full Text | Google Scholar

de Andrade Raponi, O., Barbosa, L. C. M., Junior, J. E. B., Junior, A. C. A., and Guimarães, A. (2020). Effects of the Exposition of an Autoclave Prepreg to the Processing Environment on its Properties, Curing Cycle and Final Composite Behavior. Int. J. Adv. Manuf. Technol. 106 (11-12), 5129–5136. doi:10.1007/s00170-020-05022-5

CrossRef Full Text | Google Scholar

DIN Deutsches Institut für Normung e. V. (2019). DIN EN ISO 29862:2019-09, Self Adhesive tapes - Determination of Peel Adhesion Properties (ISO 29862:2018); German Version EN ISO 29862:2019. Berlin: Beuth Verlag GmbH.

Google Scholar

Dubois, O., Le Cam, J.-B., and Béakou, A. (2010). Experimental Analysis of Prepreg Tack. Exp. Mech. 50 (5), 599–606. doi:10.1007/s11340-009-9236-7

CrossRef Full Text | Google Scholar

Ellis, B. (1993). Chemistry and Technology of Epoxy Resins. Ebrary, Inc. London, New York: Blackie Academic & Professional.

Google Scholar

Endruweit, A., Choong, G. Y. H., Ghose, S., Johnson, B. A., Younkin, D. R., Warrior, N. A., et al. (2018). Characterisation of Tack for Uni-Directional Prepreg Tape Employing a Continuous Application-And-Peel Test Method. Compos. Part A Appl. Sci. Manuf. 114, 295–306. doi:10.1016/j.compositesa.2018.08.027

CrossRef Full Text | Google Scholar

Forghani, A., Hickmott, C., Hutten, V., Bedayat, H., Wohl, C., Grimsley, B., et al. (2018). “Experimental Calibration of a Numerical Model of Prepreg Tack for Predicting Afp Process Related Defects,” in SAMPE Conference & Exhibition, Diamond Bar, CA, May 21-24, 2018 (California. Diamond Bar, CA: Society for the Advancement of Material and Process Engineering).

Google Scholar

Gillanders, A. M., Kerr, S., and Martin, T. J. (1981). Determination of Prepreg Tack. Int. J. Adhesion Adhesives 1 (3), 125–134. doi:10.1016/0143-7496(81)90035-X

CrossRef Full Text | Google Scholar

Grunenfelder, L. K., and Nutt, S. R. (2011). Out-time Effects on VBO (Vacuum Bag Only) Prepreg and Laminate Properties. SAMPE J. 47 (5), 6–13.

Google Scholar

Haanappel, S. P., and Akkerman, R. (2014). Shear Characterisation of Uni-Directional Fibre Reinforced Thermoplastic Melts by Means of Torsion. Compos. Part A Appl. Sci. Manuf. 56, 8–26. doi:10.1016/j.compositesa.2013.09.007

CrossRef Full Text | Google Scholar

Hagnell, M. K., and Åkermo, M. (2015). A Composite Cost Model for the Aeronautical Industry: Methodology and Case Study. Compos. Part B Eng. 79, 254–261. doi:10.1016/j.compositesb.2015.04.043

CrossRef Full Text | Google Scholar

Harrison, P., Clifford, M. J., and Long, A. C. (2004). Shear Characterisation of Viscous Woven Textile Composites: a Comparison between Picture Frame and Bias Extension Experiments. Compos. Sci. Technol. 64 (10-11), 1453–1465. doi:10.1016/j.compscitech.2003.10.015

CrossRef Full Text | Google Scholar

Hayes, B. S., Seferis, J. C., and Chen, J. S. (1996). Development and Hot-Melt Impregnation of a Model Controlled Flow Prepreg System. Polym. Compos.Compos 17 (5), 730–742. doi:10.1002/pc.10665

CrossRef Full Text | Google Scholar

Heller, K., Böckl, B., Ebel, C., and Drechsler, K. (2018). “Influence of Prepreg Aging and Tack on Lay-Up Effects/Defects in Thermoset Automated Fiber Placement,” in ECCM 2018 - 18th European Conference on Composite Materials, Athens, Greece, 24-28th June 2018 (Athens, Greece: European Society for Composite Materials: Applied Mechanics Laboratory).

Google Scholar

Heller, K., Seyfferth, S., Kind, K., and Drechsler, K. (2020b). “A Post Lay-up Tack Peel Test for Aerospace Grade Prepreg Tapes,” in Proceedings SE Conference Amsterdam, 29 September – 1 (Amsterdam, Netherlands: SAMPE Europe Conference and Exhibition 2020).

Google Scholar

Hexcel Corporation (2020): HexPly 8552 Epoxy matrix. Product Data Sheet. Available online at: https://www.hexcel.com/user_area/content_media/raw/HexPly_8552_eu_DataSheet.pdf, (Accessed 7 22, 2021).

Google Scholar

Heller, K., Hallmannseder, M., Colin, D., Kind, K., and Drechsler, K. (2020a). Comparing Test Methods for the Intra-ply Shear Properties of Uncured Prepreg Tapes. Sci. Eng. Compos. Mater. 27 (1), 89–96. doi:10.1515/secm-2020-0009

CrossRef Full Text | Google Scholar

Hörmann, P. (2015). Thermoset Automated Fibre Placement – on Steering Effects and Their Prediction. München: Technische Universität München. Dissertation.

Google Scholar

Hubert, P., Johnston, A., Poursartip, A., Nelson, K., Repecka, L., and Saremi, F. F. (2001). “Cure Kinetics and Viscosity Models for Hexcel 8552 Epoxy Resin,” in International SAMPE Symposium and Exhibition (Proceedings), Long Beach CA, 6-10 2001 (Long Beach CA: SKU).

Google Scholar

Larberg, Y. R., Åkermo, M., and Norrby, M. (2012). On the In-Plane Deformability of Cross-Plied Unidirectional Prepreg. J. Compos. Mater. 46 (8), 929–939. doi:10.1177/0021998311412988

CrossRef Full Text | Google Scholar

Lengsfeld, H., Wolff-Fabris, F., Krämer, J., Lacalle, J., and Altstädt, V. (2016). Composite Technology. Prepregs and Monolithic Part Fabrication Technologies. Munich, Cincinnati: Hanser Publishers; Hanser Publications.

Google Scholar

Lukaszewicz, D. H.-J. A., and Potter, K. D. (2011). The Internal Structure and Conformation of Prepreg with Respect to Reliable Automated Processing. Compos. Part A Appl. Sci. Manuf. 42 (3), 283–292. doi:10.1016/j.compositesa.2010.11.014

CrossRef Full Text | Google Scholar

Lukaszewicz, D. H.-J. A., Ward, C., and Potter, K. D. (2012). The Engineering Aspects of Automated Prepreg Layup: History, Present and Future. Compos. Part B Eng. 43 (3), 997–1009. doi:10.1016/j.compositesb.2011.12.003

CrossRef Full Text | Google Scholar

Margossian, A., Bel, S., and Hinterhoelzl, R. (2016). On the Characterisation of Transverse Tensile Properties of Molten Unidirectional Thermoplastic Composite tapes for Thermoforming Simulations. Compos. Part A Appl. Sci. Manuf. 88, 48–58. doi:10.1016/j.compositesa.2016.05.019

CrossRef Full Text | Google Scholar

Margossian, A., Hörmann, P., Zemliana, K., Avila-Gray, L., Bel, S., and Hinterhoelzl, R. (2015). Shear Characterisation of Unidirectional Thermoset Pre-impregnated Composites Using a Rheometre. Compos. Part A Appl. Sci. Manuf. 56, 8–26. doi:10.1016/j.compositesa.2013.09.007

CrossRef Full Text | Google Scholar

Matveev, M. Y., Schubel, P. J., Long, A. C., and Jones, I. A. (2016). Understanding the Buckling Behaviour of Steered Tows in Automated Dry Fibre Placement (ADFP). Compos. Part A Appl. Sci. Manuf. 90, 451–456. doi:10.1016/j.compositesa.2016.08.014

CrossRef Full Text | Google Scholar

Miller, S. G., Hou, T.-H., Sutter, J. K., Scheiman, D. A., Martin, R. E., Maryanski, M., et al. (2010). “Out-life Characteristics of IM7/977-3 Composites,” in SAMPE fall technical conference & exhibition, Salt Lake City, UT, 11 - 14 October 2010 (Salt Lake City, Utah. Covina, Calif: SAMPE).

Google Scholar

Nguyen, C. D., and Krombholz, C. (2016). “Influence of Process Parameters and Material Aging on the Adhesion of Prepreg in AFP Processes,” in ECCM17 - 17th European Conference on Composite Materials, 26-30th June 2016 (Munich, Germany: European Society for Composite Materials).

Google Scholar

O’Brien, D. J., Sottos, N. R., and White, S. R. (2007). Cure-dependent Viscoelastic Poisson's Ratio of Epoxy. Exp. Mech. 47 (2), 237–249. doi:10.1007/s11340-006-9013-9

CrossRef Full Text | Google Scholar

Pascault, J. P., and Williams, R. J. J. (1990). Glass Transition Temperature versus Conversion Relationships for Thermosetting Polymers. J. Polym. Sci. B Polym. Phys. 28 (1), 85–95. doi:10.1002/polb.1990.090280107

CrossRef Full Text | Google Scholar

Potter, K. (2002a). Bias Extension Measurements on Cross-Plied Unidirectional Prepreg. Compos. Part A Appl. Sci. Manuf. 33 (1), 63–73. doi:10.1016/S1359-835X(01)00057-4

CrossRef Full Text | Google Scholar

Potter, K. (2002b). In-plane and Out-Of-Plane Deformation Properties of Unidirectional Preimpregnated Reinforcement. Compos. Part A Appl. Sci. Manuf. 33 (11), 1469–1477. doi:10.1016/S1359-835X(02)00138-0

CrossRef Full Text | Google Scholar

Putnam, J. W., Seferis, J. C., Pelton, T., and Wilhelm, M. (1995). Perceptions of Prepreg Tack for Manufacturability in Relation to Experimental Measures. Sci. Eng. Compos. Mater. 4 (3), 143. doi:10.1515/SECM.1995.4.3.143

CrossRef Full Text | Google Scholar

Rajan, S., Sutton, M. A., Sockalingam, S., McMakin, W., Gurdal, Z., and Kidane, A. (2020). Simulations and Experiments for Automated Fiber Placement of Prepreg Slit Tape: Wrinkle Formation and Fundamental Observations. Compos. Part B Eng. 201, 108287. doi:10.1016/j.compositesb.2020.108287

CrossRef Full Text | Google Scholar

Rajan, S., Sutton, M. A., Wehbe, R., Gurdal, Z., Kidane, A., and Emri, I. (2021). Characterization of Viscoelastic Bending Stiffness of Uncured Carbon-Epoxy Prepreg Slit Tape. Compos. Struct. 275, 114295. doi:10.1016/j.compstruct.2021.114295

CrossRef Full Text | Google Scholar

Rajan, S., Sutton, M. A., Wehbe, R., Tatting, B., Gürdal, Z., Kidane, A., et al. (2019). Experimental Investigation of Prepreg Slit Tape Wrinkling during Automated Fiber Placement Process Using StereoDIC. Compos. Part B Eng. 160, 546–557. doi:10.1016/j.compositesb.2018.12.017

CrossRef Full Text | Google Scholar

Rousseau, R., Egghe, L., and Guns, R. (2018). “Statistics,” in Becoming Metric-Wise. Editors R. Rousseau, L. Egghe, and R. Guns (Cambridge, MA: Elsevier), 67–97. doi:10.1016/b978-0-08-102474-4.00004-2

CrossRef Full Text | Google Scholar

Saseendran, S., Wysocki, M., and Varna, J. (2017). Cure-state Dependent Viscoelastic Poisson's Ratio of LY5052 Epoxy Resin. Adv. Manuf. Polym. Compos. Sci. 3 (3), 92–100. doi:10.1080/20550340.2017.1348002

CrossRef Full Text | Google Scholar

Smith, A. W., Endruweit, A., Choong, G. Y. H., De Focatiis, D. S. A., and Hubert, P. (2020). Adaptation of Material Deposition Parameters to Account for Out-Time Effects on Prepreg Tack. Compos. Part A Appl. Sci. Manuf. 133, 105835. doi:10.1016/j.compositesa.2020.105835

CrossRef Full Text | Google Scholar

Smith, E. J., Grubb, C., Misasi, J., and Larson, N. (2019). “Developing a Procedure for Prepreg Tack Characterization,” in 6th Annual Composites and Advanced Materials Expo, CAMX 2019, September 23-26, 2019 (Anaheim, USA: CAMX).

Google Scholar

Timmis, A. J., Hodzic, A., Koh, L., Bonner, M., Soutis, C., Schäfer, A. W., et al. (2015). Environmental Impact Assessment of Aviation Emission Reduction through the Implementation of Composite Materials. Int. J. Life Cycle Assess. 20 (2), 233–243. doi:10.1007/s11367-014-0824-0

CrossRef Full Text | Google Scholar

van Ee, D., and Poursartip, A. (2009). HexPly 8552 Material Properties Database for Use with COMPRO CCA and Raven. Created for NCAMP National Center for Advanced Materials Performance. Wichita, KS: National Center for Advanced Materials Performance. Available online at: https://www.wichita.edu/industry_and_defense/NIAR/Research/hexcel-8552/Additional-Documents-2.pdf(Accessed 1115, 2009).

Google Scholar

Wang, Y., Chea, M. K., Belnoue, J. P.-H., Kratz, J., Ivanov, D. S., and Hallett, S. R. (2020). Experimental Characterisation of the In-Plane Shear Behaviour of UD Thermoset Prepregs under Processing Conditions. Compos. Part A Appl. Sci. Manuf. 133, 105865. doi:10.1016/j.compositesa.2020.105865

CrossRef Full Text | Google Scholar

Wehbe, R., Tatting, B., Rajan, S., Harik, R., Sutton, M., and Gürdal, Z. (2020). Geometrical Modeling of Tow Wrinkles in Automated Fiber Placement. Compos. Struct. 246, 112394. doi:10.1016/j.compstruct.2020.112394

CrossRef Full Text | Google Scholar

Wohl, C., Palmieri, F. L., Forghani, A., Hickmott, C., Bedayat, H., Coxon, B., et al. (2017). “Tack Measurements of Prepreg Tape at Variable Temperature and Humidity,” in Composites and Advanced Materials Expo (CAMX 2017), September 2017 (Orlando, FL: CAMX 2017).

Google Scholar