Theoretical Analysis on the Stability of Single Bulk Nanobubble

As predicted by classical macroscopic theory, the lifetime for nanoscale gas bubbles is extremely short, which causes conflict when detecting stable bulk nanobubbles experimentally in recent years. In fact, the stability of bulk nanobubbles depends on the surrounding liquid environment. Also, the dynamic process of gas in water involves the dissolution, diffusion, release, and transportation of gas as well as the properties of nanobubbles inside. Here, based on previous reports, we introduce the gas transport parameter $\ell$ in the classical diffusion equation by considering the gas diffusion near the bulk nanobubble at different locations in a container and consider the MacLeod-Sugden relationship between the surface tension and densities of liquid and gas for computing the lifetime of single bulk nanobubbles in an open system. The results show that the single nanobubble lifetime depends on the inner density and gas transport length. It could reach the order of 10–100 s for a single nanobubble with an initial radius of 200 nm, and provides a new idea to prolong the lifetime of the single bulk nanobubble. Meanwhile, compared with the continuous influence of the inner density on the gas diffusion flux near the nanobubble, the range of the gas transport near the nanobubble on the gas diffusion flux is limited, which is affected by the dissolution time of the nanobubble. Our findings would be helpful to explore the storage conditions of nanobubbles and the mechanism of mass transfer at the gas-liquid interface at the micro-scale.

Introduction

Long-lived, freely suspended, and spherical nanoscopic bubbles are called bulk nanobubbles (Seddon and Lohse, 2011; Attard, 2014; Zhang and Lohse, 2015; Fang et al., 2020). The applications of bulk nanobubbles have sprung up in the last decade. They exhibit excellent impacts such as in the bioremediation of groundwater pollution and water treatment (Agarwal et al., 2011; Li et al., 2014; Wang et al., 2018; Zhang et al., 2018), mineral separations using froth flotation (Sedlák and Rak, 2014), depletion flocculation for the dewatering of mineral tailings (Ngai et al., 2008), etc. However, the study of their underlying mechanisms is behind that of their applications. There are still many significant questions that need to be answered. For example, their long lifetimes could not be explained by classical theories (Zhang et al., 2008). Other applications, such as the electrification of gas-liquid interfaces (Bunkin et al., 1996), high mass transfer efficiency (Xiao and Xu, 2019), and the tensile strength discrepancy of water between experiment and theory (Mørch, 2007) are also lacking in reasonable explanations.

The basic question is the explanation of the stability of bulk nanobubbles. The diffusive dynamics of a spherical bubble in a liquid is described by the Epstein-Plesset (EP) theory (Plesset and Sadhal, 1982), which predicts that bubbles in solution will shrink or expand, depending on whether the dissolved gas in solution is oversaturated or not. Significantly, the survival time for nano-sized bubbles should be less than 0.02 s, fueling long-standing suspicion over the existence of bulk nanobubbles (Jadhav and Barigou, 2020).

In contrast to the theoretical prediction, numerous experimental results indicated that bulk nanobubbles do exist using dynamic light scattering (Alheshibri et al., 2016) Nanoparticle Tracking Analysis (Oh et al., 2015; Midtvedt et al., 2019). Although many theories reported try to explain the stability of bulk nanobubbles—for example, contaminant mechanism (Sedlák and Rak, 2014; Li et al., 2016; Yasui et al., 2016), dynamic equilibrium theory (Yasui et al., 2016), surface charge adsorption (Millare and Basilia, 2018; Tan et al., 2020), and the high-density mechanism (Zhang et al., 2008; Zhang et al., 2013)—they may partially lift the veil of mystery surrounding bulk nanobubbles under some limited conditions.

Different from surface nanobubbles, bulk nanobubbles usually exist in the bubble suspension, and their stability is easily influenced by the liquid environment surrounding them. It was reported that the storage condition may also influence the lifetime of bulk nanobubbles (Kanematsu et al., 2020). Zhou et al. reported that the high-resolution soft X-ray imaging of a single oxygen nanobubble and its near-edge fine structure absorption spectra of oxygen K-edge were obtained by scanning transmission X-ray microscopy (STXM) (Zhou et al., 2020). During the STXM nanobubble measurement the highly supersaturated liquid environment in which bubbles were sealed in between two Si3N4 membranes. This liquid environment is a confined and closed system in which no gas is exchanged with the external atmosphere. But for an open system, dissolved gas would exchange with the gas inside of the bubble near the gas/water interface and the distance of nanobubbles from the gas/water interface would also influence the stability. The process will involve dissolution, diffusion, release and transport of gas, as well as the density of nanobubbles inside.

Herein, considering the complicated processes above, we mainly focus on the effects of gas transport around nanobubbles at different horizontal positions in a container and combine new inner density data to theoretically analyze the stability of bulk nanobubbles. We numerically simulate how gas diffusion to the atmosphere influences the lifetime of a single bulk nanobubble. On the basis of the diffusion equation, we reconsider the initial condition and derive the relevant equations for a single nanobubble. In addition, the Macleod-Sugden relationship is considered to estimate the gas-liquid interfacial tension in the case of high density inside a single bulk nanobubble. The relevant parameter is varied to demonstrate the robustness of a single nanobubble’s long lifetime in varying conditions. The numerical simulation results show that the lifetime of a single bulk nanobubble lifetime could reach the order of 10–100 s, and approaches to the timescale for experimental observations depending on inner density and gas transport near bulk phase nanobubbles at different horizontal positions in a container.

The Analysis of the Stability of a Single Nanobubble

First, in order to study the effect of gas diffusion to the atmosphere on bulk nanobubble lifetime, we consider the initial condition to consist of a linear concentration profile around a single bulk nanobubble. The schematic diagram of a single bulk nanobubble is shown in Figure 1. The opening system is studied and it is supposed that bulk nanobubbles are stored in an unsealed container. In this system, we presume that a single bulk nanobubble is located in a super-saturated liquid environment and has a high density inside as reported (Zhou et al., 2020). The MacLeod-Sugden relationship for the gas-liquid interfacial tension is adopted. We conduct the numerical simulation to study the distribution of gas concentration and the evolution of the single nanobubble in order to acquire the effect of the diffusion distance and inner density on the lifetime of the nanobubble.

FIGURE 1

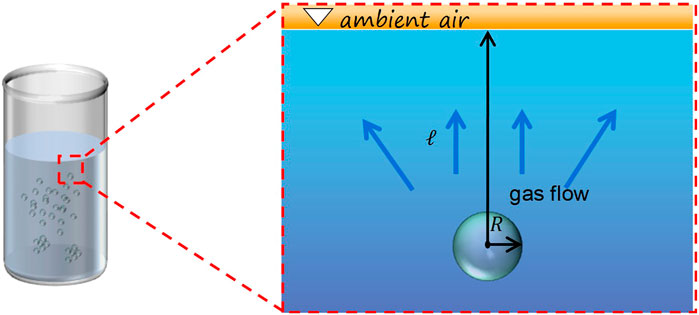
FIGURE 1. The schematic diagram of a single bulk nanobubble stored in an open system in which there is gas exchange between the bubble and the atmosphere. $\ell$ is the length of the nanobubble from air/water surface, which is also the distance of gas diffusion from the bubble to the air/water surface. The initial radius of the nanobubble is $R$.

A key point for the study of bubble diffusion dynamics is to describe the change rate of bubble mass by Fick’s diffusion law (Plesset and Sadhal, 1982):

$J=dS\cdot dm/dt=D\cdot {\partial C/\partial r|}_{r=R}(1)$

$J$ is the diffusion flux through the unit cross-sectional area ($dS$) perpendicular to the diffusion direction in unit time; $D$ is the diffusion coefficient of dissolved gas in water; $m$ is the nanobubble mass, $C$ is the mass concentration of the gas. In the diagram shown in Figure 1, we only consider the gas diffusion of a single bulk nanobubble (ignoring the influence between bubbles). The length $\ell$ between the bubble and the air/water surface determines the gas diffusion distance. The key is to solve the gas concentration gradient in the radial direction near the nanobubble: ${\partial C/\partial r|}_{r=R}$. The gas diffusion related to the gas concentration gradient is governed by the spherical diffusion equation:

$\partial C/\partial t=D\mathrm{\Delta }C(2)$

We now fully describe the boundary conditions for the above differential equation. They are given by Henry’s law and Laplace’s law, which relates the gas concentration in the liquid to the gas pressure outside the liquid near the interfaces: $C\left(r=\ell ,t\right)=P_{atm}/k$, $C\left(r=R,t\right)=\left(P_{atm}+\frac{2\gamma }{R}\right)/k$. $\gamma$ is the interfacial tension, $P_{atm}$ is the standard atmosphere, $k$ is Henry constant, $r$ is the radial coordinate.

The survival environment of surface nanobubbles during the STXM nanobubble measurement can help us effectively describe the initial conditions of bulk nanobubbles. Due to the “traffic jam effect” which lowers the diffusion rate of gas or even a chemical equilibrium in a closed system, high-density bubbles are expected to be stable in a high gas concentration environment. The high gas concentration at the nucleation site of bulk nanobubbles indicates that bulk nanobubbles also have the “traffic jam effect” similar to surface nanobubbles. In a closed system, a steady gas-saturated environment can stabilize bulk nanobubbles, but in an open system, the gas diffusion to the atmosphere is inevitable. So we simplify the gas concentration around the mature bulk nanobubble decays radially to $C\left(r=\ell ,t\right)=P_{atm}/k$ linearly in an open system (Weijs and Lohse, 2013). Based on the above considerations, the initial condition consists of a linear concentration profile (t = 0):

$C\left(r,0\right)=\frac{2\gamma }{Rk}\cdot \left(1-\frac{r}{\ell -R}\right)+\frac{P_{atm}}{k}\left(r\ge R\right)(3)$

Solving Eqs (2, 3) simultaneously, we first compute the diffusion Eq. 2 numerically. The simulations were done for the initial condition.

How long does the “traffic jam effect” stabilize a single nanobubble according to this description? Eq. 3 directly shows that the time scale of the “traffic jam effect” is related to the gas diffusion distance $\ell$ from the single bulk nanobubble to the air-water surface. Using typical parameters ($\gamma =0.072N/m$, $D=2\times {10}^{-9}{m}^2/s$, $k=5.57\times {10}^{6}Pa\cdot m^3/kg$) and the initial condition, we obtain the results corresponding to $\ell =1\mu m$ and $\ell =25mm$ shown in Figures 2A,B. Figure 2A shows time snapshots of the concentration profile $C\left(r\right)$ with gas diffusion distance $\ell =1\mu m$. It is evident from these curves that the gas diffusion away from the bubble is limited by the diffusion rate of the gas through the water far away from the bubble. This leads to an almost flat concentration profile near the bubble through which the diffusive gas flux is very small, which makes the duration of the “traffic jam effect” 0.2 ms. More details are shown in Figure 2B, which corresponds to $\ell =25mm$. It is clear from the curve that the diffusion rate of gas through water is affected by gas diffusion distance. The concentration distribution around the bubble decays slowly until it reaches the equilibrium after 200 h, forming a long-lasting “traffic jam effect”. Here we can see that the time for the system to reach the equilibrium increases from 0.2 ms to 200 h as the diffusion distance of the gas around the bubble with a radius of 200 nm increases from 1 μm to 25 mm.

FIGURE 2

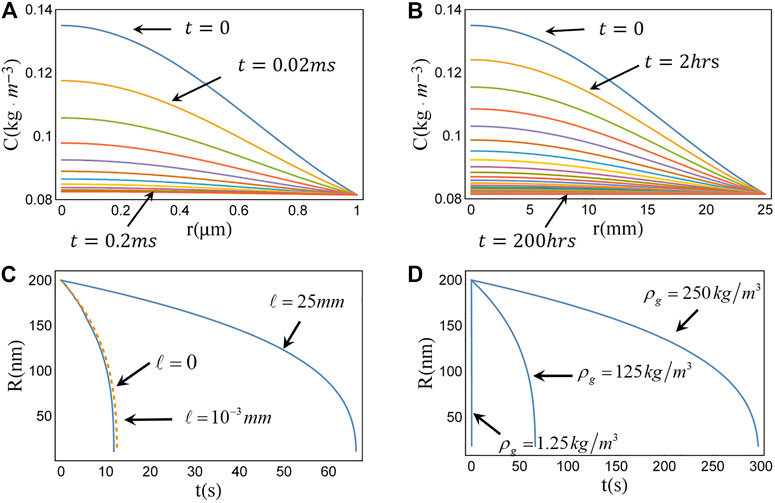
FIGURE 2. Evolution of gas concentration around the single bulk nanobubble and the dissolution process of single bulk nanobubble with different conditions. (A) In the initial moment, the gas is uniformly distributed in the fluid layer with 1 μm. At t = 0.2 ms, the gas concentration reaches an equilibrium. (B) When the liquid layer thickness is 25 mm, the gas diffusion near a single nanobubble reaches equilibrium 200 h later, indicating that the gas near the nanobubble forms a long-time “traffic jam effect”. (C) The dissolution times of bulk nanobubbles at different positions (gas diffusion distance is different) in the container while supposing inner density of bubble was ${\rho }_g=125kg/m^3$. (D) The dissolution times of bulk nanobubble with different inner densities as that proposed in Zhang et al. (2008) while supposing gas diffusion distance was $\ell =25mm$ (located a certain distance inside of the container).

The time for gas diffusion to reach an equilibrium discussed above is the result of a stationary bubble boundary and the non-zero concentration gradient of the gas near the bubble will cause the bubbles to dissolve. The gas concentration distribution around the nanobubble with the updating radius will also be updated. According to Henry’s law and Laplace’s law, the gradient of the updating gas concentration distribution is higher, and the dissolution rate of the updating nanobubble can be predicted to be accelerated. In the next section, we will solve the evolution equation of the single bulk nanobubble analytically.

According to the diffusion law, the mass that flows out of the bubble per unit time could be $dm/dt=D\cdot 4\pi R^2\cdot {\partial C/\partial r|}_{r=R}$. It should be noted that the above equations are valid only for a stationary bubble boundary, which is assumed as a reasonable physical approximation for a nanoscale bubble boundary which varies slowly with time as proposed in reference (Zhang et al., 2008). Accordingly, one has $dm/dt=4\pi R^2{\rho }_g\left(dR/dt\right)$, where ${\rho }_g$ is the inner density of nanobubble. From the above equation, we can get:

$\frac{dR}{ dt}=\frac{D}{{\rho }_g}\cdot {\frac{\partial C}{\partial r}|}_{r=R}=\frac{J}{{\rho }_g}(4)$

Eq. 4 immediately shows how the inner density and the diffusion flux affect the dissolution rate of a single bulk nanobubble. According to Eq. 2, the concentration gradient $r=R$ in relation to diffusion flux is

${\frac{\partial C}{ \partial r}|}_{r=R}=-\frac{2\gamma }{\text{k}{R}^2}\cdot \left(1+{\displaystyle \sum _{\xi =1}^{\infty }}\frac{4\left(-1+{(-1)}^{\xi }\right)e^{\frac{-D{\pi }^{2}t{\xi }^2}{{\ell }^2}}\cdot \cos \left[\frac{\pi R\xi }{\ell }\right]}{{\pi }^2{\xi }^2}\right)(5)$

$\xi$ is the summation subscript. The results of the published experiments and molecule dynamic (MD) simulation (Zhou et al., 2020) indicate that gas molecules within confinement such as the nanobubbles could maintain a dense state. In addition, MacLeod and Sugden (Robert et al., 1958) suggest an empirical relationship between the surface tension and densities of liquid and gas affecting the gas diffusion flux near the nanobubble as $\gamma ={\left[A\cdot \left({\rho }_l-{\rho }_g\right)/M\right]}^4$, where M, A and ${\rho }_l$ are molecular weight (kg/mol), parachor, and the density of the liquid (kg/m³), respectively. Then, we get:

$\frac{\text{d}R}{ \text{d}t}=-\frac{2D{\gamma }_0{(1-{\rho }_g/{\rho }_i)}^4}{\text{k}{\rho }_g{R}^2}\cdot \left(1+{\displaystyle \sum _{\xi =1}^{\infty }}\frac{4\left(-1+{(-1)}^{\xi }\right)e^{\frac{-D{\pi }^{2}t{\xi }^2}{{\ell }^2}}\cdot \cos \left[\frac{\pi R\xi }{\ell }\right]}{{\pi }^2{\xi }^2}\right)(6)$

where ${\gamma }_0$ is the surface tension of liquid on the macroscopic scale.

It follows from Eq. 6 that nanobubble lifetime depends on the initial radius $R_0$, the diffusion distance $\ell$ , and the inside density ${\rho }_g$. Here, we will computer numerical simulation on the evolution process of nanobubbles under different gas diffusion distances ($\ell =0$, $\ell =1\mu m$, $\ell =25mm$). In addition, the analysis of absorption spectra of a single surface nanobubble and MD simulation reveal that the density inside the nanobubble mainly ranges from 100 to 250 kg/m³ (Zhou et al., 2020). So, we will examine the cases with an inner density of 1.25 kg/m³, 125 kg/m³, and 250 kg/m³ to correspond to the properties of the surface nanobubble, and the results are plotted in Figures 2C,D. By changing $\ell$ and ${\rho }_g$ in the numerical calculation, we verify the result from the analytical solution to the evolutionary equation for which it holds that the single bulk nanobubble’s lifetime only depends on $\ell$ and ${\rho }_g$. In order to translate the properties of the surface nanobubble into our study, here we consider a typical nanobubble with an initial radius of 200 nm.

First, we focus on the gas diffusion distance $\ell$. The gas diffusion around a single nanobubble is actually determined by its position in the container, and bulk nanobubbles with the same size are homogeneity, so $\ell$ represents the gas diffusion distance of identical nanobubbles at different horizontal positions in the container. Meanwhile, the bulk nanobubble diffusion equation is established in the spherical coordinate system and $\ell$ is also the limit distance of gas diffusion. As observed in Figure 2C, the lifetime will increase from 11.8 to 65 s as the gas diffusion distance changes from 0 to 25 mm, where the initial radius of N₂ nanobubbles is 200 nm and the density inside the bubble is 125 kg/m³ (100 times the density of bulk gas N₂ (1.25 kg/m³) at 273 K and 1 atm). The coincidence of curves $\ell =0$ and $\ell =1\mu m$ indicates that gas diffusion has an obvious influence on the dissolution of nanobubbles only when it reaches a certain length. More details are shown in Figure 3.

FIGURE 3

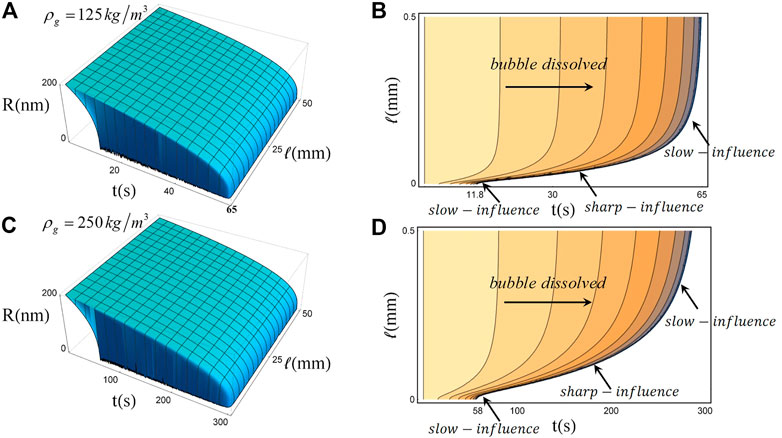
FIGURE 3. Evolution of single bulk nanobubble per unit time. (A) Development of a single bubble with an initial radius of 200 nm (${\rho }_g$ = 125 kg/m3): The gas transport near the nanobubble can effectively delay the dissolution of the nanobubble. For the nanobubble with an inner density of 125 kg/m3, the effect of gas diffusion can prolong the nanobubble lifetime by nearly six times. (B) Contour diagram of Figure 3A. Gas diffusion has a small effect range (0.5 mm) on limiting nanobubble dissolution. (C) Development of a single bubble with an initial radius of 200 nm (${\rho }_g$ = 250 kg/m3). (D) Contour diagram of Figure 3C: as the gas diffusion distance increases gradually from 0, its influence range on the life of a single nanobubble has a slow-sharp-slow process. The higher the density inside the bubble, the more obvious this process is.

Then, we further consider the gas density ${\rho }_g$ inside the nanobubble. MacLeod and Sugden correlated the gas density with the surface tension by parachor. Indeed, a higher surface tension increases the Laplace pressure, thus increasing the driving force that leads to dissolution. It is expected that achieving a low surface tension will play a positive role in prolonging nanobubble lifetime. For a gas diffusion distance of 25 mm, snapshots of different inner densities are shown in Figure 2D. From the divergence of these curves, the gas density inside the nanobubble limits the dissolution of the nanobubble, and the dissolution time could reach several hundred seconds. On the one hand, this denser reservoir requires a longer time to drain. On the other hand, high inner density reduces surface tension, resulting in smaller gas flux at the same time. In this work, we assume that the gas density inside the nanobubble has a constant value during dissolution, and the lifetime of a single bulk nanobubble is computed to be higher than that of the classical diffusion theory which considers the Young–Laplace equation. In fact, the results of STXM show that the inner density is negatively correlated with the nanobubble size (Zhou et al., 2020). During the actual dissolution process, the inner density increases, and the surface tension of the nanobubble decreases, requiring more time to expel the gas. In addition, we do not consider the effect of multi-bubble effects on gas diffusion around bulk nanobubbles because we only study the dynamic behavior of single bulk nanobubble here. Of course, those effects would act to reduce the gas flux around a single nanobubble and are a stabilizing force. It is, therefore, possible that the derived lifetimes in this work are an underestimation of real lifetimes.

Next, we further simulate the response of the dissolution process of bulk nanobubbles with internal densities of 125 kg/m³ and 250 kg/m³ to different positions of the single bulk nanobubble (which determines the distance of gas diffusion) as shown in Figures 3A,C. The evolution of nanobubbles with different inner densities at different horizontal positions in the container gives a maximum lifetime of 300 s. The change of the dissolution time of nanobubbles to the gas diffusion distance indicates that the nanobubble near the air/water interface would have a shorter lifetime. It also would provide theoretical guidance for experimental preparation and preservation of bulk phase nanobubbles: 1) requiring a high gas supersaturation environment; 2) avoiding the existence of gas/liquid interfaces.

In addition, the effect of gas diffusion distance on a single bulk nanobubble lifetime decreases with the increase of the diffusion distance, until the transport length has no effect obtained from Figures 3B,D: If $\ell$ is large enough ($\ell \gg \sqrt{D{t}_0}$), Eq. 5, and Eq. 6 are $\ell$-independent: ${\frac{\partial C}{\partial r}|}_{r=R}=-\frac{2\gamma }{{\text{kR}}^2}\left(1-\frac{8}{{\pi }^2}\right)$, $R\left(t\right)=\frac{{\left(48D{\pi }^2\text{t}\gamma +{\pi }^4\left(\text{k}{R}_0^3{\rho }_g-6D\text{t}\gamma \right)\right)}^{1/3}}{{\text{k}}^{1/3}{\pi }^{4/3}{\rho }_g^{1/3}}$. $t_0$ is the lifetime of a bulk nanobubble. Obviously, the analytical results show that the limited gas transport provides a characteristic gas diffusion layer ${\ell }_0\sim \sqrt{D{t}_0}$ for the bulk nanobubble. Constrained by $t_0$, ${\ell }_0$ ∼1.0–0.1 mm, which indicates that if a single nanobubble is too close to the air/water interface, the gas diffusion has no positive effect on its lifetime. The nanobubble lifetime can be considered uniform in a typical container for storing bulk nanobubbles (the thickness of the liquid layer in a container considered in this paper is 50 mm), which is 10–100 s. The curves in Figure 3 reveals how gas diffusion affects the dynamic behavior of single bulk nanobubble: The effect range of gas diffusion is limited, and the effect range expands with the increase of gas density within the nanobubble, and for the internal densities of 125 kg/m³ and 250 kg/m³, the effect range is (0, 0.5 mm), indicating that most nanobubbles have uniform lifetimes in the model we considered.

Finally, we obtain a possible evolution mechanism of single bulk nanobubble: the high gas concentration around mature nanobubbles leads to a long gas diffusion distance in the open system, which limits the gas diffusion flux near the nanobubbles. The high gas density inside the nanobubbles further limits the diffusion flux by reducing the surface tension at the gas-liquid interface, which is the driving force of nanobubble dissolution. In addition, higher density bubbles require a longer dissolution time at lower gas flux.

In summary, based on our previous experimental results, we simulate the gas flow of a single bulk nanobubble through a liquid to the atmosphere in an open system to study the lifetime of the single bulk nanobubble. In the vicinity of nanobubbles, we find that a nanobubble is not stable, and would dissolve by diffusion. However, due to the influence of high inner density and gas transport on gas diffusion flux near nanobubbles, the time scale of a single nanobubble dissolution is different from that of a free bubble in infinite liquid. The position of the nanobubble in a container determines the gas diffusion distance around the nanobubble. The limited operating distance of gas diffusion makes the nanobubble lifetime differ at different positions in the container. When the density inside the nanobubble is small, the nanobubble lifetime is less affected by the container position.

It should be noted that here we only study the stability of a single nanobubble and do not consider the electrostatic effect and the multi-bubble cluster effect (Du et al., 2020; Jadhav and Barigou, 2021). It may prolong the lifetime of bulk nanobubbles when considering their electrostatic effect and multi-bubble cluster effect in a multi-bubble system because they can reduce the gas flux near the nanobubble and make the nanobubble more stable. Furthermore, it may need to reevaluate the rules on the nanoscale, including the relationship between surface tension and densities of liquid and gas, Henry’s law in the case of the dense gas, and the influence of the structure of water and gas molecules at the interface on the diffusion coefficient. It is also possible that the structure of water and gas molecules at the gas-liquid interface may be different from that in the conventional case when there is a high concentration of gas diffusion layer around the bubble (Nguyen et al., 2020), which may explain the mechanism of mass transfer at the gas-liquid interface at the micro-scale. Further experimental studies, including the influence of electrostatic effect and multi-bubble effect on the existence time of nanobubbles and the analysis of hydrogen bond structure at the bubble/water interface, need to be explored.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

LZ and JH put forward the general idea of the article, YW completed the theoretical calculation of the article and the writing of the main body of the paper, LZ improved the details of the article.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 11874379, 11575281, 11305252, and U1532260), and the Knowledge Innovation Program of the Chinese Academy of Sciences (No. QYZDJ-SSW-SLH019).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agarwal, A., Ng, W. J., and Liu, Y. (2011). Principle and Applications of Microbubble and Nanobubble Technology for Water Treatment. Chemosphere 84, 1175–1180. doi:10.1016/j.chemosphere.2011.05.054

PubMed Abstract | CrossRef Full Text | Google Scholar

Alheshibri, M., Qian, J., Jehannin, M., and Craig, V. S. J. (2016). A History of Nanobubbles. Langmuir 32, 11086–11100. doi:10.1021/acs.langmuir.6b02489

PubMed Abstract | CrossRef Full Text | Google Scholar

Attard, P. (2014). The Stability of Nanobubbles. Eur. Phys. J. Spec. Top. 223, 893–914. doi:10.1140/epjst/e2013-01817-0

CrossRef Full Text | Google Scholar

Bunkin, N. F., Kochergin, A. V., Lobeyev, A. V., Ninham, B. W., and Vinogradova, O. I. (1996). Existence of Charged Submicrobubble Clusters in Polar Liquids as Revealed by Correlation between Optical Cavitation and Electrical Conductivity. Colloids Surf. A Physicochem. Eng. Aspects 110, 207–212. doi:10.1016/0927-7757(95)03422-6

CrossRef Full Text | Google Scholar

Du, T., Wang, J., Wang, Y., and Huang, C. (2020). A Study of the Collapse Speed of Bubble Clusters. Int. J. Multiphase Flow 129, 103322. doi:10.1016/j.ijmultiphaseflow.2020.103322

CrossRef Full Text | Google Scholar

Fang, Z., Wang, X., Zhou, L., Zhang, L., and Hu, J. (2020). Formation and Stability of Bulk Nanobubbles by Vibration. Langmuir 36, 2264–2270. doi:10.1021/acs.langmuir.0c00036

PubMed Abstract | CrossRef Full Text | Google Scholar

Jadhav, A. J., and Barigou, M. (2020). Bulk Nanobubbles or Not Nanobubbles: That Is the Question. Langmuir 36, 1699–1708. doi:10.1021/acs.langmuir.9b03532

PubMed Abstract | CrossRef Full Text | Google Scholar

Jadhav, A. J., and Barigou, M. (2021). On the Clustering of Bulk Nanobubbles and Their Colloidal Stability. J. Colloid Interf. Sci. 601, 816–824. doi:10.1016/j.jcis.2021.05.154

CrossRef Full Text | Google Scholar

Kanematsu, W., Tuziuti, T., and Yasui, K. (2020). The Influence of Storage Conditions and Container Materials on the Long Term Stability of Bulk Nanobubbles - Consideration from a Perspective of Interactions between Bubbles and Surroundings. Chem. Eng. Sci. 219, 115594. doi:10.1016/j.ces.2020.115594

CrossRef Full Text | Google Scholar

Li, H., Hu, L., Song, D., and Lin, F. (2014). Characteristics of Micro-Nano Bubbles and Potential Application in Groundwater Bioremediation. Water Environ. Res. 86, 844–851. doi:10.2175/106143014x14062131177953

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M., Tonggu, L., Zhan, X., Mega, T. L., and Wang, L. (2016). Cryo-EM Visualization of Nanobubbles in Aqueous Solutions. Langmuir 32, 11111–11115. doi:10.1021/acs.langmuir.6b00261

PubMed Abstract | CrossRef Full Text | Google Scholar

Midtvedt, D., Eklund, F., Olsén, E., Midtvedt, B., Swenson, J., and Höök, F. (2019). Size and Refractive index Determination of Subwavelength Particles and Air Bubbles by Holographic Nanoparticle Tracking Analysis. Anal. Chem. 92, 1908–1915. doi:10.1021/acs.analchem.9b04101

PubMed Abstract | CrossRef Full Text | Google Scholar

Millare, J., and Basilia, B. (2018). Nanobubbles from Ethanol-Water Mixtures: Generation and Solute Effects via Solvent Replacement Method. Chemistryselect 3, 9268–9275. doi:10.1002/slct.201801504

CrossRef Full Text | Google Scholar

Mørch, K. A. (2007). Reflections on Cavitation Nuclei in Water. Phys. Fluids 19, 1063. doi:10.1063/1.2747210

CrossRef Full Text | Google Scholar

Ngai, T., Xing, X., and Jin, F. (2008). Depletion Attraction between a Polystyrene Particle and a Hydrophilic Surface in a Pluronic Aqueous Solution. Langmuir 24, 13912–13917. doi:10.1021/la802529q

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, N. N., Galib, M., and Nguyen, A. V. (2020). Critical Review on Gas Hydrate Formation at Solid Surfaces and in Confined Spaces-Why and How Does Interfacial Regime Matter? Energy Fuels 34, 6751–6760. doi:10.1021/acs.energyfuels.0c01291

CrossRef Full Text | Google Scholar

Oh, S. H., Han, J. G., and Kim, J.-M. (2015). Long-term Stability of Hydrogen Nanobubble Fuel. Fuel 158, 399–404. doi:10.1016/j.fuel.2015.05.072

CrossRef Full Text | Google Scholar

Plesset, M. S., and Sadhal, S. S. (1982). On the Stability of Gas Bubbles in Liquid-Gas Solutions. Appl. Scientific Res. 38, 133–141. doi:10.1007/bf00385944

CrossRef Full Text | Google Scholar

Robert, J. M. P., Reid, C. R., and Sherwood, T. K. (1958). The Properties of Gases and Liquids. Aiche J. 24, 38–40.

Google Scholar

Seddon, J. R. T., and Lohse, D. (2011). Nanobubbles and Micropancakes: Gaseous Domains on Immersed Substrates. J. Phys. Condens. Matter 23, 133001. doi:10.1088/0953-8984/23/13/133001

PubMed Abstract | CrossRef Full Text | Google Scholar

Sedlák, M., and Rak, D. (2014). On the Origin of Mesoscale Structures in Aqueous Solutions of Tertiary Butyl Alcohol: The Mystery Resolved. J. Phys. Chem. B 118, 2726–2737. doi:10.1021/jp500953m

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, B. H., An, H., and Ohl, C.-D. (2020). How Bulk Nanobubbles Might Survive. Phys. Rev. Lett. 124, 134503. doi:10.1103/physrevlett.124.134503

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Miao, X., Ali, J., Lyu, T., and Pan, G. (2018). Quantification of Oxygen Nanobubbles in Particulate Matters and Potential Applications in Remediation of Anaerobic Environment. ACS Omega 3, 10624–10630. doi:10.1021/acsomega.8b00784

PubMed Abstract | CrossRef Full Text | Google Scholar

Weijs, J. H., and Lohse, D. (2013). Why Surface Nanobubbles Live for Hours. Phys. Rev. Lett. 110, 054501. doi:10.1103/PhysRevLett.110.054501

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, W., and Xu, G. (2019). Mass Transfer of Nanobubble Aeration and its Effect on Biofilm Growth: Microbial Activity and Structural Properties. Sci. Total Environ. 703, 134976. doi:10.1016/j.scitotenv.2019.134976

PubMed Abstract | CrossRef Full Text | Google Scholar

Yasui, K., Tuziuti, T., Kanematsu, W., and Kato, K. (2016). Dynamic Equilibrium Model for a Bulk Nanobubble and a Microbubble Partly Covered with Hydrophobic Material. Langmuir 32, 11101–11110. doi:10.1021/acs.langmuir.5b04703

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., and Lohse, D. (2015). Surface Nanobubbles and Nanodroplets. Rev. Mod. Phys. 87, 981–1035. doi:10.1103/RevModPhys.87.981

CrossRef Full Text | Google Scholar

Zhang, L., Chen, H., Li, Z., Fang, H., and Hu, J. (2008). Long Lifetime of Nanobubbles Due to High Inner Density. Sci. China Ser. G-phys. Mech. Astron. 51, 219–224. doi:10.1007/s11433-008-0026-5

CrossRef Full Text | Google Scholar

Zhang, M., Tu, Y.-s., and Fang, H.-p. (2013). Concentration of Nitrogen Molecules Needed by Nitrogen Nanobubbles Existing in Bulk Water. Appl. Math. Mech. Engl. Ed. 34, 1433–1438. doi:10.1007/s10483-013-1757-x

CrossRef Full Text | Google Scholar

Zhang, H., Lyu, T., Bi, L., Tempero, G., Hamilton, D. P., and Pan, G. (2018). Combating Hypoxia/anoxia at Sediment-Water Interfaces: A Preliminary Study of Oxygen Nanobubble Modified clay Materials. Sci. Total Environ. 637-638, 550–560. doi:10.1016/j.scitotenv.2018.04.284

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, L., Wang, X., Shin, H.-J., Wang, J., Tai, R., Zhang, X., et al. (2020). Ultrahigh Density of Gas Molecules Confined in Surface Nanobubbles in Ambient Water. J. Am. Chem. Soc. 142, 5583–5593. doi:10.1021/jacs.9b11303

PubMed Abstract | CrossRef Full Text | Google Scholar