Digital Twins for Materials

Digital twins are emerging as powerful tools for supporting innovation as well as optimizing the in-service performance of a broad range of complex physical machines, devices, and components. A digital twin is generally designed to provide accurate in-silico representation of the form (i.e., appearance) and the functional response of a specified (unique) physical twin. This paper offers a new perspective on how the emerging concept of digital twins could be applied to accelerate materials innovation efforts. Specifically, it is argued that the material itself can be considered as a highly complex multiscale physical system whose form (i.e., details of the material structure over a hierarchy of material length) and function (i.e., response to external stimuli typically characterized through suitably defined material properties) can be captured suitably in a digital twin. Accordingly, the digital twin can represent the evolution of structure, process, and performance of the material over time, with regard to both process history and in-service environment. This paper establishes the foundational concepts and frameworks needed to formulate and continuously update both the form and function of the digital twin of a selected material physical twin. The form of the proposed material digital twin can be captured effectively using the broadly applicable framework of n-point spatial correlations, while its function at the different length scales can be captured using homogenization and localization process-structure-property surrogate models calibrated to collections of available experimental and physics-based simulation data.

1 Introduction

Recent forward-looking roadmaps (Gil and Selman, 2019; Jenks et al., 2020) have identified the development of a fully digital framework that fuses human-subject matter expertise, process and performance modeling, experimental in-situ diagnostics, and data science algorithms as one of the most important areas to transform manufacturing and surveillance of components throughput their life cycle. Indeed, the digitization of product lifecycle management (PLM) has led to the emergence and deployment of digital threads (Kapteyn et al., 2021; Niederer et al., 2021; Zeb et al., 2021) in a broad spectrum of manufacturing industries. These digital threads collect, curate, and archive all of the data/information generated from all stages of the product life cycle: conceptualization, design, prototype, manufacturing, operation, and retirement (Singh and Willcox, 2018; Margaria and Schieweck, 2019). Digital threads open multiple new avenues for fostering innovation and improving the in-service performance of a wide range of products. A necessary feature of the digital threads is that they encompass both the in-silico activities (e.g., model-based or virtual engineering) and the physical activities (e.g., measurements made during the different stages of manufacturing, testing, and operation of the product) conducted in the PLM. An important outcome from the deployment of digital threads is that they have opened new opportunities for the creation and use of in-silico analogues to the physical product. The recent advances in digital and sensor technologies (Mei et al., 2019; Ullo and Sinha, 2020) enable the in-silico objects to co-exist along with their physical counterparts. In addition to mimicking the physical products, the in-silico analogues offer unprecedented potential for consistent change management, allowing the optimization of intentional or unintentional product evolution over time. Therefore, within this context, a digital twin can be defined as a high-fidelity in-silico representation closely mirroring the form (i.e., appearance) and the functional response of a specified (unique) physical twin. Digital twins have thus far been used in the manufacturing and performance evaluation of complex engineered physical systems (e.g., turbine engines) (Tao et al., 2018; Zaccaria et al., 2018; Raj and Surianarayanan, 2020; Lim et al., 2021; Xie et al., 2021) and/or their components, where the focus has been largely on capturing accurately the macroscale geometry and the component-level performance metrics. Current digital twins do not address adequately the capture and archival of the materials data, which typically deals with physical phenomena occurring at the lower material length scales (typically ranging from the atomic to the macroscale). This disconnect is not surprising given the siloed nature of current materials research and product design/manufacturing communities. However, it is abundantly clear that a successful extension of digital twins to include the materials data/information in a comprehensive manner can allow for a holistic co-design of material, manufacturing process, and product in fully integrated innovation cycles, possibly resulting in dramatic improvements in the overall part performance.

Materials, in their own right, represent highly complex multiscale and multi-physics systems. Their production and in-service responses are controlled by a wide range of phenomena occurring at length scales ranging from the atomic to the macroscale and an equally broad range of associated time scales. Figure 1 depicts schematically the hierarchical nature of materials systems with examples of a wide variety of physical phenomena that occur at the nano- and micro-scales. Clearly, the materials phenomena occurring at the lower material length scales play important roles in controlling the macro- and component-scale performances of the part. In the current research paradigm, the considerations at the component/part scale and the material scale are studied in a mostly de-coupled manner by different groups of researchers. The former are the domain of mechanical designers and manufacturing specialists, while the latter are addressed by materials science and engineering specialists. More specifically, the field of materials science and engineering focuses on understanding how the different processing histories (e.g., thermo-mechanical processing) influence the material structure (includes information on the many aspects of order and disorder seen at different length scales cf. Figure 1) and their associated properties. However, understanding and quantifying accurately the underlying process-structure-property (PSP) relationships (Kalidindi, 2015; McDowell and LeSar, 2016) at the different material length and time scales is quite arduous. This is mainly because the diverse physical phenomena occurring at these scales are necessarily related and co-dependent with one another. Therefore, adopting a systems approach that manages the complex trade-offs between potentially conflicting multifunctional requirements at the different length scales spanning across the complete range of material and product scales would yield significant benefits.

FIGURE 1

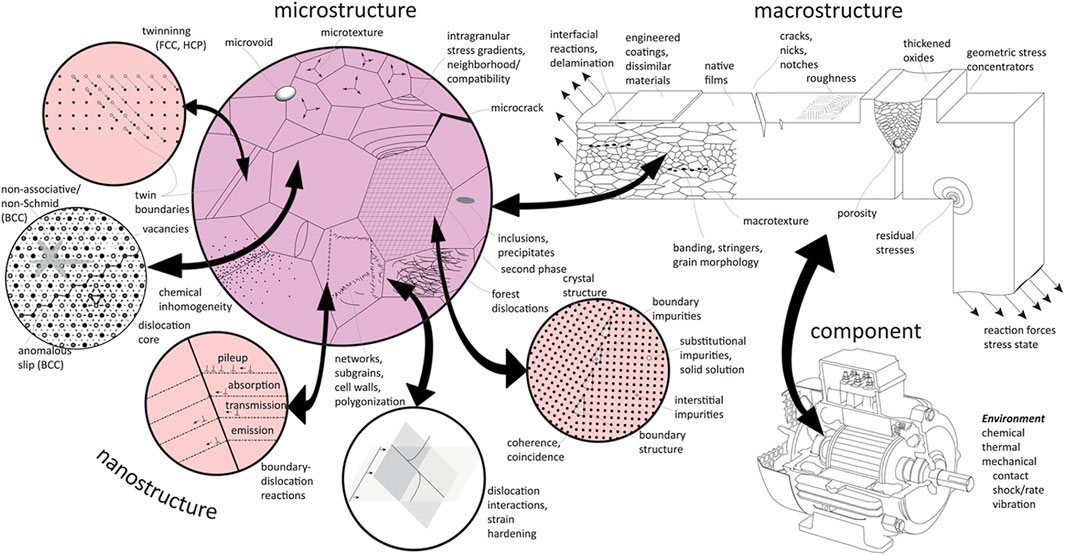
FIGURE 1. A schematic depiction of the multiscale and multi-physics nature of material systems and their relationship with the component performance. A comprehensive understanding of material performance requires a complete hierarchical representation of structural/chemical features, the relationship between those features and material properties, and the mechanisms that drive their evolution either through processing or service history. All arrows represent scale bridging, i.e., upscaling via homogenization and downscaling via localization.

However, this task faces many hurdles. The most significant of these hurdles comes from the fact that the relevant data, even for a selected single material system, is necessarily generated by distributed teams of researchers with the requisite expertise. For example, on the experimental front, materials data comes from a wide range of imaging modalities (e.g., optical microscopy, scanning and transmission electron microscopy, various diffraction and spectroscopic techniques, X-ray tomography, atomic force microscopy) (Belianinov et al., 2018; Polonsky and Pandey, 2021) and property evaluations (e.g., mechanical testing in different modes and at different spatial resolutions, thermal conductivity, diffusivities) (Khosravani et al., 2020:; Khosravani et al., 2021). On the modelling front, the data comes from an equally disparate set of sources that aim to faithfully simulate specific selected sub-phenomena at different material length scales (e.g., density functional theory computations, molecular dynamics, discrete dislocation dynamics, kinetic Monte-Carlo simulations, cellular automata, phase-field simulations, finite element models) (Horstemeyer, 2009; Panchal et al., 2013; Matouš et al., 2017). Although each individual dataset often provides a partial insight, only a systems approach can provide the comprehensive holistic view needed to objectively drive materials innovation in an accelerated manner; this is indeed the goal of many national and international materials research initiatives [e.g., ICME (Allison et al., 2006), MGI (National Science and Technology Council, 2011; de Pablo et al., 2019)].

Figure 2 illustrates the large variety of data sources involved in formulating a systems approach to understanding and optimizing materials for desired combinations of macroscale (effective) properties. As already noted, the datasets collected from any one data source (refers to either a single experimental protocol or a single physics-based simulation tool) often provides incomplete and uncertain insights into the physics controlling the materials phenomena of interest. At a high level, it should be recognized that physics-based simulations are designed to provide predictions of the material response to imposed (thermo-mechanical) environments for user-specified physics. On the other hand, experiments are generally designed to provide observations of material response to specific imposed environments, for as yet unknown (or uncertain) materials physics. Clearly, all individual datasets (from any individual data source) should be treated as being incomplete and/or uncertain. However, if the insights from the datasets collected from the different data sources can be effectively fused in a consistent framework, it is likely to produce much more comprehensive and valuable insights. Currently, there does not yet exist an overarching mathematical framework for such data fusion. The development and utilization of such a framework is likely to open new avenues for major time and effort savings in materials-product co-design and innovation efforts by optimally guiding the effort investment (i.e., objectively identifying the next best steps based on a rigorous statistical analyses of all previously aggregated data).

FIGURE 2

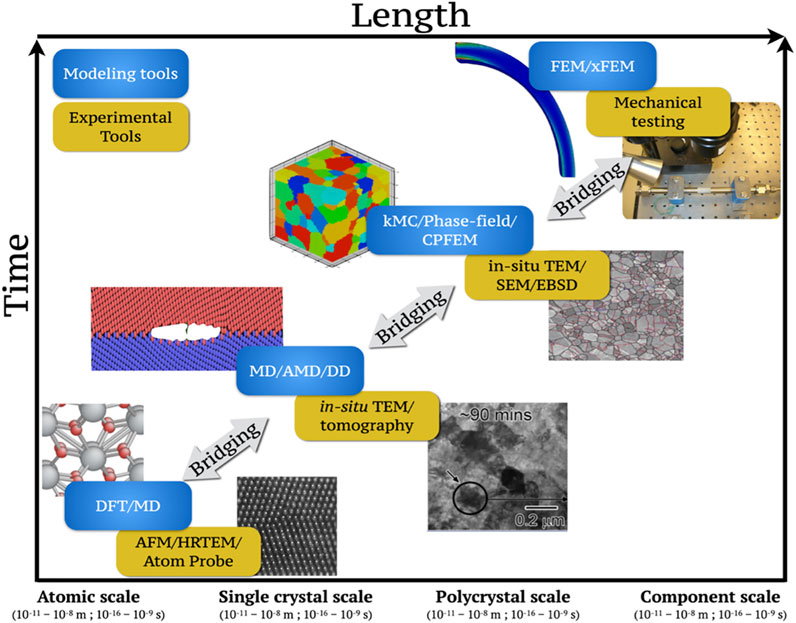
FIGURE 2. Modeling and experimental tools typically used to obtain relevant materials data at different length and time scales. Example of modeling tools used include Density Functional Theory (DFT), Molecular Dynamics (MD), Accelerated MD (AMD), Dislocation Dynamics (DD), kinetic Monte Carlo (kMC), Crystal Plasticity Finite Element Modeling (CPFEM), FEM, and extended FEM (xFEM). Examples of experimental tools used include Atomic Force Microscopy (AFM), High Resolution Transmission Microscopy (HRTEM), in situ TEM, tomography, Scanning Electron Microscopy (SEM), Electron Backscattered Diffraction (EBSD), and mechanical testing.

As already noted, the perspectives presented above build on multiple national and international initiatives. Specifically, ICME (Allison et al., 2006), and MGI (de Pablo et al., 2019) have articulated the need for increased use of computational tools and data sciences [including artificial intelligence/machine learning toolsets (AI/ML)] to accelerate the rate of materials discovery, development, and deployment in advanced technologies. Indeed, much progress has been made in organizing and disseminating materials data (The Minerals, Metals & Materials Society TMS, 2017), and physics-based simulation toolsets (The Minerals, Metals & Materials Society TMS, 2015). There has also been a strong injection of data sciences and AI/ML into materials research, especially in aspects related to data ingestion (e.g., experimental laboratory automation) (Kalidindi et al., 2019), curation (e.g., ontologies) (Morgado et al., 2020; Voigt and Kalidindi, 2021), feature engineering (Kalidindi, 2020; Xiang et al., 2021), and automated generation of surrogate models (Generale and Kalidindi, 2021; Marshall and Kalidindi, 2021). These recent advances in materials research have set the stage for the extension and application of the emerging concept of digital twins described earlier to include the multiscale details of the material. This paper establishes a roadmap for the pursuit of this goal, i.e., the extension of digital twins to include materials data over a hierarchy of length scales. Specifically, we identify the key foundational elements that currently exist and outline the gaps that need to be overcome for success in this endeavor (Figure 3).

FIGURE 3

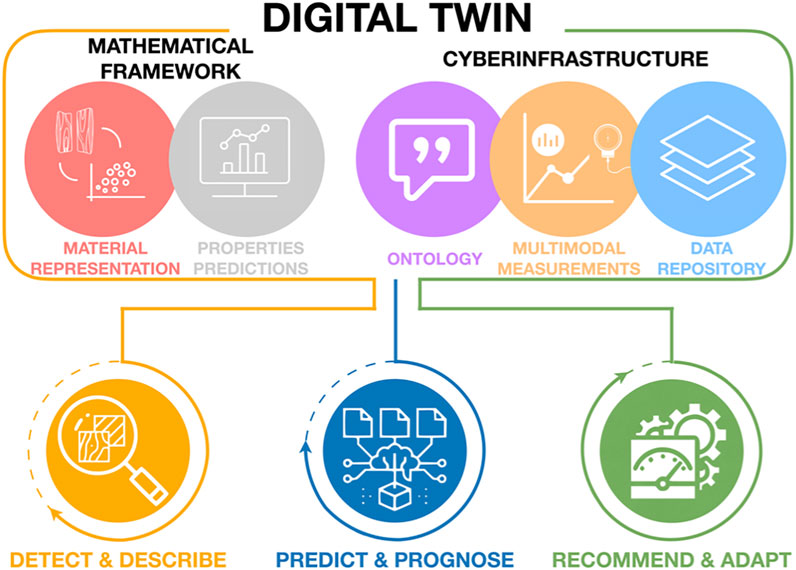
FIGURE 3. The main components of the proposed roadmap for building digital twins for material systems.

2 Main Elements of Digital Twins for Materials Systems

2.1 Physical Twin of a Material System

Digital twins of macroscale engineered components and machines typically aim to represent a uniquely identified single physical twin. For example, a digital twin might target a specific turbine engine in service on an airplane. However, in building digital twins for a material system, it becomes intractable to consider each individual material sample as the physical twin. This is not only because of the large number of distinct material samples that can be produced for a nominally specified chemical composition and processing history, but also due to the fact that non-destructive characterization techniques are not yet mature for evaluating both the three-dimensional structure of the material as well as its properties of interest. Furthermore, even with the use of destructive techniques for materials characterization, one can only hope to establish distributions that adequately quantify the material structure and properties in a stochastic framework (i.e., accounting for the significant uncertainty associated with these quantities for any given material sample). Given these considerations, it is readily apparent that the digital twins for materials systems can only be established in a stochastic framework at the present time. In other words, we propose here that digital twins of materials systems should aim to produce multiple instantiations (as many as needed) sampled from the distributions of the possible material structure and their associated properties (with both structure and properties defined over a hierarchy of material length scales). Therefore, in our proposed framework, we will associate the digital twins of the material system to the nominal chemical composition and processing/service history that created the material samples. In doing so, we will implicitly define the material by the controllable details (each of which is identified with aleatoric uncertainty) of the generative process used to create the material samples (i.e., instantiations of the physical twin). This, we believe, will result in a much more pragmatic approach to building digital twins for material systems that will have high value for the design and in-service prognosis of engineered components and devices.

2.2 Mathematical Framework for Digital Twins of Material Systems

The mathematical framework underpinning the digital twins for material systems should address two main needs: (i) the statistical quantification of the material structure over a hierarchy of material length scales¹ and its suitable representation in practically useful low-dimensional forms, and (ii) the reliable prediction of the material properties of interest given information about the material structure and the processing/service history. These tasks indeed correspond to defining the form and the function of the digital twins for material systems. As already noted, both these tasks need to be addressed in a stochastic framework that rigorously tracks the uncertainty associated with all of the available data and propagates it into the predictions of the material properties.

2.2.1 Material Structure Representation and Quantification

The term material structure is used here to describe the spatial arrangement of structural and chemical heterogeneities, which constitute a material at a specified instant of time and govern its properties at that instant of time. For a given chemical composition, thermodynamics predicts an equilibrium crystallographic phase (or a multiphase mixture), and at finite temperature, an equilibrium vacancy concentration. Yet materials are rarely in their thermodynamic ground state. Essentially, an overwhelming subset of the material structural features represent metastable or unstable defects created throughout the process history. Conventionally, material structure defects have been classified based on their dimensionality as planar grain boundaries, linear dislocations, and point-wise atomic impurities; these are but the simplest examples of a myriad of complex microstructural features (see Figure 1). The material structure is not usually static but evolves when stimulated by exposure to energy (thermal, mechanical, chemical, etc.). Through state-of-the-art processing, the most perfect undoped, isotopically pure silicon single crystals have been produced to purity levels of >99.9999%. On the other hand, the most sophisticated structural alloys benefit from their complex, multiscale arrangement of the lower length scale structural features, reminiscent of the hierarchical nature of biological systems. Hence, the challenge for a digital twin of a material system is to represent the necessary complexity of the inherently high-dimensional material structure features with sufficient fidelity to capture the relevant subset that controls the material response of interest. Complicating matters, no single experimental technique is capable of comprehensively digitizing the material’s complete internal structure.

A digital twin of a material system should be able to instantiate a representative volume of the material with sufficient statistical sampling of all the relevant lower length-scale structural features and their spatial arrangements. Given the roughly eight orders of magnitude in length scales (from ∼Å to ∼ cms) involved, it should become clear that such instantiations cannot be deterministic or unique. Therefore, what is required here is the ability to produce multiple instantiations that reflect as accurately as possible the inherent stochasticity of the material structure for a given nominal composition and process history. Laplace conjectured that by knowing every atom, its position and momentum, we could anticipate the behavior of the material (marquis de Laplace, 1814). While this statement reflects accurately the expected causal relationship between the material structure and its associated properties, it reflects a practically impossible pursuit. Therefore, we take the viewpoint that the digital twin of a material system is intended to be a minimally sufficient reduced-order representation of Laplace’s “demon.” A tractable digital twin of a material system should therefore utilize a versatile (broadly applicable to all material classes and length scales) low-dimensional representation of the material structure that would allow efficient learning of the functional response of the material system. Based on the earlier discussion, it is also clear that the low-dimensional representation of the material structure can only reflect suitably defined statistical measures at different material length scales; henceforth, such salient statistical measures of the material structure will be referred as features. Because of our interest in instantiating the material structure in our digital twins, it is important that the selected feature set should produce realistic, sufficiently accurate, instantiations of the material structure that can be subsequently correlated with its functional response. This is not a trivial requirement. For example, most of the conventionally used statistical measures of the material structure, such as the overall alloy composition, phase volume fractions, and the averaged grain sizes are woefully inadequate for producing the required instantiations of the multiscale material structure for our digital twins. More advanced approaches involving a richer set of microstructure statistics (e.g., orientation and mis-orientation distributions, grain aspect ratio distributions) have led to concepts such as statistically equivalent representative volume elements (McDowell and LeSar, 2016; Ghosh and Groeber, 2020). Some of these concepts have also been implemented in open-source codes such as DREAM.3D (Groeber and Jackson, 2014; Ghosh and Groeber, 2020).

A comprehensive and systematic framework available today that is capable of providing the requisite feature engineering capabilities for the material structure is the framework of n-point spatial correlations (Torquato and Stell, 1982; Torquato and Haslach, 2002; Fullwood et al., 2010; Niezgoda et al., 2011; Adams et al., 2012; Niezgoda et al., 2013). In recent work, Kalidindi and co-workers (e.g., Kalidindi, 2015) have developed and demonstrated an efficient and broadly applicable computational framework and toolsets for addressing this task. Broadly referred as Materials Knowledge Systems (MKS), this framework takes advantage of the computational efficiency of voxelated representations and Fast Fourier Transform (FFT) algorithms to implement the theoretical framework of n-point spatial correlations. The feasibility and benefits of this approach have been demonstrated on a wide variety of material classes and material structures at different length scales [from the atomic (Gomberg et al., 2017; Kaundinya et al., 2021) to dislocation length scales (Robertson and Kalidindi, 2021a) to microscale (Generale and Kalidindi, 2021)].

At its core, MKS defines and utilizes a material structure function (Kalidindi, 2015) that maps a selected combination of spatial position $\mathit{x}\in \text{Ω}$ (the physical volume of the material domain) and a local material state $\mathit{h}\in \text{H}$ (includes information such as phase identifiers, chemical compositions, lattice orientations, defect densities) to suitable measures (e.g., density) that reflect the intensity of $\mathit{h}$ at $\mathit{x}$. Mathematically, one can express this function as $m\left(\mathit{h},\mathit{x}\right)$. Implicit in this definition is the expectation that $\text{H}$ needs to be identified suitably to capture the complete set of material states of interest at the different material structure length scales. Features of the material structure can then be defined as expectations of suitably scaled moments of $m\left(\mathit{h},\mathit{x}\right)$. For example, the expected value of $m\left(\mathit{h},\mathit{x}\right)$ over $\text{Ω}$ can provide a set of 1-point features that can be interpreted as the volume fractions of $\mathit{h}$ in $\text{Ω}$ (Kalidindi, 2015). Similarly, the expected value of $m\left(\mathit{h},\mathit{x}\right)m\left({\mathit{h}}^{\mathit{\prime }},\mathit{x}+\mathit{r}\right)$ over $\text{Ω}$ can produce a set of 2-point features that can be interpreted as the joint probability of realizing $\mathit{h}$ at $\mathit{x}$ and $\mathit{h\prime }$ at $\mathit{x}+\mathit{r}$, where $\mathit{r}$ denotes a specified vector separating the two spatial points randomly selected from $\text{Ω}$. Although, one can define higher-order features (e.g., 3-point features), one often finds a sufficiently large number of features in the 2-point feature set, as it includes all permutations of $\left(\mathit{h},\mathit{h\prime }\right)$ over a very large domain of $\mathit{r}$ (this domain includes all distinct set of all vectors of interest that can be placed in $\text{Ω}$). The adequacy of the set of 2-point features in capturing the salient features of the material structure (including the set of features identified in conventional practices in materials science and engineering) has been established for a broad range of material classes (Latypov et al., 2019; Generale and Kalidindi, 2021) as well as the different structure length scales (Fullwood et al., 2010; Robertson and Kalidindi, 2021a; Kaundinya et al., 2021) encountered in them.

The MKS framework described in Figure 4 produces a very large number of features, even when using only the 2-point feature set. For extracting a low-dimensional feature set, one needs to use a suitable dimensionality reduction technique. Of the various options for this task, principal component analysis (PCA) has been found to be particularly attractive. First, it allows for an unsupervised learning of the salient low-dimensional features based on maximization of captured variance. Therefore, it identifies a consistent set of features that can be used across multiple PSP surrogate models, allowing for full interoperability among collections of such models. In other words, since the salient features are identified without the knowledge of the specific targets (i.e., outputs) of the surrogate model, they can be used for different targets (for example, in the predictions of very different properties of a given material system). Second, the PCA basis can be inspected and interpreted to a limited extent, allowing for the low-dimensional features to be associated with some (limited) physical meaning. Third, since PCA essentially involves a rotational transform of the original space, it preserves distances between datapoints in the original space. Finally, the orthogonal decomposition involved in the PCA allows for practically useful reconstructions of the full feature list, i.e., a reconstruction of the high-dimensional feature list from the low-dimensional feature list. Of course, these reconstructions are approximate because of PC truncation. However, since the PC representations are maximized to capture variance, it is possible to make sure that the approximation introduced by the truncation is within acceptable tolerance. The PC scores obtained from the application of PCA on an ensemble of 2-point feature sets (one set corresponds to one material structure) serve as a highly effective low-dimensional feature set for the material structure in our digital twins. There exist a multitude of other options for dimensionality reduction of the feature space, such as isomap or kernel PCA. However, the nonlinear embeddings employed in these techniques can introduce distortions into the latent space that negate the benefits of PCA identified above (Hu et al., 2022).

FIGURE 4

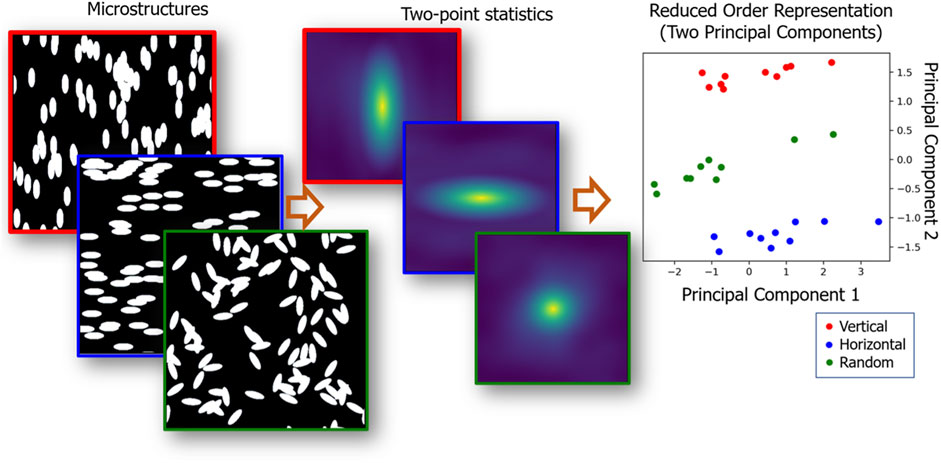
FIGURE 4. The MKS workflow for feature engineering of material structure. In this example, we start with microstructures belonging to three distinct classes (corresponding to vertical, horizontal, or random ellipses), with one example of each class shown on the left. Their corresponding 2-point features are shown in the middle and reflect a large number of statistics (including volume fractions, size and shape distributions) for each microstructure. The low-dimensional representations of the microstructure statistics are shown on the right, in the subspace of the first two PC scores. The clusters in the PC plots successfully classify the microstructures in the three classes. The intra-class variance between microstructures within each class can also be quantified from the PC representations.

As stated earlier in Section 2.1, the physical twin is not defined as a single instantiation of a material structure, but rather as the outcome of a stochastic generative process that yields instantiations that we then observe. The MKS framework described above provides a mathematically compact representation using computationally efficient tools. However, many tools (e.g., phase-field simulations, micromechanical finite element models) only take specific instantiations of the material structure as inputs. Therefore, successful creation of digital twins for materials requires the ability to move between statistical representations of material structure and their three-dimensional physical instantiations at low computational cost. While the computation of 2-point spatial correlations from instantiations is relatively easy (Cecen et al., 2016), the inverse computation is not trivial. Very recently, it has been shown that the three-dimensional material structures can be instantiated from their 2-point feature sets with minimal computational cost (Robertson and Kalidindi, 2021b). As a result of the many advantages described above, the MKS framework along with its open-source code repository PyMKS (Brough et al., 2017) offers a powerful, currently available, toolset for addressing the challenges of building digital twins of materials systems.

It is also noted that there are a number of other options based on neural networks that allow one to combine feature engineering and property prediction into a single-step framework. These approaches offer attractive avenues when one is interested in a limited number of properties as targets. If one insists on de-coupling the form and function of the digital twins (as we have argued here), then it is imperative to pursue feature engineering of the material structure independently from establishing property predictors (discussed in the next section). In this context, it should be recognized that the autoencoder-decoder networks (Herr et al., 2019) offer an interesting option. These networks do address the unsupervised feature engineering of the material structure. Therefore, the features identified from such networks can then be input into other neural networks for property predictions. This idea represents an open research avenue that merits further exploration.

2.2.2 Predictions of Material Properties

Reliable prediction of the effective properties of a given material sample is a challenging task. At a high level, the main options are to either measure experimentally the properties of interest or to leverage known physics (often delivered in physics-based simulation packages) to estimate their values. Both approaches face hurdles when one desires to produce a multiscale, digital twin for materials. On the experimental front, the effort and cost involved in measuring all of the properties of interest along with the related information (e.g., anisotropy, variances) over the multiple material length scales of interest are often prohibitive. On the modelling front, there is substantial uncertainty in the model forms and/or parameter values used in the physics-based models. It is therefore clear that neither approach by itself is optimal in getting us the requisite information. In this regard, the recent emergence and successful application of materials data analytics tools has opened up new avenues for addressing these gaps.

Recently (Kalidindi, 2015; Kalidindi, 2020), it has been argued that process-structure-property (PSP) linkages can be defined over different material-structure length scales to capture the core knowledge needed to study multiscale material responses. It is argued here that the same PSP linkages can be utilized to predict the functional response of the material digital twin. This is because the PSP linkages can be used to update both the changes in the multiscale material structure due to the imposed service conditions (using suitably defined process-structure evolution linkages) but also their associated properties (using structure-property linkages). The required PSP linkages need to be formulated using available data that might often be disparate, incomplete and/or uncertain. Most importantly, the framework for predicting the function of the material digital twin should allow easy (and possibly frequent) updates as new data becomes available. It is also likely that one needs to chain together multiple PSP models in order to make the predictions of the function of the material digital twin.

A Bayesian framework has the potential to address scale-bridging with uncertain physics. The proposed Bayesian framework will be described next using the structure-property (SP) linkages as an example. However, they will be formulated such that they can also be easily applied to capturing process-structure linkages (PS). Typically, SP linkages are formulated to take structure variables as inputs and predict property values as output. The mapping implied in these linkages can be expressed as $P\mathrm{ }=\mathrm{ ℱ}\left(\mathit{\mu }\right),$ where $P$ is a property variable and $\mathit{\mu }$ denotes a vector of structure features (e.g., the PC scores of the 2-point feature set described in Section 2.2.1). Both P and $\mathit{\mu }$ should be treated as stochastic variables. This naïve definition makes the governing physics implicit in the formulation of $\mathrm{ℱ}$. It would be much more desirable for SP linkages to explicitly treat the governing physics as additional input variables to the mapping, i.e., to refine the desired mapping as $P\mathrm{ }=\mathrm{ ℱ}(\mathit{\mu },\mathit{\phi })$, where $\mathit{\phi }$ denotes the governing physics. In practice, $\mathit{\phi }$ would represent a vector of parameters defining the physical mechanisms controlling the response of the material physical twin (e.g., parameters used in constitutive modeling of the material response). This refinement is advantageous in two ways. Firstly, it allows one to treat $\mathit{\phi }$ as a stochastic vector variable, which often exhibits a significant amount of uncertainty for a selected material physical twin. Secondly, it allows for the uncertain physics to be passed between linkages. This is particularly useful for the multiscale phenomenon that occur in material systems, as the uncertain physics learned in one length scale can still be utilized at another length scale. An example of this scale-bridging is depicted schematically in Figure 5. The first linkage estimates the indentation yield strength (effective property) of a single grain given the grain’s orientation (structure variable) and critically resolved shear strengths (physics variables). The second linkage estimates the bulk yield strength (property) given the two-point statistics of the grain orientations (structure variables) and the same critically resolved shear strengths (physics variables). Since the physics variables in these two linkages are the same, the uncertain knowledge of the physics variables extracted in the grain-scale data (could come from experiments and/or simulations) can be upscaled and utilized in making predictions of the effective properties at the polycrystal scale.

FIGURE 5

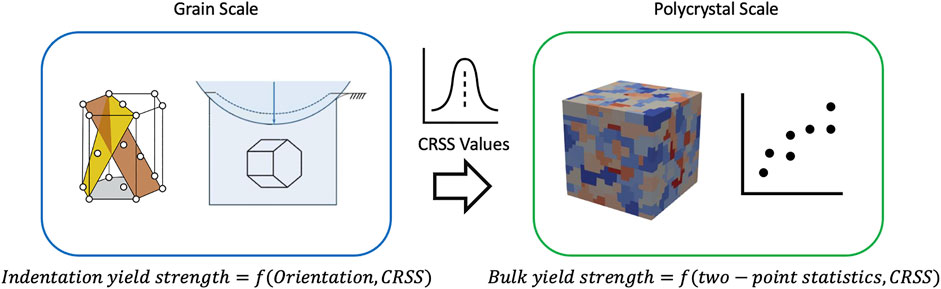
FIGURE 5. Schematic illustration of the scale-bridging between the response of an individual grain and the response of a polycrystalline aggregate. At the grain scale, the structure-property linkage is formulated to take grain orientation (structure variable) and critical resolved shear strength(s) (CRSS; physics variables) as input and predict the overall property of interest (e.g., indentation yield strength of grains of different orientations). This linkage is used with both experimental and modeling datasets to extract a posterior on the CRSS for a given material system (see Panel 6 for more details). At the polycrystal scale, the structure-property linkage is formulated to take the 2-point spatial correlations of orientation (structure variables) and CRSS (physics variables) to make a prediction of the bulk (effective) yield strength of the polycrystal (c.f., Paulson et al., 2017).

In establishing the material physics parameters, one has to exploit all of the available data, collected from disparate sources (e.g., experiments and physics-based simulations). Machine learning of $\mathit{\phi }$ for a selected material physical twin can be accomplished using a Bayesian update strategy expressed as:

$p\left(\mathit{\phi }\text{|}\mathit{E}\right)\propto p\left(\mathit{E}\text{|}\mathit{\phi }\right) p\left(\mathit{\phi }\right)(1)$

where $\mathit{E}$ denotes the set of available experimental observations, $p\left(\mathit{\phi }\right)$ is the prior (reflecting our best initial guess), $p\left(\mathit{E}\text{|}\mathit{\phi }\right)$ is the likelihood of realizing the observations in $\mathit{E}$, and $p\left(\mathit{\phi }\text{|}\mathit{E}\right)$ denotes the updated posterior on $\mathit{\phi }$. Although Eq. 1 looks very simple, its practical usage for learning the controlling physics in multiscale material phenomena has been hindered by several factors. First, only the physics-based simulation tools that faithfully mimic the experiments performed to obtain $\mathit{E}$ can allow for the computation of the likelihood term in Eq. 1. This is because only these tools allow arbitrary specification of the governing physics $\mathit{\phi }$. However, a brute-force application of physics-based tools for computing the likelihood is prohibitively expensive because of the extremely large number of simulations one needs to perform to accomplish this task since it entails performing simulations covering a large domain of likely governing physics for all of the experimental observations in $\mathit{E}$. Second, the proportionality in Eq. 1 implies that one needs to develop and implement a suitable strategy for establishing the proportionality factor. Recent work (Castillo et al., 2021) has demonstrated that it is possible to train AI/ML models on simulation results produced by physics-based models, which can then be used to compute the likelihood term in Eq. 1. Furthermore, they would also allow for the implementation of Markov-Chain Metropolis-Hastings (MCMH) approaches for sampling the posterior in Eq. 1 without explicitly computing the proportionality factor. It is important to note that the posterior estimate of $\mathit{\phi }$ is not restricted to come from any single source of data. As an example, let us consider the situation where the data becomes available from different test modes (these could be indentation tests and micro-pillar tests for grain-scale mechanical measurements). In such situations, we need to establish different surrogate models for each test mode. Let $P_1=\mathrm{ ℱ}(\mathit{\mu },\mathit{\phi })$ and $P_2=\mathrm{ ℱ}(\mathit{\mu },\mathit{\phi })$ represent such surrogate models. Since the underlying microstructure and physics variables have the exact same meanings in both models, one can use both models with their respective experimental datasets for sampling a consistent posterior for $\mathit{\phi }$. Once the posterior is established, one can establish the desired SP linkage in a stochastic framework by marginalizing as:

$p\left(\mathit{\mu }|\mathit{E}\right)={\displaystyle \int f\left(\mathit{\mu },\mathit{\phi }\right)p\left(\mathit{\phi }|\mathit{E}\right)}\mathit{d}\mathit{\phi }(2)$

As noted above, the practical implementation of Eqs 1, 2 needs the establishment of suitable AI/ML surrogates. These usually take the form $\mathrm{ℱ}\left(\mathit{\mu },\mathit{\phi }\right)$, and can be accomplished using Gaussian Process Regression (GPR). The central advantage of the proposed strategy here is that the formulation of the needed AI/ML models is generally a one-time effort. In other words, when these are properly designed to cover large input domains in the space of the controlling physical parameters and the space of relevant material structures, they only need to be performed once [examples can be seen in prior work (Castillo and Kalidindi, 2019; Castillo et al., 2021)]. This feature allows for a relatively low-computational cost update of the surrogate model as new experimental data becomes available. It is also possible to suggest new experiments that maximize the potential for improving the accuracy of the predictions (i.e., reducing the prediction uncertainty). This is most efficiently accomplished using established concepts of information gain such as the posterior predictive variance (Castillo and Kalidindi, 2019; Castillo et al., 2021; Castillo and Kalidindi, 2021), expected improvement (Solomou et al., 2018; Takhtaganov and Müller, 2018; Talapatra et al., 2018; Ghoreishi and Allaire, 2019), and expected information gain (Pandita et al., 2019).

An example application of the proposed Bayesian approach methodology is depicted in Figure 6, taken from the work of Castillo et al. (2021). In this example, the information from spherical indentation measurements on individual grains in a polycrystalline sample and the corresponding simulations using crystal plasticity finite element models are combined to establish distributions on the unknown values of the critical resolved shear strengths of four different families of potentially active slip systems in a selected Ti alloy. The approach described in this study resulted in at least one order of magnitude savings in both the overall cost and effort expended, when compared to the conventional approaches that employed small-scale testing to obtain the same information.

FIGURE 6

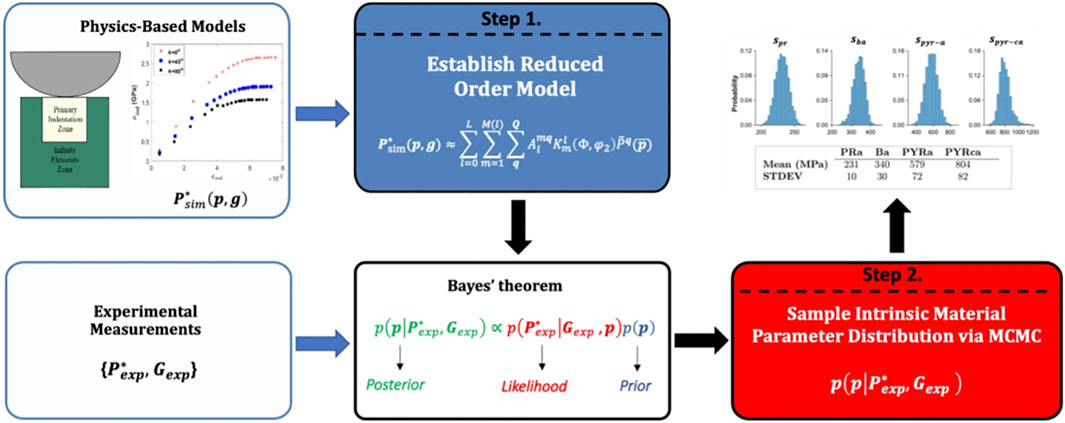
FIGURE 6. An example application of the Bayesian update strategy for the fusion of experimental and simulation datasets from indentation of a-Ti grains in a polycrystalline sample (Castillo et al., 2021).

2.3 Cyberinfrastructure for Digital Twins of Materials

Cyberinfrastructure supports the acquisition, storage, management, and fusion of data within a collaborative, but distributed, research environment. The creation of a robust cyberinfrastructure is critical to the realization of a digital twin, as digital twins exist at the confluence of multiple disparate data streams (e.g., simulation data, experimental data, real time sensor data). These data streams present challenges in managing both the variety and volume of data ingested, as well as any associated metadata needed to ensure high utility of the data for future use. Challenges in the variety of data come from the multimodal nature of materials data, meaning that the data in question stems from a variety of data sources (e.g., different imaging or analysis modalities). For example, materials data can take many forms: scalar parameters (e.g., diffraction line profile), time series (e.g., fatigue response), and spatially resolved (2-D and 3-D) image data (e.g., SEM image, tomography scan), and each modality is accompanied by its own unique forms of metadata that describe pre-process, in-process, and post-process information. Challenges in the volume of data stem from advancements in acquisition resolution and high-throughput experimental capabilities (hyperspectral imaging, x-ray computed tomography, etc.). For example, it is now commonplace to collect a large ensemble of images with high spatial resolution at a high frame rate using a variety of microscopes (e.g., optical, scanning electron, transmission electron), producing gigabytes-to-terabytes of observations of a single material (Dingreville et al., 2016). Similarly, expanded computational resources and multiscale modeling capabilities can also generate large amounts of data related to a material’s response to variety of environments (de Oca Zapiain et al., 2021). The main challenge lies in collecting and curating this large collection of heterogeneous data into the high-value information needed for the creation of a digital twin.

2.3.1 Data Sources

Material structure measurements capture the state of the material before, during, and after evolution, and material property measurements quantify various characteristics of evolution (e.g., resistance to evolution, evolution rates). The constellation of methods used to measure material structure and properties is extensive, and here we only mention two general trends. First, the digital data stream is becoming more entrenched in the instruments used to measure material properties. Just a generation ago, material structures were documented on film and quantification was performed by manual measurements; lab instruments utilized strip-chart recorders that created an analog graphical representation of the data. Now, not only have data streams become digitized, but increasingly, the data collection instruments are networked and remotely accessible. Yet significant concerns remain regarding the cyber vulnerability of both the data and the instrument, and institutional regulations regarding interconnectivity are highly disparate. Second, with the continuing advances in measurement sensors, data transfer, and data storage, the data streams are becoming increasingly dense, requiring thoughtful strategies for intelligent data reduction. Additionally, unconventional datasets, collected with alternative low-cost methods are proving to have utility. Previous trends in measurement science have focused on increases in precision and accuracy of data. Now, the focus is shifting to affordable high-density data streams that can provide similar or complementary information content to the existing suite of ultra-precise measurements.

The external stimuli (e.g., thermo-chemo-mechanical loading) driving material structure evolution need to be tracked through the use of suitable sensors. Sensors generally transduce various forms of energy (Table 1) into electrical signals that can be transformed into digital data. The transduction can also involve intermediate forms of energy, e.g., magnetic or optical. All forms of sensing have limits in resolution, range, accuracy, and precision. The fidelity of the digitized resolution of the external stimulus captured by the sensor is limited by the accuracy of the correlation of the electrical signal to the intensity of the imposed stimulus, and the bit-depth of the stored information. The fidelity of an environmental measurement can also be limited by the temporal and spatial resolution of the sensor. Sensor arrays allow for spatial mapping of a field (e.g., temperature field on a sample surface) of interest, with the spatial resolution limited by the spacing between individual sensors in the array. Alternately, one can acquire such information using a single sensor and rapidly scanning a region of interest; this strategy will lead to some degree of temporal disregistry between individual measurements.

TABLE 1

TABLE 1. Example of energy forms that drive changes in material state and the transducers employed to observe the corresponding exposure history.

2.3.2 Data Management (Ontology, Data Software Platforms)

The high volume and high variety of materials data quickly outpaces rudimentary data organization techniques typically used by humans (project specific folder structures, ad hoc organization or note taking). We therefore require more sophisticated data management tools to manage the storage and organization of the materials data relevant to the digital twin. In their most basic forms data management tools act as simple data repositories, centralized locations where data is held and made accessible to others. However, simple data repositories do not necessarily provide a systematic scheme for the organization of the data or metadata therein. Digital twins require the establishment of standards and protocols to catalogue, vet, compare, and use data reliably and credibly in automated (and possibly autonomous) protocols (Kalidindi and De Graef, 2015; Sorkin et al., 2020). Consequently, data management solutions for digital twins should aim to at least meet FAIR data principles: Findability, Accessibility, Interoperability, and Reusability (Wilkinson et al., 2016). FAIR data should have: (1) globally assigned, rich, searchable metadata with a unique persistent identifier and clear provenance; (2) standardized communication protocols for data storage and retrieval; (3) consistent, widely utilized, non-proprietary standards employed for data formatting. Data repositories generally only meet the most basic aspects of FAIR—namely accessibility. Materials databases progress further towards FAIR principles by providing greater searchability. Databases allow users to construct and carry out complex queries to search for information, and therefore improve searchability. However, their searchability is generally limited to tabular data. Furthermore, databases are also generally limited in their interoperability and reusability. In particular, they are not well suited for the materials data needed for digital twins as there is no natural way to describe the relational connections between disparate materials data (e.g., temporal variations along process paths, nested composition relationships, multimodal data describing single sample).

In order to truly realize FAIR data principles for materials data, we need to adopt emerging software tools in ontologies and linked data. Ontologies for data management are an open-world framework where we construct a standardized language to connect and describe objects. There currently exists many standardized languages used to describe ontologies such as OWL (McGuinness and Van Harmelen, 2004), RDF (Lassila and Swick, 1998), or JSONLD (Sporny et al., 2014). These languages all describe data in subject-predicate-object triples where we link the subject and the object through some rule (the predicate). One way to capture this information is through the formation of knowledge graph consisting of nodes (subjects, objects) and edges (predicates). Knowledge graphs allow for easily understood visual depictions of metadata, and for the application of emergent graph-based AI toolsets for the automated identification of new connections between aggregated elements of a complex heterogeneous dataset.

A recently proposed materials ontology (Voigt and Kalidindi, 2021) shown in Figure 7A can prove valuable in our effort to collect and curate the data needed for a materials digital twin. This ontology consists of four primary classes of entities (denoted by circles) that can serve as subjects or objects: Process, Material, Tool, and Data. A total of nine predicates (denoted by arrows) have been defined to link these objects. Process nodes hold information about process parameters, tool nodes describe the settings and characteristics of machines, and data nodes hold the payloads of interest (images, tabular data, etc). A material node describes the state of the material along a nominal process. Therefore, every time an action is taken on a material, we produce a new material node. This allows us to easily associate data with a point along a process path. As an example, a given steel (Material) produced after a specified thermo-mechanical processing route (Process) can be studied in a microscope (Tool); the results of the study are captured in a file (Data). Figure 7B depicts an example knowledge graph for a steel. The process begins with a generic low carbon steel node (seen at the bottom of the knowledge graph). It then undergoes a standard annealing step to get a uniform starting material, and proceeds through a specialized intercritical annealing and quench steps to its final form (labelled as 750-00-000 in the knowledge graph). Along the processing route shown, we are able to connect the various data/metadata collected. For example, it is seen that both the starting material and the final material have associated SEM images. The final material also has a datasheet generated using a known software package (defined by a Tool node) which took a known load-displacement curve (defined by a Data node) as input. Ontologies allow us to systematically capture interconnected materials data and allow for the context of a dataset to be robustly described and communicated, thus enhancing the reusability of the data.

FIGURE 7

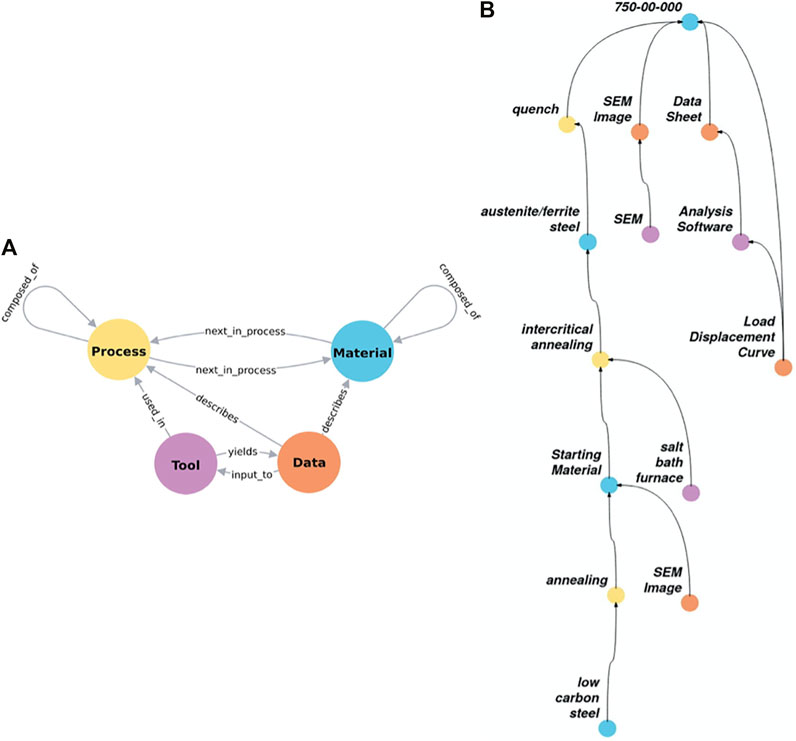
FIGURE 7. (A) The constitutive elements of a recently proposed materials ontology (Voigt and Kalidindi, 2021). The four main elements are Material (blue), Process (yellow), Tool (purple), and Data (orange) are shown in different colors along with the allowed connections between them. (B) An example of a knowledge graph constructed using the ontology.

2.3.3 AI Tools

There currently exist several software packages than can be used to support the mathematical framework proposed in Section 2.2. For structure quantification PyMKS (Brough et al.) offers computationally efficient tools for the feature engineering of material internal structures. PyMKS supports various data transformations needed to capture information on a wide range of material local states encountered in different material classes at different material structure length scales. PyMKS utilizes Dask, a distributed framework for developing python applications, to facilitate computations involving large datasets on supercomputers and large clusters (Rocklin, 2015). Subsequent to feature engineering, surrogate model building can be accomplished via a wide variety of popular python packages; examples include Statsmodels (Seabold and Perktold, 2010) for basic statistical models, SKLearn (Pedregosa et al., 2011) for machine learning tools, PyTorch (Paszke et al., 2019) and TensorFlow (Abadi et al., 2016) for neural networks/deep learning tools.

AI tools support digital twins beyond the needs of the mathematical framework alone. AI based segmentation strategies have gained traction, and Bayesian CNNs have recently been used to characterize the segmentation uncertainty in materials images (LaBonte et al., 2020). AI tools have also been effective in fusing multimodal materials data. Multi-input NNs have proven effective in combining data from multiple sources and different data types. For example, numeric and categorical data, assessed via multi-layer perceptron algorithms can be directly combined with image-based convolutional NNs (Azim and Aggarwal, 2014). While data streams are typically experimental, it can sometimes be beneficial to integrate high-fidelity simulation data from traditional high-performance computing approaches (e.g., atomistic modeling, phase-field, finite element) to augment “missing” experimental data or to represent functional dependencies/sensitivities that were not exposed in the experimental datasets. For instance, well-established experimental methods such as diffraction measurements are being implemented into computational models as a complement of the interpretation of experimental results (Coleman et al., 2014; Kunka et al., 2021). Alternatively, researchers have recently used generative machine learning algorithms such as generative adversarial network (GAN) to generate large materials and process libraries (Banko et al., 2020).

3 Applications

The ability to use a digital twin to provide an accurate picture of the corresponding physical twin at any given point in time is expected to significantly improve the guidance to subject-matter experts towards rational (and optimized) material/process improvements. Additionally, predictions of component performance can drive upstream changes in design or manufacturing process. To date, the development of detection and prognosis-driven planning strategies has largely focused on tuning individual process parameters such as temperature or materials composition for example, despite the urge to devise efficient strategies for the selection of multiple interdependent variables to substantially accelerate and improve scientific discovery. Digital twins open up new opportunities to enable such strategies and accelerate autonomous experimental design and exploration. Autonomous experiments are emerging in materials research leading to the acceleration of materials design and discovery (Nikolaev et al., 2016; Correa-Baena et al., 2018; Hase et al., 2018; Häse et al., 2019; Pendleton et al., 2019; Gongora et al., 2020). The idea is to integrate automation with some form of machine learning or artificial intelligence framework to accelerate experimentation or to guide and discover the next set of experiments. Most of the work to date is dedicated to materials discovery, i.e., autonomously predict and synthesize materials with targeted properties. For instance, Nikolaev et al. (2016) presented a closed-loop iterative method that automatically analyzes experimental results from carbon nanotubes grown from chemical vapor deposition to design or alter the next set of growth experiments to best reach a designated design target growth. Expanding autonomous loops to encompass more complex workflows will require the integration of the digital twin elements described in Section 2 with the automation of expert decisions. One interesting direction is to use the digital twins as a tool to autonomously test hypothesis during an experimental design. In this case, the practitioner would simply state the Process, Material, Tool, and Data and have the automation process decide whether the hypothesis is supported or refuted in order to decide on the potential next set of experiments. In this context, each automated trial would be guided by the knowledge collected and curated by the digital twin.

One particular application domain of interest for digital twins is the material/process exploration in additive manufacturing, with origins in rapid prototyping. There are extensive model-based simulations of the additive manufacturing process, ranging from powder packing through the entire laser-matter interaction and solidification process that can be taken as input into the Bayesian update strategy described in Section 2.2.2. The range of physical considerations in this process are daunting. In addition to these process models, there are complementary and similarly extensive set of structure-property models. Currently, a comprehensive digital representation of the entire spectrum of governing equations is beyond the state-of-the-art. A digital twin composed of many surrogate models utilizing the Bayesian update strategy could be formulated to optimize the parameters of these models for use in material design as well as process optimization.

4 Conclusion

Digital twins of the components in devices have enabled the in-service monitoring, prognosis, and design of complex systems. This work proposes both the conceptual framework and the cyberinfrastructure required to extend the concept of digital twins to the material level. Digital twins for materials provide a statistical in-silico materials representation of both structure and performance. The proposed framework consists of a materials representation based on n-point spatial correlations and PCA, a performance prediction framework centered around a two-step Bayesian framework, and a cyberinfrastructure that leverages new material ontologies for the management of multimodal materials data. Together, these foundational elements offer new opportunities for the extension of current digital twins to include important details of the material over a multitude of material structure length scales (from the macroscale to the atomistic).

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

MB and SRK acknowledge support from NSF DMREF Award# 2119640. This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In PSP linkages, one associates a material structure to an instant of time. The structure is then assumed to be responsible completely for the properties exhibited by the sample. In any imposed process, the structure is assumed to evolve with time. When the structure evolves, its associated properties are also expected to evolve.

References

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., et al. (2016). “Tensorflow: A System for Large-Scale Machine Learning,” in 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), 265–283.

Google Scholar

Adams, B. L., Kalidindi, S., and Fullwood, D. T. (2012). Microstructure Sensitive Design for Performance Optimization. Butterworth-Heinemann

Google Scholar

Allison, J., Backman, D., and Christodoulou, L. (2006). Integrated Computational Materials Engineering: a New Paradigm for the Global Materials Profession. Jom 58 (11), 25–27. doi:10.1007/s11837-006-0223-5

CrossRef Full Text | Google Scholar

Azim, S., and Aggarwal, S. (2014). Hybrid Model for Data Imputation: Using Fuzzy C Means and Multi Layer Perceptron. in IEEE International Advance Computing Conference (IACC), Gurgaon, India, February 21-22, 2014. IEEE, 1281–1285. doi:10.1109/iadcc.2014.6779512

CrossRef Full Text | Google Scholar

Banko, L., Lysogorskiy, Y., Grochla, D., Naujoks, D., Drautz, R., and Ludwig, A. (2020). Predicting Structure Zone Diagrams for Thin Film Synthesis by Generative Machine Learning. Commun. Mater. 1 (1), 1–10. doi:10.1038/s43246-020-0017-2

CrossRef Full Text | Google Scholar

Belianinov, A., Ievlev, A. V., Lorenz, M., Borodinov, N., Doughty, B., Kalinin, S. V., et al. (2018). Correlated Materials Characterization via Multimodal Chemical and Functional Imaging. ACS nano 12 (12), 11798–11818. doi:10.1021/acsnano.8b07292

PubMed Abstract | CrossRef Full Text | Google Scholar

Brough, D. B., Wheeler, D., and Kalidindi, S. R. (2017). Materials Knowledge Systems in Python-A Data Science Framework for Accelerated Development of Hierarchical Materials. Integr. Mater. Manuf Innov. 6 (1), 36–53. doi:10.1007/s40192-017-0089-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Castillo, A., and Kalidindi, S. R. (2019). A Bayesian Framework for the Estimation of the Single crystal Elastic Parameters from Spherical Indentation Stress-Strain Measurements. Front. Mater. 6, 136. doi:10.3389/fmats.2019.00136

CrossRef Full Text | Google Scholar

Castillo, A. R., and Kalidindi, S. R. (2021). Bayesian Estimation of Single Ply Anisotropic Elastic Constants from Spherical Indentations on Multi-Laminate Polymer-Matrix Fiber-Reinforced Composite Samples. Meccanica 56 (6), 1575–1586. doi:10.1007/s11012-020-01154-w

CrossRef Full Text | Google Scholar

Castillo, A. R., Venkatraman, A., and Kalidindi, S. R. (2021). Mechanical Responses of Primary-α Ti Grains in Polycrystalline Samples: Part II-Bayesian Estimation of Crystal-Level Elastic-Plastic Mechanical Properties from Spherical Indentation Measurements. Integr. Mater. Manuf Innov. 10 (1), 99–114. doi:10.1007/s40192-021-00204-9

CrossRef Full Text | Google Scholar

Cecen, A., Fast, T., and Kalidindi, S. R. (2016). Versatile Algorithms for the Computation of 2-point Spatial Correlations in Quantifying Material Structure. Integr. Mater. Manuf Innov. 5 (1), 1–15. doi:10.1186/s40192-015-0044-x

CrossRef Full Text | Google Scholar

Coleman, S. P., Sichani, M. M., and Spearot, D. E. (2014). A Computational Algorithm to Produce Virtual X-ray and Electron Diffraction Patterns from Atomistic Simulations. Jom 66 (3), 408–416. doi:10.1007/s11837-013-0829-3

CrossRef Full Text | Google Scholar

Correa-Baena, J.-P., Hippalgaonkar, K., van Duren, J., Jaffer, S., Chandrasekhar, V. R., Stevanovic, V., et al. (2018). Accelerating Materials Development via Automation, Machine Learning, and High-Performance Computing. Joule 2 (8), 1410–1420. doi:10.1016/j.joule.2018.05.009

CrossRef Full Text | Google Scholar

de Oca Zapiain, D. M., Stewart, J. A., and Dingreville, R. (2021). Accelerating Phase-Field-Based Microstructure Evolution Predictions via Surrogate Models Trained by Machine Learning Methods. npj Comput. Mater. 7 (1), 1–11. doi:10.1038/s41524-020-00471-8

CrossRef Full Text | Google Scholar

de Pablo, J. J., Jackson, N. E., Webb, M. A., Chen, L. Q., Moore, J. E., Morgan, D., et al. (2019). New Frontiers for the Materials Genome Initiative. npj Comput. Mater. 5 (1), 1–23. doi:10.1038/s41524-019-0173-4

CrossRef Full Text | Google Scholar

Dingreville, R., Karnesky, R. A., Puel, G., and Schmitt, J.-H. (2016). Review of the Synergies between Computational Modeling and Experimental Characterization of Materials across Length Scales. J. Mater. Sci. 51 (3), 1178–1203. doi:10.1007/s10853-015-9551-6

CrossRef Full Text | Google Scholar

Fullwood, D. T., Niezgoda, S. R., Adams, B. L., and Kalidindi, S. R. (2010). Microstructure Sensitive Design for Performance Optimization. Prog. Mater. Sci. 55 (6), 477–562. doi:10.1016/j.pmatsci.2009.08.002

CrossRef Full Text | Google Scholar

Generale, A. P., and Kalidindi, S. R. (2021). Reduced-order Models for Microstructure-Sensitive Effective thermal Conductivity of Woven Ceramic Matrix Composites with Residual Porosity. Compos. Structures 274, 114399. doi:10.1016/j.compstruct.2021.114399

CrossRef Full Text | Google Scholar

Ghoreishi, S. F., and Allaire, D. (2019). Multi-information Source Constrained Bayesian Optimization. Struct. Multidisc Optim 59 (3), 977–991. doi:10.1007/s00158-018-2115-z

CrossRef Full Text | Google Scholar

Ghosh, S., and Groeber, M. A. (2020). Developing Virtual Microstructures and Statistically Equivalent Representative Volume Elements for Polycrystalline Materials. Methods Theor. Model, 1631–1656. doi:10.1007/978-3-319-44677-6_13

CrossRef Full Text | Google Scholar

Gil, Y., and Selman, B. (2019). A 20-year Community Roadmap for Artificial Intelligence Research in the US.arXiv preprint arXiv:1908.02624

Google Scholar

Gomberg, J. A., Medford, A. J., and Kalidindi, S. R. (2017). Extracting Knowledge from Molecular Mechanics Simulations of Grain Boundaries Using Machine Learning. Acta Materialia 133, 100–108. doi:10.1016/j.actamat.2017.05.009

CrossRef Full Text | Google Scholar

Gongora, A. E., Xu, B., Perry, W., Okoye, C., Riley, P., Reyes, K. G., et al. (2020). A Bayesian Experimental Autonomous Researcher for Mechanical Design. Sci. Adv. 6 (15), eaaz1708. doi:10.1126/sciadv.aaz1708

PubMed Abstract | CrossRef Full Text | Google Scholar

Groeber, M. A., and Jackson, M. A. (2014). DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf Innov. 3 (1), 56–72. doi:10.1186/2193-9772-3-5

CrossRef Full Text | Google Scholar

Häse, F., Roch, L. M., and Aspuru-Guzik, A. (2019). Next-generation Experimentation with Self-Driving Laboratories. Trends Chem. 1 (3), 282. doi:10.1016/j.trechm.2019.02.007

CrossRef Full Text | Google Scholar

Häse, F., Roch, L. M., Kreisbeck, C., and Aspuru-Guzik, A. (2018). Phoenics: a Bayesian Optimizer for Chemistry. ACS Cent. Sci. 4 (9), 1134–1145. doi:10.1021/acscentsci.8b00307

PubMed Abstract | CrossRef Full Text | Google Scholar

Herr, J. E., Koh, K., Yao, K., and Parkhill, J. (2019). Compressing Physics with an Autoencoder: Creating an Atomic Species Representation to Improve Machine Learning Models in the Chemical Sciences. J. Chem. Phys. 151 (8), 084103. doi:10.1063/1.5108803

CrossRef Full Text | Google Scholar

Horstemeyer, M. F. (2009). Multiscale Modeling: A Review. Pract. aspects Comput. Chem, 87–135. doi:10.1007/978-90-481-2687-3_4

CrossRef Full Text | Google Scholar

Hu, C., Martin, S., and Dingreville, R. (2022). Accelerating Phase-Field Predictions via Recurrent Neural Networks Learning the Microstructure Evolution in Latent Space. Comput. Methods Appl. Mech. Eng.. doi:10.2172/1618267

CrossRef Full Text | Google Scholar

Jenks, , Cynthia, , Lee, , Nyung, H., Lewis, , Jennifer, P., et al. (2020). Basic Research Needs for Transformative Manufacturing (Report). United States: USDOE Office of Science

Google Scholar

Kalidindi, S. R., and De Graef, M. (2015). Materials Data Science: Current Status and Future Outlook. Annu. Rev. Mater. Res. 45, 171–193. doi:10.1146/annurev-matsci-070214-020844

CrossRef Full Text | Google Scholar

Kalidindi, S. R. (2020). Feature Engineering of Material Structure for AI-Based Materials Knowledge Systems. J. Appl. Phys. 128 (4), 041103. doi:10.1063/5.0011258

CrossRef Full Text | Google Scholar

Kalidindi, S. R. (2015). Hierarchical Materials Informatics: Novel Analytics for Materials Data. Elsevier.

Google Scholar

Kalidindi, S. R., Khosravani, A., Yucel, B., Shanker, A., and Blekh, A. L. (2019). Data Infrastructure Elements in Support of Accelerated Materials Innovation: ELA, PyMKS, and MATIN. Integr. Mater. Manuf Innov. 8 (4), 441–454. doi:10.1007/s40192-019-00156-1

CrossRef Full Text | Google Scholar

Kapteyn, M. G., Pretorius, J. V. R., and Willcox, K. E. (2021). A Probabilistic Graphical Model Foundation for Enabling Predictive Digital Twins at Scale. Nat. Comput. Sci. 1 (5), 337–347. doi:10.1038/s43588-021-00069-0

CrossRef Full Text | Google Scholar

Kaundinya, P. R., Choudhary, K., and Kalidindi, S. R. (2021). Machine Learning Approaches for Feature Engineering of the crystal Structure: Application to the Prediction of the Formation Energy of Cubic Compounds. Phys. Rev. Mater. 5 (6), 063802. doi:10.1103/physrevmaterials.5.063802

CrossRef Full Text | Google Scholar

Khosravani, A., Caliendo, C. M., and Kalidindi, S. R. (2020). New Insights into the Microstructural Changes during the Processing of Dual-phase Steels from Multiresolution Spherical Indentation Stress–Strain Protocols. Metals 10 (1), 18. doi:10.3390/met10010018

CrossRef Full Text | Google Scholar

Khosravani, A., Thadhani, N., and Kalidindi, S. R. (2021). Microstructure Quantification and Multiresolution Mechanical Characterization of Ti-Based Bulk Metallic Glass-Matrix Composites. JOM, 1–11. doi:10.1007/s11837-021-04864-y

CrossRef Full Text | Google Scholar

Kunka, C., Shanker, A., Chen, E. Y., Kalidindi, S. R., and Dingreville, R. (2021). Decoding Defect Statistics from Diffractograms via Machine Learning. npj Comput. Mater. 7 (1), 1–9. doi:10.1038/s41524-021-00539-z

CrossRef Full Text | Google Scholar

LaBonte, T., Martinez, C., and Roberts, S. (2020). We Know Where We Don't Know: 3D Bayesian CNNs for Uncertainty Quantification of Binary Segmentations for Material Simulations.osti

Google Scholar

Lassila, O., and Swick, R. R. (1998). Resource Description Framework (RDF) Model and Syntax Specification. W3C.

Google Scholar

Latypov, M. I., Toth, L. S., and Kalidindi, S. R. (2019). Materials Knowledge System for Nonlinear Composites. Comput. Methods Appl. Mech. Eng. 346, 180–196. doi:10.1016/j.cma.2018.11.034

CrossRef Full Text | Google Scholar

Lim, J., Perullo, C. A., Milton, J., Whitacre, R., Jackson, C., Griffin, C., et al. (2021). The EPRI Gas Turbine [43] Digital Twin–A Platform for Operator Focused Integrated Diagnostics and Performance Forecasting.

Google Scholar

Margaria, T., and Schieweck, A. (2019). “The Digital Thread in Industry 4.0,” in International Conference on Integrated Formal Methods (Cham: Springer), 3–24. doi:10.1007/978-3-030-34968-4_1

CrossRef Full Text | Google Scholar

Marquis de Laplace, P. S. (1814). A Treatise upon Analytical Mechanics: Being the First Book of the Mécanique Céleste. Boston, Massachusetts: Hilliard, Gray, Little, and Wilkins.

Google Scholar

Marshall, A., and Kalidindi, S. R. (2021). Autonomous Development of a Machine-Learning Model for the Plastic Response of Two-phase Composites from Micromechanical Finite Element Models. JOM, 1–11. doi:10.1007/s11837-021-04696-w

CrossRef Full Text | Google Scholar

Matouš, K., Geers, M. G., Kouznetsova, V. G., and Gillman, A. (2017). A Review of Predictive Nonlinear Theories for Multiscale Modeling of Heterogeneous Materials. J. Comput. Phys. 330, 192–220.

Google Scholar

McDowell, D. L., and LeSar, R. A. (2016). The Need for Microstructure Informatics in Process–Structure–Property Relations. MRS Bull. 41 (8), 587–593. doi:10.1557/mrs.2016.163

CrossRef Full Text | Google Scholar

McGuinness, D. L., and Van Harmelen, F. (2004). OWL Web Ontology Language Overview. W3C recommendation 10 (10), 2004.

Google Scholar

Mei, H., Haider, M., Joseph, R., Migot, A., and Giurgiutiu, V. (2019). Recent Advances in Piezoelectric Wafer Active Sensors for Structural Health Monitoring Applications. Sensors 19 (2), 383. doi:10.3390/s19020383

PubMed Abstract | CrossRef Full Text | Google Scholar

Morgado, J. F., Ghedini, E., Goldbeck, G., Hashibon, A., Schmitz, G. J., Friis, J., et al. (2020). “Mechanical Testing Ontology for Digital-Twins: a Roadmap Based on EMMO,” in SeDiT@ ESWC. CEUR Workshop Proceedings.

Google Scholar

National Science and Technology Council (Us), (2011). “Materials Genome Initiative for Global Competitiveness,” in Executive Office of the President (Washington, DC: National Science and Technology Council).

Google Scholar

Niederer, S. A., Sacks, M. S., Girolami, M., and Willcox, K. (2021). Scaling Digital Twins from the Artisanal to the Industrial. Nat. Comput. Sci. 1 (5), 313–320. doi:10.1038/s43588-021-00072-5

CrossRef Full Text | Google Scholar

Niezgoda, S. R., Kanjarla, A. K., and Kalidindi, S. R. (2013). Novel Microstructure Quantification Framework for Databasing, Visualization, and Analysis of Microstructure Data. Integr. Mater. Manuf Innov. 2 (1), 54–80. doi:10.1186/2193-9772-2-3

CrossRef Full Text | Google Scholar

Niezgoda, S. R., Yabansu, Y. C., and Kalidindi, S. R. (2011). Understanding and Visualizing Microstructure and Microstructure Variance as a Stochastic Process. Acta Materialia 59 (16), 6387–6400. doi:10.1016/j.actamat.2011.06.051

CrossRef Full Text | Google Scholar

Nikolaev, P., Hooper, D., Webber, F., Rao, R., Decker, K., Krein, M., et al. (2016). Autonomy in Materials Research: a Case Study in Carbon Nanotube Growth. npj Comput. Mater. 2 (1), 1–6. doi:10.1038/npjcompumats.2016.31

CrossRef Full Text | Google Scholar

Panchal, J. H., Kalidindi, S. R., and McDowell, D. L. (2013). Key Computational Modeling Issues in Integrated Computational Materials Engineering. Computer-Aided Des. 45 (1), 4–25. doi:10.1016/j.cad.2012.06.006

CrossRef Full Text | Google Scholar

Pandita, P., Bilionis, I., and Panchal, J. (2019). Bayesian Optimal Design of Experiments for Inferring the Statistical Expectation of Expensive Black-Box Functions. J. Mech. Des. 141 (10). doi:10.1115/1.4043930

CrossRef Full Text | Google Scholar

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). Pytorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 32, 8026–8037.

Google Scholar

Paulson, N. H., Priddy, M. W., McDowell, D. L., and Kalidindi, S. R. (2017). Reduced-order Structure-Property Linkages for Polycrystalline Microstructures Based on 2-point Statistics. Acta Materialia 129, 428–438. doi:10.1016/j.actamat.2017.03.009

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine Learning in Python. J. machine Learn. Res. 12, 2825–2830.

Google Scholar

Pendleton, I. M., Cattabriga, G., Li, Z., Najeeb, M. A., Friedler, S. A., Norquist, A. J., et al. (2019). Experiment Specification, Capture and Laboratory Automation Technology (ESCALATE): a Software Pipeline for Automated Chemical Experimentation and Data Management. MRS Commun. 9 (3), 846–859. doi:10.1557/mrc.2019.72

CrossRef Full Text | Google Scholar

Polonsky, A. T., and Pandey, A. (2021). Advances in Multimodal Characterization of Structural Materials. JOM, 1–2. doi:10.1007/s11837-021-04895-5

CrossRef Full Text | Google Scholar

Raj, P., and Surianarayanan, C. (2020). Digital Twin: the Industry Use casesAdvances in Computers. Elsevier 117 (1), 285–320. doi:10.1016/bs.adcom.2019.09.006

CrossRef Full Text | Google Scholar

Robertson, A. E., and Kalidindi, S. R. (2021a). Digital Representation and Quantification of Discrete Dislocation Networks.arXiv preprint arXiv:2101.03925

Google Scholar

Robertson, A. E., and Kalidindi, S. R. (2021b). Efficient Generation of Anisotropic N-Field Microstructures from 2-Point Statistics Using Multi-Output Gaussian Random Fields. Rochester, NY: SSRN 3949516

Google Scholar

Rocklin, M. (2015). Dask: Parallel Computation with Blocked Algorithms and Task Scheduling. in Proceedings of the 14th python in science conference, Austin, TX, July 6-12, 2009, 130. Austin, TX: SciPy, 136.

CrossRef Full Text | Google Scholar

Seabold, S., and Perktold, J. (2010). Statsmodels: Econometric and Statistical Modeling with python. in Proceedings of the 9th Python in Science Conference, Pasadena, CA, August 18-23, 2009 (Vol. 57, p. 61).doi:10.25080/majora-92bf1922-011

CrossRef Full Text | Google Scholar

Singh, V., and Willcox, K. E. (2018). Engineering Design with Digital Thread. AIAA J. 56 (11), 4515–4528. doi:10.2514/1.j057255

CrossRef Full Text | Google Scholar

Solomou, A., Zhao, G., Boluki, S., Joy, J. K., Qian, X., Karaman, I., et al. (2018). Multi-objective Bayesian Materials Discovery: Application on the Discovery of Precipitation Strengthened NiTi Shape Memory Alloys through Micromechanical Modeling. Mater. Des. 160, 810–827. doi:10.1016/j.matdes.2018.10.014

CrossRef Full Text | Google Scholar

Sorkin, B. C., Betz, J. M., and Hopp, D. C. (2020). Toward FAIRness and a User-Friendly Repository for Supporting NMR Data. doi:10.1021/acs.joc.0c00800

CrossRef Full Text | Google Scholar

Sporny, M., Longley, D., Kellogg, G., Lanthaler, M., and Lindström, N. (2014). JSON-LD 1.0. W3C recommendation 16, 41.

Google Scholar

Takhtaganov, T., and Müller, J. (2018). Adaptive Gaussian Process Surrogates for Bayesian Inference. SIAM/ASA Journal on Uncertainty Quantification.arXiv preprint arXiv:1809.10784

Google Scholar

Talapatra, A., Boluki, S., Duong, T., Qian, X., Dougherty, E., and Arróyave, R. (2018). Autonomous Efficient experiment Design for Materials Discovery with Bayesian Model Averaging. Phys. Rev. Mater. 2 (11), 113803. doi:10.1103/physrevmaterials.2.113803

CrossRef Full Text | Google Scholar

Tao, F., Zhang, M., Liu, Y., and Nee, A. Y. C. (2018). Digital Twin Driven Prognostics and Health Management for Complex Equipment. Cirp Ann. 67 (1), 169–172. doi:10.1016/j.cirp.2018.04.055

CrossRef Full Text | Google Scholar

The Minerals, Metals & Materials Society Tms, (2017). Building a Materials Data Infrastructure: Opening New Pathways to Discovery and Innovation in Science and Engineering. Pittsburgh, PA: TMS. Electronic copies available at www.tms.org/mdistudy.

Google Scholar

The Minerals, Metals & Materials Society Tms, (2015). Modeling across Scales: A Roadmapping Study for Connecting Materials Models and Simulations across Length and Time Scales. Warrendale, PA: TMS. Electronic copies available at www.tms.org/multiscalestudy.

Google Scholar

Torquato, S., and Haslach, H. (2002). Random Heterogeneous Materials: Microstructure and Macroscopic Properties. Appl. Mech. Rev. 55 (4), B62–B63. doi:10.1115/1.1483342

CrossRef Full Text | Google Scholar

Torquato, S., and Stell, G. (1982). Microstructure of Two‐phase Random media. I. The N‐point Probability Functions. J. Chem. Phys. 77 (4), 2071–2077. doi:10.1063/1.444011

CrossRef Full Text | Google Scholar

Ullo, S. L., and Sinha, G. R. (2020). Advances in Smart Environment Monitoring Systems Using IoT and Sensors. Sensors 20 (11), 3113. doi:10.3390/s20113113

PubMed Abstract | CrossRef Full Text | Google Scholar

Voigt, S. P., and Kalidindi, S. R. (2021). Materials Graph Ontology. Mater. Lett. 295, 129836. doi:10.1016/j.matlet.2021.129836

CrossRef Full Text | Google Scholar

Wilkinson, M. D., Dumontier, M., Aalbersberg, I. J., Appleton, G., Axton, M., Baak, A., et al. (2016). The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Data 3 (1), 160018–160019. doi:10.1038/sdata.2016.18

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, Z., Fan, M., Tovar, G. V., Trehem, W., Yoon, B. J., Qian, X., et al. (2021). Physics-constrained Automatic Feature Engineering for Predictive Modeling in Materials Science. in Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 35, No. 12, pp. 10414–10421). The AAAI Digital Library.

Google Scholar

Xie, R., Chen, M., Liu, W., Jian, H., and Shi, Y. (2021). Digital Twin Technologies for Turbomachinery in a Life Cycle Perspective: A Review. Sustainability 13 (5), 2495. doi:10.3390/su13052495

CrossRef Full Text | Google Scholar

Zaccaria, V., Stenfelt, M., Aslanidou, I., and Kyprianidis, K. G. (2018). “Fleet Monitoring and Diagnostics Framework Based on Digital Twin of Aero-Engines,” in Turbo Expo: Power for Land, Sea, and Air American Society of Mechanical Engineers (ASME), 51128, V006T05A021. doi:10.1115/gt2018-76414

CrossRef Full Text | Google Scholar

Zeb, S., Mahmood, A., Hassan, S. A., Piran, M. J., Gidlund, M., and Guizani, M. (2021). Industrial Digital Twins at the Nexus of nextG Wireless Networks and Computational Intelligence: A Survey. Journal of Network and Computer Applications, 103309. doi:10.1016/j.jnca.2021.103309

CrossRef Full Text | Google Scholar