The promotion effect of uniaxial strain on hydrogen aggregation in tungsten

The aggregation behavior of hydrogen (H) isotopes after low-energy plasma irradiation is particularly important for tungsten (W) in future fusion devices. Here, using the first-principles calculation, we demonstrated an interesting strain effect that may drive the planar aggregation of interstitial H atoms in W. Although there are attractive interactions between H atoms, the spontaneous nucleation of these platelet-like H clusters in strain-free W appears impossible even at high H concentrations (up to 0.1 at.%) because of the extremely low configurational entropy. However, applied uniaxial strain significantly increased the binding energy of H platelets and enabled planar H clusters to form. These results suggest that uniaxial strain enhances the nucleation and growth of H platelets in W, regardless of whether it is a compressive or tensile strain. Moreover, the binding energy of one-layer H clusters was lower than that of parallel H platelets, implying that the formation of multi-layer H clusters in W and their stability is also promoted by uniaxial strain. Meanwhile, the presence of planar H clusters dramatically reduced the vacancy formation energy in W, which in turn provided an extra trapping site to accommodate excessive H atoms. These results provide an important reference for understanding the H evolution in W-PFMs.

1 Introduction

Tungsten (W) is currently used as a plasma-facing material (PFM) in ITER and future fusion reactors (Noda et al., 1997) because of its excellent high-temperature performance, low hydrogen (H) isotope retention, and high sputtering threshold. In fusion devices, the W-PFMs are exposed to fusion fuels (e.g., deuterium and tritium) and fusion products (e.g., helium and neutron), leading to a significant degradation of material performance and a major concern for the long-term operation of reactors (Loarte et al., 2007; Roth et al., 2009). Considering tritium’s self-sufficiency and radioactivity, a full understanding of the interaction of H isotopes with W is particularly important, and has been extensively investigated both computationally (Zhou et al., 2012; Hodille et al., 2018; Hou, et al., 2018; Smirnov and Krasheninnikov, 2018; Hou et al., 2019; Ren et al., 2019; Hou, et al., 2020) and experimentally (Tokunaga et al., 2005; Shu et al., 2007; Shu, et al., 2009; Alimov, et al., 2012).

As the essential process of H evolution, the dissolution and retention of H play a key role in the H-related phenomena (e.g., H bubbles) in W. In thermodynamic equilibrium, the solubility of H in W is around 10⁻¹⁸–10⁻⁸ atomic fractions in the temperature range of room temperature to 1,000 K (Frauenfelder, 1969; Hodille et al., 2018). However, after low-energy H plasma irradiation, the total H concentration can reach up to ∼1 at.% in W, especially in the surface layers (∼10 at.%) (Gao et al., 2017). Since the kinetic energy of H plasma is far below the displacement energy threshold needed to create a stable Frenkel pair, collision-induced vacancies alone cannot be responsible for H oversaturation in W. Despite intensive investigations (Terentyev et al., 2014; Gonzalez et al., 2015; De Backer et al., 2018), the underlying mechanisms for this super-saturated H retention in plasma-loaded W remain elusive, and controversies abound in literature. For example, using density functional theory (DFT) data and thermodynamic models, Hodille et al. (2018) and Middleburgh et al. (2014) believed the oversaturation originates from the H-induced reduction of vacancy formation energy, which promotes the vacancy amount that may accommodate excessive H atoms. Meanwhile, Gao et al. (2017), Gao et al. (2020) and Kato et al. (2015) claimed that high concentrations of pre-existing H prevent the recombination of vacancies with self-interstitial atoms, and thus significantly reduce the displacement threshold energy and facilitate vacancy formation in W. In addition to vacancies, dislocations (Terentyev et al., 2014; Chen et al., 2020) and grain boundaries (GBs) (Chen et al., 2020) have also been considered to be main contributors to H retention, although H oversaturation has been widely observed in recrystallized and/or single crystal W with very low dislocations/GBs density (Alimov et al., 2005; Zibrov et al., 2017; Zhang et al., 2021). To complicate matters further, recent experiments demonstrated that super-saturated H retention is almost independent of pre-existing impurities and defects (Jia et al., 2017), suggesting that the evolution of H itself is of high importance for such oversaturation.

In this paper, we provide a new perspective for understanding H retention in W, which implicates the strain-enhanced self-clustering of interstitial H atoms. Despite the repulsive or weak interaction of H-H pairs, there are attractive interactions of large platelet-like H clusters in W along {001} planes. However, when configurational entropies are taken into account, the spontaneous formation of H platelets at room temperature is extremely difficult even at high H concentrations (up to 0.1 at.%). It is interesting to note that applied uniaxial strain significantly enhances the stability of H platelets, and enables planar H clusters to form. Furthermore, the binding energy of one-layer H clusters is lower than that of parallel H platelets, which can be promoted by uniaxial strain, implying the formation of multi-layer H clusters in W. Meanwhile, the desorption temperature of these platelet-like H clusters and their influence on vacancy formation are also calculated and discussed.

2 Computational method

First-principles calculations on the basis of DFT were performed in the Vienna Ab initio Simulation Package (VASP) with projected augmented wave (PAW) potentials (Blöchl, 1994). The electronic exchange-correlation effects were described by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (Perdew et al., 1996). Bcc supercells containing 128 lattice points (4a₀ × 4a₀ × 4a₀, a₀ of the lattice constant in W) and 216 lattice points (3a₀ × 3a₀ × 12a₀) were used to determine the gradual aggregation of interstitial H atoms and the properties of the “infinite” H platelet along (001) planes in W, respectively. The corresponding k-point mesh densities in the Brillouin zone were set as 3 × 3 × 3 and 4 × 4 × 1, respectively, based on the Monkhorst-Pack approach (Monkhorst and Pack, 1976). Through the convergence tests, a cutoff energy of 350 eV was used in all calculations. The structure iteration and electronic optimization were complete when the forces on all atoms and the energy difference was less than 0.01 eV Å⁻¹ and 10⁻⁶ eV, respectively. Lattice relaxation in strain-free W occurs when the atomic position and the shape/size of the supercell along all directions are fully relaxed. For cases under uniaxial strain, only the parameter of supercells along xy directions are relaxed with the optimization of all atomic positions, while the in-plane lattice parameters (i.e., z direction) are fixed at given strain values. Moreover, the zero-point energy (ZPE) corrections have significant effect on H behaviors in materials. Here, similar to previous studies (Hou et al., 2018; Hou et al., 2020), only the contribution of H to the zero-point energy (ZPE) was taken into account, because the vibrational energies of W were assumed to be much smaller than that of H due to their differing mass. Accordingly, the ZPE corrections could be calculated by ${\mathrm{E}}_{\mathrm{Z}\mathrm{P}\mathrm{E}}=\frac{1}{2}\sum \mathrm{h}{\nu }_{\mathrm{i}}$, where $\mathrm{h}$ and ${\nu }_{\mathrm{i}}$ are Plank’s constant and the normal vibration frequencies, respectively.

3 Results and discussion

3.1 Aggregation of H atoms in strain-free W

A single interstitial H atom energetically prefers to occupy the tetrahedral interstitial site (TIS) rather than the octahedral interstitial site (OIS) in most bcc metals (Henriksson et al., 2005; Wang et al., 2020; Yang et al., 2020). In our calculations, the solution energy of an interstitial H at TIS and OIS was 0.95 eV and 1.33 eV (or 1.06 eV and 1.43 eV with ZPE correction) in bulk W, respectively, in good agreement with previous experimental data (1.04 ± 0.17 eV) (Oates and McLellan, 1972). Next, we examined the self-clustering of interstitial H atoms in W by calculating their sequential and average binding energies, which are defined as:

$E_{nH,\epsilon }^{b,seq}=E_{NW+\left(n-1\right)H,\epsilon }+E_{H,\epsilon }-E_{NW+nH,\epsilon }-E_{NW,\epsilon }(1)$

$E_{nH,\epsilon }^{b,ave}=\left({nE}_{H,\epsilon }+{\left(n-1\right)E}_{NW,\epsilon }-E_{NW+nH,\epsilon }\right)/n(2)$

where $E_{NW+\left(n-1\right)H,\epsilon }$ and $E_{NW+nH,\epsilon }$ are the total energies of a strained (ε) system containing n-1 and n interstitial H atoms, respectively. $E_H$ and $E_{NW}$ are the energies of bcc W with and without a single TIS-H, respectively.

Here, many possible configurations (e.g., spherical, linear and planar) were considered in our calculations, but, similar to a previous DFT study (Hou et al., 2018), the stability of platelet-like H clusters along {001} planes (see Figures 1A, B) was much higher than the other configurations in strain-free W. Accordingly, only the binding energies of this planer structure as a function of H numbers are presented in Figure 1C. The sequential binding energies of planer H clusters along {001} planes were always positive, except for H₂ and H₃ clusters, indicating the attractive interaction of pre-existing H platelets and subsequent interstitial H atoms in W. Furthermore, although there were pronounced fluctuations of sequential binding energy, it generally increased with the increase in H numbers, from −0.020 eV for the second H atom to 0.205 eV for the 16^th H atom. Namely, the larger the H numbers along {001} planes, the higher the stability of the planer H clusters.

FIGURE 1

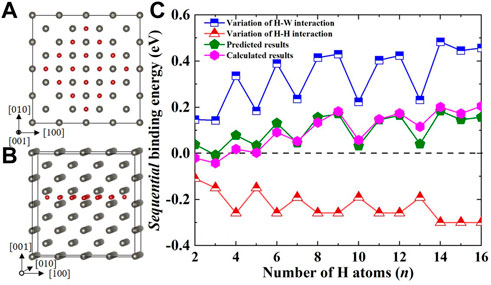
FIGURE 1. (A) The top and (B) the side views of the most stable planar H_2∼16 cluster in W along (001) planes. The small red and large grey balls represent H and W atoms, respectively; (C) shows the calculated and predicted sequential binding energies of planar H clusters, based on the linear elasticity model of Eq. 3 and the repulsive interactions of H-H pairs.

To quantitatively understand the energetics of H and the stability of planar H clusters, the sequential binding energies were decomposed into the energy variation of H-W interactions and the repulsive energy of H-H pairs. The first part originates from the volume change of neighboring TISs (to accommodate the subsequent H) induced by the pre-existing H atoms, because they share the lattice with W atoms. This alters the dissolution of H atoms at neighboring TISs, and can be roughly estimated by the linearly elasticity theory and force dipole tensor (i.e., the stress tensor induced by a H atom at TIS), which can be defined as:

$E_{\epsilon }^{H-Winteraction}=E_H^{sol}+V\left({\sigma }_{\left[100\right]}{\epsilon }_{\left[100\right]}+{\sigma }_{\left[010\right]}{\epsilon }_{\left[010\right]}+{\sigma }_{\left[001\right]}{\epsilon }_{\left[001\right]}\right)(3)$

where $E_H^{sol}$ is the solution energy of an interstitial H at TIS in strain-free W, $V$ is the volume of the bcc W supercell at equilibrium, $\sigma$ is the lattice stress induced by TIS-H, and $\epsilon$ is the atomic strain of neighboring TISs along (100), (010), and (001) directions. The strain obtained here is based on the distance between W atoms in the neighboring tetrahedron ($d_{W-W,H_{n-1}}$) when a planar H_n-1 cluster is pre-existing, i.e., $\epsilon =\frac{d_{W-W,H_{n-1}}-d_{W-W,bulk}}{d_{W-W},bulk}$. The interaction between H atoms should be repulsive and weaken with the increase in H-H distance (d). Here, similar to previous studies (Conrad and, 1996; Hou et al., 2019), the electronic repulsion of H-H pairs can be described by a power law and expressed as:

$E_{\mathit{int}}^{H-H}={-A}_s{d}^{-5}(4)$

where $A_s$ is a fitting constant (∼5.27 in our calculations). Based on this equation, the H-H interaction part of a H_n cluster is determined by summing up all the repulsions of a nth H with pre-existing (n-1) H atoms. More details and results related to the above are presented in the Supplementary Data.

As illustrated in Figure 1C, the energy variation of H-W interactions was positive for all cases, suggesting volume expansion of neighboring TISs induced by the pre-existing H atoms, which facilitates the dissolution of subsequent H and makes a positive contribution to the sequential binding energies. In contrast, the interaction energies of H-H pairs were negative and gave a negative contribution to the formation of planar H clusters. It is interesting to note that both the contribution of H-W and H-H interactions showed distinct energy levels, especially for the large planar H clusters. This was due to the fact that the volume expansion induced by pre-existing H atoms and the electronic interaction of H-H pairs were very local, and their contribution to the sequential binding energy became negligible if the H-H distance was longer than 3.19 Å. More importantly, the sequential binding energies of planar H clusters obtained by our DFT calculations were in good agreement with the model predictions by summing up the energy variation of the H-W interaction and the repulsion energy between H atoms, confirming the validity of these approximations in describing the energetics of planar H clusters in W.

Figure 2A shows the average binding energy of planar H clusters along {001} planes in W as a function of H numbers. Similar to the sequential binding energy, the average binding energy gradually increased with the increase in cluster size, from −0.01 eV/H for H₂ to 0.103 eV for H₁₆ cluster. Despite the overall increase of average binding energy, it was expected to reach a steady state eventually, corresponding to “infinitely” large H clusters, with every TIS along {001} planes being occupied by interstitial H atoms. Thanks to the periodic boundary conditions, the maximum (or steady-state) average binding energy (referring to H_∞) of planar H clusters in W could be examined and calculated to be ∼0.29 eV/H. Moreover, as displayed in Figure 2A, the variation of average binding energy followed a simple exponential function, i.e., $E_b^{H_n}=0.29-0.31\exp \left(\frac{-n}{28.41}\right)$.

FIGURE 2

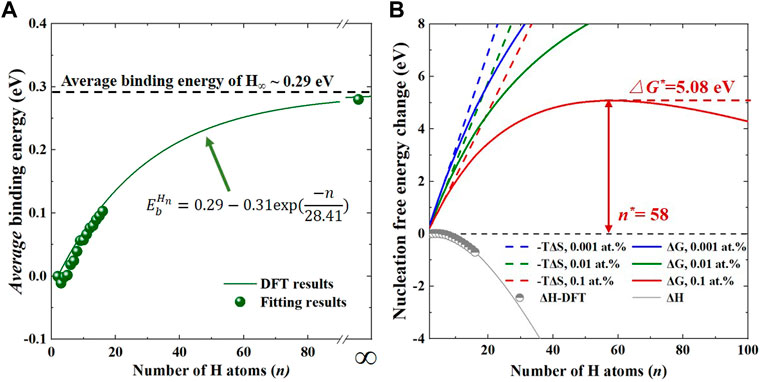
FIGURE 2. (A) The average binding energy of a planar H cluster in W as a function of cluster size. The fitting curve (solid green line) using a simple exponential function is also provided; (B) Nucleation free energy changes of H_n clusters at 300 K with different hydrogen concentrations (0.001/0.01/0.1 at.%).

According to classical nucleation theory (CNT), the nucleation of solute clusters in materials is dependent not only on their binding energies, but also on entropy contributions (Seko et al., 2004; Yuge et al., 2005). Thus, we further examined the nucleation free energy change (△G) of planar H clusters in W by considering both the enthalpy and entropy, which can be expressed as (Seko et al., 2004; Yuge et al., 2005):

$∆G=\left(∆H+H_s\right)-T∆S_{vib}-T∆S_{config}(5)$

where the first term $\left(∆H+H_s\right)$ represents the enthalpy variation for the planar H cluster from isolated H atoms, including the interface energy and the clustering energy. This part can be calculated using DFT calculations directly and precisely, and is equivalent to the opposite value of the total binding energy. The second $∆S_{vib}$ and third term $∆S_{config}$ denote the vibrational and configurational entropy changes due to the cluster formation, respectively. Here, similar to previous studies (Li, et al., 2017; Hou, et al., 2018), the contribution of vibrational entropy is neglected, and the entropy loss is approximated by (see more details in Supplementary Data):

$\frac{∆S_{config}}{k_B}=\left(n-1\right)\mathit{ln}{C}_H+\frac{3}{2}\mathit{ln}\left(n\right)-\left(1+\mathit{ln}6\right)n+\mathit{ln}6+\frac{1}{2}\mathit{ln}2\pi (6)$

where $C_H$ is the atomic concentration of H atoms in W, and $n$ is the number of H atoms in the cluster. Here, the configurational entropy change is estimated at room temperature (∼300 K) and three different H concentrations (i.e., 0.001, 0.01, and 0.1 at.%).

The nucleation free energy change and corresponding enthalpy and entropy contributions for planar H clusters in W are plotted in Figure 2B as a function of cluster size. It was found that the enthalpy change was negative and decreased with the increase in H numbers, providing the driving force for H cluster formation, while the entropy term was positive and increased linearly with the increase in H numbers, leading to a positive effect on the cluster dissociation. Notably, when the H concentration was assumed to be 0.001 and 0.01 at.%, the total nucleation free change of H platelets at 300 K was positive and monotonically increased with increasing cluster size. Thus, in this scenario, the planar H clusters were likely to be dissolved at independent TISs in W in order to reduce △G. Intriguingly, if the H content was increased to 0.1 at.%, the variation of nucleation free energy change had different characteristics. As illustrated in Figure 2B, there was a critical number of H atoms (∼58) to classify the growth of planar H clusters in W. In this case, when the H number was less than this critical value, the clusters were likely to dissociate to lower △G, while they energetically preferred to grow spontaneously with lower △G if the H number was higher than the critical value. Accordingly, the activation energy barrier (that is the top of △G, △G^*) for the nucleation of H cluster in W was calculated to be 5.08 eV at temperature of 300 K and H concentration of 0.1 at.%. Such high activation energy barrier at room temperature suggests that the probability of planar H cluster formation is extremely low because the nucleation rate is proportional to exp(−△G^*/k_BT) in the CNT. As seen in Eq. 5, temperature has a significant effect on the variation of configurational entropy and thus the nucleation free energy change of planar H clusters. Therefore, in order to show the temperature effect, we also calculated the nucleation free energy change of H platelets in strain-free W at 500 K. In this case, even when the H concentration could reach up to 0.1 at.%, the nucleation free energy change always increased with the increase in cluster sizes. This was due to the increase of configuration entropy change at high temperatures, which had a negative effect on the nucleation and growth of H clusters. Therefore, despite the attractive interactions between H atoms, the nucleation of these platelet-like H clusters in strain-free W seems impossible.

3.2 Influence of uniaxial strain on the stability of planar H clusters

Generally, applied strain/stress has significant effect on the evolution of H in W (Zhou et al., 2012; Terentyev et al., 2015a; Terentyev et al., 2015b; Smirnov and Krasheninnikov, 2018; Hou et al., 2020) due to the variation of the local atomic environment. Also, as demonstrated in a recent experiment (Gao, et al., 2017), the highly-distorted near-surface region is clearly observed in plasma-loaded W, and intimately linked with H oversaturation. However, how this H-induced lattice distortion affects the growth and nucleation of planar H clusters remains unclear. Here, taking uniaxial strain as examples, we investigated the influence of external strain/stress on the stability of H clusters by considering their binding energies in strained W.

Since uniaxial strain breaks the symmetry of the bcc lattice, two different planar H clusters along {001} planes in strained W should be considered, including (010) and (001) planes. It is interesting to note that there are two types of high stability H clusters in W under 1% tensile strain (referred to as +1% strain), the H platelets at TISs along (001) planes and at OISs along (101) planes (see Supplementary Figure S2), and the associated average binding energies are presented in Figure 3A. Although the average binding energies of these two planar H clusters were always positive and increased with the increase in H numbers, the stability of H platelets at TISs along (001) planes was much higher than that at OISs along (101) planes. Thus, the platelet-like structure along (001) planes was the most favorable configuration for H clusters under +1% strain. Furthermore, as seen in Figure 3A, the maximum average binding energy of planar H clusters (corresponding to the infinite large H platelets) along (001) planes under +1% strain was calculated to be 0.34 eV/H, which was larger than that without strain (∼0.29 eV/H). This indicates the enhancing effect of tensile strain on the stability of planar H clusters, which was also confirmed by the sequential binding energy. As displayed in Figure 3B, similar to the results in strain-free W, the sequential binding energy of H clusters under +1% strain was also volatile but generally increased with the increase in H numbers. Specifically, by comparing the data in Figures 1C, 3C, the applied tensile strain obviously promoted the formation of planar H clusters, because the sequential binding energy under +1% strain (from 0.19 eV for the second H to 0.30 eV for 16^th H) was much higher than that in strain-free W (from −0.02 eV to 0.20 eV). In the case of 1% compressive strain (refer to as −1% strain), the most favorable configuration of H clusters in W was the platelet-like structures at TISs along (010) planes, despite the positive binding energy of planar H clusters at OISs along (110) planes, as illustrated in Figure 3C. Notably, in comparison with H platelets along (001) planes in strain-free W and under 1% tensile strain, the binding energy of H platelets under −1% strain along (010) planes was much higher. For example, the largest sequential and average binding energies of H platelets reach up to 0.81 eV and 0.53 eV in compressive strained W, while in planar H clusters along (001) planes in strain-free/tensile strained W, they were only 0.61/0.74 and 0.29/0.34 eV, respectively. Overall, the growth of planar H clusters in W was enhanced by uniaxial strain, almost independent of the signs of strain. This is consistent with previous studies (Smirnov and Krasheninnikov, 2018; Hou et al., 2020) in which the anisotropic strain facilitates the formation of H platelets in W.

FIGURE 3

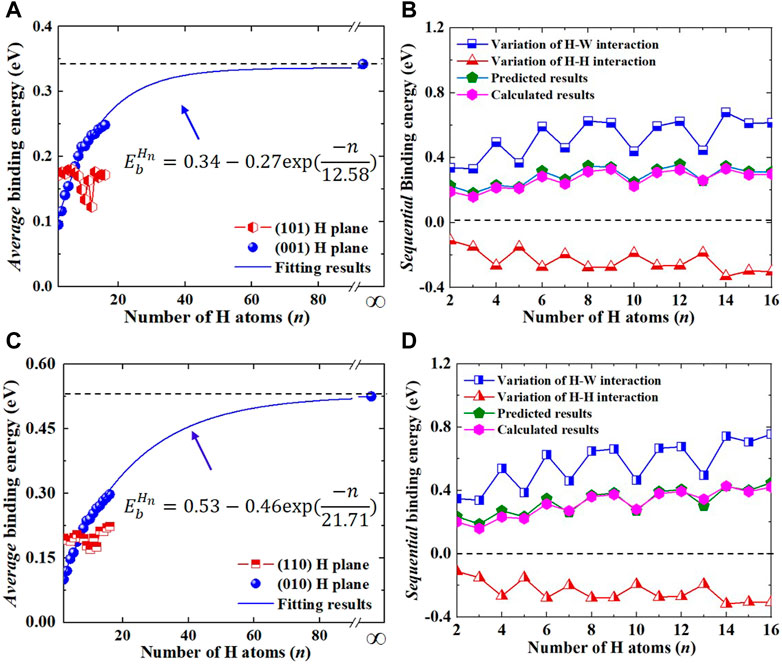
FIGURE 3. (A) shows the average binding energies of the planar H_n clusters on (001) and (101) planes under +1% strain; (B) shows the calculated and predicted sequential binding energies of H clusters on (001) planes under +1% strain; (C) shows the average binding energies of the planar H_n clusters on (010) and (110) planes under −1% strain; (D) shows the calculated and predicted sequential binding energies of H clusters on (010) planes under −1% strain.

In order to clarify the underlying mechanism of strain-enhanced H cluster formation, the sequential binding energies of H platelets in strained W were also divided into the energy variation of H-W interactions and the repulsive energy of H-H pairs. As displayed in Figures 3B, D, the sequential binding energies predicted by considering the lattice distortion induced by pre-existing H and the direct repulsion of H-H pairs were consistent with the DFT-calculated values, regardless of whether there was a compressive or tensile strain, verifying the reliability of the theoretical model. It was found that the influence of strain on the repulsive interaction between H atoms for (001) and (010) H platelets was very slight. For example, the maximum and average energies of H-H repulsion for the first 16 H atoms along (001) and (010) planes were 0.299/0.317/0.302 eV and 0.215/0.224/0.222 eV in strain-free/compressive/tensile strained W, respectively. This was due to the fact that the distance of H-H pairs in planar structures remained essentially unchanged, from 2.22 Å in strain-free W to 2.17/2.2 Å under 1% compressive/tensile strain. Thus, the promoting effect of strain on the stability of (001) and (010) platelets could be mainly attributed to the H-induced volume expansion of neighboring interstitial sites, which originated from the repulsive interaction of H-W pairs. Atomic configuration showed that the application of uniaxial strain reduced the first nearest neighboring (1NN) distance between H and its neighboring W atoms, independent of the signs of strain, leading to strong H-W repulsion and large volume expansion. For example, when a H₉ cluster was introduced, the expansion of neighboring TISs in strain-free W along [100], [010], and [001] directions was −0.01, −0.01, and 0.06, respectively. In tensile/compressive strained W, it was −0.01/−0.008, −0.01/0.074, and 0.07/−0.02, respectively. Such large volume expansion induced the high sequential binding energy of H platelets and facilitated H cluster formation in W.

Figure 4 shows the nucleation free energy change of planar H clusters along (001) and (010) planes in strain-free and strained W (−1% or +1%) at 300 K as a function of cluster size. In the case of a low H concentration of ∼0.001 at.% (see Figure 4A), although the applied strain reduced the free energy change of H clusters, it was always positive and increased with the increase in cluster size in +1% strained W, implying that the planar H clusters were unstable in thermal equilibrium. When the H concentration was increased to 0.01 at.%, the free energy change in strain-free W was still positive and monotonically increased with the increase in H numbers. However, as seen in Figure 4B, the free energy change in strained W increased initially with the increasing cluster size, and then decreased with the increase in H numbers. Furthermore, the critical size and energy barrier of planar H clusters in W under +1%/−1% strain was estimated to be 27/16 and 1.82/1.28 eV, respectively. With the further increase of H concentrations up to .1 at.%, as displayed in Figure 4C, the variation trend of free energy change in strain-free W was similar to that in strained W, but the corresponding critical size and energy barrier were reduced, from 58 to 5.08 eV in strain-free W to 16/10 and 0.73/0.56 eV in tensile/compressive strained W, respectively. These results suggest that uniaxial strain enhances the growth of H platelets in W, regardless of whether it is a compressive or tensile strain.

FIGURE 4

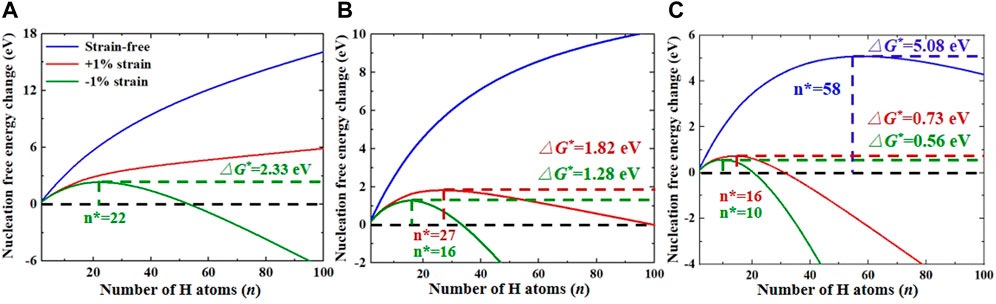
FIGURE 4. Nucleation free energy changes of planar H_n clusters at 300 K with (A) 0.001 at.%, (B) 0.01 at.% and (C) 0.1 at.% H concentrations in strain-free and strained W (−1% or +1%).

3.3 Interaction between parallel H platelets

Physically, the formation of pure planar H clusters should be very difficult due to the extremely small configurational entropy, especially for the large H platelets. Thus, to estimate the possibility of multi-layer H cluster formation, we further investigated the interaction between two planar H clusters in W along parallel {001} planes. Namely, an “infinite” H platelet was set at TISs along a {001} plane, while the other “infinite” H platelet was located at a series of parallel {001} planes with different vertical distances, as illustrated in Figure 5A. Then, the binding energy of the two parallel H clusters could be expressed as:

$E_{HP-HP}^b=2E_{HP}-E_{HP-HP}-E_W(7)$

where $E_{HP}$ and $E_{HP-HP}$ are total energies of the system containing an {001} H platelet and two parallel {001} H platelets with different vertical distances, respectively.

FIGURE 5

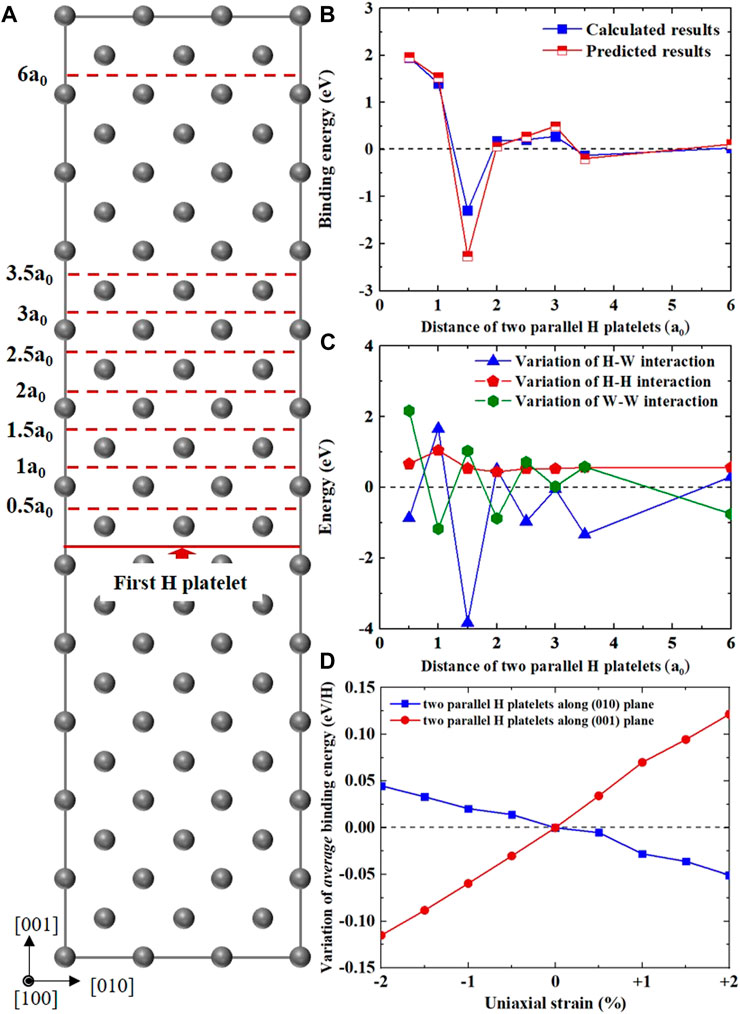
FIGURE 5. Interaction between two planar H clusters in W along parallel {001} planes. (A) Configuration of two parallel H platelets along {001} planes with different vertical distances, from .5a₀ to 6a₀. The solid and dash red lines denotes the position of first and second planar H clusters, respectively; (B) The calculated/predicted binding energies of two parallel H platelets as a function of their vertical distance, and corresponding variation of H-W/H-H/W-W interactions are presented in (C); (D) displays the average binding energy variation of two parallel H clusters in W as a function of uniaxial strain from −2% (compressive) to +2% (tensile).

Figure 5B shows the binding energy of two parallel H platelets in W along the {001} plane as a function of their vertical distance. Apparently, there were strong interactions between two planar H clusters, which was closely related to their vertical distance. When the vertical distance was only only 0.5a₀ (∼2.17 Å), their binding energy could reach up to 1.96 eV, suggesting a strong attractive interaction of two parallel H platelets. Following this, the binding energy rapidly decreased with the increase in vertical distance (except at 1.5a₀, ∼5.47 Å), from 1.41 eV at 1a₀ to −1.29 eV at 1.5 a₀, and asymptotically converged to zero. Such strong attraction between two parallel H clusters should be understood by summing up the variation of H-H repulsive interactions, H-W interactions, and W-W interactions. The first two parts are described in detail in Section 3.1, while the third term originates from the total lattice distortion induced by H atoms and can be obtained by DFT calculations, i.e.,:

$E_b^{LD}={2∆E}^{LD}\left(onelayer\right)-{∆E}^{LD}\left(twolayer\right)(8)$

where ${∆E}^{LD}\left(onelayer\right)$ and ${∆E}^{LD}\left(twolayer\right)$ are the energy released during the lattice relaxation of W containing one and two “infinite” H platelets, respectively, after all H atoms are removed. As illustrated in Figure 5B, the predicted binding energies were in good agreement with DFT-calculated values, confirming the reliability of this model. It is interesting to note that, different from the results of a planar H cluster (see Figure 1C), the energy variation of the H-W interaction was negative at a distance of 0.5a₀, leading to a negative effect on the formation of multi-layer H clusters in W. In contrast, the variation of H-H and W-W interactions induced a positive binding energy at this distance, as seen in Figure 5C, and the latter was mainly responsible for the attractive interaction of two parallel H platelets. Therefore, the strong coupling between the stress fields induced by the H platelets provided a driving force for the formation of nearest neighboring di-layer H clusters in W. Similar results were also obtained at vertical distance of 1.5/2.5/3.5a₀. However, when the vertical distance was set as 1/2/3/6a₀, as seen in Figure 5C, the energy variation of H-W and W-W interaction was both positive and negative, promoting and suppressing the attractive interaction between parallel H platelets, respectively.

Next, we determined the influence of uniaxial strain on the interaction between two “infinite” H platelets in W. Since anisotropic strain breaks the symmetry of the lattice, two types of {001} planes were taken into account, the (001) and (010) planes. Figure 5D displays the average binding energy variation (eV/H) of two parallel planar H clusters in W as a function of uniaxial strain. Here, only the results with 1NN vertical distance (∼0.5a₀) were calculated, and the reference state (i.e., binding energy variation of ∼0 eV) was the two parallel H platelets in W under 0% strain (note that the 0% strain is different from the strain-free case). As seen in Figure 5D, the applied uniaxial strain had significant effects on the average binding energy of two parallel H clusters. For the case along the (001) plane, the average binding energy variation of two parallel H clusters monotonically increased with the increase (decrease) in tensile (compressive) strain, from −0.11 eV under −2% strain to 0.12 eV under +2% strain. Notably, the results of H clusters along the (010) plane had an opposite trend, which was a monotonic decrease with the decrease (increase) in tensile (compressive strain), from 0.04 eV under −2% strain to −0.05 eV under +2% strain. This was due to the Poisson effect and strain anisotropy. Furthermore, in comparison with W under 0% strain, a high average binding energy of two parallel H clusters could be obtained in strained systems, i.e., the larger the uniaxial strain, the higher the binding energy. These suggest that the applied anisotropic strain promotes the stability of multi-layer H clusters in W, almost independent of the signs of strain.

3.4 Influence of planar clusters on vacancy formation and H retention in W

Recent experiments suggest that over-saturated H retentions may remarkably reduce the threshold displacement energy in W (Gao et al., 2017; Gao et al., 2020), which in turn provides an extra trapping site to accommodate excessive H atoms. Accordingly, we further investigated the influence of planar H clusters on the formation energy of neighboring vacancy. As listed in Table 1, the vacancy formation energy in pure W was found to be 3.19 eV, in good agreement with previous DFT results (Huang et al., 2016). More importantly, the presence of H platelets dramatically reduced the formation energy of vacancy nearby, from 3.19 eV in pure W to to 0.47/−2.24 eV with a mono-/bi-layer H clusters (see the atomic configurations of these clusters in the Supplementary Data). Such significant reduction of formation energy indicated the promoting effect of H on the vacancy formation, and potentially contributed to the H-induced decrease of the threshold displacement energy in W. This should be attributed to the strong attraction interaction of the H-vacancy complex, which lowered the formation energy of vacancy in W. Similar results were also observed in previous studies (Kirchheim, 2007; Kirchheim, 2012). Besides H addition, applied uniaxial strain also affected the energetics of vacancy formation. As seen in Table 1, when +1% and −1% uniaxial strain was applied, the formation energy of a single vacancy slightly increased and decreased, respectively. This suggests that the tensile (compressive) strain facilitated (suppresses) the vacancy formation in W, which originated from the electronic states variation of W atoms induced by the strain, as analyzed and discussed in previous studies (Hossain and Marian, 2014; Li et al., 2020). However, in comparison with the influence of H platelets, that of uniaxial strain on vacancy formation energy was negligible (≤0.11 eV), regardless of whether it was with or without planar H clusters. Thus, the enhancing effect of H on the vacancy formation in W was almost independent to the applied uniaxial strain.

TABLE 1

TABLE 1. The influence of planar H clusters (i.e., mono-layer and bi-layer H clusters) on the formation energy (eV) of vacancy nearby in strain-free and strained W.

As mentioned above, planar H clusters may be formed in W due to positive binding energies, and applied uniaxial strain dramatically enhances their nucleation and growth. However, the stability of these H platelets at finite temperatures remains to be elucidated. In experiments, the de-trapping temperature of H in materials at various states is usually determined by the thermal desorption spectroscopy (TDS) measurement, in which the samples are heated to high temperatures until all H atoms are desorbed from the materials. Here, based on the DFT-calculated binding energies and Polanyi-Wigner equation, we examined the temperature of H desorption with maximum release rate (i.e., T_max) to estimate the stability of various H clusters in W. As demonstrated in previous studies (Heinola et al., 2010; Fernandez et al., 2015), the maximum desorption temperature can be derived from the following equation:

$\frac{E^{de-trap}}{k{T}_{\mathit{max}}^2}=\frac{\nu }{\beta }{e}^{\left(\frac{{-E}^{de-trap}}{k{T}_{\mathit{max}}}\right)}(9)$

where E^de-trap is the de-trapping energy, and equals the migration energy barrier of H in pure W (0.21 eV in strain-free condition and 0.22/0.24 eV under +1%/−1% strain) plus the sequential binding energy of H, i.e., $E^{de-trap}=E^{mig}+E^b$. To simplify the calculation, the attempt frequency was assumed to be a constant value of 10 THz, which is the typical lattice vibration frequency in W (Bakaev, et al., 2017) and of the same order of magnitude for H in vacancy (Fernandez, et al., 2015). Note that three different heating rates were selected, including 0.25 K/s, 1 K/s and 4 K/s, because TDS experiments are always conducted at different heating rates (Lee, et al., 2007; Shu, et al., 2007).

Figure 6 shows the maximum desorption temperature of H from “infinite” H platelets in W with and without uniaxial strain. For comparison, the release temperature of H in a mono-vacancy is also provided, and the corresponding binding energy between H and vacancy was calculated to be 1.17 eV. As seen in Figure 6, the temperature of maximum H release rate increased slightly with the increase in heat rate (∼30 K for an order of magnitude variation), which had been proposed in a previous experiment (Yajima et al., 2014). It is important to note that several experiments have been conducted to explore the desorption of H isotopes in low-energy plasma-loaded W (Ogorodnikova et al., 2003; Quastel et al., 2006; Poon et al., 2008). The analysis of TDS spectra has always shown the presence of three peaks, corresponding to the temperatures of 400–500 K, 550–650 K, and ∼750 K. The large variation of release peak temperature in experiments should be attributed to differing conditions (e.g., plasma energy, flux and fluence, sample, and heating ramp rate). But, generally, the first peak is explained by the trapping of H at dislocations and dislocation loops (Ogorodnikova et al., 2003), and the latter two rationalized by the desorption of H from vacancy and large vacancy clusters (Quastel et al., 2006; Poon et al., 2008). Our results suggested that the release temperature of H from H platelets in strain-free W is only 301–326 K, which is slightly higher than room temperature (∼300 K) and much lower than the experimental release peak. This is due to the fact that the plasma exposure is always conducted at temperatures of 300–320 K (or above) and the H atoms are already de-trapped during irradiation. However, when uniaxial strain was applied, the desorption temperature of H increased to 354–384 K under +1% strain and 384–419 K under −1% strain. These release temperatures are comparable with those of H in dislocation loops, and may contribute to the desorption of H at 400–500 K in TDS experiments (Ogorodnikova et al., 2003). Furthermore, as displayed in Figure 6, the desorption temperature of H from mono-vacancy (which may be induced by planar H clusters, see Table 1) reached up to 504–544 K, thus contributing to the release peak temperature of 550–600 K in TDS analysis.

FIGURE 6

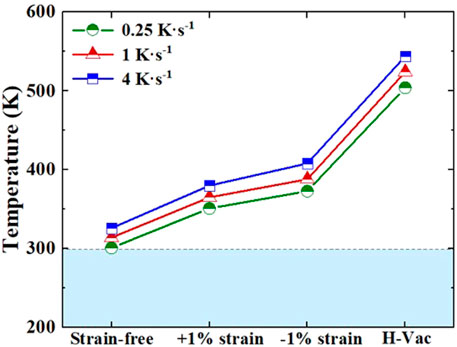
FIGURE 6. The calculated desorption temperature (with maximum release rate) of H from “infinite” H platelets in W with and without uniaxial strain. For comparison, the desorption temperature of H from mono-vacancy is also presented.

4 Conclusion

We systematically investigated the aggregation of interstitial H atoms in W and the influence of uniaxial strain using the first-principles method. It was found that when the number of H atoms was larger than 3, the sequential binding energy of planar H clusters along {001} planes was positive and generally increased with the increase in H numbers, indicating the trapping effect of planar H clusters on subsequent H atoms. Despite the attractive interaction between H atoms, the formation of planar H clusters in strain-free W was very difficult due to configurational entropy. For example, even at high H concentrations (0.1 at.%) at 300 K, the activation energy barrier for the nucleation of planar H clusters reached up to 5.08 eV, leading to an extremely low possibility of the nucleation of H clusters in strain-free W.

More importantly, the applied anisotropic strain significantly promoted the stability of planar H clusters in W. For example, the largest average binding energy of planar H clusters reach up to 0.53 eV/H and 0.34 eV/H in W under 1% compressive and tensile uniaxial strain, respectively, while in strain-free strained W, it was only .29 eV/H. Accordingly, the nucleation free energy change of H platelets was dramatically reduced by anisotropic strain, and thus enhanced the nucleation and growth of H clusters. Moreover, our calculations suggested that there were attractive interactions between two parallel H platelets at 1NN vertical distance, implying the formation of multi-layer H clusters in W, and their stability was also promoted by uniaxial strain, independent of the signs of strain. It is worthy to point out that the presence of planar H clusters remarkably reduced the formation energy of vacancies nearby, which increased the vacancy amount that may accommodate the excessive H atoms. Our calculations provide a potential mechanism to account for the super-saturation of H isotopes in W-PFMs and have broad implications for the evolution of H in materials.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

F-FM performed the numerical simulations, produced the figures, conducted analysis, and wrote the draft of the manuscript. Q-YR, Y-HL, H-BZ, and G-HL made substantial contributions to the analysis of the simulation results. Y-HL and H-BZ proposed the idea, revised it critically for important intellectual content, and approved the final version to be published. All authors contributed to the article and approved the submitted version.

Funding

This research is financially supported by the National MCF Energy R&D Program with Grant No. 2018YFE0308103, the National Natural Science Foundation of China with Grant Nos. 11905135, 12075022, and 12192281.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.1122135/full#supplementary-material

References

Alimov, V. K., Roth, J., and Mayer, M. (2005). Depth distribution of deuterium in single- and polycrystalline tungsten up to depths of several micrometers. J. Nucl. Mat. 337, 619–623. doi:10.1016/j.jnucmat.2004.10.082

CrossRef Full Text | Google Scholar

Alimov, V. K., Tyburska-Puschel, B., Lindig, S., Hatano, Y., Balden, M., Roth, J., et al. (2012). Temperature dependence of surface morphology and deuterium retention in polycrystalline ITER-grade tungsten exposed to low-energy, high-flux D plasma. J. Nucl. Mat. 420, 519–524. doi:10.1016/j.jnucmat.2011.11.003

CrossRef Full Text | Google Scholar

Bakaev, A., Grigorev, P., Terentyev, D., Bakaeva, A., Zhurkin, E., and Mastrikov, Y. A. (2017). Trapping of hydrogen and helium at dislocations in tungsten: An ab initio study. Nucl. Fusion 57, 126040. doi:10.1088/1741-4326/aa7965

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Chen, W. Q., Wang, X. Y., Li, K. L., Wang, Y., Morgan, T., Xu, B., et al. (2020). Nucleation mechanism of intra-granular blisters in tungsten exposed to hydrogen plasma. Scr. Mat. 187, 243–249. doi:10.1016/j.scriptamat.2020.06.024

CrossRef Full Text | Google Scholar

Chen, Y. S., Lu, H. Z., Liang, J. T., Rosenthal, A., Liu, H., Sneddon, G., et al. (2020). Observation of hydrogen trapping at dislocations, grain boundaries, and precipitates. Science 367, 171–175. doi:10.1126/science.aaz0122

PubMed Abstract | CrossRef Full Text | Google Scholar

Conrad and, E. (1996). Handbook of surface science. Elsevier 3, 271–360. doi:10.1016/S1573-4331(96)80012-6

CrossRef Full Text | Google Scholar

De Backer, A., Mason, D. R., Domain, C., Nguyen-Manh, D., Marinica, M. C., Ventelon, L., et al. (2018). Multiscale modelling of the interaction of hydrogen with interstitial defects and dislocations in BCC tungsten. Nucl. Fusion 58, 016006. doi:10.1088/1741-4326/aa8e0c

CrossRef Full Text | Google Scholar

Fernandez, N., Ferro, Y., and Kato, D. (2015). Hydrogen diffusion and vacancies formation in tungsten: Density Functional Theory calculations and statistical models. Acta Mater 94, 307–318. doi:10.1016/j.actamat.2015.04.052

CrossRef Full Text | Google Scholar

Frauenfelder, R. (1969). Solution and diffusion of hydrogen in tungsten. J. Vac. Sci. Technol. 6, 388–397. doi:10.1116/1.1492699

CrossRef Full Text | Google Scholar

Gao, L., Jacob, W., von Toussaint, U., Manhard, A., Balden, M., Schmid, K., et al. (2017). Deuterium supersaturation in low-energy plasma-loaded tungsten surfaces. Nucl. Fusion 57, 016026. doi:10.1088/0029-5515/57/1/016026

CrossRef Full Text | Google Scholar

Gao, L., Wilde, M., Manhard, A., von Toussaint, U., and Jacob, W. (2020). Hydrogen atom-ion synergy in surface lattice modification at sub-threshold energy. Acta Mater 201, 55–62. doi:10.1016/j.actamat.2020.09.065

CrossRef Full Text | Google Scholar

Gonzalez, C., Panizo-Laiz, M., Gordillo, N., Guerrero, C., Tejado, E., Munnik, F., et al. (2015). H trapping and mobility in nanostructured tungsten grain boundaries: A combined experimental and theoretical approach. Nucl. Fusion 55, 113009. doi:10.1088/0029-5515/55/11/113009

CrossRef Full Text | Google Scholar

Heinola, K., Ahlgren, T., Nordlund, K., and Keinonen, J. (2010). Hydrogen interaction with point defects in tungsten. Phys. Rev. B 82, 094102. doi:10.1103/PhysRevB.82.094102

CrossRef Full Text | Google Scholar

Henriksson, K. O. E., Nordlund, K., Krasheninnikov, A., and Keinonen, J. (2005). Difference in formation of hydrogen and helium clusters in tungsten. Appl. Phys.Lett. 87, 163113. doi:10.1063/1.2103390

CrossRef Full Text | Google Scholar

Hodille, E. A., Fernandez, N., Piazza, Z. A., Ajmalghan, M., and Ferro, Y. (2018). Hydrogen supersaturated layers in H/D plasma-loaded tungsten: A global model based on thermodynamics, kinetics and density functional theory data. Phys. Rev. Mat. 2, 093802. doi:10.1103/PhysRevMaterials.2.093802

CrossRef Full Text | Google Scholar

Hossain, M. Z., and Marian, J. (2014). Stress-dependent solute energetics in W-Re alloys from first-principles calculations. Acta Mater 80, 107–117. doi:10.1016/j.actamat.2014.07.028

CrossRef Full Text | Google Scholar

Hou, J., Kong, X. S., Liu, C. S., and Song, J. (2020). Hydrogen clustering in bcc metals: Atomic origin and strong stress anisotropy. Acta Mater 201, 23–35. doi:10.1016/j.actamat.2020.09.048

CrossRef Full Text | Google Scholar

Hou, J., Kong, X. S., Sun, J. J., You, Y. W., Wu, X., Liu, C. S., et al. (2018). Hydrogen bubble nucleation by self-clustering: Density functional theory and statistical model studies using tungsten as a model system. Nucl. Fusion 58, 096021. doi:10.1088/1741-4326/aacdb6

CrossRef Full Text | Google Scholar

Hou, J., Kong, X. S., Wu, X. B., Song, J., and Liu, C. S. (2019). Predictive model of hydrogen trapping and bubbling in nanovoids in bcc metals. Nat. Mat. 18, 833–839. doi:10.1038/s41563-019-0422-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, G. Y., Juslin, N., and Wirth, B. D. (2016). First-principles study of vacancy, interstitial, noble gas atom interstitial and vacancy clusters in bcc-W. Comput. Mat. Sci. 123, 121–130. doi:10.1016/j.commatsci.2016.06.022

CrossRef Full Text | Google Scholar

Jia, Y. Z., Liu, W., Xu, B., Qu, S., Shi, L., and Morgan, T. (2017). Subsurface deuterium bubble formation in W due to low-energy high flux deuterium plasma exposure. Nucl. Fusion 57, 034003. doi:10.1088/1741-4326/57/3/034003

CrossRef Full Text | Google Scholar

Kato, D., Iwakiri, H., Watanabe, Y., Morishita, K., and Muroga, T. (2015). Super-saturated hydrogen effects on radiation damages in tungsten under the high-flux divertor plasma irradiation. Nucl. Fusion 55, 083019. doi:10.1088/0029-5515/55/8/083019

CrossRef Full Text | Google Scholar

Kirchheim, R. (2007). Reducing grain boundary, dislocation line and vacancy formation energies by solute segregation. I. Theoretical background. Acta Mater 55, 5129–5138. doi:10.1016/j.actamat.2007.05.047

CrossRef Full Text | Google Scholar

Kirchheim, R. (2012). Solid solution softening and hardening by mobile solute atoms with special focus on hydrogen. Scr. Mat. 67, 767–770. doi:10.1016/j.scriptamat.2012.07.022

CrossRef Full Text | Google Scholar

Lee, H. T., Haasz, A. A., Davis, J. W., Macaulay-Newcombe, R., Whyte, D., and Wright, G. (2007). Hydrogen and helium trapping in tungsten under simultaneous irradiations. J. Nucl. Mat. 363, 898–903. doi:10.1016/j.jnucmat.2007.01.111

CrossRef Full Text | Google Scholar

Li, Y. H., Zhou, H. B., Jin, S., Zhang, Y., Deng, H., and Lu, G. H. (2017). Behaviors of transmutation elements Re and Os and their effects on energetics and clustering of vacancy and self-interstitial atoms in W. Nucl. Fusion 57, 046006. doi:10.1088/1741-4326/aa5893

CrossRef Full Text | Google Scholar

Li, Z.-Z., Li, Y.-H., Ren, Q.-Y., Ma, F. F., Yue, F. Y., Zhou, H. B., et al. (2020). Strain dependence of energetics and kinetics of vacancy in tungsten. Materials 13, 3375. doi:10.3390/ma13153375

PubMed Abstract | CrossRef Full Text | Google Scholar

Loarte, A., Lipschultz, B., Kukushkin, A. S., Matthews, G., Stangeby, P., Asakura, N., et al. (2007). Chapter 4: Power and particle control. Nucl. Fusion 47, S203–S263. doi:10.1088/0029-5515/47/6/s04

CrossRef Full Text | Google Scholar

Middleburgh, S. C., Voskoboinikov, R. E., Guenette, M. C., and Riley, D. P. (2014). Hydrogen induced vacancy formation in tungsten. J. Nucl. Mat. 448, 270–275. doi:10.1016/j.jnucmat.2014.02.014

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Noda, N., Philipps, V., and Neu, R. (1997). A review of recent experiments on W and high Z materials as plasma-facing components in magnetic fusion devices. J. Nucl. Mat. 241-243, 227–243. doi:10.1016/S0022-3115(97)80042-6

CrossRef Full Text | Google Scholar

Oates, W. A., and McLellan, R. B. (1972). The solubility of hydrogen in molybdenum. Scr. Metal. 6, 349–352. doi:10.1016/0036-9748(72)90201-3

CrossRef Full Text | Google Scholar

Ogorodnikova, O. V., Roth, J., and Mayer, M. (2003). Deuterium retention in tungsten in dependence of the surface conditions. J. Nucl. Mat. 313, 469–477. doi:10.1016/S0022-3115(02)01375-2

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Poon, M., Haasz, A. A., and Davis, J. W. (2008). Modelling deuterium release during thermal desorption of D+-irradiated tungsten. J. Nucl. Mat. 374, 390–402. doi:10.1016/j.jnucmat.2007.09.028

CrossRef Full Text | Google Scholar

Quastel, A. D., Davis, J. W., Haasz, A. A., and Macaulay-Newcombe, R. G. (2006). Effect of post-D+-irradiation time delay and pre-TDS heating on D retention in single crystal tungsten. J. Nucl. Mat. 359, 8–16. doi:10.1016/j.jnucmat.2006.07.012

CrossRef Full Text | Google Scholar

Ren, Q. Y., Li, Y. H., Zhou, H. B., Li, Z. Z., Cheng, L., and Lu, G. H. (2019). Characterization of the energetics and configurations of hydrogen in vacancy clusters in tungsten. Nucl. Fusion 59, 106032. doi:10.1088/1741-4326/ab36a4

CrossRef Full Text | Google Scholar

Roth, J., Tsitrone, E., Loarte, A., Loarer, T., Counsell, G., Neu, R., et al. (2009). Recent analysis of key plasma wall interactions issues for ITER. J. Nucl. Mat. 390-91, 1–9. doi:10.1016/j.jnucmat.2009.01.037

CrossRef Full Text | Google Scholar

Seko, A., Nishitani, S. R., Tanaka, I., Adachi, H., and Fujita, E. F. (2004). First-principles calculation on free energy of precipitate nucleation. CALPHAD 28, 173–176. doi:10.1016/j.calphad.2004.07.003

CrossRef Full Text | Google Scholar

Shu, W. M., Kawasuso, A., and Yamanishi, T. (2009). Recent findings on blistering and deuterium retention in tungsten exposed to high-fluence deuterium plasma. J. Nucl. Mat. 386-388, 356–359. doi:10.1016/j.jnucmat.2008.12.129

CrossRef Full Text | Google Scholar

Shu, W. M., Wakai, E., and Yamanishi, T. (2007). Blister bursting and deuterium bursting release from tungsten exposed to high fluences of high flux and low energy deuterium plasma. Nucl. Fusion 47, 201–209. doi:10.1088/0029-5515/47/3/006

CrossRef Full Text | Google Scholar

Smirnov, R. D., and Krasheninnikov, S. I. (2018). Stress-induced hydrogen self-trapping in tungsten. Nucl. Fusion 58, 126016. doi:10.1088/1741-4326/aae2c7

CrossRef Full Text | Google Scholar

Terentyev, D., De Temmerman, G., Minov, B., Zayachuk, Y., Lambrinou, K., Morgan, T., et al. (2015a). Synergy of plastic deformation and gas retention in tungsten. Nucl. Fusion 55, 013007. doi:10.1088/0029-5515/55/1/013007

CrossRef Full Text | Google Scholar

Terentyev, D., De Temmerman, G., Morgan, T. W., Zayachuk, Y., Lambrinou, K., Minov, B., et al. (2015b). Effect of plastic deformation on deuterium retention and release in tungsten. J. Appl. Phys. 117, 083302. doi:10.1063/1.4913478

CrossRef Full Text | Google Scholar

Terentyev, D., Dubinko, V., Bakaev, A., Zayachuk, Y., Van Renterghem, W., and Grigorev, P. (2014). Dislocations mediate hydrogen retention in tungsten. Nucl. Fusion 54, 042004. doi:10.1088/0029-5515/54/4/042004

CrossRef Full Text | Google Scholar

Tokunaga, K., Baldwin, M. J., Doerner, R. P., Noda, N., Kubota, Y., Yoshida, N., et al. (2005). Blister formation and deuterium retention on tungsten exposed to low energy and high flux deuterium plasma. J. Nucl. Mat. 337, 887–891. doi:10.1016/j.jnucmat.2004.10.137

CrossRef Full Text | Google Scholar

Wang, J. W., Shao, B., Shan, D. B., Guo, B., and Zong, Y. Y. (2020). Effect of strain on solution energy of hydrogen in alpha-zirconium from first-principle calculations. Int. J. Hydrogen Energy 45, 18001–18009. doi:10.1016/j.ijhydene.2020.04.244

CrossRef Full Text | Google Scholar

Yajima, M., Yoshida, N., Kajita, S., Tokitani, M., Baba, T., and Ohno, N. (2014). In situ observation of structural change of nanostructured tungsten during annealing. J. Nucl. Mat. 449, 9–14. doi:10.1016/j.jnucmat.2014.02.027

CrossRef Full Text | Google Scholar

Yang, K. J., Liu, Y. L., Shao, P., Zhang, X., Han, Q. F., and Ma, Y. (2020). First-principles simulation of h interacting with transition elements in molybdenum for nuclear material application. J. Nucl. Mat. 541, 152437. doi:10.1016/j.jnucmat.2020.152437

CrossRef Full Text | Google Scholar

Yuge, K., Seko, A., Tanaka, I., and Nishitani, S. R. (2005). First-principles study of the effect of lattice vibrations on Cu nucleation free energy in Fe-Cu alloys. Phys. Rev. B 72, 174201. doi:10.1103/PhysRevB.72.174201

CrossRef Full Text | Google Scholar

Zhang, X. X., Qiao, L., Zhang, H., Li, Y. H., Wang, P., and Liu, C. S. (2021). Surface blistering and deuterium retention behaviors in pure and ZrC-doped tungsten exposed to deuterium plasma. Nucl. Fusion 61, 046026. doi:10.1088/1741-4326/abdfda

CrossRef Full Text | Google Scholar

Zhou, H.-B., Jin, S., Zhang, Y., Lu, G.-H., and Liu, F. (2012). Anisotropic strain enhanced hydrogen solubility in bcc metals: The independence on the sign of strain. Phys. Rev. Lett. 109, 135502. doi:10.1103/PhysRevLett.109.135502

PubMed Abstract | CrossRef Full Text | Google Scholar

Zibrov, M., Balden, M., Morgan, T. W., and Mayer, M. (2017). Deuterium trapping and surface modification of polycrystalline tungsten exposed to a high-flux plasma at high fluences. Nucl. Fusion 57, 046004. doi:10.1088/1741-4326/aa5898

CrossRef Full Text | Google Scholar