Frequency-diverse MIMO metasurface antenna for computational imaging with aperture rotation technique

Metasurface antennas have been proposed for computational imaging (CI) systems, which can reconstruct images without using mechanical scanning or large antenna arrays. In a CI system based on metasurface antennas, a variety of different radiation fields, which can be applied to sample the objects, are generated by exciting different frequency points in broadband. According to the compressed sensing theory, the imaging performance of the system is mainly limited by frequency-diversity radiation modes. In general, it is difficult to achieve rich radiation modes; therefore, a special design of metasurface aperture is required. In this paper, we propose a frequency-diversity MIMO metasurface antenna that consists of 2 × 2 sub-apertures with randomly distributed surface impedance. By employing the aperture rotation technique (ART) which rotates the MIMO metasurface antenna around the panel axis, the pseudo-randomness of the radiation fields is utilized. The diversity of the radiation field is improved on the premise of ensuring the relatively low complexity of the system. The ART significantly improves the measurement richness at the cost of increasing the measurement time. The performance of the proposed method is evaluated through simulations and experiments, suggesting that the proposed 2 × 2 MIMO metasurface antenna and the ART are effective to reconstruct high-quality images.

1 Introduction

In recent years, microwave imaging system has gradually gained the attention of researchers. Compared with optical imaging systems, microwave imaging systems work in the microwave frequency band and are less affected by the weather. In addition, microwaves can penetrate some opaque objects (Pastorino, 2010), such as clothes, ceramics, and other objects. Therefore, microwave imaging systems are gradually applied in many scenarios, including security, automatic driving, safety inspection, medical detection, and other fields (Sheen et al., 2001; Ahmed et al., 2012; Zhou et al., 2019). Generally, there are two types of active imaging aperture, including real aperture (Howard, 1975) and synthetic aperture (SA) (Cetin and Karl, 2001; Zhang et al., 2009; Zhao et al., 2014). Imaging radars using SA include synthetic aperture radar (SAR) and Inverse synthetic aperture radar (ISAR). SAR uses moving targets as a vehicle to image stationary targets on the ground, while ISAR does the opposite. Real aperture imaging radar usually requires a large array of antennas to increase the aperture of the system, leading to high complexity, large size, high cost, and limited applications.

In the last decade, a new method called compression sensing imaging has emerged in the field of optical imaging. The microwave metamaterial aperture imaging system uses the metamaterial aperture to generate rich radiation fields to illuminate the forward-looking target, which can also use the optimized compressed sensing (CS) algorithm for inversion calculations to reconstruct the two-dimensional sparse target in the scene. Since the image is restored through calculation, this new imaging technology is also called computational imaging (Mait et al., 2018). Metamaterials and metasurfaces can be applied because they are artificial electromagnetic structures formed by the periodic arrangement of subwavelength elements (Imani et al., 2020), which can flexibly adjust the amplitude, phase, and polarization mode of electromagnetic waves (Pfeiffer and Grbic, 2013; Chen et al., 2020; Li et al., 2022a; Li et al., 2022b; Li et al., 2022c). In (Hunt et al., 2013), a metamaterial aperture for microwave computational imaging was proposed. With the frequency domain dispersion characteristics of metamaterial structure, microwave computational imaging could be realized at the physical layer by taking each frequency point as a measurement mode in broadband. In (Yurduseven et al., 2016a), the design method of an aperiodic cavity metamaterial antenna was adopted to increase the degree of freedom of the imaging system. In (Imani et al., 2016; Marks et al., 2017; Fromenteze1 et al., 2015; Yurduseven et al., 2016b), the metamaterial aperture of computational imaging was realized by using frequency diversity characteristic elements. In (Sleasman et al., 2015; Pulido-Mancera et al., 2016; Wu et al., 2016; Diebold et al., 2017; Han et al., 2020), a dynamic metasurface antenna (DMA) is designed for a microwave imaging system to alleviate the demand for UWB antenna and obtain greater freedom. Different from fixed structure antenna with frequency diversity characteristic (FDMA), each component of DMA is loaded with an independently regulated PIN diode to form a dynamic imaging aperture, which increases the system complexity and hardware cost. In the low-complexity and low-cost microwave CI systems, researchers have been pursuing to obtain the optimal imaging effect with the least imaging time. Based on the current research status and limitations, the research work of this paper is carried out.

By applying the aperture rotation technique (ART) in a passive frequency-diverse 2 × 2 MIMO metasurface antenna, we achieve high-quality imaging reconstruction, approaching the resolution of about one working wavelength. Compared with the existing literature on metasurface antenna for CI, the proposed MIMO metasurface antenna possesses a low profile, low cost, and simple system configuration. The rest of this article is structured as follows. First, the frequency-diverse holographic metasurface (FDHM) antenna which is adopted to build the 2 × 2 MIMO is introduced, fabricated, and measured. The mathematical description of the CI system based on the MIMO metasurface antenna is then presented. Next, the degree of freedom of the CI system and the ART are discussed to reduce the mutual coherence. Finally, simulation and experiment are carried out to verify the performance of the designed system.

2 System components and principles of the CI system

In this section, we mainly introduce the FDHM antenna and the operation principle of microwave CI using the 2 × 2 MIMO metasurface antenna.

2.1 The design of FDHM

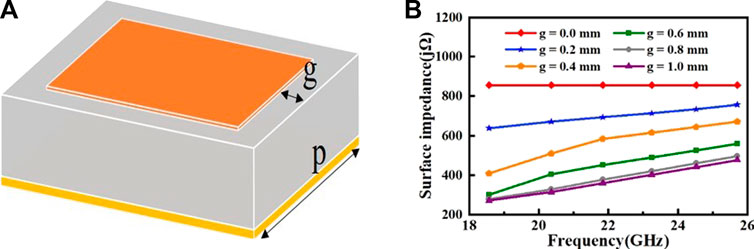
The FDHM antenna and the corresponding CI system were numerically investigated in our previous work (Han et al., 2021). The FDHM antenna is designed with frequency diversity characteristics. Similar to the concept of frequency diversity, polarization diversity in optics is also an interesting direction (Hu et al., 2021). The structure of the metasurface element is shown in Figure 1A. The top layer of the element is a square patch that is printed on a Rogers 3006 substrate backed by a ground plane. The gap g is modified in the operating band to change the surface impedance of the element. The surface impedance of the element can be calculated as

$Z=j{Z}_0\sqrt{{\left(\frac{\phi c}{\omega p}\right)}^2-1},(1)$

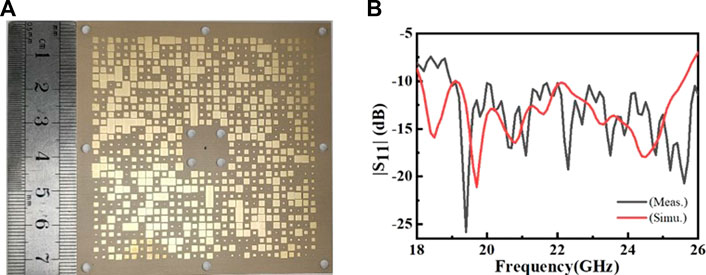
where Z₀ is the impedance of the free space wave, p = 2.2 mm is the period of elements, φ is the phase difference of elements, ω is the angular frequency, and c is the speed of light. The relationship between surface impedance and frequency corresponding to different g values is shown in Figure 1B. As can be seen, for a fixed gap g, the surface impedance of the element changes along with the frequency. On the other hand, for a fixed frequency, the gap g can also modulate the surface impedance of the element. Therefore, by randomly designing the gap g for each element, one could realize a frequency-diverse metasurface antenna, which has been validated through full-wave simulation (Han et al., 2021). The fabricated FDHM antenna used in this paper is shown in Figure 2A. The panel size of the FDHM is 70 mm × 70 mm, operating from 18 GHz to 26 GHz. The gap g of each element is randomly generated within the working frequency band. A monopole antenna is designed at the center to excite the surface waves. When the antenna is working, various radiation patterns at different frequencies are formed. The measured |S₁₁| is in accord with the simulated one, as plotted in Figure 2B, suggesting that the proposed FDHM antenna can operate in broadband from 18 to 26 GHz.

FIGURE 1

FIGURE 1. (A) Geometrical structure. (B) Surface impedance versus frequency for different gap g.

FIGURE 2

FIGURE 2. (A) Fabricated FDHM antenna. (B) Simulated and measured |S₁₁|.

The frequency-diverse 2-D pattern of the FDHM antenna is measured by planar near-field scanning in a microwave anechoic chamber. The measurements range from 18 to 26 GHz, with a frequency step of 100 MHz. The scanning grid along the horizontal and vertical directions is 6 mm by 6 mm. The center of the scanning plane is aligned with the center of the entire array at a distance of 200 mm. The patterns at 18, 20, 21, 22, 24z, and 26 GHz are shown in Figure 3A. To more clearly see the correlation between different frequency patterns, correlation analysis was conducted on the above 81 groups of patterns. The correlation results are shown in Figure 3B. From the results, it can be clearly seen that two-dimensional patterns of different frequencies differ greatly from each other, which is exactly the requirement of the CI system (Zhao et al., 2020; Gollub et al., 2017).

FIGURE 3

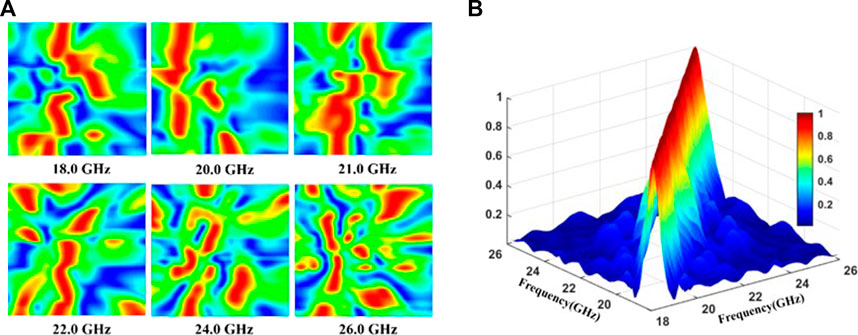
FIGURE 3. (A) Measured 2-D patterns of FDHM antenna at different frequencies. (B) 2-D pattern correlation between different frequencies.

2.2 Mathematical model of the CI system

The mathematical model of CI imaging is briefly introduced. Consider a 2 × 2 MIMO metasurface antenna using the fabricated FDHM antenna as the sub-aperture. Among the four sub-apertures, two FDHM antennas act as transmitters while the other two antennas act as receivers. According to the first Born approximation condition, the mathematical model of the 2 × 2 MIMO metasurface antenna can be expressed as

$\mathbf{g}=\mathbf{H}\mathbf{f}+\mathbf{n},(2)$

where g is a column vector of echo signals that are radiated from the two transmitters and acquired by the two receivers, H is the measurement matrix, f is the objects column vector to be imaged, and n represents the noise vector. Because the 2 × 2 MIMO metasurface antenna is utilized, for each frequency measurement, we could obtain four equations in Eq. 2, which are

$g_m^{i,j}={\displaystyle \sum }_{n=1}^N{E}_m^i\left({\overrightarrow{r}}_n\right)·E_m^j\left({\overrightarrow{r}}_n\right)·f_n,i,j=\mathrm{1,2},(3)$

where m denotes the frequency domain sensing index, i denotes the transmitter, j denotes the receiver, n denotes the pixel of the scene, $E_m^i\left({\overrightarrow{r}}_n\right)$ and $E_m^j\left({\overrightarrow{r}}_n\right)$ denote the transmitted and received electric fields. Actually, we could drop the i and j indices of Eq. 3 because one can readily swap the row vectors in a linear equation formulated by Eq. 2. Thus, the element in the measurement matrix can be denoted as $H_{m,n}^T\cdot H_{m,n}^R$, which is the multiplication of the transmitted and received patterns. We note that these patterns had been measured in an anechoic chamber as mentioned before.

It is assumed that the total number of frequency measurement modes is M and the scene is discrete with N pixels. Generally, the number of measurement modes is much smaller than scene pixels (M < N), which means Eq. 2 is a sick problem and cannot be directly analyzed. Based on the CS theory, we can solve this problem when the object is a compressible image with randomly distributed patterns. Researchers have proposed many algorithms from different angles to deal with Eq. 2 defined in the CS reconstruction problem (Bioucas-Dias and Figueiredo, 2007; Zhu and Bamler, 2012; Rao et al., 2013), and the imaging system in this paper is solved by TwIST algorithm.

3 Evaluation of H and system degree of freedom

In the above mathematical model of the CI system, the measurement matrix H is usually regarded as the sensor matrix in the CS theory. The CS theory indicates that when the sensor matrix meets certain constraints, the sparse signal can be well reconstructed from the low-dimensional measurement. In this section, we introduce the evaluation index of H and discuss the ART to increase the degree of freedom of the CI system based on the proposed 2 × 2 MIMO metasurface antenna.

3.1 Evaluation index of H

The complex matrix H in the imaging system is not a full-rank matrix, so it is necessary to evaluate the performance of matrix H. As presented above, the designed FDHM antenna can generate multiple distinct radiation patterns in the frequency domain. It is important to evaluate the correlation between various radiation patterns. In this paper, we use µ (H) to describe the mutual interference characteristics of the measurement matrix H, which can be defined as

$\mu \left(\mathbf{H}\right)=\frac{{\sum }_{m\ne n}{\left|{\stackrel{\sim }{H}}_{m,n}^{\mathrm{T}}\cdot {\stackrel{\sim }{H}}_{m,n}\right|}^2}{M\left(M-1\right)},(4)$

where $\stackrel{\sim }{H}$ is the sensing matrix with all columns normalized and T denotes the transpose symbol (Duarte-Carvajalino and Sapiro, 2009). The smaller the coherence is, the better imaging reconstruction becomes. At the same time, the singular value analysis of the matrix is introduced to characterize the coherence of the measurement modes.

3.2 The improvement of degree of freedom system

As mentioned above, the measurement matrix H in this paper is constructed by the discrete sampling of radiation field patterns of various frequency points in broadband. Generally speaking, the imaging performance depends on the orthogonal measurement modes, and this conclusion can be obtained from Eq. 3. It is worth noting that the orthogonal characteristics between the measurement matrix of the FDHM antenna are essentially the pseudo-random characteristics of the radiation modes in the target field, namely the dispersion characteristics. FDHM antenna has the characteristic of frequency diversity, and the number of different measurement modes in the target scene is determined by the system bandwidth. If the frequency sampling interval is dense, it will lead to different degrees of radiation mode overlap, increase data redundancy, and weaken the performance of the system. This characteristic also limits the performance of the frequency diversity antenna imaging system.

In this paper, ART is adopted, which can obtain more radiation modes and significantly improve the imaging performance of the system. In this section, the ART of the MIMO system is mainly discussed. The ART increases the system degree of freedom from two aspects: 1) The spatial position of multiple aperture antennas is different; 2) as the aperture antenna rotates around its panel axis, the field pattern in the target scene changes. In theory, the aperture antenna can be rotated around the axis at any angle, and a new measurement matrix can be obtained with each rotation while maintaining a low correlation with each other. For the imaging scene, the radiation pattern of the target scene changes with the rotation operation. The designed antenna has the characteristic of polarization insensitivity, which is conducive to the MIMO aperture rotation technology. According to the method, the number of measurement modes can be effectively increased. Considering the complexity of calculation, only four special angles 0°, 90°, 180°, and 270° are discussed in this paper. The rotation diagram of the 2 × 2 MIMO metasurface antenna integrating four FDHM antennas using ART is presented, including the states of 0°, 90°, 180°, and 270° as shown in Figures 4A–D. The two transmitters are labeled as Tx1 and Tx2, while the two receivers are labeled as Rx1 and Rx2.

FIGURE 4

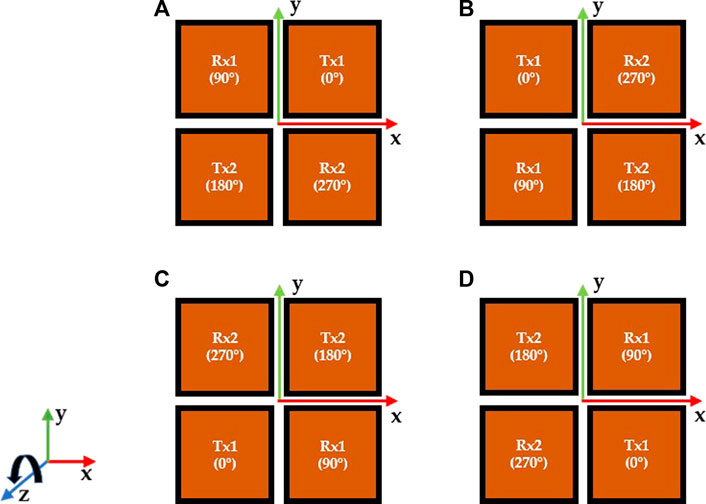
FIGURE 4. Rotation diagram of the 2 × 2 MIMO metasurface antenna integrating four FDHM antennas with rotation angles of (A) 0°, (B) 90°, (C) 180°, and (D) 270°.

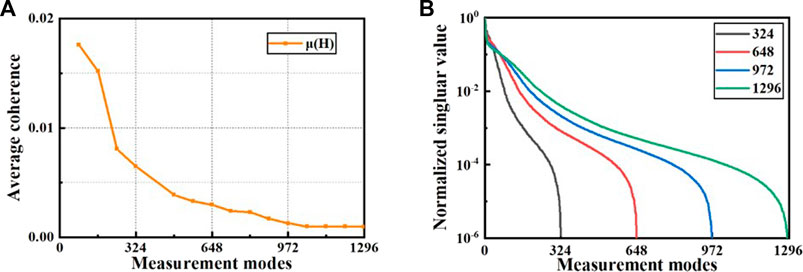
The correlation of the measurement matrix generated by different rotation operations is shown in Figure 5. During this process, the whole aperture is rotated at 0°, 90°, 180°, and 270° four modes. Note that the premise of this process is that the four antennas in Figure 4 rotate 0°, 90°, 180° and 270° around their panel axes respectively. It can be seen from Figure 5A that the average correlation value µ (H) gradually decreases with the rotation operation. The singular value curve flattens with the increase of measurement modes in Figure 5B, which further verifies the effectiveness of our proposed method. We found that this method can reduce the correlation values, produce more efficient radiation patterns, and also greatly increase the number of measurement patterns. The imaging performance of the proposed method will be verified in the next section.

FIGURE 5

FIGURE 5. (A) µ (H) of the measurement modes. (B) The singular value of the measurement modes.

4 Experiment and result of imaging system

In this section, we demonstrate the imaging performance of the proposed MIMO sub-aperture rotation method through an imaging experiment. The experimental photo of the imaging system is shown in Figure 6A. The CI system has four antennas, as aforementioned, two transmitters (Tx1 and Tx2) and two receivers (Rx1 and Rx2). The four ports of the four FDHM antennas are connected to a four-channel vector network analyzer (VNA). Therefore, we can obtain the acquired signals from the four-port S-parameters. The imaging scene is discrete into 61 × 61 = 3,721 square pixels and the size of each pixel is 6 mm × 6 mm. Three copper sheets with different sizes are selected as the object for imaging reconstruction, as shown in Figure 6B. The distance between the target object and the signal acquisition structure is 200 mm.

FIGURE 6

FIGURE 6. (A) Antenna with four-channel VNA. (B) Antenna with metallic objects.

The experimental method is based on the MIMO metasurface antenna with ART in Section 3. The imaging results are shown in Figure 7. The result in Figure 7A is solved by analyzing the measurement matrix without the rotation method, however, the target object cannot be distinguished. Note that, in this case, only 81 × 4 = 324 sampling modes are used. Accordingly, compared with Figure 7A, as shown in Figure 7B, the quality of the reconstructed image is much better with the measurement matrix analysis solution of the MIMO rotation method. In this case, the total available sensing modes are 81 × 4 × 4 = 1,296. From the comparison, it can be readily found that by applying the ART the proposed MIMO metasurface antenna could achieve high-quality imaging reconstruction with very low-cost hardware.

FIGURE 7

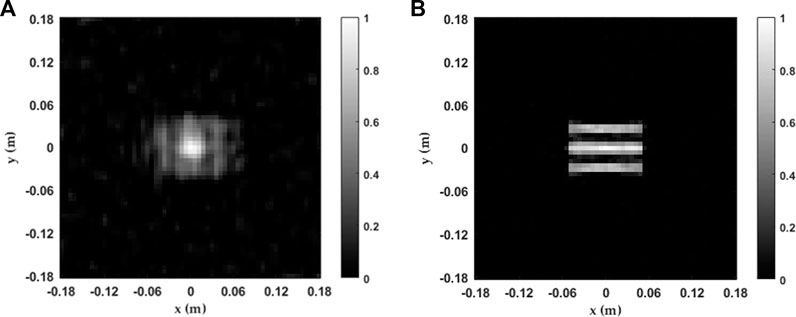
FIGURE 7. (A) Imaging reconstruction result without rotation synthesis. (B) Imaging reconstruction result with rotation synthesis.

Mean square error (MSE) was used to evaluate the imaging recovery performance (Han et al., 2021), which is defined as:

$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{N}{‖{\mathbf{f}}^{meas}-{\mathbf{f}}^{sta}‖}_2^2,(5)$

where ${‖\cdot ‖}_2^2$ denotes the l²-norm operator, ${\mathbf{f}}^{meas}$ represents the scattering characteristic value obtained by measurement and ${\mathbf{f}}^{sta}$ represents the comparison standard. The MSE is used to evaluate the image quality with ART and without ART. The calculated MSEs with ART and without ART are .003 and .02 respectively. The results show that the imaging performance of the ART system is excellent.

5 Conclusion

In this paper, we propose an aperture rotation synthesis method for the MIMO metasurface antenna to enhance the imaging performance of the CI system, which takes advantage of the diversity of radiation fields in the space and frequency domain. Through the MIMO structure and ART, one can obtain more effective measurement modes for sensing the objects, which can enhance the imaging performance while spending more time on the rotating antenna. In conclusion, the proposed method can effectively improve imaging performance while keeping the relatively low complexity of the system.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

JH and LL proposed the idea. JH, TW, and XM conceived and performed the metasurface antenna fabtication and built the imaging system. HL guided the data post-process. All authors analyzed and discussed the results.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant Nos 62288101, 62001342, in part by the National Key Research and Development Program of China under Grant No. 2021YFA1401001, in part by the Joint Foundation of Key Laboratory of Shanghai Jiao Tong University-Xidian University, Ministry of Education under Grant No. LHJJ/2020-02, in part by the China Postdoctoral Science Foundation under Grant No. 2021M692496.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, S. S., Schiessl, A., Gumbmann, F., Tiebout, M., Methfessel, S., and Schmidt, L. (2012). Advanced microwave imaging. IEEE Microw. Mag. 13 (6), 26–43. doi:10.1109/MMM.2012.2205772

CrossRef Full Text | Google Scholar

Bioucas-Dias, J. M., and Figueiredo, M. A. T. (2007). A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 16 (12), 2992–3004. doi:10.1109/TIP.2007.909319

PubMed Abstract | CrossRef Full Text | Google Scholar

Cetin, M., and Karl, W. C. (2001). Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization. IEEE Trans. Image Process. 10 (4), 623–631. doi:10.1109/83.913596

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Xue, W., Shi, H., Yi, J., and Sha, W. E. I. (2020). Orbital angular momentum multiplexing in highly reverberant environments. IEEE Microw. Wirel. Components Lett. 30 (1), 112–115. doi:10.1109/LMWC.2019.2952975

CrossRef Full Text | Google Scholar

Diebold, A. V., Pulido-Mancera, L., Sleasman, T., Boyarsky, M., Imani, M. F., and Smith, D. R. (2017). Gen. range Migr. algorithm synthetic aperture radar image Reconstr. metasurface antenna 34 (12). doi:10.1364/JOSAB.34.002610

CrossRef Full Text

Duarte-Carvajalino, J. M., and Sapiro, G. (2009). Learning to sense sparse signals: Simultaneous sensing matrix and sparsifying dictionary optimization. IEEE Trans. Image Process. 18 (7), 1395–1408. doi:10.1109/TIP.2009.2022459

PubMed Abstract | CrossRef Full Text | Google Scholar

Fromenteze1, T., Yurduseven, O., Imani, M. F., Gollub, J., Decroze1, C., Carsenat1, D., et al. (2015). Computational imaging using a mode-mixing cavity at microwave frequencies. Appl. Phys. Lett. 106 (19), 194104. doi:10.1063/1.4921081

CrossRef Full Text | Google Scholar

Gollub, J. N., Yurduseven, O., Trofatter, K. P., Arnitz, D., Imani, M. F., Sleasman, T., et al. (2017). Large metasurface aperture for millimeter wave computational imaging at the human-scale. Large Metasurface Aperture Millim. Wave Comput. Imaging A. T. Human-Scale 7, 42650. doi:10.1038/srep42650

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, J., Li, L., Tian, S., Liu, G., Liu, H., and Shi, Y. (2020). Millimeter-wave imaging using 1-bit programmable metasurface: Simulation model, design, and experiment. IEEE J. Emerg. Sel. Top. Circuits Syst. 10 (1), 52–61. doi:10.1109/JETCAS.2020.2973466

CrossRef Full Text | Google Scholar

Han, J., Li, L., Tian, S., Ma, X., Feng, Q., Liu, H., et al. (2021). Frequency-diverse holographic metasurface antenna for near-field microwave computational imaging. Front. Mater. 8. doi:10.3389/fmats.2021.766889

CrossRef Full Text | Google Scholar

Howard, D. D. (1975). High range-resolution monopulse tracking radar. IEEE Trans. Aerosp. Electron. Syst. AES- 11 (5), 749–755. doi:10.1109/TAES.1975.307984

CrossRef Full Text | Google Scholar

Hu, Q., Chen, K., Zhang, N., Zhao, J., Jiang, T., Zhao, J., et al. (2021). Arbitrary and dynamic poincaré sphere polarization converter with a time-varying metasurface. Adv. Opt. Mater. 10 (4), 2101915. doi:10.1002/adom.202101915

CrossRef Full Text | Google Scholar

Hunt, J., Driscoll, T., Mrozack, A., Lipworth, G., Reynolds, M., Brady, D., et al. (2013). Metamaterial apertures for computational imaging. Science 339 (6117), 310–313. doi:10.1126/science.1230054

PubMed Abstract | CrossRef Full Text | Google Scholar

Imani, M. F., Gollub, J. N., Yurduseven, O., Diebold, A. V., Boyarsky, M., Fromenteze, T., et al. (2020). Review of metasurface antennas for computational microwave imaging. IEEE Trans. Antennas Propag. 68 (3), 1860–1875. doi:10.1109/TAP.2020.2968795

CrossRef Full Text | Google Scholar

Imani, M. F., Sleasman, T., Gollub, J. N., and Smith, D. R. (2016). Analytical modeling of printed metasurface cavities for computational imaging. J. Appl. Phys. 120 (14), 144903. doi:10.1063/1.4964336

CrossRef Full Text | Google Scholar

Li, S., Han, B., Li, Z., Liu, X., Huang, G., Li, R., et al. (2022). Transmissive coding metasurface with dual-circularly polarized multi-beam. Opt. Express 30 (15), 26362. doi:10.1364/OE.466036

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Li, Z., Han, B., Huang, G., Liu, X., Yang, H., et al. (2022). Multifunctional coding metasurface with left and right circularly polarized and multiple beams. Front. Mater. 9. doi:10.3389/fmats.2022.854062

CrossRef Full Text | Google Scholar

Li, S., Li, Z., Huang, G., Liu, X., Li, R., and Cao, X. (2022). Digital coding transmissive metasurface for multi-OAM-beam. Front. Phys. 17 (6), 62501. doi:10.1007/s11467-022-1179-9

CrossRef Full Text | Google Scholar

Mait, J. N., Euliss, G. W., and Athale, R. A. (2018). Computational imaging. Adv. Opt. Phot. 10 (2), 409. doi:10.1364/AOP.10.000409

CrossRef Full Text | Google Scholar

Marks, D., Yurduseven, O., and Smith, D. (2017). Cavity-backed metasurface antennas and their application to frequency diversity imaging. J. Opt. Soc. Am. A 34 (4), 472. doi:10.1364/JOSAA.34.000472

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastorino, M. (2010). Microwave imaging. Hoboken, NJ, USA: Wiley.

Google Scholar

Pfeiffer, C., and Grbic, A. (2013). Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 110 (19), 197401. doi:10.1103/physrevlett.110.197401

PubMed Abstract | CrossRef Full Text | Google Scholar

Pulido-Mancera, L., Fromenteze, T., Sleasman, T., Boyarsky, M., Imani, M. F., Reynolds, M., et al. (2016). Application of range migration algorithms to imaging with a dynamic metasurface antenna. J. Opt. Soc. Am. B 33 (10), 2082. doi:10.1364/JOSAB.33.002082

CrossRef Full Text | Google Scholar

Rao, W., Li, G., Wang, X., and Xia, X. -G. (2013). Adaptive sparse recovery by parametric weighted L$_{1}$ minimization for ISAR imaging of uniformly rotating targets. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 6 (2), 942–952. doi:10.1109/JSTARS.2012.2215915

CrossRef Full Text | Google Scholar

Sheen, D. M., McMakin, D. L., and Hall, T. E. (2001). Three-dimensional millimeter-wave imaging for concealed weapon detection. IEEE Trans. Microw. Theory Tech. 49 (9), 1581–1592. doi:10.1109/22.942570

CrossRef Full Text | Google Scholar

Sleasman, T., Imani, M. F., Gollub, J. N., and Smith, D. R. (2015). Dyn. metamaterial aperture Microw. imaging 107 (20). doi:10.1063/1.4935941

CrossRef Full Text

Wu, Z., Zhang, L., Liu, H., and Kou, N. (2016). Enhancing microwave metamaterial aperture radar imaging performance with rotation synthesis. IEEE Sensors J. 16 (22), 8035–8043. doi:10.1109/JSEN.2016.2609200

CrossRef Full Text | Google Scholar

Yurduseven, O., Gollub, J. N., Marks, D. L., and Smith, D. R. (2016). Frequency-diverse microwave imaging using planar Mills-Cross cavity apertures. Opt. express 24 (8), 8907. doi:10.1364/OE.24.008907

PubMed Abstract | CrossRef Full Text | Google Scholar

Yurduseven, O., Gowda, V. R., Gollub, J. N., and Smith, D. R. (2016). Printed aperiodic cavity for computational and microwave imaging. IEEE Microw. Wirel. Components Lett. 26 (5), 367–369. doi:10.1109/LMWC.2016.2548443

CrossRef Full Text | Google Scholar

Zhang, L., Xing, M., Qiu, C. W., Li, J., and Bao, Z. (2009). Achieving higher resolution ISAR imaging with limited pulses via compressed sampling. IEEE Geoscience Remote Sens. Lett. 6 (3), 567–571. doi:10.1109/LGRS.2009.2021584

CrossRef Full Text | Google Scholar

Zhao, L., Wang, L., Bi, G., and Yang, L. (2014). An autofocus technique for high-resolution Inverse synthetic aperture radar imagery. IEEE Trans. Geoscience Remote Sens. 52 (10), 6392–6403. doi:10.1109/TGRS.2013.2296497

CrossRef Full Text | Google Scholar

Zhao, M., Zhu, S., Huang, H., Chen, X., Chen, J., and Zhang, A. (2020). Frequency-diverse metasurface antenna with hybrid bunching methods for coincidence imaging. IEEE Access 8. doi:10.1109/ACCESS.2020.3012545

CrossRef Full Text | Google Scholar

Zhou, J., Zhu, R., Jiang, G., Zhao, L., and Cheng, B. (2019). A precise wavenumber domain algorithm for near range microwave imaging by cross MIMO array. IEEE Trans. Microw. Theory Tech. 67 (4), 1316–1326. doi:10.1109/TMTT.2018.2890473

CrossRef Full Text | Google Scholar

Zhu, X. X., and Bamler, R. (2012). Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR. IEEE Trans. Geoscience Remote Sens. 50 (1), 247–258. doi:10.1109/TGRS.2011.2160183

CrossRef Full Text | Google Scholar