The morphologies of twins in tetragonal ferroelectrics

Twins, as a special structure, have been observed in a small number of experiments on ferroelectrics. A good understanding of the morphologies of twins is very important for twin engineering applications in ferroelectric materials. In this work, the morphologies of twins in tetragonal ferroelectrics are investigated using the compatibility analysis of the transformation strains and spontaneous polarization and the energetic analysis. The tetragonal BaTiO₃ single crystal is chosen as an example for the material system. The results show that the lamellar twin structures with $\left\{111\right\}$ as the twin plane have been identified by both compatibility analysis and energetic analysis, which is consistent with the experimental observations. In addition to $\left\{111\right\}$ twin structures, $\left\{1\overline{2}1\right\}$ and $\left\{2\overline{1}5\right\}$ twin structures can also appear in tetragonal ferroelectrics. Furthermore, stable state uncharged twin boundaries and metastable charged twin boundaries are distinguished by energetic analysis, where the spontaneous polarization is compatible across the uncharged twin boundaries, while it is not compatible across the charged twin boundaries. The results predicted by the compatibility analysis and energetic analysis are consistent, thus providing a pathway for understanding the morphologies of twins.

1 Introduction

Due to their piezoelectric, dielectric, pyroelectric, ferroelectric, and electrocaloric properties, ferroelectric materials have shown great potential in sensors, actuators, capacitors, memories, solid-state refrigeration, and micro-electromechanical systems (Garcia and Bibes, 2012; Hwang et al., 2014; Martin and Rappe, 2016; Li et al., 2018a; Stadlober et al., 2019; Isaeva and Topolov, 2021; Manan et al., 2021; Shan et al., 2021; Asapu et al., 2022; Dan et al., 2022). The region with the same polarization is known as the ferroelectric domain, which corresponds to a ferroelectric variant. Different ferroelectric domains correspond to different ferroelectric variants with different transformation strains and spontaneous polarizations (Liu and Li, 2009). To form stable domain configurations, these variants must satisfy the compatibility conditions on transformation strains and spontaneous polarizations, leading to minimum energy. In tetragonal ferroelectrics, 90° and 180° domains have been observed (Le et al., 2013). In rhombohedral ferroelectrics, 71°, 109°, and 180° domains have been observed (Chen et al., 2007; Anthoniappen et al., 2017; Wan et al., 2021). In addition, the charged domain walls, across which the strain compatibility condition is satisfied, but the polarization compatibility condition is not satisfied, have been reported in the theoretical and experimental aspects (Liu et al., 2007; Liu and Li, 2009; Li et al., 2016). Therefore, the formation of domain structure is the basis for understanding the functional properties of ferroelectric materials. It is also the technological application of underpinned ferroelectric materials, making domain engineering being an effective way to enhance the performance of ferroelectrics (Shelke et al., 2011; Li et al., 2017; Geng et al., 2020; Qiu et al., 2020; Chen et al., 2022; Lei and Liu, 2022; Liu et al., 2022; Xu et al., 2022).

Domain engineering for ferroelectric materials has been extensively studied from both experimental and theoretical perspectives (Shelke et al., 2011; Li et al., 2017; Geng et al., 2020; Qiu et al., 2020; Chen et al., 2022; Lei and Liu, 2022; Liu et al., 2022; Xu et al., 2022). It is well known that twin structures are often observed in metals and alloys (Li et al., 2018b; Song et al., 2020; Li et al., 2023). Based on the formation of twins, twin engineering is widely used to enhance the mechanical properties of materials (Cheng et al., 2018; Li et al., 2022; Chen et al., 2023), thermal properties (Gao et al., 2021), electrical properties (Lei et al., 2018). Although domain engineering in ferroelectrics has received extensive attention, twins in ferroelectrics have rarely been reported. It is noticed that the 90° ferroelectric domain in some literature is called “twin”, but it is not a twin structure whose lattice should be symmetrical about the twin planes.

Twin structures have been experimentally observed in BaTiO₃ powders (Eibl et al., 1987; Qin et al., 2010). For example, Qin et al. synthesized twinned BaTiO₃ powders using BaCl₂ and TiO₂ at low temperatures, and their twin plane is $\left(111\right)$ plane (Qin et al., 2010). By calcining a powder mixture of BaCO₃ and TiO₂ at 1100°C, Eibl et al. observed a $\left(111\right)$ twin structures in the BaTiO₃ ceramics (Eibl et al., 1987). Also, Cao et al. fabricated twinned structures in BaTiO₃ films by a thermomechanical treatment technique, and BaTiO₃ films with twin structures exhibit a smaller coercive field (Cao et al., 2015). This suggests that twin engineering may be used to enhance the properties of ferroelectrics. However, there are currently few reports on ferroelectric twinning, while the morphologies of ferroelectric twin, including its grain shape and orientation remain unclear. In addition to the $\left(111\right)$ twin plane, it is still unclear whether ferroelectric materials can form other twin planes, while the revealing of morphologies and twin planes for ferroelectric twins is very important for utilizing twin engineering to enhance the performance of ferroelectrics. It is well known that the stable structures in ferroelectrics are energetically stable states, which should satisfy compatibility conditions on transformation strains and spontaneous polarization. Our previous work developed an energetic analysis method for ferroelectric domain patterns based on the equivalent inclusion method (Liu et al., 2007; Liu and Li, 2009). Thus, in this article, we analyze the morphologies of twins in tetragonal ferroelectrics by using compatibility analysis and energetic analysis, and the energy minimizing twin morphologies, including orientation and shape, are identified, as well as the determined twin planes.

2 Theoretical frameworks

2.1 Tetragonal twin variants

In experiments, (111) twins have been observed in BaTiO₃ powders and films at room temperature (Eibl et al., 1987; Qin et al., 2010; Cao et al., 2015; Cao et al., 2017). It is well known that BaTiO₃ is tetragonal at room temperature. Guided by the experimental results (Eibl et al., 1987; Qin et al., 2010; Cao et al., 2015), the schematic of a tetragonal twin structure is plotted in Figure 1A, where the tetragonal unit cells TW1 and TW2 are symmetric about the twin plane. Each tetragonal unit cell has six possible polarization directions, corresponding to the six ferroelectric variants. Thus, there are a total of 12 ferroelectric variants in tetragonal twinned ferroelectrics. In their respective cubic crystallographic axes, such as TW1 in its local coordinate system $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ and TW2 in its local coordinate system $x_1^{\mathrm{T}\mathrm{W}2}{x}_2^{\mathrm{T}\mathrm{W}2}{x}_3^{\mathrm{T}\mathrm{W}2}$, the transformation strain ${\mathbf{\epsilon }}_{\mathit{i}}$ (i = 1,…,6) and the spontaneous polarization ${\mathbf{P}}_{\mathit{i}}$ of each variant are given as:

$\begin{array}{c}{\mathbf{\epsilon }}_{\mathbf{1}}={\mathbf{\epsilon }}_{\mathbf{2}}=\left[\begin{array}{ccc}\beta & 0& 0\\ 0& \alpha & 0\\ 0& 0& \alpha \end{array}\right],{\mathbf{P}}_{\mathbf{1}}=-{\mathbf{P}}_{\mathbf{2}}=\left[\begin{array}{c}{P}_t\\ 0\\ 0\end{array}\right],\\ {\mathbf{\epsilon }}_{\mathbf{3}}={\mathbf{\epsilon }}_{\mathbf{4}}=\left[\begin{array}{ccc}\alpha & 0& 0\\ 0& \beta & 0\\ 0& 0& \alpha \end{array}\right],{\mathbf{P}}_{\mathbf{3}}=-{\mathbf{P}}_{\mathbf{4}}=\left[\begin{array}{c}0\\ P_t\\ 0\end{array}\right],\\ {\mathbf{\epsilon }}_{\mathbf{5}}={\mathbf{\epsilon }}_{\mathbf{6}}=\left[\begin{array}{ccc}\alpha & 0& 0\\ 0& \alpha & 0\\ 0& 0& \beta \end{array}\right],{\mathbf{P}}_{\mathbf{5}}=-{\mathbf{P}}_{\mathbf{6}}=\left[\begin{array}{c}0\\ 0\\ P_t\end{array}\right],\end{array}(1)$

where $\alpha$ and $\beta$ are lattice constants of the materials, and $P_t$ is the module of the spontaneous polarization. It is noticed that the variants with opposite spontaneous polarizations have the same transformation strains. Considering that the tetragonal unit cells TW1 and TW2 have different local crystallographic axes, they have different transformation strains and spontaneous polarizations, which can be obtained by the tensor rotation of Eq. 1, which are denoted by $\left({\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left({\mathbf{\epsilon }}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathbf{P}}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, where the superscripts TW1 and TW2 indicate the symmetric unit cells about the twin boundary (TB), and the subscripts i and j (i, j = 1,…,6) label the ferroelectric variants on the sides of the TB.

FIGURE 1

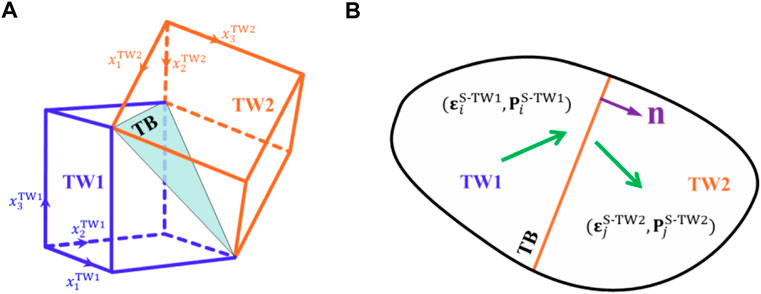
FIGURE 1. (A) Schematic of the tetragonal ferroelectric twin structure, where twin boundary (TB) represents the twin plane, TW1 and TW2 respectively denote the symmetric unit cells about the twin boundary. ${\mathrm{x}}_1^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_2^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_3^{\mathrm{T}\mathrm{W}1}$ and ${\mathrm{x}}_1^{\mathrm{T}\mathrm{W}2}{\mathrm{x}}_2^{\mathrm{T}\mathrm{W}2}{\mathrm{x}}_3^{\mathrm{T}\mathrm{W}2}$ are the local coordinate systems along cubic crystallographic axes of TW1 and TW2; (B) the twin boundary formed by different variants, where n represents the normal to the twin plane, $\left({\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left({\mathbf{\epsilon }}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathbf{P}}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ are the transformation strains and spontaneous polarizations of the variants on either side of the twin boundary.

2.2 Compatibility condition

In ferroelectrics, the stable interface between various ferroelectric variants is a consequence of energy minimization, across which the transformation strains and spontaneous polarizations of the variants satisfy the compatibility conditions (Shu and Bhattacharya, 2001; Li and Liu, 2004; Liu and Li, 2009; O'Reilly et al., 2022). For twin structures, the variants quantified by $\left({\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left({\mathbf{\epsilon }}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathbf{P}}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ form a twin boundary, as shown in Figure 1B. Thus, the compatibility conditions on the transformation strains and the spontaneous polarizations across the twin boundary are given by:

$\left({\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}-{\mathbf{P}}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)\cdot \mathbf{n}=0,(2)$

${\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}-{\mathbf{\epsilon }}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\frac{1}{2}\left(\mathbf{a}\otimes \mathbf{n}+\mathbf{n}\otimes \mathbf{a}\right),(3)$

where $\mathbf{n}$ represents the normal to the twin boundary, $\mathbf{a}$ represents the shear vector along the TB, and $\otimes$ refers to the standard tensor product of two vectors. Thus, the compatibility conditions Eqs 2, 3 allow us to determine the variants $\left({\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left({\mathbf{\epsilon }}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathbf{P}}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ that form an energetically stable twin boundary plane.

2.3 Energetic of morphology

While the compatibility analysis is capable of identifying the orientation of twin structures, it cannot identify the grain shapes of the twins, as well as the charged interface, which is energetically metastable due to polarizations incompatibility (Liu et al., 2007; Liu and Li, 2009). These deficiencies can be overcome by energy analysis using the equivalent inclusion method, which has been successfully applied to analyze the morphologies of ferroelectric domain patterns (Liu et al., 2007) and the precipitates in thermoelectric compounds (Liu et al., 2014).

For a ferroelectric crystal possessing a transformation strain ${\mathbf{\epsilon }}^{\mathrm{s}}$ and spontaneous polarization ${\mathbf{P}}^{\mathrm{s}}$, the electromechanical behavior is governed by the following constitutive equations:

$\mathbf{\epsilon }={\mathbf{F}}^{\mathbf{E}}\mathbf{\sigma }+{\mathbf{d}}^{\mathrm{t}}\mathbf{E}+{\mathbf{\epsilon }}^{\mathrm{s}},(4)$

$\mathbf{D}=\mathbf{d}\mathbf{\sigma }+{\mathbf{k}}^{\mathbf{\sigma }}\mathbf{E}+{\mathbf{P}}^{\mathrm{s}},(5)$

where $\mathbf{\epsilon }$ and $\mathbf{\sigma }$ are the strain and stress, respectively. $\mathbf{D}$ and $\mathbf{E}$ are the electric displacement and field, respectively. ${\mathbf{F}}^{\mathbf{E}}$ is the elastic compliance tensor under constant electric field, ${\mathbf{k}}^{\mathbf{\sigma }}$ is the dielectric constant under constant stress, $\mathbf{d}$ is the piezoelectric coefficient. The superscript $\mathrm{t}$ denotes the transpose of the tensor. By change of variables, the ferroelectric constitutive Eqs 4, 5 can be transformed into:

$\mathbf{\sigma }={\mathbf{C}}^{\mathbf{D}}\left(\mathbf{\epsilon }-{\mathbf{\epsilon }}^{\mathrm{s}}\right)-{\mathbf{h}}^{\mathrm{t}}\left(\mathbf{D}-{\mathbf{P}}^{\mathrm{s}}\right),(6)$

$\mathbf{E}=-\mathbf{h}\left(\mathbf{\epsilon }-{\mathbf{\epsilon }}^{\mathrm{s}}\right)+{\mathbf{\zeta }}^{\mathbf{\epsilon }}\left(\mathbf{D}-{\mathbf{P}}^{\mathrm{s}}\right).(7)$

The two types of constitutive Eqs. 4–7 can be rewritten as the following matrix forms:

$\mathbf{Y}=\mathbf{M}\mathbf{X}+{\mathbf{Y}}^{\mathrm{s}},(8)$

$\mathbf{X}=\mathbf{L}\left(\mathbf{Y}-{\mathbf{Y}}^{\mathrm{s}}\right),(9)$

where

$\begin{array}{c}\mathbf{Y}=\left[\begin{array}{c}\mathbf{\epsilon }\\ \mathbf{D}\end{array}\right],\mathbf{X}=\left[\begin{array}{c}\mathbf{\sigma }\\ \mathbf{E}\end{array}\right],{\mathbf{Y}}^{\mathrm{s}}=\left[\begin{array}{c}{\mathbf{\epsilon }}^{\mathrm{s}}\\ {\mathbf{P}}^{\mathrm{s}}\end{array}\right],\mathbf{M}=\left[\begin{array}{cc}{\mathbf{F}}^{\mathbf{E}}& {\mathbf{d}}^{\mathrm{t}}\\ \mathbf{d}& {\mathbf{k}}^{\mathbf{\sigma }}\end{array}\right],\mathbf{L}={\mathbf{M}}^{-\mathbf{1}}=\left[\begin{array}{cc}{\mathbf{C}}^{\mathbf{D}}& {-\mathbf{h}}^{\mathrm{t}}\\ -\mathbf{h}& {\mathbf{\zeta }}^{\mathbf{\epsilon }}\end{array}\right]\end{array}$

with the superscript $-1$ denoting matrix inverse. Since the electromechanical moduli M and $\mathbf{L}$ are positive definite, it is convenient to analyze the energy of twin structures using the above constitutive Eqs. 4–7.

In order to analyze the stable morphologies of stable twin structures in tetragonal ferroelectrics, the equivalent inclusion method is adopted (Dunn and Taya, 1993; Liu et al., 2007; Liu and Li, 2009). The twin structure is treated as a matrix region D and an inhomogeneous inclusion Ω, where the matrix is composed of TW1 with electromechanical moduli denoted by ${\mathbf{L}}^{\mathrm{T}\mathrm{W}1}$ and transformation strain and spontaneous polarization given by ${\mathbf{Y}}^{\mathrm{S}-\mathrm{T}\mathrm{W}1}$, while the inhomogeneous inclusion is composed of TW2 with ${\mathbf{L}}^{\mathrm{T}\mathrm{W}2}$ and ${\mathbf{Y}}^{\mathrm{S}-\mathrm{T}\mathrm{W}2}$, as shown in Figure 2. Using the matrix TW1 as a reference, the effective transformation strain and spontaneous polarization of the inhomogeneous inclusion TW2 can be written as:

${\mathbf{Y}}^{\mathbf{S}}={\mathbf{Y}}^{\mathrm{S}-\mathrm{T}\mathrm{W}2}-{\mathbf{Y}}^{\mathrm{S}-\mathrm{T}\mathrm{W}1}.(10)$

The electromechanical fields can be obtained by Eshleby’s classical solution (Liu et al., 2007; Liu and Li, 2009).

FIGURE 2

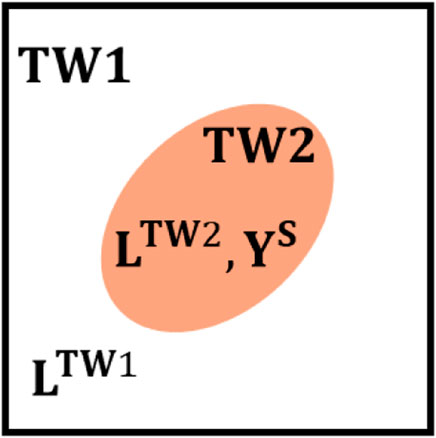
FIGURE 2. Schematic of the inhomogeneous inclusion, where TW1 and TW2 represent the unit cells in the twin structure.

Consider a uniform external field ${\mathbf{X}}^{\mathbf{0}}$ is applied to the twin structure in Figure 2. If an inhomogeneous inclusion does not exist, a uniform ${\mathbf{Y}}^{\mathbf{0}}$ will be induced in matrix. But due to the emergence of inhomogeneous inclusion TW2, the additional disturbance fields ${\mathbf{X}}^{\prime }$ and ${\mathbf{Y}}^{\prime }$ are induced. Thus, the electromechanical field for the inhomogeneous inclusion TW2 can be expressed by (Liu and Li, 2009):

${\mathbf{X}}^{\mathbf{0}}+{\mathbf{X}}^{\prime }={\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{2}}\left({\mathbf{Y}}^{\mathbf{0}}+{\mathbf{Y}}^{\prime }-{\mathbf{Y}}^{\mathbf{S}}\right),(11)$

which can be computed by Eshelby’s equivalent inclusion method (Liu et al., 2007; Liu and Li, 2009), such as:

${\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{2}}\left({\mathbf{Y}}^{\mathbf{0}}+{\mathbf{Y}}^{\prime }-{\mathbf{Y}}^{\mathbf{S}}\right)={\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}\left({\mathbf{Y}}^{\mathbf{0}}+{\mathbf{Y}}^{\prime }-{\mathbf{Y}}^{\mathbf{S}}-{\mathbf{Y}}^{**}\right),(12)$

where the inhomogeneous inclusion TW2 is replaced by an equivalent inclusion, which has the same electromechanical moduli ${\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}$ of matrix and additional transformation strain and spontaneous polarization Y^**, which ensures the equivalency of electromechanical fields between TW2 and the equivalent inclusion. For ellipsoidal inclusion, it is well known that the disturbance electromechanical field in the inclusion can be calculated by (Wang, 1992; Dunn and Taya, 1993; Liu et al., 2007; Liu and Li, 2009):

${\mathbf{Y}}^{\prime }=\mathbf{T}{\left(\mathbf{Y}\right.}^{\mathbf{S}}+{\mathbf{Y}}^{**}),(13)$

where

$\mathbf{T}=\left({\mathbf{N}}_{\mathbf{2}}\mathbf{S}-{\mathbf{N}}_{\mathbf{3}}\right)\mathbf{N}$

with

${\mathbf{N}}_{\mathbf{2}}=\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ {\mathbf{e}}^{\mathrm{t}}& {-\mathbf{k}}^{\mathbf{\epsilon }}\end{array}\right],{\mathbf{N}}_{\mathbf{3}}=\left[\begin{array}{cc}0& 0\\ {\mathbf{e}}^{\mathrm{t}}& {-\mathbf{k}}^{\mathbf{\epsilon }}\end{array}\right],\mathbf{N}=\left[\begin{array}{cc}\mathbf{I}& -\mathbf{d}{\left({\mathbf{k}}^{\mathbf{\sigma }}\right)}^{-\mathbf{1}}\\ 0& {\left({\mathbf{k}}^{\mathbf{\sigma }}\right)}^{-\mathbf{1}}\end{array}\right].$

In the above expressions, I is the unit four-rank tensor,

$\mathbf{e}={\left({\mathbf{F}}^{\mathbf{E}}\right)}^{-\mathbf{1}}\mathbf{d},{\mathbf{k}}^{\mathbf{\epsilon }}={\mathbf{k}}^{\mathbf{\sigma }}-{\mathbf{d}}^{\mathrm{t}}{\left({\mathbf{F}}^{\mathbf{E}}\right)}^{-\mathbf{1}}\mathbf{d}.$

S is the piezoelectric Eshelby’s tensors, which is a function of the electromechanical modulus ${\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}$ of the matrix TW1, as well as a function of the shape and orientation of the inclusion TW2 (Dunn and Taya, 1993). Combining Eqs 12, 13, the fictitious transformation strain and spontaneous polarization ${\mathbf{Y}}^{**}$ can be expressed as

$\begin{array}{c}{\mathbf{Y}}^{**}={\left[\left({\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}-{\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{2}}\right)\mathbf{T}-{\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}\right]}^{-\mathbf{1}}\left({\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{2}}-{\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}\right){\mathbf{Y}}^{\mathbf{0}}\\ -{\left[\left({\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}-{\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{2}}\right)\mathbf{T}-{\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{1}}\right]}^{-\mathbf{1}}{\mathbf{L}}^{\mathbf{T}\mathbf{W}\mathbf{2}}{\mathbf{Y}}^{\mathbf{S}}-{\mathbf{Y}}^{\mathbf{S}},\end{array}(14)$

from which the electromechanical field in the twin structure can be determined.

The potential energy of the twin structure system can then be expressed by:

$W=\underset{\mathbf{D}}{{\displaystyle \int }}\left[\left.\frac{\mathbf{1}}{\mathbf{2}}{\left(\mathbf{X}\right.}^{\mathbf{0}}+{\mathbf{X}}^{\prime })\cdot {\left(\mathbf{Y}\right.}^{\mathbf{0}}+{\mathbf{Y}}^{\prime }-{\mathbf{Y}}^{\mathbf{S}})-{\mathbf{X}}^{\mathbf{0}}\cdot {\left(\mathbf{Y}\right.}^{\mathbf{0}}+{\mathbf{Y}}^{\prime })\right)\right]\mathbf{d}\mathbf{x},(15)$

where the first term represents the elastic and electric energies, and the second term represents the work done by external loading. In the absence of the inhomogeneous inclusion TW2, the effective transformation strain and spontaneous polarization ${\mathbf{Y}}^{\mathbf{S}}$ and the disturbance fields vanish, leading to the potential energy expressed by:

$W_0=-\frac{1}{2}\underset{\mathbf{D}}{{\displaystyle \int }}{\mathbf{X}}^{\mathbf{0}}\cdot {\mathbf{Y}}^{\mathbf{0}}\mathbf{d}\mathbf{x}.(16)$

Thus, due to the existence of the inhomogeneous inclusion TW2, which infers the formation of a twin structure, the resulting energy variation is

$∆\mathit{W}=\mathit{W}-{\mathit{W}}_0=-\frac{1}{2}\underset{\mathbf{\Omega }}{{\displaystyle \int }}\left({\mathbf{X}}^{\mathbf{0}}\cdot {\mathbf{Y}}^{**}+{\mathbf{X}}^{\prime }\cdot {\mathbf{Y}}^{\mathbf{S}}+\mathbf{2}{\mathbf{X}}^{\mathbf{0}}\cdot {\mathbf{Y}}^{\mathbf{S}}\right)\mathbf{d}\mathbf{x},(17)$

where the Hill’s condition is adopted for simplification (Dunn and Taya, 1993; Li and Dunn, 1999). In this work, we consider the scenario of no external field, and the energy variation is further reduced to:

$∆\mathit{W}=-\frac{1}{2}\underset{\mathbf{\Omega }}{{\displaystyle \int }}{\mathbf{X}}^{\prime }\cdot {\mathbf{Y}}^{\mathbf{S}}\mathbf{d}\mathbf{x}.(18)$

Eq. 18 allows us to analyze the energy variation due to the emergence of twin structures, including its orientation and shape of the inhomogeneous inclusion TW2. The equilibrium morphologies of the twins can be identified by minimizing the energy variation with respect to the orientation and shape of the inhomogeneous inclusion TW2. For the inhomogeneous inclusion TW2, its shape can be assumed to be ellipsoidal, and the orientation can be described using Euler angles in the global coordinate system.

3 Results and discussions

In order to determine the morphologies of twins in tetragonal ferroelectrics, we employ the above theory to implement the compatibility analysis and energetic analysis of twin structures. We choose BaTiO₃ as the material system, whose electromechanical moduli associated with the single domain with the polarization along $\left[001\right]$ in its cubic crystallographic axes is $\mathbf{M}$. The transformation strain and spontaneous polarization are listed in Table 1. Notice that the physical quantities of other variants in different coordinate systems can be obtained by tensor rotations.

TABLE 1

TABLE 1. The electromechanical moduli M of single-domain with polarization along [001] in its cubic crystallographic axes (F^E: 10^–12 m²/N; d: 10^–12 C/N; ${\mathbf{\kappa }}^{\sigma }/{\kappa }_0$; where ${\kappa }_0$ = 8.85 $\times$ 10^–12 C²/Nm² is the permittivity of free space), transformation strain ε; and spontaneous polarization P(C/m²) of tetragonal BaTiO₃ single crystal (Zgonik et al., 1994; Liu and Li, 2009).

3.1 Compatibility analysis

Guided by the experimental results (Eibl et al., 1987; Qin et al., 2010; Cao et al., 2015), the tetragonal twin structure is schematically illustrated in Figure 1A. There are six variants with polarizations along the cubic crystallographic axes of TW1 unit cell. More explicitly, the polarizations are $:{\mathbf{P}}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\parallel {\left[100\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\parallel {\left[\overline{1}00\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\parallel {\left[010\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\parallel {\left[0\overline{1}0\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\parallel {\left[001\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_6^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\parallel {\left[00\overline{1}\right]}_{\mathrm{T}\mathrm{W}1}$ in the coordinate system $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$. Also, there are six variants with polarizations along the cubic crystallographic axes of TW2 unit cells, which are denoted by ${\mathbf{P}}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\parallel {\left[1\overline{2}\overline{2}\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\parallel {\left[\overline{1}22\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\parallel {\left[\overline{2}1\overline{2}\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\parallel {\left[2\overline{1}2\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\parallel {\left[22\overline{1}\right]}_{\mathrm{T}\mathrm{W}1}$, ${\mathbf{P}}_6^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\parallel {\left[\overline{2}\overline{2}1\right]}_{\mathrm{T}\mathrm{W}1}$ in the coordinate system $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$. Note that the orientational correspondences between TW1 unit cells and TW2 unit cells are: ${\left[\begin{array}{ccc}1& 0& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}2}\parallel {\left[\begin{array}{ccc}\frac{1}{3}& -\frac{2}{3}& -\frac{2}{3}\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, ${\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}2}\parallel {\left[-\begin{array}{ccc}\frac{2}{3}& \frac{1}{3}& -\frac{2}{3}\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, and ${\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_{\mathrm{T}\mathrm{W}2}\parallel {\left[\begin{array}{ccc}\frac{2}{3}& \frac{2}{3}& -\frac{1}{3}\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$. The transformation matrix that rotates from the $x_1^{\mathrm{T}\mathrm{W}2}{x}_2^{\mathrm{T}\mathrm{W}2}{x}_3^{\mathrm{T}\mathrm{W}2}$ coordinate to the $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ coordinate is then given by:

${\mathrm{R}}_{\mathrm{T}\mathrm{W}2\to \mathrm{T}\mathrm{W}1}=\frac{1}{3}\left[\begin{array}{ccc}1& -2& 2\\ -2& 1& 2\\ -2& -2& -1\end{array}\right].(19)$

In the $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ coordinate, the transformation strain ${\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}$ and spontaneous polarization ${\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}$ of each variant for TW1 have been given in Eq. 1, while the transformation strain ${\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}2}$ and spontaneous polarization ${\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}2}$ of TW2 can be obtained by the tensor rotation of Eq. 1 as:

${\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}2}={\mathrm{R}}_{\mathrm{T}\mathrm{W}2\to \mathrm{T}\mathrm{W}1}{\mathbf{P}}_i,(20)$

${\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}2}={\mathrm{R}}_{\mathrm{T}\mathrm{W}2\to \mathrm{T}\mathrm{W}1}{\mathbf{\epsilon }}_i{\mathrm{R}}_{\mathrm{T}\mathrm{W}2\to \mathrm{T}\mathrm{W}1}^{-1},(21)$

resulting in:

$\begin{array}{c}{\mathbf{\epsilon }}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}={\mathbf{\epsilon }}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\left[\begin{array}{ccc}\frac{8\alpha +\beta }{9}& \frac{2\alpha -2\beta }{9}& \frac{2\alpha -2\beta }{9}\\ \frac{2\alpha -2\beta }{9}& \frac{5\alpha +4\beta }{9}& \frac{-4\alpha +4\beta }{9}\\ \frac{2\alpha -2\beta }{9}& \frac{-4\alpha +4\beta }{9}& \frac{5\alpha +4\beta }{9}\end{array}\right],{\mathbf{P}}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=-{\mathbf{P}}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\left[\begin{array}{c}\frac{P_t}{3}\\ -\frac{2P_t}{3}\\ -\frac{2P_t}{3}\end{array}\right],\\ {\mathbf{\epsilon }}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}2}={\mathbf{\epsilon }}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\left[\begin{array}{ccc}\frac{5\alpha +4\beta }{9}& \frac{2\alpha -2\beta }{9}& \frac{-4\alpha +4\beta }{9}\\ \frac{2\alpha -2\beta }{9}& \frac{8\alpha +\beta }{9}& \frac{2\alpha -2\beta }{9}\\ \frac{-4\alpha +4\beta }{9}& \frac{2\alpha -2\beta }{9}& \frac{5\alpha +4\beta }{9}\end{array}\right],{\mathbf{P}}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=-{\mathbf{P}}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\left[\begin{array}{c}-\frac{{2P}_t}{3}\\ \frac{P_t}{3}\\ -\frac{2P_t}{3}\end{array}\right],\\ {\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}={\mathbf{\epsilon }}_6^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\left[\begin{array}{ccc}\frac{5\alpha +4\beta }{9}& \frac{-4\alpha +4\beta }{9}& \frac{2\alpha -2\beta }{9}\\ \frac{-4\alpha +4\beta }{9}& \frac{5\alpha +4\beta }{9}& \frac{2\alpha -2\beta }{9}\\ \frac{2\alpha -2\beta }{9}& \frac{2\alpha -2\beta }{9}& \frac{8\alpha +\beta }{9}\end{array}\right],{\mathbf{P}}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=-{\mathbf{P}}_6^{\mathrm{S}-\mathrm{T}\mathrm{W}2}=\left[\begin{array}{c}\frac{{2P}_t}{3}\\ \frac{2P_t}{3}\\ -\frac{P_t}{3}\end{array}\right].\end{array}(22)$

For the twin structure composed of TW1 $\left({\mathbf{\epsilon }}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathbf{P}}_i^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and TW2 $\left({\mathbf{\epsilon }}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathbf{P}}_j^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, the normal to the twin plane can be computed by solving Eqs. 2 and 3. Based on this compatibility analysis of the transformation strains and spontaneous polarizations, the twin planes between different tetragonal variants from TW1 and TW2 that may form twin structures are summarized in Table 2. It is found that the following pairs of variants can form (111)-twin in tetragonal ferroelectric: variants $\left({\epsilon }_1^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathrm{P}}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left({\epsilon }_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathrm{P}}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, variants $\left({\epsilon }_2^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathrm{P}}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left({\epsilon }_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathrm{P}}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, variants $\left({\epsilon }_3^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathrm{P}}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left({\epsilon }_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathrm{P}}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, variants $\left({\epsilon }_4^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathrm{P}}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left({\epsilon }_3^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathrm{P}}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, variants $\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathrm{P}}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathrm{P}}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, and variants $\left({\epsilon }_6^{\mathrm{S}-\mathrm{T}\mathrm{W}1},{\mathrm{P}}_6^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left({\epsilon }_6^{\mathrm{S}-\mathrm{T}\mathrm{W}2},{\mathrm{P}}_6^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, which have also been observed in experiments (Eibl et al., 1987; Cheng et al., 2006; Wu et al., 2006; Qin et al., 2010; Cao et al., 2015). Three representatives of these (111)-twins are schematically shown in Figure 3. Additionally, Table 2 shows that $\left\{1\overline{2}1\right\}$ and $\left\{2\overline{1}5\right\}$ twinned structures may also exist in tetragonal ferroelectrics, which have not been observed in currently reported experiments. Some predicted structures of $\left\{1\overline{2}1\right\}$ and $\left\{2\overline{1}5\right\}$ twins are schematically shown in Figure 4.

TABLE 2

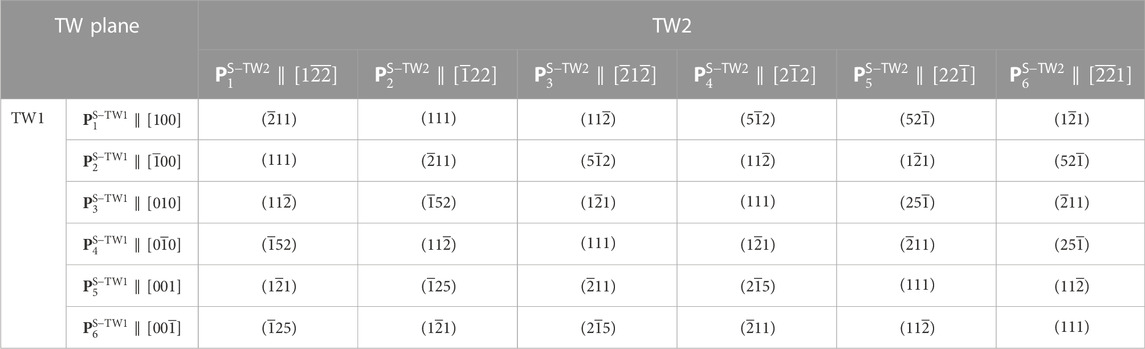
TABLE 2. The possible twin planes formed between various tetragonal variants identified by compatibility analysis. Note that all the polarization directions and twin plane normal are indicated in the local coordinate system $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$.

FIGURE 3

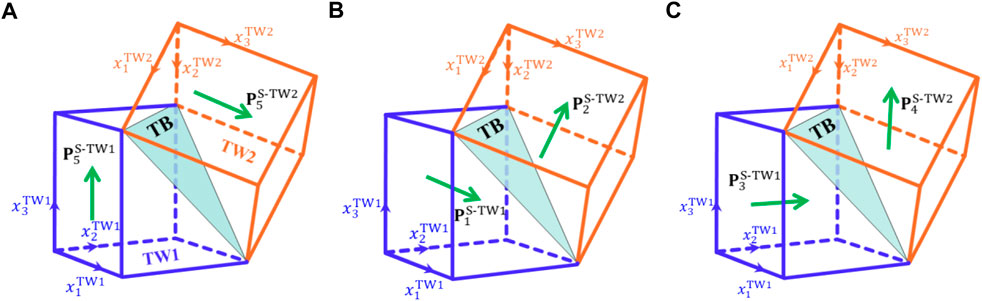
FIGURE 3. Schematics of the possible (111)-twins in tetragonal ferroelectrics; (A) Tetragonal ferroelectric variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$; (B) Tetragonal ferroelectric variants $\left.{\left({\mathbf{\epsilon }}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_2^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$; (C) Tetragonal ferroelectric variants $\left.{\left({\mathbf{\epsilon }}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_3^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$. Here $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ and ${\mathrm{x}}_1^{\mathrm{T}\mathrm{W}2}{\mathrm{x}}_2^{\mathrm{T}\mathrm{W}2}{\mathrm{x}}_3^{\mathrm{T}\mathrm{W}2}$ indicate the local coordinate system along cubic crystallographic axes of TW1 and TW2, respectively.

FIGURE 4

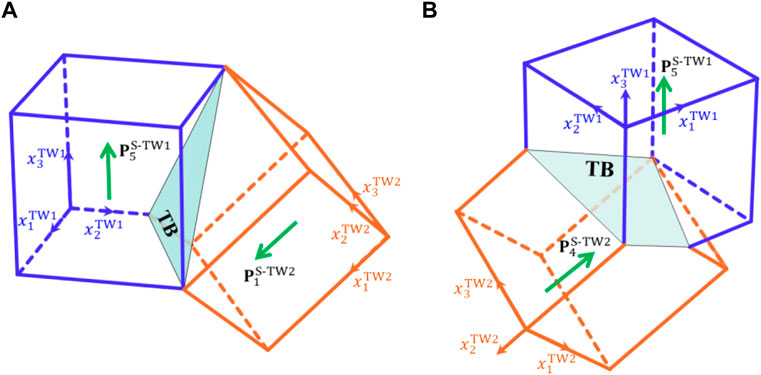
FIGURE 4. Schematics of the possible $\left(1\overline{2}1\right)$-twin and $\left(2\overline{1}5\right)$-twin in tetragonal ferroelectrics. (A) Tetragonal ferroelectric variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$; (B) Tetragonal ferroelectric variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$. Here $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ and $x_1^{\mathrm{T}\mathrm{W}2}{x}_2^{\mathrm{T}\mathrm{W}2}{x}_3^{\mathrm{T}\mathrm{W}2}$ indicate the local coordinate system along cubic crystallographic axes of TW1 and TW2, respectively.

3.2 Energetic analysis

Via the compatibility analysis, it is found that twin structures can be formed between different ferroelectric variants, and the twin planes are mainly $\left\{111\right\},\left\{1\overline{2}1\right\},\left\{2\overline{1}5\right\}$. But the compatibility analysis cannot determine the shapes of the twin grains. To this end, we apply Eq. 18 to perform an energetic analysis of tetragonal ferroelectric twins. Guided by the results of compatibility analysis, three types of twinned structures with variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\mathbf{\epsilon }}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ are considered in energetic analysis, which may form $\left(111\right),\left(1\overline{2}1\right),\left(2\overline{1}5\right)$ twinned structures respectively.

3.2.1 Twinned structure with variants $\left.{\left({\mathbf{\epsilon }}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{1}},\mathbf{P}\right.}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{1}}\right)$ and $\left.{\left({\mathbf{\epsilon }}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{2}},\mathbf{P}\right.}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{2}}\right)$

To be specific, the inhomogeneous inclusion TW2 is assumed to be spheroidal. For the twinned structure with variants $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, for the convenience of calculation, we choose the global coordinate system $x_1{x}_2{x}_3$ as shown in Figure 5A, where ${x_1\parallel \left[\begin{array}{ccc}1& 0& 0\end{array}\right]}_G\parallel {\left[-\begin{array}{ccc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, ${x_2\parallel \left[\begin{array}{ccc}0& 1& 0\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$ and ${x_3\parallel \left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, which makes the polarization vectors of the two variants lie on the same plane denoted by HJOQ, as shown in Figure 5B. The orientation of inhomogeneous inclusion TW2 can then be described by only one Euler angle θ, which is the angle between the $x_3$ axis and the rotational axis $X_3$ of the spheroid, as shown in Figure 5B. Notice that $x_2\parallel X_2$. The transformation matrix that rotates from local $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ and $x_1^{\mathrm{T}\mathrm{W}2}{x}_2^{\mathrm{T}\mathrm{W}2}{x}_3^{\mathrm{T}\mathrm{W}2}$ coordinates to the global $x_1{x}_2{x}_3$ coordinate are respectively:

${\mathrm{R}}_{\mathrm{T}\mathrm{W}1\to G}=\left[\begin{array}{ccc}-\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0\\ 0& 0& 1\end{array}\right],{\mathrm{R}}_{\mathrm{T}\mathrm{W}2\to G}=\left[\begin{array}{ccc}\frac{1}{3\sqrt{2}}& \frac{1}{3\sqrt{2}}& -\frac{4}{3\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0\\ -\frac{2}{3}& -\frac{2}{3}& -\frac{1}{3}\end{array}\right].(23)$

FIGURE 5

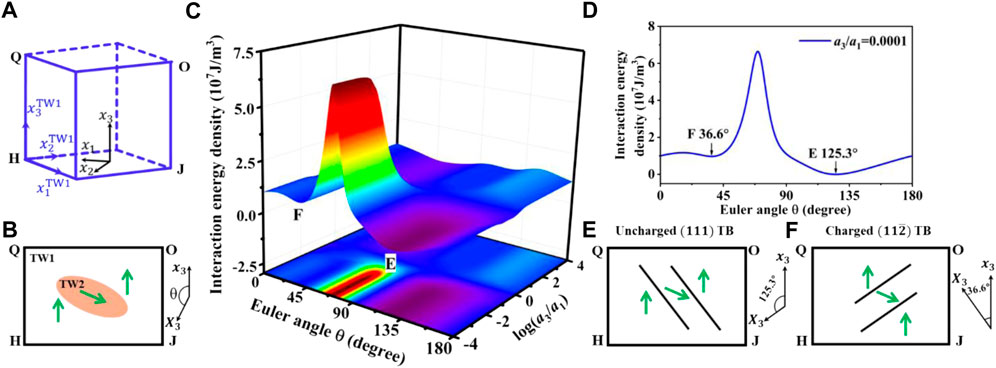
FIGURE 5. Energetic analysis of twinned structure with variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$: (A) Schematic of the relationship between the global coordinate system ${\mathrm{x}}_1{\mathrm{x}}_2{\mathrm{x}}_3$ and local coordinate system ${\mathrm{x}}_1^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_2^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_3^{\mathrm{T}\mathrm{W}1}$; (B) Schematic of variant $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ as an inhomogeneous inclusion within the variant $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ as the matrix; (C) the potential energy variation as a function of the shape aspect ratio ${\mathrm{a}}_3/{\mathrm{a}}_1$ and orientation angle $\theta$ of the inhomogeneous inclusion TW2; and (D) the corresponding potential energy variation at ${\mathrm{a}}_3/{\mathrm{a}}_1$ = 0.0001; The schematics of the uncharged (E) and charged (F) twin boundaries corresponding to the two wells in the energy landscape.

The shape aspect ratio of the inhomogeneous inclusion TW2 can be defined by $a_3/a_1=a_3/a_2$, where $a_1,a_2,a_3$ are the dimensions along the principal axes of the spheroidal. Based on Eq. 18, we calculate the potential energy variation as a function of the shape aspect ratio $a_3/a_1$ and the orientation angle $\theta$ of inhomogeneous inclusion TW2, as shown in Figure 5C. It is found that, when the aspect ratio $a_3/a_1$ approaches zero, two energy wells exist in the energy landscape, indicating that the stable twin structure is lamellar. Indeed, lamellae twins have been observed in BaTiO₃ ceramics (Oppolzer and Schmelz, 1983). Furthermore, one of the energy wells occurs at $\theta =125.3°$, while another occurs at $\theta =36.6°$. The well at $\theta =125.3°$ refers to the uncharged twin boundary with $\left(111\right)$ as the twin plane, across which the transformation strains and spontaneous polarizations are compatible, as shown in Figure 5E, which is consistent with those predicted by the compatibility analysis [as listed in Table 2]. On the other hand, the well at $\theta =36.6°$ refers to the charged twin boundary with $\left(11\overline{2}\right)$ as the twin plane, across which only the transformation strain is compatible, but the spontaneous polarization is not compatible, as shown in Figure 5F. Figure 5D reveals that the energy well at $\theta =125.3°$ is lower than that at $\theta =36.6°$, suggesting that the uncharged twin boundary is in a stable state, while the charged twin boundary is in a metastable state. A steep energy barrier exists between the two energy wells, making it hard to convert from the charged twin boundary to the uncharged twin boundary. The charged domain walls have been observed in many experiments (Sluka et al., 2012; Li et al., 2016; Wu et al., 2021), which are similar to the charged twin boundaries. Both of them are in metastable states, across which the spontaneous polarizations are also not compatible.

3.2.2 Twinned structure with variants $\left.{\left({\mathbf{\epsilon }}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{1}},\mathbf{P}\right.}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{1}}\right)$ and $\left.{\left({\mathbf{\epsilon }}_{\mathbf{1}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{2}},\mathbf{P}\right.}_{\mathbf{1}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{2}}\right)$

For the twinned structure with $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left.{\left({\epsilon }_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathrm{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, for the convenience of calculation, we choose the global coordinate system $x_1{x}_2{x}_3$ as shown in Figure 6A, where $x_1\parallel {\left[\begin{array}{ccc}1& 0& 0\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}-\frac{1}{\sqrt{5}}& \frac{2}{\sqrt{5}}& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, $x_2\parallel {\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}-\frac{2}{\sqrt{5}}& -\frac{1}{\sqrt{5}}& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, and $x_3\parallel {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, such that polarization vectors of the two variants lie on the same plane HJOQ, as shown in Figure 6B. For this case, the potential energy variation due to the emergence of the inhomogeneous inclusion TW2 as a function of its shape aspect ratio $a_3/a_1$ and the orientation angle $\theta$ is plotted in Figure 6C. It is observed that one energy well occurs at $\theta =114.1°$ in the energy landscape with $a_3/a_1$ approaching zero, which corresponds to the uncharged twin boundary with $\left(1\overline{2}1\right)$ as the twin plane, across which the transformation strains and spontaneous polarizations are compatible, as shown in Figure 6E, consistent with the prediction by the compatibility analysis [as listed in Table 2].

FIGURE 6

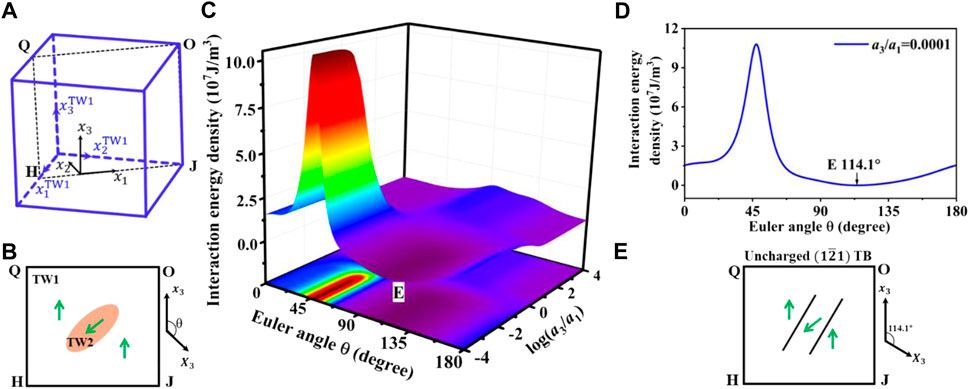
FIGURE 6. Energetic analysis of twinned structure with variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left.{\left({\mathbf{\epsilon }}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$: (A) Schematic of the relationship between the global coordinate system ${\mathrm{x}}_1{\mathrm{x}}_2{\mathrm{x}}_3$ and local coordinate system ${\mathrm{x}}_1^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_2^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_3^{\mathrm{T}\mathrm{W}1}$; (B) Schematic of variant $\left.{\left({\mathbf{\epsilon }}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ as an inhomogeneous inclusion within the variant $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ as the matrix; (C) the potential energy variation as a function of the shape aspect ratio ${\mathrm{a}}_3/{\mathrm{a}}_1$ and orientation angle $\theta$ of the inhomogeneous inclusion TW2; and (D) the corresponding potential energy variation at ${\mathrm{a}}_3/{\mathrm{a}}_1$ = 0.0001; The schematic of the uncharged (E) twin boundary corresponding to the well in the energy landscape.

3.2.3 Twinned structure with variants $\left.{\left({\mathbf{\epsilon }}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{1}},\mathbf{P}\right.}_{\mathbf{5}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{1}}\right)$ and $\left.{\left({\mathbf{\epsilon }}_{\mathbf{4}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{2}},\mathbf{P}\right.}_{\mathbf{4}}^{\mathbf{S}-\mathbf{T}\mathbf{W}\mathbf{2}}\right)$

For the twinned structure with $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left.{\left({\epsilon }_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathrm{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, we choose the global coordinate $x_1{x}_2{x}_3$, as shown in Figure 7A, where ${x_1\parallel \left[\begin{array}{ccc}1& 0& 0\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}-\frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, $x_2\parallel {\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}-\frac{1}{\sqrt{5}}& -\frac{2}{\sqrt{5}}& 0\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$, and $x_3\parallel {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_G\parallel {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}_{\mathrm{T}\mathrm{W}1}$. In the global coordinate $x_1{x}_2{x}_3$, the polarization vectors of the two variants lie on the same plane HJOQ, as shown in Figure 7B. We calculate the potential energy variation due to the emergence of the inhomogeneous inclusion TW2 as a function of its shape aspect ratio $a_3/a_1$ and orientation angle $\theta$ in Figure 7C. It can be seen that, when the aspect ratio $a_3/a_1$ approaches zero, there exists two energy wells, at $\theta =155.9°$ and $\theta =69.3°$ respectively. The energy well at $\theta =155.9°$ corresponds to the uncharged twin boundary with $\left(2\overline{1}5\right)$ as the twin plane. The transformation strains and spontaneous polarizations across this twin plane are compatible, as shown in Figure 7E, which is consistent with the prediction by the compatibility analysis [as listed in Table 2]. The other energy well located at $\theta =69.3°$ is metastable, resulting in the charged twin boundary with $\left(\overline{2}11\right)$ as the twin plane, across which only the transformation strains are compatible, while the spontaneous polarizations are not compatible, as shown in Figure 7F.

FIGURE 7

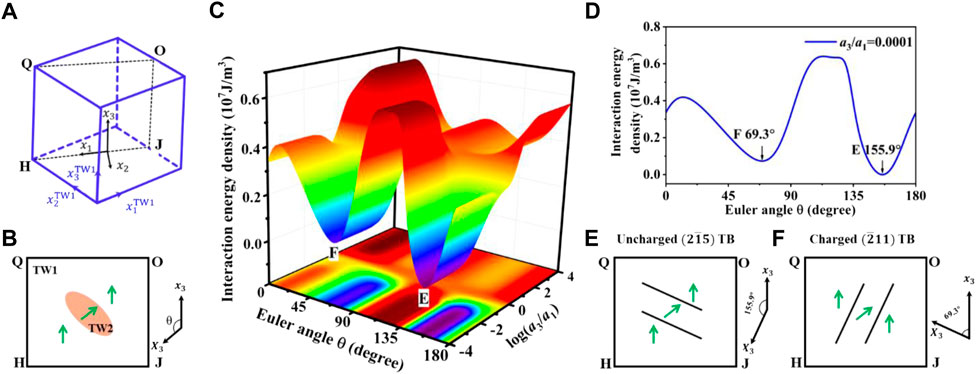
FIGURE 7. Energetic analysis of twinned structure with variants $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ and $\left.{\left({\mathbf{\epsilon }}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$: (A) Schematic of the relationship between the global coordinate system ${\mathrm{x}}_1{\mathrm{x}}_2{\mathrm{x}}_3$ and local coordinate system ${\mathrm{x}}_1^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_2^{\mathrm{T}\mathrm{W}1}{\mathrm{x}}_3^{\mathrm{T}\mathrm{W}1}$; (B) Schematic of variant $\left.{\left({\mathbf{\epsilon }}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathbf{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$ as an inhomogeneous within the variant $\left.{\left({\mathbf{\epsilon }}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathbf{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ as the matrix; (C) the potential energy variation as a function of the shape aspect ratio ${\mathrm{a}}_3/{\mathrm{a}}_1$ and orientation angle $\theta$ of the inhomogeneous inclusion TW2; and (D) the corresponding potential energy variation at ${\mathrm{a}}_3/{\mathrm{a}}_1$ = 0.0001; The schematics of the uncharged (E) and charged (F) twin boundaries corresponding to the two wells in the energy landscape.

3.3 Comparison between compatibility analysis and energetic analysis

For different combinations of variants, including the pairs $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\epsilon }_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathrm{P}\right.}_1^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, $\left.{\left({\epsilon }_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1},\mathrm{P}\right.}_5^{\mathrm{S}-\mathrm{T}\mathrm{W}1}\right)$ with $\left.{\left({\epsilon }_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2},\mathrm{P}\right.}_4^{\mathrm{S}-\mathrm{T}\mathrm{W}2}\right)$, the predicted results of the compatibility analysis and energetic analysis are summarized in Table 3. It can be found that the compatibility analysis on transformation strains can identify twin planes, but it cannot distinguish whether the twin plane is uncharged or charged. The energetic analysis not only can identify the twin plane, but also can further determine whether the twin plane is uncharged in a steady state or charged in a metastable state. The compatibility analysis on both transformation strains and spontaneous polarizations can only determine uncharged twin planes, as charged twin planes do not satisfy the compatibility in spontaneous polarizations. Overall, the results from compatibility analysis and energetic analysis are consistent. It has been demonstrated that twin engineering can reduce the coercive field of ferroelectric materials (Cao et al., 2015) due to the increased ferroelectric variants, suggesting that twin engineering may be used to enhance the other properties of ferroelectrics.

TABLE 3

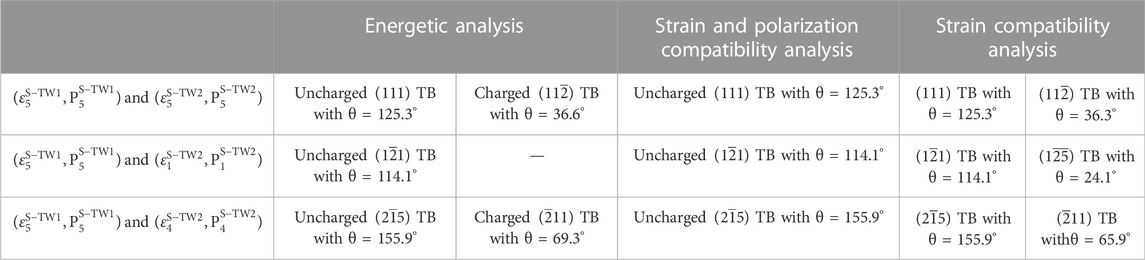
TABLE 3. Comparison of prediction results between compatibility analysis and energetic analysis. Note that the twin planes are specified in the $x_1^{\mathrm{T}\mathrm{W}1}{x}_2^{\mathrm{T}\mathrm{W}1}{x}_3^{\mathrm{T}\mathrm{W}1}$ coordinate.

4 Conclusion

We have investigated the morphologies of twins in tetragonal BaTiO₃ single crystals by using the compatibility analysis of the transformation strains and spontaneous polarizations and the energetic analysis. It is found that the lamellar twin structures with $\left\{111\right\}$ as the twin plane have been identified by both compatibility analysis and energetic analysis, which agrees well with experimental observations. The results also show that the $\left\{1\overline{2}1\right\}$ and $\left\{2\overline{1}5\right\}$ twin structures can exist in tetragonal ferroelectrics. In addition, the stable state uncharged twin boundaries and metastable charged twin boundaries are distinguished by energetic analysis, since the spontaneous polarizations are compatible across the uncharged twin boundaries, while the spontaneous polarizations are not compatible across the charged twin boundaries. The results predicted by the compatibility analysis and energetic analysis agree well with each other, offering a pathway for understanding the morphologies of twins in ferroelectrics.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, upon reasonable request.

Author contributions

NH and CL have contributed equally to this work. All authors contributed to conceptualization, theoretical calculations, analysis and writing the original draft. CL and YL revised the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially supported by the National Natural Science Foundation of China (11572276 and 12172318), the Hunan Provincial Natural Science Foundation of China (2021JJ10006), and the science and technology innovation Program of Hunan Province (2022RC3069). He also acknowledges support from Hunan Provincial Innovation Foundation for Postgraduate (CX20200628). Lei acknowledges the startup fund supported jointly by the Dean of Parks College and the Provost of Saint Louis University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anthoniappen, J., Chang, W. S., Soh, A. K., Tu, C. S., Vashan, P., and Lim, F. S. (2017). Electric field induced nanoscale polarization switching and piezoresponse in Sm and Mn co-doped BiFeO₃ multiferroic ceramics by using piezoresponse force microscopy. Acta Mater. 132, 174–181. doi:10.1016/j.actamat.2017.04.034

CrossRef Full Text | Google Scholar

Asapu, S., Pagaduan, J. N., Zhuo, Y., Moon, T., Midya, R., Gao, D., et al. (2022). Large remnant polarization and great reliability characteristics in W/HZO/W ferroelectric capacitors. Front. Mater. 9, 969188. doi:10.3389/fmats.2022.969188

CrossRef Full Text | Google Scholar

Cao, S. G., Li, Y. S., Wu, H. H., Wang, J., Huang, B. L., and Zhang, T. Y. (2017). Stress-induced cubic-to-hexagonal phase transformation in perovskite nanothin films. Nano Lett. 17 (8), 5148–5155. doi:10.1021/acs.nanolett.7b02570

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, S. G., Wu, H. H., Ren, H., Chen, L. Q., Wang, J., Li, J. Y., et al. (2015). A novel mechanism to reduce coercive field of ferroelectric materials via {111} twin engineering. Acta Mater. 97, 404–412. doi:10.1016/j.actamat.2015.07.009

CrossRef Full Text | Google Scholar

Chen, C., Liu, H., Lai, Q., Mao, X., Fu, J., Fu, Z., et al. (2022). Large-scale domain engineering in two-dimensional ferroelectric CuInP₂S₆ via giant flexoelectric effect. Nano Lett. 22 (8), 3275–3282. doi:10.1021/acs.nanolett.2c00130

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Li, F., Gao, B. T., Zhou, C., Wu, J., Deng, S. Q., et al. (2023). Excellent energy storage and mechanical performance in hetero-structure BaTiO₃-based relaxors. Chem. Eng. J. 452, 139222. doi:10.1016/j.cej.2022.139222

CrossRef Full Text | Google Scholar

Chen, Y. B., Katz, M. B., Pan, X. Q., Das, R. R., Kim, D. M., Baek, S. H., et al. (2007). Ferroelectric domain structures of epitaxial (001) BiFeO₃ thin films. Appl. Phys. Lett. 90 (7), 072907. doi:10.1063/1.2472092

CrossRef Full Text | Google Scholar

Cheng, S.-Y., Ho, N.-J., and Lu, H.-Y. (2006). Crystallographic relationships of the {111} growth twins in tetragonal barium titanate determined by electron-backscatter diffraction. J. Am. Ceram. Soc. 89 (11), 3470–3474. doi:10.1111/j.1551-2916.2006.01231.x

CrossRef Full Text | Google Scholar

Cheng, Z., Zhou, H. F., Lu, Q. H., Gao, H. J., and Lu, L. (2018). Extra strengthening and work hardening in gradient nanotwinned metals. Science 362 (6414), eaau1925. doi:10.1126/science.aau1925

PubMed Abstract | CrossRef Full Text | Google Scholar

Dan, H. Y., Li, H. Y., and Yang, Y. (2022). Flexible ferroelectric materials-based triboelectric nanogenerators for mechanical energy harvesting. Front. Mater. 9, 939173. doi:10.3389/fmats.2022.939173

CrossRef Full Text | Google Scholar

Dunn, M. L., and Taya, M. (1993). An analysis of piezoelectric composite materials containing ellipsoidal inhomogeneities. Proc. R. Soc. Lond. A 443 (1918), 265–287. doi:10.1098/rspa.1993.0145

CrossRef Full Text | Google Scholar

Eibl, O., Pongratz, P., Skalicky, P., and Schmelz, H. (1987). Formation of (111) twins in BaTiO₃ ceramics. J. Am. Ceram. Soc. 70 (8), C-195–C-197. doi:10.1111/j.1151-2916.1987.tb05724.x

CrossRef Full Text | Google Scholar

Gao, Y. F., Ning, W. B., Zhang, X. L., Liu, Y. Z., Zhou, Y. G., and Tang, D. W. (2021). The effective regulation of nanotwinning on the multichannel thermal transport in hybrid organic–inorganic halide perovskite. Nano Energy 82, 105747. doi:10.1016/j.nanoen.2021.105747

CrossRef Full Text | Google Scholar

Garcia, V., and Bibes, M. (2012). Inside story of ferroelectric memories. Nature 483 (7389), 279–280. doi:10.1038/483279a

PubMed Abstract | CrossRef Full Text | Google Scholar

Geng, W. R., Guo, X. W., Zhu, Y. L., Wang, Y. J., Tang, Y. L., Han, M. J., et al. (2020). Oxygen octahedral coupling mediated ferroelectric-antiferroelectric phase transition based on domain wall engineering. Acta Mater. 198, 145–152. doi:10.1016/j.actamat.2020.08.007

CrossRef Full Text | Google Scholar

Hwang, G. T., Park, H., Lee, J. H., Oh, S., Park, K. I., Byun, M., et al. (2014). Self-powered cardiac pacemaker enabled by flexible single crystalline PMN-PT piezoelectric energy harvester. Adv. Mater. 26 (28), 4880–4887. doi:10.1002/adma.201400562

PubMed Abstract | CrossRef Full Text | Google Scholar

Isaeva, A. N., and Topolov, V. Y. (2021). Lead-free 0–3-type composites: From piezoelectric sensitivity to modified figures of merit. J. Adv. Dielect. 11 (02), 2150010. doi:10.1142/S2010135X21500107

CrossRef Full Text | Google Scholar

Le, D.-T., Kwon, S.-J., Yeom, N.-R., Lee, Y.-J., Jeong, Y.-H., Chun, M.-P., et al. (2013). Effects of the domain size on local d₃₃ in tetragonal (Na_0.53K_0.45Li_0.02)(Nb_0.8Ta_0.2)O₃ ceramics. J. Am. Ceram. Soc. 96 (1), 174–178. doi:10.1111/j.1551-2916.2012.05445.x

CrossRef Full Text | Google Scholar

Lei, C. H., and Liu, Y. Y. (2022). Correlations between local electrocaloric effect and domains in ferroelectric crystals. Appl. Phys. Lett. 121 (10), 102902. doi:10.1063/5.0094473

CrossRef Full Text | Google Scholar

Lei, S. H., Fan, H. Q., Fang, J. W., Ren, X. H., Ma, L. T., and Tian, H. L. (2018). Unusual devisable high-performance perovskite materials obtained by engineering in twins, domains, and antiphase boundaries. Inorg. Chem. Front. 5 (3), 568–576. doi:10.1039/C7QI00711F

CrossRef Full Text | Google Scholar

Li, F., Zhang, S. J., Xu, Z., and Chen, L.-Q. (2017). The contributions of polar nanoregions to the dielectric and piezoelectric responses in domain-engineered relaxor-PbTiO₃ crystals. Adv. Funct. Mater. 27 (18), 1700310. doi:10.1002/adfm.201700310

CrossRef Full Text | Google Scholar

Li, J. L., Li, F., Xu, Z., and Zhang, S. J. (2018a). Multilayer lead-free ceramic capacitors with ultrahigh energy density and efficiency. Adv. Mater. 30 (32), 1802155. doi:10.1002/adma.201802155

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J. Y., and Dunn, M. L. (1999). Analysis of microstructural fields in heterogeneous piezoelectric solids. Int. J. Eng. Sci. 37 (6), 665–685. doi:10.1016/S0020-7225(98)00091-3

CrossRef Full Text | Google Scholar

Li, J. Y., and Liu, D. (2004). On ferroelectric crystals with engineered domain configurations. J. Mech. Phys. Solids 52 (8), 1719–1742. doi:10.1016/j.jmps.2004.02.011

CrossRef Full Text | Google Scholar

Li, L. H., Liu, W. H., Qi, F. G., Wu, D., and Zhang, Z. Q. (2022). Effects of deformation twins on microstructure evolution, mechanical properties and corrosion behaviors in magnesium alloys - a review. J. Magnes. Alloy. 10 (9), 2334–2353. doi:10.1016/j.jma.2022.09.003

CrossRef Full Text | Google Scholar

Li, L. L., Zhang, Z. J., Zhang, P., and Zhang, Z. F. (2023). A review on the fatigue cracking of twin boundaries: Crystallographic orientation and stacking fault energy. Prog. Mater. Sci. 131, 101011. doi:10.1016/j.pmatsci.2022.101011

CrossRef Full Text | Google Scholar

Li, L. Z., Britson, J., Jokisaari, J. R., Zhang, Y., Adamo, C., Melville, A., et al. (2016). Giant resistive switching via control of ferroelectric charged domain walls. Adv. Mater. 28 (31), 6574–6580. doi:10.1002/adma.201600160

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Xue, S. C., Wang, J., Shao, S., Kwong, A. H., Giwa, A., et al. (2018b). High-strength nanotwinned al alloys with 9R phase. Adv. Mat. 30 (11), 1704629. doi:10.1002/adma.201704629

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Yang, B., Lan, S., Pan, H., Nan, C.-W., and Lin, Y.-H. (2022). Perspectives on domain engineering for dielectric energy storage thin films. Appl. Phys. Lett. 120 (15), 150501. doi:10.1063/5.0090739

CrossRef Full Text | Google Scholar

Liu, Y. Y., Chen, L. Q., and Li, J. Y. (2014). Precipitate morphologies of pseudobinary Sb₂Te₃–PbTe thermoelectric compounds. Acta Mater. 65, 308–315. doi:10.1016/j.actamat.2013.10.072

CrossRef Full Text | Google Scholar

Liu, Y. Y., and Li, J. Y. (2009). Energetic analysis of ferroelectric domain patterns by equivalent inclusion method. J. Mater. Sci. 44 (19), 5214–5224. doi:10.1007/s10853-009-3536-2

CrossRef Full Text | Google Scholar

Liu, Y. Y., Liu, J. J., Xie, S. H., and Li, J. Y. (2007). Energetics of charged domain walls in ferroelectric crystals. Appl. Phys. Lett. 91 (17), 172910. doi:10.1063/1.2803765

CrossRef Full Text | Google Scholar

Manan, A., Rehman, M. U., Ullah, A., Ahmad, A. S., Iqbal, Y., Qazi, I., et al. (2021). High energy storage density with ultra-high efficiency and fast charging–discharging capability of sodium bismuth niobate lead-free ceramics. J. Adv. Dielect. 11 (04), 2150018. doi:10.1142/S2010135X21500181

CrossRef Full Text | Google Scholar

Martin, L. W., and Rappe, A. M. (2016). Thin-film ferroelectric materials and their applications. Nat. Rev. Mater. 2 (2), 16087. doi:10.1038/natrevmats.2016.87

CrossRef Full Text | Google Scholar

O'Reilly, T., Holsgrove, K., Gholinia, A., Woodruff, D., Bell, A., Huber, J., et al. (2022). Exploring domain continuity across BaTiO₃ grain boundaries: Theory meets experiment. Acta Mater. 235, 118096. doi:10.1016/j.actamat.2022.118096

CrossRef Full Text | Google Scholar

Oppolzer, H., and Schmelz, H. (1983). Investigation of twin lamellae in BaTiO₃ ceramics. J. Am. Ceram. Soc. 66 (6), 444–446. doi:10.1111/j.1151-2916.1983.tb10078.x

CrossRef Full Text | Google Scholar

Qin, S. B., Liu, D., Zheng, F. F., Zuo, Z. Y., Liu, H., and Xu, X. G. (2010). (111) Twinned BaTiO₃ microcrystallites. CrystEngComm 12 (10), 3003–3007. doi:10.1039/B925863A

CrossRef Full Text | Google Scholar

Qiu, C., Wang, B., Zhang, N., Zhang, S., Liu, J., Walker, D., et al. (2020). Transparent ferroelectric crystals with ultrahigh piezoelectricity. Nature 577 (7790), 350–354. doi:10.1038/s41586-019-1891-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Shan, D. L., Lei, C. H., Cai, Y. C., Pan, K., and Liu, Y. Y. (2021). Mechanical control of electrocaloric response in epitaxial ferroelectric thin films. Int. J. Solids Struct. 216, 59–67. doi:10.1016/j.ijsolstr.2021.01.020

CrossRef Full Text | Google Scholar

Shelke, V., Mazumdar, D., Srinivasan, G., Kumar, A., Jesse, S., Kalinin, S., et al. (2011). Reduced coercive field in BiFeO₃ thin films through domain engineering. Adv. Mater. 23 (5), 669–672. doi:10.1002/adma.201000807

PubMed Abstract | CrossRef Full Text | Google Scholar

Shu, Y. C., and Bhattacharya, K. (2001). Domain patterns and macroscopic behaviour of ferroelectric materials. Philos. Mag. B 81 (12), 2021–2054. doi:10.1080/13642810108208556

CrossRef Full Text | Google Scholar

Sluka, T., Tagantsev, A. K., Damjanovic, D., Gureev, M., and Setter, N. (2012). Enhanced electromechanical response of ferroelectrics due to charged domain walls. Nat. Commun. 3 (1), 748. doi:10.1038/ncomms1751

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, M., Zhou, G., Lu, N., Lee, J., Nakouzi, E., Wang, H., et al. (2020). Oriented attachment induces fivefold twins by forming and decomposing high-energy grain boundaries. Science 367 (6473), 40–45. doi:10.1126/science.aax6511

PubMed Abstract | CrossRef Full Text | Google Scholar

Stadlober, B., Zirkl, M., and Irimia-Vladu, M. (2019). Route towards sustainable smart sensors: Ferroelectric polyvinylidene fluoride-based materials and their integration in flexible electronics. Chem. Soc. Rev. 48 (6), 1787–1825. doi:10.1039/C8CS00928G

PubMed Abstract | CrossRef Full Text | Google Scholar

Wan, H., Luo, C. T., Liu, C., Chang, W. Y., Yamashita, Y., and Jiang, X. N. (2021). Alternating current poling on sliver-mode rhombohedral Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ single crystals. Acta Mater. 208, 116759. doi:10.1016/j.actamat.2021.116759

CrossRef Full Text | Google Scholar

Wang, B. (1992). Three-dimensional analysis of an ellipsoidal inclusion in a piezoelectric material. Int. J. Solids Struct. 29 (3), 293–308. doi:10.1016/0020-7683(92)90201-4

CrossRef Full Text | Google Scholar

Wu, H. J., Ning, S. C., Waqar, M., Liu, H. J., Zhang, Y., Wu, H.-H., et al. (2021). Alkali-deficiency driven charged out-of-phase boundaries for giant electromechanical response. Nat. Commun. 12 (1), 2841. doi:10.1038/s41467-021-23107-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y.-C., Lee, C.-C., Lu, H.-Y., McCauley, D. E., and Chu, M. S. H. (2006). The {111} growth twins in tetragonal barium titanate. J. Am. Ceram. Soc. 89 (5), 1679–1686. doi:10.1111/j.1551-2916.2006.00948.x

CrossRef Full Text | Google Scholar

Xu, X. Y., Wang, T. X., Chen, P. C., Zhou, C., Ma, J. N., Wei, D. Z., et al. (2022). Femtosecond laser writing of lithium niobate ferroelectric nanodomains. Nature 609 (7927), 496–501. doi:10.1038/s41586-022-05042-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Zgonik, M., Bernasconi, P., Duelli, M., Schlesser, R., Günter, P., Garrett, M. H., et al. (1994). Dielectric, elastic, piezoelectric, electro-optic, and elasto-optic tensors of BaTiO₃ crystals. Phys. Rev. B 50 (9), 5941–5949. doi:10.1103/PhysRevB.50.5941

PubMed Abstract | CrossRef Full Text | Google Scholar