
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 06 December 2022
Sec. Polymeric and Composite Materials
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.1081613
This article is part of the Research Topic Advances in Wellbore Servicing Fluids and Materials View all 6 articles
The dispersion of particle clusters is relevant to a high concentration carrying fluid such as fracturing and drilling fluid, and the fiber-containing fluid could improve the carrying performance of particles. In the present study, the settling dynamics behavior of clusters is investigated using the CFD-DEM method. The numerical simulation method employed was able to accurately predict the deformation and velocity change rules, which express the cluster settling dynamics behavior. The velocity variation of particles is affected by hindrance and contact inside the cluster, and the velocity contrast leads to particle leakage and cluster deformation. The cluster will have regular shape changes and break up in the settlement process under gravity and fluid drag force. According to the sensitivity parameter analysis, the deformation of clusters is mainly affected by the fluid rheological properties. Different from glycerol, the settling cluster in viscoelastic HPG has a more complex dynamic behavior and a better fiber barrier effect. The fiber barrier between particles in the cluster can be regarded as a weakly constrained fiber grid structure. Due to the contact force, fiber grid structure formed in the cluster could effectively restrain the shape change and break up trend in the settlement process. The design also considers the influence of fiber and HPG concentration, and we analyze the settling velocity of the mixed-fiber cluster. Overall, the research on the cluster settling dynamics behavior is helpful in analyzing the effect of fiber-containing fluid in the carrying performance of particles.
The carrying efficiency of fluid is an important problem in the study of multiphase flow. The solid phase in the transport process is mainly composed of bed load and suspended load, and the cluster can be regarded as a suspended unit. The fibers help smooth the construction process by improving the efficiency of solid suspensions such as proppant and drill cuttings. Under the same settling velocity of a single particle, the settling velocity of multiple particles in the non-Newtonian fluid is 2–3 times higher than that in the Newtonian fluid. Clark et al. (Clark, Harkin et al., 1977) simulated the proppant settling in the vertical fracture and found that the aggregation of the proppant would increase the settling velocity. According to the calculation and analysis of the force conditions, the average drag coefficient of the particles in the cluster is smaller than that of single particles. According to the research of Elgaddafi, A. Medvedev et al. (Elgaddafi, Ahmed et al., 2012; Medvedev, Kraemer et al., 2013) on the uneven proppant distribution process, it can be found that the formation effect of clusters in fractures is greatly affected by fluid rheological properties. Using uncross-linked fracture fluid base fluid as a sand carrier allows the formation of a large number of independent clusters in the fracture, so the transport efficiency is improved as compared to bed load (Rahim, Waheed et al., 2022). Combined with relevant engineering studies, it can also be found that suspended particles will form clusters during the settling process, which will affect the transportation efficiency of particles (Daugan, Talini et al., 2002; Yamashiro and Tomac 2021; Deepwell and Sutherland 2022). The fluid inertial lift force is the main reason causing the particle aggregation (Volpe, Gaudiuso et al., 2019). The simulation results showed a lift zero point on the transverse surface of the fluid, which is the particle aggregation position (Tang, Zhu et al., 2020). The inertia accumulation of particles is affected by fluid rheological properties and particle size (Hu, Lin et al., 2020), and the intensity of inertia accumulation is related to the Reynolds number (Liu, Hu et al., 2014). So, the distribution of the aggregate can be adjusted by the injection conditions.
Robinson et al. (Robinson, Ramaioli et al., 2014; Zhang, Tan et al., 2014) used the DEM method to simulate and describe the settlement process of aggregate particles and discussed the deformation process of the aggregate according to the trajectory of particles. In the simulation study of droplet settlement deformation, Guo et al. (Guo, Zhou et al., 2022) found that clusters and drops have similar shape changes, so similar shape characterization methods can be adopted. There are more complex mechanical behaviors in the cluster during the settlement process (Guazzelli and Pouliquen 2018; Lobry, Lemaire et al., 2019; Papadopoulou, Gillissen et al., 2020), which are generally considered to be caused by two aspects. On one hand, it is affected by external effects such as inertia force and viscous force; on the other hand, it is affected by internal flow field and interaction, contact, and collision of particles (Zenit and Feng 2018; Wang, Wan et al., 2019). To facilitate the analysis of the internal mechanical behavior of clusters during the settlement process, it is assumed that the particles are non-viscous materials. When the liquid pressure is equal to or greater than the air pressure, the adhesion between particles is ignored (Dizaji, Marshall et al., 2019; Guo, Zhou et al., 2021). Metzger et al. (Metzger, Nicolas et al., 2007) discussed the deformation law of particle cluster on one hand and the interference effect of hydrodynamics on cluster settlement on the other hand based on the interaction force between a small number of particles. According to the research results of Sun et al. (Mingyang and Lubin 2018), the final velocity of particle interference settlement is positively correlated with particle size and density and negatively correlated with particle volume fraction in unit volume space.
Based on the mechanism study of suspension flow, the dynamics behavior of themixed-fiber multiphase fluid is considered. (Gillard et al. (2010); Guo, Ma et al. (2015) proposed the method of fiber-containing fluid carrying to control the low transport efficiency of a dispersed phase in oil and gas exploitation. This phenomenon is due to the fiber barrier between particles in carrying fluids, which can be considered a weakly constrained fiber grid structure. The fiber grid structure formed in the fluid can effectively restrain the diffusion trend of particles in the movement process. Guo proposed that the grid structure of fibers is easier to form or the strength of it is enhanced in HPG. There are few studies on the stress of fiber barrier, and the interaction between the fiber and particle is simplified. Wang et al. (Wang and Zhao 2022) analyzed the mechanical action mechanism of the fiber on pulverized coal and characterized the improvement effect by comparing the conductivity changes after the process’s implementation. As for the interaction between particles and fiber barrier, Wang et al. conducted stress analysis in combination with supported beams. Ghommem et al. (Ghommem, Abbad et al., 2021) studied the fiber clustering and bridging in incompressible fluid flow and analyzed the mechanisms of interaction between internal fibers during fiber bridging and fiber flocs grid structure forming.
According to the study on cluster settling and fiber barrier, the mechanism of fiber action on suspended particles was analyzed. Then, the movement law of particles in mixed-fiber clusters was characterized, which was verified by experiments. The mechanical interactions involved in the research include fiber–particle, particle–particle, and particle–fluid. Due to the complexity of microscopic mechanics, this paper adopts a simplified model to quantitatively characterize the settlement characteristics of mixed-fiber clusters from a macroscopic perspective by combining the shape and velocity change rules to provide a reference for further research in this direction.
The static settlement experiment of clusters is proposed to reduce the influence of fluid flow on experimental results. The particle trajectory inside the cluster is affected by many factors, and the settling dynamics behavior can be analyzed through sensitivity parameters. Mylyk A et al. (Mylyk, Meile et al., 2011) studied the settling law of clusters in viscous fluids and proved that wall distance would affect the cluster deformation degree. When the distance from the wall to the cluster is more than three times the cluster diameter, the hinder of the wall on the cluster velocity can be ignored. This is the method to determine the cluster size. The cluster shape was set by Batchelor experiment research, and the initial shape is shown in Figure 1 (Nitsche and Batchelor 1997). The particles inside the cluster as shown in the Figure are closely arranged, and the orange particles are the center of the target area.
The primary measuring device for the settling experiment was a plexiglass round tube with an inner diameter of 55 mm, and the outer tube was covered with a circular water-proof plexiglass cylinder. As shown in Figure 2, the fluid temperature in the tube can be controlled by connecting the water bath heating device, and the experimental temperature is set to 25°C ± 0.5. To facilitate the deformation and dispersion of observation clusters at different stages, observation points were marked at 0.05-m intervals from the upper part of the pipeline. At the same time, a length of 0.1 m was left at the bottom to eliminate the influence of accumulated particles on the settlement velocity of clusters.
Before the experiment, the required fluid is poured into the inner tube of the device and heated for 2–4 h. The experiment begins when the gas in the fluid entirely escapes and reaches the set temperature. To eliminate the influence of the wake of the previous group during the experiment, each group should be static for 10–15 min after the experiment to make the flow field of the fluid in the tube reach a stable state. To reduce the error caused by the operation, the experiment was repeated 8–10 times for each group. During the experiment, the particle was classified according to the sieve diameter, and the particle surface was rough and varied. However, the single-particle size is much smaller than the cluster size, so the influence of particle irregularity is ignored in the analysis process.
In this paper, the cluster mold with regular cylinder shape is made by referring to the cluster initial shape in the literature. The mold is made of a copper circular cylinder with an inner diameter of 10 mm and a height of 3.5 mm. The particle and mold are wetted with solution, and the particle is packed in clusters within the mold. In order to analyze the effect of fiber mesh structure on particles, polyester fibers with length of 3 mm and diameter of 6 μm were evenly mixed into particles.
For the purpose of comparing the effects of different rheological properties, glycerin and HPG base fluids were used in this work. Glycerol is a typical Newtonian fluid. The density is about 1.26 g/cm3. A ZNN-D6 six-speed rotational viscometer was measured in glycerol (80%, 85%, and 95%) at fixed temperature (25°C). HPG is a galactomannan with linear macromolecule structure, good water solubility, and pH stability. HPG is often used to configure slick water fracturing fluid base fluids during fracturing operations. A Physica MCR301 rheometer was used to measure the rheological properties of HPG (0.3%, 0.4%, and 0.5%) at fixed temperature (25°C).
Figure 3 shows the viscosity variation laws in different concentrations of the fracturing fluid. The measured results showed that with the shear rate changing from low to high, the fluid apparent viscosity change range becomes small. The viscosity decreases with the increase of shear rate in the initial stage and then the change rules similar to Newtonian fluid characteristics in the middle region. By further fitting the shear stress test results of HPG, the variation trend in the measured interval conforms to the characteristics of the power-law fluid. The power-law fluid constitutive model is used to characterize fluid rheological properties.
where K is the consistency coefficient and n is the rheological index. The viscosity of glycerol decreased exponentially after dilution, and fitting parameters are shown in Table 1.
where c is the concentration of fluid and ρf is the fluid density. In order to achieve better simulation effect, the simulation parameters are set according to the measurement results. Using a viscometer to measure the apparent viscosity of the two types of fluid, it can be found that the values are relatively close, so the two groups of experiments have a certain comparative value.
It is difficult to analyze the action mechanism only using experiments because cluster shape and velocity variation are complicated. This paper uses the discrete element method to couple the motion process of particles and fluid. The changing trend of clusters can be predicted by analyzing the force of particles at different positions.
1) Particle governing equation
The interaction between particles can be described in terms of forces and torques only when they are in contact with each other and their motion is independent.
where fci is the contact force between particles; ff,pi is the interaction between the fluid and particles; vi is the speed of particles; mi is the mass of particles; Ii is the moment of inertia of particles; Ti is the moment generated by the tangential component of the contact force between particles; and ωi is the angular velocity of particles.
The interaction between particles was characterized by the Hertz–Mindlin contact model, and the contact force between particles was calculated by a soft sphere model. This model is also known as “elastic - damped - friction contact mechanical model".
2) Incompressible fluid governing equation
The fluid calculation model is based on Navier–Stokes equation, and the effect of solid particles on the fluid is considered. An additional volume fraction phase ε is added into the conservation equation to obtain the fluid continuous phase equation and momentum conservation equation.
where u is the fluid velocity, τf is the fluid viscous stress, ff,pi is the fluid–particle interaction force acting on particles, and nc is the number of particles in the fluid element with volume ΔVc. During the study, fluid mechanical properties can be obtained by assuming that the fluid has a viscous stress tensor.
where μb is the volume viscosity of the fluid, μs is the shear viscosity of the fluid, and vpi is the volume of particles in the fluid. At the same time, the fluid volume fraction can be obtained according to the proportion of sample points on the surface of the particle boundary in the fluid grid cell.
Because the Reynolds number of settling particles in the stationary fluid is relatively small and the fluid flow state is simple, the laminar flow model is usually used to simulate the fluid part.
3) CFD-DEM coupling
In the coupling process, the Di Felice (Di Felice 1994) resistance calculation model was adopted. A void fraction correction term was added based on the free flow model to consider the influence of void fraction on the resistance of adjacent particles.
where χ is the variable introduced to consider the influence of fluid on other particles in the calculation process, the subscript j represents the fluid unit where particle i resides, CDi is the fluid resistance coefficient suffered by the particle, and Repi is the Reynolds number under the relative velocity of particle and fluid. The expressions of different calculation parameters are given as follows:
During the numerical simulation process, the computational domain is discretized into several fluid elements. All the fluid parameters are averaged within the CFD grid element, and the particles are smaller in volume than the fluid grid element, so the fluid parameters around the particles are basically unchanged.
The experiment research shows that the cluster shape change is non-equilibrium in different directions. So the dynamic behavior of cluster settling can be divided into long-range interaction (i. e., the interaction of the cluster and fluid) and short-range interaction (i. e., interaction between particles inside the cluster), according to the difference in the scale of the research objects. To characterize the long-range interaction change rules in the settlement process, the dimensionless inertial length l* (Pignatel, Nicolas et al., 2011) can be obtained as follows:
where a is the particle radius; Rc is the equivalent hydraulic radius; Rep is the Reynolds number of particles. According to the results of rheological measurement and settling velocity calculation results, the fluid Reynolds number in different conditions can be obtained.
Reynolds number for Newtonian fluids
where v is the velocity of particle and d is the diameter of the particle.
Reynolds number for non-Newtonian fluids
In addition, the particle inertial length l* was used as the criterion for the deformation condition of clusters. The aspect ratio γ = L/D (Metzger 2007; Lin, Tan et al., 2016) is used to express the shape change rules of clusters, where L is the length of clusters in the horizontal direction and D is the height of clusters in the vertical direction. Each frame was thresholded, and the cloud contour was fitted with an ellipse under ImageJ. The Reynolds number of cluster Rec and the number of particles N are also important indicators to measure clusters. The equivalent hydraulic radius Rc = Na (6v/5V), and V is the velocity of cluster. We also consider the cluster settling model in non-Newtonian fluids (Xu, Song et al., 2019) and Newtonian fluids (Chen, Chen et al., 2021).
The diffusion trend of particles in the vortex is mainly affected by Stokes force, so the clusters aggregate during the transport process could be called Stokes clouds. The repulsion interactions decrease between particles during the diffusion of clusters, so the clusters in the process of subsidence deformation are dominated by the long-range interaction. The dynamics characteristics of clusters are analyzed through the change rules of inertial length and aspect ratio in different conditions, and the variation law of particle velocity at different positions could refer to the numerical simulation results.
In the coupling simulation process, CFD simulation calculation is carried out at first, and then the DEM solver is used for iterative calculation according to the fluid conditions in the grid cell where the particles are located, and the model parameters were set up according to the experimental results. In the high-viscosity fluid, the diffusion trend of particles decreases obviously and the shape changes are more regular. Therefore, the experiment and numerical simulation results were compared with the settling characteristics of clusters in the 95% glycerol. A 0.425–0.600 mm ceramic particle with a density of 2.7137 g/cm3 was used. For the purpose of proving the accuracy of simulation results through experiment, the distance between recording points is 0.05 m.
The shape change rules of numerical simulation are similar to those of the experimental simulation as shown in Figure 4A, and we can see the velocity variation law of particles at different positions in Figure 4B. The velocity fluctuations arising from hydrodynamic interactions cause particles to depart from the closed toroidal circulation. Due to the vortex expansion trend of internal flow field, the contact between particles is weakened, and the particles hindered is strength. In the cluster settlement process, particles on the cluster surface will move along the boundary layer of the fluid due to drag force. Under the impact of Magnus effect, the particle in the cluster tends to move outward. The cluster breaks up while settling, with leakage particles from the cloud due to differential velocity. The effect of leakage particles on cluster shape was neglected in 95% glycerol.

FIGURE 4. Shape and velocity change rules of the cluster in 95% glycerol. (A) Experiment results of settling cluster. (B) Simulation results of settling cluster.
The basic settling dynamics was revealed by numerical results. In the settling stage, the shape of clusters was compressed vertically and stretched horizontally shown in Figure 4, calculating variables of the cluster shape by each frame. Comparing the change rules of simulation with the experiment in Figure 5, the average error is about 4.72% from results. In summary, the numerical results compared well to the experimental data that verified the applicability of the numerical approach.
1) Cluster shape change rules in glycerol
Different from the dynamics behavior of single particles in the settlement process, the drag force on particles in the cluster is related to the position of particles. With the hydrodynamic behavior of the flow field, the settling cluster has different shape change degrees. The vortex expansion of the fluid results in the enhancement of particle hindered velocity, which leads to cluster break up. The velocity of the particle inside the cluster not only shows the intensity of short-range interactions but also shows the effect of fluid drag force.
At the initial stage, the difference in particle settling velocity inside the cluster is small and the cluster shape change rules are regular. From Figure 6, it can be seen that the cluster shape is affected by fluid viscosity during the settlement process significantly. In the process of cluster settlement, the difference in particle velocity between the middle and the border increases gradually. When settling in Figure 6A with low viscosity, the cluster disperses rapidly along both sides of the central axis in a cloud shape and the distance between particles increases. With the increase of fluid viscosity, the degree of sub-cluster shape change and dispersion decreases Figure 6B. When the dynamics behavior between viscosity fluid and particle cluster are close to the equilibrium state, the cluster shape tends to be stable in Figure 6C gradually.
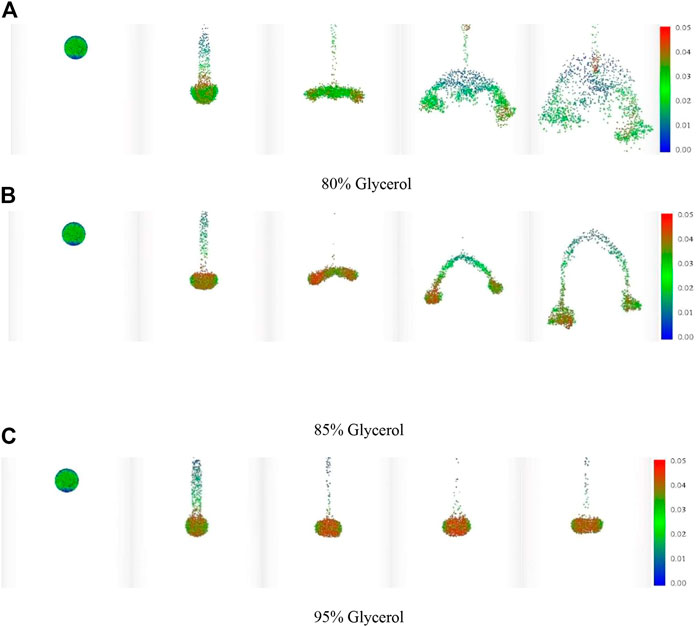
FIGURE 6. Particle velocity inside the cluster in glycerol (N = 5,000). (A) 80% Glycerol, (B) 85% Glycerol, (C) 95% Glycerol.
Under the action of fluid viscous force, a large number of particles fall off from the cluster during the settling process. With the effect of particle fall-off and interference inside the cluster, the clusters show different deformation trends. In terms of shape and velocity changes, the vertical components of clusters have great differences, and there is an obvious diffusion trend. Compared with the dynamics behavior of the vertical component, the horizontal component has little difference and certain symmetry.
2) Cluster shape change rules in HPG
According to the study of the cluster settling characteristics in glycerol, the hydrodynamic behavior of the fluid is the main factor affecting the particle trajectory. As a viscoelastic fluid, the dynamic behavior of particles inside the clusters in HPG is more complex. The influence of fluid rheological property on the particle trajectory was analyzed, by comparing with the change rules of cluster shape and velocity in different HPG concentrations.
The shape change rules of settling clusters in Figure 6 are similar to those of Figure 7 clusters, but there are also obvious differences. The sub-cluster breakup is observed along the parabolic trajectory in Figure 6A , and the particles inside the sub-cluster still have an obvious aggregation trend in low concentration. According to the cluster simulation results in HPG, the variation range of particle velocity increases significantly. Figure 7A shows the initial cluster breakup to sub-cluster secondary clusters with low viscosity in HPG. Figure 7B shows the diffusion trend of cluster decreases obviously with viscosity increase in HPG. Compared with the settling velocity of clusters in glycerol, it can be seen that the effect of the internal flow field is weakened after the shape is stabilized. With the increasing concentration, the stability of the cluster settlement process in the HPG is enhanced gradually in Figure 7C. This is because the viscoelastic fluid exhibits viscosity and elasticity at the same time. According to the experimental study of Cressman et al. (Cressman, Bailey et al., 2001), compared with Newtonian fluid, the wake vortex shedding in the wake field of cylinder flow around a cylinder in the viscoelastic fluid was significantly inhibited, resulting in a significantly elongated reflux region. The results show that viscoelastic fluid can suppress the three-dimensional instability and disorder of the flow field, reduce the vortex near the settling particles, and thus weaken the interference between particles.
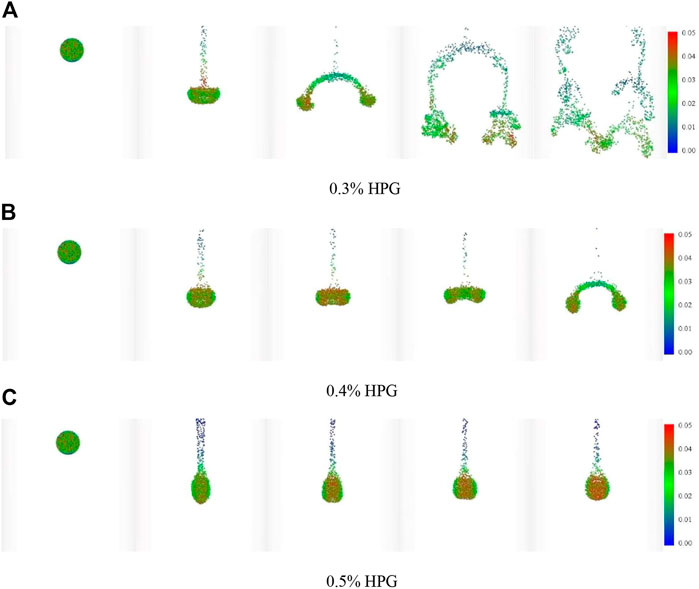
FIGURE 7. Particle velocity inside the cluster in HPG (N = 5,000). (A) 0.3% HPG, (B) 0.4% HPG, (C) 0.5% HPG.
As can be seen from Figure 6 and Figure 7, the cluster first compresses vertically and expands horizontally. Particles circulate inside clusters, which is similar to the circulation of the internal flow field during droplet movement (Yang, Li et al., 2015). At the same time, particle escape can be observed at the tail of the particle swarm. The flattened particle groups continue to expand and break into multiple sub-particle groups. These characteristics are similar to the settlement experiment and simulation results of particle groups in the literature. The particle cluster evolution in glycerol is affected by viscosity. The viscous force and inertia force jointly determine the motion trend of particles, and the viscous force dominates when the Reynolds number is low. We can confirm in power-law fluid that this change would be amplified. The cluster is more difficult to break up in the power-law flow. Under low Reynolds number conditions, the ability to maintain cluster shape stability in HPG fluid is greater than in glycerol.
The numerical model was verified by the experiment result, so the dynamics behavior of particles inside the settling cluster is characterized by the simulation results. It shows the trajectory and velocity of particles, so we can analyze the resistance change in the settlement process. The cluster deformation affects the drag force of particles at different positions, and then particle transport at different positions causes the cluster shape change. Through the short-range interaction, the particle settling velocity and fluid drag force can characterize the dynamic behavior inside the cluster.
The cluster Reynolds number Rec = 112 (80% glycerol), 57 (85% glycerol), and 15 (95% glycerol) in simulations. In Figure 8, we can see the variation of particle average velocity at different positions and the average velocity of all particles inside the clusters. The middle is the center of mass, left and right were distributed at both ends of the horizontal direction, and the upside and bottom were distributed at both ends of vertical direction. In addition, the solid and hollow points (same color) represent the average settling velocity of particles in the same area at different sections. The variation of particle velocity at different positions corresponds to the shape change rules. The velocity increases at the initial state while cluster deformation is little, and then the velocity decreases because particles leak off and cluster breakup in Figures 8A,B.
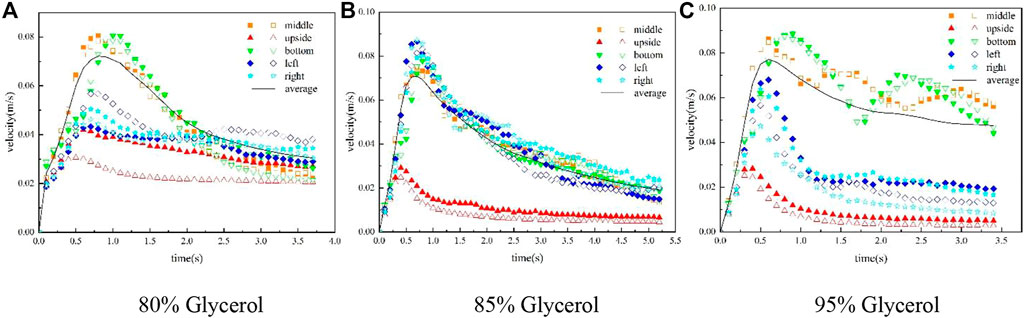
FIGURE 8. Particle velocity inside the clusters in glycerol. (A) 80% Glycerol (B) 85% Glycerol (C) 95% Glycerol.
According to the research results of Metzger B, a vortex is generated in the flow field inside the undispersed cluster during the settling process. Some particles transport with the fluid inside the cluster because of the vortex, while others move to the boundary and then slowed down and separated. This hypothesis was verified by analyzing the velocity fluctuation of internal particles in a 95% glycerol, and the particle velocity at the center and bottom positions fluctuates significantly due to eddy current from Figure 8C.
The cluster Reynolds number Rec = 155 (0.3% HPG), 51 (0.4% HPG), and 16 (0.5% HPG) in simulations. Figure 9 shows particle velocity inside the clusters in HPG during the settlement process, and the fluctuation range of velocity variation law is larger than that in Figure 8. The particle velocity change is similar to Figures 9A, B, which decreased significantly after cluster dispersion. This is caused by shear thinning of the fluid. The viscoelasticity hinders the cluster of fluid breakup and weakens vortex flow strength and the transport trend of particle velocity at different positions. Comparing Figure 8C with Figure 9C, the change range of particle velocity in the middle area inside the cluster decreased obviously. The sub-cluster deformation in HPG is weak, and the particle settling velocity variation in glycerol amplitude reduces. On one hand, due to the rheological characteristics, the settling velocities of clusters and single particles in HPG are more different than those in glycerol. On the other hand, under the influence of the deformation process, the particle velocity changes differently at different positions.
According to the literature research and dynamic behavior analysis results, HPG is more suitable for the study of settling characteristics. Based on the research of cluster shape and particle velocity change rules, the sensitivity parameters of settling characteristics with different particle physical properties in 0.4% HPG were analyzed.
A parametric study with five simulations was implemented covering three sizes and three densities of particles. The cluster Reynolds number Rec = 61 (case A), 51 (case B), 44 (case C), 61 (case D), and 79 (case E) in simulations. The particle cases are summarized in Table 2, which lists the corresponding property. The effect of particle size could be compared by cases A, B, and C. The effect of particle density could be compared by cases B, D, and E.
As shown in Figure 10, the magnitude of shape change of the cluster is similar in most cases. The deformation with different physical properties of particles has little difference at the initial state and then the cluster shape changes with the increase of settlement distance. According to the simulation results, the settlement is accompanied by particle leakage and it is obvious when the particle density is large like in case E.
The average settling velocity of particles inside the cluster is shown in Figure 11, and the variation law of settling velocity is closed with different physical properties in most cases. It increases to a different degree in the initial stage and then reduces to a fixed value gradually. Comparing five simulations in Figure 11, the settling velocity is greatly affected by particle density. The results of cases A, B, and C are similar throughout the whole settlement process; the size of particles has little effect on the dynamics behavior relatively.
1) Comparison with different concentrations of HPG
The interaction of particles, fibers, and fluids is characterized by studying the dynamic behavior of mixed-fiber clusters in the settlement process. Through the research of numerical simulation mentioned previously, the fluid rheological characteristic is the main factor that affects the cluster shape and velocity change rules. The effect of fiber barrier is obvious in HPG from experimental results, so the characteristics of cluster settlement in different fluids are compared.
During the experimental study on the dynamics behavior of the mixed-fiber clusters, the fiber volume concentration always holds at 0.5%. Figure 12 shows the shape changes rules of the mixed-fiber clusters under different HPG concentrations. The shape of clusters in Figures 12A,B did not reach to stable state, and Figure 12C is dynamic equilibrium. The cluster shape in the vertical component decreases with the increase of HPG concentration, which due to the influence of hydrodynamic behavior. With the HPG concentration increasing, the deformation of the mixed-fiber clusters in the horizontal component decreased gradually. The cluster reaches dynamic equilibrium when the HPG increases to 0.5%, and the cluster shape hardly changes during the settlement process.
(2) Comparison with different fiber concentrations
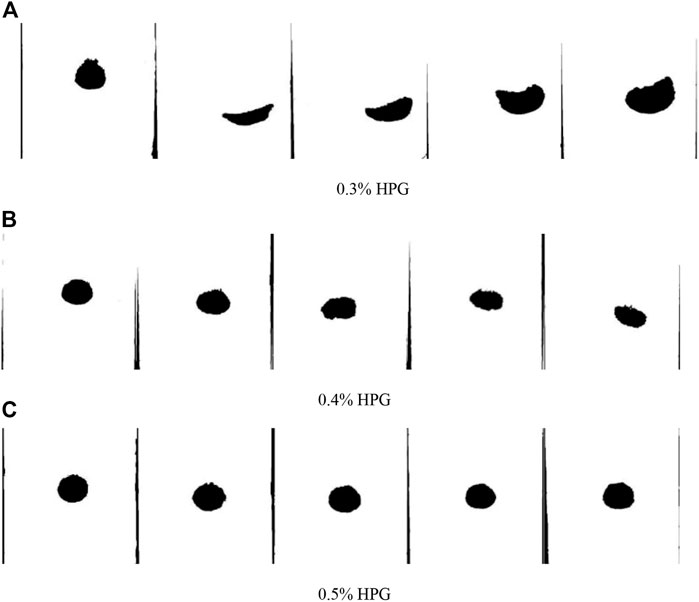
FIGURE 12. Shape change rules of 0.5% fiber-containing cluster. (A) 0.3% HPG, (B) 0.4% HPG, (C) 0.5% HPG.
The dynamic behavior of mixed-fiber clusters during the settlement process reflects the constraint effect of the fiber grid structure. By studying the influence of fiber concentration on the cluster settling characteristics, the fiber barrier can be recognized more intuitively. To produce a better comparison, 0.3% HPG was used as the base fluid to analyze the impact of different mixed-fiber concentrations on the shape changes of clusters.
Under the condition without the fiber, the settling clusters can be divided into several sub-clusters with locally high concentrations. The shape of the sub-clusters under the low fiber concentration in Figure 13A is relatively regular compared with Finger 7 (A) variation law. In the unbreak-up stage with Figures 13B, C, the deformation of mixed fiber clusters is similar to that of charged particles in the electrostatic field under strong Coulomb force. After an initial stage of slight compression, the shape remains self-similar, but the cluster size increases.

FIGURE 13. Cluster shape change rules in 0.3% HPG-based fluid. (A) 0.3% Fiber, (B) 0.4% Fiber, (C) 0.5% Fiber.
Fiber grid structure not only resists the cluster shape change rules but also affects the cluster settling velocity in the equilibrium state. Based on the study of particle dynamics behavior inside the cluster, it can be seen that the fluid rheological property is the main factor affecting the settling characteristics. Richardson (Richardson and Zaki 1997) proposed a calculation method of hindered settling velocity for coarse sediment, and parameters in this model are modified by considering the dynamic behavior of the cluster region. It is reasonable to refer to this method because of the large particle concentration in the cluster area.
where wc is the cluster hindered settling velocity, m/s; ws is the single-particle settling velocity, m/s; ϕ is the particle-fiber mixed phase volume fraction inside the cluster; k is a dimensionless parameter, which used to characterize the influence by particle–fiber interaction, fluid rheology, and other factors.
where n is the rheological index and cf is the fiber content in the cluster. It is hard to measure the settling velocity at low concentrations because the settling cluster shape changes constantly. In the settlement process, the cluster can be regarded as being in the equilibrium state at 0.5% HPG from Figure 7C. To compare the effects of HPG and fiber concentration on settling characteristics at an equilibrium state, the settling velocity of clusters in 0.5% and 0.6% HPG was measured under different fiber concentrations.
We can see the average relative error is about 2.32% from Figure 14, the point is the experiment result, and the line is the calculation result. With the increasing fiber concentration, the settling velocity of clusters decreases exponentially. Under the different fiber concentrations, the average deviation of cluster settling velocity in 0.5% and 0.6% HPG is small. By measuring the settling velocity of clusters under different conditions, this work modifies the dimensionless parameters in the model. Based on the variation law of the cluster settling velocity in the equilibrium state, the dynamic behavior affected by the fiber barrier is known.
Combined with the numerical and experimental research results, this paper analyzes the dynamical behavior of particles in settling clusters in different conditions. The results show the different change degrees in the fluid rheological properties and particle properties on cluster dynamics behavior. In addition, the contact conditions between particles can change by fibers mixed into the cluster.
1) The simulation system reveals the dynamic behavior of the clusters in the settlement process. To gain insight into the influence of hindered flow upon the interactions of settling particles, we examined the evolution of settling velocity at different positions by CFD-DEM. It is the main reason for the different deformation trends between horizontal and vertical components. The cluster break up in the settlement process affects the shape change rules and velocity variation law. The numerical simulation results have high accuracy and meet the data requirements in the process of dynamic behavior analysis.
2) The process of settling clusters is affected by the fluid rheological properties. We can find that the change degree of the cluster shape in HPG is weaker than that in glycerol with similar apparent viscosity. Numerical simulation results show that guanidine gum solution increases the resistance to particles and inhibits the intensity of vortex in clusters, thus weakening the interference between particles.
3) The experiment results show that mixed-fiber clusters can affect the hindered settling process of particles, and the shape change degree of the settling clusters decreases. The fiber barrier resists the diffusion tendency of particles. So, with the increase in fiber concentration, the cluster settling velocity decreased exponentially.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
ZB: Writing–Original Draft; ML: Methodology and Writing–Review & Editing; FL: Formal analysis; QD: Investigation.
This study was funded by the China National Natural Science Foundation (Grant No. 52174056).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Chen, P., Chen, S., Yang, M., and Li, S. (2021). Falling clouds of particles with finite inertia in viscous flows. Phys. Fluids 33, 033314. doi:10.1063/5.0042658
Clark, P. E., Harkin, M. W., Wahl, H. A., and Sievert, J. A. (1977). “Design of A Large vertical prop transport model,” in Proceedings of the SPE annual fall technical conference and exhibition (Denver, Colorado:October 1977, Society of Petroleum Engineers).
Cressman, J. R., Bailey, Q., and Goldburg, W. I. (2001). Modification of a vortex street by a polymer additive. Phys. Fluids 13 (4), 867–871. doi:10.1063/1.1347962
Daugan, S., Talini, L., Herzhaft, B., and Allain, C. (2002). Aggregation of particles settling in shear-thinning fluids. Eur. Phys. J. E 7 (1), 73–81. doi:10.1140/epje/i200101116
Deepwell, D., and Sutherland, B. R. (2022). Cluster formation during particle settling in stratified fluid. Phys. Rev. Fluids 7 (1), 014302. doi:10.1103/PhysRevFluids.7.014302
Di Felice, R. (1994). The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 20 (1), 153–159. doi:10.1016/0301-9322(94)90011-6
Dizaji, F. F., Marshall, J. S., and Grant, J. R. (2019). Collision and breakup of fractal particle agglomerates in a shear flow. J. Fluid Mech. 862, 592–623. doi:10.1017/jfm.2018.959
Elgaddafi, R., Ahmed, R., George, M., and Growcock, F. (2012). Settling behavior of spherical particles in fiber-containing drilling fluids. J. Petroleum Sci. Eng. 84-85, 20–28. doi:10.1016/j.petrol.2012.01.020
Ghommem, M., Abbad, G., Aidagulov, D., Brady, D., and Science, P. (2021). Modeling of fiber bridging in fluid flow for well stimulation applications. Pet. Sci. 17, 671–686. doi:10.1007/s12182-019-00398-w
Gillard, M., Medvedev, O., Peña, A., Medvedev, A., Peñacorada, F., and d’Huteau, E. (2010). “A new approach to generating fracture conductivity,” in Proceedings of the SPE annual technical conference and exhibition (Florence, Italy:September 2010 Society of Petroleum Engineers). doi:10.2118/135034-MS
Guazzelli, É., and Pouliquen, O. (2018). Rheology of dense granular suspensions. J. Fluid Mech. 852, P1. doi:10.1017/jfm.2018.548
Guo, J., Ma, J., Zhao, Z., and Gao, Y. (2015). Effect of fiber on the rheological property of fracturing fluid. J. Nat. Gas. Sci. Eng. 23, 356–362. doi:10.1016/j.jngse.2015.02.017
Guo, J., Zhou, Q., and Wong, R. C.-K. (2022). Numerical investigation of particle cloud sedimentation in power-law shear-thinning fluids for moderate Reynolds number. Chem. Eng. Sci. 247, 117066. doi:10.1016/j.ces.2021.117066
Guo, J., Zhou, Q., and Wong, R. (2021). Effects of volume fraction and particle shape on the rheological properties of oblate spheroid suspensions. Phys. Fluids 33, 081703. doi:10.1063/5.0059346
Hu, X., Lin, J., Chen, D., and Ku, X. (2020). Influence of non-Newtonian power law rheology on inertial migration of particles in channel flow. Biomicrofluidics 14, 014105. doi:10.1063/1.5134504
Lin, Y., Tan, J., Phan-Thien, N., and Khoo, B. (2016). Settling of particle-suspension drops at low to moderate Reynolds numbers. Eur. J. Mech. - B/Fluids 61, 72–76. doi:10.1016/j.euromechflu.2016.11.003
Liu, C., Hu, G., Jiang, X., and Sun, J. (2014). Inertial focusing of spherical particles in rectangular microchannels over a wide range of Reynolds numbers. Lab. Chip 15, 1168–1177. doi:10.1039/c4lc01216j
Lobry, L., Lemaire, E., Blanc, F., Gallier, S., and Peters, F. (2019). Shear thinning in non-Brownian suspensions explained by variable friction between particles. J. Fluid Mech. 860, 682–710. doi:10.1017/jfm.2018.881
Medvedev, A. V., Kraemer, C. C., Pena, A. A., and Panga, M. K. R. (2013). “On the mechanisms of channel fracturing,” in Proceedings of the SPE hydraulic fracturing technology conference (The Woodlands, Texas, USA:February 2013 Society of Petroleum Engineers). doi:10.2118/163836-MS
Metzger, B., Nicolas, M., and Guazzelli, E. (2007). Falling clouds of particles in viscous fluids. J. Fluid Mech. 580, 283–301. doi:10.1017/S0022112007005381
Mingyang, S., and Lubin, W. (2018). A hindered settling velocity model based on pseudo-fluid analogy. J. China Coal Soc. 43 (2), 540–545. doi:10.13225/j.cnki.jccs.2017.0537
Mylyk, A., Meile, W., Brenn, G., and Ekiel-Jezewska, M. L. (2011). Break-up of suspension drops settling under gravity in a viscous fluid close to a vertical wall. Phys. Fluids 23 (6), 063302. doi:10.1063/1.3600660)
Nitsche, J., and Batchelor, G. (1997). Break-up of a falling drop containing dispersed particles. J. Fluid Mech. 340, 161–175. doi:10.1017/S0022112097005223
Papadopoulou, A., Gillissen, J. J., Wilson, H. J., Tiwari, M. K., and Balabani, S. (2020). On the shear thinning of non-Brownian suspensions: Friction or adhesion? J. Newt. Fluid Mech. 281, 104298. doi:10.1016/j.jnnfm.2020.104298
Pignatel, F., Nicolas, M., and Guazzelli, E. (2011). A falling cloud of particles at a small but finite Reynolds number. J. Fluid Mech. 671, 34–51. doi:10.1017/S0022112010005501
Rahim, Z., Waheed, A., Al-Kanaan, A., Yudin, A., Kayumov, R., Mauth, K., et al. (2022). Improved materials and modeling extend channel fracturing revolution. Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, March 2022 doi:10.2118/200060-MS
Richardson, J. F., and Zaki, W. N. (1997). Sedimentation and fluidisation: Part I. Chem. Eng. Res. Des. 75, S82–S100. doi:10.1016/S0263-8762(97)80006-8
Robinson, M., Ramaioli, M., and Luding, S. (2014). Fluid–particle flow simulations using two-way-coupled mesoscale SPH–DEM and validation. Int. J. Multiph. Flow 59, 121–134. doi:10.1016/j.ijmultiphaseflow.2013.11.003
Tang, W., Zhu, S., Jiang, D., Zhu, L., Yang, J., and Xiang, N. (2020). Channel innovations for inertial microfluidics. Lab. Chip 20 (19), 3485–3502. doi:10.1039/D0LC00714E
Volpe, A., Gaudiuso, C., and Ancona, A. (2019). Sorting of particles using inertial focusing and laminar vortex technology: A review. Micromachines 10 (9), 594. doi:10.3390/mi10090594
Wang, G., Wan, D., Peng, C., Liu, K., and Wang, L.-P. (2019). LBM study of aggregation of monosized spherical particles in homogeneous isotropic turbulence. Chem. Eng. Sci. 201, 201–211. doi:10.1016/j.ces.2019.03.004
Wang, W., and Zhao, H. (2022). Study on the mechanism of fiber fracturing fluid controlling pulverized coal transportation. Energies 15, 2165. doi:10.3390/en15062165
Xu, Z., Song, X., Li, G., Pang, Z., and Zhu, Z. (2019). Settling behavior of non-spherical particles in power-law fluids:Experimental study and model development. Particuology 46, 30–39. doi:10.1016/j.partic.2018.07.006
Yamashiro, B. D., and Tomac, I. (2021). Particle clustering dynamics in dense-phase particle-fluid slurries. Comput. Geotechnics 132, 104038. doi:10.1016/j.compgeo.2021.104038
Yang, M., Li, S., and Marshall, J. S. (2015). Effects of long-range particle-particle hydrodynamic interaction on the settling of aerosol particle clouds. J. Aerosol Sci. 90, 154–160. doi:10.1016/j.jaerosci.2015.08.002
Zenit, R., and Feng, J. J. (2018). Hydrodynamic interactions among bubbles, drops, and particles in non-Newtonian liquids. Annu. Rev. Fluid Mech. 50 (1), 505–534. doi:10.1146/annurev-fluid-122316-045114
Keywords: fiber barrier, CFD-DEM method, cluster settling, hydrodynamics behavior, rheological properties
Citation: Bai Z, Li M, Li F and Du Q (2022) Study on particle cluster dynamics behavior in settling and the influence by fiber barrier. Front. Mater. 9:1081613. doi: 10.3389/fmats.2022.1081613
Received: 27 October 2022; Accepted: 15 November 2022;
Published: 06 December 2022.
Edited by:
Jiapei Du, RMIT University, AustraliaReviewed by:
Shiqian Xu, Southwest Petroleum University, ChinaCopyright © 2022 Bai, Li, Li and Du. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mingzhong Li, bGltaW5nemhvbmdfdXBjQGhvdG1haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.