Numerical analysis of non-Newtonian nanofluids under double-diffusive regimes

In the present study, the slip velocity of a non-Newtonian fluid flowing above a continuously stretching surface with double-diffusive nanofluid is examined at prespecified values of surface temperature, while also accounting for salt concentration. An initial set of partial differential equations, along with the boundary conditions, are first cast into a dimensionless form; subsequently, the comparation variables are invoked to reduce the partial differential equations to ordinary differential equations; and finally, the reduced ordinary differential equations are solved numerically via the shooting method. Values for dimensionless velocity, temperature, salt concentration distribution, local Nusselt number, and Sherwood number are calculated numerically and presented visually in a set of graphs. A extensive parametric study is conducted to probe the effects of adjusting various parameters in the cases of both assisting and opposing flow.

Introduction

Non-Newtonian fluids moving over a porous, continuously stretching sheet, especially in the presence of slip, have generally garnered extensive attention owing to their numerous applications in engineering processes for both micro- and macro-scale apparatuses (Kim et al., 2002; Johnson et al., 2008). In manufacturing, it has been generally recognized that non-Newtonian fluids are more suitable than Newtonian fluids, perhaps due to their wide range of applications in fluid mechanics. Examples of such fluids include shampoo, paints, clay coatings and suspensions, grease, cosmetic products, blood, and body fluids, among many others (Jang and Lee, 2000; Iverson and Garimella, 2008). As we know, biological fluids are characteristically non-Newtonian. A detailed non-Newtonian fluid analysis with different (Ellahi, 2009; Ellahi and Afzal, 2009; Ellahi and Riaz, 2010; Nadeem et al., 2013a; Sher Akbar et al., 2013a).

A nanofluid is a fluid containing nanometer-sized particles, called nanoparticles. For more than half a century, nanofluids have been developed and used in anticancer drug targeting; see (Folkman and Long, 1964) and (Xiao et al., 2018). Beyond the pharmaceutical industry, nanofluids have a major set of applications in the study of processes involving heat generation, including space heating, power generation, transportation, and manufacturing. The presence of nanoparticles may lead to significant modification of the thermodynamic properties of the base fluid. Thus, nanoparticles enable tailoring of important properties of their base fluids. Accounts of the development of various nanofluids and investigations of their thermal conductivity can be found in (Choi et al., 1995; Xuan and Li, 2000; Choi et al., 2001). Choi (Choi et al., 1995), in this context, discusses the role of low thermal conductivity and is of the opinion that this limits the development of energy-efficient heat transfer fluids, which have become a key requirement in many industrial applications. Choi (Choi et al., 1995) proposes that it may be possible to design a new class of heat transfer fluids by omitting the metallic nanoparticles contained in conventional heat transfer fluids. In (Xuan and Li, 2000), a theoretical model is proposed to promote the transmission of heat laterally with dispersion of solid particles. Discussion of the shapes, sizes, and volume fraction of nanoparticles can also be found in (Xuan and Li, 2000). Masuda et al. (Masuda et al., 1993) propose the modification of the thermal conductivity and viscidness of liquids by means of scattering of ultra-fine particles. Furthermore, deliberations on nanofluid coolants for progressive nuclear power plants are presented by Buongiorno and Hu (Buongiorno and Hu, 1920). Analyses of heat transfer in relation to nanofluids are provided by Xuan and Roetzel (Xuan and Roetzel, 2000). Recently, boundary-layer flow and heat transfer in a viscous fluid comprising metallic nanoparticles over a non-linearly stretching sheet have been examined by Hamad and Ferdows (Hamad and Ferdows, 2012). They discuss multiple dissimilar types of nanoparticles and propose that the behavior of the fluid flow varies with the type of nanoparticles. The Oldroyd-B model is well known for elucidating the behavior of polymeric fluids in terms of retardation time, relaxation time, and viscosity. A significant study on Oldroyd-B fluids can be found in (Lozinski and Owens, 2003), wherein Lozinski and Ownes offer a numerical scheme for energy estimates for the stresses of an Oldroyd-B fluid and suggest that conventional schemes may lead to a violation of energy evaluation. It is clear from this overview that work on Oldroyd-B fluids and nanofluids is very limited. Nadeem et al. (Nadeem et al., 2013b) measure two-dimensional steady incompressible Oldroyd-B nanofluid flow past a stretching sheet. According to these authors, the various Oldroyd-B parameters exert conflicting effects on behavior in terms of velocity, temperature, and mass fraction function. Recently, the effects of heat on an Oldroyd-B nanofluid flowing over a bidirectional stretching sheet have been examined in (Azeem Khan et al., 2014). More recently still, Sandeep et al. (Sandeep et al., 2015) have conducted a comparative study examining heat and mass transfer in non-Newtonian nanofluids flowing over a stretching sheet. According to (Sandeep et al., 2015), the heat and mass transfer rate is higher in Oldroyd-B nanofluids than in Jeffery and Maxwell nanofluids. New publications in the literature on nanofluids include (Noreen et al., 2013; Sher Akbar et al., 2013b; Zaib et al., 2019; Khan et al., 2021a; Khan et al., 2021b).

In the current study, we consider Oldroyd-B double-diffusive nanofluid flow over a stretching sheet at prespecified values for surface temperature and salt concentration. The partial differential equations governing this system, along with the boundary conditions, are reduced to ordinary differential equations using similarity transformation; subsequently, these reduced ordinary differential equations are solved numerically using the shooting method. A complete parametric study is presented to explore the effects of the relevant parameters on both assisting and opposing flow both explicitly and in physical terms.

Mathematical development

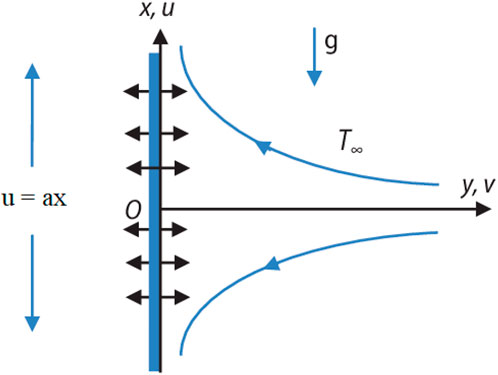
We consider the two-dimensional, laminar boundary layer flow of an Oldroyd-B nanofluid over a continuously stretching surface at a prespecified surface temperature in the presence of a particular salt concentration. It is assumed in solving the problem that the Oldroyd-B non-Newtonian nanofluid is incompressible. The governing equations for velocity under slip-flow boundary conditions at the walls are considered to capture the relevant physical processes. The model used for the fluid incorporates the effects of double diffusion. The positive y-coordinate is measured normal to the sheet, while the x-coordinate is taken transverse to it. The corresponding velocity components in the x and y directions are u and v, respectively. The physical model for the flow geometry is shown in Figure 1.

FIGURE 1

FIGURE 1. Physical model.

We now make the standard boundary layer approximation, based on a scale analysis, and write the governing equations:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$\begin{array}{l}u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}+{\mathrm{\Lambda }}_1\left(u^2\frac{{\partial }^{2}u}{\partial x^2}+v^2\frac{{\partial }^{2}u}{\partial y^2}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}\right)=\nu \frac{{\partial }^{2}u}{\partial y^2}\\ +{\mathrm{\Lambda }}_2\left(u\frac{{\partial }^{3}u}{\partial x\partial y^2}+v\frac{{\partial }^{3}u}{\partial y^3}-\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}-\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}\right)\\ +\left[-g\left({\rho }_p-\rho \right)\left(\varphi -{\varphi }_{\infty }\right)+\left(1-{\varphi }_{\infty }\right)\rho \left(g{\beta }_T\left(T-T_{\infty }\right)+g{\beta }_C\left(C-C_{\infty }\right)\right)\right]\end{array}(2)$

$\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\tau \left[D_B\frac{\partial T}{\partial y}\frac{\partial \phi }{\partial y}+\left(\frac{D_T}{T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}^2\right]+D_{TC}\frac{{\partial }^{2}C}{\partial y^2},(3)$

$\left(u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}\right)=D_S\frac{{\partial }^{2}C}{\partial y^2}+D_{CT}\frac{{\partial }^{2}T}{\partial y^2},(4)$

$\left(u\frac{\partial \phi }{\partial x}+v\frac{\partial \phi }{\partial y}\right)=D_B\frac{{\partial }^2\varphi }{\partial y^2}+\left(\frac{D_T}{T_{\infty }}\right)\frac{{\partial }^{2}T}{\partial y^2}.(5)$

$u=u_w\left(x\right)=ax,v=0,T=T_w,C=C_w,\varphi ={\varphi }_w,\mathrm{a}\mathrm{t}\mathrm{y}=0(\mathrm{6a})$

$u\to 0,v\to 0,T\to T_{\infty },C\to C_{\infty },\varphi \to {\varphi }_{\infty },\mathrm{a}\mathrm{s}y\to \infty ,(\mathrm{6b})$

where $\alpha =\frac{k}{{\left(\rho c\right)}_p},\tau =\frac{{\left(\rho c\right)}_p}{{\left(\rho c\right)}_f}$.

The similarity transformations for this problem can be written as:

$u=ax{f}^{\prime }\left(\eta \right)v=-\sqrt{\left(a\nu \right)}f\left(\eta \right),\eta =\sqrt{\left(\frac{a}{\nu }\right)},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\gamma \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\xi \left(\eta \right)=\frac{\varphi -{\varphi }_{\infty }}{{\varphi }_w-{\varphi }_{\infty }},(7)$

$f^{‴}-{\left(f^{\prime }\right)}^2+f{f}^{″}-{\beta }_1(f^2{f}^{″}-2ff\prime f^{″})-{\beta }_2{\left(f{f}^{⁗}-(f^{″}\right))}^2+G_r\left(\theta +N_c\gamma -N_r\xi \right)=0,(8)$

${\theta }^{″}+\mathrm{Pr}f{\theta }^{\prime }+N_b{\theta }^{\prime }{\xi }^{\prime }+N_t{{\theta }^{\prime }}^2+N_d{\xi }^{″}=0,(9)$

${\gamma }^{″}+\mathrm{Pr}Lef{\gamma }^{\prime }+Ld\mathrm{Pr}{\theta }^{″}=0,(10)$

${\xi }^{″}+\mathrm{Pr}Lnf{\xi }^{\prime }+\frac{N_t}{N_b}{\theta }^{″}=0,(11)$

$f\left(0\right)=0,f^{\prime }\left(0\right)=1+\beta f^{″}\left(0\right),\theta \left(0\right)=1,\gamma \left(0\right)=1,Nb{\xi }^{\prime }\left(0\right)+Nt{\theta }^{\prime }\left(0\right)=0,f^{\prime }\left(\infty \right)=0,\theta \left(\infty \right)=0,\gamma \left(\infty \right)=0,\xi \left(\infty \right)=0,(12)$

where

$R_{ax}=\frac{u_w\left(x\right)x}{\nu },G_T=\frac{\left(1-{\phi }_{\infty }\right){\rho }_{f\infty }g{x}^3{\beta }_T\left(T_w-T_{\infty }\right)}{{\nu }^2},G_r=\frac{G_T}{{R_{ax}}^2},\beta =\frac{N_{1}v{R_{ax}}^{\frac{1}{4}}}{L},N_c=\frac{B_r}{G_r}=\frac{B_C}{G_T}=\frac{{\beta }_C\left(C_w-C_{\infty }\right)}{{\beta }_T\left(T_w-T_{\infty }\right)},\mathit{Pr}=\frac{\mathit{\nu }}{\mathit{\alpha }}.{\mathit{N}}_{\mathit{d}}=\frac{{\mathit{D}}_{\mathit{T}\mathit{C}}\left({\mathit{C}}_{\mathit{w}}-{\mathit{C}}_{\infty }\right)}{\mathit{\alpha }\mathit{\Delta }\mathit{T}},{\mathit{L}}_{\mathit{e}}=\frac{\mathit{\alpha }}{{\mathit{D}}_{\mathit{B}}},N_t=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{\nu T_{\infty }}.{\mathit{N}}_{\mathit{b}}=\frac{\mathit{\tau }{\mathit{D}}_{\mathit{B}}\left({\mathit{\phi }}_{\mathit{w}}-{\mathit{\phi }}_{\infty }\right)}{\mathit{\nu }},L_d=\frac{∆T{D}_{TC}}{∆C{D}_S},L_n=\frac{\alpha }{D_B},N_{\gamma }=\frac{\left({\rho }_{p-}{\rho }_{f\propto }\right)∆\varnothing }{\left({\rho }_p-{\rho }_{f\propto }\right)\beta ∆T\left(1-{\phi }_{\infty }\right)}.(13)$

in which $R_{ax}$ is the local Reynolds number, $\beta =\frac{N_{1}v{R_{ax}}^{\frac{1}{4}}}{L}$ G_T is the local thermal Grashof number, G_r is the local Grashof number, β is the slip parameter, N_c is the ratio of the buoyancy forces B_r to the local Grashof number, Pr is the effective Prandtl number, N_d is the modified Dufour parameter, Le is the Lewis number, N_t is the thermophoresis parameter, N_b is the Brownian motion parameter, L_d is the Dufour Lewis number, L_n is the nanofluid Lewis number, and $N_{\gamma }$ is the nanofluid buoyancy ratio.

Expressions for the local Nusselt number and the local Sherwood number are defined as:

$\mathit{N}\mathit{u}=\frac{{\mathit{x}\mathit{q}}_{\mathit{w}}}{\mathit{\alpha }\left({\mathit{T}}_{\mathit{w}}-{\mathit{T}}_{\infty }\right)},Sh=\frac{x{q}_m}{\alpha \left(C_w-C_{\infty }\right)},(14)$

$q_w=-\alpha \left(\frac{\partial T}{\partial y}\right),q_m=-\alpha \left(\frac{\partial C}{\partial y}\right).(15)$

$\mathrm{R}{{\mathrm{e}}_x}^{-1/2}N{u}_x=-{\theta }^{\prime }\left(0\right),\mathrm{R}{{\mathrm{e}}_x}^{-\frac{1}{2}}S{h}_x=-{\gamma }^{\prime }\left(0\right).(16)$

Discussion

The initial differential equations, along with the appropriate boundary conditions, were solved using the shooting method. The effects of various relevant parameters on double-diffusive absorption can also be examined for the Oldroyd-B fluid. A range of graphs are presented below for comparison of the properties of assisting and opposing flow. Figures 2A–C illustrates the effects on local Grashof number of variation in Deborah number (as a relaxation parameter) and nanofluid buoyancy ratio. It is realistic that, in the case of both assisting and opposing flow, the velocity profile decreases with an increase in local Grashof number. The rise in the local Grashof number shows that the buoyancy effects supersede those of the viscous forces. Deborah number is associated with the nature of the fluid material: low Deborah number values indicate that the fluid will act like a Newtonian fluid, and higher values correspond to non-Newtonian fluid behavior. Figure 2B illustrates that the velocity profile decreases with an increase in Deborah number, while Figure 2C illustrates that the velocity profile decreases with an increase in the nanofluid buoyancy ratio. Figures2A–C illustrate that whether an assisting or opposing flow regime is in operation does not affect the behavior of the velocity profile.

FIGURE 2

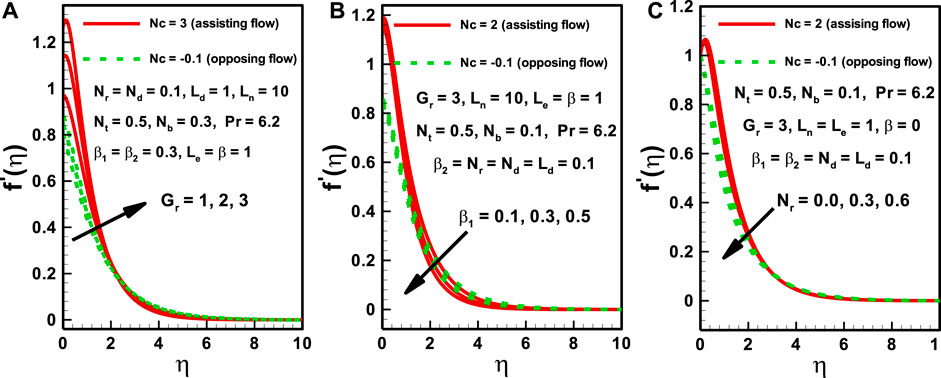
FIGURE 2. Effects of various parameters on dimensionless velocity for both assisting and opposing flows.

The plots in Figures 3A–C present the effects of local Grashof number, Deborah number, and nanofluid buoyancy ratio on temperature profile for assisting and opposing flow regimes. The temperature profile decreases with an increase in local Grashof number, while it increases with an increase in Deborah number and nanofluid buoyancy ratio. Once again, it can be observed that the temperature profile behaves similarly for the assisting and opposing flow regimes. The thickness of the thermal boundary layer decreases with an increase in local Grashof number, while it increases with an increase in Deborah number and nanofluid buoyancy ratio.

FIGURE 3

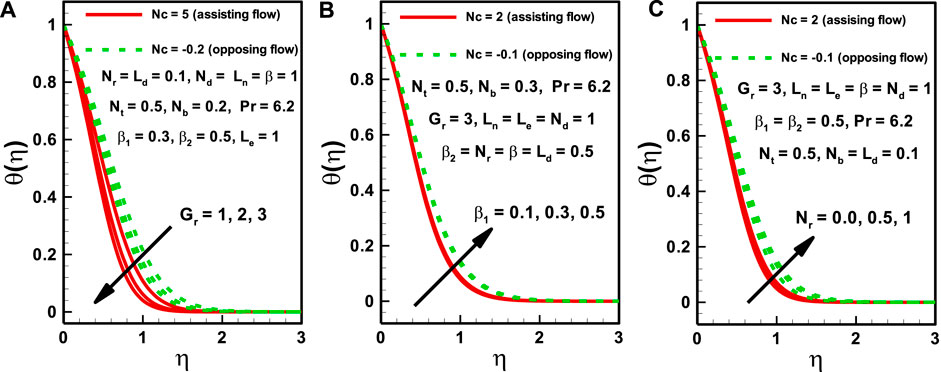
FIGURE 3. Effects of various parameters on dimensionless temperature for both assisting and opposing flows.

The plots in Figures 4A–C are presented to examine the effects of Dufour number and Lewis number on the salt concentration profile for assisting and opposing flow regimes. The salt concentration profile appears to increase with an increase in the Dufour Lewis number, while it decreases with an increase in the modified Dufour number and Lewis number. The Dufour number reflects the energy flux in a fluid flow due to the concentration gradient. The behavior of salt concentration against various parameters is not affected by whether an assisting or opposing flow regime is in operation. The Lewis number measures the ratio of thermal diffusivity to mass diffusivity. A Lewis number greater than one indicates that thermal diffusivity is higher than the mass diffusivity. The gradient of the salt concentration profile becomes less steep at a Lewis number of 5, which means that the variation in salt concentration is lower for higher Lewis numbers.

FIGURE 4

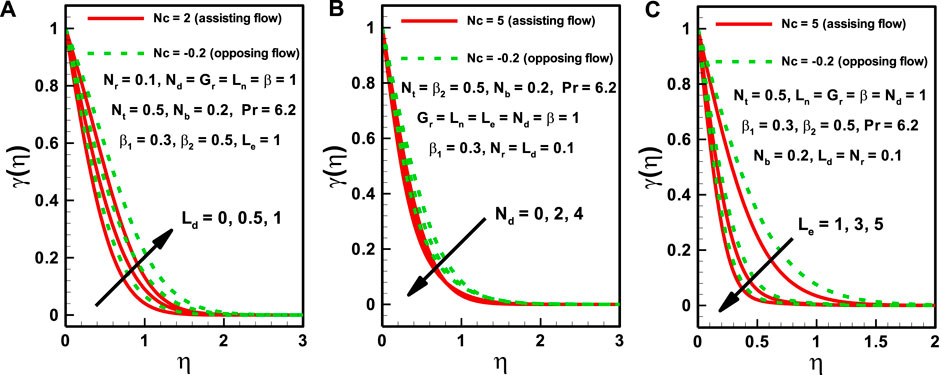
FIGURE 4. Effects of various parameters on dimensionless salt concentration distribution for both assisting and opposing flows.

In Figures 5A–C, three important parameters (the thermophoresis parameter, Brownian motion parameter, and nanofluid Lewis number) are considered in order to determine their effects on the rescaled nanoparticle volume fraction. It can be observed that the rescaled nanoparticle volume fraction increases with an increase in thermophoresis and in the Brownian parameter, but this cannot be generalized throughout the boundary layer. The effect near the wall is in the opposite direction to the effect that is visible near the free stream region. This effect occurs due to the heated surface, which significantly affects the motion of particles near it. The increase in nanofluid Lewis number causes a decrease in nanoparticle concentration near the free stream region, while the concentration increases near the heated surface.

FIGURE 5

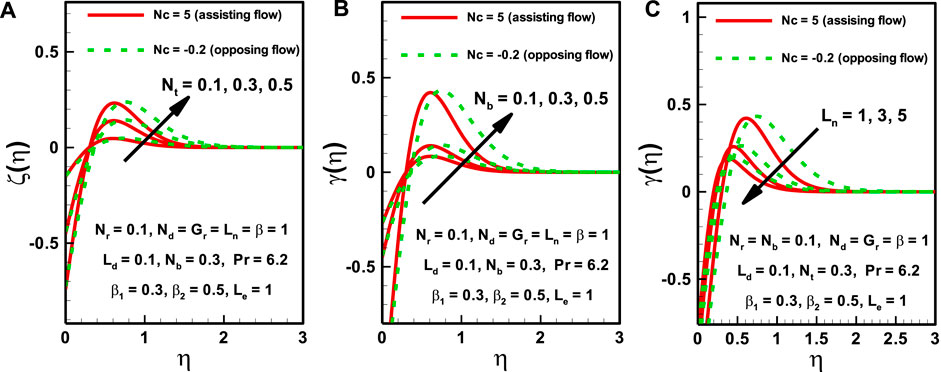
FIGURE 5. Effects of nanofluid parameters on rescaled nanoparticle volume fraction distribution for both assisting and opposing flows.

Heat transfer is an important phenomenon for nanofluid flow and is significantly affected by the heat transfer parameters involved in the equations presented above. In Figures 6A–C, we plot Nusselt number against only six of the relevant parameters. Nusselt number decreases as the slip velocity parameter increases, while it increases as the local Grashof number increases, and it is also higher for the assisting flow regime in comparison to the opposing flow regime. Figure 6B illustrates the effect of Dufour number on the heat transfer profile. It can be observed that Nusselt number responds in opposing directions to a rise in the relaxation and retardation parameters. Specifically, it increases as the retardation parameter increases, while it decreases as the relaxation parameter increases. Figure 6C illustrates the effect on Nusselt number of variation in the thermophoresis parameter and Dufour Lewis number. The heat transfer rate decreases as the thermophoresis parameter increases, and it increases as Dufour Lewis number increases. Once again, it can be observed that the assisting flow regime produces a higher Nusselt number in comparison to the opposing flow regime.

FIGURE 6

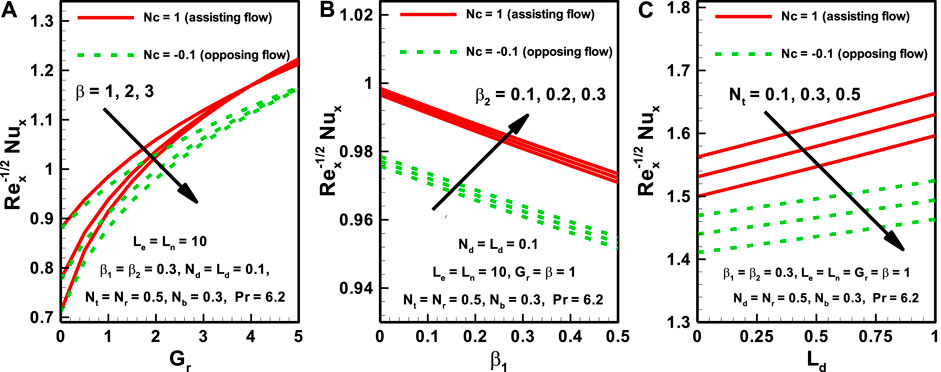
FIGURE 6. Variation in Nusselt number with variation in the values of several parameters for both assisting and opposing flows.

Sherwood number is plotted against various parameters in Figures 7A–C. It can be observed that, generally, the Sherwood number is higher for the assisting flow regime in comparison to the opposing flow regime. Figure 7A illustrates the effects of the relaxation and slip velocity parameters on Sherwood number. It can be observed that Sherwood number decreases as the slip velocity parameter and relaxation parameter increase. Figure 7B shows that Sherwood number decreases as the Dufour Lewis parameter increases, and increases against the Lewis number. The last figure shows that Sherwood number increases with an increase in the thermophoresis parameter and nanofluid Lewis number.

FIGURE 7

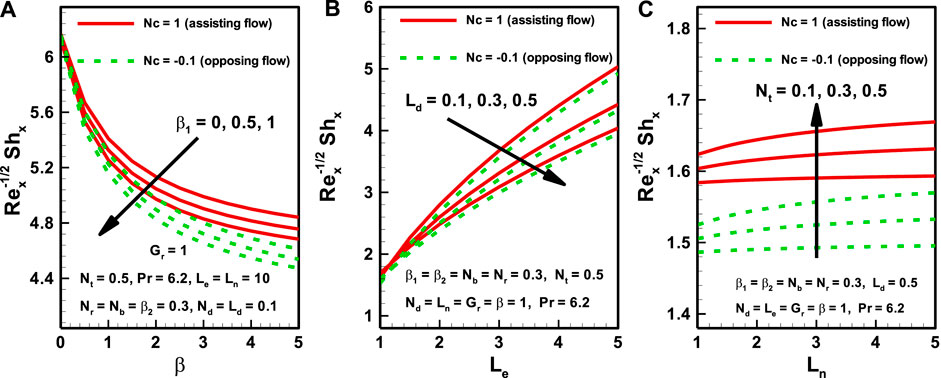
FIGURE 7. Variation in Sherwood number with variation in the values of several parameters for both assisting and opposing flows.

Conclusion

The present study considers the effects of slip velocity on the double-diffusive flow of an Oldroyd-B fluid in the case of assisting and opposing flow regimes. Diffusion of nanoparticles is considered, along with salt concentration, and separate concentration equations are considered for each of these parameters. The governing partial differential equations, along with the boundary conditions, are reduced to ordinary differential equations using similarity transformation; subsequently, the reduced ordinary differential equations are solved numerically using the shooting method. The following important conclusions can be drawn from the above analysis.

1. Whether an assisting or opposing flow regime is in operation exerts a strong effect on the temperature, velocity, and concentration profiles.

2. The profiles for Nusselt number and Sherwood number cover higher values for the assisting flow regime in comparison to the opposing flow regime.

3. Nusselt number values increase against the retardation parameter and decrease with increasing values of the relaxation parameter.

4. The Nusselt and Sherwood numbers decrease with increasing values of the slip velocity parameter.

5. The presence of nanoparticles and the salt concentration significantly affect the heat transfer characteristics of an ordinary non-Newtonian Oldroyd-B fluid.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia has funded this project under Grant No. RG-11-130-43.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azeem Khan, W., Khan, M., and Malik, R. (2014). Three-dimensional flow of an Oldroyd-B nanofluid towards stretching surface with heat generation/absorption. PLOS ONE 9 (8), e105107. doi:10.1371/journal.pone.0105107

PubMed Abstract | CrossRef Full Text | Google Scholar

Buongiorno, J., and Hu, W. (1920). “Nanofluid coolants for advanced nuclear power plants,” in Proceedings of ICAPP ’05. Seoul. Paper no. 5705.

Google Scholar

Choi, S. (1995). “Enhancing thermal conductivity of fluids with nanoparticle,” in Developments and applications of non-Newtonian flows. Editors D. A. Siginer, and H. P. Wang (Argonne: ASME MD), 231, 99–105. and FED vol. 66.

Google Scholar

Choi, S. U. S., Zhang, Z. G., Yu, W., Lockwood, F. E., and Grulke, E. A. (2001). Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 79 (14), 2252–2254. doi:10.1063/1.1408272

CrossRef Full Text | Google Scholar

Ellahi, R., and Afzal, S. (2009). Effects of variable viscosity in a third grade fluid with porous medium: An analytic solution. Commun. Nonlinear Sci. Numer. Simulat. 14, 2056–2072. doi:10.1016/j.cnsns.2008.05.006

CrossRef Full Text | Google Scholar

Ellahi, R. (2009). Effects of the slip boundary condition on non-Newtonian flows in a channel. Commun. Nonlinear Sci. Numer. Simulat. 14, 1377–1384. doi:10.1016/j.cnsns.2008.04.002

CrossRef Full Text | Google Scholar

Ellahi, R., and Riaz, A. (2010). Analytical solutions for MHD flow in a third-grade fluid with variable viscosity. Math. Comput. Model. 52, 1783–1793. doi:10.1016/j.mcm.2010.07.005

CrossRef Full Text | Google Scholar

Folkman, J., and Long, D. M. (1964). The use of silicone rubber as a carrier for prolonged drug therapy. J. Surg. Res. 4 (3), 139–142. doi:10.1016/s0022-4804(64)80040-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamad, M. A. A., and Ferdows, M. (2012). Similarity solutions to viscous flow and heat transfer of nanofluid over nonlinearly stretching sheet. Appl. Math. Mech. Engl. Ed. 33 (33), 923–930. doi:10.1007/s10483-012-1595-7

CrossRef Full Text | Google Scholar

Iverson, B. D., and Garimella, S. V. (2008). Recent advances in microscale pumping technologies: A review and evaluation. Microfluid. Nanofluidics 5 (2), 145–174. doi:10.1007/s10404-008-0266-8

CrossRef Full Text | Google Scholar

Jang, J., and Lee, S. S. (2000). Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sensors Actuators A Phys. 80 (1), 84–89. doi:10.1016/s0924-4247(99)00302-7

CrossRef Full Text | Google Scholar

Johnson, R. D., Gavalas, V. G., Daunert, S., and Bachas, L. G. (2008). Microfluidic ion-sensing devices. Anal. Chim. Acta 613 (1), 20–30. doi:10.1016/j.aca.2008.02.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Abu Bakar, S., and Ishak, A. (2021). Stagnation-point flow of a hybrid nanoliquid over a non-isothermal stretching/shrinking sheet with characteristics of inertial and microstructure. Case Stud. Therm. Eng. 26, 101150. doi:10.1016/j.csite.2021.101150

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., and Ishak, A. (2021). Magnetic field effect on sisko fluid flow containing gold nanoparticles through a porous curved surface in the presence of radiation and partial slip. Mathematics 9 (9), 921. doi:10.3390/math9090921

CrossRef Full Text | Google Scholar

Kim, J. H., and Yoon, J. Y. (2002). “Protein adsorption on polymer particles,” in Encyclopedia of surface and colloidal science. Editor T. A. Hubbard (New York: Marcel Dekker), 4373–4381.

Google Scholar

Lozinski, A., and Owens, R. G. (2003). An energy estimate for the Oldroyd B model: Theory and applications. J. Newt. Fluid Mech. 112 (2–3), 161–176. doi:10.1016/s0377-0257(03)00096-x

CrossRef Full Text | Google Scholar

Masuda, H., Ebata, A., Teramae, K., and Hishinuma, N. (1993). Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bussei 7, 227–233. doi:10.2963/jjtp.7.227

CrossRef Full Text | Google Scholar

Sher Akbar, N., Nadeem, S., Haq, R. U., and Khan, Z. H. (2013a). Numerical solutions of Magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 87 (11), 1121–1124. doi:10.1007/s12648-013-0339-8

CrossRef Full Text | Google Scholar

Nadeem, S., Ul Haq, R., and Khan, Z. H. (2013). MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alexandria Eng. J. 52, 577–582. doi:10.1016/j.aej.2013.08.005

CrossRef Full Text | Google Scholar

Nadeem, S., Ul Haq, R., Sher Akbar, N., Lee, C., and Khan, Z. H. (2013). Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet. PLoS ONE 8 (8), e69811. doi:10.1371/journal.pone.0069811

PubMed Abstract | CrossRef Full Text | Google Scholar

Noreen, S. A., Nadeem, S., Haq, R. Ul., and Khan, Z. H. (2013). Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition. Chin. J. Aeronautics 26 (6), 1389–1397. doi:10.1016/j.cja.2013.10.008

CrossRef Full Text | Google Scholar

Sandeep, N., Rushi Kumar, B., and Jagadeesh Kumar, M. S. (2015). A comparative study of convective heat and mass transfer in non-Newtonian nanofluid flow past a permeable stretching sheet. J. Mol. Liq. 212, 585–591. 585-591ISSN 0167-7322. doi:10.1016/j.molliq.2015.10.010

CrossRef Full Text | Google Scholar

Sher Akbar, N., Nadeem, S., Lee, C., Khan, Z. H., and Ul Haq, R. (2013b). Numerical study of Williamson nano fluid flow in an asymmetric channel. Results Phys. 3, 161–166. doi:10.1016/j.rinp.2013.08.005

CrossRef Full Text | Google Scholar

Xiao, H., Yan, L., Dempsey, E. M., Song, W., Qi, R., Li, W., et al. (2018). Recent progress in polymer-based platinum drug delivery systems. Prog. Polym. Sci. 87, 70–106. doi:10.1016/j.progpolymsci.2018.07.004

CrossRef Full Text | Google Scholar

Xuan, Y., and Li, Q. (2000). Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 21 (1), 58–64. doi:10.1016/s0142-727x(99)00067-3

CrossRef Full Text | Google Scholar

Xuan, Y., and Roetzel, W. (2000). Conceptions for heat transfer correlation of nanofluids. Int. J. Heat. Mass Transf. 43, 3701–3707. doi:10.1016/s0017-9310(99)00369-5

CrossRef Full Text | Google Scholar

Zaib, A., Khan, U., Khan, I., and Asiful, H. (2019). Numerical investigation of aligned magnetic flow comprising nanoliquid over a radial stretchable surface with cattaneo–christov heat flux with entropy generation. Symmetry 11 (12), 1520. doi:10.3390/sym11121520

CrossRef Full Text | Google Scholar