Transition of electrochemical measurement to machine learning in the perspective of two-dimensional materials

Two-dimensional materials (e.g. graphene, and transition metal dichalcogenides) have become ubiquitous in electrochemical contexts including energy storage, electrocatalyst, and ion-selective membranes. This is due to its superior electrochemical properties, specifically “capacitance”, which can be referred to the storage ions at the electrolyte/materials interfaces. Experimental work and computational chemistry were carried out in the past decade for solving and improving the understanding of two-dimensional materials; however, these techniques are relatively expensive, complex, and time-consuming. Therefore, we accentuate the future trend of two-dimensional material study with machine learning as the modest alternative. In this perspective, the intrinsic capacitance properties of the two dimension materials were described from an atomic level, explaining the heteroatom doping to a nanoscopic level, showing (basal vs edge capacitance). The studies also extended to the macroscopic level i.e., the flake size of the two-dimensional materials. We then shed more light on the applicability of machine learning coupled with the “fundamental measurement” for solving electrochemistry of two-dimensional materials. The shallow artificial neural network was demonstrated for the prediction of CV curves using the data from size-dependent graphene. In addition, the application of deep neural networks with complicated architecture has also been explored through the prediction of capacitance for heteroatom-doped graphene. This perspective provides a clear background and creates the connection between fundamental measurement and machine learning for understanding the capacitance properties of two-dimensional materials.

Introduction

The two-dimensional (2D) materials have arisen from the discovery of graphene by exfoliating “bulk” graphite in 2004, it was soon recognized as a promising material due to its high electrical conductivity (∼2 × 10³ S cm⁻¹), high charge carrier density (Novoselov et al., 2004), high theoretical surface area (2,630 m² g⁻¹) (Stoller et al., 2008). Hence, there is a progressive trend of exploring novel 2D materials, in which the structure of those materials is similar to graphene. Due to the superior properties of those two-dimensional materials, it is obvious that the search for 2D materials was then expanded to the transition metal dichalcogenides (TMDs) family (Bissett et al., 2016), hexagonal boron nitride (also known as “white graphene”) (Gautam and Chelliah, 2021), Mxene (Gogotsi and Anasori, 2019), and some heterostructure forming from those original materials (Keerthi et al., 2021). In recent years, 2D materials become central to the most in the context of many electrochemical applications including energy storage (Nualchimplee et al., 2022), electrocatalysts (McAteer et al., 2016), ions selective membrane (Hirunpinyopas et al., 2020) and so on. It is undeniable that the development of the as-mentioned electrochemical applications requires the understanding of fundamentals from a nanoscale using either experiment or the computational-based method. However, those experimental and computational techniques require a consumable budget and time. In recent years, machine learning has been of great interest, and applied to various studies in the area of electrochemistry (Min et al., 2018). Machine learning has shown a high capability to predict and analyse various thermodynamic properties, capacitance, and quantification of chemicals in electrochemical systems (Yoon et al., 2021). Hence, the development of machine learning algorithms to study the underlying properties or predict the future outcome from an experiment of 2D materials would be a cutting-edge of material science future. In this perspective, we discussed the background research of the two-dimensional materials from the experimental views, and offer an alternative method for the computational techniques, particularly machine learning, for the study of electrochemical systems. Machine learning (artificial neural network, ANN) was also then demonstrated for predicting the electrochemical response (CVs), which is to the best of our knowledge. This work describes the insight into the electrochemistry of two-dimensional materials, suggesting the research direction of two-dimensional materials using machine learning. This should improve the understanding of two-dimensional material, especially energy storage applications, which should lead the way of the development of energy materials.

Capacitance of two-dimensional materials

The understanding of electrochemistry at the nanoscale electrode/electrolyte interfaces is the key to the development of energy materials, particularly the capacitive properties at the basal and edge plane. This perspective shed more light on two-dimensional materials, especially graphene, and TMDs. (Yuan et al. (2013)Demonstrated that the capacitance of graphene can be divided into two positions: 1) basal plane and 2) edge plane. These two position exhibit different capacitance properties. The basal plane provides a small value of interfacial capacitance of about 4 μF cm⁻², while the edge plane shows much higher orders of magnitude up to ×1.0 10⁵ μF cm⁻². This intrinsic capacitance can be used for determining the capacitance of the macro level (Unsuree et al., 2021). For example, the proposed theoretical capacitance of graphene, which is quoted to be 550 F g⁻¹ (∼21 μF cm⁻², in areal basis (Liu et al., 2010; Sawangphruk et al., 2013); however, this is not valid for most of case. This is because the capacitance from the original work by Xia et al. (2009) measured the capacitance using a platinum electrode on behalf of graphene, assuming the equivalent interfacial properties between graphene and platinum, ignoring the nanoscale quantum capacitance (known as space charge capacitance for higher dimension materials (Iamprasertkun and Dryfe, 2020) In fact, the pristine graphene shows far beyond those theoretical approach providing less than half of theoretical value (Wang et al., 2009). This is due to the Helmholtz, diffuse layer, quantum, as well as space charge capacitance of those two-dimensional materials, which can be varied by the operating conditions (Unsuree et al., 2021). Our group also demonstrates that the basal plane capacitance depends on the hydrated ionic size showing the basal plane capacitance of 4.7–9.4 μF cm⁻² while the capacitance follows the following order Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺ (Iamprasertkun et al., 2019). The basal plane capacitance also varies when applying different electrolyte concentrations as we have reported the capacitance from the diluted aqueous electrolyte to “water-in-salt” conditions (Iamprasertkun et al., 2020). Not only those effects but also the effect of adventitious hydrocarbon adsorption, this effect could reduce the intrinsic capacitance by the exposure time to the ambient of 2D materials (Hurst et al., 2018). By simply leaving the samples in the ambient, the airborne organic compound could be adsorbed on the surface of materials forming a thick hydrocarbon layer leading to poor capacitance (Zou et al., 2016). At this stage, it is seen that the measurement of intrinsic capacitance is complex, requiring the understanding of fundamental materials. The capacitance of transition metal dichalcogenides (TMDs) e.g. MoS₂ was reported by Velický et. al., it is found that MoS₂ exhibits a lower interfacial capacitance (1.5 μF cm⁻²) than that of pristine graphene. The benefit of using MoS₂ is that MoS₂ is a light sensitive material. It provides a band gap energy of 1.29 eV in which the capacitance can be increased by illuminating the samples (capacitance enhance up to 20%). Moreover, it is reported that the basal plane capacitance of MoS₂ relates to the flake thickness, which increase from 1.5 μF cm⁻²–3.0 μF cm⁻² when increasing the dimension from monolayer to bulk MoS₂ (Velický et al., 2016). Apart from the basal plane, it is no doubt that the edge plane displays higher activity than the basal plane in many perspectives e.g., capacitance, charge transport, and electron transfer kinetic (Shen et al., 2014; Velický et al., 2016). The steric accessibility of metallic orbitals at the edge site could increase the electrochemical activity, and lead to a high interfacial capacitance (Velický et al., 2017); however, this is not only due to the edge density and defect but also the redox activity of the doped atom at the edge oriented. The atom at the edge site is reactive and unstable, which can be terminated by some reactive species e.g. hydrogen, oxygen, nitrogen, and so on. These terminated species such as oxygen (quinone species) can greatly enhance the pseudocapacitive performance as reported by Iamprasertkun et al. (2019), where there is no effect of the ion identity on the edge plane. The major capacitive contribution of the edge oriented is the surface redox of quinone to hydroquinone, giving the high interfacial capacitance of up to 700 μF cm⁻². This could explain why the reduced graphene oxide displays high gravimetric capacitance. The doped species displays potential in energy storage and electrocatalyst applications. The pseudocapacitance effect which is due to surface faradaic reactions from heteroatom dopants such as nitrogen, sulfur, and oxygen accompanies the electric double-layer effect, resulting in a high-capacitance supercapacitor (Béguin et al., 2014; Parveen et al., 2016; Zhao et al., 2016), and also enhance the electrocatalyst activity (Wang L. et al., 2020). However, it is not clear yet which doped atoms or contents exhibit the highest electrochemical activity, and this led to some unclear explanations in this field; hence, many researchers have demonstrated an insight study using machine learning, in recent years (describe in a later section). Note that further information on TMDs doping were reported (Zhu et al., 2020; Yoo et al., 2021) through a variety of techniques e.g. chemical vapour deposition (Jin et al., 2019; Zhang et al., 2020). This may be enabling some electrochemical applications and insight studies for 2D materials and machine learning. However, it is noted that it is difficult to control exactly the doped element; hence, it is impossible to draw a conclusion from a single experiment. This can be referred in the statement by A. K. Geim quoted as “graphene oxide (also referred to as the reduced graphene oxide family) is not suitable for the fundamental measurement as it uncontrollable structure” (Geim and Novoselov, 2007). Thus, machine learning may be one of the strategies for solving this complexity. Remarks, the artificial neural network for solving the heteroatom doped was proposed in this work (describe in the machine learning session). Apart from graphene, the termination at the edge site of TMDs is also found when exfoliated from bulk materials. For example, the edge site of MoS₂ can be terminated by the oxygen species turning MoS₂ to MoO₃. This structure could enable larger interlayer spacing, which gives a higher ion intercalation degree than that of MoS₂ (Nualchimplee et al., 2022). From the macro scale, it is no doubt that controlling the structural properties is one of the most interesting parts of the material context. One of the simplest ways for preparing 2D materials is through the solvent-assist liquid phase exfoliation method, which was introduced by Coleman’s group (Coleman, 2009; Coleman et al., 2011). The exfoliated flakes can be controlled using the centrifugal technique by increasing/decreasing the revolution speed, generating different gravitational forces. The large flakes are then settling down to the bottom and the tiny flakes are then floated on the top as supernatant (Iamprasertkun et al., 2021; Hirunpinyopas et al., 2022). Evidently, the different flakes dimension displayed a variety of structural, chemical, and electrochemical properties; thus, the selection of those dimensions plays a significant role in enhancing the performance of the as-interested applications, giving some room for the exploration using machine learning in this perspective. This perspective also provides the idea of using a shallow artificial neural network for predicting the electrochemical response from size-dependent graphene. The coupling between measurement and machine learning could grow the understanding of the work in this area in the next decade.

Machine learning in 2D materials

Over the past decades, machine learning, a tool of artificial intelligence that aims to learn the underlying relationship among data and predicts outcomes for new data sets, is increasingly gaining popularity, and can be considered as an alternative method for the study of 2D material (Ryu et al., 2022). In general, machine learning consists of three major processes which are data preparation, the learning process, and performance evaluation (Zhou et al., 2020). After the initial objectives of the study have been set, the data preparation can be initiated which includes data collection and data inspection to eliminate outliers, and visualise the correlation of data. Afterward, the cleaned data normally split into two separate datasets so-called “train set” and “test set” with a random seed or pre-assigned seed. Then, the machine learning algorithm will be selected based on training purposes. The training process will utilise the “train set” with the selected algorithm, and regularisation or “early stopping” is recommended. This prevent overtraining, and improve the predictive performance of the trained model. For example, splitting the “train set” into an additional dataset so-called “validation set” to invoke the “early stopping” in the case that the error is persisted. Moreover, the validation dataset can be used to assess, and finely tune the optimum hyperparameters of the model. The performance of the trained model will be evaluated by both train and test datasets which present in form of the learning curve and statistical evaluation such as coefficient of determination or R² (Wang A. Y.-T. et al., 2020). Herein, the general workflow of machine learning for the study of 2D material was summarised as illustrated in Figure 1. Zhou et.al., demonstrated the electrochemical performances of N-doped graphene supercapacitors, and employed a machine learning technique (artificial neural network, ANN). The relationship between the chemical/morphological characteristics of the electrode, and the performance of the supercapacitor were then demonstrated. The developed model can precisely predict the capacitance at the coefficient of determination (R²) of 0.8495, and root mean square error of 31.5491 F/g, in which that model could be able to provide a relationship between the capacitance, and interesting feature (e.g. surface area, doping, pore structure) (Zhou et al., 2020). Consequently, machine learning not only considerably saves cost and time, but also allows convenient exploration through combinations of design features such as the effect of nitrogen configuration and surface area on the capacitance (Zhou et al., 2020). The studies of two-dimentional materials were expanded using other machine learning techniques e.g., Support Vector Machine algorithms (SVM) (Yang and Yao, 2020), and Random Forest algorithm (Wang et al., 2019). The techniques were further applied for either calculate the band gap energy (Mishra et al., 2019) or optimised the defects of 2D materials (Frey et al., 2020).

FIGURE 1

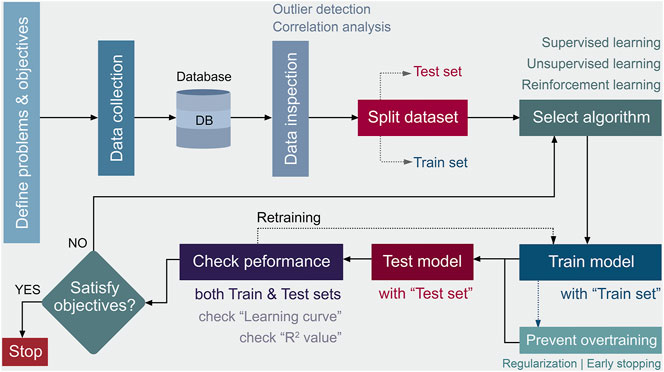
FIGURE 1. Logical and workflow of machine learning techniques for the data analysis and prediction in two-dimensional materials perspective.

Prediction ability of machine learning

The review of recent works in the previous section highlights the applicability of machine learning on a variety of 2D materials studies. To further demonstrate the prediction ability of machine learning, we have adopted the shallow artificial neural network (ANN) for the prediction of the cyclic voltammetry profiles (CV curves) of graphene based on our experimental data (Deerattrakul et al., 2021) as shown in Figure 2A (the training data are reported in the supplementary). Deerattrakul et al. reported that graphene with a larger flake size tends to have a narrower CV curve due to the poor capacitive properties while increase the scan rate could produce a wider CVs. It is clear that the CVs profiles is dominated by the flake sizes, scan rates, and quality of the samples. Due to the distinct and clear relationship between CVs profile, and the involved features such as flake sizes and scan rates, their behavior has low complexity. For this reason, the shallow artificial neural network comprised of one hidden layer with non-linear transfer function should be sufficient for this predictive task (Lopez-Martin et al., 2019). To further predict the CVs responses in the different situation, the CV profiles from three graphene flake sizes (100, 350, and 942 nm), and five scan rates (10, 25, 50, 75, and 100 mV s⁻¹) were then collected. Only 14 C V curve profiles were included for training the ANN, and the leftover CV curve data is used to evaluate the prediction ability of the trained model. The inputs for the network are graphene flake sizes, and scan rates where the CV profiles are the output. The data has been randomly split into three datasets which are the train set, validation set, and test set with an 80:10:10 ratio (Joseph, 2022). The double loop training with different numbers of nodes in the hidden layer is employed to identify the optimum hyperparameters (e.g., number of nodes and number of epochs). Levenberg-Marquardt backpropagation (Levenberg, 1944; Marquardt, 1963) is selected as the training algorithm with a hyperbolic tangent sigmoid transfer function used in the hidden layer and a learning rate of 0.01. As illustrated in Figure 2, the trained and tested CV profiles (red dashed line) are in good agreement with the experimental profiles (light blue line), which result in a high coefficient of determination (R²) of 0.98, and low mean squared error (MSE) of 0.02. The optimum hyperparameters can also be summarised as follow; the number of epochs is equal to 21 and the number of hidden nodes required is 7. Even though we have obtained the trained ANN model with a high value of R², overtraining is not our concern because we have utilised the “early stopping” using a validation dataset (Thike et al., 2020). Therefore, we can achieve high precision of the CVs prediction (black dashed line) as shown in the far-right subplot located in the last row of Figure 2A. It is suggested that the high prediction ability, and the sufficient generalisation of ANN model can be obtained by determining the optimum hyperparameters, and exercising the appropriate overtraining prevention strategies without the need of complicated ANN architecture or deep learning, especially for small datasets. Moreover, we demonstrated the application of ANN to the prediction of heteroatom-doped graphene capacitance based on multiple features such as the amount of heteroatom doped, current density, and structural properties (e.g., specific surface area). However, instead of the conventional linear function assigned for the output layer, we switched the activation function to Rectified Linear Unit (ReLU) function (Hanin, 2019). In addition, the ANN architecture has been expanded to a deep neural network with five hidden layers and hundreds of hidden neurons for each layer. The L1 and L2 regularisation are included to prevent overtraining by adding the penalty to the loss function (Yang et al., 2023). As illustrated in Figure 2B, the predicted capacitance profile (red line) has a similar trend to the experimental capacitance (blue line). Even though the precision of capacitance prediction is not high but it produces a considerably satisfactory result with low mean squared error (MSE) of 0.04 (see Figure 2C), which may provide a universal model for further usage. This result could emphasise our preliminary suggestion that the complicated neural network design does not guarantee training, and prediction performances.

FIGURE 2

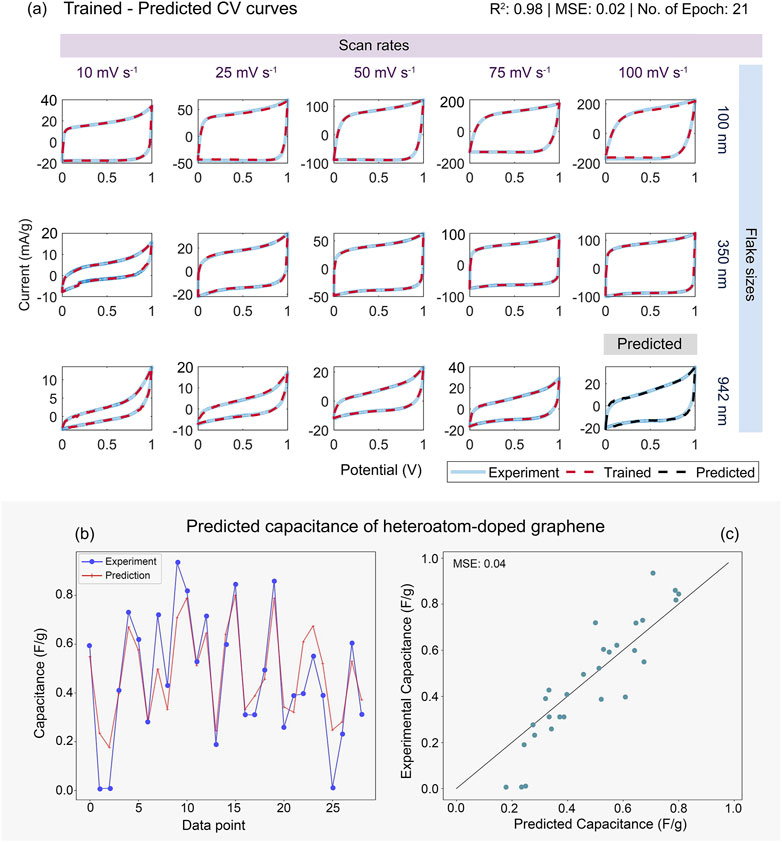
FIGURE 2. (A) Trained and Predicted CVs plotted in comparison with experimental CVs of different graphene flake sizes and scan rates. (B) The predicted capacitance of heteroatom-doped graphene plotted with experimental data. (C) Linear regression plot of predicted capacitance versus experimental capacitance.

Conclusion and outlook

In summary, various 2D materials have shown tremendous benefit to electrochemical applications, especially in the development of energy storage. The nanoscale capacitance of those two-dimensional materials depends on a variety of features such as positions (edge plane vs basal plane) or heteroatom doping. Obviously, those features can be projected using machine learning, which depended on available experimental data. We successfully predicted the cyclic voltammetry profiles of graphene with multiple flake sizes, and capacitance of heteroatom-doped graphene, we have found that the prediction performance of artificial neural networks largely depends on hyperparameter tuning. Interestingly, the complicated network does not guarantee the precision of prediction. The simple architecture can be powerful and provide satisfactory results with modest computational time. However, it should be aware that the reliability of this data-driven approach depends heavily on the acquired data, and the challenge is sometimes the limited size of the dataset due to the difficulty of the data acquisition process. The understanding of fundamental concepts especially in the nanoscale experiment is yet crucial. Thus, the coupling between fundamental experiment and machine learning should lead the way for the development of electrochemical applications in the next decade.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PI. initiated, directed, and designed the project and wrote the manuscript with KJ, and AC. KJ. performed the ANN model, in which the data were collected by AC. All authors have given approval to the final version of the manuscript.

Funding

This study was supported by Thammasat University Research Fund (Sustainable Development Gols-SDG, UN-SDGs7), under contract No. TUSDG2/2565. P.I. acknowledged the SIIT Young Researcher Grant (under contract No. SIIT 2021-YRG-PI02). K.J. acknowledge Thammasat Postdoctoral Fellowship (TUPD17/2565)

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.1070608/full#supplementary-material

References

Béguin, F., Presser, V., Balducci, A., and Frackowiak, E. (2014). Carbons and electrolytes for advanced supercapacitors. Adv. Mat. 26, 2219–2251. doi:10.1002/adma.201304137

Bissett, M. A., Worrall, S. D., Kinloch, I. A., and Dryfe, R. A. W. (2016). Comparison of two-dimensional transition metal dichalcogenides for electrochemical supercapacitors. Electrochimica Acta 201, 30–37. doi:10.1016/j.electacta.2016.03.190

Coleman, J. N. (2009). Liquid-phase exfoliation of nanotubes and graphene. Adv. Funct. Mat. 19, 3680–3695. doi:10.1002/adfm.200901640

Coleman, J. N., Lotya, M., O’neill, A., Bergin, S. D., King, P. J., Khan, U., et al. (2011). Two-dimensional nanosheets produced by liquid exfoliation of layered materials. Science 331, 568–571. doi:10.1126/science.1194975

Deerattrakul, V., Hirunpinyopas, W., Pisitpipathsin, N., Saisopa, T., Sawangphruk, M., Nualchimplee, C., et al. (2021). The electrochemistry of size dependent graphene via liquid phase exfoliation: Capacitance and ionic transport. Phys. Chem. Chem. Phys. 23, 11616–11623. doi:10.1039/d1cp00887k

Frey, N. C., Akinwande, D., Jariwala, D., and Shenoy, V. B. (2020). Machine learning-enabled design of point defects in 2D materials for quantum and neuromorphic information processing. ACS Nano 14, 13406–13417. doi:10.1021/acsnano.0c05267

Gautam, C., and Chelliah, S. (2021). Methods of hexagonal boron nitride exfoliation and its functionalization: Covalent and non-covalent approaches. RSC Adv. 11, 31284–31327. doi:10.1039/d1ra05727h

Geim, A. K., and Novoselov, K. S. (2007). The rise of graphene. Nat. Mat. 6, 183–191. doi:10.1038/nmat1849

Gogotsi, Y., and Anasori, B. (2019). The rise of MXenes. ACS Nano 13, 8491–8494. doi:10.1021/acsnano.9b06394

Hanin, B. (2019). Universal function approximation by deep neural nets with bounded width and ReLU activations. Mathematics 7, 992. doi:10.3390/math7100992

Hirunpinyopas, W., Iamprasertkun, P., Bissett, M. A., and Dryfe, R. A. W. (2020). Tunable charge/size selective ion sieving with ultrahigh water permeance through laminar graphene membranes. Carbon 156, 119–129. doi:10.1016/j.carbon.2019.09.030

Hirunpinyopas, W., Iamprasertkun, P., Fevre, L. W. L., Panomsuwan, G., Sirisaksoontorn, W., Dryfe, R. A. W., et al. (2022). Insights into binding mechanisms of size-selected graphene binders for flexible and conductive porous carbon electrodes. Electrochimica Acta 403, 139696. doi:10.1016/j.electacta.2021.139696

Hurst, J. M., Li, L., and Liu, H. (2018). Adventitious hydrocarbons and the graphite-water interface. Carbon 134, 464–469. doi:10.1016/j.carbon.2018.04.020

Iamprasertkun, P., and Dryfe, R. A. W. (2020). The capacitance of graphene: From model systems to large-scale devices. Nanocarbon Electrochem., 33–84. doi:10.1002/9781119468288.ch2

Iamprasertkun, P., Ejigu, A., and Dryfe, R. A. W. (2020). Understanding the electrochemistry of “water-in-salt” electrolytes: Basal plane highly ordered pyrolytic graphite as a model system. Chem. Sci. 11, 6978–6989. doi:10.1039/d0sc01754j

Iamprasertkun, P., Hirunpinyopas, W., Deerattrakul, V., Sawangphruk, M., and Nualchimplee, C. (2021). Controlling the flake size of bifunctional 2D WSe2 nanosheets as flexible binders and supercapacitor materials. Nanoscale Adv. 3, 653–660. doi:10.1039/d0na00592d

Iamprasertkun, P., Hirunpinyopas, W., Keerthi, A., Wang, B., Radha, B., Bissett, M. A., et al. (2019). Capacitance of basal plane and edge-oriented highly ordered pyrolytic graphite: Specific ion effects. J. Phys. Chem. Lett. 10, 617–623. doi:10.1021/acs.jpclett.8b03523

Jin, Y., Zeng, Z., Xu, Z., Lin, Y.-C., Bi, K., Shao, G., et al. (2019). Synthesis and transport properties of degenerate P-type Nb-doped WS2 monolayers. Chem. Mat. 31, 3534–3541. doi:10.1021/acs.chemmater.9b00913

Joseph, V. R. (2022). Optimal ratio for data splitting. Stat. Anal. 15, 531–538. doi:10.1002/sam.11583

Keerthi, A., Goutham, S., You, Y., Iamprasertkun, P., Dryfe, R. a. W., Geim, A. K., et al. (2021). Water friction in nanofluidic channels made from two-dimensional crystals. Nat. Commun. 12, 3092. doi:10.1038/s41467-021-23325-3

Levenberg, K. (1944). A method for the solution of certain NON – linear problems in least squares. Q. Appl. Math. 2, 164–168. doi:10.1090/qam/10666

Liu, C., Yu, Z., Neff, D., Zhamu, A., and Jang, B. Z. (2010). Graphene-based supercapacitor with an ultrahigh energy density. Nano Lett. 10, 4863–4868. doi:10.1021/nl102661q

Lopez-Martin, M., Carro, B., Sanchez-Esguevillas, A., and Lloret, J. (2019). Shallow neural network with kernel approximation for prediction problems in highly demanding data networks. Expert Syst. Appl. 124, 196–208. doi:10.1016/j.eswa.2019.01.063

Marquardt, D. W. (1963). An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Industrial Appl. Math. 11, 431–441. doi:10.1137/0111030

Mcateer, D., Gholamvand, Z., Mcevoy, N., Harvey, A., O’malley, E., Duesberg, G. S., et al. (2016). Thickness dependence and percolation scaling of hydrogen production rate in MoS₂ nanosheet and nanosheet–carbon nanotube composite catalytic electrodes. ACS Nano 10, 672–683. doi:10.1021/acsnano.5b05907

Min, K., Choi, B., Park, K., and Cho, E. (2018). Machine learning assisted optimization of electrochemical properties for Ni-rich cathode materials. Sci. Rep. 8, 15778. doi:10.1038/s41598-018-34201-4

Mishra, A., Satsangi, S., Rajan, A. C., Mizuseki, H., Lee, K.-R., and Singh, A. K. (2019). Accelerated data-driven accurate positioning of the band edges of MXenes. J. Phys. Chem. Lett. 10, 780–785. doi:10.1021/acs.jpclett.9b00009

Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric field effect in atomically thin carbon films. Science 306, 666–669. doi:10.1126/science.1102896

Nualchimplee, C., Jitapunkul, K., Deerattrakul, V., Thaweechai, T., Sirisaksoontorn, W., Hirunpinyopas, W., et al. (2022). Auto-oxidation of exfoliated MoS₂ in N-methyl-2-pyrrolidone: From 2D nanosheets to 3D nanorods. New J. Chem. 46, 747–755. doi:10.1039/d1nj05384a

Parveen, N., Ansari, M. O., Ansari, S. A., and Cho, M. H. (2016). Simultaneous sulfur doping and exfoliation of graphene from graphite using an electrochemical method for supercapacitor electrode materials. J. Mat. Chem. A Mat. 4, 233–240. doi:10.1039/c5ta07963b

Ryu, B., Wang, L., Pu, H., Chan, M. K. Y., and Chen, J. (2022). Understanding, discovery, and synthesis of 2D materials enabled by machine learning. Chem. Soc. Rev. 51, 1899–1925. doi:10.1039/d1cs00503k

Sawangphruk, M., Srimuk, P., Chiochan, P., Krittayavathananon, A., Luanwuthi, S., and Limtrakul, J. (2013). High-performance supercapacitor of manganese oxide/reduced graphene oxide nanocomposite coated on flexible carbon fiber paper. Carbon 60, 109–116. doi:10.1016/j.carbon.2013.03.062

Shen, A., Zou, Y., Wang, Q., Dryfe, R. a. W., Huang, X., Dou, S., et al. (2014). Oxygen reduction reaction in a droplet on graphite: Direct evidence that the edge is more active than the basal plane. Angew. Chem. Int. Ed. Engl. 53, 10980–10984. doi:10.1002/ange.201406695

Stoller, M. D., Park, S., Zhu, Y., An, J., and Ruoff, R. S. (2008). Graphene-based ultracapacitors. Nano Lett. 8, 3498–3502. doi:10.1021/nl802558y

Thike, P. H., Zhao, Z., Liu, P., Bao, F., Jin, Y., and Shi, P. (2020). An early stopping-based artificial neural network model for atmospheric corrosion prediction of carbon steel. Comput. Mater. Continua 65, 2091–2109. doi:10.32604/cmc.2020.011608

Unsuree, N., Phanphak, S., Prajongtat, P., Bunpheng, A., Jitapunkul, K., Kongputhon, P., et al. (2021). A review: Ion transport of two-dimensional materials in novel technologies from macro to nanoscopic perspectives. Energies 14, 5819. doi:10.3390/en14185819

Velický, M., Bissett, M. A., Woods, C. R., Toth, P. S., Georgiou, T., Kinloch, I. A., et al. (2016). Photoelectrochemistry of pristine mono- and few-layer MoS2. Nano Lett. 16, 2023–2032. doi:10.1021/acs.nanolett.5b05317

Velický, M., Toth, P. S., Rakowski, A. M., Rooney, A. P., Kozikov, A., Woods, C. R., et al. (2017). Exfoliation of natural van der Waals heterostructures to a single unit cell thickness. Nat. Commun. 8, 14410. doi:10.1038/ncomms14410

Wang, A. Y.-T., Murdock, R., Kauwe, S. K., Oliynyk, A. O., Gurlo, A., Brgoch, J., et al. (2020a). Machine learning for materials scientists: An introductory guide toward best practices. Chem. Mat. 32 (12), 4954–4965. doi:10.1021/acs.chemmater.0c01907

Wang, L., Sofer, Z., and Pumera, M. (2020b). Will any crap we put into graphene increase its electrocatalytic effect? ACS Nano 14, 21–25. doi:10.1021/acsnano.9b00184

Wang, X., Han, D., Hong, Y., Sun, H., Zhang, J., and Zhang, J. (2019). Machine learning enabled prediction of mechanical properties of tungsten disulfide monolayer. ACS Omega 4, 10121–10128. doi:10.1021/acsomega.9b01087

Wang, Y., Shi, Z., Huang, Y., Ma, Y., Wang, C., Chen, M., et al. (2009). Supercapacitor devices based on graphene materials. J. Phys. Chem. C 113, 13103–13107. doi:10.1021/jp902214f

Xia, J., Chen, F., Li, J., and Tao, N. (2009). Measurement of the quantum capacitance of graphene. Nat. Nanotechnol. 4, 505–509. doi:10.1038/nnano.2009.177

Yang, J., and Yao, H. (2020). Automated identification and characterization of two-dimensional materials via machine learning-based processing of optical microscope images. Extreme Mech. Lett. 39, 100771. doi:10.1016/j.eml.2020.100771

Yang, M., Lim, M. K., Qu, Y., Li, X., and Ni, D. (2023). Deep neural networks with L1 and L2 regularization for high dimensional corporate credit risk prediction. Expert Syst. Appl. 213, 118873. doi:10.1016/j.eswa.2022.118873

Yoo, H., Heo, K., Raza, H., and Cho, S. (2021). Recent advances in electrical doping of 2D semiconductor materials: Methods, analyses and applications. Nanomaterials 11, 832. doi:10.3390/nano11040832

Yoon, Y., Kim, M. J., and Kim, J. J. (2021). Machine learning to electrochemistry: Analysis of polymers and halide ions in a copper electrolyte. Electrochimica Acta 399, 139424. doi:10.1016/j.electacta.2021.139424

Yuan, W., Zhou, Y., Li, Y., Li, C., Peng, H., Zhang, J., et al. (2013). The edge- and basal-plane-specific electrochemistry of a single-layer graphene sheet. Sci. Rep. 3, 2248. doi:10.1038/srep02248

Zhang, P., Cheng, N., Li, M., Zhou, B., Bian, C., Wei, Y., et al. (2020). Transition-metal substitution-induced lattice strain and electrical polarity reversal in monolayer WS2. ACS Appl. Mat. Interfaces 12, 18650–18659. doi:10.1021/acsami.9b22004

Zhao, X., Dong, H., Xiao, Y., Hu, H., Cai, Y., Liang, Y., et al. (2016). Three-dimensional Nitrogen-doped graphene as binder-free electrode materials for supercapacitors with high volumetric capacitance and the synergistic effect between nitrogen configuration and supercapacitive performance. Electrochimica Acta 218, 32–40. doi:10.1016/j.electacta.2016.09.096

Zhou, M., Vassallo, A., and Wu, J. (2020). Data-driven approach to understanding the in-operando performance of heteroatom-doped carbon electrodes. ACS Appl. Energy Mat. 3, 5993–6000. doi:10.1021/acsaem.0c01059

Zhu, H., Gan, X., Mccreary, A., Lv, R., Lin, Z., and Terrones, M. (2020). Heteroatom doping of two-dimensional materials: From graphene to chalcogenides. Nano Today 30, 100829. doi:10.1016/j.nantod.2019.100829

Zou, Y., Walton, A. S., Kinloch, I. A., and Dryfe, R. a. W. (2016). Investigation of the differential capacitance of highly ordered pyrolytic graphite as a model material of graphene. Langmuir 32, 11448–11455. doi:10.1021/acs.langmuir.6b02910