Thermally conductive electro-osmotic propulsive pressure-driven peristaltic streaming flow study with a suspended nanomaterial in a micro-ciliated tube

This article focuses on the peristaltic flow of carbon nanoparticle-suspended nanofluids under the influence of electroosmosis. The flow is considered inside a vertical tube with ciliated boundary walls. This study holds great importance because it represents the flow inside the esophagus of the human body. Nanoparticles are inserted in blood for diagnosing diseases like cancer and are also useful in angiography, angioplasty, etc. A comparative study is conducted for single-walled carbon nanotubes and multi-walled carbon nanotubes. We used the analytical method to obtain exact solutions of the velocity, temperature, and pressure profiles. The results have been presented graphically. Streamlines are also plotted to visualize the difference with SWCNT and MWCNT. We found that the use of CNT in the base fluid significantly enhances the thermal conductivity and helps increase the velocity of the fluid.

Introduction

Peristaltic pumping, driven due to contraction or expansion of a distensible tube, is an obvious phenomenon of physiological fluids. Several pertinent examples include digestive tract movement in food transportation, urine transport via the bladder, bile flow from the gall bladder, ovum motion in the fallopian tube, blood circulation in vessels, and ciliary movement (Latham, 1966; Fung and Yih, 1968; Shapiro et al., 1969). Several modern day medical, industrial, and technological equipment include dialysis machines, heart–lung machines, and blood pumping devices. Similarly, the noxious food transport mechanisms in nuclear industries all involve the peristaltic transport mechanism. Owing to such fascinating applications, physiological fluid dynamics has been a subject of core interest for researchers for the past several decades now. Numerous studies have been conducted to explore the peristaltic transport of physiological fluids with various physical characteristics. Mishra and Rao (2003) discussed the peristaltic flow of Newtonian fluids in an asymmetric channel and found out that trapping and reflux regions are directly related to the symmetry of the channel. Reddy et al. (2005) explored the influence of lateral walls on the peristaltic flow by considering the rectangular duct and discussed the effect of the aspect ratio on the pumping characteristics. Ebaid et al. (Elshehawey et al., 2006) considered a similar kind of problem but with the supposition of a porous medium. They concluded that the phase shift between the two walls is strongly effective on transport phenomena, while the axial velocity enhances with the permeability parameter. Nadeem and Akbar (2010) discussed the heat and mass transport in a vertical annulus using the Carreau fluid as a working fluid model and observed smaller trapped boluses for the case of a triangular wave when compared with other waveforms. In another study, Nadeem and Akram (2010) explored the peristaltic phenomenon of the Williamson fluid in an asymmetric channel. Ellahi et al. (2012) discussed the Carreau fluid in a rectangular duct through the porous medium. Their study showed that velocity magnitude increases with an enhancement in the Weissenberg number.

Over the past several years, cilia-driven flows have become a topic of hot research for scientists and engineers. These microscopic hair-like structures which extend from the surface of all mammalian cells, e.g., lungs, kidneys, and respiratory tract, play a critical role in the human physiological system, owing to its visibility in several natural and technological phenomena, microfluidic devices (which uses hair-like structures of artificial cilia), gamete transport in human physiology, respiratory mucus clearance, and embryo development; numerous theoretical studies have been conducted to explore this significant phenomenon. Awais et al. (Awais et al., 2020a; Awais et al., 2020b) have studied the effects of nanoparticles and cilia on the peristaltic motion. Ali et al. (2019) studied the entropy generation of nanofluids in the peristaltic motion. Akbar and Butt (2014) presented the heat transfer analysis due to the metachronal wave of cilia for a viscoelastic fluid. They presented exact solutions for the velocity, temperature, and pressure gradient profiles. A trapping phenomenon along with isotherms was also presented against pertinent parameters. Maqbool et al. (2017) explored the ciliary fluid dynamics in an inclined tube using the fractional generalized Burgers’ fluid model. They observed that relaxation time has a positive impact on the flow region thickness; thus, a greater pressure gradient is desired for the required fluid flow. Bhatti et al. (2017) applied thermal radiation on the MHD particle–fluid suspension induced due to the metachronal wave. Their computed results showed that the fluid parameter augments while the Hartman number suppresses the velocity profile. In another study, Sadaf et al. (2020) scrutinized the cilia-driven flow of a viscoelastic Jeffery fluid within a vertical tube and analyzed that the pumping mechanism is more efficient for the case of the Jeffery fluid than the Newtonian fluid. Farooq et al. (2020) explored the cilia-assisted flow of a magneto-biofluid with chemical reactions using the Darcy–Boussinesq model. Their computed flow rate was extremely close to the flow rate in the ductile efferent and further suggested implementation of their findings in the artificial cilia pumping systems in micro channels. Similarly, the impact of cilia walls on the magneto-fluid peristaltic motion through a porous medium at a moderate Reynolds number has been presented by Abo-Elkhair et al. (2017). The core findings of their study showed a lesser axial velocity without ciliated walls, while a higher pressure gradient in both directions was observed for the case of ciliated channel walls. They also found out that the number of trapped boluses significantly increases without eccentricity of the cilia elliptic path.

Carbon nanotubes (CNTs) are rolled-up graphene sheets having unique thermal, electric, and mechanical properties. In addition, these cylindrical-shaped tubes possess remarkable mechanical tensile strength; these are light in weight and possess good thermal conductivity. Such astonishing properties make them an ideal choice for usage in several biosensors, hydrogen storage cells, transistor batteries, and numerous other electrical shielding applications (Akhtar et al., 2021; Saleem et al., 2021). These nanotubes can be single-walled or multi-walled depending upon the usage of a single layer/multi-layer of carbon atoms. Single- and multi-walled carbon nanotubes are offering promising applications in several modern day industries such as anti-corrosion paints, coatings and thin films, conductive electrodes, engineering plastics, polymers, and many more for the last few decades or so. Meyer et al. (2013) examined the pressure drop characteristics within smooth tubes by utilizing multi-walled carbon nanotubes. Akbar (2015) analyzed the heat transfer in a peristaltic tube using carbon nanotubes and provided the exact analytical expressions for velocity and pressure gradients dependent upon the volume fraction of carbon nanotubes. Hayat et al. (2016) explored the peristaltic flow of a water-based fluid using carbon nanotubes with different thermal conductivity models and reported an increase in the heat transfer rate at the boundaries with a higher volume fraction of carbon nanotubes, while a decline in the velocity profile in the presence of carbon nanotubes was observed. Some more studies on CNTs can be found in the literature (Akbar and Butt, 2014; Khan et al., 2021; Khan et al., 2022; Waini et al., 2022).

In several areas of biotechnology, numerous micro-channel processes involve chemical separation where the electro-osmotic flow is inevitable due to charge disequilibrium (Nadeem et al., 2015). Some significant applications include tissue culture, cell scaffolding systems, pharmacodynamics, and medical electro-osmotic nanoscale devices (Abbasi and Shehzad, 2021). Tripathi et al. (Abbasi and Shehzad, 2021) inspected the electro-thermal peristaltic transport of nanofluids in a finite micro channel by adopting Chakraborty–Roy nanofluid electro kinetic formulation. Ijaz et al. (Tripathi et al., 2017) computed the influence of electroosmosis on the bio-nanofluid with non-spherical particles in a curved channel. The computed results revealed a rise in heat transfer due to the insertion of blade-shaped particles. Noreen et al. (Ijaz et al., 2018) considered the non-Darcy porous medium to present the heat transfer analysis in the electro-osmotic peristaltic flow and concluded that axial velocity declines with the Darcy number, while the heat transfer rate is significantly influenced with energy dissipation due to Joule heating. Recently, Khan et al. (Noreen and Tripathi, 2019) explored the impact of radiation on the electroosmosis-modulated peristaltic flow inside a tapered channel by using the Prandtl nanofluid and found that isothermal lines enhance with the electro-osmotic parameter.

After a comprehensive review of the existing published literature, it is quite evident that the cilia-driven peristaltic fluid using carbon nanotubes has not been given much attention despite its enormous practical significance. Most of the research on the peristaltic flows has been conducted in the absence of electroosmotic forces. As of authors’ knowledge, the thermally conductive nanotube analysis of such fluid models caused by the effects of electroosmosis has not been studied so far. Since this model is studied under the influence of ciliated boundary conditions, the same contributes toward the drug delivery inside the human body.

Problem formulation

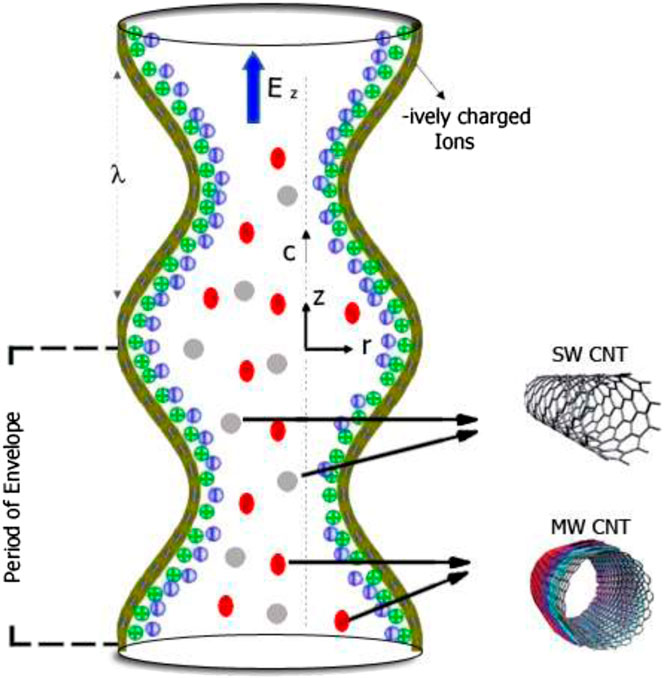
Consider an electroosmosis regulated peristaltic fluid flow of an aqueous ionic nanofluid through a vertical micro-ciliated tube of constant radius $d$. The carbon nanotubes are suspended in the base fluid to prepare the nanofluid. The fluid flow is driven by the combined effect of electroosmosis and peristaltic pumping. Furthermore, it is assumed that ionic species present in the aqueous ionic solution have an equal valence, i.e., the solution is symmetric. These ionic species are set into motion by enforcing an external electric field across the electric double layer carrying the nearby fluid molecules with them. The fluid flow is moving inside a plumb duct under the influence of gravitational force. Peristaltic pumping is generated by the propagation of the sinusoidal waves along the walls of the tube with a constant wave speed $c$ and wavelength $\lambda$. The cylindrical coordinate system $\left(\overline{r},\overline{z},\overline{t}\right)$ is found to be more suitable to perform the mathematical formulation of the flow problem in which $\overline{r}$ and $\overline{z}$ represent the radial and axial directions, respectively, and $\overline{t}$ represents time. The deformation in the tube walls is physically shown in Figure 1 and mathematically represented as follows:

FIGURE 1

FIGURE 1. Geometry of the problem.

The envelops of the cilia tips can be expressed Figure 2 mathematically as $\left[\mathrm{1,2}\right]$:

$\overline{\mathit{R}}=\overline{\mathit{H}}=\overline{\mathit{f}}\left(\overline{\mathit{Z}},\overline{\mathit{t}}\right)=\mathit{a}+\mathit{a}\mathit{\epsilon }\mathit{cos}\left(\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\left(\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}}\right)\right),(\mathrm{1a})$

$\overline{\mathit{Z}}=\overline{\mathit{g}}\left(\overline{\mathit{Z}},\overline{\mathit{t}}\right)=\mathit{a}+\mathit{a}\mathit{\epsilon }\mathit{\alpha }\mathit{sin}\left(\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\left(\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}}\right)\right),(\mathrm{1b})$

where $a$ denotes the mean radius of the tube, $\epsilon$ is the non-dimensional measure with respect to the cilia length, and $\lambda$ and $c$ are the wavelength and wave speed of the metachronal wave, respectively. ${\overline{Z}}_0$ is the reference position of the particle, and $\alpha$ is the measure of the eccentricity of the elliptical motion.

FIGURE 2

FIGURE 2. Movement of cilia causing fluid transport near the walls.

Governing equations

The governing set of equations formulated under the effect of mixed convection, heat source, and electroosmosis is given as follows:

$\frac{\partial \overline{\mathit{U}}}{\partial \overline{\mathit{R}}}+\frac{\overline{\mathit{U}}}{\overline{\mathit{R}}}+\frac{\partial \overline{\mathit{W}}}{\partial \overline{\mathit{Z}}}=\mathbf{0},(1)$

${\mathit{\rho }}_{\mathit{n}\mathit{f}}\left(\frac{\partial \overline{\mathit{U}}}{\partial \overline{\mathit{t}}}+\overline{\mathit{U}}\frac{\partial \overline{\mathit{U}}}{\partial \overline{\mathit{R}}}+\overline{\mathit{W}}\frac{\partial \overline{\mathit{U}}}{\partial \overline{\mathit{Z}}}\right)=-\frac{\partial \overline{\mathit{P}}}{\partial \overline{\mathit{R}}}+{\mathit{\mu }}_{\mathit{n}\mathit{f}}\left(\frac{{\partial }^{\mathbf{2}}\overline{\mathit{U}}}{\partial {\overline{\mathit{R}}}^{\mathbf{2}}}+\frac{\mathbf{1}}{\overline{\mathit{R}}}\frac{\partial \overline{\mathit{U}}}{\partial \overline{\mathit{R}}}-\frac{\overline{\mathit{U}}}{{\overline{\mathit{R}}}^{\mathbf{2}}}+\frac{{\partial }^{\mathbf{2}}\overline{\mathit{U}}}{\partial {\overline{\mathit{Z}}}^{\mathbf{2}}}\right)+{\mathit{\rho }}_{\mathit{e}}{\mathit{E}}_{\overline{\mathit{R}},}(2)$

${\mathit{\rho }}_{\mathit{n}\mathit{f}}\left(\frac{\partial \overline{\mathit{W}}}{\partial \overline{\mathit{t}}}+\overline{\mathit{U}}\frac{\partial \overline{\mathit{W}}}{\partial \overline{\mathit{R}}}+\overline{\mathit{W}}\frac{\partial \overline{\mathit{W}}}{\partial \overline{\mathit{Z}}}\right)=-\frac{\partial \overline{\mathit{P}}}{\partial \overline{\mathit{Z}}}+{\mathit{\mu }}_{\mathit{n}\mathit{f}}\left(\frac{{\partial }^{\mathbf{2}}\overline{\mathit{W}}}{\partial {\overline{\mathit{R}}}^{\mathbf{2}}}+\frac{\mathbf{1}}{\overline{\mathit{R}}}\frac{\partial \overline{\mathit{W}}}{\partial \overline{\mathit{R}}}+\frac{{\partial }^{\mathbf{2}}\overline{\mathit{W}}}{\partial {\overline{\mathit{Z}}}^{\mathbf{2}}}\right)+{\mathit{\rho }}_{\mathit{e}}{\mathit{E}}_{\overline{\mathit{Z}}}+{\left(\mathit{\rho }\mathit{\gamma }\right)}_{\mathit{n}\mathit{f}}\left(\overline{\mathit{T}}-{\mathit{T}}_{\mathbf{0}}\right),(3)$

${\left(\mathit{\rho }\mathit{c}\right)}_{\mathit{n}\mathit{f}}\left(\frac{\partial \overline{\mathit{T}}}{\partial \overline{\mathit{t}}}+\overline{\mathit{U}}\frac{\partial \overline{\mathit{T}}}{\partial \overline{\mathit{R}}}+\overline{\mathit{W}}\frac{\partial \overline{\mathit{T}}}{\partial \overline{\mathit{Z}}}\right)={\mathit{k}}_{\mathit{n}\mathit{f}}\left(\frac{{\partial }^{\mathbf{2}}\overline{\mathit{T}}}{{\partial \overline{\mathit{R}}}^{\mathbf{2}}}+\frac{\mathbf{1}}{\overline{\mathit{R}}}\frac{\partial \overline{\mathit{T}}}{\partial \overline{\mathit{R}}}+\frac{{\partial }^{\mathbf{2}}\overline{\mathit{T}}}{{\partial \overline{\mathit{Z}}}^{\mathbf{2}}}\right)+{\mathit{Q}}_{\mathbf{0}},(4)$

in which $E_{\overline{R},}$ and $E_{\overline{Z}}$ specify the electric body forces in the radial and axial directions, respectively, $\overline{U}$ is the velocity component in the radial direction, $\overline{W}$ is the velocity in the axial direction, $\overline{T}$ is the temperature of the fluid, $k_{nf}$ is the effective thermal conductivity of the nanofluid, $Q_0$ is the heat source parameter, ${\left(\rho c\right)}_{nf}$ is the specific heat of the nanofluid, ${\rho }_{nf}$ and ${\mu }_{nf}$ are the effective density and the viscosity of the nanofluid, respectively, ${\left(\rho \gamma \right)}_{nf}$ is the thermal expansion coefficient of the nanofluid, and ${\rho }_e$ is the eclectic number density of the electrolyte solution.

If no slip condition is applied, then the velocities of the transporting fluid are just those caused by the cilia tips, which can be given as follows:

$\overline{\mathit{W}}={\frac{\mathbf{\partial }\overline{\mathit{Z}}}{\mathbf{\partial }\overline{\mathit{t}}})}_{{\overline{\mathit{Z}}}_0}=\frac{\partial \overline{\mathit{g}}}{\partial \overline{\mathit{t}}}+\frac{\partial \overline{\mathit{g}}}{\partial \overline{\mathit{Z}}}\frac{\partial \overline{\mathit{Z}}}{\partial \overline{\mathit{t}}}=\frac{\partial \overline{\mathit{g}}}{\partial \overline{\mathit{t}}}+\frac{\partial \overline{\mathit{g}}}{\partial \overline{\mathit{Z}}}\overline{\mathit{W}},(5)$

$\overline{\mathit{U}}={\frac{\mathit{\partial }\overline{\mathit{R}}}{\mathit{\partial }\overline{\mathit{t}}})}_{{\overline{\mathit{Z}}}_0}=\frac{\partial \overline{\mathit{f}}}{\partial \overline{\mathit{t}}}+\frac{\partial \overline{\mathit{f}}}{\partial \overline{\mathit{Z}}}\frac{\partial \overline{\mathit{Z}}}{\partial \overline{\mathit{t}}}=\frac{\partial \overline{\mathit{f}}}{\partial \overline{\mathit{t}}}+\frac{\partial \overline{\mathit{f}}}{\partial \overline{\mathit{Z}}}\overline{\mathit{W}}.(6)$

Using equations (1) and (2) in equations (5) and (6), we obtain

$\overline{\mathit{W}}=\frac{-\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\left(\mathit{\epsilon }\mathit{\alpha }\mathit{a}\mathit{c}\mathbf{cos}\left(\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\right)\left(\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}}\right)\right)}{\mathbf{1}-\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\left(\mathit{\epsilon }\mathit{\alpha }\mathit{a}\mathbf{cos}\left(\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\right)\left(\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}}\right)\right)},(7)$

$\overline{\mathit{U}}=\frac{\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\left(\mathit{\epsilon }\mathit{a}\mathit{c}\mathit{sin}\left(\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\right)\left(\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}}\right)\right)}{\mathbf{1}-\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\left(\mathit{\epsilon }\mathit{\alpha }\mathit{a}\mathit{cos}\left(\frac{\mathbf{2}\mathit{\pi }}{\mathit{\lambda }}\right)\left(\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}}\right)\right)}.(8)$

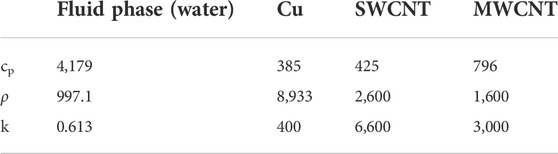
From the general mixture rule, the effective density, specific heat, and thermal expansion coefficient of the Cu–water nanofluid are determined, and the Brinkman’s relation and the Maxwell model are employed to specify the viscosity and thermal conductivity of the nanofluid as follows:

${\mathit{\rho }}_{\mathit{n}\mathit{f}}=\left(\mathbf{1}-\mathit{\varphi }\right){\mathit{\rho }}_{\mathit{f}}+\mathit{\varphi }{\mathit{\rho }}_{\mathit{C}\mathit{N}\mathit{T}},{\mathit{\mu }}_{\mathit{n}\mathit{f}}=\frac{{\mathit{\mu }}_{\mathit{f}}}{{\left(\mathbf{1}-\mathit{\varphi }\right)}^{\mathbf{2.5}}},(9)$

${\left(\mathit{\rho }{\mathit{c}}_{\mathit{p}}\right)}_{\mathit{n}\mathit{f}}=\left(\mathbf{1}-\mathit{\varphi }\right){\left(\mathit{\rho }{\mathit{c}}_{\mathit{p}}\right)}_{\mathit{f}}+\mathit{\varphi }{\left(\mathit{\rho }{\mathit{c}}_{\mathit{p}}\right)}_{\mathit{f}},{\mathit{\alpha }}_{\mathit{n}\mathit{f}}=\frac{{\mathit{k}}_{\mathit{n}\mathit{f}}}{{\left(\mathit{\rho }{\mathit{c}}_{\mathit{p}}\right)}_{\mathit{n}\mathit{f}}},$

${\left(\mathit{\rho }\mathit{\gamma }\right)}_{\mathit{n}\mathit{f}}=\left(\mathbf{1}-\mathit{\varphi }\right){\left(\mathit{\rho }\mathit{\gamma }\right)}_{\mathit{f}}+\mathit{\varphi }{\left(\mathit{\rho }\mathit{\gamma }\right)}_{\mathit{C}\mathit{N}\mathit{T}},{\mathit{k}}_{\mathit{n}\mathit{f}}={\mathit{k}}_{\mathit{f}}\left(\frac{\left(\mathbf{1}-\mathit{\varphi }\right)+\frac{\mathbf{2}\mathit{\varphi }{\mathit{k}}_{\mathit{C}\mathit{N}\mathit{T}}}{{\mathit{k}}_{\mathit{C}\mathit{N}\mathit{T}}-{\mathit{k}}_{\mathit{f}}}\mathit{log}\left(\frac{{\mathit{k}}_{\mathit{C}\mathit{N}\mathit{T}}+{\mathit{k}}_{\mathit{f}}}{\mathbf{2}{\mathit{k}}_{\mathit{f}}}\right)}{\left(\mathbf{1}-\mathit{\varphi }\right)+\frac{\mathbf{2}\mathit{\varphi }{\mathit{k}}_{\mathit{f}}}{{\mathit{k}}_{\mathit{C}\mathit{N}\mathit{T}}-{\mathit{k}}_{\mathit{f}}}\mathit{log}\left(\frac{{\mathit{k}}_{\mathit{C}\mathit{N}\mathit{T}}+{\mathit{k}}_{\mathit{f}}}{\mathbf{2}{\mathit{k}}_{\mathit{f}}}\right)}\right).$

Here, $\varphi$ designates the nanoparticle volume fraction, the subscript “$f$” is used to denote the properties of the base fluid, and “$p$” denotes the solid particle properties. The distribution of the electric potential within the fluid medium is described by the Poisson equation as follows:

${\nabla }^{\mathbf{2}}\overline{\mathit{\phi }}=\frac{{\partial }^{\mathbf{2}}\overline{\mathit{\phi }}}{{\partial \overline{\mathit{R}}}^{\mathbf{2}}}+\frac{\mathbf{1}}{\overline{\mathit{r}}}\frac{\partial \overline{\mathit{\phi }}}{\partial \overline{\mathit{R}}}+\frac{{\partial }^{\mathbf{2}}\overline{\mathit{\phi }}}{{\partial \overline{\mathit{Z}}}^{\mathbf{2}}}=-\frac{{\mathit{\rho }}_{\mathit{e}}}{{\mathit{\epsilon }}_{\mathit{r}}{\mathit{\epsilon }}_{\mathbf{0}}}.(10)$

Here, ${\epsilon }_r$ represents the relative permittivity of the medium, ${\epsilon }_0$ is the permittivity of the vacuum, and the electric number density in terms of the number density of cations $n^{+}$ and the anions $n^{-}$ is described as follows:

${\mathit{\rho }}_{\mathit{e}}=\mathit{e}\mathit{z}\left({\mathit{n}}^{+}-{\mathit{n}}^{-}\right).(11)$

Defining the transformation of velocity components and the coordinates from the stationary frame to the wave frame (moving frame of reference), to observe the steady fluid flow, as follows:

$\overline{\mathit{z}}=\overline{\mathit{Z}}-\mathit{c}\overline{\mathit{t}},\overline{\mathit{r}}=\overline{\mathit{R}},\overline{\mathit{w}}=\overline{\mathit{W}}-\mathit{c},\overline{\mathit{u}}=\overline{\mathit{U}},\overline{\mathit{p}}\left(\overline{\mathit{r}},\overline{\mathit{z}}\right)=\overline{\mathit{P}}\left(\overline{\mathit{R}},\overline{\mathit{Z}},\overline{\mathit{t}}\right).(12)$

The considered flow problem can be simplified by performing the non-dimensional analysis by introducing the following dimensionless parameters:

$\begin{array}{ll}\hfill \mathit{r}=& \frac{\overline{\mathit{r}}}{\mathbf{\lambda }},\mathit{z}=\frac{\overline{\mathit{z}}}{\mathit{d}},\mathit{p}=\frac{\overline{\mathit{p}}{\mathit{d}}^{\mathbf{2}}}{{\mathit{\mu }}_{\mathit{f}}\mathit{c}\lambda },\mathit{n}=\frac{\overline{\mathit{n}}}{{\mathit{n}}_{\mathbf{0}}},\mathit{R}\mathit{e}=\frac{{\mathit{\rho }}_{\mathit{f}}\mathit{c}\mathit{d}}{{\mathit{\mu }}_{\mathit{f}}},\overline{\mathit{\Psi }}=\frac{\mathit{\Psi }}{\mathit{c}\mathit{d}},\mathit{h}=\frac{\overline{\mathit{H}}}{\mathit{d}},\mathit{Pr}=\frac{{\mathit{\mu }}_{\mathit{f}}{\mathit{c}}_{\mathit{p}}}{{\mathit{k}}_{\mathit{f}}},\mathit{\delta }=\frac{\mathit{d}}{\lambda },\mathit{\theta }=\frac{\overline{\mathit{T}}-{\mathit{T}}_{\mathbf{0}}}{{\mathit{T}}_{\mathbf{0}}},\hfill \\ \hfill & {\mathit{G}}_{\mathit{r}}=\frac{{\mathit{\rho }}_{\mathit{f}}\mathit{g}{\mathit{\gamma }}_{\mathit{f}}{\mathit{d}}^{\mathbf{2}}{\mathit{T}}_{\mathbf{0}}}{{\mathit{\mu }}_{\mathit{f}}\mathit{c}},\mathit{U}=-\frac{{\mathit{\epsilon }}_{\mathbf{0}}{\mathit{\epsilon }}_{\mathit{r}}{\mathit{k}}_{\mathit{f}}{\widehat{\mathit{T}}}_{\mathit{a}\mathit{v}\mathit{g}}{\mathit{E}}_{\mathit{z}}}{\mathit{e}\mathit{z}{\mathit{\mu }}_{\mathit{f}}\mathit{c}},\mathit{\kappa }=\sqrt{\frac{\mathbf{2}{\mathit{n}}_{\mathbf{0}}{\mathit{e}}^{\mathbf{2}}{\mathit{z}}^{\mathbf{2}}{\mathit{d}}^{\mathbf{2}}}{{\mathit{\epsilon }}_{\mathbf{0}}{\mathit{\epsilon }}_{\mathit{r}}{\mathit{k}}_{\mathit{f}}{\widehat{\mathit{T}}}_{\mathit{a}\mathit{v}\mathit{g}}}}=\frac{\mathit{d}}{{\mathit{\lambda }}_{\mathit{d}}},\mathit{\phi }=\frac{\mathit{e}\mathit{z}\overline{\mathit{\phi }}}{{\mathit{k}}_{\mathit{f}}{\widehat{\mathit{T}}}_{\mathit{a}\mathit{v}\mathit{g}}},\mathit{\beta }=\frac{{\mathit{Q}}_{\mathbf{0}}{\mathit{d}}^{\mathbf{2}}}{{\mathit{T}}_{\mathbf{0}}{\mathit{k}}_{\mathit{f}}},\mathit{L}=\frac{{\left(\mathit{\rho }\mathit{\gamma }\right)}_{\mathit{n}\mathit{f}}}{{\left(\mathit{\rho }\mathit{\gamma }\right)}_{\mathit{f}}}.\hfill \end{array}(13)$

Then, applying the lubrication linearization theory of long wavelength and the low Reynolds number, we are left with the following simplified set of equations:

$\frac{\partial \mathit{p}}{\partial \mathit{r}}=\mathbf{0},(14)$

$\frac{\mathit{d}\mathit{p}}{\mathit{d}\mathit{z}}=\frac{{\mathit{\mu }}_{\mathit{n}\mathit{f}}}{{\mathit{\mu }}_{\mathit{f}}}\frac{\mathbf{1}}{\mathit{r}}\frac{\partial }{\partial \mathit{r}}\left(\mathit{r}\frac{\partial \mathit{w}}{\partial \mathit{r}}\right)+{\mathit{G}}_{\mathit{r}}\mathit{L}\mathit{\theta }+\mathit{U}\frac{\mathbf{1}}{\mathit{r}}\frac{\partial }{\partial \mathit{r}}\left(\mathit{r}\frac{\partial \mathit{\phi }}{\partial \mathit{r}}\right),(15)$

$\frac{\mathbf{1}}{\mathit{r}}\frac{\partial }{\partial \mathit{r}}\left(\mathit{r}\frac{\partial \mathit{\theta }}{\partial \mathit{r}}\right)+\mathit{\beta }\frac{{\mathit{k}}_{\mathit{f}}}{{\mathit{k}}_{\mathit{n}\mathit{f}}}=\mathbf{0},(16)$

$\frac{\mathbf{1}}{\mathit{r}}\frac{\partial }{\partial \mathit{r}}\left(\mathit{r}\frac{\partial \mathit{\phi }}{\partial \mathit{r}}\right)={\mathit{\kappa }}^{\mathbf{2}}\left(\frac{{\mathit{n}}^{-}-{\mathit{n}}^{+}}{\mathbf{2}}\right),(17)$

where U designates the Helmholtz–Smoluchowski velocity or the electro-osmotic velocity parameter, $G_r$ is the Grashof number, $\beta$ is the dimensionless heat source parameter, $\theta$ is the dimensionless temperature parameter, and $\kappa$ is the ratio of the characteristic traverse length to the Debye length parameter.

The local ionic distribution of ionic species can be specified by the linearized Boltzmann distribution for low zeta potential which accurately estimates the electric potential established in the fluid medium without increasing the complexity of the flow problem; as for most of the electrolyte solution, the generated electric potential lies in the range less than or equal to 25 mV.

${\mathit{n}}^{\pm }={\mathit{e}}^{\mp \mathit{\phi }}.(18)$

Using equation (14) in (13), we get the linearized Poisson–Boltzmann paradigm (Tripathi et al., 2017) as follows:

$\frac{\mathbf{1}}{\mathit{r}}\frac{\partial }{\partial \mathit{r}}\left(\mathit{r}\frac{\partial \mathit{\phi }}{\partial \mathit{r}}\right)={\mathit{\kappa }}^{\mathbf{2}}\mathbf{sinh}\left(\mathit{\phi }\right),(19)$

which is further simplified under the Debye–Hückel approximation (Tripathi et al., 2017), i.e., $\sinh \left(\phi \right)\approx \phi$, as follows:

$\frac{\mathbf{1}}{\mathit{r}}\frac{\partial }{\partial \mathit{r}}\left(\mathit{r}\frac{\partial \mathit{\phi }}{\partial \mathit{r}}\right)={\mathit{\kappa }}^{\mathbf{2}}\mathit{\phi }.(20)$

The dimensionless form of the no-slip boundary conditions for velocity temperature and electric potential enforced along the tube walls is given by the following equations:

$\mathit{\phi }=\mathit{\xi },\mathit{w}=\frac{-\mathbf{2}\mathit{\pi }\mathit{ϵ}{\mathit{\beta }}_{\mathbf{1}}\mathbf{cos}\left(\mathbf{2}\mathit{\pi }\mathit{z}\right)}{\mathbf{1}-\mathbf{2}\mathit{\pi }\mathit{ϵ}{\mathit{\beta }}_{\mathbf{1}}},\mathit{\theta }=\mathbf{0},\mathit{a}\mathit{t}\mathit{r}=\mathit{h}=\mathbf{1}+\mathit{ϵ}\mathbf{cos}\left(\mathbf{2}\mathit{\pi }\mathit{z}\right),(21)$

$\frac{\partial \mathit{\phi }}{\partial \mathit{r}}=\mathbf{0},\frac{\partial \mathit{w}}{\partial \mathit{r}}=\mathbf{0},\frac{\partial \mathit{\theta }}{\partial \mathit{r}}=\mathbf{0},\mathit{a}\mathit{t}\mathit{r}=\mathbf{0}.$

Solution profiles

An analytical expression for velocity profile, temperature distribution, and electric potential can be obtained by integrating equations (11), (12), and (16) with the help of appropriate boundary conditions. The resulting velocity profile, temperature distribution, and electric potential are given as follows:-

$w\left(r,z\right)=\frac{\left(h^2-r^2\right)\left(G_{r}L\frac{k_f}{k_{nf}}\beta \left(3h^2-r^2\right)-16\frac{dp}{dz}\right)+64\left(U\xi -\frac{{\mu }_{nf}}{{\mu }_f}\right)-64U\xi \frac{{\mathrm{I}}_0\left(r\kappa \right)}{{\mathrm{I}}_0\left(h\kappa \right)}}{64\frac{{\mu }_{nf}}{{\mu }_f}},(22)$

$\theta \left(r,z\right)=\frac{1}{4}\frac{k_f}{k_{nf}}\left(h^2-r^2\right)\beta ,(23)$

$\phi =\xi \frac{{\mathrm{I}}_0\left(r\kappa \right)}{{\mathrm{I}}_0\left(h\kappa \right)}.(24)$

To find the pressure gradient, we use the flow rate in the moving frame given by the following equation:

$F=2\pi \underset{0}{\overset{h}{{\displaystyle \int }}}rwdr.(25)$

From Equation 21, the pressure gradient can be obtained in terms of flow rate as follows:

$\frac{dp}{dz}=\frac{7}{40}{G}_{r}L{h}^2\frac{k_f}{k_{nf}}\beta +\frac{3F}{h^3}\frac{{\mu }_{nf}}{{\mu }_f}+\frac{3\pi U\xi }{h^2{\mathrm{I}}_0\left(h\kappa \right)}\left[{\mathrm{I}}_1\left(h\kappa \right){\mathrm{L}}_0\left(h\kappa \right)-{\mathrm{I}}_0\left(h\kappa \right){\mathrm{L}}_1\left(h\kappa \right)\right],(26)$

where ${\mathrm{I}}_0\left(x\right)\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{I}}_1\left(x\right)$ are the modified Bessel function of the first kind, defined as follows:

${\mathrm{I}}_j\left(x\right)={\displaystyle \sum }_{i=0}^{\infty }\frac{1}{i!\mathrm{\Gamma }\left(i+j+1\right)}{\left(\frac{x}{2}\right)}^{2i+j}(27)$

and ${\mathrm{L}}_0\left(x\right),{\mathrm{L}}_1\left(x\right)$ are the modified Struve functions, defined as follows:

${\mathrm{L}}_j\left(x\right)={\displaystyle \sum }_{i=0}^{\infty }\frac{1}{i!\mathrm{\Gamma }\left(\frac{3}{2}+i\right)\mathrm{\Gamma }\left(\frac{3}{2}+i+j\right)}{\left(\frac{x}{2}\right)}^{2i+j+1}.(28)$

Using the aforementioned equation (22), we can evaluate the pressure rise $∆P$ as follows:

$∆P=\underset{0}{\overset{1}{{\displaystyle \int }}}\frac{dP}{dz}dz.(29)$

The exact solutions of all equations have been formulated using Mathematical 11.0.

Results and discussion

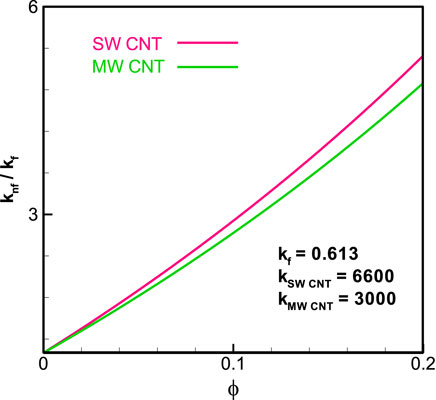
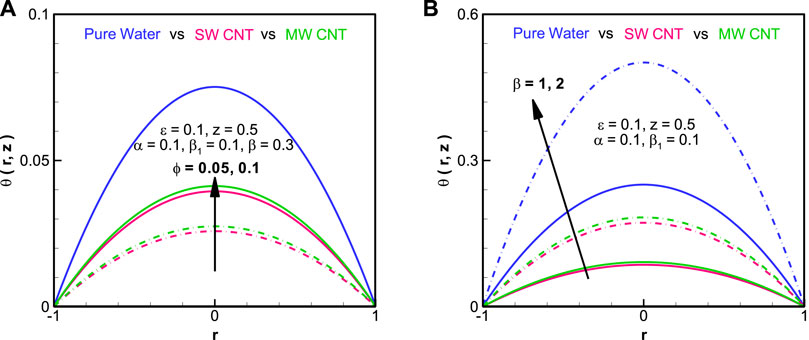
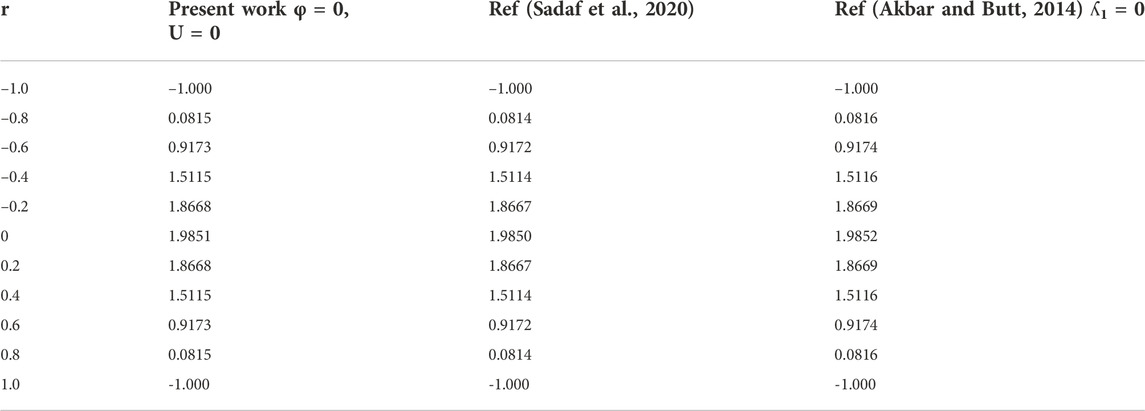
We have plotted the graphs for the temperature, electric potential, velocity, and pressure distribution of the given problem. Figure 3, Table 1 tells us about the effective thermal conductivity of the nanofluid while using the single-walled carbon nanotube (SWCNT) and multi-walled carbon nanotube (MWCNT). We can see that the thermal conductivity enhances in case of MWCNT as compared to the SWCNT. Moreover, the greater the amount of copper in the nanofluid ($\varphi >0$), the more will be the difference in SWCNT and MWCNT. Figure 4 shows the temperature profile of the nanofluid in case of pure water, SWCNT, and MWCNT. Color profiles are utilized in graphs to efficiently differentiate between the different forms of fluids. We can observe that without the addition of copper in the nanofluid (in case of pure water), the temperature is maximum. For SWCNT, the temperature is lower than that of MWCNT. Figure 4A indicates that the addition of copper in the base nanofluid significantly reduces the temperature of the fluid. Figure 4B indicates that if we increase the heat source parameter ($\beta )$, the temperature increases. In addition, we can see that the temperature increases toward the center of the tube ($r=0$) and decreases at the boundaries of the tube ($r=1,-1$).

TABLE 1

TABLE 1. Thermal properties of the base fluid (water) and nanoparticles.

FIGURE 3

FIGURE 3. Effective thermal conductivity of the nanofluid.

FIGURE 4

FIGURE 4. Temperature profile of the nanofluid.

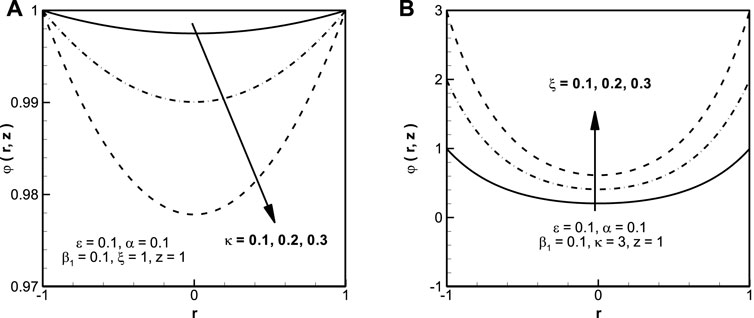
Figure 5 depicts the electric potential of the nanofluid against the radial distance. Contrary to the temperature profile, the electric potential is minimum at the center of the tube and maximum toward the boundaries of the tube. Furthermore, the electric potential decreases with an increase in the ratio of the characteristic traverse length to the Debye length parameter ($\kappa )$ and increases with an increase in the zeta potential ($\xi$). Figure 6 has been plotted to visualize the behavior of the velocity profile in contrast with the radial distance of the tube. We can see that the velocity profile has a sinusoidal behavior due to the presence of the to and fro motion of cilia. Velocity is minimally differentiated with the use of SWCNT and MWCNT nanofluids. However, at the center of the tube, larger values of the Grashof number ($G_r$) and the heat source parameter indicate higher values of the velocity, whereas larger values of the nanoparticle volume fraction ($\varphi$), the ratio of the characteristic traverse length to the Debye length parameter, and the Helmholtz–Smoluchowski velocity indicate a decline in the velocity of the fluid.

FIGURE 5

FIGURE 5. Electric potential of the nanofluid.

FIGURE 6

FIGURE 6. Velocity profile of the nanofluid.

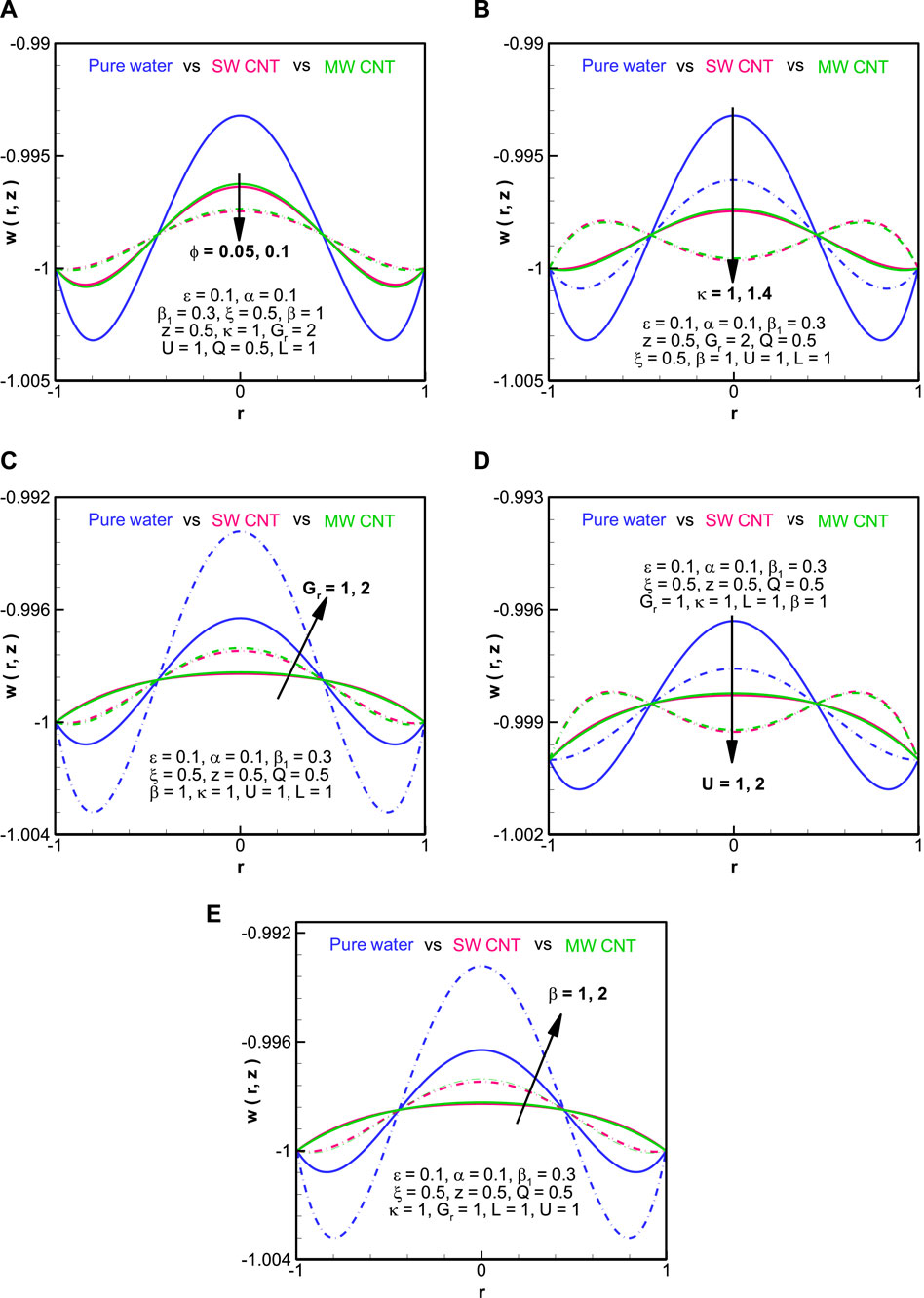
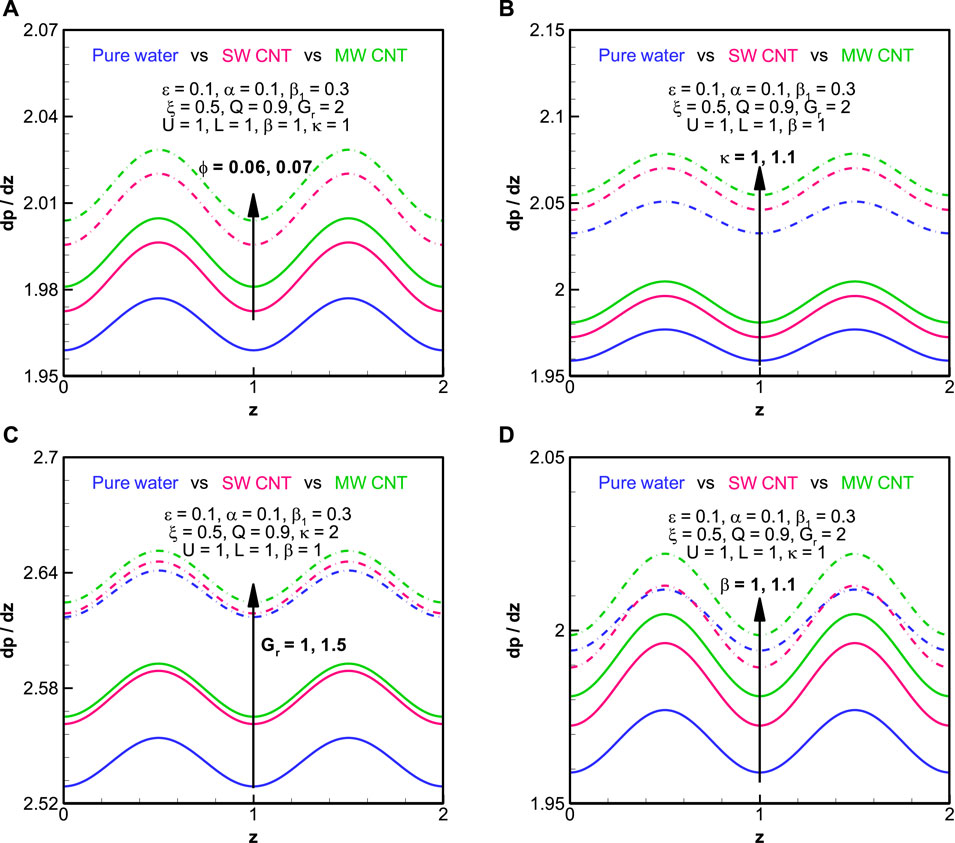
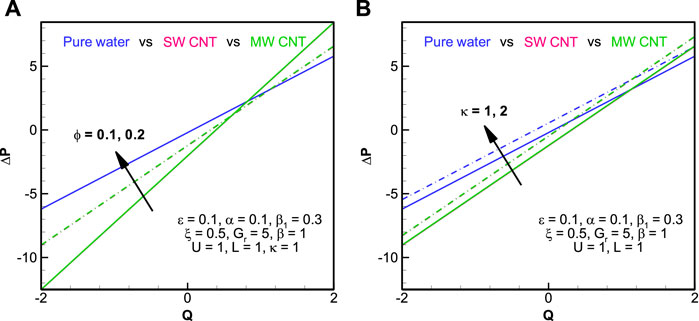
Figure 7 shows the graphical profile of the pressure gradient against the axial distance of the fluid. We can see that the pressure gradient of the nanofluids increases with the amount of copper addition in the base fluid. For MWCNT, the pressure gradient remains greater than SWCNT, which remains greater than pure water. The pressure gradient appears to gain volume with the increase in either the ratio of the characteristic traverse length to the Debye length parameter, the Grashof number, or the heat source parameter. Throughout the length of the tube, the behavior of the pressure gradient remains sinusoidal. In Figure 8, we have demonstrated the pressure rise of the nanofluid in contrast with the flow rate parameter ($Q$). There is a marginal difference in the pressure rise of the nanofluid in case of SWCNT and MWCNT. However, in the peristaltic pumping region ($∆P>0$), the pressure rise is mostly maximum for MWCNT as compared to SWCNT and pure water; opposite behavior can be seen in the augmented pumping region ($∆P<0$). The amount of the nanoparticle volume fraction increases the pressure gradient in the augmented peristaltic region and reduces it in the peristaltic region. Similar behavior is seen in the case of the ratio of the characteristic traverse length to the Debye length parameter.

FIGURE 7

FIGURE 7. Pressure gradient of the nanofluid.

FIGURE 8

FIGURE 8. Pressure rise of the nanofluid.

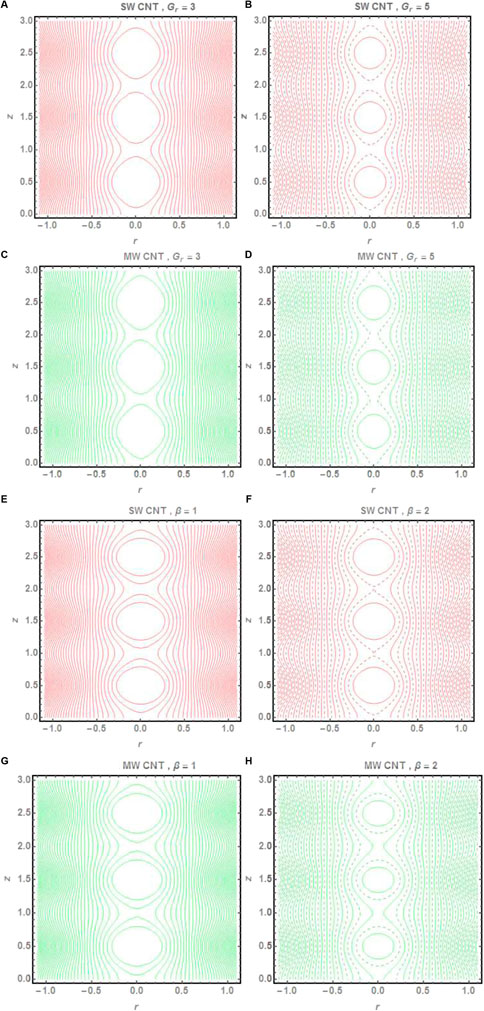
Streamlines depicting the peristaltic flow of the fluid is represented in Figure 9. Streamlines are plotted both for SWCNT and MWCNT for variation in the values of the Grashof number and the heat absorption parameter. The trapped bolus inside the streamlines depicts the transport of the fluid through the peristaltic movement with the help of the ciliated boundary walls. We can see that with the increase in the values in the Grashof number, the number of trapped boluses increases in the fluid flow and the size of the bolus decreases in both cases of CNTs. However, the trapped bolus appears to be greater in size in the case of MWCNT. A similar pattern and behavior is witnessed when we increase the values of the heat absorption parameter Table 2.

TABLE 2

TABLE 2. Comparison of the present results with the existing literature.

FIGURE 9

FIGURE 9. Streamlines of the fluid flow for SWCNT and MWCNT.

Conclusion

This article focuses on the peristaltic flow of carbon nanoparticle-suspended nanofluids under the influence of electroosmosis. Main findings of the current study are listed as follows.

1) It is found that the use of CNT in the base fluid significantly enhances the thermal conductivity and helps increase the velocity of the fluid.

2) We can observe that without the addition of copper in the nanofluid (in case of pure water), the temperature is maximum. For SWCNT, the temperature is lower than that of MWCNT.

3) We can see that the pressure gradient of the nanofluids increases with the amount of copper addition in the base fluid. For MWCNT, the pressure gradient remains greater than SWCNT.

4) There is a marginal difference in the pressure rise of the nanofluid in the case of SWCNT and MWCNT.

5) We can see that with the increase in the values in the Grashof number, the number of trapped bolus increases in the fluid flow and the size of the bolus decreases in both cases of CNTs

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

AB worked on the solution section and graphs section, NK carried out mathematical modeling, RM worked on the introduction section, and SF carried out the final proof reading and suggested mathematical techniques.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasi, F. M., and Shehzad, S. A. (2021). Heat transfer analysis for EMHD peristalsis of ionic-nanofluids via curved channel with Joule dissipation and Hall effects. J. Biol. Phys. 23, 1–22.

Google Scholar

Abo-Elkhair, R., Mekheimer, K. S., and Moawad, A. (2017). Cilia walls influence on peristaltically induced motion of magneto-fluid through a porous medium at moderate Reynolds number: Numerical study. J. Egypt. Math. Soc. 25, 238–251. doi:10.1016/j.joems.2017.01.001

CrossRef Full Text | Google Scholar

Akbar, N. S., and Butt, A. W. (2014). Heat transfer analysis of viscoelastic fluid flow due to metachronal wave of cilia. Int. J. Biomath. 7, 1450066. doi:10.1142/s1793524514500661

CrossRef Full Text | Google Scholar

Akbar, N. S. (2015). Heat transfer and carbon nano tubes analysis for the peristaltic flow in a diverging tube. Meccanica 50, 39–47. doi:10.1007/s11012-014-0067-y

CrossRef Full Text | Google Scholar

Akhtar, S., McCash, L. B., Nadeem, S., Saleem, S., and Issakhov, A. (2021). Convective heat transfer for Peristaltic flow of SWCNT inside a sinusoidal elliptic duct. Sci. Prog. 104 (2), 003685042110236–17. doi:10.1177/00368504211023683

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, A., Shah, Z., Mumraiz, S., Kumam, P., and Awais, M. (2019). Entropy generation on MHD peristaltic flow of Cu-water nanofluid with slip conditions. Heat. Trans. Asian. Res. 48, 4301–4319. doi:10.1002/htj.21593

CrossRef Full Text | Google Scholar

Awais, M., Kumam, P., Parveen, N., Ali, A., Shah, Z., and Thounthong, P. (2020). Slip and Hall effects on peristaltic rheology of copper-water nanomaterial through generalized complaint walls with variable viscosity. Front. Phys. 7, 249. doi:10.3389/fphy.2019.00249

CrossRef Full Text | Google Scholar

Awais, M., Shah, Z., Perveen, N., Ali, A., Kumam, P., Rehman, H., et al. (2020). MHD effects on ciliary-induced peristaltic flow coatings with rheological hybrid nanofluid. Coatings 10 (2), 186. doi:10.3390/coatings10020186

CrossRef Full Text | Google Scholar

Bhatti, M., Zeeshan, A., and Ellahi, R. (2017). Heat transfer with thermal radiation on MHD particle–fluid suspension induced by metachronal wave. Pramana -. J. Phys. 89, 48–9. doi:10.1007/s12043-017-1444-6

CrossRef Full Text | Google Scholar

Ellahi, R., Riaz, A., Nadeem, S., and Ali, M. (2012). Peristaltic flow of Carreau fluid in a rectangular duct through a porous medium. Math. problems Eng. 2012, 1–24. doi:10.1155/2012/329639

CrossRef Full Text | Google Scholar

Elshehawey, E., Eldabe, N. T., Elghazy, E., and Ebaid, A. (2006). Peristaltic transport in an asymmetric channel through a porous medium. Appl. Math. Comput. 182, 140–150. doi:10.1016/j.amc.2006.03.040

CrossRef Full Text | Google Scholar

Farooq, A. A., Shah, Z., Kumam, P., O Alzahrani, E., Shutaywi, M., and Anwar, T. (2020). Darcy–Boussinesq model of cilia-assisted transport of a non-Newtonian magneto-biofluid with chemical reactions. Appl. Sci. 10, 1137. doi:10.3390/app10031137

CrossRef Full Text | Google Scholar

Fung, Y., and Yih, C. (1968). Peristaltic transport. China

Google Scholar

Hayat, T., Ahmed, B., Abbasi, F., and Ahmad, B. (2016). Mixed convective peristaltic flow of carbon nanotubes submerged in water using different thermal conductivity models. Comput. methods programs Biomed. 135, 141–150. doi:10.1016/j.cmpb.2016.07.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Ijaz, N., Zeeshan, A., and Rehman, S. (2018). Effect of electro-osmosis and mixed convection on nano-bio-fluid with non-spherical particles in a curved channel. Mech. Industry 19, 108. doi:10.1051/meca/2017040

CrossRef Full Text | Google Scholar

Khan, U., Ishak, A., and Zaib, A. (2021). Hybrid nanofluid flow containing single-wall and multi-wall CNTs induced by a slender stretchable sheet. Chin. J. Phys. 74, 350–364. doi:10.1016/j.cjph.2021.10.009

CrossRef Full Text | Google Scholar

Khan, U., Zaib, A., Ishak, A., Bakar, S. A., Animasaun, I. L., and Yook, S. J. (2022). Insights into the dynamics of blood conveying gold nanoparticles on a curved surface when suction, thermal radiation, and Lorentz force are significant: The case of Non-Newtonian Williamson fluid. Math. Comput. Simul. 193, 250–268. doi:10.1016/j.matcom.2021.10.014

CrossRef Full Text | Google Scholar

Latham, T. (1966). “Motion in a peristaltic pump,” in MS thesis (Cambridge, Mass, USA: MIT-Press).

Google Scholar

Maqbool, K., Mann, A., Siddiqui, A., and Shaheen, S. (2017). Fractional generalized Burgers’ fluid flow due to metachronal waves of cilia in an inclined tube. Adv. Mech. Eng. 9, 168781401771556–1687814017715565. doi:10.1177/1687814017715565

CrossRef Full Text | Google Scholar

Meyer, J. P., McKrell, T., and Grote, K. (2013). The influence of multi-walled carbon nanotubes on single-phase heat transfer and pressure drop characteristics in the transitional flow regime of smooth tubes. Int. J. Heat Mass Transf. 58, 597–609. doi:10.1016/j.ijheatmasstransfer.2012.11.074

CrossRef Full Text | Google Scholar

Mishra, M., and Rao, A. R. (2003). Peristaltic transport of a Newtonian fluid in an asymmetric channel. Z. für. Angew. Math. Phys. 54, 532–550. doi:10.1007/s00033-003-1070-7

CrossRef Full Text | Google Scholar

Nadeem, S., and Akbar, N. S. (2010). Effects of heat and mass transfer on peristaltic flow of Carreau fluid in a vertical annulus. Z. für Naturforsch. A 65, 781–792. doi:10.1515/zna-2010-1004

CrossRef Full Text | Google Scholar

Nadeem, S., and Akram, S. (2010). Peristaltic flow of a Williamson fluid in an asymmetric channel. Commun. Nonlinear Sci. Numer. Simul. 15, 1705–1716. doi:10.1016/j.cnsns.2009.07.026

CrossRef Full Text | Google Scholar

Nadeem, S., Mehmood, R., and Akbar, N. S. (2015). Oblique stagnation point flow of carbon nano tube based fluid over a convective surface. J. Comput. Theor. Nanosci. 12, 605–612. doi:10.1166/jctn.2015.3774

CrossRef Full Text | Google Scholar

Noreen, S., and Tripathi, D. (2019). Heat transfer analysis on electroosmotic flow via peristaltic pumping in non-Darcy porous medium. Therm. Sci. Eng. Prog. 11, 254–262. doi:10.1016/j.tsep.2019.03.015

CrossRef Full Text | Google Scholar

Reddy, M. S., Mishra, M., Sreenadh, S., and Rao, A. R. (2005). Influence of lateral walls on peristaltic flow in a rectangular duct.

Google Scholar

Sadaf, H., Kiani, A., and Mir, N. A. (2020). Mixed convection analysis of cilia-driven flow of a Jeffrey fluid in a vertical tube. Can. J. Phys. 98, 111–118. doi:10.1139/cjp-2018-0753

CrossRef Full Text | Google Scholar

Saleem, A., Akhtar, S., Nadeem, S., and Ghalambaz, M. (2021). Microphysical analysis for peristaltic flow of SWCNT and MWCNT carbon nanotubes inside a catheterised artery having thrombus: Irreversibility effects with entropy. Int. J. Exergy 34 (3), 301–314. doi:10.1504/ijex.2021.10036473

CrossRef Full Text | Google Scholar

Shapiro, A. H., Jaffrin, M. Y., and Weinberg, S. L. (1969). Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 37, 799–825. doi:10.1017/s0022112069000899

CrossRef Full Text | Google Scholar

Tripathi, D., Sharma, A., and Bég, O. A. (2017). Electrothermal transport of nanofluids via peristaltic pumping in a finite micro-channel: Effects of Joule heating and Helmholtz-Smoluchowski velocity. Int. J. Heat Mass Transf. 111, 138–149. doi:10.1016/j.ijheatmasstransfer.2017.03.089

CrossRef Full Text | Google Scholar

Waini, I., Khan, U., Zaib, A., Ishak, A., and Pop, I. (2022). Inspection of TiO2-CoFe2O4 nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer. J. Mol. Liq. 361, 119615. doi:10.1016/j.molliq.2022.119615

CrossRef Full Text | Google Scholar