Testing the validity of the core-shell-surface layer model on the size dependence of effective magnetic anisotropy in magnetic nanoparticles

The stability of the stored information in magnetic recording media depends on the anisotropy energy E_a (=K_eff V) of nanoparticles (NPs) of volume V or diameter D. Therefore, it is important to know how the effective anisotropy constant K_eff varies with size D of the NPs. In a recent paper [Appl. Phys. Lett. 110, 222409 (2017)], the observed K_eff versus D variation in NPs of maghemite (γ-Fe₂O₃) was explained on the basis of the core-shell-surface layer (CSSL) model given by Eq.: K_eff = K_b + (6K_S/D) +K_sh{[1-(2d/D)]⁻³–1}, where K_b, K_S, and K_sh are the anisotropy constants of spins in the core, surface layer, and a shell of thickness d, respectively. This CSSL model is an extension of an earlier core-surface layer (CSL) model described by K_eff = K_b + (6K_S/D) [Phys. Rev. Lett. 72, 282 (1994)] proposed to explain the K_eff versus D variation in Fe NPs. For the NPs of γ-Fe₂O₃, the additional term of the CSSL model involving K_sh was found to be necessary to fit the data for sizes D < 5 nm. In this paper, we report the validity of the CSSL model for NPs of several other systems viz. Co, Ni, NiO, and Fe₃O₄ using the available data from literature. In selecting the data, care was taken to consider data only for non-interacting NPs since the interparticle interactions generally overshadow the actual value of K_eff in NPs. It is shown that the new CSSL model describes very well the K_eff vs. D variation for all particle sizes whereas the CSL model fails for smaller particles with the notable exception of Fe NPs. This validation of the CSSL model for the NPs of Co, Ni, NiO, Fe₃O₄, and γ-Fe₂O₃ suggests its general validity for magnetic NPs. Discussion is also presented on the comparative magnitudes of the parameters K_b, K_S, and K_sh obtained from the fits to the CSSL model.

Introduction

The increasing demand of magnetic nanoparticles (NPs) for applications in compact magnetic storage media, catalysis, ferrofluids, sensors, magnetic drug delivery, and biomedicine have secured a unique place for nanoparticle research in the scientific community (Fiorani, 2005; Gubin, 2009; Thanh, 2012; Fuxi and Yang, 2015; Seehra, 2017). A particularly interesting feature of magnetic NPs is their size-dependent magnetic properties, both due to finite-size effects and the increasing role of surface spins with decreasing particle size. With decreasing particle size (D), the concentration of unsaturated surface spins increases as 1/D causing reduction in the net magnetization and enhancement in the effective magnetic anisotropy (K_eff) of NPs. Details of the size-dependence of K_eff is of primary interest for applications in magnetic data storage technology since the stability of the stored information in recording media depends on the anisotropy energy E_a = K_effV of NPs of volume V. Large anisotropy energy is desired to keep the stored information robust against the thermal activation of spins. Generally, a ratio (K_effV)/(k_BT) > 40 is required for reliable storage of data for ∼10 years, k_BT being the average thermal energy (Fuxi and Yang, 2015).

The spins on the surface of the NPs experience a different anisotropy compared to those in the bulk (core) of the NPs due to the broken exchange bonds and reduced crystalline symmetry of the surface. Taking this fact into consideration, Bodker et al. (1994) proposed a core-surface layer (CSL) model to describe the linear trend of K_eff versus 1/D data for Fe NPs and to separate the contributions of the surface and bulk spins in the total effective anisotropy energy of magnetic NPs. Although this CSL model has been often used to describe the K_eff versus 1/D data for magnetic NP systems, deviations from this model have been reported for ultra-fine magnetic NPs (Chen et al., 1995; Yanes et al., 2007; Shim et al., 2008; Laha et al., 2014; Singh et al., 2017a; Singh et al., 2017b; Pisane et al., 2017). The main reason for the limitation of the CSL model for ultra-fine magnetic NPs is that the model does not account for the spins in the shell layer. Recent experimental, theoretical, and computational studies have shown that the surface spin disorder in NPs is not localized at the surface layer only, but it tends to gradually propagate towards the core forming a shell of finite thickness d (Kachkachi et al., 2000; Millan et al., 2007; Dutta et al., 2009; Krycka et al., 2010; Krycka et al., 2014). This makes the ordering of spins and hence the magnetic anisotropy in the shell layer quite different from that of in the core or at the surface. Here we show that the effects of the shell layer become prominent only for very small particle sizes D < 5 nm.

In a recent work, Pisane et al. (2017) reported an extension of the CSL model to account the effect of shell layer in the total effective magnetic anisotropy data of maghemite (γ-Fe₂O₃) NPs. The new model considers the core-shell-surface layer (CSSL) geometry of NPs, and it has been proven successful to adequately describe the K_eff versus 1/D data in NPs of Ni and NiO systems (Singh et al., 2017b) in addition to NPs of γ-Fe₂O₃ (Pisane et al., 2017). In this paper, we test the validity of the CSSL model for additional NP systems of Co, Fe, and magnetite (Fe₃O₄) since it is important to test the validity of the CSSL model for all magnetic NPs. The K_eff vs. D data used here for testing the model was taken from the published papers in literature (Mørup et al., 1982; Bødker et al., 1992; Bodker et al., 1994; Bødker and Mørup, 1994; Chen et al., 1995; Petit et al., 1998; Sun and Murray, 1999; Kumar et al., 2001; Fonseca et al., 2002; Goya et al., 2003a; Goya et al., 2003b; Petit et al., 2005; Lima et al., 2006; Guardia et al., 2007; Wu et al., 2007; Dutta et al., 2009; Masunaga et al., 2009; Singh et al., 2009; Parker et al., 2010; Díaz et al., 2011; Fonseca et al., 2011; Lisiecki, 2012; Ruano et al., 2013; Chesnel et al., 2014; Yang et al., 2014), selecting data only for the non-interacting NPs since the interparticle interactions generally overshadow the actual value of K_eff in NPs and often lead to various emergent magnetic phases such as superparamagnetism, superspin glass, and superferromagnetism (Majetich and Jin, 1999; Majetich and Sachan, 2006; Bedanta and Kleemann, 2009). This analysis shows that the CSL model only captures the size-variation of K_eff for larger size Ni, Co, and magnetite NPs, whereas the CSSL model adequately describes the K_eff versus 1/D data for all particle sizes of Ni, Co, and magnetite (Fe₃O₄) NPs. The only exception appears to be the NPs of Fe for which the linear behavior of K_eff vs. 1/D data as predicted by the CSL model is valid (Bodker et al., 1994). Details of these results and discussion are presented below.

Interparticle interactions and effective magnetic anisotropy

It is important to first discuss the role of interparticle interactions (IPI) and its effect on the measured blocking temperature T_B which is often used to determine K_eff. The dipolar interactions between the magnetic moments of the NPs yield an additional enhancement in the magnetic anisotropy of NPs (Bedanta et al., 2005; Chen et al., 2005; Majetich and Sachan, 2006; Petracic et al., 2006; Bedanta et al., 2007), causing a noticeable increase in T_B, as schematically demonstrated in Figure 1A. To reduce IPI due to dipole-dipole interactions, experimentalists often use following two methods: 1) proper coating of NPs by surfactants, and 2) dispersion/separation of NPs on a non-magnetic matrix or in suitable solvent. The strength of the IPI in blocking temperature (T_B) measurements can be characterized by an effective T₀ leading to (Seehra and Pisane, 2016)

$T_B=T_0+\frac{K_{eff}V}{k_B\mathit{ln}\left(f_0/f_m\right)}.(1)$

Here k_B is the Boltzmann constant, f₀ ∼ 10¹⁰–10¹² Hz is the system-dependent attempt frequency varying only weakly with temperature, f_m is the experimental measurement frequency, and T₀ is an effective temperature representing the strength of the IPI. To determine T₀, one can measure T_B at two different measurement frequencies and evaluate the following quantities (Seehra and Pisane, 2016)

$\Phi =\frac{T_B\left(2\right)-T_B\left(1\right)}{T_B\left(1\right)\left[\log f_m\left(2\right)-\log f_m\left(1\right)\right]},(2)$

$\Phi ={\Phi }_o\left\{1-\left[T_o/T_B\left(1\right)\right]\right\},(3)$

FIGURE 1

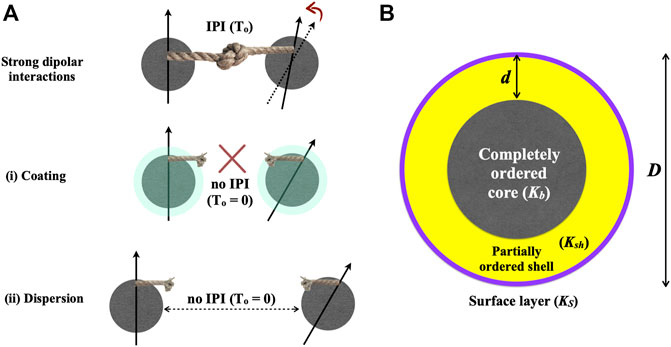
FIGURE 1. (A) Schematic representation of the effect of IPI on the effective magnetic anistropy (K_eff) of NPs. The black arrow represents the magnetization easy axis and rope depicts the effect of IPI on K_eff. (B) Core-shell-surface layer (CSSL) geometry of a spherical magnetic NP of diameter D and shell thickness d. T₀ represents temperature corresponding to the strength of IPI.

and

${\Phi }_o=2.3026/\left\{\ln \left[f_o/f_m\left(2\right)\right]\right\}.(4)$

Here T_B (1) and T_B (2) are the blocking temperature measured at two sufficiently different frequencies f_m (1) and f_m (2), respectively. For no IPI (T₀ = 0), $\Phi ={\Phi }_o$ ∼ 0.13 and for $\Phi$ < 0.13, the magnitude of IPI and T₀ increases with decreasing magnitude of $\Phi$ (Seehra et al., 2010; Pisane et al., 2015; Seehra and Pisane, 2016; Pramanik et al., 2017). Since IPI play a crucial role in the determination of K_eff by renormalizing its actual value, it is important to carefully separate the contribution of IPI in the actual K_eff value. In this work, we took care to consider only those data in which IPI effects were properly considered. In Seehra and Pisane (2016), Singh et al. (2017b), and Pisane et al. (2017), the details of the systematic evaluation of the strength of IPI using data from ac-magnetic susceptibility measurements are described. For a detailed discussion on the IPI-induced emergent magnetic phenomena in magnetic NPs, we refer reader to Majetich and Jin (1999), Majetich and Sachan (2006), and Bedanta and Kleemann (2009).

The core-shell-surface layer model

Figure 1B shows a pictorial representation of the CSSL model. The spins in core (shell) are well-ordered (partially ordered), whereas the ordering of spins is disrupted at the surface layer due to the broken crystalline symmetry and presence of dangling bonds. The formation of shell layer is preferred because it reduces the total energy of the magnetic NPs (Krycka et al., 2014). Neutron diffraction measurements have confirmed the existence of shell layer in magnetite NPs (Krycka et al., 2010). Furthermore, by means of Monte-Carlo simulations, Kachkachi et al. (2000) have demonstrated the formation of a shell layer of finite thickness in maghemite NPs. Since the magnetic anisotropy constants K_b, K_S, and K_sh corresponding to the spins in the core, at surface layer, and in a shell of thickness d, respectively, are expected to be different, it is essential to separate the contributions of K_sh from K_b and K_S in the K_eff versus D data of magnetic NPs. According to the core-surface layer (CSL) model (Bodker et al., 1994)

$K_{eff}=K_b+\frac{6K_S}{D}.(5)$

The factor 6/D in Eq. 5 represents the surface/volume ratio of spherical NPs with diameter D. The CSSL model represents an extension of the CSL model of Eq. 5 in which we include an extra term addressing the contribution of magnetic anisotropy from the spin in the spherical shell of thickness d (Pisane et al., 2017)

$K_{eff}=K_b+\frac{6K_S}{D}+K_{sh}\left\{{\left(1-\frac{2d}{D}\right)}^{-3}-1\right\}.(6)$

The term {[1-(2d/D)]⁻³–1}in Eq. 6 represents the ratio of the shell volume to the core volume, and it represents the contribution of a fraction of the spins in a shell with effective anisotropy K_sh different from K_b and K_S. The K_sh contribution particularly dominates the K_b and K_S contributions in ultra-fine magnetic NPs. For example, it was found that for maghemite NPs, the total contribution of the K_sh term to K_eff is about 38% for D = 3 nm NPs but it rapidly decreases to ∼13% for D = 4 nm, to ∼3.7% for D = 8 nm and to ∼2% for D = 15 nm (Pisane et al., 2017). However, the contribution of the K_S term remains significant even for D = 20 nm (Pisane et al., 2017). The validity of the CSSL model is limited to D > 2d since only in this limit the NPs have a core of nonzero diameter (D-2d > 0). For morphologies different from a sphere, the factor 6 in Eqs 5, 6 should be replaced by a proper factor representing the non-spherical morphology of NPs.

Here, it is important to comment on the size dependence of shell thickness, i.e., d(D). In the semi-empirical CSSL model, the shell thickness is assumed to be same for all particle sizes for simplicity and to avoid any additional fitting parameters in Eq. 6. Although this assumption is not very accurate, it can be justified by reported experimental observations (Chen et al., 1996; Goya et al., 2003b; Caruntu et al., 2007; Millan et al., 2007; Dutta et al., 2009; Krycka et al., 2010). Magnetic measurements on magnetic NPs with a wide range of particle sizes yield almost similar shell thickness for a given magnetic NP system (Chen et al., 1996; Goya et al., 2003b; Caruntu et al., 2007; Dutta et al., 2009; Krycka et al., 2010). For instance, Millan et al. reported a shell (magnetic dead layer) of ∼1 nm constant thickness for maghemite NPs in size range 1.6–15 nm with 10% size dispersion (Millan et al., 2007). Also, a maximum deviation of 0.2 nm was observed for the shell thickness of Fe₃O₄ NPs in 4–12 nm size range (Dutta et al., 2009). Motivated from these studies, a constant d, independent of D, can be justified at the simplest level in the CSSL model.

Validation of the CSSL model

Now we test the validity of the CSSL model for four different magnetic NP systems, namely–Ni, Co, Fe, and magnetite (Fe₃O₄). Figures 2, 3 show variation in K_eff vs. 1/D data for these four NPs. The data was collected from available reports in the literature, where the effects due to IPI were taken into account, with the relevant references listed in the figures. Deviations from the linear trend of the K_eff vs. 1/D variations predicted by the CSL model (Eq. 5) are for smaller sizes of the Ni, Co and magnetite NPs, the exception being the Fe NPs which follow a linear trend. The red line shows the best fit of the data to Eq. 6 and green line shows the best fit to Eq. 5. Although, all the data points do not exactly fall on the fitted curve, the overall trend of K_eff vs. 1/D variation is well-captured by Eq. 6 within the experimental uncertainties.

FIGURE 2

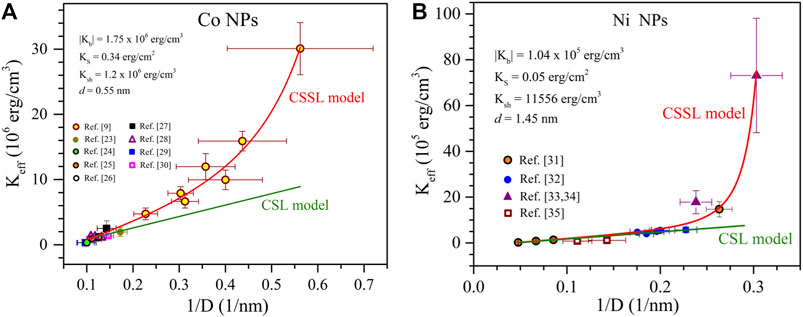
FIGURE 2. The K_eff vs. 1/D variation of (A) Co, and (B) Ni NPs. The red (green) line shows the best fit to the CSSL (CSL) model. The best fitting parameters along with the sources of the data (Chen et al., 1995; Petit et al., 1998; Sun and Murray, 1999; Fonseca et al., 2002; Goya et al., 2003a; Petit et al., 2005; Masunaga et al., 2009; Singh et al., 2009; Parker et al., 2010; Díaz et al., 2011; Fonseca et al., 2011; Lisiecki, 2012; Ruano et al., 2013; Yang et al., 2014) are given in the inset.

FIGURE 3

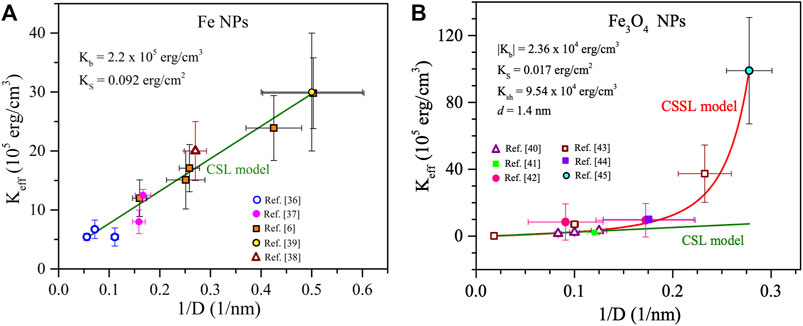
FIGURE 3. The K_eff vs. 1/D variation of (A) Fe, and (B) magnetite (Fe₃O₄) NPs. The red (green) line shows the best fit of the data to the CSSL (CSL) model. The best fitting parameters along with the sources of the data (Mørup et al., 1982; Bødker et al., 1992; Bodker et al., 1994; Bødker and Mørup, 1994; Kumar et al., 2001; Goya et al., 2003b; Lima et al., 2006; Guardia et al., 2007; Wu et al., 2007; Dutta et al., 2009; Chesnel et al., 2014) are given in the inset.

It is important to describe the procedure used for fitting the data to the CSSL model since there are four fitting parameters (K_b, K_S, K_sh, and d). To gain confidence in the procedure, this 4-parameter problem was split into two 2-parameters problems. First, we fitted the linear part of K_eff vs. 1/D data for larger NPs (D > 5 nm) using Eq. 5 and determined the magnitudes of K_b and K_S from the linear fitting. Next, we used the obtained values of K_b and K_S as guidelines to determine the magnitudes of K_sh and d by fitting the overall data for all size ranges. The magnitudes of the best fitting parameters along with the references of the sources of the data are listed in the inset of figures. Note that these parameters obtained from the fits give important physical insights into magnetic ordering of the spins in the NPs. The magnitudes of the obtained magnetic anisotropy constants and the shell thickness are in excellent agreement with the reported experimental data on Ni, Co, and Fe₃O₄ NPs (Amighian and Corner, 1976; Birss et al., 1977; Wohlfarth, 1980; Kachkachi et al., 2000; Dutta et al., 2009; Krycka et al., 2010).

A comparison of the magnitudes of the fitted parameters K_b, K_S, K_sh, and d on the six systems of NPs (γ-Fe₂O_3, NiO, Fe₃O₄, Ni, Co, and Fe) on which the CSSL system has been tested so far is given in Table 1. Among these systems, NPs of two systems stand out: Fe for zero values of d and K_sh, and Co for the largest magnitudes of K_b, K_S, and K_sh and smallest value of non-zero d. For Co, the large magnitude of K_S, and K_sh are likely related to its large K_b which is due to its hexagonal structure. Bare Fe is easily oxidized to one of its oxides (α-Fe₂O₃, Fe₃O₄, γ-Fe₂O₃, etc.) depending on the experimental conditions and this may be the reason for the absence of the formation of a shell in this case (d = 0). Our efforts to find sufficient published data of K_eff vs. D for NPs of other magnetic systems for testing the CSSL model in which IPI has been adequately addressed have not yet been successful.

TABLE 1

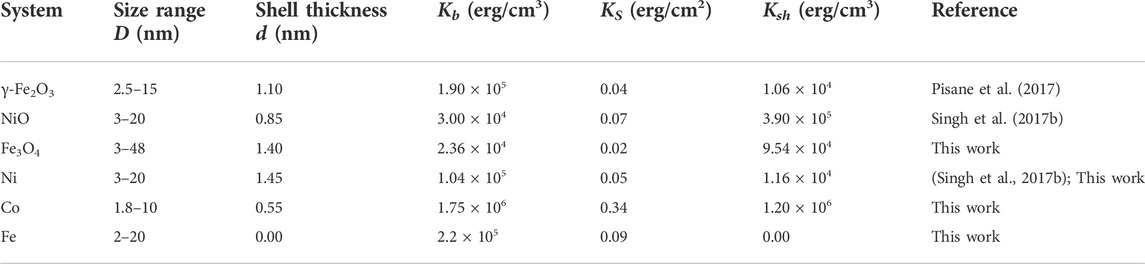
TABLE 1. The effective bulk (K_b), surface (K_S), and shell (K_sh) magnetic anisotropies along with the shell thickness (d) obtained from fitting the CSSL model for maghemite (γ-Fe₂O₃), NiO, Fe₃O₄, Ni, Co, and Fe nanoparticles.

Conclusion

In this paper, we have tested the validity of the CSSL model on the variation of K_eff vs. D for NPs of six systems of γ-Fe₂O_3, NiO, Fe₃O₄, Ni, Co, and Fe, the results presented here for Fe₃O₄, Co, and Fe being the new contributions. For the NPs of Ni, Co, and Fe₃O₄ discussed here and those of NiO (Pisane et al., 2017) and maghemite (Singh et al., 2017b) reported recently, the variation of K_eff vs. 1/D is best described by the CSSL model. For the NPs of Fe, the CSL model appears to be quite adequate as if the Fe NPs do not have a shell. These differences for the Fe NPs might be related to how the Fe NPs were prepared, or perhaps, peculiar and yet un-understood physics of the Fe nanoparticles. The analysis presented here also shows that the CSSL model and hence contributions of the spins in the shell to K_eff become important only for sizes D < ∼5 nm and that for larger NPs, the CSL model appears to be quite adequate to describe the linear variation of K_eff vs. 1/D. It is likely that the CSSL may also be applicable for other magnetic NP systems where K_eff vs. D data becomes available over a large enough size range without the interference of the interparticle interactions. An improved model considering the particle size dependent shell thickness d (D) and core-shell mixing terms of magnetic anisotropy would be desired in future. Results reported here may be particularly important for computational modelling of the studied magnetic nanoparticles (Reeves and Weaver, 2014; Winkler, 2017; Mahmood and Yingling, 2022).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amighian, J., and Corner, W. D. (1976). Measurement of the anisotropy constants K₃and K₁for nickel and a dilute nickel-vanadium alloy. J. Phys. F. Met. Phys. 6 (11), L309–L312. doi:10.1088/0305-4608/6/11/004

CrossRef Full Text | Google Scholar

Bedanta, S., Eimüller, T., Kleemann, W., Rhensius, J., Stromberg, F., Amaladass, E., et al. (2007). Overcoming the Dipolar Disorder in Dense CoFe nanoparticle Ensembles: Superferromagnetism. Phys. Rev. Lett. 98, 176601. doi:10.1103/physrevlett.98.176601

CrossRef Full Text | Google Scholar

Bedanta, S., and Kleemann, W. (2009). Supermagnetism. J. Phys. D. Appl. Phys. 42, 013001. doi:10.1088/0022-3727/42/1/013001

CrossRef Full Text | Google Scholar

Bedanta, S., Sahoo, S., Chen, X., Kleemann, W., Sudfeld, D., Wojczykowski, K., et al. (2005). Intra- and interparticle interaction in a dense frozen ferrofluid. Phase Transitions 78, 121–129. doi:10.1080/01411590412331316654

CrossRef Full Text | Google Scholar

Birss, R. R., Keeler, G. J., and Shepherd, C. H. (1977). Measurements of the anisotropy energy of nickel in the (100) plane. Phys. B+C 86, 257–258. doi:10.1016/0378-4363(77)90304-7

CrossRef Full Text | Google Scholar

Bodker, F., Morup, S., and Linderoth, S. (1994). Surface effects in metallic iron nanoparticles. Phys. Rev. Lett. 72, 282–285. doi:10.1103/physrevlett.72.282

PubMed Abstract | CrossRef Full Text | Google Scholar

Bødker, F., and Mørup, S. (1994). Magnetic properties of 2 nm α-Fe particles. Hyperfine Interact. 93 (1), 1421–1425. doi:10.1007/bf02072887

CrossRef Full Text | Google Scholar

Bødker, F., Mørup, S., Oxborrow, C. A., Linderoth, S., Madsen, M. B., and Niemansverdriet, J. W. (1992). Mossbauer studies of ultrafine iron-containing particles on a carbon support. J. Phys. Condens. Matter 4, 6555–6568. doi:10.1088/0953-8984/4/31/008

CrossRef Full Text | Google Scholar

Caruntu, D., Caruntu, G., and J O’Connor, C. (2007). Magnetic properties of variable-sized Fe₃O₄nanoparticles synthesized from non-aqueous homogeneous solutions of polyols. J. Phys. D. Appl. Phys. 40, 5801–5809. doi:10.1088/0022-3727/40/19/001

CrossRef Full Text | Google Scholar

Chen, J. P., Sorensen, C. M., Klabunde, K. J., Hadjipanayis, G. C., Devlin, E., and Kostikas, A. (1996). Size-dependent magnetic properties ofMnFe2O4fine particles synthesized by coprecipitation. Phys. Rev. B 54, 9288–9296. doi:10.1103/physrevb.54.9288

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J. P., Sorensen, C. M., Klabunde, K. J., and Hadjipanayis, G. C. (1995). Enhanced magnetization of nanoscale colloidal cobalt particles. Phys. Rev. B 51, 11527–11532. doi:10.1103/physrevb.51.11527

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Bedanta, S., Petracic, O., Kleemann, W., Sahoo, S., Cardoso, S., et al. (2005). Superparamagnetism versus superspin glass behavior in dilute magnetic nanoparticle systems. Phys. Rev. B 72, 214436. doi:10.1103/physrevb.72.214436

CrossRef Full Text | Google Scholar

Chesnel, K., Trevino, M., Cai, Y., Hancock, J. M., Smith, S. J., and Harrison, R. G. (2014). Particle size effects on the magnetic behaviour of 5 to 11 nm Fe₃O₄nanoparticles coated with oleic acid. J. Phys. Conf. Ser. 521 (1), 012004. doi:10.1088/1742-6596/521/1/012004

CrossRef Full Text | Google Scholar

Díaz, M., Martínez, L., Ruano, M. M., Llamosa, P. D., Román, E., García-Hernandez, M., et al. (2011). Morphological, structural, and magnetic properties of Co nanoparticles in a silicon oxide matrix. J. Nanoparticle Res. 13 (10), 5321.

Google Scholar

Dutta, P., Pal, S., Seehra, M. S., Shah, N., and Huffman, G. P. (2009). Size dependence of magnetic parameters and surface disorder in magnetite nanoparticles. J. Appl. Phys. 105, 07B501. doi:10.1063/1.3055272

CrossRef Full Text | Google Scholar

Fiorani D. (Editor) (2005). Surface effects in magnetic nanoparticles (New York, NY: Springer).

Google Scholar

Fonseca, F. C., Goya, G. F., Jardim, R. F., Muccillo, R., Carreno, N. L., Longo, E., et al. (2002). Superparamagnetism and magnetic properties of Ni nanoparticles embedded inSiO2. Phys. Rev. B 66, 104406. doi:10.1103/physrevb.66.104406

CrossRef Full Text | Google Scholar

Fonseca, F. C., Jardim, R. F., Escote, M. T., Gouveia, P. S., Leite, E. R., and Longo, E. (2011). Superparamagnetic Ni:SiO2–C nanocomposites films synthesized by a polymeric precursor method. J. Nanopart. Res. 13 (2), 703–710. doi:10.1007/s11051-010-0068-2

CrossRef Full Text | Google Scholar

Fuxi G., and Yang W. (Editors) (2015). Data storage at the Nanoscale: Advances and applications (Singapore: CRC Press).

Google Scholar

Goya, G. F., Berquo, T. S., Fonseca, F. C., and Morales, M. P. (2003). Static and dynamic magnetic properties of spherical magnetite nanoparticles. J. Appl. Phys. 94 (5), 3520–3528. doi:10.1063/1.1599959

CrossRef Full Text | Google Scholar

Goya, G. F., Fonseca, F. C., Jardim, R. F., Muccillo, R., Carreno, N. L. V., Longo, E., et al. (2003). Magnetic dynamics of single-domain Ni nanoparticles. J. Appl. Phys. 93 (10), 6531–6533. doi:10.1063/1.1540032

CrossRef Full Text | Google Scholar

Guardia, P., Batlle-Brugal, B., Roca, A. G., Iglesias, O., Morales, M. P., Serna, C. J., et al. (2007). J. Magn. Magn. Mater. 316 (2), e756–e759.

Gubin S. P. (Editor) (2009). Magnetic nanoparticles (John Wiley & Sons).

Google Scholar

Kachkachi, H., Nogues, M., Tronc, E., and Garanin, D. A. (2000). Finite-size versus surface effects in nanoparticles. J. Magn. Magn. Mater. 221, 158–163. doi:10.1016/s0304-8853(00)00390-5

CrossRef Full Text | Google Scholar

Krycka, K. L., Booth, R. A., Hogg, C. R., Ijiri, Y., Borchers, J. A., Chen, W. C., et al. (2010). Core-shell magnetic morphology of Structurally Uniform magnetite nanoparticles. Phys. Rev. Lett. 104, 207203. doi:10.1103/physrevlett.104.207203

PubMed Abstract | CrossRef Full Text | Google Scholar

Krycka, K. L., Borchers, J. A., Booth, R. A., Ijiri, Y., Hasz, K., Rhyne, J. J., et al. (2014). Kryckaet al.Reply:. Phys. Rev. Lett. 113, 149702. doi:10.1103/physrevlett.114.149702

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, D., Narayan, J., Kvit, A. V., Sharma, A. K., and Sankar, J. (2001). High coercivity and superparamagnetic behavior of nanocrystalline iron particles in alumina matrix. J. Magn. Magn. Mater. 232 (3), 161–167. doi:10.1016/s0304-8853(01)00191-3

CrossRef Full Text | Google Scholar

Laha, S. S., J Tackett, R., and Lawes, G. (2014). Interactions in γ-Fe2O3 and Fe3O4 nanoparticle systems. Phys. B Condens. Matter 448, 69–72. doi:10.1016/j.physb.2014.03.036

CrossRef Full Text | Google Scholar

Lima, E., Brandl, A. L., Arelaro, A. D., and Goya, G. F. (2006). J. Appl. Phys. 99 (8), 083908.

Lisiecki, I. (2012). From the Co nanocrystals to their Self-organizations: Towards Ferromagnetism at Room temperature. Acta Phys. Pol. A 121 (2), 426–433. doi:10.12693/aphyspola.121.426

CrossRef Full Text | Google Scholar

Mahmood, A. U., and Yingling, Y. G. (2022). All-atom simulation method for Zeeman Alignment and Dipolar assembly of magnetic nanoparticles. J. Chem. Theory Comput. 18 (5), 3122–3135. doi:10.1021/acs.jctc.1c01253

PubMed Abstract | CrossRef Full Text | Google Scholar

Majetich, S. A., and Jin, Y. (1999). Magnetization Directions of Individual nanoparticles. Science 284 (5413), 470–473. doi:10.1126/science.284.5413.470

PubMed Abstract | CrossRef Full Text | Google Scholar

Majetich, S. A., and Sachan, M. (2006). Magnetostatic interactions in magnetic nanoparticle assemblies: Energy, time and length scales. J. Phys. D. Appl. Phys. 39, R407–R422. doi:10.1088/0022-3727/39/21/r02

CrossRef Full Text | Google Scholar

Masunaga, S. H., Jardim, R. F., Fichtner, P. F. P., and Rivas, J. (2009). Role of dipolar interactions in a system of Ni nanoparticles studied by magnetic susceptibility measurements. Phys. Rev. B 80, 184428. doi:10.1103/physrevb.80.184428

CrossRef Full Text | Google Scholar

Millan, A., Urtizberea, A., Silva, N. J., Palacio, F., Amaral, V. S., Snoeck, E., et al. (2007). Surface effects in maghemite nanoparticles. J. Magn. Magn. Mater. 312, L5.

CrossRef Full Text | Google Scholar

Mørup, S., Topsøe, H., and Clausen, B. S. (1982). Magnetic properties of Microcrystals studied by Mössbauer Spectroscopy. Phys. Scr. 25 (6A), 713–719. doi:10.1088/0031-8949/25/6a/015

CrossRef Full Text | Google Scholar

Parker, D., Lisiecki, I., and Pileni, M. P. (2010). Do 8 nm Co nanocrystals in Long-range-ordered Face-Centered Cubic (fcc) supracrystals show superspin glass behavior? J. Phys. Chem. Lett. 1, 1139–1142. doi:10.1021/jz1001874

CrossRef Full Text | Google Scholar

Petit, C., Taleb, A., and Pileni, M. P. (1998). Self-organization of magnetic Nanosized cobalt particles. Adv. Mater. 10 (3), 259–261. doi:10.1002/(sici)1521-4095(199802)10:3<259:aid-adma259>3.0.co;2-r

CrossRef Full Text | Google Scholar

Petit, C., Wang, Z. L., and Pileni, M. P. (2005). Seven-nanometer hexagonal Close Packed cobalt nanocrystals for High-temperature magnetic applications through a Novel Annealing process. J. Phys. Chem. B 109 (32), 15309–15316. doi:10.1021/jp052487+

PubMed Abstract | CrossRef Full Text | Google Scholar

Petracic, O., Chen, X., Bedanta, S., Kleemann, W., Sahoo, S., Cardoso, S., et al. (2006). Collective states of interacting ferromagnetic nanoparticles. J. Magn. Magn. Mater. 300, 192–197. doi:10.1016/j.jmmm.2005.10.061

CrossRef Full Text | Google Scholar

Pisane, K. L., Singh, S., and Seehra, M. S. (2015). Synthesis, structural characterization and magnetic properties of Fe/Pt core-shell nanoparticles. J. Appl. Phys. 117, 17D708. doi:10.1063/1.4908304

CrossRef Full Text | Google Scholar

Pisane, K. L., Singh, S., and Seehra, M. S. (2017). Unusual enhancement of effective magnetic anisotropy with decreasing particle size in maghemite nanoparticles. Appl. Phys. Lett. 110, 222409. doi:10.1063/1.4984903

CrossRef Full Text | Google Scholar

Pramanik, P., Thota, S., Singh, S., Joshi, D. C., Weise, B., Waske, A., et al. (2017). Effects of Cu doping on the electronic structure and magnetic properties of MnCo₂O₄nanostructures. J. Phys. Condens. Matter 29, 425803. doi:10.1088/1361-648x/aa839d

PubMed Abstract | CrossRef Full Text | Google Scholar

Reeves, D. B., and Weaver, J. B. (2014). Approaches for modeling magnetic nanoparticle Dynamics. Crit. Rev. Biomed. Eng. 421, 85–93. doi:10.1615/critrevbiomedeng.2014010845

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruano, M., Diaz, M., Martinez, L., Navarro, E., Roman, E., Garcia-Hernandez, M., et al. (2013). Matrix and interaction effects on the magnetic properties of Co nanoparticles embedded in gold and vanadium. Phys. Chem. Chem. Phys. 15, 316–329. doi:10.1039/c2cp42769a

PubMed Abstract | CrossRef Full Text | Google Scholar

Seehra M. S. (Editor) (2017). Nanostructured materials - Fabrication to application (London: InTech).

Google Scholar

Seehra, M. S., and Pisane, K. L. (2016). Relationship between blocking temperature and strength of interparticle interaction in magnetic nanoparticle systems. J. Phys. Chem. Solids 93, 79–81. doi:10.1016/j.jpcs.2016.02.009

CrossRef Full Text | Google Scholar

Seehra, M. S., Singh, V., Dutta, P., Neeleshwar, S., Chen, Y. Y., Chen, C. L., et al. (2010). Size-dependent magnetic parameters of fcc FePt nanoparticles: Applications to magnetic hyperthermia. J. Phys. D. Appl. Phys. 43 (14), 145002. doi:10.1088/0022-3727/43/14/145002

CrossRef Full Text | Google Scholar

Shim, H., Dutta, P., Seehra, M. S., and Bonevich, J. (2008). Size dependence of the blocking temperatures and electron magnetic resonance spectra in NiO nanoparticles. Solid State Commun. 145, 192–196. doi:10.1016/j.ssc.2007.10.026

CrossRef Full Text | Google Scholar

Singh, S., Pisane, K. L., and Seehra, M. S. (2017). “A core-shell-surface layer model to explain the size dependence of effective magnetic anisotropy in magnetic nanoparticles,” in 2017 IEEE 17th International Conference on Nanotechnology (IEEE-NANO), Pittsburgh, PA, July 2017 (IEEE), 1014–1018.

CrossRef Full Text | Google Scholar

Singh, S., Pramanik, P., Sangaraju, S., Mallick, A., Giebeler, L., and Thota, S. (2017). Size-dependent structural, magnetic, and optical properties of MnCo₂O₄nanocrystallites. J. Appl. Phys. 121 (19), 194303. doi:10.1063/1.4983360

CrossRef Full Text | Google Scholar

Singh, V., Seehra, M. S., and Bonevich, J. (2009). Ac susceptibility studies of magnetic relaxation in nanoparticles of Ni dispersed in silica. J. Appl. Phys. 105, 07B518. doi:10.1063/1.3073949

CrossRef Full Text | Google Scholar

Sun, S., and Murray, C. B. (1999). Synthesis of monodisperse cobalt nanocrystals and their assembly into magnetic superlattices (invited). J. Appl. Phys. 85, 4325–4330. doi:10.1063/1.370357

CrossRef Full Text | Google Scholar

Thanh N. T. K. (Editor) (2012). Magnetic nanoparticles: From Fabrication to Clinical applications (Boca Raton, FL: CRC Press).

Google Scholar

Winkler, D. A. (2017). Curr. Med. Chem. 24 (5), 483–496.

PubMed Abstract |

Wohlfarth, E. P. (1980). Iron, cobalt and nickel. Handb. Ferromagn. Mater. 1, 1–70.

Google Scholar

Wu, Jun-Hua, Ko, S. P., Liu, H.-L., Kim, S., Ju, J.-S., and Kim, Y. K. (2007). Sub 5 nm magnetite nanoparticles: Synthesis, microstructure, and magnetic properties. Mater. Lett. 61 (14), 3124.

CrossRef Full Text | Google Scholar

Yanes, R., Chubykalo-Fesenko, O., Kachkachi, H., Garanin, D. A., Evans, R., and Chantrell, R. W. (2007). Effective anisotropies and energy barriers of magnetic nanoparticles with Néel surface anisotropy. Phys. Rev. B 76, 064416. doi:10.1103/physrevb.76.064416

CrossRef Full Text | Google Scholar

Yang, J., Khazen, K., and Pileni, M. P. (2014). How nanocrystallinity and order define the magnetic properties ofε-Co supracrystals. J. Phys. Condens. Matter 26, 295303. doi:10.1088/0953-8984/26/29/295303

PubMed Abstract | CrossRef Full Text | Google Scholar