Atomistic simulations of dislocation plasticity in concentrated VCoNi medium entropy alloys: Effects of lattice distortion and short range order

Face-centered cubic (fcc) high and medium entropy alloys (H/MEAs) have been shown to display superior mechanical properties at low temperatures, but significant improvement of their strength at high temperatures is required for industrial applications at extreme conditions. Recently, it has been shown that the breakthrough of the MEAs from equiatomic/near-equiatomic to non-equiatomic ratios leads to strong MEAs with good ductility. To design new H/MEAs, we consider two important factors that may influence strength: the chemical composition and chemical short range order (CSRO). In this study, we investigate the depinning stress (σ_c) as a criterion of strength of several compositions of VCoNi concentrated solid solution alloys (CSSAs) including V_0.33Co_0.33Ni_0.33, V_0.35Co_0.2Ni_0.45, V_0.33Co_0.17Ni_0.5, and V_0.17Co_0.33Ni_0.5 at 5 K and 300 K, using atomistic simulations. The chosen interatomic potential is shown to be reliable by comparing experimental/ab initio values and calculated parameters such as lattice constant, shear modulus, depinning stress, and temperature variation of stacking fault width for equimolar VCoNi. We find a good agreement between experimental friction stress and the depinning stress extracted from our results for equimolar VCoNi. Also, we find that Vclusters are the main pinning points of dislocations, and With a random distribution of atoms, we find that the alloy composition V_0.33Co_0.17Ni_0.5 displays the largest depinning stress at both 5 and 300 K. Furthermore, to investigate how CSRO affects the strength of these alloys, we design CSRO into the microstructure using two different methods: In the first method, hybrid Molecular-dynamics/Monte-Carlo simulations were employed to simulate annealing at various temperatures. We observe that such simulations create CSRO so that it increases with decreasing annealing temperature. Recently, the CSRO motif and its concentration in an equimolar VCoNi have been determined by experiment. By modeling this experiment, we also implemented the CSRO into microstructure as the second method. By using both methods, the effect of CSRO on the magnitude of the depinning stress is discussed. It was shown that in both methods, CSRO significantly influences the strength of non-equimolar VCoNi alloys.

1 Introduction

Concentrated solid solution high and medium-entropy alloys have been found to display excellent mechanical properties Senkov et al. (2011); Zhang et al. (2018); Jiang et al. (2022); Luoet al. (2021). Balancing between strength and ductility is an important issue in designing such materials and in general, body-centered cubic (bcc) high and medium entropy alloys (H/MEAs) have high strength while face-centered cubic (fcc) H/MEAs show high ductility Hu et al. (2021). According to solid solution strengthening theory Varvenne et al. (2016), the flow stress exhibits a decreasing trend with increasing temperature which is modulated by the zero temperature flow stress. Thus, improving the strength at low temperatures should lead to improving the strength at finite temperatures. One of the strategies to consider for designing new solid solution alloys (SSAs) could be related to increasing the strength of fcc solid solution alloys. Such a strategy may become possible by choosing compositional elements that increase lattice distortion based on the solid solution strengthening theory Esfandiarpour et al. (2022); Varvenne et al. (2016). One of the most characteristic cases is that of equiatomic CrCoNi solid solution alloys, that show higher yield strengths than traditional alloys, as well as more complex Cantor CrMnFeCoNi high entropy alloys at cryogenic and room temperatures Esfandiarpour et al. (2022); Wu et al. (2014). Deformation twins (especially at cryogenic temperature) Chen et al. (2021a) and larger atomistic mismatch (larger lattice distortion), induced by Cr atoms, are the main explanation for the exceptional behavior of CrCoNi solid solutions Varvenne et al. (2016). We propose that the design of new MEAs that have higher strength than CrCoNi, it is imperative to add elements that can induce higher local lattice distortion. Vanadium can play such an important role for strengthening in fcc HEAs due to its large atomic volume in the fcc matrix Esfandiarpour and Nasrabadi (2019); Yin et al. (2020). Furthermore, it has been shown that changing the concentration of H/MEAs from equiatomic/near-equiatomic to non-equiatomic ratios can improve the mechanical properties of these materials Coury et al. (2018); Yan et al. (2022). For instance, Coury et al. (2018) reported that Cr_0.45Co_0.275Ni_0.275 alloy shows yield strength over 50% greater with equivalent ductility than equimolar CrCoNi MEA. In this work, we develop such alloys by altering the composition of VCoNi MEAs and calculate the depinning stress of edge dislocations through molecular dynamics simulations.

Recent experiments showed a high strength of VCoNi medium entropy alloys at low and room temperature Yang et al. (2021); Hu et al. (2021). For example, in Ref. Hu et al.(2021), mechanical properties of equimolar VCoNi with various different mean grain sizes were relatively compared with CrCoNi. Their main findings were focused on that VCoNi alloys display higher strength and friction stress than CrCoNi while their ductility still is much higher than bcc HEAs. In association, Ref. Yang et al. (2021) concludes that at cryogenic temperatures, twinning is absent in VCoNi under tension or impact, while pinning of dislocations is primarily observed. Furthermore, the strength of equimolar VCoNi may be predicted by the Labusch-Varvenne class of solid solution analytical models Labusch (1970); Varvenne et al. (2016); Yin et al. (2020), which use the large atomistic mismatch of vanadium, to show that strength shall increase with respect to equiatomic CrCoNi. A major contributor to the strength of VCoNi alloys has been conjectured to relate to chemical short range order (CSRO) that may form in the solid solution microstructure Antillon et al. (2020); Cheng et al. (2021). Atomistic simulations have already shown that nanoscale strength and hardness of CoCrNi MEAs increase with increasing the CSRO order parameter Chen et al. (2022); Li et al. (2019), while stacking fault widths decrease Zhang et al. (2020). MD simulations have been widely used to describe the microstructure of materials under deformation Antillon et al. (2020); Jia et al.(2022); Zhou et al. (2022); Esfandiarpour et al. (2022); Karimiet al. (2022). In this work, we focus on the understanding of the basic mechanism and dynamics of strengthening in non-equiatomic and equiatomic VCoNi single-crystal SSAs. We investigate the effect of CSRO and the strength of VCoNi alloys, by calculating structural features, the depinning stress, and stacking fault widths for edge dislocations in four fcc VCoNi SSAs including V_0.33Co_0.33Ni_0.33, V_0.35Co_0.2Ni_0.45, V_0.33Co_0.17Ni_0.5, and V_0.17Co_0.33Ni_0.5 at 5 and 300 K using molecular dynamics (MD) simulations. We choose these four alloys because they form single phase fcc solid solutions King et al. (2016), according to semi-empirical rules used for predicting the alloy phase of SSAs. The depinning stress (σ_c) appears as a very reliable quantity for the estimation of strength of SSAs Esfandiarpour et al. (2022) and more specifically, VCoNi alloys, given that friction stress estimates Sohn et al. (2019) are very close to σ_c calculations, as shown here. The depinning stress refers to the stress required to depin a dislocation in a single crystal, and can be accurately calculated using stress-controlled loading, using atomistic simulations Esfandiarpour et al. (2022); Antillon et al. (2020). In classical solute-dislocation hardening models, it is predicted that the required stress that is needed to move an edge dislocation is 1/(1−ν) greater than the screw dislocation. The theory of strengthening for edge dislocations has predicted the flow stress for fcc H/MEAs, in very good agreement with experiments, over a range of concentrations and temperatures Varvenne et al. (2016). For this reason, in this study, we calculate the depinning stress of edge dislocations. In the second part of this study, we investigate the effect of CSRO on depinning stress and lattice distortion. We investigate two different scenarios for the CSRO formation in these alloys, by using two different methods: In the first method, hybrid Molecular-dynamics (MD)—Monte-Carlo (MC) simulations are employed to facilitate thermally induced kinetics at high temperatures, and emulate thermal annealing effects in chemical ordering patterns. In this way, we investigate possible effects of annealing at various temperatures, and investigate the possible correlation to CSRO effects. In the second method, a recent experimentally identified CSRO motif for VCoNi alloys Chen et al. (2022) is used to model CSRO.

2 Simulation techniques

2.1 Calculating depinning stress using molecular dynamics simulations

To calculate depinning stress, a stress-controlled loading method was applied using MD. The periodic array of dislocations (PAD) model Osetsky and Bacon (2003) was used to insert a perfect edge dislocation between two central $(\bar{1}11)$ planes in the cell. This model was employed to have periodicity along the Burger vector (X = [110]), and dislocation line direction $(Z=[1\bar{1}2])$. To apply the PAD model, one should join two crystals in the $[\bar{1}11]$ direction, while one of them (top) contains an atomic column in excess, in the X direction, rather than the other (bottom). The top crystal is compressed by b/2 (b is the magnitude of Burger vector), while the bottom crystal is elongated by b/2 to both have the same length along X. For each composition, four simulation cells with fcc crystal and different random distribution of constituent elements were created along $X=[110]\left(l_x\sim 380\right.$Å), $Y=[\bar{1}11]\left(l_y\sim 110\right.$Å), and $Z=[1\bar{1}2]\left(l_z\sim 1103\right.$Å) containing 4,036,500 atoms (Figure 1). Periodic boundary conditions (PBC) are applied in both X and Z directions, while the fixed boundary condition was used in the Y direction. After minimization of the system using molecular statics, the system is equilibrated to the target temperatures (5 and 300 K) using NpT for 100 ps by considering the zero pressure in x and z direction, ${\tau }_d^{\text{therm}}=100$ fs, and ${\tau }_d^{\text{bar}}=1000$ fs. Stress-controlled loading was considered where the force F_x = σAN_±e_xz was applied to the top and bottom Y-layers with the area of A, and N± is the number of atoms in the top (bottom) layers. A time step of 4 fs was used. The temperature is controlled by a Berendsen thermostat at the target temperatures Berendsen et al. (1984). The loading stress increases with 20 MPa ramp till dislocation starts continuous moving. Dislocation and crystal structures are analyzed using dislocation extraction algorithm (DXA) Stukowski et al. (2012) and common neighbor analysis that are implemented in OVITO software Stukowski (2009). The simulations performed in this work use the large-scale molecular dynamics massively parallel simulator (LAMMPS) Thompson et al. (2022), and the modified embedded atom method (MEAM) interatomic potential has been recently developed by Choi et al. (2021). To evaluate this interatomic potential, elastic constants are calculated using LAMMPS. To estimate elastic constants at zero temperature, the derivative of stress with respect to strain is calculated by deforming the box in various directions. To estimate the elastic constants at room temperature, the variation in the average stress tensor for an NVT simulation is calculated when the cell volume is under finite deformation. Both methods are implemented in LAMMPS. Furthermore, shear modulus (μ) and Poisson’s ratio (ν) are calculated based on Liebfried’s effective isotropic elastic constants Eshelby (1955).

FIGURE 1

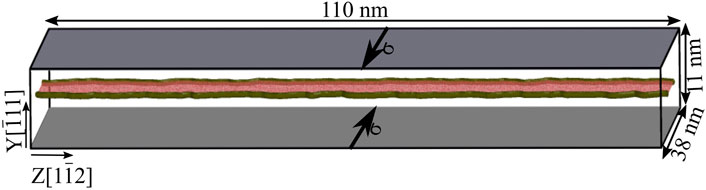
FIGURE 1. Simulation box for stress-control loading test. The red area represents the region between two partial dislocation lines dissociated from an edge dislocation. The stress is applied to the top and bottom Y-layer (grey area).

2.2 Modeling chemical short range order

Hybrid MD-MC is utilized in a canonical ensemble to simulate annealing of crystals at different temperatures. The details of the simulations are performed through several steps Antillon et al. (2020). In the first step, two different chemical compositions are selected randomly in the simulations and tried to swap the position so that the kinetic energy keeps constant by swapping. In the second step, Metropolis criterion is used and each swap attempt is accepted if $ϵ<\frac{P_f}{P_i}$, where ϵ is a random number between [0,1] and $P_i=e^{-\beta U_i}$, where β is the inverse of k_BT and U_i is the potential energy of the system. Swapping is tried 200 times for all pair-types. Since we have three distinct pairs, a MC cycle includes 600 swaps. To relax any local residual stress that is induced by swapping, 50 molecular dynamic time steps under constant pressure (NpT) conditions are performed. We repeat these hybrid MD/MC steps until we reach reasonable convergence of the system’s potential energy. These simulations have been done at 750, 1,000, and 1,400 K temperatures. Supplementary Figure S1A shows, for V_0.35Co_0.2Ni_0.45 alloy, the potential energy per atom as a function of the parameter MCsteps, which is the number of swap attempts normalized by the total number of atoms. For example, in a small system containing 48600 atoms, at MCsteps = 10 (810 MC cycles), you can see convergence in the potential energy. In this work, we simulate 4.5 million atoms and four different compositions, for dislocation dynamics purposes. This is a computationally demanding task, so we follow the simulation till MCsteps = 2 (15000 MC cycles), while we can see a reasonable convergence of potential energy for three different temperatures. To characterize the degree of CSRO at the various annealed temperatures, we used the following formula Li et al. (2019):

${\alpha }_{ij}^n=\frac{P_{ij}^n-C_j}{{\delta }_{ij}-C_j}(1)$

where n means the nth nearest-neighbor shell of the central atom i, P_ij is the average probability of finding a j-type atom around an i-type atom in the nth shell, C_j is the average concentration of j-type atom in the system, and α_ij is the Kronecker delta function. For pairs of the same types (i.e., i = j), a positive αⁿ represents the clustering tendency in the nth shell and a negative αⁿ means the opposite. While, we can have opposite interpretations for pairs of different types (i.e., i ≠ j).

2.2.1 Modelling from experimental chemical short range order motif

Recently for equimolar VCoNi, CSRO motif which has some similarity to L1₁ intermetallic compounds has been observed experimentally Chen et al. (2022). We modelled this motif (Supplementary Figure S2) and inserted it into the four compositions. It should be noticed that for non-equimolar VCoNi alloys we focus on just investigating the effect of CSRO on the strength of these alloys, if the CSRO motif is similar to the ones that formed in the case of equimolar VCoNi. In model 1 (CSROm1) we insert such motif so that 23.3% of the whole atoms (and thus with 0.132 V concentration) have such phases. This selection is close to the percentage observed for equimolar VCoNi in the experiments (25%) Chen et al. (2021b). To investigate how such a motif can affect mechanical properties, we considered another model (CSROm2) so that half of the Vanadium atoms in each composition belong to such motif.

3 Results and discussions

Table 1 shows the lattice constant, elastic constant, shear modulus μ, and Poisson’s ratio ν for four different VCoNi alloys at 0 K using the interatomic potential Choi et al. (2021). The available experimental values Hu et al. (2021) for equimolar VCoNi at room temperature are presented. To compare experiments and simulations, elastic constants, μ, and ν at room temperature have been calculated for equimolar VCoNi. The percentage differences between experimental values and calculated ones are presented. A reasonably good agreement between experiment and simulation values can be observed.

TABLE 1

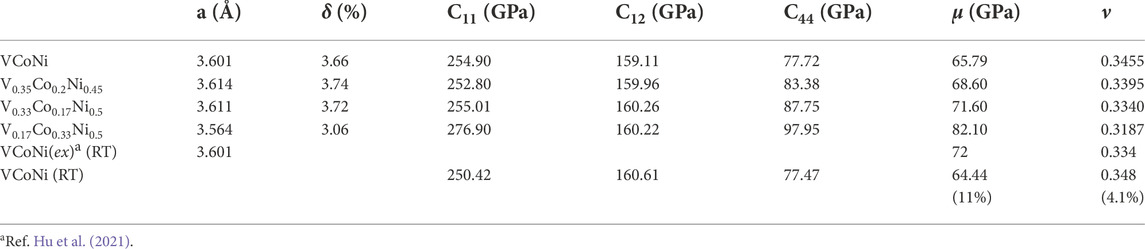
TABLE 1. Lattice constant (a (Å)), atomic mismatch (δ), elastic constants, shear modulus (μ) and Poisson’s ratio (ν) are presented for four different VCoNi alloys at 0 K using MD simulations. For equimolar VCoNi available experimental values are presented at room temperature (RT). To compare the experiments and simulation, elastic constants, μ, and ν at room temperature have been calculated for equimolar VCoNi. The percentage differences between the experimental value and the calculated value are shown in the parenthesis.

First, we focus on the depinning stress dependence on composition. Figures 2A,B show the depinning stress for all the compositions in two different temperatures. The depinning stress for equimolar VCoNi at 300 K is 410 ± 20 MPa, which is in good agreement with the experimental value of friction stress (383 MPa) for VCoNi at room temperature. The results show increasing the depinning stress by decreasing temperature from 300 to 5 K. This trend is in agreement with the experimental result for VCoNi Yang et al. (2021); Hu et al. (2021). Atomic mismatch (δ) for different compositions is calculated by $\delta =\sqrt{\mathrm{\Sigma }{c}_n\mathrm{\Delta }{\overline{V_n}}^2}/(3V_{\mathit{alloy}})$ where V_alloy = a³/4, c_n is concentration of each element and $\overline{V_n}=V_n-\bar{V}$ with $\bar{V}=\mathrm{\Sigma }{c}_n{V}_n$ Varvenne et al. (2016). The apparent volume $V_V=3.18{\mathring{A}}^3$ was obtained from DFT calculations Yin et al. (2020). $V_{Co}=11.12{\mathring{A}}^3$ and $V_{Ni}=10.94{\mathring{A}}^3$ were deduced from experiments Varvenne et al. (2016). Although we can see a relatively good correlation between atomic mismatch and depinning stress, V_0.33Co_0.17Ni_0.5 with lower atomic mismatch than V_0.35Co_0.2Ni_0.45 shows higher depinning stress. If we compare equimolar VCoNi with V_0.33Co_0.17Ni_0.5, we can see that by just changing the concentration of Ni and Co (decreasing Co concentration from 0.33 to 0.20 and increasing Ni concentration from 0.33 to 0.50), we can increase the depinning stress around 21.9% at 300 K and 27.2% at 5 K. Figure 5C represents the higher bond distances for Ni-V pairs rather than Co-V. It could be a source of higher depinning stress of V_0.33Co_0.17Ni_0.5 rather than equimolar VCoNi, where the number of V-Ni pairs is higher than Co-V in V_0.33Co_0.17Ni_0.5 which leads to higher lattice distortion. To see the effect of local atomic clusters on pinning dislocations, the atomic Virial stress in x-direction was calculated using lammps. Figures 2C,D represent the Virial atomic stress (σ_x) of random equimolar VCoNi at 5 K on the $(\bar{1}11)$ glide plane for two local pinning stages when the applying external stress increased from 1,060 to 1,080 MPa. Supplementary Movie S1 [see Supplementary Material (SM)] shows a movie of a dislocation avalanche across pinning centers, combining snapshots such as the ones shown in Figures 2C,D, where dislocation transfers from one local pinning to the others. As it is obvious from this figure, V-clusters (with the highest atomic pressure) play an important role in dislocation pinning. In contrast to CrCoNi, deformation twinning has not been observed in deforming VCoNi at cryogenic temperatures Yang et al. (2021). As reported in Ref. Yang et al. (2021), this can be connected to fairly high stacking fault energy (SFE) associated with VCoNi at low temperatures. Furthermore, it was shown that planer dislocation glides remain almost insensitive to variations temperature owing to very minimal SFE differences within the temperature range of interest Yang et al. (2021). In this framework, we investigated the temperature-dependence of the stacking fault width. Figure 3 shows a slight increase of the stacking fault width $W_{S{F}_c}$ with temperature, measured as a distance between the two partial dislocations, slightly below the depinning transition. Given that $W_{S{F}_c}$ is proportional to the inverse of stacking fault energy Vaid et al. (2022), our finding is consistent with ab initio calculations of equimolar VCoNi Yang et al. (2021) indicating a slight decrease of stacking fault energy with temperature. It can be seen that random equimolar VCoNi shows the highest stacking fault widths than the other non-equimolar VCoNi alloys.

FIGURE 2

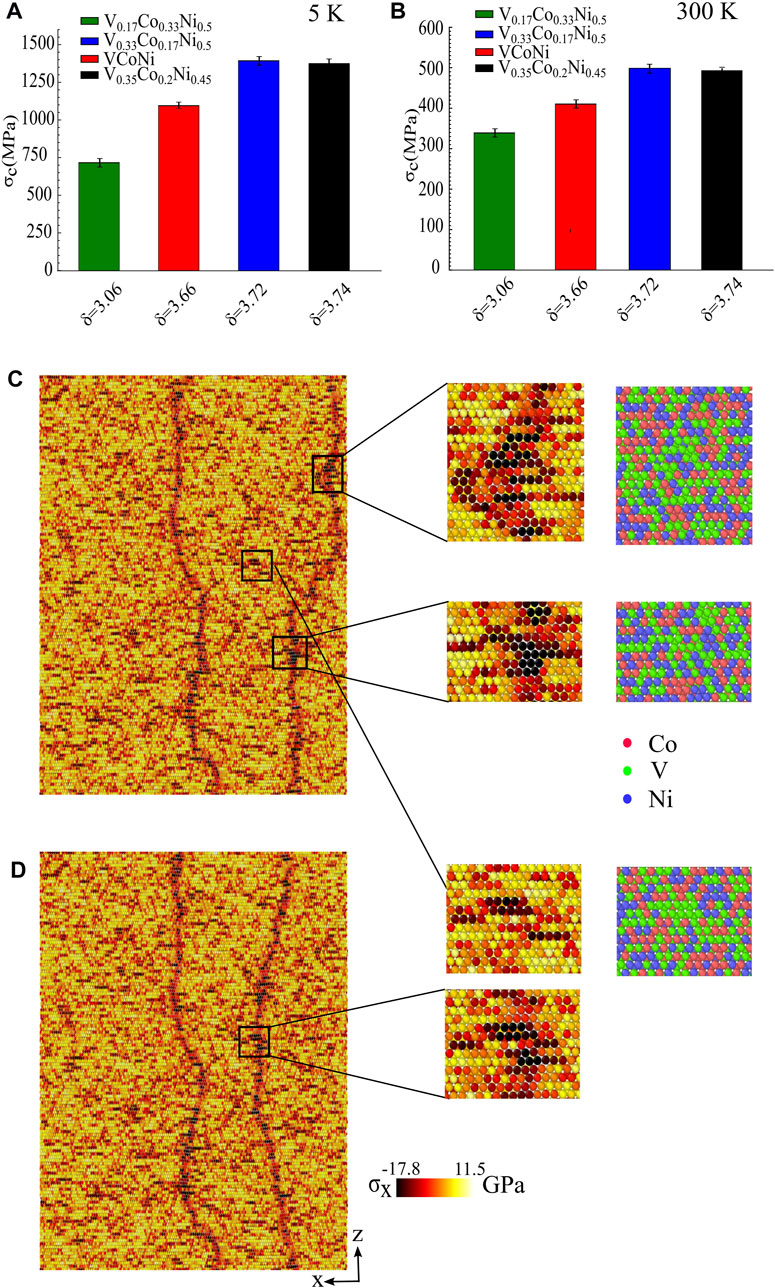
FIGURE 2. The depinning stress for all the random compositions at (A) 5 K. and (B) 300 K. The bars are ordered based on atomic mismatch (δ). Snapshot of two local pinning stages of dislocations in the random equimolar VCoNi at 5 K on the $(\bar{1}11)$ glide plane when the applying external stress is (C) 1,060 MPa and (D) 1,080 MPa pining points are zoomed in and color coded by Virial atomic stress in the glide direction (σ_x) as well as atomic type.

FIGURE 3

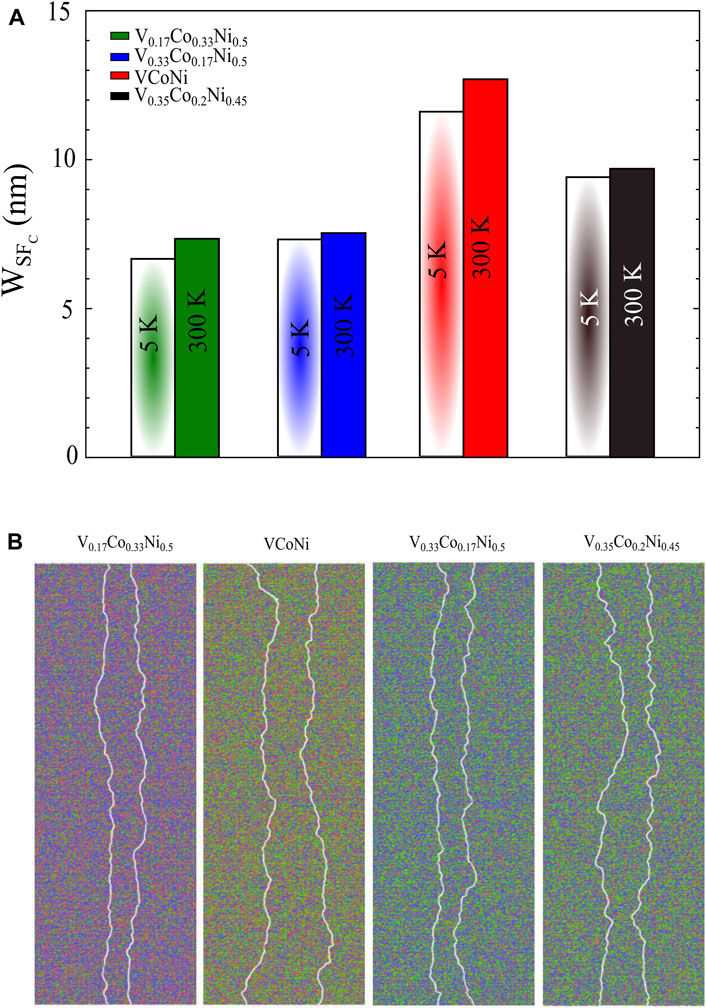
FIGURE 3. (A) Stacking fault width slightly below the depinning transition $(W_{S{F}_c})$ between two partial dislocations for four compositions at two different temperatures. (B) Atomic snapshot of four compositions at the verge of depinning. White line represents two partial dislocations. The red, blue and green, represent Co, Ni and V atoms respectively.

To see the effect of CSRO on the depinning stress, hybrid MD/MC simulations have been performed. Supplementary Figure S1B shows the acceptance rate as a function of MCsteps for different pair types in V_0.35Co_0.2Ni_0.45 alloy. It can be seen that Co-Ni has the highest acceptance rate of swapping. It makes sense because the electronegativity and atomic radius of Co and Ni are much closer to each other rather than V. Figure 4A depicts CSRO in the first neighbor shell. The interpretation of the results tells us the CSRO originates from the nearest neighbor preference towards V-Co and V-Ni pairs and avoidance of V-V pairs. Figure 4A indicates that CSRO increases with decreasing annealing temperature, which is analogous to the behavior seen numerically and experimentally in CrCoNi solid solutions. Figure 4B shows the variation of α¹ for different compositions which are annealed at 750 K. One can see from Figure 4B the same trend of CSRO for the three other compositions, where V_0.17Co_0.33Ni_0.5 shows the lowest CSRO among all. Figures 5A,B show how the annealing at 750 K affects depinning stress at 5 and 300 K. These Figs indicate that annealing does not affect the strength of equimolar VCoNi and V_0.17Co_0.33Ni_0.5, while it makes V_0.33Co_0.17Ni_0.5 and V_0.35Co_0.2Ni_0.45 softer. Softening by annealing was reported in another hybrid MD/MC study Antillon et al. (2020).

FIGURE 4

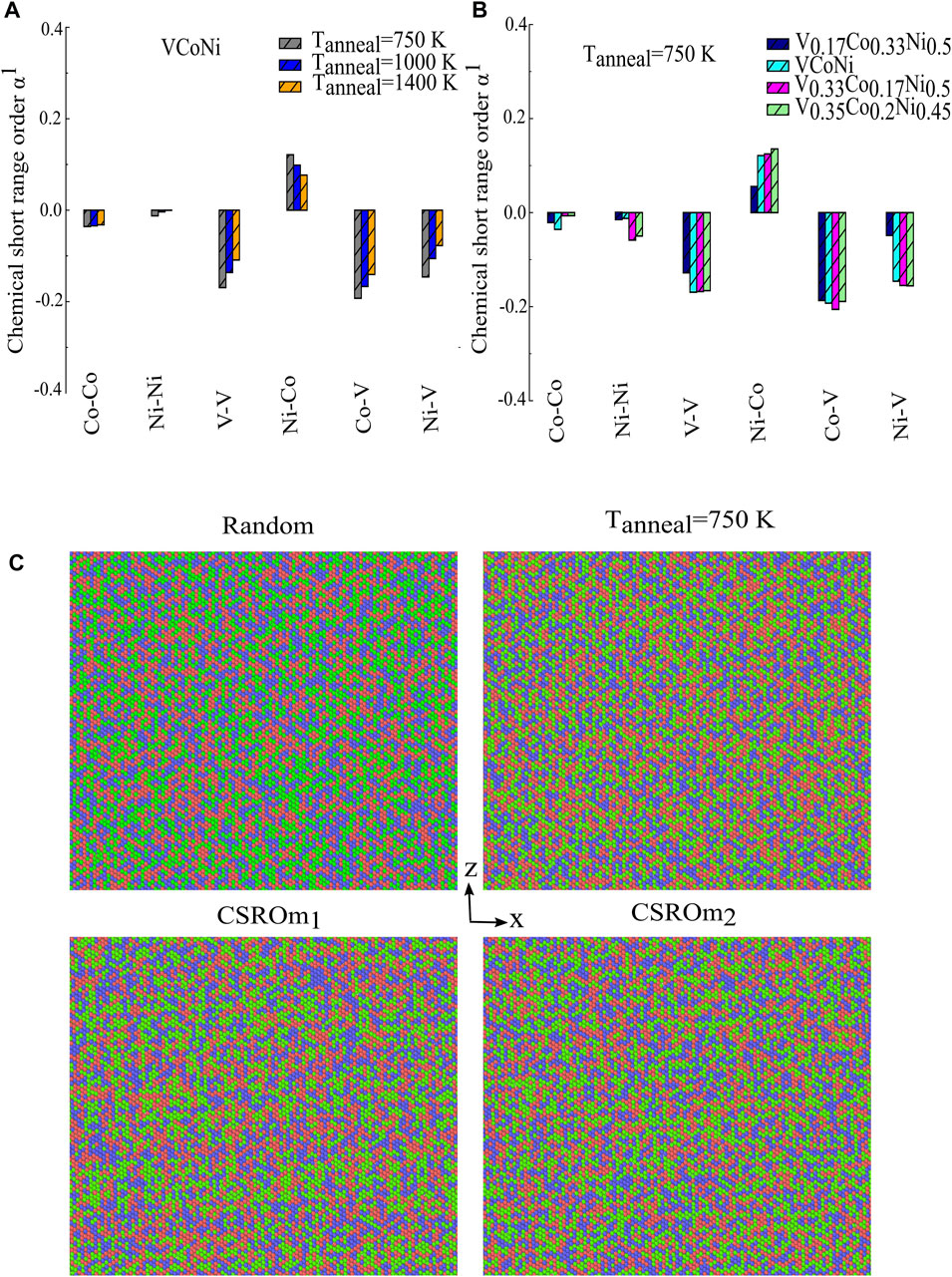
FIGURE 4. (A) The variation of α¹ (CSRO at first shell) in VCoNi for three different annealing temperatures (750, 1,100, 1,400 K). (B) The variation of α¹ for different compositions which are annealed at 750 K. (C) Equimolar VCoNi atomic structure in an x-z plane for random, the one that annealed at 750 K, and two CSRO models which experimental CSRO motifs are inserted into microstructure. The red, blue and green, represent Co, Ni and V atoms respectively.

FIGURE 5

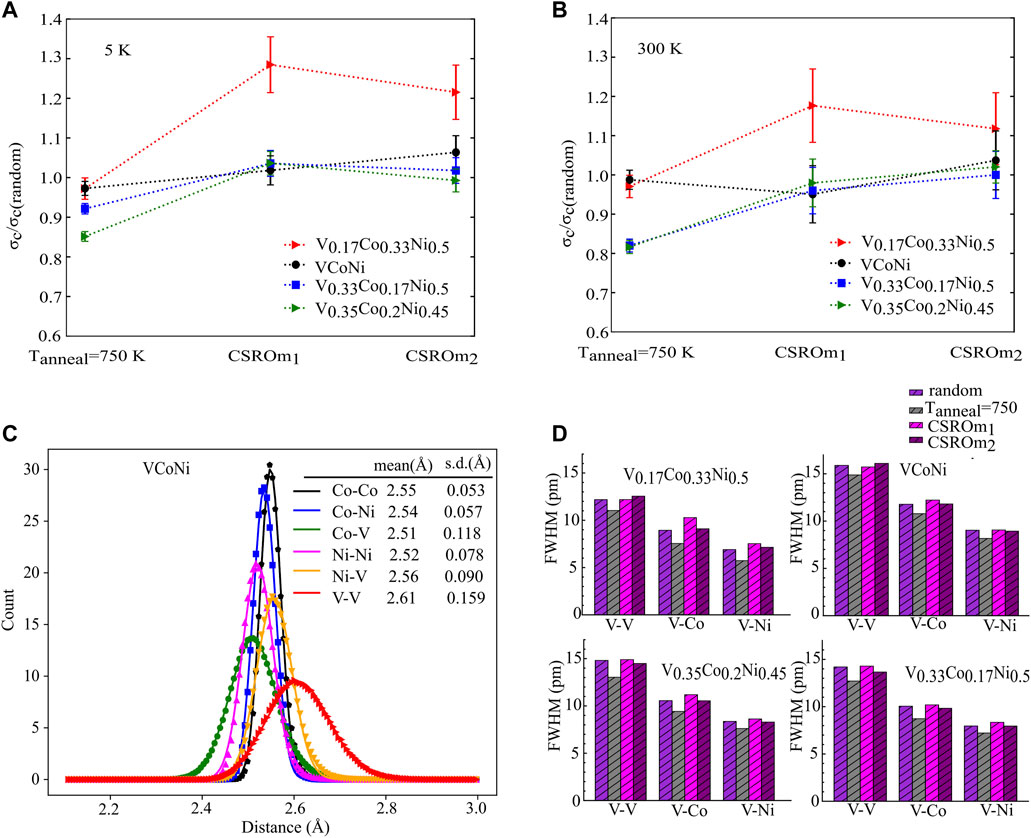
FIGURE 5. The ratio of ${\sigma }_c/{\sigma }_{c_{random}}$ (A) At 5 K and (B) 300 K for annealed compositions at 750 K as well as the compositions containing experimental CSRO motif (CSROm₁ and CSROm₁). (C) Bond distances in equimolar VCoNi random alloy and its fluctuation by analysing the radial pair distribution function in the first nearest neighbors and fitting it to normal distribution. (D) Effect of CSRO on bond fluctuations for different compositions by calculating full width at half maximum of the fitted normal distribution.

It should be mentioned that, despite softening of V_0.35Co_0.2Ni_0.45 and V_0.33Co_0.17Ni_0.5 due to annealing at 750 K, the depinning values remain higher than for equimolar random annealed VCoNi, especially at 5 K. The depinning values for annealed VCoNi, V_0.33Co_0.17Ni_0.5, and V_0.35Co_0.2Ni_0.45 at 5 K and 300 K are (1070, 1290, 1175) MPa and (400, 410, 400) MPa, respectively. To interpret the results, bond distance, and bond fluctuation in the first nearest neighbor are calculated using the radial pair distribution function and fitted to normal distribution functions (Figure 5C). Figure 5D shows such bond fluctuations for all compositions and the bonds with the highest fluctuations. Among the top-three highest fluctuation bonds, V-V and V-Ni with the bigger bond distance and fluctuations play an important role in lattice distortion, while V-Co shows a lower bond distance. It seems that annealing decreases bond fluctuations of V-V, Ni-V, and Co-V for all four compositions. These fluctuations are the least in V_0.17Co_0.33Ni_0.5 which is consistent with Figure 4B where the CSRO is the least in this composition. We should notice that the difference in the populations of the bonds in the first shell gives a weight for the lattice distortion so that for V_0.33Co_0.17Ni_0.5 and V_0.35Co_0.2Ni_0.45 alloys, lower bond fluctuations leads to lower depinning stress. This can be more understood when we notice that in V_0.35Co_0.2Ni_0.45 and V_0.33Co_0.17Ni_0.5, the number of V-Ni bonds are more than V-Co bonds rather the concentration of these bonds in equimolar VCoNi.

We also investigate the effect of CSRO on the depinning stress by modeling the microstructure based on the recently experimentally identified CSRO motif for equimolar VCoNi alloy. It should be noted that for non-equimolar VCoNi alloys there are no experimental observations to date. For these alloys, we conjecture a similar CSRO motif to the one forming in the equimolar VCoNi alloy. The reason for this choice is the fact that in the hybrid MD/MC simulation, the SRO patterns for V_0.35Co_0.2Ni_0.45 and V_0.33Co_0.17Ni_0.5 are very close to the one forming in the case of equimolar VCoNi. However, we believe that in the case of V_0.17Co_0.33Ni_0.5, such considerations may be far from reality, since there is a big apparent difference in the SRO pattern, compared to the one of an equimolar VCoNi alloy, based on hybrid MD/MC simulation. Figure 4C shows the atomic structure of the CSROm1 and CSROm2 models on x-z plane. The effect of such considerations on depinning stress and bond fluctuations is presented in Figure 5. The results show that the depinning stress of equimolar VCoNi is almost unchanged by considering the CSRO motifs. This is the same for V_0.33Co_0.17Ni_0.5 and V_0.35Co_0.2Ni_0.45 alloys, while for V_0.17Co_0.33Ni_0.5 considering the CSRO motifs (especially in model 1) increase the depinning stress. The main reason for that could be the very high concentration of V (0.132 from 0.17) that belong to such pseudo L1₁ phase in V_0.17Co_0.33Ni_0.5.

4 Concluding remarks

In conclusion, we performed a thorough molecular dynamics study of the effect of V, Co and Ni in the mechanical properties of VCoNi MEAs, which are potentially significant for future industrial applications. In summary, we find that:

1) V_0.33Co_0.17Ni_0.5 shows the highest depinning stress among the alloys studied, which means that changing Co and Ni concentrations from equimolar composition (decreasing Co concentration from 0.33 to 0.20 and increasing Ni concentration from 0.33 to 0.50) makes VCoNi alloys stronger.

2) Stacking fault width does not change significantly by decreasing temperature from 300 to 5 K.

3) V-clusters are the main source of dislocation pinning in solid solution VCoNi alloys.

4) We identify the emergence of chemical short range order that increases with decreasing annealing temperature.

5) CSRO affects the strength of non-equimolar VCoNi alloys

6) Annealing of V_0.35Co_0.2Ni_0.45 and V_0.33Co_0.17Ni_0.5 alloys leads to decreasing their depinning stress. This softening may be related to decreasing bond fluctuations in the annealed systems.

7) If the CSRO motif is similar to the experimental one in the equimolar VCoNi, it may lead to a meaningful increase in the strength of the composition with the lowest concentration of vanadium (V_0.17Co_0.33Ni_0.5).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

AE: Conception and design of study, Acquisition of data, Analysis and/or interpretation of data, Writing—original draft, Writing—review and editing, RA-D: Analysis and/or interpretation of data, Writing—original draft, Writing—review and editing, SP: Analysis and/or interpretation of data, Writing—original draft, Writing—review and editing, MA: Conception and design of study, Analysis and/or interpretation of data, Writing—original draft, Writing—review and editing.

Funding

This work has been supported by the European Union Horizon 2020 research and innovation program under grant agreement No. 857470 and by the European Regional Development Fund via the Foundation for Polish Science International Research Agenda PLUS program grant No. MAB PLUS/2018/8.

Acknowledgments

We acknowledge the computational resources provided by the High Performance Cluster at the National Centre for Nuclear Research in Poland.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.1046291/full#supplementary-material

References

Antillon, E., Woodward, C., Rao, S., Akdim, B., and Parthasarathy, T. (2020). Chemical short range order strengthening in a model fcc high entropy alloy. Acta Mater. 190, 29–42. doi:10.1016/j.actamat.2020.02.041

CrossRef Full Text | Google Scholar

Berendsen, H. J., Postma, J. v., Van Gunsteren, W. F., DiNola, A., and Haak, J. R. (1984). Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690. doi:10.1063/1.448118

CrossRef Full Text | Google Scholar

Chen, C., Ge, Y., Fang, W., Zhang, X., Liu, B., Feng, J., et al. (2021a). Multilayer maraging/cocrni composites with synergistic strengthening-toughening behavior. Front. Mat. 7, 619315. doi:10.3389/fmats.2020.619315

CrossRef Full Text | Google Scholar

Chen, X., Wang, Q., Cheng, Z., Zhu, M., Zhou, H., Jiang, P., et al. (2021b). Direct observation of chemical short-range order in a medium-entropy alloy. Nature 592, 712–716. doi:10.1038/s41586-021-03428-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Yuan, F., Zhou, H., and Wu, X. (2022). Structure motif of chemical short-range order in a medium-entropy alloy. Mater. Res. Lett. 10, 149–155. doi:10.1080/21663831.2022.2029607

CrossRef Full Text | Google Scholar

Cheng, W., Yuan, F., and Wu, X. (2021). Coupled strengthening effects by lattice distortion, local chemical ordering and nanoprecipitates in medium entropy alloys. Front. Mat. 8, 444. doi:10.3389/fmats.2021.767795

CrossRef Full Text | Google Scholar

Choi, W.-M., Kim, J.-S., Ko, W.-S., Kim, D. G., Jo, Y. H., Sohn, S. S., et al. (2021). Computational design of v-cocrfemnni high-entropy alloys: An atomistic simulation study. Calphad 74, 102317. doi:10.1016/j.calphad.2021.102317

CrossRef Full Text | Google Scholar

Coury, F. G., Clarke, K. D., Kiminami, C. S., Kaufman, M. J., and Clarke, A. J. (2018). High throughput discovery and design of strong multicomponent metallic solid solutions. Sci. Rep. 8, 8600–8610. doi:10.1038/s41598-018-26830-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Esfandiarpour, A., and Nasrabadi, M. (2019). Investigation of the effect of composing elements of cunicofev high entropy alloy on thermal-elastic properties: An ab initio study. Intermetallics 104, 59–65. doi:10.1016/j.intermet.2018.10.019

CrossRef Full Text | Google Scholar

Esfandiarpour, A., Papanikolaou, S., and Alava, M. (2022). Edge dislocations in multicomponent solid solution alloys: Beyond traditional elastic depinning. Phys. Rev. Res. 4, L022043. doi:10.1103/physrevresearch.4.l022043

CrossRef Full Text | Google Scholar

Eshelby, J. (1955). The elastic interaction of point defects. Acta metall. 3, 487–490. doi:10.1016/0001-6160(55)90140-1

CrossRef Full Text | Google Scholar

Hu, M., Cao, Q., Wang, X., Zhang, D., and Jiang, J.-Z. (2021). Ultra-strong nanostructured co-ni-v medium entropy alloy thin film designed by interface strengthening. Thin Solid Films 734, 138866. doi:10.1016/j.tsf.2021.138866

CrossRef Full Text | Google Scholar

Jia, Q., He, W., Hua, D., Zhou, Q., Du, Y., Ren, Y., et al. (2022). Effects of structure relaxation and surface oxidation on nanoscopic wear behaviors of metallic glass. Acta Mater. 232, 117934. doi:10.1016/j.actamat.2022.117934

CrossRef Full Text | Google Scholar

Jiang, W., Zhu, Y., and Zhao, Y. (2022). Mechanical properties and deformation mechanisms of heterostructured high-entropy and medium-entropy alloys: A review. Front. Mat. 8. doi:10.3389/fmats.2021.792359

CrossRef Full Text | Google Scholar

Karimi, K., Esfandiarpour, A., Alvarez-Donado, R., Alava, M. J., and Papanikolaou, S. (2022). Shear banding instability in multicomponent metallic glasses: Interplay of composition and short-range order. Phys. Rev. B 105, 094117. doi:10.1103/physrevb.105.094117

CrossRef Full Text | Google Scholar

King, D., Middleburgh, S., McGregor, A., and Cortie, M. (2016). Predicting the formation and stability of single phase high-entropy alloys. Acta Mater. 104, 172–179. doi:10.1016/j.actamat.2015.11.040

CrossRef Full Text | Google Scholar

Labusch, R. (1970). A statistical theory of solid solution hardening. Phys. Stat. Sol. 41, 659–669. doi:10.1002/pssb.19700410221

CrossRef Full Text | Google Scholar

Li, Q.-J., Sheng, H., and Ma, E. (2019). Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways. Nat. Commun. 10, 1–11. doi:10.1038/s41467-019-11464-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, D., Zhou, Q., Ye, W., Ren, Y., Greiner, C., He, Y., et al. (2021). Design and characterization of self-lubricating refractory high entropy alloy-based multilayered films. ACS Appl. Mat. Interfaces 13, 55712–55725. doi:10.1021/acsami.1c16949

PubMed Abstract | CrossRef Full Text | Google Scholar

Osetsky, Y. N., and Bacon, D. J. (2003). An atomic-level model for studying the dynamics of edge dislocations in metals. Model. Simul. Mat. Sci. Eng. 11, 427–446. doi:10.1088/0965-0393/11/4/302

CrossRef Full Text | Google Scholar

Senkov, O. N., Wilks, G., Scott, J., and Miracle, D. B. (2011). Mechanical properties of nb25mo25ta25w25 and v20nb20mo20ta20w20 refractory high entropy alloys. Intermetallics 19, 698–706. doi:10.1016/j.intermet.2011.01.004

CrossRef Full Text | Google Scholar

Sohn, S. S., Kwiatkowski da Silva, A., Ikeda, Y., Körmann, F., Lu, W., Choi, W. S., et al. (2019). Ultrastrong medium-entropy single-phase alloys designed via severe lattice distortion. Adv. Mat. 31, 1807142. doi:10.1002/adma.201807142

PubMed Abstract | CrossRef Full Text | Google Scholar

Stukowski, A., Bulatov, V. V., and Arsenlis, A. (2012). Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mat. Sci. Eng. 20, 085007. doi:10.1088/0965-0393/20/8/085007

CrossRef Full Text | Google Scholar

Stukowski, A. (2009). Visualization and analysis of atomistic simulation data with ovito–the open visualization tool. Model. Simul. Mat. Sci. Eng. 18, 015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2022). Lammps-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171. doi:10.1016/j.cpc.2021.108171

CrossRef Full Text | Google Scholar

Vaid, A., Wei, D., Bitzek, E., Nasiri, S., Zaiser, M., et al. (2022). Pinning of extended dislocations in atomically disordered crystals. Acta Mater. 236, 118095. doi:10.1016/j.actamat.2022.118095

CrossRef Full Text | Google Scholar

Varvenne, C., Luque, A., and Curtin, W. A. (2016). Theory of strengthening in fcc high entropy alloys. Acta Mater. 118, 164–176. doi:10.1016/j.actamat.2016.07.040

CrossRef Full Text | Google Scholar

Wu, Z., Bei, H., Pharr, G. M., and George, E. P. (2014). Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 81, 428–441. doi:10.1016/j.actamat.2014.08.026

CrossRef Full Text | Google Scholar

Yan, J., Zhang, Z., Zhang, P., Liu, J., Yu, H., Hu, Q., et al. (2022). Design and optimization of the composition and mechanical properties for non-equiatomic cocrni medium-entropy alloys. J. Mater. Sci. Technol. doi:10.1016/j.jmst.2022.07.031

CrossRef Full Text | Google Scholar

Yang, D. C., Jo, Y. H., Ikeda, Y., Körmann, F., and Sohn, S. S. (2021). Effects of cryogenic temperature on tensile and impact properties in a medium-entropy vconi alloy. J. Mater. Sci. Technol. 90, 159–167. doi:10.1016/j.jmst.2021.02.034

CrossRef Full Text | Google Scholar

Yin, B., Maresca, F., and Curtin, W. (2020). Vanadium is an optimal element for strengthening in both fcc and bcc high-entropy alloys. Acta Mater. 188, 486–491. doi:10.1016/j.actamat.2020.01.062

CrossRef Full Text | Google Scholar

Zhang, R., Zhao, S., Ding, J., Chong, Y., Jia, T., Ophus, C., et al. (2020). Short-range order and its impact on the crconi medium-entropy alloy. Nature 581, 283–287. doi:10.1038/s41586-020-2275-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W., Liaw, P. K., and Zhang, Y. (2018). Science and technology in high-entropy alloys. Sci. China Mat. 61, 2–22. doi:10.1007/s40843-017-9195-8

CrossRef Full Text | Google Scholar

Zhou, Q., Luo, D., Hua, D., Ye, W., Li, S., Zou, Q., et al. (2022). Design and characterization of metallic glass/graphene multilayer with excellent nanowear properties. Friction, 1–14. doi:10.1007/s40544-021-0581-6

CrossRef Full Text | Google Scholar