Theoretical analysis and experimental study on physical explosion of stratospheric airship envelope

The shock wave released from physical explosion of a pressurized stratospheric airship can produce serious damage to the environment. Shock wave overpressure can measure the degree of damage that an explosion can cause to such things as buildings and the human body. To obtain the overpressure from an airship envelope explosion, explosion energy must first be conducted. Explosion energy is derived based on Brode’s equation, Brown’s equation, and Crowl’s equation. An equivalent TNT computational model is then applied to calculate the overpressure of the explosion energy. In order to verify the accuracy of the computational model, a ground test must be conducted. The experimental result shows that a computational model based on Crowl’s equation is more accurate than the other two. Finally, the effect of geometric scale ratio, pressure difference, and the gas of the explosion overpressure is discussed. This paper can provide a relatively effective calculation method for shock wave overpressure for an airship envelope explosion.

Introduction

A stratospheric airship is a kind of lighter-than-air vehicle which depends on buoyant floating at high altitudes, as opposed to satellites or airplanes. Its internal pressurized gases are helium and air. The pressure difference between the internal gas and external environment of the airship envelope maintains the envelope’s shape and determines the airship’s floating altitude. Therefore, the construction material of airships must exhibit a high strength-to-weight ratio and excellent tear resistance (Zhai and Anthony, 2005). Most common failures of airship envelopes are caused by tear propagation, which generally develops from a tiny crack and causes a large area tear or even eventually an explosion. Much research on the tear properties of stratospheric airship envelope materials has been published, including analysis methods (Galliot and Luchsinger, 2009; Ma, 2011; Wang et al., 2013; Min et al., 2014; Meng et al., 2016; Yi et al., 2020; Ding et al., 2021), test methods (Miller and Mandel, 2000; Bai et al., 2011; Wang et al., 2012; Chen et al., 2018), and fracture propagation models (Maekawa et al., 2008; Cao et al., 2015; Xu et al., 2017). However, there has been no research on calculating the energy and shock wave of an airship explosion. To assess the physical explosion damage from pressurized stratospheric airship envelopes, Brode’s equation (Brode, 1959), Brown’s equation (Brown, 1985), and Crowl’s equation (Crowl, 1992) are applied to estimate explosion energy. Prugh’s correction TNT equivalent method (Dennis et al., 2000) is applied to estimate the explosion overpressure. A pressurized airship envelope explosion test is proposed to rationality verify the estimation methods.

Theory

Overpressure of explosion from a pressurized stratospheric airship envelope

Shock wave overpressure can measure the degree of damage that an explosion can cause to things such as buildings and the human body. An explosion from a pressurized stratospheric airship envelope is a typical physical explosion. The stored energy is released instantly, producing a shock wave and accelerating airship envelope fragments. To determine the overpressure from an airship envelope explosion, explosion energy must first be conducted. Prugh (Dennis et al., 2000) proposed a correction TNT equivalent method using virtual distance from an explosion center to estimate shock wave effects; this can be applied to explosion research from a pressurized stratospheric airship. The procedure is as follows.

Determine the energy of explosion

There are various expressions which can be developed to calculate the energy released by a physical explosion from a pressurized vessel. Brode (Brode, 1959) developed the simplest expression 1), which expressed the energy required to raise the pressure of the inflated gas at a constant volume from atmospheric pressure to the explosion pressure E:

$E=\frac{\left(P_1-P_0\right)V}{\gamma -1}(1)$

where E is the explosion energy, $P_1$ is the initial pressure of the vessel, $P_0$ is the standard pressure, V is the volume of the vessel, and $\gamma$ is the heat capacity ratio of the expanding gas.

Brown (Brown, 1985) assumed that explosion 2) occurs isothermally and derived an expression based on the ideal gas law.

$E=P_{1}V\ln \left(\frac{P_1}{P_0}\right)(2)$

Crowl (Crowl, 1992) proposed another approach which assumed that available energy represented the maximum mechanical energy which could be extracted from a material as it moves into equilibrium with the environment. Regarding non-reactive material initially at pressure P and temperature T and expanding into pressure $P_E$, the maximum mechanical energy E can be expressed as Eq. 3:

$E=RT\left[\ln \left(\frac{P}{P_E}\right)-\left(1-\frac{P_E}{P}\right)\right](3)$

Determine the blast pressure at the surface of the airship envelope

The blast pressure Ps at the surface of the envelope can be determined by Eq. 4. This equation assumes that the expansion will occur into the air at atmospheric pressure at a temperature of 25°C and that the explosion energy is distributed uniformly across the vessel. Therefore, this equation is a trial-and-error solution.

$P_b=P_s{\left[1-\frac{3.5\left(\gamma -1\right)\left(P_s-1\right)}{\sqrt{\left(\gamma T/M\right)\left(1+5.9P_s\right)}}\right]}^{-2\gamma /\left(\gamma -1\right)}(4)$

where $P_s$ is the pressure at the surface of the vessel (bar abs), $P_b$ is the burst pressure of the vessel (bar abs), T is the absolute temperature of the expanding gas (K), and M is the molecular weight of the expanding gas (mass/mole).

Calculate the scaled distance

The scaled distance Z for the explosion can be obtained from Eq. 5:

${\log }_{10}{P}_s={\displaystyle \sum }_{i=0}^n{c}_i{\left(a+b{\log }_{10}Z\right)}^i(5)$

where Z is the scale distance (m/kg^1/3) and $c_i$, a, b are the constants shown in Table 1.

TABLE 1

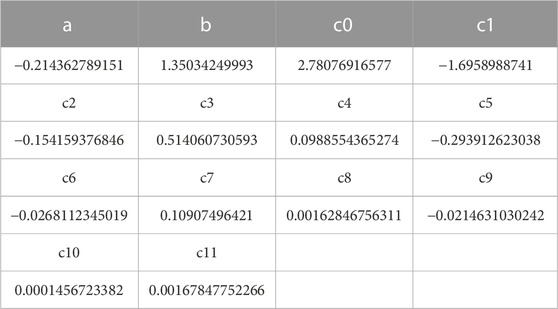
TABLE 1. Function parameters for Eq. 5.

Calculate a value for the distance from the explosion center

The value for the distance R from the explosion can be calculated using Eqs. 6, 7:

$Z=\frac{R}{W^{1/3}}(6)$

$W=\frac{E}{E_{TNT}}(7)$

where $W$ is the equivalent mass of TNT, $\eta$ is an empirical efficiency, M is the mass of hydrocarbon, and $E_{TNT}$ is the combustion heat of TNT (4437–4765 kJ/kg or 1943–2049 Bru/lb).

Calculate the virtual distance $R_x$ and the scaled distance from the center to the surface of container $Z_R$

$R_x=R-r(8)$

$Z_R=\frac{R+R_x}{W_E^{1/3}}(9)$

where $r$ is the distance from the center of the pressurized gas container to its surface.

Determine the overpressure $P_{ZR}$

The overpressure at object distance is determined using Eq. 5:

${\log }_{10}{P}_{ZR}={\displaystyle \sum }_{i=0}^n{c}_i{\left(a+b{\log }_{10}{Z}_R\right)}^i(10)$

Experiment

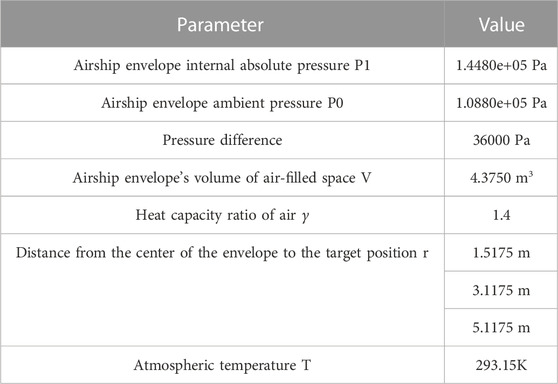
An airship envelope model was designed and produced from the envelope material FV1160. The geometrical dimension of the airship envelope model was determined to be 5 m in length and 1.28 m in radius (Figure 1). An air pump was employed to pump air into the airship envelope until it exploded. The differential pressure recorder was used to record the pressure difference of the envelope through the whole process. Two high speed cameras were utilized of capture the exploding process of the airship envelope. Three pressure gauges were located, respectively, at distances of 1.1175 m, 2.6175 m, and 4.6175 m from the blasting position to measure the shock pressure.

FIGURE 1

FIGURE 1. Ground explosion test for an airship envelope.

As the envelope was continuously pressurized by the pump, it exploded at the pressure difference of 36 kPa. Table 2 lists the overpressure at different positions.

TABLE 2

TABLE 2. Test parameters.

Results and discussion

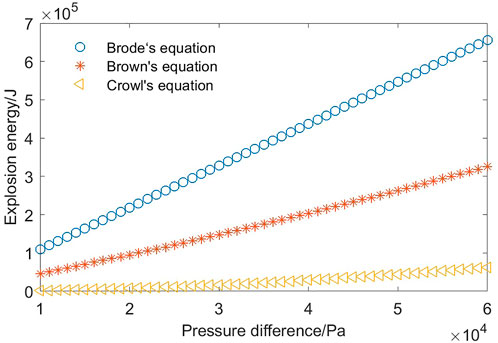
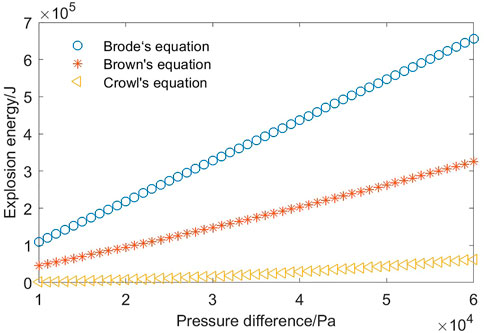
The correction TNT equivalent method was applied to calculate the overpressure of the shock from this airship envelope explosion. At first, the explosion energy was calculated using the equations of Brode, Brown, and Crowl (Figure 2). The explosion energies at the pressure difference of 36 kPa between the airship envelope’s internal and external gas were, respectively, 393.8 kJ, 181.5 kJ, and 23.95 kJ. The three methods thus provided considerably different results.

FIGURE 2

FIGURE 2. Explosion energy at various pressure differences.

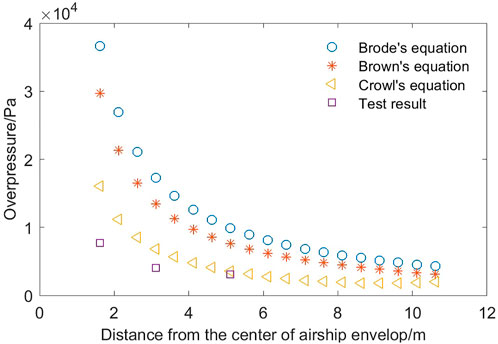
Using the explosion energy calculated by these three methods, Prugh’s correction TNT equivalent method was applied to estimate the overpressure at the explosion pressure difference of 36 kPa. As shown in Figure 3, this correction TNT equivalent method is based on the three explosion energy calculation methods for estimating overpressure as a trial-and-error solution. The theoretical calculation result and experiment results are listed in Table 3, and the error values for three calculation methods are listed in Table 4. All the computational and experimental results show low accuracy. However, the values of explosion overpressure using Crowl’s equation are closest to the test result, especially as the distance from the center of airship envelope increases. Brode’s equation assumes that the value of the vessel’s volume is constant during this explosion process, ignoring the work carried out by gas expansion. Brown’s equation assumes that the expansion occurs isothermally and that all compression energy is used in the explosion. Crowl’s equation assumes that maximum mechanical energy can be extracted from a material as it moves into equilibrium with the environment. The first term within the brackets of Crowl’s equation is equivalent to the isothermal energy of expansion. The second term within the parenthesis represents the loss of energy as a result of the second law of thermodynamics. Therefore, the results calculated by Crowl’s equation are smaller than the results predicted by Brown.

FIGURE 3

FIGURE 3. Computational and experimental value for overpressure at difference positions.

TABLE 3

TABLE 3. Computational and experimental value for overpressure at three positions.

TABLE 4

TABLE 4. Computational error for overpressure using three computational models.

Effect of the geometric scale ratio

Scale models for airship envelopes are generally used in ground explosion tests to study the envelope explosion characteristics for cost savings and convenient operation. Rupture is likely to occur at the location of the largest radius R because this position suffers the most hoop and axial stress.

$f_h=\frac{\Delta \mathit{PR}}{t},(11)$

$f_a=\frac{\Delta \mathit{PR}}{2t},(12)$

where $f_h$ is hoop stress, $f_a$ is axial stress, t is the thickness of the envelope material, and $\Delta P$ is the pressure difference between the internal and external gas of the airship envelope.

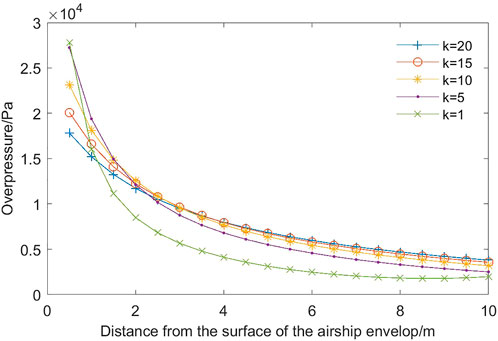
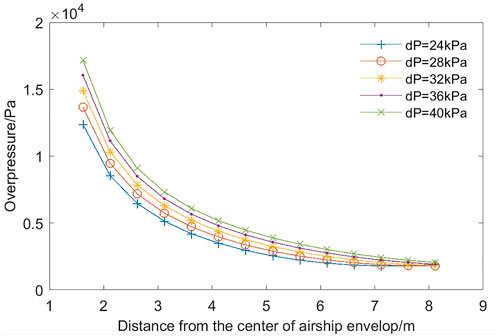
Therefore, if the dimension of the airship envelope is the k time of the ground test model, its estimated explosion pressure difference becomes 1/k time. Crowl’s equation is applied to calculate explosion energy, and the correction TNT equivalent method is used to estimate the overpressure for the airship envelope with the geometric scale ratio k at 1, 5, 10, 15, and 20. As shown in Figures 4 and 5, explosion energy increases linearly as the geometric dimension increases. At the position near the surface of the airship envelope, the overpressure increases with the rising geometric dimension. However, the opposite is true for the position far away from the envelope (Figure 6).

FIGURE 4

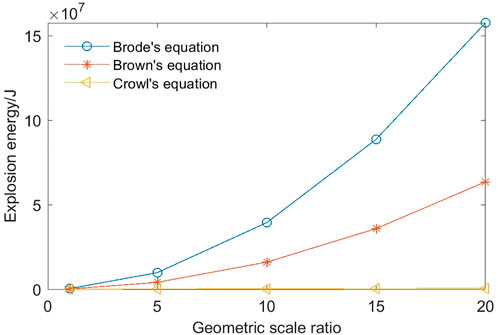
FIGURE 4. Explosion energy for envelopes with different geometric scale ratios calculated by Brode’s, Brown’s, and Crowl’s equations.

FIGURE 5

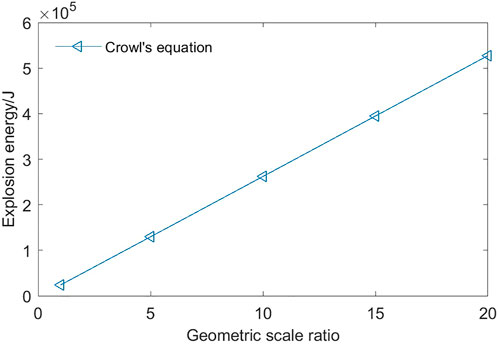
FIGURE 5. Explosion energy for envelopes with different geometric scale ratios calculated by Crowl’s equations.

FIGURE 6

FIGURE 6. Overpressure for envelopes with different geometric scale ratios.

Effects of the pressure difference

In general, rupture is caused by the reduction in envelope strength due to material defects in the subsequent development of fracture- or fatigue-induced weakening of the envelope material. Rupture may thus occur at a relatively lower pressure difference than the value of the material’s theoretical strength. Therefore, it is necessary to analyze the effect of the pressure difference on explosion energy and overpressure. As shown in Figure 7, explosion energy grows significantly as the pressure difference increases. In comparison to Brode’s and Brown’s equations, the explosion energy derived by Crowl’s equation rises slowly. Figure 8 shows that the pressure difference has a significant effect on overpressure at the position near the center of the airship envelope, and that overpressure increases with the rising pressure difference. However, as the distance from the envelope center increases to 8 m, the overpressure slightly increases as the pressure difference increases.

FIGURE 7

FIGURE 7. Explosion energy for envelopes at different pressure differences.

FIGURE 8

FIGURE 8. Overpressure for envelopes at different pressure differences.

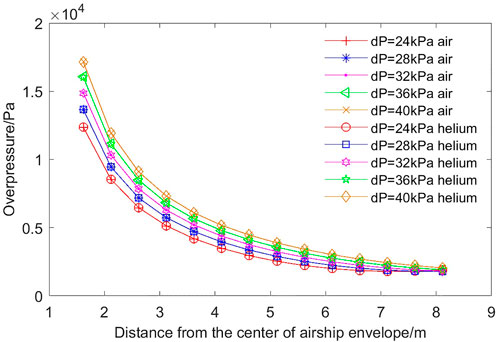
Effects of the variety of gas

Normally, airship envelopes are partly filled with helium floating in the air at 20 km altitude. The heat capacity ratio $\gamma$ for helium is 1.6 and that for air is 1.4. Figure 9 shows that values of overpressure are almost the same as each other at the same distance for different pressure differences and variety of gas. Because the explosion energy model derived by Crowl’s equation does not consider the heat transfer process, air could be replaced by helium filled into envelopes during the ground explosion tests of airship envelopes to save cost.

FIGURE 9

FIGURE 9. Overpressure for envelopes at different pressure differences and sorts of gas.

Conclusion

Three methods were used to calculate the explosion energy of a pressurized airship envelope. A ground explosion test was conducted, and the results showed that Crowl’s equation for calculating explosion energy is relatively more accurate than Brode’s and Brown’s equations. Based on Crowl’s equation for estimating energy, a correction TNT equivalent method was applied to calculate overpressure at different distances from the envelope’s center.

At the position near the surface of the airship envelope, the overpressure increased with the rising dimensions. However, the opposite is true for the position far from the envelope.

Pressure difference has a significant effect on overpressure near the center of the airship envelope. However, as the distance from the envelope center increases, the effect increasingly lessens.

The heat capacity ratio $\gamma$ for filled gas had a slight effect on the overpressure of the pressurized envelope. Helium could be replaced by air and pumped into envelopes during the ground explosion tests for airship envelopes.

This paper can provide a calculation method for overpressure for ground explosion testing of airship envelopes for safe operation. It provides a relatively effective calculation method for shock wave and explosion energy in the event of an airship explosion during a possible flight accident.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

LS: proposing the idea, theoretical calculation, experiment performance, and data collection. YY and ZH: theoretical calculation and analysis. XZ, XG, ZZ, and HG: experiment performance, data collection, and data processing. All authors have agreed to submit the manuscript.

Funding

The first author acknowledges the funding support from the Strategic Priority Research Program of China Academy of Sciences (Grant No. XDA20100200).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, J., Xiong, J., and Cheng, X. (2011). Tear resistance of orthogonal kevlar-PWF-reinforced TPU film. J. Aeronautics 24 (1), 113–118. doi:10.1016/s1000-9361(11)60014-9

CrossRef Full Text | Google Scholar

Brode, H. L . (1959). Blast wave from a spherical charge. Phys. Fluids 2 (2), 217. doi:10.1063/1.1705911

CrossRef Full Text | Google Scholar

Brown, S. J. (1985). Energy release protection for pressurized systems. Part I: Review of studies into blast and fragmentation. Appl. Mech. Rev. 38 (12), 1625–1651. doi:10.1115/1.3143700

CrossRef Full Text | Google Scholar

Cao, S., Liu, L. B., Meng, J. H., and Lv, M. Y. (2015). Tearing propagation of stratospheric airship envelope based on the link model[J]. J. Harbin Inst. Technol. 47 (11), 5. doi:10.11918/j.issn.0367-6234.2015.11.010

CrossRef Full Text | Google Scholar

Chen, Y. F., Chen, Y. L., Wang, F. X., and Fu, G. Y. (2018). Tearing properties of a stratospheric airship envelope material[J]. Spat. Struct. 24 (3), 10. doi:10.13849/j.issn.1006-6578.2018.03.066

CrossRef Full Text | Google Scholar

Crowl, D. A. (1992). Calculating the energy of explosion using thermodynamic availability. J. Loss Prev. Process Industries 5 (2), 109–118. doi:10.1016/0950-4230(92)80007-u

CrossRef Full Text | Google Scholar

Dennis, C. H., Brian, R. D., and Arthur, G. M. (2000). Guidelines for chemical process quantitative risk analysis[M]. New York: John Wiley & Sons International Rights, Inc, 157–186. doi:10.1002/9780470935422

CrossRef Full Text | Google Scholar

Ding, K., Chen, Y. L., Chen, Y. F., and Fu, G. Y. (2021). Study on factors influencencing tearing properties of stratospheric airship envelope materials [J]. Spat. Struct. 27 (3), 7. doi:10.13849/j.issn.1006-6578.2021.03.061

CrossRef Full Text | Google Scholar

Galliot, C., and Luchsinger, R. H. (2009). A simple model describing the non-linear biaxial tensile behaviour of PVC-coated polyester fabrics for use in finite element analysis. Compos. Struct. 90 (4), 438–447. doi:10.1016/j.compstruct.2009.04.016

CrossRef Full Text | Google Scholar

Ma, Q. (2011). Finite element analyses of woven fabrics tearing damage[D]. Shanghai: Dong Hua Univesity.

Google Scholar

Maekawa, S., Shibasaki, K., Kurose, T., Maeda, T., Sasaki, Y., and Yoshino, T. (2008). Tear propagation of a high-performance airship envelope material. J. Aircr. 45 (5), 1546–1553. doi:10.2514/1.32264

CrossRef Full Text | Google Scholar

Meng, J. H., Li, P. H., Ma, G. Y., Du, H., and Lv, M. (2016). Tearing behaviors of flexible fiber-reinforced composites for the stratospheric airship envelope. Appl. Compos. Mater. 24 (3), 735–749. doi:10.1007/s10443-016-9539-7

CrossRef Full Text | Google Scholar

Miller, T., and Mandel, M. (2000). “Airship envelopes: Requirements, materials and test methods[C],” in The 3rd International Airship Convention and Exhibition, Friedrichshafen, Germany, 1-5 July 2000.

Google Scholar

Min, J. B., Xue, D., and Shi, Y. (2014). Micromechanics modeling for fatigue damage analysis designed for fabric reinforced ceramic matrix composites. Compos. Struct. 111, 213–223. doi:10.1016/j.compstruct.2013.12.025

CrossRef Full Text | Google Scholar

Wang, P., Sun, B. Z., and Gu, B. H. (2012). Comparisons of trapezoid tearing behaviors of uncoated and coated woven fabrics from experimental and finite element analysis. Int. J. Damage Mech. 22 (4), 464–489. doi:10.1177/1056789512450524

CrossRef Full Text | Google Scholar

Wang, S., Sun, B., and Gu, B. (2013). Analytical modeling on mechanical responses and damage morphology of flexible woven composites under trapezoid tearing. Text. Res. J. 83 (12), 1297–1309. doi:10.1177/0040517512468824

CrossRef Full Text | Google Scholar

Xu, W., Wang, F. X., Chen, Y. L., and Fu, G. Y. (2017). Tearing propagation on a new airship envelope material[J]. Spat. Struct. 23 (2), 7. doi:10.13849/j.issn.1006-6578.2017.02.035

CrossRef Full Text | Google Scholar

Yi, F. W., Chen, Y. L., and Wang, F. J. (2020). Tearing test and numerical simulation of airship envelope material[J]. J. hefei Univ. Technol. Nat. Sci. 43 (1), 8.

Google Scholar

Zhai, H. L., and Anthony, E. (2005). “Material challenges for lighterthan-air systems in high altitude applications,” in AIAA 5th ATIO conference, Arlington, VA, 26–28 September 2005 (Reston, VA: AIAA), 1–12.

CrossRef Full Text | Google Scholar