- 1School of Civil Engineering, Shenyang Urban Construction Institute, Shenyang, China
- 2School of Transportation and Geomatics Engineering, Shenyang Jianzhu University, Shenyang, China
- 3Transportation Engineering College, Dalian Maritime University, Dalian, China
To reasonably describe the damage characteristics of composite modified open graded friction course (OGFC) after multiple freeze-thaw cycles, based on the Able viscoelastic constitutive equation, a viscoelastic model of freeze-thaw damage was constructed and analyzed using the Weibull distribution function, damage mechanics, and fractional derivative theory. Under the conditions of composite modified OGFC mixtures with different mixing ratios (12%, 0%), (12%, 1%), and (12%, 2%), and multiple freeze-thaw cycles (0–16), low-temperature bending and creep tests of the mixtures were carried out. The stress-strain curve data obtained were fitted to analyze the physical significance of the model parameters. The results show that the model is suitable for characterizing the viscoelastic stage of composite modified OGFC under 10 freeze-thaw cycles. The freeze-thaw damage model parameters of three types of composite modified OGFC with different mixing ratios were compared and analyzed. The order of the fractional derivative of the composite modified OGFC model (12%, 1%) was 0.2223, the maximum damage threshold was 1.108, and the maximum viscosity coefficient was 371.84. This composite modified OGFC had the best low-temperature crack resistance.
1 Introduction
Because of the dense structure of dense-graded asphalt mixtures, discharging surface water is challenging and the water mist and reflected light produced by vehicles traveling at high speed can seriously affect the safety of vehicles (Goetz and Schoch, 1995). Open graded friction course (OGFC) asphalt mixtures have the potential to reduce splash and water mist and improve road friction. Since the 1950s, OGFC has been widely used globally. As a typical large-gap asphalt mixture, OGFC was initially used to reduce noise pollution and improve road visibility by reducing the air pump effect between the tires and the road (Meiarashi et al., 1996). Moreover, it was found that OGFC can eliminate road surface water accumulation, resolve urban waterlogging, and has good anti-sliding performance, thus improving the safety of vehicles traveling on rainy days (Elvik and Greibe, 2005; Rungruangvirojn and kantipong, 2010; Donavan, 2011; Estakhri et al., 2012; Poulikakos et al., 2013). However, OGFC also has the disadvantage of low strength. When the asphalt binder between the aggregate particles breaks or the bond between the asphalt binder and aggregate particles is lost, pavement distress can result from loosening of the asphalt mixture. Moreover, the large gaps expose more binder to the air and increase the aging speed relative to that of the general dense-graded structure; thus OGFC has relatively low durability and a short service life (Allen Cooley et al., 2000; Alvarez et al., 2011; Apostolidis et al., 2020). To enhance the cohesiveness and improve the road performance of OGFC, fibers are usually added to the mixture to reinforce it (Lou et al., 2021). Punith and Veeraragavan. (2011) found that the OGFC mixture containing recycled polyethylene fiber had a higher resistance to permanent deformation, fatigue damage, and moisture sensitivity compared to the mixture without fiber. Using freeze-thaw splitting tests and economic analysis, Xu et al. (2020) found that optimized modifiers could improve the low-temperature performance and rutting resistance of the reactive elastomeric terpolymer modified asphalt mixture (RETM) to varying degrees; however, it had little effect on the economy of RETM.
In the parts of coastal regions with middle to high latitudes, rainfall is abundant in summer and thus, pavement structures are susceptible to water damage. Further, these areas are in the seasonal freezing zone; therefore, the pavement is susceptible to low-temperature cracking from the combined effects of freezing and swelling of snow, and traffic loads. At present, existing research is aimed at material selection and the structural design of OGFC in humid and rainy areas, whereas research on the damage characteristics of OGFC permeable asphalt mixture at low temperature is insufficient. The damage mechanism and characteristics of the material should be comprehensively considered when the permeable asphalt mixture is subject to seasonal freezing. At present, research on the damage mechanism of materials can be obtained using macro- and microanalysis experiments, such as image processing and industrial computed tomography (CT) scanning technology. An asphalt mixture was scanned after a freeze–thaw cycle using X-ray CT technology, the meso-characteristic parameters (porosity, connected porosity, number of voids, and average void diameter) were extracted, and the freeze-thaw evolution of its internal structure was quantified (Gong et al., 2018; Ji et al., 2019; Xu et al., 2021). The new and connected voids of the mixture after freeze-thaw were found to be the direct factors influencing the amount of damage to the mixture. Li et al. (2019a) obtained the internal microstructure of AC-13 using X-ray CT technology and simulated the critical crack stress in the process of freeze-thaw damage, considering that the critical crack stress weakened with an increase in freeze–thaw cycles. Lövqvist et al. (2021) established a comprehensive multi-scale model including water permeability, temperature, and mechanical properties to simulate the influence of freeze–thaw cycles, freezing time, etc. on the asphalt mixture structure. Tarefder et al. (2018) conducted fatigue and indirect tensile strength tests on asphalt mixtures after freeze–thaw cycles and found that the low-temperature crack resistance of the mixture decreased with an increase in freeze-thaw cycles. Using splitting tensile strength and indirect tensile stiffness modulus tests, Wang et al. (2018) found that a basalt fiber-reinforced asphalt mixture had good mechanical properties before and after freeze–thaw cycles. Guo et al. (2020) conducted indirect tensile (IDT) tests at low temperatures and found that the addition of fibers enhanced the ultimate tensile strain of the asphalt mixture and that the fiber type made an important contribution to the low-temperature ductility of the mixture. Li et al. (2019b) and Wei et al. (2021) simulated the two-dimensional structure of asphalt mixture by discrete element method and found that the numerical results of asphalt mixture were in good agreement with the indoor test results in terms of cracking distribution and statistical probability. Further, it was found that the acoustic emission (AE) parameters are relatively sensitive to the temperature-influenced deformation damage of asphalt mixtures and that the cumulative probabilities of AE ringing counts and microcrack counts obey the Weibull distribution (Wei et al., 2021).
Theoretical models can also be used to analyze damage characteristics. Kassem et al. (2019) developed a linear viscoelastic function model of an asphalt mixture based on the viscoelastic continuous damage model using complex modulus tests to characterize its damage characteristics. Zhang et al. (2019) combined the fatigue damage theory with viscoelastic mechanics to establish a viscoelastic damage constitutive model of an asphalt mixture under cyclic loading using the Burgers viscoelastic and modified Chaboche damage models. They also analyzed the damage development and fatigue life of the asphalt mixture using an indirect tensile fatigue test. Cherif et al. (2021) studied the complex modulus of recycled asphalt mixture and predicted the mechanical properties of a recycled asphalt mixture based on the generalized self-consistent scheme (GSCS). The predicted model concurred with the measured results. Kuchiishi et al. (2019) conducted dynamic modulus tests on a cold recycled asphalt mixture and analyzed its viscoelastic behavior by establishing a principal curve that played an important role in the construction and repair of the cold recycled asphalt pavement.
Several studies have been performed on the low-temperature cracking behavior of asphalt mixtures using fine-scale analysis methods such as CT scan, AE, and digital image correlation (DIC). The research has gradually gone from macro-level fracture to fine-scale crack sprouting. Moreover, research has been carried out on the viscoelastic properties of asphalt mixtures in characterizing their damage properties and fatigue life. However, to date, there is limited research on the viscoelastic model of asphalt mixtures after the freeze-thaw damage evolution, and the primary goal of related research on the composite modified OGFC mixture is to develop a reasonable freeze-thaw damage evolution model. In the road pavement field, asphalt mixtures are generally considered to be a typical viscoelastic material at normal temperature (Kumar and Veeraragavan, 2011); however, at low temperature, its performance becomes more elastic and the viscosity decreases (Taherkhania, 2011). The static bending creep test is a simple method to test the viscoelastic behavior of an asphalt mixture, while maintaining the applied stress and obtaining the strain as the response function changes with time (Jahangiri et al., 2021). Therefore, an appropriate viscoelastic constitutive equation can be selected to mathematically describe the viscoelastic behavior of an asphalt mixture at low temperature, and in conjunction with the freeze–thaw damage evolution model of the composite modified OGFC mixture, the freeze–thaw damage characteristics can be studied. Based on the fractional derivative Abel viscoelastic and Weibull distribution damage models, this study analyzes the mechanical behavior of a composite modified OGFC asphalt mixture under multiple freeze-thaw cycles to better understand its low-temperature failure characteristics and provide a reference for further application.
2 Theoretical research
Based on the fractional derivative Abel viscoelastic and Weibull distribution damage models, the optimization model is the Weibull fractional derivative freeze-thaw damage viscoelastic model, making it more suitable to describe the damage characteristics of a composite modified OGFC asphalt mixture under multiple freeze-thaw cycles.
2.1 Weibull fractional derivative viscoelastic model of freeze–thaw damage
A composite modified OGFC mixture deforms under the action of the freeze-thaw cycle, and internal micro-cracks develop and cause damage similar to that of cement concrete materials (Li et al., 2021). The Weibull distribution function can be used to describe the freeze-thaw damage behavior of a composite modified OGFC mixture if the composite modified OGFC mixture can meet the four basic hypotheses of the model:
Hypothesis 1: The composite modified OGFC mixture is considered a continuous homogeneous body. The size of the high-viscosity modifier and length of the chopped basalt fiber is smaller than those of the test specimen. After the mixture is mixed and molded, the high-viscosity modifier swells in the asphalt, and the basalt fibers are uniformly and disorderedly dispersed in all directions and positions of the specimen. The aggregate, mortar, and void sizes meet the requirements of a small and disorderly distribution. Macroscopically, the mixture specimen can be considered a statistical average of the performance of each component.
Hypothesis 2: All boundaries of a composite modified OGFC are subjected to the same freeze-thaw action, an equal damage gradient caused by freeze-thaw develops from all sides toward the interior of the asphalt mixture, and micro-element points with identical short distances from the interior of the asphalt mixture specimen all obey the same damage evolution law.
Hypothesis 3: Freeze-thaw damage of the mixture is caused by the gradual accumulation of internal damage with freeze–thaw cycles. The failure probability of each component in the mixture increases with the damage and is positively correlated to the number of freeze-thaw cycles. Therefore, the freeze-thaw damage of a composite modified OGFC mixture gradually increases with an increase in the number of cycles; this concurs with the Weibull distribution (Shi et al., 2021), and the function expression is:
where m is the shape factor, n is the material parameter, λ is the damage threshold parameter, and b is the number of freezing and thawing cycles.
Hypothesis 4: All points inside the asphalt mixture are affected by the same damage conditions, and the failure curves have the same shape and factor m.
According to the theory of damage mechanics, the damage factor (degree) is expressed by Eqn. 2. In this paper, the modulus ratio of mixture under multiple freeze-thaw cycles is calculated as EE_0^(-1) in Eqn. 2.
where D is the damage factor, E is the residual modulus of the material, and E_0 is the initial modulus of the material.
Assuming that the derivative of damage factor to number of freeze–thaw cycles is the Weibull distribution function:
The integral Eqn. 3 is used to obtain the relationship between the damage factor and number of freeze-thaw cycles:
Then, the following equation results:
2.2 Constitutive relationship of the fractional derivative viscoelastic model
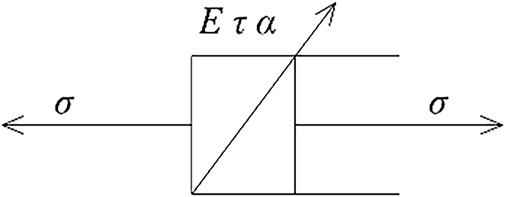
Because viscoelastic solid materials have complex constitutive relationships, they are easily influenced by temperature, loading, vibration frequencies, and other factors that change their mechanical properties (Kawada et al., 2013). Therefore, scholars in China and abroad have completed much exploration and research regarding the accuracy and applicability of the constitutive model relationship under different conditions. The constitutive relationship of viscoelastic materials can be divided into integral and differential types. These models mainly include the Maxwell, Kelvin, and Burgers models. These models are intuitive, easy to understand, and the physical meaning of the parameters is clear. However, to use an element model to accurately describe the mechanical behavior of complex viscoelastic materials, more elements need to be combined. A complex viscoelastic model will acquire more parameters after fitting, and is not easily applied in engineering practice (Xu and Jiang, 2017; Luo et al., 2020). Fractional derivative models are widely used because they have fewer determinable parameters, can more accurately describe the material stress–strain relationship, and can describe the mechanical properties of viscoelastic solid materials in a wide frequency range (Zhang et al., 2021). The Abel dashpot element with fractional derivative describing the viscoelastic behavior is shown in Figure 1.
The constitutive equation is as follows:
where α is the order of fractional derivative, E_∞ = Eτ^α, and τ = η⁄E. When α = 0, the element has degenerated into Hooke spring element. When α = 1, the element has degenerated into Newton’s dashpot element. When the order of fractional derivative ranges between 0 and 1, Eqn. 6 can characterize the mechanical properties of the asphalt mixture from the solid to the fluid state.
2.3 Damage factor of the fractional derivative viscoelastic model
A damage factor is introduced into the constitutive equation of the fractional derivative Abel dashpot element to obtain the Weibull fractional derivative freeze-thaw damage viscoelastic model, that is, Eqn. 5 is incorporated into Eqn. 6, and the damage model is obtained after simplifying the coefficient as follows:
where A is the viscosity coefficient, and γ is the order of fractional derivative.
3 Materials and methods
3.1 Raw material index
In this study, basalt fiber, a high-viscosity modifier, and LiaoHe 90# asphalt were used to prepare composite modified asphalt. Table 1 lists the basic indexes of the asphalt. Basalt fiber is produced by HaiNing AnJie Company, as shown in Figure 2, and its basic technical indexes are listed in Table 2. The high-viscosity modifier is domestic OLB-1, which is composed of a variety of polymers. Its appearance is light yellow with hemispherical translucent particles, as shown in Figure 3.
Basalt was used as the coarse aggregate, and composed of three ranges of graded materials, namely 9.5–13.2 mm, 4.75–9.5 mm, and 2.36–4.75 mm. The fine aggregate was alkaline-manufactured sand in the range of 0.075–2.36 mm. The mineral fines were made up of fine limestone.
3.2 Preparation of composite modified asphalt
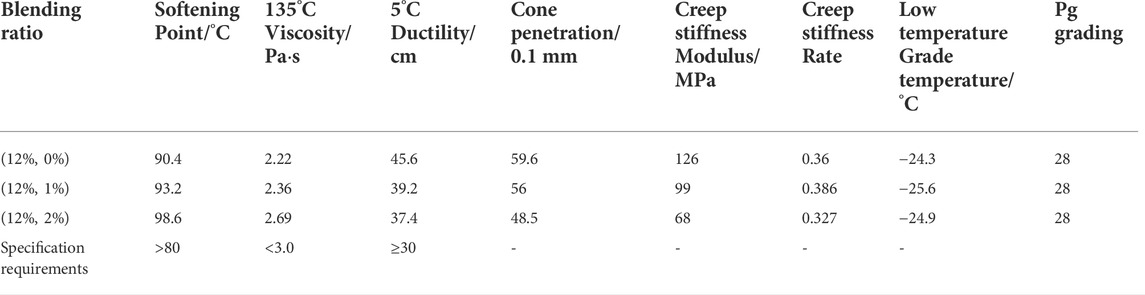
The composite modified asphalt was prepared by a high-speed shearing machine. The basalt fiber content was taken as the ratio of fiber mass to base asphalt mass, expressed by a mass fraction of 0%, 1%, or 2%. The high-viscosity modifier content is the ratio of modifier mass to matrix asphalt mass expressed as a mass fraction. The softening point, ductility, taper and shear strength tests of compound modified asphalt were performed at 0%, 4%, 8% and 12% doping ratios, and the test results are listed in Table 3. We therefore used a 12% doping ratio as it produced the best results. The technical indexes of the composite modified asphalt with different mixing ratios of the high-viscosity modifier and basalt fiber were tested, namely (12%, 0), (12%, 1%), and (12%, 2%), and the test results are listed in Table 4.
According to the softening point and 135°C viscosity data in Table 4, the three types of composite modified asphalt have good high-temperature performance. In addition, the low-temperature grade temperature determined according to 5°C ductility and bending beam rheometer (BBR) test data is lower than the daily average minimum temperature of cities in the seasonal frozen areas of northeast Liaoning Province, China. Therefore, all three types of composite modified asphalt can be used in the seasonal frozen areas of northeast Liaoning Province. The climatic conditions and performance grade (PG) low temperature classification in the northeast Liaoning Province are listed in Table 5.
3.3 OGFC gradation design and sample preparation
According to the technical specification for permeable asphalt pavement (CJJ/T190-2012, 2012) (Technical specification for permeable asphalt pavement, 2012), a range of gradation curve was determined and composite gradation curve was selected for the gradation studied in this paper, as shown in Figure 4. The optimum asphalt-aggregate ratio of the mixture was determined to be 5.1%. According to the standard test methods of asphalt and asphalt mixtures for highway engineering (JTG E20-2011, 2011) (Ministry of transport. Standard test methods of bitumen and bituminous mixtures for highway engineering, 2001), different mixing ratios of high-viscosity modifier and basalt fiber were adopted, namely (12%, 0), (12%, 1%), and (12%, 2%). The cutting size of the composite modified OGFC permeable asphalt mixture with the best asphalt-aggregate ratio of 5.1% was determined to be the cuboid trabeculae with a length of 250 mm, width of 30 mm, and height of 35 mm. The test sample is shown in Figure 5.
3.4 Determination of multiple freeze-thaw cycle methods
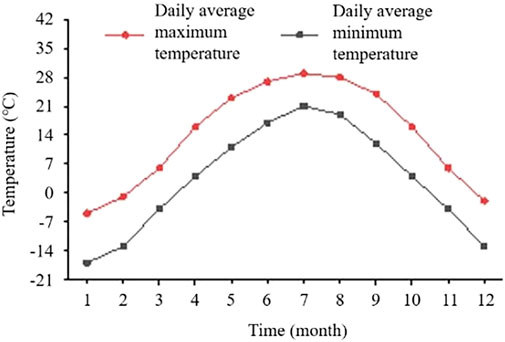
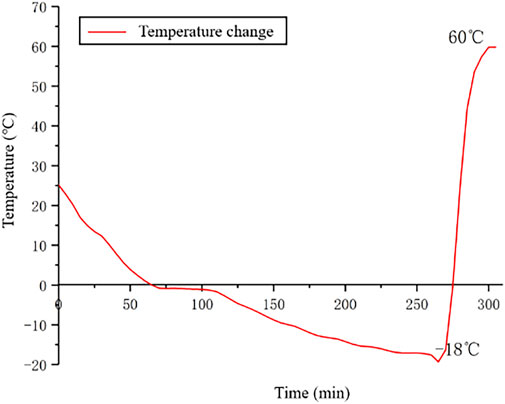
During the seasonal shift from winter to spring the seasonal frozen region of northeast Liaoning Province, the temperatures are usually higher than 0°C during the day and lower than 0°C at night. The pavement structures are often damaged by this freezing and thawing because the asphalt mixture is a viscoelastic material that is extremely sensitive to temperature. Therefore, the asphalt mortar is greatly influenced by temperature and water. The asphalt mixture may freeze and crack, leading to a decline in the performance of the mixture (Ud Din et al., 2020). For example, the daily minimum temperature in Shenyang between April and October is higher than 0°C. In contrast, the average daily maximum temperature in December, January, and February is lower than 0°C, thus the road structure is in a frozen state and less freezing and thawing occurs. In November and March, the daily average maximum temperature is higher than 0°C, whereas the daily average minimum temperature is lower than 0°C. During these 2 months, the pavement structure is repeatedly subjected to freeze-thaw cycles. The annual temperature distribution in Shenyang is shown in Figure 6. In this study, three groups of composite modified OGFC Marshall specimens were drilled in the center, and the temperature variation law of the specimens under freeze-thaw cycles was observed using a TORRIE temperature sensor. The results are shown in Figure 7.
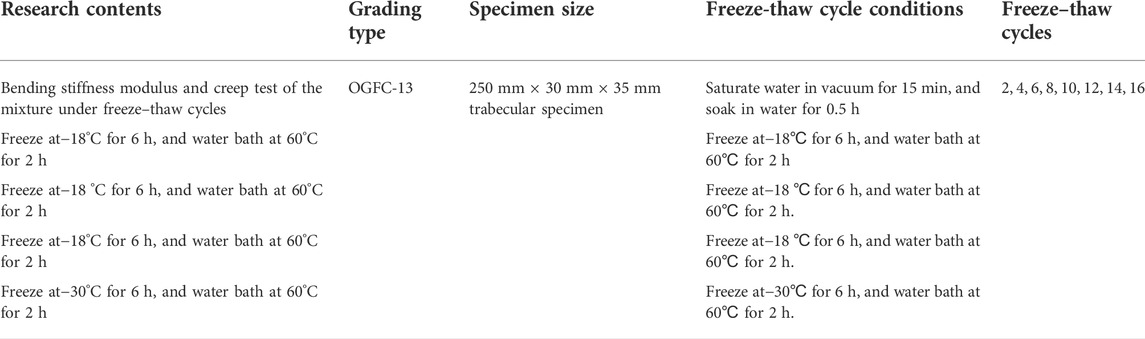
In this study, the freeze-thaw method used in the test was determined according to the analysis of the measured temperature change inside the freeze-thaw Marshall specimen and the city temperature in the northeast Liaoning Province. The specific method is listed in Table 6
4 Results
4.1 Low-temperature bending test and results of multiple freeze-thaw mixtures
In this study, the freeze-thaw cycle method in Table 6 was used to freeze–thaw the composite modified OGFC trabecular specimens with three different mixing ratios for 2, 4, 6, 8, 10, 12, 14, and 16 cycles. The first group of specimens was maintained at 20 ± 5°C, and the remaining specimens were subjected to freeze-thaw cycles. Thereafter, the specimens were placed into a 25°C water bath at a constant temperature for 2 h and then subjected to a low-temperature trabecula test. The SANS universal testing machine was used to conduct a three-point low temperature bending test on the composite modified OGFC rectangular beam specimen, which was placed in a low temperature chamber at (-10 ± 0.5) °C for 1.5 h before the test, and then the mechanical properties of the bending damage of the mixture were measured at the specified temperature of (-10 ± 0.5) °C at a loading rate of 50 mm/min. The test results are shown in Figure 8.
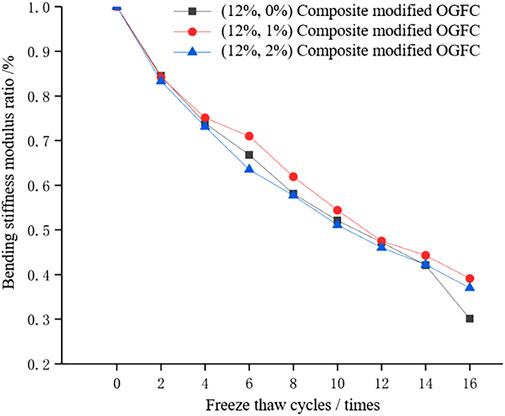
FIGURE 8. Variation diagram of trabecula stiffness modulus ratio of different blending ratio specimens.
Figure 8 shows that with an increase in the number of freeze-thaw cycles, the trabecula stiffness modulus of the composite modified OGFC with the mixing ratio of (12%, 0%) decreased the most, and dropped to approximately 30% after 16 freeze–thaw cycles. However, the trabecula stiffness modulus of the composite modified OGFC with the mixing ratio of (12%, 1%) and (12%, 2%) decreased to approximately 40%. This indicates that with the increase in number of freeze-thaw cycles, the basalt fiber provides more obvious resistance to trabecula and stretching.
4.2 Low-temperature bending creep test and results of multiple freeze-thaw mixtures
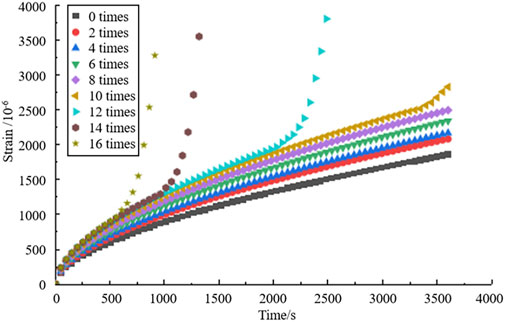
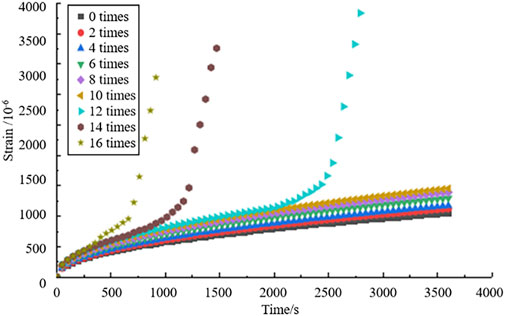
To analyze the low-temperature viscoelasticity of composite modified OGFC under freeze-thaw cycles, the failure load of composite modified OGFC specimens without freeze-thaw cycles with three mixing ratios was measured, and the creep stress level was determined. The bending test was conducted on the mixture at 0°C, and the failure loads of the small beams of the mixture determined for the mixing ratios of (12%, 0), (12%, 1%), and (12%, 2%) were 598, 632, and 614 N, respectively. Theoretically, the recommended load of the bending creep test of small beams is 0.1 times the failure stress [34]. Therefore, under the condition of 0°C, a load of 60 N and loading time of 3,600 s were selected to conduct the low-temperature bending creep test of the composite modified OGFC trabecula. The time-strain curves of the mixture after repeated freezing and thawing are shown in Figures 9–11.
Figures 9–11 show that when the freeze-thaw cycles of the mixture are less than 10, the three types of composite modified OGFC creep tests are still in the transition and stable periods within 3,600 s. When the freeze-thaw cycles reaches 12, 14, and 16, the three types of composite modified OGFC creep tests are all destroyed within 3,600 s. Comparing the strain changes of the three mixtures subject to freeze-thaw cycles, we found that when 2% basalt fiber was added, the strain increased minimally with the freeze–thaw cycles. However, when the basalt fiber content was 0%, the initial strain value was greater at 3,600 s, indicating that the addition of basalt fiber improves the low-temperature crack resistance of OGFC.
4.3 Model analysis
According to Eqn. 5, the modulus ratio data of the freeze-thaw bending stiffness in Figure 8 was fitted by MATLAB, in which the Weibull probability distribution has a nonlinear fitting and the data is logarithmic in the fitting process. Three types of modulus ratio performance attenuation models of the freeze-thaw bending stiffness of OGFC with mixed ratio were obtained:
The modulus ratio of freeze-thaw bending stiffness was taken as the damage factor of the attenuation model, and the fractional derivative Abel dashpot component constitutive equation was introduced to form three Weibull fractional derivative freeze-thaw damage viscoelastic models of OGFC with mixed ratios:
The original data in Figures 9–11 were substituted into Eqs. 11–13 to fit the creep data of three types of OGFC mixtures with mixed proportions using the Weibull fractional derivative freeze-thaw damage viscoelastic model. The fitting parameter results are listed in Table 7, and the fitting strain–time curves are shown in Figures 12–14.
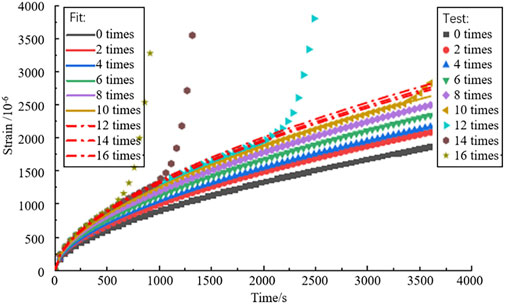
FIGURE 12. Creep fitting curve of composite modified OGFC freeze-thaw damage at mixing ratios of (12%,0%).
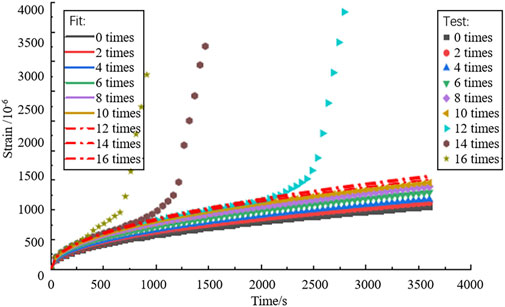
FIGURE 13. Creep fitting curve of composite modified OGFC freeze-thaw damage at mixing ratios of (12%,1%).
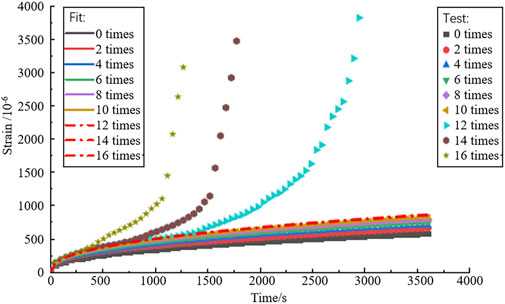
FIGURE 14. Creep fitting curve of composite modified OGFC freeze-thaw damage at mixing ratios of (12%,2%).
Figures 12–14 show that after 12, 14, and 16 freeze-thaw cycles, the three types of composite modified OGFC were all destroyed in the creep test within 3,600 s. During this process, the specimens first went through the viscoelastic migration and stability periods, then entered the plastic deformation stage, and were finally destroyed. In this study, the viscoelastic model was only suitable for describing the viscoelastic stage of the mixture and could not characterize the plastic deformation stage of the specimen. Therefore, when fitting the model, the creep data of the three types of composite modified OGFC with freeze–thaw cycles less than or equal to 10 were fitted. The fitting results of the Weibull fractional derivative freeze-thaw damage viscoelastic model are similar to the experimental results, and the fitting correlation is greater than 0.9, indicating that the model can characterize the low-temperature viscoelasticity of composite modified OGFC after freeze-thaw cycles. After substituting the creep data of 12, 14, and 16 freeze-thaw cycles into the model fitting, the fitting accuracy of the model was found to be poor, and the model lost its characterization function, further proving that the viscoelastic model is not applicable to the plastic deformation of an asphalt mixture.
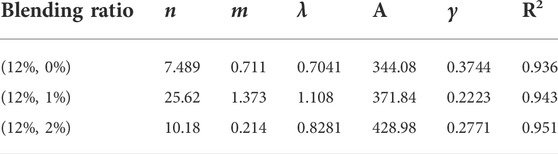
According to the analysis in Table 7, the viscosity coefficients of (12%, 0), (12%, 1%), and (12%, 2%) composite modified OGFC were 344.08, 371.84, and 428.98, respectively, and the fractional derivatives were 0.3744, 0.2223, and 0.2771, respectively. The viscosity coefficient increases with the increase in basalt fiber content, and the viscosity performance of the composite modified asphalt or asphalt binder also increased. Because the order of fractional derivative represents the creep rate of the mixture, the order of fractional derivative of (12%, 1%) composite modified OGFC model was 0.2223 at the minimum and the damage threshold was 1.108 at the maximum. This proves that the low-temperature crack resistance of (12%, 1%) composite modified OGFC was the best after the mixture was subjected to multiple freeze-thaw cycles.
5 Discussion
1) Adding an appropriate amount of basalt fiber can improve the water stability and low-temperature deformation resistance of an OGFC mixture. Basalt fiber can provide more obvious resistance to bending and stretching when the number of freeze-thaw cycles is increased.
2) Based on the Weibull distribution model, the modulus ratio of the freeze-thaw bending stiffness of composite modified OGFC mixture is nonlinearly fitted, and the performance attenuation models of the three types of mixed mixtures under freeze-thaw cycles are established.
3) Based on the fractional derivative Abel dashpot constitutive equation and freeze-thaw bending stiffness modulus ratio performance attenuation model, a Weibull fractional derivative freeze-thaw damage viscoelastic model suitable for composite modified OGFC mixture with less than 10 freeze-thaw cycles is established. The viscosity coefficient of 371.84, fractional derivative is 0.223, and low-temperature crack resistance of the (12%, 1%) composite modified OGFC show that it has the superior mixing ratio.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
LQ provided ideas and supervised the experiments. BY and JS conducted experiments and data analysis. LQ and CZ directed manuscript writing and checking. JS and CZ compiled the figures and tables in the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the General Project of Liaoning Provincial Department of Education (No. LJKZ1358).
Acknowledgments
This study was completed at the School of Civil Engineering in Shenyang Urban Construction Institute, Transportation Engineering College in Dalian Maritime University, and School of Transportation and Geomatics Engineering in Shenyang Jianzhu University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allen Cooley, L., Ray Brown, E., and Watson, D. E. (2000). Evaluation of open-graded friction course mixtures containing cellulose fibers. Transp. Res. Rec. 1723, 19–25. doi:10.3141/1723-03
Alvarez, A. E., Martin, A. E., and Estakhri, C. (2011). A review of mix design and evaluation research for permeable friction course mixtures. Constr. Build. Mat. 25, 1159–1166. doi:10.1016/j.conbuildmat.2010.09.038
Apostolidis, P., Liu, X., Erkens, S., and Scarpas, A. (2020). Use of epoxy asphalt as surfacing and tack coat material for roadway pavements. Constr. Build. Mat. 250, 118936. doi:10.1016/j.conbuildmat.2020.118936
Cherif, R., Eddhahak, A., Gabet, T., Hammoum, F., and Neji, J. (2021). Effect of the processing conditions on the viscoelastic properties of a high-RAP recycled asphalt mixture: Micromechanical and experimental approaches. Int. J. Pavement Eng. 22, 708–717. doi:10.1080/10298436.2019.1640363
CJJ/T190-2012 (2012). Technical specification for permeable asphalt pavement CJJ/T190-2012, 2012. Beijing: China Construction Industry Press.
Donavan, P. R. (2011). Tire noise generation and propagation over porous and nonporous asphalt pavements. Transp. Res. Rec. 2233, 135–144. doi:10.3141/2233-16
Elvik, R., and Greibe, P. (2005). Road safety effects of porous asphalt: A systematic review of evaluation studies. Accid. Analysis Prev. 37, 515–522. doi:10.1016/j.aap.2005.01.003
Estakhri, C., Scullion, T., and Hu, X. (2012). Design and performance evaluation of fine-graded permeable friction course. Transp. Res. Rec. 2293, 48–54. doi:10.3141/2293-06
Goetz, H. D. I., and Schoch, R. (1995). Reducing splash and spray of trucks and passenger cars. SAE Trans. 104, 950631–951172. doi:10.4271/950631
Gong, Y., Bi, H., Liang, C., and Wang, S. (2018). Microstructure analysis of modified asphalt mixtures under freeze-thaw cycles based on CT scanning technology. Appl. Sci. (Basel). 8, 2191. doi:10.3390/app8112191
Guo, Q., Wang, H., Gao, Y., Jiao, Y., Liu, F., and Dong, Z. (2020). Investigation of the low-temperature properties and cracking resistance of fiber-reinforced asphalt concrete using the DIC technique. Eng. Fract. Mech. 229, 106951. doi:10.1016/j.engfracmech.2020.106951
Jahangiri, B., Karimi, M. M., Giraldo-Londoño, O., and Buttlar, W. G. (2021). Characterization of viscoelastic properties of asphalt mixture at low temperatures using DC(T) creep test. Constr. Build. Mat. 298, 123731. doi:10.1016/j.conbuildmat.2021.123731
Ji, J., Yao, H., Yuan, Z., Suo, Z., Xu, Y., Li, P., et al. (2019). Moisture susceptibility of warm mix asphalt (WMA) with an organic wax additive based on X-ray computed tomography (CT) technology. Adv. Civ. Eng. 2019, 1–12. doi:10.1155/2019/7101982
JTG E20-2011 (2011). Standard test methods of bitumen and bituminous mixtures for highway engineering JTG E20-2011. Beijing: Chinese Communications Press.
Kassem, H., Chehab, G., and Najjar, S. (2019). Development of probabilistic viscoelastic continuum damage model for asphalt concrete. Transp. Res. Rec. 2673, 285–298. doi:10.1177/0361198119838980
Kawada, Y., Yajima, T., Nagahama, H., Czechowski, Z., and Białecki, M. (2013). Fractional-order derivative and time-dependent viscoelastic behaviour of rocks and minerals. Acta Geophys. 61, 1690–1702. doi:10.2478/s11600-013-0153-x
Kuchiishi, A. K., Santos Antão, C. C. D., Vasconcelos, K., and Bernucci, L. L. B. (2019). Influence of viscoelastic properties of cold recycled asphalt mixtures on pavement response by means of temperature instrumentation. Road Mater. Pavement Des. 20, S710–S724. doi:10.1080/14680629.2019.1633781
Kumar, S. A., and Veeraragavan, A. (2011). Dynamic mechanical characterization of asphalt concrete mixes with modified asphalt binders. Mater. Sci. Eng. A 528, 6445–6454. doi:10.1016/j.msea.2011.05.008
Li, H., Zhang, Y., and Guo, H. (2021). Numerical simulation of the effect of freeze–thaw cycles on the durability of concrete in a salt frost environment. Coatings (Basel) 11, 1198. doi:10.3390/coatings11101198
Li, J., Wang, F., Yi, F., Ma, J., and Lin, Z. (2019a). Fractal analysis of the fracture evolution of freeze-thaw damage to asphalt concrete. Mater. (Basel) 12, 88. doi:10.3390/ma12142288
Li, J., Zhang, J., Qian, G., Zheng, J., and Zhang, Y. (2019b). Three-dimensional simulation of aggregate and asphalt mixture using parameterized shape and size gradation. J. Mat. Civ. Eng. 31 (3), 04019004. doi:10.1061/(asce)mt.1943-5533.0002623
Lou, K., Xiao, P., Kang, A., Wu, Z., Li, B., and Lu, P. (2021). Performance evaluation and adaptability optimization of hot mix asphalt reinforced by mixed lengths basalt fibers. Constr. Build. Mat. 292, 123373. doi:10.1016/j.conbuildmat.2021.123373
Lövqvist, L., Balieu, R., and Kringos, N. (2021). A micromechanical model of freeze-thaw damage in asphalt mixtures. Int. J. Pavement Eng. 22, 1017–1029. doi:10.1080/10298436.2019.1656808
Luo, W., Li, B., Zhang, Y., Yin, B., and Dai, J. (2020). A creep model of asphalt mixture based on variable order fractional derivative. Appl. Sci. (Basel). 10, 3862. doi:10.3390/app10113862
Meiarashi, S., Ishida, M., Fujiwara, T., Hasebe, M., and Nakatsuji, T. (1996). Noise reduction characteristics of porous elastic road surfaces. Appl. Acoust. 47, 239–250. doi:10.1016/0003-682x(95)00050-j
Poulikakos, L. D., Sedighi Gilani, M., Derome, D., Jerjen, I., and Vontobel, P. (2013). Time resolved analysis of water drainage in porous asphalt concrete using neutron radiography. Appl. Radiat. Isot. 77, 5–13. doi:10.1016/j.apradiso.2013.01.040
Punith, V. S., and Veeraragavan, A. (2011). Characterization of OGFC mixtures containing reclaimed polyethylene fibers. J. Mat. Civ. Eng. 23, 335–341. doi:10.1061/(asce)mt.1943-5533.0000162
Rungruangvirojn, P., and Kanitpong, K. (2010). Measurement of visibility loss due to splash and spray: Porous, SMA and conventional asphalt pavements. Int. J. Pavement Eng. 11, 499–510. doi:10.1080/10298430903578945
Shi, L., Liu, Y., Meng, X., Zhang, H., and Dede, T. (2021). Study on mechanical properties and damage characteristics of red sandstone under freeze-thaw and load. Adv. Civ. Eng. 2021, 1–13. doi:10.1155/2021/8867489
Taherkhania, H. (2011). Compressive creep behaviour of asphalt mixtures. Procedia Eng. 10, 583–588. doi:10.1016/j.proeng.2011.04.097
Tarefder, R., Faisal, H., and Barlas, G. (2018). Freeze-thaw effects on fatigue LIFE of hot mix asphalt and creep stiffness of asphalt binder. Cold Reg. Sci. Technol. 153, 197–204. doi:10.1016/j.coldregions.2018.02.011
Ud Din, I. M., Mir, M. S., and Farooq, M. A. (2020). Effect of freeze-thaw cycles on the properties of asphalt pavements in cold regions: A review. Transp. Res. Procedia 48, 3634–3641. doi:10.1016/j.trpro.2020.08.087
Wang, W., Cheng, Y., Ma, G., Tan, G., Sun, X., and Yang, S. (2018). Further investigation on damage model of eco-friendly basalt fiber modified asphalt mixture under freeze-thaw cycles. Appl. Sci. (Basel). 9, 60. doi:10.3390/app9010060
Wei, H., Li, J., Wang, F., Zheng, J., Tao, Y., and Zhang, Y. (2021). Numerical investigation on fracture evolution of asphalt mixture compared with acoustic emission. Int. J. Pavement Eng. 23, 3481–3491. doi:10.1080/10298436.2021.1902524
Xu, C., Zhang, Z., and Liu, F. (2020). Improving the low-temperature performance of RET modified asphalt mixture with different modifiers. Coatings (Basel) 10, 1070. doi:10.3390/coatings10111070
Xu, G., Chen, X., Cai, X., Yu, Y., and Yang, J. (2021). Characterization of three-dimensional internal structure evolution in asphalt mixtures during freeze–thaw cycles. Appl. Sci. (Basel). 11, 4316. doi:10.3390/app11094316
Xu, H., and Jiang, X. (2017). Creep constitutive models for viscoelastic materials based on fractional derivatives. Comput. Math. Appl. 73, 1377–1384. doi:10.1016/j.camwa.2016.05.002
Zhang, J., Li, Z., Chu, H., and Lu, J. (2019). A viscoelastic damage constitutive model for asphalt mixture under the cyclic loading. Constr. Build. Mat. 227, 116631. doi:10.1016/j.conbuildmat.2019.08.012
Keywords: freeze-thaw damage, viscoelasticity, fractional derivative, composite modification, OGFC, mixing ratio
Citation: Qi L, Yu B, Song J and Zhang C (2022) Freeze–Thaw damage characteristics of composite modified open graded friction course. Front. Mater. 9:1040349. doi: 10.3389/fmats.2022.1040349
Received: 12 September 2022; Accepted: 04 October 2022;
Published: 13 October 2022.
Edited by:
Jian Ouyang, Dalian University of Technology, ChinaReviewed by:
Jue Li, Chongqing Jiaotong University, ChinaDi Wang, Technische Universitat Braunschweig, Germany
Copyright © 2022 Qi, Yu, Song and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Baoyang Yu, Ynl5dUBzanp1LmVkdS5jbg==
 Lin Qi1
Lin Qi1 Baoyang Yu
Baoyang Yu