- 1State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang, China
- 2School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang, China
- 3Department of Engineering Mechanics, Shijiazhuang Tiedao University, Shijiazhuang, China
We study the propagation of bending waves along the free edge of a semi-infinite piezoelectric plate within the framework of two-variable refined plate theory (TVPT, a high-order plate theory), Reissner-Mindlin refined plate theory (RMPT, a first-order plate theory), and the classical plate theory (CPT). The piezoelectric plate has macroscopic symmetry of orthogonal mm2 The governing equations are derived using Hamilton principle. The dispersion relations for electrically open and shorted boundary conditions at the free edge are obtained analytically. The difference in dispersion property between the three plate theories is analyzed. The numerical results show that the dispersion curves predicted by TVPT and RMPT are similar and have small difference over the complete frequency range, which means both the two theories are valid for the analysis of edge waves in a piezoelectric plate. But the wave velocity calculated by CPT is much larger than the two theories above and is no longer valid for high frequency and thick plate. The electrical boundary condition at the free edge has an insignificant effect on phase velocity and group velocity which can be ignored for the analysis of edge waves in a piezoelectric plate governed by bending deformation. The velocity of bending edge waves in a semi-infinite piezoelectric plate is positively related to that of Rayleigh surface wave in a traction-free piezoelectric half-space. The edge wave velocity can be enhanced when the piezoelectric plate is considered as one with weaker anisotropy.
Introduction
Edge waves, which propagate along the edge of a thin plate and decay transversely with distance from the edge, have attracted much attention in the past 60 years since the existence of a flexural wave guided by the free edge of a semi-infinite isotropic elastic thin plate was reported by Konenkov (1960). Edge waves have great potential for the applications in the measurement of material properties and non-destructive evaluation of thin elastic structures, such as aircraft wings, submarine hulls, rotor blades, and so on (Lawrie and Kaplunov, 2012). In view of these important application, the existence and propagation of edge waves in various elastic thin plates, such as transversely isotropic plates (Piliposian et al., 2010), orthotropic plates (Norris, 1994; Thompson et al., 2002), cubic symmetric materials (Belubekyan and Engibaryan, 1996), anisotropic materials (Fu, 2003), and laminated plates (Liu et al., 1991; Zakharov and Becker, 2003; Fu and Brookes, 2006; Lu et al., 2007), have been well studied. Lawrie and Kaplunov (2012) gave a periodic overview of edge waves and resonance on elastic structures before the 2010s. Most of the above results were derived using Kirchhoff plate theory. It was demonstrated that the edge waves in elastic thin plate were also theoretically predicted by Mindlin plate theory including shear deformation and rotatory inertia (Norris et al., 1998) and Ambartsumian refined plate theory considering high-order shear deformation (Piliposian and Ghazaryan, 2011). The former was proved to be in agreement with experimental and finite element results (Lagasse and Oliner, 1976; Norris et al., 1998). It was shown that the velocity of edge waves predicted by Kirchhoff plate theory, which is valid only for very low frequency, is much larger than the results of experiment and finite element.
Piezoelectric materials are widely used to develop electro-mechanical transducers for converting mechanical energy to electric energy or vice versa, and acoustic wave devices for frequency operation and sensing. The subject of elastic wave propagation in various piezoelectric materials and structures has received increasing attention from the mechanics community in the last few decades. Recent results mainly include surface waves in piezoelectric half-space (Collet and Destrade, 2004; Collet and Destrade, 2005), elastic half-space covered by piezoelectric layer (Nie et al., 2020a; Zhang et al., 2022) or the reverse configuration (Liu and He, 2010; Huang et al., 2014), interface waves in piezoelectric bi-material (Yang and Yang, 2009; Otero et al., 2012), guided waves in piezoelectric plate (Zhang et al., 2012; Nie et al., 2020b), and multilayered plate (Gao and Zhang, 2020; Xia et al., 2021), functionally graded piezoelectric material (Liu et al., 2021; Lakshman, 2022) and so on. So far, most of the available results on elastic wave in piezoelectric materials and structures are for the infinite media extended in one or two dimensions. It is known that the vibration energy carried by edge waves can be confined to the edge region of the plate and decays rapidly with distance from the edge which means that there will be very little motion away from the active edge. This property has unique advantage in fixing and support of acoustic wave device compared to that of bulk wave and surface wave, since devices can be mounted to supporting structures at the side very close to the active edge without affecting the device performance. From this, the edge waves have great promise for achieving the miniaturisation of acoustic wave devices which is exactly demand for the future development of micro-electro-mechanical systems (MEMS). Compared with elastic waves propagation in the infinite piezoelectric materials, which have been widely studied and also have been used in many engineering fields, the results related to edge waves in the thin piezoelectric plates are still limited, and some interesting properties are waiting to be further revealed. Recently, Piliposian and Ghazaryan (2011) studied the existence and propagation of bending waves localized at the free edge of a piezoelectric plate within the framework of Ambartsumian refined plate theory. The condition for existence of a localized bending wave was given. Nie et al. (2021) investigated bending waves propagation along the free edge of a semi-infinite piezoelectric plate perfectly bonded with a metal strip plate using the first-order Reissner-Mindlin refined plate theory. The propagation of bending wave with multi-mode was shown. Piezoelectric plates considered in (Piliposian and Ghazaryan, 2011) and (Nie et al., 2021) are both assumed as the transversely isotropic media. In this paper, we study the propagation of bending waves localized along the free edge of a semi-infinite piezoelectric plate of orthogonal symmetry using two-variable refined plate theory (TVPT, a high-order shear deformation theory), Reissner-Mindlin refined plate theory (RMPT, a first-order shear deformation theory), and the classical plate theory (CPT). Our aim is to examine the difference in dispersion property between the three plate theories and to reveal the effects of electrical boundary applied on the free edge and material property on wave propagation. To the best of our knowledge, the propagation of edge waves in an orthogonal piezoelectric plate has not been previously studied and also has not been analyzed in the context of TVPT.
Problem formulation and plate theories
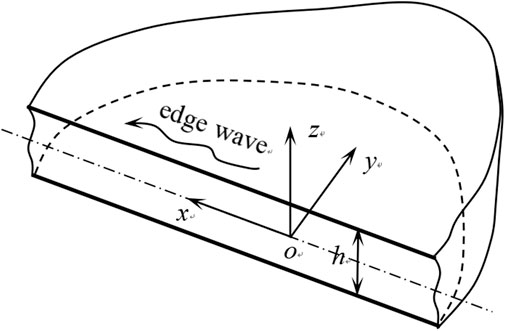
A semi-infinite piezoelectric plate of thickness h is shown in Figure 1. The plate (
where cij, κij and eij (i, j = 1–6) are the elastic constants, dielectric and piezoelectric constants; σkl, εkl, Ek, and Dk (k, l = x, y, and z) are the stress, strain, electric field and electric displacement, respectively. The non-trivial strain-displacement and electric field-potential relations are as follows
where u, v, and w are the mechanical displacement components along the x-axis, y-axis and z-axis; φ is the electric potential.
Two-variable refined plate theory
According to the TVPT (Shimpi, 2002; Shimpi and Patel, 2006), the transversal displacement w, which is independent of z, can be expressed as a combination of the bending component and the shear component, i.e.,
where wb and ws denote the bending component and shear component of transversal displacement w, respectively.
Also, the in-plane displacements u and v consisting of bending and shear components are
where ub and vb represent the bending components of in-plane displacement u and v; us, and vs are the shear components of u and v, respectively.
Assuming that the bending components of in-plane displacement ub and vb play the same roles as u and v in CPT, gives
The shear components of in-plane displacement are considered as the following functions
where f (z) signifies the generalized shape function describing the transverse shear deformation and stress distribution through the thickness of the piezoelectric plate. In this two-variable refined plate theory (Shimpi, 2002; Shimpi and Patel, 2006), we assume.
The mechanical displacements can be rewritten as
The non-zero strains are
First-order Reissner-Mindlin refined plate theory
According to the RMPT (Reissner, 1945; Mindlin, 1951), the transversal displacement only includes a bending component and is also independent of z. The shear components of in-plane displacement vary linearly through the plate thickness. From this, the displacement fields for RMPT can be obtained by letting the shape function be linear, i.e., f(z) = z in Eq. 9, which gives
where w (x,y,t) = wb (x,y,t) is the transversal displacement of middle plane of the plate. ϑx (x,y,t) and ϑy (x,y,t) are unknown functions defining transversal shears. The non-zero strains are reduced to
Classical plate theory
Neglect of the transversal shears, i.e., ϑx (x,y,t) = ϑy (x,y,t) = 0 in Eq. 12, we obtain displacement fields for the CPT
The non-zero strains can be further reduced to
For the above three plate theories, the distribution of the electric potential φ in the piezoelectric plate should satisfy the Maxwell equation which is approximately assumed as a combination of a half-cosine and linear variation (Quek and Wang, 2000; Ke et al., 2014)
where β = π/h.
Using Eq. 3, the electric fields can be written as
Derivation of governing equations
Two-variable refined plate theory
The strain energy Πu of the piezoelectric plate is given by
where A denotes the domain occupied by the mid-plane of piezoelectric plate. Substituting Eqs 10, 16 into Eq. 17 yields
where the bending moments Mx1, Mx2, My1 and My2, the twisting moments Mxy1 and Mxy2, the shearing forces Qx and Qy, are respectively defined by
The kinetic energy Πk of the piezoelectric plate is calculated by
The work done by external force Πw is
where
The governing equations can be derived by Hamilton principle
Substituting Eqs 18, 20, 21 into the above equation, letting the coefficients of
First-order Reissner-Mindlin refined plate theory
Using Hamilton principle and taking account of Eqs 12, 16, the governing equations for the RMPT can be obtained as
where the bending moments Mx and My, the twisting moment Mxy, the shearing forces Qx and Qy, are respectively defined by
Classical plate theory
The governing equations for CPT are
where the bending moments Mx, My, and the twisting moment Mxy are
Solution of the localized bending waves
Two-variable refined plate theory
For bending wave propagating along x-direction we seek the general solution satisfying the governing Eq. 23 in the form
where
where η = kh is the non-dimensional wavenumber. Eq. 29 is a system of linear homogeneous equations with respect to the unknown amplitudes A, B and D. A non-trivial solution requires that the determinant of coefficient matrix of Eq. 29 vanishes which obtains a 10-order equation in undetermined parameter b. There are ten roots of b representing the propagation direction of the ten partial waves, respectively. In order to satisfy the attenuation condition that the displacements and electric potential should vanish as
where
At the free edge y = 0, the bending moments and twisting moments should be zero, i.e., My1 = My2 = Mxy1 = Mxy2 = 0. We further consider two types of electrical boundary conditions at the edge y = 0, i.e.,
The elements of matrix T for electrically shorted case are the same except for
First-order Reissner-Mindlin refined plate theory
We consider the following solution satisfying the governing Eq. 24
where A, B, D and F are unknown amplitudes. Substituting Eq. 32 into Eq. 24 obtains
Equation 33 is a system of linear homogeneous equations with respect to the unknown amplitudes A, B, D, and F. A non-trivial solution requires that the determinant of coefficient matrix vanishes which obtains an 8-order equation in b. To satisfy the attenuation condition, only the four negative roots denoted by bn (n = 1–4) are remained. The general solution can be written as
where
At the free edge y = 0, the bending moment, twisting moment and shear force should be zero, i.e., My = Mxy = Qy = 0. The electrical boundary conditions at the free edge are the same as the case of TVPT. Using the general solution Eq. 34 and the corresponding boundary conditions, a system of 4-order linear homogeneous equations with unknown amplitudes An can be obtained, i.e.,
The elements of matrix T for electrically shorted case are the same except for
Classical plate theory
We consider the following solution of Eq. 26
where K and J are unknown amplitudes. Substituting Eq. 36 into Eq. 26 obtains
Equation 37 is a system of linear homogeneous equations with respect to the unknown amplitudes K and J. A non-trivial solution requires that the determinant of coefficient matrix vanishes which yields a 6-order equation in b. To satisfy the attenuation condition, we only take the three negative roots denoted by bj (j = 1–3). Eq. 36 is rewritten as
where βj is the amplitude ratio given by
At the edge y = 0, the traction-free criterion requires My = Mxy = 0. Based on the general solution Eq. 38 and the corresponding boundary conditions, a system of 3-order linear homogeneous equations with constants Aj can be obtained, i.e.,
The elements of matrix T for electrically shorted case are the same except for
When the determinant of the matrix T carried out within the framework of TVPT, RMPT and CPT vanishes, we obtain the dispersion relations for localized bending waves propagating in the semi-infinite piezoelectric plate.
Numerical results and discussions
In this section, we give some numerical results to demonstrate the dispersion property of localized bending waves propagating along the free edge of an orthogonal piezoelectric plate. The piezoelectric plate is considered as PZN-0.07PT with material constants listed in Table 1 (Zhang et al., 2002).
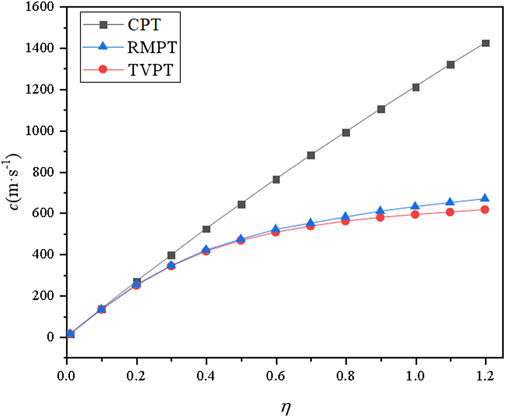
Based on the dispersion relations derived using TVPT, RMPT and CPT, we calculate the dispersion curves of localized bending waves for the three plate theories shown in Figure 2, where boundary condition at the free edge is imposed as electrically open case, the external electric voltage
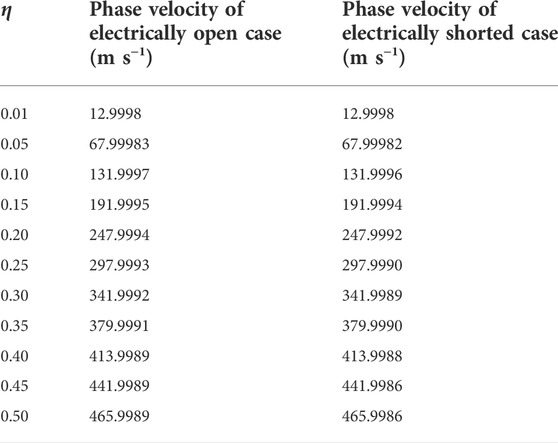
Based on the dispersion relations derived by TVPT, we calculate the phase velocity and group velocity of localized bending waves for electrically open case and shorted case listed in Tables 2, 3, respectively. The group velocity cg is calculated through cg = c + kdc/dk. It is observed that the phase velocity and group velocity of electrically open case are slightly larger than that of electrically shorted case. In view of the unnoticeable differences in phase velocity and group velocity between the two electrical boundary conditions, one can ignore the effect of electrical boundary imposed at the free edge when propagation of localized edge waves in a piezoelectric plate is considered. The acceptable results can be obtained through either electrically open boundary condition or electrically shorted boundary condition.
Figure 3 shows the effect of external electric voltage
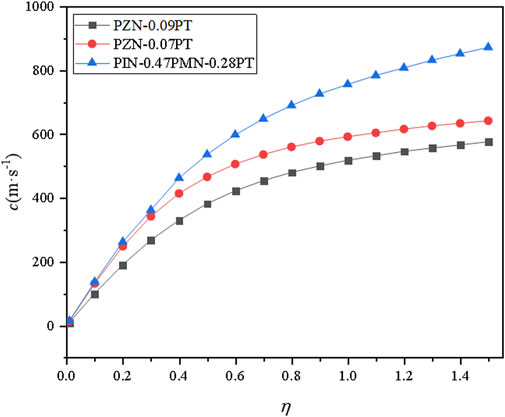
To demonstrate the effect of material property on dispersion curve of localized bending waves we calculate the wave velocities for three different piezoelectric materials all with symmetry of orthogonal mm2, i.e., PZN-0.07PT, PZN-0.09PT and PIN-0.47PMN-0.28PT. The used material constants are found in Table 1 (Zhang et al., 2002; He et al., 2011; Zhang et al., 2011). Figure 4 shows the dispersion curves of the above three piezoelectric plates for electrically shorted case at the free edge, where
To reveal the effect of anisotropy on dispersion property of bending edge waves, comparison of dispersion characteristics for orthogonal piezoelectric plate (class mm2) and for transverse isotropic piezoelectric plate (class 6 mm) in the context of TVPT, is shown in Figure 5. The materials parameters used in this calculation are taken as follows: PZN-0.07PT is used as the mm2 piezoelectric plate whose material constants is found in Table 1; the 6 mm piezoelectric plate is reduced by assuming c22 = c11 = 18 Nm−2 × 1010 Nm−2, c23 = c13 = 15 Nm−2 × 1010 Nm−2, c55 = c44 = 0.34 Nm−2 × 1010 Nm−2, e24 = e15 = 3.24 cm−2, e32 = e31 = –17.44 cm−2, and κ22 = κ11 = 1847κ0 from the PZN-0.07PT. It is shown from Figure 5 that the edge wave velocity of the 6 mm piezoelectric plate is higher than the mm2 piezoelectric plate, for a fixed non-dimensional wavenumber η. It means that the wave velocity of bending edge wave increases when the piezoelectric plate is considered as a weaker anisotropic medium.
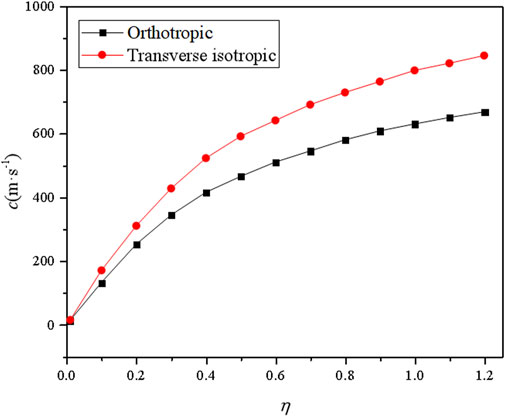
FIGURE 5. Comparison of the dispersion characteristics of bending edge waves in mm2 piezoelectric plate and 6 mm piezoelectric plate under TVPT.
Conclusion
Propagation of localized bending waves along the free edge of a semi-infinite piezoelectric plate of orthogonal mm2 is studied using TVPT, RMPT, and CPT. The dispersion relations for electrically open and shorted cases at the free edge are obtained analytically. The difference in wave velocity between the three plate theories is analyzed. The effects of electrical boundary condition at the edge, material property as well as the external electric voltage on dispersion characteristic are discussed through some numerical examples. It is found that the wave velocity calculated by TVPT and RMPT are very close over the complete frequency range, which means both the two theories are valid for the analysis of edge waves in a piezoelectric plate. But CPT result, which shows a significant difference in wave velocity comparing with that of TVPT and RMPT, is unacceptable for high frequency and thick plate. The electrically boundary condition at the free edge of the semi-infinite piezoelectric plate has an insignificant effect on phase velocity and group velocity. Either electrically open boundary or electrically shorted boundary can produce an acceptable result. The velocity of bending edge waves in a piezoelectric plate is positively related to that of Rayleigh surface wave in a traction-free piezoelectric half-space. A large velocity of Rayleigh surface wave results in a large velocity of bending wave propagating along the edge of a semi-infinite piezoelectric plate. The edge wave velocity is enhanced when the piezoelectric plate is considered as a weaker anisotropic medium.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
GN: Conceptualization, methodology, formal analysis, writing-original draft. ZL: software, visualization. JL: conceptualization, writing-review and editing. LZ: methodology, writing-review and editing.
Funding
This study is supported by the National Natural Science Foundation of China (Nos. 11872041 and 11802185), the Natural Science Foundation of Hebei Province of China (No. A2019210203) and the Top-notch Young Talent Program of Hebei Province Education Department of China (No. BJK2022055).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Appendix A
The expressions of Am, Bm and Dm related to the amplitude ratios αm and βm are given by
Appendix B
The expressions of An, Bn, Dn and Fn related to the amplitude ratios αn, βn and χn are given by
References
Belubekyan, M. V., and Engibaryan, A. I. (1996). Waves localized along the free edge of a plate with cubic symmetry. Mech. Solids [MTT] 31 (6), 117.
Collet, B., and Destrade, M. (2005). Explicit secular equations for piezoacoustic surface waves: Rayleigh modes. J. Appl. Phys. 98, 054903. doi:10.1063/1.2031948
Collet, B., and Destrade, M. (2004). Explicit secular equations for piezoacoustic surface waves: Shear-horizontal modes. J. Acoust. Soc. Am. 116 (6), 3432–3442. doi:10.1121/1.1819503
Fu, Y. B., and Brookes, D. W. (2006). Edge waves in asymmetrically laminated plates. J. Mech. Phys. Solids 54 (1), 1–21. doi:10.1016/j.jmps.2005.08.007
Fu, Y. B. (2003). Existence and uniqueness of edge waves in a generally anisotropic elastic plate. Q. J. Mech. Appl. Math. 56 (4), 605–616. doi:10.1093/qjmam/56.4.605
Gao, Q., and Zhang, Y. H. (2020). An accurate method for guided wave propagation in multilayered anisotropic piezoelectric structures. Acta Mech. 231, 1783–1804. doi:10.1007/s00707-020-02619-5
He, C. J., Jing, W. P., and Wang, F. F. (2011). Full tensorial elastic, piezoelectric, and dielectric properties characterization of [011]-poled PZN-9%PT single crystal. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 (6), 1127–1130. doi:10.1109/tuffc.2011.1921
Huang, N. X., Lu, T. Q., Zhang, R., Wang, Y. L., and Cao, W. W. (2014). Guided wave propagation in a gold electrode film on a Pb(Mg1/3Nb2/3)O3-33%PbTiO3 ferroelectric single crystal substrate. Chin. Phys. Lett. 31 (10), 104302. doi:10.1088/0256-307x/31/10/104302
Ke, L. L., Wang, Y. S., Yang, J., and Kitipornchai, S. (2014). Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech. Sin. 30, 516–525. doi:10.1007/s10409-014-0072-3
Lagasse, P. E., and Oliner, A. A. (1976). Acoustic flexural mode on a ridge of semi-infinite height. Electron. Lett. 12 (1), 11–13. doi:10.1049/el:19760009
Lakshman, A. (2022). Propagation characteristic of Love-type wave in different types of functionally graded piezoelectric layered structure. Waves Random Complex Media 32 (3), 1424–1446. doi:10.1080/17455030.2020.1822562
Lawrie, J. B., and Kaplunov, J. (2012). Edge waves and resonance on elastic structures: An overview. Math. Mech. Solids 17 (1), 4–16. doi:10.1177/1081286511412281
Liu, C. C., Yu, J. G., Zhang, B., Zhang, X., and Elmaimouni, L. (2021). Analysis of Lamb wave propagation in a functionally graded piezoelectric small-scale plate based on the modified couple stress theory. Compos. Struct. 265, 113733. doi:10.1016/j.compstruct.2021.113733
Liu, G. R., Tani, J., Ohyoshi, T., and Watanabe, K. (1991). Characteristics of surface wave propagation along the edge of an anisotropic laminated semi-infinite plate. Wave Motion 13 (3), 243–251. doi:10.1016/0165-2125(91)90061-r
Liu, J. S., and He, S. T. (2010). Properties of Love waves in layered piezoelectric structures. Int. J. Solids Struct. 47 (2), 169–174. doi:10.1016/j.ijsolstr.2009.06.018
Lu, P., Chen, H. B., Lee, H. P., and Lu, C. (2007). Further studies on edge waves in anisotropic elastic plates. Int. J. Solids Struct. 44 (7-8), 2192–2208. doi:10.1016/j.ijsolstr.2006.07.005
Mindlin, R. D. (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 18, 31–38. doi:10.1115/1.4010217
Nie, G. Q., Dai, B., Liu, J. X., and Zhang, L. (2021). Bending waves in a semi-infinite piezoelectric plate with edge coated by a metal strip plate. Wave Motion 103 (4), 102731. doi:10.1016/j.wavemoti.2021.102731
Nie, G. Q., Zhang, K. K., and Liu, J. X. (2020). Love-type wave in PMN-PT single crystal layered structures with periodic undulations. Int. J. Acoust. Vib. 25 (2), 173–182. doi:10.20855/ijav.2020.25.21544
Nie, G. Q., Zhang, K. K., Liu, J. X., and Zhang, L. (2020). Effect of periodic corrugation on Lamb wave propagation in PMN-PT single crystal bilayer plates. Ultrasonics 108, 106176. doi:10.1016/j.ultras.2020.106176
Norris, A. N. (1994). Flexural edge waves. J. Sound Vib. 171 (4), 571–573. doi:10.1006/jsvi.1994.1141
Norris, A. N., Krylov, V. V., and Abrahams, I. D. (1998). Flexural edge waves and Comments on “A new bending wave solution for the classical plate equation” [J. Acoust. Soc. Am.104, 2220–2222 (1998)]. J. Acoust. Soc. Am.The J. Acoust. Soc. Am. 104107 (3), 22201781–22221784. doi:10.1121/1.428457
Otero, J. A., Ramos, R. R., Castillero, J. B., and Monsivais, G. (2012). Interfacial waves between two piezoelectric half-spaces with electro-mechanical imperfect interface. Philos. Mag. Lett. 92 (10), 534–540. doi:10.1080/09500839.2012.698758
Piliposian, G. T., Belubekyan, M. V., and Ghazaryan, K. B. (2010). Localized bending waves in a transversely isotropic plate. J. Sound Vib. 329 (17), 3596–3605. doi:10.1016/j.jsv.2010.03.019
Piliposian, G. T., and Ghazaryan, K. B. (2011). Localized bending vibrations of piezoelectric plates. Waves Random Complex Media 23 (3), 418–433. doi:10.1080/17455030.2011.576712
Quek, S. T., and Wang, Q. (2000). On dispersion relations in piezoelectric coupled-plate structures. Smart Mat. Struct. 9 (6), 859–867. doi:10.1088/0964-1726/9/6/317
Reissner, E. (1945). The effect of transverse shear deformation on the bending of elastic plates. J. Appl. Mech. 12 (3), 69–77. doi:10.1115/1.4009435
Shimpi, R. P., and Patel, H. G. (2006). A two variable refined plate theory for orthotropic plate analysis. Int. J. Solids Struct. 43 (22-23), 6783–6799. doi:10.1016/j.ijsolstr.2006.02.007
Shimpi, R. P. (2002). Refined plate theory and its variants. AIAA J. 40 (1), 137–146. doi:10.2514/3.15006
Thompson, I., Abrahams, I. D., and Norris, A. N. (2002). On the existence of flexural edge waves on thin orthotropic plates. J. Acoust. Soc. Am. 112 (5), 1756–1765. doi:10.1121/1.1506686
Xia, R. Y., Zhu, J. Y., Yi, J. L., Shao, S., and Li, Z. (2021). Guided wave propagation in multilayered periodic piezoelectric plate with a mirror plane. Int. J. Mech. Sci. 204 (2), 106539. doi:10.1016/j.ijmecsci.2021.106539
Yang, Z. T., and Yang, J. S. (2009). Effects of electric field gradient on the propagation of short piezoelectric interface waves. Int. J. Appl. Electromagn. Mech. 29 (2), 101–108. doi:10.3233/jae-2009-1006
Zakharov, D. D., and Becker, W. (2003). Rayleigh type bending waves in anisotropic media. J. Sound Vib. 261 (5), 805–818. doi:10.1016/s0022-460x(02)00996-3
Zhang, C. L., Chen, W. Q., and Zhang, C. Z. (2012). On propagation of anti-plane shear waves in piezoelectric plates with surface effect. Phys. Lett. A 376 (45), 3281–3286. doi:10.1016/j.physleta.2012.09.027
Zhang, L. L., Zhao, J., Nie, G. Q., and Liu, J. (2022). Propagation of Rayleigh-type surface waves in a layered piezoelectric nanostructure with surface effects. Appl. Math. Mech. 43 (3), 327–340. doi:10.1007/s10483-022-2824-7
Zhang, R., Jiang, B., Cao, W. W., and Amin, A. (2002). Complete set of material constants of 0.93Pb(Zn1/3Nb2/3)O3-0.07PbTiO3 domain engineered single crystal. J. Mater. Sci. Lett. 21 (23), 1877–1879. doi:10.1023/a:1021573431692
Keywords: piezoelectric plate, edge wave, bending wave, dispersion relation, plate theory
Citation: Nie G, Lei Z, Liu J and Zhang L (2022) Bending waves localized along the edge of a semi-infinite piezoelectric plate with orthogonal symmetry. Front. Mater. 9:1031538. doi: 10.3389/fmats.2022.1031538
Received: 30 August 2022; Accepted: 15 September 2022;
Published: 07 October 2022.
Edited by:
Chunli Zhang, Zhejiang University, ChinaReviewed by:
Xu Liang, Xi’an Jiaotong University, ChinaZhijing Wu, Harbin Engineering University, China
Copyright © 2022 Nie, Lei, Liu and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lele Zhang, emhhbmdsbEBzdGR1LmVkdS5jbg==
 Guoquan Nie
Guoquan Nie Zhenyu Lei3
Zhenyu Lei3 Jinxi Liu
Jinxi Liu Lele Zhang
Lele Zhang