Mechanical properties of PVC-based wood–plastic composites effected by temperature

Compared with traditional wooden building materials, polyvinyl chloride (PVC)-based wood–plastic composites have advantages of good weather resistance, easy processing capability, energy conservation, and environmental protection and have been popular and widely used in the field of civil construction and garden engineering in recent years. Due to the difference in the thermal expansion coefficient between its component materials, the stress will accumulate in the wood–plastic composites (WPCs) when the temperature changes, which will affect the mechanical properties of the material and structure. In order to explore the changes in mechanical properties of WPCs under different temperatures and achieve a safe and controllable design, the differential scanning calorimetry (DSC) method was used in this study to measure the glass transition temperature of the WPC between 78.45°C and 88.30°C, and the glass transition temperature (T_g) was about 83.54°C. The tensile, compressive, and bending mechanical property tests of PVC-based wood–plastic composite materials under different temperatures were carried out in the ambient temperature chamber to obtain the failure characteristics, the load–displacement curve, and the influence of temperature on their mechanical properties.

1 Introduction

Low forest coverage rates and shortage of wood resources are problems faced by many countries in the world. Using renewable crop straw and fast-growing wood to develop green and energy-saving bio-based building materials and build resource-saving and environment-friendly engineering facilities are an urgent need for sustainable and developmental construction of human beings (Wang, 2018; Wang et al., 2010; Liu, 2013; Zahedi et al., 2013; Sudar shan Rangara, 1999; Brandt, 2001; pooler, 2001; Parsons and Bender, 2004). Plastic products can be seen everywhere in modern life. They have the advantages of being lightweight, durability, and low price but also have the disadvantages of environmental pollution and difficult recycling. There is a growing demand for plastic products year by year, and the world plastic industry keeps a trend of rapid development (Pilarski and Matuana, 2005; Goertzen and Kessler, 2006; Soury et al., 2009; Leu et al., 2012; Homkhiew et al., 2014; Zhang, 2014; Zhang et al., 2016; Ghorbani et al., 2019; Vedrtnam et al., 2019; Yu et al., 2020). According to statistics, the annual global plastic usage exceeds 350 million tons, and the main disposal methods of waste plastic include landfill, incineration, and recycling, with an effective recycling rate of less than 20% (Qi, 2011; Xiao et al., 2018; Wang et al., 2019; Feng et al., 2020). The landfill method has a certain effect in the short term, but it is simple and negative. The waste plastic buried in the landfill cannot be exposed to the sun and air, and it is difficult to degrade. Waste plastics in the soil not only damage the permeability of the soil, reduce the water-holding capacity of the soil, and affect the growth of crops but also pollute groundwater. The incineration method will release a large number of harmful gases into the air, polluting the air quality and exacerbating the greenhouse effect. The recycling method can be used through a variety of equipment and processes to recycle plastic decomposition and reuse; the current technology has been very mature and will not cause secondary pollution, but the cost is higher, and the process is more complex. Therefore, it is necessary to seek the disposal method of waste plastics which can protect the environment and improve the efficiency.

The wood–plastic composite (WPC) is a new environment-friendly building material, which is mainly made of high-performance matrix resins such as PVC, reinforced by wood chips, bamboo chips, straw, plant straws, and other waste biomass fiber materials. The water absorption of WPC is much smaller than natural wood. It is less affected by the atmospheric temperature environment, has good dimensional stability, wear resistance, chemical corrosion resistance, and has the excellent characteristics of wood and plastic. It has a beautiful appearance in many kinds of colors, and the manufacturing technique contains extrusion, injection molding, and plastic molding. It satisfies the needs of industrial production of products and has the following characteristics: 1) low requirements for wood materials such as waste wood chips, bamboo chips, and plant straw; 2) with a strong dimensional stability, it can help solve the problems of wooden building materials such as joint, cracking, moth-eaten, and rot; 3) by adjusting the composition of the resin matrix, the strength and functional requirements of WPC products can be improved to achieve the goals of corrosion resistance, aging resistance, and being flame retardant; and 4) solve the problem that plastic products cannot be recycled and crop straw burning environmental pollution. The products can be recycled for reproduction by 100%, which can effectively reduce construction waste and carbon emission, saving energy and conforming to the design concept of green building and sustainable development. PVC-based wood–plastic composite material has the texture and diverse appearance of wood, low price, convenient production and preparation, and can be used as building wall panels, floors, railings, maintenance facilities, etc. Furthermore, it has broad application prospects in the field of civil architecture and garden engineering (Klyosov, 2010; Wang, 2010; Tamrakar et al., 2011; Zahedi et al., 2013; Bai, 2014; Di and Wang, 2016; Pulngern et al., 2016; Liu, 2018; Shi et al., 2019). PVC-based wood–plastic composites are often faced with the dual test of temperature and load in the process of use. The thermal expansion properties of their component materials are quite different, and the resin matrix is a thermal sensitive material; in order to study the mechanical properties of the material at different temperatures, compressive, tensile, and bending tests of PVC-based WPC composites under temperature-load coupling were carried out systematically in this study.

2 Experimental program

2.1 Specimens

WPCs can be prepared through pressing, extrusion, and other processes with resin matrix materials such as polyvinyl chloride (PVC), polypropylene (PP), and polyethylene (PE) at one time. The main material components of specimens are the poplar wood powder, PVC resin, foaming agent, stabilizer, coupling agent, combustive agent, etc. The plating density is 0.82 g/cm³. According to the national standards GB/T 29418-2012, 2012 and GB/T 1040.4-2006, 2006, the dimension of the specimens in the linear thermal expansion coefficient test, compressive test, tensile test, and bending test is as shown in Table 1.

TABLE 1

TABLE 1. Details of specimens.

2.2 Experimental instrumentation and results

2.2.1 Glass transition temperature test

The glass transition temperature (T_g) is a very important physical parameter of the crystalline polymer, referring to the temperature of the amorphous polymer (including an amorphous component in the crystalline polymer) transitioning from the glassy state to the high elastic state. The temperature is the highest temperature of plastic products, which directly affects the functional performance and process performance of the material (Harris., 2004).

The experiment was carried out in the laboratory of the physical and chemical properties of composites. Before the mechanical property test of WPC under temperature-load coupling, the glass transition temperature (T_g) of WPCs should be measured by DSC to determine the maximum temperature of the test. The WPC was ground into powder, weighed on the electronic scales, and then put into the differential scanning calorimeter to measure the glass transition temperature.

Figure 1 shows the glass transition temperature curve of WPCs measured by DSC; as shown in the figure, the temperature interval of glass transition of PVC-based WPCs is 78.45°C–88.30°C, and T_g is about 83.54°C. It is suggested to set 70°C as the upper limit of the application temperature environment of WPCs.

FIGURE 1

FIGURE 1. Curve of the glass transition temperature.

2.2.2 Linear thermal expansion coefficient test

Before the test, we should ensure that the section of the specimen is smooth and flat, and a center line should be drawn on the surface of the specimen along the direction of the length. According to the specification, the test was divided into three groups, with 10 specimens in each group; the size of which is 300 mm × 20 mm × 18 mm. Each group of specimens was placed in a temperature-controlled environment of 10°C, 30°C, and 60°C for 48 h, and then, the length of the marking line was measured quickly after taking out the specimens one by one. The test temperature T_i (i = 1, 2, and 3) and the arithmetic mean value L_i (i = 1, 2, 3) of the line length of each group of samples were recorded in 30 s after the specimens were taken out, as quickly as possible.

According to the results, the average linear thermal expansion coefficient of PVC-based WPC is about 55.49 × 10⁻⁶/°C and that of PVC is about 80 × 10⁻⁶/°C in the temperature range of 10°C–60°C. The thermal expansion coefficient of WPC is reduced by 30.64% compared with that of PVC resin matrix material. It is related to lignocellulose in WPCs. Lignin in lignocellulose has a stable three-dimensional spatial structure and can cross-link with cellulose and hemicellulose through the hydrogen bond and covalent bond to inhibit the thermal expansion of cellulose and hemicellulose (Sain et al., 2005). Also, the wood powder fiber in the WPC can be closely connected with the resin molecules to inhibit the expansion of the resin matrix (PVC), thus reducing the thermal expansion phenomenon of the WPC system.

2.2.3 Tensile property test under temperature-load coupling

The tensile strength of WPC is always lower than that of wood because of the high proportion of resin components; the more the resin matrix is contained, the lower the tensile strength is. In order to study the mechanical properties of PVC-based WPCs under the influence of temperature, six kinds of temperature test conditions were set as 10°C, 20°C, 30°C, 40°C, 50°C, and 60°C, with five specimens in each group. The size of the specimens was 250 mm × 25 mm × 8 mm, and both ends were reinforced with aluminum sheets 50 mm in length and 3 mm in thickness. The test was carried out on the MTS universal testing machine, and the ambient temperature is provided by the temperature control test box matching the testing machine.

During the process of the test, there was no obvious change in the specimens in the early loading stage, but when the loading was close to the failure load, the specimens suddenly broke, showing the characteristics of brittle fracture. As shown in Figure 2, the fracture surface of the specimen is rough, and the roughness of the fracture surface increases with the increase of temperature. The higher the temperature is, the longer it takes for the specimen to fracture, and the elongation of the specimen before brittle fracture is also increasing. After the fracture, observing the fracture surface of the specimen, the middle part of the specimen produces more particle debris, while the upper and lower surfaces have less particle debris. It shows that there is good continuity between the outer layers of PVC-based WPCs produced by the co-extrusion process.

FIGURE 2

FIGURE 2. Typical tensile failure mode of WPC specimens: (A) 10°C, (B) 30°C, and (C) 60°C.

According to the results, the maximum tensile load at different temperatures was obtained, and then the tensile strength, tensile modulus, and Poisson’s ratio at different temperatures were calculated, as shown in Figure 3.

FIGURE 3

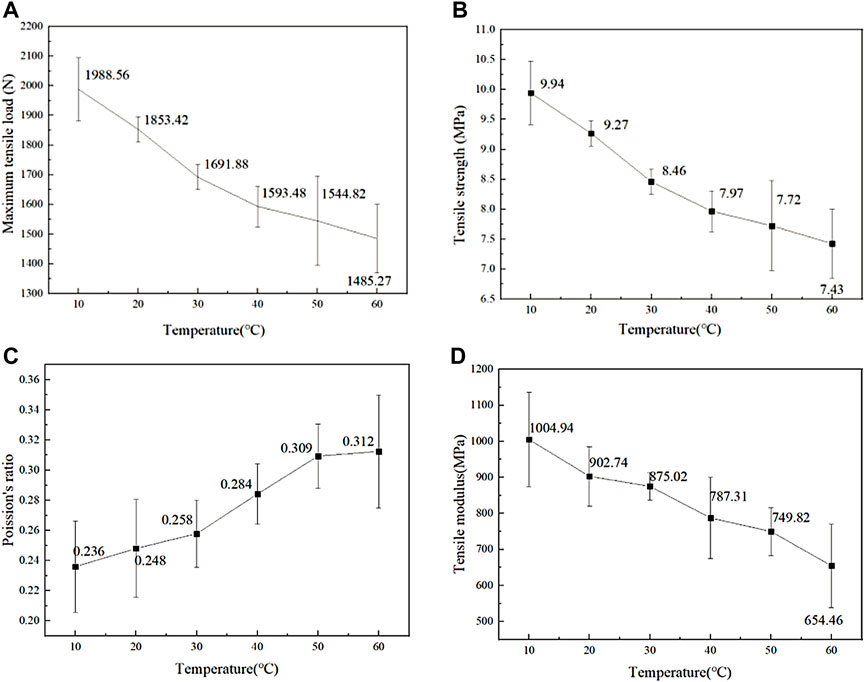
FIGURE 3. Maximum tensile load, tensile strength, Poisson’s ratio, and tensile modulus of WPCs at different temperatures: (A) maximum load, (B) tensile strength, (C) Poisson’s ratio, and (D) tensile modulus.

As shown in Figure 3, the tensile strength of the specimen is between 7 MPa and 10 MPa. When the temperature rises from 10°C to 40°C, the tensile strength decreases from 9.94 MPa to 7.97 MPa, decreasing by 19.82%. When the temperature rises from 40°C to 60°C, the tensile strength drops from 7.97 MPa to 7.43 MPa, decreasing by 5.43%. With the rising of the temperature, the tensile strength decreased by 25.25%. The closer the temperature is to T_g, the lower the tensile strength will be, but the dispersion of tensile strength will increase with the increase of temperature.

Poissons ratio is an elastic constant of the material, reflecting the proportion of elongation (or shortening) deformation of material along the direction of the load and perpendicular to the direction of the load (Zhang et al., 2018). As shown in Figure 3C, the Poisson’s ratio of WPC increases with the temperature rising from 10°C to 60°C, and the Poisson’s ratio increases from 0.236 to 0.312, with an increase of 30.2%.

The tensile modulus decreased with the increase in the test temperature and decreased from 1,004.94 MPa to 654.46 MPa in the whole temperature range, decreasing by 34.87%. It can be seen that with the increase in temperature, the tensile modulus is most sensitive to temperature change and decreases the most.

The increase in temperature will cause the movement of the polymer chain segment, leading to the reorganization of the micro-molecular chain segment, thus affecting the macroscopic mechanical properties of the material (Isa et al., 2016). With the increasing temperature of the test, the motion amplitude of the polymer chain segment becomes larger and larger, eventually changing the original solid state. The weakening of van der Waals forces between molecules, coupled with the difference in thermal expansion properties of the material itself and the action of external loads, damages the state of the material itself to a greater extent. Many microscopic cracks appear inside the specimen, and damaged cracks accumulate continuously at the interface between the material structure resin and wood powder particles, leading to the reduction of the mechanical properties of WPCs (Aklonis and MacKnight, 1983).

The tensile load–displacement curves of WPCs at different temperatures are shown in Figure 4. It can be seen from the figure that at the initial stage of loading, load displacement changes linearly, and the elastic stage is gradually shortened with the increase of temperature. The PVC-based WPC shows good ductility when it is close to the failure load. The tensile failure load decreases with the increase in the test temperature, when it rises from 10°C to 60°C, the failure load drops from 1908.43 N to 1,429.68 N, with a total decrease of 25.08%. The maximum tensile displacement increases with the increase in the test temperature, from 3.97 mm to 6.93 mm, showing an increase of 74.56%. It shows that the higher the temperature, the better the tensile failure ductility is. The effect of temperature on mechanical properties of WPC is mainly through changing the motion state of the polymer. In the range of 10°C–20°C, the displacement of the maximum load increases by 0.31 mm. An increase of 0.85 mm in the range of 30°C–40°C and 0.9 mm in the range of 50°C–60°C. It indicates that the ductility of the material will continue to increase when the temperature is dropped below the glass transition temperature, and the higher the temperature (the closer to the glass transition temperature), the better the ductility of the specimen is.

FIGURE 4

FIGURE 4. Load–displacement curves of WPCs in the tensile test at different temperatures.

According to the tensile property test data on WPCs at six different temperatures, the influences of temperature on the maximum load (F_t), tensile strength (σ_t), and modulus (E_t) of WPCs were obtained, and F_t, σ_t, and E_t were variables related to temperature (T). The origin fitting method was used to obtain the function relations of F_t, σ_t, and E_t, as shown in Eqs. 1–3. The fitting results are shown in Figure 5.

FIGURE 5

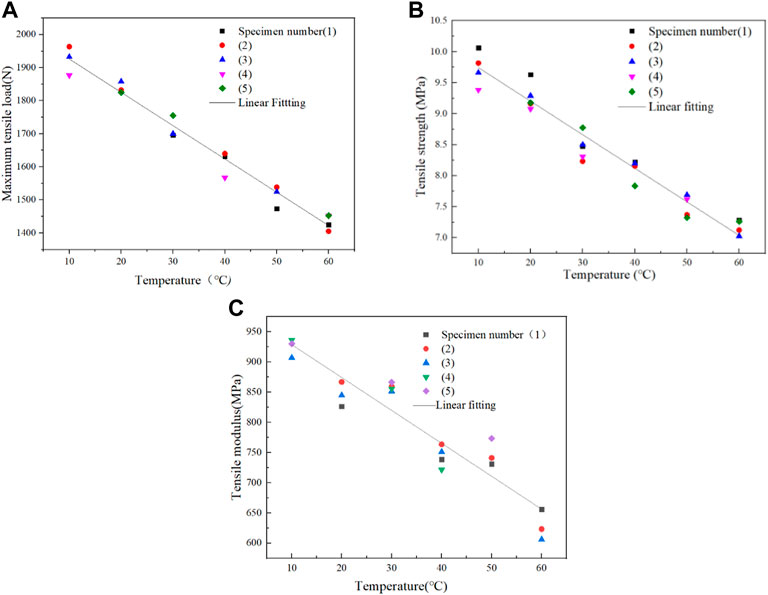
FIGURE 5. Fitting of tensile mechanical properties of WPCs at different temperatures: (A) maximum tensile load, (B) tensile strength, and (C) tensile modulus.

The following shows the fitting results of tensile mechanical properties:

$F_t=2026.92-10.08T,(1)$

${\sigma }_t=10.28-0.05T,(2)$

$E_t=983.22-5.45T.(3)$

Also, the correlation coefficients (R²) of F_t, σ_t, and E_t are 0.973,0.960, and 0.880, respectively.

2.2.4 Compressive property test under temperature-load coupling

The test temperature condition was set the same as the tensile test, and the size of the specimen was 108 mm × 40 mm × 36 mm. The compressive test equipment is shown in Figure 6. The specimen was placed between two pressure plates to ensure that the center of the specimen and the center of the pressure plate coincide to avoid eccentricity when loading. The thermocouple was tightly pasted on the specimen, and an identical reference specimen was also placed. The WRNT-01 thermocouple was inserted into the specimen, and the temperature inspection instrument was connected. When the specimen temperature displayed by the temperature inspection instrument was consistent with the temperature inside the temperature box, the compressive test was carried out at the rate of 5 mm/min, and the data acquisition frequency is 1 Hz.

FIGURE 6

FIGURE 6. Specimen and instruments for the compressive test of WPCs: (A) compressive specimen, (B) temperature inspection instrument, and (C) temperature control instrument.

There was no obvious change in the specimens in the early loading stage. However, with the progress of the test, lateral bending began to occur in the middle of the specimen, a white area gradually appeared on the surface of the specimen side, and cracks appeared in the middle of the specimen along the loading direction longitudinally. With the increase of load, side bending occurred in the middle part of the specimen, and cracks occurred at the interface between the middle layer and the inner and outer layers of the bent part. The crack from the middle to the surface expanded diagonally until it passed through the entire cross section of the component; then, the specimen failed, reaching the preset displacement range of 10 mm. Failure modes at 10°C, 30°C, and 60°C are shown in Figure 7.

FIGURE 7

FIGURE 7. Typical compressive failure mode of WPC specimens: (A) 10°C, (B) 30°C, and (C) 60°C.

The results of the maximum compressive load and compressive strength in compressive tests at different temperatures are shown in Figure 8.

FIGURE 8

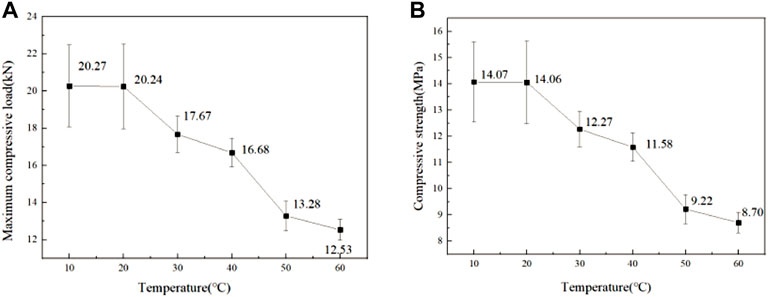
FIGURE 8. Maximum compressive load and compressive strength of WPCs at different temperatures: (A) maximum compressive load and (B) compressive strength.

With the rising test temperature, the compressive strength of WPC decreases from 14.07 MPa to 8.70 MPa, and the maximum compressive load decreases from 20.27 kN to 12.53 kN. Compared with the tensile strength, the compressive strength decreases more, so the compressive strength of WPCs is affected by temperature more easily. The compressive strength at each temperature is higher than the corresponding tensile strength, and the maximum compressive load is about 10 times the maximum tensile load. This indicates that WPC material has stronger compressive resistance. As can be seen from Figure 9, the compressive strength decreases by 34.39% from 20°C to 50°C and by 5.65% from 50°C to 60°C. In the range of 20°C–50°C, the compressive strength of WPCs shows some discreteness, and the discreteness decreases when the temperature exceeds 50°C. The compressive properties are relatively stable, and the compressive strength will not decrease significantly and tends to be stable. When the temperature is very close to the range of T_g, the stiffness begins to decrease obviously. This is consistent with the effect of temperature on the tensile strength and modulus of WPCs.

FIGURE 9

FIGURE 9. Load–displacement curves of WPCs in the compressive test at different temperatures.

Load–displacement curves of the wood–plastic composite under compressive tests at different temperatures are shown in Figure 9. The maximum compressive load of PVC-based WPCs decreases with the rising test temperature, and the displacement increases with the rising test temperature under the maximum compressive load. In the temperature range of 10°C–60°C, the peak load displacement increased from 3.02 mm to 4.81 mm, increasing more than 37.21%.

Considering the influence of temperature on the maximum compressive load ($F_{\mathrm{c}}$) and compressive strength (${\sigma }_{\mathrm{c}}$) of wood–plastic composite material, $F_{\mathrm{c}}\mathrm{a}\mathrm{n}\mathrm{d}{\sigma }_{\mathrm{c}}$are variables related to temperature ($T$). The fitting results are shown in Figure 10.

FIGURE 10

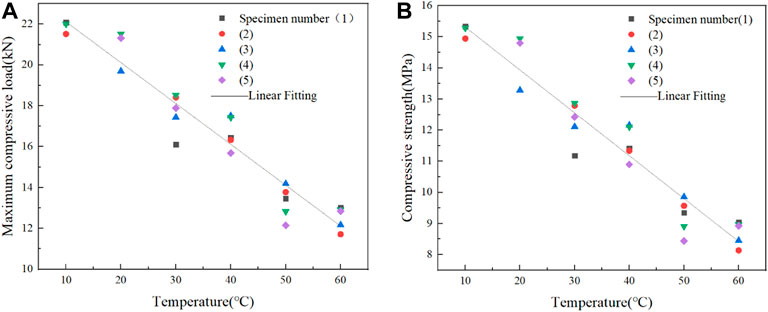
FIGURE 10. Fitting of compressive mechanical properties of WPCs at different temperatures: (A) maximum compressive load and (B) compressive strength.

The following equations show the fitting results of compressive mechanical properties:

$F_{\mathrm{c}}=24.112-0.199T,(4)$

${\sigma }_{\mathrm{c}}=16.689-0.137T.(5)$

Also, the correlation coefficients (R2) of Fc and σc are 0.925 and 0.922, respectively.

2.2.5 Bending property test under temperature-load coupling

The bending property test was carried out according to the national standard GB/T 29418-2012. The set temperature condition of the test was the same as that of the tensile and compressive tests. The size of the specimens was 340 mm × 40 mm × 18 mm, with five specimens at each temperature condition. The test was carried out on an MTS micro-controlled electronic universal testing machine. The ambient temperature was controlled by high- and low-temperature control testing instruments, and the thermocouple was tightly glued on the specimen to measure the surface temperature of the specimen. The span of the two supports was adjusted to 16 times (288 mm) the nominal thickness of the sample. The two-point loading test method is shown in Figure 11. During the test, the loading roller axis line is parallel to the supporting roller axis line and perpendicular to the center line of the long axis of the sample, which is placed at 1/3 of the span.

FIGURE 11

FIGURE 11. Four-point bending load test.

The main components of WPC are wood or various plant fibers. Low temperature has less influence on the wood or plant fibers in WPCs, and temperature mainly affects the bending performance of WPCs by affecting the plastic. With the increase in temperature, the molecular movement in the plastic is intensified, and the intermolecular van der Waals force is reduced, which leads to the decrease in the bending resistance of WPCs.

The bending failure pattern of the specimens is shown in Figure 12. There was no crack on the side of the specimen before failure, and it suddenly broke from the tension zone below the loading point. The fracture surface of the lower part of the specimen is rough, which is similar to the tensile failure of WPCs. The fracture surface of the upper compressive zone is very smooth and flat, which is very different from the form of compressive failure of WPCs. There is no rough section caused by irregular crack development. This indicates that in the bending test, the lower tensile side of the specimen belongs to tensile failure, while the upper part does not have compressive failure. The stress whitening phenomenon occurs at the loading point and becomes more obvious with the increase in temperature, which is consistent with the compressive characteristics of WPCs.

FIGURE 12

FIGURE 12. Typical bending failure mode of WPC specimens: (A) 10°C, (B) 30°C, and (C) 60°C.

The bending failure load under different temperatures was obtained, and the bending strength and bending modulus were calculated. The results are shown in Figure 13.

FIGURE 13

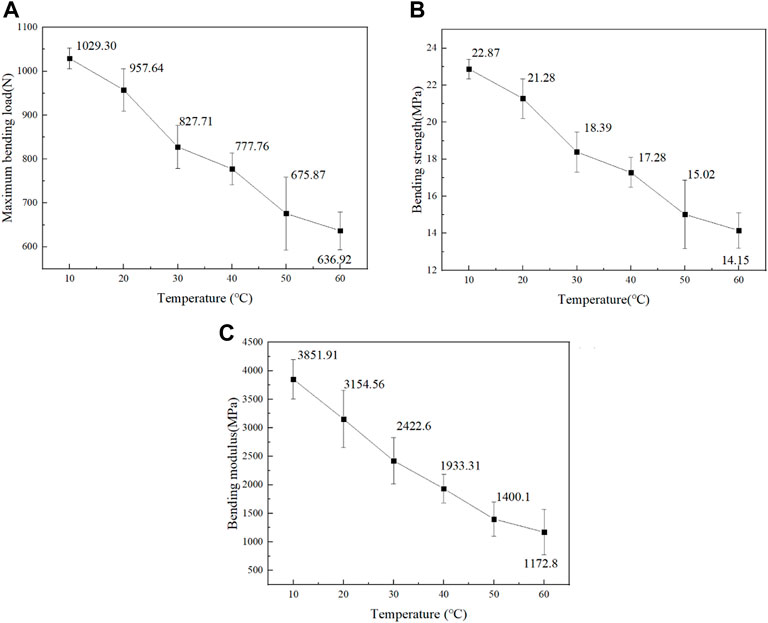
FIGURE 13. Bending behavior of WPCs at different temperatures: (A) maximum bending load, (B) bending strength, and (C) bending modulus.

As can be seen in Figure 13, when the temperature rises from 10°C to 60°C, the bending property of the four-point bending specimen decreases gradually. The bending strength decreased from 22.87 MPa to 14.15 MPa, decreasing by 38.13% with a linear downward trend. The bending modulus decreased from 3,851.91 MPa to 1,172.8 MPa, decreasing by 69.55%. The bending modulus is more susceptible to the temperature environment. Decline modes of the bending strength and bending modulus show an obvious characteristic of the two stages. At the early stage of a low temperature (10°C–40°C), the bending strength decreased from 22.87 MPa to 17.28 MPa, accounting for 64.11% of the total strength. The bending modulus decreased from 3,851.91 MPa to 1933.31 MPa, decreasing about 1918.6 MPa, accounting for 71.61% of the total modulus. At the second stage of high temperature (40°C–60°C), the bending strength decreased from 17.28 MPa to 14.15 MPa, decreasing about 3.13 MPa, accounting for 35.89% of the total strength decreased. The bending modulus decreased from 71.91% to 71.61%, decreasing by 760.51 MPa, accounting for 28.09% of the total modulus. The trend is consistent with the decreasing law of tensile strength and modulus.

Load–displacement curves of the four-point bending test of WPCs at different temperatures are shown in Figure 14. The maximum bending load of the specimen decreases with the rising test temperature, from 1,021.2 N to 624.80 N, decreasing by 38.82%. The maximum midspan displacement increases with the rising test temperature, from 15.18 mm to 20.49 mm, increasing by 34.98%. The bending failure load of WPCs decreases and ductility increases with the rising temperature.

FIGURE 14

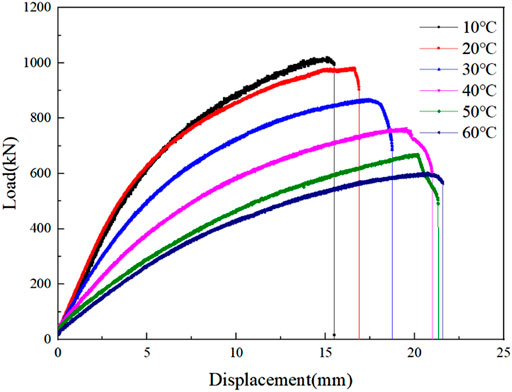
FIGURE 14. Load-midspan displacement curves of the four-point bending test of WPCs at different temperatures.

2.2.6 Theoretical analysis of the bending property

Based on the theory of first-order shear deformation, the deflection formula of WPCs in the four-point bending test is presented as follows:

${\Delta }_f={\Delta }_b+{\Delta }_s=\frac{Pa\left(3l^2-4a^2\right)}{48EI}+\frac{Pa}{2G{\rm A}},(\mathrm{1a})$

where a is the net distance between the loading point and the support, and l is the net span of the beam. Based on the test results with the theoretical results, the deflection can be deduced as follows:

${\Delta }_f={\Delta }_b+{\Delta }_s=\frac{Pa\left[3l^2-4a^2+4h^2\left(1+\mu \right)\right]}{4b{h}^3\left(4234.963-54.665T\right)}.(\mathrm{2a})$

According to the Euler beam theory, the deflection of the four-point bending test of WPCs is shown as follows:

${\Delta }_o=\frac{Pa\left(3l^2-4a^2\right)}{48EI},(\mathrm{3a})$

where E is fitted from the bending test results as

$E=4234.963-54.665T.$

Also, the inertia moment (I) of the rectangular cross section is

$I=\frac{b{h}^3}{12}.$

By substitution into Eq. 3, the deflection is obtained as follows:

${\Delta }_o=\frac{Pa\left(3l^2-4a^2\right)}{4b{h}^3\left(4234.963-54.665T\right)}.(\mathrm{4a})$

If the load is 300 N, when the temperature increases, compared with the test value, the calculation error of the Euler beam theory is stable within 2.2 mm, and the minimum error is 0.22 mm. As the temperature rises, the error increases. Although the first-order shear deformation theory considers the shear deformation, the accuracy of its calculation results is not significantly improved, and the error is similar to that of the Euler beam theory. In the initial low-temperature environment, the error between the theoretically calculated value and the test value of the Euler beam and first-order shear deformation is within 0.7 mm, and the fitting result is good. However, when the temperature exceeds 40°C, the error between the calculated value and the test value is larger, and the fitting result is poor.

The failure modes of the WPC beam in the four-point bending test are mainly 1) tensile failure and 2) buckling failure. The calculation formula of the ultimate bearing capacity is as follows:

Tensile failure is expressed as follows

$P_{f1}=b{d}_{t1}{\left(\frac{{\pi }^2{\sigma }_t^2{E}_{t}d}{3\left(l-a\right)}\right)}^{1/3}.(\mathrm{5a})$

Buckling failure is expressed as follows

$P_{f2}=\frac{2b{d}_{t2}d}{l-a}\sqrt[3]{EG}.(6)$

In Eq. 5, b is the width of the beam, l is the calculated length of the beam, and d_t1 is the thickness of the panel. According to the test data, d_t1 is 0.8 and d is the thickness of the beam. E_t is the tensile modulus, σ_t is the tensile strength, and a is the net distance between the loading point and the support. In Eq. 6, when d_t2 is close to 0.76, the fitting results are more accurate. E is the elastic modulus, and G is the shear modulus.

3 Conclusion

The compressive, tensile, and bending properties of PVC-based WPCs were studied under the influence of temperature. The main conclusions are summarized as follows:

(1) The glass transition temperature of PVC-based WPCs is measured by means of DSC; the results are in the range of 78.45°C and 88.30°C, which is about 83.54°C. The designed application temperature environment for PVC-based WPC is suggested to be lower than 70°C.

(2) The average linear thermal expansion coefficient of WPC is about 55.49 × 10⁻⁶/°C, and PVC is about 80 × 10⁻⁶/°C in the temperature between 10°C and 60°C. The thermal expansion coefficient is related closely to lignocellulose in WPC.

(3) The tensile and compressive tests of WPCs were carried out, and the tensile failure load decreased with the rising test temperature. When the test temperature rose from 10°C to 60°C, the failure load decreased by 25.08%. The maximum tensile displacement increased with the rising test temperature by 74.56%. The displacement of the maximum compressive load increases with the rising test temperature by 37.21%. The results show that the higher the temperature, the better the tensile failure ductility is. The tensile and compressive mechanical formulas were fitted in consideration of the temperature effect.

(4) The four-point bending test of WPCs under temperature-load coupling was carried out. The results showed that the maximum bending load, bending strength, and bending modulus were reduced under the influence of temperature. The bending failure characteristics of WPCs were analyzed, and the influence law of temperature on the bending characteristics was obtained. The load–displacement curves of WPCs at different temperatures were fitted.

(5) The formulas to calculate the deflection and ultimate bending capacity were obtained based on the first-order shear deformation theory and the Euler–Bernoulli beam theory, and the results are very close to the experimental results under a low-temperature environment.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JL is the first author in charge of carrying out the test and writing. RH is the corresponding author in charge of the test plan and analysis. WL and LJ were in charge of data fitting and writing. HF and DZ were in charge of the load-temperature coupling test and analysis.

Funding

This research is financially supported by the National Key Research and Development Program of China (Grant No. 2019YFD1101205), the National Natural Science Foundation of China (Grant No. 51978336), and the Natural Science Foundation for Distinguished Young Scholars of Jiangsu Province (Grant No. BK20190034).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aklonis, J. J., and MacKnight, W. J. (1983). Introduction to polymer viscoelasticity [M]. New York, NY: John Wiley & Sons. doi:10.1016/j.matchar.2007.05.008

CrossRef Full Text | Google Scholar

Bai, X. (2014). PVC wood-plastic composites[M], 04. Beijing: Beijing Jiaotong University Press, 2–3.

Google Scholar

Brandt, C. W. (2001). Load-duration behavior of extruded wood-plastic composite. Washington, DC. Washington State University. Master Thesis.

Google Scholar

Di, M., and Wang, Q. (2016). Surface treatment and cementation of wood-plastic composites[M], 03. Beijing: Science Press, 1–3.

Google Scholar

Feng, Z., Liping, N., and Lu, X. (2020). Effect of two plasticizers on properties of bamboo flour/waste PVC composites[J]. J. Mater. Sci. Eng. 38 (01), 123–128. doi:10.14136/j.cnki.issn1673-2812.2020.01.023

CrossRef Full Text | Google Scholar

GB/T 1040.4-2006 (2006). Plastics-Determination of tensile properties-Part 4: Test conditions for isotropic and orthotropic fibre-reinforced plastic composites[S].

Google Scholar

GB/T 29418-2012 (2012). Test methods for mechanical and physical properties of wood-plastic composite product[S].

Google Scholar

Ghorbani, M., Aghmashadi, Z. A., Seyed Mojtaba, A., and Abedini, R. (2019). Effect of different coupling agents on chemical structure and physical properties of vinyl acetate/wood polymer composites. J. Appl. Polym. Sci. 136 (19), 47467. doi:10.1002/app.47467

CrossRef Full Text | Google Scholar

Goertzen, W. K., and Kessler, M. R. (2006). Creep behavior of carbon fiber/epoxy matrix composites. Mater. Sci. Eng. A 421 (1-2), 217–225. doi:10.1016/j.msea.2006.01.063

CrossRef Full Text | Google Scholar

Harris., B. (2004). Engineering composites[M]. London. Chemical Industry Press, 213–215.

Google Scholar

Homkhiew, C., Ratanawilai, T., and Thongruang, W. (2014). Time–temperature and stress dependent behaviors of composites made from recycled polypropylene and rubberwood flour. Constr. Build. Mater. 66, 98–104. doi:10.1016/j.conbuildmat.2014.05.048

CrossRef Full Text | Google Scholar

Isa, A., Minamino, J., Kojima, Y., Suzuki, S., Ito, H., Makise, R., et al. (2016). The influence of dry-milled wood flour on the physical properties of wood flour/polypropylene composites. J. Wood Chem. Technol. 36 (2), 105–113. doi:10.1080/02773813.2015.1083583

CrossRef Full Text | Google Scholar

Klyosov, A. A. (2010). Wood-plastic composites[M]. Beijing: Science Press, 1–7. doi:10.3969/j.issn.1009-797X.2004.08.007

CrossRef Full Text | Google Scholar

Leu, S-Y., Tsu-Hsien, Y., Lo, S-F., and Yang, T. H. (2012). Optimized material composition to improve the physical and mechanical properties of extruded wood–plastic composites (WPCs). Constr. Build. Mater. 29, 120–127. doi:10.1016/j.conbuildmat.2011.09.013

CrossRef Full Text | Google Scholar

Liu, G. (2013). Study on properties of wood-plastic composites. Guide Sci-tech Mag.. 08 (8), 110. doi:10.3969/j.issn.1007-1547.2013.06.092

CrossRef Full Text | Google Scholar

Liu, W. (2018). Research on innovation and development of recycling technology for waste plastics[M], 09. Beijing: Scientific and Technical Documents Publishing House, 1–4.

Google Scholar

Parsons, W. R., and Bender, D. A. (2004). Energy-based design of dowel connections in wood-plastic composites hollow sections[J]. J. Struct. Eng. 130130 (4), 4. doi:10.1061/(ASCE)0733-9445

CrossRef Full Text | Google Scholar

Pilarski, J. M., and Matuana, L. M. (2005). Durability of wood flour-plastic composites exposed to accelerated freeze-thaw cycling. Part I. Rigid PVC matrix. J. Vinyl Addit. Technol. 11 (1), 1–8. doi:10.1002/vnl.20029

CrossRef Full Text | Google Scholar

pooler, D. J. (2001). The temperature dependent non-linear response of a wood plastic composite. Washington, DC. Washington State University. Master Thesis. Available at: https://www.researchgate.net/publication/35733405.

Google Scholar

Pulngern, T., Chitsamran, T., Chucheepsakul, S., Rosarpitak, V., Patcharaphun, S., and Sombatsompop, N. (2016). Effect of temperature on mechanical properties and creep responses for wood/PVC composites. Constr. Build. Mater. 111, 191–198. doi:10.1016/j.conbuildmat.2016.02.051

CrossRef Full Text | Google Scholar

Qi, G. (2011). Practical technology of recycling waste plastics[M], 10. Beijing: Machinery Industry Press, 1.

Google Scholar

Sain, M., Suhara, P., Law, S., and Bouilloux, A. (2005). Interface modification and mechanical properties of natural fiber-polyolefin composite products. J. Reinf. Plast. Compos. 24 (2), 121–130. doi:10.1177/0731684405041717

CrossRef Full Text | Google Scholar

Shi, T., Zhu, L., and Li, X. (2019). Research progress in anti-aging properties of wood-plastic composite[J]. For. Mach. Woodwork. Equip. 47 (04), 7–10. doi:10.3969/j.issn.2095-2953.2019.04.002

CrossRef Full Text | Google Scholar

Soury, E., Behravesh, A. H., Rouhani Esfahani, E., and Zolfaghari, A. (2009). Design, optimization and manufacturing of wood–plastic composite pallet. Mater. Des. 30 (10), 4183–4191. doi:10.1016/j.matdes.2009.04.035

CrossRef Full Text | Google Scholar

Sudar shan Rangara, J. (1999). Durability assessment and modeling of wood-thermoplastic composites. Washington, DC. Washington State University. Master Thesis. Available at: https://www.researchgate.net/publication/35020162.

Google Scholar

Tamrakar, S., Kiziltas, A., and Douglas, J. (2011). Gardner. Time and temperature dependent response of a wood–polypropylene composite[J]. Compos. Part A 42 (7). doi:10.1016/j.compositesa.2011.03.011

CrossRef Full Text | Google Scholar

Vedrtnam, A., Kumar, S., and Shashikant, S. (2019). Experimental study on mechanical behavior, biodegradability, and resistance to natural weathering and ultraviolet radiation of wood-plastic composites[J]. Compos. Part B, 176. doi:10.1016/j.compositesb.2019.107282

CrossRef Full Text | Google Scholar

Wang, D., Chong, L., and Li, S. (2019). Influence of foaming agent on interface properties of wood-plastic composites[J]. Plastics Sci. Technol. 47 (05), 27–30. doi:10.15925/j.cnki.issn1005-3360.2019.05.006

CrossRef Full Text | Google Scholar

Wang, Q. (2010). Wood plastic composites manufacture and application[M]. Beijing: Science Press, 12–14.

Google Scholar

Wang, W., Li, C., and Wang, Q. (2010). Industrial development status and key technologies of wood plastics composites[J]. Mod. Chem. Ind. 30 (01), 6–10. doi:10.16606/j.cnki.issn0253-4320.2010.01.021

CrossRef Full Text | Google Scholar

Wang, Y. (2018). Research on green building design for sustainable development[M], 05. Beijing: China Atomic Energy Press, 1.

Google Scholar

Xiao, L., Cui, Y., and Liu, Q. (2018). Analysis on situation of waste plastics recycling industry in China[J]. China Resour. Compr. Util. 12, 99–102. doi:10.3969/j.issn.1008-9500.2018.12.028

CrossRef Full Text | Google Scholar

Yu, W., Liu, Q., and Chen, Y. (2020). Comparative study on the properties of different plastic-based plastic-wood composites[J]. China Plast. Ind. 48 (06), 121–125. doi:10.3969/j.issn.1005-5770.2020.06.023

CrossRef Full Text | Google Scholar

Zahedi, M., Tabarsa, T., Ashori, A., Madhoushi, M., and Shakeri, A. (2013). A comparative study on some properties of wood plastic composites using canola stalk, Paulownia, and nanoclay. J. Appl. Polym. Sci. 129 (3), 1491–1498. doi:10.1002/app.38849

CrossRef Full Text | Google Scholar

Zhang, H. (2014). Effect of a novel coupling agent, alkyl ketene dimer, on the mechanical properties of wood–plastic composites. Mat. Des. 59, 130–134. doi:10.1016/j.matdes.2014.02.048

CrossRef Full Text | Google Scholar

Zhang, X., Hao, X., Hao, J., and Wang, Q. (2018). Heat transfer and mechanical properties of wood-plastic composites filled with flake graphite. Thermochim. Acta, 26–31. doi:10.1016/j.tca.2018.04.003

CrossRef Full Text | Google Scholar

Zhang, Y., Xue, P., Ding, Y., Jia, M., Cai, J., and Jin, X. (2016). Improvement of mechanical properties of wood-plastic composite floors based on the optimum structural design. Acta Mech. Solida Sin. 29 (04), 444–454. doi:10.1016/S0894-9166(16)30246-4

CrossRef Full Text | Google Scholar