Structural, vibrational and transport properties of liquid and amorphous alumina: A molecular dynamics simulation study

Structural, vibrational and transport properties of liquid alumina at 2500 K and amorphous alumina at 300 K were studied by molecular dynamics simulations using an empirical Born-Mayer-Huggins potential with the recently optimized parameters. The investigations were conducted for the predicted densities at almost zero pressure, as well as the experimentally reported densities of 2.81 g/cm³ and 3.175 g/cm³. A detailed examination of the interatomic correlations showed that for both liquid and amorphous alumina, the short-range order was dominated by the slightly distorted (AlO₄)⁵⁻ tetrahedra. Vibrational density of states (VDOS) was obtained from the Fourier transform of the velocity autocorrelation functions (VACF), which exhibited broader ranges for the liquid phases compared with those for the amorphous phases. Each VDOS spectrum was divided into two primary frequency bands for both liquid and amorphous alumina. Thermal conductivities (κ) and viscosities (η) were estimated respectively through the heat-current autocorrelation functions (HCACFs) and stress autocorrelation functions (SACF) by the equilibrium molecular dynamics (EMD) simulations using the Green-Kubo relation. And the results were shown to be consistent with the experimental data, especially that κ was equal to 2.341 ± 0.039 Wm⁻¹K⁻¹ for amorphous alumina at 2.81 g/cm³ and 300 K, η was equal to 0.0261 ± 0.0017 Pa·s and 0.0272 ± 0.0018 Pa·s for the liquid phases at 2500 K with densities of 2.81 g/cm³ and 2.863 g/cm³, respectively. Mean squared displacements (MSDs) were employed for the self-diffusion coefficients (D) estimation.

1 Introduction

Alumina in various phases has received a great deal of research interest due to the wide range of technical applications (Es-Souni and Habouti, 2014; Hadjicharalambous et al., 2015; Tabandeh-Khorshid et al., 2016; Li et al., 2019; Shaikh and Hosan, 2019; Shi et al., 2019; Couto et al., 2020; Pan et al., 2020; Deng et al., 2021; Zhao et al., 2021). The most frequently occurring form in nature is α-Alumina (hexagonal), which is a thermodynamically stable phase at room temperature. Moreover, there exist several metastable polycrystals, for example, β (hexagonal), γ (cubic), δ (tetragonal), η (cubic), θ (monoclinic), κ (orthorhombic), and χ (cubic) phases. Amorphous alumina, unlike crystalline polymorphs, has a disordered, non-crystalline structure, and exhibits some attractive properties, such as high dielectric constant (Segda et al., 2001; Momida et al., 2006, 2007b), low band gap energy (Jennison et al., 2004; Adiga et al., 2006; Novikov et al., 2009; Lizárraga et al., 2011), and excellent mechanical and optical properties (Nayar et al., 2014; Paz et al., 2014; Orosco and Coimbra, 2018). Benefiting from these remarkable properties, amorphous alumina has been successfully used as insulators (Rashkeev et al., 2003; Katiyar et al., 2005; Avis and Jang, 2011), corrosion protection (Boisier et al., 2008; Singh et al., 2015; Daubert et al., 2017), capacitors (Blonkowski, 2007; Fukuhara et al., 2021), and catalysis (Yoon and Cocke, 1986; Nagaraju et al., 2002). Meanwhile, molten alumina has also attracted a lot of attention because of its utilization in producing large sapphire single crystals (Will et al., 1992; Golubović et al., 2001; Farr et al., 2013) and in the analysis of the behavior of aluminum-fueled rocket engine effluent (Jani et al., 2013; Skinner et al., 2013).

Knowledge of the structure at the atomic level is necessary for understanding the physical and chemical properties. The main challenge in performing experiments on liquid alumina is that contamination of the container from high temperatures affects the structural information. Therefore, most experimental investigations on the structural properties were carried out by non-destructive testing, for instance, X-ray diffraction (Waseda et al., 1995; Stuart and Krishnan, 1997; Hennet et al., 2002; Krishnan et al., 2005; Kohara et al., 2007), nuclear magnetic resonance measurements (NMR) (Coutures et al., 1990; Poe et al., 1992; Florian et al., 1995), neutron scattering measurements (Landron et al., 2001a; Landron et al., 2001b), and a joint of X-ray and neutron diffraction (Skinner et al., 2013). Additionally, for the structural analysis of amorphous alumina, extended X-ray absorption fine structure (EXAFS) (El-Mashri et al., 1983) and electron extended energy loss fine structure (EXELFS) (Bourdillon et al., 1984) were used. The majority of the experimental findings demonstrated that for both amorphous and liquid alumina, the coordination number of the Al-O pair was between 4 and 5, with the 4-fold coordination (AlO₄) predominating.

Unfortunately, owing to the difficulties encountered during the experiments, the experimental data was often insufficient and unreproducible. To alleviate the lack of experimental data, an alternative approach was to anticipate the properties of liquid and amorphous alumina using molecular dynamics (MD) simulations. Considerable efforts in the structure (Ahuja et al., 1998; Gutierrez and Johansson, 2002; Van Hoang, 2004; Van Hoang and Oh, 2004; Vashishta et al., 2008; Sergio and Gonzalo, 2011; Skinner et al., 2013; Shi et al., 2019), pore aggregation (Van Hoang, 2004; Hung et al., 2006; Nhan et al., 2006), and structural transformation at high pressures (Hoang and Oh, 2005; Van Hoang and Oh, 2005; Hung et al., 2006) of liquid and amorphous alumina have been made, in order to gain a better understanding of the structural information at the atomic scale and its relationship to macroscopic properties. Similar to the experimental results, most simulations revealed that in the liquid and amorphous states of alumina, the short-range order was dominated by slightly distorted (AlO₄)⁵⁻ tetrahedra (Gutierrez and Johansson, 2002; Chang et al., 2004; Van Hoang, 2004; Van Hoang and Oh, 2004; Nhan et al., 2006; Cristiglio et al., 2007; Vashishta et al., 2008; Skinner et al., 2013; Shi et al., 2019). However, there were some divergences, with some research suggesting that besides AlO₄, a significant fraction of AlO₅ was found in liquid and amorphous alumina (Van Hoang and Oh, 2005; Hung et al., 2006; Sergio and Gonzalo, 2011). And even Hemmati et al. (1999) indicated that liquid alumina was mainly composed of AlO₅ units, with a fair amount of AlO₄ and AlO₆ units present.

It is worth mentioning that most of the computational investigations of the liquid and amorphous alumina were focused on structural information, with only a few ones examining the dynamical properties. Regarding liquid alumina, Jahn and Madden (2008) calculated frequency-dependent viscosity, and self-diffusion coefficient from the zero frequency limit of the vibrational spectrum, despite the fact that this value was usually determined by the slope of the mean squared displacement (Van Hoang, 2004; Van Hoang and Oh, 2004, 2005; Hung et al., 2006). In addition, for amorphous alumina, the vibrational (Gutiérrez et al., 2010; Sergio and Gonzalo, 2011), and dielectric properties (Momida et al., 2006; Momida et al., 2007a) were explored using the first-principles calculation. So far, only Vashishta et al. (2008) provided a relatively comprehensive study on the dynamical properties of the liquid and amorphous alumina with different densities, including the vibrational density of states, specific heat, and frequency-dependent ionic conductivity. Significantly, few explorations concentrated on transport coefficients have been reported for either liquid or amorphous alumina. Moreover, previous simulation studies on the liquid and amorphous alumina were mostly concerned with the performances at ambient or high pressures, yielding less information on the relaxed models at zero pressure.

The purpose of this paper is to present a detailed theoretical investigation of the structural, vibrational, and transport properties of the liquid and amorphous alumina using classical MD simulations. Meanwhile, a comparison study was carried out on three densities, in addition to the experimentally reported densities of 2.81 g/cm³ and 3.175 g/cm³ (Tyrolerova and Lu, 1969; Landron et al., 2001a), the relaxed configurations with almost zero pressure were also examined, with the predicted densities of 2.863 g/cm³ at 2500 K, and 3.159 g/cm³ at 300 K. Atomic interactions in classical MD were taken in the form of the Born-Mayer-Huggins (BMH) type, whose parameters were recently optimized by Bouhadja and Jakse (2019) and proved to be efficient in describing the structural and dynamical properties of Calcium oxide (CaO) (Alvares et al., 2020), aluminosilicate (AS) (Bouhadja and Jakse, 2019) binary and calcium aluminosilicate (CAS) (Bouhadja et al., 2013; 2014b; a) ternary systems. These parameters have not, however, been employed in the pure liquid and amorphous alumina systems.

Structural properties were determined by pair distribution functions, coordination numbers, and bond-angle distributions. Vibrational density of states (VDOS) was obtained from the Fourier transform of the velocity autocorrelation function (VACF). Transport coefficients as thermal conductivities and viscosities were investigated by the Green-Kubo formula using the equilibrium molecular dynamics (EMD) simulations, while the mean squared displacements (MSD) were employed for the estimation of the self-diffusion coefficients.

2 Simulation background

Atomic interactions for the liquid and amorphous alumina system were described by the Born-Mayer-Huggins (BMH) potential, for which interactions between Al and O atoms are given by

$\begin{array}{c}V\left(r_{ij}\right)=\frac{q_i{q}_j}{r_{ij}}+A_{ij}\exp \left(\frac{{\sigma }_{ij}-r_{ij}}{{\rho }_{ij}}\right)-{\left(\frac{C_{ij}}{r_{ij}}\right)}^6-{\left(\frac{D_{ij}}{r_{ij}}\right)}^8\end{array}(1)$

where the first term of this pair potential corresponds to the long-range Coulomb potential, the second one to the Born repulsive, and the third and the fourth ones are referred to the dipolar expansion, in which only the van der Waals term was considered. For the ith ion and the jth ion, the distance between the centers is given by r_ij, while q_i and q_j are the effective charges, and A_ij, σ_ij, ρ_ij, and C_ij are some parameters recently optimized by Bouhadja and Jakse (2019), as shown in Table 1.

TABLE 1

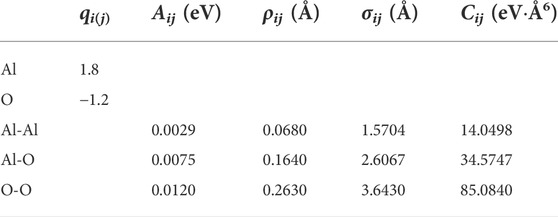
TABLE 1. Parameters for the alumina potentials taken from Bouhadja and Jakse (2019) study.

Using the LAMMPS package (Thompson et al., 2022), classical MD simulations were performed to investigate the structural and dynamic properties of the liquid and the amorphous alumina. The Ewald summation method with a cutoff of 12 Å was used to account for Coulomb interactions, which meant that pairwise interactions within 12 Å were computed directly, and those outside this range were computed in reciprocal space. The short-range interaction was truncated at 8.0 Å. All MD simulations reported in this paper were performed for a system with 2000 atoms (800 Al+1200 O), which was generated by placing the atoms randomly in a basic cube. Periodic boundary conditions were imposed, and the equations of motion were solved using the velocity Verlet algorithm with a time step of 10⁻³ ps. Firstly, the system was equilibrated for 1 ns at a temperature of 4500 K in the isobaric-isothermal ensemble (NPT) with zero pressure, and a well-thermalized liquid was obtained. Subsequently, this liquid was cooled at a rate of 1 K/ps to T = 300 K. During this process, the configurations were stored and equilibrated at intervals of 500 K for 1,000 ps at the corresponding temperature and zero pressure. Moreover, using this relaxed configuration, two models with densities equal to 2.81 g/cm³ and 3.175 g/cm³ (Tyrolerova and Lu, 1969; Landron et al., 2001a) were prepared respectively by volume change, which corresponded to the experimentally reported densities for the liquid alumina at 2500 K and the amorphous alumina at 300 K, respectively. Thus, in this study, the structural and dynamical properties for amorphous alumina were produced at 300 K, while those for liquid alumina were produced at 2500 K, to make it easier to compare the simulation results with the experimental data. Meanwhile, simulations were conducted for three densities at each temperature, besides the experimental densities of 2.81 g/cm³ and 3.175 g/cm³, the predicted densities at almost zero pressure (2.863 g/cm³ at 2500 K, and 3.159 g/cm³ at 300 K) were also explored. The density and the mean pressure in each model are shown in Table 2.

TABLE 2

TABLE 2. Density and mean pressure in each configuration.

3 Results and discussion

3.1 Structural correlations for amorphous and liquid alumina

3.1.1 Structural correlations for amorphous alumina

Structural properties were analyzed through testing atomic correlations, such as pair distribution functions (g(r)), coordination numbers, bond-angle distributions, and the nearest-neighbor connectivity of the basic structural units. The partial pair distribution functions g_ij(r) give the probability of finding a particle j in a spherical shell between r and r+Δr, relative to a particle i located at the origin. And it is calculated from:

$\begin{array}{c}{g}_{ij}\left(r\right)=\frac{\langle n_{ij}\left(r,r+\Delta r\right)\rangle }{\mathrm{4}\pi r^{\mathrm{2}}{\rho }_j\Delta r}\left(i,j=\mathrm{A}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{O}\right)\end{array}(2)$

where $\langle n_{ij}\left(r,r+\Delta r\right)\rangle$ is the number of the j particles in the distance between r and r+Δr around an i particle, ${\rho }_j=N_j/V$ represents the number density of the particle j (N_j is the total number of the j particles). The total pair-distribution function is determined by:

$\begin{array}{c}g\left(r\right)={\displaystyle \sum }_{i,j}{c}_i{c}_j{g}_{ij}\left(r\right)\end{array}(3)$

here, $c_{i\left(j\right)}=N_{i\left(j\right)}/N$ represents the concentration of the i or j particles ($N=N_i+N_j$, the total number of particles). The coordination number Z_ij(R), which determines the average number of the j particles around an i particle, is obtained by integration around the first peak of the corresponding g_ij(r):

$\begin{array}{c}{Z}_{ij}\left(R\right)=\mathrm{4}\pi {\rho }_j{\int }_{\mathrm{0}}^{\mathrm{R}}{g}_{ij}\left(r\right)r^{\mathrm{2}}\mathrm{d}r\end{array}(4)$

where R is a cutoff, usually chosen as the position of the minimum after the first peak of g_ij(r). In this study, the fixed values of R were chosen as R_Al-Al = 3.76 Å, R_Al-O = 2.38 Å, and R_O-O = 3.65 Å to calculate the coordination number distributions and the bond-angle distributions.

Figure 1 shows the total and partial pair distribution functions for amorphous alumina at 300 K. As can be seen, the peak positions of the predicted total pair distribution functions (g(r)) corresponded well with the experimental data reported by Lamparter and Kniep (1997) (Figure 1D). The first peak in the g_Al-O correlation (Figure 1A), which related to the Al-O bond length, was observed at 1.797 Å for the density of 2.81 g/cm³, and shifted respectively to 1.776 Å and 1.775 Å for the two larger densities of 3.159 g/cm³ and 3.175 g/cm³. Similarly, the first peaks in the g_O-O and g_Al-Al correlations (Figures 1B,C) moved to small values as density increased. The initial peak positions in all partial pair distribution functions as well as the average coordination numbers for all the atom pairs are displayed in Table 3. Notably, the average coordination numbers for all the atom pairs increased along with density, although the distances between atoms decreased, which denoted that both the sizes of the structural units and the lengths of the connections decreased, indicating a densely packed-like structure.

FIGURE 1

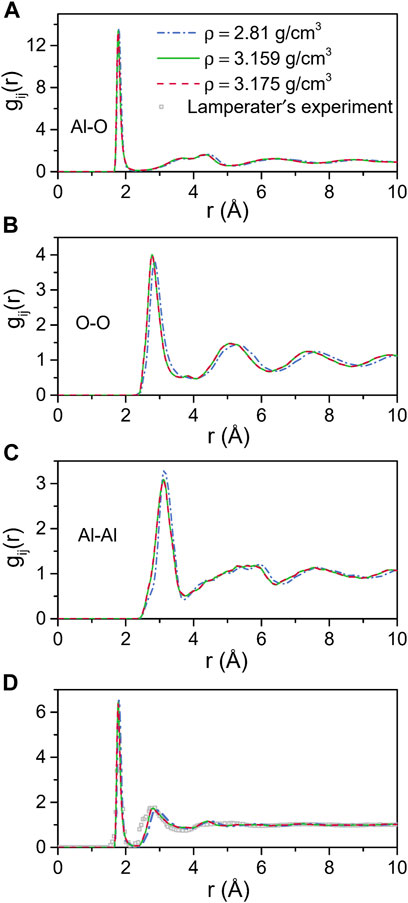
FIGURE 1. MD results for total and partial pair distribution functions for amorphous alumina at 300 K and three densities. (A) Al-O, (B) O-O and (C) Al-Al partial pair distribution functions, (D) Comparison with the neutron pair distribution function from Lamperater’s experiment.

TABLE 3

TABLE 3. Structural characteristics of amorphous alumina at 300 K and three densities. r_ij-positions of the first peaks in partial pair distribution functions; Z_ij-the average coordination number.

More details about the coordination number distributions for amorphous alumina at 300 K are shown in Figure 2. The coordination number distribution of the Al-O pair could be used to infer the network structure. As shown in Figure 2A, each Al atom was principally surrounded by four O atoms, although there was also some AlO₅ and AlO₆ present, especially for ρ = 3.159 g/cm³ and ρ = 3.175 g/cm³. The coordination number for the O-Al pair exhibited a similar narrow distribution to that of the Al-O pair, falling between 2 and 5 (Figure 2B). The ranges of the coordination numbers, however, were wider for O-O and Al-Al, with maximums of 9 or 10 for the O-O pair (Figure 2C), and 8 or 9 for the Al-Al pair (Figure 2D).

FIGURE 2

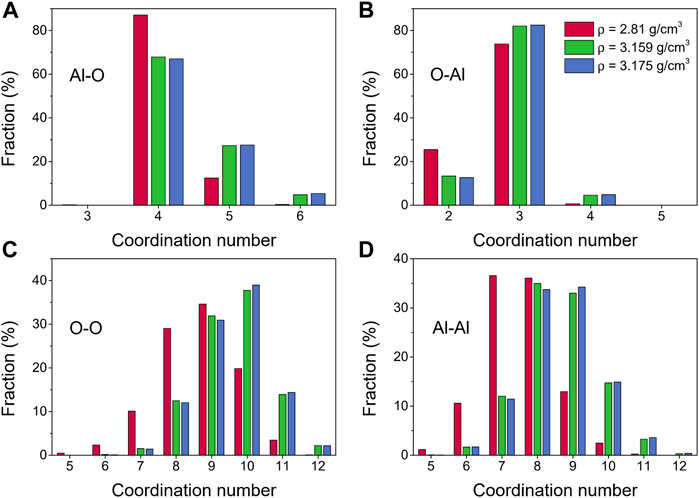
FIGURE 2. Coordination number distributions for amorphous alumina at 300 K and three densities, (A) Al-O, (B) O-Al, (C) O-O and (D) Al-Al.

The bond-angle distributions, as illustrated in Figure 3, provided additional information regarding the structure of amorphous alumina at 300 K. It is well known that for an ideal AlO₄ tetrahedron, ∠Al-O-O = 35.26°, ∠O-O-O = 60°, and ∠O-Al-O = 109.47°. In this study, as the densities ranged from 2.81 g/cm³ to 3.175 g/cm³, the bond-angle distributions for∠O-Al-O, O-O-O, and Al-O-O respectively displayed the main peaks around 37.77°–38.68°, 57.49°–57.06°, and 104.32°–103.22° (Figures 3A,B,F). Combining this information with the interatomic distances and coordination numbers, it could be inferred that a slightly distorted (AlO₄)⁵⁻ tetrahedron was the main basic unit for the formation of the amorphous alumina system. Additionally, two peaks around 91° and 169°, indicating the presence of AlO₅ and AlO₆, were observed in the O-Al-O bond-angle distribution for ρ = 3.159 g/cm³ and 3.175 g/cm³ (Figure 3F), which corresponded to the changes in the coordination number distributions for Al-O pair, demonstrating a trend of transition from tetrahedral to octahedral networks of the structural basic units.

FIGURE 3

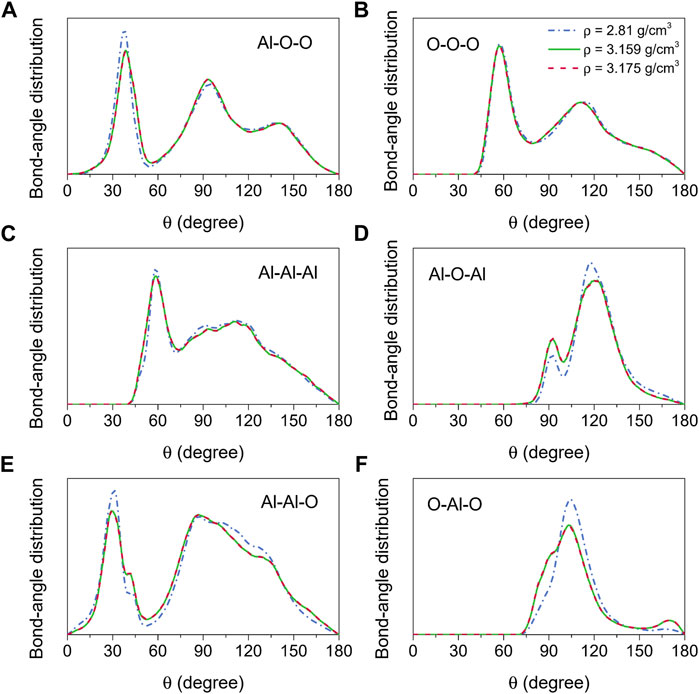
FIGURE 3. Bond-angle distributions for amorphous alumina at 300 K and three densities, (A) Al-O-O, (B) O-O-O, (C) Al-Al-Al, (D) Al-O-Al, (E) Al-Al-O and (F) O-Al-O.

3.1.2 Structural correlations for liquid alumina

The total and partial pair distribution functions for the liquid models at 2500 K are shown in Figure 4. Figure 4D compared the total pair distribution functions to the neutron radial distribution function derived from the experimental data given by Landron et al. (2001a). Although there were some differences in the amplitude and the shape of the peaks, the positions of the peaks were nearly coincident. The initial peaks in the partial pair distribution functions for the Al-O correlations (Figure 4A) were found to be at 1.765 Å and 1.766 Å when ρ = 2.81 g/cm³ and 2.863 g/cm³, respectively, which were in excellent agreement with the experimental findings of 1.76 ± 0.01 Å (Landron et al., 2001a; Landron et al., 2001b), and shifted to 1.772 Å when ρ = 3.175 g/cm³. Numerical values of the peak positions in partial pair distribution functions and the average coordination numbers are summarized in Table 4. When density increased from 2.81 g/cm³ to 3.175 g/cm³, r_ij changed in ways that were consistent with Hoang and Oh (2005) study, with r_Al-Al and r_O-O decreasing and r_Al-O slightly increasing.

FIGURE 4

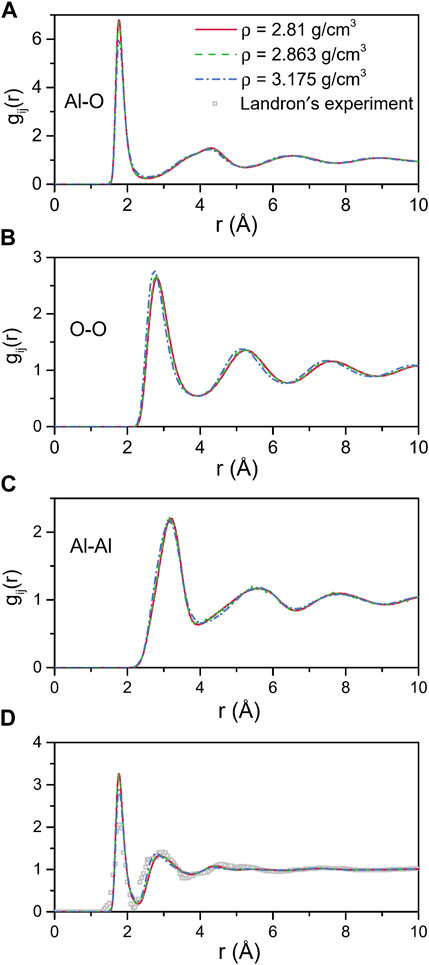
FIGURE 4. MD results for total and partial pair distribution functions for liquid alumina at 2500 K and three densities. (A) Al-O, (B) O-O and (C) Al-Al partial pair distribution functions, (D) Comparison with the neutron pair distribution function from Landron’s experiment.

TABLE 4

TABLE 4. Structural characteristics of liquid alumina at 2500 K and three densities. r_ij-positions of the first peaks in partial pair distribution functions; Z_ij-the average coordination number.

Further information about the liquid alumina structure at 2500 K can be obtained from the coordination number distributions, as displayed in Figure 5. The coordination numbers of liquid alumina have been explored by some experimental studies so far, especially for the Al-O pair, with the most common result being ∼ 4 (Coutures et al., 1990; Poe et al., 1992; Florian et al., 1995; Hennet et al., 2002; Krishnan et al., 2005; Kohara et al., 2007). However, Waseda et al. (1995) indicated that in both corundum and liquid alumina, the octahedrally coordinated aluminum was the main structural basic unit. In accordance with most of the previous experimental research, the coordination numbers for the Al-O pair obtained by our study were mainly distributed at 4 (Figure 5A). The fractions of the 5-fold and 6-fold Al increased with density, just as the cases at 300 K, suggesting that the structural transition also happened in the liquid state.

FIGURE 5

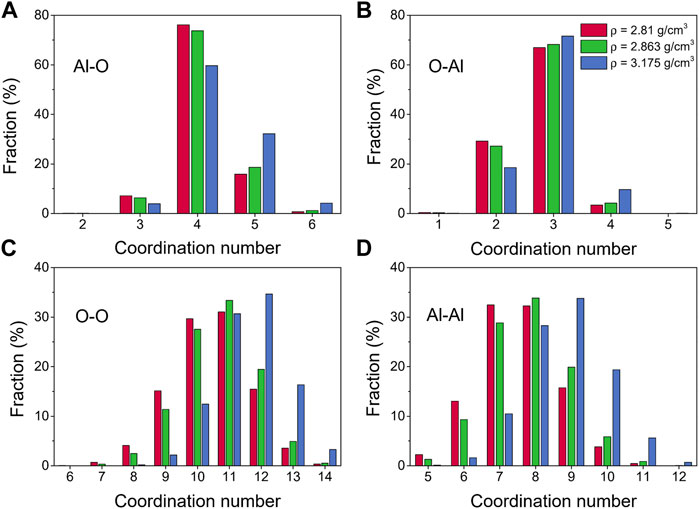
FIGURE 5. Coordination number distributions for liquid alumina at 2500 K and three densities, (A) Al-O, (B) O-Al, (C) O-O and (D) Al-Al.

Bond-angle distributions for the liquid alumina at 2500 K are shown in Figure 6. The initial peaks in the O-Al-O bond-angle distribution moved toward small values with density raising, and were located at 98.63° and 97.03° (Figure 6F) respectively for ρ = 2.81 g/cm³ and 2.863 g/cm³, which were very close to Greaves et al. (2001) experimental value of 97°. As density increased to 3.175 g/cm³, the initial peak appeared at 92.18°, moreover, the intensity of the minor peak around 164.34° also increased. According to Hung et al. (2006) analysis, these two peaks suggested the presence of some AlO₅ and AlO₆, which can be observed more intuitively from the coordination number distribution for the Al-O pair, as shown in Figure 5A.

FIGURE 6

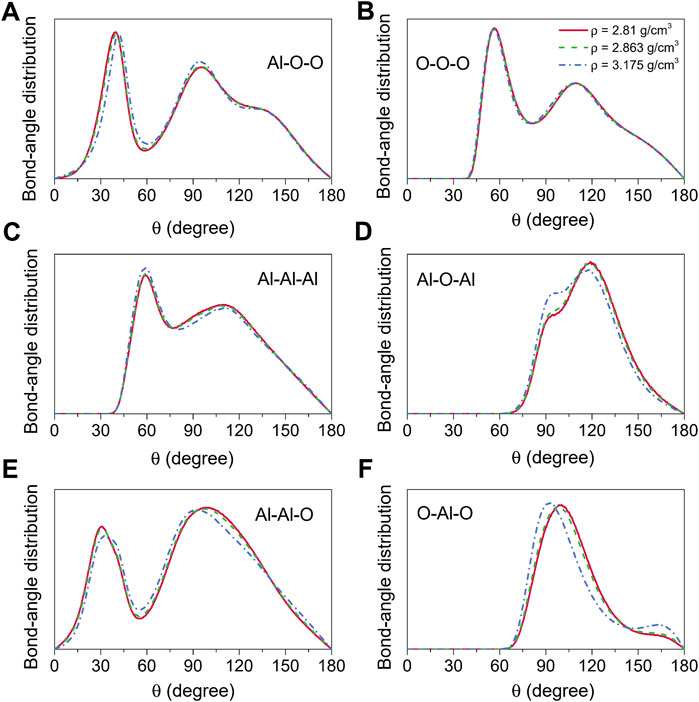
FIGURE 6. Bond-angle distributions for liquid alumina at 2500 K and three densities, (A) Al-O-O, (B) O-O-O, (C) Al-Al-Al, (D) Al-O-Al, (E) Al-Al-O and (F) O-Al-O.

By using the BMH potential with the recently optimized parameters, the predicted densities of 3.159 g/cm³ and 2.863 g/cm³ were obtained at zero pressure with temperatures of 300 K and 2500 K respectively, which were very close to the experimental results of 3.175 g/cm³ and 2.81 g/cm³. Additionally, for both amorphous and liquid alumina, good agreements in the short-range order were found between the simulation and the experimental findings. These results demonstrated a well reproducibility of the chemical order, indicating the high reliability of the potential.

3.1.3 Connectivity of the basic units

The Al-O-Al bond-angle distribution can be used to analyze the nearest-neighbor connectivity of the basic structural units AlO_x in terms of the structure beyond the short-range order. There are two principal ways for the basic units linked to each other, one is the edge/face-sharing network, which is compatible with the peak at 90° in the Al-O-Al bond-angle distribution, and the other is the corner-sharing network, which corresponds to the peak observed at 120°. In this study, for the amorphous models at 300 K, two peaks around 92° and 120° could be found in the Al-O-Al bond-angle distribution (Figure 3D), whereas they were located at 94° and 119° for the liquid models at 2500 K (Figure 6D). These findings indicated that the basic units were linked together not only by sharing corners but also by sharing edges and faces in both amorphous and liquid states.

3.2 Vibrational and transport properties of amorphous and liquid alumina

3.2.1 Velocity autocorrelation function

The velocity autocorrelation function (VACF) represents the correlation between the velocity of the particle at time t and its velocity at time t = 0, and is defined as:

$\begin{array}{c}Z\left(t\right)=\frac{\langle v_i\left(t\right)\bullet v_i\left(\mathrm{0}\right)\rangle }{\langle v_i^{\mathrm{2}}\left(\mathrm{0}\right)\rangle }\end{array}(5)$

where v_i(t) is the velocity of the ith particle at time t, and the brackets mean averages over atoms and a suitable ensemble.

As illustrated in Figure 7, the density dependence was negligible for this density range. The VACF curves rapidly decreased from the initial value of 1 to a negative well in a short time, indicating a back-scattering effect caused by the cages of the nearest neighbor atoms. And then, it damped rapidly toward zero. Compared with those for 300 K, the minimum values of the curves for 2500 K were less deep, which demonstrated that the motional randomness increased with temperature, implying the tendency to Brownian motion as described by the Langevin equation.

FIGURE 7

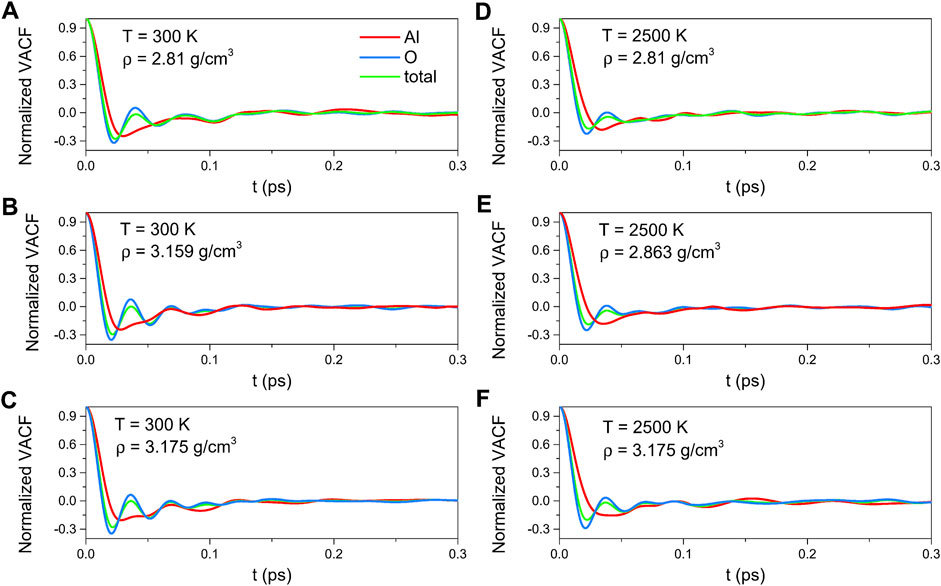
FIGURE 7. Velocity autocorrelation functions for amorphous alumina at 300 K, (A) ρ = 2.81 g/cm³, (B) ρ = 3.159 g/cm³ and (C) ρ = 3.175 g/cm³, and for liquid alumina at 2500 K, (D) ρ = 2.81 g/cm³, (E) ρ = 2.863 g/cm³ and (F) ρ = 3.175 g/cm³.

3.2.2 Vibrational density of states

The vibrational density of states (VDOS) was predicted by computing the Fourier-transform of the VACF as follows:

$\begin{array}{c}G\left(\omega \right)=\frac{\mathrm{1}}{\mathrm{2}\pi }{\int }_{\mathrm{0}}^{\mathrm{\infty }}Z\left(t\right)e^{-i\omega t}\mathrm{d}t\end{array}(6)$

The total and partial VDOSs for liquid alumina at 2500 K and amorphous alumina at 300 K with different densities are shown in Figure 8. Each VDOS spectrum was divided into two primary bands: a lower frequency band ranging from 0 THz up to about 20 THz, and a higher frequency band ranging from about 20 THz to 37 THz for the amorphous states, or from 20 THz to 45 THz for the liquid states. Based on the participation ratio of each species (Al or O) to the total VDOSs, the lower frequency band was mainly profiled from the vibration of Al atoms, whereas the higher frequency band was due to the vibration of O atoms, in agreement with the ab initio calculation results of Gutiérrez et al (Sergio and Gonzalo, 2011). Furthermore, these VDOSs findings for the amorphous alumina were comparable to those for other amorphous networks, such as GeO₂ and SiO₂ (Giacomazzi et al., 2005; Giacomazzi and Pasquarello, 2007), which were primarily composed of a basic tetrahedron. According to Bell (1972) report, the lower band was related to the bond-bending modes, associating with inter-tetrahedra vibrations, while the higher band was related to the bonding-stretching modes, associating with intra-tetrahedra vibrations.

FIGURE 8

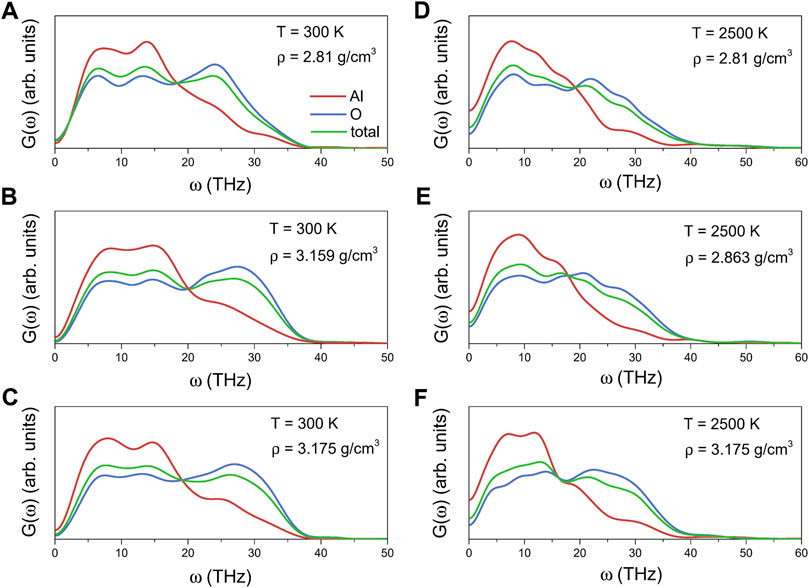
FIGURE 8. Total and partial vibrational density of states for amorphous alumina at 300 K, (A) ρ = 2.81 g/cm³, (B) ρ = 3.159 g/cm³ and (C) ρ = 3.175 g/cm³, and for liquid alumina at 2500 K, (D) ρ = 2.81 g/cm³, (E) ρ = 2.863 g/cm³ and (F) ρ = 3.175 g/cm³.

3.2.3 Self-diffusion coefficient

Due to the sensitivity of the transport coefficients (self-diffusion coefficients, thermal conductivities and viscosities) to the initial conditions, for each configuration, five independent simulations with different starting momenta were conducted to reduce the statistical errors. And the results were obtained by averaging and calculating the standard deviations over the independent simulations.

For a pure liquid in thermodynamic equilibrium, the self-diffusion of the particles is defined as the translational motion caused by thermal agitation. And the self-diffusion coefficient (D) describes the single-particle motion on a microscopic level from the molecular point of view, which can be calculated from the long-time limit of the mean squared displacement (MSD) via the Einstein relation:

$\begin{array}{c}{D}_i=\frac{\mathrm{1}}{\mathrm{6}N}\underset{t\to \infty }{\lim }\frac{\mathrm{d}}{\mathrm{d}t}\langle {\displaystyle \sum }_{i=\mathrm{1}}^N{\left|r_i\left(t\right)-r_i\left(\mathrm{0}\right)\right|}^{\mathrm{2}}\rangle \end{array}(7)$

where N is the number of the ith atom, r_i(t) is the position vector of the ith atom at the time t, and the brackets denote averages over the ensemble.

Figures 9A–C show the time dependence of MSDs at 2500 K and three densities, while the corresponding self-diffusion coefficients are displayed in Figure 9D. The slopes of the MSDs for Al were larger than those of O at densities ranging from 2.81 g/cm³ to 3.175 g/cm³, indicating that the motion of the Al particles was faster. This result was in agreement with those reported by Liang and Hoang (Liang et al., 1996; Van Hoang and Oh, 2004), and was most probably caused by the different diffusion mechanisms between Al and O particles. Besides being in the free state, Al particles diffused through the breaking or reforming of Al-O bonds, whereas the conversion of bridging O to nonbridging O, which required higher energies, had an impact on the diffusion of O particles (Liang et al., 1996). Moreover, D decreased with density increasing, from 0.1208 ± 0.0018 Ų/ps to 0.0926 ± 0.0041 Ų/ps for Al particles, from 0.1078 ± 0.0031 Ų/ps to 0.0733 ± 0.0028 Ų/ps for O particles, and from 0.1131 ± 0.0019 Ų/ps to 0.0811 ± 0.0032 Ų/ps for the total systems.

FIGURE 9

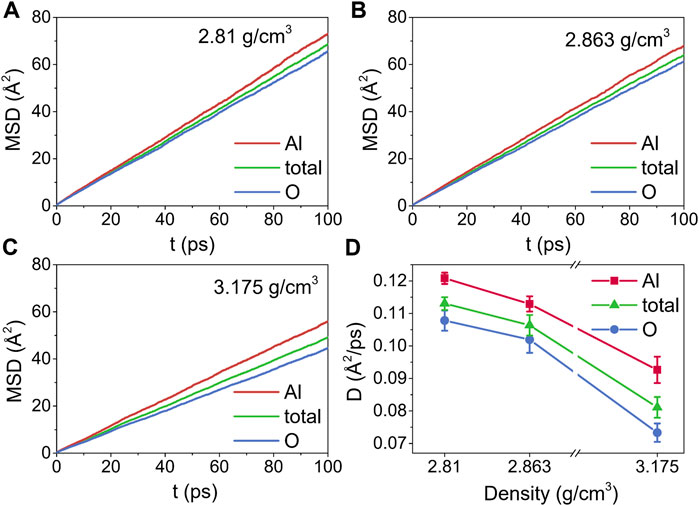
FIGURE 9. The time dependence of mean-squared displacements (MSDs) for liquid alumina at 2500 K, (A) ρ = 2.81 g/cm³, (B) ρ = 2.863 g/cm³ and (C) ρ = 3.175 g/cm³, (D) self-diffusion coefficients (D) for liquid alumina at 2500 K and three densities.

3.2.4 Thermal conductivity

The thermal conductivity (κ) was calculated by EMD simulations through a time integral of the heat current autocorrelation function (HCACF) using the Green-Kubo formulation:

$\begin{array}{c}\kappa \left(t\right)=\frac{V}{\mathrm{3}{k}_B{T}^{\mathrm{2}}}{\int }_{\mathrm{0}}^{\mathrm{t}}\langle J\left(t\right)\bullet J\left(\mathrm{0}\right)\rangle \mathrm{d}t\end{array}(8)$

here, V is the system volume, k_B is the Boltzmann constant, T is the equilibrium temperature, and $\langle J\left(t\right)\bullet J\left(\mathrm{0}\right)\rangle$ is HCACF averaged over the ensemble. The heat current J is defined as:

$\begin{array}{c}J=\frac{{\displaystyle \sum }_i{e}_i{v}_i-{\displaystyle \sum }_i{S}_i{v}_i}{V}\end{array}(9)$

where e_i is the kinetic and potential energy of the ith atom, v_i is the velocity of the ith atom, and S_i is the atomic stress of the ith atom. The normalized HCACF was calculated as $\langle J\left(t\right)\bullet J\left(\mathrm{0}\right)\rangle ∕\langle J\left(\mathrm{0}\right)\cdot J\left(\mathrm{0}\right)\rangle$.

Figures 10, 11 illustrate the normalized HCACFs and thermal conductivities as a function of the correlation time respectively for the amorphous (300 K) and liquid (2500 K) alumina at three densities. Details of the normalized HCACF and thermal conductivity curves over the correlation time of 0–0.5 ps are shown in the insets. The normalized HCACFs declined rapidly from positive to negative and ultimately decayed to zero, as can be observed in the insets of the normalized HCACFs. Correspondingly, the curves of κ first increased to a maximum value, then decreased and oscillated around a constant value, which was taken as the thermal conductivity value of the equilibrated system. In this study, the thermal conductivity values were obtained by averaging, which were taken from 2 to 6 ps for 300 K, and 9–15 ps for 2500 K.

FIGURE 10

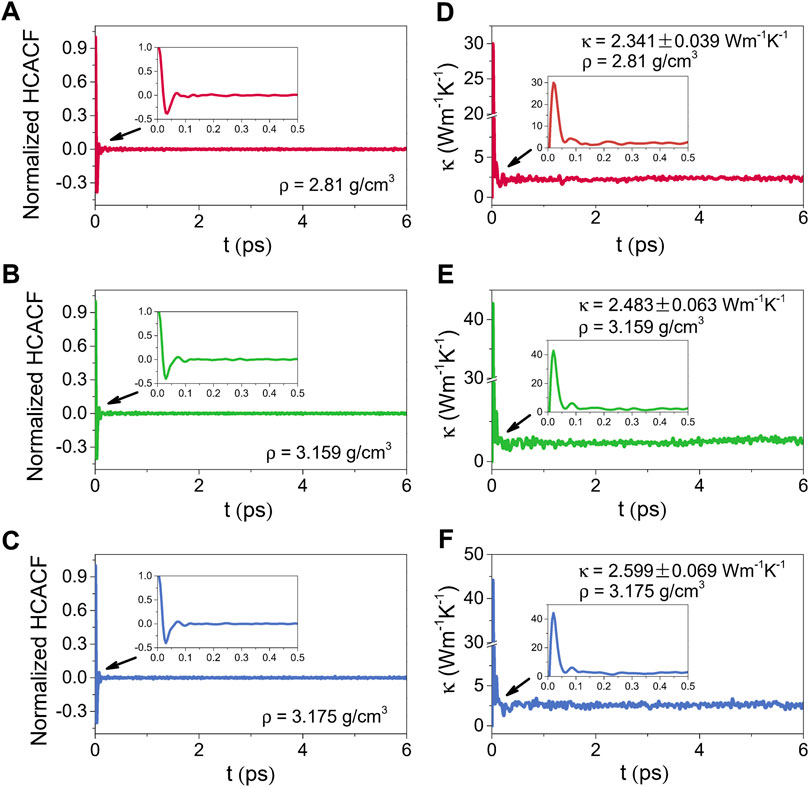
FIGURE 10. Normalized HCACFs for (A) ρ = 2.81 g/cm³, (B) ρ = 3.159 g/cm³ and (C) ρ = 3.175 g/cm³, and thermal conductivities (κ) for (D) ρ = 2.81 g/cm³, (E) ρ = 3.159 g/cm³ and (F) ρ = 3.175 g/cm³ as a function of the correlation time for amorphous alumina at 300 K, insets: the normalized HCACFs and thermal conductivities over the correlation time of 0–0.5 ps.

FIGURE 11

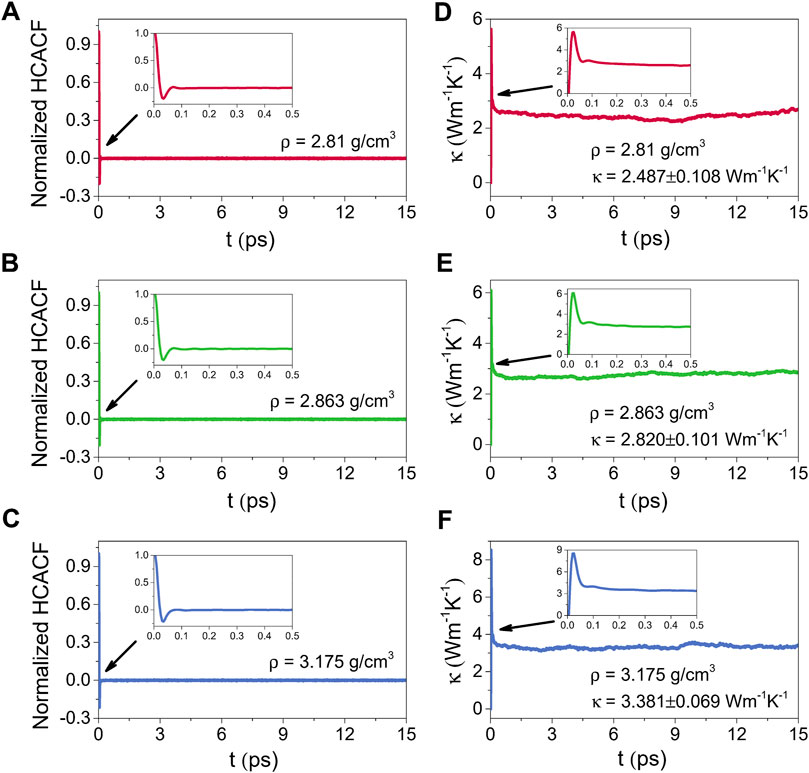
FIGURE 11. Normalized HCACFs for (A) ρ = 2.81 g/cm³, (B) ρ = 2.863 g/cm³ and (C) ρ = 3.175 g/cm³, and thermal conductivities (κ) for (D) ρ = 2.81 g/cm³, (E) ρ = 2.863 g/cm³ and (F) ρ = 3.175 g/cm³ as a function of the correlation time for liquid alumina at 2500 K, insets: the normalized HCACFs and thermal conductivity curves over the correlation time of 0–0.5 ps.

Compared the thermal conductivities at 2500 K with those at 300 K, because phonon scattering was more intense at higher temperatures, the normalized HCACFs decayed faster at 2500 K, converging at zero after 0.1 ps, whereas it takes 0.2 ps at 300 K. The κ for the liquid phases raised obviously as the density increased from 2.81 g/cm³ to 3.175 g/cm³, with the averaged values from 2.487 ± 0.108 Wm⁻¹K⁻¹ to 3.381 ± 0.069 Wm⁻¹K⁻¹. Simultaneously, the increase in κ for the amorphous phases was slower, from 2.341 ± 0.039 Wm⁻¹K⁻¹ to 2.599 ± 0.069 Wm⁻¹K⁻¹, which was much lower than the values for the single crystal (∼53 Wm⁻¹K⁻¹) (Slack, 1962) and polycrystalline (∼30 Wm⁻¹K⁻¹) (Williams et al., 1987) Al₂O₃. However, these results, especially for the density of 2.81 g/cm³, were extremely near to the experimental value of ∼ 2.3 Wm⁻¹K⁻¹ reported by Luo et al. (2014), who measured the thermal conductivity of amorphous alumina using the micro-Raman technique.

3.2.5 Viscosity

The viscosity (η) is also calculated by the Green-Kubo relation, using a time integral of the stress autocorrelation function (SACF), the Green-Kubo relation is given as:

$\begin{array}{c}\eta \left(\tau \right)=\frac{V}{k_{B}T}{\int }_{\mathrm{0}}^{\mathrm{\tau }}\langle P_{\alpha \beta }\left(t\right)\cdot P_{\alpha \beta }\left(\mathrm{0}\right)\rangle \mathrm{d}t\end{array}(10)$

where V is the system volume, k_B is the Boltzmann constant, T is the equilibrium temperature, and $\langle P_{\alpha \beta }\left(t\right)\cdot P_{\alpha \beta }\left(\mathrm{0}\right)\rangle$ is SACF averaged over the ensemble. P_αβ(t) is the component in αβ = xy, xz, and yz directions of the molecular stress tensor of the system:

$\begin{array}{c}{P}_{\alpha \beta }=\frac{\mathrm{1}}{V}\left[m_i\cdot v_{i\alpha }\cdot v_{i\beta }+{\displaystyle \sum }_{j\ne i}{r}_{ij}\cdot F_{ij}\right]\end{array}(11)$

and m_i represents the mass of the ith atom, v_iα and v_iβ are the velocities of the ith atom, $r_{ij}=r_i-r_j$ is the relative position of the ith atom in relation to the jth atom, and F_ij is the force acting upon the ith atom due to interaction with the jth atom.

Figure 12 shows the normalized SACFs and viscosities for liquid alumina at 2500 K and three densities. As illustrated in Figures 12A–C, the SACF curves for three densities monotonically decreased and decayed to 0 within 4 ps. The viscosities initially increased along with the correlation time, and then stabilized around a constant value after about 10 ps, as seen in Figure 12D. Thus, the viscosities between 10 and 17 ps were averaged, which were equal to 0.0261 ± 0.0017 Pa·s, 0.0272 ± 0.0018 Pa·s, and 0.0425 ± 0.0043 Pa·s respectively for densities of 2.81 g/cm³, 2.863 g/cm³, and 3.175 g/cm³. Significantly, the predicted viscosity values at ρ = 2.81 g/cm³ and 2.863 g/cm³ were both in excellent agreement with the experimental data given by Blomquist et al. (1978), where the viscosities of molten alumina at 2458 K and 2509 K were equal to 0.0264 Pa·s and 0.0243 Pa·s respectively, with densities of 2.85 g/cm³ and 2.79 g/cm³.

FIGURE 12

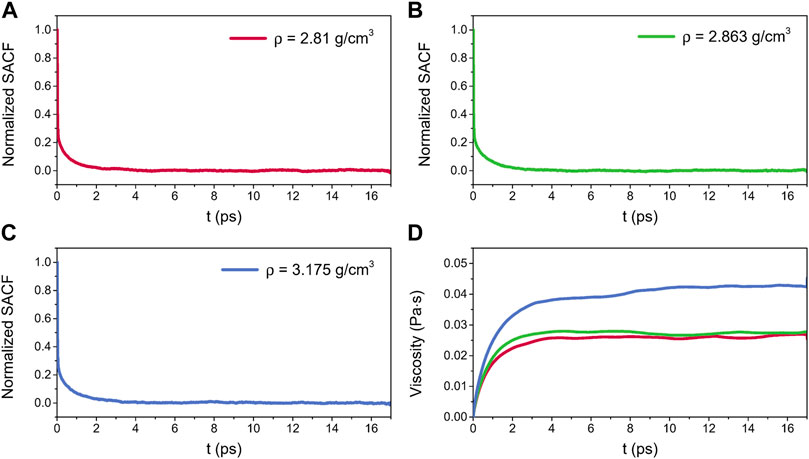
FIGURE 12. Normalized SACFs for liquid alumina at 2500 K as a function of the correlation time, (A) ρ = 2.81 g/cm³, (B) ρ = 2.863 g/cm³ and (C) ρ = 3.175 g/cm³, (D) viscosities for liquid alumina at 2500 K and three densities as a function of the correlation time.

4 Conclusion

In the present investigation, a detailed theoretical study of the structural, vibrational, and transport properties of the liquid and amorphous alumina was provided. The investigations were conducted not only for the experimental densities of 2.81 g/cm³ and 3.175 g/cm³, but also for the predicted densities at almost zero pressure, which were equal to 2.863 g/cm³ at 2500 K, and 3.159 g/cm³ at 300 K, respectively. Classical MD simulations were conducted using an empirical BMH potential with the parameters initially designed for the ternary calcium aluminosilicate system. The results of our study showed that these optimized parameters were also efficient in describing the structural and dynamical properties of the pure liquid and amorphous alumina.

The investigation of the interatomic correlations showed that for both liquid and amorphous alumina, the short-range order was dominated by the slightly distorted (AlO₄)⁵⁻ tetrahedra, with a small amount of AlO₅ and AlO₆ present. Moreover, as the density increased, there was a trend of structural transition from tetrahedral to octahedral networks of the basic units.

The VDOSs for the liquid phases exhibited broader ranges compared with those for the amorphous phases. Each VDOS spectrum was divided into two primary frequency bands for both liquid and amorphous alumina, with the low frequencies for inter-tetrahedra vibrations, and the higher ones for intra-tetrahedra vibrations.

The density dependence of transport properties was also investigated, with self-diffusion coefficients (D) calculated via the slopes of mean squared displacements (MSDs), and shown to be decreased with increasing density. Furthermore, thermal conductivities (κ) and viscosities (η) were obtained using the Green-Kubo relation, and the results from our EMD simulations agreed well with the experimental data, especially that κ was equal to 2.341 ± 0.039 Wm⁻¹K⁻¹ for amorphous alumina at 300 K and 2.81 g/cm³, and η was equal to 0.0261 ± 0.0017 Pa·s and 0.0272 ± 0.0018 Pa·s for the liquid phases at 2500 K with densities of 2.81 g/cm³ and 2.863 g/cm³, respectively.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XLZ, YFZ, and YMZ contributed to the conception and design of the research. XLZ performed the simulations. XLZ, YFZ, and YD conducted the statistical analysis. XLZ wrote the draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Science Foundation of the National Key Laboratory of Science and Technology on Advanced Composites in Special Environments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adiga, S., Zapol, P., and Curtiss, L. (2006). Atomistic simulations of amorphous alumina surfaces. Phys. Rev. B 74 (6), 064204. doi:10.1103/physrevb.74.064204

CrossRef Full Text | Google Scholar

Ahuja, R., Belonoshko, A., and Johansson, B. (1998). Melting and liquid structure of aluminum oxide using a molecular-dynamics simulation. Phys. Rev. E 57 (2), 1673–1676. doi:10.1103/physreve.57.1673

CrossRef Full Text | Google Scholar

Alvares, C. M., Deffrennes, G., Pisch, A., and Jakse, N. (2020). Thermodynamics and structural properties of CaO: A molecular dynamics simulation study. J. Chem. Phys. 152 (8), 084503. doi:10.1063/1.5141841

PubMed Abstract | CrossRef Full Text | Google Scholar

Avis, C., and Jang, J. (2011). High-performance solution processed oxide TFT with aluminum oxide gate dielectric fabricated by a sol-gel method. J. Mat. Chem. 21 (29), 10649–10652. doi:10.1039/c1jm12227d

CrossRef Full Text | Google Scholar

Bell, R. (1972). The dynamics of disordered lattices. Rep. Prog. Phys. 35 (3), 306–1409. doi:10.1088/0034-4885/35/3/306

CrossRef Full Text | Google Scholar

Blomquist, R. A., Fink, J., and Leibowitz, L. (1978). Viscosity of molten alumina. IL, USA: Argonne National Laboratory Lemont.

Google Scholar

Blonkowski, S. (2007). Nonlinear capacitance variations in amorphous oxide metal-insulator-metal structures. Appl. Phys. Lett. 91 (17), 172903. doi:10.1063/1.2800291

CrossRef Full Text | Google Scholar

Boisier, G., Raciulete, M., Samélor, D., Pébère, N., Gleizes, A., and Vahlas, C. (2008). Electrochemical behavior of chemical vapor deposited protective aluminum oxide coatings on Ti6242 titanium alloy. Electrochem. Solid-State Lett. 11 (10), C55. doi:10.1149/1.2968109

CrossRef Full Text | Google Scholar

Bouhadja, M., Jakse, N., and Pasturel, A. (2014a). Stokes-einstein violation and fragility in calcium aluminosilicate glass formers: a molecular dynamics study. Mol. Simul. 40 (1-3), 251–259. doi:10.1080/08927022.2013.840893

CrossRef Full Text | Google Scholar

Bouhadja, M., Jakse, N., and Pasturel, A. (2014b). Striking role of non-bridging oxygen on glass transition temperature of calcium aluminosilicate glass-formers. J. Chem. Phys. 140 (23), 234507. doi:10.1063/1.4882283

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouhadja, M., Jakse, N., and Pasturel, A. (2013). Structural and dynamic properties of calcium aluminosilicate melts: a molecular dynamics study. J. Chem. Phys. 138 (22), 224510. doi:10.1063/1.4809523

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouhadja, M., and Jakse, N. (2019). Structural and dynamic properties of aluminosilicate melts: A molecular dynamics study. J. Phys. Condens. Matter 32 (10), 104002. doi:10.1088/1361-648x/ab58ea

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourdillon, A., El-Mashri, S., and Forty, A. (1984). Application of TEM extended electron energy loss fine structure to the study of aluminium oxide films. Philos. Mag. A 49 (3), 341–352. doi:10.1080/01418618408233278

CrossRef Full Text | Google Scholar

Chang, H., Choi, Y., Kong, K., and Ryu, B.-H. (2004). Atomic and electronic structures of amorphous Al₂O₃. Chem. Phys. Lett. 391 (4-6), 293–296. doi:10.1016/s0009-2614(04)00716-x

CrossRef Full Text | Google Scholar

Couto, M., Vasconcelos, D. P., Sousa, D. M., Sousa, B., Conceição, F., Neto, E., et al. (2020). The mechanisms underlying the biological response to wear debris in periprosthetic inflammation. Front. Mat. 7, 274. doi:10.3389/fmats.2020.00274

CrossRef Full Text | Google Scholar

Coutures, J. P., Massiot, D., Bessada, C., Echegut, P., and Taulelle, F. (1990). Etude par RMN 27A1 d'aluminates liquides dans le domaine 1600-2100 °C. Comptes Rendus l'Académie Sci. Paris 310, 1041.

Google Scholar

Cristiglio, V., Hennet, L., Cuello, G., Johnson, M., Fernandez-Martinez, A., Fischer, H., et al. (2007). Ab-initio molecular dynamics simulations of the structure of liquid aluminates. J. non-crystalline solids 353 (18-21), 1789–1792. doi:10.1016/j.jnoncrysol.2007.01.075

CrossRef Full Text | Google Scholar

Daubert, J. S., Hill, G. T., Gotsch, H. N., Gremaud, A. P., Ovental, J. S., Williams, P. S., et al. (2017). Corrosion protection of copper using Al₂O₃, TiO₂, ZnO, HfO₂, and ZrO₂ atomic layer deposition. ACS Appl. Mat. Interfaces 9 (4), 4192–4201. doi:10.1021/acsami.6b13571

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, N., Zhao, J., Yang, L., and Zheng, Z. (2021). Effects of brazing technology on hermeticity of alumina ceramic-metal joint used in nuclear power plants. Front. Mat. 7, 580938. doi:10.3389/fmats.2020.580938

CrossRef Full Text | Google Scholar

El-Mashri, S., Jones, R., and Forty, A. (1983). An electron-yield EXAFS study of anodic-oxide and hydrated-oxide films on pure aluminium. Philos. Mag. A 48 (5), 665–683. doi:10.1080/01418618308236536

CrossRef Full Text | Google Scholar

Es-Souni, M., and Habouti, S. (2014). Ordered nanomaterial thin films via supported anodized alumina templates. Front. Mat. 1, 19. doi:10.3389/fmats.2014.00019

CrossRef Full Text | Google Scholar

Farr, W. G., Creedon, D. L., Goryachev, M., Benmessai, K., and Tobar, M. E. (2013). Ultrasensitive microwave spectroscopy of paramagnetic impurities in sapphire crystals at millikelvin temperatures. Phys. Rev. B 88 (22), 224426. doi:10.1103/physrevb.88.224426

CrossRef Full Text | Google Scholar

Florian, P., Massiot, D., Poe, B., Farnan, I., and Coutures, J. P. (1995). A time resolved 27Al NMR study of the cooling process of liquid alumina from 2450 C to crystallisation. Solid state Nucl. magn. Reson. 5 (3), 233–238. doi:10.1016/0926-2040(95)01188-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukuhara, M., Kuroda, T., Hasegawa, F., Hashida, T., Takeda, M., Konno, K., et al. (2021). AlO6 clusters’ electric storage effect in amorphous alumina supercapacitors. Sci. Rep. 11 (1), 1699–1706. doi:10.1038/s41598-021-81483-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Giacomazzi, L., and Pasquarello, A. (2007). Vibrational spectra of vitreous SiO₂ and vitreous GeO₂ from first principles. J. Phys. Condens. Matter 19 (41), 415112. doi:10.1088/0953-8984/19/41/415112

PubMed Abstract | CrossRef Full Text | Google Scholar

Giacomazzi, L., Umari, P., and Pasquarello, A. (2005). Medium-range structural properties of vitreous germania obtained through first-principles analysis of vibrational spectra. Phys. Rev. Lett. 95 (7), 075505. doi:10.1103/physrevlett.95.075505

PubMed Abstract | CrossRef Full Text | Google Scholar

Golubović, A., Nikolić, S., Đurić, S., and Valčić, A. (2001). The growth of sapphire single crystals. J. Serbian Chem. Soc. 66 (6), 411–418. doi:10.2298/jsc0106411g

CrossRef Full Text | Google Scholar

Greaves, G. N., Jenkins, T. E., Soper, A. K., Landron, C., and Coutures, J. P. (2001). Neutron scattering experiments on solids and liquids at elevated temperatures using an aerodynamic laser-heated furnace. Microgravity Res. Appl. Phys. Sci. Biotech. 454, 699–706.

Google Scholar

Gutierrez, G., and Johansson, B. (2002). Molecular dynamics study of structural properties of amorphous Al₂O₃. Phys. Rev. B 65 (10), 104202. doi:10.1103/physrevb.65.104202

CrossRef Full Text | Google Scholar

Gutiérrez, G., Menéndez-Proupin, E., Loyola, C., Peralta, J., and Davis, S. (2010). Computer simulation study of amorphous compounds: structural and vibrational properties. J. Mat. Sci. 45 (18), 5124–5134. doi:10.1007/s10853-010-4579-0

CrossRef Full Text | Google Scholar

Hadjicharalambous, C., Prymak, O., Loza, K., Buyakov, A., Kulkov, S., and Chatzinikolaidou, M. (2015). Effect of porosity of alumina and zirconia ceramics toward pre-osteoblast response. Front. Bioeng. Biotechnol. 3, 175. doi:10.3389/fbioe.2015.00175

PubMed Abstract | CrossRef Full Text | Google Scholar

Hemmati, M., Wilson, M., and Madden, P. A. (1999). Structure of liquid Al₂O₃ from a computer simulation model. J. Phys. Chem. B 103 (20), 4023–4028. doi:10.1021/jp983529f

CrossRef Full Text | Google Scholar

Hennet, L., Thiaudiere, D., Gailhanou, M., Landron, C., Coutures, J.-P., and Price, D. L. (2002). Fast x-ray scattering measurements on molten alumina using a 120 curved position sensitive detector. Rev. Sci. Instrum. 73 (1), 124–129. doi:10.1063/1.1426228

CrossRef Full Text | Google Scholar

Hoang, V. V., and Oh, S. K. (2005). Simulation of pressure-induced phase transition in liquid and amorphous Al₂O₃. Phys. Rev. B 72 (72), 054209. doi:10.1103/physrevb.72.054209

CrossRef Full Text | Google Scholar

Hung, P., Vinh, L., Nghiep, D., and Nguyen, P. (2006). Computer simulation of liquid Al₂O₃. J. Phys. Condens. Matter 18 (41), 9309–9322. doi:10.1088/0953-8984/18/41/001

CrossRef Full Text | Google Scholar

Jahn, S., and Madden, P. (2008). Atomic dynamics of alumina melt: A molecular dynamics simulation study. Condens. Matter Phys. 11, 169–178. doi:10.5488/cmp.11.1.169

CrossRef Full Text | Google Scholar

Jani, A. M. M., Losic, D., and Voelcker, N. H. (2013). Nanoporous anodic aluminium oxide: Advances in surface engineering and emerging applications. Prog. Mater. Sci. 58 (5), 636–704. doi:10.1016/j.pmatsci.2013.01.002

CrossRef Full Text | Google Scholar

Jennison, D., Schultz, P., and Sullivan, J. (2004). Evidence for interstitial hydrogen as the dominant electronic defect in nanometer alumina films. Phys. Rev. B 69 (4), 041405. doi:10.1103/physrevb.69.041405

CrossRef Full Text | Google Scholar

Katiyar, P., Jin, C., and Narayan, R. (2005). Electrical properties of amorphous aluminum oxide thin films. Acta Mater. 53 (9), 2617–2622. doi:10.1016/j.actamat.2005.02.027

CrossRef Full Text | Google Scholar

Kohara, S., Itou, M., Suzuya, K., Inamura, Y., Sakurai, Y., Ohishi, Y., et al. (2007). Structural studies of disordered materials using high-energy x-ray diffraction from ambient to extreme conditions. J. Phys. Condens. Matter 19 (50), 506101. doi:10.1088/0953-8984/19/50/506101

CrossRef Full Text | Google Scholar

Krishnan, S., Hennet, L., Jahn, S., Key, T. A., Madden, P. A., Saboungi, M. L., et al. (2005). Structure of normal and supercooled liquid aluminum oxide. Chem. Mat. 17 (10), 2662–2666. doi:10.1021/cm050254p

CrossRef Full Text | Google Scholar

Lamparter, P., and Kniep, R. (1997). Structure of amorphous Al₂O₃. Phys. B Condens. Matter 234, 405–406. doi:10.1016/s0921-4526(96)01044-7

CrossRef Full Text | Google Scholar

Landron, C., Hennet, L., Jenkins, T., Greaves, G., Coutures, J., and Soper, A. (2001a). Liquid alumina: detailed atomic coordination determined from neutron diffraction data using empirical potential structure refinement. Phys. Rev. Lett. 86 (21), 4839–4842. doi:10.1103/physrevlett.86.4839

PubMed Abstract | CrossRef Full Text | Google Scholar

Landron, C., Soper, A., Jenkins, T., Greaves, G., Hennet, L., and Coutures, J. (2001b). Measuring neutron scattering structure factor for liquid alumina and analysing the radial distribution function by empirical potential structural refinement. J. non-crystalline solids 293, 453–457. doi:10.1016/s0022-3093(01)00839-0

CrossRef Full Text | Google Scholar

Li, H., Liu, Y., Liu, Y., Zeng, Q., and Liang, J. (2019). Thermal treatment of γ- Al₂O₃ for the preparation of stereolithography 3D printing ceramic slurries. Front. Mat. 6, 295. doi:10.3389/fmats.2019.00295

CrossRef Full Text | Google Scholar

Liang, Y., Richter, F. M., Davis, A. M., and Watson, E. B. (1996). Diffusion in silicate melts: . Self diffusion in CaO-Al₂O₃-SiO₂ at 1500 °C and 1 GPa. Geochimica Cosmochimica Acta 22, 4353, doi:10.1103/physrevb.83.094201

CrossRef Full Text | Google Scholar

Lizárraga, R., Holmström, E., Parker, S. C., and Arrouvel, C. (2011). Structural characterization of amorphous alumina and its polymorphs from first-principles XPS and NMR calculations. Phys. Rev. B 83 (9), 094201. doi:10.1103/PhysRevB.83.094201

CrossRef Full Text | Google Scholar

Luo, Z., Liu, H., Spann, B. T., Feng, Y., Ye, P., Chen, Y. P., et al. (2014). Measurement of in-plane thermal conductivity of ultrathin films using micro-Raman spectroscopy. Nanoscale Microscale Thermophys. Eng. 18 (2), 183–193. doi:10.1080/15567265.2014.892553

CrossRef Full Text | Google Scholar

Momida, H., Hamada, T., and Ohno, T. (2007a). First-principles study of dielectric properties of amorphous high-k materials. Jpn. J. Appl. Phys. (2008). 46 (5S), 3255–3260. doi:10.1143/jjap.46.3255

CrossRef Full Text | Google Scholar

Momida, H., Hamada, T., Takagi, Y., Yamamoto, T., Uda, T., and Ohno, T. (2007b). Dielectric constants of amorphous hafnium aluminates: First-principles study. Phys. Rev. B 75 (19), 195105. doi:10.1103/physrevb.75.195105

CrossRef Full Text | Google Scholar

Momida, H., Hamada, T., Takagi, Y., Yamamoto, T., Uda, T., and Ohno, T. (2006). Theoretical study on dielectric response of amorphous alumina. Phys. Rev. B 73 (5), 054108. doi:10.1103/physrevb.73.054108

CrossRef Full Text | Google Scholar

Nagaraju, N., Fonseca, A., Konya, Z., and Nagy, J. B. (2002). Alumina and silica supported metal catalysts for the production of carbon nanotubes. J. Mol. Catal. A Chem. 181 (1-2), 57–62. doi:10.1016/s1381-1169(01)00375-2

CrossRef Full Text | Google Scholar

Nayar, P., Khanna, A., Kabiraj, D., Abhilash, S., Beake, B. D., Losset, Y., et al. (2014). Structural, optical and mechanical properties of amorphous and crystalline alumina thin films. Thin Solid Films 568, 19–24. doi:10.1016/j.tsf.2014.07.053

CrossRef Full Text | Google Scholar

Nhan, N. T., Hung, P. K., Nghiep, D. M., Thang, T. Q., and Kim, H. S. (2006). Molecular dynamics study on local structure of amorphous and liquid Al₂O₃. Met. Mat. Int. 12 (2), 167–172. doi:10.1007/bf03027474

CrossRef Full Text | Google Scholar

Novikov, Y. N., Gritsenko, V., and Nasyrov, K. (2009). Charge transport mechanism in amorphous alumina. Appl. Phys. Lett. 94 (22), 222904. doi:10.1063/1.3151861

CrossRef Full Text | Google Scholar

Orosco, J., and Coimbra, C. (2018). Optical response of thin amorphous films to infrared radiation. Phys. Rev. B 97 (9), 094301. doi:10.1103/physrevb.97.094301

CrossRef Full Text | Google Scholar

Pan, Y., Li, H., Liu, Y., Liu, Y., Hu, K., Wang, N., et al. (2020). Effect of holding time during sintering on microstructure and properties of 3D printed alumina ceramics. Front. Mat. 7, 54. doi:10.3389/fmats.2020.00054

CrossRef Full Text | Google Scholar

Paz, A. P., Lebedeva, I. V., Tokatly, I. V., and Rubio, A. (2014). Identification of structural motifs as tunneling two-level systems in amorphous alumina at low temperatures. Phys. Rev. B 90 (22), 224202. doi:10.1103/physrevb.90.224202

CrossRef Full Text | Google Scholar

Poe, B. T., McMillan, P. F., Cote, B., Massiot, D., and Coutures, J. P. (1992). Silica-alumina liquids: in-situ study by high-temperature aluminum-27 NMR spectroscopy and molecular dynamics simulation. J. Phys. Chem. 96 (21), 8220–8224. doi:10.1021/j100200a005

CrossRef Full Text | Google Scholar

Rashkeev, S. N., Sohlberg, K., Glazoff, M., Novak, J., Pennycook, S. J., and Pantelides, S. T. (2003). Transition metal atoms on different alumina phases: The role of subsurface sites on catalytic activity. Phys. Rev. B 67 (11), 115414. doi:10.1103/physrevb.67.115414

CrossRef Full Text | Google Scholar

Segda, B., Jacquet, M., and Besse, J. (2001). Elaboration, characterization and dielectric properties study of amorphous alumina thin films deposited by rf magnetron sputtering. Vacuum 62 (1), 27–38. doi:10.1016/s0042-207x(01)00114-2

CrossRef Full Text | Google Scholar

Sergio, D., and Gonzalo, G. (2011). Structural, elastic, vibrational and electronic properties of amorphous Al₂O₃ from ab initio calculations. J. Phys. Condens. Matter 23, 495401. doi:10.1088/0953-8984/23/49/495401

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaikh, F. U. A., and Hosan, A. (2019). Effect of nano alumina on compressive strength and microstructure of high volume slag and slag-fly ash blended pastes. Front. Mat. 6, 90. doi:10.3389/fmats.2019.00090

CrossRef Full Text | Google Scholar

Shi, C., Alderman, O. L., Berman, D., Du, J., Neuefeind, J., Tamalonis, A., et al. (2019). The structure of amorphous and deeply supercooled liquid alumina. Front. Mat. 6, 38. doi:10.3389/fmats.2019.00038

CrossRef Full Text | Google Scholar

Singh, I., Gupta, P., Maheshwari, A., and Agrawal, N. (2015). Corrosion resistance of sol-gel alumina coated Mg metal in 3.5% NaCl solution. J. Solgel. Sci. Technol. 73 (1), 127–132. doi:10.1007/s10971-014-3503-5

CrossRef Full Text | Google Scholar

Skinner, L. B., Barnes, A. C., Salmon, P. S., Hennet, L., Fischer, H. E., Benmore, C. J., et al. (2013). Joint diffraction and modeling approach to the structure of liquid alumina. Phys. Rev. B 87 (2), 024201. doi:10.1103/physrevb.87.024201

CrossRef Full Text | Google Scholar

Slack, G. A. (1962). Thermal conductivity of MgO, Al₂O₃, MgAl₂O_4, and Fe₃O₄ crystals from 3° to 300° K. Phys. Rev. 126 (2), 427.

Google Scholar

Stuart, A. S., Krishnan, J., K., Weber, J. K. R., Felten, J. J., Nordine, P. C., Beno, M. A., et al. (1997). Structure of liquid aluminum oxide. Phys. Rev. Lett. 78 (3), 464–466. doi:10.1103/physrevlett.78.464

CrossRef Full Text | Google Scholar

Tabandeh-Khorshid, M., Schultz, B. F., Rohatgi, P. K., and Elhajjar, R. (2016). The diametrically loaded cylinder for the study of nanostructured aluminum–graphene and aluminum–alumina nanocomposites using digital image correlation. Front. Mat. 3, 22. doi:10.3389/fmats.2016.00022

CrossRef Full Text | Google Scholar

Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2022). LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171. doi:10.1016/j.cpc.2021.108171

CrossRef Full Text | Google Scholar

Tyrolerova, P., and Lu, W. K. (1969). Volume change on freezing of ALO. J. Am. Ceram. Soc. 52 (2), 77–79. doi:10.1111/j.1151-2916.1969.tb13344.x

CrossRef Full Text | Google Scholar

Van Hoang, V. (2004). Molecular dynamics study on structure and properties of liquid and amorphous Al₂O₃. Phys. Rev. B 70 (13), 134204. doi:10.1103/physrevb.70.134204

CrossRef Full Text | Google Scholar

Van Hoang, V., and Oh, S. K. (2005). Computer simulation of the structural transformation in liquid Al₂O₃. J. Phys. Condens. Matter 17 (19), 3025–3033. doi:10.1088/0953-8984/17/19/016

CrossRef Full Text | Google Scholar

Van Hoang, V., and Oh, S. K. (2004). Structure and diffusion simulation of liquid Al₂O₃. Phys. B Condens. Matter 352 (1-4), 342–352. doi:10.1016/j.physb.2004.08.011

CrossRef Full Text | Google Scholar

Vashishta, P., Kalia, R. K., Nakano, A., and Rino, J. P. (2008). Interaction potentials for alumina and molecular dynamics simulations of amorphous and liquid alumina. J. Appl. Phys. 103 (8), 083504. doi:10.1063/1.2901171

CrossRef Full Text | Google Scholar

Waseda, Y., Sugiyama, K., and Toguri, J. (1995). Direct determination of the local structure in molten alumina by high temperature X-ray diffraction. Z. fur Naturforsch. A 50 (8), 770–774. doi:10.1515/zna-1995-0809

CrossRef Full Text | Google Scholar

Will, F. G., DeLorenzi, H. G., and Janora, K. H. (1992). Conduction mechanism of single‐crystal alumina. J. Am. Ceram. Soc. 75 (2), 295–304. doi:10.1111/j.1151-2916.1992.tb08179.x

CrossRef Full Text | Google Scholar

Williams, R., Graves, R., Janney, M., Tiegs, T., and Yarbrough, D. (1987). The effects of Cr₂O₃ and Fe₂O₃ additions on the thermal conductivity of Al₂O₃. J. Appl. Phys. 61 (10), 4894–4901. doi:10.1063/1.338356

CrossRef Full Text | Google Scholar

Yoon, C., and Cocke, D. L. (1986). Potential of amorphous materials as catalysts. J. non-crystalline solids 79 (3), 217–245. doi:10.1016/0022-3093(86)90224-3

CrossRef Full Text | Google Scholar

Zhao, Y., Cui, N., Zhao, S., Zhu, Y., Hou, P., Feng, L., et al. (2021). Aggressive Environment resistance of concrete products modified with nano alumina and nano silica. Front. Mat. 8, 223. doi:10.3389/fmats.2021.695624

CrossRef Full Text | Google Scholar