Role of cross-diagonal reinforcements in lieu of seismic confining stirrups in the performance enhancement of square RC columns carrying axial load subjected to close-range explosive loading

Exposure of building infrastructures to accidental or intentional blasts is an extreme load condition that may cause irreparable damage leading to the collapse of buildings. Columns being principal elements are the most important for the stability and safety of the buildings under accidental explosions and subversive blast events and therefore attract the attention of structural engineers and researchers. Some recent examples are the Beirut seaport explosion (August 2020), the explosion at an ammunition warehouse in Ryazan City of Russia (October 2020), the gas explosion in China’s Hubei Province (June 2021), a blast at a chemical factory on the outskirts of Bangkok (July 2021), and the explosion on a container ship docked at Dubai’s Jebel Ali Port (July 2021). In the crises like ongoing conflict between Russia and Ukraine, the enhanced response of the principal components of a structure may save the life of the building users by limiting severe damage to the structure. In this study, three experimentally tested 3000-mm-long normal strength concrete columns, 300mm x 300mm, provided with (i) conventional reinforcement, (ii) seismic reinforcements over top and bottom confining regions (600 mm), and (iii) seismic reinforcement over confining and mid-height regions, carrying an axial working load of 950 kN available in the literature, are modeled in the ABAQUS 2020 code and are subjected to 82 kg TNT close-range explosive load at a scaled distance 1.0 m/kg^1/3 using the software’s explicit module. In addition to this, one column with seismic reinforcement over its entire length has been considered and modeled. The concrete damage plasticity model is explored for nonlinear elastic and inelastic behaviors, degradation of stiffness, and loading rate effect on concrete. Following the validation of the numerical models, the seismic reinforcements of the columns have been replaced by the cross-diagonal reinforcements between the conventional stirrups with the same axial load. Blast performance of the columns with the seismic reinforcements and with replaced diagonal reinforcements is critically examined and discussed. The results show that the application of cross-diagonal reinforcements as a replacement for the seismic reinforcements enhances the blast resistance of the reinforced concrete column significantly by reducing the damage and displacement.

1 Introduction

Several studies have been conducted in the past 2 decades addressing the behavior of reinforced concrete (RC) columns under extreme blast loadings (Elsanadedy et al., 2011; Mutalib and Hao, 2011; Bogosian and Heidenreich, 2012; Fujikake and Aemlaor, 2013; Jayasooriya et al., 2014; Li and Hao, 2014; Burrell et al., 2015; Cui et al., 2015; Jacques et al., 2015; Zhang et al., 2015; Zhang et al., 2016; Hu et al., 2018; Wang et al., 2018; Rajkumar et al., 2019; Alsendi and Eamon, 2020; Anas et al., 2022e; Anas et al., 2022h; Shariq et al., 2022a; Tahzeeb et al., 2022a; Tahzeeb et al., 2022b; Tahzeeb et al., 2022c; Anas and Alam, 2022d; Anas et al., 2022I; Shariq et al., 2022c). Moretti and Tassios (2018) tested eight RC columns with additional transverse reinforcement in the form of open ties in both directions under axial compression. It was concluded that a higher transverse ratio improves the ductility of the columns. Previous experimental research on beams with diagonal shear reinforcements showed that the application of diagonal reinforcement not only reduces the flexure–shear cracks but also enhances the ductility and shear capacity of the beams (Demir et al., 2016; Ozturk, 2016). Elsanadedy et al. (2011) examined the level of damage on the circular RC column by the variation of charge weight, scaled distance, and boundary conditions. The dynamic characteristic of a circular RC column was studied using a numerical approach in LS-DYNA software, and a comparison was made between blast performance of the retroftted and non-retrofitted column. Rodriguez-Nikl et al. (2012) conducted a quasistatic experimental test on the RC column to determine the blast performance of as-built and carbon-fiber-jacketed columns. The failure mode of the jacketed column changed from brittle the shear to ductile flexure and therefore increased the blast-resistance of the column. Roller et al. (2012) carried out a series of tests on the exposed hardened concrete surface to study the residual axial load-carrying capacity of the circular column under contact as well as close-in detonations. Abladey and Braimah (2014) presented a numerical study AUTODYN to investigate the effect of close-in explosion on the behavior of the square RC column designed and reinforcement detailed with different levels of seismicity. Li and Hao (2014) proposed various numerical models to predict concrete spall damage in the RC columns under different combinations of explosive charges and standoff distances. Li et al. (2015) carried out an experimental and numerical study (LS-DYNA) to determine the axial load-carrying capacity of the square column. It was noted that the application of axial load provides smaller mid-span flexural deflection and residual deflection. Kyei and Braimah (2017) carried out experimental and numerical investigation on the square RC column with and without seismic reinforcement over the confining region, and seismic reinforcement over the confining region and mid-region was subjected to 82 kg and 123 kg-TNT at a scaled distance varying from 0.25 to 0.85m/kg^1/3. Performance of the column with seismic reinforcement over the confining region as well as mid-height region was found to be superior. An experimental and computational analysis was carried out by Chen et al. (2019) to study the behavior of the RC column considering the variation in the axial load ratio (ALR). At a scaled distance greater than 0.40 m/kg^1/3, increment in ALR was found to be in favor of the RC column subjected to close-in blast loading, and the increment in ALR accentuates the shear damage of the RC column. However, at a scaled distance less than 0.40 m/kg^1/3, with an increase in ALR, the failure mode changes from flexural failure to compression–shear failure and at a scaled distance of 0.40 m/kg^1/3 and ALR of more than 0.40, the column suffers compression–shear failure.

Safety of buildings that are part of critical infrastructures against extreme loadings such as those generated by the explosion is of concern to the government and for designers, and it is a challenge to design the buildings as blast-resistant. Compression members of the buildings in the ground-storey particularly are more important because of their exposure to blast, and their failure may be instrumental to disproportionate or progressive collapse. In this study, the blast performance of conventionally reinforced axially loaded square RC columns with the cross-diagonal reinforcement between the conventional stirrups over the confining zones (top and bottom 600 mm), over-confining zones as well as mid-height zone, and over the entire length of the column has been examined using the ABAQUS code equipped with the concrete damage plasticity model and comparisons with their respective seismically reinforced RC columns are the novelty of the study. The three columns, namely, conventionally reinforced (C1), seismically reinforced over the confining regions (S1), and seismically reinforced over the confining regions as well as mid-height regions (S2), experimentally tested by Kyei and Braimah (2017) under an axial compressive load of 950 kN and blast load of 82 kg-TNT equivalent, are considered reference columns. In addition to this, one column with the seismic reinforcement over its entire length (S3) is also considered a reference column in the study. The present research investigates the role of the diagonal reinforcements on the performance of the columns subjected to the close-in explosion loading and suggests provisions to reduce explosion-generated risk.

2 Finite element modeling of the RC column under explosive loading

A commercial code, ABAQUS with an inbuilt explicit module (ABAQUS/Explicit FEA program, 2020) is used in this study to investigate the effect of the seismic reinforcements and additional reinforcements in the form of cross-diagonal between the conventional stirrups on the air-blast response of the axially loaded RC column under a high explosive load of 100 kg ANFO (≈82 kg-TNT). The height of the burst is 1.50 m from the ground. The ductile detailing of the columns has been provided following the guidelines of CSA A23.3–04 (R2010) (CSA A23.3-04, 2010) and IS 13920:2016 (IS 13920, 1968). The three columns, namely, C1, S1, and S2, tested by Kyei and Braimah (2017), were not designed against seismic loading but were assumed to be part of the seismic force-resisting system (SFRS) of the building with sufficient ductility to undergo lateral deformation (Kyei and Braimah, 2017).

2.1 Description of the models

Nine FE column models have been developed. The first model (C1) is of 3000 mm long, 300mm x 300mm conventionally reinforced RC column with 4 bars of 25 mm diameter and transverse reinforcement in the form of 10 mm diameter stirrups of a yield strength 500 MPa at a uniform spacing of 150 mm center-to-center (c/c), as illustrated in Figure 1A. In the second model (S-1), the seismic reinforcement has been provided over a length of 600 mm at each end of the column, as shown in Figure 1B. The third model (S-2) consists of seismic reinforcement over the confining regions as well as the mid-height (600 mm), Figure 1C. The fourth column model (S-3) is having seismic reinforcement throughout the length, as shown in Figure 1D. The spacing of stirrups in the seismic regions is 75 mm c/c. Model nos. 5, 6, and 7, i.e., C-2, C-3, and C-4 have been obtained by replacing seismic reinforcement over the confining regions, over confining regions as well as mid-height, and over the entire column length with the cross-diagonal reinforcement (8 mm), as shown in Figure 1E–Figure 1G. It is worth mentioning that the inner member of the cross-diagonal is connected to longitudinal re-bars and conventional stirrups, while the outer one is connected to the conventional stirrups. It is to be pointed out that the weight of the replaced cross-diagonal reinforcement is higher than the seismic reinforcement. Model nos. 8 and 9, i.e., C-5 and C-6 have the reinforcement layout of model nos. 6 and 7 but with a difference that the diagonal reinforcement is of 10 mm diameter, as shown in Figure 1H and Figure 1I. The finite element models are illustrated in Figure 2. The slenderness ratio of the columns is 10 (<12, short columns). All the columns are subjected to an axial gravity load of 950 kN and blast pressure of 8.60 MPa generated from the 100 kg ANFO charge. Single-diagonal reinforcement is blast face specific; therefore, it is not considered in the study as blast face, in general, is not predefined.

FIGURE 1

FIGURE 1. Dimensions (mm) and details of the reinforcements.

FIGURE 2

FIGURE 2. Three-dimensional view of the reinforcements of the columns.

2.2 FE mesh, idealized support conditions, and explicit module

The columns are discretized with C3D8R elements of an explicit type available in ABAQUS/Explicit FEA program, 2020. Generally, the average mesh size of 10 mm has been adopted following the convergence test conducted at a scaled distance of 1.00m/kg^1/3. The compressive strength, tensile strength, Young’s modulus, and Poisson’s ratio of the concrete taken from Kyei and Braimah (2017) are 30 MPa, 3.00 MPa, 26.60 GPa, and 0.20 GPa, respectively. The mass density, ultimate tensile strength, yield strength, Young’s modulus, and Poisson’s ratio of the steel are 7800kg/m³, 545MPa, 500MPa, 210GPa, and 0.30, respectively (Kyei and Braimah, 2017). The thickness of the concrete cover to the longitudinal steel bar is 40 mm. The reinforcements are discretized with B31 elements (ABAQUS/Explicit FEA program, 2020). The re-bars are embedded in the column using the EMBEDDED_REGION constraint command (ABAQUS/Explicit FEA program, 2020). The host region is chosen as the concrete, while the embedded region is chosen as the reinforcements. Moreover, the TIE_CONSTRAINT command has been used to provide the interaction between the steel bars and the lateral reinforcements (ABAQUS/Explicit FEA program, 2020). The axial load-carrying columns are modeled with no translational degree-of-freedom restraint in the direction of the applied load (Kyei and Braimah, 2017). However, the bottom of the columns is assumed fixed (Kyei and Braimah, 2017).

In the current study, the air-blast pressure is defined as pressure versus time application and subsequently applied to the surface of the column facing the explosion (-Z direction) using the explicit solver available in the ABAQUS code (ABAQUS/Explicit FEA program, 2020; Anas et al., 2020a; Anas et al., 2020b; Anas et al., 2020c; Anas and Ansari, 2021; Anas and Alam, 2022a; Anas et al., 2021a; Kyei and Braimah, 2017; Pereira et al., 2015). The explicit solver incrementally solves the equation of motion and updates the stiffness matrix at the end of each increment of load and displacement based on changes in geometry and material (ABAQUS/Explicit FEA program, 2020; Anas et al., 2021a; Hao et al., 2016).

2.3 Concrete modeling

The material constitutive model is one of the factors responsible for the accuracy of numerical results (Tahzeeb et al., 2022a; Tahzeeb et al., 2022b; Tahzeeb et al., 2022c). Concrete damage plasticity (CDP) is such a model employed to model the plastic behavior of the concrete in the present work from ABAQUS/EXPLICIT software.

The concrete model has been developed to analyze the failure of the concrete using the damage plasticity constitutive model, which is a combination of isotropic damage elasticity and isotropic compressive and tensile plasticity (Lee and Fenves, 1998; Lubliner et al., 2003). It defines an important characteristic of the failure mechanism of the concrete in an elastic–plastic manner (ABAQUS/Explicit FEA program, 2020; Hafezolghorani et al., 2017; Lee and Fenves, 1998). The damage plasticity model assumes to influence the axial compression and tension response of the concrete (ABAQUS/Explicit FEA program, 2020). Experimental data of Hafezolghorani et al. (2017) are utilized to model the inelastic response of the concrete under a blast. The strain-rate or loading rate effects on materials’ strength are considered per UFC3-340–02 (2008) and fib Model Code 2010, reported in Refs. (Shariq et al., 2022a; Tahzeeb et al., 2022a; Anas et al., 2022e). General CDP parameter values used for concrete modeling are listed in Table 1.

TABLE 1

TABLE 1. Default parameters for the CDP concrete model, taken from Ahmadi et al. (2022), Anas et al. (2022J), Anas et al. (2022K), Anas et al. (2022L), Anas et al. (2022M), Anas et al. (2022N), Anas et al. (2022O), Shariq et al. (2022b), Shariq et al. (2022c), and Anas and Alam (2022d).

In numerical simulations involving the reinforced concrete, which involves separately meshing the concrete and steel reinforcement, there are basically two ways of ensuring a bond between the concrete and the reinforcing bars. The first method requires meshing the concrete and reinforcing bars in such a way that they share common nodes on the interface (Ahmadi et al., 2022; Anas et al., 2022J; Anas et al., 2022K; Anas et al., 2022L; Anas et al., 2022M; Anas et al., 2022N; Anas et al., 2022O; Shariq et al., 2022b; Shariq et al., 2022c; Anas and Alam, 2022d). This, however, tends to be a very laborious process. The second method allows for meshing the concrete and the reinforcement separately and coupling the concrete and reinforcing bar nodes using the CONSTRAINED_EMBBEDED_REGION keycard in ABAQUS (ABAQUS/Explicit FEA program, 2020). The CONSTRAINED_EMBBEDED_REGION keycard requires, as input, the master (in this case concrete) and slave (reinforcing bars and stirrups) components of the meshed parts (Anas and Alam, 2022e).

2.4 Explosive load modeling

An explosion is the combustion of a chemical explosive that is initiated suddenly through rapid oxidation, and the generated wave propagates at an expeditious speed (Anas et al., 2021a; IS 4991, 1968; Goel and Matsagar, 2014; TM 5-1300, 1990; Anas et al., 2021b; Anas and Alam, 2021; Anas et al., 2021c; Anas et al., 2021d; Anas et al., 2022a; Anas et al., 2022b; Anas and Alam, 2022b; Anas et al., 2022c; Anas et al., 2022d; Ahmadi et al., 2021; Anas et al., 2021e; Anas et al., 2021f; Anas and Alam, 2022c; Anas et al., 2022e; Anas et al., 2022f; Anas et al., 2022g; Anas et al., 2022h; Anas et al., 2022I; Shariq et al., 2022a; Tahzeeb et al., 2022a; Tahzeeb et al., 2022b; Tahzeeb et al., 2022c; Ul Ain et al., 2021; Ul Ain et al., 2022). The speed of the explosion wave varies from 6000m/s to 8000m/s (Anas et al., 2021a; TM 5-1300, 1990). Blast is an explicit dynamic event having a non-linear response to structure and materials with a very fast varying transient nature involving the complex stress state and high magnitude of peak load. The explosion loading terminates with the blast wave propagation through the atmosphere which impinges on the target structure surface conduce with an extremely robust release of energy resulting in expeditious augmentation in the intensity of light, heat, sound, and dense gases with high-pressure gas in a very short duration of time. The peak blast pressure is dependent on explosive weight (W), standoff distance (S), and the incidence angle of the blast wave with the striking surface (IS 4991, 1968; TM 5-1300, 1990). Air-blast loading characteristics and related blast parameters are discussed by the authors in detail (Anas et al., 2020a; Anas et al., 2020b; Anas et al., 2020c; Anas et al., 2021a; Anas and Ansari, 2021; Anas and Alam, 2022a). Blast pressure–time history variation following a detonation can be expressed by the empirical-based model proposed by Wu and Hao (2005), represented in Eq. 1, shown in Figure 3A.

$\mathit{P}\left(\mathbf{t}\right)=\left\{\begin{array}{c}{\mathit{P}}_{\mathit{o}},\left(\mathbf{0}\le \mathbf{t}<{\mathbf{t}}_{\mathit{A}}\right),\\ {\mathit{P}}_{\mathit{o}}+{\mathit{P}}_{\mathit{O}\mathit{P}}\left(\frac{\mathbf{t}}{{\mathbf{t}}_{\mathbf{1}}}\right),\left({\mathbf{t}}_{\mathit{A}}\le \mathbf{t}\le {\mathbf{t}}_{\mathbf{1}}\right),\\ {\mathit{P}}_{\mathit{o}}+{\mathit{P}}_{\mathit{O}\mathit{P}}\left(\mathbf{1}-\frac{\mathbf{t}-{\mathbf{t}}_{\mathbf{1}}}{{\mathbf{t}}_{\mathbf{2}}}\right).\mathbf{exp}\left(-\frac{\mathbf{\Psi }\left(\mathbf{t}-{\mathbf{t}}_{\mathbf{1}}\right)}{{\mathbf{t}}_{\mathbf{2}}}\right),\left({\mathbf{t}}_{\mathbf{1}}\le \mathbf{t}\right),\end{array}\right\}(1)$

where pp(t) = blast pressure at time “t”; P_O = ambient air-pressure (0.10 MPa); P_OP = peak overpressure; t_A = arrival time of the shock wave; t₁ = rising time; t₂ = decreasing time; t^- = negative blast phase duration; t_d = positive phase duration, and $\Psi$ = decay coefficient. Figure 3B shows the air-blast profile for a scaled distance of 1.00 m/kg^1/3 in free air, experimentally recorded by Kyei and Braimah (2017). Current blast design provisions have been followed to model the blast history illustrated in Figure 3B (Anas et al., 2020a; Anas et al., 2020b; Anas et al., 2020c; Anas et al., 2021a; Anas and Ansari, 2021; Anas and Alam, 2022a; IS 4991, 1968; TM 5-1300, 1990; Goel and Matsagar, (2014); Hao et al., 2016).

FIGURE 3

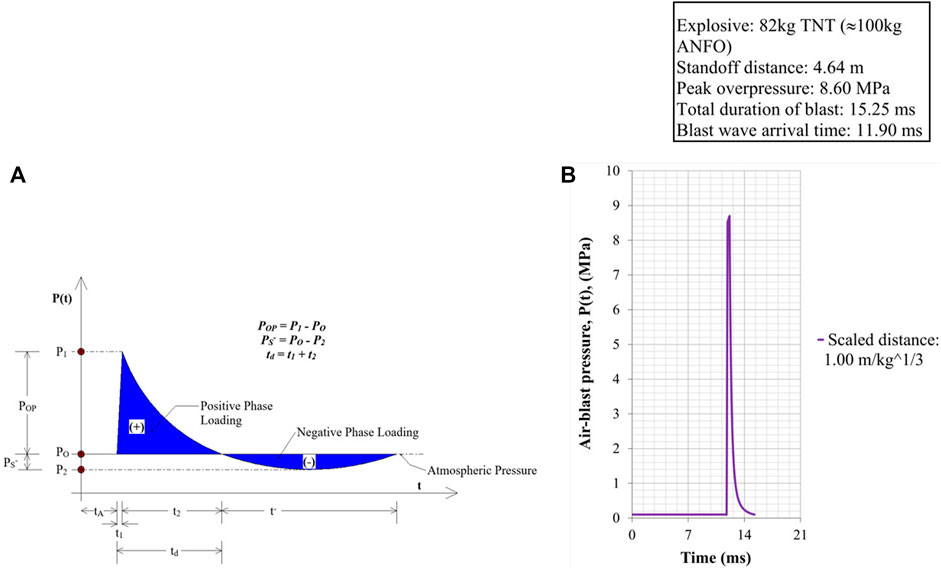
FIGURE 3. (A) Time evolution of air-blast pressure due to an explosion acting on a target structure (TM 5-1300, 1990; Wu and Hao, 2005) and (B) experimentally recorded history adapted from Kyei and Braimah (2017).

The loading on the RC columns in the numerical simulations was accomplished in two phases, as the same reported in Anas and Alam (2022d). In the first phase, the axial loading was applied to the top surface nodes as linearly increasing load to the axial load level. The load is maintained for a few milliseconds until the internal stress stabilizes at the stress corresponding to the ALR considered in the simulation. The static pressure is then maintained throughout the second phase of the loading which involves lateral blast loading on the column.

3 Results and discussions

Maximum transverse displacements of the axially loaded square RC columns C-1, S-1, and S-2 under 82 kg TNT blast loading are in good agreement with the experimentally measured maximum displacements by Kyei and Braimah (2017) (Lubliner et al., 2003) with an average percentage difference less than 4%, shown in Table 2. The crack pattern obtained on the side face of column S-1 as illustrated in Figure 4 is quite similar to the available blast test results and therefore approves the application of employed software to predict the dynamic response of the column.

TABLE 2

TABLE 2. Comparison of maximum transverse mid-height displacement (mm).

FIGURE 4

FIGURE 4. Comparison of the cracking profile of column S-1.

3.1 Effect of seismic reinforcements (S-1, S-2, and S-3)

The maximum damage dissipation energy (DDE) of the conventionally reinforced RC column C-1 is found to be 763.17 J, shown in Table 2 and Figure 5B. The application of the seismic reinforcements reduces the maximum displacement and DDE, as shown in Figure 5. The decrease in the DDE represents less damage commensurate to the formation of fewer cracks and lesser concrete spalling/crushing in the columns than the reference column C-1. The percentage reductions in columns S-1, S-2, and S-3 are 4, 10, and 15%, respectively, with respect to column C-1, as shown in Table 2.

FIGURE 5

FIGURE 5. (A) Displacement time histories and (B) DDE profiles.

The re-bars facing the explosion experience the maximum principal compressive stress of 200.03 MPa (< f_y = 500 MPa) at the bottom region of column C-1, while the re-bars on the rear side experience the maximum tensile stress of 100.68 MPa at the mid-height level of the column, as shown in Figure 6. The concrete on the blast face at the bottom and near the top of column C-1 experiences the maximum compressive stress of 28.02 MPa (< f_c = 30 MPa) which implies that the conventional stirrups with four corner longitudinal bars are not able to confine to the concrete, as shown in Table 2. The top and bottom portions of column C-1 are severely damaged with the concrete crushing on the explosion face, while the tension face suffers from concrete spalling and flexure–shear cracks with an average crack depth of 220 mm, as shown in Figure 7 and Figure 8. Provision of seismic reinforcement over the confining regions (S1), over the confining regions as well as mid-height (S2), and over the entire column length (S3) reduces the maximum compressive stress in the re-bars by 6, 5, and 2%, respectively, while the percentage reductions of maximum tensile stress in the re-bars are 5, 15, and 18% with respect to column C-1, as shown in Figure 6. The stirrups near the top and bottom of column C-1 facing the explosion experience the maximum tensile stress of 251.03 MPa, as shown in Figure 6. A noticeable reduction in the tensile stress in the stirrups and average crack depth is observed with the application of seismic reinforcements; however, the percentage reduction is found to be maximum with the application of seismic reinforcement over the entire column length in comparison to column C-1. Referring to Table 4, the maximum crushing stress in the concrete of columns S-1, S-2, and S-3 is more than the compressive strength of the concrete (30 MPa).

FIGURE 6

FIGURE 6. Principal stress (MPa) contour of the columns’ reinforcements.

FIGURE 7

FIGURE 7. Profile of concrete crushing in the columns.

FIGURE 8

FIGURE 8. Profile of cracking and spalling of the concrete of the columns.

TABLE 4

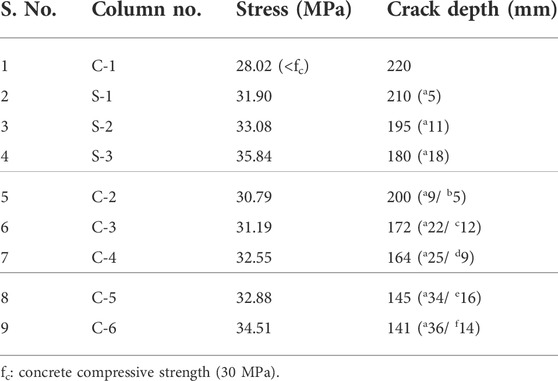
TABLE 4. Summary of maximum principal compressive stress in the concrete and average crack depth of flexure–shear cracks.

3.2 Effect of cross-diagonal reinforcements (8 mm and 10 mm)

Columns C-2 and C-3 obtained by replacing the seismic reinforcements with the cross-diagonal reinforcements (8 mm) between the conventional stirrups display significant improvement in their blast performance by reducing the maximum transverse displacement, DDE, stresses, and average flexure crack depth with reference to their respective seismically reinforced RC columns, as shown in Table 3, Table 4, and Figure 5. Column C-4 with cross-diagonal reinforcement (8 mm) further improves the deflection response and cracking resistance. An increase in the cross-diagonal reinforcement from 8 to 10 mm marginally reduces the maximum displacement in columns C5 and C6, but the cross-diagonal reinforcement in column C6 throughout its length more effectively contributes to reducing the concrete crushing as well as cracking than all other columns considered in the study, as shown in Table 3, Figure 7, and Figure 8.

TABLE 3

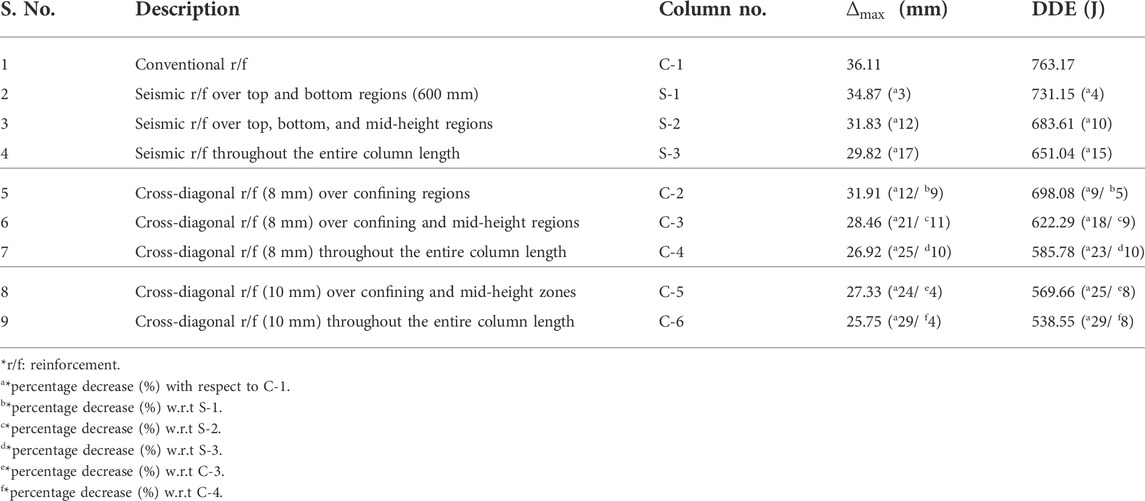
TABLE 3. Summary of maximum transverse mid-height displacement (${∆}_{\max })$ and damage dissipation energy (DDE).

4 Conclusion

Different techniques have been adopted by the researchers to enhance the blast performance of the RC columns of the square cross section. In the present research work, the seismic reinforcement over the confining regions, over the confining regions as well as mid-height, and over the entire length of the column and the replacement for the seismic reinforcements by the cross-diagonal reinforcements between the conventional stirrups are considered to improve the response of the axially loaded square RC columns subjected to 82 kg-TNT equivalent close-in explosion loading.

The major conclusions drawn from the analyses’ results are as follows:

a) Provision of the seismic confining lateral reinforcements improves the deflection response of the column; however, it does not contribute to controlling the damage (concrete crushing/cracking) under the high explosion loading.

b) The technique of using the cross-diagonal reinforcements as a replacement for the seismic reinforcements enhances the blast performance of the column significantly.

c) Higher diameter (10 mm) of the cross-diagonal reinforcement throughout the length of the column is found most effective to control the concrete crushing and cracking among the seismic reinforcements in the square column.

The technique followed in this study can be used for strengthening the square columns in the existing buildings and also for the design of the blast-resistant square RC columns of the buildings vulnerable to blasts.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

SA performed the numerical simulations and measurements. MA supervised this work. HI organized the database. HN and MS wrote the sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The research was partially funded by the Ministry of Science and Higher Education of the Russian Federation under the strategic academic leadership program “Priority 2030” (Agreement 075–15-2021-1333 dated 09/30/2021).

Acknowledgments

The authors extend their thanks to the Ministry of Science and Higher Education of the Russian Federation for funding this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

ABAQUS/Explicit FEA program (2020). 2020 Concrete-damaged plasticity model, explicit solver, three dimensional solid element library ABAQUS DS-SIMULIA User Manual. AvaliableAt: https://sites.engineering.ucsb.edu.

Google Scholar

Abladey, L., and Braimah, A. (2014). Near-field explosion effects on the behaviour of reinforced concrete columns: A numerical investigation. Int. J. Prot. Struct. 5, 475–499. doi:10.1260/2041-4196.5.4.475

CrossRef Full Text | Google Scholar

Ahmadi, E., Alam, M., and Anas, S. M. (2022). Behaviour of C-FRP laminate strengthened masonry and unreinforced masonry compound walls under blast loading, Afghanistan scenario. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10049968

CrossRef Full Text | Google Scholar

Ahmadi, E., Alam, M., and Anas, S. M. (2021). “Blast performance of RCC slab and influence of its design parameters,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 389–402. doi:10.1007/978-981-16-6978-1_31

CrossRef Full Text | Google Scholar

Alsendi, A., and Eamon, D. C. (2020). Quantitative resistance assessment of sfrp-strengthened RC bridge columns subjected to blast loads. J. Perform. Constr. Facil. 34 (4), 1–9. doi:10.1061/(asce)cf.1943-5509.0001458

CrossRef Full Text | Google Scholar

Anas, S. M., and Alam, M. (2021a). “Air-blast response of free-standing: (1) unreinforced brick masonry wall, (2) cavity RC wall, (3) RC walls with (i) bricks, (ii) sand, in the cavity: A macro-modeling approach,” in Proceedings of SECON’21. SECON 2021. Editors G. C. Marano, S. Ray Chaudhuri, G. Unni Kartha, P. E. Kavitha, R. Prasad, and R. J. Achison (Cham: Springer), Vol. 171, 921–930. doi:10.1007/978-3-030-80312-4_78

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Alam, M. (2022O). “Performance prediction of axially loaded square reinforced concrete column with additional transverse reinforcements in the form of (1) master ties, (2) diamond ties, and (3) open ties under close-in blast,” in Proceedings of the 2nd international symposium on disaster resilience and sustainable development lecture notes in civil engineering (Springer), 294. (article in press). doi:10.1007/978-981-19-6297-4_12

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Alam, M. (2022N). Reinforced cement concrete (RCC) shelter and prediction of its blast loads capacity. Mater. Today Proc. doi:10.1016/j.matpr.2022.09.125

CrossRef Full Text | Google Scholar

Anas, S. M., and Alam, M. (2022a). Close-range blast response prediction of hollow circular concrete columns with varied hollowness ratio, arrangement of compression steel, and confining stirrups’ spacing. Iran. J. Sci. Technol. Trans. Civ. Eng. doi:10.1007/s40996-022-00951-5

CrossRef Full Text | Google Scholar

Anas, S. M., and Alam, M. (2021b). Comparison of existing empirical equations for blast peak positive overpressure from spherical free air and hemispherical surface bursts. Iran. J. Sci. Technol. Trans. Civ. Eng. 46, 965–984. doi:10.1007/s40996-021-00718-4

CrossRef Full Text | Google Scholar

Anas, S. M., and Alam, M. (2022b). Dynamic behavior of free-standing unreinforced masonry and composite walls under close-range blast loadings: A finite element investigation. Int. J. Mason. Res. Innovation. (article in press).

Google Scholar

Anas, S. M., and Alam, M. (2022c). Performance of brick-filled reinforced concrete composite wall strengthened with C-FRP laminate(s) under blast loading. Mater. Today Proc. 65, 1–11. doi:10.1016/j.matpr.2022.03.162

CrossRef Full Text | Google Scholar

Anas, S. M., and Alam, M. (2022d). Performance of simply supported concrete beams reinforced with high-strength polymer re-bars under blast-induced impulsive loading. Int. J. Struct. Eng. 12 (1), 62–76. doi:10.1504/IJSTRUCTE.2022.119289

CrossRef Full Text | Google Scholar

Anas, S. M., and Alam, M. (2022e). Role of shear reinforcements on the punching shear resistance of two-way RC slab subjected to impact loading. Mater. Today Proc. doi:10.1016/j.matpr.2022.08.510

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Shariq, M. (2022a). Behavior of two-way RC slab with different reinforcement orientation layouts of tension steel under drop load impact. Mater. Today Proc. doi:10.1016/j.matpr.2022.08.509

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Shariq, M. (2022b). Damage response of conventionally reinforced two-way spanning concrete slab under eccentric impacting drop weight loading. Def. Technol. doi:10.1016/j.dt.2022.04.011

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Tahzeeb, R. (2022M). Impact response prediction of square RC slab of normal strength concrete strengthened with (1) laminates of (i) mild-steel and (ii) C-FRP, and (2) strips of C-FRP under falling-weight load. Mater. Today Proc. doi:10.1016/j.matpr.2022.07.324

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2021). Air-blast and ground shockwave parameters, shallow underground blasting, on the ground and buried shallow underground blast-resistant shelters: A review. Int. J. Prot. Struct. 13 (1), 99–139. doi:10.1177/20414196211048910

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022L). “Air-blast response of axially loaded clay brick masonry walls with and without reinforced concrete core,” in ASMA 2021, advances in structural mechanics and applications, STIN 19 (Spinger), 1–18. doi:10.1007/978-3-030-98335-2_4

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022). Effect of design strength parameters of conventional two-way singly reinforced concrete slab under concentric impact loading. Mater. Today Proc. 62, 2038–2045. doi:10.1016/j.matpr.2022.02.441

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2021). Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. Structures 31, 428–461. doi:10.1016/j.istruc.2021.01.102

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022K). Experimental studies on blast performance of unreinforced masonry walls of clay bricks and concrete blocks: A state-of-the-art review. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2022.10049719

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2021). “Influence of charge locations on close-in air-blast response of pre-tensioned concrete U-girder,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 513–527. doi:10.1007/978-981-16-6978-1_40

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., Umair, M., and Kanaan, M. H. G. (2022J). Strengthening of unreinforced braced masonry wall with (1) CFRP laminate and (2) mild-steel strips: Innovative techniques, against close-range explosion. Int. J. Mason. Res. Innovation. (article in press).

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2021). “Out-of-plane response of clay brick unreinforced and strengthened masonry walls under explosive-induced air-blast loading,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 477–491. doi:10.1007/978-981-16-6978-1_37

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022a). Performance based strengthening with concrete protective coatings on braced unreinforced masonry wall subjected to close-in explosion. Mater. Today Proc. 64, 161–172. doi:10.1016/j.matpr.2022.04.206

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022b). Performance of (1) concrete-filled double-skin steel tube with and without core concrete, and (2) concrete-filled steel tubular axially loaded composite columns under close-in blast. Int. J. Prot. Struct. doi:10.1177/20414196221104143

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2021). Performance of on-ground double-roof RCC shelter with energy absorption layers under close-in air-blast loading. Asian J. Civ. Eng. 22, 1525–1549. doi:10.1007/s42107-021-00395-8

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2020b). “Performance of one-way composite reinforced concrete slabs under explosive-induced blast loading,” in IOP conference series: Earth and environmental science, volume 614, 1st international conference on energetics (Tashkent, Uzbekistan: Civil and Agricultural Engineering 2020). doi:10.1088/1755-1315/614/1/012094

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2020a). “Performance of one-way concrete slabs reinforced with conventional and polymer re-bars under air-blast loading,” in Recent advances in structural engineering. Editors S. Chandrasekaran, S. Kumar, and S. Madhuri (Jamshedpur, India: Springer), 135, 179–191. doi:10.1007/978-981-33-6389-2_18

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022I). Role of UHPC in-lieu of ordinary cement-sand plaster on the performance enhancement of masonry wall under close-range blast loading: A finite element investigation. Int. J. Mason. Res. Innovation. (article in press).

CrossRef Full Text | Google Scholar

Anas, S. M., Alam, M., and Umair, M. (2022). Strengthening of braced unreinforced brick masonry wall with (i) C-frp wrapping, and (ii) steel angle-strip system under blast loading. Mater. Today Proc. 58, 1181–1198. doi:10.1016/j.matpr.2022.01.335

CrossRef Full Text | Google Scholar

Anas, S. M., and Ansari, M. I. (2021). A study on existing masonry heritage building to explosive-induced blast loading and its response. Int. J. Struct. Eng. 11 (4), 387–412. doi:10.1504/IJSTRUCTE.2021.118065

CrossRef Full Text | Google Scholar

Anas, S. M., Ansari, Md I., and Alam, M. (2020). Performance of masonry heritage building under air-blast pressure without and with ground shock. Aust. J. Struct. Eng. 21 (4), 329–344. doi:10.1080/13287982.2020.1842581

CrossRef Full Text | Google Scholar

Anas, S. M., Shariq, M., and Alam, M. (2022). Performance of axially loaded square RC columns with single/double confinement layer(s) and strengthened with C-frp wrapping under close-in blast. Mater. Today Proc. 58, 1128–1141. doi:10.1016/j.matpr.2022.01.275

CrossRef Full Text | Google Scholar

Anas, S. M., Shariq, M., Alam, M., and Umair, M. (2022). Evaluation of critical damage location of contact blast on conventionally reinforced one-way square concrete slab applying CEL-FEM blast modeling technique. Int. J. Prot. Struct. doi:10.1177/20414196221095251

CrossRef Full Text | Google Scholar

Bogosian, D. D., and Heidenreich, A. N. (2012). An evaluation of engineering methods for predicting close-in air blast. Struct. Congr. ASCE 2, 90–101.

CrossRef Full Text | Google Scholar

Burrell, P. R., Aoude, H., and Saatcioglu, M. (2015). Response of SFRC columns under blast loading. J. Struct. Eng. 141 (9), 1–15.

CrossRef Full Text | Google Scholar

Chen, L., Hu, Y., Ren, H., Xiang, H., Zhai, C., and Fang, Q. (2019). Performances of the RC column under close-in explosion induced by the double end-initiation explosive cylinder. Int. J. Impact Eng. 132, 103326. doi:10.1016/j.ijimpeng.2019.103326

CrossRef Full Text | Google Scholar

CSA A23.3-04 (2010). Design of concrete structures. Ontario: Canadian Standards Association.

Google Scholar

Cui, J., Shi, Y., Li, X. Z., and Chen, L. (2015). Failure analysis and damage assessment of RC columns under close-in explosions Journal of Performance of Constructed Facilities. J. Perform. Constr. Facil. 29 (5), 766. doi:10.1061/(asce)cf.1943-5509.0000766

CrossRef Full Text | Google Scholar

Demir, A., Caglar, N., Ozturk, H., and Sumer, Y. (2016). Nonlinear finite element study on the improvement of shear capacity in reinforced concrete T-Section beams by an alternative diagonal shear reinforcement. Eng. Struct. 120, 158–165. doi:10.1016/j.engstruct.2016.04.029

CrossRef Full Text | Google Scholar

Elsanadedy, H. M., Almusallam, T. H., Abbas, H., Al-Salloum, Y. A., and Al-Salloum, S. H. (2011). Effect of blast loading on CFRP-retrofitted RC columns - a numerical study effect of blast loading on CFRP-retrofitted RC columns – A numerical study. Lat. Am. J. solids Struct. 8, 55–81. doi:10.1590/s1679-78252011000100004

CrossRef Full Text | Google Scholar

Fujikake, K., and Aemlaor, P. (2013). Damage of reinforced concrete columns under demolition blasting. Eng. Struct. 55, 116–125. doi:10.1016/j.engstruct.2011.08.038

CrossRef Full Text | Google Scholar

Goel, D. M., and Matsagar, A. V. (2014). Blast-resistant design of structures practice Periodical on structural Design and construction. ASCE 19 (2), 040140071–040140079.

CrossRef Full Text | Google Scholar

Hafezolghorani, M., Hejazi, F., Vaghei, R., Jaafar, B. S. M., and Karimzade, K. (2017). Simplified damage plasticity model for concrete. Struct. Eng. Int. 27 (1), 68–78. doi:10.2749/101686616x1081

CrossRef Full Text | Google Scholar

Hao, H., Hao, Y., Li, J., and Chen, W. (2016). Review of the current practices in blast-resistant analysis and design of concrete structures. Adv. Struct. Eng. 19 (8), 1193–1223. doi:10.1177/1369433216656430

CrossRef Full Text | Google Scholar

Hu, Y., Chen, L., Fang, Q., and Xiang, H. (2018). Blast loading model of the RC column under close-in explosion induced by the double-end-initiation explosive cylinder. Eng. Struct. 175, 304–321. doi:10.1016/j.engstruct.2018.08.013

CrossRef Full Text | Google Scholar

IS 13920 (1968). Indian Standard ductile detailing of reinforced concrete structures subjected to seismic forces – code of practice. New Delhi, India: Bureau of Indian Standards.

Google Scholar

IS 4991 (1968). Criteria for blast resistant design of structures for explosions above ground. New Delhi, India: Bureau of Indian Standards.

Google Scholar

Jacques, E., Lloyd, A., Imbeau, P., Palermo, D., and Quek, J. (2015). GFRP-retrofitted reinforced concrete columns subjected to simulated blast loading. J. Struct. Eng. (N. Y. N. Y). 141 (11), 1–13. doi:10.1061/(asce)st.1943-541x.0001251

CrossRef Full Text | Google Scholar

Jayasooriya, R., Thambiratnam, P. D., and Perera, J. N. (2014). Blast response and safety evaluation of a composite column for use as key element in structural systems. Eng. Struct. 61, 31–43. doi:10.1016/j.engstruct.2014.01.007

CrossRef Full Text | Google Scholar

Kyei, C., and Braimah, A. (2017). Effects of transverse reinforcement spacing on the response of reinforced concrete columns subjected to blast loading. Eng. Struct. 142, 148–164. doi:10.1016/j.engstruct.2017.03.044

CrossRef Full Text | Google Scholar

Lee, J., and Fenves, L. G. (1998). Plastic-damage model for cyclic loading of concrete structures Journal of Engineering Mechanics. J. Eng. Mech. 124 (8), 892–900. doi:10.1061/(asce)0733-9399(1998)124:8(892)

CrossRef Full Text | Google Scholar

Li, J., and Hao, H. (2014). Numerical study of concrete spall damage to blast loads. Int. J. Impact Eng. 68, 41–55. doi:10.1016/j.ijimpeng.2014.02.001

CrossRef Full Text | Google Scholar

Li, J., Wi, C., and Hao, H. (2015). Residual loading capacity of ultra-high performance concrete columns after blast loads. Int. J. Prot. Struct. 6, 649–669.

Google Scholar

Lubliner, J., Oliver, J., Oller, S., and Onate, E. (2003). A plastic-damage model for concrete. Int. J. Solids Struct. 25 (3), 299–326. doi:10.1016/0020-7683(89)90050-4

CrossRef Full Text | Google Scholar

Moretti, M., and Tassios, T. P. (2018). Behavior of short columns subjected to cyclic shear displacements: Experimental results. J. Eng. Struct. 29 (1), 2018–2029. doi:10.1016/j.engstruct.2006.11.001

CrossRef Full Text | Google Scholar

Mutalib, A. A., and Hao, H. (2011). Development of P-I diagrams for FRP strengthened RC columns. Int. J. Impact Eng. 38, 290–304. doi:10.1016/j.ijimpeng.2010.10.029

CrossRef Full Text | Google Scholar

Ozturk, H. (2016). Improving the shear strength of reinforced concrete short beams with diagonal shear reinforcement. Sakarya, Turkey: Sakarya University. PhD Thesis.

Google Scholar

Pereira, M. J., Campos, J., and Lourenco, B. P. (2015). Masonry infill walls under blast loading using confined underwater blast wave generators (WBWG). Eng. Struct. 92 (1), 69–83. doi:10.1016/j.engstruct.2015.02.036

CrossRef Full Text | Google Scholar

Rajkumar, D., Senthill, R., Kumar, M. B. B., Gomathi, A. K., and Velan, M. S. (2019). Numerical study on parametric analysis of reinforced concrete column under blast loading. J. Perform. Constr. Facil. 34 (1), 1–12. doi:10.1061/(asce)cf.1943-5509.0001382

CrossRef Full Text | Google Scholar

Rodriguez-Nikl, T., Lee, C.-S., Hegemier, G. A., and Seible, F. (2012). Experimental performance of concrete columns with composite jackets under blast loading. J. Struct. Eng. (N. Y. N. Y). 138, 81–89. doi:10.1061/(asce)st.1943-541x.0000444

CrossRef Full Text | Google Scholar

Roller, C., Mayrhofer, C., Riedel, W., and Thoma, K. (2012). Residual load capacity of exposed and hardened concrete columns under explosion loads. Eng. Struct. 28, 66–72. doi:10.1016/j.engstruct.2011.12.004

CrossRef Full Text | Google Scholar

Shariq, M., Alam, M., Anas, S. M., Islam, N., and Hussain, A. (2022). Performance enhancement of square RC column carrying axial compression by (1) C-frp wrapping, and (2) steel angle system under air-blast loading. Int. J. Comput. Mater. Sci. Surf. Eng. (article in press).

Google Scholar

Shariq, M., Alam, M., Husain, A., and Anas, S. M. (2022). Jacketing with steel angle sections and wide battens of RC column and its influence on blast performance. Asian J. Civ. Eng. 23, 487–500. doi:10.1007/s42107-022-00437-9

CrossRef Full Text | Google Scholar

Shariq, M., Anas, S. M., and Alam, M. (2022). Blast resistance prediction of clay brick masonry wall strengthened with steel wire mesh, and C-frp laminate under explosion loading: A finite element analysis. Int. J. Reliab. Saf. (article in press).

Google Scholar

Tahzeeb, R., Alam, M., and Mudassir, S. M. (2022). A comparative performance of columns: Reinforced concrete, composite, and composite with partial C-frp wrapping under contact blast. Mater. Today Proc. 62, 2191–2202. doi:10.1016/j.matpr.2022.03.367

CrossRef Full Text | Google Scholar

Tahzeeb, R., Alam, M., and Mudassir, S. M. (2022). Effect of transverse circular and helical reinforcements on the performance of circular RC column under high explosive loading. Mater. Today Proc. 64, 315–324. doi:10.1016/j.matpr.2022.04.676

CrossRef Full Text | Google Scholar

Tahzeeb, R., Alam, M., and Mudassir, S. M. (2022). Performance of composite and tubular columns under close-in blast loading: A comparative numerical study. Mater. Today Proc. 65, 51–62. doi:10.1016/j.matpr.2022.04.587

CrossRef Full Text | Google Scholar

TM 5-1300 (1990). “Structures to resist the effects of accidental explosions-Technical Manual,” in The navy, and the air force (United States: Department of the Army, the Navy, and the Air Force).

Google Scholar

Ul Ain, Q., Alam, M., and Anas, S. M. (2021). “Behavior of ordinary load-bearing masonry structure under distant large explosion, Beirut scenario,” in Resilient infrastructure, lecture notes in civil engineering. Editors S. Kolathayar, C. Ghosh, B. R. Adhikari, I. Pal, and A. Mondal (Singapore: Springer), 239–253. doi:10.1007/978-981-16-6978-1_19

CrossRef Full Text | Google Scholar

Ul Ain, Q., Alam, M., and Anas, S. M. (2022). “Response of two-way RCC slab with unconventionally placed reinforcements under contact blast loading,” in ASMA 2021, advances in structural mechanics and applications, STIN 19 (Silchar, India: Structural Integrity, Springer), 1–18. (article in press). doi:10.1007/978-3-031-04793-0_17

CrossRef Full Text | Google Scholar

Wang, W., Wu, C., and Li, J. (2018). Numerical simulation of hybrid frp-concrete-steel double-skin tubular columns under close-range blast loading. J. Compos. Constr. 22 (5), 1–15. doi:10.1061/(asce)cc.1943-5614.0000871

CrossRef Full Text | Google Scholar

Wu, C., and Hao, H. (2005). Modeling of simultaneous ground shock and airblast pressure on nearby structures from surface explosions. Int. J. Impact Eng. 31 (6), 699–717. doi:10.1016/j.ijimpeng.2004.03.002

CrossRef Full Text | Google Scholar

Zhang, F., Wu, C., Zhao, L. X., Heidarpour, A., Li, Z., and Huang, Y. H. (2016). Tanshinone ⅡA inhibits human esophageal cancer cell growth through miR-122-mediated PKM2 down-regulation. Arch. Biochem. Biophys. 149, 50–56. doi:10.1016/j.abb.2016.03.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, F., Wu, C., Zhao, L. X., Li, X. Z., Heidarpour, A., and Wang, H. (2015). Numerical modeling of concrete-filled double-skin steel square tubular columns under blast loading. J. Perform. Constr. Facil. 29 (5). doi:10.1061/(asce)cf.1943-5509.0000749

CrossRef Full Text | Google Scholar