Multiple linear-crossing metamaterials for directional refraction

Recently, linear-crossing metamaterials (LCMMs) in the hyperbolic topological transition of iso-frequency contour, have attracted people’s great attention. Due to the novel linear dispersion, LCMM provides a new platform to control and enhance the light-matter interactions, such as all-angle negative refraction, filters, super-lens, etc. However, the narrow-band working frequency is currently the major limitation in LCMMs. In this work, we propose two methods to realize multiple linear-crossing metamaterials (MLCMMs), including a basic Drude-Lorenz model and an actual step-like multilayer structure. Especially, in order to identify the designed two kinds of MLCMMs, we numerically demonstrate the unique beam splitting and directional refraction of MLCMM at different frequencies. Our findings may not only provide a new platform for the fundamental study of LCMM, but also facilitate some broadband applications.

Introduction

Metamaterials are fundamental building blocks in a number of optical applications due to their ability to efficiently and flexibly manipulate light (Pendry, 2000; Shelby et al., 2001; Engheta and Ziolkowsky, 2006). Among the abundant metamaterials, hyperbolic metamaterials (HMMs) (Poddubny et al., 2013; Smolyaninov, 2018; Guo et al., 2020a; Lee et al., 2022) and zero-index metamaterials (ZIMs) (Liberal and Engheta, 2017; Niu et al., 2018) are undoubtedly remarkable because of their diverse counterintuitive attributes. Recently, linear-crossing metamaterials (LCMMs) with linear dispersion, which combine the properties of both HMM and ZIM, have been proposed in the study of topological phase transition between two kinds of HMMs (Guo et al., 2018a). Take the electric LCMM ($\epsilon \to 0$; ${\mu }_{//}{\mu }_{\perp }<0$) for example, because the permittivity is close to zero, it has characteristics similar to ZIMs, that is, there will be no phase accumulation along the transmission path. Besides, the anisotropic permeability ensures the electric LCMM support high-k modes like HMMs. LCMMs open a new avenue for controlling light propagation and verifying abnormal phenomena involving ZIMs and HMMs (Guo et al., 2022a).

Although LCMMs have some physical properties similar to ZIMs and HMMs, which have been widely studied in the last two decades, the novel linear dispersion also enables LCMMs to have many unique properties that are worth exploring. The light-matter interactions depend on the dispersion in wave-vector space characterized by the isofrequency contours (IFCs). Similar to the Fermi plane in electronic systems, the IFCs of photonic systems determine the transmission properties of light in various materials (Guo et al., 2020a). The complex dispersive control of beam propagation is a very interesting topic (Fan et al., 2016; Tsilipakos et al., 2018; Zhu et al., 2022). It is well known that the normal topological transition of dispersion in anisotropic metamaterials, in which IFC changes from a closed ellipsoid to an open hyperboloid, can lead to many unusual propagation phenomena of electromagnetic waves in media, such as all-angle negative refraction (High et al., 2015), focusing (Martín-Sánchez et al., 2021), and self-collimation (Yu et al., 2016). Especially, the open IFCs of hyperbolic dispersion can support high-k modes and possess an enhanced photonic density of states (Smolyaninov and Narimanov, 2010; Krishnamoorthy et al., 2012), leading to promising applications such as super-resolution imaging that can overcome diffraction limits (Liu et al., 2007; Smolyaninov et al., 2007; Duan et al., 2021a), long-range atom-atom interaction (Guo et al., 2018b; Newman et al., 2018), optical forces engineering (Li et al., 2020a; Li et al., 2020b), sub-wavelength cavities (Yang et al., 2012; Wang et al., 2020; Guo et al., 2022b) and waveguides (Guo et al., 2021a; Fu et al., 2021; Ji et al., 2022). Similar to the normal topological transition, the LCMMs existing in the novel hyperbolic topological transition of dispersion can also be well studied based on IFC, which reveals that LCMMs have some unique properties in the field of designing superior optical devices, such as the super-resolution imaging (Guo et al., 2018a), diffraction free beam (Guo et al., 2020b), and robust spatial filtering (Guo et al., 2020c). It should be emphasized that although LCMM was proposed in the transmission lines system based on effective circuit model, it has recently been extended to photonic crystal (Yang et al., 2019), phononic crystal (Xu et al., 2022), and even the $\alpha$-MoO₃ biaxial slab with phonon polaritons (Duan et al., 2021b). Nevertheless, similar to most critical situations of photonic systems, LCMMs suffer from single frequency response for the near-zero permittivity or permeability, which is a significant disadvantage for practical applications. A natural question is whether we can achieve multi-frequency LCMM?

In this work, we propose the multi-frequency LCMM from the basic Drude-Lorenz model and actual step-like multilayer structure. Specifically, from the perspective of basic dispersive electromagnetic parameters, when the permittivity meets the Drude-Lorenz model, a double-LCMM will be achieved. In addition, multiple structure is a very special topic because it has more physical properties than a single counterpart. When considering an actual composite stepped multilayer structure, a quintuple-LCMM will also be achieved. Since the two open branches of IFC intersect in LCMMs, multi-frequency beam splitting will occur when light is normally incident on LCMMs. Besides, the unidirectional refraction will happen if the light is incident on the material at oblique angles. Based on the findings in this study, a series of important applications based on these novel properties may be applied, such as broadband 50/50 beam splitter, unidirectional refraction, zero-phase delay device and so on.

Results and discussion

The novel physical properties of LCMMs have motivated extensive studies of linear dispersion in photonic and acoustic systems. However, as introduced in previous works, the LCMMs suffer from single frequency response for the near-zero permittivity or permeability, which greatly hamper the related applications. Once the multiple linear-crossing metamaterials (MLCMM) can be realized, broadband directional refraction becomes possible. Due to the special linear dispersion characteristics of MLCMM, it will open up a new way for energy directional collection and filtering when the natural light incident on the material, as shown schematically in Figure 1. Generally speaking, the electromagnetic response of uniaxial materials is described by the permittivity and permeability (Guo et al., 2020a)

$\widehat{\mathrm{\epsilon }}=\left(\begin{array}{ccc}{\epsilon }_{\perp }& 0& 0\\ 0& {\epsilon }_{\perp }& 0\\ 0& 0& {\epsilon }_{\parallel }\end{array}\right),\widehat{\mathrm{\mu }}=\left(\begin{array}{ccc}{\mu }_{\perp }& 0& 0\\ 0& {\mu }_{\perp }& 0\\ 0& 0& {\mu }_{\parallel }\end{array}\right)(1)$

where the subscript $\perp$ and $\parallel$ represent the components perpendicular and parallel to the optical axis (z axis), respectively. In particular, by substituting Eq. 1 into Maxwell’s equations, the corresponding dispersion relationship can be obained as (Ferrari et al., 2015)

$\left(\frac{k_{\perp }^2}{{\epsilon }_{\parallel }}+\frac{k_{\parallel }^2}{{\epsilon }_{\perp }}-{\mu }_{\perp }{k}_0^2\right)\left(\frac{k_{\perp }^2}{{\mu }_{\parallel }}+\frac{k_{\parallel }^2}{{\mu }_{\perp }}-{\epsilon }_{\perp }{k}_0^2\right)=0(2)$

where $k_{\perp }=\pm \sqrt{k_x^2+k_y^2}$ and $k_{\parallel }=k_z$ are the wave vector in the perpendicular and parallel directions, respectively. $k_0$ is the wave vector in free space. Especially, the first and second terms of brackets in Eq. 2 describe the transverse electric (TE,$H_x,E_y,H_z$) and transverse magnetic (TM, $E_x,H_y,E_z$) polarized waves, respectively.

FIGURE 1

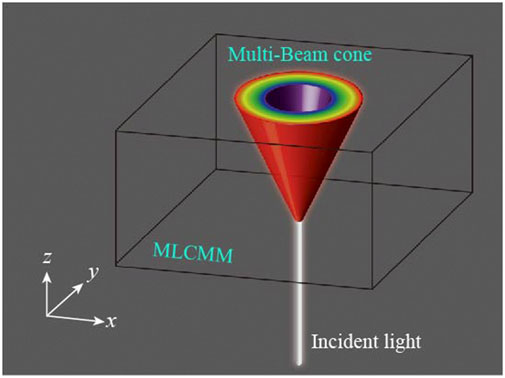
FIGURE 1. Schematic of the multi-beam cone in the MLCMM. The beam splitting will occur when the light incident on the MLCMM.

Considering the TE polarized wave propagating in the x–z plane, the simply dispersion equation of the uniaxial media is expressed as (Guo et al., 2020a)

$\frac{k_x^2}{{\mu }_z}+\frac{k_z^2}{{\mu }_x}={\epsilon }_y{k}_0^2(3)$

where $k_x$ and $k_z$ are the wave vector along x and z directions, respectively. According to Eq. 3, considering the anisotropic permeability ${\mu }_x{\mu }_z<0$ like the magnetic HMM, the hyperbolic topological transition between two kinds of HMMs can be realized by tuning the sign of ${\epsilon }_y$ from negative to positive while the signs of the ${\mu }_x$ and ${\mu }_z$ are unchanged. Especially, the transition phase at ${\epsilon }_y\to 0$ corresponds to LCMM with linear crossing IFC. To illustrate the mechanism for the formation of MLCMM with multi-frequency linear dispersion, we consider that the permittivity satisfies the basic Drude-Lorenz model as (Hashimoto et al., 2016; Sehmi et al., 2017)

${\epsilon }_y={\epsilon }_{\infty }-\frac{{\omega }_p^2}{i\omega \gamma +{\omega }^2}-\frac{\Delta {\mathrm{\Omega }}_L^2}{i{\mathrm{\Gamma }}_L+{\omega }^2-{\mathrm{\Omega }}_L^2}(4)$

where ${\epsilon }_{\infty }=0.5$, $\gamma ={\mathrm{\Gamma }}_L=0$, ${\omega }_p=2.51\times {10}^{15}$ rad/s, $\mathrm{\Delta }=0.1$, and ${\mathrm{\Omega }}_L=3.77\times {10}^{15}$ rad/s. Without losing any generality, the anisotropic permeability are satisfy the simply Drude model as (Guo et al., 2018a)

${\mu }_x={\mu }_{\infty }-\frac{{\omega }_{px}^2}{i\omega {\gamma }_x+{\omega }^2},{\mu }_z={\mu }_{\infty }-\frac{{\omega }_{pz}^2}{i\omega {\gamma }_z+{\omega }^2}(5)$

where ${\epsilon }_{\infty }=1$, ${\gamma }_x={\gamma }_z=0$, ${\omega }_{px}=7.67\times {10}^{15}$ rad/s, and ${\omega }_{pz}=4.46\times {10}^{15}$ rad/s. The electromagnetic parameters calculated by Eqs. 4, 5 are shown in Figure 2A as a function of frequency. It can be clearly seen that ${\mu }_x$ and ${\mu }_z$ increase monotonically with the increase of frequency. However, with increasing frequency, ${\epsilon }_y$ changes from negative to positive twice, which indicates the double-LCMM can be realized based on the basic Drude-Lorenz model. We can clearly see that permittivity have two zero point in the visible region. The inset color map shows that LCMM1 and LCMM2 in the double-LCMM correspond to the red and purple light, which are marked by the red and purple stars, respectively. Based on Eq. 3, the 3D dispersion relationship can be obtained, as is shown in Figure 2B. It can be clearly seen that the first (second) hyperbolic topological transition from dielectric-type HMM (DHMM) to metal-type HMM (MHMM) can be realized when the frequency increases from 400 THz (600 THz) to 600 THz (800 THz). In order to intuitively show the hyperbolic topological transitions, Figures 2C,D give three different IFCs near LCMM1 and LCMM2, respectively. Especially, IFCs of low-frequency (high-frequency) DHMM, LCMM1 (LCMM2), and low-frequency (high-frequency) MHMM at 400 THz (650 THz), 463 THz (733 THz), and 550 THz (900 THz) are marked by green dashed line, red (purple) solid line and blue dash dotted line in Figures 2C,D respectively.

FIGURE 2

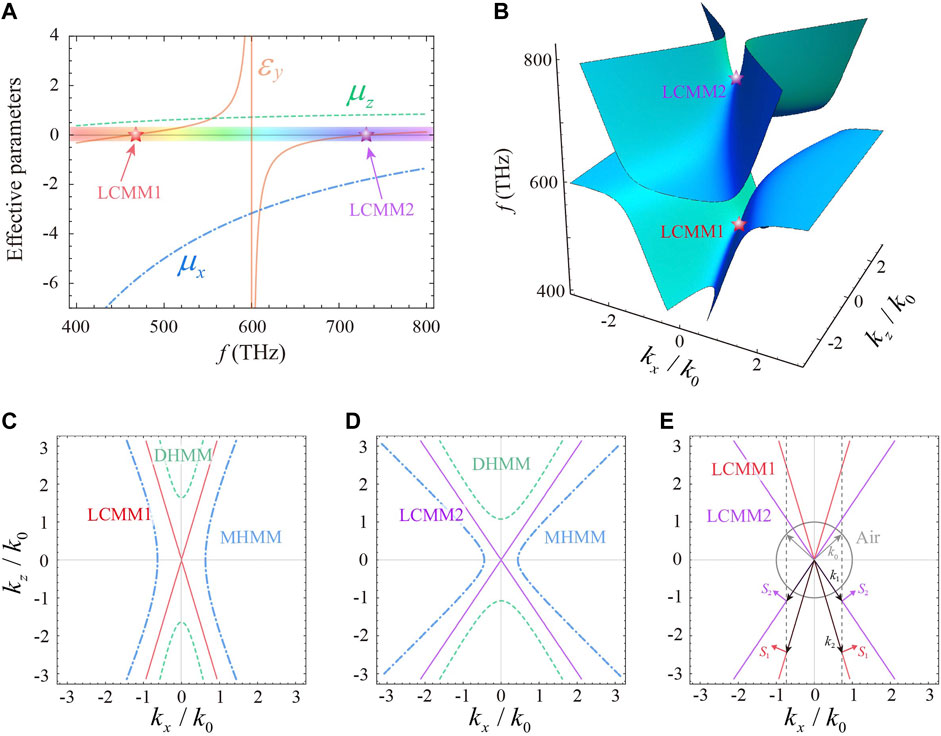
FIGURE 2. MLCMM based on the Drude-Lorenz model. (A) Effective anisotropic electromagnetic parameters of the MLCMM based on the Drude-Lorenz model. ${\mu }_x$, ${\epsilon }_y$, and ${\mu }_z$ are represented by blue dash dotted line, red solid line, and green dashed line, respectively. (B) The 3D dispersion relationships of two kinds of hyperbolic topological transitions. LCMM1 and LCMM2 are marked by red and purple stars, respectively. (C) The cross graphs of the 3D dispersion relationships for the low frequency hyperbolic topological transition in (B). IFCs of dielectric-type HMM (DHMM), LCMM1, and metal-type HMM (MHMM) at 400 THz, 463 THz, and 550 THz are marked by green dashed line, red solid line and blue dashdotted line, respectively. (D) Similar to (C), but for the high frequency hyperbolic topological transition. (E) Multi-frequency directional refraction expressed from the linear dispersion when the light incident from air to double-LCMM.

The beam splitting and directional refraction of double-LCMM are clarified from the linear dispersion, which is shown in Figure 2E. The gray arrows and black arrows denote the wave vectors in free space (the incident medium) and double-LCMM (the refracted medium), respectively. According to the boundary conditions and the causality law, we can determine that the energy flow of the refractive waves can only propagate in two fixed directions, which are marked respectively by the red and purple arrows for LCMM1 and LCMM2 in Figure 2E. Because of the novel linear dispersion, when light incident from air to the double-LCMM the refracted angle is fixed as

$\theta =\mathit{arctan}\left({\left|{\mu }_x/{\mu }_z\right|}^{1/2}\right)(6)$

For the LCMM1 (LCMM2) at 463 THz (733 THz), the anisotropic permeability corresponds to ${\mu }_x=-6\left(-1.79\right)$ and ${\mu }_z=0.53\left(0.81\right)$, which indicates the refracted angle is ${\theta }_1={73.5}^o$ (${{\theta }_2=56.1}^o$). In order to verify the multi-frequency directional refraction of the multi-LCMM with basic Drude-Lorenz model, the simulated field distributions of LCMM1 and LCMM2 are shown in Figure 3. It can be seen that when the light is normally incident on the multilayered LCMM, the beam will split into two directions, as shown in Figures 3A,D for LCMM1 (f₁ = 463 THz) and LCMM2 (f₂ = 733 THz), respectively (Erçağlar et al., 2021; Hu et al., 2021; Phon et al., 2021). The wave vector and energy flow are marked by blue and red arrows, respectively. Because the group velocity and phase velocity in an LCMM are perpendicular to each other, which leads to zero phase accumulation along the propagation path as in a ZIM. On the other hand, when the beam is obliquely incident on the double-LCMM structure at f₁ = 463 THz with incident angle of -5° (or 5°), the beam will be refracted at the fixed angle ${\theta }_1={73.5}^o$, as is shown in Figure 3B (Figure 3C). Similarly, Figures 3E,F give the electric field distributions of when the beam is obliquely incident on the double-LCMM structure at f₂ = 733 THz with incident angle of -5 degrees and 5°, respectively. In this case, the beam will be refracted at the fixed angle ${\theta }_1={56.1}^o$. It should be emphasized that for HMM to achieve directional transition, the near-field spin source or Huygens’ source is required, while LCMM can only be achieved when incident at an oblique angle (Guo et al., 2021b).

FIGURE 3

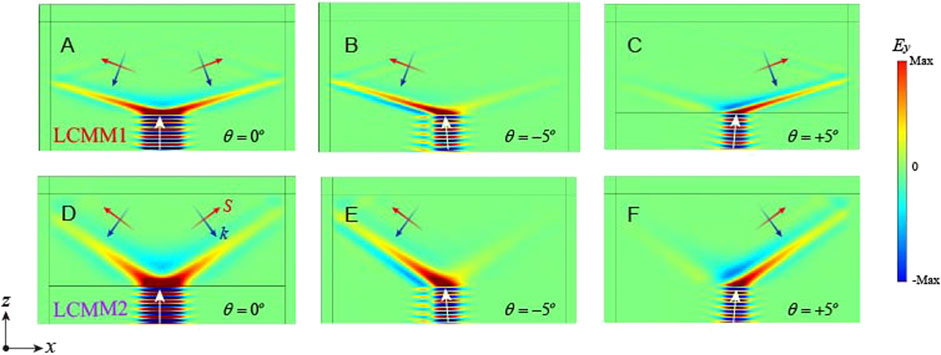
FIGURE 3. Beam splitting and unidirectional refraction of MLCMM based on the Drude-Lorenz model. (A) Beam splitting when the light is normally incident on the LCMM1. (B), (C) The directional refraction of LCMM1 when the incident angle is ${-\mathit{5}}^o$ and ${+\mathit{5}}^o$, respectively. (D–F) Similar to (A–C), but for the LCMM2. The incident Gaussian beam is marked by the white arrows.

From Figure 3, it is clear that incident red and purple light will trigger beam splitting and directional refraction with different refraction angles. In order to further verify the multi-frequency directional refraction of MLCMM, we study the electric field distributions at more incident angles in Figure 4. When the incident angle increases from ${+10}^o$ to ${+45}^o$, the beam will still be refracted at the fixed angle ${\theta }_1={73.5}^o$ (${{\theta }_2=56.1}^o$) for LCMM1 (LCMM2), as shown in Figures 4A–F). It should be emphasized that the beam splitting and directional refraction of MLCMM remain even for the lossy materials, but the transmission distance will be shortened due to the influence of absorption. Recently, the pseudo-magnetic field controlled beam bending is a very interesting research topic, in which the external-field-free photonic transportation behavior comes from the introduction of structural gradient (Zhang et al., 2014; Deng et al., 2015). The similar phenomenon can also be expected in the LCMM with crossing IFCs when the structural gradient is considered.

FIGURE 4

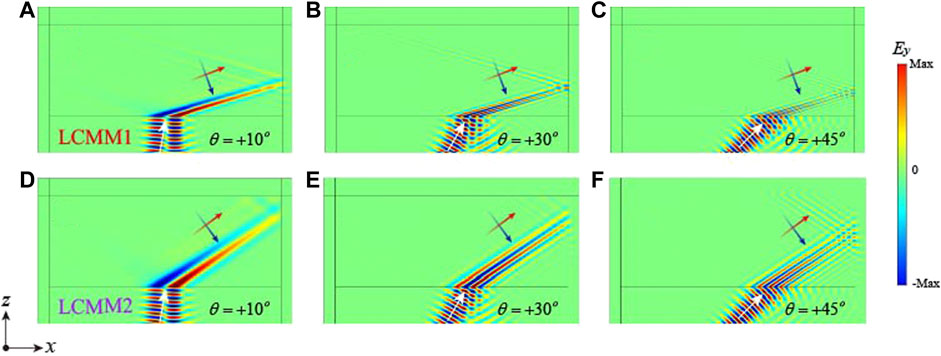
FIGURE 4. Directional refraction of the MLCMM based on the Drude-Lorenz model. (A–C) The positive refraction of LCMM1 with different incident angles: (A) ${\theta =+\mathit{10}}^o$, (B) ${\theta =+\mathit{30}}^o$, (C) ${\theta =+\mathit{45}}^o$. (D–F) Similar to (A–C), but for the LCMM2.

After using the basic Drude-Lorenz model to study the multi-frequency directional refraction of MLCMM, we also design a practical composite stepped multilayer structure to realize the MLCMM. At present, although multilayered structures containing two kinds of single-negative media have been proposed for the single-frequency LCMM, the multiple-LCMM with broadband properties remains elusive (Guo et al., 2020b). Fortunately, based on the Bergman spectral representation of the effective permittivity, the step-like design has been successfully used in realizing the multi frequency near-zero effective permittivity (Sun et al., 2013). Very recently, the all-angle broadband near-zero effective permittivity property also has been demonstrated in the symmetric step-like multilayer structure (Sun et al., 2022). Inspired by these pioneering works, in this section we propose the composite stepped multilayer structure to realize the MLCMM. The component DPS (${\epsilon }_1$ > 0, ${\mathrm{\mu }}_1$ > 0), ENG (${\epsilon }_2$ < 0, ${\mathrm{\mu }}_2$ > 0), DNS (${\epsilon }_3$ < 0, ${\mathrm{\mu }}_3$ < 0) and MNG (${\epsilon }_4$ > 0, ${\mathrm{\mu }}_4$ < 0) media are respectively marked by brown, green, blue, and pink in the electromagnetic parameter space, as shown in Figure 5A. The corresponding composite stepped multilayer structure is shown in Figure 5B. So far, DPS, ENG, DNS and MNG media have been conveniently constructed using circuit-based metamaterials in microwave regime (Guo et al., 2020d; Long et al., 2020). The optical nanocircuit-based metamaterials provide a good platform for realizing isotropic electromagnetic parameters in higher frequency bands (Engheta, 2007; Alù and Engheta, 2009). The proposed step-like multilayer structure for MLCMM is a two-dimensional three-layer stack, and layer A (B) is a mixture with A1 (B1) as the inclusion and A2 (B2) as the host medium. Moreover, cross graphs of multilayer structure in the plane of x-z and composite layer A (B) in the plane of y-z are shown in Figures 5C–E, respectively. The thickness of composite layer A (layer B) is $d_A=d_B=15$ nm. The filling ratio of width and height for A1 (B1) in the composite layer A (B) is $w_i/w_0=0.22,0.19,0.16$ and $h_i/h_0=0.44,0.19,0.37\left(i=\mathrm{1,2,3}\right)$.

FIGURE 5

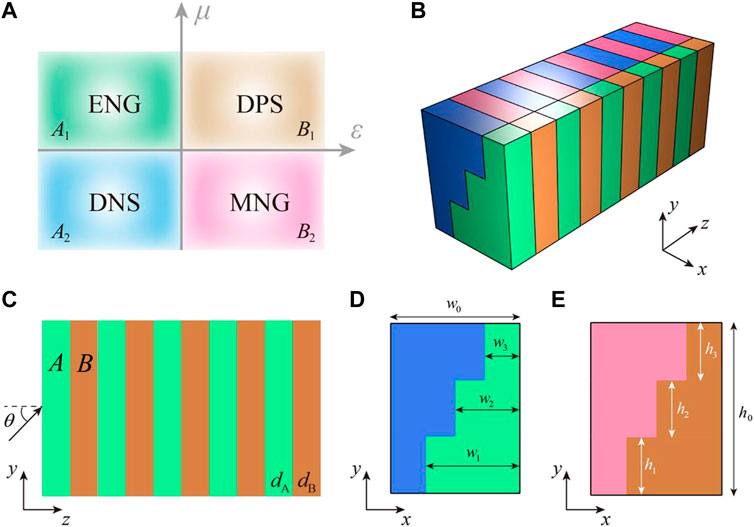
FIGURE 5. Step-like multilayer structure for MLCMM. (A) Electromagnetic parameter space of the isotropic media. DPS (${\epsilon }_{\mathit{1}}$ > 0, ${\mathrm{\mu }}_{\mathit{1}}$ > 0), ENG (${\epsilon }_{\mathit{2}}$ < 0, ${\mathrm{\mu }}_{\mathit{2}}$ > 0), DNS (${\epsilon }_{\mathit{3}}$ < 0, ${\mathrm{\mu }}_{\mathit{3}}$ < 0) and MNG (${\epsilon }_{\mathit{4}}$ > 0, ${\mathrm{\mu }}_{\mathit{4}}$ < 0) media are marked by brown, green, blue, and pink, respectively. (B) Schematic of the step-like multilayer structure composed of four kinds of media in (A). (C) The cross graph of multilayer structure in the plane of x-z. (D) The cross graph of composite layer A in the plane of y-z. (E) The cross graph of composite layer B in the plane of y-z. All the geometric parameters are marked as $d_A=d_B=\mathit{15}$ nm, The filling ratio of width and height for A1 (B1) in the composite layer A (B) is $w_i/w_{\mathit{0}}=0.22,0.19,0.16$ and $h_i/h_{\mathit{0}}=0.44,0.19,0.37\left(i=\mathit{1,2,3}\right)$.

Considering the simplicity of the structure, we assume that the dispersion electromagnetic parameters are described by the simple Drude model (Guo et al., 2020b)

${\mathrm{\epsilon }}_1={\mathrm{\epsilon }}_4={\mathrm{\epsilon }}_a,{\mathrm{\epsilon }}_2={\mathrm{\epsilon }}_3={\mathrm{\epsilon }}_b-\frac{{\alpha }^2}{{\omega }^2+i\omega \gamma }(7)$

${\mu }_1={\mu }_4={\mu }_a-\frac{{\beta }^2}{{\omega }^2+i\omega \gamma },{\mu }_2={\mu }_3={\mu }_b(8)$

In the following calculation, we choose ${\mathrm{\epsilon }}_a={\mu }_b=2.13$, ${\mathrm{\epsilon }}_b={\mu }_a=5.7$, $\alpha =\beta =1.37\times {10}^{16}$ rad/s, and $\gamma =1.22\times {10}^{14}$ rad/s. Considering the TE polarized wave propagating in the x–z plane, the effective anisotropic permittivity and permeability of the step-like multilayer structure can be obtained based on the effective medium theory (Sun et al., 2013)

${\mathrm{\epsilon }}_y={\mathrm{\epsilon }}_1{\displaystyle \sum }_{i=1}^3{\left(\frac{h_i/h_0}{1-w_i\left({\mathrm{\epsilon }}_1-{\mathrm{\epsilon }}_2\right)/{\mathrm{\epsilon }}_1}\right)}^{-1}(9)$

and

${\mu }_x=\frac{{\mu }_1{d}_A+{\mu }_2{d}_B}{d_A+d_B},{\mu }_z={\left(\frac{d_A/{\mu }_1+d_B{/\mu }_2}{d_A+d_B}\right)}^{-1}(10)$

respectively. Based on Eqs. 9 and (10), the effective permittivity and anisotropic permeability of the step-like multilayer structure are shown in Figure 6A. The dependence of ${\mu }_x$, ${\epsilon }_y$, and ${\mu }_z$ on the frequency are represented by blue dash dotted line, red solid line, and green dashed line, respectively. There are five zero points of ${\epsilon }_y$ while ${\mu }_x{\mu }_z<0$ when the frequency increases from 550 THz to 680 THz. Therefore, the quintuple-LCMM can be realized by the composite step-like multilayer structure. In order to show the directional refraction of green light, cyan light and blue light, we selected three frequencies at 595 THz, 610 THz, and 650 THz for LCMM1, LCMM2, and LCMM3, respectively. Similar to Figure 2E, the IFCs corresponding to the selected frequencies are shown in Figure 6B.

FIGURE 6

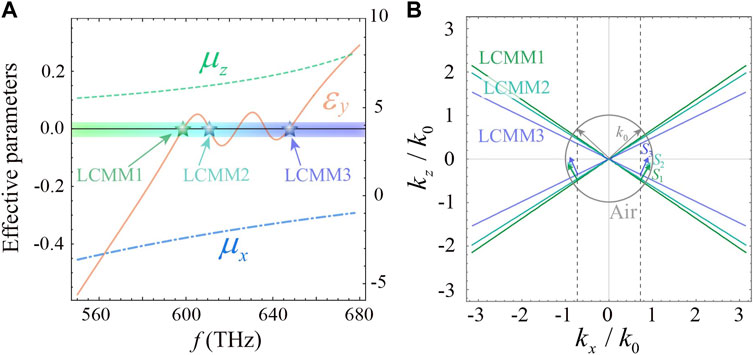
FIGURE 6. MLCMM based on the step-like multilayer structure. (A) Effective real part of anisotropic electromagnetic parameters based on the step-like multilayer structure. ${\mu }_x$, ${\epsilon }_y$, and ${\mu }_z$ are represented by blue dash dotted line, red solid line, and green dashed line, respectively. (B) Directional refraction of three LCMMs expressed from the linear dispersion.

For the LCMM1, LCMM2, and LCMM3, the anisotropic permeability in x (z) direction correspond to ${\mu }_x=-2.76,-2.43,\mathrm{a}\mathrm{n}\mathrm{d}-1.68$ (${\mu }_z=5.91,6.12,\mathrm{a}\mathrm{n}\mathrm{d}6.96$), respectively. According to Eq. 6, the corresponding fixed refracted angles are ${\theta }_1={34.3}^o$, ${{\theta }_2=32.2}^o$ and ${{\theta }_3=26.2}^o$, respectively. When the light is normally incident on the structure, the multi-frequency beam splitting has been demonstrated from the simulated electric field distributions of LCMM1, LCMM2, and LCMM3 in Figures 7A,D,G, respectively. However, when the beam is obliquely incident on the MLCMM structure with incident angle of -5° (or 5°), the beam will be refracted at the fixed angle ${\theta }_1={34.3}^o$, ${{\theta }_2=32.2}^o$ and ${{\theta }_3=26.2}^o$ for LCMM1, LCMM2, and LCMM3, as shown in Figures 7B,C,E,F,H,I respectively.

FIGURE 7

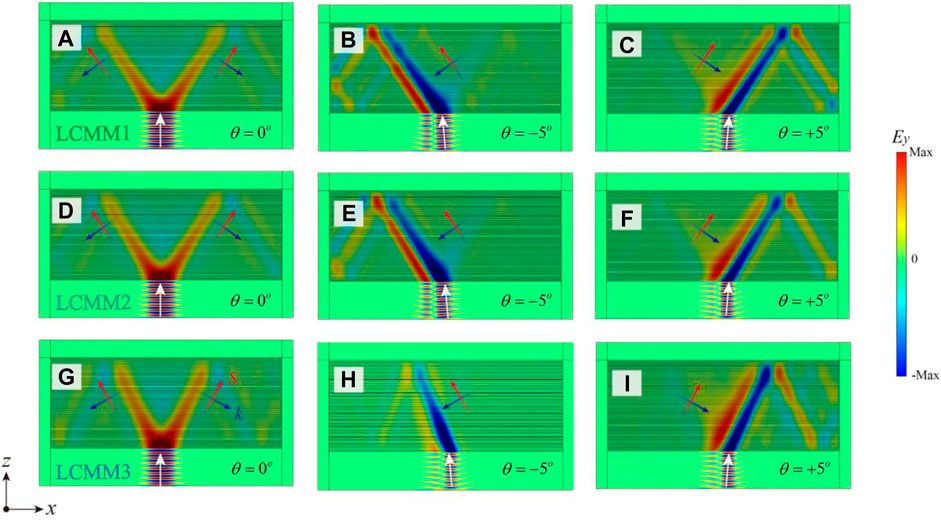
FIGURE 7. Beam splitting and unidirectional refraction of MLCMM based on the step-like multilayer structure. (A) Beam splitting when the light is normally incident on the LCMM1. (B), (C) The directional refraction of LCMM1 when the incident angle is ${-\mathit{5}}^o$ and ${+\mathit{5}}^o$, respectively. (D–F) (G–I) Similar to (A–C), but for the LCMM2 and LCMM3, respectively.

Similar to the MLCMM based on the basic Drude-Lorenz model in Figure 4, the directional refraction with different refraction angles of MLCMM based on the step-like multilayer structure is demonstrated in Figure 8. When the incident angle increases from ${+10}^o$ to ${+45}^o$, the beam will still be refracted at the fixed angle ${\theta }_1={34.3}^o$, ${{\theta }_2=32.2}^o$ and ${{\theta }_3=26.2}^o$ for LCMM1, LCMM2, and LCMM3, as are shown in Figures 8A–C,D–F,G–I, respectively. Although the directional positive refraction of LCMM is studied in this paper, by exchanging the signs of anisotropic permeability, we can also achieve novel directional negative refraction (Guo et al., 2018a). In addition, the results of this paper are based on electric MLCMM in the magnetic hyperbolic topological transition, but when the permittivity and permeability are exchanged, similar results can be extended to the magnetic MLCMM in the electric hyperbolic topological transition according to the duality (Kruk et al., 2016; Yermakov et al., 2018). Especially, considering the degree of freedom of rotation (Guo et al., 2020c; DuanCapote-Robayna et al., 2020; Shen et al., 2020; Liu et al., 2022a), the Moire lattice also provides a good research idea for the further study of MLCMMs (Chen et al., 2020; Hu et al., 2020; Liu et al., 2022b). Finally, tunable LCMM provides another effective manner to achieve linear dispersion at multiple frequencies. Recently, tunable metamaterials have been widely studied by using voltage controlled graphene (Vakil and Engheta, 2011; Guo et al., 2018c; Fan et al., 2019) and temperature controlled vanadium oxide (Liu et al., 2012; Taboada-Gutiérre et al., 2020). However, it should be emphasized that compared with actively controlled tunable LCMM, although MLCMM cannot achieve broadband linear dispersion in continuous frequency band, the multi-frequency linear dispersion of MLCMM is an inherent characteristic of materials, and no additional external field is required. Overall, due to the multi-frequency linear dispersion characteristics of MLCMM, it will open a new way for energy directional collection and filtering at different working frequencies and refraction angles.

FIGURE 8

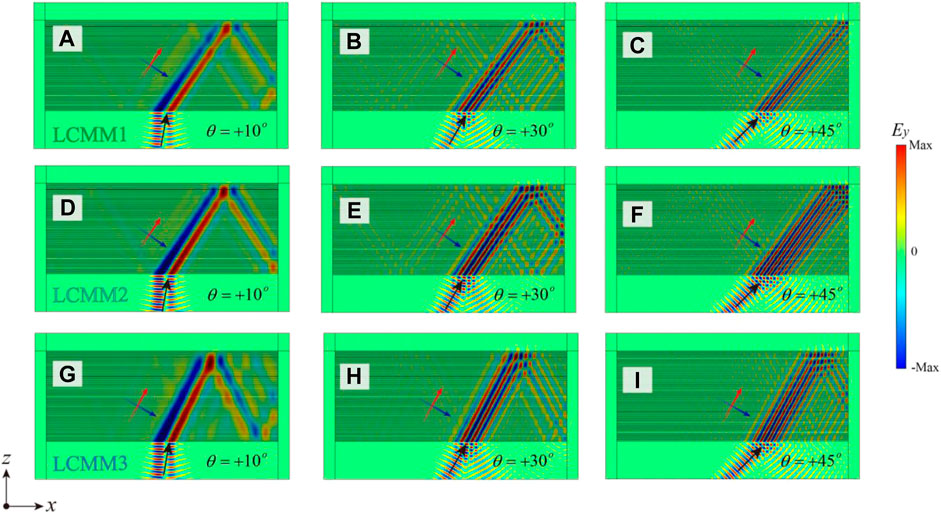
FIGURE 8. Directional refraction of the MLCMM based on the step-like multilayer structure. (A–C) The positive refraction of LCMM1 with different incident angles: (A) ${\theta =+\mathit{10}}^o$, (B) ${\theta =+\mathit{30}}^o$, (C) ${\theta =+\mathit{45}}^o$. (D–F) (G–I) Similar to (A–C), but for the LCMM2 and LCMM3, respectively.

Conclusion

In summary, we theoretically propose the MLCMM in the hyperbolic topological transition. Starting from basic Drude-Lorenz model and the effective composite step-like multilayer structure, we demonstrate that the MLCMMs can be used to realize the multi-frequency beam splitting and directional refraction for the normal and oblique incident beams, respectively. The results not only combine two independent concepts of ZIM and HMM to construct a new multi-frequency optical metamaterial, but also provide a way to design novel optical devices with excellent performance, which overcomes the single-frequency limitation of conventional LCMM.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZG and HC put forward the initial idea and supervised the project. ZG and YJ performed the theoretical calculations and wrote the manuscript. XW, FD, and LD helped with the theoretical analyses. All authors fully contribute to the research. ZG and YJ contribute equally to this work.

Funding

This work was supported by the National Key R&D Program of China (Grant No. 2021YFA1400602), the National Natural Science Foundation of China (NSFC; Grant Nos. 12004284 and 61621001), the Central Government Guides Local Science and Technology Development Fund Projects (Grant No. YDZJSX 2021B011), the Fundamental Research Funds for the Central Universities (Grant No. 22120210579), and the Shanghai Chenguang Plan (Grant No.21CGA22).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alù, A., and Engheta, N. (2009). All optical metamaterial circuit board at the nanoscale. Phys. Rev. Lett. 103, 143902. doi:10.1103/physrevlett.103.143902

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, M., Lin, X., Dinh, T. H., Zhang, Z., Shen, J., Ma, Q., et al. (2020). Configurable phonon polaritons in twisted α-MoO3. Nat. Mat. 19, 1307–1311. doi:10.1038/s41563-020-0732-6

CrossRef Full Text | Google Scholar

Deng, F., Li, Y., Sun, Y., Wang, X., Guo, Z., Shi, Y., et al. (2015). Valley-dependent beams controlled by pseudomagnetic field in distorted photonic graphene. Opt. Lett. 40, 3380. doi:10.1364/ol.40.003380

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, J., Álvarez-Pérez, G., Tresguerres-Mata, A. I. F., Taboada-Gutiérrez, J., Voronin, K. V., Bylinkin, A., et al. (2021). Planar refraction and lensing of highly confined polaritons in anisotropic media. Nat. Commun. 12, 4325. doi:10.1038/s41467-021-24599-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, J., Alvarez-Pérez, G., Voronin, K. V., Prieto, I., Taboada-Gutiérrez, J., Volkov, V. S., et al. (2021). Enabling propagation of anisotropic polaritons along forbidden directions via a topological transition. Sci. Adv. 7, eabf2690. doi:10.1126/sciadv.abf2690

PubMed Abstract | CrossRef Full Text | Google Scholar

DuanCapote-Robayna, J. N., Taboada-Gutiérrez, J., ÁlvarezPérez, G., Prieto, I., Martín-Sánchez, J., Nikitin, A. Y., et al. (2020). Twisted nano-optics: Manipulating light at the nanoscale with twisted phonon polaritonic slabs. Nano Lett. 20, 5323–5329. doi:10.1021/acs.nanolett.0c01673

PubMed Abstract | CrossRef Full Text | Google Scholar

Engheta, N. (2007). Circuits with light at nanoscales: Optical nanocircuits inspired by metamaterials. Science 317, 1698–1702. doi:10.1126/science.1133268

PubMed Abstract | CrossRef Full Text | Google Scholar

Engheta, N., and Ziolkowsky, R. W. (2006). Metamaterials, physics and engineering exploration. New York: John Wiley & Sons.

Google Scholar

Erçağlar, V., Hajian, H., Serebryannikov, A. E., and Ozbay, E. (2021). Multifunctional tunable gradient metasurfaces for terahertz beam splitting and light absorption. Opt. Lett. 46, 3953. doi:10.1364/ol.435197

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Y., Shen, N. H., Zhang, F., Wei, Z., Li, H., Zhao, Q., et al. (2016). Electrically tunable Goos–Hänchen effect with graphene in the terahertz regime. Adv. Opt. Mat. 4, 1824–1828. doi:10.1002/adom.201600303

CrossRef Full Text | Google Scholar

Fan, Y., Shen, N., Zhang, F., Zhao, Q., Wu, H., Fu, Q., et al. (2019). Graphene plasmonics: A platform for 2D optics. Adv. Opt. Mat. 7, 1800537. doi:10.1002/adom.201800537

CrossRef Full Text | Google Scholar

Ferrari, L., Wu, C. H., Lepage, D., Zhang, X., and Liu, Z. W. (2015). Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 40, 1. doi:10.1016/j.pquantelec.2014.10.001

CrossRef Full Text | Google Scholar

Fu, M., Jin, Y., Evans, J., and He, S. L. (2021). Microwave waveguide-type hyperbolic metamaterials. Adv. Photonics Res. 2, 2000043. doi:10.1002/adpr.202000043

CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., and Chen, H. (2020). Abnormal wave propagation in tilted linear-crossing metamaterials. Adv. Photonics Res. 2, 2000071. doi:10.1002/adpr.202000071

CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., and Chen, H. (2020). Hyperbolic metamaterials: From dispersion manipulation to applications. J. Appl. Phys. 127, 071101. doi:10.1063/1.5128679

CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., and Chen, H. (2022). Linear-crossing metamaterials and their applications. Acta Phot. Sin. 51, 0151111.

Google Scholar

Guo, Z., Jiang, H., and Chen, H. (2020). Linear-crossing metamaterials mimicked by multi-layers with two kinds of single negative materials. J. Phys. Photonics 2, 011001. doi:10.1088/2515-7647/ab5ecb

CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., and Chen, H. (2022). Zero-index and hyperbolic metacavities: Fundamentals and applications. J. Phys. D. Appl. Phys. 55, 083001. doi:10.1088/1361-6463/ac2e89

CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., Li, Y., Chen, H., and Agarwal, G. S. (2018). Enhancement of electromagnetically induced transparency in metamaterials using long range coupling mediated by a hyperbolic material. Opt. Express 26, 627. doi:10.1364/oe.26.000627

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., Sun, Y., Li, Y., and Chen, H. (2018). Actively controlling the topological transition of dispersion based on electrically controllable metamaterials. Appl. Sci. (Basel). 8, 596. doi:10.3390/app8040596

CrossRef Full Text | Google Scholar

Guo, Z., Jiang, H., Zhu, K., Sun, Y., Li, Y., and Chen, H. (2018). Focusing and super-resolution with partial cloaking based on linear-crossing metamaterials. Phys. Rev. Appl. 10, 064048. doi:10.1103/physrevapplied.10.064048

CrossRef Full Text | Google Scholar

Guo, Z., Long, Y., Jiang, H., Ren, J., and Chen, H. (2021). Anomalous unidirectional excitation of high-k hyperbolic modes using all-electric metasources. Adv. Phot. 3, 036001. doi:10.1117/1.ap.3.3.036001

CrossRef Full Text | Google Scholar

Guo, Z., Song, J., Jiang, H., and Chen, H. (2021). Miniaturized backward coupler realized by the circuit-based planar hyperbolic waveguide. Adv. Photonics Res. 2, 2100035. doi:10.1002/adpr.202100035

CrossRef Full Text | Google Scholar

Guo, Z., Sun, Y., Jiang, H., Ding, Y.-Q., Li, Y., Zhang, Y., et al. (2020). Experimental demonstration of an anomalous Floquet topological insulator based on negative-index media. Available at: https://arxiv.org/abs/2006.12252.

Google Scholar

Hashimoto, Y., Seniutinas, G., Balčytis, A., Juodkazis, S., and Nishijima, Y. (2016). Au-Ag-Cu nano-alloys: Tailoring of permittivity. Sci. Rep. 6, 25010. doi:10.1038/srep25010

PubMed Abstract | CrossRef Full Text | Google Scholar

High, A. A., Devlin, R. C., Dibos, A., Polking, M., Wild, D. S., Perczel, J., et al. (2015). Visible frequency hyperbolic metasurface. Nature 522, 192–196. doi:10.1038/nature14477

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, F., Du, S., Li, J., and Gu, C. (2021). Multidimensional image and beam splitter based on hyperbolic metamaterials. Nano Lett. 21, 1792–1799. doi:10.1021/acs.nanolett.0c04795

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, G., Ou, Q., Si, G., Wu, Y., Wu, J., Dai, Z., et al. (2020). Topological polaritons and photonic magic angles in twisted α-MoO₃ bilayers. Nature 582, 209–213. doi:10.1038/s41586-020-2359-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Ji, W., Zhou, X., Chu, H., Luo, J., and Lai, Y. (2022). Theory and experimental observation of hyperbolic media based on structural dispersions. Phys. Rev. Mat. 4, 105202. doi:10.1103/physrevmaterials.4.105202

CrossRef Full Text | Google Scholar

Krishnamoorthy, H. N., Jacob, Z., Narimanov, E., Kretzschmar, I., and Menon, V. M. (2012). Topological transitions in metamaterials. Science 336, 205–209. doi:10.1126/science.1219171

PubMed Abstract | CrossRef Full Text | Google Scholar

Kruk, S. S., Wong, Z. J., Pshenay-Severin, E., O’Brien, K., Neshev, D. N., Kivshar, Y. S., et al. (2016). Magnetic hyperbolic optical metamaterials. Nat. Commun. 7, 11329. doi:10.1038/ncomms11329

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, D., So, S., Hu, G., Kim, M., Badloe, T., Cho, H., et al. (2022). Hyperbolic metamaterials: Fusing artificial structures to natural 2D materials. Elight 2, 1. doi:10.1186/s43593-021-00008-6

CrossRef Full Text | Google Scholar

Li, H., Cao, Y., Shi, B., Zhu, T., Geng, Y., Feng, R., et al. (2020). Momentum-topology-induced optical pulling force. Phys. Rev. Lett. 124, 143901. doi:10.1103/physrevlett.124.143901

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Cao, Y., Zhou, L. M., Xu, X., Zhu, T., Shi, Y., et al. (2020). Optical pulling forces and their applications. Adv. Opt. Phot. 12, 288. doi:10.1364/aop.378390

CrossRef Full Text | Google Scholar

Liberal, I., and Engheta, N. (2017). Near-zero refractive index photonics. Nat. Photonics 11, 149–158. doi:10.1038/nphoton.2017.13

CrossRef Full Text | Google Scholar

Liu, M., Hwang, H. Y., Tao, H., Strikwerda, A. C., Fan, K., Keiser, G. R., et al. (2012). Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348. doi:10.1038/nature11231

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Ouyang, C., Xu, Q., Su, X., Ma, J., Zhao, J., et al. (2022). Negative refraction in twisted hyperbolic metasurfaces. Nanophotonics 11, 1977–1987. doi:10.1515/nanoph-2021-0561

CrossRef Full Text | Google Scholar

Liu, Y., Ouyang, C., Xu, Q., Su, X., Yang, Q., Ma, J., et al. (2022). Moiré-driven electromagnetic responses and magicangle in sandwiched hyperbolic metasurface. Phot. Res 10, 2056–2065. doi:10.1364/prj.462119

CrossRef Full Text | Google Scholar

Liu, Z., Lee, H., Xiong, Y., Sun, C., and Zhang, X. (2007). Far field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686. doi:10.1126/science.1137368

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Y., Ren, J., Guo, Z., Jiang, H., Wang, Y., Sun, Y., et al. (2020). Designing all-electric subwavelength metasources for near-field photonic routings. Phys. Rev. Lett. 125, 157401. doi:10.1103/physrevlett.125.157401

PubMed Abstract | CrossRef Full Text | Google Scholar

Martín-Sánchez, J., Duan, J. H., Taboada-Gutiérrez, J., Álvarez-Pérez, G., Voronin, K. V., Prieto, I., et al. (2021). Focusing of in-plane hyperbolic polaritons in van der Waals crystals with tailored infrared nanoantennas. Sci. Adv. 7, eabj0127. doi:10.1126/sciadv.abj0127

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, W. D., Cortes, C. L., Afshar, A., Cadien, K., Meldrum, A., Fedosejevs, R., et al. (2018). Observation of long-range dipole-dipole interactions in hyperbolic metamaterials. Sci. Adv. 4, eaar5278. doi:10.1126/sciadv.aar5278

PubMed Abstract | CrossRef Full Text | Google Scholar

Niu, X. X., Hu, X. Y., Chu, S. S., and Gong, Q. H. (2018). Epsilon-near-zero photonics: A new platform for integrated devices. Adv. Opt. Mat. 6, 1701292. doi:10.1002/adom.201701292

CrossRef Full Text | Google Scholar

Pendry, J. B. (2000). Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969. doi:10.1103/physrevlett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

Phon, R., Kim, Y., Park, E., Jeong, H., and Lim, S. (2021). Mechanical and self-deformable spatial modulation beam steering and splitting metasurface. Adv. Opt. Mat. 9, 2100821. doi:10.1002/adom.202100821

CrossRef Full Text | Google Scholar

Poddubny, A., Iorsh, I., Belov, P., and Kivshar, Y. (2013). Hyperbolic metamaterials. Nat. Photonics 7, 948–957. doi:10.1038/nphoton.2013.243

CrossRef Full Text | Google Scholar

Sehmi, H. S., Langbein, W., and Muljarov, E. A. (2017). Optimizing the Drude-Lorentz model for material permittivity: Method, program, and examples for gold, silver, and copper. Phys. Rev. B 95, 115444. doi:10.1103/physrevb.95.115444

CrossRef Full Text | Google Scholar

Shelby, R. A., Smith, D. R., and Schultz, S. (2001). Experimental verification of a negative index of refraction. Science 292, 77–79. doi:10.1126/science.1058847

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, L., Lin, X., Shalaginov, M. Y., Low, T., Zhang, X. M., Zhang, B. L., et al. (2020). Broadband enhancement of on-chip single-photon extraction via tilted hyperbolic metamaterials. Appl. Phys. Rev. 7, 021403. doi:10.1063/1.5141275

CrossRef Full Text | Google Scholar

Smolyaninov, I. I., Hung, Y.-J., and Davis, C. C. (2007). Magnifying superlens in the visible frequency range. Science 315, 1699–1701. doi:10.1126/science.1138746

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolyaninov, I. I. (2018). Hyperbolic metamaterials. London: Morgan & Claypool/Institute of Physics.

Google Scholar

Smolyaninov, I. I., and Narimanov, E. E. (2010). Metric signature transitions in optical metamaterials. Phys. Rev. Lett. 105, 067402. doi:10.1103/physrevlett.105.067402

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, L., Gao, J., and Yang, X. D. (2013). Broadband epsilon-near-zero metamaterials with steplike metal-dielectric multilayer structures. Phys. Rev. B 87, 165134. doi:10.1103/physrevb.87.165134

CrossRef Full Text | Google Scholar

Sun, L., Lin, Y., Yu, K. W., and Wang, G. P. (2022). All-angle broadband ENZ metamaterials. New J. Phys. 24, 073016. doi:10.1088/1367-2630/ac7d02

CrossRef Full Text | Google Scholar

Taboada-Gutiérre, J., Álvarez-Pérez, G., Duan, J., Ma, W., Crowley, K., Prieto, I., et al. (2020). Broad spectral tuning of ultra-low-loss polaritons in a van der Waals crystal by intercalation. Nat. Mat. 19, 964–968. doi:10.1038/s41563-020-0665-0

CrossRef Full Text | Google Scholar

Tsilipakos, O., Koschny, T., and Soukoulis, C. M. (2018). Antimatched electromagnetic metasurfaces for broadband arbitrary phase manipulation in reflection. ACS Photonics 5, 1101–1107. doi:10.1021/acsphotonics.7b01415

PubMed Abstract | CrossRef Full Text | Google Scholar

Vakil, A., and Engheta, N. (2011). Transformation optics using graphene. Science 332, 1291–1294. doi:10.1126/science.1202691

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Guo, Z., Chen, Y., Chen, X., Jiang, H., and Chen, H. (2020). Circuit-based magnetic hyperbolic cavities. Phys. Rev. Appl. 13, 044024. doi:10.1103/physrevapplied.13.044024

CrossRef Full Text | Google Scholar

Xu, C., Huang, S., Guo, Z., Jiang, H., Li, Y., Wu, Y., et al. (2022). Acoustic beam splitting and cloaking based on a compressibility-near-zero medium. Phys. Rev. Appl. 17, 054025. doi:10.1103/physrevapplied.17.054025

CrossRef Full Text | Google Scholar

Yang, X. D., Yao, J., Rho, J., Yin, X. B., and Zhang, X. (2012). Experimental realization of three-dimensional indefinite cavities at the nanoscale with anomalous scaling laws. Nat. Photonics 6, 450–454. doi:10.1038/nphoton.2012.124

CrossRef Full Text | Google Scholar

Yang, Y., Jia, Z., Xu, T., Luo, J., Lai, Y., and Hang, Z.-H. (2019). Beam splitting and unidirectional cloaking using anisotropic zero-index photonic crystals. Appl. Phys. Lett. 114, 161905. doi:10.1063/1.5088837

CrossRef Full Text | Google Scholar

Yermakov, O. Y., Hurshkainen, A. A., Dobrykh, D. A., Kapitanova, P. V., Iorsh, I. V., Glybovski, S. B., et al. (2018). Experimental observation of hybrid TE-TM polarized surface waves supported by a hyperbolic metasurface. Phys. Rev. B 98, 195404. doi:10.1103/physrevb.98.195404

CrossRef Full Text | Google Scholar

Yu, K., Guo, Z. W., Jiang, H. T., and Chen, H. (2016). Loss-induced topological transition of dispersion in metamaterials. J. Appl. Phys. 119, 203102. doi:10.1063/1.4952378

CrossRef Full Text | Google Scholar

Zhang, D. B., Seifert, G., and Chang, K. (2014). Strain-induced pseudomagnetic fields in twisted graphene nanoribbons. Phys. Rev. Lett. 112, 096805. doi:10.1103/physrevlett.112.096805

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, W., Fan, Y., Yang, R., Geng, G., Fu, Q., Gu, C., et al. (2022). Polarization-multiplexed silicon metasurfaces for multi-channel visible light modulation. Adv. Funct. Mat. 32, 2200013. doi:10.1002/adfm.202200013

CrossRef Full Text | Google Scholar