- 1Multi-Functional Shaking Tables Laboratory, Beijing University of Civil Engineering and Architecture, Beijing, China
- 2School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing, China
- 3Beijing Institute of Architectural Design, Beijing, China
It is critical to ensure the seismic resilience of super-tall buildings using high performance materials. The seismic resilience of these buildings can be enhanced by simultaneously controlling the maximum and residual inter-story drift ratios. To realize such dual-objective control, a prevailing trend is to adopt self-centering energy dissipation outriggers. In this study, taking a real engineering practice as the prototype building, super-tall building study cases with energy dissipation outriggers, and with self-centering energy dissipation outriggers are designed. Based on nonlinear time-history analysis, the seismic performances of these study cases are evaluated and compared with emphasis on the maximum, and residual inter-story drift ratios. The dual-objective control effect of self-centering energy dissipation outriggers and energy dissipation outriggers are analyzed and compared. The results indicate that self-centering energy dissipation outriggers are more effective than energy dissipation outriggers for achieving the dual-objective control of the maximum and residual drift ratios of super-tall buildings.
1 Introduction
Super-tall buildings are important parts of most cities, and their seismic performance and post-earthquake recoverability are critical factors affecting the seismic resilient performance of cities. Energy dissipation technology is typically introduced in real engineering practice to ensure and improve the seismic performance of such buildings (Yang, 2020; Oviedo-Amezquita et al., 2021). Existing investigations and engineering practices indicate that such technology can effectively control the maximum deformation and damage to the structure. However, excessive post-earthquake residual deformation of the structure increases its repair difficulty and cost (Pettinga et al., 2007; Mao and Wang, 2021). Compared with multistory and tall buildings, post-earthquake residual deformation affects super-tall building structures more significantly, primarily because of the large height of the building and the large volume of components, which render post-earthquake residual deformation difficult to repair or recover. Hence, it is critical to realize dual-objective control of the maximum deformation during an earthquake and the post-earthquake residual deformation of the structure to improve the seismic resilient performance of super-tall buildings.
Currently, high-performance concrete and steel are adopted to design and construct vertical components in super-tall buildings to improve the deformation limits corresponding to each damage stage and then alleviate the damage to the main structure under the same deformation (Nehdi, 2013; Liew et al., 2016; Hassan et al., 2017; Zhang et al., 2020). Regarding the horizontal components (e.g., coupling beam and outrigger), high-performance energy dissipation components can be introduced to dissipate plastic energy, and reduce damage to the vertical components to ensure the seismic performance of the main structure (Yang et al., 2016; Ding et al., 2018). Frame-core tube-outrigger systems, which are typical hybrid lateral load-resisting systems, and have been widely used in modern super-tall buildings (Park and Oh, 2018; Zhang et al., 2018; Shim et al., 2019; Alhaddad et al., 2020; Huang et al., 2021). In this system, the outrigger is typically designed as an energy dissipation component that is elastic under the service level earthquake (SLE) and the design basis earthquake (DBE). Under the maximum considered earthquake (MCE), the web member of the outrigger is expected to yield and dissipate energy, and thereby controlling the maximum inter-story drift ratio (MIDR) of the structure. Hence, various studies regarding energy dissipation outriggers have been conducted. Two methods are typically used to realize an energy dissipation outrigger. One method is to maintain the original structural system of the outrigger; energy dissipation components are directly introduced to replace the web member. For example, a buckling restrained brace (BRB) can be adopted to prevent the buckling of web members and offer the expected excellent energy dissipation capacity and ductility (Youssef et al., 2010; Yang et al., 2018; Lin et al., 2018; Lin et al., 2019). The other method is to change the construction or connection method using the vertical components (i.e., columns and core tube) of the outrigger (Smith and Willford, 2007; Wu et al., 2014; Zhou and Li, 2014), e.g., by introducing a viscous damper to vertically connect the outrigger and column. The first method is primarily used because it involves a convenient design and will not significantly change the conventional design and construction method, particularly for the outrigger with a BRB.
Notably, the energy dissipation capacity of the outrigger can be effectively enhanced using the BRB as a web member. However, because such energy dissipation capacity is realized based on the yielding and significant plastic deformation of steel, considerable residual deformation of the BRB is typically observed after unloading. Such features may result in significant residual deformations of the outrigger and overall structure, thereby hindering the post-earthquake recovery of super-tall buildings (Kiggins and Uang, 2006; Lu and Lu, 2019). The SC-BRB provides a potential solution for balancing the energy dissipation capacity and controlling the brace residual deformation. It is composed of a self-centering system (e.g., prestressed steel strands or shape memory alloys) and energy dissipation cores of the BRB in parallel. After unloading, the residual deformation of the brace can be alleviated by the self-centering system, whereas the energy dissipation capacity can be maintained through the cores of the BRB, and which can control the maximum deformation of the structure (Erochko et al., 2013; Liu et al., 2018; Fan et al., 2019; Qing et al., 2021; Zhou et al., 2021). The seismic performance of three-story steel frame buildings with a BRB and an SC-BRB was compared by Zeng (2014). The results indicated that using an SC-BRB can reduce the residual inter-story drift ratio by 60%, and the maximum deformation during the earthquake can be controlled more effectively because a higher post-yield stiffness can be achieved. Based on nonlinear time-history analyses (NTHAs) of 4- and 12-story SC-BRB frame structures, Xie et al. (2016b) identified the critical parameters of SC-BRBs that affect the seismic performance of braced steel frame structures. Furthermore, a seismic design method was developed for such structures with emphasis on post-earthquake repairability. Qiu et al. (2020) proposed a new type of SC-BRB using a novel buckling-restrained super-elastic shape memory alloy, and the seismic responses of structures with and without SC-BRBs were compared. The results indicated that compared with the structure without SC-BRB, the MIDR and maximum residual inter-story drift ratio (MRIDR) were reduced by 15 and 70% for this with SC-BRBs, respectively. The studies above showed that the SC-BRB offered significant benefits in the dual control of the MIDR and MRIDR. However, these investigations focused on multistory and tall buildings; studies regarding the dual control of super-tall buildings using SC-BRBs for the outrigger are scarce.
To investigate the feasibility of MIDR and MRIDR dual control in super-tall buildings using the self-centering energy dissipation outrigger with SC-BRBs, a 75-story frame-core tube-outrigger super-tall building with a total height of 344.85 m is selected and designed using the energy dissipation outrigger with BRBs and the self-centering energy dissipation outrigger with SC-BRBs. The seismic performance of the buildings with BRB under two different earthquake levels is evaluated, and the characteristics of the MIDR and MRIDR are identified. Subsequently, four cases with SC-BRBs are established to investigate the control effect of the MIDR and MRIDR; the critical design parameters of the SC-BRB for the dual-objective control effect and the corresponding effect on the damage to the connected vertical components are identified. The feasibility of the SC-BRB for self-centering energy dissipation outriggers was validated.
2 Seismic Performance of Prototype Building With Energy Dissipation Outriggers
2.1 Prototype Structure
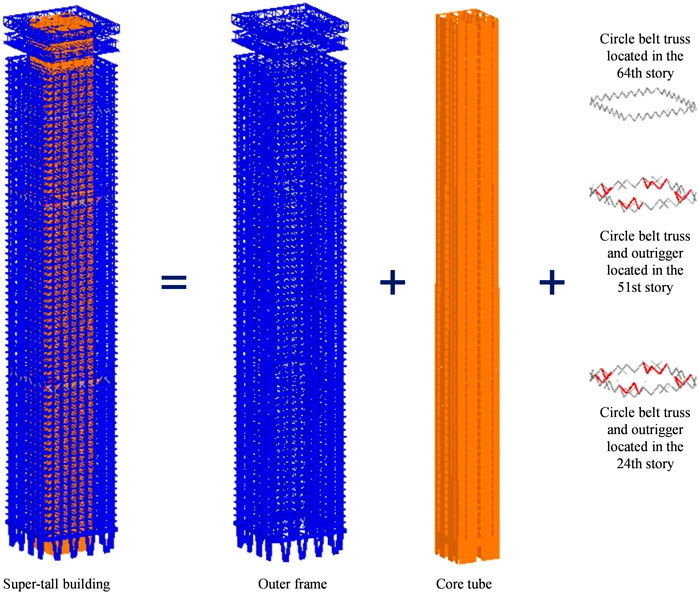
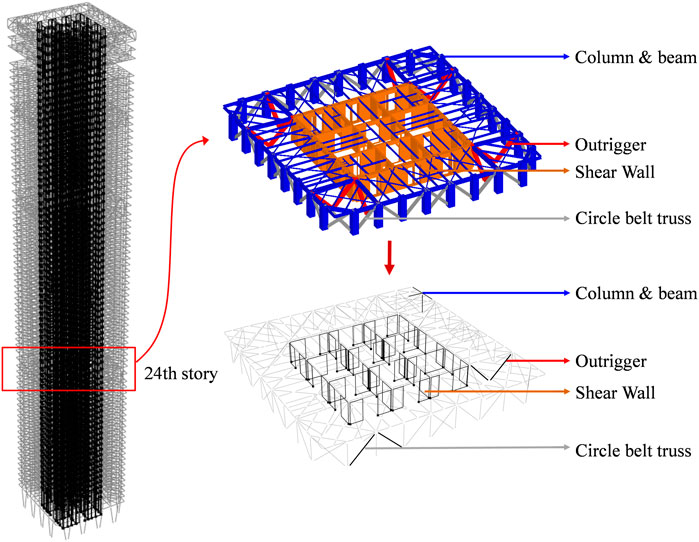
A super-tall building located in Xi’an is selected as the prototype building for this study. The design seismic intensity of the building is 8°. The corresponding peak ground acceleration (PGA) values are 70, 200, and 400 cm/s2 for the SLE, DBE, and MCE, respectively. The characteristic period of the site is 0.40 s. The building comprises 75 stories and measures 344.85 m in height. The planar sizes of the outer frame and core tube are 53.8 × 53.8 m and 29.6 × 30.0 m, respectively. A hybrid lateral-load-resisting system, known as the frame-core tube-outrigger system, is adopted to achieve a desirable seismic performance. A three-dimensional (3D) view of the building and its corresponding structural system are presented in Figure 1.
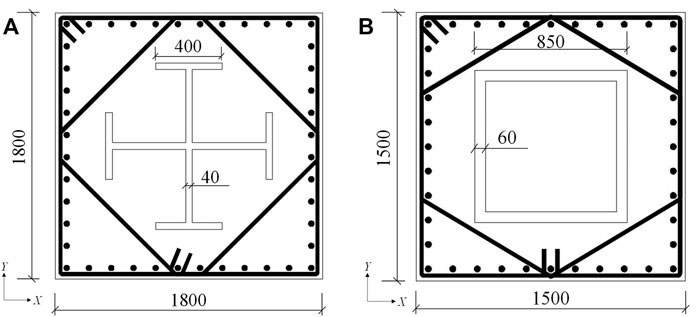
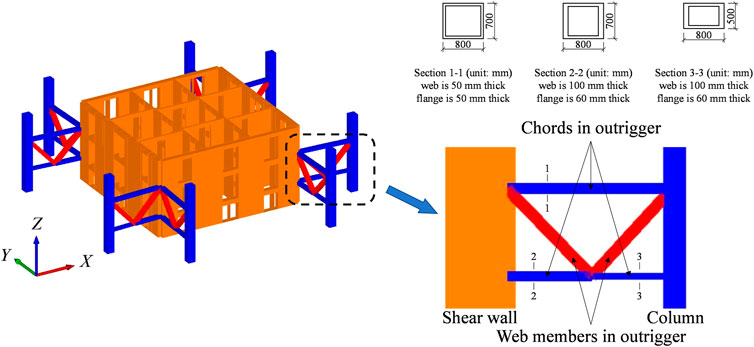
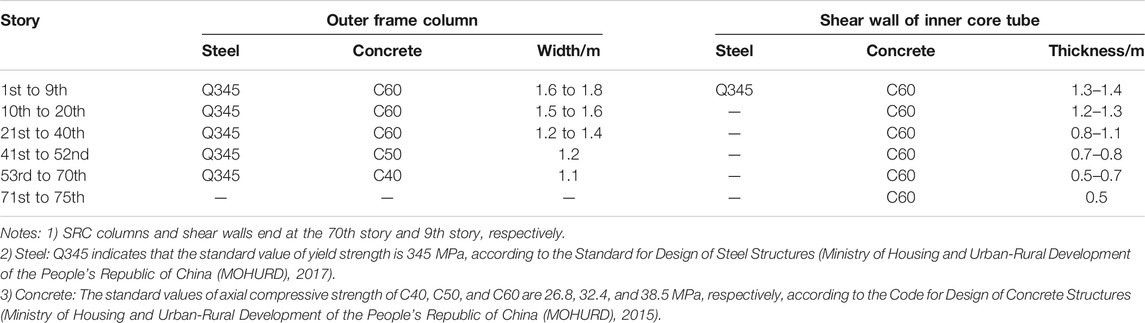
The outer frame of the structure comprises cross- and box-shaped steel-reinforced concrete (SRC) columns and I-shaped steel beams. Typical sections of the SRC columns are presented in Figure 2. Based on the requirements of the building function, 16 groups of V-shaped SRC columns with a square section measuring 1.8 × 1.8 m are adopted to realize the first story with a height of 15.3 m. SRC shear walls and reinforced concrete (RC) shear walls are adopted for the core tube. The thickness of the shear walls decreases gradually with the height of the building. The thickness of the SRC shear walls in the bottom strengthening region (first to ninth stories) is 1.4 m. The yield strength of the steel plates embedded in such shear walls is 345 MPa; the thickness of the steel plates in the outer wall is 30 mm, whereas that in the inner wall ranges from 14 to 20 mm. To improve the lateral stiffness of the structure and coordinate the outer frame with the inner core tube, two groups of outriggers are installed at the 24th and 51st stories, and three groups of circle belt trusses are installed on the 24th, 51st, and 64th stories. The arrangement of outriggers is schematically presented in Figure 3. Sixteen BRBs are adopted in each story as the web members of the outrigger. The yield load, pre-yield stiffness, and post-yield stiffness of the BRB are 3 × 104 kN, 3.7 × 103 kN/mm, and 74 kN/mm, respectively. A steel box section (700 mm (height) × 800 mm (width) × 50 mm (thickness of the web) × 50 mm (thickness of the flange)) is adopted for the outrigger chord, and the associated yield strength is 390 MPa. The material strength grades and sectional dimensions of the main structural components are presented in Table 1. The yield strength of most of the rebars in the structure is 400 MPa.
2.2 Finite Element Model
To investigate the characteristics of the seismic responses of the prototype building during and after an earthquake, a refined finite element model is established using the commercial software Perform-3D. It is notable that Lu X. L. et al. (2015), Lu X. L. et al. (2016) have provided a benchmark model for a typical frame-core tube-outrigger super-tall building using Perform-3D, which is a widely acknowledged software in China. Hence, the corresponding recommended simulation method is adopted in this study. Specifically, SRC columns, steel beams, SRC shear walls, and RC shear walls are modeled using fiber elements. The bilinear kinematic hardening plasticity model is used for the steel and rebar, and the parameters of the confined and unconfined concrete are determined using the model proposed by Mander and Cheng (1997). Because a relatively large span-to-height ratio is adopted for the coupling beams, the fiber element is also used to simulate the coupling beams dominated by flexural behavior (Lu, X. Z. et al., 2013; Lu X. et al., 2013; Lu et al., 2016; Lu and Guan, 2017). The BRB element in Perform-3D is adopted for the web members in the outrigger. Based on the abovementioned simulation method, the refined finite element model is established, as presented in Figure 4.
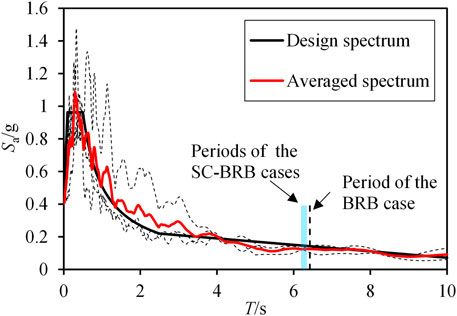
Gravity and modal analyses are conducted based on the refined finite element model. The total mass of the structure is 315,310 t. The first six vibration periods and the corresponding modal properties are presented in Table 2. The ratio of the first-order torsional period (4.32 s) to the first-order translational period (6.42 s) is 0.673, which is much lower than the limit value of 0.85 (Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD), 2010), indicating that the torsional effect is controlled effectively. Three (two natural and one artificial) ground motions are then selected for the NTHAs. A comparison between the response spectra of these ground motions and the design spectrum is shown in Figure 5, and they exhibit good agreement. A damping ratio of 4% is adopted for the NTHAs (Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD), 2016). NTHAs with PGA values of 400 and 510 cm/s2 are conducted for the prototype building along the Y-direction of the building, which is the direction of the first mode. Two PGA levels are considered for the NTHAs. Specifically, a PGA of 400 cm/s2 is used to satisfy the general requirements of the code. In addition, a PGA of 510 cm/s2, equivalent to increasing the seismic design intensity from 8° to 8.5°, is taken to evaluate the seismic performance under extremely strong earthquakes. Such procedure is widely adopted in engineering practices.
2.3 Nonlinear Time-History Analysis
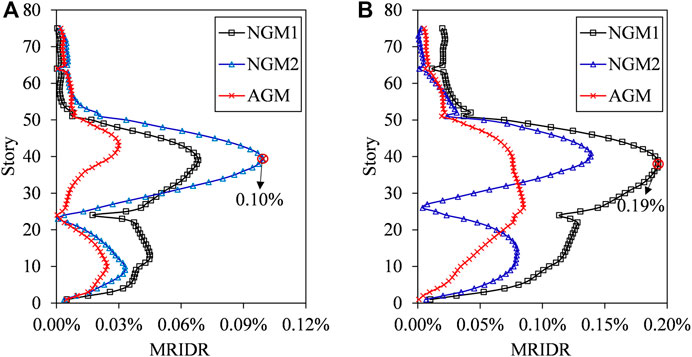
Three critical seismic responses of the super-tall structure are discussed herein and presented in Figures 6–8, including the MIDR, MRIDR, and hysteretic behavior of the web members in the outrigger. Free vibration (i.e., the acceleration keeps at 0) of 100 s is added to the end of the selected ground motions for time-history analysis. Based on this, the residual story drift ratio can be determined by checking the stabilized structural response at the end of the time-history analysis. The inter-story drift ratios of the story with outrigger are significantly smaller than those of the adjacent stories, which is attributed to the high stiffness of the outriggers and circle belt trusses. At a PGA of 400 cm/s2, the envelope value of the MIDR is observed at the 36th story, i.e., 0.94%, which is lower than the limit value of 1% specified by the code. The web members in the outrigger using the BRB can stably dissipate energy and control the maximum deformation. The MRIDR is 0.10% at the 39th story. As the PGA increases to 510 cm/s2, the envelope values of the MIDR and MRIDR increase to 1.26 and 0.19%, respectively, indicating that a 27.5% increase in the PGA results in a 34 and 90% increase in the MIDR and MRIDR, respectively. Although the energy dissipated by the BRB increases, a large MRIDR is introduced. Notably, the MRIDR at the 24th story with outriggers increases significantly as the PGA increases under natural ground motion 1 (NGM1), i.e., from 0.02% at 400 cm/s2 to 0.11% at 510 cm/s2. This is because more energy is dissipated when the PGA reaches 510 cm/s2, and the increase in the MRIDR of the outrigger results in an increase in the MRIDR of the entire structure. This phenomenon is more evident in artificial ground motion (AGM). When the PGA increases from 400 to 510 cm/s2, the MRIDR at the 24th story increases from approximately 0–0.08% and is the maximum residual inter-story drift ratio of the structure; this implies that considerable plastic behavior occurs in this region and dominates the residual deformation of the structures.
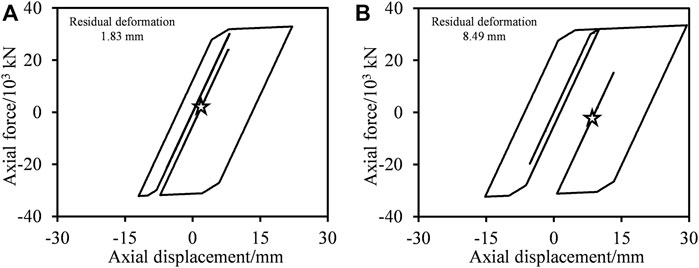
FIGURE 8. Load-displacement hysteretic curves of BRB in the 24th story under NGM1. (A) PGA = 400 cm/s2. (B) PGA = 510 cm/s2.
As shown in Figure 8, the BRB of the outrigger in the 24th story yields under NGM1, indicating that the BRB provides energy dissipation capacity and controls the maximum response of the building. It is noteworthy that the residual deformations of the BRB under the PGAs of 400 cm/s2 and 510 cm/s2 are 1.83 and 8.49 mm, respectively. The residual deformation of BRB is considerable and thus leads to the abovementioned residual deformation of the structures. Hence, the introduction of a self-centering BRB may have the potential to control the residual deformation of the outrigger and even that of the entire structure.
3 Seismic Performance of a Building With Self-Centering Energy Dissipation Outriggers
3.1 Self-Centering Outrigger Using SC-BRB
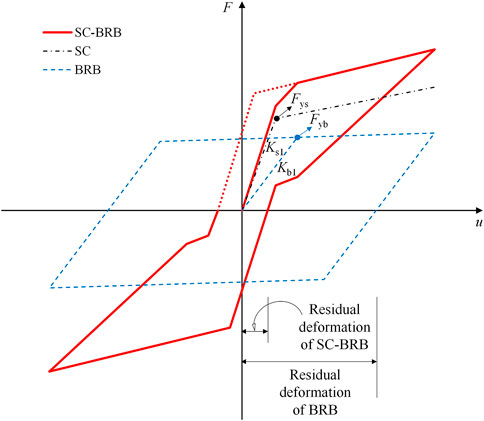
The SC-BRB is composed of a self-centering system and an energy dissipation system. Existing studies (Zeng, 2014; Xie, 2018; Zhou et al., 2021) show that its high post-yield stiffness and energy dissipation capacity is desirable for controlling the maximum deformation of a structure during an earthquake, and its self-centering capacity is desirable for controlling the post-earthquake residual deformation. The hysteretic curves of the SC-BRB and BRB are schematically compared in Figure 9. Flag-shaped hysteretic behavior is observed for the SC-BRB, indicating good residual deformation control capacity. Fys and Ks1 represent the yield force and initial stiffness of the self-centering system, respectively; Fyb and Kb1 denote the yield force and initial stiffness of the energy dissipation system, respectively.
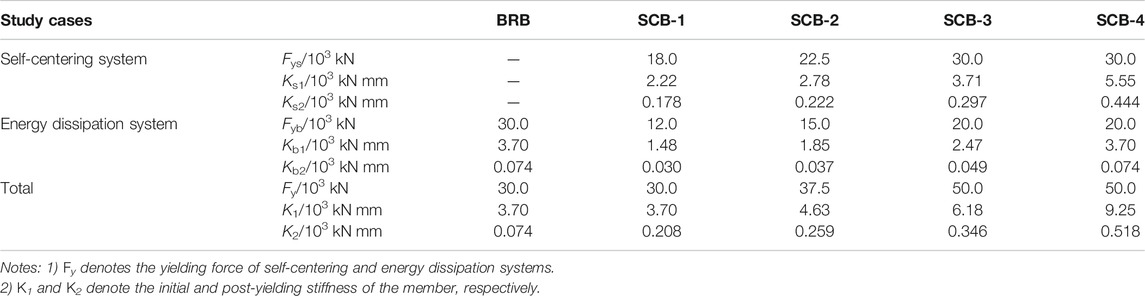
In this study, to achieve dual-objective control of the maximum and residual deformations of super-tall buildings, SC-BRB is adopted for the web members to replace the BRB in the prototype building, and which results in the self-centering energy dissipation outrigger. Various forms of SC-BRBs have been proposed and investigated by scholars based on prestressed strand (Xie et al., 2017; Liu et al., 2018; Qiu et al., 2020), pre-compressed disc spring (Fan et al., 2019), and shape memory alloy (Qiu et al., 2020). It is noteworthy that the skeleton curve and hysteretic behavior of these SC-BRBs are similar despite their different forms. Therefore, in this study, the SC-BRB used in self-centering energy dissipation outrigger is not limited to a specific form. The effect of SC-BRBs on the seismic performance of super-tall buildings is investigated based on the theoretical model of SC-BRB. The critical parameters of the SC-BRB in this outrigger are set to Fys/Fyb = Ks1/Kb1 = 1.5, based on Xie et al. (2016a), Xie et al. (2017), which allows a good balance to be achieved between the energy dissipation capacity and self-centering capacity. As the outriggers are only set in the 24th and 51st stories, all the BRB web members of these outriggers are replaced with SC-BRBs to realize dual-objective control of the maximum deformation during earthquake and post-earthquake residual deformation. Four cases with different SC-BRB design schemes are considered, and the corresponding parameters of the two SC-BRB systems are presented in Table 3. For SCB-1, the total yield force and initial stiffness are identical to those of the BRB in the prototype building. The values for the parameters of SCB-2 and SCB-3 are 1.25 and 1.67 times those of SCB-1, respectively. SCB-4 is a design case that only increases the initial stiffness based on SCB-3. Based on the NTHAs of these four cases, the effect of the SC-BRB on the control effect of the MIDR and MRIDR can be identified, and the dual-objective control mechanism of the SC-BRB as well as the self-centering energy dissipation outrigger can be investigated.
3.2 Finite Element Model of Buildings With Self-Centering Energy Dissipation Outrigger
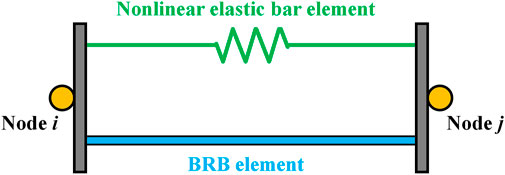
As shown in Figure 10, SC-BRB is modeled in Perform-3D with a BRB element and a nonlinear elastic bar in parallel. The BRB element is adopted for simulating the energy dissipation system and the nonlinear elastic bar is adopted for simulating the self-centering system.
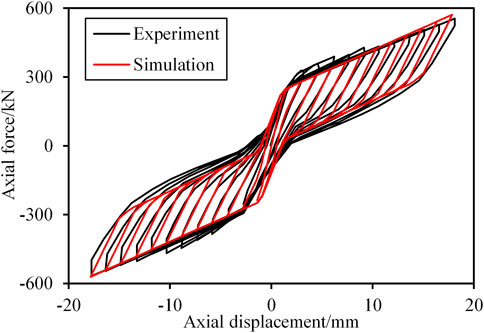
To validate the reliability of such a simulation method, a numerical simulation is conducted for the SC-BRB experimentally tested by Xie (2018) under cyclic loads. The mechanical properties of the two systems are presented in Table 4. A comparison between the numerical and experimental results shows good agreement between them, as shown in Figure 11, indicating that this method can effectively capture the energy dissipation and self-centering capacities of the SC-BRB.

TABLE 4. Mechanical properties of the tested SC-BRB of Xie (2018).
Based on the abovementioned simulation method, refined numerical models of the four study cases are established, and modal analyses are also conducted. The first three fundamental periods of the prototype building and four study cases are compared, as shown in Table 5. Although the stiffness of the web members of SCB-2, SCB-3, and SCB-4 increases, the variation in the fundamental periods is no more than 3.27%. Therefore, the ground motions selected for the prototype building can be used for the four study cases.
3.1.1 Hysteretic Responses of SC-BRB and Damage of Main Components
To identify the control effect of the SC-BRB, the hysteretic responses of typical web members using BRBs and SC-BRBs are required to be compared. This comparison based on a PGA of 510 cm/s2 under NGM1 is shown in Figure 12. The results under NGM1 are presented because it yielded the maximum MIDR under two earthquake levels and the maximum MRIDR under 510 cm/s2. Flag-shaped hysteretic curves are observed for the SC-BRBs; moreover, the maximum and residual axial deformations of the SC-BRBs are generally lower than those of BRBs except for SCB-1, which has the initial stiffness and yield load identical to those of the BRB. In addition, the maximum and residual axial deformations of the SC-BRB decrease as the initial stiffness and yield load of the SC-BRB increase. For the web members located in the 24th and 51st stories, the corresponding residual axial deformations are reduced by 56–77% and 55–86%, respectively. Such a feature provides the foundation for the dual-objective control of the outrigger and entire building.
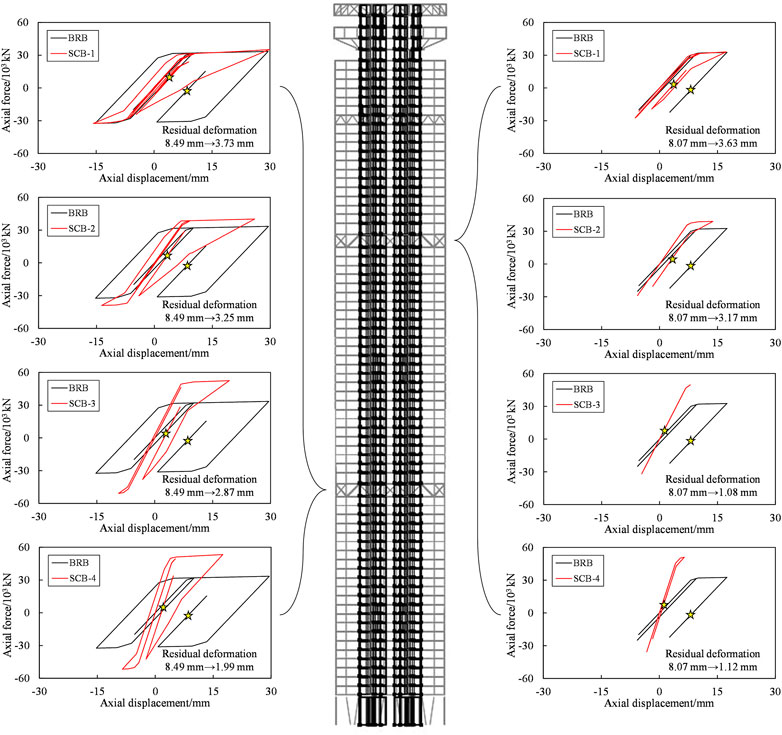
FIGURE 12. Comparison of the hysteretic curves and residual deformation of web members in an outrigger.
It is notable that the increase in the stiffness and yield load of web members may transfer a larger load to the adjacent vertical components (e.g., columns and shear walls), as compared with prototype buildings. Hence, it is necessary to check the damage state of these components adjacent to the outrigger, which can be reflected by the maximum strain. Compared with the prototype building, case SCB-1 exhibits similar maximum strains because the SC-BRB in this case is designed with identical initial stiffness and yield load. For SCB-2 and SCB-3, the maximum strains of the components adjacent to the upper outrigger (i.e., the 51st story) are also identical, whereas the maximum strains of the components adjacent to the lower outrigger (i.e., the 24th story) increased by approximately 10 and 15% for SCB-2 and SCB-3, respectively. However, the damage state is not changed for all these adjacent components. For SCB-4, the significant increase in the stiffness of the self-centering system results in a 20% increase in the maximum strain of the components adjacent to the 24th story and changes the damage state.
The discussion above indicates that the SC-BRB can function well at the structural level, can effectively control the residual axial deformation of web members, and will not significantly change the damage states of the components adjacent to the outrigger.
3.1.2 Comparison of MIDR During an Earthquake
The distributions of the envelope values of MIDR for all the study cases are compared, as shown in Figure 13. It is noteworthy that the introduction of the self-centering energy dissipation outrigger using the SC-BRB as web members will not change the deformation mode of super-tall buildings. Additionally, the MIDR of the four cases using such outriggers reduces as compared with that of the prototype building. For the self-centering energy dissipation outrigger with the original initial stiffness and yield load (SCB-1), although the energy dissipation capacity of the web member decreases significantly, the post-yield stiffness of SC-BRB is approximately three times that of the BRB, and the MIDR is identical to that of the prototype building. For SCB-2 with a relatively high initial stiffness and yield load (25% greater than that of BRB), the MIDR under PGAs of 400 and 510 cm/s2 are reduced by 3 and 2%, respectively. When the initial stiffness and yield load of the SC-BRB are significantly higher (i.e., SCB-3, 67%) than those of the BRB, the MIDR under PGAs of 400 and 510 cm/s2 are reduced by 6 and 4%, respectively. For SCB-4, the MIDR under PGAs of 400 and 510 cm/s2 are reduced by 7 and 6%, respectively, indicating that the continuous increase in the stiffness of the energy dissipation system could not further improve such reduction.
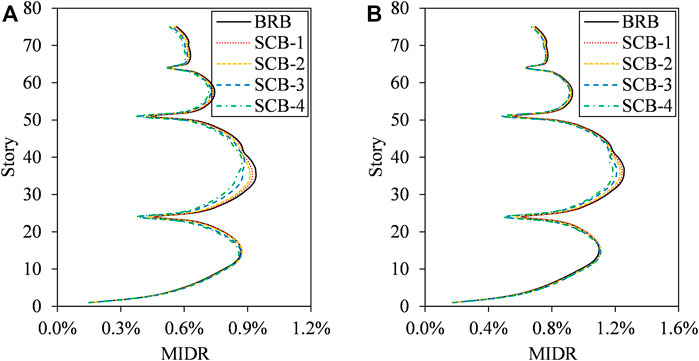
FIGURE 13. Comparison of distribution of MIDR of study cases. (A) PGA = 400 cm/s2. (B) PGA = 510 cm/s2.
Based on the discussion above, it can be concluded that the introduction of self-centering energy dissipation outriggers using SC-BRBs as web members will not change the deformation mode of super-tall buildings. Although the SC-BRB will sacrifice a certain extent of the energy dissipation capacity of the web member, the increase in the post-yield stiffness can ensure the control effect of the MIDR during an earthquake. In addition, a better control effect is generally achieved for the study cases if the stiffness and yield load of the SC-BRB are greater than those of the BRB. The continuous increase in these parameters will not significantly increase the control effect of the MIDR.
3.1.3 Comparison of MRIDR After an Earthquake
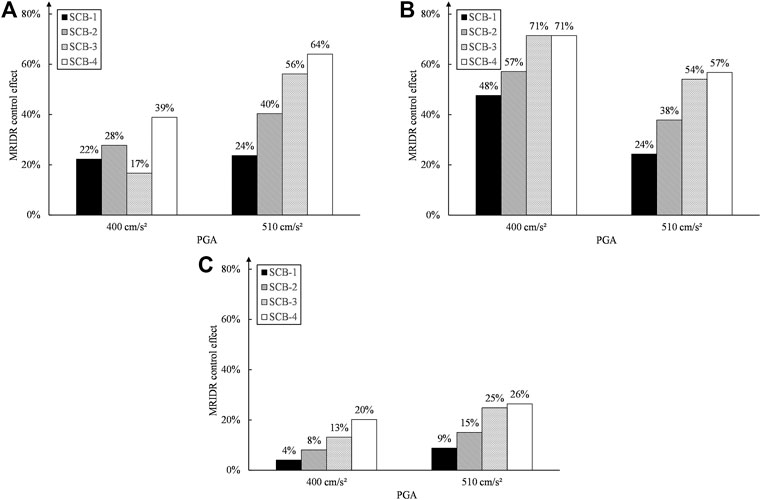
The distributions of the envelope values of the MRIDR for all cases are compared, as shown in Figure 14. The maximum MRIDR of the entire structure and the MRIDR of the stories where the outrigger was located are listed and compared, as shown in Table 6 and Figure 15, respectively. The self-centering energy dissipation outrigger using the SC-BRB can control the MRIDR to a certain extent, and this control effect becomes more evident as the PGA increases. In addition, as the stiffness and yield load of the SC-BRB increases, a better control effect can be realized. When the PGA reaches 510 cm/s2, the MRIDRs of the entire building and the stories with an outrigger are two to six times and two times those of 400 cm/s2, respectively. Hence, the results with PGA of 510 cm/s2 are discussed herein.
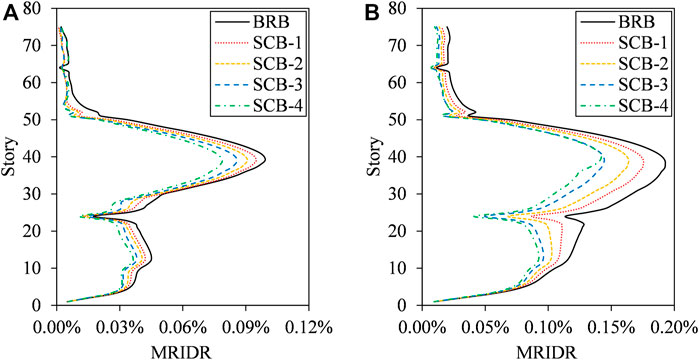
FIGURE 14. Comparison of distribution of MRIDR of study cases. (A) PGA = 400 cm/s2. (B) PGA = 510 cm/s2.
For SCB-1 with the original initial stiffness and yield load, the MRIDRs of the stories with outriggers are both reduced by 24%, and the MRIDR of the entire building is reduced by 9%. When the initial stiffness and yield load of the SC-BRB are slightly higher than those of the BRB (i.e., SCB-2, 25% higher), a significant control effect is observed in the stories with an outrigger, which is consistent with the control effect of the residual axial deformation of the SC-BRB. Specifically, the MRIDRs of these stories reduce by 40 and 38% at the 24th and 51st stories, respectively. It is noteworthy that the difference between the distributions of the MIDR of SCB-1 and SCB-2 is negligible, as shown in Figure 13, i.e., the damage states of the shear walls and columns are basically identical, and their residual states should be similar. However, as shown in Figure 14, owing to the desirable control effect on the MRIDRs of the stories with outriggers, a further reduction in the MRIDR of the entire building (i.e., from 9 to 15%) is achieved. As the initial stiffness and yield load of SC-BRB increased, the abovementioned phenomenon becomes more evident. Specifically, the MRIDRs of the stories with outriggers reduce further by 54–56% and 57–64% for SCB-3 and SCB-4, respectively. The reduction in the MRIDR of the entire building stabilized at approximately 25% owing to SCB-3.
The above discussion reveals that the self-centering energy dissipation outrigger can effectively provide self-centering capacity and control the residual deformation of the super-tall building, especially for the story where the outriggers locate. Therefore, the dual-objective control of maximum and residual drift ratios of super-tall buildings could be achieved by introducing a self-centering energy dissipation outrigger.
4 Conclusion
To investigate the feasibility of dual control of MIDR and MRIDR of super-tall buildings based on self-centering energy dissipation outriggers with SC-BRBs, a 75-story frame-core tube-outrigger super-tall building with a total height of 344.85 m is selected and designed using the energy dissipation outriggers with BRBs and self-centering energy dissipation outriggers with SC-BRBs. The seismic performance of the building with the BRBs under two different levels of earthquakes is evaluated, and the characteristics of the MIDR and MRIDR identified. Subsequently, four cases with SC-BRBs are established to investigate the control effect of the MIDR and MRIDR, where the critical design parameters of the SC-BRB for the dual-objective control effect, and the corresponding effect on the damage to the connected vertical components are identified. The feasibility of the SC-BRB for self-centering energy dissipation outriggers is validated. The main conclusions of this study are as follows:
1) The SC-BRB can function well at the structural level, can effectively control the residual axial deformation of web members, and will not significantly change the damage states of the components adjacent to the outrigger.
2) The introduction of a self-centering energy dissipation outrigger using SC-BRBs as web members will not change the deformation mode of super-tall buildings. A better control effect on the MIDR is generally achieved in the study cases when the stiffness and yield load of the SC-BRB are greater than those of the BRB. A continuous increase in these parameters will not significantly increase the control effect.
3) The self-centering energy dissipation outrigger significantly controls the residual deformation in the story where the outriggers are located by up to 64%. The MRIDR of the entire structure can be reduced by 26%, which is attributed to the control effect of the story with the outrigger. To further improve the control effect of the MRIDR, high-performance shear walls, and columns constructed using high-performance are required to be introduced to control the corresponding damage.
The results of this study can provide a reference for the dual-objective control of the maximum and residual deformations of super-tall buildings.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
LX: Conceptualization, methodology, investigation, writing, and funding acquisition. NA: Methodology, investigation, and writing. XW: Methodology, investigation, and writing. QL: Design of the prototype building. CY: Conceptualization, methodology, and writing.
Funding
The authors are grateful for the financial support received from the National Natural Science Foundation of China (51808029) and the Pyramid Talent Training Project of Beijing University of Civil Engineering and Architecture (Grant No JDYC20200306).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alhaddad, W., Halabi, Y., Xu, H., and Lei, H. (2020). Outrigger and Belt-Truss System Design for High-Rise Buildings: A Comprehensive Review Part II-Guideline for Optimum Topology and Size Design. Adv. Civil Eng. 2020, 2589735. doi:10.1155/2020/2589735
Ding, J., Wang, S., and Wu, H. (2018). Seismic Performance Analysis of Viscous Damping Outrigger in Super High-Rise Buildings. Struct. Des. Tall Spec. Build 27, e1486. doi:10.1002/tal.1486
Erochko, J., Christopoulos, C., Tremblay, R., and Kim, H.-J. (2013). Shake Table Testing and Numerical Simulation of a Self-Centering Energy Dissipative Braced Frame. Earthquake Engng Struct. Dyn. 42, 1617–1635. doi:10.1002/eqe.2290
Fan, X., Xu, L., and Li, Z. (2019). Seismic Performance Evaluation of Steel Frames with Pre-pressed spring Self-Centering Braces. J. Constructional Steel Res. 162, 105761. doi:10.1016/j.jcsr.2019.105761
Hassan, W. M., Hodhod, O. A., Hilal, M. S., and Bahnasaway, H. H. (2017). Behavior of Eccentrically Loaded High Strength concrete Columns Jacketed with FRP Laminates. Construction Building Mater. 138, 508–527. doi:10.1016/j.conbuildmat.2017.02.016
Huang, X., Lv, Y., Chen, Y., Qi, L., Zhu, X. D., and Hu, X. Y. (2021). Performance‐Based Seismic Design of the Outrigger of a High‐rise Overrun Building with Asymmetric Vertical Setback in a Strong Earthquake Area. Struct. Des. Tall Spec. Build 30, e1834. doi:10.1002/tal.1834
Kiggins, S., and Uang, C.-M. (2006). Reducing Residual Drift of Buckling-Restrained Braced Frames as a Dual System. Eng. Structures 28, 1525–1532. doi:10.1016/j.engstruct.2005.10.023
Liew, J. Y. R., Xiong, M., and Xiong, D. (2016). Design of concrete Filled Tubular Beam-Columns with High Strength Steel and concrete. Structures 8, 213–226. doi:10.1016/j.istruc.2016.05.005
Lin, P.-C., Takeuchi, T., and Matsui, R. (2018). Seismic Performance Evaluation of Single Damped-Outrigger System Incorporating Buckling-Restrained Braces. Earthquake Engng Struct. Dyn. 47, 2343–2365. doi:10.1002/eqe.3072
Lin, P.-C., Takeuchi, T., and Matsui, R. (2019). Optimal Design of Multiple Damped-Outrigger System Incorporating Buckling-Restrained Braces. Eng. Structures 194, 441–457. doi:10.1016/j.engstruct.2019.05.078
Liu, L., Zhao, J., and Li, S. (2018). Nonlinear Displacement Ratio for Seismic Design of Self-Centering Buckling-Restrained Braced Steel Frame Considering Trilinear Hysteresis Behavior. Eng. Structures 158, 199–222. doi:10.1016/j.engstruct.2017.12.026
Lu, X. Z., and Guan, H. (2017). Earthquake Disaster Simulation of Civil Infrastructures: From Tall Buildings to Urban Areas. Beijing: Science press.
Lu, X., and Lu, Q. L. (2019). Study on the Mechanics Principle and Hysteretic Behavior of Self-Centering Viscoelastic diagonal Members. Eng. Mech. 36, 138–146. doi:10.6052/j.issn.1000-4750.2018.05.0265
Lu, X. L., Jiang, C., and Jiang, H. J. (2015). A Benchmark Model of Mega-Tall Buildings and Analysis of its Seismic Responses. Struct. Eng. 31, 100–107. doi:10.15935/j.cnki.jggcs.2015.04.015
Lu, X., Lu, X., Guan, H., and Ye, L. (2013). Collapse Simulation of Reinforced Concrete High-Rise Building Induced by Extreme Earthquakes. Earthquake Engng Struct. Dyn. 42, 705–723. doi:10.1002/eqe.2240
Lu, X., Lu, X., Guan, H., and Xie, L. (2016). Application of Earthquake-Induced Collapse Analysis in Design Optimization of a Supertall Building. Struct. Des. Tall Spec. Build 25, 926–946. doi:10.1002/tal.1291
Lu, X. L., Jiang, C., and Jiang, H. J. (2016). Seismic Damage Analysis of a Benchmark Model for Mega-Tall Buildings. J. Build. Struct. 37, 1–7. doi:10.14006/j.jzjgxb.2016.09.001
Lu, X. Z., Lu, X., Guan, H., Zhang, W. K., and Ye, L. P. (2013). Earthquake-Induced Collapse Simulation of a Super-Tall Mega-Braced Frame-Core Tube Building. J. Constructional Steel Res. 82, 59–71. doi:10.1016/j.jcsr.2012.12.004
Mander, J. B., and Cheng, C. T. (1997). Seismic Resistance of Bridge Piers Based on Damage Avoidance Design. Technical Report US National Center for Earthquake Engineering Research.
Mao, C., and Wang, Z. (2021). Seismic Performance Evaluation of a Self-Centering Precast Reinforced concrete Frame Structure. Earthq. Eng. Eng. Vib. 20, 943–968. doi:10.1007/s11803-021-2062-3
Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD) (2015). Code for Design of concrete Structures (GB 50010-2010). Beijing: China Architecture and Building Press.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China MOHURD (2016). Code for Seismic Design of Buildings (GB 50011-2010). Beijing: China Architecture and Building Press.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD) (2017). Standard for Design of Steel Structures (GB 50017-2017). Beijing: China Architecture and Building Press.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China MOHURD (2010). Technical Specification for concrete Structures of Tall Building (JGJ 3-2010). Beijing: China Architecture and Building Press.
Nehdi, M. L. (2013). Only Tall Things Cast Shadows: Opportunities, Challenges and Research Needs of Self-Consolidating concrete in Super-Tall Buildings. Construction Building Mater. 48, 80–90. doi:10.1016/j.conbuildmat.2013.06.051
Oviedo-Amezquita, J. A., Jaramillo-Santana, N., Blandon-Uribe, C. A., and Bernal-Zuluaga, A. M. (2021). Development and Validation of an Acceptance Criteria and Damage Index for Buckling-Restrained Braces (BRB). J. Building Eng. 43, 102534. doi:10.1016/j.jobe.2021.102534
Park, H. S., and Oh, B. K. (2018). Real-Time Structural Health Monitoring of a Supertall Building under Construction Based on Visual Modal Identification Strategy. Automation in Construction 85, 273–289. doi:10.1016/j.autcon.2017.10.025
Pettinga, D., Christopoulos, C., Pampanin, S., and Priestley, N. (2007). Effectiveness of Simple Approaches in Mitigating Residual Deformations in Buildings. Earthquake Engng Struct. Dyn. 36, 1763–1783. doi:10.1002/eqe.717
Qing, Y., Wang, C.-L., Zhou, Z., and Zeng, B. (2021). Seismic Responses of Multistory Buildings with Self-Centering Buckling-Restrained Braces: Influence of the Pretension Force. Eng. Structures 238, 112249. doi:10.1016/j.engstruct.2021.112249
Qiu, C., Fang, C., Liang, D., Du, X., and Yam, M. C. (2020). Behavior and Application of Self-Centering Dampers Equipped with Buckling-Restrained SMA Bars. Smart Mater. Struct. 29, 035009. doi:10.1088/1361-665X/ab6883
Shim, H. B., Kim, Y., and Park, H. S. (2019). Verification of Structural Performance of Connections between Reinforced Concrete Shear walls and Outriggers in High‐rise Buildings. Struct. Concrete 20, 932–941. doi:10.1002/suco.201800209
Smith, R. J., and Willford, M. R. (2007). The Damped Outrigger Concept for Tall Buildings. Struct. Des. Tall Spec. Build. 16, 501–517. doi:10.1002/tal.413
Wu, H. L., Ding, J. M., Cui, J. Q., and Zhang, B. (2014). Study on Energy Dissipation Technology and Connection Design for Outriggers and belt Members of Super High-Rise Buildings. J. Build. Struct. 35, 8–15. doi:10.14006/j.jzjgxb.2014.03.003
Xie, Q., Zhou, Z., Huang, J. H., Zhu, D. P., and Meng, S. P. (2016a). Finite-element Analysis of Dual-Tube Self-Centering Buckling-Restrained Braces with Composite Tendons. J. Compos. Constr. 21, 04016112. doi:10.1061/(ASCE)CC.1943-5614.0000778
Xie, Q., Zhou, Z., Huang, J.-H., and Meng, S.-P. (2016b). Influence of Tube Length Tolerance on Seismic Responses of Multi-Storey Buildings with Dual-Tube Self-Centering Buckling-Restrained Braces. Eng. Structures 116, 26–39. doi:10.1016/j.engstruct.2016.02.023
Xie, Q., Zhou, Z., Li, C., and Meng, S. (2017). Parametric Analysis and Direct Displacement-Based Design Method of Self-Centering Energy-Dissipative Steel-Braced Frames. Int. J. Str. Stab. Dyn. 17, 1750087. doi:10.1142/S0219455417500870
Xie, Q. (2018). Seismic Performance and Design Method of an Innovative Self-Centering BRB Frame with Pre-Tensioned Tendons. [dissertation]. Nanjing (JS): Southeast University.
Yang, Q., Lu, X., Yu, C., and Gu, D. (2016). Experimental Study and Finite Element Analysis of Energy Dissipating Outriggers. Adv. Struct. Eng. 20, 1196–1209. doi:10.1177/1369433216677122
Yang, Q. S., Zhen, W., Lu, X. Z., Xie, L. L., and Lin, K. Q. (2018). Experimental Study on the Seismic Performance of Damped Outriggers. Eng. Mech. 35, 47–58. doi:10.6052/j.issn.1000-4750.2017.04.0318
Yang, S. (2020). Application of Energy Dissipation and Damping Structure in the Reinforcement of Shear wall in concrete Engineering. Open Phys. 18, 631–641. doi:10.1515/phys-2020-0149
Youssef, N., Wilkerson, R., Fischer, K., and Tunick, D. (2010). Seismic Performance of a 55-Storey Steel Plate Shear wall. Struct. Des. Tall Spec. Build. 19, 139–165. doi:10.1002/tal.545
Zeng, P. (2014). Investigation on Seismic Performance of Steel Frames with All-Steel Self-Centering Buckling-Restrained Braces. [master’s thesis]. Nanjing (JS): Southeast University.
Zhang, Y., He, Z., and Yang, Y. (2018). A Spectral-Velocity-Based Combination-Type Earthquake Intensity Measure for Super High-Rise Buildings. Bull. Earthquake Eng. 16, 643–677. doi:10.1007/s10518-017-0224-5
Zhang, J., Cai, R., Li, C., and Liu, X. (2020). Seismic Behavior of High-Strength concrete Columns Reinforced with High-Strength Steel Bars. Eng. Structures 218, 110861. doi:10.1016/j.engstruct.2020.110861
Zhou, Y., and Li, H. (2014). Analysis of a High-Rise Steel Structure with Viscous Damped Outriggers. Struct. Des. Tall Spec. Build. 23, 963–979. doi:10.1002/tal.1098
Keywords: dual-objective control, super-tall building, outrigger, self-centering, energy dissipation
Citation: Xie L, An N, Wang X, Liu Q and Yang C (2022) Dual-Objective Control of Maximum and Residual Drift Ratios of Super-Tall Buildings Based on Self-Centering Energy Dissipation Outriggers. Front. Mater. 8:838597. doi: 10.3389/fmats.2021.838597
Received: 18 December 2021; Accepted: 27 December 2021;
Published: 14 February 2022.
Edited by:
Zhigang Zhang, Chongqing University, ChinaReviewed by:
Xiao Lu, Beijing Jiaotong University, ChinaWanrun Li, Lanzhou University of Technology, China
Copyright © 2022 Xie, An, Wang, Liu and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Cantian Yang, eWFuZ2NhbnRpYW5Ab3V0bG9vay5jb20=
 Linlin Xie
Linlin Xie Nan An1,2
Nan An1,2 Cantian Yang
Cantian Yang