
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 18 January 2022
Sec. Ceramics and Glass
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.825327
Thermal shock is one of the main causes for the fracture of ceramic materials due to their inherent brittleness. Aiming to explore the mechanism of thermal shock cracking behavior of ceramics under different thermal shock conditions, a novel temperature-dependent failure criterion of thermal shock fracture of the ceramic materials was deduced based on the force-heat equivalence energy density principle. Combining this failure criterion and the finite element method, the thermal shock cracking behaviors of the thin circular and rectangular ceramic slabs under different thermal shock initial temperature were simulated. Results show that the morphology, periodicity, hierarchy, and number of thermal shock cracks obtained by numerical simulation are in good agreement with the experimental results. These essential characteristics verify the validity of the temperature-dependent failure criterion for thermal shock fracture. Furthermore, the strain energy of tension produced by thermal shock is proved to be the dominated mechanism for thermal shock-induced fracture.
Because of the good thermophysical properties and chemical stability, such as high melting point and corrosion resistance, ceramic materials are widely used in high-temperature fields such as aerospace technology, metallurgy, and machinery (Cui et al., 2021a; Wang et al., 2021). However, thermal shock is an important cause of fracture to ceramic materials (Neuman et al., 2016) due to the poor thermal shock resistance (TSR). Therefore, to improve the TSR of ceramic materials and explore the mechanism of thermal shock damage of ceramic materials has become a key problem to be solved urgently. Many researchers have used experiments, theories, and numerical simulation methods to study the thermal shock behaviors of ceramics and discuss the TSR of ceramics, and they have achieved important results (Cui et al., 2021b; Zhang et al., 2022).
In terms of theoretical study, the thermal shock fracture theory deduced by Kingery (1955) and the thermal shock damage theory deduced by Hasselman (1963) and Hasselman (1969) are two widely accepted thermal shock theories of ceramics. Thereafter, researchers (Swain, 1990; Zhou et al., 2005; Salvini et al., 2012) further improved the theories of thermal shock fracture for ceramics. However, the initiation and propagation of thermal shock cracks have not been characterized in the existing theoretical studies. Even though the theoretical analysis utilized fracture mechanics, it still failed to characterize the cracking process.
In experimental studies, Pettersson et al. (2002) used the indentation quenching method to study the effect of thickness and initial crack length of specimen on the TSR of ceramics. Collin and Rowcliffe (2000) used the quenching method to prove that the thermal shock crack propagation of materials is jointly controlled by residual stress and thermal stress. The multiple-crack propagation with periodic and hierarchical characteristics caused by water quenching were observed by Jiang et al. (2012) and Liu et al. (2015) using thin rectangle and circular slab specimens of ceramics. The factors that affected the thermal shock-induced crack propagation of ceramics also studied by experiments (Shao et al., 2010; Shao et al., 2017; Shao et al., 2018). Different shapes and sizes (Becher and Warwick, 1993; Wang et al., 2018), temperature of cooling media (Seok Hahn and Lee, 1999; Li W. et al., 2015), and surface treatments (Song et al., 2010) had been also investigated in thermal shock experiments. However, the current experimental methods cannot real-time capture the crack nucleation and propagation process of thermal shock and cannot effectively uncover the corresponding mechanisms in ceramics. This limits the development of ceramic materials.
Because of the limitation of theoretical and experimental studies in characterizing the thermal shock crack initiation and propagation process, the finite element method was used to simulate the crack nucleation and propagation of ceramics under thermal shock, and the factors that control the cracking behavior. Henneberg et al. (2013) proposed a thermal shock damage model of brittle materials to simulate the thermal shock damage process of ceramics during heating and cooling. Wang et al. (2019) established a new weakly coupled thermoelastic normal creep model to study the influence of size and crack propagation energy evolution on the thermal shock crack morphology of ceramic plates in the water quenching tests. Tang et al. (2016) and Jiang et al. (2012) discussed the periodic and hierarchical characteristics of thermal shock-induced cracks of ceramics by numerical simulation. Li D. et al. (2015) proposed a non-local fracture modeling method. And its numerical simulation results showed that the crack patterns had the same periodicity and hierarchy as the experiment. Because the application of ceramic materials in the high-temperature field, strict requirements have been put forward for the service environment. However, the above-mentioned numerical simulation methods did not consider the influence of temperature dependence of the criterion on thermal shock while the importance of considering the temperature dependence of material properties in evaluating the TSR of ceramic materials had been clarified by Han and Wang (2011). Therefore, the temperature dependence of the thermophysical properties of materials should be considered in the numerical simulation. Li et al. (2019), Li et al. (2020) derived the temperature-dependent critical failure energy density criterion suitable for complex stress conditions according to the energy storage limit of the material and explored the thermal shock fracture behavior of the ceramics and thermal barrier coating systems under thermal shock conditions.
Although some of the above-mentioned numerical simulation methods considered the temperature dependence of thermophysical properties in thermal shock, some of the thermal shock failure criteria, i.e., the maximum tensile stress and maximum principal stress, are valid in complex thermal shock condition. Therefore, based on the force-heat equivalence energy density principle, this paper establishes a novel temperature-dependent failure criterion and combines the finite element method to carry out the numerical simulation. The results are compared with experimental results to study the thermal shock damage behavior and the mechanism of ceramics thermal protection materials under different service environments, which provides a theoretical reference for the study of thermal shock resistance of ceramic materials.
Li et al. (2010) considered that: for a specific material, both mechanical work and heat can destroy the structure of the material. When the material fails, it corresponds to a constant of maximum energy value, which belongs to the energy storage limit (critical failure energy density) of the material itself. This energy storage limit can be characterized by strain energy or thermal energy. The premise of the material being destroyed is the failure energy density of the material reaches the critical value, that is, the sum of the equivalent thermal energy density and the strain density reaches the critical value. At this time, the material will rupture, and then crack nucleation and propagation will occur, as shown in the following equation:
where,
Assuming that the reference temperature is 0°C, the corresponding heat energy density can be expressed as
According to Eqs 1, 2, when
where Tm is the melting point of material. According to Eq. 1,
Therefore,
Substituting Eq. 6 into Eq. 1, we can obtain:
To prevent the occurrence of the pseudo-bifurcation phenomenon, the strain energy is decomposed. According to the method proposed by Miehe et al. (2010), the elastic strain energy is decomposed in tensile and compressive part so that the tensile part of the strain energy drives the evolution of cracks, for which the strain tensor is first spectrally decomposed as follows:
In the formula,
According to the strain after spectral decomposition, the strain energy density at current temperature T can be decomposed into:
where λ and μ are temperature-dependent Lamé constants, and tr(•) represents the trace. According to the above equation, the strain energy density of the tensile part is
Substituting Eq. 10 into Eq. 7, the critical failure energy density can be obtained as
The numerical simulation of ceramic materials is carried out by using the finite element software ABAQUS combining with the subroutine USDFLD which embedded the proposing temperature-dependent failure criterion in Temperature-Dependent Failure Criterion of Thermal Shock Based on the Force-Heat Equivalence Energy Density Principle. The mechanical properties of the ceramics showed brittle behavior in the studied temperature range, the thermal shock crack growth rate is fast, and when the failure energy density reached the critical value, the material is destroyed, that is, in the process of model calculation, the material only exists in two states before- and after- fracture. To facilitate the convergence of the calculation results, we set the elastic modulus of the material after fracture to 0.0001 E0 (E0 is the initial elastic modulus of the material before failure), and the conductivity is set to 0.1 k0 (k0 is the conductivity before failure).
Temperature-dependent failure criteria combined with the finite element software ABAQUS were used to model the thermal shock behavior of the alumina ceramic circular slices, as shown in Figure 1, with a diameter of 13 mm. The thermal shock experiments of the specimens by water quenching were demonstrated by Liu et al. (2015) in detail. The material parameters are shown in Table 1 and Figure 2 (Shao et al., 2011; Jiang et al., 2012; Liu et al., 2015; Li et al., 2016). The thermal conductivity, thermal expansion coefficient, and specific heat are all temperature-dependent, and the heat transfer coefficient is ts = 48 kW/(m2 K) according to the experiments (Liu et al., 2015).
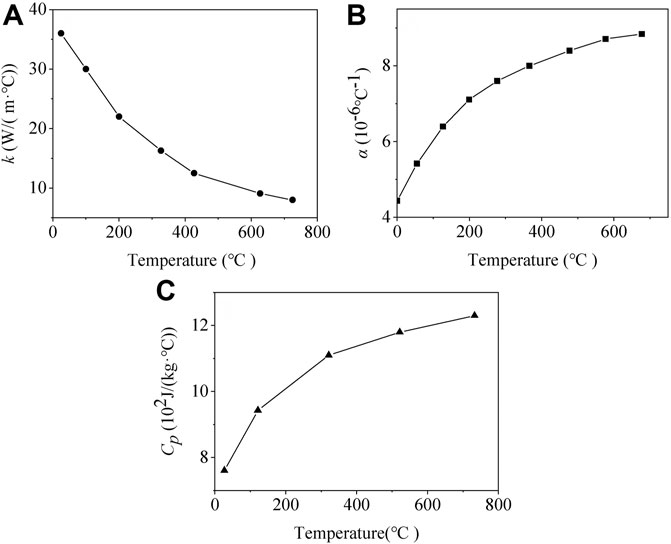
FIGURE 2. Thermal properties of Al2O3 versus temperature. (A) the conductivity k, (B) the thermal expansion coefficient α, and (C) the specific heat Cp.
The water quenching test is the most widely used method to evaluate the TSR of ceramics. In the experimental studies demonstrated by Shao et al. (2010) and Jiang et al. (2012), the ceramic slabs were first heated to different initial thermal shock temperatures and then dropped freely into a water bath. Taking into account the symmetry of the model, only 1/4 of the specimen was needed for modeling, and the symmetry boundary conditions were used. The model size is 25 mm × 5 mm ×1 mm, as shown in Figure 3 (the shaded part is the actual modeling). The material parameter settings of the model are the same as those in Table 1 and Figure 2. The initial ambient temperature is 20°C, and the heat transfer coefficient is ts = 65 kW/(m2 K).
As shown in Figure 4, when the initial temperature is 300°C, the alumina ceramic numerical model has fewer cracks and larger crack spacing. As the initial temperature increases, the number of cracks in the model increases, and the crack spacing gradually decreases. This indicates that the thermal shock initial temperature is one of the main factors affecting the crack spacing. The cracks show periodicity and hierarchy. Short cracks appear between every two long cracks. Consequently, the numerical simulation results are in good agreement with the experimental results. Moreover, the rationality and validity of the proposed temperature-dependent failure criterion are proved.
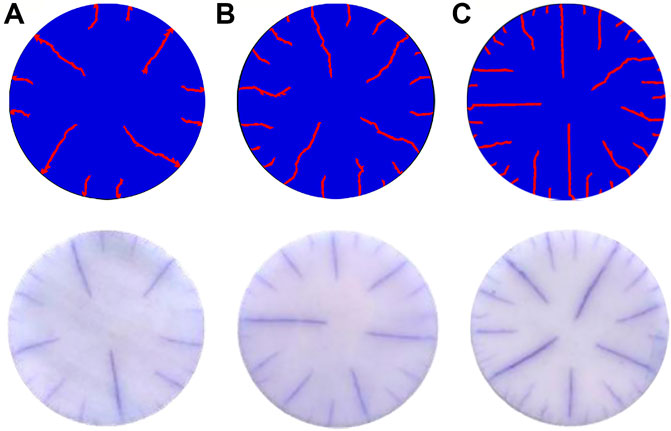
FIGURE 4. Comparison of simulation results and experimental results (Liu et al., 2015) of thermal shock in circular Al2O3 specimens at different initial thermal shock temperatures ((A) T0 = 300°C, (B) T0 = 400°C, (C) T0 = 500°C).
At the beginning of thermal shock, the temperature of the ceramic specimen decreases sharply the edge. This results in great temperature gradient in a short time and cause severe tensile strain energy which controls the initiation and propagation of the thermal shock crack. Along with the time of thermal shock continue, the internal temperature of the ceramic sheet sample also decreases. In the temperature field shown in Figure 5, the tangent direction of the temperature at the crack propagation area jumps obviously. This indicates that during the initiation and propagation of thermal shock cracks, the original continuity of the material at the crack is destroyed, and the heat transfer in the material are influenced. Therefore, the propagation of thermal shock cracks and the heat transfer of materials are mutually affected.
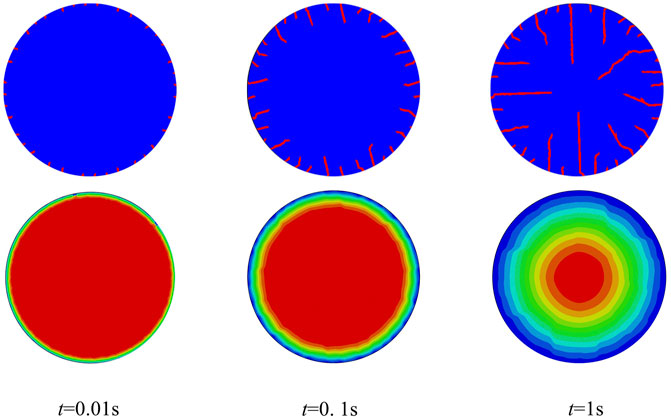
FIGURE 5. Thermal shock-induced crack evolution and its corresponding temperature field of circular Al2O3 under the initial temperature of 500°C.
As shown in Figure 6, when the temperature is 300°C, four long cracks appear in the numerical simulation, and six appear in the experimental model. When the initial temperature is 400°C, the number of long cracks in the numerical simulation is seven and that in the experimental result is eight. When the temperature rises to 600°C, the number of long cracks in the numerical simulation and experimental result are all 11. Obviously, the number of long cracks increases with the increase of the initial temperature. Because the inhomogeneity of the material is not considered, a certain error occurs between the experimental results and the numerical simulation results. However, the overall tendency is consistent with the experimental results.
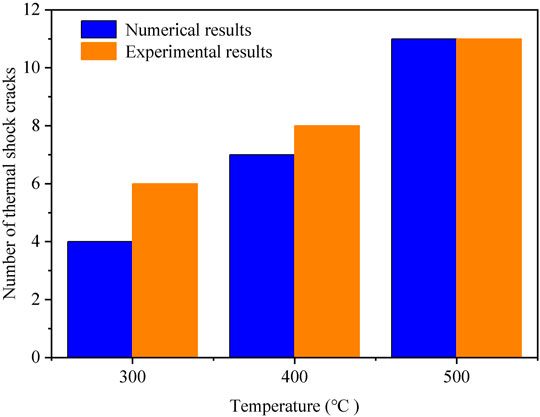
FIGURE 6. Comparison of the number of long cracks in simulation results and experimental results (Liu et al., 2015) of the circular Al2O3 specimen.
The crack initiation and propagation process of the circular ceramic specimen under the initial temperature of 500°C is shown in Figure 7. Before 0.1 s, the number of cracks increased fast. On the contrary, the cracks propagated slowly. After 0.1 s, the number of cracks did not change overall. The cracks only propagated along the original path to the final length. Therefore, no cracks initiate in the thermal shock crack propagation stage. The final number of the thermal shock cracks is determined in the crack nucleation stage.
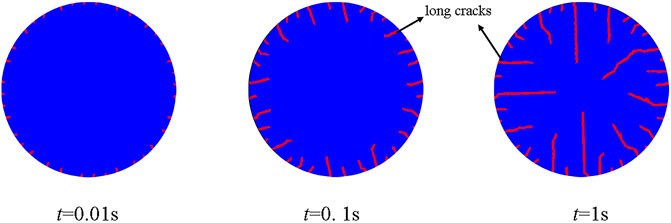
FIGURE 7. Thermal shock-induced crack initiation and propagation process of circular Al2O3 under the initial temperature of 500°C. Thermal shock behavior of rectangular Al2O3 slabs.
Crack morphology of thin Al2O3 specimens after thermal shock of different initial thermal shock temperature and its comparison with experimental results are shown in Figure 8. The higher the initial temperature of thermal shock, the greater the number of cracks and the smaller the spacing are acquired. Because higher temperature will result in more severe stress mismatch during cooling and more cracks nucleate (Zhang et al., 2021). The regularity of crack morphology is demonstrated periodically with long and short cracks. The morphology obtained by the finite element simulation is in good agreement with the experimental results, proving that the temperature-dependent failure criterion is accurate and effective.

FIGURE 8. Comparison of simulation results and experimental results (Jiang et al., 2012) of thermal shock in rectangle Al2O3 specimens at different initial thermal shock temperatures.
As shown in Figure 9, before 0.01 s, the thermal shock process is in the crack nucleation stage, the cracks formed uniformly at equal intervals. The cracks propagate rapidly between 0.01 and 0.2003 s, the thermal shock cracks selectively stop and propagate in this period, and the long and short cracks form hierarchy. After 0.2003 s, as the thermal stress decreases, the crack propagation speed slows down. From the crack morphology of the specimen under different initial thermal shock temperatures, we can conclude that the total number of cracks is determined by the nucleation stage. The more cracks that appear in the crack nucleation stage, the more the number of cracks that will eventually be formed.
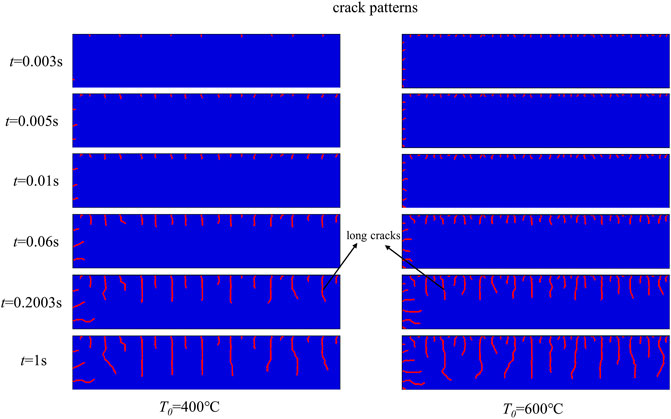
FIGURE 9. Thermal shock crack evolution process of the rectangular Al2O3 specimens under the initial temperatures of 400 and 600°C.
Statistics of the average long crack spacing of different thermal shock initial temperature are shown in Figure 10. With the increase of the initial temperature, the crack spacing becomes increasingly smaller. The Figure shows that the crack spacing obtained by numerical simulation is close to the experimental results (Jiang et al., 2012), again verifying the accuracy and the validity of the new failure criterion.
The comparison of the number of long cracks between simulation and experimental results (Jiang et al., 2012) is shown in Figure 11. When the temperature is 400°C, seven long cracks appear in the numerical result and eight in the experimental result, with short cracks sandwiched between the long cracks. When the temperature is 500°C, 11 long cracks appear in the numerical simulation results, four more than those at 400°C. The number of cracks in the experimental results is also 11. When the temperature is 600°C, 12 long cracks appear both in the numerical simulation and the experiment. As the initial temperature increases, the thermal shock condition is more severe, leading to more cracks.
This paper derives a new temperature-dependent failure criterion based on the force-heat equivalence energy density principle. With the use of this criterion, the finite element simulation was applied to the thin rectangular and circular Al2O3 ceramic slab specimens under different thermal shock conditions. The finite element numerical simulation results are in good agreement with the experimental results, because they reproduced the periodicity and hierarchy of the cracks in the experiment, crack spacing, and the number of cracks gradually increased with the increase of the initial temperature. It was found that there existed two stage of thermal shock cracking and the final number of the thermal shock cracks was determined in the initial crack nucleation stage. Higher temperature resulted in more severe stress mismatch during cooling and more cracks nucleate. Therefore, the tensile part of the strain energy produced by thermal shock was proved to be the controlling mechanism of thermal shock fracture, and the temperature-dependent failure criterion proposed in this paper overcomes the limitations of the previous maximum principal stress and maximum tensile stress criteria.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
DL deduced the temperature-dependent failure criterion. YP and TL finished the calculation and original manuscript. ZL and SC revised the manuscript.
This work was supported by the National Natural Science Foundation of China under Grant Nos. 11972100, 11602043, and 5180040902 and the National Science Foundation Project of Chongqing CSTC (Grant Nos. cstc2019jcyjmsxmX0298 and cstc2019jcyj-msxm1870).
Author ZL was employed by the company China Merchants Chongqing Communications Research & Design Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Becher, P. F., and Warwick, W. H. (1993). “Factors Influencing the Thermal Shock Behavior of Ceramics,” in Thermal Shock and thermal Fatigue Behavior of Advanced Ceramics (Dordrecht: Springer), 37–48. doi:10.1007/978-94-015-8200-1_4
Collin, M., and Rowcliffe, D. (2000). Analysis and Prediction of thermal Shock in Brittle Materials. Acta Mater. 48, 1655–1665. doi:10.1016/S1359-6454(00)00011-2
Cui, K., Fu, T., Zhang, Y., Wang, J., Mao, H., and Tan, T. (2021b). Microstructure and Mechanical Properties of CaAl12O19 Reinforced Al2O3-Cr2O3 Composites. J. Eur. Ceram. Soc. 41 (15), 7935–7945. doi:10.1016/j.jeurceramsoc.2021.08.024
Cui, K., Zhang, Y., Fu, T., Hussain, S., Saad AlGarni, T., Wang, J., et al. (2021a). Effects of Cr2O3 Content on Microstructure and Mechanical Properties of Al2O3 Matrix Composites. Coatings 11 (2), 234. doi:10.3390/coatings11020234
Han, J.-C., and Wang, B.-L. (2011). Thermal Shock Resistance of Ceramics with Temperature-Dependent Material Properties at Elevated Temperature. Acta Materialia 59, 1373–1382. doi:10.1016/j.actamat.2010.10.068
Hasselman, D. P. H. (1963). Elastic Energy at Fracture and Surface Energy as Design Criteria for Thermal Shock. J. Am. Ceram. Soc. 46, 535–540. doi:10.1111/j.1151-2916.1963.tb14605.x
Hasselman, D. P. H. (1969). Unified Theory of Thermal Shock Fracture Initiation and Crack Propagation in Brittle Ceramics. J. Am. Ceram. Soc. 52, 600–604. doi:10.1111/j.1151-2916.1969.tb15848.x
Henneberg, D., Ricoeur, A., and Judt, P. (2013). Multiscale Modeling for the Simulation of Damage Processes at Refractory Materials Under Thermal Shock. Comput. Mater. Sci. 70, 187–195. doi:10.1016/j.commatsci.2013.01.002
Jiang, C. P., Wu, X. F., Li, J., Song, F., Shao, Y. F., Xu, X. H., et al. (2012). A Study of the Mechanism of Formation and Numerical Simulations of Crack Patterns in Ceramics Subjected to Thermal Shock. Acta Mater. 60, 4540–4550. doi:10.1016/j.actamat.2012.05.020
Kingery, W. D. (1955). Factors Affecting thermal Stress Resistance of Ceramic Materials. J. Am. Ceram. Soc. 38, 3–15. doi:10.1111/j.1151-2916.1955.tb14545.x
Li, D., Wang, R., and Li, W. (2019). Research on Thermal Shock Damage Behavior of Thermal Barrier Coating Based on Critical Failure Energy Density Criterion. Surf. Techn. 48, 56–61. doi:10.16490/j.cnki.issn.1001-3660.2019.01.008
Li, D., Wang, R., Wang, X., and Li, W. (2020). Simulation of the Thermal Shock Cracking Behaviors of Ceramics Under Water Quenching for 3-Dimension Conditions. Eur. J. Mech. A/Solids 84, 104080. doi:10.1016/j.euromechsol.2020.104080
Li, J., Song, F., and Jiang, C. (2015). A Non-Local Approach to Crack Process Modeling in Ceramic Materials Subjected to thermal Shock. Eng. Fracture Mech. 133, 85–98. doi:10.1016/j.engfracmech.2014.11.007
Li, W., Wang, R., Li, D., Shen, X., Kou, H., and Fang, D. (2015). Effect of the Cooling Medium Temperature on the thermal Shock Resistance of Ceramic Materials. Mater. Lett. 138, 216–218. doi:10.1016/j.matlet.2014.09.137
Li, D., Li, W., Wang, R., and Fang, D. (2016). The Effects of Water Entry Postures on the Thermal Shock Behavior of Alumina. Int. J. Appl. Ceramic Technol. 13 (1). doi:10.1111/ijac.12411
Li, W., Yang, Y., and Fang, D. (2010). The Temperature-Dependent Fracture Strength Model for Ultra-High Temperature Ceramics. Acta Mech. Sinica 26 (2), 235–239. doi:10.1007/s10409-009-0326-7
Liu, Y., Wu, X., Guo, Q., Jiang, C., Song, F., and Li, J. (2015). Experiments and Numerical Simulations of thermal Shock Crack Patterns in Thin Circular Ceramic Specimens. Ceram. Int. 41 (1), 1107–1114. doi:10.1016/j.ceramint.2014.09.036
Miehe, C., Hofacker, M., and Welschinger, F. (2010). A Phase Field Model for Rate-Independent Crack Propagation: Robust Algorithmic Implementation Based on Operator Splits. Comput. Methods Appl. Mech. Eng. 199 (145-48), 2765–2778. doi:10.1016/j.cma.2010.04.011
Neuman, E. W., Hilmas, G. E., and Fahrenholtz, W. G. (2016). Ultra-High Temperature Mechanical Properties of a Zirconium Diboride-Zirconium Carbide Ceramic. J. Am. Ceram. Soc. 99 (2), 597–603. doi:10.1111/jace.13990
Pettersson, P., Johnsson, M., and Shen, Z. (2002). Parameters for Measuring the Thermal Shock of Ceramic Materials with an Indentation-Quench Method. J. Eur. Ceram. Soc. 22, 1883–1889. doi:10.1016/S0955-2219(01)00504-0
Salvini, V. R., Pandolfelli, V. C., and Bradt, R. C. (2012). Extension of Hasselman’s Thermal Shock Theory for Crack/Microstructure Interactions in Refractories. Ceram. Int. 38, 5369–5375. doi:10.1016/j.ceramint.2012.03.046
Seok Hahn, B., and Lee, H. L. (1999). Effect of Environmental Factors on Thermal Shock Behaviour of Polycrystalline Alumina Ceramics. J. Mater. Sci. 34, 3623–3630. doi:10.1023/A:1004686918618
Shao, Y., Liu, B., Wang, X., Li, L., Wei, J., and Song, F. (2018). Crack Propagation Speed in Ceramic during Quenching. J. Eur. Ceram. Soc. 38, 2879–2885. doi:10.1016/j.jeurceramsoc.2018.02.028
Shao, Y., Song, F., Liu, B., Li, W., Li, L., and Jiang, C. (2017). Observation of Ceramic Cracking during Quenching. J. Am. Ceram. Soc. 100, 520–523. doi:10.1111/jace.14674
Shao, Y., Xu, X., Meng, S., Bai, G., Jiang, C., and Song, F. (2010). Crack Patterns in Ceramic Plates after Quenching. J. Am. Ceram. Soc. 93, 3006–3008. doi:10.1111/j.1551-2916.2010.03971.x
Shao, Y., Zhang, Y., Xu, X., Zhou, Z., Li, W., and Liu, B. (2011). Effect of Crack Pattern on the Residual Strength of Ceramics After Quenching. J. Am. Ceram. Soc. 94 (9), 2804–2807. doi:10.1111/j.1551-2916.2011.04728.x
Song, F., Meng, S., Xu, X., and Shao, Y. (2010). Enhanced Thermal Shock Resistance of Ceramics through Biomimetically Inspired Nanofins. Phys. Rev. Lett. 104, 125502. doi:10.1103/PhysRevLett.104.125502
Swain, M. V. (1990). R-Curve Behavior and Thermal Shock Resistance of Ceramics. J. Am. Ceram. Soc. 73, 621–628. doi:10.1111/j.1151-2916.1990.tb06562.x
Tang, S. B., Zhang, H., Tang, C. A., and Liu, H. Y. (2016). Numerical Model for the Cracking Behavior of Heterogeneous Brittle Solids Subjected to thermal Shock. Int. J. Sol. Structures 80, 520–531. doi:10.1016/j.ijsolstr.2015.10.012
Wang, J., Zhang, Y., Cui, K., Fu, T., Gao, J., Hussain, S., et al. (2021). Pyrometallurgical Recovery of Zinc and Valuable Metals from Electric Arc Furnace Dust - A Review. J. Clean. Prod. 298, 126788. doi:10.1016/j.jclepro.2021.126788
Wang, R., Li, W., Li, D., Wang, S., Wu, X., and Fang, D. (2018). An Ascending Thermal Shock Study of Ceramics: Size Effects and the Characterization Method. Mater. Chem. Phys. 203, 34–39. doi:10.1016/j.matchemphys.2017.09.042
Wang, Y., Zhou, X., and Zhang, T. (2019). Size Effect of thermal Shock Crack Patterns in Ceramics: Insights from a Nonlocal Numerical Approach. Mech. Mater. 137, 103133. doi:10.1016/j.mechmat.2019.103133
Zhang, Y., Cui, K., Fu, T., Wang, J., Shen, F., Zhang, X., et al. (2021). Formation of MoSi2 and Si/MoSi2 Coatings on TZM (Mo-0.5Ti-0.1Zr-0.02C) Alloy by Hot Dip Silicon-Plating Method. Ceramics Int. 47 (16), 23053–23065. doi:10.1016/j.ceramint.2021.05.020
Zhang, Y., Yu, L., Fu, T., Wang, J., Shen, F., and Cui, K. (2022). Microstructure Evolution and Growth Mechanism of Si-MoSi2 Composite Coatings on TZM (Mo-0.5Ti-0.1Zr-0.02 C) Alloy. J. Alloys Compd. 894, 162403. doi:10.1016/j.jallcom.2021.162403
Keywords: ceramics, force-heat equivalence energy density, thermal shock, crack, failure criterion
Citation: Li D, Pang Y, Lu T, Liu Z and Chen S (2022) Numerical Analysis of Thermal Shock Cracking Behaviors of Ceramics Based on the Force-Heat Equivalence Energy Density Principle. Front. Mater. 8:825327. doi: 10.3389/fmats.2021.825327
Received: 09 December 2021; Accepted: 27 December 2021;
Published: 18 January 2022.
Edited by:
Shahid Hussain, Jiangsu University, ChinaReviewed by:
Yingyi Zhang, Anhui University of Technology, ChinaCopyright © 2022 Li, Pang, Lu, Liu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhongshuai Liu, bGl1emhvbmdzaHVhaUBjbWhrLmNvbQ==; Shiwei Chen, MjAxMzAwMUBjcXVzdC5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.