Magnetic-Optic Effect-Based Topological State: Realization and Application

The topological state in photonics was first realized based on the magnetic-optic (MO) effect and developed rapidly in recent years. This review summarizes various topological states. First, the conventional topological chiral edge states, which are accomplished in periodic and aperiodic systems based on the MO effect, are introduced. Some typical novel topological states, including valley-dependent edge states, helical edge states, antichiral edge states, and multimode edge states with large Chern numbers in two-dimensional and Weyl points three-dimensional spaces, have been introduced. The manifest point of these topological states is the wide range of applications in wave propagation and manipulation, to name a few, one-way waveguides, isolator, slow light, and nonreciprocal Goos–Hänchen shift. This review can bring comprehensive physical insights into the topological states based on the MO effect and provides reference mechanisms for light one-way transmission and light control.

Introduction

Topology, which began as a mathematical concept, studies the properties of geometry or space that remain unchanged with continuous deformations (Xu et al., 2015). Topology is initially observed in the solid-state electron systems with the fountainhead of topological order (Ozawa et al., 2019). It was first introduced as a new property of the full energy band along with the discovery of the quantum Hall effect in 1980 (von Klitzing, 1986; Chen and Wu, 2016). It sufficiently explained the phenomenon of Hall conductance of a two-dimensional (2D) electron gas under an external magnetic field, which had a quantized value with remarkable precision regardless of the charge density and impurities in the sample (Klitzing et al., 1980). The quantized Hall conductance is categorized by a nonzero topological invariant (the Chern number), which is an integer-quantity value that defines the universal structure of the wave function in the momentum space over the Brillouin zone (Chen and Wu, 2016).

After the topological invariant in electronics was proposed, it was introduced in photonics (Haldane and Raghu, 2008) and phononics (Wang et al., 2020). Magnetic-optical (MO) effects are used to break time-reversal symmetry (TRS) to realize topological states in photonics (Haldane and Raghu, 2008; Raghu and Haldane, 2008). The effects of MO represent the phenomena in which electromagnetic (EM) waves propagate in materials with a static magnetic field, such as the Faraday effect (Dannegger et al., 2021; Kazemi et al., 2021; Majedi, 2021; Yertutanol et al., 2021), the MO Kerr effect (Borovkova et al., 2016; Amanollahi et al., 2018; Diaz-Valencia, 2021; Papusoi et al., 2021), and the Zeeman effect (Márquez and Esquivel-Sirvent, 2020; Li et al., 2021). The medium is called gyrotropic (including gyromagnetic and gyroelectric), in which EM parameters can be easily tuned by external field (Wang et al., 2018). When the TRS of the photonic system is broken, the degenerate points of photonic bands split apart, and each nondegenerate band is associated with a nonzero Chern number (Raghu and Haldane, 2008). The Chern number of the bandgap is the sum of all the bands below this gap (Haldane and Raghu, 2008). If the gap Chern number changes when it is across an interface of two media, states localized along the interface, namely, topological edge states (TESs), will occur, which are immune to defects and disorders (Xu et al., 2015). TESs provide ideal platforms for realizing one-way states with low feedback and loss, which is a challenge in ordinary waveguides because backscattering is a primary-significant source of unwanted feedback and loss in ordinary waveguides. The backscattering hinders large-scale optical integration, so resistance to it is the main task (Ma et al., 2011; Kumar and Chaubey, 2012). More interesting physical phenomena and applications of TESs based on the MO effect are explored theoretically and experimentally (Skirlo et al., 2015; Chen et al., 2017; Lu et al., 2018a; Chen et al., 2019a; Chen et al., 2020; Ma et al., 2020; Wang et al., 2021).

This review summarizes the recent progress and applications of TESs in periodic and aperiodic systems based on the MO effect. We begin with an itemized exposition of topological one-way chiral edge states, whose corresponding propagating direction can be reversed by the opposite external magnetic field. The mechanisms of realizing topological states are introduced, and the achievements of topological one-way chiral states in different configurations are concluded. Then, other novel TESs, including valley-dependent edge states, helical edge states, antichiral edge states, multimode edge states in 2D space, and Weyl point in three-dimensional (3D) space, are presented. The final section mainly introduces the applications based on these TESs, including one-way fiber, isolator, large-area waveguide, slow light, rainbow effect, and nonreciprocal Goos–Hänchen (GH) shift.

Ordinary Topological Chiral Edge State Based on MO Effect

The chiral edge state, related to the nontrivial topological properties of the band structure, implies a unique one-way flow of light that possesses group velocities pointing in only one direction, which is determined by the direction of a magnetic field. A one-way waveguide can be formed based on these properties, and the propagating direction can be reversed by applying an opposite external magnetic field (He et al., 2010). Because of the tunability and the robustness against defects and disorders, TESs are widely concerned by researchers.

Theory

Dirac point, an isolated point where two bands become degenerate but with a linear dispersion for nearby Bloch vectors, can be found in graphene’s electronic band structure. For a graphene ribbon with zigzag edges, there are peculiar localized electronic states at each edge (Nakada et al., 1996). Haldane and Raugh proposed the theory to realize a topological state in photonics by transcribing the key feature of the electronic Haldane model to the photonic context (Haldane and Raghu, 2008; Raghu and Haldane, 2008). Electrons as fermions are very different from photons as bosons. However, the edge states belong to one-particle eigenstate problems similar to the Maxwell normal-mode problem, which is a generalized self-consistent Hermitian eigenproblem. The generalized eigenproblem has the structure (Haldane and Raghu, 2008):

${\mathit{U}}^{+}\left(\mathit{k}\right)\mathit{AU}\left(\mathit{k}\right)|u_n\left(\mathit{k}\right)\rangle ={\omega }_n\left(\mathit{k}\right)\mathit{B}\left({\omega }_n\left(\mathit{k}\right)\right)|u_n\left(\mathit{k}\right)\rangle$

The eigenfunction $|{\mathit{u}}_n\left(\mathit{k},r\right)\rangle =\langle \mathit{r}\text{|}{u}_n\left(\mathit{k}\right)\rangle$ has the form (Haldane and Raghu, 2008):

$|{\mathit{u}}_n\left(\mathit{k},\mathit{r}\right)\rangle \equiv \left(\begin{array}{c}{\mathit{E}}_n(\mathit{k}, \mathit{r})\\ {\mathit{H}}_n(\mathit{k}, \mathit{r})\end{array}\right)$

On this basis, $\mathit{U}\left(\mathit{k},\mathit{r}\right)=\text{exp}\left(i\mathit{k}\cdot \mathit{r}\right)$, $\mathbf{A}=-\text{i}{\mathit{J}}^a{\nabla }_a$ and $\mathbf{B}=\left(\begin{array}{cc}\mathit{\epsilon }\left(\mathbf{r},\omega \right)& 0\\ 0& \mathit{\mu }\left(\mathit{r},\omega \right)\end{array}\right)$ are chosen, where ${\mathit{J}}^a=\left(\begin{array}{cc}0& i{\mathit{L}}^a\\ -i{\mathit{L}}^a& 0\end{array}\right)$, ${\mathit{L}}^a$ are the $3\times 3$ Pauli matrices.

By deducing the eigenfunction, Berry connection is obtained, which is gauge dependent (Haldane and Raghu, 2008):

${\mathit{A}}_n^a=\frac{\langle u_n\text{|}{\mathit{B}}_0\left({\omega }_{\text{n}}\right)\text{|}{\nabla }_k^a{u}_n\rangle -\langle {\nabla }_k^a{u}_n\text{|}{\mathit{B}}_0\left({\omega }_{\text{n}}\right)\text{|}{u}_n\rangle }{2i\langle u_n\text{|}{\mathit{B}}_0\left({\omega }_{\text{n}}\right)\text{|}{u}_n\rangle }$

The associate gauge-invariant function is Berry curvature that can be obtained from Berry connection:

${\mathit{F}}_n^{ab}\left(\mathit{k}\right)=\nabla \times \mathit{A}$

For adiabatic evolution around a closed path Γ, the Berry phase is given by

${\mathrm{\Phi }}_{\text{n}}=\underset{\Gamma }{{\displaystyle \mathit{\oint }}}{\mathit{A}}_n^{a}d{\mathit{k}}_a=\underset{\Sigma }{{\displaystyle \mathit{\iint }}}d{\mathit{k}}_a\wedge d{\mathit{k}}_b{\mathit{F}}_n^{ab}$

where Σ is a surface bounded by Γ. In the case of 2D band structure, Σ means the Brillouin zone. The integer Chern number of a band is $C_n=\frac{{\mathrm{\Phi }}_{\text{n}}}{2\pi }$. The 2D photonic band with a nonzero Chern number has nontrivial topology property. The Chern number of a bandgap is the sum of the Chern number of all the bands below this gap, which is the topological invariant of a structure (Haldane and Raghu, 2008).

Pairs of Dirac points are allowed to exist when inversion symmetry (IS) and TRS are existed, which means $F_n^{ab}\left(\mathit{k}\right)=0$. When IS is alone broken, $F_n^{ab}\left(-\mathit{k}\right)=-F_n^{ab}\left(\mathit{k}\right)$, Chern number is zero, but another topological invariant named the valley Chern number can be created (Chen et al., 2018; Tang et al., 2020; Shi et al., 2021). When TRS is alone broken by adding a Faraday term in permittivity tensor or permeability tensor (applying an external magnetic field on gyrotropic medium), tensors acquire imaginary off-diagonal components having the periodicity of the unit cell (Haldane and Raghu, 2008):

$\widehat{\mathit{\mu }}=\left(\begin{array}{ccc}\mu & i\kappa & 0\\ -i\kappa & \mu & 0\\ 0& 0& {\mu }_0\end{array}\right),\widehat{\mathit{\epsilon }}=\alpha \left(\begin{array}{ccc}\nu & i\lambda & 0\\ -i\lambda & \nu & 0\\ 0& 0& {\nu }_0\end{array}\right)$

$F_n^{ab}\left(-\mathit{k}\right)=F_n^{ab}\left(\mathit{k}\right)$ is now achieved, and each band that splits apart due to the Faraday coupling will have equal and opposite nonzero Chern number, which means nontrivial topology of the bands. A topological gap can be obtained by separating Dirac points as Haldane et al. proposed (Haldane and Raghu, 2008) and separating quadratic degeneracy points (Wang et al., 2008). The one-way edge states are confined at the interface between specific topological structures and possess group velocities pointing at only one direction that is determined by the direction of a magnetic field. The commonly used gyromagnetic materials are yttrium–iron–garnet (YIG) (Wang et al., 2008; Lian et al., 2012; Li et al., 2020; Ma et al., 2020; Wang et al., 2021), vanadium-doped calcium–iron–garnet (Shen et al., 2012), and gyroelectric material such as CuFe₂O₄ (Wu et al., 2018).

Realization in Periodic Optical Systems

After Haldane and Raghu put forward the theory of TES in the photonic system, Wang et al. demonstrated it first in 2D photonic crystals (PhCs) with square lattice theoretically and experimentally (Wang et al., 2008; Wang et al., 2009). In 2008, Wang et al. achieved one-way edge states in PhC with gyrotropic constituents in transverse magnetic (TM) polarization mode, without the restriction of having Dirac points in the band structure and using gyroelectric materials for transverse electric (TE) polarization mode proposed by (Haldane and Raghu, 2008). They designed an experimentally feasible one-way waveguide using a 2D MO square lattice YIG PhC that lacks Dirac point operating at microwave frequencies but has the relevant quadratic degeneracy point (Wang et al., 2008). When an external magnetic field is applied in the out-of-plane direction, strong gyromagnetic anisotropic is induced with the permeability tensor acquiring imaginary off-diagonal components, and the degenerate points are lifted, resulting in the given nonzero Chern number bands. The dispersion curve for the one-way edge state is achieved, which is shown in Figure 1A. The corresponding waveguides, interfaced the MO crystal with an upper cladding, support no bulk states at the second MO crystal band gap frequency, which are demonstrated to be immune against defects by simulation calculation, as shown in Figure 1B. Then, they experimentally achieved one-way backscattering-immune topological EM states for TM polarization (Wang et al., 2009). Their experimental system involves a gyromagnetic 2D periodic PhC bounded on one side by a nonmagnetic metallic cladding. The robustness of the one-way propagation is verified by studying the effect of a large obstacle on transmission. In 2010, a one-way waveguide made from gyromagnetic PhCs and normal dielectric PhCs was also realized with an external static magnetic field applied (Fu et al., 2010).

FIGURE 1

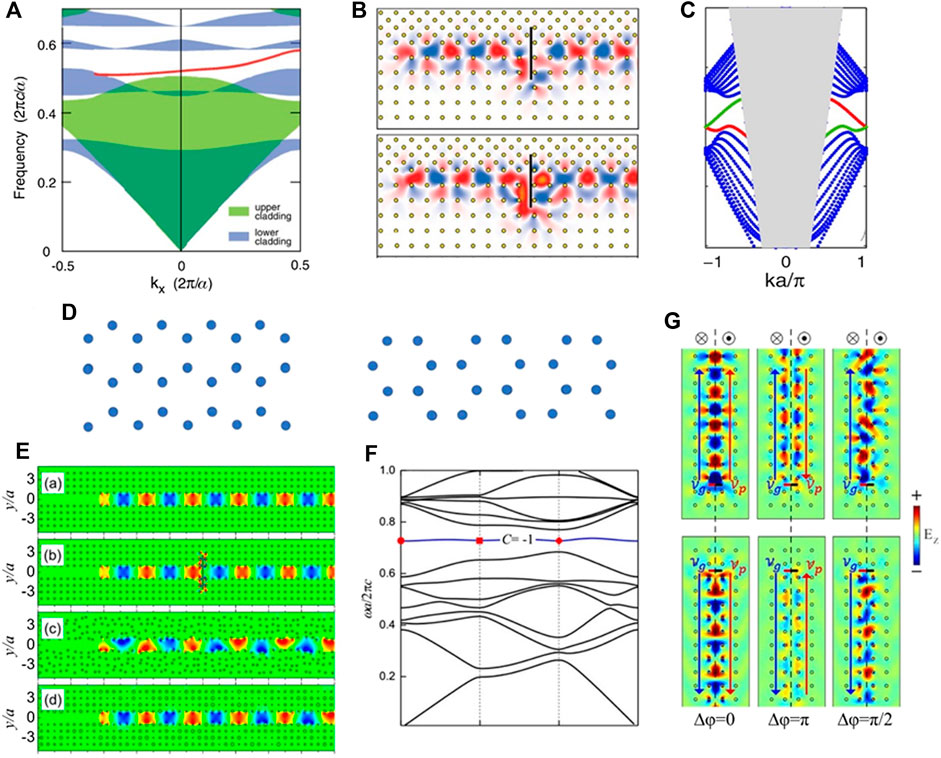
FIGURE 1. (A) The dispersion curve of the one-way edge state spans the bandgap for the cladding crystals (Wang et al., 2008). (B) The simulation of the one-way waveguide with t = 0 and t = 0.25T₀ (T₀ is the optical period) maintains complete transmission even inserting a slab of a perfect electrical conductor (Wang et al., 2008). (C) Band structure of self-guiding edge state, in which the light cone is shaded and the edge states are shown in red and green (Ao et al., 2009). (D) The zigzag edge and the armchair edge. (E) The one-way transportation of EM wave in four configurations: without defects and disorder, with defects, with position disorder, and with radius disorders (Liu et al., 2010). (F) Flat band with nonzero Chern number is denoted by colored lines (Yang et al., 2017b). (G) Symmetrical and antisymmetrical one-way transportation of EM wave (Lai et al., 2020).

Considering the case of PhC with finite size, the edge states are categorized into leaky and guided states, depending on whether they are inside or outside the light cone (Ochiai, 2010). For the guided state (or self-guiding state), the electric field is strongly localized at edge sites, forming a one-way propagating surface wave without an ancillary cladding. For the leaky state, the one-way waveguide is realized by the assisting cladding. Without the help of an assisting cladding, the radiation leakage will completely ruin the one-way propagation. As the one-way edge states mentioned previously are the leaky states (inside the light cone), the PhCs are all assisted with another gapped material to form waveguides. If the assisted material is removed in these systems, the propagating wave along the edge will disappear.

Without assisting another gapped material, a honeycomb gyromagnetic PhC with a self-guiding waveguide at the zigzag ribbon is designed, where TES is outside the light cone and is immune against defects (Ao et al., 2009), as shown in Figure 1C. Then, it was experimentally demonstrated (Poo et al., 2011). In addition to the zigzag ribbon edge, Ochiai and Onoda have realized it by using the armchair edge of honeycomb gyromagnetic PhCs (Ochiai and Onoda, 2009; Ochiai, 2010). The two different edge morphologies are shown in Figure 1D. The band-edge states of them possess different shapes and slopes, which influence the one-way self-guiding transmission performance. In their works, the bulk band structure exhibits a topological phase transition by changing the degree of the broken symmetries including IS and TRS, and the so-called bulk-edge correspondence is verified. The self-guiding edge state was also demonstrated in triangular gyromagnetic PhCs (Liu et al., 2012).

Surface plasmons originate from the collective electronic density wave in a system consisting of metallic building blocks. They have attracted much recent interest for their promising applications in subwavelength nanophotonics (Barnes et al., 2003; Luo and Ishihara, 2004). There is a magnetic counterpart of it in the magnetic system, known as “magnetic surface plasmons”, which inhabit in the magnetic system due to the coupling of EM waves to the collective resonance of spin wave (Chern, 2008; Hu et al., 2012; Ding et al., 2020). When a periodic array of such material is assembled together, the photonic states that hop from one magnetic surface plasmons state to another can form a magnetic surface plasmons band (Shen et al., 2012). By combining the magnetic surface plasmons resonance and the TRS breaking, one-way edge states, including leaky (Lian et al., 2012; Shen et al., 2012; Liu et al., 2010)and self-guiding (Poo et al., 2012) states, can be realized within the magnetic resonance-induced bandgap in gyromagnetic PhCs, which are not only immune to interstitial metal defects but also robust against the disorders of rods position, as shown in Figure 1E (Liu et al., 2010). In addition, the magnetic surface plasmons waveguide exhibits remarkable tunability with an external static magnetic field (Liu et al., 2010; Lian et al., 2012; Shen et al., 2012), which has a broad prospect of applications.

The TESs are also controllable even without magnetic surface plasmons resonances, which have an extensive application prospect. In 2017, Yang et al. explored the generic method that allows us to engineer TESs by altering the parameters of the original microstructure (Yang et al., 2017a). The TESs in the structures can be constructed and varied by altering the parameters of the structure according to the field-energy distributions of the Bloch states at the related Bloch wave vectors. In 2020, Li et al. explored how the surface morphology, from zigzag edge to bearded edge, influences the one-way self-guiding transmission performances of topological honeycomb gyromagnetic PhC (Li et al., 2020). From the band diagrams of PhC and transmission spectrum, the surface morphology changes the shape, slope and frequency range of TESs, which effectively improves one-way waveguides transmission performance.

However, the working waveband of above works is limited to microwaves, limiting its application in optical communication because the natural materials usually have a weak response to the magnetic field in optical frequency range. It is vital to extend the working frequency to the optical regime for practical applications. In 2018, Wu et al. utilized gyroelectric material with breaking TRS by applying an external magnetic field to realize TESs (Wu et al., 2018). The plasmo-gyroelectric metamaterials are designed to have a large ratio of off-diagonal to diagonal components of the dielectric permittivity tensor by suppressing the diagonal components via the plasmonic response of the metallic films. Because of this large ratio, a TES is realized even at optical frequency and keeps robustness that characterized by suppressing backscattering. Then, another group constructed metamaterials by combining the layered metal and gyroelectric media as the background, and by combining the layered metal and ordinary media as the dielectric rods (Wu et al., 2020). The TESs are achieved at the optical frequency with a large MO effect and can be dynamical controlled by altering the external magnetic field. The authors revealed a new mechanism for generating the photonic topological states at optical frequencies, and proposed a new method for controlling the transmission direction of topological states.

There are also some exciting novel phenomena in gyromagnetic PhC. In 2017, Yang et al. explored that there is a flat nontrivial topological band with a nonzero Chern number in gyromagnetic PhC, which comes from strong gyromagnetic coupling interactions of fields among neighboring unit cells (Yang et al., 2017b). The nearly flat band diagram of this PhC is denoted by a colored line with nonzero Chern number, as shown in Figure 1F. A gapless one-way leaky edge state is achieved when this PhC is interfaced with a metallic boundary, which shows robustness against defects. In 2020, symmetrical and antisymmetrical TESs, as shown in Figure 1G, are designed at the boundary of two adjacent MO PhC with opposite magnetic biases (Lai et al., 2020). These two edge states possess the same direction of backscattering-immune chiral energy propagation, but their directions of phase propagation are opposite, i.e., forward phase propagation for the symmetrical state while backward for the anti-symmetric alone. Based on these properties, an all-photonic tunable splitter by hybridizing these two topological states is designed and offers promising applications in tunable photonic devices.

Realization in Aperiodic Optical Systems

Amorphous phases of matter, aperiodic and lack long-range order but maintain short-range order (Berthier and Biroli, 2011), exhibit an interesting phenomenon known as the “glass transition,” whereby an amorphous medium experiences a dramatic structural change from a glass-like phase into a liquid-like phase (Zhou et al., 2020a). The topological one-way waveguides against defects in periodic PhCs were mentioned earlier (Liu et al., 2010; Lian et al., 2012; Poo et al., 2012; Shen et al., 2012), in which both long-range and short-range orders exist (Yang et al., 2019). This section will focus solely on TESs in aperiodic optical systems of short-range orders.

In amorphous lattices, the spectral gaps can continue to exist if there is sufficient short-range order. Such gaps have been found in TRS amorphous photonic structures numerically and experimentally (Ballato et al., 1999; García et al., 2007; Yang et al., 2010; Mansha et al., 2016). In 2017, Mansha et al. presented a numerical study of 2D TRS broken photonic lattices that are amorphous, only possessing short-range position order (Mansha and Chong, 2017). The amorphous lattices are generated by molecular dynamics simulations. The behavior of the topological bandgaps and edge states, as the level of short-range positional order, is varied by tuning the packing algorithm. The edge states in the form of strongly nonreciprocal transmission at frequencies coinciding with the ordered lattice’s topological gaps are evidence of robust propagation. Furthermore, the field distributions for circular and triangular boundaries also demonstrate the robustness of propagation around curves and sharp corners, as shown in Figure 2A. The robust nonreciprocal, ballistic, and edge-localized transmission observed at frequencies corresponding to the topologically nontrivial gaps confirms the principle that TESs should be protected against disorders.

FIGURE 2

FIGURE 2. (A) Robust edge propagation in amorphous lattices with circular and triangular shapes (Mansha and Chong, 2017). (B) One-way waveguide propagation field profiles at the edge of the supercell gyromagnetic PhC configuration with star source in different frequency (Yang et al., 2019).

In 2019, Yang et al. constructed 2D amorphous magnetic photonic lattices that have only short-range orders and used the supercell method with full-wave simulation to study their topological properties in TM mode (Yang et al., 2019). The supercell method is to build super gyromagnetic PhCs that are approximately equivalent to the studied amorphous magnetic photonic lattices by gradually increasing the sizes of the supercells. There are single-mode and multimode TESs in these amorphous magnetic photonic lattices. The one-way waveguide propagation field profiles of single-mode edge states are shown in Figure 2B, where metallic boundaries are placed on the top. Moreover, in 2020, this group numerically investigated the details of the disorder-induced topological state transition in photonic systems composed of 2D gyromagnetic PhCs (Yang et al., 2020). The topological state transition is gradually accompanied by some interesting phenomena as the disorder of rod positions increases. Their studies give an intuitive understanding of the topology underlying aperiodic optical systems and pave a way to manufacture topological optical devices in applications.

Novel Topological Edge States Based on MO Effect

In addition to the one-way chiral edge states mentioned previously, more topological states will be discussed in this section, including valley-dependent edge state, helical edge state, antichiral edge state, multimode edge state with large Chern number in 2D, and Weyl points in 3D space. They show robustness against defects as well. The realization of various topological states based on the MO effect shows that gyrotropic materials with an external magnetic field are still valuable to be explored in topological photonics.

Valley-Dependent Edge State and Helical Edge State

When Dirac point is separated by breaking IS, the Chern number is zero, but the structures with valley Chern numbers (another topological invariant) can be constructed to realize TESs (Chen et al., 2018; Tang et al., 2020; Shi et al., 2021). In 2018, Lu et al. introduced the valley concept in magnetic PhC with broken IS and TRS (Lu et al., 2018a). Two pseudogaps where the bulk states exit only at one single valley are obtained. Changing the strength of broken IS by altering this structure’s parameter (the external magnetic field is still applied), the topological phase characterized by nonzero Chern number transits to another one characterized by nonzero valley Chern number. The one-way valley-dependent edge states appeared at the photonic boundary between these topological distinct PhCs. The projected band structure is shown in Figure 3A, which shows the valley-dependent edge states at two inequivalent valleys. It was demonstrated that the edge states are robust against certain defects, which have potential to realize topological waveguides in microwave range (Lu et al., 2018a).

FIGURE 3

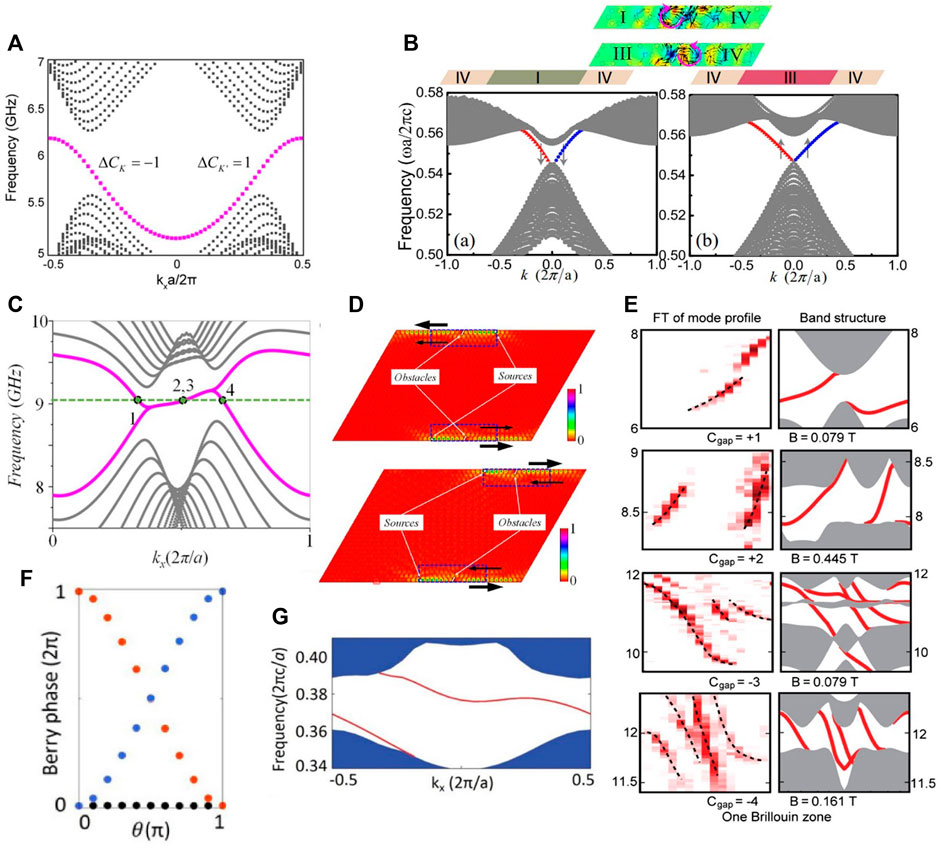
FIGURE 3. (A) Projected band of bulk states and valley-dependent edge states found at two inequivalent valleys (Lu et al., 2018a). (B) Projected band structures and edge states with various pseudospins (Chen et al., 2017). (C) Projected band structures of antichiral edge states (Chen et al., 2020). (D) The diagram of wave transporting of Chiral and antichiral edge states that can bypass obstacles (Chen et al., 2020). (E) Experimental Fourier transforms of edge-mode profiles (left) and the theoretical edge band structures (right) with the edge states in red and the bulk bands in gray (Skirlo et al., 2015). (F) The berry phase was calculated to verify that the Weyl point has topological charge (Yang et al., 2017c). © The Optical Society. (G) Topologically protected Fermi arc-like surface states (Yang et al., 2017c). © The Optical Society.

Quantum spin Hall effect (QSH) of light has a robust and gapless pair of topological helical edge states locked by different specific pseudospins. It has the advantages of one-way transmission and robustness, which plays a key role in realizing topological integrated photonic devices (Khanikaev et al., 2012; Xie et al., 2020). In 2017, the topological phase transition, from QSH insulator to a TRS-broken-QSH insulator and then to a Chern insulator (structure with nonzero gap Chern number) or a transition from a conventional insulator to a Chern insulator, is analyzed in a 2D triangular lattice PhC of hexagonal clusters made from a gyromagnetic material by applying a gradually enhanced external magnetic field (Chen et al., 2017). The helical edge state with various pseudospins appeared on the interfaces between insulators with different topological phases, as shown in Figure 3B. The robustness of the helical edge state is demonstrated by introducing a magnetic impurity or geometric deformations on the interface, which implies potential applications in spin splitter devices.

Antichiral Edge State

Antichiral edge states, in contrast to chiral edge states that transport along the opposite direction on two parallel boundaries, means one-way edge states transporting along the same direction on two parallel boundaries, which are realized in electrics (Colomés and Franz, 2018; Bhowmick and Sengupta, 2020) and photonics (Mandal et al., 2019). To overcome the limitation that the environment for achieving antichiral edge states must be low temperature in practical experiments in Mandal et al. (2019), Chen et al. realized antichiral edge states in a gyromagnetic PhC with a honeycomb lattice consisting of two interpenetrating triangular sublattices A and B that are immersed in opposite external magnetic fields, respectively, in 2020 (Chen et al., 2020). From the projected band structure of the antichiral edge state as shown in Figure 3C, we can see antichiral edge states acquire dispersion with the same velocity. Both edge states propagate in the same direction, which differs from chiral edge states with opposite velocity. The comparison of transport phenomena of chiral and antichiral edge state is shown in Figure 3D. Therefore, two copropagating one-way transport channels are created on the paralleled boundaries. Based on these effects, a three-channel one-way waveguide with a simpler and more compact structure have been created, which offers valuable insights and routines to design novel EM and functional optical devices. In the same year, Zhou et al. have reported the experimental observation of antichiral edge states in gyromagnetic PhCs (Zhou et al., 2020b) with the lattice same to Chen et al. (2020). The chiral-like robust propagation in samples with certain shapes and the 100% scattering into backward bulk states at certain terminations have been further demonstrated in their experiment. These results extend and supplement the current understanding of chiral edge state.

Multimode Edge State With a Large Chern Number

For an edge formed by joining two materials with bandgaps overlapping in frequency, the number of one-way edge states is equal to the difference of gap Chern numbers across the interface (Hatsugai, 1993). Therefore, to create a multimode edge state, namely increasing the Chern number of gaps, band structure requires involving more pairs of Dirac points and more quadratic points. Two approaches are proposed to implement bulk bands with multiple pairs of Dirac cones and multiple quadratic points by Skirlo et al. (2014). New topological phases with large Chern numbers are found by simultaneously gapping these degenerate points in PhCs with material parameters of YIG. A possible practical application as an adjustable power splitter has been proposed experimentally to verify the existence of a large Chern number for multimode edge states.

The following year, they experimentally realized the large Chern number in PhCs with a square lattice ferrimagnetic PhC (Skirlo et al., 2015). The band structure comprising high Chern number (−4 to 3) bandgaps is verified by calculating the multimode one-way edge state’s bulk transmission, edge transmission, and edge-mode dispersion relations. The dispersion relations of the multimode one-way edge states are achieved through Fourier transform experimentally, which show excellent agreement with theory predictions, as shown in Figure 3E. The large Chern number was also realized in structures with mirror symmetry and TRS both broken (He and Chan, 2015). The number of equivalent mirror planes in PhC potentially determines how many pairs of Dirac points can be created; breaking TRS by MO effect straightforward combines these with Chern number, which indicates that the multihelical edge state can be created. In the work of Yang et al. mentioned in section Realization in Periodic Optical Systems (Yang et al., 2017a), they also give an example to engineer multimode TESs by tuning structure’s parameters. The multimode edge state was also realized in the amorphous system (Yang et al., 2019). Compared with their single-mode counterparts, these one-way multimode waveguides have a much larger density of states and give a much higher input coupling efficiency, which inspires the functional device research of topological photonic materials.

Weyl Point in 3D

A Dirac point in 3D is a linear point-degeneracy between four bands, consisting of two Weyl points with opposite Chern numbers sitting on top of each other in frequency (Young et al., 2012). Weyl point is a topological band degeneracy and is linearly dispersed in all three directions, which is governed by the Weyl Hamiltonian (Wan et al., 2011):

$H\left(\mathit{k}\right)=k_i{\nu }_{ij}{\sigma }_j\left(i,j=1, 2, 3\right)$

where k is wave vector, v is velocity, and σ is Pauli matrix. Weyl point, the source of Berry flux, is the monopole of Berry flux: a closed surface in a 3D ΒΖ containing a single Weyl point has a nonzero Chern number of ±1 (Lu et al., 2016). Gapless surface states corresponding to Weyl points are topologically protected. Weyl Hamiltonian have occurred in condensed-matter physics (Wan et al., 2011; Xu et al., 2015), acoustics (Xiao et al., 2015; Yang and Zhang, 2016), and photonics (Lu et al., 2013; Lu et al., 2015). As for the MO effect in photonics, a pair of Weyl points is realized theoretically in PhCs with a tetrahedral lattice at microwave regime (Yang et al., 2017c). The existence of topological charge is verified by calculating the berry phase and the topologically protected Fermi arc-like surface states, which are shown in Figures 3F,G, respectively. Research on Weyl points inspires researchers to explore more topological states in gyrotropic material structures.

Applications

Recently, there has been an increase in attempts to implement topologically protected edge states because of the application potential of backscattering immune against perturbations, robust transmission and field localization (Lu et al., 2014; Lu et al., 2016; Shi et al., 2016). These properties play an important role on light transmission and control, which have wide applications, such as one-way fiber, isolator, and slow light device.

One-Way Optical Waveguide

Topological one-way edge states are immune to defects and disorders, so they bring hope to realize scattering-free and low-loss one-way waveguide. A tunable one-way cross-waveguide splitter controlled by altering structural parameters of gyromagnetic PhC is designed based on the property of chiral edge states (He et al., 2010). Moreover, based on the side-cavity coupling property with nonreciprocal gyromagnetic PhC, a one-way channel-drop filter that the robust one-way wave can be downloaded by another one-way waveguide is realized, which opens up a window to explore the one-way edge state for controlling EM wave propagation (Fu et al., 2011).

Based on the one-way edge states, one-way fibers are designed in a 3D magnetic Weyl PhC by Lu et al., which is realized at microwave regime. The comparison of regular fiber and one-way fiber is shown in Figure 4A, the latter shows strong resistance to backscattering (Lu et al., 2018b). Their start point is a crystal in the double gyroid made of gyroelectric material with a pair of Weyl points. Then the crystal with a nonzero first Chern number by annihilating the Weyl points is obtained through supercell modulation. These single-polarization single-mode and multimode one-way fibers, having nearly identical group and phase velocities, are topological-protected by the second Chern number in the 4D parameters space of the winding angle of the helix and the 3D wave vectors. This work solves the problems in traditional optical fiber, such as the intense light scattering loss caused by material inhomogeneity, nonlinear effect and unevenness of end face.

FIGURE 4

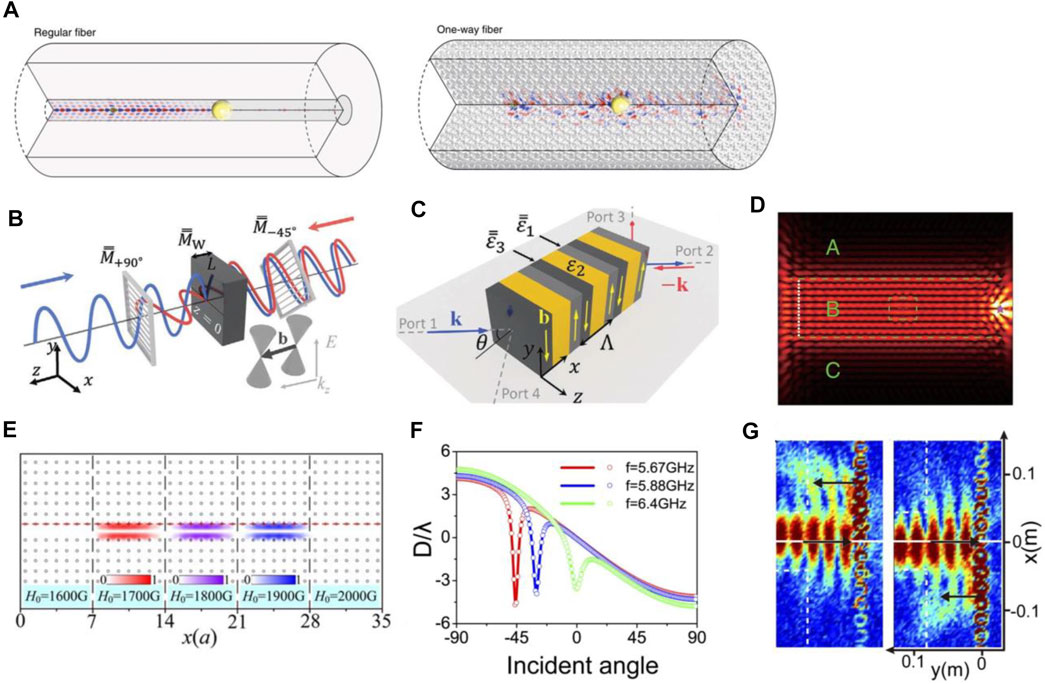
FIGURE 4. (A) Comparison of a regular fiber and a one-way fiber (Lu et al., 2018b). (B) The Faraday isolator and (C) more compact Voigt isolator (Asadchy et al., 2020). (D) Simulated electric field intensity distributions of the one-way large transport at 11.9 GHz in the heterostructures with a void defect (Wang et al., 2021). (E) Electric field profiles at the frequencies of 4.292, 4.346, and 4.393 GHz with different magnetic field strengths H₀ (Chen et al., 2019b). (F) The relationship between GH shift, the incident angle and bias magnetic field (Ma et al., 2020). © The Optical Society. (G) Experimental demonstration of nonreciprocal property of GH shift even at normal incidence (Ma et al., 2020). © The Optical Society.

Isolators are nonreciprocal devices that allow light propagation in one direction but block it in the opposite direction. Based on Weyl semimetals, Asadchy et al. proposed two designs of isolators at mid-infrared wavelengths with Faraday and Voigt geometries (Asadchy et al., 2020). These bulk topological materials can simultaneously exhibit broadband and giant MO effect without an external magnetic bias. The two designs provide good performance with considerable isolation and slight insertion loss. The geometry of the designed Faraday isolator and the more compact Voigt isolator are shown in Figures 4B,C, respectively. The above two examples of compact optical isolators demonstrate that magnetic Weyl semimetals provide an unprecedented material response that will open new avenues for designing nonreciprocal components.

In 2021, large-area one-way transport, as shown in Figure 4D, is achieved both theoretically and experimentally by using heterostructures consisting of a domain of an ordinary PhC sandwiched between two domains of gyromagnetic PhCs (Wang et al., 2021). A and C are topological PhCs, whose TRS is broken by applied two opposite biased magnetic fields; B is a trivial PhC sandwiched by A and C, which exhibits one-way transmission robust to imperfections and defects. Such one-way waveguide states can be used to abruptly narrow the beam width of an extended state to concentrate energy. It shows robustness against defects and imperfections and is immune to the Anderson-type localization when large randomness is introduced.

Slow Light and Rainbow Effect

The slow light effect can reduce the speed of light to an extremely low value and play a vital role in the applications of photonic devices, such as optical delay line or buffer, signal processing, optical switch, and light-matter interaction (Baba, 2008; Krauss, 2008; Bortolozzo et al., 2010; Figotin and Vitebskiy, 2011; Colman et al., 2012; Zhang et al., 2021). Gyromagnetic PhC with simple structure, fast response, high spatial resolution, etc. is considered a considerable method to achieve slow light. The tunable flat band slow light is proposed based on line-defect PhC waveguide infiltrated with magnetic fluids (Pu et al., 2013; Guillan-Lorenzo and Diaz-Otero, 2016). Topology provides a new and attractive platform to manipulate photonic states due to the unique properties with backscattering elimination and structural disorder immunity. Thus, a one-way slow-light waveguide made of gyromagnetic PhC and a metal cladding in microwave regime is realized (Yang et al., 2013). Moreover, in 2019, Chen et al. realized a unique slow-light state by the waveguide composed of two MO PhCs, owing to the strong interaction of the two counterpropagating topological one-way edge states (Chen et al., 2019a).

One of the splendid conclusions of the slow light effect is rainbow trapping. This effect means the states with different frequencies can be trapped at different positions and inspire wide attention. Compared with classical systems, such as nanowires (Hussein et al., 2016), metamaterials (Gan et al., 2009; Hu et al., 2013), plasmonic chirped waveguide (Chen et al., 2010), magnetic surface plasmons (Xu et al., 2021), and PhCs (Romero-García et al., 2013; Hayran et al., 2017; Tian and Yu, 2017), topological PhCs have great advantages to achieve rainbow effect with robustness. In 2019, a switchable slow light rainbow trapping was designed using a special gradient magnetic field in a line defect waveguide channel (Chen et al., 2019b). The EM waves with different frequency components are trapped in different regions under the gradient magnetic field, as shown in Figure 4E. Topological rainbow provides a new scheme to achieve robust nanophotonic wavelength routers, multichannel optical amplifiers, optical storages, and optical buffers. In 2021, Zhuang et al. considered a double-channel square MO PhC waveguide formed by introducing a two-stranded Al₂O₃ PhC as the coupling layer (Zhuang et al., 2021). One-way slow-light with zero group velocity dispersion and near-zero group velocity can be obtained with an appropriate radius of Al₂O₃ rods. The simulation results show that the slow-light modes are extremely strong against perfect electric conductor defects and the one-way transmittance is close to 100%. These results hold promise for the design of various topological devices.

Nonreciprocal GH Shift

The GH shift is that the reflected light beam will have a lateral shift along the interface from the ideal position predicted by the geometric optics when a light beam impinges on the interface of two media with different refractive indices (Goos and Hänchen, 1947). The phenomenon was first experimentally observed by Goos and Hänchen in total internal reflection (Goos and Hänchen, 1947), which is further developed again because of the finding of giant and negative GH shifts (Shadrivov et al., 2003; Wang et al., 2005). In 2019, magnetic plasmonic gradient metasurfaces have been designed, which can be operated as a platform to implement nonreciprocal GH shift (Wu et al., 2019). The GH shift is controlled intrinsically by tuning the rotational gradient, or extrinsically by tuning the bias magnetic field for specified magnetic gradient metasurfaces. The demonstration of the nonreciprocal GH effect in this work can serve as a guide for experimental verification and potential applications. In 2020, the GH effect was explored using MO PhC made of YIG ferrite rings in square lattice (Ma et al., 2020). A significant nonreciprocal negative GH shift for total reflection waves is realized through the excitation of TESs. The GH shifts depend on the incident angle and bias magnetic field, as shown in Figure 4F, and keep nonreciprocity even at normal incidence, which is verified experimentally, as shown in Figure 4G. The enhanced nonreciprocal negative GH shifts provide a new way to control the flow of light, which can be used in designing new devices and integrated optics.

Discussion and Perspective

In the past decades, topological photonics have developed surprisingly rapidly. The topological photonic states with the MO effect are essential for exploring abundant physical laws and unique physical effects. In addition to utilizing the MO effect, other configurations can achieve photonic topological states, such as the systems breaking IS (Chen et al., 2018; Tang et al., 2020; Shi et al., 2021) or the systems breaking TRS with an effective magnetic field (Fang et al., 2016). Topological protected edge states ensure the absence of backscattering of waves by defects and disorders, which suggest abundant applications, such as one-way fiber, on-chip isolation, and slow light effect. Understanding and mastering the state control mechanism can provide a rich experience and reference for the further study of other topological optical systems and provide helpful guidance for designing various topological optical devices.

So far, there are still some challenges waiting to be solved, such as the realization of TES in the visible range, more compact devices with less loss. Furthermore, in recent years, topological photonics has extended to nonlinearity (Lan et al., 2020; Xia et al., 2020), non-Hermitian (Martinez Alvarez et al., 2018; Pan et al., 2018; Höckendorf et al., 2019; Liu et al., 2020; Xia et al., 2021), and synthetic dimension scales (Lin et al., 2016; Lu et al., 2021; Ni and Alù, 2021); it is worth trying to implement them based on MO effects.

Author Contributions

CL conceived the idea to write this review. XW wrote the most of the manuscript, and WZ and HZ wrote part of it. CL and SE revised the manuscript. CL supervised the project. All authors participated in discussions and contributed to this work.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

CL acknowledges the support from the National Natural Science Foundation of China (Nos 11654003 and 91850117).

References

Amanollahi, M., and Zamani, M. (2018). Wide-Angle Giant Transverse Magneto-Optical Kerr Effect in a Gyromagnetic Superlens. Opt. Lett. 43 (19), 4851. doi:10.1364/OL.43.004851

PubMed Abstract | CrossRef Full Text | Google Scholar

Ao, X., Lin, Z., and Chan, C. T. (2009). One-Way Edge Mode in a Magneto-Optical Honeycomb Photonic crystal. Phys. Rev. B 80 (3), 33105. doi:10.1103/PhysRevB.80.033105

CrossRef Full Text | Google Scholar

Asadchy, V. S., Guo, C., Zhao, B., and Fan, S. (2020). Sub‐Wavelength Passive Optical Isolators Using Photonic Structures Based on Weyl Semimetals. Adv. Opt. Mater. 8 (16), 2000100. doi:10.1002/adom.202000100

CrossRef Full Text | Google Scholar

Baba, T. (2008). Slow Light in Photonic Crystals. Nat. Photon. 2 (8), 465–473. doi:10.1038/nphoton.2008.146

CrossRef Full Text | Google Scholar

Ballato, J., Dimaio, J., James, A., and Gulliver, E. (1999). Photonic Band Engineering through Tailored Microstructural Order. Appl. Phys. Lett. 75 (11), 1497–1499. doi:10.1063/1.124734

CrossRef Full Text | Google Scholar

Barnes, W. L., Dereux, A., and Ebbesen, T. W. (2003). Surface Plasmon Subwavelength Optics. Nature 424 (6950), 824–830. doi:10.1038/nature01937

PubMed Abstract | CrossRef Full Text | Google Scholar

Berthier, L., and Biroli, G. (2011). Theoretical Perspective on the Glass Transition and Amorphous Materials. Rev. Mod. Phys. 83 (2), 587–645. doi:10.1103/RevModPhys.83.587

CrossRef Full Text | Google Scholar

Bhowmick, D., and Sengupta, P. (2020). Antichiral Edge States in Heisenberg Ferromagnet on a Honeycomb Lattice. Phys. Rev. B 101 (19), 195133. doi:10.1103/PhysRevB.101.195133

CrossRef Full Text | Google Scholar

Borovkova, O., Kalish, A., and Belotelov, V. (2016). Transverse Magneto-Optical Kerr Effect in Active Magneto-Plasmonic Structures. Opt. Lett. 41 (19), 4593. doi:10.1364/OL.41.004593

PubMed Abstract | CrossRef Full Text | Google Scholar

Bortolozzo, U., Residori, S., and Huignard, J.-P. P. (2010). Slow and Fast Light: Basic Concepts and Recent Advancements Based on Nonlinear Wave-Mixing Processes. Laser Photon. Rev. 4 (4), 483–498. doi:10.1002/lpor.200910022

CrossRef Full Text | Google Scholar

Chen, Z.-G., and Wu, Y. (2016). Tunable Topological Phononic Crystals. Phys. Rev. Appl. 5 (5), 54021. doi:10.1103/PhysRevApplied.5.054021

CrossRef Full Text | Google Scholar

Chen, L., Wang, G. P., Gan, Q., and Bartoli, F. J. (2010). Rainbow Trapping and Releasing by Chirped Plasmonic Waveguides at Visible Frequencies. Appl. Phys. Lett. 97 (15), 153115. doi:10.1063/1.3502487

CrossRef Full Text | Google Scholar

Chen, Z.-G., Mei, J., Sun, X.-C., Zhang, X., Zhao, J., and Wu, Y. (2017). Multiple Topological Phase Transitions in a Gyromagnetic Photonic crystal. Phys. Rev. A. 95 (4), 43827. doi:10.1103/PhysRevA.95.043827

CrossRef Full Text | Google Scholar

Chen, X.-D., Deng, W.-M., Lu, J.-C., and Dong, J.-W. (2018). Valley-Controlled Propagation of Pseudospin States in Bulk Metacrystal Waveguides. Phys. Rev. B 97 (18), 184201. doi:10.1103/PhysRevB.97.184201

CrossRef Full Text | Google Scholar

Chen, J., Liang, W., and Li, Z.-Y. (2019). Strong Coupling of Topological Edge States Enabling Group-Dispersionless Slow Light in Magneto-Optical Photonic Crystals. Phys. Rev. B 99 (1), 14103. doi:10.1103/PhysRevB.99.014103

CrossRef Full Text | Google Scholar

Chen, J., Liang, W., and Li, Z.-Y. (2019). Switchable Slow Light Rainbow Trapping and Releasing in Strongly Coupling Topological Photonic Systems. Photon. Res. 7 (9), 1075. doi:10.1364/PRJ.7.001075

CrossRef Full Text | Google Scholar

Chen, J., Liang, W., and Li, Z.-Y. (2020). Antichiral One-Way Edge States in a Gyromagnetic Photonic crystal. Phys. Rev. B 101 (21), 214102. doi:10.1103/PhysRevB.101.214102

CrossRef Full Text | Google Scholar

Chern, R.-L. (2008). Magnetic and Surface Plasmon Resonances for Periodic Lattices of Plasmonic Split-Ring Resonators. Phys. Rev. B 78 (8), 85116. doi:10.1103/PhysRevB.78.085116

CrossRef Full Text | Google Scholar

Colman, P., Combrié, S., Lehoucq, G., de Rossi, A., and Trillo, S. (2012). Blue Self-Frequency Shift of Slow Solitons and Radiation Locking in a Line-Defect Waveguide. Phys. Rev. Lett. 109 (9), 93901. doi:10.1103/PhysRevLett.109.093901

CrossRef Full Text | Google Scholar

Colomés, E., and Franz, M. (2018). Antichiral Edge States in a Modified Haldane Nanoribbon. Phys. Rev. Lett. 120 (8), 86603. doi:10.1103/PhysRevLett.120.086603

CrossRef Full Text | Google Scholar

Dannegger, T., Berritta, M., Carva, K., Selzer, S., Ritzmann, U., Oppeneer, P. M., et al. (2021). Ultrafast Coherent All-Optical Switching of an Antiferromagnet with the Inverse Faraday Effect. Phys. Rev. B 104 (6), L60413. doi:10.1103/PhysRevB.104.L060413

CrossRef Full Text | Google Scholar

Diaz-Valencia, B. F. (2021). Extraordinary Transverse Magneto-Optical Kerr Effect through Excitation of Bulk Plasmon Polariton Modes in Type II Magneto-Optical Hyperbolic Metamaterials. Opt. Lett. 46 (19), 4863. doi:10.1364/OL.437519

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Z.-x., Huang, Z.-N., Chen, Y., Mou, C., Lu, Y.-Q., and Xu, F. (2020). All-fiber Ultrafast Laser Generating Gigahertz-Rate Pulses Based on a Hybrid Plasmonic Microfiber Resonator. Adv. Photon. 2 (2), 26002. doi:10.1117/1.AP.2.2.026002

CrossRef Full Text | Google Scholar

Fang, Y. N., Shen, Y., Ai, Q., and Sun, C. P. (2016). Negative Refraction in Möbius Molecules. Phys. Rev. A. 94 (4), 43805. doi:10.1103/PhysRevA.94.043805

CrossRef Full Text | Google Scholar

Figotin, A., and Vitebskiy, I. (2011). Slow Wave Phenomena in Photonic Crystals. Laser Photon. Rev. 5 (2), 201–213. doi:10.1002/lpor.200900049

CrossRef Full Text | Google Scholar

Fu, J.-X., Liu, R.-J., and Li, Z.-Y. (2010). Robust One-Way Modes in Gyromagnetic Photonic crystal Waveguides with Different Interfaces. Appl. Phys. Lett. 97 (4), 041112. doi:10.1063/1.3470873

CrossRef Full Text | Google Scholar

Fu, J.-X., Lian, J., Liu, R.-J., Gan, L., and Li, Z.-Y. (2011). Unidirectional Channel-Drop Filter by One-Way Gyromagnetic Photonic crystal Waveguides. Appl. Phys. Lett. 98 (21), 211104. doi:10.1063/1.3593027

CrossRef Full Text | Google Scholar

Gan, Q., Ding, Y. J., and Bartoli, F. J. (2009). "Rainbow" Trapping and Releasing at Telecommunication Wavelengths. Phys. Rev. Lett. 102 (5), 56801. doi:10.1103/PhysRevLett.102.056801

CrossRef Full Text | Google Scholar

García, P. D., Sapienza, R., Blanco, Á., and López, C. (2007). Photonic Glass: A Novel Random Material for Light. Adv. Mater. 19 (18), 2597–2602. doi:10.1002/adma.200602426

CrossRef Full Text | Google Scholar

Goos, F., and Hänchen, H. (1947). Ein neuer und fundamentaler Versuch zur Total reflexion. Ann. Phys. 436 (7-8), 333–346. doi:10.1002/andp.19474360704

CrossRef Full Text | Google Scholar

Guillan-Lorenzo, O., and Diaz-Otero, F. J. (2016). Slow Light in Tunable Low Dispersion Wide Bandwidth Photonic Crystal Waveguides Infiltrated with Magnetic Fluids. Opt. Commun. 359, 49–52. doi:10.1016/j.optcom.2015.09.057

CrossRef Full Text | Google Scholar

Haldane, F. D. M., and Raghu, S. (2008). Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 100 (1), 13904. doi:10.1103/PhysRevLett.100.013904

CrossRef Full Text | Google Scholar

Hatsugai, Y. (1993). Chern Number and Edge States in the Integer Quantum Hall Effect. Phys. Rev. Lett. 71 (22), 3697–3700. doi:10.1103/PhysRevLett.71.3697

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayran, Z., Kurt, H., and Staliunas, K. (2017). Rainbow Trapping in a Chirped Three-Dimensional Photonic crystal. Sci. Rep. 7, 3046. doi:10.1038/s41598-017-03454-w

PubMed Abstract | CrossRef Full Text | Google Scholar

He, W.-Y., and Chan, C. T. (2015). The Emergence of Dirac Points in Photonic Crystals with Mirror Symmetry. Sci. Rep. 5, 8186. doi:10.1038/srep08186

PubMed Abstract | CrossRef Full Text | Google Scholar

He, C., Chen, X.-L., Lu, M.-H., Li, X.-F., Wan, W.-W., Qian, X.-S., et al. (2010). Tunable One-Way Cross-Waveguide Splitter Based on Gyromagnetic Photonic crystal. Appl. Phys. Lett. 96 (11), 111111. doi:10.1063/1.3358386

CrossRef Full Text | Google Scholar

Höckendorf, B., Alvermann, A., and Fehske, H. (2019). Non-Hermitian Boundary State Engineering in Anomalous Floquet Topological Insulators. Phys. Rev. Lett. 123 (19), 190403. doi:10.1103/PhysRevLett.123.190403

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, B., Wang, Q. J., and Zhang, Y. (2012). Broadly Tunable One-Way Terahertz Plasmonic Waveguide Based on Nonreciprocal Surface Magneto Plasmons. Opt. Lett. 37 (11), 1895. doi:10.1364/OL.37.001895

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, H., Ji, D., Zeng, X., Liu, K., and Gan, Q. (2013). Rainbow Trapping in Hyperbolic Metamaterial Waveguide. Sci. Rep. 3, 1249. doi:10.1038/srep01249

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussein, M., Hameed, M. F. O., Areed, N. F. F., Yahia, A., and Obayya, S. S. A. (2016). Funnel-Shaped Silicon Nanowire for Highly Efficient Light Trapping. Opt. Lett. 41 (5), 1010. doi:10.1364/OL.41.001010

PubMed Abstract | CrossRef Full Text | Google Scholar

Kazemi, A. H., Mokhtari, A., and Zamani, M. (2021). The Effect of Using Coated Graphene in Enhancing Faraday Rotation in Gyroelectric and Gyromagnetic Materials. J. Magnetism Magn. Mater. 537, 168219. doi:10.1016/j.jmmm.2021.168219

CrossRef Full Text | Google Scholar

Khanikaev, A. B., Hossein Mousavi, S., Tse, W.-K., Kargarian, M., MacDonald, A. H., and Shvets, G. (2012). Photonic Topological Insulators. Nat. Mater. 12, 233–239. doi:10.1038/NMAT3520

PubMed Abstract | CrossRef Full Text | Google Scholar

Klitzing, K. V., Dorda, G., and Pepper, M. (1980). New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 45 (6), 494–497. doi:10.1103/PhysRevLett.45.494

CrossRef Full Text | Google Scholar

Krauss, T. F. (2008). Why Do We Need Slow Light? Nat. Photon. 2 (8), 448–450. doi:10.1038/nphoton.2008.139

CrossRef Full Text | Google Scholar

Kumar, R., and Chaubey, P. N. (2012). Design of Coplanar Waveguide-Feed Pentagonal-Cut Ultra-Wide Bandwidth Fractal Antenna and its Backscattering. IET Microw. Antenna. P. 6 (13), 1407–1414. doi:10.1049/iet-map.2011.0188

CrossRef Full Text | Google Scholar

Lai, H.-S., Chen, H., He, B., He, C., and Chen, Y.-F. (2020). Symmetrical and Anti-symmetrical Topological Edge States Based on Two-Dimensional Magneto-Optical Photonic Crystals. AIP Adv. 10 (6), 065029. doi:10.1063/5.0011727

CrossRef Full Text | Google Scholar

Lan, Z., You, J. W., and Panoiu, N. C. (2020). Nonlinear One-Way Edge-Mode Interactions for Frequency Mixing in Topological Photonic Crystals. Phys. Rev. B 101 (15), 155422. doi:10.1103/PhysRevB.101.155422

CrossRef Full Text | Google Scholar

Li, Z., Ma, H., Wu, R.-x., and Wu, G.-z. (2020). Tuning the Chiral Edge States and Unidirectional Transmission by Surface Morphology of Gyromagnetic Photonic crystal. J. Opt. 22 (9), 095101. doi:10.1088/2040-8986/aba3b4

CrossRef Full Text | Google Scholar

Li, W., Lu, X., Wu, J., and Srivastava, A. (2021). Optical Control of the valley Zeeman Effect through many-exciton Interactions. Nat. Nanotechnol. 16, 148–152. doi:10.1038/s41565-020-00804-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lian, J., Fu, J.-X., Gan, L., and Li, Z.-Y. (2012). Robust and Disorder-Immune Magnetically Tunable One-Way Waveguides in a Gyromagnetic Photonic crystal. Phys. Rev. B 85 (12), 125108. doi:10.1103/PhysRevB.85.125108

CrossRef Full Text | Google Scholar

Lin, Q., Xiao, M., Yuan, L., and Fan, S. (2016). Photonic Weyl point in a Two-Dimensional Resonator Lattice with a Synthetic Frequency Dimension. Nat. Commun. 7, 13731. doi:10.1038/ncomms13731

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Lu, W., Lin, Z., and Chui, S. T. (2010). Magnetically Controllable Unidirectional Electromagnetic Waveguiding Devices Designed with Metamaterials. Appl. Phys. Lett. 97 (20), 201113. doi:10.1063/1.3520141

CrossRef Full Text | Google Scholar

Liu, K., Shen, L., and He, S. (2012). One-Way Edge Mode in a Gyromagnetic Photonic Crystal Slab. Opt. Lett. 37 (19), 4110. doi:10.1364/OL.37.004110

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, T., Guo, H., Pu, Y., and Longhi, S. (2020). Generalized Aubry-André Self-Duality and Mobility Edges in Non-Hermitian Quasiperiodic Lattices. Phys. Rev. B 102 (2), 24205. doi:10.1103/PhysRevB.102.024205

CrossRef Full Text | Google Scholar

Lu, L., Fu, L., Joannopoulos, J. D., and Soljačić, M. (2013). Weyl Points and Line Nodes in Gyroid Photonic Crystals. Nat. Photon. 7 (4), 294–299. doi:10.1038/nphoton.2013.42

CrossRef Full Text | Google Scholar

Lu, L., Joannopoulos, J. D., and Soljačić, M. (2014). Topological Photonics. Nat. Photon. 8 (11), 821–829. doi:10.1038/NPHOTON.2014.248

CrossRef Full Text | Google Scholar

Lu, L., Wang, Z., Ye, D., Ran, L., Fu, L., Joannopoulos, J. D., et al. (2015). Experimental Observation of Weyl Points. Science 349 (6248), 622–624. doi:10.1126/science.aaa9273

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, L., Fang, C., Fu, L., Johnson, S. G., Joannopoulos, J. D., and Soljačić, M. (2016). Symmetry-Protected Topological Photonic Crystal in Three Dimensions. Nat. Phys. 12 (4), 337–340. doi:10.1038/nphys3611

CrossRef Full Text | Google Scholar

Lu, J.-C., Chen, X.-D., Deng, W.-M., Chen, M., and Dong, J.-W. (2018). One-Way Propagation of Bulk States and Robust Edge States in Photonic Crystals with Broken Inversion and Time-Reversal Symmetries. J. Opt. 20 (7), 075103. doi:10.1088/2040-8986/aac3a1

CrossRef Full Text | Google Scholar

Lu, L., Gao, H., and Wang, Z. (2018). Topological One-Way Fiber of Second Chern Number. Nat. Commun. 9, 5384. doi:10.1038/s41467-018-07817-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Wang, C., Xiao, M., Zhang, Z. Q., and Chan, C. T. (2021). Topological Rainbow Concentrator Based on Synthetic Dimension. Phys. Rev. Lett. 126 (11), 113902. doi:10.1103/PhysRevLett.126.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, X., and Ishihara, T. (2004). Surface Plasmon Resonant Interference Nanolithography Technique. Appl. Phys. Lett. 84 (23), 4780–4782. doi:10.1063/1.1760221

CrossRef Full Text | Google Scholar

Ma, H., He, Z., and Hotate, K. (2011). Reduction of Backscattering Induced Noise by Carrier Suppression in Waveguide-Type Optical Ring Resonator Gyro. J. Lightwave Technol. 29 (1), 85–90. doi:10.1109/JLT.2010.2092751

CrossRef Full Text | Google Scholar

Ma, H., Ju, C., Xi, X., and Wu, R.-X. (2020). Nonreciprocal Goos-Hänchen Shift by Topological Edge States of a Magnetic Photonic crystal. Opt. Express 28 (14), 19916. doi:10.1364/OE.394286

PubMed Abstract | CrossRef Full Text | Google Scholar

Majedi, A. H. (2021). Microwave-Induced Inverse Faraday Effect in Superconductors. Phys. Rev. Lett. 127 (8), 87001. doi:10.1103/PhysRevLett.127.087001

CrossRef Full Text | Google Scholar

Mandal, S., Ge, R., and Liew, T. C. H. (2019). Antichiral Edge States in an Exciton Polariton Strip. Phys. Rev. B 99 (11), 115423. doi:10.1103/PhysRevB.99.115423

CrossRef Full Text | Google Scholar

Mansha, S., and Chong, Y. D. (2017). Robust Edge States in Amorphous Gyromagnetic Photonic Lattices. Phys. Rev. B 96 (12), 121405. doi:10.1103/PhysRevB.96.121405

CrossRef Full Text | Google Scholar

Mansha, S., Yongquan, Z., Wang, Q. J., and Chong, Y. D. (2016). Optimization of TM Modes for Amorphous Slab Lasers. Opt. Express 24 (5), 4890. doi:10.1364/OE.24.004890

PubMed Abstract | CrossRef Full Text | Google Scholar

Márquez, A., and Esquivel-Sirvent, R. (2020). Terahertz Response of Plasmonic Nanoparticles: Plasmonic Zeeman Effect. Opt. Express 28 (26), 39005. doi:10.1364/OE.412585

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinez Alvarez, V. M., Barrios Vargas, J. E., Berdakin, M., and Foa Torres, L. E. F. (2018). Topological States of Non-Hermitian Systems. Eur. Phys. J. Spec. Top. 227 (12), 1295–1308. doi:10.1140/epjst/e2018-800091-5

CrossRef Full Text | Google Scholar

Nakada, K., Fujita, M., Dresselhaus, G., and Dresselhaus, M. S. (1996). Edge State in Graphene Ribbons: Nanometer Size Effect and Edge Shape Dependence. Phys. Rev. B 54 (24), 17954–17961. doi:10.1103/PhysRevB.54.17954

PubMed Abstract | CrossRef Full Text | Google Scholar

Ni, X., and Alù, A. (2021). Higher-Order Topolectrical Semimetal Realized via Synthetic Gauge fields. APL Photonics 6, 050802. doi:10.1063/5.0041458

CrossRef Full Text | Google Scholar

Ochiai, T., and Onoda, M. (2009). Photonic Analog of Graphene Model and its Extension: Dirac Cone, Symmetry, and Edge States. Phys. Rev. B 80 (15), 155103. doi:10.1103/PhysRevB.80.155103

CrossRef Full Text | Google Scholar

Ochiai, T. (2010). Topological Properties of Bulk and Edge States in Honeycomb Lattice Photonic Crystals: the Case of TE Polarization. J. Phys. Condens. Matter 22 (22), 225502. doi:10.1088/0953-8984/22/22/225502

CrossRef Full Text | Google Scholar

Ozawa, T., Price, H. M., Amo, A., Goldman, N., Hafezi, M., Lu, L., et al. (2019). Topological Photonics. Rev. Mod. Phys. 91 (1), 15006. doi:10.1103/RevModPhys.91.015006

CrossRef Full Text | Google Scholar

Pan, M., Zhao, H., Miao, P., Longhi, S., and Feng, L. (2018). Photonic Zero Mode in a Non-Hermitian Photonic Lattice. Nat. Commun. 9, 1308. doi:10.1038/s41467-018-03822-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Papusoi, C., Le, T., Admana, R., Mani, P., and Desai, M. (2021). Evaluation of the Exchange Coupling between Adjacent Magnetic Layers Using Time-Resolved Magneto-Optic Kerr Effect (TRMOKE). J. Phys. D: Appl. Phys. 54, 365004. doi:10.1088/1361-6463/ac0a08

CrossRef Full Text | Google Scholar

Poo, Y., Wu, R.-X., Lin, Z., Yang, Y., and Chan, C. T. (2011). Experimental Realization of Self-Guiding Unidirectional Electromagnetic Edge States. Phys. Rev. Lett. 106 (9), 93903. doi:10.1103/PhysRevLett.106.093903

CrossRef Full Text | Google Scholar

Poo, Y., Wu, R.-X., Liu, S., Yang, Y., Lin, Z., and Chui, S. T. (2012). Experimental Demonstration of Surface Morphology Independent Electromagnetic Chiral Edge States Originated from Magnetic Plasmon Resonance. Appl. Phys. Lett. 101 (8), 081912. doi:10.1063/1.4747810

CrossRef Full Text | Google Scholar

Pu, S., Wang, H., Wang, N., and Zeng, X. (2013). Tunable Flat Band Slow Light in Reconfigurable Photonic Crystal Waveguides Based on Magnetic Fluids. Opt. Commun. 311, 16–19. doi:10.1016/j.optcom.2013.08.051

CrossRef Full Text | Google Scholar

Raghu, S., and Haldane, F. D. M. (2008). Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys. Rev. A 78 (3), 33834. doi:10.1103/PhysRevA.78.033834

CrossRef Full Text | Google Scholar

Romero-García, V., Picó, R., Cebrecos, A., Sánchez-Morcillo, V. J., and Staliunas, K. (2013). Enhancement of Sound in Chirped Sonic Crystals. Appl. Phys. Lett. 102 (9), 091906. doi:10.1063/1.4793575

CrossRef Full Text | Google Scholar

Shadrivov, I. V., Zharov, A. A., and Kivshar, Y. S. (2003). Giant Goos-Hänchen Effect at the Reflection from Left-Handed Metamaterials. Appl. Phys. Lett. 83 (13), 2713–2715. doi:10.1063/1.1615678

CrossRef Full Text | Google Scholar

Shen, J., Liu, S., Zhang, H., Chui, S. T., Lin, Z., Fan, X., et al. (2012). Robust and Tunable One-Way Magnetic Surface Plasmon Waveguide: An Experimental Demonstration. Plasmonics 7 (2), 287–291. doi:10.1007/s11468-011-9305-5

CrossRef Full Text | Google Scholar

Shi, X., Xue, C., Jiang, H., and Chen, H. (2016). Topological Description for Gaps of One-Dimensional Symmetric All-Dielectric Photonic Crystals. Opt. Express 24 (16), 18580. doi:10.1364/OE.24.018580

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, F.-L., Cao, Y., Chen, X.-D., Liu, J.-W., Chen, W.-J., Chen, M., et al. (2021). Distortionless Pulse Transmission in valley Photonic crystal Slab Waveguide. Phys. Rev. Appl. 15 (2), 24002. doi:10.1103/PhysRevApplied.15.024002

CrossRef Full Text | Google Scholar

Skirlo, S. A., Lu, L., and Soljačić, M. (2014). Multimode One-Way Waveguides of Large Chern Numbers. Phys. Rev. Lett. 113 (11), 113904. doi:10.1103/PhysRevLett.113.113904

PubMed Abstract | CrossRef Full Text | Google Scholar

Skirlo, S. A., Lu, L., Igarashi, Y., Yan, Q., Joannopoulos, J., and Soljačić, M. (2015). Experimental Observation of Large Chern Numbers in Photonic Crystals. Phys. Rev. Lett. 115 (25), 253901. doi:10.1103/PhysRevLett.115.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, G.-J., Chen, X.-D., Shi, F.-L., Liu, J.-W., Chen, M., and Dong, J.-W. (2020). Frequency Range Dependent Topological Phases and Photonic Detouring in valley Photonic Crystals. Phys. Rev. B 102 (17), 174202. doi:10.1103/PhysRevB.102.174202

CrossRef Full Text | Google Scholar

Tian, Z., and Yu, L. (2017). Rainbow Trapping of Ultrasonic Guided Waves in Chirped Phononic crystal Plates. Sci. Rep. 7, 40004. doi:10.1038/srep40004

PubMed Abstract | CrossRef Full Text | Google Scholar

von Klitzing, K. (1986). The Quantized Hall Effect. Rev. Mod. Phys. 58 (3), 519–531. doi:10.1103/RevModPhys.58.519

CrossRef Full Text | Google Scholar

Wan, X., Turner, A. M., Vishwanath, A., and Savrasov, S. Y. (2011). Topological Semimetal and Fermi-Arc Surface States in the Electronic Structure of Pyrochlore Iridates. Phys. Rev. B 83 (20), 205101. doi:10.1103/PhysRevB.83.205101

CrossRef Full Text | Google Scholar

Wang, L.-G., Chen, H., and Zhu, S.-Y. (2005). Large Negative Goos-Hänchen Shift from a Weakly Absorbing Dielectric Slab. Opt. Lett. 30 (21), 2936. doi:10.1364/ol.30.002936

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Chong, Y. D., Joannopoulos, J. D., and Soljačić, M. (2008). Reflection-free One-Way Edge Modes in a Gyromagnetic Photonic crystal. Phys. Rev. Lett. 100 (1), 13905. doi:10.1103/PhysRevLett.100.013905

CrossRef Full Text | Google Scholar

Wang, Z., Chong, Y., Joannopoulos, J. D., and Soljačić, M. (2009). Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature 461 (7265), 772–775. doi:10.1038/nature08293

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X. Z., Yu, G. X., Fu, J. J., Dong, J. Y., and Luo, M. (2018). The Nonreciprocal Properties of Lateral Shift in the Gyrotropic Medium Slab. Optik 157, 63–67. doi:10.1016/j.ijleo.2017.09.070

CrossRef Full Text | Google Scholar

Wang, Y.-F., Wang, Y.-Z., Wu, B., Chen, W., and Wang, Y.-S. (2020). Tunable and Active Phononic Crystals and Metamaterials. Appl. Mech. Rev. 72 (4), 40801. doi:10.1115/1.4046222

CrossRef Full Text | Google Scholar

Wang, M., Zhang, R.-Y., Zhang, L., Wang, D., Guo, Q., Zhang, Z.-Q., et al. (2021). Topological One-Way Large-Area Waveguide States in Magnetic Photonic Crystals. Phys. Rev. Lett. 126 (6), 67401. doi:10.1103/PhysRevLett.126.067401

CrossRef Full Text | Google Scholar

Wu, H., Luo, Q., Chen, H., Han, Y., Yu, X., and Liu, S. (2019). Magnetically Controllable Nonreciprocal Goos-Hänchen Shift Supported by a Magnetic Plasmonic Gradient Metasurface. Phy. Rev. A 99 (3), 033820. doi:10.1103/PhysRevA.99.033820

CrossRef Full Text | Google Scholar

Wu, X., Ye, F., Merlo, J. M., Naughton, M. J., and Kempa, K. (2018). Topologically Protected Photonic Edge States in the Visible in Plasmo-Gyroelectric Metamaterials. Adv. Opt. Mater. 6 (15), 1800119. doi:10.1002/adom.201800119

CrossRef Full Text | Google Scholar

Wu, Y., Li, X., and Fang, Y. (2020). Evolution and Reversal of Topological Edge States at Optical Frequencies from a Two-Dimensional Photonic crystal. J. Opt. 22 (10), 105102. doi:10.1088/2040-8986/abae78

CrossRef Full Text | Google Scholar

Xia, S., Jukić, D., Wang, N., Smirnova, D., Smirnov, L., Tang, L., et al. (2020). Nontrivial Coupling of Light into a Defect: the Interplay of Nonlinearity and Topology. Light Sci. Appl. 9, 147. doi:10.1038/s41377-020-00371-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, S., Kaltsas, D., Song, D., Komis, I., Xu, J., Szameit, A., et al. (2021). Nonlinear Tuning of PT Symmetry and Non-hermitian Topological States. Science 372 (6537), 72–76. doi:10.1126/science.abf6873

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, M., Chen, W.-J., He, W.-Y., and Chan, C. T. (2015). Synthetic Gauge Flux and Weyl Points in Acoustic Systems. Nat. Phys. 11 (11), 920–924. doi:10.1038/nphys3458

CrossRef Full Text | Google Scholar

Xie, B., Su, G., Wang, H.-F., Liu, F., Hu, L., Yu, S.-Y., et al. (2020). Higher-order Quantum Spin Hall Effect in a Photonic crystal. Nat. Commun. 11 (1), 3768. doi:10.1038/s41467-020-17593-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S.-Y., Belopolski, I., Alidoust, N., Neupane, M., Bian, G., Zhang, C., et al. (2015). Discovery of a Weyl Fermion Semimetal and Topological Fermi Arcs. Science 349 (6248), 613–617. doi:10.1126/science.aaa9297

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, J., He, P., Feng, D., Yong, K., Hong, L., Shen, Y., et al. (2021). Slow Wave and Truly Rainbow Trapping in a One-Way Terahertz Waveguide. Opt. Express 29 (7), 11328. doi:10.1364/OE.422274

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., and Zhang, B. (2016). Acoustic Type-II Weyl Nodes from Stacking Dimerized Chains. Phys. Rev. Lett. 117 (22), 224301. doi:10.1103/PhysRevLett.117.224301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J.-K., Schreck, C., Noh, H., Liew, S.-F., Guy, M. I., O’Hern, C. S., et al. (2010). Photonic-band-gap Effects in Two-Dimensional Polycrystalline and Amorphous Structures. Phys. Rev. A 82 (5), 53838. doi:10.1103/PhysRevA.82.053838

CrossRef Full Text | Google Scholar

Yang, Y., Poo, Y., Wu, R.-x., Gu, Y., and Chen, P. (2013). Experimental Demonstration of One-Way Slow Wave in Waveguide Involving Gyromagnetic Photonic Crystals. Appl. Phys. Lett. 102 (23), 231113. doi:10.1063/1.4809956

CrossRef Full Text | Google Scholar

Yang, B., Wu, T., and Zhang, X. (2017). Engineering Topological Edge States in Two Dimensional Magnetic Photonic crystal. Appl. Phys. Lett. 110 (2), 021109. doi:10.1063/1.4973990

CrossRef Full Text | Google Scholar

Yang, B., Wu, T., and Zhang, X. (2017). Topological Properties of Nearly Flat Bands in Two-Dimensional Photonic Crystals. J. Opt. Soc. Am. B 34 (4), 831. doi:10.1364/JOSAB.34.000831

CrossRef Full Text | Google Scholar

Yang, Z., Xiao, M., Gao, F., Lu, L., Chong, Y., and Zhang, B. (2017). Weyl Points in a Magnetic Tetrahedral Photonic crystal. Opt. Express 25 (14), 15772. doi:10.1364/OE.25.015772

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, B., Zhang, H., Wu, T., Dong, R., Yan, X., and Zhang, X. (2019). Topological States in Amorphous Magnetic Photonic Lattices. Phys. Rev. B 99 (4), 45307. doi:10.1103/PhysRevB.99.045307

CrossRef Full Text | Google Scholar

Yang, B., Zhang, H., Shi, Q., Wu, T., Ma, Y., Lv, Z., et al. (2020). Details of the Topological State Transition Induced by Gradually Increased Disorder in Photonic Chern Insulators. Opt. Express 28 (21), 31487. doi:10.1364/OE.405820

PubMed Abstract | CrossRef Full Text | Google Scholar

Yertutanol, A., Akçaalan, Ö., Öğüt, S., Özbay, E., and Ceylan, A. (2021). Fiber-optic Gyroscope for the Suppression of a Faraday-Effect-Induced Bias Error. Opt. Lett. 46 (17), 4328. doi:10.1364/OL.436195

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, S. M., Zaheer, S., Teo, J. C. Y., Kane, C. L., Mele, E. J., and Rappe, A. M. (2012). Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 108 (14), 140405. doi:10.1103/PhysRevLett.108.140405

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, R., He, Y., Zhang, Y., An, S., Zhu, Q., Li, X., et al. (2021). Ultracompact and Low-Power-Consumption Silicon Thermo-Optic Switch for High-Speed Data. Nanophotonics 10 (2), 937–945. doi:10.1515/nanoph-2020-0496

CrossRef Full Text | Google Scholar

Zhou, P., Liu, G.-G., Ren, X., Yang, Y., Xue, H., Bi, L., et al. (2020a). Photonic Amorphous Topological Insulator. Light Sci. Appl. 9 (1), 133. doi:10.1038/s41377-020-00368-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, P., Liu, G. G., Yang, Y., Hu, Y. H., Ma, S., Xue, H., et al. (2020b). Observation of Photonic Antichiral Edge States. Phys. Rev. Lett. 125 (26), 263603. doi:10.1103/PhysRevLett.125.263603

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuang, S., Chen, J., Liang, W., and Li, Z. (2021). Zero GVD Slow-Light Originating from a Strong Coupling of One-Way Modes in Double-Channel Magneto-Optical Photonic Crystal Waveguides. Opt. Express 29 (2), 2478. doi:10.1364/OE.412460

PubMed Abstract | CrossRef Full Text | Google Scholar