Exploring the Compositional Space of High-Entropy Alloys for Cost-Effective High-Temperature Applications

High-entropy alloys (HEAs) are nearly equimolar multi-principal element alloys, exhibiting exceptional thermal and mechanical properties at extreme conditions such as high-temperatures and stresses. Since the first discovery and early conceptualization of conventional HEAs nearly two decades ago, HEAs with far-from-equimolar compositions have attracted substantial interest to provide a broader range of material properties and to adjust price fluctuations and availability of commodities. Here, we present a first-principles investigation of non-equimolar chromium-manganese-iron-cobalt-nickel (CrMnFeCoNi) HEAs and effects of molybdenum (Mo) and niobium (Nb) substitutions on cost, phase stability and solubility, and mechanical and thermal performance up to 1000 K operational temperature. Virtual-crystal approximation is used to expediently approximate random solid solutions at the disordered mean-field limit. Using multi-objective metaheuristics built on a first-principles database, golden compositions are predicted for thermally well-insulated components and effective heat sinks. Replacing Co with Fe lowers commodity costs without hindering phase stability and solubility. Lower Ni concentration leads to lower thermal conductivity, indicating better thermal insulation, while reducing Mn concentration significantly increases the thermal conductivity, indicating better performing heat sinks. Moving away from equimolar ratios commonly increases the thermal expansion coefficient, which could generate higher thermal stresses. Nb and Mo substitution always lead to substantially higher commodity cost and density but with an increment in the mechanical performance due to solid-solution hardening. However, alloying with Mo and Nb is the only compositional space that reduces the thermal conductivity and thermal expansion coefficient.

1 Introduction

High-entropy alloys (HEAs) are single-phase multi-principal element alloys exhibiting solid solution and are conventionally mixed with equimolar fractions (Chen et al., 2018). Among conventional HEAs, the face-centered cubic (FCC) chromium-manganese-iron-cobalt-nickel (CrMnFeCoNi), also called Cantor alloy, (Cantor et al., 2004) has been extensively studied due to its remarkable mechanical properties such as high yield strength (Kim et al., 2020), tensile strength (Gali and George, 2013; Otto et al., 2013), hardness (Liu et al., 2013), and fracture toughness (Gludovatz et al., 2014). The early concept behind the formation of HEAs has been mostly attributed to high configurational entropy (S_conf) due to configurational disorderliness (Yeh et al., 2004). By definition, S_conf is the highest for equimolar mixture, for which it substantially reduces mixing Gibbs free energy. However, there has been a rapidly growing literature on the development and manufacturing strategies of non-equimolar HEAs (Miracle and Senkov, 2017), in particular, Cantor-like HEAs (Cantor, 2021).

Non-equimolar HEAs provide a broad compositional space for multi-objective materials design for diverse engineering applications for extreme conditions such as aerospace (Dada et al., 2021a), nuclear reactors (Tong et al., 2005), and biomedical (Varalakshmi et al., 2010) applications. In such applications, conventional alloys commonly have severe limitations to achieve more cost-effective, long-living, and more green designs (Dada et al., 2021b). In particular, low Co non-equimolar HEAs are an appealing system for diverse applications and the replacement of high-strength steel components (Li et al., 2022).

Ad-hoc design of engineering materials is a multi-faceted task requiring consideration of material properties, manufacturability, operational conditions, compatibility to the current design, and environmental impact (Mouritz, 2012; Edwards, 2014). Multi-objective metaheuristics (Liu et al., 2020) serve as powerful tools for compositional optimization during materials selection (Ashby, 2000). There have been previous works such as composition selection based on commodity availability and cost (Fu et al., 2017) and phase-stability prediction based on thermodynamic multi-objective criteria (Gheribi et al., 2018). However, such works are severely limited to a single aspect of materials selection due to a lack of available materials data. First-principles simulations provide tractable tools to calculate material properties highly suitable for multi-objective optimization (Liu et al., 2020).

This work presents a systematic first-principles investigation of composition- and temperature-dependent material properties of non-equimolar Cantor-like HEAs. We also investigate the effects of Nb and Mo substitutions. First-principle materials database and available commodity cost are used to perform multi-objective optimizations within fundamental materials objectives and constraints for high-temperature applications (T > 800 K), particularly thermally well-insulated components and effective heat sinks.

2 Materials and Methods

The equimolar CrMnFeCoNi, labeled by X⁵, serves as the reference system. Two compositional spaces are derived starting from X⁵. The first compositional space was spanned by non-equimolar five-principal-elements (5-PEs) HEAs. It was sampled using a discrete mesh of compositions, obtained by individually varying molar fractions of each PE in between x = 0.05 − 0.3, where x is the atomic molar fraction while keeping the remaining PEs equimolar among themselves. For instance, the non-equimolar 5-PE HEAs are Cr_x(MnFeCoNi)_1−x, labeled by ${\mathrm{C}\mathrm{r}}_x{\mathrm{X}}_{1-x}^4$, where x = 0.05, 0.1, 0.15, 0.25, 0.3 when varying Cr concentration. The second compositional space was spanned by 6- and 7-PE HEAs. It was sampled using a discrete mesh of compositions, obtained one-by-one by substituting half each PE of X⁵ with Nb and Mo. For instance, the 6- and 7-PE HEAs are ${\mathrm{C}\mathrm{r}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{N}\mathrm{b}}_y$Mo_0.1−y where y = 0.1, 0.075, 0.05, 0.025 when the molar fraction of Cr is halved. Relevant symbols and molar fractions of available compositions are listed in Supplementary Tables S1, S2.

2.1 Objectives and Constraints for Optimization

Inspired by the most common ambient conditions for high-stress and high-temperature applications, four main objective categories were determined for multi-objective optimization, schematically illustrated in Figure 1. The main objectives and constraints (whenever present) are also summarized in Figure 1. We focus on fundamental material properties rather than design-specific performance metrics as they are more suitable for general assessments. Moreover, they are also used to determine the most common specific performance metrics (Ashby, 2000).

FIGURE 1

FIGURE 1. Schematic illustration of multi-objective optimization for thermal insulation and heat sinks, operating at high-stress and high-temperature. Abbreviation list: ρ: Solid density, G_free: Gibbs free energy, n_v: Valence electron concentration, χ: Mulliken electronegativity, δr: Atomic-size mismatch parameter, E: Young’s modulus, σ_y: Yield strength, K: Bulk modulus, G: Shear modulus, κ: Thermal conductivity, β: Thermal expansion coefficient.

The first objective category is economics, aiming to minimize commodity price and solid density (ρ). Economics, associated with materials design, is far more complex due to manufacturing, repair, replacement, and recycling costs. While these are highly dependent on the particular design, commodity cost is a fundamental factor. It is particularly crucial when considering large fluctuations in unit prices, shown in Supplementary Figure S1. Solid density is an indirect contributing factor, particularly for transportation technologies, determining fuel consumption. For instance, estimations indicate that a 1 kg reduction on an average-sized airplane may reduce fuel consumption by $\sim 800$ liters per year (Mouritz, 2012). Beyond reducing operation costs, lower density also reduces carbon footprint and associated costs.

The second objective category is related to the phase-stability and solubility of a multi-principal-elements alloy. Relative phase stability of non-equimolar compositions with respect to X⁵ was assessed by Gibbs free energy (GFE) difference (ΔG_free). In addition to the GFE difference, likelihood of solid-solution formation is assessed by valence electron concentration (Δn_v), Mulliken electronegativity (Δχ), and atomic-size mismatch parameter (Δ(δr)) differences (Qin et al., 2019; Rojas et al., 2022). A limit of 5% increase G_free compared to that of X⁵ is chosen as the upper-bound constraint to ensure that comparable phase stability is attained. Rojas et al. (2022) have shown that good solubility of Mo and Nb solute atoms was achieved when Δn_v and Δχ were below ±2%. These conditions are imposed as constraints during the optimizations. Lastly, minimizing Δ(δr) serves as an optimization objective when Mo and Nb are considered.

The third objective category is mechanical properties for which Young’s modulus (E), yield strength (σ_y), and Pugh ratio (ratio between bulk (K) and shear (G) moduli) serve as objectives. E and σ_y commonly serve as figures of merits (FOMs) for mechanical strength (Ashby, 2000), while K/G serves as a figure of merit for ductility, thus leading to better workability (Boucetta, 2014). For most engineering applications, these FOMs are desired to be maximized.

The last objective category is related to the thermal behavior, expediently assessed through thermal conductivity (κ) and thermal-expansion coefficient (β). A low κ is preferred for thermal insulation such as in jet-engine components (Mouritz, 2012), while a higher κ is required for effective heat sinks to dissipate the excess of heat rapidly. In general, a low β is highly preferable to avoid thermal dilatation in integrated components.

2.2 Theoretical Methodology for First-Principles Material Properties

The Kohn–Sham density-functional theory (KS-DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) with semi-local electronic exchange-correlation functionals (Kohn and Sham, 1965; Perdew et al., 1992) is an almost-universal approach to study ground-state properties of solids. Its perturbative extension, namely, density-functional perturbation theory (DFPT) (Gonze, 1997; Gonze and Lee, 1997), also provides a parameter-free approach to simulate lattice dynamics. These theories offer parameter-free approaches to calculate elastic and anharmonic thermodynamic properties (Corso, 2016; Palumbo and Corso, 2017).

Despite rapidly growing computational resources and state-of-the-art algorithms in recent decades, practical implementations of the approximate KS-DFT are still severely limited by system size and spatial complexity, particularly for metallic systems (Ponga et al., 2016; Ponga et al., 2020). It becomes more infeasible for HEAs as they require many well-converged super-cell simulations to achieve an accurate statistical representation of configurational disorderliness. Virtual-crystal approximation (VCA) (Bellaiche and Vanderbilt, 2000) offers a less robust yet expedient method to simulate such systems. A linear mixing scheme is applied to atomic pseudo-potentials (Heine, 1970) to achieve a virtual representation at the disordered mean-field limit (Bellaiche and Vanderbilt, 2000). Although VCA has been commonly deemed over-simplified, it is entirely accurate when calculating elastic constant, simple-phase transformation, and thermodynamic functions of HEAs (Tian, 2017).

Random solid solutions such as HEAs do not exhibit long-range ordering due to spatial disorder; however, they still may have short-range ordering (SRO), which can play crucial roles in the local chemical environment and lattice distortions (Miracle and Senkov, 2017). Such local effects may significantly contribute to superior thermal stability, sluggish diffusion, and exceptional mechanical strength (Zhang et al., 2015; Miracle and Senkov, 2017). SRO may also be necessary for capturing fine details of electronic band structures (Maurizio et al., 2003). By definition, VCA does not include any SRO. There have been considerable efforts to include SRO within VCA by using tight-binding model-like approaches to explicitly include interactions of unlike first and second neighbors (Baldereschi and Maschke, 1975; Porod and Ferry, 1983). Despite their relative simplicity, such corrective approaches are unsuitable for high-throughput materials research due to additional computational costs.

2.2.1 Figures of Merits for Phase Stability and Solubility

GFE serves as a universal FOM when comparing the relative phase stability of solids. For non-magnetic HEAs, it is given by the sum of the enthalpy of mixing (H_mix), the electronic Helmholtz free energy (F_el), the vibrational Helmholtz energy (F_vib), and the configurational-entropy contribution ( − TS_conf). H_mix is commonly approximated using the enthalpy of mixing of binary bulk metallic glasses (Youssef et al., 2015), while F_el and F_vib can be approximately calculated within the KS-DFT-based methods (Wang et al., 2004; Shang et al., 2010), and S_conf is given by

$S_{\text{conf}}=-R\sum _i^M{c}_{i}ln\left(c_i\right),(1)$

where R is the gas constant, M is the number of PEs, and c_i is the molar fraction (Santodonato et al., 2015). By definition, Eq. 1 reaches its maximum for equimolar mixture of M PEs. Antiferromagnetic ordering of Cr atoms against significant local magnetic moments of Fe and Mn atoms commonly leads to weak paramagnetism in X⁵ and its FCC derivatives (Tian et al., 2013; Schneeweiss et al., 2017; Šebesta et al., 2019). Hence, the magnetic contribution to GFE due to the total magnetic moment is negligible. For instance, it is −3.23 × 10⁻⁷ eV per unit cell for a magnetic field of 500 Oe which induces a total magnetic moment of $\sim 4\times 10^{-3}$ emu on a sample of X⁵ with a dimension of 10, ×, 2 × 0.02 mm at 300 K.

We define n_v as the electron number at outermost shell per unit volume to include temperature effects due to thermal expansion. It is also more convenient when comparing different phases of an alloy with the same ratio of PEs. Within KS-DFT, χ is approximately equal to the negative of chemical potential (Parr et al., 1978), which is a temperature-dependent quantity. Finally, δr is simply given by

$\delta r=\sqrt{\sum _i^M{c}_i\left(1-\frac{r_i}{r_{\text{avr}}}\right)},(2)$

where r_i and r_avr are the atomic radius of PEs and their arithmetic averaging, respectively.

2.2.2 Approximate Mechanical Properties

It is a challenging task to calculate technologically relevant mechanical properties such as Vickers hardness, yield strength, or ductility/brittleness, for which even experimental measurements are highly dependent on morphology, choice of indenter, the direction of loading forces relative to the microstructure orientation, and impurity of samples (Chen et al., 2011). Despite that, there are some expedient macroscopic semi-empirical connections between such quantities and the HEA’s second-order elastic tensor, which is well-defined in the linear elastic regime (Corso, 2016). Pugh ratio, given by the ratio between bulk and shear moduli (K/G), is commonly used as a FOM for ductility and workability. A Pugh ratio above 1.75 indicates good workability (Boucetta, 2014).

Vickers hardness is commonly used as an industry-standard measure for wear resistance. It is approximated by $H_{\text{V}}^{\text{Teter}}=0.151G$ (Teter, 1998), or $H_{\text{V}}^{\text{Tian}}=0.92{(G/K)}^{1.137}{G}^{0.708}$ (Tian et al., 2012). The former one tends to underestimate, whereas the latter expression tends to overestimate the material hardness. Thus, we used their averaging to approximate Vickers hardness, given by $H_{\text{V}}=0.5(H_{\text{V}}^{\text{Teter}}+H_{\text{V}}^{\text{Tian}})$. Following this approximation, the semi-empirical relation between H_V and yield strength (σ_y) is given by H_V ≈ 3σ_y (in MPa units) (Tiryakioğlu, 2015). Within this definition and in the context of our calculations, σ_y can be interpreted as the lattice friction as it does not account for dislocation density, grain-size, solid-solution hardening (SSH), and precipitation hardening, which can synergetically increase σ_y. In 5-PE CrMnFeCoNi HEAs, it has been shown that the lattice friction value is in the neighborhood of ∼ 164 MPa (Zhao and Nieh, 2017), which is considerably higher than in other single-phase metals such as Ni.

Temperature dependence of macroscopic elastic properties was carried out through temperature dependence of K, E, and G. Temperature-dependent K was obtained from the Murnaghan equation of state at each temperature (Palumbo and Corso, 2017), while temperature-dependent E and G were carried out using temperature-dependent longitudinal and transverse sound velocities, respectively, and solid density (Farraro and Mclellan, 1977).

2.2.3 Approximate Solid-Solution Hardening due to Nb and Mo Substitution

Introducing additional PEs, in particular, with different atomic radii such as Nb and Mo to X⁵, commonly improve mechanical strength through SSH (Fleischer, 1963; Labusch, 1970). SSH can be expediently estimated by the sum of individual SSH of each solute atom, given by (Toda-Caraballo and del Castillo, 2015),

$\mathrm{\Delta }{\sigma }_{\text{SSH}}=\sum _i{B}_i{c}_i^{2/3},(3)$

where c_i is the molar fraction of i^th solute atom, α is the theory-dependent parameter which is commonly 3 < α < 16 and α > 16 for screw and edge dislocations, respectively.

$B_i=3G{ϵ}_i^{4/3}Z,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{ϵ}_i=\sqrt{{\eta }_i^{\prime 2}+{\left(\alpha {\delta }_i\right)}^2},(4)$

${\delta }_i=\frac{\partial a}{\partial c_i}\frac{1}{a}\mathrm{a}\mathrm{n}\mathrm{d}{\eta }_i^{\prime }=\frac{{\eta }_i}{1+0.5|{\eta }_i|},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\eta }_i=\frac{\partial G}{\partial c_i}\frac{1}{G},(5)$

G is the composition-dependent shear modulus, Z is the fitting constant, and a is the composition-dependent lattice parameter.

2.2.4 Approximate Thermal Properties

Thermal-expansion coefficient is a key FOM to assess thermal dilatation of components exposed to high temperatures. It can be calculated within the quasi-harmonic approximation starting from well-converged electronic structure at different volumes (Palumbo and Corso, 2017). Thermal conductivity was used to assess the ability of dissipating excess heat in solids. For metallic systems, it is predominantly mediated by free electrons and phonons, given by their respective contribution, symbolically κ = κ_el + κ_lat. Electronic thermal conductivity can be approximated by

${\kappa }_{\text{el}}=\frac{2{\pi }^2{k}_{\text{B}}^{2}T}{9}\frac{N\left(E_{\text{F}}\right)}{V}\frac{⟨v_{\text{F}}^2⟩}{{\left(1+\lambda \right)}^2}{\tau }_{\text{p}},(6)$

where k_B is the Boltzmann constant, N(E_F) is the density-of-state at the Fermi level, V is the unit-cell volume, v_F is the Fermi velocity, λ is the electron–phonon mass enhancement parameter, and τ_p is plasmon lifetime (Orhan and Ponga, 2021). Lattice thermal conductivity (in W⋅m⁻¹ ⋅K⁻¹ unit) is given by the semi-empirical formula:

${\kappa }_{\text{lat}}=f\left(\gamma \right)\frac{m_{\text{avr}}{V}_0^{1/3}{\mathrm{\Theta }}_{\text{D}}^3}{\gamma N^{2/3}T},\mathrm{a}\mathrm{n}\mathrm{d}f\left(\gamma \right)=\frac{2.42814\times 10^7}{1+0.228/{\gamma }^2-0.514/\gamma },(7)$

where m_avr (in kg unit) is the average mass, V₀ (in m³ unit) is the equilibrium volume, N is the number of atoms in unit cell, Θ_D is the Debye temperature, and γ is the Grüneisen parameter (Morelli and Slack, 2006). We refer the reader to the recent work of Orhan and Ponga (2021) for details on obtaining κ within fully first principles.

2.2.5 Computational Details

Ground-state and lattice-dynamics simulations were performed using the Quantum ESPRESSO (QE) software (Giannozzi et al., 2009, 2017). Virtual-atomic pseudo-potentials within VCA were generated using the SG15 optimized norm-conserving Vanderbilt scalar-relativistic pseudo-potentials of PEs (Hamann, 2013; Schlipf and Gygi, 2015). A generic FCC crystal was used for initial crystallographic information. Variable-cell optimizations were performed with a 150 Ry kinetic-energy cutoff for wavefunctions (E_cut), and a choice of smearing parameter for the Marzari–Vanderbilt cold smearing (Marzari et al., 1999) equivalent to 300 K at a 12 × 12 × 12 Monkhorst-Pack–equivalent (Monkhorst and Pack, 1976) uniform Brillouin zone with a 10⁻⁷ Ry total energy, 10⁻⁶ Ry/a₀ total force convergence, and 10⁻¹⁰ self-consistency thresholds.

Equilibrium crystal structures were used to perform three sets of simulations. For subsequent simulations, E_cut was set to a common converged value of 100 Ry. Phonon dispersion was calculated on a uniform 4 × 4 × 4 mesh. In the first set, electronic structures, elastic properties, and anharmonic thermodynamic properties were calculated on a shifted 12 × 12 × 12 uniform Brillouin zone on a temperature grid in between 0 − 1000 K with a step size of 5 K. In the second set, a series of sequential simulations were performed to obtain electron–phonon coupling on an electronic temperature grid in between 100 − 1000 K with a step size of 100 K. Ground-state simulations on a highly dense Brillouin zone sampling of 36 × 36 × 36 were performed to be used for interpolating electron–phonon coupling coefficients in the following simulations. Subsequent simulations in the second set were performed with a 12 × 12 × 12 uniform Brillouin zone. High-symmetry points on the first Brillouin zone of primitive FCC symmetry were used for a weighted sum of electron–phonon coupling coefficients to obtain an electron–phonon mass enhancement parameter (λ). In the last set, electronic band structures were calculated on a 36 × 36 × 36 uniform Brillouin zone to be used as input database for calculating Fermi velocities using an in-house code available online (Orhan, 2020).

2.3 Multi-Objective Optimization

In this work, our composition spaces represent design spaces where each available combination is a particle. We use the particle-swarm optimization (PSO) (Kennedy and Eberhart, 1995), a stochastic multi-objective metaheuristics method that has been extensively used in diverse optimization problems such as nano-structure design (Jiao et al., 2021) and data processing (Song et al., 2021). A multi-objective function with goals shown in Figure 1 was defined using the constant-weighting method (Lian, 2010). Thus, the multi-objective problem was solved as a linear combination of weights and single-objective function by satisfying the imposed phase stability and solubility constraints through the feasibility method (He and Wang, 2007). Compositions were promoted to explore regions where feasible solutions exist. For our particular problem, feasible-solution regions satisfied phase-stability and solubility conditions.

2.3.1 Interpolating Compositional Spaces Using the Higher-Order Maximum-Entropy Scheme

Conventionally, PSO is performed on continuous design spaces while available compositions are obtained on a discrete mesh of molar fractions at different temperatures. Thus, a fitting scheme is required at the end of each iterative solution to ensure the multi-objective functions represent the original discrete composition space, spanned by the available first-principles database. Two interpolation schemes were tested.

The higher-order maximum entropy scheme (HOLMES) is an approximation method designed to operate over unstructured multidimensional data (Bompadre et al. 2012). Within HOLMES, a shape function provides a balance between maximizing information entropy for least-biased statistical inference and minimizing shape-function width for computational efficiency. Moreover, HOLMES allows higher orders of polynomial consistency, enabling high-order interpolation of sparse data. HOLMES was explicitly designed to operate over unstructured multidimensional data. It is robust for situations where data points are spaced in widely varying manners and do not require complicated tinkering of its shape parameter to achieve consistent results. Additionally, because the shape functions achieve maximum entropy for their width, the resulting approximation is more resilient to uncertainty in the data than other methods. This property makes HOLMES a good choice in scenarios where clumping of data points may occur, such as exploring a design space for optimization. However, being an approximate rather than an exact interpolant means the HOLMES scheme will not necessarily duplicate data points values.

In practice, HOLMES is a set of shape functions, w_a(x), centered around a corresponding set of data points or nodes, x_a. Interpolation is performed as per any standard interpolation scheme. For some function u(x), the HOLMES approximant is

$u_I\left(x\right)=\sum _{a=1}^{{\mathcal{N}}_a\left(x\right)}{w}_a\left(x\right)u\left(x_a\right),(8)$

where ${\mathcal{N}}_a(x)$ is the number of nodes within a neighborhood of the query point x. Within the context of this work, the functions u(x_a) are the composition-dependent response functions of material properties of HEAs, listed in Figure 1, at each temperature point. Smooth response functions were obtained a high-dimensional space as required by the optimization process.

To compare the optimization procedure results, we also implemented the radial basis function (RBF) interpolation. RBF interpolation is a well-known alternative interpolation technique operating over unstructured multidimensional data (Buhmann, 2003). RBF uses kernel functions centered at each data point to create a system of equations with the shape functions as unknowns. Polynomial consistency of the desired dimension and order can be achieved by expanding the system of equations to include polynomial coefficients and suitable orthogonality constraints Wendland (2005). The reader is referred to Fasshauer (2007) for practical implementation details. RBF interpolation in its standard form is an exact interpolation, meaning it duplicates known values at data points. For some choices of kernel and data set, RBF has even achieved spectral rates of convergence (Madych and Nelson, 1992). However, in scenarios with extreme clumping of data points, the linear system may become ill-conditioned and ruin interpolation accuracy. Furthermore, performance is highly dependent on the choice of kernel and kernel parameters. The compact Wendland C2 kernels from Wendland (2005) produce sparse matrices and are less parameter-sensitive than most other kernels. Given the small size of the data set and its regular spacing, the kernel support radius is allowed to encompass all data points.

2.3.2 Computational Details

Multi-objective optimizations were performed using the numerical computing software MATLAB(R2021a) following (Isiet and Gadala, 2019). Global solutions were obtained by 100 independent runs with each 1000 iterations to ensure the robustness of the stochastic process. 100 randomly generated compositions were used for the discrete representation of composition space. Multi-objective functions were evaluated for each temperature.

Despite evaluating the same amount of multi-objective function, the computational demands of RBF and LME differ due to the nature of the methods. For a single processor, the ratio of time taken for a single evaluation of a 5-PEs composition between LME:RBF was 0.013. However, when evaluating a large number of compositions, as is in the case here, the computational demands for LME increase sharply. For example, for 100 evaluations, the ratio LME:RBF ratio is 0.6181, and for 1000 evaluations, the ratio increases to 5.0426. Therefore, it could be said that LME is more appropriate for problems where limited sampling is required, while RBF performs better when dealing with a large number of evaluations across a compositional space. For multi-dimensional problems with low-order nonlinearity, like here, RBF performs better as it is computationally more efficient, but in problems with high-order nonlinearity, LME has been shown to interpolate data with a higher accuracy (Fan et al., 2018).

3 Results and Discussion

We start with relative phase stability and solubility of non-equimolar HEAs with respect to the reference system (X⁵). In Figure 2, three general trends arise in ΔG_free of 5-PE non-equimolar HEAs. The first one is that moving further away in the equimolar case (x = 0.2) leads to larger |ΔG_free|. The second one is that this behavior is not symmetric, and ΔG_free increases more rapidly for compositions that increase the GFE. The last one is that increasing (decreasing) molar fractions of lighter (heavier) PEs decrease (increase) ΔG_free. As Fe is at the middle in terms of atomic number and mass, its ΔG_free is relatively small, almost within the practical KS-DFT accuracy threshold of ∼ 1 meV.

FIGURE 2

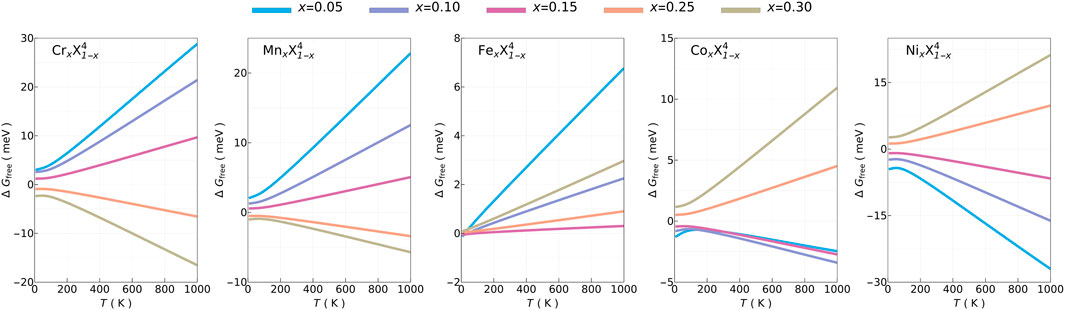
FIGURE 2. Temperature dependence of Gibbs free energy differences (ΔG_free) of non-equimolar five-principal-elements high-entropy alloys with respect to CrMnFeCoNi (X⁵). Note that the vertical scale is not the same for these plots.

In Supplementary Figure S2, the four terms contributing to ΔG_free are shown. ΔH_mix and ΔF_el are in the orders $\le 10^{-1}$ meV which are below practical KS-DFT accuracy threshold and are negligible. Thus, ΔF_vib and ΔS_conf determine relative phase stability. By definition, S_conf is lower for non-equimolar 5-PE cases compared to X⁵; thus, − (TΔS_conf) is always positive. This leaves ΔF_vib to determine the sign of ΔG_free. In Supplementary Figure S2, ΔF_vib takes positive values for reduced molar-fractions of lighter elements (i.e., Cr and Mn), while it takes negative values for heavier elements (i.e., Co and Ni). It becomes insignificant in the case of ${\mathrm{F}\mathrm{e}}_x{\mathrm{X}}_{1-x}^4$. When ΔF_vib is positive, it works with ΔS_conf in the same direction. Thus, |ΔG_free| is asymmetrical with respect to deviation from the equimolar case as shown in Figure 2.

The trend in ΔF_vib can be traced back to phonon density of states (PDOS), as shown in Supplementary Figure S3. Increasing (decreasing) Cr or Mn (Co or Ni) shifts PDOS to lower (higher) energies and leads to higher (lower) F_vib and lower (higher) ΔF_vib. Tracing back further, ΔF_vib follows an almost identical trend seen in the average atomic mass difference (Δm_avr), shown in Supplementary Figure S4, except Fe_xX_1−x for which changes are negligible. This indicates that interatomic force constants (IFC) (hence, the second derivative of energies with respect to ionic displacements) do not change substantially while shifts in PDOS are mostly due to Δm_avr as its square-root is used to normalized IFC before calculating phonon frequencies (Baroni et al., 2001).

Supplementary Figure S5 shows the changes in χ, Δn_v, and Δ(δr) compared to the X⁵ HEAs. The relative small changes, all below 2%, suggest high-solubility of these compositions. Moreover, moving further away from the equimolar case leads to larger solubility FOMs which provide a large compositional space for optimization for 5-PE cases.

In the case of additions of Nb and Mo, despite ΔG_free being always negative in Figure 3, the underlying mechanisms are more complex. The main factor leading to negative ΔG_free is higher S_conf due to additional element(s), resulting in large negative − (TΔS_conf), as shown in Supplementary Figure S6. Furthermore, ΔF_vib is also negative except in the cases of ${\mathrm{C}\mathrm{r}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{M}\mathrm{o}}_{0.1}$ and ${\mathrm{C}\mathrm{r}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{N}\mathrm{b}}_{0.025}{\mathrm{M}\mathrm{o}}_{0.075}$ for which − TΔS_conf is large enough to compensate. Unlike previous cases, ΔF_vib is not simply determined by Δm_avr. A more complex behavior is present in PDOS, shown in Supplementary Figure S7, such as larger energies shift to lower energies when substituting a heavier element with Nb and Mo despite lower Δm_avr as shown in Supplementary Figure S8. For instance, despite overall highest Δm_avr, there is almost no shift in the case of ${\mathrm{C}\mathrm{r}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{N}\mathrm{b}}_y$Mo_0.1−y. On the other hand, for a given substituted PE, higher Δm_avr leads to smaller shifts and lower energies. It indicates that effects of Δm_avr are over-compensated by higher IFC.

FIGURE 3

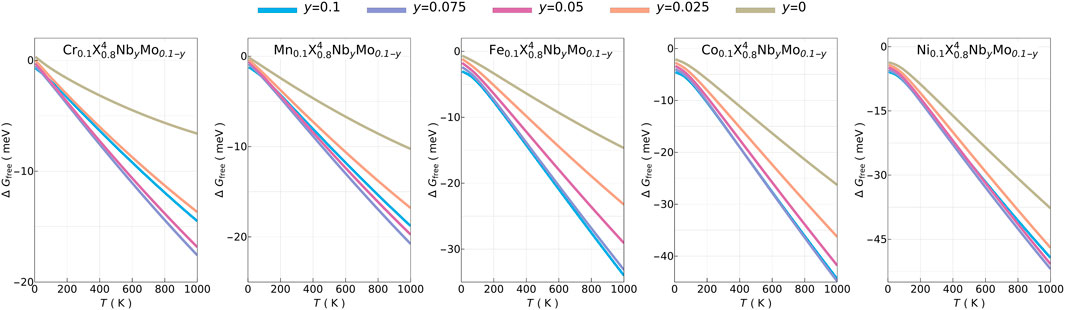
FIGURE 3. Temperature dependence of Gibbs free energy differences of non-equimolar six- and seven-principal-elements high-entropy alloys with respect to CrMnFeCoNi (X⁵).

In Supplementary Figure S9, three FOMs for solubility are shown for T = 1000 K when No and Mo are used as solute atoms. δχ and Δn_v have weak temperature dependence while Δ(δr) is independent of temperature. These FOMs are desired to be kept as low as possible to reduce affinity for phase segregation (Rojas et al., 2022). For additions of Nb and Mo, the solubility FOMs indicate that some phase segregation in the form of precipitations may not be avoidable (Rojas et al., 2022).

3.1 Temperature Dependence of Material Properties

Temperature dependence of mechanical and thermal properties has to be taken into account when optimizing compositions for a range of operational temperatures. In Supplementary Figure S10 and Supplementary Figure S11, material properties in between the room temperature (300 K) and 1000 K are presented for 5-, 6-, and 7-PE HEAs. Prior to an in-depth analysis, there are some general trends arising throughout compositions. In general, ρ and E do not have strong temperature dependence; Pugh ratios, σ_y, and β exhibit moderate temperature dependence, while κ_el and κ_lat vary substantially with temperature. Since ${\sigma }_{\text{y}}\stackrel{\propto }{\sim }{G}^2/K$ while the Pugh ratio is K/G, they always have opposite trends with respect to temperature. Also, β mostly determines temperature dependence of E and G through longitudinal and transverse sound velocities, respectively, as ρ has a weak temperature dependence.

Temperature dependence of relevant quantities in Eq. 6 and Eq. 7 are presented in Supplementary Figure S12 and Supplementary Figure S13 to investigate strong temperature dependence in κ_el and κ_lat. Strong temperature dependence of κ_el is mostly due to τ_p in Eq. 6, such as τ_p ∝ (λT)⁻¹. Indeed, $\lambda \stackrel{\propto }{\sim }{T}^{-1}$; however, λ is in the order of 1. In the case of κ_lat, it is almost entirely due to κ_lat ∝ T⁻¹, as for which f[γ]/γ is mostly constant.

3.2 Composition Dependence of Material Properties at High Temperature

We shift our focus on the high-temperature case where T = 1000 K ($\sim 725°$C). In Figure 4, materials objective for non-equimolar 5-PE HEAs alongside X⁵ are shown with re-scaled by-values of X⁵ (black solid lines). Increasing Fe content or decreasing Co content is the most reliable option to reduce commodity cost. Remarkably, changing Fe content does not significantly change material properties. In the case of Co reduction, κ decreases while β becomes larger, hinting better thermal insulation at the expense of higher thermal expansion. Tuning Cr, Mn, or Ni content gives wider range control over σ_y, the Pugh ratio, κ, and β; however, it does not lead to any significant cost reduction. In the case of κ, in particular for ${\mathrm{N}\mathrm{i}}_x{\mathrm{X}}_{1-x}^4$, it varies over a wide range, in between $\sim 0.25-1.25$ times compared to that of X⁵.

FIGURE 4

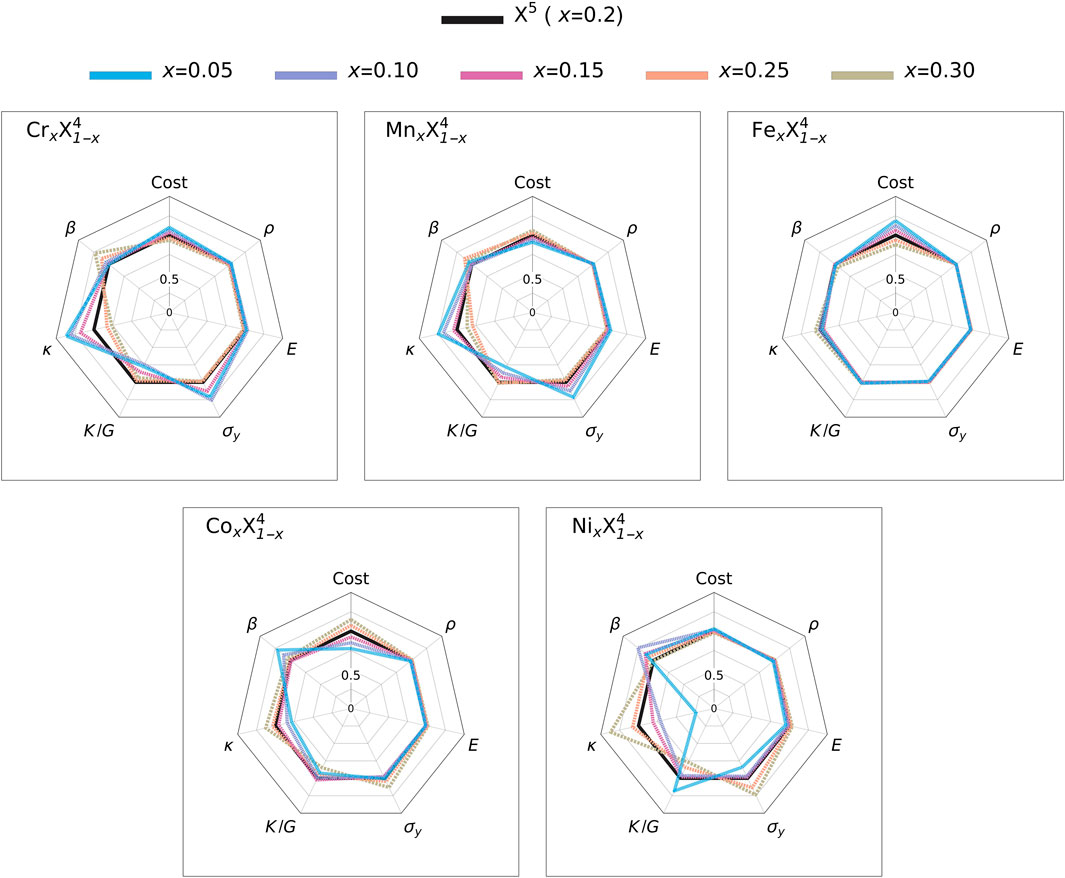
FIGURE 4. Composition dependence of material properties of non-equimolar five-principal-elements high-entropy alloys, shown by their ratio to those of CrMnFeCoNi (X⁵), at T = 1000 K.

Results for additions of Nb and Mo in the composition are shown in Figure 5. Substituting any other PE by Nb drives the cost up as it is the most expensive metal (shown in Supplementary Figure S1). Replacing Co or Mn by Mo keeps the cost almost fixed. Substituting Cr with Nb or Mo does not have any significant benefit except slight reduction of thermal conductivity and thermal expansion coefficient. ${\mathrm{N}\mathrm{i}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{N}\mathrm{b}}_y$Mo_0.1−y is also not quite favorable as they have lower strength at a higher cost. Despite higher mechanical strength, ${\mathrm{F}\mathrm{e}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{N}\mathrm{b}}_y$Mo_0.1−y is not a good choice as well due to its higher thermal expansion and lower ductility. Among remaining options, ${\mathrm{C}\mathrm{o}}_{0.1}{\mathrm{X}}_{0.8}^4{\mathrm{N}\mathrm{b}}_y$Mo_0.1−y is the most promising as it provides a compositional range for simultaneously improving mechanical strength and ductility while keeping thermal expansion almost constant.

FIGURE 5

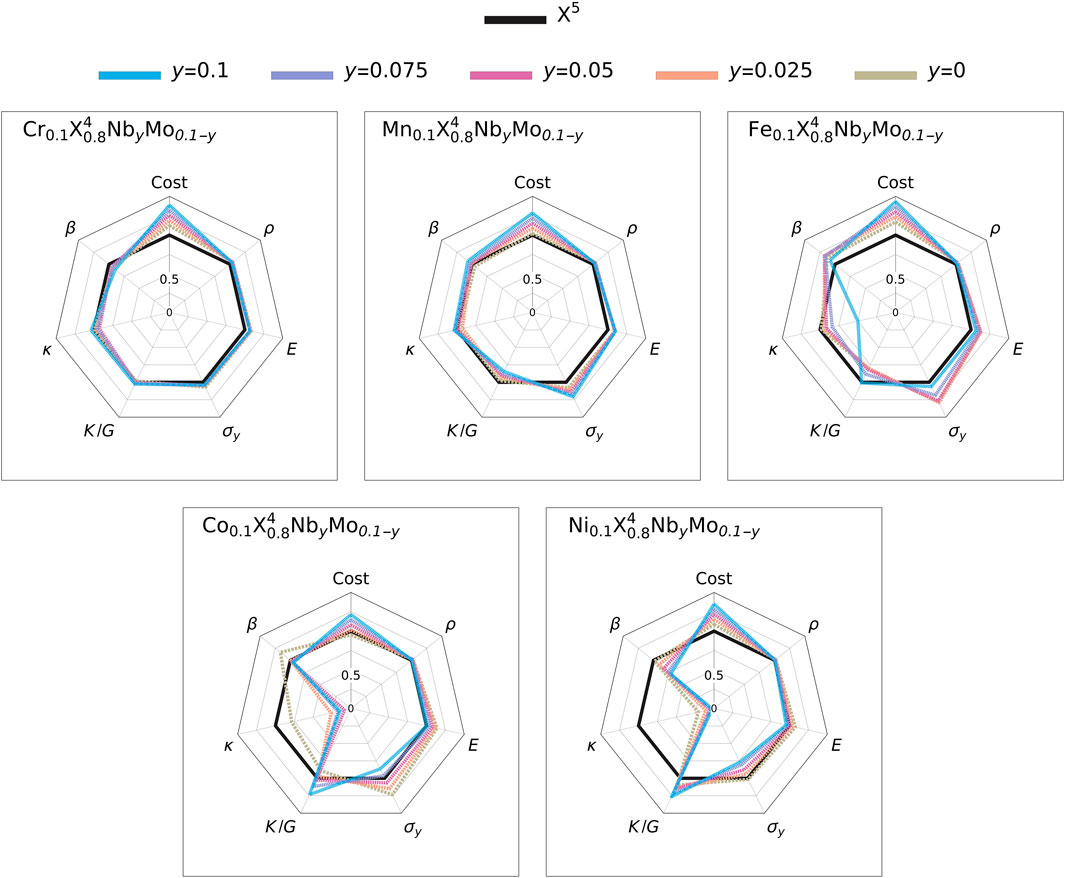
FIGURE 5. Composition dependence of material properties of non-equimolar six- and seven-principal-elements high-entropy alloys, shown by their ratio to those of CrMnFeCoNi (X⁵), at T = 1000 K.

In Supplementary Figure S14 and Supplementary Figure S15, composition-dependent quantities, used to calculate κ_el and κ_lat in Eq. 6 and Eq. 7, are shown to further analyze this trend. For the 5-PE cases, κ_lat is one order higher than κ_el. Thus, κ shows the same trend with κ_lat in Supplementary Figure S14 regardless of how κ_el behaves. The most visible clue of this behavior is in ${\mathrm{N}\mathrm{i}}_x{\mathrm{X}}_{1-x}^4$ in Supplementary Figure S14, where the term f[γ]/γ in Eq. 7 determines this trend. This term monotonically decreases for increasing γ between 0.5 − 4.5, representing the approximate lower and upper bounds for HEAs in this work. Thus, γ predominantly determines trends in κ of 5-PE HEAs, and higher γ leads to lower κ. For Nb and Mo substitutions, the general trend in κ is subtle changes for Cr and Mn while there are substantial reductions for Fe, Co, and Ni. In the case of substituting Cr, Mn, and some cases of Fe, κ_lat does not change significantly, and lower κ_el leads to quite subtle changes in total thermal conductivity.

In other cases, κ_lat and κ_el are substantially lowered by Mo and Nb substitution for which κ_lat sets the trends in κ. Similar to the previous case, changes in κ_lat (or lack of) are driven by γ as other terms in Eq. 7 are not strongly composition-dependent. Since ${\tau }_{\text{p}}\stackrel{\propto }{\sim }{\lambda }^{-1}$, ${\kappa }_{\text{el}}\stackrel{\propto }{\sim }{\lambda }^{-3}$ while ${\kappa }_{\text{el}}\propto N(E_{\text{F}})/V$ and ${\kappa }_{\text{el}}\propto v_{\text{F}}^2$. As shown in Figure 5, N(E_F)/V is almost constant throughout the compositional space and v_F varies between higher and lower energies, while higher λ compared to that of X⁵ leads substantially lower κ_el. One step further, this trend can be traced back trend in PDOS (Supplementary Figure S7) for which more shifts to lower energies lead to lower κ_el due to higher $\lambda \stackrel{\propto }{\sim }PDOS(E)/E^2$.

3.3 Solid-Solution Hardening due to Nb and Mo Substitution

It is now interesting to analyze the effect of strengthening of solutes (i.e., Mo and Nb) into the HEAs. Remarkably, their large radii difference will pin dislocations near the solutes, and this can be quantified using the approach presented by (Toda-Caraballo and del Castillo, 2015). We also point out that this effect is added to the one computed through the elastic interactions –also known as lattice friction – of the matrix presented in the previous sections.

Figure 6 shows the effect of SSH for several compositions of Nb and Mo at 1000 K Figures 6A,C and the temperature dependence of SSH when the same molar fraction of Mo and Nb is used (y = 0.05) Figures 6B,D. SSH for screw (top panel) and edge (bottom panel) dislocations were obtained by setting the theory-dependent parameter α in Eq. 4 to 4 and 16, respectively, and Z = 1/700 (see Supplementary Figure S16 for the full composition-temperature space). SSHs were calculated by adding up all the individual contributions due to Nb and Mo contents, shown in Supplementary Figure S16. In Figures 6A,C, SSHs generally reach a maximum between y = 0.025 or y = 0.075, hinting that 1 : 3 or 3 : 1 ratio of Nb:Mo is most favorable to have maximum additional hardening. This composition also stabilizes the changes in electronegativity with respect to the base alloy, as shown by Rojas et al., (2022). In Figures 6B,D, SSHs have subtle temperature dependence which is a general trend throughout compositional space as seen in Supplementary Figure S16. Temperature and composition dependence is mostly determined by shear modulus rather than lattice parameters (shown in Supplementary Figure S17), which lead to a SSH optimal value when y = 0.025 − 0.075 (see Supplementary Figure S18).

FIGURE 6

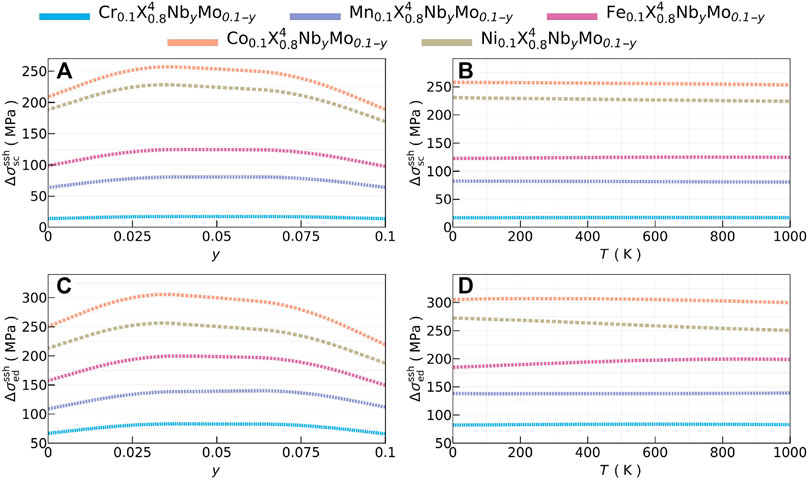
FIGURE 6. Composition dependence at T = 1000 K and temperature dependence at y = 0.05 of solid-solution hardening (in MPa units) due to Nb and Mo substitution for screw ($\mathrm{\Delta }{\sigma }_{sc}^{\text{ssh}}$) (A,B), respectively) and edge ($\mathrm{\Delta }{\sigma }_{ed}^{\text{ssh}}$) (C,D), respectively) dislocations, for which theory-dependent α parameters were set to 4 and 16, respectively.

3.4 Optimized Candidate Compositions

Compositional space (design space) for the 5-PE HEAs was discretely sampled by eleven points for each PE, whereas it was halved for the original PEs with Nb and Mo at four different sampling points in the case of 6- and 7-PEs. Thus, we constrained compositional spaces to the discrete compositions during optimizations for which the 5-PEs case had a large design space compared to the 6- and 7-PE cases. With that in mind, two general cases were studied within two interpolation schemes. Comparing Supplementary Figures S19, S20, the RBF interpolation scheme performs better than HOLMES for the 5-PEs compositional space. This is not surprising as HOLMES maximizes information entropy and thus smooth data out. Thus, they result in different optimal compositions, listed in Supplementary Tables S3, S4 for thermally well-isolated components, and Supplementary Tables S5, S6 for effective heat sinks. In the case of 7-PE HEAs, the two interpolation schemes perform quite similarly, as shown in Supplementary Figures S21, S22, resulting in the same optimal compositions, as listed in Supplementary Tables S7, S8 for thermally well-isolated components, and Supplementary Tables S9, S10 for effective heat sinks. Thus, the RBF interpolations scheme is used to determine optimal compositions.

3.4.1 Thermally Well-Insulated Components

The first case is where a component is operating at a high temperature and required to be thermally well-insulated to protect other components. In this scenario, the key quantity is the total thermal thermal conductivity which is required to be as low as possible. In Figure 7, the relative gains/losses on materials objectives of the two optimal compositions are shown for T = 1000 K.

FIGURE 7

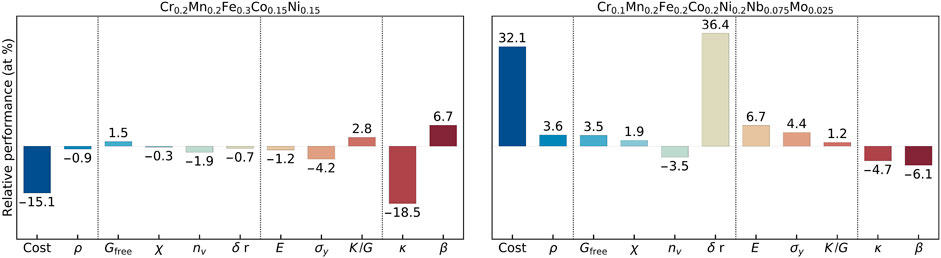
FIGURE 7. Optimized candidate compositions for five- and seven-principal-elements high-entropy alloys for thermally well-insulated components, operating at high temperatures. The Wendland radial basis functions are used for interpolating the compositional spaces.

For the 5-PEs compositional space, three predominant objectives are the commodity cost, κ, and β during optimization. This is due to fact that these objectives deviate most from the reference system within the feasible compositional space. In Figure 4, changing the Fe concentration has almost no effects on material properties except the average commodity cost, while lower Co and Ni concentrations reduce κ at the expense of increment in β. Thus, the optimum candidate composition is predicted as Cr_0.2Mn_0.2Fe_0.3Co_0.15Ni_0.15 for which the relative gains/losses in objectives are shown in 7 (left). Since Co and Ni are the two most expansive elements among the original PEs, partially replacing them with Fe, which is the cheapest element, leads to a 15.1% reduction in the average commodity. It also reduces ρ by only 1% which leads to $\sim 90$ kg mass reduction per 1 m³, implying further cost reduction due to lower density. Lower Co and Ni concentration reduces κ by 18.5% at the expense of a 6.7% increase in β, and sight worsened mechanical strength. Overall gain may compensate these relatively small losses as long as they are still within safety ranges of the particular design.

When Nb and Mo were introduced in the design, it was not feasible to reduce the commodity cost and ρ, as indicated by fittings in Supplementary Figures S21, S22. Furthermore, the cost and κ have generally inverse composition dependence in Figure 5, and it is challenging to simultaneously optimize these two predominant objectives within the feasible-solution region, determined by the phase stability and solubility constraints. Thus, the gain κ is relatively small to keep the cost lower. Nevertheless, Nb and Mo substitutions are quite promising to improve the mechanical and thermal properties. As shown in Figure 7 right panel, the composition Cr_0.1Mn_0.2Fe_0.2Co_0.2Ni_0.2Nb_0.075Mo_0.025 is promising as it provides significant improvements in material properties They simultaneously reduce κ and β, hinting better thermal insulation and less thermal expansion. There is also improvement of the lattice friction value σ_y and K/G by 4.4% and 1.2%, respectively. Moreover, the SSH hardening of using simultaneous additions of Nb and Mo could lead to significant increments in the yield strength, as shown in Section 3.3. The 3 : 1 ratio of Nb:Mo substitution leads to 16.7 MPa SSH in the case of screw dislocations (α = 4), and 80.6 MPa SSH in the case of edge dislocations (α = 16). Supplementary Figure S23 shows the homologous optimized solutions obtained with the HOLMES interpolation scheme.

3.4.2 Effective Heat Sinks

For effective heat sinks, the main objective is to reach the highest κ for an optimal dissipation of excess heat. Two relative gains/losses in two optimal compositions are shown in Figure 8 for T = 1000 K. In this particular case, a lower Mn fraction is the key to achieve the main objective as it increases κ in Figure 4.

FIGURE 8

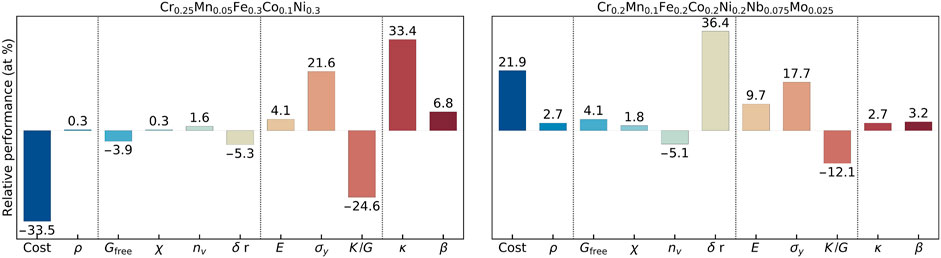
FIGURE 8. Optimized candidate compositions for five- and seven-principal-elements high-entropy alloys for effective heat sinks, operating at high temperatures. The Wendland radial basis functions are used for interpolating the compositional spaces.

Thus, the optimal composition is predicted as Cr_0.25Mn_0.05Fe_0.3Co_0.1Ni_0.3. It has a κ 33.4% higher compared to that of X⁵. Similar to the previous case, reducing Co while increasing Fe results in a considerable reduction ( − 33.5%) in the average commodity cost. Unlike the previous case, there is also considerable improvement in mechanical strength such as 21.6% higher σ_y and 4.1% higher E at the expense of considerably lower Pugh ratio ( − 24.6%), indicating less ductility.

The 7-PEs optimal composition is predicted as Cr_0.2Mn_0.1Fe_0.2Co_0.2Ni_0.2Nb_0.075Mo_0.025. It also relies on reducing the Mn concentration to increase κ for which a subtle 2.7% gains is achieved. Similar to the previous case, Nb and Mo substitution substantially increases the commodity cost and density. It also improves mechanical strength; however, not as much as in the case of Cr_0.25Mn_0.05Fe_0.3Co_0.1Ni_0.3. On the other hand, it also has additional SSH similar to Cr_0.1Mn_0.2Fe_0.2Co_0.2Ni_0.2Nb_0.075Mo_0.025. Despite some improvements in the mechanical and thermal properties, it is application-dependent to understand whether they are sufficient enough to compensate the increased cost. Supplementary Figure S24 shows the homologous optimized solution obtained with the HOLMES interpolation scheme.

4 Discussion

This work explored the non-equimolar compositional space of five multi-principal elements (Co, Cr, Fe, Mn, and Ni) with and without additions of Mo and Nb using first-principles simulations. We found that the solubility FOMs and mechanical properties have commonly weak temperature dependence while thermal properties exhibited significant temperature dependence. This temperature dependence of G_free is predominantly due to S_conf and ΔF_vib. Thus, while the configurational entropy is maximized when equimolar fractions are used, the vibrational contributions play a critical role in stabilizing HEAs. This observation is crucial as it opens up the possibility of stabilizing diverse compositions by contributing to the GFE.

Another important aspect of our first-principles data is that the changes in compositions go beyond affecting the average mass (m_avr), change in electronegativity (Δχ) and charge density (Δn_v), and misfit parameter (Δ(δr) which are widely used and computed using classical models. For instance, the phonon DOS critically changed compared to the equimolar case except for changes in Fe. These results, which were achieved due to the use of DFT calculations, point out the possibility to control phonon-dominated properties such as thermal conductivity, wave velocity, and phase transformation by tuning the HEAs composition (Li et al., 2022). Indeed, the analyzed compositions, whose values are provided in the SI for the maximum reproducibility, indicated that thermal conductivity and the coefficient of thermal expansion could be drastically changed among all properties.

Of particular interest, we also explored non-equimolar compositions with additions of Mo and Nb. The trend of incorporating Mo and Nb is starting to gain momentum in the HEA community, with some experimental studies showing the synergistic effects of these two solutes (Fan et al., 2022; Rojas et al., 2022). Our results showed that small additions of both Mo and Nb could significantly improve the yield strength thanks to SSH. Indeed, we showed that a ratio of Nb:Mo of 1 : 3 is optimal to retain the electronegativity of the base alloy while providing significant SSH (i.e., ∼ 80 MPa). Remarkably, this ratio of Nb and Mo also maximizes the SSH value, as shown in Section 3.3 and Figure 6. An essential outcome of the SSH calculations is that the increment of the yield strength was weakly dependent on the temperature, and thus, can play a significant role in contributing to mechanical performance at high temperatures.

While the first-principles simulations and optimized compositions provide valuable insights, there are several limitations in our approach. For instance, the use of VCA is limited to HEAs that are in solid solution, and it is not possible to assess the thermodynamic stability of intermetallic phases that could appear in it. This limitation is more critical in HEAs combining Mo and Nb, where experimental works have shown that the volume fraction of σ, μ, and Laves phases increase with Mo and Nb content. For instance, Liu et al. (2016) and Shun et al. (2012) investigated CoCrFeNiMo_x with x = 0.1 − 0.8. Others have investigated the effect of Nb in non-equimolar HEAs, including Liu et al. (2015), and later He et al. (2016) and Jiang et al. (2017) studied the effect of Nb in the CoCrFeNiNb_x system, with x = 0.1 − 1.2. More recently, Sunkari et al. (2020) investigated a non-equimolar CoCrFeNi_2.1Nb_0.2 HEA, and found excellent properties when it was cryo-rolled. These works revealed that these two solute atoms could be solved in the FCC matrix, although precipitation of intermetallic phases could appear for large molar fractions, that is, x ≥ 0.1. Thus, these observations suggest that controlled proportions of Mo and Nb should be employed. Remarkably, our study suggests that small proportions, that is, x = 0,−, 0.1, could be employed to maximize SSH. Additionally, the proportion of Mo:Nb 3: 1 seems to be optimal in preserving electronegativity and maximization of SSH while being an economically viable option. This result is in agreement with the recent experimental work presented by Rojas et al. (2022).

In summary, we have systematically investigated non-equimolar CoCrFeMnNi with and without Mo and Nb additions. We have used thermalized first-principles simulations to construct a reasonably large data set. Based on this set, we have created a smooth high-dimensional interpolated space with LME and RDF to predict the highly non-linear response function of the HAEs properties as a function of composition and temperature. Combining the first-principles set with the interpolation scheme allowed us to find optimal compositions for two applications of interest related to optimal heat insulation and heat conduction using multi-objective metaheuristics optimization. The 5-PEs compositional space provides cost and density reductions with good phase stability and solubility thresholds and relatively small performance gains/losses in material properties. Thus, the non-equimolar 5-PE HEAs offer significant advantages when the cost is the most crucial factor when designing a component.

Data Availability Statement

The first-principles materials data is available online in the repository Orhan, 2021. Further inquiries can be directed to the corresponding author.

Author Contributions

OO contributed to the original research topic, performed first-principles simulations, generated and analyzed materials database, and prepared the original manuscript. MI and LC performed multi-objective optimizations and contributed to the original manuscript. MP developed the original research topic, supervised, managed the funding acquisition, and revised the original manuscript.

Funding

We acknowledge the support from the Natural Sciences and Engineering Research Council of Canada (NSERC) through the Discovery Grant under Award Application Number RGPIN’2016’06 114 and the New Frontiers in Research Fund (NFRFE’2019’01 095). This research was supported in part through computational resources and services provided by Advanced Research Computing at the University of British Columbia.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.816610/full#supplementary-material

References

Ashby, M. F. (2000). Multi-Objective Optimization in Material Design and Selection. Acta Materialia 48, 359–369. doi:10.1016/S1359-6454(99)00304-3

CrossRef Full Text | Google Scholar

Baldereschi, A., and Maschke, K. (1975). Band Structure of Semiconductor Alloys Beyond the Virtual crystal Approximation. Effect of Compositional Disorder on the Energy Gaps in GaPxAs1−x. Solid State. Commun. 16, 99–102. doi:10.1016/0038-1098(75)90799-1

CrossRef Full Text | Google Scholar

Baroni, S., de Gironcoli, S., Dal Corso, A., and Giannozzi, P. (2001). Phonons and Related crystal Properties from Density-Functional Perturbation Theory. Rev. Mod. Phys. 73, 515–562. doi:10.1103/RevModPhys.73.515

CrossRef Full Text | Google Scholar

Bellaiche, L., and Vanderbilt, D. (2000). Virtual Crystal Approximation Revisited: Application to Dielectric and Piezoelectric Properties of Perovskites. Phys. Rev. B 61, 7877–7882. doi:10.1103/PhysRevB.61.7877

CrossRef Full Text | Google Scholar

Bompadre, A., Perotti, L. E., Cyron, C. J., and Ortiz, M. (2012). Convergent Meshfree Approximation Schemes of Arbitrary Order and Smoothness. Comput. Methods Appl. Mech. Eng. 221-222, 83–103. doi:10.1016/j.cma.2012.01.020

CrossRef Full Text | Google Scholar

Boucetta, S. (2014). Theoretical Study of Elastic, Mechanical and Thermodynamic Properties of Mgrh Intermetallic Compound. J. Magnesium Alloys 2, 59–63. doi:10.1016/j.jma.2014.04.001

CrossRef Full Text | Google Scholar

Buhmann, M. (2003). Radial Basis Functions. Cambridge, UK: Cambridge University Press.

Google Scholar

Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural Development in Equiatomic Multicomponent Alloys. Mater. Sci. Eng. A 375-377, 213–218. doi:10.1016/j.msea.2003.10.257

CrossRef Full Text | Google Scholar

Cantor, B. (2021). Multicomponent High-Entropy Cantor Alloys. Prog. Mater. Sci. 120, 100754. doi:10.1016/j.pmatsci.2020.100754

CrossRef Full Text | Google Scholar

Chen, J., Zhou, X., Wang, W., Liu, B., Lv, Y., Yang, W., et al. (2018). A Review on Fundamental of High Entropy Alloys with Promising High–Temperature Properties. J. Alloys Compd. 760, 15–30. doi:10.1016/j.jallcom.2018.05.067

CrossRef Full Text | Google Scholar

Chen, X.-Q., Niu, H., Li, D., and Li, Y. (2011). Modeling Hardness of Polycrystalline Materials and Bulk Metallic Glasses. Intermetallics 19, 1275–1281. doi:10.1016/j.intermet.2011.03.026

CrossRef Full Text | Google Scholar

Corso, A. D. (2016). Elastic Constants of Beryllium: A First-Principles Investigation. J. Phys. Condens. Matter 28, 075401. doi:10.1088/0953-8984/28/7/075401

CrossRef Full Text | Google Scholar

Dada, M., Popoola, P., Adeosun, S., and Mathe, N. (2021a). “High Entropy Alloys for Aerospace Applications,” in Aerodynamics. Editors M. Gorji-Bandpy, and A.-M. Aly (Rijeka: IntechOpen). chap. 7. doi:10.5772/intechopen.84982

CrossRef Full Text | Google Scholar

Dada, M., Popoola, P., and Mathe, N. (2021b). Recent Advances of High Entropy Alloys for Aerospace Applications: A Review. World J. Eng. ahead-of-print. doi:10.1108/WJE-01-2021-0040

CrossRef Full Text | Google Scholar

Edwards, K. (2014). “Interaction between Functional and Human-Centered Attributes in Materials Selection,” in Materials Experience. Editors E. Karana, O. Pedgley, and V. Rognoli (Boston: Butterworth-Heinemann), 287–299. doi:10.1016/B978-0-08-099359-1.00020-5

CrossRef Full Text | Google Scholar

Fan, J., Liao, H., Wang, H., Hu, J., Chen, Z., Lu, J., et al. (2018). Local Maximum-Entropy Based Surrogate Model and its Application to Structural Reliability Analysis. Struct. Multidisciplinary Optimization 57, 373–392. doi:10.1007/s00158-017-1760-y

CrossRef Full Text | Google Scholar

Fan, R., Wang, L., Zhao, L., Wang, L., Zhao, S., Zhang, Y., et al. (2022). Synergistic Effect of Nb and Mo Alloying on the Microstructure and Mechanical Properties of Cocrfeni High Entropy alloy. Mater. Sci. Eng. A 829, 142153. doi:10.1016/j.msea.2021.142153

CrossRef Full Text | Google Scholar

Farraro, R., and Mclellan, R. B. (1977). Temperature Dependence of the Young's Modulus and Shear Modulus of Pure Nickel, Platinum, and Molybdenum. Metallurgical Trans. A 8, 1563–1565. doi:10.1007/BF02644859

CrossRef Full Text | Google Scholar

Fasshauer, G. E. (2007). “Meshfree Approximation Methods in MATLAB,” in Interdisciplinary Mathematical Sciences (World Scientific). Singapore: World Scientific Publisher, 6.

Google Scholar

Fleischer, R. L. (1963). Substitutional Solution Hardening. Acta Metallurgica 11, 203–209. doi:10.1016/0001-6160(63)90213-X

CrossRef Full Text | Google Scholar

Fu, X., Schuh, C. A., and Olivetti, E. A. (2017). Materials Selection Considerations for High Entropy Alloys. Scripta Materialia 138, 145–150. doi:10.1016/j.scriptamat.2017.03.014

CrossRef Full Text | Google Scholar

Gali, A., and George, E. P. (2013). Tensile Properties of High- and Medium-Entropy Alloys. Intermetallics 39, 74–78. doi:10.1016/j.intermet.2013.03.018

CrossRef Full Text | Google Scholar

Gheribi, A. E., Pelton, A. D., Bélisle, E., Le Digabel, S., and Harvey, J.-P. (2018). On the Prediction of Low-Cost High Entropy Alloys Using New Thermodynamic Multi-Objective Criteria. Acta Materialia 161, 73–82. doi:10.1016/j.actamat.2018.09.001

CrossRef Full Text | Google Scholar

Giannozzi, P., Andreussi, O., Brumme, T., Bunau, O., Nardelli, M. B., Calandra, M., et al. (2017). Advanced Capabilities for Materials Modelling with Q Uantum Espresso. J. Phys. Condensed Matter 29, 465901. doi:10.1088/1361-648x/aa8f79

CrossRef Full Text | Google Scholar

Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum Espresso: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condensed Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502

CrossRef Full Text | Google Scholar

Gludovatz, B., Hohenwarter, A., Catoor, D., Chang, E. H., George, E. P., and Ritchie, R. O. (2014). A Fracture-Resistant High-Entropy alloy for Cryogenic Applications. Science 345, 1153–1158. doi:10.1126/science.1254581

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonze, X. (1997). First-Principles Responses of Solids to Atomic Displacements and Homogeneous Electric Fields: Implementation of a Conjugate-Gradient Algorithm. Phys. Rev. B 55, 10337–10354. doi:10.1103/PhysRevB.55.10337

CrossRef Full Text | Google Scholar

Gonze, X., and Lee, C. (1997). Dynamical Matrices, Born Effective Charges, Dielectric Permittivity Tensors, and Interatomic Force Constants from Density-Functional Perturbation Theory. Phys. Rev. B 55, 10355–10368. doi:10.1103/PhysRevB.55.10355

CrossRef Full Text | Google Scholar

Hamann, D. R. (2013). Optimized Norm-Conserving vanderbilt Pseudopotentials. Phys. Rev. B 88, 085117. doi:10.1103/PhysRevB.88.085117

CrossRef Full Text | Google Scholar

He, F., Wang, Z., Cheng, P., Wang, Q., Li, J., Dang, Y., et al. (2016). Designing Eutectic High Entropy Alloys of CoCrFeNiNbx. J. Alloys Compd. 656, 284–289. doi:10.1016/j.jallcom.2015.09.153

CrossRef Full Text | Google Scholar

He, Q., and Wang, L. (2007). A Hybrid Particle Swarm Optimization with a Feasibility-Based Rule for Constrained Optimization. Appl. Math. Comput. 186, 1407–1422. doi:10.1016/j.amc.2006.07.134

CrossRef Full Text | Google Scholar

Heine, V. (1970). The Pseudopotential Concept. J. Phys. C: Solid State. Phys. 24, 1–36. doi:10.1016/s0081-1947(08)60069-7

CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, B864–B871. doi:10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

Isiet, M., and Gadala, M. (2019). Self-Adapting Control Parameters in Particle Swarm Optimization. Appl. Soft Comput. 83, 105653. doi:10.1016/j.asoc.2019.105653

CrossRef Full Text | Google Scholar

Jiang, H., Jiang, L., Qiao, D., Lu, Y., Wang, T., Cao, Z., et al. (2017). Effect of Niobium on Microstructure and Properties of the CoCrFeNbxNi High Entropy Alloys. J. Mater. Sci. Technol. 33, 712–717. doi:10.1016/j.jmst.2016.09.016

CrossRef Full Text | Google Scholar

Jiao, J., Ghoreishi, S.-M., Moradi, Z., and Oslub, K. (2021). Coupled Particle Swarm Optimization Method with Genetic Algorithm for the Static–Dynamic Performance of the Magneto-Electro-Elastic Nanosystem. Eng. Comput., 1–15. doi:10.1007/s00366-021-01391-x

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle Swarm Optimization,” in Proceedings of ICNN’95-international conference on neural networks, Perth, WA, Australia, November 27–December 1, 1995 (IEEE), 4, 1942–1948.

Google Scholar

Kim, Y.-K., Yang, S., and Lee, K.-A. (2020). Superior Temperature-Dependent Mechanical Properties and Deformation Behavior of Equiatomic Cocrfemnni High-Entropy alloy Additively Manufactured by Selective Laser Melting. Sci. Rep. 10, 8045. doi:10.1038/s41598-020-65073-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

Labusch, R. (1970). A Statistical Theory of Solid Solution Hardening. Phys. Stat. Sol. (B) 41, 659–669. doi:10.1002/pssb.19700410221

CrossRef Full Text | Google Scholar

Li, H., Shao, C., Orhan, O. K., Rojas, D. F., Ponga, M., and Hogan, J. D. (2022). Strain-Rate-Dependent Mechanical Behavior of a Non-Equimolar CoCrFeMnNi High Entropy alloy with a Segmented Coarse Grain Structure, In press. Materialia 21, 101271. doi:10.1016/j.mtla.2021.101271

CrossRef Full Text | Google Scholar

Lian, Z. (2010). A United Search Particle Swarm Optimization Algorithm for Multiobjective Scheduling Problem. Appl. Math. Model. 34, 3518–3526. doi:10.1016/j.apm.2010.03.001

CrossRef Full Text | Google Scholar

Liu, Q., Li, X., Liu, H., and Guo, Z. (2020). Multi-Objective Metaheuristics for Discrete Optimization Problems: A Review of the State-Of-The-Art. Appl. Soft Comput. 93, 106382. doi:10.1016/j.asoc.2020.106382

CrossRef Full Text | Google Scholar

Liu, W. H., He, J. Y., Huang, H. L., Wang, H., Lu, Z. P., and Liu, C. T. (2015). Effects of Nb Additions on the Microstructure and Mechanical Property of CoCrFeNi High-Entropy Alloys. Intermetallics 60, 1–8. doi:10.1016/j.intermet.2015.01.004

CrossRef Full Text | Google Scholar

Liu, W. H., Lu, Z. P., He, J. Y., Luan, J. H., Wang, Z. J., Liu, B., et al. (2016). Ductile CoCrFeNiMox High Entropy Alloys Strengthened by Hard Intermetallic Phases. Acta Materialia 116, 332–342. doi:10.1016/j.actamat.2016.06.063

CrossRef Full Text | Google Scholar

Liu, W. H., Wu, Y., He, J. Y., Nieh, T. G., and Lu, Z. P. (2013). Grain Growth and the Hall-Petch Relationship in a High-Entropy FeCrNiCoMn alloy. Scripta Materialia 68, 526–529. doi:10.1016/j.scriptamat.2012.12.002

CrossRef Full Text | Google Scholar

Madych, W. R., and Nelson, S. A. (1992). Bounds on Multivariate Polynomials and Exponential Error Estimates for Multiquadric Interpolation. J. Approximation Theor. 70, 94–114. doi:10.1016/0021-9045(92)90058-V

CrossRef Full Text | Google Scholar

Marzari, N., Vanderbilt, D., De Vita, A., and Payne, M. C. (1999). Thermal Contraction and Disordering of the Al(110) Surface. Phys. Rev. Lett. 82, 3296–3299. doi:10.1103/PhysRevLett.82.3296

CrossRef Full Text | Google Scholar

Maurizio, C., Mattei, G., Mazzoldi, P., Padovani, S., Cattaruzza, E., Gonella, F., et al. (2003). Deviation from the Virtual crystal Approximation in Disordered Au–Cu Alloy Nanocrystals: Exafs and Gixrd Investigation. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 200, 178–184. doi:10.1016/S0168-583X(02)01716-0

CrossRef Full Text | Google Scholar

Miracle, D. B., and Senkov, O. N. (2017). A Critical Review of High Entropy Alloys and Related Concepts. Acta Materialia 122, 448–511. doi:10.1016/j.actamat.2016.08.081

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Morelli, D. T., and Slack, G. A. (2006). “High Lattice thermal Conductivity Solids,” in High Thermal Conductivity Materials. Editors S. L. Shindé, and J. S. Goela (New York, NY: Springer New York), 37–68. doi:10.1007/0-387-25100-6_2

CrossRef Full Text | Google Scholar

Mouritz, A. P. (2012). “Materials Selection for Aerospace,” in Introduction to Aerospace Materials (Sawston, Cambridge: Woodhead Publishing), 569–600. doi:10.1533/9780857095152.569

CrossRef Full Text | Google Scholar

[Dataset] Orhan, O. K. (2020). Drude Plasmon Energy. Available at: https://github.com/okorhan/Drude-plasmon-energy. (Accessed October 14, 2021).

Google Scholar

Orhan, O. K. (2021). First-Principles Materials Properties of the Face-Centered Cubic CrMnFeCoNi-based High-Entropy Alloys. GitHub. Available at: https://github.com/okorhan/CrMnFeCoNi_Based_HEAs_First_Principles_Database.

Orhan, O. K., and Ponga, M. (2021). Surface-plasmon Properties of Noble Metals with Exotic Phases. J. Phys. Chem. C 125, 21521–21532. doi:10.1021/acs.jpcc.1c06110

CrossRef Full Text | Google Scholar

Otto, F., Dlouhý, A., Somsen, C., Bei, H., Eggeler, G., and George, E. P. (2013). The Influences of Temperature and Microstructure on the Tensile Properties of a Cocrfemnni High-Entropy Alloy. Acta Materialia 61, 5743–5755. doi:10.1016/j.actamat.2013.06.018

CrossRef Full Text | Google Scholar

Palumbo, M., and Dal Corso, A. (2017). Lattice Dynamics and Thermophysical Properties of h.c.P. Os and Ru from the Quasi-Harmonic Approximation. J. Phys. Condens. Matter 29, 395401. doi:10.1088/1361-648x/aa7dca

PubMed Abstract | CrossRef Full Text | Google Scholar

Parr, R. G., Donnelly, R. A., Levy, M., and Palke, W. E. (1978). Electronegativity: The Density Functional Viewpoint. J. Chem. Phys. 68, 3801–3807. doi:10.1063/1.436185

CrossRef Full Text | Google Scholar

Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., et al. (1992). Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 46, 6671–6687. doi:10.1103/PhysRevB.46.6671

CrossRef Full Text | Google Scholar

Ponga, M., Bhattacharya, K., and Ortiz, M. (2016). A Sublinear-Scaling Approach to Density-Functional-Theory Analysis of crystal Defects. J. Mech. Phys. Sol. 95, 530–556. doi:10.1016/j.jmps.2016.05.029

CrossRef Full Text | Google Scholar

Ponga, M., Bhattacharya, K., and Ortiz, M. (2020). Large Scale Ab-Initio Simulations of Dislocations. J. Comput. Phys. 407, 109249. doi:10.1016/j.jcp.2020.109249

CrossRef Full Text | Google Scholar

Porod, W., and Ferry, D. K. (1983). Modification of the Virtual-Crystal Approximation for Ternary Iii-V Compounds. Phys. Rev. B 27, 2587–2589. doi:10.1103/PhysRevB.27.2587

CrossRef Full Text | Google Scholar

Qin, G., Chen, R., Zheng, H., Fang, H., Wang, L., Su, Y., et al. (2019). Strengthening Fcc-Cocrfemnni High Entropy Alloys by Mo Addition. J. Mater. Sci. Technol. 35, 578–583. doi:10.1016/j.jmst.2018.10.009

CrossRef Full Text | Google Scholar

Rojas, D. F., Li, H., Orhan, O. K., Shao, C., Hogan, J. D., and Ponga, M. (2022). Mechanical and Microstructural Properties of a CoCrFe_0.75NiMo_0.3Nb_0.125 High-Entropy Alloy Additively Manufactured via Cold-Spray. J. Alloys Compd. 893, 162309. doi:10.1016/j.jallcom.2021.162309

CrossRef Full Text | Google Scholar

Santodonato, L. J., Zhang, Y., Feygenson, M., Parish, C. M., Gao, M. C., Weber, R. J. K., et al. (2015). Deviation from High-Entropy Configurations in the Atomic Distributions of a Multi-Principal-Element Alloy. Nat. Commun. 6, 5964. doi:10.1038/ncomms6964

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlipf, M., and Gygi, F. (2015). Optimization Algorithm for the Generation of Oncv Pseudopotentials. Comput. Phys. Commun. 196, 36–44. doi:10.1016/j.cpc.2015.05.011

CrossRef Full Text | Google Scholar

Schneeweiss, O. C. V., Friák, M., Dudová, M., Holec, D., Šob, M., Kriegner, D., et al. (2017). Magnetic Properties of the Crmnfeconi High-Entropy Alloy. Phys. Rev. B 96, 014437. doi:10.1103/physrevb.96.014437

CrossRef Full Text | Google Scholar

Šebesta, J., Carva, K., and Legut, D. (2019). Role of Magnetism in the Stability of the High-Entropy Alloy Cocrfemnni and its Derivatives. Phys. Rev. Mater. 3, 124410. doi:10.1103/PhysRevMaterials.3.124410

CrossRef Full Text | Google Scholar

Shang, S.-L., Wang, Y., Kim, D., and Liu, Z.-K. (2010). First-Principles Thermodynamics from Phonon and Debye Model: Application to Ni and Ni₃Al. Comput. Mater. Sci. 47, 1040–1048. doi:10.1016/j.commatsci.2009.12.006

CrossRef Full Text | Google Scholar

Shun, T.-T., Chang, L.-Y., and Shiu, M.-H. (2012). Microstructure and Mechanical Properties of Multiprincipal Component CoCrFeNiMox Alloys. Mater. Characterization 70, 63–67. doi:10.1016/j.matchar.2012.05.005

CrossRef Full Text | Google Scholar

Song, X.-F., Zhang, Y., Gong, D.-W., and Sun, X.-Y. (2021). Feature Selection Using Bare-Bones Particle Swarm Optimization with Mutual Information. Pattern Recognition 112, 107804. doi:10.1016/j.patcog.2020.107804

CrossRef Full Text | Google Scholar

Sunkari, U., Reddy, S. R., Rathod, B. D. S., Kumar, S. S. S., Saha, R., Chatterjee, S., et al. (2020). Heterogeneous Precipitation Mediated Heterogeneous Nanostructure Enhances Strength-Ductility Synergy in Severely Cryo-Rolled and Annealed CoCrFeNi2.1Nb0.2 High Entropy alloy. Scientific Rep. 10, 6056. doi:10.1038/s41598-020-63038-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Teter, D. M. (1998). Computational Alchemy: The Search for New Superhard Materials. MRS Bull. 23, 22–27. doi:10.1557/S0883769400031420

CrossRef Full Text | Google Scholar

Tian, F. (2017). A Review of Solid-Solution Models of High-Entropy Alloys Based on Ab Initio Calculations. Front. Mater. 4, 36. doi:10.3389/fmats.2017.00036

CrossRef Full Text | Google Scholar

Tian, F., Varga, L. K., Chen, N., Delczeg, L., and Vitos, L. (2013). Ab Initioinvestigation of High-Entropy Alloys of 3delements. Phys. Rev. B 87, 075144. doi:10.1103/PhysRevB.87.075144

CrossRef Full Text | Google Scholar

Tian, Y., Xu, B., and Zhao, Z. (2012). Microscopic Theory of Hardness and Design of Novel Superhard Crystals. Int. J. Refractory Met. Hard Mater. 33, 93–106. doi:10.1016/j.ijrmhm.2012.02.021

CrossRef Full Text | Google Scholar

Tiryakioğlu, M. (2015). On the Relationship between Vickers Hardness and Yield Stress in Al-Zn-Mg-Cu Alloys. Mater. Sci. Eng. A 633, 17–19. doi:10.1016/j.msea.2015.02.073

CrossRef Full Text | Google Scholar

Toda-Caraballo, I., and Rivera-Díaz-del-Castillo, P. E. J. (2015). Modelling Solid Solution Hardening in High Entropy Alloys. Acta Materialia 85, 14–23. doi:10.1016/j.actamat.2014.11.014

CrossRef Full Text | Google Scholar

Tong, C.-J., Chen, Y.-L., Yeh, J.-W., Lin, S.-J., Chen, S.-K., Shun, T.-T., et al. (2005). Microstructure Characterization of Alxcocrcufeni High-Entropy Alloy System with Multiprincipal Elements. Metallurgical Mater. Trans. A 36, 881–893. doi:10.1007/s11661-005-0283-0

CrossRef Full Text | Google Scholar

Varalakshmi, S., Kamaraj, M., and Murty, B. S. (2010). Formation and Stability of Equiatomic and Nonequiatomic Nanocrystalline Cunicoznalti High-Entropy Alloys by Mechanical Alloying. Metall. Mat Trans. A. 41, 2703–2709. doi:10.1007/s11661-010-0344-x

CrossRef Full Text | Google Scholar

Wang, Y., Liu, Z.-K., and Chen, L.-Q. (2004). Thermodynamic Properties of Al, Ni, NiAl, and Ni3Al from First-Principles Calculations. Acta Materialia 52, 2665–2671. doi:10.1016/j.actamat.2004.02.014

CrossRef Full Text | Google Scholar

Wendland, H. (2005). Scattered Data Approximation. New York: Cambridge University Press.

Google Scholar

Yeh, J.-W., Chen, S.-K., Lin, S.-J., Gan, J.-Y., Chin, T.-S., Shun, T.-T., et al. (2004). Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel alloy Design Concepts and Outcomes. Adv. Eng. Mater. 6, 299–303. doi:10.1002/adem.200300567

CrossRef Full Text | Google Scholar

Youssef, K. M., Zaddach, A. J., Niu, C., Irving, D. L., and Koch, C. C. (2015). A Novel Low-Density, High-Hardness, High-Entropy Alloy with Close-Packed Single-Phase Nanocrystalline Structures. Mater. Res. Lett. 3, 95–99. doi:10.1080/21663831.2014.985855

CrossRef Full Text | Google Scholar

Zhang, Y., Stocks, G. M., Jin, K., Lu, C., Bei, H., Sales, B. C., et al. (2015). Influence of Chemical Disorder on Energy Dissipation and Defect Evolution in Concentrated Solid Solution Alloys. Nat. Commun. 6, 8736. doi:10.1038/ncomms9736

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y. Y., and Nieh, T. G. (2017). Correlation between Lattice Distortion and Friction Stress in Ni-Based Equiatomic Alloys. Intermetallics 86, 45–50. doi:10.1016/j.intermet.2017.03.011

CrossRef Full Text | Google Scholar