Theoretical Insight Into Diamond Doping and Its Possible Effect on Diamond Tool Wear During Cutting of Steel

Natural diamond tools experience wear during cutting of steel. As reported in our previous work, Ga doping of diamond has an effect on suppressing graphitization of diamond which is a major route of wear. We investigate interstitial and substitutional dopants of different valence and different ionic radii (Ga, B, and He) to achieve a deeper understanding of inhibiting graphitization. In this study, ab initio calculations are used to explore the effects of three dopants that might affect the diamond wear. We consider mechanical effects via possible solution strengthening and electronic effects via dopant-induced modifications of the electronic structure. We find that the bulk modulus difference between pristine and doped diamond is clearly related to strain energies. Furthermore, boron doping makes the resulting graphite with stable sp2 hybridization more perfect than diamond, but Ga-doped diamond needs 2.49 eV to form the two graphene-like layers than only one layer, which would result in the suppressed graphitization and reduced chemical wear of the diamond tool.

Introduction

In the 21st century, miniaturization has gained rising importance owing to the increasing demand for higher precision and further downsizing of various devices. The ultra-precision processing technology has allowed for higher quality and reliability of products with complex shapes and micro-features. Natural single crystal diamond, said to be the hardest natural material on the Earth, is considered to be an excellent precision cutting tool in high-accuracy microscopic processing due to the excellent thermal conductivity, low thermal expansion, low coefficient of friction, and high wear resistance. It can be machined to form nanometric scale cutting edges and is widely used in ultra-precision machining of non-ferrous metals, optical components, molds, and other parts [Gao and Huang (2017), Wang et al. (2012), Zong et al. (2007), Uddin et al. (2007)].

However, single crystal diamond tools easily suffer excessive wear on their cutting edges when machining ferrous metals [Shimada et al. (2004); de Oliveira et al. (2007)]. Under the catalytic effect of ferrous metals and high interface temperatures, graphitization occurs and diamond in a metastable state transforms into stable layer graphite [Paul et al. (1996), Narulkar et al. (2009)]. Multiple experimental tests were developed to reduce the chemical wear through tool modification techniques to alter the diamond tool properties and suppress the wear initiation process. We reported in a previous study that gallium doping reduced diamond tool wear when cutting steels [Lee et al. (2019)]. Boron-doped diamond, a semiconducting material, has attracted much attention in physics and electrochemistry [Zhao and Larsson (2014), The Anh et al. (2021), Garcia-Segura et al. (2015)]. However, the addition of boron, which in the same group and has a smaller ionic radius than gallium, makes the resulting graphite more perfect [Gu et al. (2016), Bagramov (2021)]. Therefore, it is necessary to have a further understanding of the effects of different dopants on diamond properties and the wear process. The doping effect can differ not only due to different dopant atoms but also due to different doping sites. For example, the same dopant atom can cause p-type doping in substitutional doping and n-type doping in an interstitial position. The smallest inert element He, which has been used to modify the structure and strength of diamond, was also studied as the interstitial dopant [Chen et al. (2020)]. In this study, we investigate ab initio calculations, using density functional theory, the effects of doping that might affect the diamond wear. We consider mechanical effects via possible solution strengthening and thermodynamic effects via dopant-induced modifications at the diamond surface. We compute the effect of interstitial and substitutional dopants of different valence and different ionic radii (Ga, B, and He) to help disambiguate mechanical and thermodynamic effects.

Ab Initio Calculations

To verify the implications of B-, Ga-, and He-doping in a diamond cutting tool, periodic ab initio simulations were performed on pristine and doped diamond materials. The mechanical and thermodynamic effects were assessed with interstitial (I) and substitutional (S) dopants in a cubic diamond cell with 64 C atoms, as shown in Figure 1.

FIGURE 1

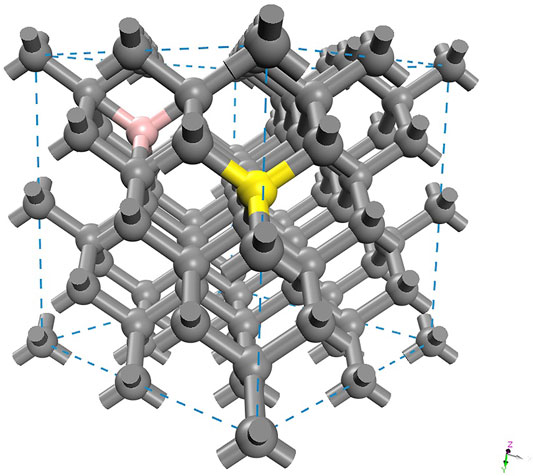
FIGURE 1. Simulation cell of diamond (dark gray) showing interstitial (pink) and substitutional (golden) positions.

B-, Ga-, and He-doped diamond materials were investigated by density functional theory (DFT) performed in the Vienna ab initio simulation package (VASP) [Kresse and Hafner (1993), Kresse and Furthmüller (1996), Kresse and Furthmüller (1996)] with the projector-augmented plane-wave method (PAW) [Blöchl (1994), Kresse and Joubert (1999)]. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional [Perdew et al. (1996), Perdew et al. (1997)] was used, and a kinetic energy cutoff of 520 eV was selected for the plane wave basis set. Energy and force convergence criteria for electronic and structural relaxations (ion positions and cell vectors) were set at 1 × 10⁻⁶ eV and 0.01 eV/Å, respectively. Based on our past theoretical work [Lee et al. (2019)], the theoretical bulk lattice constant of diamond (3.573 A˚) was used, and the Brillouin zone is sampled using a 3 × 3×3Monkhorst–Pack k-point mesh in conventional standard cubic diamond cells (64 C atoms, 7.14 Å × 7.14 Å × 7.14Å). We computed the defect formation energies (E_f), strain energies (E_s), bulk moduli BM, and electronic structures.

For both I and S configurations, the energy required to dope the material is represented by E_f which is expressed as follows:

In the case of substitutional doping:

${\mathrm{E}}_{\mathrm{f}}=\mathrm{E}\left({\mathrm{C}}_{63}\mathrm{M}\right) -\frac{63}{64}\mathrm{E}\left({\mathrm{C}}_{64}\right)-\mathrm{E}\left(\mathrm{M}\right).(1)$

In the case of interstitial doping:

${\mathrm{E}}_{\mathrm{f}}=\mathrm{E}\left({\mathrm{C}}_{64}\mathrm{M}\right)-\mathrm{E}\left({\mathrm{C}}_{64}\right)-\mathrm{E}\left(\mathrm{M}\right),(2)$

where M represents the dopant (B, Ga, or He). E(M) is the energy per atom of M in its bulk He, B, or Ga. E (C₆₄) is the energy of the pure diamond cell with 64 atoms. E (C₆₄M) and E (C₆₃M) are the energies of I- and S-doped systems.

The energy required to deform the diamond cell induced by the dopants can be estimated by E_s, where E (MC₆₄—M) is the energy of the distorted diamond material excluding the dopant atom, and E (C₆₄) is the energy of a fully relaxed pristine. In order to exclude the effect of a single vacancy defect on the strain energy, the dopant is replaced by a C atom with the same fractional coordinates in the case of S-doping, while the structure remains distorted.

${\mathrm{E}}_{\mathrm{s}}=\mathrm{E}\left(\mathrm{M}{\mathit{C}}_{64}-\mathrm{M}\right)-\mathrm{E}\left({\mathrm{C}}_{64}\right).(3)$

To assess the effects of dopants on the diamond mechanical properties, we also computed the bulk moduli BM. The value was obtained via a linear fitting equation with five data points, where P and V are the pressure and volume of a fully relaxed structure. The data points were computed by an isotropic compression and expansion of a simulation cell by −0.5, −0.1, 0.1, and 0.5% of the cell volume, as shown in Figure 2. The bulk modulus was computed as

$\mathrm{BM}=-\mathrm{VdP}/\mathrm{dV},(4)$

where V and the derivative are taken at the optimized geometry (V₀ and -a of the linear equation, as marked in Figure 2).

FIGURE 2

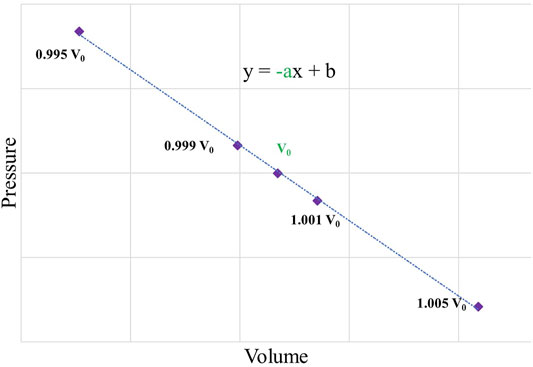
FIGURE 2. A pressure–volume diagram with the isotropic compression and expansion by −0.5, −0.1, 0.1, and 0.5% of the volume.

We also studied the effect of doping on surface energy γ, where ${\mathrm{E}}_{\mathrm{slab}}^{\mathrm{hlk}}$ is the total energy of the slab structure, ${\mathrm{E}}_{\mathrm{bulk}}^{\mathrm{hlk}}$ is the energy of the oriented bulk, and ${\mathrm{A}}_{\mathrm{slab}}$ is the surface area.

$\mathrm{\gamma }=\frac{{\mathrm{E}}_{\mathrm{slab}}^{\mathrm{hlk}}-{\mathrm{E}}_{\mathrm{bulk}}^{\mathrm{hlk}}}{2\times {\mathrm{A}}_{\mathrm{slab}}}.(5)$

The effect of doping on the surface energy can be related to stability against exfoliation (graphitization) (Lee et al., 2019).

Computational Results

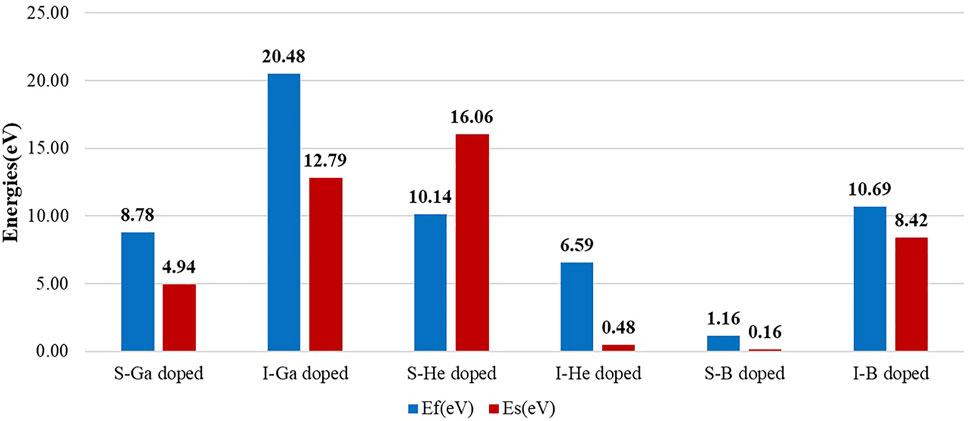
The defect formation energies of all dopants in interstitial sites are strongly positive, which means that doping is thermodynamically unfavored. Substitutional dopants are strongly energetically preferred to interstitials for both Ga and B dopants. The defect formation energy for a C vacancy in bulk diamond is 5.32 eV. For both substitutional and interstitial doping, the defect formation energies of He doping are strongly positive, 10.14 and 6.59 eV, as shown in Figure 3. There is an obvious difference in strain energies with He, 16.06 and 0.48 eV for substitutional and interstitial doping, respectively. The inert element is not chemically reactive and will not bond with other atoms, which results in significant displacements of surrounding C atoms for substitution and a very difficult way to insert but keeping the diamond crystal structure very well. But for B doping, it is obvious to see that the end state of substitution with a formation energy of 1.16 eV is much preferred to an interstitial position (10.69 eV).

FIGURE 3

FIGURE 3. Formation and strain energies for doped diamond materials.

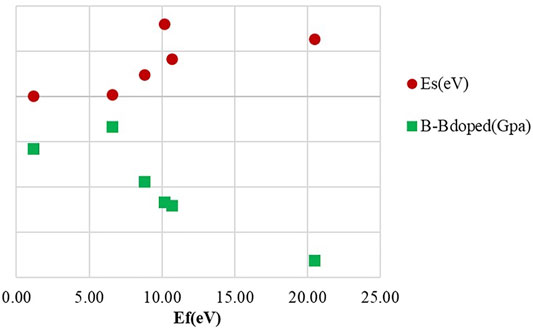
The effects of dopants on the bulk modulus are summarized in Table 1. The bulk modulus of pristine diamond is computed to be 434 GPa, in good agreement with previously reported values [Brazhkin and Solozhenko (2019)]. The small size of B leads to less softening (422.94 GPa for substitution and 410.33 GPa for insertion) than Ga doping of diamond (415.74 GPa for substitution and 398.30 GPa for insertion) for the same doping position. For He and B dopants, we get close numbers as cross interstitial and substitutional positions. As shown in Figure 4, the bulk modulus difference between pristine and doped diamond is clearly related to strain energies. It can be deduced that the larger strain energies led to mechanical softening. Although the reduction in the bulk modulus is observed under the influence of a dopant and may promote wear, the mechanical property is still acceptable for machining purposes. Based on the above results, we will only discuss one favor configuration for each dopant in the following calculation, interstitial He and substitutional structures of B and Ga.

TABLE 1

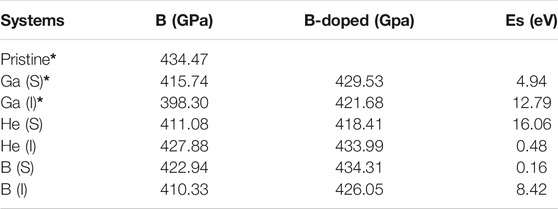
TABLE 1. The bulk modulus and strain energies of pristine and doped diamond materials. I and S are short for interstitial and substitutional positions. {^*labeled results based on the previous theoretical work [Lee et al. (2019)]}.

FIGURE 4

FIGURE 4. Strain energies and the reduction of bulk modulus for diamond with different dopants.

We compute the surface energy of pristine diamond for both (110) and (111) facets, as summarized in Table 2. The effects of dopants on the surface energy are summarized in Table 2. The surface energy decreasing (%) between pristine and doped diamond systems with 64 C atoms is calculated by the formula: ($\frac{\mathrm{E}1-\mathrm{E}2}{\mathrm{E}1}\times 100\%$).

TABLE 2

TABLE 2. Surface energies for pristine and doped diamond systems with 64°C atoms [Decreasing (%) is calculated by the formula: $\frac{\mathrm{E}1-\mathrm{E}2}{\mathrm{E}1}\times 100\%$]. {^*labeled results based on the previous theoretical work [Lee et al. (2019)]}.

Here, the decrease in surface energy is within 10% as compared with pure diamond but varies with that of different dopants. The surface energy of the (110) face decreases by 4.39 ∼9.44%. The surface energy of the (111) face decreases by 3.33% for Ga doping, 9.10% for He doping, and 6.67% for B doping. This trend shows that the higher the concentration, the greater will be the decrease. The positive impact of the dopant comes with the lowering of the surface energy of the diamond. Dopants would reduce the surface energy and increase the surface stability of the diamond tool, which can reduce the interaction at the surface.

The density of states of diamond with three different dopants is provided in Figure 5. The total DOS presents separated conduction bands (CB) and valence bands (VB). Partial DOS (PDOS) of B, Ga, and He is also presented as green lines. Compared to the DOS of pure diamond, the DOS is strongly influenced by dopants. Substitutional doping (B and Ga) in diamond moves the Fermi level downward with the reduced band gap. Additionally, interstitial doping (He) moves the Fermi level upward and introduces new energy states in the bandgap. Dopant-induced modifications would have effects on the band alignment at the diamond–iron interface and thereby on possible electrochemical reactions that might facilitate or inhibit the diamond wear.

FIGURE 5

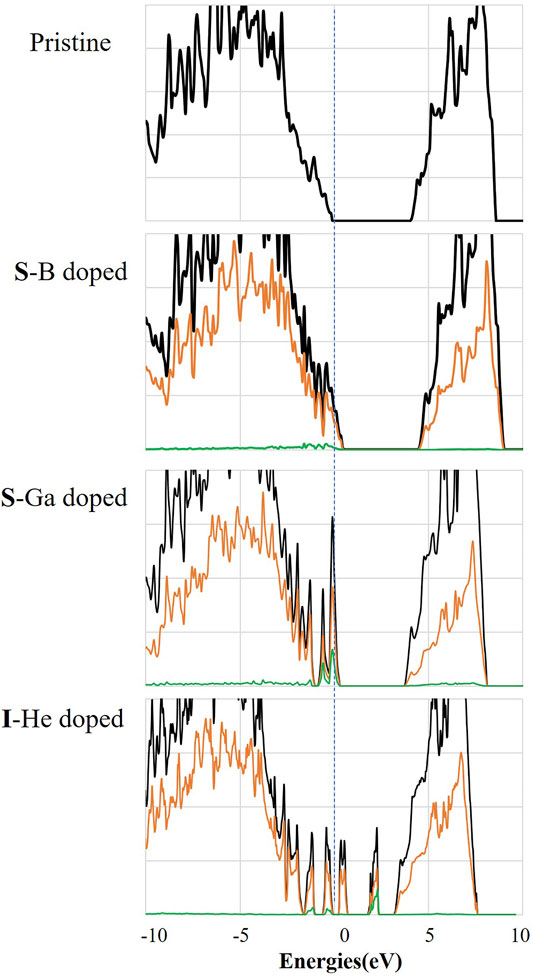
FIGURE 5. Calculated density of states (DOS) of diamond with different dopants. (The black lines represent the total DOS; brown and green lines represent the PDOS of C atoms and the dopant).

The diamond cutting ability of ferrous materials is strongly limited due to its extreme affinity to iron; diffusion of Fe is reported into the diamond layer at higher temperatures (from 600°C) [Zenkin et al. (2018)]. In DSC (differential scanning calorimetry) curves, they observed inflection points about 890 °C corresponding to the transition temperature of the diamond graphitization reaction Lee et al., 2019. The {111} plane of diamond would graphitize preferentially, and graphitization occurs when the rings of the {111} plane are flattened [Liang et al. (2012)]. To assess effects of the three dopants on the graphitization process, a diamond (111) surface (5.05 Å × 5.05 Å, 64 C atoms) was constructed with a 15 Å vacuum layer, as shown in Figure 6.

FIGURE 6

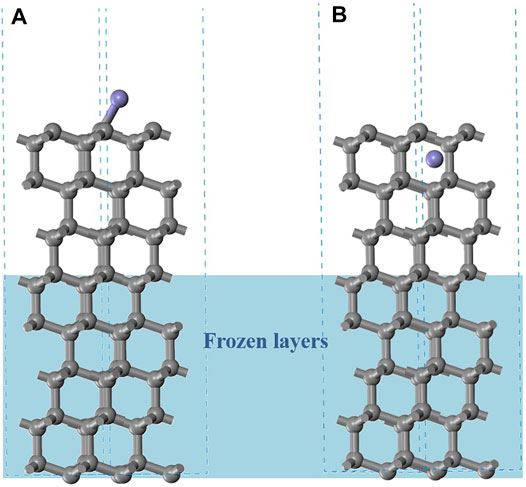
FIGURE 6. The initial structures of diamond (111) surface with different Fe diffusion locations (purple marked Fe atom position). (A) Fe binding on diamond (111) surface, (B) Fe inserted into diamond.

In the diffusion process, the Fe atom will be absorbed on the diamond surface first, as shown in (A) of Figure 6. The energy required to remove the Fe atom from the diamond (111) surface can be estimated by the binding energy E_bind, where E_slab+Fe is the total energy of the adsorption configuration. E_slab is the energy of the base fragment (diamond surface), and E_cell is the energy of unicell Fe in the face-centered cubic (fcc) arrangement with 2 Fe atoms (n = 2). The lower the bind energy, the weaker and harder is the Fe atom absorbed on the surface, and this is assumed to reduce the cutting tool wear.

${\mathrm{E}}_{\mathrm{bind}}={\mathrm{E}}_{\mathrm{slab}+\mathrm{Fe}}–{\mathrm{E}}_{\mathrm{slab}}–{\mathrm{E}}_{\mathrm{cell}}/\mathrm{n}(6)$

According to Figure 7, there is no significant difference in the binding energy between He doping and pristine materials (6.81 and 6.78 eV). Ga doping gives a higher binding energy (7.04 eV), and B doping shows the biggest value (8.79 eV). The results indicate that the Fe atom should be much easier to bond to the diamond (111) surface after B doping. It also suggests that B doping might enhance cutting tool wear more than Ga and He doping.

FIGURE 7

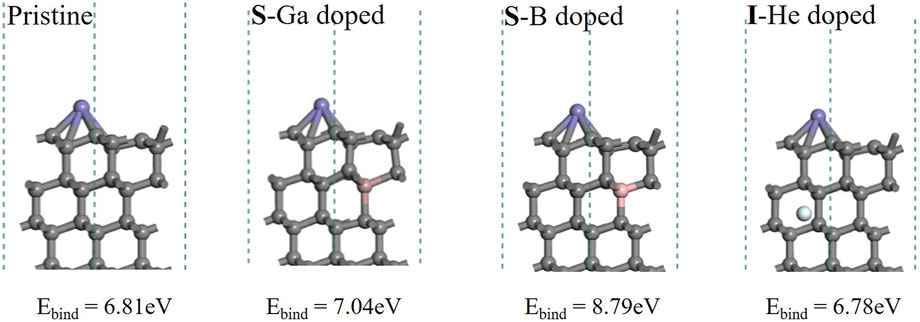
FIGURE 7. Optimized structures of adsorption configurations with Fe atoms on pristine and doped diamond (111) surfaces.

As shown in Figure 8, adsorption configurations display that all systems retain the diamond structure very well. Most C-C bonds between different layers change less than 0.1 Å. The structure is distorted only near the doping site with the large size of the Ga atom. As Fe atoms diffuse into diamond, the graphitization process appears with the surface diamond (111) bilayer morphing into a graphene-like layer. Based on Bader charge analysis, the electrons localized in the Fe atoms are listed at the bottom. Compared to pristine (6.91e), Ga doping will reduce the charge transfer from the Fe atom to surrounding C atoms (7.16e). B and He doping resulted in the graphene-like structure around the doping site.

FIGURE 8

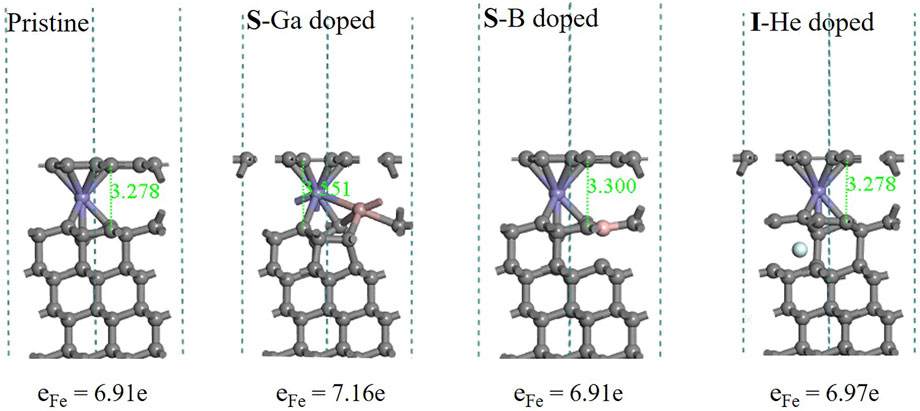
FIGURE 8. Optimized structures of pristine and doped diamond (111) surfaces with Fe atoms diffused through the top bilayer.

Figure 9 shows that there is a strong correlation between the degree of graphitization and the position of Fe sites. With Fe atoms diffusing into the diamond lattice, the deeper the Fe position, the more graphene-like layers are formed. The layers are sp² hybridized in the plane and weak π bonds to Fe atoms and the diamond substrate. It can be clearly seen that Ga doping makes a C-C bond in the substrate shorter (1.539 Å) than that in pristine diamond (1.685 Å).

FIGURE 9

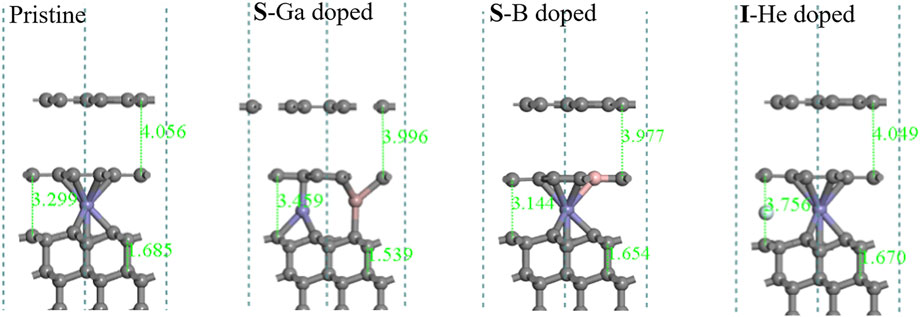
FIGURE 9. Optimized structures of pristine and doped diamond (111) surfaces with Fe atoms diffused through the second bilayer.

Figure 10 reveals thermodynamic effects of different doping on graphitization as Fe atoms diffuse into the diamond lattice. After Fe atoms diffused through the first diamond (111) bilayer, all dopants make sp3-hybridized carbon atoms more susceptible to graphitization in thermodynamics. In the pristine system, there is only 2.42 eV released as one graphene-like layer is formed (3.08, 3.26 and even 9.06 eV released as B, He, and Ga doped). Furthermore, the different and interesting phenomenon occurred while Fe atoms diffused through the second C-C bilayer in the next step. The interstitial He atom is located in the same intermediate layer. He doping made reactants release more energy (5.06), and the exothermic reaction would be much more favorable. Compared to the pristine system, B atoms are given the same fundamental sp² hybridized bonds and are more stable than sp³ hybridized atoms. Therefore, B doping demonstrated a similar phenomenon and may slightly accelerate the reaction. The larger ion radius of Ga results in a stronger interaction with the neighboring C atoms. Ga doping of diamond exhibited a completely opposite trend. It needs 2.49 eV to form another graphene-like layer. It is explained that the graphitization process is inhibited to some extent, with Ga dopants and the chemical wear of the diamond tool being reduced.

FIGURE 10

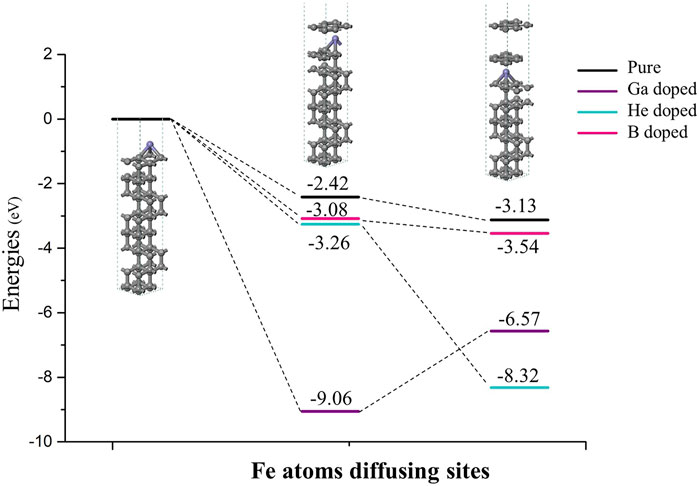
FIGURE 10. As Fe atoms diffusing into the diamond lattice, thermodynamic effects of different doping on graphitization. The black lines represent the pristine systems without dopants; purple, sky blue and pink lines represent the Ga, He and B doped systems.

Conclusion

In this study, ab initio calculations are adopted to investigate the mechanical and thermodynamic effects of doping that might affect the diamond wear. We consider interstitial and substitutional dopants of different valence and different ionic radii (Ga, B, and He) to help identify the working principle. To summarize, some conclusions can be drawn.

1) The bulk modulus difference between pristine and the doped diamond is clearly related to strain energies. The larger strain energies led to mechanical softening.

2) All three dopants could reduce the surface energy and increase the surface stability of the diamond tool, which can reduce the interaction at the surface.

3) Three dopants make the diamond (111) surface more susceptible to graphitization in thermodynamics. It is especially favorable for the Ga-doped diamond, 9.06 eV released as the top graphene-like layer formed. The sp² hybridized B atoms demonstrated a similar phenomenon with the pristine system. The interstitial He atom was located in the same intermediate layer with diffused Fe atoms, which made the reaction much more favorable.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author Contributions

LH carried out the formal analysis, investigation, data curation, writing of the original draft, and review and editing. SM was responsible for conceptualization, formal analysis, and revision. ZZ conducted the formal analysis, investigation, data curation, funding acquisition, and review and editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bagramov, R. H., Filonenko, V. P., Zibrov, I. P., Skryleva, E. A., Nikolaev, A. V., Pasternak, D. G., et al. (2021). Highly Boron-Doped Graphite and Diamond Synthesized from Adamantane and Ortho-Carborane under High Pressure. Available at: https://arxiv.org/abs/2108.04709.

Google Scholar

Blöchl, P. E. (1994). Projector Augmented-Wave Method. Phys. Rev. B 50, 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Brazhkin, V. V., and Solozhenko, V. L. (2019). Myths about New Ultrahard Phases: Why Materials that Are Significantly superior to diamond in Elastic Moduli and Hardness Are Impossible. J. Appl. Phys. 125, 130901. doi:10.1063/1.5082739

CrossRef Full Text | Google Scholar

Chen, M., Best, J. P., Shorubalko, I., Michler, J., Spolenak, R., and Wheeler, J. M. (2020). Influence of Helium Ion Irradiation on the Structure and Strength of diamond. Carbon 158, 337–345. doi:10.1016/j.carbon.2019.10.078

CrossRef Full Text | Google Scholar

de Oliveira, L. J., Bobrovnitchii, G. S., and Filgueira, M. (2007). Processing and Characterization of Impregnated diamond Cutting Tools Using a Ferrous Metal Matrix. Int. J. Refractory Met. Hard Mater. 25, 328–335. doi:10.1016/j.ijrmhm.2006.08.006

CrossRef Full Text | Google Scholar

Gao, S., and Huang, H. (2017). Recent Advances in Micro- and Nano-Machining Technologies. Front. Mech. Eng. 12, 18–32. doi:10.1007/s11465-017-0410-9

CrossRef Full Text | Google Scholar

Garcia-Segura, S., Vieira dos Santos, E., and Martínez-Huitle, C. A. (2015). Role of Sp3/sp2 Ratio on the Electrocatalytic Properties of boron-doped diamond Electrodes: A Mini Review. Electrochemistry Commun. 59, 52–55. doi:10.1016/j.elecom.2015.07.002

CrossRef Full Text | Google Scholar

Gu, C., Li, W., Xu, J., Xu, S., Lu, C., Xu, L., et al. (2016). Graphene Grown Out of diamond. Appl. Phys. Lett. 109, 162105. doi:10.1063/1.4964710

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab Initiomolecular Dynamics for Liquid Metals. Phys. Rev. B 47, 558–561. doi:10.1103/physrevb.47.558

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Lee, Y. J., Hao, L., Lüder, J., Chaudhari, A., Wang, S., Manzhos, S., et al. (2019). Micromachining of Ferrous Metal with an Ion Implanted diamond Cutting Tool. Carbon 152, 598–608. doi:10.1016/j.carbon.2019.06.043

CrossRef Full Text | Google Scholar

Liang, Y. C., Wang, Z. G., Chen, M. J., and Chen, J. X. (2012). The Influence of Crystal Plane on Graphitization of Diamond by Structure Analysis. Key Eng. Mater. 522, 142–146. doi:10.4028/www.scientific.net/kem.522.142

CrossRef Full Text | Google Scholar

Narulkar, R., Bukkapatnam, S., Raff, L. M., and Komanduri, R. (2009). Graphitization as a Precursor to Wear of diamond in Machining Pure Iron: A Molecular Dynamics Investigation. Comput. Mater. Sci. 45, 358–366. doi:10.1016/j.commatsci.2008.10.007

CrossRef Full Text | Google Scholar

Paul, E., Evans, C. J., Mangamelli, A., McGlauflin, M. L., and Polvani, R. S. (1996). Chemical Aspects of Tool Wear in Single point diamond Turning. Precision Eng. 18, 4–19. doi:10.1016/0141-6359(95)00019-4

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396. doi:10.1103/physrevlett.78.1396

CrossRef Full Text | Google Scholar

Shimada, S., Tanaka, H., Higuchi, M., Yamaguchi, T., Honda, S., and Obata, K. (2004). Thermo-Chemical Wear Mechanism of Diamond Tool in Machining of Ferrous Metals. CIRP Ann. 53, 57–60. doi:10.1016/S0007-8506(07)60644-1

CrossRef Full Text | Google Scholar

The Anh, L., Catalan, F. C. I., Kim, Y., Einaga, Y., and Tateyama, Y. (2021). Boron Position-dependent Surface Reconstruction and Electronic States of boron-doped diamond(111) Surfaces: an Ab Initio Study. Phys. Chem. Chem. Phys. 23, 15628–15634. doi:10.1039/D1CP00689D

PubMed Abstract | CrossRef Full Text | Google Scholar

Uddin, M. S., Seah, K. H. W., Rahman, M., Li, X. P., and Liu, K. (2007). Performance of Single crystal diamond Tools in Ductile Mode Cutting of Silicon. J. Mater. Process. Technol. 185, 24–30. doi:10.1016/j.jmatprotec.2006.03.138

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z. Y., Dong, L. H., Wang, D. S., and Dong, Y. H. (2012). Study of HPHT Single crystal diamond as Precision Cutting Tool Material. Precision Eng. 36, 162–167. doi:10.1016/j.precisioneng.2011.07.009

CrossRef Full Text | Google Scholar

Zenkin, S., Gaydaychuk, A., Okhotnikov, V., and Linnik, S. (2018). CVD Diamond Interaction with Fe at Elevated Temperatures. Materials 11, 2505. doi:10.3390/ma11122505

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, S., and Larsson, K. (2014). Theoretical Study of the Energetic Stability and Geometry of Terminated and B-Doped Diamond (111) Surfaces. J. Phys. Chem. C 118, 1944–1957. doi:10.1021/jp409278x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zong, W. J., Cheng, K., Li, D., Sun, T., and Liang, Y. C. (2007). The Ultimate Sharpness of Single-crystal diamond Cutting Tools-Part I: Theoretical Analyses and Predictions. Int. J. Machine Tools Manufacture 47, 852–863. doi:10.1016/j.ijmachtools.2006.04.001

CrossRef Full Text | Google Scholar