- 1Department of Civil Engineering, National Taiwan University, Taipei, Taiwan
- 2Physics Department, National Taiwan University, Taipei, Taiwan
- 3Institute of Physics, Academia Sinica, Taipei, Taiwan
- 4Physics Department, National Taiwan Normal University, Taipei, Taiwan
- 5Department of Biomedical Engineering, National Taiwan University, Taipei, Taiwan
The emerging demand for advanced structural and biological materials calls for novel modeling tools that can rapidly yield high-fidelity estimation on materials properties in design cycles. Lattice spring model , a coarse-grained particle spring network, has gained attention in recent years for predicting the mechanical properties and giving insights into the fracture mechanism with high reproducibility and generalizability. However, to simulate the materials in sufficient detail for guaranteed numerical stability and convergence, most of the time a large number of particles are needed, greatly diminishing the potential for high-throughput computation and therewith data generation for machine learning frameworks. Here, we implement CuLSM, a GPU-accelerated compute unified device architecture C++ code realizing parallelism over the spring list instead of the commonly used spatial decomposition, which requires intermittent updates on the particle neighbor list. Along with the image-to-particle conversion tool Img2Particle, our toolkit offers a fast and flexible platform to characterize the elastic and fracture behaviors of materials, expediting the design process between additive manufacturing and computer-aided design. With the growing demand for new lightweight, adaptable, and multi-functional materials and structures, such tailored and optimized modeling platform has profound impacts, enabling faster exploration in design spaces, better quality control for 3D printing by digital twin techniques, and larger data generation pipelines for image-based generative machine learning models.
1 Introduction
Materials with complex geometry and multiple constituents can be difficult to predict the mechanical properties, such as elasticity, plasticity, hysteresis, and fracture. The properties are usually coupled with the structure and topology of materials, and in many cases change under different boundary conditions. Classical solid mechanics are highly accurate if the assumptions of homogeneity and small deformation are practical. Problems arise when materials become nonhomogeneous and undergo large deformation. Multiple assumptions and parameter fittings are often required, engendering intensive computational cost and prolonged calibration. In particular, many biomimetic and bioinspired motifs involve complex structures and composite materials by design (Wegst et al., 2015). For example, birds have hollow and pneumatized bones for avian purpose. Inside the dense and thin exterior, there are hollows with internal reinforcing structures, including ridges, struts, and foams (Sullivan et al., 2017) (Figure 1). These complex structures pose nearly insurmountable challenges to continuum approaches (such as finite element methods, FEMs) since the number of elements required by sufficiently detailed characteristics increases dramatically. To resolve the computational intractability of ultra-high mesh models, homogenization techniques are often adopted to replace the materials at smaller scales by the equivalent larger ones (Roters et al., 2010). The degrees of freedom therefore decrease correspondingly in favor of the computing capability and desired scalability. However, the process of homogenization inevitably losses information content and geometry details, leading to inaccurate evaluation on the mechanical properties. In this regard, a different perspective is necessary for describing the materials in an efficient approach but without much loss of details.
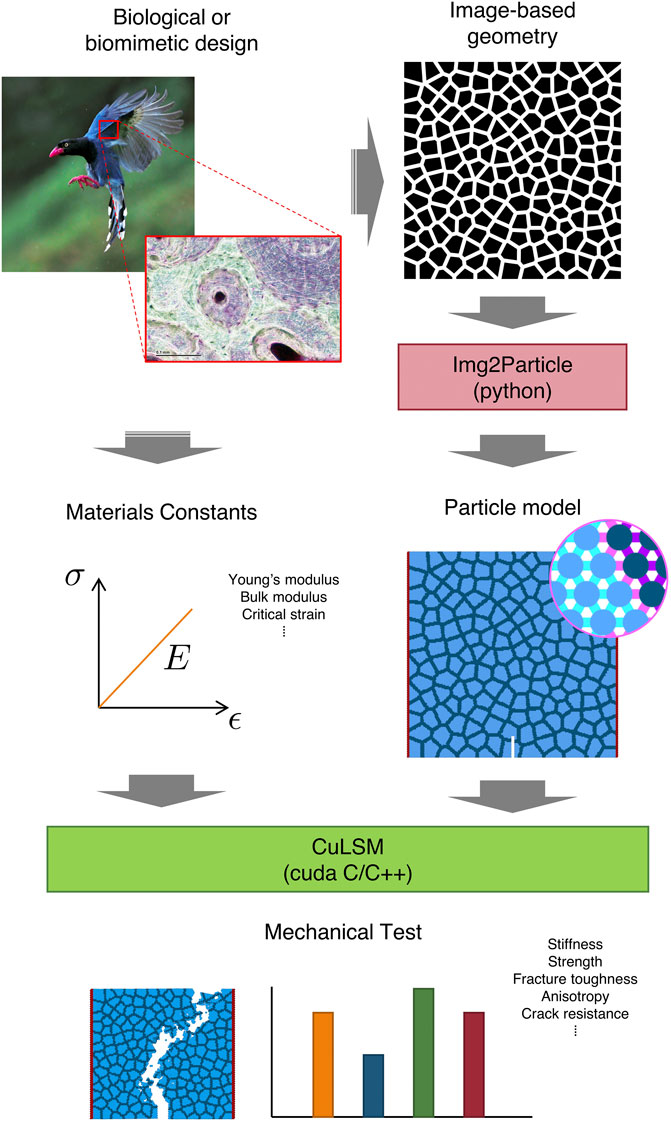
FIGURE 1. ImageMech platform from image to mechanical properties. Taiwan blue magpie (Urocissa caerulea) (photo credit: John & Fish on Flickr, CC BY-NC-ND 2.0). Cross section of bird bone (photo credit: Josef Reischig, CC BY-SA 3.0).
Lattice spring model (LSM) has been proved to be an effective tool to predict the elasticity, plasticity, and fracture behaviors of metals (Buxton et al., 2001; Chen et al., 2014), osteon-inspired cellular composites (Libonati et al., 2017), and geometrically toughened structural composites (Chiang et al., 2020; Tsai et al., 2021). The underlying physics of LSM is simply the truncated potential of springs between particles (or beads), which are the representative volume element (RVE) of the discrete material bodies. The fracture occurs when the length of elongated spring exceeds the critical length, leading to the spring breakage and the release of stored elastic strain energy. This straightforward criteria has provided predictive insights in the fracture behaviors of many brittle materials.
One of the most popular codes for large-scale particle dynamics simulations is LAMMPS (http://lammps.sandia.gov). The current acceleration of LSM calculation in LAMMPS package relies on spatial decomposition rather than spring list (bond list) parallelization. Parallelization on large spring list is crucial for LSM acceleration since the spring force calculation is the major bottleneck of time integration. Each particle in the middle of triangular packing lattice, for example, has six springs connected with its first nearest neighbors. To enhance the performance of LSM simulation, we develop a CUDA-enhanced lattice spring model code (CuLSM), which implements GPU parallelization on particle and spring lists. CuLSM provides a great speedup for large particle-spring networks with tens of thousands of particles and springs. This work as well as associated codes is important for future large-scale LSM simulations where a large number of particles are necessary to provide enough resolution for biological/biomimetic geometries and complex physical phenomena such as stress concentration, shielding, and plastic zone.
Here we present a handy platform to evaluate the mechanical properties of biological or biomimetic materials design based on 2D image geometry and prescribed materials constants. The images can be obtained from microscopy, computed tomography scan (Liang et al., 2009; Bibb et al., 2011), or other imaging methods and artificial design (such as generative adversarial networks) and can be converted into different types of particles based on the gray-scale pixel values. We report an image-particle conversion tool—Img2Particle, which takes the image and number of particle types as input, and outputs the triangular packing particle model with boundary and notch for mechanical characterization. CuLSM subsequently performs displacement-control mechanical test to determine the mechanical properties. System energies, particle trajectories and other derived attributes are computed using various parallelism scheme. The platform provides reliable pipeline from image to mechanical properties and meanwhile achieves high-performance speedup compared with CPU-centered programs.
2 Materials and Methods
2.1 Force Calculation
Consider two particles i, j connected by a harmonic spring of stiffness k. The potential energy (elastic strain energy) stored in the spring can be expressed in a function of two particle coordinates ri and rj. For a system with N particles and M springs, the total potential energy is
where rij = ‖ri − rj‖ and
The force exerted on the individual particle i can be obtained through the gradient of potential energy
where Fji is the force applied by the spring (i, j) on the particle i.
2.2 Velocity Verlet Integration
Velocity Verlet integration is used to solve the second-order ODE of Newton’s equation of motion
Second, the accelerations at the next timestep are obtained from the forces using the configuration at the next timestep x(t + Δt).
Third, the velocities at the next timestep are then updated as
In code implementation, we use the half-step velocity scheme to further reduce the memory usage of acceleration vectors. Velocity verlet integration has been proved to be numerically stable and possess important properties for physics such as time reversibility.
2.3 GPU Parallelization
Instead of using spatial decomposition which requires prior knowledge of particle coordinates and multiple CPU threads to divide entire domain into several computing subdomains, this work applies GPU parallelization to the force calculations of spring list. By doing so, the algorithm focuses on the pair relations between particles connected by springs regardless of their separating distance. The method has a merit that the examination of particle coordinates is unnecessary and therefore accelerates the computing speed.
Simulations are implemented by the in-house CUDA C++ code CuLSM on a desktop with Intel i5-8400 and Nvidia GeForce GTX 1060. First, vectors of positions, velocities, and accelerations of all particles are copied from host to device memory. All of the subsequent boundary displacement and velocity Verlet integration are executed on the device, with periodic callback copying from device to host when the output of particle states are needed. Five GPU kernel functions for boundary displacement, updating position, calculating force, updating acceleration, and updating velocity are implemented at each timestep controlled sequentially by CPU.
Positions, velocities, and accelerations vectors of all particles are flattened into 1D array and assigned continuously in both host and device memory. 1D block in 1D grid is used, and the block size is fixed as 256 for both particle and spring list. The grid size is dynamically allocated according to the model size of LSM.
Figure 2 shows the computing flowchart in CuLSM. In the preprocessing stage, the initial particle-spring network is constructed from the desirable geometry. Particle masses and spring parameters are then assigned according to their specific types. After the model is constructed, the boundary conditions and simulation configurations are set. At this stage, CuLSM has read model input, boundary conditions, and simulation configurations and has stored the data in host memory. Before simulation starts, particle and bond vectors are copied from host memory to device memory. At each timestep, boundary displacements are first applied using a GPU kernel function. Another three GPU kernel functions for updating positions, velocities, and accelerations are then initialized for velocity Verlet integration. The position, velocity, and acceleration vectors are flattened into 1D arrays and are allocated continuously in the global memory space. Due to the independence of vector spaces, each thread takes care of single component at a time. However, in the force calculation, the race condition emerges when multiple spring forces try to access and add particle forces at the same time, leading to memory conflicts and unexpected results. Thus, the atomic operation is used to serializing the requests (access and addition) from threads across the entire grid. The particle forces are first set as zeros and then summed over spring forces using atomicAdd function, as shown in the following code.
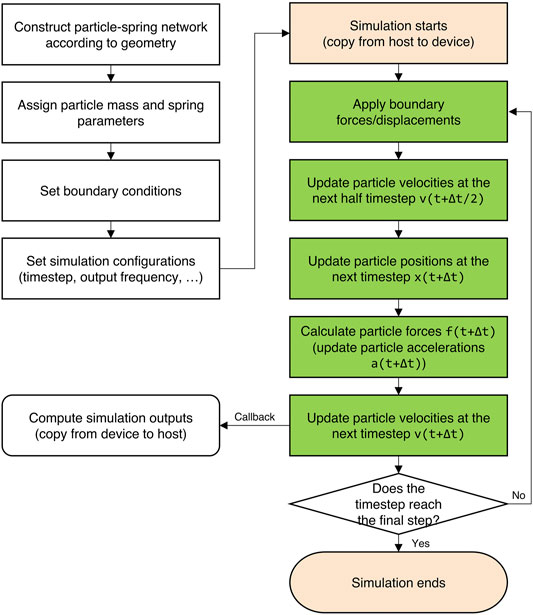
FIGURE 2. Computing flowchart in CuLSM. The green blocks are implemented by GPU kernels, which parallelize particle and spring vectors. At each iteration, timestep is checked if satisfying the conditions for callback or termination.
At each iteration, timestep is checked if satisfying the conditions for callback or termination. Once the condition for simulation output is satisfied, particle position and velocity vectors are copied back from device to host memory. The spring stiffness vector is also copied for calculating potential energy. The system potential energy and kinetic energy are calculated on CPU.
3 Results
3.1 CuLSM Demonstrates Strong Validity Against Analytical and Numerical Results
We first compare the trajectory of a simple harmonic oscillator solved numerically by CuLSM with the analytical solution. For a system consisting of two particles with mass m = 1 kg connected by a harmonic spring with spring constant k = 1 × 10−4 N/m and equilibrium distance r0 = 10 m, the equation of motion is a second-order ordinary differential equation:
We fix one particle at the origin x = 0 m and place another one still at x = 3r0/2 m when time t = 0 s, as shown in Figure 3A. The time integral interval δt for CuLSM is set as 1 s. The simulation was run for 1,000 s and the output interval is 10 s. As depicted by Figure 3B, our model provides an accurate numerical solution for a simple harmonic oscillator without error accumulation over time.
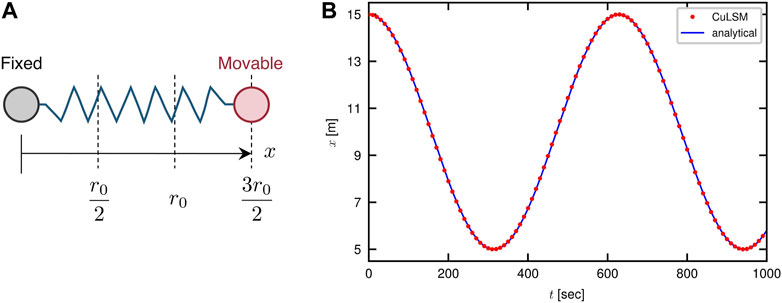
FIGURE 3. Validation of CuLSM against the analytical solution of a simple harmonic oscillator. (A) Boundary and initial conditions of the oscillator. (B) Trajectory computed by CuLSM compared to analytical solution.
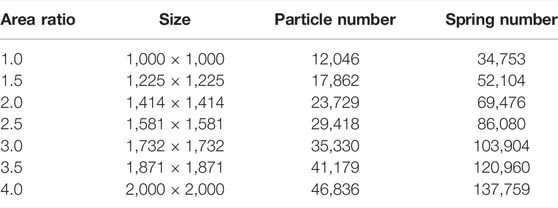
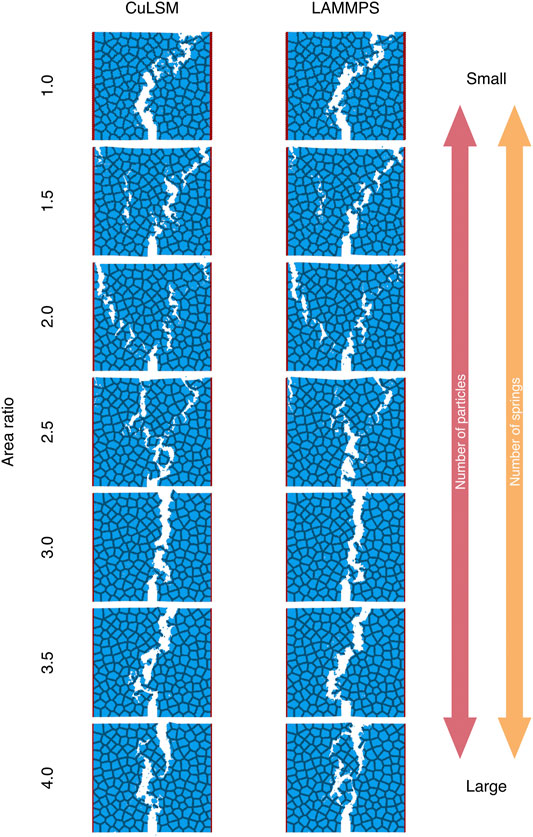
We also test our code against LAMMPS (Mar 3, 2020, stable release) and compare the performance in the next subsection. As illustrated by Figure 4A, we construct a series of 2D composite materials with the soft inclusions arranged in a Poisson distribution (Chiang et al., 2020). Three kinds of linear fracture springs, including stiff-stiff, soft-soft, and stiff-soft springs, are used to model stiff, soft and interfacial materials (Table 1). The stiff, soft, and boundary particles are marked as dark blue, light blue, and red, respectively. To model the mode-I fracture behaviors, boundary particles were displaced apart along x axis at the strain rate of 10–6. The size of composites increases from 1,000 × 1,000 to 2,000 × 2,000 squared unit length, with area ratio ρA linearly increasing from 1.0 to 4.0 (Table 2). The uniaxial tensile tests are performed to validate the results by CuLSM against those by LAMMPS. As shown in Figure 4B, the potential and kinetic energies computed by CuLSM perfectly coincide with those computed by LAMMPS before the peaks of potential energies. We also note that the potential and kinetic energies increase as the size of Poisson composite become large. Small energy discrepancies at large strain are observed, but the tendencies are similar. We further compare the fracture patterns obtained from CuLSM and LAMMMPS (Figure 5). Regardless of the size of the composites, CuLSM and LAMMPS yield akin fracture patterns. The cracks nucleate, propagate, and bifurcate at strikingly similar locations in CuLSM and LAMMPS series, proving strong fidelity of CuLSM. CuLSM reads input of particle geometry from LAMMPS Data file formatted in bond atom style. During simulation output, CuLSM outputs particle coordinates in LAMMPS Dump file. The outputted files are readily readable and operable by visualization tools such as OVITO (Stukowski, 2009).
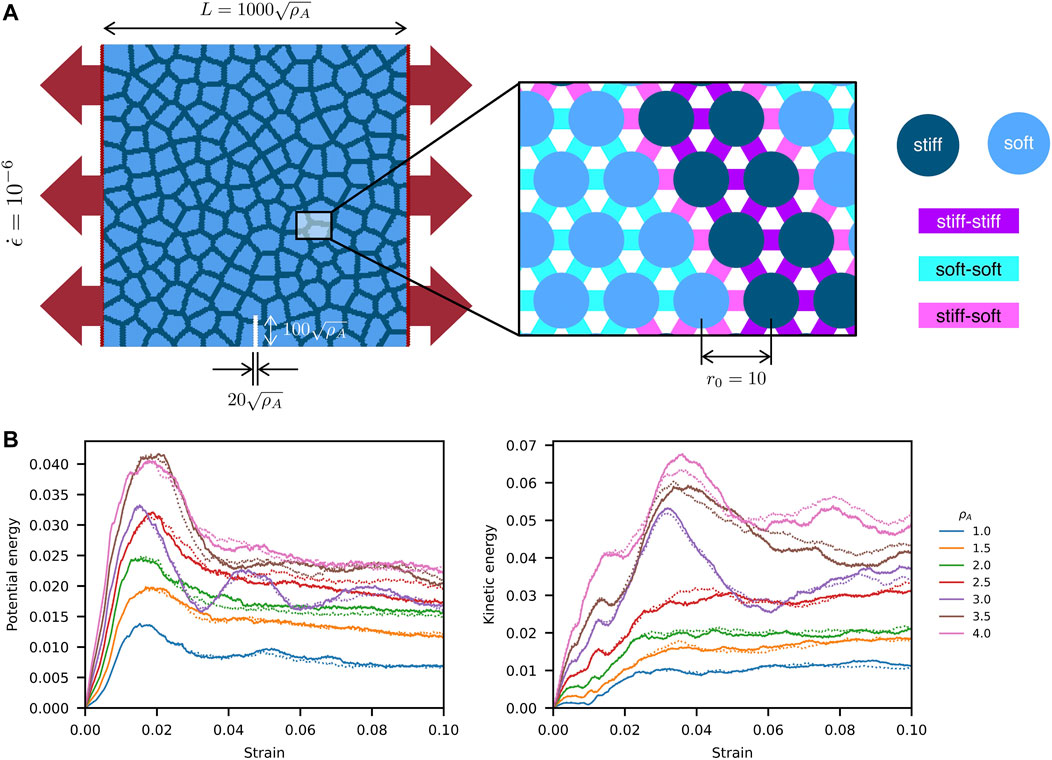
FIGURE 4. Mode-I fracture simulation of Poisson composites by LSM. (A) Model size, notch size, and boundary conditions. Stiff-stiff, stiff-soft, and soft-soft springs are used to model stiff, soft, and interfacial materials. (B) Potential and kinetic energies of LSMs with different area ratios ρA ranging from 1.0 to 4.0. The solid lines are computed by CuLSM, and the dashed lines are computed by LAMMPS.
In Figure 6, we present virial stress σV (Subramaniyan and Sun, 2008; Thompson et al., 2009) and Lagrangian strain ϵL (Shimizu et al., 2007) fields of Poisson composite at bulk engineering strain ϵ = 0.02:
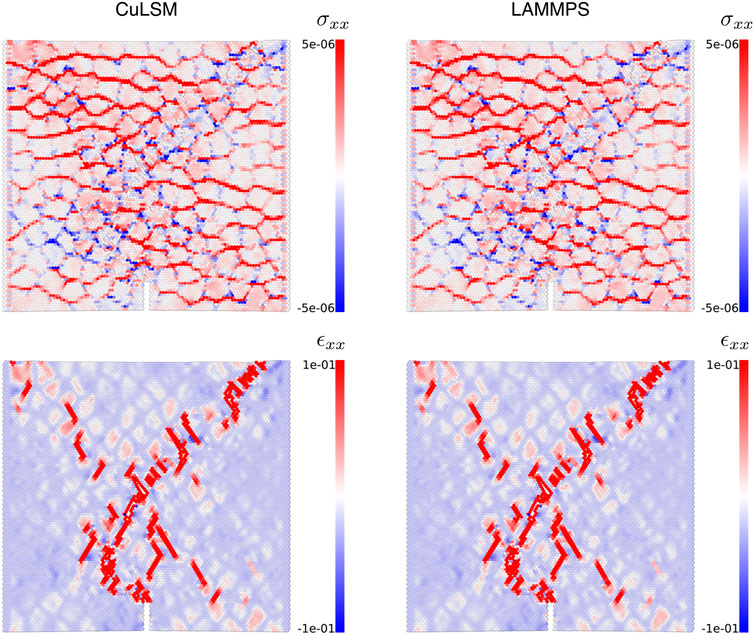
FIGURE 6. Stress and strain fields in Poisson composites calculated by CuLSM and LAMMPS at engineering strain ϵ = 0.02.
where Ω is the finite domain volume considered, x, v are particle position and velocity, f is the force between particle pairs; J is the locally affine transformation matrix considering the relative displacement of particle with its first nearest neighbors, and δ is the Kronecker delta. The result indicates that the discrepancies of stress and strain fields calculated by CuLSM and LAMMPS are negligible.
3.2 CuLSM Achieves Superior Computing Speed
To benchmark the performance of CuLSM, we record the computing time of mode-I fracture simulations on Poisson composites of different sizes, as listed in Table 2. In Figure 7, we compare the total wall time of simulations by CuLSM (1 CPU + 1 GPU) and LAMMPS with 1 CPU, 2 CPUs, 4 CPUs, and 1 CPU + 1 GPU. With inter-processor communication cutoff rcomm = 100r0 and default step interval for neighbor list update Tn = 10, LAMMPS with 1 CPU can be one to two orders slower than CuLSM. With these settings, LAMMPS is unfavorably slow and the spatial decomposition scheme is incapable of accelerating the LSM simulation efficiently. Note that LAMMPS does not currently support GPU acceleration on bond potentials. Therefore, LAMMPS 1 CPU + 1 GPU shows no speedup compared to LAMMPS 1 CPU. With communication cutoff (rcomm = 4r0) and turning off the neighbor list update (Tn = ∞), the total wall time of LAMMPS scales in the same order as CuLSM with respect to the particle number. CuLSM can be up to 4.4 times faster than LAMMPS with 1 CPU and have around 1.5 speedup compared to LAMMPS with 4 CPUs. CuLSM-CPU with 1 CPU has comparable speed with LAMMPS with 2 CPUs. Note that the optimal neighbor setting depends on the simulation cases for the spatial decomposition scheme. The GPU speedup of CuLSM, i.e., the speedup of CuLSM 1 CPU + 1 GPU against CuLSM-CPU 1 CPU, is also presented in the bottom panel of Figure 7. On the machine with Intel i5-8400 and Nvidia GeForce GTX 1060, the GPU speedup of CuLSM is about 2.5. CuLSM reduces the total wall time (including input, output, and copying) by a considerable margin, with only 1 CPU and 1 GPU. The enhanced performance results from the parallelization on particle and spring lists. The input files for all the benchmarks and more information can be found online at the link in Data Availability Statement.
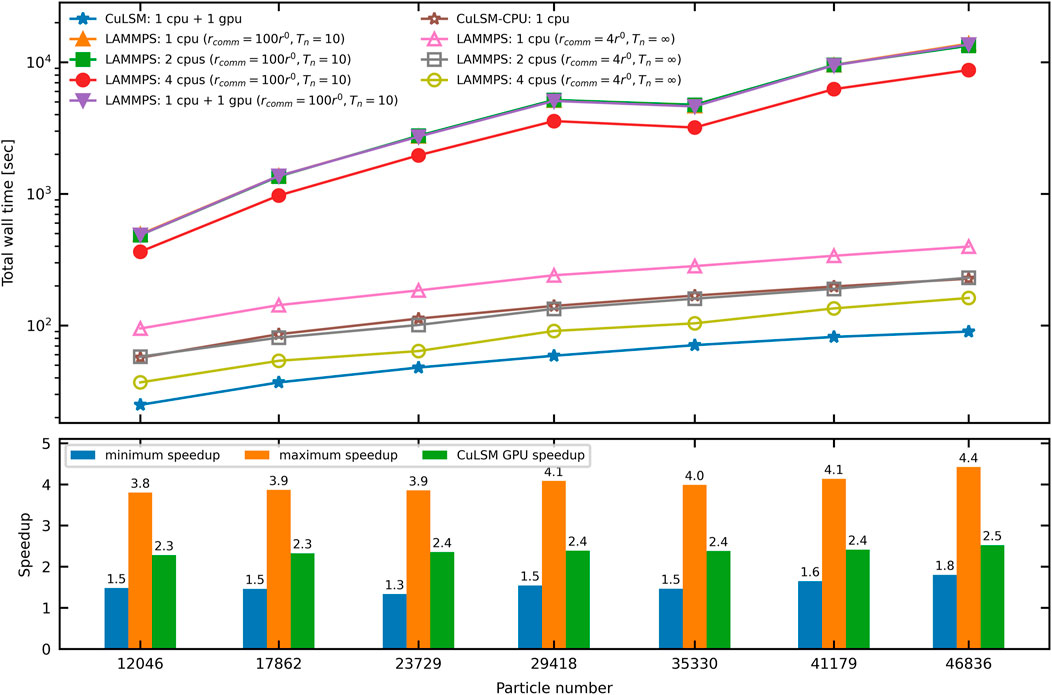
FIGURE 7. Comparison of the total computing wall time by CuLSM and LAMMPS. The insets enlarge the regions around LAMMPS: 1 CPU, LAMMPS: 2 CPUs, and LAMMPS: 1 CPU + 1 GPU. Note that LAMMPS: 1 CPU + 1 GPU does not support parallelism on spring list. The maximum and minimum speedup of CuLSM compared with other four models are illustrated in the bottom panel.
4 Discussion and Conclusion
In this work, we present a CUDA C++ code CuLSM for large-scale LSM simulations. By realizing the parallelism on particle and spring lists, CuLSM has been optimized for LSM simulations and secures a remarkable boost in computing speed in comparison with general-purpose LAMMPS package. Since all of the interactions in LSM are harmonic pair potentials, the speedup of spatial decomposition used in LAMMPS is limited. Without updating neighbor list during simulations, CuLSM remarkably accelerates the time integration on GPU and only copy data from device to host when needed.
Currently, the broken springs are not deleted from the spring list but are irreversibly assigned zero stiffness to emulate the free deformation. We deliberately retain these broken springs since in future studies the stiffness may need to recover when the materials is subject to compression, bending, and cyclic loading. Indeed, different spring properties and mechanical elements, e.g., non-linear elasticity, viscocity, and plasticity, are worth being added into the particle-spring networks. Multi-body potentials such as angle potential and volume-compensated particle method (Chen et al., 2014) are also of interest in future studies. More in-depth theoretical formulations are required for investigating high-level phenomena such as dislocation, Bauschinger effect, and yield surface evolution.
CuLSM is readily extensible to multi-GPUs and can be further incorporated with multithread environment for the larger and three-dimensional models. To further reduce the memory copying time between host and device, the unified memory can be used to allocate memory address space accessible from any CPUs and GPUs in the system. Moreover, the parallel reduction scheme can be adopted to speed up the calculation of the global attributes, such as potential and kinetic energies.
The future opportunities this work brings include:
• The toolkit we developed provides a faster and more flexible structure-properties platform, which expedites the particle-based simulation and materials design procedures.
• CuLSM opens the venue for high-throughput and high-fidelity data generation to meet the increasing need for machine learning aided materials design protocols (Kim et al., 2021; Sui et al., 2021).
• The work largely reduces the computational cost for predicting elasticity and fracture behaviors of complex materials systems, further accelerating the design phase through offering predictive insights for additive manufacturing and mechanical experimentation.
• The LSM simulations provide rich and detailed geometric and topological data where the relationship with high-level mechanical properties underlies. One future research direction would be finding out the physics rules from local to global hierarchy that govern the macroscopic behavior of structural materials.
In conclusion, we provide a powerful and efficient framework to characterize and predict the elasticity and fracture mechanism of materials. The remarkable speedup CuLSM enables entails more extensive application in sophisticated materials design. The robustness and adroitness it promises drive new design perspective other than continuity in practical circumstances. With the emerging new intersection between physics-based simulation and deep learning, the toolkit holds exciting key to advanced materials design.
Data Availability Statement
The CuLSM code associated with this paper is publicly available on GitHub (https://github.com/Chiang-Yuan/culsm). The Img2Particle code is available on GitHub (https://github.com/Chiang-Yuan/Img2Particle).
Author Contributions
YC conceived the idea and developed the research. YC coded the program and performed simulations with advice from T-WC. YC wrote the manuscript with input and advice from T-WC and S-WC.
Funding
The authors appreciate the financial support from the Ministry of Science and Technology, Taiwan (109-2224-E-007-003, 110-2112-M-003-009, 110-2636-E-002-013).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bibb, R., Thompson, D., and Winder, J. (2011). Computed Tomography Characterisation of Additive Manufacturing Materials. Med. Eng. Phys. 33 (5), 590–596. doi:10.1016/j.medengphy.2010.12.015
Buxton, G. A., Care, C. M., and Cleaver, D. J. (2001). A Lattice spring Model of Heterogeneous Materials with Plasticity. Model. Simul. Mater. Sci. Eng. 9 (6), 485–497. doi:10.1088/0965-0393/9/6/302
Chen, H., Lin, E., and Liu, Y. (2014). A Novel Volume-Compensated Particle Method for 2d Elasticity and Plasticity Analysis. Int. J. Sol. Structures 51 (9), 1819–1833. doi:10.1016/j.ijsolstr.2014.01.025
Chiang, Y., Tung, C.-C., Lin, X.-D., Chen, P.-Y., Chen, C.-S., and Chang, S.-W. (2020). Geometrically Toughening Mechanism of Cellular Composites Inspired by Fibonacci Lattice in Liquidambar Formosana. Composite Structures, 113349.
Kim, Y., Kim, Y., Yang, C., Park, K., Gu, G. X., and Ryu, S. (2021). Deep Learning Framework for Material Design Space Exploration Using Active Transfer Learning and Data Augmentation. npj Comput. Mater. 7 (1), 1–7. doi:10.1038/s41524-021-00609-2
Liang, X., Jacobs, R., Martens, W., Hu, Y., Adriaensens, P., Quirynen, M., et al. (2009). Macro- and Micro-anatomical, Histological and Computed Tomography Scan Characterization of the Nasopalatine Canal. J. Clin. Periodontol. 36 (7), 598–603. doi:10.1111/j.1600-051x.2009.01429.x
Libonati, F., Cipriano, V., Vergani, L., and Buehler, M. J. (2017). Computational Framework to Predict Failure and Performance of Bone-Inspired Materials. ACS Biomater. Sci. Eng. 3 (12), 3236–3243. doi:10.1021/acsbiomaterials.7b00606
Roters, F., Eisenlohr, P., Hantcherli, L., Tjahjanto, D. D., Bieler, T. R., and Raabe, D. (2010). Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in crystal Plasticity Finite-Element Modeling: Theory, Experiments, Applications. Acta Materialia 58 (4), 1152–1211. doi:10.1016/j.actamat.2009.10.058
Shimizu, F., Ogata, S., and Li, J. (2007). Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mater. Trans. 48, 0710160231. doi:10.2320/matertrans.mj200769
Stukowski, A. (2009). Visualization and Analysis of Atomistic Simulation Data with OVITO-The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18 (1), 015012. doi:10.1088/0965-0393/18/1/015012
Subramaniyan, A. K., and Sun, C. (2008). Continuum Interpretation of Virial Stress in Molecular Simulations. Int. J. Sol. Structures 45 (14-15), 4340–4346. doi:10.1016/j.ijsolstr.2008.03.016
Sui, F., Guo, R., Zhang, Z., Gu, G. X., and Lin, L. (2021). Deep Reinforcement Learning for Digital Materials Design. ACS Mater. Lett. 3 (10), 1433–1439. doi:10.1021/acsmaterialslett.1c00390
Sullivan, T. N., Wang, B., Espinosa, H. D., and Meyers, M. A. (2017). Extreme Lightweight Structures: Avian Feathers and Bones. Mater. Today 20 (7), 377–391. doi:10.1016/j.mattod.2017.02.004
Thompson, A. P., Plimpton, S. J., and Mattson, W. (2009). General Formulation of Pressure and Stress Tensor for Arbitrary many-body Interaction Potentials under Periodic Boundary Conditions. J. Chem. Phys. 131 (15), 154107. doi:10.1063/1.3245303
Tsai, Y.-Y., Chiang, Y., Buford, J. L., Tsai, M.-L., Chen, H.-C., and Chang, S.-W. (2021). Mechanical and Crack Propagating Behavior of Sierpiński Carpet Composites. ACS Biomaterials Science & Engineering.
Keywords: CUDA (compute unified device architecture), parallel computing, modeling and simulation, lattice spring model (LSM), mechanical characterisation
Citation: Chiang Y, Chiu T-W and Chang S-W (2022) ImageMech: From Image to Particle Spring Network for Mechanical Characterization. Front. Mater. 8:803875. doi: 10.3389/fmats.2021.803875
Received: 28 October 2021; Accepted: 22 December 2021;
Published: 12 January 2022.
Edited by:
Flavia Libonati, University of Genoa, ItalyReviewed by:
Alfonso Gautieri, Politecnico di Milano, ItalySumit Sharma, Dr. B. R. Ambedkar National Institute of Technology Jalandhar, India
Chi-Hua Yu, Massachusetts Institute of Technology, United States
Copyright © 2022 Chiang, Chiu and Chang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shu-Wei Chang, Y2hhbmdzd0BudHUuZWR1LnR3
 Yuan Chiang
Yuan Chiang Ting-Wai Chiu
Ting-Wai Chiu Shu-Wei Chang
Shu-Wei Chang