Temperature and Stress Dependence of Screw Dislocation Mobility in Nb-V-Ta Alloys Using Kinetic Monte Carlo Simulations

In this work we present simulations of thermally-activated screw dislocation motion in Nb-Ta-V alloys for two distinct scenarios, one where kink propagation is solely driven by chemical energy changes, i.e., thermodynamic energy differences, and another one where a migration barrier of 1.0 eV is added to such changes. The simulations have been performed using a kinetic Monte Carlo model for screw dislocation kinetics modified for complex lattice-level chemical environments. At low stresses, we find that dislocation motion in the case with no barrier is controlled by long waiting times due to slow nucleation rates and extremely fast kink propagation. Conversely, at high stress, the distribution of sampled time steps for both kink-pair nucleation and kink propagation events are comparable, resulting in continuous motion and faster velocities. In the case of the 1.0-eV kink propagation energy barrier, at low stresses kink motion becomes the rate-limiting step, leading to slow dynamics and large kink lateral pileups, while at high stresses both kink pair nucleation and kink propagation coexist on similar time scales. In the end, dislocation velocities differ by more than four orders of magnitude between both scenarios, emphasizing the need to have accurate calculations of kink energy barriers in the complex chemical environments inherent to these alloys.

1 Introduction

Among the several hundred or so different high-entropy alloy (HEA) combinations currently in existence (Kozak et al., 2015; Senkov et al., 2015; Gao et al., 2018), refractory multi-element alloys (RMEA) are a special type composed of four or more refractory metal elements (Nb, Mo, Ta, V, W, Cr, Hf, Zr). While compositionally complex, these systems generally crystallize into a simple body-centered cubic (bcc) phase, found to be stable up to very high temperatures (Senkov et al., 2011; Zou et al., 2014; Dobbelstein et al., 2016; Körmann and Sluiter, 2016; Yao et al., 2016; Yao et al., 2017; Senkov et al., 2018; Kube et al., 2019). RMEA display sluggish self-diffusion rates (Chang et al., 2014; Beke and Erdaglyi, 2015; Zhao et al., 2017; Roy et al., 2021) and, similar to their pure bcc metal counterparts, suffer from a lack of ductility at low temperatures (Senkov et al., 2011; Soni et al., 2018). However, they retain high mechanical strength and ductility at high temperature, making them attractive candidates for structural applications in the power, aerospace, or nuclear sectors (Miracle et al., 2014; Xia et al., 2015, 2016; Kumar et al., 2016; Yeh and Lin, 2018). Figure 1 shows compression test results for the Nb₂₅Mo₂₅Ta₂₅W₂₅ system, clearly illustrating both of the points just discussed.

FIGURE 1

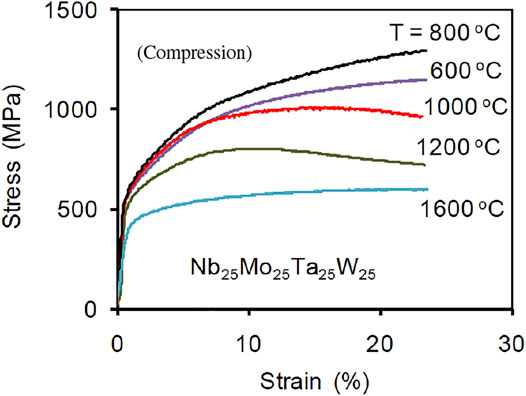
FIGURE 1. Engineering strain versus engineering stress curves for the Nb₂₅Mo₂₅Ta₂₅W₂₅ alloy obtained during compression testing at elevated temperature [from Senkov et al. (2011)] (Reprinted with permission from Elsevier).

While the deformation mechanisms of bcc metals and their alloys are relatively well understood, theories that explain the behavior observed in body-centered cubic RMEA have only recently begun to be developed (Rao et al., 2019; Maresca and Curtin, 2020a; Maresca and Curtin, 2020b; Yin and Curtin, 2020). These theories are built around the idea that each atom in the alloy can be regarded as a solute atom in an effective matrix defined by the average properties of the constituent elements. As such, every single atom in the lattice contributes to (solution) hardening, potentially resulting in a large strengthening effect (often referred to as “cocktail” effect). At the same time, these local chemical fluctuations enhance the concentration of equilibrium kinks on screw dislocation lines, potentially reducing the importance of kink-pair nucleation and shifting it instead to kink lateral motion (Zhou et al., 2021). This signifies a departure from “classical” bcc metal plasticity, which is known to be controlled by the thermally-activated glide of 1/2⟨111⟩ screw dislocations on close-packed planes (Gilbert et al., 2011; Stukowski et al., 2015; Cereceda et al., 2016). A natural consequence of the proliferation of kink pairs along a screw dislocation line is the enhanced formation of cross kinks, i.e., adjacent kinks on different glide planes (Marian et al., 2004). Cross-kinks are non-glissile structures (see Figure 2) that can be resolved either conservatively, by closing on themselves by the subsequent nucleation of kinks on complementary slip planes, or non-conservatively by emission of point defects. In both cases, this can lead to considerable self-pinning, which may also help explain the high-temperature strength of RMEA.

FIGURE 2

FIGURE 2. Simulated steady-state configuration of a screw dislocation line at 600 K in a Nb-Ta-V alloy showing the presence of kinks and cross-kinks at zero stress [from Zhou et al. (2021)].

A crucial factor to investigate plastic deformation in these systems is to understand dislocation motion and its dependence on deformation conditions. Molecular dynamics (MD) is a natural choice to carry out these studies provided that accurate interatomic potentials are available. While RMEA present an exceptionally challenging paradigm from the standpoint of fitting traditional potentials, recent machine-learned force fields for complex multi-element alloys are gradually enabling more accurate atomistic simulations (Zhou et al., 2019; Li et al., 2020; Rickman et al., 2020). For example, recent MD simulations based on these potentials have revealed a complex relationship between dislocation motion and the existence of short-range order in Nb-Mo-Ta-W alloys (Yin et al., 2021). However, MD simulations are still subjected to the usual time and length scale limitations, which often overlook the importance of thermally-activated mechanisms and their role in dislocation motion.

In a previous work, we have developed a kinetic Monte Carlo (kMC) model to simulate screw dislocation motion in Nb-Ta-V alloys (Zhou et al., 2021). The model is built by adding dislocation-solute interaction energies to a pure bcc metal description of kink-pair nucleation and kink propagation rates (Stukowski et al., 2015). These interaction energies are pre-computed by using first-principles atomistic methods in supercells containing dislocations with the appropriate alloy composition (Ghafarollahi et al., 2019). Here, we conduct stress-driven simulations of screw dislocation motion as a function of temperature to calculate dislocation velocities and study the relevant mechanisms. While the kMC model makes use of a number of approximations, it allows us to explore the features of slip associated with three-dimensional behavior and long dislocation lines. Thus, this model is a first attempt to embed some of the complexites of the highly-random alloy into a mesoscale framework with the aim of capturing time and length scales more suitable for experiments, as compared to MD.

The paper is organized as follows. First, we provide the theoretical framework for the kinetic Monte Carlo model. This is followed by a description of the numerical implementation and modifications of the kMC simulator to adapt it to the alloy of choice. Next we calculate dislocation velocities in the alloy as a function of temperature and stress. We finalize the paper with a discussion of the results and the conclusions.

2 Methods: Kinetic Monte Carlo Model of Screw Dislocation Motion in a Multielement Alloy

2.1 Pure Metal Formulation

As discussed above, plasticity in bcc metals is governed by the motion of screw dislocations on close-packed planes. Generally, this motion is understood to occur over a periodic energy landscape known as the Peierls potential U_P. U_P is typically quite stiff, resulting in high critical (Peierls) stresses, τ_P, (Weinberger et al., 2013; Dezerald et al., 2015), and at low-to-medium homologous temperatures slip proceeds via thermally-activated nucleation of steps on the dislocation line, known as kink pairs, and their subsequent sideward relaxation. Kink-pair nucleation is a rare event, i.e., one that occurs with a low probability over the scale of atomic vibrations. Thus, methods with high temporal resolution such as molecular dynamics are not suitable for simulating the long-term kinetics of the system. Instead, kinetic Monte Carlo evolves the system efficiently through a sequence of thermalized states connected by transitions that define “events”. In kMC, one simply specifies the transition rates of different events, which represent the probabilities per unit time that they will occur, and then time evolves in discrete increments. With this approach, the atomistic features of the dislocation core, such as atomic vibrations and local distortions, are not directly resolved, but their effective kinetic behavior is condensed into physical transition rates that can be characterized atomistically. This is what allows us to explore mesoscopic length and time scales. Adaptations of the kMC method to simulate thermally-activated screw dislocation motion have been successfully applied to pure bcc crystals (Cai et al., 2001; Stukowski et al., 2015) and dilute alloys (Zhao and Marian, 2018; Shinzato et al., 2019; Zhao et al., 2020).

The kink-pair nucleation rate for a segment i of length ℓ_i (note that the total screw length line L is conserved: L = ∑_iℓ_i) is expressed as a function of stress and temperature as (Stukowski et al., 2015):

${{\omega }_{\text{kp}}}_i\left({\tau }_i,T\right)={\nu }_0\frac{{\ell }_i-w}{b}\exp \left(-\frac{\mathrm{\Delta }{H}_{\text{kp}}\left({\tau }_i\right)}{kT}\right)(1)$

where τ_i and T are the local resolved shear stress and the absolute temperature, respectively, ν₀ is an attempt frequency, ℓ_i is the dislocation segment length, w is the total width extent of a kink pair, b is the Burgers vector’s modulus, and ΔH_kp is the kink-pair activation enthalpy. ℓ_i is itself delimited by kinks on both sides, while w includes the distance between kinks, λ_kp, at the point of nucleation plus the spread, a, of each kink, i.e., w = λ_kp + 2a. The above expression is only defined for positive nucleation lengths, (ℓ_i − w) > 0, with segments shorter than w being discarded for the purposes of calculating ω_kp. In pure bcc metals, a common expression for ΔH_kp is the one proposed by Kocks et al. (1975):

$\mathrm{\Delta }{H}_{\text{kp}}\left(\tau \right)=\mathrm{\Delta }{H}_0{\left(1-{\left(\frac{\tau }{{\tau }_{\mathrm{P}}}\right)}^p\right)}^q(2)$

where ΔH₀ is the sum of the energies of two infinitely-separated opposite kinks, and p and q are fitting parameters. We have extended this expression to account for non-Schmid effects on dislocation glide in past works (Stukowski et al., 2015; Cereceda et al., 2016; Po et al., 2016), and dilute solid solution interactions (Zhao and Marian, 2018; Zhao et al., 2020). For their part, kinks move a distance $\delta y=v_k\delta t\pm \xi \sqrt{2D_k\delta t}$ during a given time increment δt, where v_k and D_k are the kink velocity and diffusivity, respectively, and ξ is a uniform random number. v_k and D_k represent mechanically-driven (stress-dependent) and diffusive (stress-independent) contributions to the kink motion. Generally, δt is chosen as the “waiting” time for kink pair nucleation, such that the position of existing kinks (if any) is updated prior to the next nucleation event. To avoid unphysically long kink propagation events, δy is typically capped to some distance on the order of w. Due to the finite spread, a, of individual kinks, kink pairs are considered to have a trapezoidal shape, rather than a rectangular one, for the purpose of calculating elastic stresses. However, during visualization kinks are represented as straight (i.e., pure edge) segments for simplicity.

Kink segments are identified by their non-screw character, i.e., when |t ⋅s| < 1, where t and s = b/b are the line tangent and the slip direction, respectively. Kinks are tracked in space and time throughout the simulation by monitoring their vectors t, s (constant), and n = s×t (representing the glide plane). Two kinks mutually annihilate if 1) they have opposite line directions (projected along the glide direction), 2) they share a common n vector, and 3) they are within an interaction distance a of one another. When all three conditions are met, the two kink segments are eliminated and the screw dislocation line is reconnected on the Peierls valley common to both.

The underlying topology supporting dislocation and kink segments is a discrete bcc lattice oriented along the [111] direction. The crystal model thus includes all possible lattice point locations, which in this work are assigned a chemical descriptor to represent multi-element systems. Simulations can be done with periodic boundary conditions or with finite-sized lines. Unless otherwise noted, here we use finite dislocation lines of length L = 1000b pinned at both ends to mimic the operation of a Frank-Read source in the material. Shear stress is applied such that the $\left(1\bar{1}0\right)$ plane is always the maximum resolved shear stress (MRSS) plane.

τ_i in Eqs. 1 and 2 is calculated as the Schmid stress:

$\tau =\mathit{s}\cdot \mathit{\sigma }\left({\mathit{x}}_i\right)\cdot \mathit{n}(3)$

where σ(x_i) is the local stress tensor at the location x_i of segment i. As explained by Stukowski et al. (2015), σ takes contributions from the applied stress as well as from the elastic stresses due to all unique segments i along the dislocation line. The only component of the applied stress tensor that produces a nonzero resolved shear stress with the lattice orientation considered in our model is the xz component. Thus, in this work, the stress τ_yz is a fixed input parameter that is added to the local elastic stresses everywhere in the simulation volume. In the forthcoming graphs and plots, we simply refer to this stress as the applied stress “τ.”

2.2 Environment-Dependent Kink Pair Nucleation and Kink Propagation Rates

The model employed to describe a multicomponent alloy involves the superposition of an effective substrate (often referred to as the “average” alloy) whose properties are taken as the compositional average of each of the individual element properties, and a set of lattice atoms representative of the chemical composition of the alloy. As such, Eq. 1 is modified to capture this new physical system and its effect on the dislocation kinetics. The details of these modifications have been discussed in depth by Zhou et al. (2021) and are only briefly reviewed here.

The kink-pair nucleation enthalpy in the alloy is written as a sum that includes “solute” interaction energies:

$\mathrm{\Delta }{H}_{\text{kp}}\left(\tau ;T\right)=\left(\mathrm{\Delta }{H}_0+\mathrm{\Delta }{E}_{x\to x+h}^{\text{int}}\right){\left(1-{\left(\frac{\tau }{{\tau }_{\mathrm{P}}}\right)}^p\right)}^q(4)$

where ΔH₀ is the formation energy of a pair of isolated complementary kinks in the average alloy (average across all constituent elements), $\mathrm{\Delta }{E}_{x\to x+h}^{\text{int}}$ is the change of “chemical” energy across one Peierls valley (i.e., between x and x + h) on a given dislocation segment i (with length ℓ_i), τ_P is the Peierls stress of the average alloy, and p and q are fitting parameters. The $\mathrm{\Delta }{E}_{x\to x+h}^{\text{int}}$ represent excess energies in the translation of segments of the dislocation from one location to another. As such, they are calculated for a specific spatial arrangement of lattice atoms, which reflects the composition of the random alloy. In our case, we start from a pre-generated hexagonal prism with fixed size that does not change throughout the simulation. Figure 3 shows the minimum prism size that captures all the non-MRSS {110} glide planes available to the dislocation segment for the calculation of the corresponding rates. Within these prisms,

$\mathrm{\Delta }{E}_{x\to x+h}^{\text{int}}=\sum _j{q}_j{e}_j^{\text{int}}{|}_{x+h}-\sum _i{q}_i{e}_i^{\text{int}}{|}_x(5)$

where $e_j^{\text{int}}$ are the solute (of type j) interaction energies and q_j is the number of solutes of type j surrounding the dislocation core along that segment. Note that $\mathrm{\Delta }{E}_{x\to x+h}^{\text{int}}$ may be positive or negative, indicating a favorable or unfavorable effect on kink-pair nucleation, respectively. To account for correlated transitions, both forward and backward nucleation rates are considered for each viable glide plane.

FIGURE 3

FIGURE 3. Minimal atomic environment around a dislocation line required to calculate kink event rates. The image is a view of the dislocation core along the [111] direction, showing two possible transitions to next Peierls valleys on different {110} planes. The dashed polygons represent the maximum extent of dislocation-atom interactions as indicated in Table 1.

In alloys, kink motion is itself thermally activated and thus treated also as an Arrhenius process with a propagation rate equal to:

${\omega }_{\mathrm{k}}\left(\tau ,T\right)={\nu }_1\exp \left(-\frac{\mathrm{\Delta }{E}_{\mathrm{k}}+\mathrm{\Delta }{E}_{y\to y+b}^{\text{int}}-\tau \mathrm{\Delta }{\mathrm{\Omega }}_k}{kT}\right)(6)$

where ν₁ is an attempt frequency not necessarily equal to ν₀, ΔE_k is the kink migration barrier, and $\mathrm{\Delta }{E}_{y\to y+b}^{\text{int}}$ is the excess energy that results when kinks move an amount b along the y (i.e., [111]) direction. ΔΩ_k is an activation volume, which here is taken to be the average of the excess atomic volume of Nb, Ta, and V with respect to the average alloy (Zhou et al., 2021). Defined in this fashion, ω_k represents the hopping rate of a kink segment going from a position y to another y + b. $\mathrm{\Delta }{E}_{y\to y+b}^{\text{int}}$ is obtained as the excess energy resulting from the sideward translation of a kink along the [111] direction, from position y to y + b, i.e.:

$\mathrm{\Delta }{E}_{y\to y\pm b}^{\text{int}}=\sum _k\left(e_i^{\text{int}}{|}_{y+b}\mp e_i^{\text{int}}{|}_y\right)(7)$

The kink interaction energies are calculated over the entire length of the kink spread a, as illustrated in Zhou et al. (2021). Here too, we calculate rates for forward and backward jumps to account for correlated motion (hence the ± sign). Contrary to Eq. 5, $\mathrm{\Delta }{E}_{y\to y\pm b}^{\text{int}}$ is calculated only for the glide plane on which the kink in question lies. Similarly, however, it can be positive or negative, indicating attraction towards the next atomic position or repulsion from it.

The computed values for all the e^int for the Nb-V-Ta alloy in relation to the dislocation core are given in Table 1. In this work, it is assumed that kinks are segments close to the screw orientation (based on values of a = 12b) and thus we use the same interaction energies calculated for screw cores. Values for the average alloy are given in Table 2 as averages from the known values of Nb, Ta, and V. Screw dislocation-specific properties, such as the single kink spread a, and the coefficients p and q have been obtained using a line tension model using the elastic constants for the average alloy, as demonstrated by He et al. (2019). Those constants, together with the rest of the relevant parameters are given in Table 3.

TABLE 1

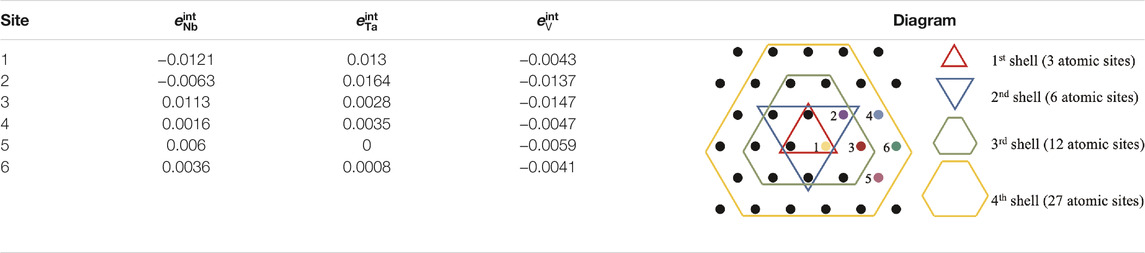
TABLE 1. Dislocation core solute-interaction energies (solute in average-atom matrix). Site numbers are given in relation to the diagram on the right column. All energies in eV [from Maresca and Curtin (2020a)]. Negative values indicate attraction.

TABLE 2

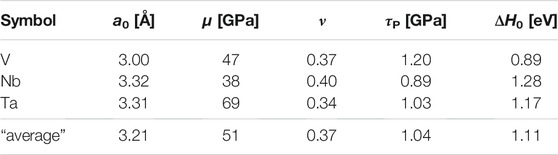
TABLE 2. Material constants for the individual constituent elements of the equiatomic NbTaV alloy. From Weinberger et al. (2013), Dezerald et al. (2015).

TABLE 3

TABLE 3. Additional material parameters for the “average” material.

Equations 4, 6 are then sampled according to the kMC algorithm for any available dislocation segment with length greater than w and for all existing kinks.

3 Results

3.1 Case ΔE_k = 0

Following our previous work in Zhou et al. (2021), we first carry out simulations assuming no migration barrier for kink propagation, i.e., ΔE_k = 0 in Eq. 6. As indicated in the previous section, we work with dislocations lines of length 1000b along the screw direction. One crucial aspect of the simulations is that screw dislocations in the Nb-Ta-V system are not perfectly straight at zero stress, as shown, e.g., in Figure 2. For this reason, all lines are first equilibrated at the corresponding temperature at zero stress, and the resulting line structures are then used as the initial configurations for the stress-driven simulations.

For each (τ, T) point, the position of the dislocation is taken as that of the center of mass of all distinct segments i along the glide direction. This average position d is plotted versus time t and the velocities are extracted from the linear d-t regions. Figure 4 shows three exemplary cases, one at high stress, Figure 4A, and two at low stresses, Figure 4B,C. Clear differences can be seen in all cases. At high stress, the dislocations go through a fast transient associated with the propagation of existing kink pairs along the line in the original configuration, and then moderate their velocity once kink-pair nucleation events become more likely. In these cases, we take the velocity after the initial transient has passed. At low stress, the dislocations are seen to intercalate stationary periods waiting for a nucleation event (horizontal time periods marked with continuous orange lines), punctuated by fast motion in between those. In those cases, the velocities are taken from the entire d-t curves.

FIGURE 4

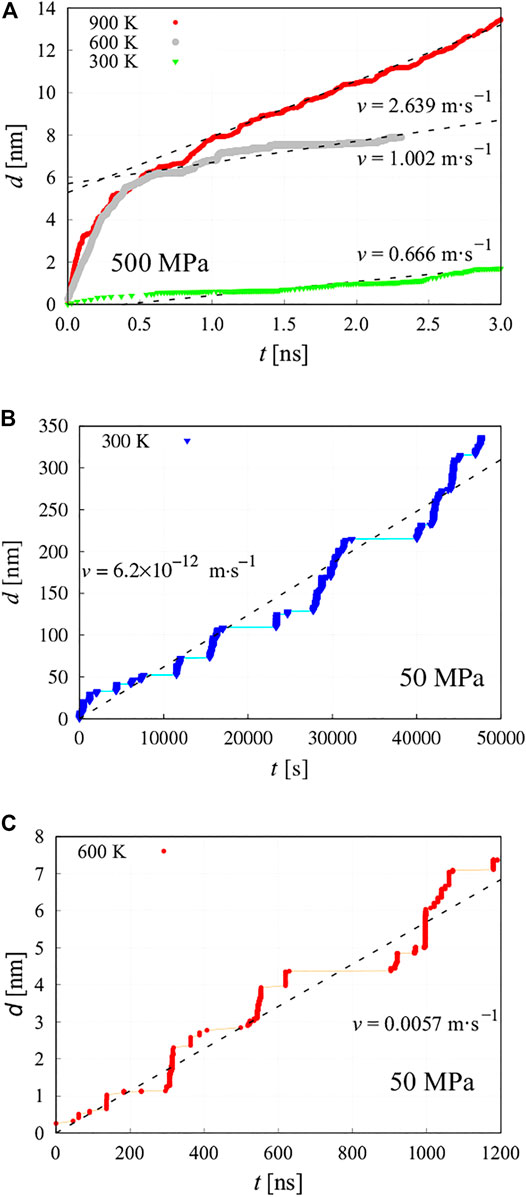
FIGURE 4. Dislocation center-of-mass position as a function of time for a few exemplary temperatures and stresses. (A) At a stress of 500 MPa, the dislocation is seen to go through a rapid transient before stabilizing into a steady state from which velocities are obtained. At low stress (50 MPa), the dislocation is seen to spend stationary periods waiting for a nucleation event (horizontal time periods marked with continuous horizontal lines), punctuated by fast motion. In those cases, the velocities are taken from the entire d-t curves as shown for (B) 300 K and (C) 600 K.

The reason for the above differences lies in the distribution of time steps sampled in the kMC algorithm, which are reflective of the chemical environment variations. Figure 5A shows the histogram of sampled time steps, δt, during the course of the simulations at 300 K and 50 MPa. While kink propagation time steps (inverse of rates obtained from Eq. 6) are narrowly distributed between 10^–12 and 10^–10 s, kink nucleation events (inverse of Eq. 1) are spread over an extraordinarily large interval ranging from 10^–14 to 10³ s. This points to the wide variability in rates obtained via Eq. 1, i.e., to the strong effect of $\mathrm{\Delta }{E}_{x\to x+h}^{\text{int}}$ on the final values of ω_kp when τ and T are small. Although the distribution of time steps for kink-pair nucleation events appears bimodal, it is likely that for the specific simulation shown, 300 K and 50 MPa, the gap shown in the figure between 10^–9 and 10^–8 s does not have a particular physical meaning and is simply a region of poor sampling.

FIGURE 5

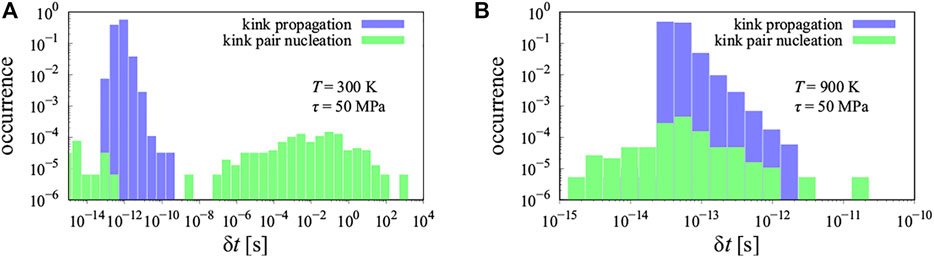
FIGURE 5. Histogram of sampled time steps throughout the course of a simulation at (A) 300 K and 50 MPa and (B) 900 K and 50 MPa. While kink propagation time steps are narrowly distributed between 10^–12 and 10^{–10 s}, kink nucleation events are spread over an extraordinarily large interval ranging from 10^–12 to 104 s.

As the figure shows, the tails of the histogram at 50 MPa and 300 K span 16 orders of magnitude in time. As well, notwithstanding the logarithmic scale, the histogram of δt is relatively flat, indicating that the tails of the distribution are sampled with probabilities that do not differ dramatically from the mode of the distribution (≈0.01 s). This is the reason behind the occurrence of long waiting periods in Figure 4B. The curves in Figure 4C, showing the d-t evolution for 600 K and 50 MPa, further substantiate this notion of long waiting times at low stresses, even at temperatures as high as 600 K.

By contrast, Figure 5B shows the histogram of time steps at 900 K and 50 MPa, all lying in a narrower interval between 10^–15 and 10^–10 s. This is a manifestation of very high event rates and no waiting time, resulting in “smooth” d-t curves such as those shown in Figure 4A.

Plots of the screw dislocation velocities as a function of stress and temperature for the ΔE_k = 0 case are shown in Figure 6. As the graphs show, the dislocation velocities display a clear temperature dependence at low stresses, while approaching 1,200 MPa the velocities seem to converge towards a value of 1.0 m ⋅s⁻¹. At T = 300 K, the dislocation is virtually stationary below 100 MPa, with velocities less than 1 Å per second due to the long waiting periods discussed above. The region below this value is shaded in the figure, as it would correspond to creep rates and is thus irrelevant for glide-controlled strength studies. All the v-τ curves follow power laws of the type v(τ) = A(T)τⁿ, where A is a temperature-dependent prefactor and n is the power law exponent. In this case, no clear temperature correlation for A was found, while n was seen to gradually decrease from 6.8 at 300 K to 0.7 at 1200 K.

FIGURE 6

FIGURE 6. Screw dislocation velocities as a function of stress and temperature for the ΔE_k = 0 case. The shaded region indicates velocities of less than 1 Å per second, which would result in strain rates of less than 10^{–6 s−1}, assumed in this work to be the creep limit and, thus, irrelevant for glide deformation purposes.

3.2 Case ΔE_k = 1.0 eV

Next, we make ΔE_k in Eq. 6 equal to 1.0 eV using the exact same conditions as in the previous section. Note that, although not directly applicable, this value is not inconsistent with energies obtained for edge dislocations in similar systems (Kubilay et al., 2021).

In this case, the extra kink migration energy leads to slow propagation rates, which shifts the distribution of δt towards long times, as shown in Figure 7. At low temperatures and moderate stresses (simulation at 300 K and 500 MPa, left-hand panel), a clear gap exists between the distribution of kink-pair nucleation times and kink propagation ones (the former clustering narrowly around 1,000 s and the latter ranging from fs to ms). In contrast, at T = 900 K and τ = 50 MPa, the effect of temperature on kink propagation rates can be clearly appreciated with a six-order-of-magnitude decrease in the histogram of time steps. Interestingly, kink-pair nucleation rates are much less sensitive to temperature and stress changes.

FIGURE 7

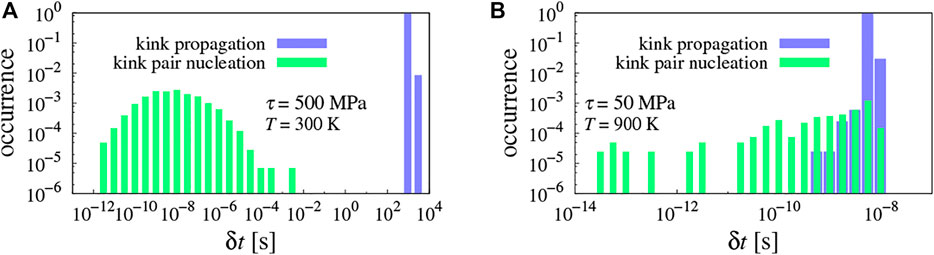
FIGURE 7. Histogram of sampled time steps throughout the course of (A) a low-temperature, low-stress simulation (300 K and 500 MPa), and (B) high-temperature, low-stress (900 K, 50 MPa). In contrast with Figure 5, kink propagation time steps represent the largest among all sampled time steps in both cases.

As expected with these sluggish kink propagation rates, the resulting dislocation velocities are overall much slower than for ΔE_k = 0. Figure 8 gives the stress and temperature dependence of the screw dislocation velocity for ΔE_k = 1.0 eV. The figure reveals a strong temperature dependence (note the logarithmic scale for the-v axis) with the v-τ relations also well described by power laws such as those for the ΔE_k = 0 case. In this case, n oscillates between 0.84 for the 300 K case, and 1.4 for the 1200 K case, but a clear temperature dependence cannot be extracted. For its part, A is well described by an exponential of the type:

$A\left(T\right)=4.8\times 10^{-15}{e}^{0.16T}\left[\mathrm{m}\cdot {\mathrm{s}}^{-1}\right]$

FIGURE 8

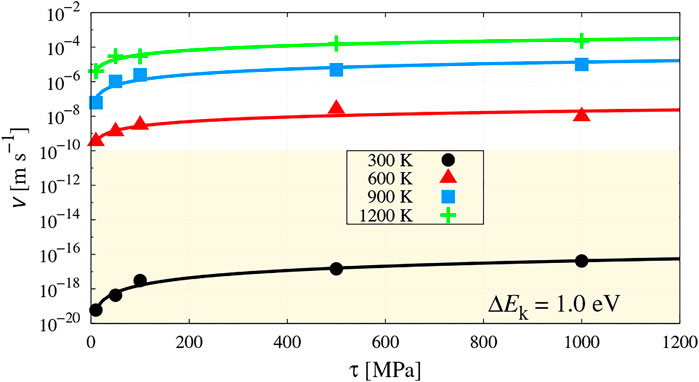
FIGURE 8. Screw dislocation velocities as a function of stress and temperature for the ΔE_k = 1.0 eV case. The shaded region indicates velocities of less than 1 Å per second, which would result in strain rates of less than 10^{–6 s−1}, assumed in this work to be the creep limit and, thus, irrelevant for glide deformation purposes.

Our results essentially indicate that for ΔE_k = 1.0 eV, the rate-limiting step is lateral kink propagation. This is particularly the case at low temperatures, where one has to wait up to thousands of seconds for kinks to move, which results in extremely low dislocation velocities. At higher temperatures, kink-pair nucleation and kink propagation times overlap around the nanosecond range, with neither clearly becoming the rate-limiting step. Dislocation velocities are then seen to increase by many orders of magnitude.

A qualitative discussion of these results is provided next.

4 Discussion

The mechanisms behind high temperature strength in chemically complex alloys are still under investigation, with inconclusive evidence about whether it is mainly screw or edge dislocations what controls deformation (Couzinié et al., 2015; Couzinié and Dirras, 2019; Bu et al., 2021; Lee et al., 2021). While reasons can be found in favor of both mechanisms, some gaps in our microscopic understanding of dislocation processes still exist, preventing us from having a complete picture of dislocation dynamics in these materials. One such gap is the detailed characterization of the energy landscape over which single kinks propagate along the screw dislocation direction. Given the nonscrew character of kink steps, one might be tempted to treat them as quasi-edge segments for which some information has recently become available (Kubilay et al., 2021). While this is not strictly correct, one can get an idea of the range of values that might be expected for the energy barriers encountered by kinks during motion. This work is an attempt to understand and quantify the effect of such barriers on net screw dislocation motion by adopting two extreme cases for these barriers: 0.0 and 1.0 eV. Our model takes atomistic information as a primary source of parameter data, and uses it to extend the physics to realistic line lengths and time scales. As such, our approach is as accurate as the data used as input and–as importantly–as the number of different mechanisms captured in its formulation.

Bearing this in mind, our results show that the two scenarios contemplated here lead to strikingly different behaviors.

1) In general, screw dislocation velocities are very low. By way of comparison, dislocation velocities in pure tungsten at 1,000 MPa in a similar temperature range as that considered here were on average approximately 100 m ⋅s⁻¹ (Stukowski et al., 2015), compared to less than 1.0 m ⋅s⁻¹.

2) When ΔE_k = 0, dislocation velocities are on average four to five orders of magnitude higher than for ΔE_k = 1.0 eV.

3) With no kink barrier, dislocation velocities converge for all temperatures at high stresses, while with ΔE_k = 1.0 the v-τ relations displays a clear separation with temperature that is maintained for all stresses.

Points 1 and 2 from the list above are consistent with the high strength generally measured in RMEA at low homologous temperature. However, what we are after explaining is less the intrinsic high temperature of these alloys (after all, they are made of heavy refractory elements, all strong by definition) but the retention of strength at high temperature. Thus, it is interesting to notice that the model with zero kink migration energy shows that the velocities become temperature independent at high stresses (at or above 1,000 MPa in Figure 6). Indeed, at high stress and with kink propagation not being the rate-limiting step, the profusion of kink pair nucleation events and cross-kinks makes temperature a secondary factor. This ultimately leads to velocities whose primary dependence is on stress, not temperature. The mechanism is illustrated in Figure 9, where similar dislocation structures can be observed at 300 and 900 K, both for τ = 500 MPa. Very rugged lines with an abundance of cross kinks and trailing loops are generated in both cases.

FIGURE 9

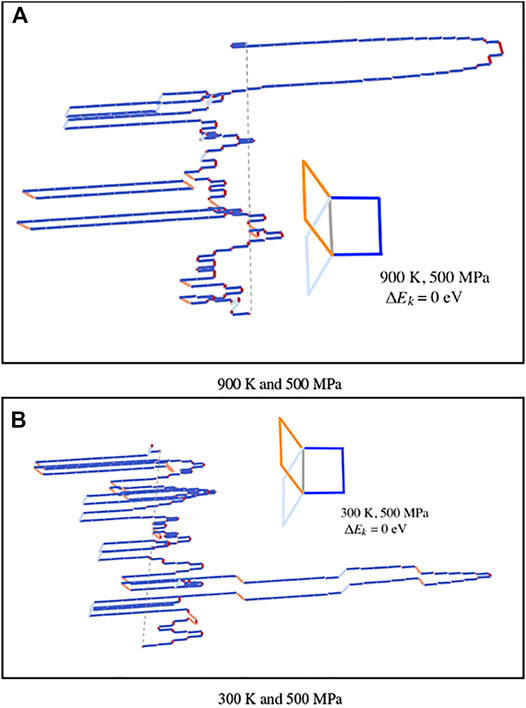
FIGURE 9. Snapshots at long times of dislocation substructures under 500 MPa of applied stress showing a profusion of cross kinks and trailing loops. Segments lying on different {110} planes are colored accordingly (color reference shown). The dark blue plane is the MRSS plane. The straight black dashed line indicates the position of the center of mass of the dislocation.

The situation is different when ΔE_k = 1.0 eV because both kink propagation and kink-pair nucleation coexist as thermally-activated processes. In that case, then, a clear temperature dependence persists regardless of how high the stress gets. Thus, while dislocation line configurations similar to those shown in Figure 9 are also seen when ΔE_k = 1.0 eV, they are strongly dependent on temperature conditions. Figure 10 shows the line configuration in this case for T = 300 K and τ = 50 MPa, with profuse generation of trailing defects and significant line roughness as well. Such abundance of “nonscrew” segments on the line results in very slow progress under stress, and–consequently–low dislocation velocities, making it potentially a contributing factor for high temperature strength.

FIGURE 10

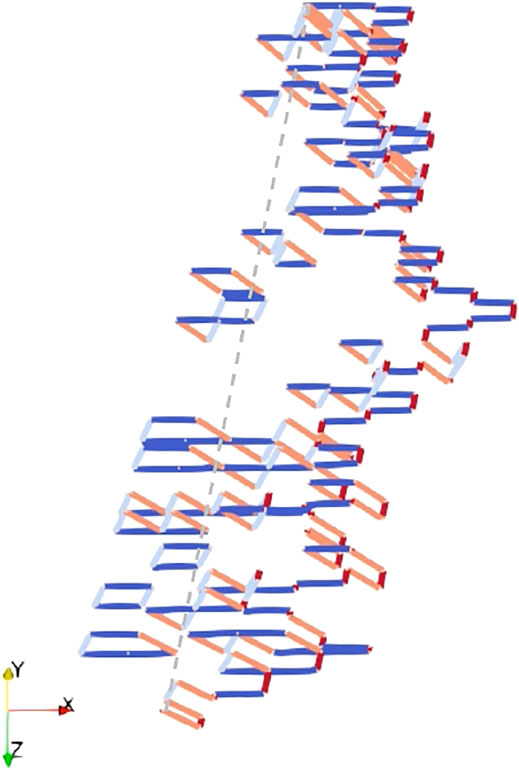
FIGURE 10. Screw dislocation configuration for the ΔE_k = 1.0 eV case at 300 K and 50 MPa. Color coding is the same is for Figure 9. The gray dashed line represents the two ends of the dislocation line, connected through periodic boundaries.

The behavior just described would suggest that a temperature independent strength might occur when the kink propagation energy is low (approaching zero perhaps). This prompts the question of why would this then not happen as well in pure bcc metals where kink propagation is basically athermal (in fact viscous, as described in Section 2.1). The answer is that, while kink-pair nucleation is unquestionably a thermally-activated process in pure metals, it is not so in RMEA. In fact, it is this lack of a clearly temperature-dominated process in RMEA at high stress what leads to a temperature insensitization of its mechanical response. Thus, while not discounting contributions from other dislocation types and other mechanisms, our results might indicate that dislocation motion is characterized by small kink propagation energy barriers. Detailed atomistic studies of these barriers will elucidate whether that is indeed the case.

Finally, in all cases studied here, the v-τ relations are well described by power laws of the type v(T, τ) = A(T)τⁿ. This clearly represents a deviation from purely thermally-activated behavior, as rationalized above. However, interestingly, studies have shown that when pure bcc metals are pushed beyond the thermally-activated limit, the dislocation velocities display strongly nonlinear dependences with stress that are well captured by power laws. In fact, exponents of up to 40 have been measured in pure Fe (Altshuler and Christian, 1967). Thus, in a certain sense, the Nb-V-Ta alloy behaves at all temperatures and stresses as some “regular” bcc metals are found to behave at high temperatures and high stresses.

5 Conclusion

We finalize with some of the most important conclusions:

1) We have developed a kinetic Monte Carlo model of thermally activated screw dislocation kinetics in the equiatomic Nb-Ta-V alloy. The model includes an extensive atomistic envelope around the dislocation to calculate all the necessary interaction energies from the surrounding atomic configurations. These environments ensure that correlated transitions are properly accounted for, and that a statistically significant material volume is sampled.

2) We have studied the relationship between dislocation velocities with stress and temperature in the range 0 ∼1,000 MPa and 300 ∼1200 K using stress-controlled simulations. We have considered two distinct scenarios, one where the kink propagation energy is zero, and another one where it is 1.0 eV.

3) In general, screw dislocation velocities are very low, never surpassing 1.0 m⋅s⁻¹ even at high stress and/or temperature. With no kink propagation energy, dislocation velocities are on average four to five orders of magnitude higher than when it is 1.0 eV.

4) With no kink barrier, dislocation velocities converge for all temperatures at high stresses, while with for 1.0 eV the v-τ relations displays a clear separation with temperature that is maintained for all stresses. This may give us a hint in terms of what kink propagation energy barriers to expect to observe a weak temperature dependence of the alloy strength.

5) In all cases, dislocation lines develop a very rough structure, characterized by a profusion of kinks on multiple slip systems, cross kinks, trailing loops, and bulging.

Data Availability Statement

The raw data generated in the work described in this article can be made available upon reasonable request to the authors.

Author Contributions

XZ developed the kMC code, carried out the simulations, analyzed and parsed all output data, and contributed to the writing of the paper. JM designed the research, guided the simulation effort, and wrote the first version of the paper.

Funding

This work has been funded by the National Science Foundation under Grant No. DMR-1611342.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank UCLA’s IDRE for computer time allocations on the Hoffman2 supercomputer. Helpful discussions with W. Curtin are gratefully acknowledged.

References

Altshuler, T., and Christian, J. W. (1967). The Mechanical Properties of Pure Iron Tested in Compression over the Temperature Range 2 to 293 K. Phil. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 261, 253–287.

Google Scholar

Beke, D. L., and Erdélyi, G. (2016). On the Diffusion in High-Entropy Alloys. Mater. Lett. 164, 111–113. doi:10.1016/j.matlet.2015.09.028

CrossRef Full Text | Google Scholar

Bu, Y., Wu, Y., Lei, Z., Yuan, X., Wu, H., Feng, X., et al. (2021). Local Chemical Fluctuation Mediated Ductility in Body-Centered-Cubic High-Entropy Alloys. Mater. Today 46, 28–34. doi:10.1016/j.mattod.2021.02.022

CrossRef Full Text | Google Scholar

Cai, W., Bulatov, V. V., Yip, S., and Argon, A. S. (2001). Kinetic Monte Carlo Modeling of Dislocation Motion in Bcc Metals. Mater. Sci. Eng. A 309-310, 270–273. doi:10.1016/s0921-5093(00)01689-0

CrossRef Full Text | Google Scholar

Cereceda, D., Diehl, M., Roters, F., Raabe, D., Perlado, J. M., and Marian, J. (2016). Unraveling the Temperature Dependence of the Yield Strength in Single-crystal Tungsten Using Atomistically-Informed crystal Plasticity Calculations. Int. J. Plastic. 78, 242–265. doi:10.1016/j.ijplas.2015.09.002

CrossRef Full Text | Google Scholar

Chang, S.-Y., Li, C.-E., Huang, Y.-C., Hsu, H.-F., Yeh, J.-W., and Lin, S.-J. (2014). Structural and Thermodynamic Factors of Suppressed Interdiffusion Kinetics in Multi-Component High-Entropy Materials. Sci. Rep. 4, 4162. doi:10.1038/srep04162

PubMed Abstract | CrossRef Full Text | Google Scholar

Couzinié, J.-P., and Dirras, G. (2019). Body-centered Cubic High-Entropy Alloys: From Processing to Underlying Deformation Mechanisms. Mater. Charact. 147, 533–544. doi:10.1016/j.matchar.2018.07.015

CrossRef Full Text | Google Scholar

Couzinié, J.-P., Lilensten, L., Champion, Y., Dirras, G., Perrière, L., and Guillot, I. (2015). On the Room Temperature Deformation Mechanisms of a Tizrhfnbta Refractory High-Entropy alloy. Mater. Sci. Eng. A 645, 255–263. doi:10.1016/j.msea.2015.08.024

CrossRef Full Text | Google Scholar

Dezerald, L., Proville, L., Ventelon, L., Willaime, F., and Rodney, D. (2015). First-principles Prediction of Kink-Pair Activation Enthalpy on Screw Dislocations in Bcc Transition Metals: V, Nb, Ta, Mo, W, and Fe. Phys. Rev. B 91, 094105. doi:10.1103/PhysRevB.91.094105

CrossRef Full Text | Google Scholar

Dobbelstein, H., Thiele, M., Gurevich, E. L., George, E. P., and Ostendorf, A. (2016). Direct Metal Deposition of Refractory High Entropy alloy Monbtaw. Phys. Proced. 83, 624–633. doi:10.1016/j.phpro.2016.08.065

CrossRef Full Text | Google Scholar

Gao, M. C., Jablonski, P. D., Hawk, J. A., and Alman, D. E. (2018). “High-Entropy Alloys: Formation and Properties,” in ASME 2018 Symposium on Elevated Temperature Application of Materials for Fossil, Nuclear, and Petrochemical Industries of Pressure Technology, Seattle, WA, April 3–5, 2018. doi:10.1115/ETAM2018-6732.V001T01A004

CrossRef Full Text | Google Scholar

Ghafarollahi, A., Maresca, F., and Curtin, W. (2019). Solute/screw Dislocation Interaction Energy Parameter for Strengthening in Bcc Dilute to High Entropy Alloys. Model. Simul. Mater. Sci. Eng. 27, 085011. doi:10.1088/1361-651x/ab4969

CrossRef Full Text | Google Scholar

Gilbert, M. R., Queyreau, S., and Marian, J. (2011). Stress and Temperature Dependence of Screw Dislocation Mobility Inα-Fe by Molecular Dynamics. Phys. Rev. B 84, 174103. doi:10.1103/PhysRevB.84.174103

CrossRef Full Text | Google Scholar

He, S., Overly, E., Bulatov, V., Marian, J., and Cereceda, D. (2019). Coupling 2d Atomistic Information to 3d Kink-Pair Enthalpy Models of Screw Dislocations in Bcc Metals. Phys. Rev. Mater. 3, 103603. doi:10.1103/physrevmaterials.3.103603

CrossRef Full Text | Google Scholar

Körmann, F., and Sluiter, M. (2016). Interplay between Lattice Distortions, Vibrations and Phase Stability in Nbmotaw High Entropy Alloys. Entropy 18, 403. doi:10.3390/e18080403

CrossRef Full Text | Google Scholar

Kocks, U., Argon, A., and Ashby, M. (1975). Progress in Materials Science. Volume 19, Thermodynamics and Kinetics of Slip.Oxford: Pergamon.

Google Scholar

Kozak, R., Sologubenko, A., and Steurer, W. (2015). Single-phase High-Entropy Alloys - an Overview. Z. für Kristallographi -Crystal. Mater. 230, 55–68. doi:10.1515/zkri-2014-1739

CrossRef Full Text | Google Scholar

Kube, S. A., Sohn, S., Uhl, D., Datye, A., Mehta, A., and Schroers, J. (2019). Phase Selection Motifs in High Entropy Alloys Revealed through Combinatorial Methods: Large Atomic Size Difference Favors Bcc over Fcc. Acta Mater. 166, 677–686. doi:10.1016/j.actamat.2019.01.023

CrossRef Full Text | Google Scholar

Kubilay, R. E., Ghafarollahi, A., Maresca, F., and Curtin, W. A. (2021). High Energy Barriers for Edge Dislocation Motion in Body-Centered Cubic High Entropy Alloys. Npj Comput. Mater. 7, 112. doi:10.1038/s41524-021-00577-7

CrossRef Full Text | Google Scholar

Kumar, N. A. P. K., Li, C., Leonard, K. J., Bei, H., and Zinkle, S. J. (2016). Microstructural Stability and Mechanical Behavior of Fenimncr High Entropy alloy under Ion Irradiation. Acta Mater. 113, 230–244. doi:10.1016/j.actamat.2016.05.007

CrossRef Full Text | Google Scholar

Lee, C., Maresca, F., Feng, R., Chou, Y., Ungar, T., Widom, M., et al. (2021). Strength Can Be Controlled by Edge Dislocations in Refractory High-Entropy Alloys. Nat. Commun. 12, 1–8. doi:10.1038/s41467-021-25807-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X.-G., Chen, C., Zheng, H., Zuo, Y., and Ong, S. P. (2020). Complex Strengthening Mechanisms in the Nbmotaw Multi-Principal Element alloy. Npj Comput. Mater. 6, 1–10. doi:10.1038/s41524-020-0339-0

CrossRef Full Text | Google Scholar

Maresca, F., and Curtin, W. A. (2020a). Mechanistic Origin of High Strength in Refractory Bcc High Entropy Alloys up to 1900k. Acta Mater. 182, 235–249. doi:10.1016/j.actamat.2019.10.015

CrossRef Full Text | Google Scholar

Maresca, F., and Curtin, W. A. (2020b). Theory of Screw Dislocation Strengthening in Random BCC Alloys from Dilute to "High-Entropy" Alloys. Acta Mater. 182, 144–162. doi:10.1016/j.actamat.2019.10.007

CrossRef Full Text | Google Scholar

Marian, J., Cai, W., and Bulatov, V. V. (2004). Dynamic Transitions from Smooth to Rough to Twinning in Dislocation Motion. Nat. Mater 3, 158–163. doi:10.1038/nmat1072

PubMed Abstract | CrossRef Full Text | Google Scholar

Miracle, D., Miller, J., Senkov, O., Woodward, C., Uchic, M., and Tiley, J. (2014). Exploration and Development of High Entropy Alloys for Structural Applications. Entropy 16, 494–525. doi:10.3390/e16010494

CrossRef Full Text | Google Scholar

Po, G., Cui, Y., Rivera, D., Cereceda, D., Swinburne, T. D., Marian, J., et al. (2016). A Phenomenological Dislocation Mobility Law for Bcc Metals. Acta Mater. 119, 123–135. doi:10.1016/j.actamat.2016.08.016

CrossRef Full Text | Google Scholar

Rao, S. I., Antillon, E., Woodward, C., Akdim, B., Parthasarathy, T. A., and Senkov, O. N. (2019). Solution Hardening in Body-Centered Cubic Quaternary Alloys Interpreted Using Suzuki's Kink-Solute Interaction Model. Scr. Mater. 165, 103–106. doi:10.1016/j.scriptamat.2019.02.012

CrossRef Full Text | Google Scholar

Rickman, J. M., Balasubramanian, G., Marvel, C. J., Chan, H. M., and Burton, M.-T. (2020). Machine Learning Strategies for High-Entropy Alloys. J. Appl. Phys. 128, 221101. doi:10.1063/5.0030367

CrossRef Full Text | Google Scholar

Roy, A., Munshi, J., and Balasubramanian, G. (2021). Low Energy Atomic Traps Sluggardize the Diffusion in Compositionally Complex Refractory Alloys. Intermetallics 131, 107106. doi:10.1016/j.intermet.2021.107106

CrossRef Full Text | Google Scholar

Senkov, O. N., Wilks, G. B., Scott, J. M., and Miracle, D. B. (2011). Mechanical Properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 Refractory High Entropy Alloys. Intermetallics 19, 698–706. doi:10.1016/j.intermet.2011.01.004

CrossRef Full Text | Google Scholar

Senkov, O. N., Miller, J. D., Miracle, D. B., and Woodward, C. (2015). Accelerated Exploration of Multi-Principal Element Alloys for Structural Applications. Calphad 50, 32–48. doi:10.1016/j.calphad.2015.04.009

CrossRef Full Text | Google Scholar

Senkov, O. N., Miracle, D. B., Chaput, K. J., and Couzinie, J.-P. (2018). Development and Exploration of Refractory High Entropy Alloys-A Review. J. Mater. Res. 33, 3092–3128. doi:10.1557/jmr.2018.153

CrossRef Full Text | Google Scholar

Shinzato, S., Wakeda, M., and Ogata, S. (2019). An Atomistically Informed Kinetic Monte Carlo Model for Predicting Solid Solution Strengthening of Body-Centered Cubic Alloys. Int. J. Plasticity 122, 319–337. doi:10.1016/j.ijplas.2019.03.004

CrossRef Full Text | Google Scholar

Soni, V., Senkov, O. N., Gwalani, B., Miracle, D. B., and Banerjee, R. (2018). Microstructural Design for Improving Ductility of an Initially Brittle Refractory High Entropy alloy. Sci. Rep. 8, 8816. doi:10.1038/s41598-018-27144-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Stukowski, A., Cereceda, D., Swinburne, T. D., and Marian, J. (2015). Thermally-activated Non-schmid glide of Screw Dislocations in W Using Atomistically-Informed Kinetic Monte Carlo Simulations. Int. J. Plastic. 65, 108–130. doi:10.1016/j.ijplas.2014.08.015

CrossRef Full Text | Google Scholar

Weinberger, C. R., Tucker, G. J., and Foiles, S. M. (2013). Peierls Potential of Screw Dislocations in Bcc Transition Metals: Predictions from Density Functional Theory. Phys. Rev. B 87, 054114. doi:10.1103/PhysRevB.87.054114

CrossRef Full Text | Google Scholar

Xia, S.-q., Wang, Z., Yang, T.-f., and Zhang, Y. (2015). Irradiation Behavior in High Entropy Alloys. J. Iron Steel Res. Int. 22, 879–884. doi:10.1016/s1006-706x(15)30084-4

CrossRef Full Text | Google Scholar

Xia, S., Gao, M. C., Yang, T., Liaw, P. K., and Zhang, Y. (2016). Phase Stability and Microstructures of High Entropy Alloys Ion Irradiated to High Doses. J. Nucl. Mater. 480, 100–108. doi:10.1016/j.jnucmat.2016.08.017

CrossRef Full Text | Google Scholar

Yao, H., Qiao, J.-W., Gao, M., Hawk, J., Ma, S.-G., and Zhou, H. (2016). Monbtav Medium-Entropy alloy. Entropy 18, 189. doi:10.3390/e18050189

CrossRef Full Text | Google Scholar

Yao, H. W., Qiao, J. W., Hawk, J. A., Zhou, H. F., Chen, M. W., and Gao, M. C. (2017). Mechanical Properties of Refractory High-Entropy Alloys: Experiments and Modeling. J. Alloys Compd. 696, 1139–1150. doi:10.1016/j.jallcom.2016.11.188

CrossRef Full Text | Google Scholar

Yeh, J.-W., and Lin, S.-J. (2018). Breakthrough Applications of High-Entropy Materials. J. Mater. Res. 33, 3129–3137. doi:10.1557/jmr.2018.283

CrossRef Full Text | Google Scholar

Yin, B., and Curtin, W. A. (2020). Origin of High Strength in the Cocrfenipd High-Entropy alloy. Mater. Res. Lett. 8, 209–215. doi:10.1080/21663831.2020.1739156

CrossRef Full Text | Google Scholar

Yin, S., Zuo, Y., Abu-Odeh, A., Zheng, H., Li, X. G., Ding, J., et al. (2021). Atomistic Simulations of Dislocation Mobility in Refractory High-Entropy Alloys and the Effect of Chemical Short-Range Order. Nat. Commun. 12, 4873–4914. doi:10.1038/s41467-021-25134-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., and Marian, J. (2018). Direct Prediction of the Solute Softening-To-Hardening Transition in W-Re Alloys Using Stochastic Simulations of Screw Dislocation Motion. Model. Simul. Mater. Sci. Eng. 26, 045002. doi:10.1088/1361-651x/aaaecf

CrossRef Full Text | Google Scholar

Zhao, S., Osetsky, Y., and Zhang, Y. (2017). Preferential Diffusion in Concentrated Solid Solution Alloys: Nife, Nico and Nicocr. Acta Mater. 128, 391–399. doi:10.1016/j.actamat.2017.01.056

CrossRef Full Text | Google Scholar

Zhao, Y., Dezerald, L., Pozuelo, M., Zhou, X., and Marian, J. (2020). Simulating the Mechanisms of Serrated Flow in Interstitial Alloys with Atomic Resolution over Diffusive Timescales. Nat. Commun. 11, 1227–1228. doi:10.1038/s41467-020-15085-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z., Zhou, Y., He, Q., Ding, Z., Li, F., and Yang, Y. (2019). Machine Learning Guided Appraisal and Exploration of Phase Design for High Entropy Alloys. Npj Comput. Mater. 5, 1–9. doi:10.1038/s41524-019-0265-1

CrossRef Full Text | Google Scholar

Zhou, X., He, S., and Marian, J. (2021). Cross-kinks Control Screw Dislocation Strength in Equiatomic Bcc Refractory Alloys. Acta Mater. 211, 116875. doi:10.1016/j.actamat.2021.116875

CrossRef Full Text | Google Scholar

Zou, Y., Maiti, S., Steurer, W., and Spolenak, R. (2014). Size-dependent Plasticity in an Nb25Mo25Ta25W25 Refractory High-Entropy alloy. Acta Mater. 65, 85–97. doi:10.1016/j.actamat.2013.11.049

CrossRef Full Text | Google Scholar