- Department of Mechanical Engineering and Mechatronics, Ariel University, Ariel, Israel
Through years of evolution, biological soft fibrous tissues have developed remarkable functional properties, unique hierarchical architectures, and -most notably, an unparalleled and extremely efficient deformation ability. Whereas the structure-function relationship is well-studied in natural hard materials, soft materials are not getting similar attention, despite their high prevalence in nature. These soft materials are usually constructed as fiber-reinforced composites consisting of diverse structural motifs that result in an overall unique mechanical behavior with large deformations. Biomimetics of their mechanical behavior is currently a significant bioengineering challenge. The unique properties of soft fibrous tissues stem from their structural complexity, which, unfortunately, also hinders our ability to generate adequate synthetic analogs, such that autografts remain the “gold standard” materials for soft-tissue repair and replacement. This review seeks to understand the structural and deformation mechanisms of soft collagenous tissues, with a particular emphasis on tendon and ligaments, the annulus fibrosus (AF) in the intervertebral disc (IVD), skin, and blood vessels. We examined and compared different mechanical and structural motifs in these different tissue types, which are subjected to complex and varied mechanical loads, to isolate the mechanisms of their deformation behavior. Herein, we focused on their composite structure from a perspective of the different building blocks, architecture, crimping patterns, fiber orientation, organization and their structure-function relationship. In the second part of the review, we presented engineered soft composite applications that used these structural motifs to mimic the structural and mechanical behavior of soft fibrous tissues. Moreover, we demonstrated new methodologies and materials that use biomimetic principles as a guide. These novel architectural materials have tailor-designed J-shaped large deformations behavior. Structural motifs in soft composites hold valuable insights that could be exploited to generate the next generation of materials. They actually have a two-fold effect: 1) to get a better understanding of the complex structure-function relationship in a simple material system using reverse biomimetics and 2) to develop new and efficient materials. These materials could revolutionize the future tailor-designed soft composite materials together with various soft-tissue repair and replacement applications that will be mechanically biocompatible with the full range of native tissue behaviors.
Introduction
From a mechanical and material point of view, natural materials and tissues are composite materials, which in thousands of years of evolution, are designed as hierarchical materials with very efficient structures (Sanchez et al., 2005; Bar-Cohen, 2006; Munch et al., 2008; Studart, 2012; Ma et al., 2013; Jang et al., 2015; Wegst et al., 2015; Kokkinis et al., 2018; Schaffner et al., 2018; Yang et al., 2019). Although these materials are composed of relatively simple building blocks, their multi-level structures and inherent structural motifs result in remarkable mechanical properties. Unfortunately, while soft fibrous tissues’ unique properties stem from their structural complexity, this complexity also hinders our ability to generate adequate synthetic analogs (Mazza and Ehret, 2015). Thus autografts remain the “gold standard” materials for soft-tissue repair and replacement.
Understanding the structure-function relationship in these structures and its mimicking will revolutionize our ability to repair organs and tissues and restore the biomechanical function of the native tissues. Moreover, using the same principles in classical engineering applications can make a new leap and revolutionize the next generation of materials.
The current review is focused on different structural motifs in functional soft fibrous tissues and their ability to function under complex loading modes. We aim to take a step forward in disentangling the structural complexity of soft fibrous tissues to explain how their different structural elements endow them with their unique large deformation behavior. We have examined the basic principles of the functional tissues as multi-scale composites and their newly developed biomimetic designs.
Building Blocks of Soft Fibrous Tissues
Despite their naturally wide structural and functional diversity, all biological soft fibrous tissues, from the cornea to tendon, have a composite structure assembled from repeating simple building blocks. In general, collagen fibers act as reinforcement and provide stiffness and strength to the tissue. Proteoglycans (PGs) and Glycosaminoglycans (GAGs) serve as a matrix and bind the fibrils and fibers. They are negatively charged, absorb water, act as a shock absorber, and provide viscoelasticity to the tissue; and elastin, which provides flexibility, recoiling ability, and fatigue resistance (Holzapfel, 2001; Meyers et al., 2013; Godinho et al., 2021). These constituents are arranged in diverse structures and allow varied mechanical functions and complex loading modes. Although these materials also have essential biological functions, this review will focus only on the mechanical and structural roles.
Soft fibrous tissues consist of multiple variations of intrinsic structural elements, such as the fiber volume fraction, orientation, crimping angles, and structural hierarchy in multiple length scales. However, they share multiple structural mechanisms such as anisotropy, large deformations, and a unique nonlinear J-shaped mechanical behavior with strain stiffening (Figure 1). The absolute values are different between diverse tissues; however, from examining their structure and mechanical behavior, we can learn about repeating structural mechanisms and their effect on the mechanical behavior for tissue repair applications and the engineering of new materials.
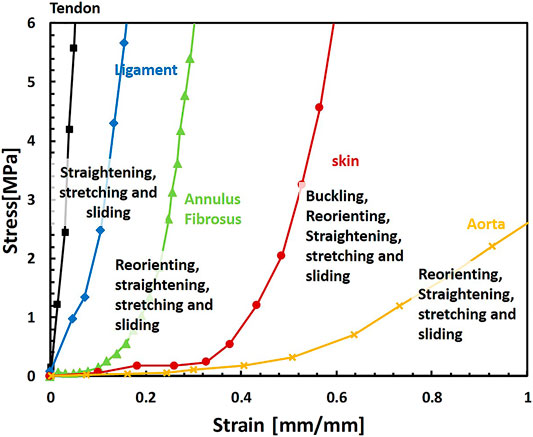
FIGURE 1. Representative mechanical behaviors of different soft fibrous tissues under uniaxial tension and related mechanisms of their deformation behavior: tendon (De Santis et al., 2004), ligament (De Santis et al., 2004), annulus fibrosus, (stretched in the fiber direction) (Shan et al., 2015), skin (Joodaki and Panzer, 2018) and aorta (Zhalmuratova et al., 2019). The Behaviors presented here are representative; different protocols, origins, and tissue types result in large variations of behaviors.
Proteoglycans and Glycosaminoglycans
PGs and GAGs are a diverse family of biomolecules with varied roles in the extracellular matrix (ECM). Biologically, they play an essential role in mediating cell-cell and cell-matrix interactions. GAGs are linear polysaccharides whose disaccharide building blocks consist of amino sugar. PGs are polysaccharide chains covalently linked to protein and may contain varying amounts of sulfate, resulting in a strong negative charge. This negative charge allows them to absorb water up to 1,000 times their volume and provide viscoelasticity to the tissues (Silbert, 1982; Lindahl et al., 2017). In tendons, they are found between collagen fibrils and bind them noncovalently (Scott, 1988), enabling load transfer, sliding, and stretching of the fibrils (Rigozzi et al., 2013), as discussed in Tendons and Ligaments section. PGs and GAGs are found in all tissue length scales as part of the noncollagenous matrix (NCM). However, the lowest level they were identified was the collagen fibril level (Figure 2).
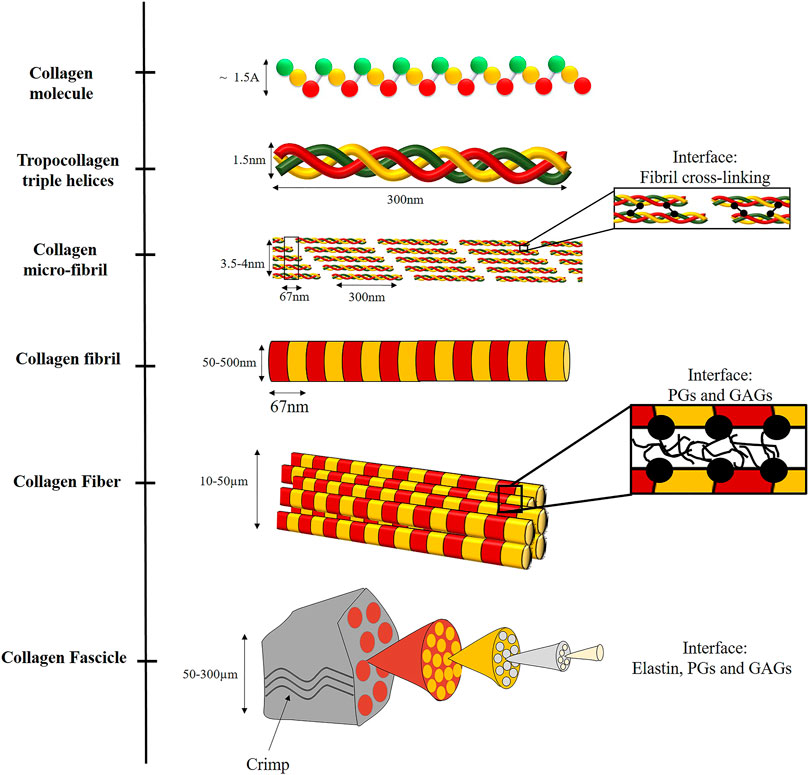
FIGURE 2. Illustration of the hierarchical structure of collagenous fibrous tissues, including the different interfaces. At the nano-scale, collagen is assembled from three left-handed alpha-helices stabilized by hydrogen bonds and covalent cross-links to form a triple helix (tropocollagen). Tropocollagens are staggered into a larger array with a repeated D-period to form fibrils, via covalent cross-linking. The fibrils are assembled to fibers, bound by weak interactions with PGs and GAGs. The fibers are assembled to fascicles. In this level, elastin, PGs and GAGs are also present. Crimping also occurs at this structural level.
The exact role of different PGs in different length scales is not entirely resolved yet (Thorpe et al., 2013). Usually, it is accepted that GAGs resist compression, and collagen resists tension in load-bearing soft tissues. Indeed, in tissues with relatively low GAG content (e.g., tendons and ligaments), enzymatic digestion of GAG had a minor effect on tensile modulus. However, in tissues with high GAG content (e.g., articular cartilage), enzymatic digestion of GAG increases tensile modulus. Therefore, the relation between the structure and mechanical function varied between different structural arrangements of the tissues (Han et al., 2012).
Elastin
Elastic fibers are a fundamental component in the ECM in all vertebrates; they are found in different amounts and orientations. Elastin is an essential component of these fibers and an insoluble polymer that is very durable with a very slow degradation rate due to extensive crosslinking of tropoelastin monomers (Mithieux and Weiss, 2005; Vindin et al., 2019). Usually, elastin is found in a complex with fibrillin 1 and 2, known as microfibrils (Kielty et al., 2002). The tropoelastin monomers are coiled along their axis. Thus, this coil provides high flexibility under tension with almost no hysteresis loss (Baldock et al., 2011). Elastin is composed of repeating structures and has a hierarchical structure at many length scales. Approximately 90% of the elastin fiber is composed of an amorphous core of highly cross-linked elastin protein, and 10% is a fibrillar layer of ∼5 nm thick microfibrils (Ross and Bornstein, 1969; Cleary, 1987; Tamburro et al., 1995; Gasser, 2020). Elastin molecules are heavily cross-linked and connected to each other and other molecules, as collagen.
Elastin demonstrates linear elastic behavior up to approximately 70% strain (Gosline, 1976). Elastic fibers have a modulus of 300–600 kPa and a maximum extension of 100–220% (Fung, 2013), with incredible fatigue resistance that includes thousands of millions of cycles of extension and recoil without failure (Gosline et al., 2002; Keeley et al., 2002). Under small loads, elastin acts as a load-bearing matrix in the toe region of several tissues (Venkatraman et al., 2008).
The primary function of elastin is to provide flexibility to different tissues by enabling elastic recoil of the collagen fibrils. This function is essential for the continuous mechanical stretching and recovery of soft load-bearing tissues, providing stretch and relaxation cycles. Mechanically, elastin acts as natural rubber and synthetic elastomers (Debelle and Tamburro, 1999). However, it is only elastic when swollen in water, and its function is critically dependent on hydrated environments (Mithieux and Weiss, 2005). When dry, it is a hard, brittle, glassy solid. On wetting, it becomes flexible and elastic. Therefore, PGs and GAGs (as versican, biglycan, and decorin) interact with elastin, providing hydration and impact absorption (Wu et al., 1999; Isogai et al., 2002; Reinboth et al., 2002).
Collagen
Collagen is a structural protein that plays a crucial role in tissue biomechanics. It is the most widespread protein in vertebrates and accounts for approximately 25–35% of the proteins. The collagen family consists of 28 types and can be divided into fibrillar and non-fibrillar types. The Fibrillar collagens include types I, II, III, V, XI, XXIV, and XXVII. The different collagens are discussed comprehensively in Fratzl (2008). Herein, a particular focus will be given to the fibrillar collagens due to their vital function in the mechanical behavior of tissues, with a specific emphasis on Type I collagen.
Type I collagen is named “the steel of biological materials” (Sherman et al., 2015). It is the most abundant and structurally essential and a crucial building block in blood vessels, ligaments, tendons, cornea, skin, bone, etc. Type I collagen is extensively studied for its structure-function relationship in tissues and nature-based materials (Sherman et al., 2015; Yang et al., 2019). However, the collagen as the fibrous phase in a complex composite material system is not fully established in means of hierarchy in different tissues, including interaction with other building blocks, interfaces, and structural motifs. The structural hierarchy of collagen and interaction with other building blocks dominate the characteristic tissues’ nonlinear J-shaped behavior and provide remarkable strength and toughness.
The Molecular Level
At the molecular level, Type I collagen is formed by three left-handed alpha-helices composed primarily of glycine, proline, and alanine amino acids coiled together to form a triple helix, stabilized by hydrogen bonds and covalent cross-links (Tropocollagen). Tropocollagen has approximately 1.5 nm in diameter and 300 nm in length (Figure 2).
The Fibrillar Level
The tropocollagen molecules are staggered to create well-organized fibril aggregates by covalent cross-linking between the helices. These fibrils are semi-crystalline aggregates of tropocollagen. The staggering of tropocollagen creates a visible characteristic D-banding pattern (D-period) of 67 nm (Orgel et al., 2011). The 2D arrangement of the fibril is illustrated in Figure 2. However, to allow 3D arrangement with one D-period, Smith (1968) suggested five-tropocollagen molecules arranged in microfibrils that can justify the fibril observation of 67 nm. Then, Orgel et al. (2006) presented the complete crystallographic structure of the microfibrils with a diameter of 3.5–4 nm (Fratzl, 2008; Yang et al., 2019).
A comparison between different tissues, such as cornea, skin, reticular tissue, etc., demonstrated that some tissues have a shorter D-period of ∼64 nm with a small and very uniform diameter (∼100 nm). These fibrils were different from those in the tendon and ligaments, which have a larger and heterogeneous fibrils diameter with a 67 nm D-period. It was suggested that the difference is attributed to other collagen types, which can bind with type I to form heterotypic fibrils and cross-links. However, this assumption was not accepted (Franchi et al., 2008). In tissues such as skin, cornea, and blood vessels, which are subjected to multiaxial loads, a molecular tilt of approximately 18° was discovered. Therefore, a shorter D-period of 64 nm (67 cos 18°) exists. However, molecular tilts of ∼5° were found in the tendon, ligament, and bone tissues, all subjected to uniaxial stresses (Fratzl, 2008).
The fibril diameter is in the range of 50–500 nm. The variation depends on different factors such as tissue type, local variability, hydration, pathologies, and age (Han et al., 2012). The fibril diameter also affects the mechanical behavior: as fibril diameter increases, tensile stiffness decreases. Namely, when the number of tropocollagen molecules in a fibril is larger, it will be less stiff.
As also seen for higher levels of collagen hierarchy, the fibril mechanical behavior is nonlinear and includes initial elastic deformation stemming from collagen molecular uncoiling. It is followed by a linear regime of molecular sliding and then an additional stiffer elastic regime that results from stretching the molecular backbone (Depalle et al., 2015). The fibril mechanical behavior is also rate-dependent with strain stiffening with susceptibility to cyclic fatigue (Shen et al., 2008; Yang et al., 2012). When comparing different scales, the collagen molecule is stiffer than fibril, which is stiffer than collagen fiber (2.4–9 GPa, 0.2–1 GPa, and 0.05–1.57 GPa for molecule, fibril, and fiber, respectively) (Sherman et al., 2015). Cross-linking in collagen fibrils affects their mechanical strength, deformation, and fracture behaviors. Thus, increased density of cross-links results in stronger but more brittle fibrils, whereas a reduced amount of cross-links results in a large yield regime and highly dissipative deformation behavior (Buehler, 2008).
Measuring the fibril length is quite challenging since it is longer than sequential microscope sections. It was estimated between 0.3 to greater than 10 mm for a rat tail tendon, depending on the developmental stage (Craig et al., 1989; Starborg et al., 2013). Thus, in some cases, the fibrils are not crossing the full fiber length, and hence load transfer between the fibrils is very important (Starborg et al., 2013). However, in a recent study by Svensson et al. (2017), due to the discovery of extremely long collagen fibrils, they can be assumed as “structurally continuous.”
Although there are differences in the collagen fibrils, the fibrillary level represents quite a similar structure when comparing different tissues. Figure 3 demonstrates transmission electron microscopy (TEM) images in the transverse section of soft fibrous tissues. In classical composite materials, the packing and fiber volume fraction significantly affect the stiffness and strength of the material. Thus, quantifying the fibril volume fraction can provide essential data regarding the tissue structure, even if partial; however, the fibril volume fraction imaged by TEM does not reflect fiber volume fraction in higher length scales.

FIGURE 3. TEM images of the transverse cross-section of collagen fibrilar structure in different fibrous tissues. Tendons present heterogenous in fibril diameter compared with aorta, which are more homogenous. (A) Rat Achilles tendon. Transversally sectioned tendon including plurimodal collagen fibrils. Reprinted from Franchi et al. (2007) under CC-BY-3.0. (B) Mouse aorta. Reprinted from Dubacher et al. (2020) under CC-BY-NC.
The main structural diversity occurs above the fibrillary scale, where suprafibrillar structures emerge and are assembled, creating diverse mechanical behaviors of different tissues. In most soft tissues, PGs and elastin are located between the fibrils and in higher length scales (Thorpe et al., 2013) (Figure 2). For example, in tendons and ligaments, the association of collagen with other biomolecules (PGs, GAGs, elastin) occurs in several length scales simultaneously, and the PGs matrix separates the fibrils, allowing mechanisms as fibril and fiber gliding, providing larger strains in the tissue level.
Collagen Hierarchy and Suprafibrillar Structures
The micrometer-scale organization of fibrils is highly diverse among different tissues. Mainly, the fibrils are organized to higher-level architectures. These structures are entangled composites consisting of various biomolecules with different mechanical functions, as mentioned in Building Blocks of Soft Fibrous Tissues section.
Suprafibrillar structures can be divided into bundles (fibers and fascicles) as in tendons, ligaments, skin, aorta, and lamellae as in AF and bone. Collagen fibers are bundles of fibrils. They may consist of up to hundreds of collagen fibrils, and their diameter can get to 10–50 µm. Not all fibrous tissues consist of the fiber level. For example, in the cornea, due to the need for transparency, the highest level of organization is the fibrils (Sherman et al., 2015). A collagen fiber consists of PGs and water molecules that mediate the sliding between the fibrils. Therefore, fiber stretching also includes fibril sliding mediated by PGs bound by weak interactions. The latter supports the larger strains observed in the fiber when comparing the fiber to the fibril strains and provides the fiber with more considerable energy dissipation and toughness under tension.
The comparison across different tissues can be challenging due to different names given to the same hierarchical level in various tissues, such as the definition of fibrils, fibers, and bundles and the exchange between them (Handsfield et al., 2016). Mechanically, the definitions are fundamental since they define the interactions in a specific hierarchical level architecture and the nature of interactions with other biomolecules. For instance, covalent crosslinks contribute differently to the mechanical behavior than the weak reversible interactions, thus having different mechanical roles. Herein, the level of the hierarchy will be defined by the length scale and the mechanical function.
Lamellae can be mineralized (bone) or non-mineralized (AF). It accounts for the directionality of the structure when parallel fibrils are oriented in specific directions. For example, in the cortical bone, mineralized fibrils self-assemble into planar fibril arrays (lamellae) with 3–5 µm thickness. These lamellae are found in a repetitive stacked arrangement with different orientations in each sublayer (plywood structure) (Weiner et al., 1999). The AF in the IVD is also assembled from lamellae. Unlike the bone, it is made of unmineralized collagen fibrils with a thickness between 0.14 and 1.10 mm, oriented in alternate orientations of approximately ±30° (Holzapfel et al., 2005). The fibrils are organized as lamellae, with parallel fibrils aligned in specific directions.
The structural hierarchy in collagen fibers, explicitly, its subdivision into fibrils and micro-fibrils significantly increases its toughness and lessens the risk of crack propagation across multiple fibrils (Launey et al., 2010; Ritchie, 2011; Schriefl et al., 2012; Yang et al., 2019). We assume that working mechanisms are shared among tissues due to similar structural architectures. Therefore, in the next section, we will examine different fibrous tissues and their structure-function relationship.
Structure of Different Fibrous Tissues
In many cases, the direct modus operandi of these suprafibrillar structures is not fully resolved yet. However, comparing and observing different composite structures reveal several common working mechanisms that may explain tissue biomechanics and contribute to tissue biomimetics since the collagen structure alone cannot explain their full deformation behavior (see Figures 1, 4).
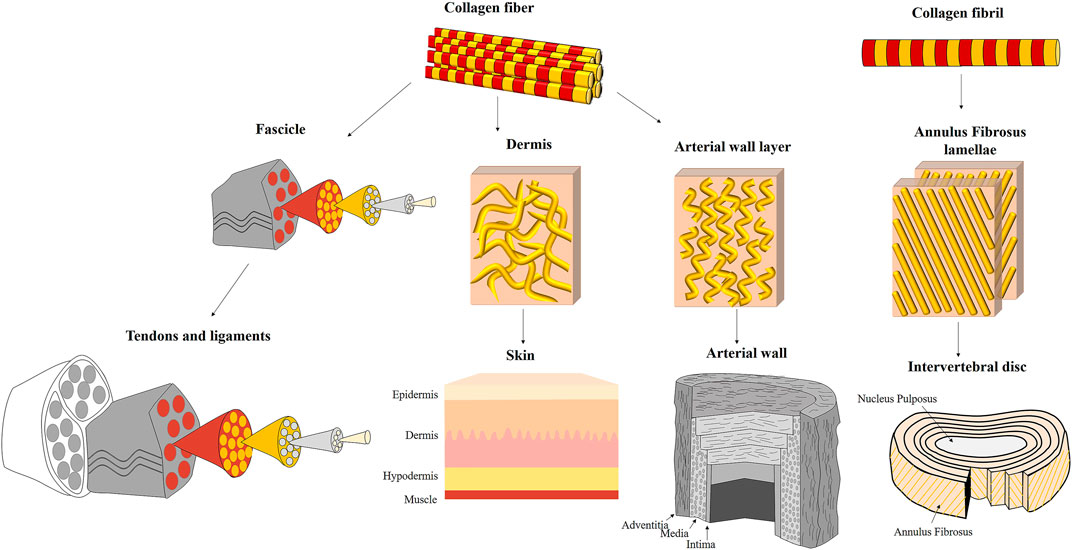
FIGURE 4. Different suprafibrillar collagenous structures of fibrous tissues: tendons and ligaments, skin, arterial wall, and intervertebral disc. Tendons and ligaments are assembled from unidirectional fascicles that are highly aligned with the tension direction. The fascicles are assembled from parallel unidirectional collagen fibers. The skin is composed of three layers: epidermis, dermis and hypodermis (endodermis). The collagen fibers in the dermis (which is the load-bearing layer) are wavy, dispersed and discontinuous. The arterial wall is composed of three layers: adventitia, media and intima. The collagen fibers in the adventitia and media (which are the load-bearing layers) are oriented in wavy and discontinuous and oriented in specific directions. However, they have a relatively large orientation distribution than tendons and ligaments. The intervertebral disc is composed of outer annulus fibrosus (AF) surrounding a gelatinous core (nucleus pulposus). The AF is constructed from 20–25 lamellae composed of parallel and crimped collagen fibrils oriented in an alternate arrangement of ±30° with the vertebral axis.
Tendons and Ligaments
Tendon and ligaments are efficient structures responsible for load transferring by enabling minimal energy loss from muscle to bone and between bones, respectively. They are composed of collagen, high water content (70% w/v), PGs, and elastin. Tendons and ligaments consist of highly organized hierarchical structures from the molecular to the organ level. This hierarchy is highly dependent on collagen architectures: from collagen molecules that are covalently bound to form nano-scale fibrils, which are assembled to micro-scale fibers arranged in fascicles to the tendon macrostructure (Figure 4). Each structural level acts as an isolated composite structure to form a “composite within composite’ or nested composite structure that functions together as a highly efficient material (Fratzl and Weinkamer, 2007; Gupta et al., 2010).
The collagen fibers in tendons and ligaments are assembled into fascicles. Rat tail tendon, for example, consists of about ten fascicles. Between the fibers, an interfascicular matrix consists of PGs and elastin. The latter is absent in lower length scales. The fascicle diameter is in the range of 50–300 µm and structured as a cylindrical array of planar zig-zag (crimped) fibrils (Figure 5A). The crimping in the micro-scale is responsible for the toe region behavior in tendons and ligaments. i.e., the toe region is larger when the crimping angle is smaller (Kastelic et al., 1978). Fibril crimping is thoroughly discussed in Collagen Crimping section.
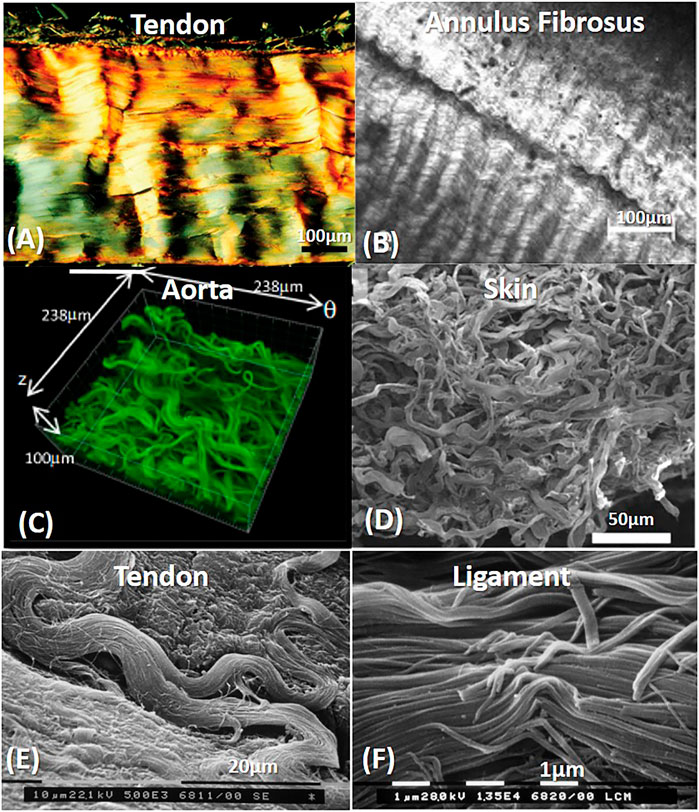
FIGURE 5. Crimping and orientation patterns in different fibrous tissues: Tendons and ligaments (A,E,F), Annulus Fibrosus (B), Aorta (C) and skin (D). (A) Polarized light micrograph of longitudinally sectioned rat Achilles tendon. Reprinted from Franchi et al. (2007) under CC-BY-3.0. (B) Annulus fibrosus second harmonic generation imaging of bovine tail AF. Reprinted from Vergari et al. (2017) under CC-BY-4.0. (C) Confocal laser scanning of the rabbit arterial adventitia. Reprinted from Rezakhaniha et al. (2012) under CC-BY-NC. (D) SEM arrangement of rabbit skin. Reprinted from Yang et al. (2015) under CC BY 4.0. (E) SEM image of a rat Achilles tendon, without fibrillary crimp when fibrils change their direction. Reprinted from Franchi et al. (2007) under CC-BY-3.0. (F) Fibril crimp in Rat medial collateral ligament (SEM). Reprinted from Franchi et al. (2010a) under CC-BY-3.0.
Some tendons also have additional sub-tendon structures. The matrix between the sub-tendons and between the fascicles allows the sliding of tendons and fascicles in small forces (toe region) (Thorpe et al., 2015; Gains et al., 2020). The primary role of the interfascicular matrix is to allow an increased extension and cyclic loading in energy-storing tendons. However, for the sub-tendon matrix, the linear region also allows load transmission (Gains et al., 2020).
Tendon and ligaments are widely investigated in different scales. Therefore, in many cases, they thus serve as a case model for collagenous tissues for structure-function relationship. They have characteristic J-shaped mechanical behavior under uniaxial tension. Tendons demonstrate remarkable mechanical behavior with stiffness of 1–2 GPa and strength of approximately 100 MPa (Mithieux and Weiss, 2005). It is important to note that structural differences in all length scales and additional mechanical mechanisms exist in other fibrous tissues that are not always given proper attention.
The Intervertebral Disc
The intervertebral disc (IVD) separates between adjacent vertebrae. It is composed of the outer annulus fibrosus (AF) surrounding the nucleus pulposus (NP) core. The AF consists of approximately 20 layers of parallel collagen fibrils called lamellae. In adjacent lamellae, the orientation alternates relative to the spinal column. The lamellar thickness is varied between the different AF regions, ranging between 50 and 260 µm (Cassidy et al., 1989). The collagen fibril angle varies between 46 and 60° with the loading direction in human discs (Cassidy et al., 1989; Marchand and Ahmed, 1990; Holzapfel et al., 2005; Guerin and Elliott, 2006). The outer AF, made of type I collagen fibril organized network with a diameter of 20–160 nm, gradually changes to type II collagen when advancing inward towards the NP (diameter of 20–140 nm). Hence, collagen organization and collagen type distinguish the inner and outer AF. A possible reason for the varying fibril diameters in the outer and inner AF may be the different types of collagen (Han et al., 2012).
Collagen lamellae have planar zig-zag crimp (Baer et al., 1991), as in the tendon fascicles (Figure 5B). The crimp angle increases in the radial direction inward from 20 to 45°, and the crimp period decreases from 26 to 20 µm (Cassidy et al., 1989). Together with the high collagen content, elastic fibers run parallel to the collagen fibrils of the lamellae to uncoil the collagen fibrils (Yu et al., 2007). The elastic fibers are oriented axially and radially, allowing them to restore more complex deformations (Roughley, 2004). The entangled network of elastic fibers is described in detail in Yu et al. (2007, 2015) and Tavakoli et al. (2017, 2020). Different PGs in the AF (such as leucine-rich repeat family, Decorin and biglycan, etc.) can interact with collagen fibrils and facilitate intermolecular interactions with varying types of collagen (Roughley, 2004).
The AF lamellae are separated via inter-lamellar matrix (ILM). The ILM thickness is approximately 30 μm, and it is composed of PGs, radial cross-bridges, elastic fibers, and cells. The ILM consist of a dense network of elastic fibers between adjacent lamellae (Yu et al., 2015). A continuous elastic network exists across the AF, connecting collagen fibrils within lamellae, and connecting lamellae to each other, holding the AF structure intact (Schollum et al., 2009; Yu et al., 2015).
Blood Vessels
Arteries are responsible for transporting blood and supply nutrients from the heart to the whole body. They are subjected to 35–40 million load cycles annually. Thus, their deformation mechanisms repeatability is crucial. Unlike tendons, ligaments, and AF, blood vessels consist of active mechanical behavior due to their muscle layer. The arteries close to the heart are mostly elastic with large diameters, whereas, in the periphery, the arteries are muscular, demonstrating pronounced viscoelastic behavior. Some arteries present mixed morphological structures (Holzapfel, 2008). Here, we will focus on the vessels’ passive mechanical behavior and the relation to their structure.
As in the other tissues, the ECM of the vessels also contains elastin, collagen, and PGs (Carey, 1991) which their hierarchical structure and three-dimensional organization enable durable support and define the mechanical behavior of the vessel (Martufi and Gasser, 2011).
Vessels are usually composed of three layers: adventitia, media, and intima (Figure 4). Collagen assembly varies between the layers but is mainly arranged in the media and adventitia, which provide the blood vessel its strength and stiffness. In the intima, collagen fibers are dispersed, while in the media, collagen fibers form an entangled tri-dimensional network with elastin and muscle cells, which are arranged into ∼10 μm thickness concentric lamellae, oriented circumferentially, to restrict rotation during pressurization. The adventitia also contains a helical arrangement of thick collagen fibers, creating a 3D network similar to the media. These fibers are crimped and oriented in different directions that change between tissues (Yang et al., 2019). For instance, in the aorta, two prominent fiber families exist in the axial and circumferential directions: in the intima-axial and circumferential, in the media-primarily circumferential and the adventitia-mainly axial (Niestrawska et al., 2016). The mechanical behavior of the different layers correlates with these directions, where the higher stiffness is seen in the axial direction of the adventitia and circumferential direction for the media. However, other families of fibers exist as well (Schriefl et al., 2012).
In vessels, approximately 10–40 collagen fibrils are cross-linked and assembled into fibers. Like tendons or ligaments, they run parallel and envelop muscle cells (O’Connell et al., 2008; Martufi and Gasser, 2011). As in tendons, fibrils are noncovalently bound using PG bridges, such as decorin (Scott, 2003; Gasser, 2020). The reversibility of these interactions is essential for the sliding between the fibrils. In the media, the collagen fibers are usually straight, whereas, in the adventitia, they have a wavy structure. Although the collagen fibers align in specific directions, unlike tendons and AF, they are separated into individual fibers and have a larger distribution than the latter tissues (Figures 4, 5C). These distributions in collagen fiber orientations vary across the vessel walls to keep their functionality (Schriefl et al., 2012).
Unlike the latter tissues discussed here, vessels consist of significantly high elastin content (Table 1). Elastin in the aorta constitutes 40–50% dry tissue weight (Holzapfel, 2001). It is mainly found in the media and organized as mostly concentric sheets with ∼1 μm thickness (71%), 100–500 nm thick rope-like interlamellar elastin fibers (27%), and ∼1.5 μm thick radial struts (2%) (Berry and Greenwald, 1976; Dingemans et al., 2000; O’Connell et al., 2008; Gasser, 2020). GAGs are often neglected in the arterial tissue; however, they exist in relatively low contents (2–5% by dry weight) (Wight, 1980) (Table 1).

TABLE 1. Representative structural and mechanical properties of different soft fibrous tissuesa.
Skin
The skin comprises the “outer layer” of the body, and it is one of the most important tissues. Its thickness is about 1.5–4 mm, it averages 1.8 m2 on surface, and it accounts for approximately 15% of the bodyweight (Breathnach et al., 2010; Benítez and Montáns, 2017) and has exceptional tear resistance to ensure that the internal organs remain intact (Yang et al., 2015). Different species consist of entirely different skin architectures. The differences between species were discussed in Sherman et al. (2015) and Yang et al. (2019).
Skin usually comprises three layers: the epidermis, dermis, and endodermis (Hypodermis). The dermis is the main load-bearing structural component of the skin. It contains PGs, elastic fibers, and collagen types I and III collagen (respectively, 80 and 15% of total collagen content) and cells. Collagen is arranged into fibers that account for approximately 70% of the weight of dry dermis. The dermis is divided into three layers: papillary, sub-papillary ant reticular. In the papillary and sub-papillary layers, the fibers are wavy, thin, and sparsely distributed. In contrast, in the reticular layer, the fibers are thick (2–15 µm), organized in bundles, and densely distributed (Limbert, 2017) (Figures 4, 5D). Several studies found a bimodal orientation of fibers in skin tissue (Jor et al., 2011; Annaidh et al., 2012). The collagen fibers are wavy with a wavelength of ∼10 μm and amplitude of ∼3 μm (Table 2). Unlike tendons, their crimping has 3D semicircular pattern. This waviness disappears after extension to failure (Pissarenko et al., 2019; Yang et al., 2019). The orientation in planes parallel to the outer surface of the human dermis follows langer lines (Langer, 1861), corresponding to the directions of pre-existing tension in the tissue.
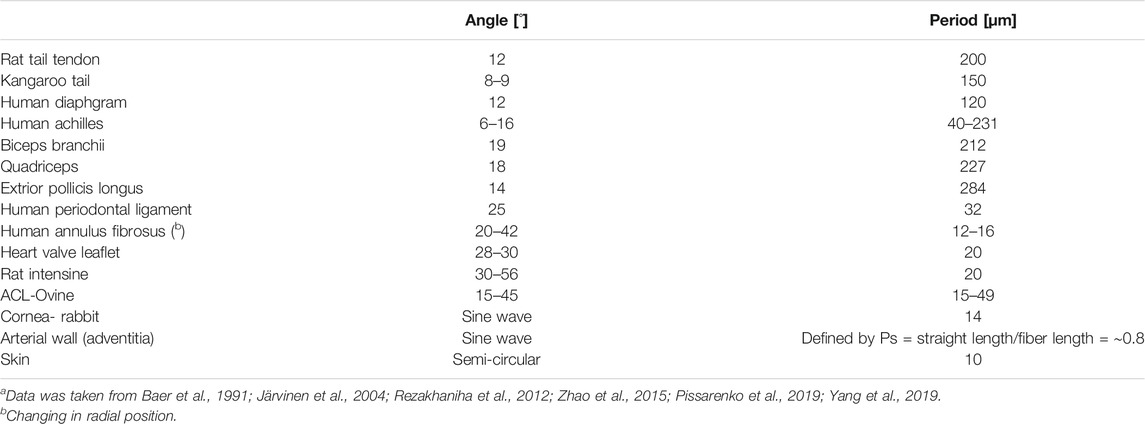
TABLE 2. Crimp properties of different fibrous tissues (a).
Mechanical Mechanisms
The mechanical behavior and structural architectures of soft fibrous tissues are extensively studied in specific tissues (Fratzl and Zizak, 1997; Schulze-Bauer et al., 2002; Holzapfel et al., 2005; Sommer et al., 2009; Yang et al., 2015; Niestrawska et al., 2016; Holzapfel and Ogden, 2018; Frank et al., 2019; Kramer et al., 2019), including the mechanical role of the tissue constituents using enzymatic digestion (Basalo et al., 2004; Barbir et al., 2010; Isaacs et al., 2014). Recently, new techniques such as multiphoton microscopy, Second-harmonic generation (SHG), and Small-angle X-ray scattering (SAXS) were used for in situ multi-scale examinations of tissues under load (Bancelin et al., 2015; Yang et al., 2015; Niestrawska et al., 2016; Lynch et al., 2017; Pissarenko et al., 2019; Amabili et al., 2021). These techniques provide valuable data regarding the structure-function relationship in different tissues and how the entangled mechanical mechanisms work simultaneously on different scales. However, understanding how each isolated structural element affects the tissue mechanical behavior is still not completely revealed. Additionally, the biomimetics of these multiscale structural designs is still not getting enough attention, as further discussed in Structural Mechanisms in Biomimetic Materials and Soft Tissue Engineering section.
Structural mechanisms in tissues include several structural motifs: such as the different composite constituents and their distribution and gradients between the different length scales, the fiber fraction, orientation and crimping of the fibrous phase (the load-bearing component, namely, the collagen), the structural hierarchy-including “composite within composite” or nested composites and the interface between the fiber and matrix that enables load transfer. Moreover, herein we aim to examine the synergy between the building blocks as composite materials and not the individual effect of the building blocks as a guideline for engineering new materials for tissue repair and replacement and the next generation of engineered materials.
Collagen Crimping
Crimping or waviness of collagen fibers is found in most collagenous tissues, like the intestine, skin, tendon, cornea, AF, blood vessels (Cassidy et al., 1989; Gathercole and Keller, 1991; Franchi et al., 2008; Zhao et al., 2015; Vergari et al., 2017). The crimping properties of different tissues are presented in Figure 5 and described in Table 2. Crimping straightening creates the toe region in tendons and ligaments, presenting large deformations under small loads (Fratzl and Weinkamer, 2007). At this region, the matrix (elastin and PGs) dominates the mechanical behavior. For other tissues, additional motifs influence simultaneously.
The AF shows a zig-zag pattern oriented with the lamellar angle, varied with the radial location of the IVD (Figure 5B) (Baer et al., 1991). The fibrils introduce a joint planar crimp waveform. The plane of the waveform is vertical to the lamellar plane and bent relative to the spinal axis by the interlamellar angle. Although the crimp length stays constant, there is a gradient in the crimp geometry: the crimp angle increases from 20 to 45°, while the crimp period decreases from 26 to 20 μm linearly from the outer region of the disc inward. This gradient influences the mechanical response to disc compression: when the IVD is compressed, axial loads are translated to radial and tangential tensile stresses in the AF lamellae. Thus, the collagen fibrils reorient in the radial direction (Klein and Hukins, 1982), and there is a decrease in the crimp angle and an increase in the crimp period. However, fiber angles increase from the anterior to the posterior region. The larger angles for the posterior fibers restrict the maximal axial distance of endplates in flexion and minimize spinal cord over-stretching (Marchand and Ahmed, 1990; Holzapfel et al., 2005).
In tendons and ligaments, crimping is parallel in the fascicle, i.e., fibrils share a zig-zag pattern in the micro-scale with bending regions that act as flexible hinges. These regions show alternating dark and light bands at polarized light microscopy (Gathercole and Keller, 1991). Different tendons have different crimping angles, such as the Patellar and Achilles tendons. The latter crimping angle was smaller than that of the patellar tendon, which allowed for a larger toe region (Amiel et al., 1983; Herod et al., 2016). The mechanical role of the tendon also influences the crimping properties. For example, energy-storing superficial digital flexor tendons (SDFTs) demonstrated much finer crimp (21.1 ± 5.5 µm) and smaller crimp angle (6.5 ± 1.4°) than positional common digital extensor tendons (CDETs) with a crimp of 135.4 ± 20.1 µm and crimp angle of 13.1 ± 2.0°. Probably due to SDFT’s adequate recoil capacity (Spiesz et al., 2018).
Fibril crimping planes are approximately parallel to the outer surface of the fascicle (Figure 5A), and adjacent fascicles have a similar crimping angle. However, crimping angle decreases significantly at the center of the fascicle (Kastelic et al., 1978). Franchi et al. (2008) found that tendon and ligament fibrils showed periodic sharp kinks in the nanometric scale, called fibrillar crimp. They found that the crimp always had local deformation (Figure 5F). However, in regions that were subjected to change in the direction, these kinks were absent (Figure 5E). These fibrils were characterized in large plurimodal diameter and a straight subfibrillar arrangement (∼5°) and subjected mainly to unidirectional tension. The fibrillar kink is composed of parallel collagen fibrils that suddenly change their direction at the top angle of each crimp. They appear distorted with a sudden change of their direction, with interfered D-periodicity and swollen microfibrillar array. It is assumed that these kinks have molecular flexibility due to different sequences of amino acids in tropocollagen: proline and hydroxyproline have the highest flexibility compared with Gly-Pro-Hyp sequence, which is very rigid. Actually, these kinks act more like knots than kinks, creating more flexible regions of the rigid thick fibrils by changing their direction and microfibrillar arrangement and allowing the local structural release of the helical constraint and recoiling capabilities (Franchi et al., 2010b).
Unlike tendons and ligaments, skin and blood vessels are subjected to multidirectional loads. They also consisted of crimping (or waviness) in the microscale (fiber level). However, every fiber had a different crimping pattern and orientation (Figures 5C,D). These tissues were composed of small collagen fibrils (25–100 nm) with a highly uniform diameter (unimodal distribution) and a sinuous or helical form with diverse curvatures (Franchi et al., 2008). These small fibrils did not show any shape deformation when they changed direction. Hence, These fibrils can adapt varied curvatures without damage, thus compatible with multidirectional loadings. Herein, the recruitment and reorientation of the fibers preceded the crimping straightening, allowing even larger deformations in the toe and heel regions. These tissues are also characterized in larger toe regions and higher elastin content (Holzapfel, 2008; Venkatraman et al., 2008).
Jan and Sigal (2018) demonstrated how collagen fiber crimp straightens (or fiber recruitment increases) in different regions of the eye sclera with increasing Intraocular pressure (IOP). While this phenomenon is well studied in tendons (Fratzl and Weinkamer, 2007; Gupta et al., 2010), it is less studied experimentally in other tissues. They found that different areas of the sclera have different crimping architectures, and with increasing IOP, different amounts of fibers are recruited (straightened). At physiologic IOP, 75% of the fibers were recruited, and 25% were reserved in both regions. This mechanism of variable crimp morphology in the different areas of the tissue allows gradual recruitment and stiffening of the fibers and is also seen for vessels (Schriefl et al., 2012), tendons (Franchi et al., 2008), and AF (Baer et al., 1991).
Orientation and Recruitment
An essential structural motif that is crucial in fibrous tissues is the directionality of the collagen fibers. Fiber orientation plays a vital role in the structure-function relationship and determines the anisotropy in the mechanical properties. Collagen fibers work in tension, and they start bearing load when they are aligned in the direction of tension. Thus, fibrous composites are stronger and stiffer in the direction of the fibers and weaker and more compliant in the direction of least orientation.
Unlike hard composites, in soft composites, collagen fiber orientation enables an additional mechanism for large deformations when collagen fibers and fibrils rotate towards the loading direction and thus, increase toughness. Fiber organization also influences cellular behavior, such as cell migration, matrix production, gene expression, cell morphology, and strain transmission (Eekhoff and Lake, 2020).
In general, there are variations in structural compositions between different species, regions, and pathologies for all tissues, affecting the local and global mechanical properties. However, for different tissues, repeated trends exist. In tendons and ligaments, collagen fibers are strongly aligned in the loading direction. Their physiological role is to provide unidirectional resistance to bind between muscle and bone and between bones, so they are stiff and strong along the primary axis of loading. In the AF, Angle-plied (±30°) fiber orientation is critical for appropriate biomechanical disc functioning. It transforms the compressive forces applied to the disc to lateral forces and makes the spine flexible enough to bend and twist in all directions. In the aorta, different fiber families are oriented mainly in the circumferential and axial directions. Fiber orientations are found in the tangential plane of the artery wall, with minimal dispersion through the wall thickness and without any radial components (Schriefl et al., 2012). However, in pathological states, such as abdominal aortic aneurism (AAA), the distribution of orientations increased significantly compared to a healthy aorta (Niestrawska et al., 2016).
Although fiber distribution is relatively small in tendons, Lake et al. (2009) have found that fiber distributions became more aligned under load, mostly in the toe region. This suggests that fiber realignment may be partly responsible for observed nonlinear behavior in the tendon as well. A relatively similar small distribution exists in the AF (Ghezelbash et al., 2021); thus, a similar influence can be assumed. On the other hand, skin consist of large distribution of fibers; though specific orientations are observed (±45°), their distribution is very wide (Annaidh et al., 2012). This structure allows multiaxial loads.
Furthermore, under load, the anisotropy considerably increases when fibers are realigned and recruited. However, for different skin types, it was found that stronger skin is associated with a smaller orientation distribution (Sizeland et al., 2013). It is important to note that unlike tendons, ligaments, and AF in skin and blood vessels, the fibers are recruited separately, enabling large deformations. Furthermore, the orientation distribution there is larger (Figure 5C,D).
Structure and Function Relationship in Different Fibrous Tissues
All soft tissues have pronounced J-shaped behavior with large deformations attributed to different recruitment mechanisms, where more mechanisms are apparent—larger deformations are demonstrated (Figure 1). Soft tissues are also characterized by viscoelasticity, prominent fatigue life, and exceptional tear resistance. Some tissues also demonstrate unique Poisson behaviors, such as Poisson value larger than one and negative Poissons (auxetic behavior) (Derrouiche et al., 2020; Pissarenko and Meyers, 2020). This review will mainly focus on the large deformation behaviors.
Tendons and Ligaments
Tendons and ligaments have pronounced J-Shaped behavior, with a very stiff slope (tendons more than ligament) (Figure 6). Upon the beginning of stretching, the crimping in the fascicles is straightened. The matrix (elastin and PGs) dominates the mechanical behavior of this toe region, where under small loads, relatively large deformation is seen. Recent publications have also shown that the matrix in other length scales, i.e., between the sub-tendons and between the fascicles, allows sliding of tendons and fascicles in the toe region (Thorpe et al., 2015; Gains et al., 2020).
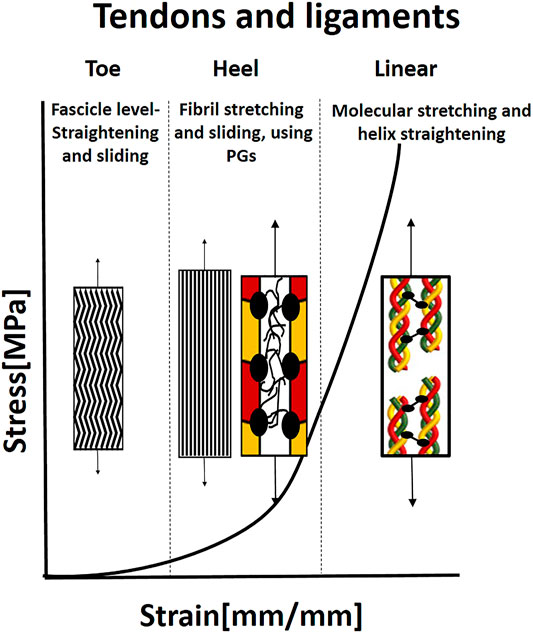
FIGURE 6. Illustration of the J-shaped behavior and mechanical mechanisms in tendon and ligaments. In the toe region, the microscopic crimping in the fascicles is straightened. When the fibrils are straight, they start carrying the load, and simultaneous sliding and stretching start, mediated by PGs, in the heel region. In the linear region, the molecular stretch of the covalent cross-links and helix straightening occurs. Based on Fratzl and Weinkamer (2007).
The toe region is followed by the heel region, where collagen starts carrying the load, and the stiffness increases considerably with extension. In this region, the kinks in the gap between the fibrils are straightened (Fratzl and Zizak, 1997), fibril sliding occurs simultaneously with fibril elongation, both mediated by the PG matrix in a critical balance (Rigozzi et al., 2013). Rigozzi et al. (2013) also demonstrated that there were not any differences in collagen fibril D-period and diameter in the heel region (5% strain) for either GAG-depleted or native tendons. However, in the linear region (15% strain), a significant increase in D-period length and a decrease in fibril diameter were seen. Longer D-period was observed in GAG-depleted tendons. Therefore, it appears that GAGs play a role in lower strains to reduce fibril stretching and facilitate sliding and maybe protect the fibrils from overstraining. In the linear region, stretching the collagen triple helices and cross-links leads to a change in helix pitch (Fratzl and Zizak, 1997; Fratzl and Weinkamer, 2007). An additional slipping mechanism in the molecular and sub-fibril level may occur due to a deficiency in covalent cross-linking between molecules in the fibrils. The main function of tendons and ligaments is force transmission, however, the specific pathways of force transmission between different hierarchical levels are unresolved yet (Zitnay and Weiss, 2018). The main explanation is that force transmission is done through the matrix that enables fiber sliding, which is also the most significant contributor to stress relaxation (Gupta et al., 2010).
The Intervertebral Disc
AF lamellae demonstrate hyperelastic J-shape stress-strain behavior, typical for type I collagen tissues under tension, with toe, heel, and linear regions (Figure 7) (Skaggs et al., 1994; Holzapfel et al., 2005). Under load, the AF lamellae reorient in the stretch direction, with an average 17.0° decrease in fiber angle for non-degenerate tissue over 10% strain (Stokes and Greenapple, 1985; Tower et al., 2002; Guerin and Elliott, 2006). This reorientation increases the rotation under torsion, AF circumferential modulus, and compressive stiffness and decreases vertical displacement under compression and AF bulging. Therefore, fiber reorientation may serve to stabilize the motion segment during axial loading. Moreover, affine fibril reorientation, that is, fibril deformations would be consistent with overall tissue deformations, was found to be primarily valid in small strains (namely, the toe region). Other mechanisms such as fibril sliding, crosslinks, fibril-fibril, or fibril-matrix interactions may constrain the reorientation at large strains to be non-affine (Guerin and Elliott, 2006).
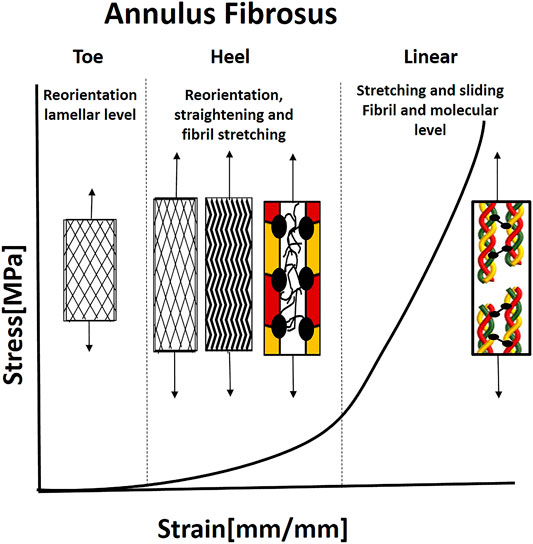
FIGURE 7. Illustration of the J-shaped behavior under uniaxial tenion and mechanical mechanisms in the annulus fibrosus. For collagen fibrils to carry the load, they need to be straight and reorient in the loading direction. Therefore, the fibrils reorient in the loading directions, and the microscopic crimp straight in the toe and heel regions. When the fibrils are straight and recruited, they start to carry the load, and simultaneous sliding and stretching start, using the PGs. Then, the molecular stretch of the covalent cross-links and helix straightening taking place. Based on Guerin and Elliott (2006).
Due to the spatial gradients in the structure, the outer lamellae are less deformable, stiffer, and have lower energy dissipation properties than the inner lamellae (Cassidy et al., 1989; Holzapfel et al., 2005). More specifically, the stiffness of the outer AF region is larger than the inner region, and the anterior region is stiffer than the posterior region. The radial variation of the lamellar stiffness is mechanically beneficial since a heterogeneous thick-walled cylinder, with internal soft layers, will reduce stress gradients compared to a homogenous inner thick-walled cylinder that yields a high gradient of circumferential stresses (Holzapfel et al., 2005). These stiffness gradients result from alternate structural collagen I and II ratio, proteoglycans type, water content, and collagen fibril diameter (Eyre and Muir, 1974; Skaggs et al., 1994; Han et al., 2012).
Isaacs et al. (2014) have tested the influence of enzymatic digestion on collagen, elastin, and PGs in different AF orientations. They found that the degradation of the elastic fibers and PGs within the lamellae resulted in deteriorated mechanical properties since these biomolecules play an essential role in load transfer between the collagen fibrils under uniaxial loading.
Michalek et al. (2009) demonstrated that the mechanical behavior under transverse shear of multilamellar sample resulted from skewing inside the lamella and fibril sliding (as in tendon and ligaments) and not from sliding between the lamellae through the ILM. The fibril sliding mechanism is similar to the one occurs in tendons and ligaments. The lack of sliding in the ILM results from the rigid fibrous connection in the transverse cross-bridges (Pezowicz et al., 2006; Michalek et al., 2009).
Blood Vessels
Arteries also have hyperelastic J-shaped behavior with toe, heel, and linear regions under tension (Figure 8). Arteries are subject to large inner pressures that stretch the arterial wall tissue. For example, human adventitia of coronary arteries demonstrated significant load-carrying capabilities with high ultimate tensile stresses of larger than 1 MPa (approximately three times more than media and intima). However, ultimate strains were similar for the three layers (Holzapfel, 2008). Thus, adventitial collagen plays a major role in arterial wall strength. In unstressed tissue, the wavy adventitial collagen fibers cause the adventitia to be less stiff than the media. However, at more significant strains, the collagen fibers are straightened and recruited. Then, the adventitia’s mechanical response changes to that of a stiff tube that protects the muscle from acute hypertension (Schulze-Bauer et al., 2002).
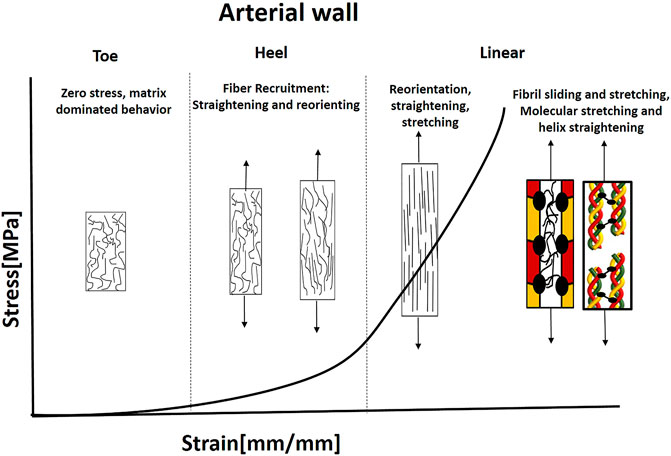
FIGURE 8. Illustration of the J-shaped behavior and mechanical mechanisms under tension in the aorta. The collagen fibers are separated and noncontinuous with preferred orientation. The distribution of orientations is larger than AF, ligaments, and tendons. Elastin is widely distributed and carries the load under small strains. Fiber recruitment starts in the heel region (Hill et al., 2012). Fibers need to reorient and straight to carry the load; therefore, larger deformations exist. Then, simultaneous sliding and stretching start, mediated by PGs. This stage is followed by a molecular stretch of the covalent cross-links and helix straightening taking place.
Hence, collagen fibers can dominate the mechanical behavior when recruited and activated. Thus, they will carry tension forces only when they are straightened and reoriented in the load direction. Therefore, for small stresses, there is no fiber contribution to the deformation of the tissue, and the elastin matrix bears the load (Roach and Burton, 1957; Venkatraman et al., 2008). Elastin has a less significant contribution at higher strains owing to the increased bearing of load through collagen. However, its primary importance stems from its ability to recoil the vessel during pulse cycles (Gasser, 2020). Recently, Amabili et al. (2021) demonstrated using SHG combined with two-photon fluorescence (TPF), 3D interconnected structure of collagen and elastin fibers in human aorta. They presented intertwined elastin and collagen fibers together with transverse elastin fibers, connecting collagen fibers.
Hill et al. (2012) examined the fiber recruitment (straightening) together with reorientation in the artery wall using a uniaxial extension device combined with a multi-photon microscope. They found that fiber recruitment starts in the heel region and continues in the linear region. When the slope changes, it indicates the specific point where fibers begin to contribute to the strain-energy function. Then, when additional load is applied, the collagen fiber becomes aligned with the stretch direction. The stretching enables storing the elastic energy in the PG matrix inside and between the fibrils (Gasser, 2020). At higher strains, sliding of collagen fibrils or damage in interfibrillar PGs bridges can result in tissue softening and failure (Gasser, 2011; Schmidt et al., 2014; Li and Holzapfel, 2019). As in tendons and ligaments, fibril stretching (increased D-space) and sliding occur in arterial collagen, and the fibrillar stretch is about one order of magnitude smaller than the macroscopic stretch, mediated by PG matrix (Holzapfel, 2008).
In addition, Mattson et al. (2017) tested the influence of GAG removal on arteries. They found that the removal of GAGs results in an earlier transition point of the nonlinear stress-strain curve. However, stiffness was not significantly changed with GAG removal. Furthermore, multiphoton microscopy examination demonstrated straighter fibers in adventitial collagen and earlier recruitment of elastin and collagen in lower strains. In addition, it was found that mechanical mechanisms work differently under different loading modes. When two types of macroscopic loading were subjected to the adventitia layer of carotid arteries: axial tension under constant pressure and inflation under constant axial length, fiber realignment was observed for the second loading regime. However, it was not observed for the first one, even for large stretches (over 1.5). This behavior was attributed to the complex tension-compression interactions between very stiff collagen fibers and compliant surrounding proteins (Krasny et al., 2018). Thus, these structures allow varied structural responses for different loading modes.
One of the roles of viscoelasticity in arterial walls is to reduce stresses and strains in sudden acute hypertension events. Additionally, energy storage and dissipation can prevent mechanical failure and increase fatigue life (Zhang et al., 2007).
Skin
Gibson et al. (1965) stated on the dermis: “In whatever direction it is stretched, all the fibers eventually become parallel.’’ Hence, the collagen fibers in the dermis are widely distributed (Figure 5D); therefore, upon applying stress in a specific direction, the fibers reorient in the loading direction, allowing very large deformations (Figure 1).
As in other fibrous tissues, the skin stress-strain behavior is nonlinear with J-shaped behavior and composed of toe, heel, and linear regions (Figure 9). The exact working mechanism in every region is different from the classical one in tendons and ligaments (Tendons and Ligaments section) due to the fiber arrangement and distribution of building blocks. The crucial role of PGs can explain their high content in skin, as it accounts for 20% of the dry weight of the skin and 80% of the volume (Benítez and Montáns, 2017).
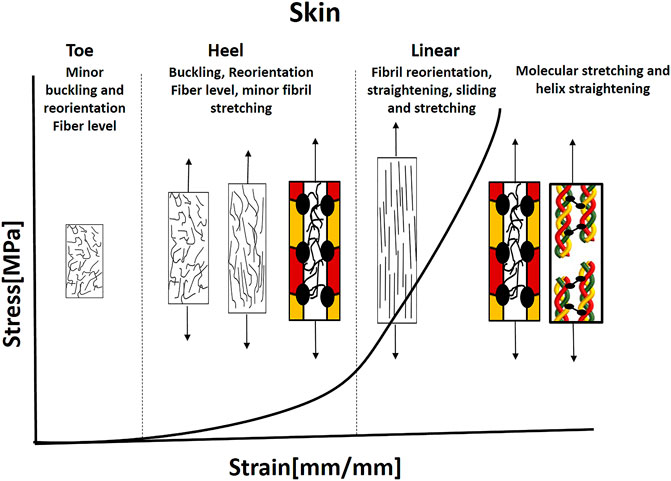
FIGURE 9. Illustration of the J-shaped behavior and mechanical mechanisms under tension in the skin. The collagen fibers are noncontinuous with bimodal orientation and distribution of orientations. In the toe and regions, buckling and bending of the fibers occur together with minor Fiber recruitment and straightening (Bancelin et al., 2015; Lynch et al., 2017). Most recruitment and straightening occurs in the linear region up to critical load when fibril sliding and stretching start, using the PGs. This is followed by a molecular stretch of the covalent cross-links and helix straightening. Based on Bancelin et al., 2015; Yang et al., 2015; Lynch et al., 2017.
Yang et al. (2015) tested the structure-function relationship in rabbit skin using in situ tension loading combined with small-angle X-ray scattering (SAXS), scanning electron microscopy (SEM), and transmission electron microscopy (TEM). They divided the mechanical behavior into four steps: 1, 2) toe and heel: collagen fibrils are oriented in varied angles. During these stages, collagen fibrils start to straighten and rotate toward the direction of tension. Fibrils are also stretched, and D-space starts to increase, and more strain is attributed to straightening than stretching. 3) Linear region: Collagen fibrils rotate at approximately 10°, becoming aligned uniformly and increasing recruitment. D-spacing of collagen fibrils increases from 64.5 to 66.9 nm together with the mechanisms of inter-and intrafibrillar sliding, and 4) Fracture: collagen fibrils fracture and curl back upon unloading (Figure 10A–D). The fibrils return to a wider range of orientations, and D-spacing decreases. These mechanisms provide skin with extraordinary tear resistance.
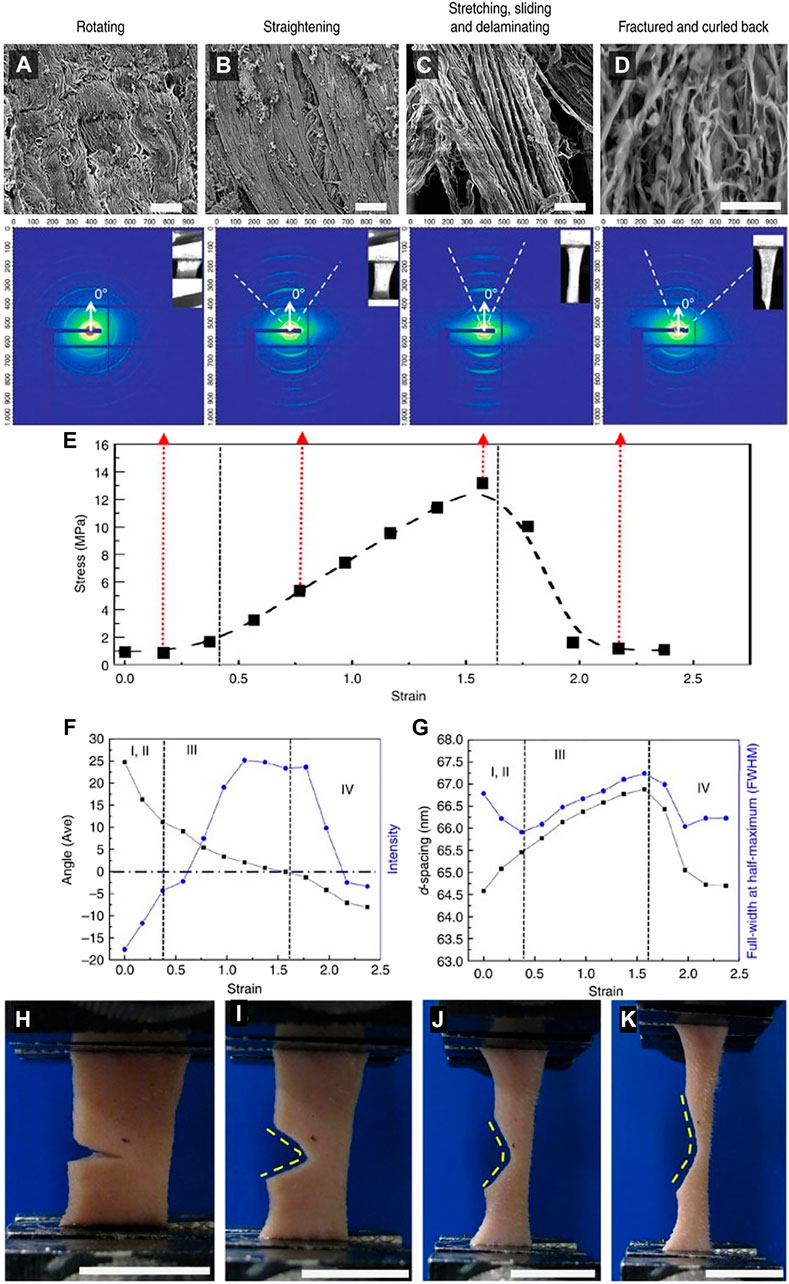
FIGURE 10. (A–D) Four structural mechanisms under tensile loading of rabbit skin: Rotating, straightening, stretching, sliding, and delaminating, and fracture. (E) Variations in SAXS peak intensity during a tensile test of rabbit skin divided into four stages 1, 2) toe and heel regions, 3) Linear region, and 4) Fracture. (F) Fibril reorientation: Angle of normal to the tensile axis (black dots) versus intensity of fibrils (blue dots) as a function of strain. (G) Fibril stretching and sliding: D-spacing (black dots) and full-width-at-half-maximum (FWHM) (blue dots) of fibrils as a function of strain. (H–K) Tear resistance of notched rabbit skin under uniaxial tension. Adapted from Yang et al. (2015) under CC BY 4.0.
Similarly, Bancelin et al. (2015) tested the multiscale mechanical behavior in mice skin using multiphoton microscopy. They found that the heel region is partly associated with fiber alignments, but the linear region corresponds to the maximal alignment of the collagen fibers. Thus, stretch in the linear region is associated with the increased alignment of fibers in the loading direction and not only due to fiber stretching. Accordingly, each aligned fiber provides specific stress to the tissue, regardless of the stretch ratio. The fiber sliding, reported for tendons (Gupta et al., 2010), probably occurs above a critical load, associated with breaking cross-bridges with the non-fibrillar matrix. Each stretched fiber contributes its critical load individually to the total stress of the tissue. Thus, the collagen fibers in the linear region do not behave elastically but plastically. This plastic response is likely due to inner sliding inside each collagen fiber assisted by the PG matrix between the fibrils.
Moreover, Lynch et al. (2017) found that in the heel region of skin stress-strain behavior, the aligned fiber fraction in the loading direction increases non-linearly with stretch. The fibers perpendicular to the traction direction would need to buckle and bend before they can reorient. Thus, a minor reorganization was measured in the toe and heel regions. A similar interpretation of buckling was also seen in recent numerical models based on low-density fibrous gels, simulating a large network of fibers connected by flexible junctions (Stein et al., 2011; Mauri et al., 2016; Bircher et al., 2017; Sopher et al., 2018). Nonetheless, these studies did not include the PG matrix and its mechanical effect on the fibers.
Structural Mechanisms in Biomimetic Materials and Soft Tissue Engineering
Biomimetics is used to imitate natural mechanisms towards developing newly designed materials with superior properties. However, due to the high complexity and multi-functionality of natural materials (such as biological, chemical, mechanical functions, etc.), a systemic biomimetic approach can verify the different functions by iterative reverse-engineering approach. Such iterative feedback can also benefit soft-tissue biomechanics (Csete and Doyle, 2002; Vincent, 2003; Fratzl, 2007; Wilson and Rosen, 2009). Therefore, engineered biomimetic composite materials that follow nature’s design principles and duplicate them in simpler material systems have a two-fold effect: they provide a better understanding of the complex natural systems and allow engineers to develop superior material systems (Bar-Cohen, 2005, 2006; Laaksonen et al., 2012). For example, in hard natural composites, biomimetics in synthetic material systems is more abundant and complex structures as nacre and bone are designed to mimic their mechanical behavior (Fratzl, 2007; Espinosa et al., 2011; Studart, 2012; Libonati and Vergani, 2016; Wilkerson et al., 2016; Greenfeld et al., 2018; Peng et al., 2019; Yang et al., 2019; Zhang et al., 2019; Grezzana et al., 2020; Zorzetto et al., 2020). Nevertheless, using the same approach in soft fibrous tissues is more scarce.
As mentioned before, soft fibrous tissues are made of the same repeating building blocks. Still, they consist of different structural motifs at different length scales, thus creating various soft tissue structures and functions (Holzapfel, 2001). Herein, we presented four different examples and tried to explain the structure-function relations known so far. The ability to mimic mechanical mechanisms and understand the structure-function relationship enables the development of custom-made hierarchical soft composite materials with tailor-designed mechanical behavior for soft tissue repair and replacement. These materials will be mechanically biocompatible with the native tissue when implanted (Mazza and Ehret, 2015). Moreover, an additional benefit that arises from this scientific advance is the ability to model tissues for medical interventions and provide improved medical care.
Engineering these mechanical motifs in simpler material systems will also allow us to isolate the effect of the structural motif on the mechanical behavior and explain how these structural elements interact in an assembly to generate the required function. Although the biological aspect is very important in this area, it was widely discussed in other reviews (Dhandayuthapani et al., 2011; Nikolova and Chavali, 2019). Herein, we will further discuss the latest advances in soft tissue biomimetics from the material and mechanical point of view. Our goal is to examine engineering principles that allow the designing of new biomimetic materials based on the reviewed structural motifs.
Material Selection
Soft tissues are constructed as composite materials consisting of collagen, elastin, and PGs. Each has its unique function. Biomaterials for soft tissue engineering are extensively explored and developed. These materials cover multiple aspects; such as cell adhesion, biocompatibility, biodegradability, bioprinting, structural hierarchy, and mechanical compatibility (Venkatraman et al., 2008; Dhandayuthapani et al., 2011; Mazza and Ehret, 2015; Nikolova and Chavali, 2019; Buwalda, 2020; Guimarães et al., 2020). Herein, we will focus on the biomimetics of structural motifs and their effect on the mechanical compatibility of the materials.
Collagen is a very important biomaterial due to its biological and mechanical properties discussed above. However, its cleaning and isolation from mammalian tissues and its fiber assembly significantly deteriorate its structural and mechanical properties, thus preventing its natural role as the load-bearing element (Bazrafshan and Stylios, 2019; Montalbano et al., 2021). Methods for collagen assembly to fibers include electrospinning and wet spinning. Other collagen sources are also widely explored (Parenteau-Bareil et al., 2010; Lim et al., 2019), including marine sourced collagens (Sharabi et al., 2014; Benayahu et al., 2018; Fassini et al., 2021). Other load-bearing biomaterials, synthetic and natural, are frequently studied as well. Elastin and Elastin-like biopolymers are also frequently used as scaffolds for tissue engineering, especially for vascular applications, due to the large content of elastin in these tissues (Daamen et al., 2007; Nettles et al., 2010). However, their structural and mechanical roles often get insufficient attention, although it is vastly known that they are responsible for the toe region behavior in vascular tissues, provide large deformation behavior, and play a role in recoiling collagen crimping (Venkatraman et al., 2008). Elastin biopolymers comprising repetitive elastin sequences can exhibit supramolecular features similar to the native protein; however, some technical problems still remain, such as stable crosslinking (Debelle and Tamburro, 1999). Proteoglycans as biomaterials have many biological functions, and they are also used as biomaterials as reviewed in Rnjak-Kovacina et al. (2018).
Although many efforts are invested in developing these building blocks, they are mostly characterized as separate biomaterials with distinct properties or as hybrid material/scaffold and not as soft composite materials, without a focus on their structure-mechanical function behavior. A combination of all the three building blocks in one construct was tested by Daamen et al. (2003). However, it did not focus on the mechanical and structural characterization discussed in this review.
Recently, attempts to mimic these combinations and examine their effect on mechanical behavior were made as nano- and microfiber-reinforced soft composites, mainly for soft-tissue repair and replacement (Caves et al., 2010a, 2011; Kumar et al., 2013b; Tonsomboon and Oyen, 2013; Naik et al., 2014; Sharabi et al., 2014, 2015; Strange et al., 2014; Jang et al., 2015; Sharabi et al., 2016, 2019; Xu et al., 2016; Tonsomboon et al., 2017; Benayahu et al., 2018; Castilho et al., 2018; Sharabi and Wagner, 2021; Wertheimer et al., 2021).
To the best of the author’s knowledge, to date, there are no engineered biomimetic constructs that consist of all three building blocks but mostly partial combinations; as soft composites made of hydrogels (polysaccharides and PGs) embedded with collagen fibers (Sharabi et al., 2014, 2015, 2016, 2019; Ayala et al., 2015; Wertheimer et al., 2021), or combinations of collagen fibers and elastin (Caves et al., 2010a, 2010c, 2011; Kumar et al., 2013b; Ryan et al., 2020).
However, these composite demonstrated superior mechanical behavior as in native soft tissues. For example, Tonsomboon et al. (2017) demonstrated the crack patterns and increased toughness of gelatin nanofiber reinforced alginate hydrogels in different fiber orientations, known for natural tissues such as skin (Yang et al., 2015, 2019) (Figures 10H–K, 11G). Alginate hydrogels are polysaccharide gels that absorb water, provide viscoelasticity, and act mechanically as the PG matrix in tissues.
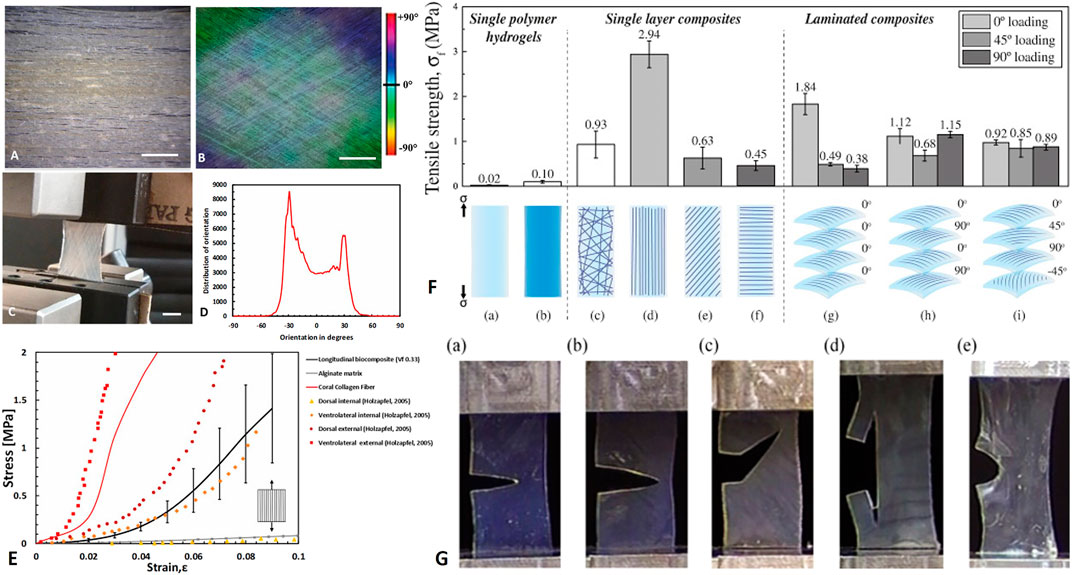
FIGURE 11. Biomimetics of soft composite fibrous structures. (A–E) biomimetics of form and function of annulus fibrosus lamellae using collagen reinforce alginate hydrogel composite. (A) Longitudinal arrangement of collagen fibers (B) Angle–plied (AP) arrangement of collagen fibers (±30°). (C) AP biocomposite under uniaxial tension test (D) Distribution of collagen fiber orientations in the AP biocomposite (scale bar 5 mm). (E) Mechanical behavior of longitudinal biocomposites, alginate matrix, and representative coral collagen fiber in comparison with in vitro uniaxial AF Single lamella measurements of (Holzapfel et al., 2005). Reprinted from Sharabi et al. (2019) with permission. (F) Electrospun gelatin nanofibers embedded in alginate hydrogel composites: Tensile failure strength σf (a) alginate and (b) gelatin; single layer composites: (c) random fiber composite, (d) longitudinal laminate, (e) 45° laminate, (f) 90° laminate; and four-layer laminate composites with a (g) uniaxial 0°/0°/0°/0°fibre orientation pattern, (h) cross-ply 0°/90°/0°/90°fiber orientation pattern, or an (i) angle-ply 0°/45°/90°/−45° fiber orientation pattern. (G) Crack patterns in alginate hydrogels with (a) no fibers, (b) 90° laminate, (c)) 45° laminate, (d) longitudinal laminate, and (e) cross-ply 0°/90°/0°/90° composite. (F–G) Reprinted from Tonsomboon et al. (2017) under CC-BY.
Moreover, in a series of papers, Chaikof and colleagues (Caves et al., 2010a, 2010b, 2010c, 2011; Kumar et al., 2013b) developed elastin-collagen composites for soft tissue repair. These composites were made of wet spun collagen microfibers (∼20–60 µm) (Caves et al., 2010b) embedded in recombinant elastin matrix (Caves et al., 2010a, 2011). As in native tissues, the mechanical behavior of these composites was non-linear, with large deformations under uniaxial tensile testing. The authors also managed to control the fiber orientation, fiber fraction, fiber spacing, and thus mechanical behavior.
In another series of papers, Sharabi and colleagues (Sharabi et al., 2014, 2015, 2016, 2019; Benayahu et al., 2018; Wertheimer et al., 2021) designed a material system comprised of coral collagen fibers that reinforce an alginate hydrogel matrix. The coral collagen fibers diameter was approximately 10 µm, and the fibers had a natural hierarchical structure and demonstrated inherent crimping, similar to the native collagen fibers (Sharabi et al., 2014). The alginate hydrogel matrix provided aqueous surrounding creating weak interactions with the collagen fibers, as in native tissues. Diverse fiber orientations and fractions were tested, and a nonlinear hyperelastic material behavior with large deformations was shown, similar to various native soft fibrous tissues, like the cornea, annulus fibrosus, and blood vessels (Sharabi et al., 2014, 2015, 2016, 2019; Benayahu et al., 2018; Wertheimer et al., 2021).
One of the major drawbacks of designing biomimetic soft composite materials is creating a stiff hierarchical fibrous phase as the naturally occurring collagen. Thus, different techniques were developed for fiber spinning. Electrospinning is an essential method for creating nanofibers from a variety of materials, synthetic and natural. This method is thoroughly discussed (Mauck et al., 2009; Sell et al., 2010; Tamayol et al., 2013; Tan and Zhou, 2019; Reid et al., 2021). The diameters of electrospun fibers can be ranging from 10 nm to 100 μm depending on the material, device configuration, and process setup. They are similar in diameter to collagen fibrils (∼100–300 nm). In addition, method modifications allow diverse fiber structures (Tan and Zhou, 2019).
Wet spinning is also a widely used method for fiber manufacturing (Puppi and Chiellini, 2017). However, the resultant fibers are usually microfibers (Caves et al., 2010b), in the same collagen fibers level range (and not fibrils, which is an essential scale). Caves et al. (2010b) created collagen microfibers from monomeric rat-tail collagen and demonstrated the alignment of the nanofibers inside the microfiber with applied deformation. Bioprinting is also an important emerging area in tissue engineering and biomimetics research (Murphy and Atala, 2014; Mandrycky et al., 2016).
Fiber Volume Fraction
In classical composites, fiber volume fraction (FVF) is an important property that dramatically influences the composites’ mechanical behavior. In native tissues, the fibril diameter is mainly measured in the cross-section view using TEM. However, different physical variables (water content, osmotic loading) and biological (age, pathology) affect the diameter of the fibrils (Han et al., 2012). Furthermore, due to the hierarchical structure of the tissues, the fibril volume function does not represent the volume fraction in other length scales as fibers, fascicles, or laminates. Spatial location and gradual tissue changes also affect this parameter. In addition, fiber volume fraction can be measured in tissues like skin and vessels using diverse imaging techniques (Rezakhaniha et al., 2012; Niestrawska et al., 2016; Pissarenko et al., 2019; Amabili et al., 2021).
However, as of today, the knowledge regarding FVF of different tissues is quite limited. It is important to note that the length of fibers/fibrils in these tissues is not entirely known, and thus the load–transfer mechanisms and interface properties are not completely revealed. Further research is also needed to allow better biomimetics, including the development of new multi-scale imaging technologies. This data is also essential for medical purposes and modeling of native physiological tissues (Holzapfel and Weizsäcker, 1998; Holzapfel et al., 2000, 2019; Niestrawska et al., 2016; Li and Holzapfel, 2019; Frank et al., 2019).
In biomimetic composites, the influence of FVF on soft synthetic composites have been investigated, mainly for tissue engineering applications (Caves et al., 2010a, 2010c, 2011; Kumar et al., 2013a, 2013b, 2014; Naik et al., 2014; Ayala et al., 2015; Sharabi et al., 2019, 2015, 2016) and found to affect different mechanical properties such as strength, stiffness, and ultimate strains.
Fiber Orientation and Recruitment
Fibrous tissues are organized in anisotropic structures as a function of their functionality. For instance, in tendons, which connect muscle to bone unidirectionally, fibrils, fibers, and fascicles are aligned with the load direction. In the AF, the parallel fibrils are oriented in what is usually defined as ±30° but actually ranges between ±22 and 50° (Holzapfel et al., 2005; Sharabi et al., 2018), due to the multiaxial loads on the IVD. Herein, the fibrils reorient under load and then recruited. In the aorta, the main orientations are circumferential and axial (depending on the layer). Still, other fiber families exist, and the orientation distribution is larger than the last two examples. A probable explanation is that reorientation and fiber recruitment allow larger deformations than in tendons and AF.
Moreover, the incontinuity of the fibers also plays a mechanical role, together with higher elastin content. Crimped isolated collagen fibers (as in skin and arterial walls) allow larger deformations without additional material stretching due to matrix interactions. Nevertheless, the main orientation allows withstanding large pressures in vessels. In the skin, the orientation is defined as bimodal but even more sparse. The large orientation distribution brings to fiber buckling and recruitment towards the loading direction. It is highly compatible with multiaxial loading, where the behavior becomes more anisotropic with applied load. This phenomenon is not similar to classical composites and unique to soft deformable composites.
Oriented biocomposites and constructs are fabricated and mechanically tested in diverse orientations mimicking native tissues, such as longitudinal (0°), transverse (90°), cross-plied (0–90°), angle-plied (±30°), and multi-laminate structures in the microfiber and nanofiber level (Figure 11) (Nerurkar et al., 2010, 2011; Caves et al., 2011; Kumar et al., 2013b; Tonsomboon and Oyen, 2013; Naik et al., 2014; Sharabi et al., 2014, 2015, 2016, 2019; Tonsomboon et al., 2017; Wertheimer et al., 2021). As more fibers are aligned in the stretching direction, the stiffer the material is. When fibers are under deflection, additional reinforcement angles are needed (Sharabi et al., 2016). Multilaminate structures are also studied in means of their mechanical behavior under different loading modes: flexure (Sharabi et al., 2016), fracture (Tonsomboon et al., 2017), and burst pressure (Kumar et al., 2013b; Wertheimer et al., 2021). Soft composites act differently as a function of the applied load. The physiological loading mode should be considered when designing a composite (Mazza and Ehret, 2015; Zhou et al., 2021). Although the oriented composites were designed and fabricated, there is not enough attention to quantifying the reorientation and fiber recruitment mechanisms, as described for tissues.
Structural Hierarchy and Nested Composites
One characteristic property of natural materials in general, and soft tissues, in particular, is their hierarchical structure composed of several structural levels, from the nano to macro-scale, such as the fibril-fiber-fascicle assembly in tendons and ligaments. One of the major drawbacks of soft tissue biomimetics is the ability to fabricate functional hierarchical materials. Nanoscale methods such as electrospinning and self-assembly enable the creation of multi-scale materials; however, these are not often assembled to higher levels structures (Doineau et al., 2021). The nanoscale level is often responsible for the toughness of materials and is characterized by increased fracture toughness and breaking energy (Evans, 1990; Launey and Ritchie, 2009; Launey et al., 2010; Yang et al., 2019); thus, nested composites fabrication is essential.
For soft composites, the multiscale behavior is not frequently studied. However, Stella et al. (2010a, 2010b) examined the multi-scale behavior of electrospun nanofibers sheets. The samples underwent planar biaxial modes of deformation. The deformation behavior was investigated across multiple scales by defining three characteristic lengths (micro (1–2 µm), meso (40–50 µm), and macro (1–3 mm). They demonstrated that even though the macro-scale behavior was similar to this of native valve tissue, the behavior in the micro and mesoscale were different and showed a heterogeneous deformation response. However, although the nanofibers were aligned in the loading direction and collected on a rotating drum, they did not consist of microscopic crimping nor aqueous matrix that enables sliding, as in soft tissues. Thus, biomimetics in multilevel scales is essential to imitate the native fibrous tissue and shed light on tissues’ multiscale behavior. Furthermore, for this type of composites, multi-scale finite element modeling is an important tool that can contribute significantly to the structure-function understanding of the construct (D’Amore et al., 2014).
Higher levels constructs that include multi-laminates for vessels and tendons biomimetics were fabricated (Caves et al., 2011; Kumar et al., 2013b; Ayala et al., 2015; Sensini et al., 2019a; Wertheimer et al., 2021). For example, Sensini et al. (2019a, 2019b, 2021) developed a morphologically bioinspired hierarchical electrospun construct to mimic the structure and mechanical function of tendon and ligaments (Figures 12A–F). They control the nanofibers’ alignment and orientation, thus creating stiffer structures like tendons and ligaments. Furthermore, they created the 2nd and 3rd levels of hierarchy, demonstrating the increased stiffness and strength arising from additional hierarchy levels. Interestingly, these constructs’ behavior is not often compared with the native tissue behavior to achieve mechanical biocompatibility (Mazza and Ehret, 2015).
FIGURE 12. Hierarchy in soft electrospun constructs. (A–F) PLLA multiscale hierarchical scaffold for ligament biomimetics. (A,B) Section of the multiscale hierarchical scaffold made of single bundles of aligned nanofibers with the electrospun sheath epitenon/epiligament-like. (C) Section of a single bundle. (E,F) Aligned nanofibers on the surface of a single bundle at different magnifications. Reprinted from (Sensini et al., 2019b) under CC-BY. (G) The hierarchical structure of crimped polyamide-soft alginate composite. Right-to-left- from electrospun nanofibers to hierarchical soft composite. Reprinted from (Sharabi and Wagner, 2021) with permission.
Sharabi and Wagner (2021) demonstrated a fiber-reinforced hydrogel hierarchical composite (Figure 12G). They fabricated a soft biomimetic composite from a hierarchical aligned electrospun polyamide fiber made of electrospun nanofibers, reinforcing an alginate hydrogel matrix. They demonstrated via SEM cross-bridges in the fiber-matrix interface, mimicking the natural form of collagen failure (Yang et al., 2019). In that case, the polyamide nanofibers created cross-bridges with the matrix and within the bundle. However, multi-scale structural and mechanical studies of the composite were not executed.
For hard tissues, hierarchy is much frequently studied and mimicked. Moreover, and very notably, the nanoscale reinforcement is known to simultaneously favor the strength and toughness of materials (Evans, 1990; Launey and Ritchie, 2009), in particular bone (Gupta et al., 2005; Gupta et al., 2006; Launey and Ritchie, 2009; Libonati and Vergani, 2016; Grezzana et al., 2020). Therefore, combining nanoscale structures in higher levels constructs may provide valuable advantages.
Fiber Crimping
Apart from the FVF and fiber orientation, fiber crimping also governs soft tissue mechanical behavior (Vidal, 2003; Zhao et al., 2015). Collagen crimping allows an additional degree of freedom in the material deformation due to its straightening ability under load that does not require applying force, thus protecting the material from wear. Crimp structure has been divided into different structures such as planar zig-zag, sinusoid, or helical with wavelength ranges between 10 and 200 μm (Caves et al., 2010c). It can appear as a parallel waveform (as in tendon, ligaments, and AF-Figures 5A,B) or distributed fibers (as in skin and arterial wall- Figures 5C,D). In naturally occurring collagen composites, hyperelastic behavior with strain stiffening was seen due to the inherent coral collagen crimping (Sharabi et al., 2014, 2015, 2016, 2019; Wertheimer et al., 2021) (Figures 13L,M).

FIGURE 13. Biomimetics of fiber and fibril crimping. (A–I) Hierarchical soft composite fabrication and mechanical behavior. (A) Electrospinning apparatus. (B) Adding nanocrimping to electrospun film. Scale bar 1 µm. (C) Rolling the electrospun film to create a bundle. Scale bar 100 µm. (D) Applying different bundle macro-crimping angles (75°, 127°, and 145°, up to bottom). Scale bar 1 mm. (E) Alginate-polyamide composite fabrication. Scale bar 1 mm. (F) the modulus of composites with a different crimping angle at 0.05, 0.1, 0.15, and 0.2 strain. (G) Stress-strain curves for composites with different crimping angles under unidirectional tension, experiments vs. FE models. (H) the influence of different crimping angles on the mechanical behavior in FE models of polyamide-alginate composites. (I) polyamide–alginate FE model and boundary conditions. Reprinted from Sharabi and Wagner (2021) with permission. (J,K) SEM images of electrospun P (LLA-AC) fibers after crimping (scale bar 200 μm). Reprinted from Chen et al. (2014) with permission. (L,M) Crimping in coral collagen fibers and collagen-based biocomposites. Scale bar 20 µm. Reprinted from Sharabi et al. (2014) with permission.
Crimped fibers were synthetically fabricated as a part of a laminate or as isolated fibers to investigate their deformation behavior (Caves et al., 2010c; Fleischer et al., 2013; Nunes et al., 2013; Chao et al., 2014; Chen et al., 2014; Kumar et al., 2014; Naik et al., 2014; Pen-hsiu Grace et al., 2014; Liu et al., 2015; Szczesny et al., 2016; Wu et al., 2017; Sharabi and Wagner, 2021). They were also beneficial for embedded cells and altered strain transmission to cells (Fleischer et al., 2013; Chao et al., 2014; Szczesny et al., 2016).
Crimping in the nanoscale can be applied on electrospun nanofibers (Figures 13J,K) by different chemical and physical methods (Chen et al., 2014; Liu et al., 2015; Szczesny et al., 2016; Zaarour et al., 2020). The degree of nanocrimping can be controlled and thus results in a changeable toe region, governable J-shaped behavior, and stiffening regime in electrospun film (Liu et al., 2015; Szczesny et al., 2016). However, in hierarchical composites consisting of nanoscale crimping, it was found not to affect the overall toe region compared with micro-and millimetric crimping. Applying different crimping degrees (experimentally and numerically) resulted in a controlled transition between the matrix and the fiber modes, where the matrix governed the toe region behavior. As was expected, the toe region was larger when the crimping angle was smaller (Sharabi and Wagner, 2021) (Figures 13A–I).
Summary and Future Prospective
Soft fibrous tissues are functional tissues that hold diverse and complex mechanical roles: from load transmission between muscle to bone – in tendons, through burst pressure under cyclic loading in arteries, mechanical barrier as in the skin, and multiaxial loads subjected to the intervertebral disc, enabling remarkable flexibility. All these abilities are the result of different combinations of the same building blocks. Nature uses simple building blocks, but its efficient use in repeating structural motifs allows it to create a set of tools that result in a wide mechanical variety. As material engineers, the building blocks we can use are much more diverse. However, understanding the structural motifs and their mechanical response can be of major importance.
We examine soft tissues that are structurally different, but similar repeating structural motifs allow their diverse unparallel mechanical behaviors. Due to the highly intricated structures and their variability, the diverse characterization methods, and protocols, the full structure-function relationship is unknown yet, and many questions still remain.
However, the comparison also reveals similar trends and motifs. As presented in the previous sections, soft fibrous tissues include multiple structural motifs that govern all fibrous tissues to allow nonlinear J-shaped behavior with large deformations. In soft tissues, nature uses motifs that control collagen’s ability to carry load, such as crimping, sliding, rotating, and stretching in multiple length scales, using nested composites and “programmed” interfaces. The simultaneous use in stretching and sliding mechanisms in different scales allows the structure to be more robust since the material itself has a finite ability to stretch.
Nature uses composites. Each of its building blocks is essential, and its assembly is responsible for the mechanical function. In different tissues, removing one constituent changes the entire behavior differently (Isaacs et al., 2014; Ross et al., 2021). Moreover, the quantities of the building blocks vastly affect the nature of the tissue. Multi-scale hierarchy and sliding mechanisms in different scales allow large deformations and failure toughness. The different length scales deflect cracks and increase the tissue robustness, and protect it from failure. Sliding is allowed due to PGs and GAGs matrix. They absorb water molecules, and the high water content results in weak hydrophilic interactions promoting collagen fibril sliding and stretching. Thus, stretching is not the main mechanical mechanism, and thus the tissue can withstand substantial deformations for a long time and under different loading conditions. Biomimetics of this mechanism can improve our ability significantly to create functioning soft composite materials. Nested composites that can be up to fiber level, like skin and aorta, or in an ordered telescopic structure like tendons are also very common. In tendons, this structure allows very efficient load-bearing with minimal diameter.
Crimping occurs in the micrometer scale for all tissues (Table 2). Usually, elastin fibers exist on the same scale to allow crimping recoil. The crimp is inherent in the fibril level (fibrillar crimp) in some tissues, mainly in unidirectional loaded tissues like tendons and ligaments. These crimps generate fibrillar marks that enable the crimping pattern (such as in origami folding). In tissues that are loaded in multiaxial directions, these crimps do not exist.
Gradual recruitment is a mechanism that occurs in different tissues at different levels. In the skin and arteries, fibers are recruited fiber by fiber, allowing large deformations. The recruitment, namely, the stage where collagen fibers can carry the load, is the joint function of crimping, straightening, and reorientating the fibers in the load direction. This mechanism also allows multiaxial loading, such as in skin, where the wide distribution of fiber directions is recruited under load, becoming more anisotropic when additional load is applied. Variations and graded changes allow different regimes and local stiffening in preferred locations. For example, different tissue layers in the aorta have the same ultimate strains but different mechanical responses (Holzapfel, 2008). Biomimetic soft multi-layered architectural composites with embedded structural mechanisms can vastly increase the mechanical abilities of new constructs.
Here, we focused on the deformation behavior and did not discuss other important mechanical behaviors such as failure, viscoelasticity, fatigue, or cyclic loading, due to the complexity of the current subject. Understanding and mimicking these structural motifs can significantly improve the future of biomedical engineering. When discussing biomimetics of tissues, mechanics is an important issue together with biology and chemistry. Mechanical biocompatibility (Mazza and Ehret, 2015) is soft composites with large deformations, cannot be only defined by specific values as modulus or strength, but by the whole deformation behavior. Therefore, to imitate this behavior in different length scales, we need to understand the structure-function relationships in different scales, implement and use the natural structural motifs. The nanoscale is vital for toughness and large deformations, but all structural levels work together in fibrous tissues’ mechanical behavior. Mismatch in the mechanical behavior between highly deformable biomedical materials and native tissue might lead to short and long-term damage, including micro-injuries, cell damage, inflammation, hyperplasia, fibrosis, or necrosis (Venkatraman et al., 2008). Therefore, multi-scale biomimetics is essential for mechanical behavior. However, one should take into account that tissue architectural variability is sometimes a result of growth and remodeling processes and does not always stem from mechanical considerations. Thus, reverse biomimetics aided with computational modeling and advanced multiscale experimental techniques can expose the desirable mechanical requirements.
These materials are highly complex in mechanical terms since the testing protocol, applied strain rate, griping influence, sample geometry, size, and even definitions of mechanical properties (e.g., Young’s modulus) differ between researchers and applications. This creates a significant variance in tissues’ mechanical behavior and the engineered structural materials characterization, in addition to inherent biological variability that already exists in biological tissues. Therefore, there is a vital need to formulate criteria of mechanical biocompatibility. Thus, instead of a trial-and-error approach, bottom-up structural design of the sub-macroscopic scale may result in novel advancements.
Proper assembly of the building blocks, together with the use in these structural motifs that appear in nature, can create the next generation of architectural materials that will be highly efficient for tissue repair applications. Moreover, these materials may lead to new types of highly deformable soft-engineered composites, ubiquitous in nature but not in our daylife engineering.
Author Contributions
MS designed the ideas, collected and analyzed the data, and wrote the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amabili, M., Asgari, M., Breslavsky, I. D., Franchini, G., Giovanniello, F., and Holzapfel, G. A. (2021). Microstructural and Mechanical Characterization of the Layers of Human Descending Thoracic Aortas. Acta Biomater. 134, 401–421. doi:10.1016/j.actbio.2021.07.036
Amiel, D., Frank, C., Harwood, F., Fronek, J., and Akeson, W. (1983). Tendons and Ligaments: a Morphological and Biochemical Comparison. J. Orthop. Res. 1, 257–265. doi:10.1002/jor.1100010305
Ayala, P., Caves, J., Dai, E., Siraj, L., Liu, L., Chaudhuri, O., et al. (2015). Engineered Composite Fascia for Stem Cell Therapy in Tissue Repair Applications. Acta Biomater. 26, 1–12. doi:10.1016/j.actbio.2015.08.012
Baer, E., Cassidy, J. J., and Hiltner, A. (1991). Hierarchical Structure of Collagen Composite Systems: Lessons from Biology. Pure Appl. Chem. 63, 961–973. doi:10.1351/PAC199163070961
Baldock, C., Oberhauser, A. F., Ma, L., Lammie, D., Siegler, V., Mithieux, S. M., et al. (2011). Shape of Tropoelastin, the Highly Extensible Protein that Controls Human Tissue Elasticity. Proc. Natl. Acad. Sci. 108, 4322–4327. doi:10.1073/pnas.1014280108
Bancelin, S., Lynch, B., Bonod-Bidaud, C., Ducourthial, G., Psilodimitrakopoulos, S., Dokládal, P., et al. (2015). Ex Vivo multiscale Quantitation of Skin Biomechanics in Wild-type and Genetically-Modified Mice Using Multiphoton Microscopy. Sci. Rep. 5, 17635. doi:10.1038/srep17635
Bar-Cohen, Y. (2006). Biomimetics-using Nature to Inspire Human Innovation. Bioinspir. Biomim. 5759, P1–P12. doi:10.1088/1748-3182/1/1/P01
Bar-Cohen, Y. (2005). “Biomimetics: Mimicking and Inspired-By Biology,” in Smart Structures and Materials 2005: Electroactive Polymer Actuators and Devices (EAPAD) (International Society for Optics and Photonics), 1–8. doi:10.1117/12.597436
Barbir, A., Michalek, A. J., Abbott, R. D., and Iatridis, J. C. (2010). Effects of Enzymatic Digestion on Compressive Properties of Rat Intervertebral Discs. J. Biomech. 43, 1067–1073. doi:10.1016/j.jbiomech.2009.12.005
Basalo, I. M., Mauck, R. L., Kelly, T.-A. N., Nicoll, S. B., Chen, F. H., Hung, C. T., et al. (2004). Cartilage Interstitial Fluid Load Support in Unconfined Compression Following Enzymatic Digestion. J. Biomech. Eng. 126, 779–786. doi:10.1115/1.1824123
Bazrafshan, Z., and Stylios, G. K. (2019). Spinnability of Collagen as a Biomimetic Material: A Review. Int. J. Biol. Macromolecules 129, 693–705. doi:10.1016/j.ijbiomac.2019.02.024
Ben-Or Frank, M., Niestrawska, J. A., Holzapfel, G. A., and deBotton, G. (2019). Micromechanically-motivated Analysis of Fibrous Tissue. J. Mech. Behav. Biomed. Mater. 96, 69–78. doi:10.1016/j.jmbbm.2019.04.007
Benayahu, D., Sharabi, M., Pomeraniec, L., Awad, L., Haj-Ali, R., and Benayahu, Y. (2018). Unique Collagen Fibers for Biomedical Applications. Mar. Drugs 16, 102. doi:10.3390/md16040102
Benítez, J. M., and Montáns, F. J. (2017). The Mechanical Behavior of Skin: Structures and Models for the Finite Element Analysis. Comput. Struct. 190, 75–107.
Berillis, P. (2013). The Role of Collagen in the Aorta's Structure. Tocvj 6, 1–8. doi:10.2174/1877382601306010001
Berry, C. L., and Greenwald, S. E. (1976). Effects of Hypertension on the Static Mechanical Properties and Chemical Composition of the Rat Aorta. Cardiovasc. Res. 10, 437–451. doi:10.1093/cvr/10.4.437
Bircher, K., Ehret, A. E., and Mazza, E. (2017). Microstructure Based Prediction of the Deformation Behavior of Soft Collagenous Membranes. Soft Matter 13, 5107–5116. doi:10.1039/c7sm00101k
Breathnach, S., Cox, N., and Griffiths, C. (2010). Rook’s Textbook of Dermatology, 4 Volume Set. Wiley.
Buehler, M. J. (2008). Nanomechanics of Collagen Fibrils under Varying Cross-Link Densities: Atomistic and Continuum Studies. J. Mech. Behav. Biomed. Mater. 1, 59–67. doi:10.1016/J.JMBBM.2007.04.001
Buwalda, S. J. (2020). Bio-based Composite Hydrogels for Biomedical Applications. Multifunct. Mater. 3, 022001. doi:10.1088/2399-7532/AB80D6
Carey, D. J. (1991). Control of Growth and Differentiation of Vascular Cells by Extracellular Matrix Proteins. Annu. Rev. Physiol. 53, 161–177. doi:10.1146/annurev.ph.53.030191.001113
Cassidy, J. J., Hiltner, A., and Baer, E. (1989). Hierarchical Structure of the Intervertebral Disc. Connect. Tissue Res. 23, 75–88. doi:10.3109/03008208909103905
Castilho, M., Hochleitner, G., Wilson, W., van Rietbergen, B., Dalton, P. D., Groll, J., et al. (2018). Mechanical Behavior of a Soft Hydrogel Reinforced with Three-Dimensional Printed Microfibre Scaffolds. Sci. Rep. 8, 1245. doi:10.1038/s41598-018-19502-y
Caves, J. M., Cui, W., Wen, J., Kumar, V. A., Haller, C. A., Chaikof, E. L., et al. (2011). Elastin-like Protein Matrix Reinforced with Collagen Microfibers for Soft Tissue Repair. Biomaterials 32, 5371–5379. doi:10.1016/j.biomaterials.2011.04.009
Caves, J. M., Kumar, V. A., Martinez, A. W., Kim, J., Ripberger, C. M., Haller, C. A., et al. (2010a). The Use of Microfiber Composites of Elastin-like Protein Matrix Reinforced with Synthetic Collagen in the Design of Vascular Grafts. Biomaterials 31, 7175–7182. doi:10.1016/j.biomaterials.2010.05.014
Caves, J. M., Kumar, V. A., Wen, J., Cui, W., Martinez, A., Apkarian, R., et al. (2009b). Fibrillogenesis in Continuously Spun Synthetic Collagen Fiber. J. Biomed. Mater. Res. 93, 24–38. doi:10.1002/jbm.b.31555
Caves, J. M., Kumar, V. A., Xu, W., Naik, N., Allen, M. G., and Chaikof, E. L. (2010c). Microcrimped Collagen Fiber-Elastin Composites. Adv. Mater. 22, 2041–2044. doi:10.1002/adma.200903612
Chen, F., Hayami, J. W. S., and Amsden, B. G. (2014). Electrospun Poly(l-Lactide-Co-Acryloyl Carbonate) Fiber Scaffolds with a Mechanically Stable Crimp Structure for Ligament Tissue Engineering. Biomacromolecules 15, 1593–1601. doi:10.1021/bm401813j
Christian Gasser, T. (2011). An Irreversible Constitutive Model for Fibrous Soft Biological Tissue: A 3-D Microfiber Approach with Demonstrative Application to Abdominal Aortic Aneurysms. Acta Biomater. 7, 2457–2466. doi:10.1016/j.actbio.2011.02.015
Cleary, E. G. (1987). The Microfibrillar Component of the Elastic Fibers. Morphology and Biochemistry. Connect. Tissue Dis. Mol. Pathol. Extracell. Matrix 12, 55–81.
Craig, A. S., Birtles, M. J., Conway, J. F., and Parry, D. A. D. (1989). An Estimate of the Mean Length of Collagen Fibrils in Rat Tail-Tendon as a Function of Age. Connect. Tissue Res. 19, 51–62. doi:10.3109/03008208909016814
Csete, M. E., and Doyle, J. C. (2002). Reverse Engineering of Biological Complexity. Science 295, 1664–1669. doi:10.1126/science.1069981
Daamen, W., Van Moerkerk, H. T. B., Hafmans, T., Buttafoco, L., Poot, A. A., Veerkamp, J. H., et al. (2003). Preparation and Evaluation of Molecularly-Defined Collagen-Elastin-Glycosaminoglycan Scaffolds for Tissue Engineering. Biomaterials 24, 4001–4009. doi:10.1016/S0142-9612(03)00273-4
Daamen, W., Veerkamp, J., Vanhest, J., and Vankuppevelt, T. (2007). Elastin as a Biomaterial for Tissue Engineering. Biomaterials 28, 4378–4398. doi:10.1016/J.BIOMATERIALS.2007.06.025
D’Amore, A., Amoroso, N., Gottardi, R., Hobson, C., Carruthers, C., Watkins, S., et al. (2014). From Single Fiber to Macro-Level Mechanics: A Structural Finite-Element Model for Elastomeric Fibrous Biomaterials. J. Mech. Behav. Biomed. Mater. 39, 146–161. doi:10.1016/j.jmbbm.2014.07.016
De Santis, R., Sarracino, F., Mollica, F., Netti, P. A., Ambrosio, L., and Nicolais, L. (2004). Continuous Fibre Reinforced Polymers as Connective Tissue Replacement. Composites Sci. Techn. 64, 861–871. doi:10.1016/J.COMPSCITECH.2003.09.008
Debelle, L., and Tamburro, A. M. (1999). Elastin: Molecular Description and Function. Int. J. Biochem. Cel Biol. 31, 261–272. doi:10.1016/s1357-2725(98)00098-3
Depalle, B., Qin, Z., Shefelbine, S. J., and Buehler, M. J. (2015). Influence of Cross-Link Structure, Density and Mechanical Properties in the Mesoscale Deformation Mechanisms of Collagen Fibrils. J. Mech. Behav. Biomed. Mater. 52, 1–13. doi:10.1016/J.JMBBM.2014.07.008
Derrouiche, A., Karoui, A., Zaïri, F., Ismail, J., Qu, Z., Chaabane, M., et al. (2020). The Two Poisson's Ratios in Annulus Fibrosus: Relation with the Osmo-Inelastic Features. Mech. Soft Mater. 2 (2), 1–12. doi:10.1007/S42558-019-0016-Y
Dhandayuthapani, B., Yoshida, Y., Maekawa, T., and Kumar, D. S. (2011). Polymeric Scaffolds in Tissue Engineering Application: A Review. Int. J. Polym. Sci. 2011, 1–19. doi:10.1155/2011/290602
Dingemans, K. P., Teeling, P., Lagendijk, J. H., and Becker, A. E. (2000). Extracellular Matrix of the Human Aortic media: an Ultrastructural Histochemical and Immunohistochemical Study of the Adult Aortic media. Anat. Rec. 258, 1–14. doi:10.1002/(sici)1097-0185(20000101)258:1<1::aid-ar1>3.0.co;2-7
Doineau, E., Cathala, B., Benezet, J.-C., Bras, J., and Le Moigne, N. (2021). Development of Bio-Inspired Hierarchical Fibres to Tailor the Fibre/Matrix Interphase in (Bio)composites. Polymers 13, 804. doi:10.3390/POLYM13050804
Dubacher, N., Münger, J., Gorosabel, M. C., Crabb, J., Ksiazek, A. A., Caspar, S. M., et al. (2020). Celiprolol but Not Losartan Improves the Biomechanical Integrity of the Aorta in a Mouse Model of Vascular Ehlers-Danlos Syndrome. Cardiovasc. Res. 116, 457–465. doi:10.1093/CVR/CVZ095
Eekhoff, J. D., and Lake, S. P. (2020). Three-dimensional Computation of Fibre Orientation, Diameter and Branching in Segmented Image Stacks of Fibrous Networks. J. R. Soc. Interf. 17, 20200371. doi:10.1098/RSIF.2020.0371
Espinosa, H. D., Juster, A. L., Latourte, F. J., Loh, O. Y., Gregoire, D., and Zavattieri, P. D. (2011). Tablet-level Origin of Toughening in Abalone Shells and Translation to Synthetic Composite Materials. Nat. Commun. 2, 173. doi:10.1038/ncomms1172
Evans, A. G. (1990). Perspective on the Development of High-Toughness Ceramics. J. Am. Ceram. Soc. 73, 187–206. doi:10.1111/J.1151-2916.1990.TB06493.X
Eyre, D. R., and Muir, H. (1974). Collagen Polymorphism: Two Molecular Species in Pig Intervertebral Disc. FEBS Lett. 42, 192–196. doi:10.1016/0014-5793(74)80783-0
Fassini, D., Wilkie, I. C., Pozzolini, M., Ferrario, C., Sugni, M., Rocha, M. S., et al. (2021). Diverse and Productive Source of Biopolymer Inspiration: Marine Collagens. Biomacromolecules 22, 1815–1834. doi:10.1021/ACS.BIOMAC.1C00013
Fleischer, S., Feiner, R., Shapira, A., Ji, J., Sui, X., Daniel Wagner, H., et al. (2013). Spring-like Fibers for Cardiac Tissue Engineering. Biomaterials 34, 8599–8606. doi:10.1016/j.biomaterials.2013.07.054
Franchi, M., De Pasquale, V., Martini, D., Quaranta, M., Macciocca, M., Dionisi, A., et al. (2010a). Contribution of Glycosaminoglycans to the Microstructural Integrity of Fibrillar and Fiber Crimps in Tendons and Ligaments. The Scientific World JOURNAL 10, 1932–1940. doi:10.1100/tsw.2010.192
Franchi, M., Ottani, V., Stagni, R., and Ruggeri, A. (2010b). Tendon and Ligament Fibrillar Crimps Give Rise to Left-Handed Helices of Collagen Fibrils in Both Planar and Helical Crimps. J. Anat. 216, 301–309. doi:10.1111/J.1469-7580.2009.01188.X
Franchi, M., Raspanti, M., Dell’Orbo, C., Quaranta, M., De Pasquale, V., Ottani, V., et al. (2008). Different Crimp Patterns in Collagen Fibrils Relate to the Subfibrillar Arrangement. Connect. Tissue Res. 49, 85–91. doi:10.1080/03008200801913635
Franchi, M., Trirè, A., Quaranta, M., Orsini, E., and Ottani, V. (2007). Collagen Structure of Tendon Relates to Function. Scientific World JOURNAL 7, 404–420. doi:10.1100/TSW.2007.92
Fratzl, P., Misof, K., Zizak, I., Rapp, G., Amenitsch, H., and Bernstorff, S. (1997). Fibrillar Structure and Mechanical Properties of Collagen. J. STRUCT. BIOL. 122, 119–122. doi:10.1006/jsbi.1998.3966
Fratzl, P. (2007). Biomimetic Materials Research: what Can We Really Learn from Nature's Structural Materials. J. R. Soc. Interf. 4, 637–642. doi:10.1098/rsif.2007.0218
Fratzl, P. (2008). “Collagen: Structure and Mechanics, an Introduction,” in Collagen (Springer), 1–13.
Fratzl, P., and Weinkamer, R. (2007). Nature's Hierarchical Materials. Prog. Mater. Sci. 52, 1263–1334. doi:10.1016/J.PMATSCI.2007.06.001
Fung, Y. (2013). Biomechanics: Mechanical Properties of Living Tissues. Springer Science & Business Media.
Gains, C. C., Correia, J. C., Baan, G. C., Noort, W., Screen, H. R. C., and Maas, H. (2020). Force Transmission between the Gastrocnemius and Soleus Sub-tendons of the Achilles Tendon in Rat. Front. Bioeng. Biotechnol. 8, 700. doi:10.3389/FBIOE.2020.00700
Gasser, T. C. (2020). “Modeling the Structural and Mechanical Properties of the normal and Aneurysmatic Aortic wall,” in Multi-scale Extracellular Matrix Mechanics and Mechanobiology (Springer), 55–82. doi:10.1007/978-3-030-20182-1_3
Gathercole, L. J., and Keller, A. (1991). Crimp Morphology in the Fibre-Forming Collagens. Matrix 11, 214–234. doi:10.1016/S0934-8832(11)80161-7
Ghezelbash, F., Eskandari, A. H., Shirazi-Adl, A., Kazempour, M., Tavakoli, J., and Baghani, M. (1994). Modeling of Human Intervertebral Disc Annulus Fibrosus with Complex Multi-Fiber Networks. Acta Biomater. 123, 208–221.
Gibson, T., Kenedi, R. M., and Craik, J. E. (2005). The mobile Micro-architecture of Dermal Collagen: A Bio-Engineering Study. Br. J. Surg. 52, 764–770. doi:10.1002/BJS.1800521017
Godinho, M. S., Thorpe, C. T., Greenwald, S. E., and Screen, H. R. C. (2021). Elastase Treatment of Tendon Specifically Impacts the Mechanical Properties of the Interfascicular Matrix. Acta Biomater. 123, 187–196. doi:10.1016/j.actbio.2021.01.030
Gosline, J., Lillie, M., Carrington, E., Guerette, P., Ortlepp, C., and Savage, K. (2002). Elastic Proteins: Biological Roles and Mechanical Properties. Phil. Trans. R. Soc. Lond. B 357, 121–132. doi:10.1098/rstb.2001.1022
Gosline, J. M. (1976). The Physical Properties of Elastic Tissue. Int. Rev. Connect. Tissue Res. 7, 211–249. doi:10.1016/b978-0-12-363707-9.50011-3
Grace Chao, P.-h., Hsu, H.-Y., and Tseng, H.-Y. (2014). Electrospun Microcrimped Fibers with Nonlinear Mechanical Properties Enhance Ligament Fibroblast Phenotype. Biofabrication 6, 035008. doi:10.1088/1758-5082/6/3/035008
Grace Chao, P.-h., Hsu, H.-Y., and Tseng, H.-Y. (2014). Electrospun Microcrimped Fibers with Nonlinear Mechanical Properties Enhance Ligament Fibroblast Phenotype. Biofabrication 6, 035008. doi:10.1088/1758-5082/6/3/035008
Greenfeld, I., Zhang, W., Sui, X., and Wagner, H. D. (2018). Intermittent Beading in Fiber Composites. Composites Sci. Techn. 160, 21–31. doi:10.1016/j.compscitech.2018.03.003
Grezzana, G., Loh, H.-C., Qin, Z., Buehler, M. J., Masic, A., and Libonati, F. (2020). Probing the Role of Bone Lamellar Patterns through Collagen Microarchitecture Mapping, Numerical Modeling, and 3D‐Printing. Adv. Eng. Mater. 22, 2000387. doi:10.1002/adem.202000387
Guerin, H. A. L., and Elliott, D. M. (2006). Degeneration Affects the Fiber Reorientation of Human Annulus Fibrosus under Tensile Load. J. Biomech. 39, 1410–1418. doi:10.1016/J.JBIOMECH.2005.04.007
Guimarães, C. F., Gasperini, L., Marques, A. P., and Reis, R. L. (2020). The Stiffness of Living Tissues and its Implications for Tissue Engineering. Nat. Rev. Mater. 5 (5), 351–370. doi:10.1038/s41578-019-0169-1
Gupta, H. S., Seto, J., Krauss, S., Boesecke, P., and Screen, H. R. C. (2010). In Situ multi-level Analysis of Viscoelastic Deformation Mechanisms in Tendon Collagen. J. Struct. Biol. 169, 183–191. doi:10.1016/j.jsb.2009.10.002
Gupta, H. S., Wagermaier, W., Raz-Ben Aroush, G. A., Funari, S. S., Roschger, P., Wagner, H. D., et al. (2005). Nanoscale Deformation Mechanisms in Bone. Nano Lett. 5, 2108–2111. doi:10.1021/NL051584B
Gupta, H. S., Wagermaier, W., Zickler, G. A., Hartmann, J., Funari, S. S., Roschger, P., et al. (2006). Fibrillar Level Fracture in Bone beyond the Yield point. Int. J. Fract 139, 425–436. doi:10.1007/s10704-006-6635-y
Han, W. M., Nerurkar, N. L., Smith, L. J., Jacobs, N. T., Mauck, R. L., and Elliott, D. M. (2012). Multi-scale Structural and Tensile Mechanical Response of Annulus Fibrosus to Osmotic Loading. Ann. Biomed. Eng. 40, 1610–1621. doi:10.1007/s10439-012-0525-4
Handsfield, G. G., Slane, L. C., and Screen, H. R. C. (2016). Nomenclature of the Tendon Hierarchy: An Overview of Inconsistent Terminology and a Proposed Size-Based Naming Scheme with Terminology for Multi-Muscle Tendons. J. Biomech. 49, 3122–3124. doi:10.1016/j.jbiomech.2016.06.028
Herod, T. W., Chambers, N. C., and Veres, S. P. (2016). Collagen Fibrils in Functionally Distinct Tendons Have Differing Structural Responses to Tendon Rupture and Fatigue Loading. Acta Biomater. 42, 296–307. doi:10.1016/J.ACTBIO.2016.06.017
Hill, M. R., Duan, X., Gibson, G. A., Watkins, S., and Robertson, A. M. (2012). A Theoretical and Non-destructive Experimental Approach for Direct Inclusion of Measured Collagen Orientation and Recruitment into Mechanical Models of the Artery wall. J. Biomech. 45, 762–771. doi:10.1016/J.JBIOMECH.2011.11.016
Holzapfel, G. A. (2008). Collagen in Arterial Walls: Biomechanical Aspects. Collagen. Editor P. Fratzl (Boston, MA, Springer), 285–324. doi:10.1007/978-0-387-73906-9_11
Holzapfel, G. A., Gasser, T. C., and Ogden, R. W. (2000). A New Constitutive Framework for Arterial wall Mechanics and a Comparative Study of Material Models. J. Elast. Phys. Sci. Solids 61, 1–48. doi:10.1023/a:1010835316564
Holzapfel, G. A., and Ogden, R. W. (2018). Biomechanical Relevance of the Microstructure in Artery walls with a Focus on Passive and Active Components. Am. J. Physiology-Heart Circulatory Physiol. 315, H540–H549. doi:10.1152/ajpheart.00117.2018
Holzapfel, G. A., Ogden, R. W., and Sherifova, S. (2019). On Fibre Dispersion Modelling of Soft Biological Tissues: a Review. Proc. R. Soc. A. 475, 20180736. doi:10.1098/rspa.2018.0736
Holzapfel, G. A., Schulze-Bauer, C. A. J., Feigl, G., and Regitnig, P. (2005). Single Lamellar Mechanics of the Human Lumbar Anulus Fibrosus. Biomech. Model. Mechanobiol. 3, 125–140. doi:10.1007/s10237-004-0053-8
Holzapfel, G. A., and Weizsäcker, H. W. (1998). Biomechanical Behavior of the Arterial wall and its Numerical Characterization. Comput. Biol. Med. 28, 377–392. doi:10.1016/s0010-4825(98)00022-5
Holzapfel, G. A. (2001). “Biomechanics of Soft Tissue”, Handbook of Material Behavior-Non Linear Models and Properties. San Diego, CA: Academic press.
Isaacs, J. L., Vresilovic, E., Sarkar, S., and Marcolongo, M. (2014). Role of Biomolecules on Annulus Fibrosus Micromechanics: Effect of Enzymatic Digestion on Elastic and Failure Properties. J. Mech. Behav. Biomed. Mater. 40, 75–84. doi:10.1016/j.jmbbm.2014.08.012
Isogai, Z., Aspberg, A., Keene, D. R., Ono, R. N., Reinhardt, D. P., and Sakai, L. Y. (2002). Versican Interacts with Fibrillin-1 and Links Extracellular Microfibrils to Other Connective Tissue Networks. J. Biol. Chem. 277, 4565–4572. doi:10.1074/jbc.m110583200
Jan, N.-J., and Sigal, I. A. (2018). Collagen Fiber Recruitment: A Microstructural Basis for the Nonlinear Response of the Posterior Pole of the Eye to Increases in Intraocular Pressure. Acta Biomater. 72, 295–305. doi:10.1016/j.actbio.2018.03.026
Jang, K.-I., Chung, H. U., Xu, S., Lee, C. H., Luan, H., Jeong, J., et al. (2015). Soft Network Composite Materials with Deterministic and Bio-Inspired Designs. Nat. Commun. 6, 6566. doi:10.1038/ncomms7566
Joodaki, H., and Panzer, M. B. (2018). Skin Mechanical Properties and Modeling: A Review. Proc. Inst. Mech. Eng. H. 232, 323–343. doi:10.1177/0954411918759801
Jor, J. W. Y., Nielsen, P. M. F., Nash, M. P., and Hunter, P. J. (2011). Modelling Collagen Fibre Orientation in Porcine Skin Based upon Confocal Laser Scanning Microscopy. Ski. Res. Technol. 17, 149–159. doi:10.1111/j.1600-0846.2011.00471.x
Järvinen, T. A., Järvinen, T. L., Kannus, P., Józsa, L., and Järvinen, M. (2004). Collagen Fibres of the Spontaneously Ruptured Human Tendons Display Decreased Thickness and Crimp Angle. J. Orthop. Res. 22, 1303–1309. doi:10.1016/J.ORTHRES.2004.04.003
Kastelic, J., Galeski, A., and Baer, E. (1978). The Multicomposite Structure of Tendon. Connect. Tissue Res. 6, 11–23. doi:10.3109/03008207809152283
Keeley, F. W., Bellingham, C. M., and Woodhouse, K. A. (2002). Elastin as a Self-Organizing Biomaterial: Use of Recombinantly Expressed Human Elastin Polypeptides as a Model for Investigations of Structure and Self-Assembly of Elastin. Phil. Trans. R. Soc. Lond. B 357, 185–189. doi:10.1098/rstb.2001.1027
Kielty, C. M., Baldock, C., Lee, D., Rock, M. J., Ashworth, J. L., and Shuttleworth, C. A. (2002). Fibrillin: from Microfibril Assembly to Biomechanical Function. Phil. Trans. R. Soc. Lond. B 357, 207–217. doi:10.1098/rstb.2001.1029
Klein, J. A., and Hukins, D. W. L. (1982). X-ray Diffraction Demonstrates Reorientation of Collagen Fibres in the Annulus Fibrosus during Compression of the Intervertebral Disc. Biochim. Biophys. Acta (Bba) - Gen. Subjects 717, 61–64. doi:10.1016/0304-4165(82)90380-4
Kokkinis, D., Bouville, F., and Studart, A. R. (2018). 3D Printing of Materials with Tunable Failure via Bioinspired Mechanical Gradients. Adv. Mater. 30, 1705808. doi:10.1002/adma.201705808
Kramer, K., Ross, C., Babu, A., Wu, Y., Towner, R., Mir, A., et al. (2019). An Investigation of Layer-specific Tissue Biomechanics of Porcine Atrioventricular Valve Anterior Leaflets. Acta Biomater. 96, 368–384. doi:10.1016/j.actbio.2019
Krasny, W., Magoariec, H., Morin, C., and Avril, S. (2018). Kinematics of Collagen Fibers in Carotid Arteries under Tension-Inflation Loading. J. Mech. Behav. Biomed. Mater. 77, 718–726. doi:10.1016/J.JMBBM.2017.08.014
Kumar, V. A., Caves, J. M., Haller, C. A., Dai, E., Liu, L., Grainger, S., et al. (2013b). Acellular Vascular Grafts Generated from Collagen and Elastin Analogs. Acta Biomater. 9, 8067–8074. Available at: http://www.sciencedirect.com/science/article/pii/S1742706113002730. doi:10.1016/j.actbio.2013.05.024
Kumar, V. A., Caves, J. M., Haller, C. A., Dai, E., Liu, L., Grainger, S., et al. (2013a). Collagen-Based Substrates with Tunable Strength for Soft Tissue Engineering. Biomater. Sci. 1, 1193–1202. doi:10.1039/C3BM60129C
Kumar, V. A., Martinez, A. W., Caves, J. M., Naik, N., Haller, C. A., and Chaikof, E. L. (2014). Microablation of Collagen-Based Substrates for Soft Tissue Engineering. Biomed. Mater. 9, 011002. doi:10.1088/1748-6041/9/1/011002
Laaksonen, P., Szilvay, G. R., and Linder, M. B. (2012). Genetic Engineering in Biomimetic Composites. Trends Biotechnol. 30, 191–197. doi:10.1016/j.tibtech.2012.01.001
Lake, S. P., Miller, K. S., Elliott, D. M., and Soslowsky, L. J. (2009). Effect of Fiber Distribution and Realignment on the Nonlinear and Inhomogeneous Mechanical Properties of Human Supraspinatus Tendon under Longitudinal Tensile Loading. J. Orthop. Res. 27, 1596–1602. doi:10.1002/JOR.20938
Langer, K. (1978). On the Anatomy and Physiology of the Skin I. The cleavability of the cutis. (Translated from Langer, K. (1861). Zur Anatomie und Physiologie der Haut. I. Uber die Spaltbarkeit der Cutis. Sitzungsbericht der Mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Academie der Wissenschaften, 44, 19. Br. J. Plast. Surg. 31, 3–8.
Launey, M. E., Buehler, M. J., and Ritchie, R. O. (2010). On the Mechanistic Origins of Toughness in Bone. Annu. Rev. Mater. Res. 40, 25–53. doi:10.1146/annurev-matsci-070909-104427
Launey, M. E., and Ritchie, R. O. (2009). On the Fracture Toughness of Advanced Materials. Adv. Mater. 21, 2103–2110. doi:10.1002/ADMA.200803322
Li, K., and Holzapfel, G. A. (2019). Multiscale Modeling of Fiber Recruitment and Damage with a Discrete Fiber Dispersion Method. J. Mech. Phys. Sol. 126, 226–244. doi:10.1016/j.jmps.2019.01.022
Libonati, F., and Vergani, L. (2016). Understanding the Structure-Property Relationship in Cortical Bone to Design a Biomimetic Composite. Compos. Structures 139, 188–198. doi:10.1016/j.compstruct.2015.12.003
Lim, Y.-S., Ok, Y.-J., Hwang, S.-Y., Kwak, J.-Y., and Yoon, S. (2019). Marine Collagen as A Promising Biomaterial for Biomedical Applications. Mar. Drugs 17, 467. doi:10.3390/MD17080467
Limbert, G. (2017). Mathematical and Computational Modelling of Skin Biophysics: a Review. Proc. R. Soc. A. 473, 20170257. doi:10.1098/rspa.2017.0257
Lindahl, U., Couchman, J., Kimata, K., and Esko, J. D. (2017). Proteoglycans and Sulfated Glycosaminoglycans. Essentials of Glycobiology. 3rd Edn. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press
Liu, W., Lipner, J., Moran, C. H., Feng, L., Li, X., Thomopoulos, S., et al. (2015). Generation of Electrospun Nanofibers with Controllable Degrees of Crimping through a Simple, Plasticizer-Based Treatment. Adv. Mater. 27, 2583–2588. doi:10.1002/adma.201500329
Lynch, B., Bancelin, S., Bonod-Bidaud, C., Gueusquin, J.-B., Ruggiero, F., Schanne-Klein, M.-C., et al. (2017). A Novel Microstructural Interpretation for the Biomechanics of Mouse Skin Derived from Multiscale Characterization. Acta Biomater. 50, 302–311. doi:10.1016/J.ACTBIO.2016.12.051
Ma, M., Guo, L., Anderson, D. G., and Langer, R. (2013). Bio-inspired Polymer Composite Actuator and Generator Driven by Water Gradients. Science 339, 186–189. doi:10.1126/science.1230262
Mandrycky, C., Wang, Z., Kim, K., and Kim, D.-H. (2016). 3D Bioprinting for Engineering Complex Tissues. Biotechnol. Adv. 34, 422–434. doi:10.1016/J.BIOTECHADV.2015.12.011
Marchand, F., and Ahmed, A. M. (1990). Investigation of the Laminate Structure of Lumbar Disc Anulus Fibrosus. Spine 15, 402–410. doi:10.1097/00007632-199005000-00011
Martufi, G., and Gasser, T. C. (2011). A Constitutive Model for Vascular Tissue that Integrates Fibril, Fiber and Continuum Levels with Application to the Isotropic and Passive Properties of the Infrarenal Aorta. J. Biomech. 44, 2544–2550. doi:10.1016/j.jbiomech.2011.07.015
Mattson, J. M., Turcotte, R., and Zhang, Y. (2017). Glycosaminoglycans Contribute to Extracellular Matrix Fiber Recruitment and Arterial wall Mechanics. Biomech. Model. Mechanobiol. 16, 213–225. doi:10.1007/s10237-016-0811-4
Matuszewski, P. E., Chen, Y.-L., Szczesny, S. E., Lake, S. P., Elliott, D. M., Soslowsky, L. J., et al. (2012). Regional Variation in Human Supraspinatus Tendon Proteoglycans: Decorin, Biglycan, and Aggrecan. Connect. Tissue Res. 53, 343–348. doi:10.3109/03008207.2012.654866
Mauck, R. L., Baker, B. M., Nerurkar, N. L., Burdick, J. A., Li, W.-J., Tuan, R. S., et al. (2009). Engineering on the Straight and Narrow: the Mechanics of Nanofibrous Assemblies for Fiber-Reinforced Tissue Regeneration. Tissue Eng. B: Rev. 15, 171–193. Available at: http://online.liebertpub.com/doi/full/10.1089/ten.teb.2008.0652 (Accessed July 23, 2014). doi:10.1089/ten.teb.2008.0652
Mauri, A., Hopf, R., Ehret, A. E., Picu, C. R., and Mazza, E. (2016). A Discrete Network Model to Represent the Deformation Behavior of Human Amnion. J. Mech. Behav. Biomed. Mater. 58, 45–56. doi:10.1016/J.JMBBM.2015.11.009
Mazza, E., and Ehret, A. E. (2015). Mechanical Biocompatibility of Highly Deformable Biomedical Materials. J. Mech. Behav. Biomed. Mater. 48, 100–124. doi:10.1016/j.jmbbm.2015.03.023
Meyers, M. A., McKittrick, J., and Chen, P.-Y. (2013). Structural Biological Materials: Critical Mechanics-Materials Connections. Science 339, 773–779. doi:10.1126/science.1220854
Michalek, A. J., Buckley, M. R., Bonassar, L. J., Cohen, I., and Iatridis, J. C. (2009). Measurement of Local Strains in Intervertebral Disc Anulus Fibrosus Tissue under Dynamic Shear: Contributions of Matrix Fiber Orientation and Elastin Content. J. Biomech. 42, 2279–2285. doi:10.1016/j.jbiomech.2009.06.047
Mikawa, Y., Hamagami, H., Shikata, J., and Yamamuro, T. (1986). Elastin in the Human Intervertebral Disk. Arch. Orth. Traum. Surg. 105, 343–349. doi:10.1007/BF00449940
Mithieux, S. M., and Weiss, A. S. (2005). Elastin. Adv. Protein Chem. 70, 437–461. doi:10.1016/s0065-3233(05)70013-9
Montalbano, G., Tomasina, C., Fiorilli, S., Camarero-Espinosa, S., Vitale-Brovarone, C., and Moroni, L. (2021). Biomimetic Scaffolds Obtained by Electrospinning of Collagen-Based Materials: Strategies to Hinder the Protein Denaturation. Materials 14, 4360. doi:10.3390/ma14164360
Munch, E., Launey, M. E., Alsem, D. H., Saiz, E., Tomsia, A. P., and Ritchie, R. O. (2008). Tough, Bio-Inspired Hybrid Materials. Science 322, 1516–1520. doi:10.1126/science.1164865
Murphy, S. V., and Atala, A. (2014). 3D Bioprinting of Tissues and Organs. Nat. Biotechnol. 32, 773–785. doi:10.1038/nbt.2958
Naik, N., Caves, J., Chaikof, E. L., and Allen, M. G. (2014). Generation of Spatially Aligned Collagen Fiber Networks through Microtransfer Molding. Adv. Healthc. Mater. 3, 367–374. doi:10.1002/adhm.201300112
Nerurkar, N. L., Mauck, R. L., and Elliott, D. M. (2011). Modeling Interlamellar Interactions in Angle-Ply Biologic Laminates for Annulus Fibrosus Tissue Engineering. Biomech. Model. Mechanobiol 10, 973–984. Available at: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3513349&tool=pmcentrez&rendertype=abstract (Accessed October 14, 2014). doi:10.1007/s10237-011-0288-0
Nerurkar, N. L., Sen, S., Huang, A. H., Elliott, D. M., and Mauck, R. L. (2010). Engineered Disc-like Angle-Ply Structures for Intervertebral Disc Replacement. Spine 35, 867–873. doi:10.1097/BRS.0b013e3181d74414
Nettles, D. L., Chilkoti, A., and Setton, L. A. (2010). Applications of Elastin-like Polypeptides in Tissue Engineering. Adv. Drug Deliv. Rev. 62, 1479–1485. doi:10.1016/J.ADDR.2010.04.002
Ní Annaidh, A., Bruyère, K., Destrade, M., Gilchrist, M. D., Maurini, C., Otténio, M., et al. (2012). Automated Estimation of Collagen Fibre Dispersion in the Dermis and its Contribution to the Anisotropic Behaviour of Skin. Ann. Biomed. Eng. 40, 1666–1678. doi:10.1007/s10439-012-0542-3
Niestrawska, J. A., Viertler, C., Regitnig, P., Cohnert, T. U., Sommer, G., and Holzapfel, G. A. (2016). Microstructure and Mechanics of Healthy and Aneurysmatic Abdominal Aortas: Experimental Analysis and Modelling. J. R. Soc. Interf. 13, 20160620. doi:10.1098/rsif.2016.0620
Nikolova, M. P., and Chavali, M. S. (2019). Recent Advances in Biomaterials for 3D Scaffolds: A Review. Bioactive Mater. 4, 271–292. doi:10.1016/j.bioactmat.2019.10.005
Nunes, J. K., Constantin, H., and Stone, H. A. (2013). Microfluidic Tailoring of the Two-Dimensional Morphology of Crimped Microfibers. Soft Matter 9, 4227–4235. doi:10.1039/C3SM27579E
O'Connell, M. K., Murthy, S., Phan, S., Xu, C., Buchanan, J., Spilker, R., et al. (2008). The Three-Dimensional Micro- and Nanostructure of the Aortic Medial Lamellar Unit Measured Using 3D Confocal and Electron Microscopy Imaging. Matrix Biol. 27, 171–181. doi:10.1016/j.matbio.2007.10.008
Orgel, J. P. R. O., Irving, T. C., Miller, A., and Wess, T. J. (2006). Microfibrillar Structure of Type I Collagen In Situ. Proc. Natl. Acad. Sci. 103, 9001–9005. doi:10.1073/PNAS.0502718103
Orgel, J. P. R. O., San Antonio, J. D., and Antipova, O. (2011). Molecular and Structural Mapping of Collagen Fibril Interactions. Connect. Tissue Res. 52, 2–17. doi:10.3109/03008207.2010.511353
Parenteau-Bareil, R., Gauvin, R., and Berthod, F. (2010). Collagen-Based Biomaterials for Tissue Engineering Applications. Materials 3, 1863–1887. doi:10.3390/MA3031863
Peng, J., Huang, C., Cao, C., Saiz, E., Du, Y., Dou, S., et al. (2020). Inverse Nacre-like Epoxy-Graphene Layered Nanocomposites with Integration of High Toughness and Self-Monitoring. Matter 2, 220–232. doi:10.1016/j.matt.2019.08.013
Pezowicz, C. A., Robertson, P. A., and Broom, N. D. (2006). The Structural Basis of Interlamellar Cohesion in the Intervertebral Disc wall. J. Anat. 208, 317–330. Available at: http://www.scopus.com/scopus/inward/record.url?eid=2-s2.0-33644818077&partnerID=40. doi:10.1111/j.1469-7580.2006.00536.x
Pissarenko, A., and Meyers, M. A. (2020). The Materials Science of Skin: Analysis, Characterization, and Modeling. Prog. Mater. Sci. 110, 100634. doi:10.1016/J.PMATSCI.2019.100634
Pissarenko, A., Yang, W., Quan, H., Brown, K. A., Williams, A., Proud, W. G., et al. (2019). Tensile Behavior and Structural Characterization of Pig Dermis. Acta Biomater. 86, 77–95. doi:10.1016/j.actbio.2019.01.023
Puppi, D., and Chiellini, F. (2017). Wet-spinning of Biomedical Polymers: from Single-Fibre Production to Additive Manufacturing of Three-Dimensional Scaffolds. Polym. Int. 66, 1690–1696. doi:10.1002/PI.5332
Reid, J. A., Dwyer, K. D., Schmitt, P. R., Soepriatna, A. H., Coulombe, K. L., and Callanan, A. (2021). Architected Fibrous Scaffolds for Engineering Anisotropic Tissues. Biofabrication 13, 045007. doi:10.1088/1758-5090/AC0FC9
Reinboth, B., Hanssen, E., Cleary, E. G., and Gibson, M. A. (2002). Molecular Interactions of Biglycan and Decorin with Elastic Fiber Components. J. Biol. Chem. 277, 3950–3957. doi:10.1074/jbc.m109540200
Rezakhaniha, R., Agianniotis, A., Schrauwen, J. T. C., Griffa, A., Sage, D., Bouten, C. V. C., et al. (2012). Experimental Investigation of Collagen Waviness and Orientation in the Arterial Adventitia Using Confocal Laser Scanning Microscopy. Biomech. Model. Mechanobiol. 11, 461–473. doi:10.1007/s10237-011-0325-z
Rigozzi, S., Müller, R., Stemmer, A., and Snedeker, J. G. (2013). Tendon Glycosaminoglycan Proteoglycan Sidechains Promote Collagen Fibril Sliding-AFM Observations at the Nanoscale. J. Biomech. 46, 813–818. doi:10.1016/j.jbiomech.2012.11.017
Ristaniemi, A., Stenroth, L., Mikkonen, S., and Korhonen, R. K. (2018). Comparison of Elastic, Viscoelastic and Failure Tensile Material Properties of Knee Ligaments and Patellar Tendon. J. Biomech. 79, 31–38. doi:10.1016/J.JBIOMECH.2018.07.031
Ritchie, R. O. (2011). The Conflicts between Strength and Toughness. Nat. Mater 10 (10), 817–822. doi:10.1038/nmat3115
Rnjak‐Kovacina, J., Tang, F., Whitelock, J. M., and Lord, M. S. (2018). Glycosaminoglycan and Proteoglycan‐Based Biomaterials: Current Trends and Future Perspectives. Adv. Healthc. Mater. 7, 1701042. doi:10.1002/ADHM.201701042
Roach, M. R., and Burton, A. C. (1957). The Reason for the Shape of the Distensibility Curves of Arteries. Can. J. Biochem. Physiol. 35, 681–690. doi:10.1139/y57-080
Ross, C. J., Laurence, D. W., Echols, A. L., Babu, A. R., Gu, T., Duginski, G. A., et al. (2021). Effects of Enzyme-Based Removal of Collagen and Elastin Constituents on the Biaxial Mechanical Responses of Porcine Atrioventricular Heart Valve Anterior Leaflets. Acta Biomater. 135, 425–440. doi:10.1016/J.ACTBIO.2021.08.043
Ross, R., and Bornstein, P. (1969). The Elastic Fiber. J. Cel Biol. 40, 366–381. doi:10.1083/jcb.40.2.366
Roughley, P. J. (2004). Biology of Intervertebral Disc Aging and Degeneration. Spine 29, 2691–2699. doi:10.1097/01.brs.0000146101.53784.b1
Rumian, A. P., Wallace, A. L., and Birch, H. L. (2007). Tendons and Ligaments Are Anatomically Distinct but Overlap in Molecular and Morphological Features-A Comparative Study in an Ovine Model. J. Orthop. Res. 25, 458–464. doi:10.1002/JOR.20218
Ryan, A. J., Ryan, E. J., Cameron, A. R., and O'Brien, F. J. (2020). Hierarchical Biofabrication of Biomimetic Collagen-Elastin Vascular Grafts with Controllable Properties via Lyophilisation. Acta Biomater. 112, 52–61. doi:10.1016/J.ACTBIO.2020.06.002
Sanchez, C., Arribart, H., and Giraud Guille, M. M. (2005). Biomimetism and Bioinspiration as Tools for the Design of Innovative Materials and Systems. Nat. Mater 4, 277–288. doi:10.1038/nmat1339
Schaffner, M., Faber, J. A., Pianegonda, L., Rühs, P. A., Coulter, F., and Studart, A. R. (2018). 3D Printing of Robotic Soft Actuators with Programmable Bioinspired Architectures. Nat. Commun. 9, 878. doi:10.1038/s41467-018-03216-w
Schmidt, T., Balzani, D., and Holzapfel, G. A. (2014). Statistical Approach for a Continuum Description of Damage Evolution in Soft Collagenous Tissues. Comput. Methods Appl. Mech. Eng. 278, 41–61. doi:10.1016/J.CMA.2014.04.011
Schollum, M. L., Robertson, P. A., and Broom, N. D. (2009). A Microstructural Investigation of Intervertebral Disc Lamellar Connectivity: Detailed Analysis of the Translamellar Bridges. J. Anat. 214, 805–816. doi:10.1111/j.1469-7580.2009.01076.x
Schriefl, A. J., Zeindlinger, G., Pierce, D. M., Regitnig, P., and Holzapfel, G. A. (2012). Determination of the Layer-specific Distributed Collagen Fibre Orientations in Human Thoracic and Abdominal Aortas and Common Iliac Arteries. J. R. Soc. Interf. 9, 1275–1286. doi:10.1098/rsif.2011.0727
Schulze-Bauer, C. A. J., Regitnig, P., and Holzapfel, G. A. (2002). Mechanics of the Human Femoral Adventitia Including the High-Pressure Response. Am. J. Physiology-Heart Circulatory Physiol. 282, H2427–H2440. doi:10.1152/ajpheart.00397.2001
Scott, J. E. (2003). Elasticity in Extracellular Matrix 'shape Modules' of Tendon, Cartilage, Etc. A Sliding Proteoglycan‐filament Model. J. Physiol. 553, 335–343. doi:10.1113/jphysiol.2003.050179
Scott, J. E. (1988). Proteoglycan-fibrillar Collagen Interactions. Biochem. J. 252, 313–323. doi:10.1042/BJ2520313
Sell, S. A., Wolfe, P. S., Garg, K., McCool, J. M., Rodriguez, I. A., and Bowlin, G. L. (2010). The Use of Natural Polymers in Tissue Engineering: A Focus on Electrospun Extracellular Matrix Analogues. Polymers 2, 522–553. doi:10.3390/polym2040522
Sensini, A., Gotti, C., Belcari, J., Zucchelli, A., Focarete, M. L., Gualandi, C., et al. (2019a). Morphologically Bioinspired Hierarchical Nylon 6,6 Electrospun Assembly Recreating the Structure and Performance of Tendons and Ligaments. Med. Eng. Phys. 71, 79–90. doi:10.1016/J.MEDENGPHY.2019.06.019
Sensini, A., Gualandi, C., Focarete, M. L., Belcari, J., Zucchelli, A., Boyle, L., et al. (2019b). Multiscale Hierarchical Bioresorbable Scaffolds for the Regeneration of Tendons and Ligaments. Biofabrication 11, 035026. doi:10.1088/1758-5090/AB20AD
Sensini, A., Santare, M. H., Eichenlaub, E., Bloom, E., Gotti, C., Zucchelli, A., et al. (2021). Tuning the Structure of Nylon 6,6 Electrospun Bundles to Mimic the Mechanical Performance of Tendon Fascicles. Front. Bioeng. Biotechnol. 9, 230. doi:10.3389/FBIOE.2021.626433
Shan, Z., Li, S., Liu, J., Mamuti, M., Wang, C., and Zhao, F. (2015). Correlation between Biomechanical Properties of the Annulus Fibrosus and Magnetic Resonance Imaging (MRI) Findings. Eur. Spine J. 24, 1909–1916. doi:10.1007/S00586-015-4061-4
Sharabi, M., Benayahu, D., Benayahu, Y., Isaacs, J., and Haj-Ali, R. (2015). Laminated Collagen-Fiber Bio-Composites for Soft-Tissue Bio-Mimetics. Composites Sci. Techn. 117, 268–276. doi:10.1016/j.compscitech.2015.06.024
Sharabi, M., Mandelberg, Y., Benayahu, D., Benayahu, Y., Azem, A., and Haj-Ali, R. (2014). A New Class of Bio-Composite Materials of Unique Collagen Fibers. J. Mech. Behav. Biomed. Mater. 36, 71–81. Available at: http://www.sciencedirect.com/science/article/pii/S175161611400109X. doi:10.1016/j.jmbbm.2014.04.008
Sharabi, M., Varssano, D., Eliasy, R., Benayahu, Y., Benayahu, D., and Haj-Ali, R. (2016). Mechanical Flexure Behavior of Bio-Inspired Collagen-Reinforced Thin Composites. Compos. Structures 153, 392–400. doi:10.1016/j.compstruct.2016.06.031
Sharabi, M., Wade, K. R., Galbusera, F., Rasche, V., Haj-Ali, R., and Wilke, H.-J. (2018). Three-dimensional Microstructural Reconstruction of the Ovine Intervertebral Disc Using Ultrahigh Field MRI. Spine J. 18, 2119–2127. doi:10.1016/j.spinee.2018.06.356
Sharabi, M., and Wagner, H. D. (2021). Structural Biomimetics in Soft Synthetic Composite Materials: A Proof-Of-Concept Alginate-Polyamide Soft Hierarchical Composite. Express Polym. Lett. 15, 708–724. doi:10.3144/EXPRESSPOLYMLETT.2021.59
Sharabi, M., Wertheimer, S., Wade, K. R., Galbusera, F., Benayahu, D., Wilke, H.-J., et al. (2019). Towards Intervertebral Disc Engineering: Bio-Mimetics of Form and Function of the Annulus Fibrosus Lamellae. J. Mech. Behav. Biomed. Mater. 94, 298–307. doi:10.1016/j.jmbbm.2019.03.023
Shen, Z. L., Dodge, M. R., Kahn, H., Ballarini, R., and Eppell, S. J. (2008). Stress-Strain Experiments on Individual Collagen Fibrils. Biophysical J. 95, 3956–3963. doi:10.1529/biophysj.107.124602
Sherman, V. R., Yang, W., and Meyers, M. A. (2015). The Materials Science of Collagen. J. Mech. Behav. Biomed. Mater. 52, 22–50. doi:10.1016/j.jmbbm.2015.05.023
Silbert, J. E. (1982). Structure and Metabolism of Proteoglycans and Glycosaminoglycans. J. Invest. Dermatol. 79, 31–37. doi:10.1038/jid.1982.7
Silver, F. H., Christiansen, D. L., and Buntin, C. M. (1989). Mechanical Properties of the Aorta: a Review. Crit. Rev. Biomed. Eng. 17, 323–358. Available at: https://europepmc.org/article/med/2676341 (Accessed October 2, 2021).
Sizeland, K. H., Basil-Jones, M. M., Edmonds, R. L., Cooper, S. M., Kirby, N., Hawley, A., et al. (2013). Collagen Orientation and Leather Strength for Selected Mammals. J. Agric. Food Chem. 61, 887–892. doi:10.1021/JF3043067
Skaggs, D. L., Weidenbaum, M., Latridis, J. C., Ratcliffe, A., and Mow, V. C. (1994). Regional Variation in Tensile Properties and Biochemical Composition of the Human Lumbar Anulus Fibrosus. Spine 19, 1310–1319. doi:10.1097/00007632-199406000-00002
Smith, J. W. (1968). Molecular Pattern in Native Collagen. Nature 219, 157–158. doi:10.1038/219157a0
Sommer, G., Regitnig, P., Költringer, L., and Holzapfel, G. A. (2009). Biaxial Mechanical Properties of Intact and Layer-Dissected Human Carotid Arteries at Physiological and Supraphysiological Loadings. Am. J. Physiol. Heart Circ. Physiol. 298, H898–H912. doi:10.1152/ajpheart.00378.2009
Sopher, R. S., Tokash, H., Natan, S., Sharabi, M., Shelah, O., Tchaicheeyan, O., et al. (2018). Nonlinear Elasticity of the ECM Fibers Facilitates Efficient Intercellular Communication. Biophysical J. 115, 1357–1370. doi:10.1016/J.BPJ.2018.07.036
Spiesz, E. M., Thorpe, C. T., Thurner, P. J., and Screen, H. R. C. (2018). Structure and Collagen Crimp Patterns of Functionally Distinct Equine Tendons, Revealed by Quantitative Polarised Light Microscopy (qPLM). Acta Biomater. 70, 281–292. doi:10.1016/j.actbio.2018.01.034
Starborg, T., Kalson, N. S., Lu, Y., Mironov, A., Cootes, T. F., Holmes, D. F., et al. (2013). Using Transmission Electron Microscopy and 3View to Determine Collagen Fibril Size and Three-Dimensional Organization. Nat. Protoc. 8, 1433–1448. doi:10.1038/nprot.2013.086
Stein, A. M., Vader, D. A., Weitz, D. A., and Sander, L. M. (2011). The Micromechanics of Three-Dimensional Collagen-I Gels. Complexity 16, 22–28. doi:10.1002/CPLX.20332
Stella, J. A., D’Amore, A., Wagner, W. R., and Sacks, M. S. (2010a). On the Biomechanical Function of Scaffolds for Engineering Load-Bearing Soft Tissues. Acta Biomater. 6, 2365–2381. doi:10.1016/j.actbio.2010.01.001
Stella, J. A., Wagner, W. R., and Sacks, M. S. (2009b). Scale-dependent Fiber Kinematics of Elastomeric Electrospun Scaffolds for Soft Tissue Engineering. J. Biomed. Mater. Res. 93, 1032–1042. doi:10.1002/jbm.a.32593
Stokes, I., and Greenapple, D. M. (1985). Measurement of Surface Deformation of Soft Tissue. J. Biomech. 18, 1–7. doi:10.1016/0021-9290(85)90040-5
Strange, D. G. T., Tonsomboon, K., and Oyen, M. L. (2014). Mechanical Behaviour of Electrospun Fibre-Reinforced Hydrogels. J. Mater. Sci. Mater. Med. 25, 681–690. doi:10.1007/s10856-013-5123-y
Studart, A. R. (2012). Towards High-Performance Bioinspired Composites. Adv. Mater. 24, 5024–5044. doi:10.1002/adma.201201471
Svensson, R. B., Herchenhan, A., Starborg, T., Larsen, M., Kadler, K. E., Qvortrup, K., et al. (2017). Evidence of Structurally Continuous Collagen Fibrils in Tendons. Acta Biomater. 50, 293–301. doi:10.1016/J.ACTBIO.2017.01.006
Szczesny, S. E., Driscoll, T. P., Tseng, H.-Y., Liu, P.-C., Heo, S.-J., Mauck, R. L., et al. (2016). Crimped Nanofibrous Biomaterials Mimic Microstructure and Mechanics of Native Tissue and Alter Strain Transfer to Cells. ACS Biomater. Sci. Eng. 3, 2869–2876. doi:10.1021/ACSBIOMATERIALS.6B00646
Tamayol, A., Akbari, M., Annabi, N., Paul, A., Khademhosseini, A., and Juncker, D. (2013). Fiber-based Tissue Engineering: Progress, Challenges, and Opportunities. Biotechnol. Adv. 31, 669–687. doi:10.1016/j.biotechadv.2012.11.007
Tamburro, A. M., Stradis, A. D., and D'Alessio, L. (1995). Fractal Aspects of Elastin Supramolecular Organization. J. Biomol. Struct. Dyn. 12, 1161–1172. doi:10.1080/07391102.1995.10508805
Tan, G. Z., and Zhou, Y. (2019). Electrospinning of Biomimetic Fibrous Scaffolds for Tissue Engineering: a Review. Int. J. Polymeric Mater. 69, 947–960. doi:10.1080/00914037.2019.1636248
Tavakoli, J., Diwan, A. D., and Tipper, J. L. (2020). The Ultrastructural Organization of Elastic Fibers at the Interface of the Nucleus and Annulus of the Intervertebral Disk. Acta Biomater. 114, 323–332. doi:10.1016/j.actbio.2020.07.021
Tavakoli, J., Elliott, D. M., and Costi, J. J. (2017). The Ultra-structural Organization of the Elastic Network in the Intra- and Inter-lamellar Matrix of the Intervertebral Disc. Acta Biomater. 58, 269–277. doi:10.1016/j.actbio.2017.05.036
Thorpe, C. T., Birch, H. L., Clegg, P. D., and Screen, H. R. C. (2013). The Role of the Non-collagenous Matrix in Tendon Function. Int. J. Exp. Path. 94, 248–259. doi:10.1111/iep.12027
Thorpe, C. T., Godinho, M. S. C., Riley, G. P., Birch, H. L., Clegg, P. D., and Screen, H. R. C. (2015). The Interfascicular Matrix Enables Fascicle Sliding and Recovery in Tendon, and Behaves More Elastically in Energy Storing Tendons. J. Mech. Behav. Biomed. Mater. 52, 85–94. doi:10.1016/J.JMBBM.2015.04.009
Tonsomboon, K., Butcher, A. L., and Oyen, M. L. (2017). Strong and Tough Nanofibrous Hydrogel Composites Based on Biomimetic Principles. Mater. Sci. Eng. C 72, 220–227. doi:10.1016/j.msec.2016.11.025
Tonsomboon, K., and Oyen, M. L. (2013). Composite Electrospun Gelatin Fiber-Alginate Gel Scaffolds for Mechanically Robust Tissue Engineered Cornea. J. Mech. Behav. Biomed. Mater. 21, 185–194. doi:10.1016/j.jmbbm.2013.03.001
Tower, T. T., Neidert, M. R., and Tranquillo, R. T. (2002). Fiber Alignment Imaging during Mechanical Testing of Soft Tissues. Ann. Biomed. Eng. 30, 1221–1233. doi:10.1114/1.1527047
Venkatraman, S., Boey, F., and Lao, L. L. (2008). Implanted Cardiovascular Polymers: Natural, Synthetic and Bio-Inspired. Prog. Polym. Sci. 33, 853–874. doi:10.1016/j.progpolymsci.2008.07.001
Vergari, C., Chan, D., Clarke, A., Mansfield, J. C., Meakin, J. R., and Winlove, P. C. (2017). Bovine and Degenerated Human Annulus Fibrosus: a Microstructural and Micromechanical Comparison. Biomech. Model. Mechanobiol. 16, 1475–1484. doi:10.1007/s10237-017-0900-z
Vidal, B. d. C. (2003). Image Analysis of Tendon Helical Superstructure Using Interference and Polarized Light Microscopy. Micron 34, 423–432. doi:10.1016/S0968-4328(03)00039-8
Vincent, J. F. V. (2003). Biomimetic Modelling. Phil. Trans. R. Soc. Lond. B 358, 1597–1603. doi:10.1098/rstb.2003.1349
Vindin, H., Mithieux, S. M., and Weiss, A. S. (2019). Elastin Architecture. Matrix Biol. 84, 4–16. doi:10.1016/j.matbio.2019.07.005
Wegst, U. G. K., Bai, H., Saiz, E., Tomsia, A. P., and Ritchie, R. O. (2015). Bioinspired Structural Materials. Nat. Mater 14, 23–36. doi:10.1038/nmat4089
Weiner, S., Traub, W., and Wagner, H. D. (1999). Lamellar Bone: Structure-Function Relations. J. Struct. Biol. 126, 241–255. doi:10.1006/jsbi.1999.4107
Wertheimer, S., Sharabi, M., Shelah, O., Lesman, A., and Haj-Ali, R. (2021). Bio-composites Reinforced with Unique Coral Collagen Fibers: Towards Biomimetic-Based Small Diameter Vascular Grafts. J. Mech. Behav. Biomed. Mater. 119, 104526. doi:10.1016/J.JMBBM.2021.104526
Wight, T. N. (1980). Vessel Proteoglycans and Thrombogenesis. Prog. Hemost. Thromb. 5, 1–39. Available at: https://europepmc.org/article/med/7422873 (Accessed October 1, 2021).
Wilkerson, R. P., Gludovatz, B., Watts, J., Tomsia, A. P., Hilmas, G. E., and Ritchie, R. O. (2016). A Novel Approach to Developing Biomimetic ("Nacre-like") Metal-compliant-phase (Nickel-Alumina) Ceramics through Coextrusion. Adv. Mater. 28, 10061–10067. doi:10.1002/adma.201602471
Wilson, J. O., and Rosen, D. (2009). “Systematic Reverse Engineering of Biological Systems,” in ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (American Society of Mechanical Engineers Digital Collection), 69–78. doi:10.1115/detc2007-35395
Wu, W. J., Vrhovski, B., and Weiss, A. S. (1999). Glycosaminoglycans Mediate the Coacervation of Human Tropoelastin through Dominant Charge Interactions Involving Lysine Side Chains. J. Biol. Chem. 274, 21719–21724. doi:10.1074/jbc.274.31.21719
Wu, Y., Wu, B., Vijayavenkataraman, S., Wong, Y. S., and Fuh, J. Y. H. (2017). Crimped Fiber with Controllable Patterns Fabricated via Electrohydrodynamic Jet Printing. Mater. Des. 131, 384–393. doi:10.1016/j.matdes.2017.06.027
Xu, S., Deng, L., Zhang, J., Yin, L., and Dong, A. (2016). Composites of Electrospun-Fibers and Hydrogels: A Potential Solution to Current Challenges in Biological and Biomedical Field. J. Biomed. Mater. Res. 104, 640–656. doi:10.1002/jbm.b.33420
Yang, L., van der Werf, K. O., Dijkstra, P. J., Feijen, J., and Bennink, M. L. (2012). Micromechanical Analysis of Native and Cross-Linked Collagen Type I Fibrils Supports the Existence of Microfibrils. J. Mech. Behav. Biomed. Mater. 6, 148–158. doi:10.1016/J.JMBBM.2011.11.008
Yang, W., Sherman, V. R., Gludovatz, B., Schaible, E., Stewart, P., Ritchie, R. O., et al. (2015). On the Tear Resistance of Skin. Nat. Commun. 6, 1–10. doi:10.1038/ncomms7649
Yang, W., Meyers, M. A., and Ritchie, R. O. (2019). Structural Architectures with Toughening Mechanisms in Nature: A Review of the Materials Science of Type-I Collagenous Materials. Prog. Mater. Sci. 103, 425–483. doi:10.1016/j.pmatsci.2019.01.002
Yu, J., Schollum, M. L., Wade, K. R., Broom, N. D., and Urban, J. P. G. (2015). ISSLS Prize Winner. Spine 40, 1149–1157. doi:10.1097/brs.0000000000000943
Yu, J., Tirlapur, U., Fairbank, J., Handford, P., Roberts, S., Winlove, C. P., et al. (2007). Microfibrils, Elastin Fibres and Collagen Fibres in the Human Intervertebral Disc and Bovine Tail Disc. J. Anat. 210, 460–471. doi:10.1111/j.1469-7580.2007.00707.x
Zaarour, B., Zhu, L., Huang, C., and Jin, X. (2020). A Mini Review on the Generation of Crimped Ultrathin Fibers via Electrospinning: Materials, Strategies, and Applications. Polym. Adv. Technol. 31, 1449–1462. doi:10.1002/PAT.4876
Zhalmuratova, D., La, T.-G., Yu, K. T.-T., Szojka, A. R. A., Andrews, S. H. J., Adesida, A. B., et al. (2019). Mimicking "J-Shaped" and Anisotropic Stress-Strain Behavior of Human and Porcine Aorta by Fabric-Reinforced Elastomer Composites. ACS Appl. Mater. Inter. 11, 33323–33335. doi:10.1021/ACSAMI.9B10524
Zhang, M., Jiao, D., Tan, G., Zhang, J., Wang, S., Wang, J., et al. (2019). Strong, Fracture-Resistant Biomimetic Silicon Carbide Composites with Laminated Interwoven Nanoarchitectures Inspired by the Crustacean Exoskeleton. ACS Appl. Nano Mater. 2, 1111–1119. doi:10.1021/acsanm.9b00063
Zhang, W., Liu, Y., and Kassab, G. S. (2007). Viscoelasticity Reduces the Dynamic Stresses and Strains in the Vessel wall: Implications for Vessel Fatigue. Am. J. Physiol. Heart Circ. Physiol. 293, H2355–H2360. doi:10.1152/ajpheart.00423.2007
Zhao, L., Thambyah, A., and Broom, N. (2015). Crimp Morphology in the Ovine Anterior Cruciate Ligament. J. Anat. 226, 278–288. doi:10.1111/joa.12276
Zhou, M., Werbner, B., and O'Connell, G. D. (2021). Fiber Engagement Accounts for Geometry-dependent Annulus Fibrosus Mechanics: A Multiscale, Structure-Based Finite Element Study. J. Mech. Behav. Biomed. Mater. 115, 104292. doi:10.1016/J.JMBBM.2020.104292
Zitnay, J. L., and Weiss, J. A. (2018). Load Transfer, Damage, and Failure in Ligaments and Tendons. J. Orthop. Res. 36, 3093–3104. doi:10.1002/JOR.24134
Keywords: biomimetics, soft tissues, mechanical mechanisms, soft composite materials, mechanical properties, structure-function relationship, architectural materials
Citation: Sharabi M (2022) Structural Mechanisms in Soft Fibrous Tissues: A Review. Front. Mater. 8:793647. doi: 10.3389/fmats.2021.793647
Received: 12 October 2021; Accepted: 02 December 2021;
Published: 05 January 2022.
Edited by:
Flavia Libonati, University of Genoa, ItalyReviewed by:
Anna Tarakanova, University of Connecticut, United StatesEttore Barbieri, Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Japan
Copyright © 2022 Sharabi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mirit Sharabi, bWlyaXRzaEBhcmllbC5hYy5pbA==
 Mirit Sharabi
Mirit Sharabi