Bearing Capacity of Hollow GFRP Pipe-Concrete-High Strength Steel Tube Composite Long Columns Under Eccentrical Compression Load

To investigate the bearing capacity of the hollow Glass Fiber Reinforced Polymer (GFRP) pipe-concrete-steel tube composite long columns subjected to eccentrical compression load, 33 hollow GFRP pipe-concrete-steel tube composite long columns have been designed. The slenderness ratio (λ), compressive strength of concrete cube (f_cu), eccentricity (e) and so on are the main parameters. Based on constitutive models for steel, GFRP and confined concrete, numerical simulation of the hollow GFRP pipe-concrete-high strength steel tube composite long columns has been carried out by using software ABAQUS. The rationality of the constitutive models and modeling method has been verified by comparing the experimental and simulated load-displacement curves. The influence of different parameters on the mechanical behavior of this kind of column has been investigated. Results show that with the increasing of t1, t2 and fcu, the ultimate eccentrical compression bearing capacity of the specimen increases. With the increasing of e, the ultimate displacement of the specimens increases, while the ultimate eccentrical compression bearing capacity decreases. The eccentricity has a significant influence on the ultimate eccentrical compression bearing capacity. With the increasing of λ, the ultimate eccentrical compression bearing capacity of the specimens gradually decreases. The specimens suffer from ductile failure. The formula of the ultimate eccentrical compression bearing capacity of the composite columns is obtained by statistical regression. The study can provide theoretical support for the application of the composite columns in practical engineering.

Introduction

Glass Fiber Reinforced Polymer (GFRP) has been widely used in acidic, alkaline and wet environments because of its advantages of light weight, high tensile strength and good corrosion resistance (Dilum et al., 2018; Ji et al., 2021a). But it also has the shortcomings of poor rigidity and low shear strength, which severely restrict its popularization and application in structural systems. The GFRP material and concrete are organically combined to form a composite structural member, which can give full play to the superior mechanical properties of the material (Wang and Dai, 2019a). Based on this, a new type of hollow GFRP pipe-concrete-high strength steel tube composite columns is proposed. This type of column is composed of an outer layer of GFRP pipe, an inner layer of high strength steel tube and sandwich concrete. The outer layer of GFRP pipe and inner layer of steel tube can provide effective confined force for the sandwich concrete, thereby the bearing capacity and ductility of the composite columns can be greatly improved (Idris and Ozbakkaloglu, 2014). In actual engineering, this new type of composite member is not only convenient for construction, but also possesses excellent seismic performance and durability (Wang et al., 2019b).

In 2015, Mohammad et al. (2015) firstly proposed a circular GFRP pipe concrete column compression model, which could better predict the stress-strain behavior of GFRP pipe concrete columns subjected to compression load. In 2016, Abdelkarim et al. (2016) found that solid-web composite columns had better overall stiffness and seismic behavior than hollow FRP-concrete-steel tube composite columns. In the same year, Abdelkarim et al. (2016) proposed a design method for hollow FRP-concrete-steel tube columns under earthquake action. In 2017, Ekmekyapar and AL-Eliwi (2017) found that the bearing capacity, ductility and stiffness of double-layer concrete filled steel tube (CFST) columns were better than those of single-layer CFST columns. In 2018, Ahmed et al. (2018) proposed a bearing capacity formula for double CFST short columns under axial compression and developed a ideal mathematical model which could reflect well the stress-strain relationship of this type of column under compression. In 2019, AlAjarmeh et al. (2019) established a theoretical model of hollow concrete columns by GFRP reinforcement, which could well predict the axial compressive bearing capacity of this type of column. In 2015, Qian et al. (2015) found that the vertical strain of the mid-span section of the eccentrically compressed double CFST column basically conformed to the plane-section assumption, and its eccentric compression bearing capacity could be obtained by the superposition method. In 2015, Feng et al. (2015) found that steel tube-concrete-FRP composite columns had superior stiffness, ductility and stable residual bearing capacity. In 2016, Cheng (2016) established a calculation method for the compressive and flexural bearing capacity of steel tube-concrete-FRP-concrete columns and proved that this type of column had superior mechanical behavior. In 2017, Zhang et al. (2017) established the medium long column model of steel-encased concrete filled GFRP tubes, and proposed the calculation formula for reduction coefficient of bearing capacity considering the effect of slenderness ratio. In 2018, Teng et al. (2018) found that FRP-concrete-high-strength steel tube-concrete composite columns had excellent short-term and long-term bearing capacity, and both FRP tubes and high-strength steel tubes generated obvious restraint effects on concrete. Ji Jing’s research group (Yu, 2020; Ji et al., 2021b) found that the thickness of the outer GFRP tube had the most significant impact on the axial compression behavior of the GFRP tube-concrete-steel tube composite columns, and proposed that the best winding angle of the GFRP tube should be ±80°. So far, the research on the GFRP tube-concrete-steel tube composite columns has mainly focused on the axial compression behavior, and there are few experiments and numerical simulations involving the eccentric compression behavior of this type of composite columns. Therefore, it is essential to carry out the research on the eccentric compression bearing behavior of this type of composite long columns through finite element software.

Combined with large-scale finite element software ABAQUS (Ji et al., 2018; Ji et al., 2021c), and considering the nonlinear contact between materials, the finite element model of the hollow GFRP pipe-concrete-high strength steel tube composite long columns is established by introducing the nonlinear constitutive model of materials. Based on the experimental verification of the material constitutive model and finite element modeling, the influence regularity of different parameters on the eccentrical compression bearing capacity of the composite columns is explored, and the calculation formula of the composite columns under eccentric compression load is obtained by statistical regression.

Specimen Design

In order to obtain the eccentric compression behavior of the hollow GFRP pipe-concrete-high strength steel tube composite long columns, the slenderness ratio (λ), compressive strength of concrete cube (f_cu), eccentricity (e), thickness of GFRP pipe (t₁) and thickness of steel tube (t₂) are taken as the main controlled parameters, and a total of 33 composite long columns are designed. The specific parameters of the specimens are shown in Table 1, and the overall diagram of the specimen is shown in Figure 1. In Table 1, H is the length of the column, D_GFRP and D_s are the outer GFRP with a diameter of 300 mm and inner steel tubes with a diameter of 219 mm respectively, and the hollow rate (ρ) is 0.6. High-strength steel that the grade is Q345 is adopted for the steel tube, and the yield strength (f_sy) is taken as 351 MPa. The modulus of elasticity and Poisson’s ratio are taken as 198.22GPa and 0.3, respectively. λ is equal to H/D_GFRP.

TABLE 1

TABLE 1. Specific parameters of 33 specimens.

FIGURE 1

FIGURE 1. Hollow GFRP pipe-concrete-steel tube composite long columns.

Finite Element Model

Material Constitutive Model

GFRP Pipe

GFRP is an orthotropic material which could provide little axial compression resistance, so only the axial tension effect of GFRP is considered in this paper. The linear elastic constitutive model is shown in Figure 2. The mechanical properties of GFRP pipes are shown in Table 2. The axial stress-strain relationship of GFRP is as follows:

$\text{When}\epsilon \le {\epsilon }_{fu},{\sigma }_f=E_f\epsilon (1)$

$\text{When}\epsilon \ge {\epsilon }_{fu},{\sigma }_f=0(2)$

Where ${\epsilon }_{fu}$ and $E_f$ are the fracture strain and elastic modulus of GFRP, respectively.

FIGURE 2

FIGURE 2. Constitutive model of GFRP pipe.

TABLE 2

TABLE 2. Mechanical properties of GFRP pipe.

Concrete

The constitutive model of confined concrete is given by Han et al. (2001), Teng et al. (2006), Mander et al. (1988) and Pagoulatou et al. (2014), and the comparisons of different constitutive models are shown in Figure 3. The constitutive model of confined concrete proposed by L. H. Han is adopted in this article and the plastic damage model of concrete is selected in the ABAQUS software.

FIGURE 3

FIGURE 3. Different constitutive models of concrete.

The stress-strain relationship of concrete under uniaxial compression:

$y=\{\begin{array}{c}2\cdot x-x^2 (x\le 1)\\ \frac{x}{{\beta }_0{\left(x-1\right)}^n+x} (x>1)\end{array}(3)$

Where:

$x=\epsilon /{\epsilon }_0(4)$

$y=\sigma /{\sigma }_0(5)$

${\sigma }_0=f_c(6)$

${\epsilon }_0={\epsilon }_c+800\cdot {\xi }^{0.2}\cdot {10}^{-6}(7)$

${\epsilon }_c=(1300+12.5\cdot f_c)\cdot {10}^{-6}(8)$

$\eta =2(9)$

${\beta }_0={\left(2.36\times {10}^{-5}\right)}^{\left[0.25+{\left(\xi -0.5\right)}^7\right]}\cdot f_c^{0.5}\cdot 0.5\ge 0.12 (10)$

The stress-strain relationship of concrete under uniaxial tension:

$y=\{\begin{array}{c}1.2\cdot x-0.2\cdot x^6 (x\le 1)\\ \frac{x}{0.31\cdot {\sigma }_P^2\cdot {\left(x-1\right)}^{1.7}+x} (x>1)\end{array}(11)$

Where, $x=\frac{{\epsilon }_c}{{\epsilon }_P}$, $y=\frac{{\sigma }_c}{{\sigma }_P}$, ${\sigma }_{\text{P}}$ is the peak tensile stress, ${\epsilon }_{\text{P}}$ is the peak tensile strain, ${\sigma }_P$ and ${\epsilon }_P$ can be calculated respectively according to the following formulas:

${\sigma }_P=0.26\times {\left(1.25\cdot f_c\right)}^{2/3}(12)$

${\epsilon }_P=34.276\times {\sigma }_P(\mu \cdot \epsilon )(13)$

Steel

The double-broken line elastoplastic constitutive model considering stress hardening is adopted as the constitutive model of the inner steel tube, as shown in Figure 4. The stress-strain relationship is shown in Eq. 14, where E₁ is taken as 0.01E_s.

$\sigma =\{\begin{array}{c}{E}_s\times \epsilon (\epsilon \le {\epsilon }_{sy})\\ f_{sy}+E_1\times \left|\epsilon -{\epsilon }_{sy}\right| (\epsilon >{\epsilon }_{sy})\end{array}(14)$

Where, E_s is the elastic modulus of the steel tube. E₁ is the modulus of the plastic stage of the steel tube. f_sy and ɛ_sy are the yield strength and its corresponding strain of the steel tube, respectively.

FIGURE 4

FIGURE 4. Bilinear constitutive model of steel tube.

Element Selection and Contact Method

Based on the finite element software ABAQUS, finite element model of the hollow GFRP pipe-concrete-high strength steel tube composite column is established. Eight-node three-dimensional solid elements (C3D8R) are adopted to simulate the steel tube, concrete and GFRP pipe. The interface contact among GFRP pipe, steel tube and concrete consisted of two aspects, including the hard contact in the normal direction and the frictional contact considering relative slip in the tangent direction, as shown in Figure 5. In the normal direction, in order to make the interaction surface fully contact, the hard contact is adopted. The interface pressure of the contact unit is p. In the tangent direction, shear stress τ can be freely transferred between the interface of steel tube and concrete. When the shear stress reaches the critical value of interface bond stress τ_bond, the interfacial bond stress failed, that is, GFRP pipe, steel tube and concrete began to slip relatively, as shown in Eq. 15. In this paper, the relative slip between the interface of steel tube and concrete is considered during the analysis process, and the friction coefficient µ is taken as 0.5 (Ji et al., 2020).

$\tau =\mu \times p\{\begin{array}{c}<{\tau }_{bond} consistent deformation\\ \ge {\tau }_{bond} relative slip\end{array}(15)$

FIGURE 5

FIGURE 5. Material contact relationship of composite long columns.

Boundary Conditions and Meshing

Two reference points RP₁ and RP₂ are set at both ends of the specimens, and RP₁ and RP₂ are coupled with the degrees of freedom at the end sections of columns. In order to ensure that the eccentric compression columns exhibits the flexure only in the XOZ plane during the loading process, the degrees of freedom (U_X, U_Y, UR_X, and UR_Y) of the eccentric compression columns are restricted at the upper end, while the degrees of freedom (U_X, U_Y, U_Z, UR_X, and UR_Y) are restricted at the lower end. Vertical displacement is applied to the reference point RP₁ at the upper end of the column. In order to ensure the accuracy and efficiency of the model calculation, a suitable mesh density is selected firstly to analyze the model, and then the density mesh of the model is taken as 2 times to analyze again. By comparing the calculation results of the two meshing methods, the error between them is less than 5%, which could be used as a suitable meshing for the composite columns. The meshing of the finite element model is shown in Figure 6.

FIGURE 6

FIGURE 6. Meshing of finite element model.

Experimental Verification of Finite Element Model

Overview of Existing Tests

In order to verify the rationality of the finite element modeling, four GFRP pipe-concrete-steel tube composite columns from the literature (Xu, 2013) are selected for finite element simulation in this paper, and the load-displacement relationship curves of the composite columns can be obtained. By comparing the results of existing tests, the rationality of the finite element modeling of the composite columns in this paper is verified. The specific parameters of four specimens are shown in Tables 3, 4, here f_c and E_c are the axial compressive strength of concrete and the elastic modulus of concrete, respectively.

TABLE 3

TABLE 3. Specific parameters of four specimens.

TABLE 4

TABLE 4. Specific parameters of four specimens of GFRP pipe and steel tube.

Comparisons of Results Between Simulations and Tests of four Specimens

The above modeling method is used to carry out numerical analysis for the eccentrical compression behavior of four test specimens, and the load-displacement relationship curves of the four specimens are obtained. The comparisons of the load-displacement curves between simulations and tests are shown in Figure 7. It can be seen by comparison that the trend of the test curves are basically consistent with that of the simulated curves, which are in good agreement. However, some specimens in the later plastic stage are in general agreement. The possible reason is that the concrete is regarded as an isotropic continuous element during the simulation analysis, while the concrete is regarded as a discrete element in the test. The ultimate eccentrical compression bearing capacity and ultimate displacement of the specimens can be extracted by load-displacement curves, as shown in Table 5.

FIGURE 7

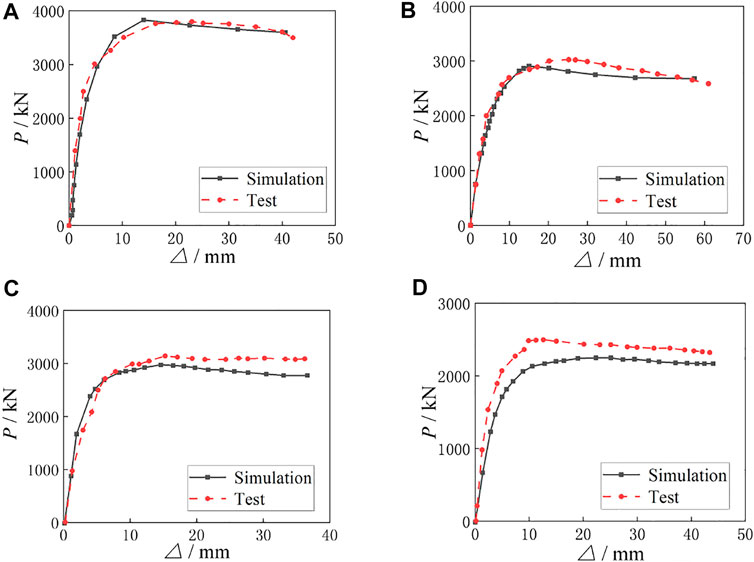
FIGURE 7. Comparisons of load-displacement curves between simulation and test. (A) Specimen 1-30-10-3. (B) Specimen 1-60-10-4. (C) Specimen 2-30-6-3. (D) Specimen 2-60-6-3.

TABLE 5

TABLE 5. Comparisons of ultimate eccentrical compression bearing capacity and ultimate displacement.

It can be seen from Table 5 that the maximum error between the simulated eccentrical compression ultimate bearing capacity (N_s) and the test ultimate bearing capacity (N_t) is less than 10%, which can be seen that the analytical results of the finite element simulations and the tests are in good agreement. The comparisons of the failure modes between the simulations and tests of four specimens are shown in Figure 8. It can be seen that the overall deformation and failure position of the simulated composite columns are basically the same as those of the test composite columns, which can verify the rationality and feasibility of the finite element modeling method.

FIGURE 8

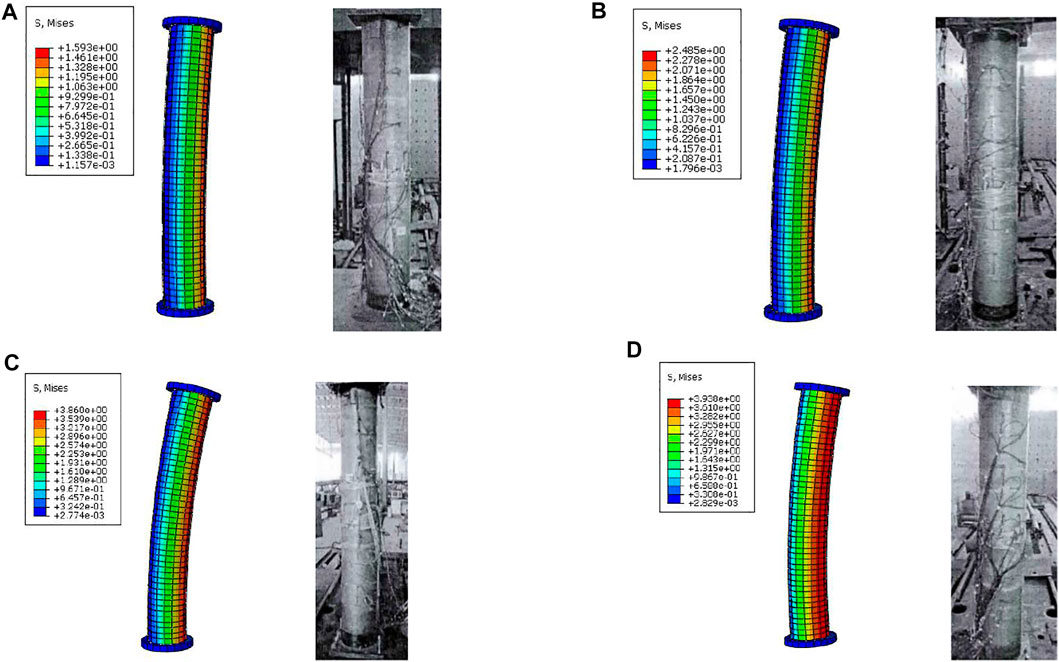
FIGURE 8. Comparisons of deformation between simulation and test for four specimens. (A) Specimen 1-30-10-3. (B) Specimen 1-60-10-4. (C) Specimen 2-30-6-3. (D) Specimen 2-60-6-3.

Analysis of Extended Parameters

Thickness of GFRP pipe (t₁)

The comparisons of load-displacement curves of specimens with different t₁ are shown in Figure 9, and the ultimate eccentrical compression bearing capacity (N_s) of the specimens is shown in Table 6. It can be seen from Figure 9 that the initial stiffness of the specimens is basically unchanged with the increasing of t₁, and with the increasing of load, the stiffness of the specimens gradually increases. As can be seen from Figure 9A, when the eccentricity (e) is 30 mm and t₁ increases from 6 to 8, 10 and 12 mm, respectively, N_s increases from 2979 to 3336kN, 3804 and 4564kN in turn, which increases by 12.0, 27.7 and 53.2%, respectively. As can be seen from Figure 9B, when e is 60 mm and t₁ increases from 6 to 8, 10 and 12 mm respectively, N_s increases from 2472 to 2736kN, 3081 and 3698kN in turn, which increases by 10.7, 24.6 and 49.6%, respectively. As can be seen from Figure 9C, when e is 0mm, t₁ increases from 6 to 8, 10 and 12 mm respectively, N_s increases from 3932 to 4404kN, 5022 and 6051kN in turn, which increases by 12.0, 27.7 and 53.9%, respectively. It can be concluded that N_s of the three groups of specimens show the same change regularity, that is, N_s increases gradually and the increase rate is larger with the increasing of t₁. All specimens show good bearing capacity.

FIGURE 9

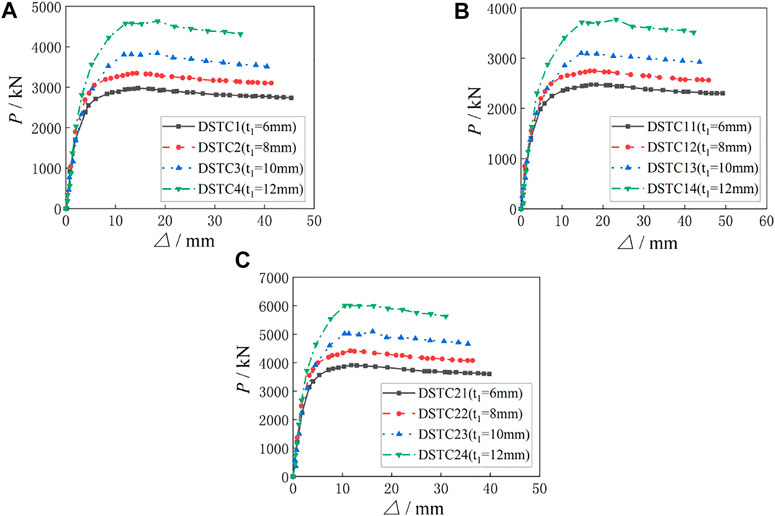
FIGURE 9. Comparisons of load-displacement curves for specimens with different GFRP thicknesses. (A) Load-displacement curves of group A specimens. (B) Load-displacement curves of group B specimens. (C) Load-displacement curves of group C specimens.

TABLE 6

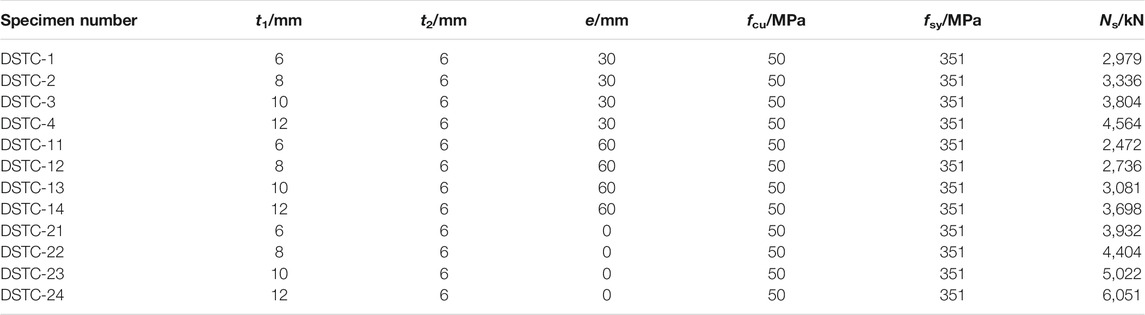
TABLE 6. Ultimate eccentrical compression bearing capacity of specimens with different thicknesses of GFRP pipe.

Thickness of Steel tube (t₂)

The comparisons of load-displacement curves of specimens with different t₂ are shown in Figure 10, and the ultimate eccentrical compression bearing capacity (N_s) of the specimens is shown in Table 7. It can be seen from Figure 10 that the initial stiffness of the specimens is basically unchanged with the increasing of t₂, while the ultimate eccentrical compression bearing capacity of the specimens increases gradually. As can be seen from Figure 10A, when the eccentricity (e) is 30 mm and t₂ increases from 6 to 8, 10 and 12 mm, respectively, N_s increases from 3804 to 3961kN, 4381 and 4822kN in turn, which increases by 4.0, 13.2 and 21.1%, respectively. As can be seen from Figure 10B, when e is 60 mm and t₂ increases from 6 to 8, 10 and 12 mm respectively, N_s increases from 3081 to 3248kN, 3589 and 3996kN in turn, which increases by 5.1, 14.2 and 22.9%, respectively. As can be seen from Figure 10C, when e is 0 mm and t₂ increases from 6 to 8, 10 and 12 mm, respectively, N_s increases from 5022 to 5229kN, 5789 and 6361kN in turn, which increases by 4, 13.2 and 21.1%, respectively. It can be concluded that N_s of the three groups of specimens show the same change regularity, that is, N_s gradually increases and the increase rate is larger with the increase of t₂. With the increasing of deformation, the curves tend to be horizontal and then begin to decrease slowly. All specimens show good bearing capacity.

FIGURE 10

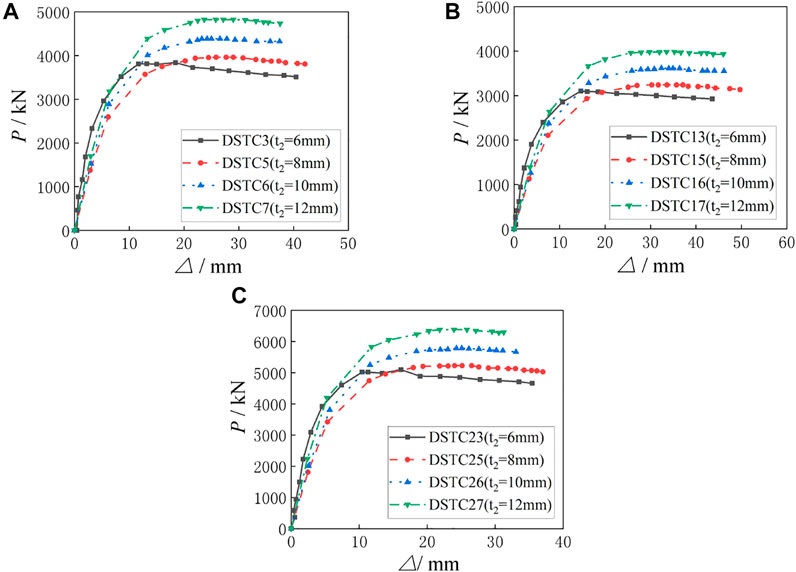
FIGURE 10. Comparisons of Load-Displacement Curves of Specimens with Different Steel Tube Thicknesses. (A) Load-displacement curves of group A specimens. (B) Load-displacement curves of group B specimens. (C) Load-displacement curves of group C specimens.

TABLE 7

TABLE 7. Ultimate eccentrical compression bearing capacity of specimens with different thicknesses.

Compressive Strength of Concrete Cube (f_cu)

The comparisons of load-displacement curves of specimens with different f_cu are shown in Figure 11, and the ultimate eccentrical compression bearing capacity of the specimens is shown in Table 8. It can be seen from Figure 11 that the initial stiffness of the specimens is basically unchanged with the increasing of f_cu, and with the increasing of load, the stiffness of the specimens gradually increases. As can be seen from Figure 11A, when e is 30 mm and f_cu increases from 30 to 40, 50 and 60 MPa, respectively, N_s increases from 2693 to 3112kN, 3804 and 4502kN in turn, which increases by 13.5, 29.2 and 40.2%, respectively. As can be seen from Figure 11B, when e is 60 mm and f_cu increases from 30 to 40, 50 and 60 MPa, respectively, N_s increases from 2235 to 2546kN, 3081 and 3737kN in turn, which increases by 12.2, 27.5 and 40.2%, respectively. As can be seen from Figure 11C, when e is 0 mm and f_cu increases from 30 to 40, 50 and 60 MPa, respectively, N_s increases from 3555 to 4075kN, 5022 and 5921kN in turn, which increases by 12.8, 29.2 and 40%, respectively. It can be concluded that N_s of the three groups of specimens show the same change regularity, that is, N_s gradually increases and the increase rate is larger with the increasing of f_cu. When f_cu reaches 60MPa, the growth rate of ultimate eccentrical compression bearing capacity begins to slow down. All specimens show good ductility and bearing capacity.

FIGURE 11

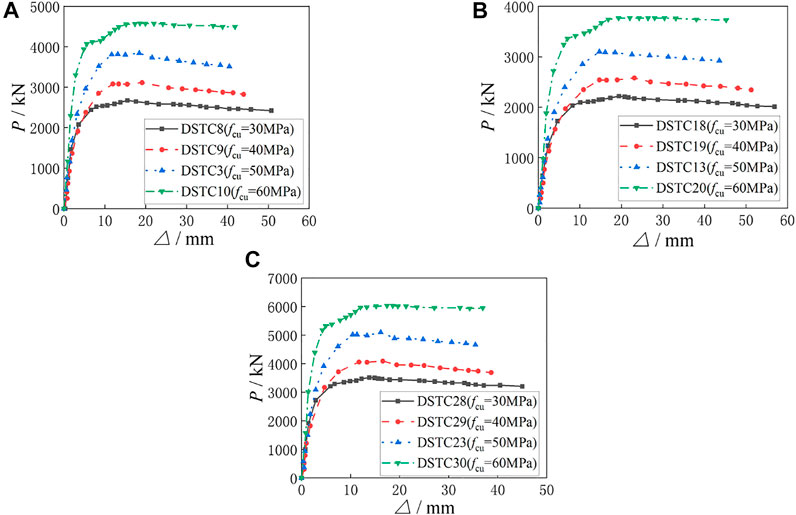
FIGURE 11. Comparisons of load-displacement curves of specimens with different concrete strengths. (A) Load-displacement curves of group A specimens. (B) Load-displacement curves of group B specimens. (C) Load-displacement curves of group C specimens.

TABLE 8

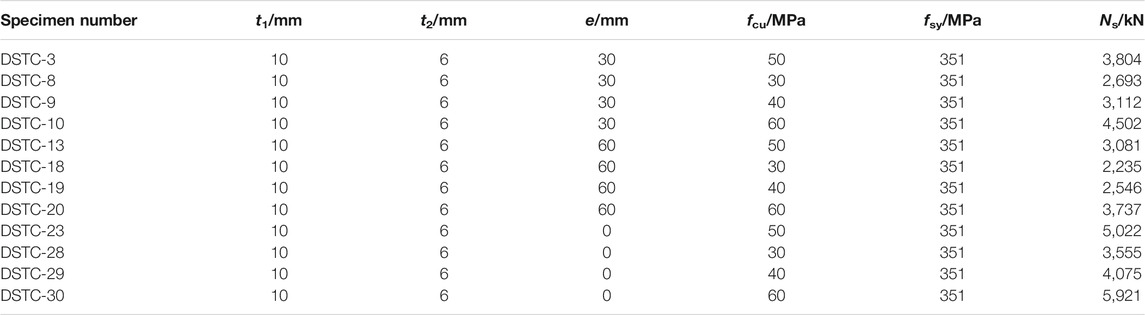
TABLE 8. Ultimate eccentrical compression bearing capacity of specimens with different compressive strengths of concrete cubes.

Eccentricity(e)

The comparisons of the ultimate eccentrical compression bearing capacity of multiple groups of specimens with eccentricities of 0, 30 and 60 mm are shown in Figure 12. It can be seen from Figure 12 that eccentricity was an essential part in the ultimate eccentrical compression bearing capacity of specimens. With the increasing of eccentricity, the ultimate eccentrical compression bearing capacity decreases gradually. Taking Figure 12A as an example, when t₁ is 6 mm and e increases from 0 to 30mm and 60 mm respectively, N_s decreases from 3932 to 2979kN and 2472kN in turn, which decreases by 32 and 59%, respectively. When t₁ is 8 mm and e increases from 0 to 30mm and 60 mm respectively, N_s decreases from 4404 to 3336kN and 2736kN in turn, which decreases by 32.4 and 60.7%, respectively. When t₁ is 10 mm and e increases from 0 to 30mm and 60 mm, respectively, N_s decreases from 5022 to 3804kN and 3081kN in turn, which decreases by 32.1 and 63.0%, respectively. When t₁ is 12 mm and e increases from 0 to 30mm and 60 mm, respectively, N_s decreases from 6051 to 4564kN and 3698kN in turn, which decreases by 42.4 and 75.8%, respectively. To sum up, the eccentricity can be regarded as the most important factor affecting the ultimate eccentrical compression bearing capacity of the specimens.

FIGURE 12

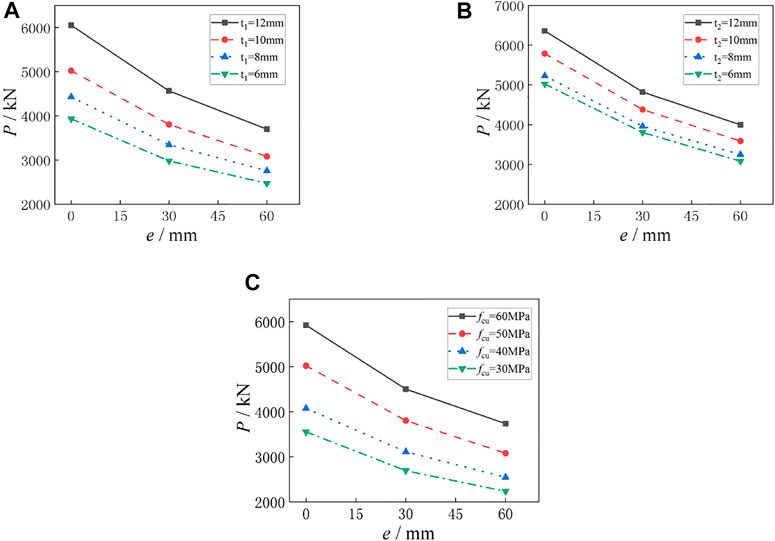
FIGURE 12. Comparisons of ultimate bearing capacity of specimens with different eccentricities. (A) Specimens with different GFRP thicknesses. (B) Specimens with different steel tube thicknesses. (C) Specimens with different concrete strengths.

Slenderness ratio (λ)

The comparisons of load-displacement curves of specimens with different slenderness ratios are shown in Figure 13. It can be seen that the initial stiffness of the specimen decreases gradually with the increasing of slenderness ratio, and with the increasing of load, the curve deviates further and further from the coordinate axis, and the specimens have low ultimate eccentrical compression bearing capacity. As can be seen from Figure 13, when the slenderness ratio of the specimens increases from 6 to 7, 8 and 9, respectively, the ultimate eccentrical compression bearing capacity of the specimens decreases from 3804 KN to 3202, 2837 and 2689 KN in turn, which decreases by 15.8, 25.4 and 29.3%, respectively. It can be concluded that with the increasing of slenderness ratio, the ultimate eccentrical compression bearing capacity of the specimens decreases gradually and the decreasing amplitude becomes smaller and smaller, but the load-holding capacity becomes better and better.

FIGURE 13

FIGURE 13. Comparisons of load-displacement curves for specimens with different slenderness ratios.

Force Mechanism

The partial pressure (N)-deformation (Δ) characteristic curve of hollow GFRP pipe-concrete-high strength steel tube composite long column subjected to eccentric compression is shown in Figure 14. At the initial loading stage, N is small and the specimen is at the elastic stage (OA segment). The longitudinal inhomogeneous compressive strain of the composite column section basically maintains a linear relationship, which conforms to the plane-section assumption. With the increasing of N, the curve gradually deviates from the ordinate, and the stiffness of the specimen decreases, then the specimen enters the elastic-plastic stage (AB segment). The longitudinal inhomogeneous compressive strain of the composite column section increases gradually, but it still conforms to the plane-section assumption. With the further increasing of N, the radial strain of sandwich concrete is greater than that of steel tube and GFRP pipe, then the deformation of concrete starts to be constrained by steel tube and GFRP pipe, which shows that the specimen enters the plastic stage (BC segment) (Yu and Hu, 2014; Zhang et al., 2015; Shen, 2019). The sandwich concrete is under triaxial compression. The outer GFRP pipe is under radial compression and hoop tension, while the inner steel tube is subjected to both radial and hoop compression, and the micro-stress state of the cross-section element is shown in Figure 15. After the peak compression load, the axial strain of GFRP pipe and steel tube at the lower compression side changes from compressive strain to tensile strain, and the steel tube at the larger compression side yields, resulting in outer bulging deformation of specimen. Then, the specimen enters the load-holding stage (CD segment), finally the GFRP pipe at the mid-span compression side of the long column breaks circumferentially. The restraint effect on the concrete disappears, and the specimen is declared to fail. All specimens show good load-holding capacity and deformation capacity. The failure process of specimens presents certain characteristics, which belongs to ductile failure.

FIGURE 14

FIGURE 14. Typical N-Δ curve.

FIGURE 15

FIGURE 15. Micro-stress state of section element. (A) GFRP pipe. (B) Concrete. (C) Steel tube.

Eccentric Compression Bearing Capacity Formula of Hollow GFRP Pipe-Concrete-High Strength Steel Tube Composite Long Columns

Since slenderness ratio and eccentricity have significant influence on the eccentric compression bearing capacity of hollow GFRP pipe -concrete-high strength steel tube composite long columns, the empirical coefficient method is adopted. Referred to the calculation formula of single-pillar bearing capacity in “Specification for Design and Construction of Concrete-filled Steel Tube Structures” (CECS28-90) (National Standards of the People’s Republic of China CECS28:901990), the calculation formula of the eccentric compression bearing capacity of hollow GFRP pipe-concrete-high strength steel tube composite long columns is given as follows:

$N_u={\phi }_l{\phi }_e{N}_0(16)$

Where, $N_u$ is the ultimate bearing capacity of the eccentric compression columns; ${\phi }_l$ is the reduction coefficient of bearing capacity considering slenderness ratio; ${\phi }_e$ is the reduction coefficient of bearing capacity considering eccentricity; $N_0$ is the ultimate axial compression capacity of hollow FRP-concrete-steel tube composite short columns.

The formula proposed in literature (Qian and Liu, 2006) is adopted as the calculation formula of axial compression capacity and slenderness ratio reduction coefficient of hollow GFRP pipe-concrete-steel tube composite short columns:

$N_0=f_{cc,m}^{\prime }{A}_c+f_{ay}{A}_a(17)$

Where, $f_{cc,m}^{\prime }$ is the peak stress of concrete, and $f_{ay}$ is the yield compressive strength of steel tube, and $A_{\text{c}}$ is the cross-sectional area of concrete, and $A_{\text{a}}$ is the cross-sectional area of steel tube.

When the steel tube diameter-thickness ratio is greater than 20 for composite columns, $f_{cc,m}^{\prime }=f_{cc,fs}^{\prime }$ is taken in the reference (Qian and Liu, 2006), where $f_{cc,fs}^{\prime }$ can be expressed by the following formula:

$f_{cc,fs}^{\prime }=\lambda f_{cc\left(solid\right)}^{\prime }(18)$

Where, A is the influencing factor considering the hollow ratio and the steel tube diameter-thickness ratio. Hollow ratio $K_V=D_a/D_0$, $D_a$ is the outer diameter of the steel tube, $D_{\text{O}}$ is the inner diameter of GFRP pipe, $f_{cc\left(core\right)}^{\prime }$ is the peak strain of the GFRP pipe confined core concrete. When $f_l/f_c\le 2.3$, core concrete peak strain of the GFRP pipe can be calculated by Eq. 19. $f_l/f_c$ is the fiber characteristic value of GFRP pipe confined concrete. When the laminate theory is used to study the material properties of the GFRP pipe at the axial and hoop directions, the formula $f_l=2f_{h,frp}/\text{D}$ can be adopted. $f_{h,frp}$ is the hoop tensile strength of the GFRP pipe, and $t_{frp}$ is the thickness of GFRP pipe, and $f_c$ is the axial compressive strength of concrete. If the steel tube diameter-thickness ratio is greater than 20, $\lambda ={\lambda }_v$, and ${\lambda }_v$ is the influencing factor considering the hollow ratio. When ${\lambda }_v<0.848$, ${\lambda }_{\text{v}}$ = 0.848. ${\lambda }_{\text{v}}$ can be calculated by Eq. 20:

$f_{cc\left(core\right)}^{\prime }=\left[1+2.91f_l/f_c-0.587{\left(f_l/f_c\right)}^2\right]f_c(19)$

${\lambda }_{\text{v}}=1+0.062k_{\text{V}}-0.74k_{\text{V}}^2(20)$

In the literature (Qian and Liu, 2006), experimental data is used to fit the reduction coefficient ${\phi }_l$ considering the slenderness ratio, and its expression is as follows:

${\phi }_l=1-0.11\sqrt{L_0/r-6}(21)$

Where, $L_0/r$ is the slenderness ratio.

In order to consider the reduction factor of eccentricity, the calculation formula is used as follows:

${\phi }_e=\frac{1}{1+c\frac{e_0}{r_c}}(22)$

Where, $e_0$ is the initial eccentricity of the eccentric composite columns; $r_c$ is the radius of the core concrete; c in Eq. 22 can be obtained by regression of the experimental data in the literature (Cao, 2013), and its calculation formula is as follows:

$c=-0.484+3.679\left(\frac{e_0}{r_c}\right)(23)$

The Eqs 17, 21, 22 are taken into Eq. 16 to obtain Eq. 24, and the calculation formula for the eccentric compression bearing capacity of the hollow GFRP pipe-concrete-high strength steel tube composite long columns is obtained.

$N_u=1-0.11\sqrt{\frac{L_0}{r}-6}\cdot \frac{1}{1+c\frac{e_0}{r_c}}\cdot \lambda f_{cc\left(solid\right)}^{\prime }{A}_C+f_{ay}{A}_a(24)$

The Eq. 24 is used to calculate the ultimate eccentric compression bearing capacity ($N_u$) of 33 composite long columns, as shown in Table 9 and Figure16. By comparing with the simulation results (N_s), it can be seen that the maximum error (Error_max) between the simulation and calculation is 10.5%, which can meet the engineering accuracy requirements.

TABLE 9

TABLE 9. Comparisons of N_s and N_u for 33 composite columns.

FIGURE 16

FIGURE 16. Comparisons of simulated and calculated bearing capacity of DSTC composite columns.

Conclusion

The finite element models of 33 hollow GFRP pipe-concrete-high strength steel tube composite long columns are established by finite element software ABAQUS, and the eccentric compression behavior analysis of the composite long columns is carried out. The load-displacement curves of the specimens can be obtained during the whole process. The influence regularity of the different parameters on the ultimate eccentric compression bearing capacity of specimens can be clarified. The specific conclusions can be drawn as follows:

1) Based on the stress-hardening double-line elastic-plastic constitutive model for steel, line elastic constitutive model for GFRP and constitutive model for confined concrete, the contact element is introduced to simulate the hollow GFRP pipe-concrete-high strength steel tube composite long columns. The load-displacement curves obtained from the tests and simulations are compared and the rationality of constitutive models and finite element modeling method can be verified.

2) With the increasing of the thickness of GFRP pipe and steel tube, the ultimate eccentric compression bearing capacity of specimens increases gradually. Under the double-layer constraint of GFRP pipe and steel tube, concrete can be under a state of triaxial compression. It can be seen that GFRP pipe has a significant constraint effect on concrete. With the increasing of the compressive strength of the cube concrete, the ultimate eccentric compression capacity of the specimens increases gradually. However, when the compressive strength of cube concrete reaches 60Mpa, the growth rate of ultimate eccentric compression capacity begins to slow down. The greater the eccentricity is, the greater the ultimate displacement of specimens is. However, the ultimate eccentrical compression bearing capacity decreases with the increasing of the eccentricity. The eccentricity can be regarded as the most important factor affecting the eccentric compression capacity of the specimens. With the increasing of slenderness ratio, the ultimate eccentric compression capacity decreases gradually.

3) The load-displacement curves of the composite long columns consist of four stages of elastic, elastoplastic, plastic and load-holding. Due to the restraint of GFRP pipe on concrete, the bearing capacity and deformation capacity of the specimens can be improved. When the specimens fail, due to the hoop fracture of GFRP pipe, the restraint effect on concrete disappears, and the specimens lose bearing capacity and fail. All specimens show good load-holding capacity and deformation capacity. The failure process of specimen presents certain characteristics, which belongs to ductile failure.

4) Based on the empirical coefficient method, the calculation formula of the eccentric compression bearing capacity of hollow GFRP pipe-concrete-high strength steel tube composite long columns can be obtained by statistical regression. It can provide theoretical support for the application of this kind of composite columns in practical engineering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

JJ and WZ: writing, simulation; RW, HR, LZ, YL, LH, and CY: translation; LJ: simulation. All authors contributed to the article and approved the submitted version.

Funding

The authors are grateful the financial support received from the National Natural Science Foundation of China (Grant No. 51808173); The Natural Science Foundation of Heilongjiang Province (Grant No. LH 2020E018); Opening Fund for Key Laboratory of The Ministry of Education for Structural Disaster and Control of Harbin Institute of Technology (Grant No. HITCE201908); The Social Science Foundation of Hebei Province (Grant No. HB20GL055); the Northeast Petroleum University Guided Innovation Fund (Grant No.2020YDL-02) and the Research on Risk Identification and Emergency Management of Buildings from the Perspective of COVID-19 (Grant No. SQ2021115).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelkarim, O. I., and ElGawady, M. A. (2016). Behavior of Hollow FRP-concrete-steel Columns under Static Cyclic Axial Compressive Loading. Eng. Structures 123, 77–88. doi:10.1016/j.engstruct.2016.05.031

CrossRef Full Text | Google Scholar

Abdelkarim, O. I., Mohamed, A. E., Gheni, A., Anumolu, S., and Abdulazeez, M. (2016). Seismic Performance of Innovative Hollow-Core FRP-concrete-steel Bridge Columns. J. Bridge Eng. 2, 04016120. doi:10.1061/(ASCE)BE.1943-5592.0000985

CrossRef Full Text | Google Scholar

Afifi, M. Z., Mohamed, H. M., and Benmokrane, B. (2015). Theoretical Stress-Strain Model for Circular concrete Columns Confined by GFRP Spirals and Hoops. Eng. Structures 102, 202–213. doi:10.1016/j.engstruct.2015.08.020

CrossRef Full Text | Google Scholar

Ahmed, M., Liang, Q. Q., Patel, V. I., and Hadi, M. N. S. (2018). Nonlinear Analysis of Rectangular Concrete-filled Double Steel Tubular Short Columns Incorporating Local Buckling. Eng. Structures 175, 13–26. doi:10.1016/j.engstruct.2018.08.032

CrossRef Full Text | Google Scholar

AlAjarmeh, O. S., Manalo, A. C., Benmokrane, B., Karunasena, W., Mendis, P., and Nguyen, K. T. Q. (2019). Compressive Behavior of Axially Loaded Circular Hollow Concrete Columns Reinforced with GFRP Bars and Spirals. Construction Building Mater. 194, 12–23. doi:10.1016/j.conbuildmat.2018.11.016

CrossRef Full Text | Google Scholar

Cao, P. P. (2013). Mechanical Behavior of Steel-Encased Concrete Filled FRP Tube Column under Unidirectional Eccentric Compression. Shenyang: Shenyang Jianzhu University.

Cheng, S. (2016). Behavior of Hybrid Columns of Concrete-filled Square Steel Tube with FRP-Confined Concrete Core under Axial Compression and Seismic Loading. Beijing: Tsinghua University.

Ekmekyapar, T., and Al-Eliwi, B. J. M. (2017). Concrete Filled Double Circular Steel Tube (CFDCST) Stub Columns. Eng. Struct 135, 68–80. doi:10.1016/j.engstruct.2016.12.061

CrossRef Full Text | Google Scholar

Feng, P., Cheng, S., Bai, Y., and Ye, L. (2015). Mechanical Behavior of Concrete-filled Square Steel Tube with FRP-Confined Concrete Core Subjected to Axial Compression. Compos. Struct 123, 312–324. doi:10.1016/j.compstruct.2014.12.053

CrossRef Full Text | Google Scholar

Fernando, D., Teng, J., Gattas, J., and Heitzmann, M. (2018). Hybrid Fibre-Reinforced Polymer-Timber Thin-Walled Structural Members. Adv. Struct. Eng. 21, 1409–1417. doi:10.1177/1369433217739709

CrossRef Full Text | Google Scholar

Han, L. H., Tao, Z. C., and Liu, W. (2001). Concrete Filled Steel Tubular Structures from Theory to Practice. J. Fuzhou Univ. (Natural Sci. Edition) 6, 24–34.

Google Scholar

Idris, Y., and Ozbakkaloglu, T. (2014). Flexural Behavior of FRP-HSC-Steel Composite Beams. Thin-Walled Struct 80, 207–216. doi:10.1016/j.tws.2014.03.011

CrossRef Full Text | Google Scholar

Ji, J., Song, H., Jiang, L., Ren, H., Zhang, Y., and Liu, Y. (2021b). Tensile Performance of High Ductility Cementitious Composites with Recycled Powder from C&D Waste. Front. Mater. 8, 1–8. doi:10.3389/FMATS.2021.673752

CrossRef Full Text | Google Scholar

Ji, J., Xu, Z., Jiang, L., Yuan, C., Zhang, Y., Zhou, L., et al. (2018). Nonlinear Buckling Analysis of H-type Honeycombed Composite Column with Rectangular Concrete-Filled Steel Tube Flanges. Int. J. Steel Struct. 18, 1153–1166. doi:10.1007/s13296-018-0084-0

CrossRef Full Text | Google Scholar

Ji, J., Yang, M., Xu, Z., Jiang, L., and Song, H. (2021c). Experimental Study of H-Shaped Honeycombed Stub Columns with Rectangular Concrete-filled Steel Tube Flanges Subjected to Axial Load. Adv. Civil Eng. 2021, 1–18. doi:10.1155/2021/6678623

CrossRef Full Text | Google Scholar

Ji, J., Yu, D. Y., and Jiang, L. Q. (2020). Research on Axial Compression Bearing Capacity of Different-Strength Concrete Filled Double Steel Tube Short Columns. Building Struct. 50, 121–129. doi:10.19701/j.jzjg.2020.05.021

CrossRef Full Text | Google Scholar

Ji, J., Zhang, R., Yu, C., He, L., Ren, H., and Jiang, L. (2021a). Flexural Behavior of Simply Supported Beams Consisting of Gradient Concrete and GFRP Bars. Front. Mater. 8, 1–14. doi:10.3389/FMATS.2021.693905

CrossRef Full Text | Google Scholar

Mander, J. B., Priestley, M. J. N., and Park, R. (1988). Theoretical Stress‐Strain Model for Confined Concrete. J. Struct. Eng. 114, 1804–1826. doi:10.1061/(asce)0733-9445(1988)114:8(1804)

CrossRef Full Text | Google Scholar

National Standards of the People's Republic of ChinaCECS28:90 (1990). Specification for Design and Construction of Concrete-filled Steel Tubular Structures. Beijing: China Architecture & Building Press.

Pagoulatou, M., Sheehan, T., Dai, X. H., and Lam, D. (2014). Finite Element Analysis on the Capacity of Circular Concrete-filled Double-Skin Steel Tubular (CFDST) Stub Columns. Eng. Structures 72, 102–112. doi:10.1016/j.engstruct.2014.04.039

CrossRef Full Text | Google Scholar

Qian, J. R., and Liu, M. X. (2006). Experiment of FRP-concrete-steel Double-Skin Tubular Long Columns under Axial Compressive Load, Concrete, 9, 31–34. CNKI:SUN:HLTF.0.2006-09-009.

Google Scholar

Qian, J. R., Zhang, Y., and Zhang, W. J. (2015). Eccentric Compressive Behavior of High Strength Concrete Filled Double-Tube Short Columns. J. Tsinghua Univ. (Natural Sci. Edition) 1, 1–7. doi:10.16511/j.cnki.qhdxxb.2015.01.001

CrossRef Full Text | Google Scholar

Shen, Q. H. (2019). Research on the Eccentric Compressive Behavior of CFRP Partially-Wrapped Circular CFST Stub Columns. Ind. Construction 49, 192–199. doi:10.13204/j.gyjz201910032

CrossRef Full Text | Google Scholar

Teng, J.-G., Wang, Z., Yu, T., Zhao, Y., and Li, L.-J. (2018). Double-tube concrete Columns with a High-Strength Internal Steel Tube: Concept and Behaviour under Axial Compression. Adv. Struct. Eng. 21, 1585–1594. doi:10.1177/1369433217746838

CrossRef Full Text | Google Scholar

Teng, J. G., Yu, T., Wong, Y. L., and Dong, S. L. (2007). Hybrid FRP-concrete-steel Tubular Columns: Concept and Behavior. Construction Building Mater. 21, 846–854. doi:10.1016/j.conbuildmat.2006.06.017

CrossRef Full Text | Google Scholar

Wang, H.-P., Ni, Y.-Q., Dai, J.-G., and Yuan, M.-D. (2019b). Interfacial Debonding Detection of Strengthened Steel Structures by Using Smart CFRP-FBG Composites. Smart Mater. Struct. 28, 115001. doi:10.1088/1361-665X/ab3add

CrossRef Full Text | Google Scholar

Wang, H., and Dai, J.-G. (2019a). Strain Transfer Analysis of Fiber Bragg Grating Sensor Assembled Composite Structures Subjected to thermal Loading. Composites B: Eng. 162, 303–313. doi:10.1016/j.compositesb.2018.11.013

CrossRef Full Text | Google Scholar

Xu, P. (2013). Experimental Study on Capacity of FRP-concrete-steel Double-Skin Tubular Columns. Zhejiang: Zhejiang University.

Yu, D. Y. (2020). Research on Axial Compression and Seismic Performance of Solid-Web GFRP-concrete-steel Tube Composite Column. Daqing: Northeast Petroleum University. doi:10.26995/d.cnki.gdqsc.2020.000549

CrossRef Full Text

Yu, T., Hu, Y. M., and Teng, J. G. (2014). FRP-confined Circular Concrete-filled Steel Tubular Columns under Cyclic Axial Compression. J. Constructional Steel Res. 94, 33–48. doi:10.1016/j.jcsr.2013.11.003

CrossRef Full Text | Google Scholar

Zhang, B., Teng, J. G., and Yu, T. (2015). Experimental Behavior of Hybrid FRP-concrete-steel Double-Skin Tubular Columns under Combined Axial Compression and Cyclic Lateral Loading. Eng. Struct 99, 214–231. doi:10.1016/j.engstruct.2015.05.002

CrossRef Full Text | Google Scholar

Zhang, H. X., Liu, H., and Sun, Y. J. (2017). Analysis of Bearing Capacity of Steel-Encased Concrete Filled GFRP Tubes Middle-Long Column Subject. J. Hefei Univ. Tech. (Natural Sci. Edition) 7, 965–970. doi:10.3969/j.issn.1003-5060.2017.07.020

CrossRef Full Text | Google Scholar