Broadband Bidirectional and Multi-Channel Unidirectional Acoustic Insulation by Mode-Conversion Phased Units

The technique of sound insulation has a wide range of potential applications in environment noise control and architectural acoustics. The rapid development of acoustic artificial materials has provided alternative solutions to design sound insulation structures. However, the realization of single-layer planar structures with bidirectional acoustic insulation (BAI) and unidirectional acoustic insulation (UAI) still poses a challenge. Here, we report the theoretical and experimental realization of two types of single-layer phased array lenses which presents the characteristics of broadband BAI and multi-channel UAI. Both types of lenses consist of 12 mode-conversion phased units which are composed of two types of unit cells (I and II) with an opposite phase and a step waveguide. Based on the phase regulation, the designed phased unit can realize the mode conversion between the zero-order and first-order waves and asymmetric sound manipulation, which enables multi-functional sound insulations. Based on the desired theoretical phase profiles, two types of lenses with BAI and UAI are realized for the incidence of the zero-order wave, and their fractional bandwidths can reach about 0.28 and 0.37, respectively. More interestingly, the UAI effect can be reversed for the incidence of the first-order wave. The proposed lenses based on the mode-conversion phased units have the advantages of single-layer planar structure, multi-functional sound insulation, and broad bandwidth, which have wide application prospect.

Introduction

The technique of sound insulation has attracted more and more attentions from both physics and engineering communities due to its wide potential applications in environment noise control and architectural acoustics. In the past decades, with the rapid development of sonic crystals (Liu et al., 2000; Torrent and Sanchez-Dehesa, 2018; Xia et al., 2018a; Yang et al., 2019) and acoustic metamaterials (Liang ad Li, 2012; Gusev and Wright, 2014; Quan et al., 2014; Cheng et al., 2015; Liu et al., 2018; Zhang et al., 2019; Cheng et al., 2019), several linear structures with the characteristic of unidirectional acoustic insulation (UAI) are realized based on different mechanisms, including sound gratings with diffraction mechanism (Li et al., 2011; He et al., 2011; Li et al., 2014; Sun et al., 2015; Zhang et al., 2016), sonic crystals with band gap property (Li et al., 2011; Huang et al., 2016; Oh et al., 2012; Yuan et al., 2012), and near-zero-index metamaterials with abnormal refraction (Li et al., 2013; Shen et al., 2016; Song et al., 2017), and so on. In addition to these structures, acoustic metasurfaces (Li et al., 2013; Xie et al., 2014; Tang et al., 2014; Mei and Wu, 2014; Tian et al., 2017; Assouar et al., 2018; Tian et al., 2019; Quan and Alù, 2019; Holloway et al., 2019; Allen et al., 2020) also provide rich possibilities to design advanced structures of sound insulation owing to its characteristics of planar structure and subwavelength thickness. By attaching a pair of metasurface structures on the inner boundary of the waveguide structures, several types of tunnels (Zhu et al., 2016) and windows (Ge et al., 2018; Ge et al., 2019) with the properties of UAI and bidirectional acoustic insulation (BAI) are realized continuously, which have practical applications in architectural acoustics and duct noise control. Furthermore, in the case of free space, dual-layer metasurfaces (Xia et al., 2018b) with asymmetric phase modulation, lossy metasurfaces (Li et al., 2017) and coding metasurfaces (Xie et al., 2017) are designed to realize UAI (Jiang et al., 2016; Wang et al., 2019). However, the realization of a single-layer phased array structure with BAI and UAI still remains a great challenge.

To overcome it, we experimentally demonstrate two types of single-layer phased array lenses composed of 12 mode-conversion phased units with the characteristics of broadband BAI and multi-channel UAI, in which each phased unit is composed of two types of unit cells (I and II) with an opposite phase and a step waveguide. Based on the phase regulation, the designed phased unit can realize the mode conversion between the zero-order and first-order waves and acoustic asymmetric modulation (AAM), enabling the realization of multi-functional sound insulations. By arranging the phased units based on the theoretical phase profiles, two types of lenses with BAI and UAI are obtained separately for the incidence of the zero-order wave, and their fractional bandwidths can reach about 0.28 and 0.37, respectively. More interestingly, for the incidence of the first-order wave, the UAI effect can be reversed. The measured and simulated results match with each other well.

Design and Performance of Mode-Conversion Phased Unit

Design of Mode-conversion Phased Unit

To construct a phased unit with the mode-conversion characteristic, we propose a type of unit cell composed of different numbers (N) of V-shaped structures (Lan et al., 2017), which is schematically shown in Figure 1A. The structure parameters are selected as l = 30 mm, h = 5.5 mm, t = 0.5 mm, and d = 0.25 mm, and its opening angle is determined by the values of N, and Throughout this work, we adopt the COMSOL Multiphysics software to numerically simulate the sound insulation. The unit cells are fabricated with epoxy resin to satisfy the sound hard-boundary condition. In the numerical models, the material parameters are used as follows, the density ρ = 1,180 kg/m³ and the sound velocity c = 2,720 m/s for epoxy resin; ρ = 1.21 kg/m³ and c = 343 m/s for air.

FIGURE 1

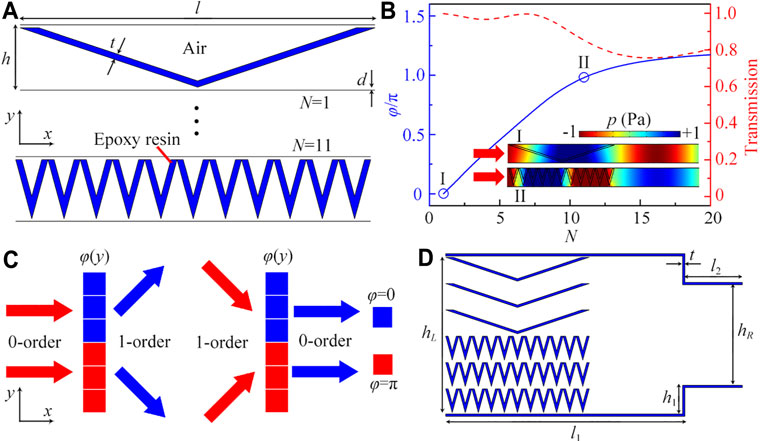
FIGURE 1. (A) Schematic of the unit cells composed different number (N) of V-shaped structures. The total length l of each unit cell is the same, and the opening angle of the V-shaped structure is determined by the values N. (B) Transmission spectrum and phase delays of the unit cell as the function of N at 7.1 kHz, which are displayed as red dashed line and blue solid line, respectively. Two insets are the pressure distributions created by the unit cells I and II. (C) Schematic of mode conversion of sound created by a phased unit composed of 6 unit cells (I and II). Red and blue solid arrows are the incident and transmitted acousitc waves, respectively. (D) Schematic of a mode-conversion phased unit.

Figure 1B shows the transmission spectrum and phase delay φ of the unit cells with different values of N at 7.1 kHz. We can see that, with the increase of N, the phase delay increases gradually, and their transmission coefficients exceed 0.7. Based on the conversion theory between the zero-order and first-order waves in a waveguide (see the Supplementary Material), we select two unit cells I and II (open blue circles) with a phase difference of π to design a mode-conversion phased unit, in which the selected values of N for the unit cells I and II are 1 and 11, and their transmission coefficients are about 0.99 and 0.85, respectively. Two insets in Figure 1B are the pressure distributions created by the unit cells I and II, separately, further demonstrating that the phase difference of both unit cells is π.

Here, it is worthy to mention that the zero-order wave can transmit through a straight waveguide without the restrictions of width. However, for the first-order wave, it can only pass through the waveguide with a width larger than a half wavelength due to a cut-off frequency of higher-order waves. Based on the desired phase profile for the mode conversion between the two types of waves (see the Supplementary Material), we can design a mode-conversion phased unit composed of 6 unit cells I and II, and its total width is 33 mm, satisfying the propagation of the first-order wave at 7.1 kHz. As shown in Figure 1C, the zero-order wave can transmit through the phased unit and convert to the first-order wave. Similarly, the first-order wave can also convert to the zero-order wave, indicating that the proposed phased unit can realize the mode conversion between the two types of waves. Here, it is noted that the first-order wave in Figure 1C is represented by two plane sound beams with the angles of ±45° with respect to the x axis. This is because the first-order wave in the waveguide with the width of 33 mm is formed as the zigzag propagation of the plane wave with the angle of 45° (see the Supplementary Material). Beyond that, to obtain the property of sound insulation, we introduce a step waveguide placed on the right side of the phased unit (Figure 1D), in which its width h_R = 21 mm is smaller than a half wavelength of sound at 7.1 kHz. Thus, the first-order wave is prohibited to pass through the step waveguide owing to the cutoff frequency. The parameters of the phased unit are selected as l₁ = 50 mm, l₂ = 12 mm, h₁ = 6 mm, h_L = 33 mm, and t = 0.5 mm.

AAM Based on Mode Conversion

The proposed phased unit has a typical characteristic of AAM based on the mode conversion. To clearly show this, we present the propagation paths in the phased unit for the incidence of the zero-order wave. The abbreviations LI and RI refer to the sound incidence from the left and right sides of the phased unit, respectively. As shown in Figures 2A,B, the zero-order wave can transmit through the phased unit and is converted to the first-order wave for RI. However, owing to its cutoff frequency of the first-order wave, it cannot pass through the step waveguide for LI. Figures 2C,D show the pressure distributions created by the phased unit under the incidence of the zero-order wave for LI and RI, respectively. The simulated pressure distributions agree well with the propagation paths shown in Figures 2A,B, showing high performance of AAM based on the mode conversion. We also simulate the reflected pressure distribution under the incidence of the zero-order wave for LI, and the results show that most of sound energy is reflected back to the incident region, which is shown in the Supplementary Material.

FIGURE 2

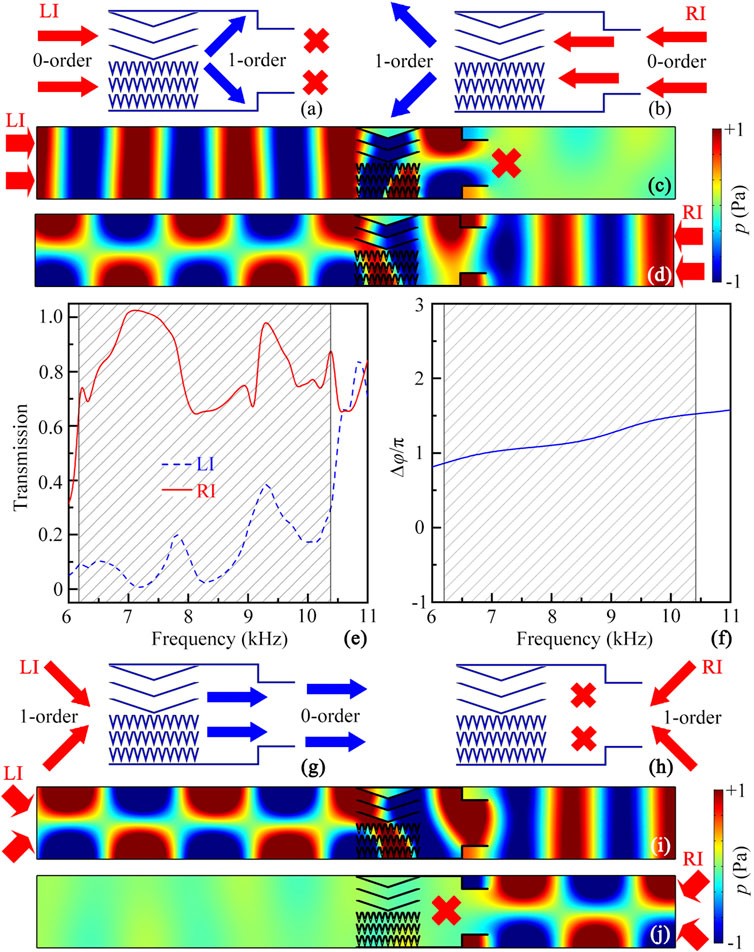
FIGURE 2. Schematic of the propagation paths through the mode-conversion phased unit under the incidence of the zero-order wave for (A) LI and (B) RI. Simulated pressure distributions created by the phased unit under the incidence of the zero-order wave for (C) LI and (D) RI at 7.1 kHz. Red solid arrows in (A–D) represent the incident zero-order wave. (E) Simulated transmission spectra through the mode-conversion phased unit under the incidence of the zero-order wave for LI (blue dashed line) and RI (red solid line). (F) Simulated phase difference spectrum of both unit cells I and II. Black shaded region (6.2–10.4 kHz) represents the working band of the AAM. Schematic of propagation paths through the phased unit for the incidence of the first-order wave for (G) LI and (H) RI. Simulated pressure distributions created by the phased unit under the incidence of the first-order wave for (I) LI and (J) RI at 7.1 kHz. Red solid arrows in (G–J) represent the incident first-order wave.

Figure 2E shows the transmission spectra through the phased unit. It is observed that, in the range of 6.2–10.4 kHz (black shaded region), the transmission coefficients are larger than 0.65 for RI, but those are lower than 0.4 for LI, showing the obvious characteristics of AAM. Thus, the bandwidth of the phased unit is about 4.2 kHz, and the fractional bandwidth is about 0.5 (viz., the center frequency is 8.3 kHz), which is much wider than that of previous AAM devices based on phase modulation. To explain it, we simulate the phase spectra of the unit cells I and II, separately, and display the phase difference spectrum of both types of units in Figure 2F. Note that, in the working band of the phased unit (black shadow region), the phase difference is in the range from 0.82π to 1.52π, which is around the value of π. Therefore, we deduce that the broadband characteristic of the proposed phased unit arises from the stable phase difference of both types of unit cells around 7.1 kHz.

Moreover, for the incidence of the first-order wave (Figures 2G,H), the characteristics of the mode conversion and sound transmission created by the phased unit are opposite to those for the incidence of the zero-order wave (Figures 2A,B). Additionally, the simulated pressure distributions under the incidence of the first-order wave for LI and RI match well with the corresponding propagation paths shown in Figures 2G,H, showing the characteristic of the reversed AAM based on the incidence of the first-order wave. In addition to the mode conversion between the zero-order and first-order waves, we can realize the mode conversion between the zero-order and other high-order waves by designing different phase profiles, which is shown in the Supplementary Material.

Design and Performances of Phased Array Lens

Based on the mode-conversion phased unit, we design two types of phased array lenses with two types of sound insulation effects, such as BAI, UAI and reversed UAI. Compared with other types of sound insulation lenses based on the phase modulation (Song et al., 2016; Zhao et al., 2017; Yu et al., 2019), the proposed lenses have the typical advantages of single-layer planar structure, multi-functional sound insulation, and broad bandwidth.

Design and Performances of BAI Lens

First, we use 12 phased units with 72 unit cells (I and II) to design a phased array lens with BAI, in which its photograph is shown in Figure 3A. By using the phase modulation of 72 unit cells, we can realize the lens of BAI with high performance. As shown in Figure 3B, for RI, the zero-order wave is converted to the surface wave based on the phase modulation of 72 unit cells, and thus the acoustic wave cannot reach the far field of the left side. To realize this, by using the generalized Snell’s law (Yu et al., 2011), the theoretical phase profile can be written as

$\phi \left(y\right)=k_0\left|y\right|.(1)$

where k₀ = 2πf/c is the wave number in air, and these parameters are selected as f = 7.1 kHz and c = 343 m/s. Based on Eq. 1, we calculate the theoretical continuous phase profile of the lens, which is shown in the Supplementary Material. By arranging the positions of 12 phased units with 72 discrete phase delays based on the theoretical phase profile, we can realize the conversion between the zero-order wave and surface wave. Here, there exist solid parts between the phased units for the BAI lens (shown in Figure 3A), this is because the phase distribution of the phased unit and the theoretical continuous profile do not agree with each other, and thus the solid parts made of epoxy resin are used to connect the phased units. However, for LI (Figure 3C), the converted first-order wave is prohibited by the step waveguide in the phased units owing to its cutoff frequency.

FIGURE 3

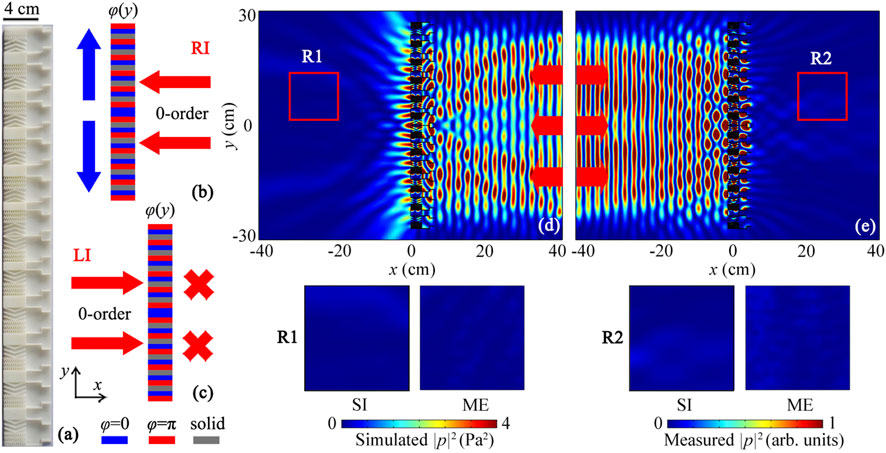
FIGURE 3. (A) Photograph of the BAI lens composed of 12 phased units. The solid parts are epoxy resin which is used to connect the phased units. Schematic of propagation paths through the BAI lens under the incidence of the zero-order wave for (B) RI and (C) LI. Simulated intensity distributions created by the BAI lens under the incidence of the zero-order wave for (D) RI and (E) LI at 7.1 kHz. Red solid arrows in (B–E) are the zero-order wave. Four insets on the bottom are the simulated (SI) and measured (ME) intensity distributions in red open squares R1 and R2.

To show the BAI performance, we simulate the intensity distributions created by the lens for LI and RI, in which the BAI effect is observed for both cases in the far field. As shown in Figure 3D, for RI, the acoustic wave can pass through the lens, but the sound energy is confined on the lens surface, forming as the surface mode. So, we observe that the sound energy in the far field on the left side is very weak. However, for LI (Figure 3E), the incident zero-order wave is converted to the first-order wave, and the sound energy is confined into the step waveguide of each phased unit. In this case, the sound energy in both near and far fields on the right side is very weak. Compared with the result for RI, the performance of sound insulation is better for LI. Therefore, we can realize the BAI based on two distinct mechanisms. To experimentally verify it, we measure the intensity distributions for RI and LI in red open squares R1 and R2. The description of the experiment setup is presented in the Supplementary Material. As shown in four insets in the bottom of Figures 3D,E, the measured results match well with the corresponding simulations, further demonstrating high BAI performance of the lens.

To display the bandwidth of the BAI lens, we simulate and measure its transmittance spectra for LI and RI, which is shown in Figure 4. Here, the transmittance can be calculated as |P_o|²/|P_i|², in which |P_i|² and |P_o|² are the integration of sound intensity in the same transmitted region (with a distance of 30 cm away from the lens) without and with the lens, respectively. We observe that, in the range 6.95–9.20 kHz (black shaded region), the transmittances are lower than 0.2 for both LI and RI, and the simulated and measured results agree with each other. Therefore, its bandwidth is about 2.25 kHz, and the fractional bandwidth can reach about 0.28, exhibiting the broadband characteristic.

FIGURE 4

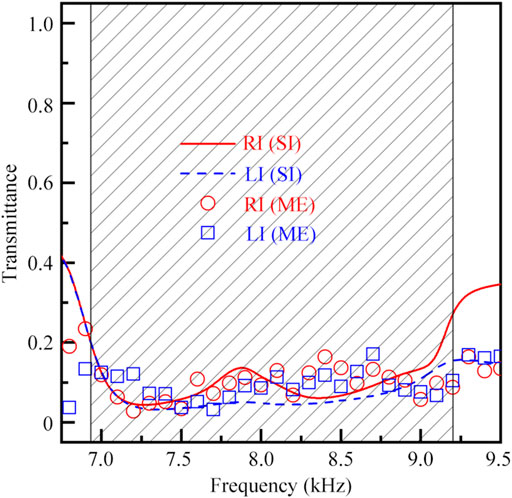
FIGURE 4. Simulated and measured transmittance spectra created by the BAI lens under the incidence of the zero-order wave for RI and LI.

Design and Performances of UAI Lens

In addition to the BAI lens, we adopt 12 phased units to design a phased array lens with UAI based on the mode-conversion mechanism, in which its photograph is shown in Figure 5A. Here, 12 phased units are placed close together, which is different from the arrangement of phased units in the BAI lens (shown in Figure 3A). The propagation paths through the lens for the incidence of the zero-order wave are shown in Figures 5B,C. Similar to those in Figures 2A,B, the first-order wave is obtained, and passes through the lens in the form of two symmetric sound beams with the refraction angles of ±45° for RI. But for LI (Figure 5C), the incident zero-order wave is prohibited by the step waveguide in each phased unit.

FIGURE 5

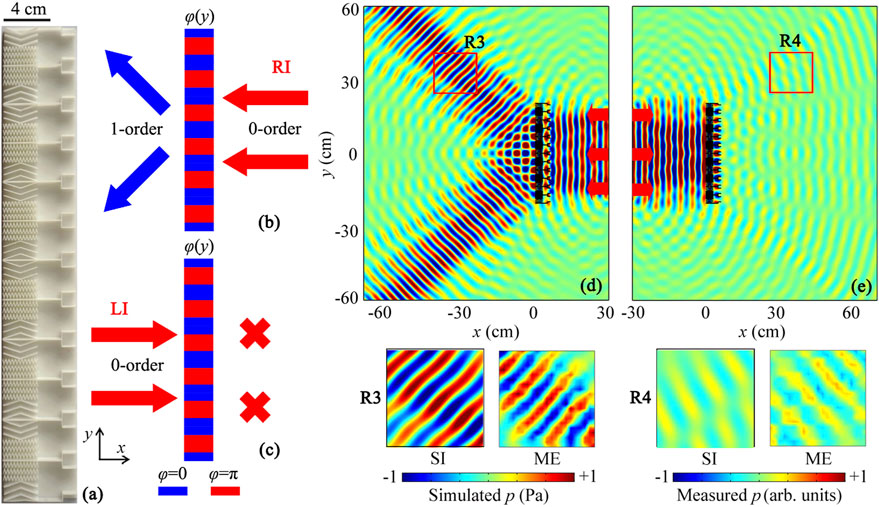
FIGURE 5. (A) Photograph of the UAI lens composed of 12 phased units. Each phased unit is placed close together. Schematic of propagation paths through the UAI lens under the incidence of the zero-order wave for (B) RI and (C) LI. Simulated pressure distributions created by the UAI lens under the incidence of the zero-order wave for (D) RI and (E) LI at 7.1 kHz. Red solid arrows in (B)–(E) are the incident wave. Four insets on the bottom are the simulated and measured intensity distributions in red open squares R3 and R4.

Figures 5D,E show the simulated pressure distributions created by the UAI lens for RI and LI, respectively. We can see that, for the incidence of the zero-order wave, the incident sound energy can pass through the lens as the form of two symmetric beams for RI, but cannot reach the right region for LI, showing typical characteristic of UAI. The four insets on the bottom of Figures 5D,E are the pressure distributions in red open squares R3 and R4. The measured results also match well with the simulated ones. Therefore, by using the proposed mode-conversion phased units, we can realize the UAI effect.

Figure 6 shows the simulated and measured the transmittance spectra of the UAI lens for LI and RI. In the frequency range 6.2–9.0 kHz (black shaded region), the transmittance spectra for LI and RI exhibit obvious characteristics of UAI. Thus, the bandwidth of the proposed UAI lens is 2.80 kHz, and the fractional bandwidth can reach about 0.37. Furthermore, both types of results are consistent with each other, and therefore the broadband feature of the proposed UAI lens is demonstrated experimentally. Beyond that, we simulate the pressure distributions created by the UAI lens for LI and RI by using the module of Acoustic-Solid Interaction, and discuss the influences of the thermoviscous loss (Shen and Cummer, 2018; Li et al., 2017; Ju et al., 2018; Gerard and Jing, 2020) on the performances of the UAI lens. The results are shown in the Supplementary Material.

FIGURE 6

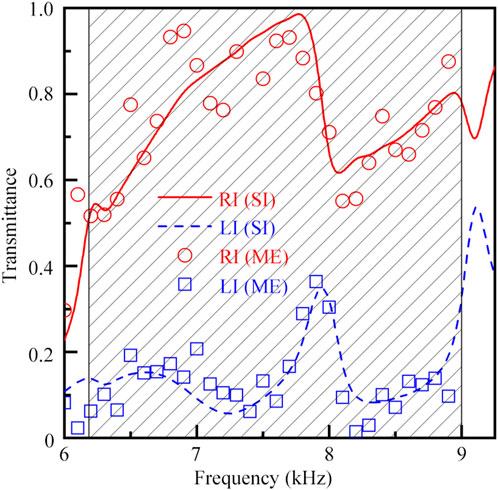
FIGURE 6. Simulated and measured transmittance spectra created by the UAI lens under the incidence of the zero-order wave for RI and LI.

Performances of Reversed UAI

In addition to the aforementioned UAI effect, we can observe the reversed UAI by using the same lens with the incidence of the first-order wave. As shown in Figures 7A,B, the propagation paths through the lens for the incidence of the first-order wave are the same as those in Figures 2G,H. The incident first-order wave is converted to the zero-order wave and transmits through the lens for LI, but cannot pass through the lens for RI. Compared with the results in Figures 5B,C, the UAI effect is reserved for the incidence of the first-order wave.

FIGURE 7

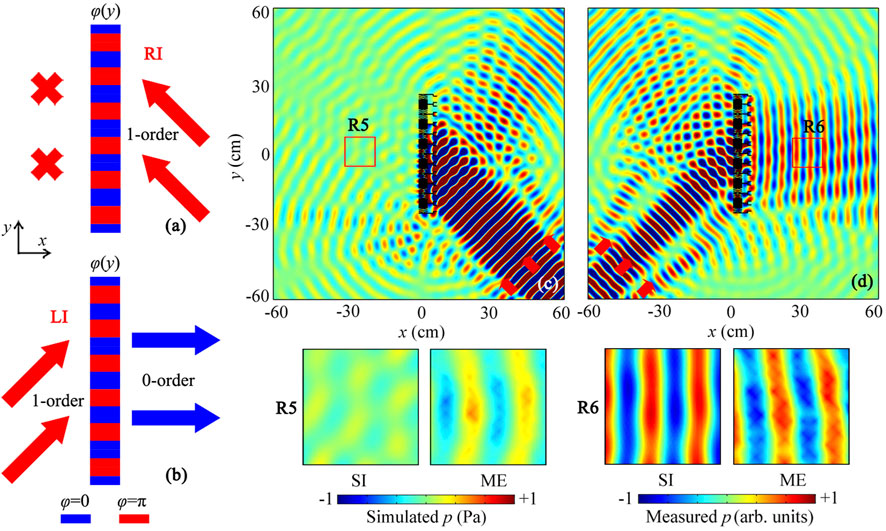
FIGURE 7. Schematic of propagation paths through the UAI lens under the incidence of the first-order wave for (A) RI and (B) LI. Simulated pressure distributions created by the UAI lens under the incidence of the first-order wave for (D) RI and (E) LI at 7.1 kHz. Red solid arrows in (A–D) are the first-order wave. Four insets on the bottom are the simulated and measured intensity distributions in red open squares R5 and R6.

Figures 7C,D show the simulated pressure distributions through the UAI lens under the incidence of the first-order wave for RI and LI, respectively. It is found that, for RI, the incident first-order wave is prohibited by the step waveguide of each phased unit, and cannot reach the left side. But for LI, the first-order wave is converted to the zero-order wave, and can pass through the lens. The transmission characteristic is opposite to that in Figures 5D,E, which indicates that the designed UAI lens can realize the effect of reversed UAI under the incidence of the first-order wave. The measured pressure distributions in red open squares R5 and R6 are shown on the bottom of Figures 7C,D, and the measured results match with the simulated ones well. Therefore, the proposed lens has the advantage of multi-channel UAI, which can realize the characteristics of UAI and reversed UAI based on the incidence of the zero-order and first-order waves, respectively.

Conclusion

In conclusion, we have experimentally demonstrated two types of single-layer phased array lenses with multi-functional sound insulation which consist of 12 mode-conversion phased units composed of two types of unit cells (I and II) with an opposite difference. The results show that, based on the phase regulation, the proposed phased unit can realize the mode conversion between two different types of waves and AAM with a fractional bandwidth of 0.5. By arranging the phased units based on the theoretical phase profiles, we have realized two types of lenses with BAI and UAI for the incidence of the zero-order wave, and their fractional bandwidths can reach about 0.28 and 0.37, respectively. More interestingly, for the incidence of the first-order wave, the UAI effect of the lens is reversed. The experimental and numerical results agree well with each other. The proposed mode-conversion phased unit and its designed phased array lenses provide diverse routes to design multi-functional sound insulation structures with versatile applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (11774137, 51779107, 11834008, 12174188, 11974176, and 12174159).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.766491/full#supplementary-material

References

Allen, K. W., Dykes, D. J. P., Reid, D. R., and Lee, R. T. (2020). Multi-objective Genetic Algorithm Optimization of Frequency Selective Metasurfaces to Engineer Ku-Passband Filter Responses. PIER 167, 19–30. doi:10.2528/PIER19112609

CrossRef Full Text | Google Scholar

Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J.-C., and Jing, Y. (2018). Acoustic Metasurfaces. Nat. Rev. Mater. 3, 460–472. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

Cheng, Y., Li, W., and Mao, X. (2019). Triple-band Polarization Angle Independent 90° Polarization Rotator Based on Fermat's Spiral Structure Planar Chiral Metamaterial. PIER 165, 35–45. doi:10.2528/PIER18112603

CrossRef Full Text | Google Scholar

Cheng, Y., Zhou, C., Yuan, B. G., Wu, D. J., Wei, Q., and Liu, X. J. (2015). Ultra-sparse Metasurface for High Reflection of Low-Frequency Sound Based on Artificial Mie Resonances. Nat. Mater 14, 1013–1019. doi:10.1038/nmat4393

PubMed Abstract | CrossRef Full Text | Google Scholar

Ge, Y., Sun, H.-X., Yuan, S.-Q., and Lai, Y. (2018). Broadband Unidirectional and Omnidirectional Bidirectional Acoustic Insulation through an Open Window Structure with a Metasurface of Ultrathin Hooklike Meta-Atoms. Appl. Phys. Lett. 112, 243502. doi:10.1063/1.5025812

CrossRef Full Text | Google Scholar

Ge, Y., Sun, H.-X., Yuan, S.-Q., and Lai, Y. (2019). Switchable Omnidirectional Acoustic Insulation through Open Window Structures with Ultrathin Metasurfaces. Phys. Rev. Mater. 3, 065203. doi:10.1103/PhysRevMaterials.3.065203

CrossRef Full Text | Google Scholar

Gerard, N. J., and Jing, Y. (2020). Loss in Acoustic Metasurfaces: a Blessing in Disguise. MRS Commun. 10, 32–41. doi:10.1557/mrc.2019.148

CrossRef Full Text | Google Scholar

Gusev, V. E., and Wright, O. B. (2014). Double-negative Flexural Acoustic Metamaterial. New J. Phys. 16, 123053. doi:10.1088/1367-2630/16/12/123053

CrossRef Full Text | Google Scholar

He, Z., Peng, S., Ye, Y., Dai, Z., Qiu, C., Ke, M., et al. (2011). Asymmetric Acoustic Gratings. Appl. Phys. Lett. 98, 083505. doi:10.1063/1.3562306

CrossRef Full Text | Google Scholar

Holloway, C. L., Kuester, E. F., and Haddab, A. H. (2019). Retrieval Approach for Determining Surface Susceptibilities and Surface Porosities of a Symmetric Metascreen from Reflection and Transmission Coefficients. PIER 166, 1–22. doi:10.2528/PIER19022305

CrossRef Full Text | Google Scholar

Huang, Y.-L., Sun, H.-X., Xia, J.-P., Yuan, S.-Q., and Ding, X.-L. (2016). Multi-band Asymmetric Acoustic Transmission in a Bended Waveguide with Multiple Mechanisms. Appl. Phys. Lett. 109, 013501. doi:10.1063/1.4955268

CrossRef Full Text | Google Scholar

Hwan Oh, J., Woong Kim, H., Sik Ma, P., Min Seung, H., and Young Kim, Y. (2012). Inverted Bi-prism Phononic Crystals for One-Sided Elastic Wave Transmission Applications. Appl. Phys. Lett. 100, 213503. doi:10.1063/1.4721485

CrossRef Full Text | Google Scholar

Jiang, X., Liang, B., Zou, X.-Y., Yang, J., Yin, L.-L., Yang, J., et al. (2016). Acoustic One-Way Metasurfaces: Asymmetric Phase Modulation of Sound by Subwavelength Layer. Sci. Rep. 6, 28023. doi:10.1038/srep28023

PubMed Abstract | CrossRef Full Text | Google Scholar

Ju, F., Tian, Y., Cheng, Y., and Liu, X. (2018). Asymmetric Acoustic Transmission with a Lossy Gradient-index Metasurface. Appl. Phys. Lett. 113, 121901. doi:10.1063/1.5032263

CrossRef Full Text | Google Scholar

Lan, J., Li, Y., and Liu, X. (2017). Broadband Manipulation of Refracted Wavefronts by Gradient Acoustic Metasurface with V-Shape Structure. Appl. Phys. Lett. 111, 263501. doi:10.1063/1.5005950

CrossRef Full Text | Google Scholar

Li, C., Ke, M., Ye, Y., Xu, S., Qiu, C., and Liu, Z. (2014). Broadband Asymmetric Acoustic Transmission by a Plate with Quasi-Periodic Surface Ridges. Appl. Phys. Lett. 105, 023511. doi:10.1063/1.4890721

CrossRef Full Text | Google Scholar

Li, X.-F., Ni, X., Feng, L., Lu, M.-H., He, C., and Chen, Y.-F. (2011). Tunable Unidirectional Sound Propagation through a sonic-crystal-based Acoustic Diode. Phys. Rev. Lett. 106, 084301. doi:10.1103/PhysRevLett.106.084301

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Liang, B., Gu, Z.-M., Zou, X.-Y., and Cheng, J.-C. (2013). Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci. Rep. 3, 2546. doi:10.1038/srep02546

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Liang, B., Gu, Z.-M., Zou, X.-Y., and Cheng, J.-C. (2013). Unidirectional Acoustic Transmission through a Prism with Near-Zero Refractive index. Appl. Phys. Lett. 103, 053505. doi:10.1063/1.4817249

CrossRef Full Text | Google Scholar

Li, Y., Shen, C., Xie, Y., Li, J., Wang, W., Cummer, S. A., et al. (2017). Tunable Asymmetric Transmission via Lossy Acoustic Metasurfaces. Phys. Rev. Lett. 119, 035501. doi:10.1103/PhysRevLett.119.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Z., and Li, J. (2012). Extreme Acoustic Metamaterial by Coiling up Space. Phys. Rev. Lett. 108, 114301. doi:10.1103/PhysRevLett.108.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C., Luo, J., and Lai, Y. (2018). Acoustic Metamaterials with Broadband and Wide-Angle Impedance Matching. Phys. Rev. Mater. 2, 045201. doi:10.1103/PhysRevMaterials.2.045201

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, J., and Wu, Y. (2014). Controllable Transmission and Total Reflection through an Impedance-Matched Acoustic Metasurface. New J. Phys. 16, 123007. doi:10.1088/1367-2630/16/12/123007

CrossRef Full Text | Google Scholar

Quan, L., and Alù, A. (2019). Hyperbolic Sound Propagation over Nonlocal Acoustic Metasurfaces. Phys. Rev. Lett. 123, 244303. doi:10.1103/PhysRevLett.123.244303

PubMed Abstract | CrossRef Full Text | Google Scholar

Quan, L., Zhong, X., Liu, X., Gong, X., and Johnson, P. A. (2014). Effective Impedance Boundary Optimization and its Contribution to Dipole Radiation and Radiation Pattern Control. Nat. Commun. 5, 3188. doi:10.1038/ncomms4188

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, C., and Cummer, S. A. (2018). Harnessing Multiple Internal Reflections to Design Highly Absorptive Acoustic Metasurfaces. Phys. Rev. Appl. 9, 054009. doi:10.1103/PhysRevApplied.9.054009

CrossRef Full Text | Google Scholar

Shen, C., Xie, Y., Li, J., Cummer, S. A., and Jing, Y. (2016). Asymmetric Acoustic Transmission through Near-Zero-index and Gradient-index Metasurfaces. Appl. Phys. Lett. 108, 223502. doi:10.1063/1.4953264

CrossRef Full Text | Google Scholar

Song, A.-L., Chen, T.-N., Wang, X.-P., and Wan, L.-L. (2016). Waveform-preserved Unidirectional Acoustic Transmission Based on Impedance-Matched Acoustic Metasurface and Phononic crystal. J. Appl. Phys. 120, 085106. doi:10.1063/1.4961659

CrossRef Full Text | Google Scholar

Song, A., Chen, T., Wang, X., and Xi, Y. (2017). Broadband Asymmetric Acoustic Transmission through an Acoustic Prism. Phys. Lett. A 381, 2283–2286. doi:10.1016/j.physleta.2017.05.034

CrossRef Full Text | Google Scholar

Sun, H.-X., Yuan, S.-Q., and Zhang, S.-Y. (2015). Asymmetric Acoustic Transmission in Multiple Frequency Bands. Appl. Phys. Lett. 107, 213505. doi:10.1063/1.4936609

CrossRef Full Text | Google Scholar

Tang, K., Qiu, C., Ke, M., Lu, J., Ye, Y., and Liu, Z. (2014). Anomalous Refraction of Airborne Sound through Ultrathin Metasurfaces. Sci. Rep. 4, 6517. doi:10.1038/srep06517

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, Y., Wei, Q., Cheng, Y., and Liu, X. (2017). Acoustic Holography Based on Composite Metasurface with Decoupled Modulation of Phase and Amplitude. Appl. Phys. Lett. 110, 191901. doi:10.1063/1.4983282

CrossRef Full Text | Google Scholar

Tian, Z., Shen, C., Li, J., Reit, E., Gu, Y., Fu, H., et al. (2019). Programmable Acoustic Metasurfaces. Adv. Funct. Mater. 29, 1808489. doi:10.1002/adfm.201808489

PubMed Abstract | CrossRef Full Text | Google Scholar

Torrent, D., and Sánchez-Dehesa, J. (2018). Anisotropic Mass Density by Radially Periodic Fluid Structures. Phys. Rev. Lett. 105, 174301. doi:10.1103/PhysRevLett.105.174301

CrossRef Full Text | Google Scholar

Wang, Y., Xia, J.-P., Sun, H.-X., Yuan, S.-Q., Ge, Y., Si, Q.-R., et al. (2019). Multifunctional Asymmetric Sound Manipulations by a Passive Phased Array Prism. Phys. Rev. Appl. 12, 024033. doi:10.1103/PhysRevApplied.12.024033

CrossRef Full Text | Google Scholar

Xia, J.-P., Jia, D., Sun, H.-X., Yuan, S.-Q., Ge, Y., Si, Q.-R., et al. (2018a). Programmable Coding Acoustic Topological Insulator. Adv. Mater. 30, 1805002. doi:10.1002/adma.201805002

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, J.-P., Zhang, X.-T., Sun, H.-X., Yuan, S.-Q., Qian, J., and Ge, Y. (2018b). Broadband Tunable Acoustic Asymmetric Focusing Lens from Dual-Layer Metasurfaces. Phys. Rev. Appl. 10, 014016. doi:10.1103/PhysRevApplied.10.014016

CrossRef Full Text | Google Scholar

Xie, B., Cheng, H., Tang, K., Liu, Z., Chen, S., and Tian, J. (2017). Multiband Asymmetric Transmission of Airborne Sound by Coded Metasurfaces. Phys. Rev. Appl. 7, 024010. doi:10.1103/PhysRevApplied.7.024010

CrossRef Full Text | Google Scholar

Xie, Y., Wang, W., Chen, H., Konneker, A., Popa, B.-I., and Cummer, S. A. (2014). Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat. Commun. 5, 5553. doi:10.1038/ncomms6553

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Sun, H.-X., Xia, J.-P., Xue, H., Gao, Z., Ge, Y., et al. (2019). Topological Triply Degenerate point with Double Fermi Arcs. Nat. Phys. 15, 645–649. doi:10.1038/s41567-019-0502-z

CrossRef Full Text | Google Scholar

Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J.-P., Capasso, F., et al. (2011). Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, X., Lu, Z., Liu, T., Cheng, L., Zhu, J., and Cui, F. (2019). Sound Transmission through a Periodic Acoustic Metamaterial Grating. J. Sound Vibration 449, 140–156. doi:10.1016/j.jsv.2019.02.042

CrossRef Full Text | Google Scholar

Yuan, B., Liang, B., Tao, J.-C., Zou, X.-Y., and Cheng, J.-C. (2012). Broadband Directional Acoustic Waveguide with High Efficiency. Appl. Phys. Lett. 101, 043503. doi:10.1063/1.4739081

CrossRef Full Text | Google Scholar

Zhang, C., Cao, W. K., Yang, J., Ke, J. C., Chen, M. Z., Wu, L. T., et al. (2019). Multiphysical Digital Coding Metamaterials for Independent Control of Broadband Electromagnetic and Acoustic Waves with a Large Variety of Functions. ACS Appl. Mater. Inter. 11, 17050–17055. doi:10.1021/acsami.9b02490

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Zhang, Y., Guo, Y., Leng, Y., Feng, W., and Cao, W. (2016). Realization of Subwavelength Asymmetric Acoustic Transmission Based on Low-Frequency Forbidden Transmission. Phys. Rev. Appl. 5, 034006. doi:10.1103/PhysRevApplied.5.034006

CrossRef Full Text | Google Scholar

Zhao, X., Cai, L., Yu, D., Lu, Z., and Wen, J. (2017). A Low Frequency Acoustic Insulator by Using the Acoustic Metasurface to a Helmholtz Resonator. AIP Adv. 7, 065211. doi:10.1063/1.4989819

CrossRef Full Text | Google Scholar

Zhu, Y.-F., Gu, Z.-M., Liang, B., Yang, J., Yang, J., Yin, L.-L., et al. (2016). Asymmetric Sound Transmission in a Passive Non-blocking Structure with Multiple Ports. Appl. Phys. Lett. 109, 103504. doi:10.1063/1.4962435

CrossRef Full Text | Google Scholar