Yi-jun Guan
Yong Ge1
Hong-xiang Sun- 1Research Center of Fluid Machinery Engineering and Technology, School of Physics and Electronic Engineering, Jiangsu University, Zhenjiang, China
- 2Key Laboratory of Modern Acoustics, National Laboratory of Solid State Microstructures, Department of Physics and Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, China
- 3State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing, China
We report, both theoretically and experimentally, a type of ultra-thin metasurface-based low-frequency sound absorber with bandwidth optimization. Such a metasurface unit consists of an ultrathin resonator (thickness∼1/90 wavelength) with a circular hole on the upper panel and four narrow slits inside a multiple-cavity structure. Eigenmode simulations of the unit show rich artificial Mie resonances, in which a type of monopolar Mie resonance mode can be obtained at 238.4 Hz. Based on the excitation of the monopolar mode, we can realize the near-perfect low-frequency sound absorption with the maximum absorption coefficient and fractional bandwidth of 0.97 and 12.9%, respectively, which mainly arises from the high thermal-viscous loss around the circular hole and four narrow slits of the unit. More interestingly, by combining 4 units with different diameters of the circular hole, we further enhance the fractional bandwidth of the compound unit to 18.7%. Our work provides a route to design ultra-thin broadband sound absorbers by artificial Mie resonances, showing great potential in practical applications of low-frequency noise control and architectural acoustics.
Introduction
Studies on low-frequency sound absorption have attracted great scientific and engineering fascination due to its extensive practical applications in noise control, architectural acoustics, and environmental protection. Traditionally, the realization of sound absorption is mainly based on porous and fibrous materials (Biot, 1956; Zarek, 1978) and micro-perforated plate structures with cavities at the back (Maa, 1998; Arenas and Crocker, 2010). However, these absorbing structures usually have imperfect impedance matching with free space and relatively large sizes comparable to working wavelengths.
In the past few years, rapid development of metamaterials (Liu et al., 2000; Fang et al., 2006; Li et al., 2009; Toyoda et al., 2011; Christensen and de Abajo, 2012; Liang and Li, 2012; Quan et al., 2014; Cummer et al., 2016; Cheng et al., 2019; Gao et al., 2021) and metasurfaces (Li et al., 2013; Tang et al., 2014; Xie et al., 2014; Xie et al., 2017; Assouar et al., 2018; Holloway et al., 2019; Quan et al., 2019; Zhu and Assouar, 2019; Gao et al., 2020; Nikkhah et al., 2020) provides an unprecedented way to overcome the limits of conventional absorption materials and realize high absorption performance. These absorbing structures usually contain subwavelength resonant units to enhance energy density and dissipate sound energy inside. The previously demonstrated resonant units mainly include Helmholtz resonators (Jimenez et al., 2016; Li et al., 2016; Romero-Garcia et al., 2016; Jimenez et al., 2017; Long et al., 2017), sound membranes (Mei et al., 2012; Ma et al., 2014; Yang et al., 2015; Yang et al., 2015), coiled Fabry-Perot resonators (Zhang and Hu, 2016; Jimenez et al., 2017; Yang et al., 2017), split-ring-resonators (Wu et al., 2016), acoustic metasurfaces (Cai et al., 2014; Li and Assouar, 2016; Tang et al., 2017; Donda et al., 2019; Ge et al., 2019; Long et al., 2019; Gao et al., 2021), etc. The above designs exhibit high efficiency for low-frequency sound absorption. However, due to their resonant nature, the design of sound absorption structures with both broad bandwidth and deep subwavelength thickness remains a challenging task. Theoretical analysis shows that broadband absorption can be achieved by dispersive dissipative meta-films (Duan et al., 2015). Meanwhile, sound absorption can also be theoretically obtained by coherent perfect absorbers based on interference cancellation (Song et al., 2014; Wei et al., 2014).
Recently, a type of maze-like unit consisting of eight zigzag channels has become a hot topic due to its rich artificial Mie resonances and subwavelength size (Cheng et al., 2015; Landi et al., 2018). Based on different types of Mie resonance modes created by the maze-like units, a variety of application designs of low-frequency sound have been realized, including rainbow trapping (Zhou et al., 2016), extraordinary transmission (Xia et al., 2015; Zhang et al., 2017), sound filtering (Sun et al., 2019), energy harvesting (Gao et al., 2019) and directional propagation (Lu et al., 2017). Additionally, a multi-band near-perfect sound absorber based on the multi-orders monopolar and dipolar Mie resonances has been designed (Long et al., 2018). However, this system is composed of a Mie resonator array backed by a rigid wall, and broadband sound absorbers designed by a single layer of Mie resonator array with deep subwavelength thickness still pose a challenge.
In this work, we propose a metasurface unit which consists of an upper surface panel with a central circular hole and a multiple-cavity structure. By applying eigenmode simulations to the unit, a series of artificial Mie resonance modes can be observed, such as a monopolar Mie resonance (MMR) mode at 238.4 Hz and a second MMR mode at 1,145.4 Hz. Based on the thermal-viscous loss created by the circular hole and four narrow slits of the unit under the excitation of the MMR mode, the near-perfect low-frequency sound absorption is observed at 239 Hz, and the maximum absorption coefficient and fractional bandwidth can reach about 0.97 and 12.9%, respectively. Additionally, we discuss the influences of structure parameters on the sound absorption performance, and design two types of broadband compound units by combining 4 units with different central circular holes. The fractional bandwidth of the compound unit can be further enhanced to 18.7%. The measured sound absorption spectra agree well with the simulated ones.
Design and Performances of Sound Absorber
Design of Unit
As schematically shown in Figure 1A, we propose an acoustic metasurface-based absorber consisting of periodic square units with a length a and a thickness h. A central circular hole with a diameter d is located at the upper surface of the unit. Each unit is composed of an upper surface panel (with a thickness t3) and a multiple-cavity structure (with a thickness t4) on the bottom (Figure 1B). As shown in Figure 1C, the multiple-cavity structure consists of a central square cavity (with a length b) surrounded by four interconnected identical cavities which are divided by four narrow slits (with a width t1), showing a high structure symmetry. The distance between the slits and the outer frame is t2, and the frames (with a thickness t) are made of epoxy resin based on 3D-printing technology. Here, the COMSOL Multiphysics software is used to numerically simulate sound absorption characteristics, and the structure parameters are selected as a = 100 mm, b = 42 mm, d = 5 mm, t = t1 = 2 mm, t2 = 10 mm, t3 = 1 mm, and t4 = 15 mm. In our work, the sound absorption is created by the thermoviscous loss of the unit structure, and we use the module of Thermoviscous Acoustic-Solid Interaction inside the unit, and the module of Acoustic Pressure outside the unit due to the huge computation load. In the simulations, the thermoviscous acoustic boundary is used for all the surfaces inside the unit (include the inner surface of the hole), and the acoustic-thermoviscous acoustic boundary is adopted for the interface between the hole and the external space. The parameters of epoxy resin are the density ρe = 1,180 kg/m3, the longitudinal wave velocity cl = 2,720 m/s, and the transversal wave velocity ct = 1,460 m/s, and those of air are calculated as
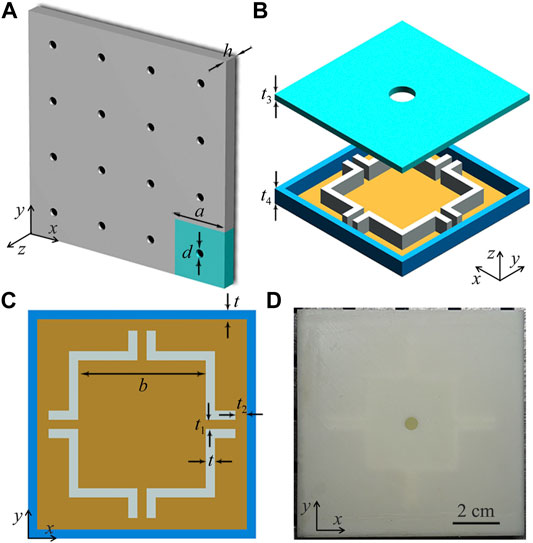
FIGURE 1. (A) Structure of acoustic metasurface-based absorber composed of periodic square units. (B) 3D structure of the unit constructed by an upper surface panel with a central circular hole and a multiple-cavity structure on the bottom. (C) 2D structure of the multiple-cavity structure. (D) Top view of paragraph of the unit.
Characteristics of Two Types of MMR Modes
Figure 2 shows the simulated pressure amplitude and phase eigenfunctions of the proposed unit. We can see that two types of eigenmodes present typical characteristics of the MMR, which are denoted as the monopole and second monopole. Additionally, due to high symmetry of the multiple-cavity structure, the Mie resonance of the dipole and quadrupole can also be observed (see Supplementary Material), showing rich Mie resonant modes of the unit. As shown in Figure 2A, for the MMR mode at 238.4 Hz, the sound energy is mainly concentrated into the surrounding four cavities, and the whole structure exhibits a collective in-phase characteristic (Figure 2B). But for the second MMR mode at 1,145.4 Hz, the sound energy is mainly in the central square cavity (Figure 2C), and an out-of-phase feature (Figure 2D) is observed between the internal and external cavities. Here, to further demonstrate the mechanism of both MMR modes, we simulate the pressure amplitude and phase eigenfunctions of the units with different number of surrounding cavities (see Supplementary Material). The results show that the eigenfrequencies of both MMR modes change greatly with different number of cavities, but their mode characteristics are almost the same.
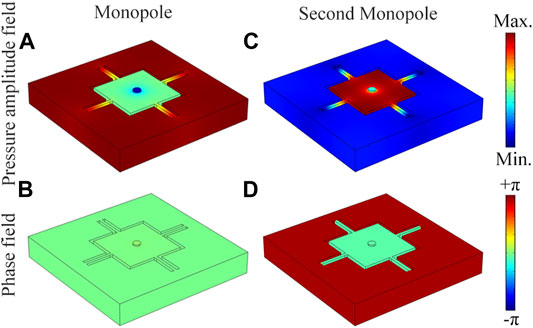
FIGURE 2. Simulated pressure amplitude and phase eigenfunctions of Mie resonance modes of the unit for (A), (B) monopole at 238.4 Hz and (C), (D) second monopole at 1,145.4 Hz.
Low-Frequency Sound Absorption Created by the MMR Mode
Next, we experimentally measure the absorption performance of low-frequency sound created by the MMR mode in Figure 2A. As shown in Figure 3A, in the experiment, the sample (shown in Figure 1D) is placed at the right side in the straight waveguide which is made of acrylic plates to satisfy sound hard boundary condition. The experimental set-up is presented in the Supplementary Material. Figure 3B shows the measured and simulated sound absorption spectra created by the unit. We find that there exists a sound absorption peak at 239 Hz for both results, and the absorption coefficient can reach about 0.97, showing a near-perfect low-frequency sound absorption. Moreover, the bandwidth of sound absorption (black shaded region) is about 31 Hz, and its corresponding fractional bandwidth (the ratio of the bandwidth to the center frequency) can reach about 12.9%. The measured and simulated sound absorption spectra match well with each other. Beyond that, the thickness h of the unit is only 16 mm, which is equal to λ/90, exhibiting a deep subwavelength thickness of the proposed low-frequency sound absorber.
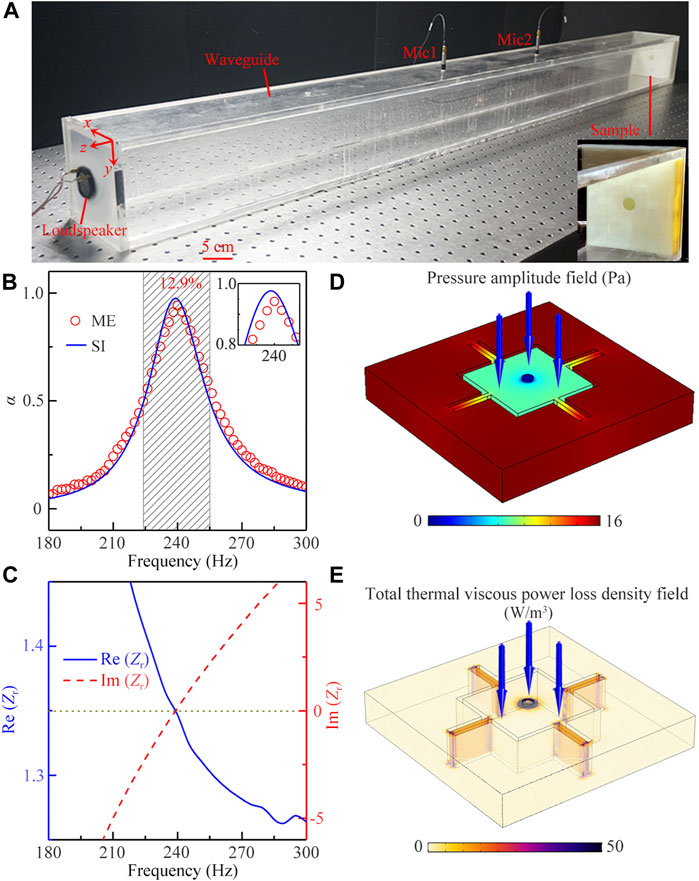
FIGURE 3. (A) Experiment set-up of sound absorption. (B) Simulated (blue solid line) and measured (red open circles) sound absorption spectra of the unit. (C) Real and imaginary parts of relative acoustic impedance Zr of the unit. Distributions of (D) the pressure amplitude and (E) total thermal viscous power loss density in the unit excited by a normal incident wave (blue solid arrows) at 239 Hz.
To explain the existence of the sound absorption peak, we introduce the relative acoustic impedance of the unit defined as
Furthermore, we find that the frequency of sound absorption peak is almost the same as that of the MMR mode, and thus the sound absorption may arise from the MMR mode of the unit. To make a further insight into it, we simulate the distributions of the pressure amplitude and total thermal-viscous power loss density in the unit created by a normal incidence of sound at 239 Hz, which are shown in Figures 3D,E, respectively. Note that the excited pressure amplitude distribution of the unit (Figure 3D) agrees well with that of the MMR mode (Figure 2A), indicating that the low-frequency sound absorption is created by the MMR mode of the unit. Moreover, as shown in Figure 3E, there exist an obvious thermal-viscous sound loss around the central circular hole and four narrow slits, especially the central circular hole. Therefore, we deduce that the sound absorption of the unit arises from the thermoviscous loss around the central circular hole and four narrow slits under the excitation of the MMR mode. Beyond that, we also simulate the sound absorption spectra created by the MMR mode of the unit with different incident angles (θ), and the absorption spectra are relatively stable below θ = 60°. (see Supplementary Material).
Besides the sound absorption created by the MMR mode, we simulate the performances of sound absorption created by the second MMR mode of the unit. The results show that the sound absorption can also be created by the second MMR mode, but its absorption performance is reduced greatly due to the sound reflection created by the impedance mismatch (see Supplementary Material). Furthermore, we simulate the sound absorption spectra of the units with different number of surrounding cavities (see Supplementary Material), in which the results further demonstrates that the sound absorption of the unit arises from the excitation of both MMR modes.
Bandwidth Optimization of Sound Absorber
Finally, we discuss the influences of the parameters b and d on the sound absorption and further optimize the working bandwidth of the sound absorber. Figures 4A,B show the simulated sound absorption spectra created by the MMR mode as a function of the parameters b and d, respectively, in which other parameters remain unchanged. It is found that, with the decrease of both parameters, the working bandwidth moves to the low-frequency region with a high sound absorption coefficient. The corresponding measured results for the parameters b and d are displayed in Figures 4C,D, which agree well with the simulation ones. Thus, we can reduce the working frequency of the sound absorption by simply decreasing the values of b and d.
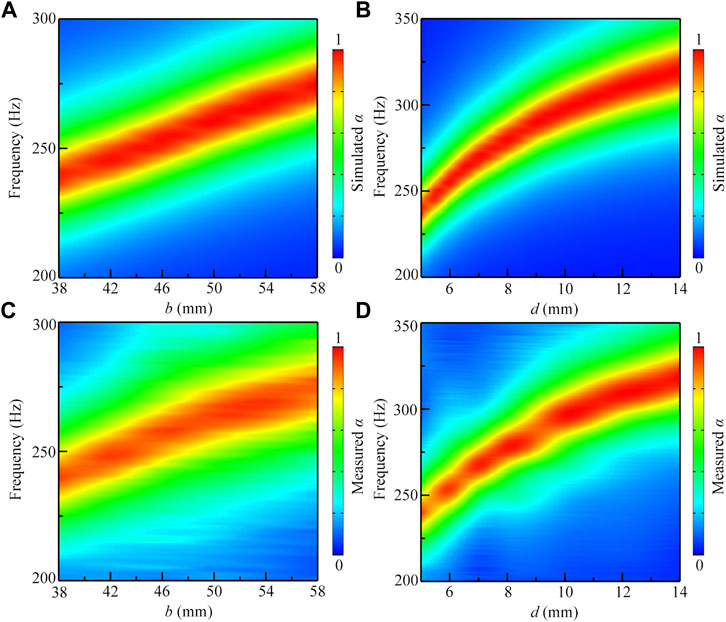
FIGURE 4. Simulated sound absorption spectra as a function of parameters (A)b and (B)d, and the corresponding measured sound absorption spectra for the parameters (C)b and (D)d, in which the other parameters remain unchanged.
To further optimize the working bandwidth, we design two types of compound units A and B consisting of 4 units (2 × 2 array) with different values of d (d = 8, 10, and 12 mm for the units I, II and III), and experimentally measure sound absorption of both compound units. The experiment set-up is shown in Figure 5A, in which the width and height of the waveguide double those in Figure 3A, and the other parameters are the same. As shown in Figure 5B, the compound unit A consists of two types of units (I and II), and the arrangement of 4 units is shown in the sample photograph (shown in bottom inset). Note that, by combining the units I and II, the fractional bandwidth of the compound unit A can reach about 16.4%, in which the working frequency range (266–313.5 Hz, black shaded region) can cover those of a single unit I or II. Compared with the result in Figure 3B, the maximum sound absorption coefficient decreases slightly, but the absorption peak becomes wide and flat due to their coupling effect of both types of units. Additionally, as shown in Figure 5C, the compound unit B is composed of three types of units (I, II and III). By introducing the unit III, the working band (266–321 Hz, black shaded region) of the compound unit B is further improved, and its fractional bandwidth can be enhanced to 18.7%, showing a broadband feature of the sound absorption. The measured sound absorption spectra for both compound units agree with the simulations. Therefore, by combining the units with different values of d, we can further enhance the working bandwidth of the proposed sound absorber. Furthermore, we simulate the sound absorption spectra of another two types of compound units C and D with different configurations (see Supplementary Material). Compared with the absorption performance of the compound units A and B, we demonstrate that the absorption performance of the compound unit is closely related to its configuration.
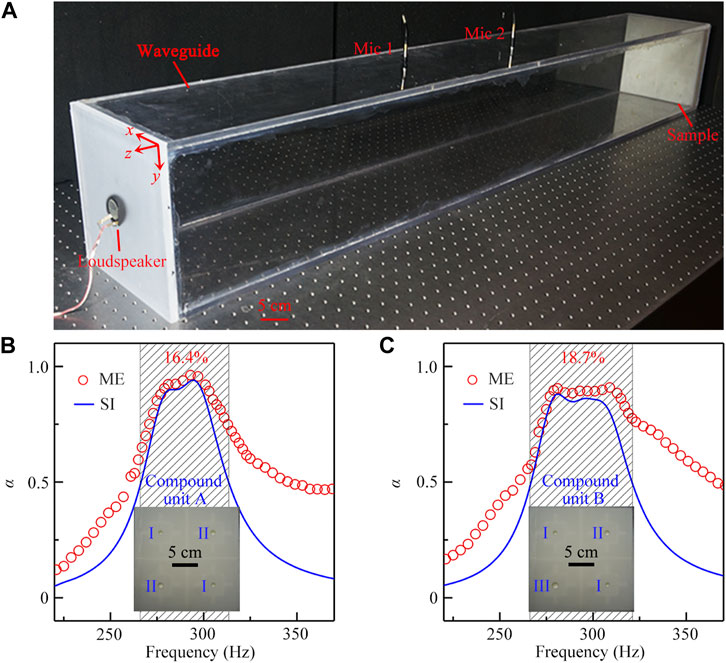
FIGURE 5. (A) Experiment set-up of sound absorption for the compound unit. Simulated (blue solid lines) and measured (red open circles) sound absorption spectra of the compound units (B) A and (C) B. The arrangement of 4 units with different values of d (d = 8, 10, and 12 mm for the units I, II, and III) are shown in the paragraphs of the compound units A and B (shown as two insets on the bottom).
Conclusion
In conclusions, we have demonstrated a metasurface-based unit with near-perfect low-frequency sound absorption based on artificial Mie resonances. The results show that a series of artificial Mie resonance modes can be observed in the unit, including the MMR mode at 238.4 Hz and the second MMR mode at 1,145.4 Hz. Based on the excited MMR mode and the thermal-viscous loss around the circular hole and four narrow slits of the unit, the near-perfect low-frequency sound absorption is achieved at 239 Hz, the maximum absorption coefficient and fractional bandwidth of the proposed unit can reach 0.97 and 12.9%. It is noted that the thickness of the unit is only about λ/90, showing a deep subwavelength thickness of the proposed metasurface-based sound absorber. In addition, we discuss the influences of structure parameters b and d on the sound absorption in detail, and find that the working bandwidth moves to the low-frequency region with a high absorption coefficient by decreasing both parameters. Finally, we improve the working bandwidth of the sound absorption by combining 4 units with different values of b, and the fractional bandwidth of the compound unit B can be further enhanced to 18.7%. The measured and simulated sound absorption spectra match well with each other. The proposed multiple-cavity units with the near-perfect sound absorption and broadband feature provide diverse routes to design advanced sound absorption structures with great potential applications in low-frequency noise control, architectural acoustics and environmental protection.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
Y-JG and YG contributed equally to this work.
Funding
This work was supported by the National Natural Science Foundation of China (11774137, 51779107, 11834008, 61671314, 11974176, and 12174159).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.764338/full#supplementary-material
References
Arenas, J. P., and Crocker, M. J. (2010). Recent Trends in Porous Sound-Absorbing Materials. Sound Vib 44, 12–17. doi:10.1007/s00397-010-0453-x
Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J.-C., and Jing, Y. (2018). Acoustic Metasurfaces. Nat. Rev. Mater. 3, 460–472. doi:10.1038/s41578-018-0061-4
Biot, M. A. (1956). Theory of Propagation of Elastic Waves in a Fluid‐Saturated Porous Solid. I. Low‐Frequency Range. The J. Acoust. Soc. America 28, 168–178. doi:10.1121/1.1908239
Cai, X., Guo, Q., Hu, G., and Yang, J. (2014). Ultrathin Low-Frequency Sound Absorbing Panels Based on Coplanar Spiral Tubes or Coplanar Helmholtz Resonators. Appl. Phys. Lett. 105, 121901. doi:10.1063/1.4895617
Cheng, Y., Li, W., and Mao, X. (2019). Triple-band Polarization Angle Independent 90° Polarization Rotator Based on Fermat's Spiral Structure Planar Chiral Metamaterial. Pier 165, 35–45. doi:10.2528/PIER18112603
Cheng, Y., Zhou, C., Yuan, B. G., Wu, D. J., Wei, Q., and Liu, X. J. (2015). Ultra-sparse Metasurface for High Reflection of Low-Frequency Sound Based on Artificial Mie Resonances. Nat. Mater 14, 1013–1019. doi:10.1038/NMAT4393
Christensen, J., and de Abajo, F. J. G. (2012). Anisotropic Metamaterials for Full Control of Acoustic Waves. Phys. Rev. Lett. 108, 124301. doi:10.1103/PhysRevLett.108.124301
Cummer, S. A., Christensen, J., and Alù, A. (2016). Controlling Sound with Acoustic Metamaterials. Nat. Rev. Mater. 1, 16001. doi:10.1038/natrevmats.2016.1
Donda, K., Zhu, Y., Fan, S.-W., Cao, L., Li, Y., and Assouar, B. (2019). Extreme Low-Frequency Ultrathin Acoustic Absorbing Metasurface. Appl. Phys. Lett. 115, 173506. doi:10.1063/1.5122704
Duan, Y., Luo, J., Wang, G., Hang, Z. H., Hou, B., Li, J., et al. (2015). Theoretical Requirements for Broadband Perfect Absorption of Acoustic Waves by Ultra-thin Elastic Meta-Films. Sci. Rep. 5, 12139. doi:10.1038/srep12139
Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C., et al. (2006). Ultrasonic Metamaterials with Negative Modulus. Nat. Mater 5, 452–456. doi:10.1038/nmat1644
Gao, N., Luo, D., Cheng, B., and Hou, H. (2020). Teaching-learning-based Optimization of a Composite Metastructure in the 0-10 kHz Broadband Sound Absorption Range. J. Acoust. Soc. America 148, EL125–EL129. doi:10.1121/10.0001678
Gao, N., Tang, L., Deng, J., Lu, K., Hou, H., and Chen, K. (2021). Design, Fabrication and Sound Absorption Test of Composite Porous Metamaterial with Embedding I-Plates into Porous Polyurethane Sponge. Appl. Acoust. 175, 107845. doi:10.1016/j.apacoust.2020.107845
Gao, N., Wu, J., Lu, K., and Zhong, H. (2021). Hybrid Composite Meta-Porous Structure for Improving and Broadening Sound Absorption. Mech. Syst. Signal Process. 154, 107504. doi:10.1016/j.ymssp.2020.107504
Gao, W.-t., Xia, J.-p., Sun, H.-x., Yuan, S.-q., Ge, Y., and Liu, X.-j. (2019). Acoustic Energy Harvesting for Low-Frequency Airborne Sound Based on Compound Mie Resonances. Appl. Phys. Express 12, 044002. doi:10.7567/1882-0786/ab07e5
Ge, Y., Sun, H.-x., Yuan, S.-q., and Lai, Y. (2019). Switchable Omnidirectional Acoustic Insulation through Open Window Structures with Ultrathin Metasurfaces. Phys. Rev. Mater. 3, 065203. doi:10.1103/PhysRevMaterials.3.065203
Holloway, C. L., Kuester, E. F., and Haddab, A. H. (2019). Retrieval Approach for Determining Surface Susceptibilities and Surface Porosities of a Symmetric Metascreen from Reflection and Transmission Coefficients. Pier 166, 1–22. doi:10.2528/PIER19022305
Jiménez, N., Huang, W., Romero-García, V., Pagneux, V., and Groby, J.-P. (2016). Ultra-thin Metamaterial for Perfect and Quasi-Omnidirectional Sound Absorption. Appl. Phys. Lett. 109, 121902. doi:10.1063/1.4962328
Jiménez, N., Romero-García, V., Pagneux, V., and Groby, J.-P. (2017). Quasiperfect Absorption by Subwavelength Acoustic Panels in Transmission Using Accumulation of Resonances Due to Slow Sound. Phys. Rev. B 95, 014205. doi:10.1103/PhysRevB.95.014205
Jiménez, N., Romero-García, V., Pagneux, V., and Groby, J.-P. (2017). Rainbow-trapping Absorbers: Broadband, Perfect and Asymmetric Sound Absorption by Subwavelength Panels for Transmission Problems. Sci. Rep. 7, 13595. doi:10.1038/s41598-017-13706-4
Landi, M., Zhao, J., Prather, W. E., Wu, Y., and Zhang, L. (2018). Acoustic purcell Effect for Enhanced Emission. Phys. Rev. Lett. 120, 114301. doi:10.1103/PhysRevLett.120.114301
Li, J., Fok, L., Yin, X., Bartal, G., and Zhang, X. (2009). Experimental Demonstration of an Acoustic Magnifying Hyperlens. Nat. Mater 8, 931–934. doi:10.1038/NMAT2561
Li, J., Wang, W., Xie, Y., Popa, B.-I., and Cummer, S. A. (2016). A Sound Absorbing Metasurface with Coupled Resonators. Appl. Phys. Lett. 109, 091908. doi:10.1063/1.4961671
Li, Y., and Assouar, B. M. (2016). Acoustic Metasurface-Based Perfect Absorber with Deep Subwavelength Thickness. Appl. Phys. Lett. 108, 063502. doi:10.1063/1.4941338
Li, Y., Liang, B., Gu, Z.-m., Zou, X.-y., and Cheng, J.-c. (2013). Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci. Rep. 3, 2546. doi:10.1038/srep02546
Liang, Z., and Li, J. (2012). Extreme Acoustic Metamaterial by Coiling up Space. Phys. Rev. Lett. 108, 114301. doi:10.1103/PhysRevLett.108.114301
Liu, Z., Zhang, X. X., Mao, Y. W., Zhu, Y. Y., Yang, Z. Y., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734
Long, H., Cheng, Y., and Liu, X. (2017). Asymmetric Absorber with Multiband and Broadband for Low-Frequency Sound. Appl. Phys. Lett. 111, 143502. doi:10.1063/1.4998516
Long, H., Gao, S., Cheng, Y., and Liu, X. (2018). Multiband Quasi-Perfect Low-Frequency Sound Absorber Based on Double-Channel Mie Resonator. Appl. Phys. Lett. 112, 033507. doi:10.1063/1.5013225
Long, H., Shao, C., Liu, C., Cheng, Y., and Liu, X. (2019). Broadband Near-Perfect Absorption of Low-Frequency Sound by Subwavelength Metasurface. Appl. Phys. Lett. 115, 103503. doi:10.1063/1.5109826
Lu, G., Ding, E., Wang, Y., Peng, X., Cui, J., Liu, X., et al. (2017). Realization of Acoustic Wave Directivity at Low Frequencies with a Subwavelength Mie Resonant Structure. Appl. Phys. Lett. 110, 123507. doi:10.1063/1.4979105
Ma, G., Yang, M., Xiao, S., Yang, Z., and Sheng, P. (2014). Acoustic Metasurface with Hybrid Resonances. Nat. Mater 13, 873–878. doi:10.1038/NMAT3994
Maa, D.-Y. (1998). Potential of Microperforated Panel Absorber. J. Acoust. Soc. America 104, 2861–2866. doi:10.1121/1.423870
Mei, J., Ma, G., Yang, M., Yang, Z., Wen, W., and Sheng, P. (2012). Dark Acoustic Metamaterials as Super Absorbers for Low-Frequency Sound. Nat. Commun. 3, 756. doi:10.1038/ncomms1758
Quan, L., Sounas, D. L., and Alù, A. (2019). Nonreciprocal willis Coupling in Zero-index Moving media. Phys. Rev. Lett. 123, 064301. doi:10.1103/PhysRevLett.123.064301
Quan, L., Zhong, X., Liu, X., Gong, X., and Johnson, P. A. (2014). Effective Impedance Boundary Optimization and its Contribution to Dipole Radiation and Radiation Pattern Control. Nat. Commun. 5, 3188. doi:10.1038/ncomms4188
Ranjbar Nikkhah, M., Hiranandani, M., and Kishk, A. A. (2020). Rotman Lens Design with Wideband DRA Array. Pier 169, 45–57. doi:10.2528/PIER20050801
Romero-García, V., Theocharis, G., Richoux, O., Merkel, A., Tournat, V., and Pagneux, V. (2016). Perfect and Broadband Acoustic Absorption by Critically Coupled Sub-wavelength Resonators. Sci. Rep. 6, 19519. doi:10.1038/srep19519
Song, J. Z., Bai, P., Hang, Z. H., and Lai, Y. (2014). Acoustic Coherent Perfect Absorbers. New J. Phys. 16, 033026. doi:10.1088/1367-2630/16/3/033026
Sun, Y. Y., Xia, J. P., Sun, H. X., Yuan, S. Q., Ge, Y., and Liu, X. J. (2019). Dual‐Band Fano Resonance of Low‐Frequency Sound Based on Artificial Mie Resonances. Adv. Sci. 6, 1901307. doi:10.1002/advs.201901307
Tang, K., Qiu, C., Ke, M., Lu, J., Ye, Y., and Liu, Z. (2014). Anomalous Refraction of Airborne Sound through Ultrathin Metasurfaces. Sci. Rep. 4, 6517. doi:10.1038/srep06517
Tang, Y., Xin, F., Huang, L., and Lu, T. (2017). Deep Subwavelength Acoustic Metamaterial for Low-Frequency Sound Absorption. Epl 118, 44002. doi:10.1209/0295-5075/118/44002
Toyoda, M., Sakagami, K., Takahashi, D., and Morimoto, M. (2011). Effect of a Honeycomb on the Sound Absorption Characteristics of Panel-type Absorbers. Appl. Acoust. 72, 943–948. doi:10.1016/j.apacoust.2011.05.017
Wei, P., Croënne, C., Tak Chu, S., and Li, J. (2014). Symmetrical and Anti-symmetrical Coherent Perfect Absorption for Acoustic Waves. Appl. Phys. Lett. 104, 121902. doi:10.1063/1.4869462
Wu, X., Fu, C., Li, X., Meng, Y., Gao, Y., Tian, J., et al. (2016). Low-frequency Tunable Acoustic Absorber Based on Split Tube Resonators. Appl. Phys. Lett. 109, 043501. doi:10.1063/1.4959959
Xia, J.-p., Sun, H.-x., Yuan, S.-q., and Zhang, S.-y. (2015). Extraordinary Acoustic Transmission Based on Source Pattern Enhancement and Reconstruction by Metal cylinder Structure. Appl. Phys. Express 8, 104301. doi:10.7567/APEX.8.104301
Xie, B., Tang, K., Cheng, H., Liu, Z., Chen, S., and Tian, J. (2017). Coding Acoustic Metasurfaces. Adv. Mater. 29, 1603507. doi:10.1002/adma.201603507
Xie, Y., Wang, W., Chen, H., Konneker, A., Popa, B.-I., and Cummer, S. A. (2014). Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat. Commun. 5, 5553. doi:10.1038/ncomms6553
Yang, M., Chen, S., Fu, C., and Sheng, P. (2017). Optimal Sound-Absorbing Structures. Mater. Horiz. 4, 673–680. doi:10.1039/c7mh00129k
Yang, M., Li, Y., Meng, C., Fu, C., Mei, J., Yang, Z., et al. (2015). Sound Absorption by Subwavelength Membrane Structures: A Geometric Perspective. Comptes Rendus Mécanique 343, 635–644. doi:10.1016/j.crme.2015.06.008
Yang, M., Meng, C., Fu, C., Li, Y., Yang, Z., and Sheng, P. (2015). Subwavelength Total Acoustic Absorption with Degenerate Resonators. Appl. Phys. Lett. 107, 104104. doi:10.1063/1.4930944
Zarek, J. H. B. (1978). Sound Absorption in Flexible Porous Materials. J. Sound Vibration 61, 205–234. doi:10.1016/0022-460X(78)90004-4
Zhang, C., and Hu, X. (2016). Three-dimensional Single-Port Labyrinthine Acoustic Metamaterial: Perfect Absorption with Large Bandwidth and Tunability. Phys. Rev. Appl. 6, 064025. doi:10.1103/PhysRevApplied.6.064025
Zhang, J., Cheng, Y., and Liu, X. (2017). Extraordinary Acoustic Transmission at Low Frequency by a Tunable Acoustic Impedance Metasurface Based on Coupled Mie Resonators. Appl. Phys. Lett. 110, 233502. doi:10.1063/1.4985154
Zhou, C., Yuan, B., Cheng, Y., and Liu, X. (2016). Precise Rainbow Trapping for Low-Frequency Acoustic Waves with Micro Mie Resonance-Based Structures. Appl. Phys. Lett. 108, 063501. doi:10.1063/1.4941664
Keywords: acoustics, absorber, low-frequency sound, metasurface, bandwidth optimization
Citation: Guan Y-j, Ge Y, Sun H-x, Yuan S-q, Lai Y and Liu X-j (2021) Ultra-Thin Metasurface-Based Absorber of Low-Frequency Sound With Bandwidth Optimization. Front. Mater. 8:764338. doi: 10.3389/fmats.2021.764338
Received: 25 August 2021; Accepted: 20 September 2021;
Published: 30 September 2021.
Edited by:
Fuyin Ma, Xi’an Jiaotong University, ChinaReviewed by:
Nansha Gao, Northwestern Polytechnical University, ChinaHui Zhang, Southeast University, China
Copyright © 2021 Guan, Ge, Sun, Yuan, Lai and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hong-xiang Sun, anNkeHNoeEB1anMuZWR1LmNu; Shou-qi Yuan, c2hvdXFpeUB1anMuZWR1LmNu; Yun Lai, bGFpeXVuQG5qdS5lZHUuY24=; Xiao-jun Liu, bGl1eGlhb2p1bkBuanUuZWR1LmNu