Effects of Aromatic Thiol Capping Agents on the Structural and Electronic Properties of CdnTen (n = 6,8 and 9) Quantum Dots

Thiols are efficient capping agents used for the synthesis of semiconductor and metal nanoparticles. Commonly, long-chain thiols are used as passivating agents to provide stabilization to nanoparticles. Theoretical methods rarely reported aromatic thiol ligands’ effects on small-sized CdTe quantum dots’ structural and electronic properties. We have studied and compared the structural and electronic properties of (i) bare and (ii) aromatic thiols (thiophenol, 4-methoxybenzenethiol, 4-mercaptobenzonitrile, and 4-mercaptobenzoic acid) capped Cd_nTe_n quantum dots (QDs). Aromatic thiols are used as thiol-radical because of the higher tendency of thiol-radicals to bind with Cd atoms. This work provides an understanding of how the capping agents affect specific properties. The results show that all aromatic thiol-radical ligands caused significant structural distortion in the geometries. The aromatic thiol-radical ligands stabilize LUMOs, stabilize or destabilize HOMOs, and decrease HOMO-LUMO gaps for all the capped QDs. The stabilization of LUMOs is more pronounced than the destabilization of HOMOs. We also studied the effect of solvent on structural and electronic properties. TD-DFT calculations were performed to calculate the absorption spectra of bare and capped QDs, and all the capping ligands resulted in the redshift of absorption spectra.

Introduction

Semiconductor quantum dots (QDs), or “nanoclusters,” or “nanoparticles” of CdTe and CdSe, are gaining significant attention due to their potential applications in various fields. Optoelectronic devices (Talapin et al., 2010; Kumar and Rao, 2014; Kershaw et al., 2017) (e.g., LEDs (Anikeena et al., 2009; Zou et al., 2017), sensors (Liang et al., 2014; Kanagasubbulakshmi et al., 2018), solar cells (Yaacobi-Gross et al., 2012; Huang et al., 2014; Carey et al., 2015; Bosio et al., 2017; Xiao et al., 2018), photodetectors (Barkhouse et al., 2008; Tu and Lin, 2008; Amelia et al., 2012)) and biomedical devices (Zheng et al., 2007; Yaghini et al., 2009; He and Ma, 2014) use QDs owing to their unique properties: size tunability, changeable surface chemistry (through capping with variety of ligands) (Hines and Kamat, 2013; Hines and Kamat, 2014), photoluminescence and absorption profile (Wuister et al., 2003; Wuister et al., 2004; Weng et al., 2006; Duan et al., 2009). The surface chemistry of semiconductor QDs is important in determining the electronic and structural properties because of their large surface-to-volume ratio.

The synthesis of semiconductor QDs is carried out in various ways, among which aqueous synthesis has considerable advantages in terms of high yield, reproducibility, and selectivity. During the synthesis of QDs, capping ligands tend to cover the surface of newly synthesized QDs and alter the structural and electronic properties of QDs. Ligands-capped CdTe QDs exhibit unique tunable structural, emission, and electronic properties (Akamatsu et al., 2005; Guo et al., 2005; Yaacobi-Gross et al., 2012; Deng et al., 2013; Lin et al., 2014; Amin et al., 2015; Liu et al., 2015; Schnitzenbaumer and Dukovic, 2018).

The presence of ligands on the surface affects the nucleation and growth of QDs considerably. Knowing the ligand effect helps develop a strategy for the synthesis and manipulating the size and properties of the QDs. Experimental characterization of structures and properties during the synthesis process remains challenging due to the minimal size and short lifetime of newly formed particles of QDs. On the other hand, first-principles computational techniques have been a good instrument for investigating the structures and properties of QDs. The cluster models have been used in several theoretical studies to investigate the structural and electronic properties of bare and ligated CdSe/CdTe QDs (Bhattacharya and Kshirsagar, 2007; Bhattacharya and Kshirsagar, 2008; Wang et al., 2009; Xu et al., 2010a; Seal et al., 2010; Haram et al., 2011; Kuznetsov et al., 2012; Lim et al., 2012; Ma et al., 2012; Leubner et al., 2013; Lin et al., 2013; Sriram and Chandiramouli, 2013; Wu et al., 2013; Alnemrat et al., 2014; Kuznetsov and Beratan, 2014; Rajbanshi et al., 2014; Sarkar et al., 2014; Shah and Roy, 2014; Aruda et al., 2016; Kilina et al., 2016; Swenson et al., 2016; Cao et al., 2018). Mainly, these studies were limited to exploring the capping effects of aliphatic ligands on the structural, electronic, and optical properties of CdTe QDs. Most of these computational studies have been conducted on small-sized QDs because of significant challenges associated with the atomistic simulation of large-sized QDs (Bhattacharya and Kshirsagar, 2007; Wang et al., 2009; Seal et al., 2010; Ma et al., 2012). These studies determined the possible lowest energy structures and optical properties of Cd_nTe_n (n = 1–16, 19, 20, 24, 28) nanoclusters employing the first-principles calculations.

Recent computational and experimental studies have confirmed the utilization of aromatic capping ligands in synthesis and the capping exchange process of CdSe/CdTe QDs (Bloom et al., 2013; Lin et al., 2013; Kumar et al., 2015; Aruda et al., 2016; Swenson et al., 2016). However, significant and systematic studies that would have investigated the effect of aromatic ligands on the structural, electronic, and optical properties of CdTe QDs are rare. Hence, the present study aims to fill that knowledge gap and provide a systematic computational analysis of the structural, electronic, and optical properties of aromatic thiol capped CdTe QDs.

In one of our previous studies, we had performed an extensive search for the lowest energy geometries of Cd_nTe_n QDs (n = 1–17) using particle swarm optimization (PSO) algorithms and density functional theory (DFT) approaches and explored structural and electronic properties (Imran et al., 2019). The present study presents structural and electronic properties of bare and capped small-sized Cd_nTe_n (n = 6,8 and 9) QDs. We have used four aromatic thiol ligands for capping: thiophenol (TP), 4-methoxybenzene-thiol (MBT), 4-mercaptobenzonitrile (MBN), and 4-mercaptobenzoic acid (MBA) (see Figure 1).

FIGURE 1

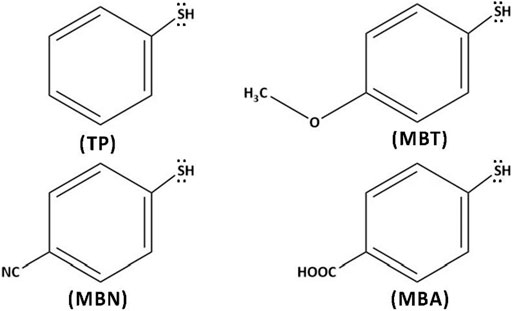
FIGURE 1. Structures of the capping ligands: thiophenol (TP), 4-methoxybenzenethiol (MBT), 4-mercaptobenzonitrile (MBN), and 4-mercaptobenzoic acid (MBA).

Computational Methods

All the calculations described here were performed using the Gaussian 09W package (Frisch et al., 2013). Recent studies have used the simulated annealing technique to find CdTe clusters’ lowest energy structures (Wang et al., 2009; Ma et al., 2012). Our previous study performed an extensive structural search for CdTe clusters using PSO algorithms as implemented in CALYPSO, evaluated the candidate clusters by DFT and MP2 theory levels. We re-used the lowest energy CdTe structures from our previous work for the sake of the present work (Imran et al., 2019). All the symmetric structures of bare and capped QDs were optimized without symmetry constraints. Vibrational frequency analysis indicated that optimized QD structures are actual minimum energy structures.

All the calculations were performed using hybrid functional B3LYP (Becke, 1993) with basis sets of Los Alamos double-ζ effective core potential (Lanl2dz) (Hay and Wadt, 1985a; Hay and Wadt, 1985b; Wadt et al., 1985) in the gas phase as implemented in the Gaussian 09W package. Earlier studies had found the B3LYP/Lanl2dz level of theory to be a practical approach in terms of accuracy and efficiency when used to study CdTe and CdSe bare and capped QDs (Kuznetsov et al., 2012; Lim et al., 2012; Kuznetsov and Beratan, 2014). However, utilizing the B3LYP functional may underestimate the HOMO-LUMO gaps and excited-state energy, which may be corrected by using range-separated functionals, as shown in previous studies (Salzner and Aydin, 2011; Kurban et al., 2019; Muz and Kurban, 2020). In small-sized QDs, all the cadmium atoms are exposed to the surface and potentially coordinated with ligands. We also varied the number of ligands attached to QDs to explore the effect of ligand density on the structural and electronic properties of QDs. Theoretical studies were simulated in toluene solvent (dielectric constant ε = 2.2706). The ligand-binding energies (BE) were calculated with the help of the following equation:

$\text{BE}=\left[\text{E}\left({\text{Cd}}_{\text{n}}{\text{Te}}_{\text{n}}{\text{L}}_{\text{n}}\right)-\left(\text{E}\left({\text{Cd}}_{\text{n}}{\text{Te}}_{\text{n}}\right)+\text{nE}\left(\text{L}\right)\right)\right]/\text{n}$

Where E(Cd_nTe_nL_n) is the energy of capped QD, E(Cd_nTe_n) is the energy of bare QD, and E(L) is the energy of the capping agent. Time-dependent DFT calculations were performed using the B3LYP/Lanl2dz approach both in the gas and implicit solvent to study the electronic transitions of both bare and capped QDs. Calculated spectra were plotted with the help of Gabedit 2.5.0 (Allouche, 2011) to determine λ_max/E_max from plots. Molecular structures and orbitals were visualized using Molden 5.8 (Schaftenaar and Noordik, 2000) and GaussView, respectively.

Results and Discussion

Bare Cd_nTe_n (n = 6,8 and 9) Quantum Dots

Figure 2 shows the minimum energy structures of bare Cd₆Te₆, Cd₈Te₈, and Cd₉Te₉ QDs in the gas phase and their Frontier molecular orbitals. Table 2 shows calculated HOMO/LUMO energies, HOMO-LUMO gaps, E_max, and λ_max.

FIGURE 2

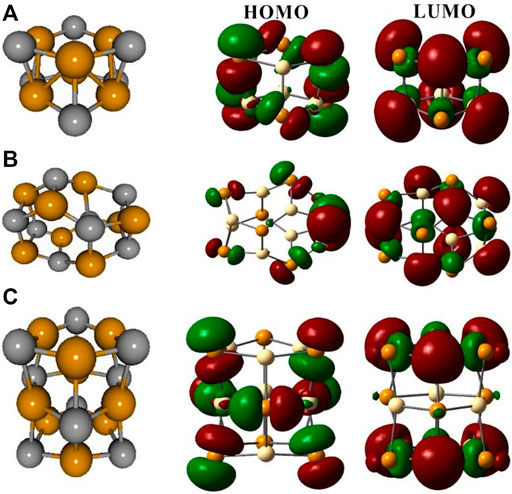
FIGURE 2. Optimized gas-phase structures and Frontier orbitals of bare Cd₆Te₆(A), Cd₈Te₈(B) and Cd₉Te₉(C) QDs. Dark yellow spheres represent Cd, and gray spheres represent Te.

Cd₆Te₆ (C_3v symmetry) structure shows that it consists of stacks of Cd₃Te₃ rings of hexagonal shape with a Cd-Te bond distance of 2.87 Å inside the hexagonal rings Cd-Te bond distance between the two layers is 3.045 Å.

Cd-Te bond lengths in Cd₈Te₈ (S₄ symmetry) are calculated to be 2.856–3.002 Å in distorted six Cd₂Te₂ rhombi and four Cd₃Te₃ hexagonal rings.

Cd₉Te₉ (D_3h symmetry) consists of three interconnected Cd₃Te₃ hexagonal rings, and Cd-Te bond lengths in upper and lower hexagonal layers are 2.85 Å, while in the middle layer, Cd-Te bond lengths expand to 2.994 Å. The interlayer Cd-Te bond lengths are calculated to be 3.163 Å which is greater than the interlayer bond length of Cd₆Te₆ QD.

Geometry optimization with implicit solvent (toluene) and gas-phase gave similar geometries for all QDs. However, the amount of NBO charges on Cd and Te atoms increased by adding implicit solvent (toluene) during calculations.

In the gas phase, HOMO-LUMO gaps of Cd6Te6, Cd8Te8, and Cd9Te9 QDs revealed that all the QDs were semiconductor-like (Table 1). The calculated HOMO-LUMO gaps are 3.05, 3.09, and 2.76 eV for Cd₆Te₆, Cd₈Te₈, and Cd₉Te₉ QDs. Generally, an increase in the size of QDs decreases HOMO-LUMO gaps, but in the present study, HOMO-LUMO gaps of Cd₉Te₉ QD are less than Cd₆Te₆ QD while Cd₈Te₈ QD shows a higher HOMO-LUMO gap than the other two species. We attribute this observation to different structural motifs of each size of QD. Cd₆Te₆ and Cd₉Te₉ are similar to wurtzite structures with six atoms in a ring, whereas Cd₈Te₈ is somewhat similar to zinc-blende structures. Probably this structural difference is the reason behind the unexpected higher bandgap of Cd₈Te₈.

TABLE 1

TABLE 1. Calculated E_HOMO and E_LUMO energies (eV), HOMO-LUMO gaps (eV) of bare Cd_nTe_n (n = 6, 8, and 9) QDs in the gas phase, and toluene with B3LYP/Lanl2dz approach.

Table 2 presents TD-DFT calculations of excitation energies (E_max) and absorption wavelengths (λ_max) of excited states with maximum oscillator strength. The calculated excitation energies (E_max) of bare QDs in the gas phase are close to the HOMO-LUMO gaps of the same QDs and consistent with the previous computational report (Lim et al., 2012). The inclusion of toluene solvent in calculations slightly increased the excitation energies. A blue shift in the absorption maxima caused by the solvent is an interesting observation. One may find few previously published studies on solvents’ effect on the absorption spectrum of CdSe clusters reporting a blue shift occurrence (Xu et al., 2010a; Xu et al., 2010b; Lim et al., 2012). In our research, we have observed a similar blue shift occurrence in the case of CdTe clusters.

TABLE 2

TABLE 2. Calculated E_HOMO energy (eV), E_LUMO energy (eV), HOMO-LUMO gaps (eV), excitation energies (E_max) (eV), and maximum absorption wavelengths (λ_max) (nm), of the excited states with maximum oscillator strength of bare Cd_nTe_n (n = 6, 8, and 9) QDs in the gas phase and toluene with TDB3LYP/Lanl2dz approach.

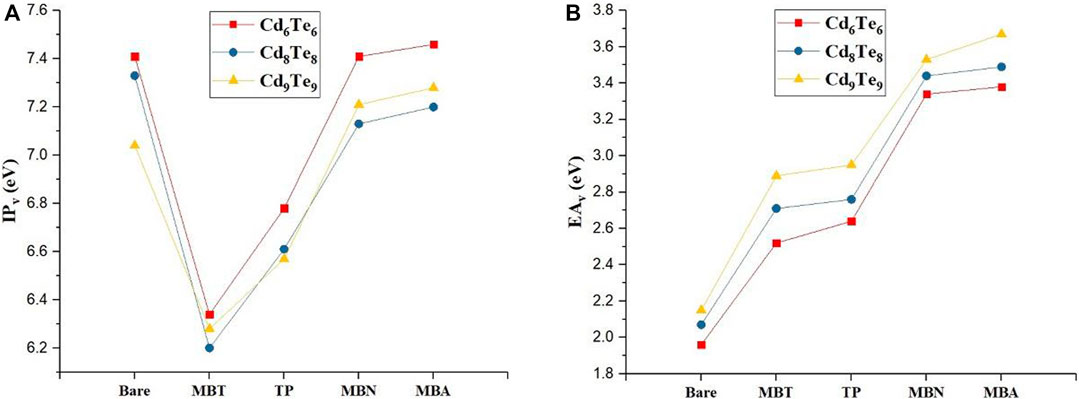
IP_v and EA_v values are considered to be an index of stability of QDs. It is energetically not favorable for QDs with large IP_v and EA_v values to be activated toward a chemical reaction. Hence, QDs with large IP_v and EA_v values can be considered more stable. Calculated IP_v/IP_ad values and EA_v/EA_ad values are given in Table 3. It is observed that IP_v/IP_ad values decrease with an increase in the size of bare QDs, while EAv/EAad values increase gradually with an increase in the size of bare QDs.

TABLE 3

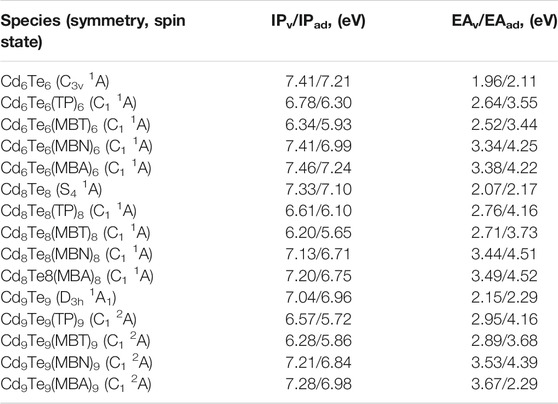
TABLE 3. Calculated vertical and adiabatic IPs and EAs (eV) in the gas phase of bare Cd_nTe_n (n = 6, 8, and 9) QDs and capped Cd_nTe_nL_n QDs (where L = TP, MBT, MBN, and MBA) using B3LYP/Lanl2dz level of theory.

Capped Cd_nTe_n (n = 6,8 and 9) Quantum Dots

We capped CdTe QDs with aromatic thiol-radical ligands: TP (C₆H₅S-), MBT (CH₃OC₆H₄S-), MBN (CNC₆H₄S-), and MBA (COOHC₆H₄S-), (see Figure 1). The aromatic ligands were coordinated to the QDs via sulfur, which significantly changed the geometries of bare QDs after geometry relaxation. We explored different numbers of capping ligands and different modes of ligands’ coordination with QD.

Cd₆Te₆L₆ and Cd₆Te₆L₄ (L = TP, MBT, MBN, and MBA) species gave stable and physically acceptable geometry after geometry relaxation. For both Cd₆Te₆L₆ and Cd₆Te₆L₄ species, different geometries arose from bare QD because of Cd-Te bond breakage and Cd-S-Te bridge formation in the form of a 5-membered ring. However, the overall structural motif remained intact, containing interconnected two hexagonal (6-membered rings) layers (see Figure 3 and Supplementary Figure S1). Closed structural configurations were observed after optimization of Cd₆Te₆L₆ and Cd₆Te₆L₄ species, and these results are different from previous works of Kuznetsov et al. (2012), Lim et al. (2012), where they had capped Cd₆Te₆ with small-sized ligands and observed open structures after geometry relaxation.

FIGURE 3

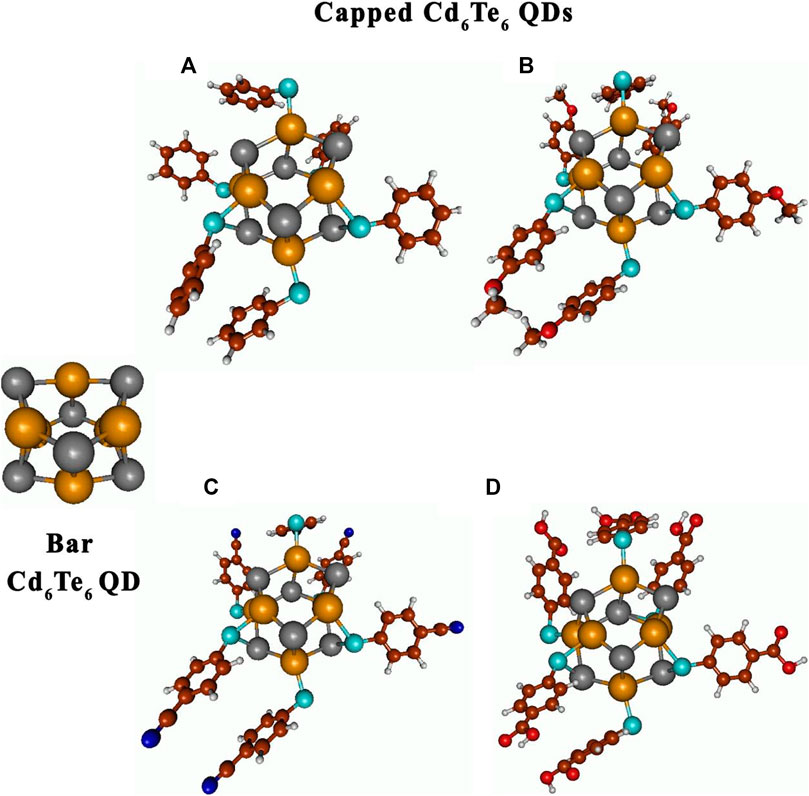
FIGURE 3. Optimized gas-phase structures of bare and capped Cd₆Te₆ QDs: Cd₆Te₆(TP)₆(A), Cd₆Te₆(MBT)₆(B), Cd₆Te₆(MBN)₆(C), and Cd₆Te₆(MBA)₆(D). Atoms are represented as follows: Cd by dark yellow spheres, Te by dark gray spheres, C brown spheres, H light gray sphere, O red spheres, S sapphire spheres, and N blue spheres.

The capping of Cd₈Te₈ QDs (with S₄ point group) by all four aromatic ligands led to a slight opening of the bare QD structure due to Cd-Te bond breakage, Cd-S-Cd bridge formation with 4-membered rings, Cd-S-Te bridge formation with 5-membered rings, and formation of one 8-membered ring. We explored the geometries of two Cd₈Te₈L₈ and Cd₈Te₈L₄ species and found that ligands caused a slight opening of the bare QD structure in both cases. On a relative scale, the coordination of eight ligands caused a larger opening than four ligands (see Figure 4 and Supplementary Figure S2).

FIGURE 4

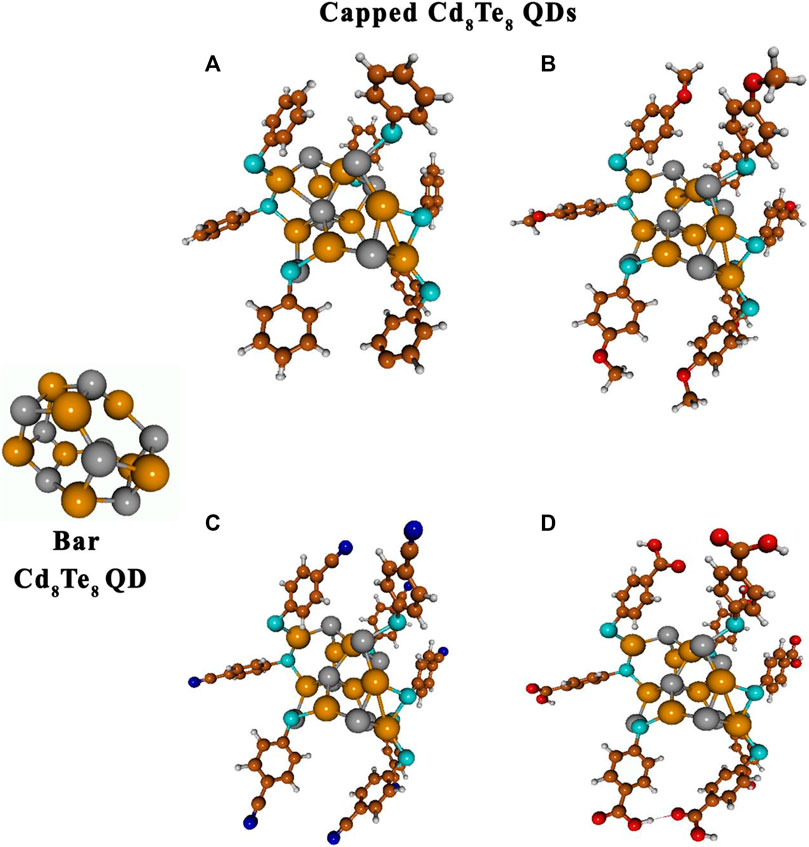
FIGURE 4. Optimized gas-phase structures of bare and capped Cd₈Te₈ QDs: Cd₈Te₈(TP)₈(A), Cd₈Te₈(MBT)₈(B), Cd₈Te₈(MBN)₈(C), and Cd₈Te₈(MBA)₈(D). Atoms are represented as follows: Cd by dark yellow spheres, Te by dark gray spheres, C brown spheres, H light gray sphere, O red spheres, S sapphire spheres, and N blue spheres.

Similarly, Cd₉Te₉ QD (with D_3h point group) was also capped with the aromatic thiol-radical ligands, which led to significant changes in QD’s structure compared to its bare lowest energy structure (see Figure 5 and Supplementary Figure S3). Optimized structures of Cd₉Te₉L₉ species showed open structures with a hexagonal ring at the center while above and lowered layer opened up to stabilize the structure. It resulted in Cd-Te bond breakage, Cd-S-Cd bridge formation with 4-membered rings, and Cd-S-Te bridge formation with 5-membered rings. However, in the case of Cd₉Te₉L₄ species with a smaller number of capping ligands attached to QDs, the closed-shell configuration of Cd₉Te₉ QDs remained intact with the slight opening of the QDs structures. These changes in the structure of capped Cd₉Te₉ QDs also arise from the formation of multiple Cd-S-Te bridges in 5-membered ring configuration and breakage of Cd-Te bonds. These findings are consistent with the previous works of Kuznetsov et al. (2012), Lim et al. (2012).

FIGURE 5

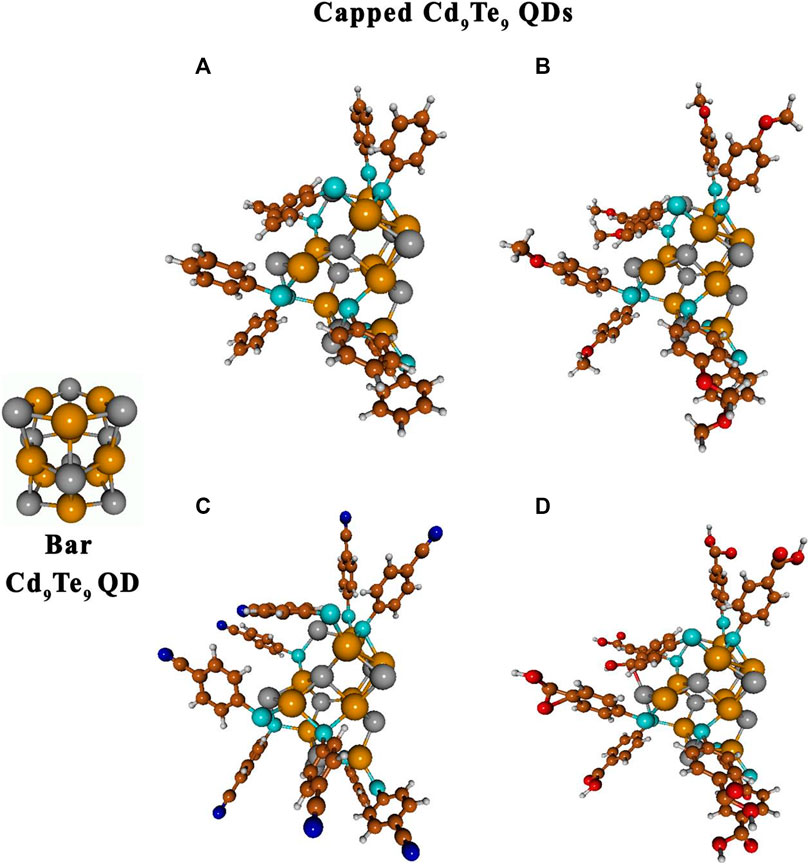
FIGURE 5. Optimized gas-phase structures of bare and capped Cd₉Te₉ QDs: Cd₉Te₉(TP)₉(A), Cd₉Te₉(MBT)₉(B), Cd₉Te₉(MBN)₉(C), and Cd₉Te₉(MBA)₉(D). Atoms are represented as follows: Cd by dark yellow spheres, Te by dark gray spheres, C brown spheres, H light gray sphere, O red spheres, S sapphire spheres, and N blue spheres.

We performed NBO charge analysis to explore the distribution of charges on QDs after capping with aromatic ligands. Cd atoms in all Cd₆Te₆L₆ species displayed positive charges that range from 0.71e to 0.85e. While positive charges on Cd atoms in bare Cd₆Te₆ QDs were 0.76e. There was an increase in the positive charge on Cd atoms in all capped QDs. The ranges of negative charges on Te atoms in capped Cd₆Te₆L₆ species were from −0.11e to −0.77e, close to −0.76e charge on Te atoms in bare Cd₆Te₆ QD.

In Cd₈Te₈L₈ species, the positive charges on the Cd atoms were also higher than bare Cd₈Te₈ QD. The positive charges on Cd atoms in ligated Cd₈Te₈L₈ species were in the range of 0.64e to 0.94e. Compared to bare Cd₈Te₈ QD, there was no significant negative charge change on Te atoms in ligated Cd₈Te₈L₈ species. However, those Te atoms which formed a bridge configuration of Cd-S-Te in capped Cd₈Te₈L₈ species displayed low negative charges.

In bare Cd₉Te₉ QD, the range of positive charges on Cd atoms and negative charges on Te atoms were (0.71–0.79)e and -(0.72–0.85)e, respectively. The range of positive charges on Cd atoms in Cd₉Te₉L₉ species was 0.74e to 0.91e. The negative charges on the Te atom in ligated Cd₉Te₉L₉ species varied from −0.05e to −0.87e. Both positive and negative charge distribution in capped Cd₉Te₉L₉ species varied tremendously. A significant negative charge accumulates on the oxygen of the methoxy group of MBT, the nitrogen of the nitrile group of MBN, and oxygens of the carboxyl group of MBA.

At the CdTe-ligand interface, the charge interchange between the ligand and the QD produces a dipole layer that could influence the oxidation potential of QDs. The extent of charge transfer between the ligand and the QDs determines the strength of the dipole layer. Adsorption of ligands to the QDs causes a change in the net charge of the capping ligands. Table 4 presents the total net change in the NBO charge of capping ligands and the net change in the NBO charge per ligand for all capped QDs. A negative value of net charge transfer by ligands indicates that ligands withdraw electron density from the QDs. The net NBO charge change is in the following order: Cd_nTe_n(MBA)_n > Cd_nTe_n(MBN)_n > Cd_nTe_n(TP)_n > Cd_nTe_n(MBT)_n for each value of n.

TABLE 4

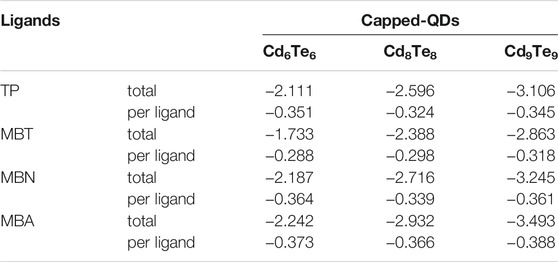
TABLE 4. Ligand’s total net charge change and net charge change per ligand (in e unit) for capped Cd_nTe_nL_n (n = 6, 8, and 9) QDs (where L = TP, MBT, MBN, and MBA) calculated with B3LYP/Lanl2dz approach in the gas phase.

Calculated ligand binding energies are given in Table 5. The ligand-binding energies of all ligated QDs decrease in the following order: Cd_nTe_n(MBA)_n > Cd_nTe_n(MBN)_n > Cd_nTe_n(TP)_n > Cd_nTe_n(MBT)_n for each value of n. A possible explanation of this sequence of ligand binding energies can be the HOMOs, and LUMOs stabilization, and higher IP_v and EA_v values depicted by MBA and MBN capped QDs (see Table 1, 2, and 5). On the other hand, Cd_nTe_n(MBT)_n and Cd_nTe_n(TP)_n present lower ligand binding energy due to their HOMOs destabilization and low IP_v and EA_v values. These results are also reflected in NBO charge analysis, where MBA exhibits the biggest charge change by withdrawing electrons density from the QDs. Charge analysis also reveals that oxygens of -COOH groups in Cd_nTe_n(MBA)_n possess greater charges about −(0.598–0.787)e compared to the nitrogen of -CN groups in Cd_nTe_n(MBN)_n that shows charges about −(0.308–0.363)e. This could be another reason for higher ligand binding energies of Cd_nTe_n(MBA)_n. Our calculated ligand binding energies values are close to the previous findings of Lim and co-workers (Lim et al., 2012), who calculated binding energies with the B3LYP/Lanl2dz approach in the gas phase for Cd_nSe_n/Cd_nTe_n QDs (n = 3,4,6, and 9) capped with SCH₂COOH–, SCH₂CH₂CO₂H–, and SCH₂CH₂NH₂ ligands. Our calculated values also agree with the work of Kuznetsov and co-workers (Kuznetsov et al., 2012), who studied Cd_nSe_n/Cd_nTe_n QDs (n = 6,9) capped with NH₃, SCH₃, and OPH₃ ligands in the gas phase using B3LYP/Lanl2dz approach.

TABLE 5

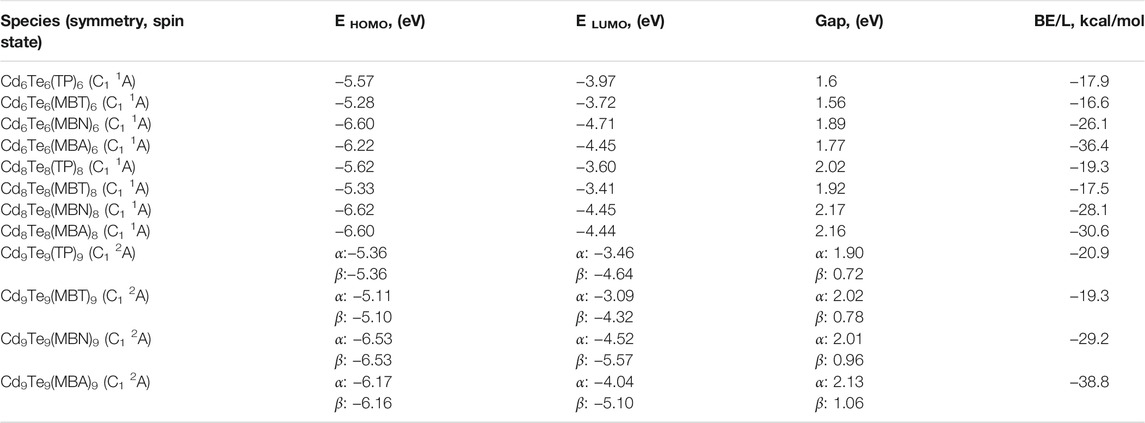
TABLE 5. E_HOMO and E_LUMO energies (eV), HOMO-LUMO gaps (eV), and binding energy (BE/L) in kcal/mol of capped Cd_nTe_nL_n (n = 6, 8, and 9) QDs (where L = TP, MBT, MBN, and MBA) calculated with B3LYP/Lanl2dz approach.

Figure 6 presents the interaction of S containing ligands with Cd₆Te₆ QD frontier orbitals. The partial density of states (PDOS) plots (see Figure 7) shows the dominant contributions of sulfur 3p orbitals of the aromatic thiol-radical ligands in the HOMOs of capped Cd₆Te₆ QDs with minor contributions from QD atoms. On the other hand, the LUMOs of the capped Cd₆Te₆ QD show high contributions from both QD atoms and ligand groups: with slightly higher contributions from Te atoms (see Figure 7). The S containing ligands tend to use their lone pair and their unpaired electrons to interact with Cd and Te atoms. An unpaired electron is present in the sulfur 3p orbital of thiol-radical ligands. Seemingly, the singly occupied β-LUMOs of thiol-radical ligands favorably interact with the doubly occupied HOMO of the QD, which possesses some d-character from Cd atoms. This interaction destabilizes the HOMO of the capped QDs, as depicted in Figures 7A,B. The interaction of the LUMOs of QD with the α-LUMOs and β-LUMOs of thiol-radical ligands highly stabilizes the LUMOs of the capped QDs.

FIGURE 6

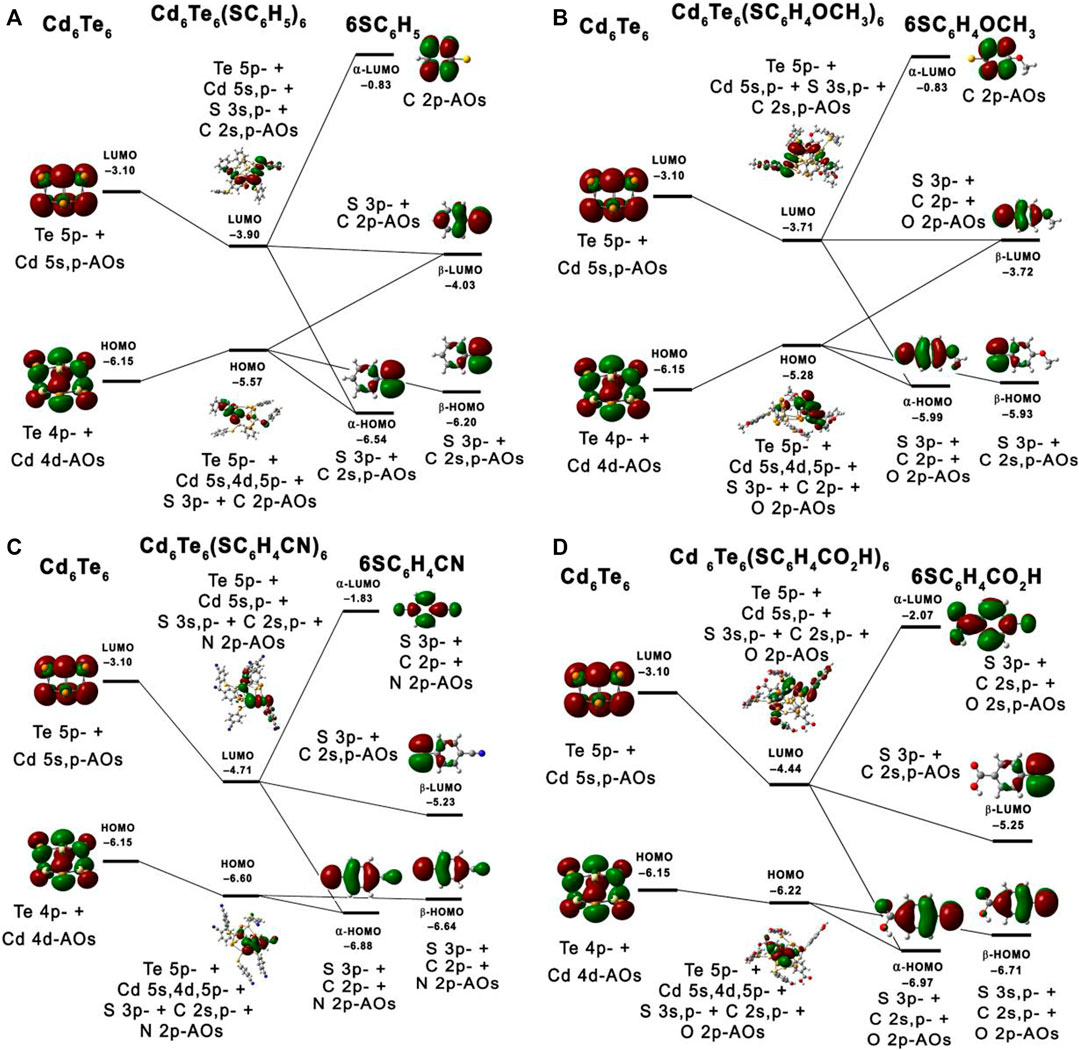
FIGURE 6. Orbital mixing diagram depicting interactions between HOMOs and LUMOs of the capped Cd₆Te₆(TP)₆(A), Cd₆Te₆(MBT)₆(B), Cd₆Te₆(MBN)₆(C) and Cd₆Te₆(MBA)₆(D) QDs.

FIGURE 7

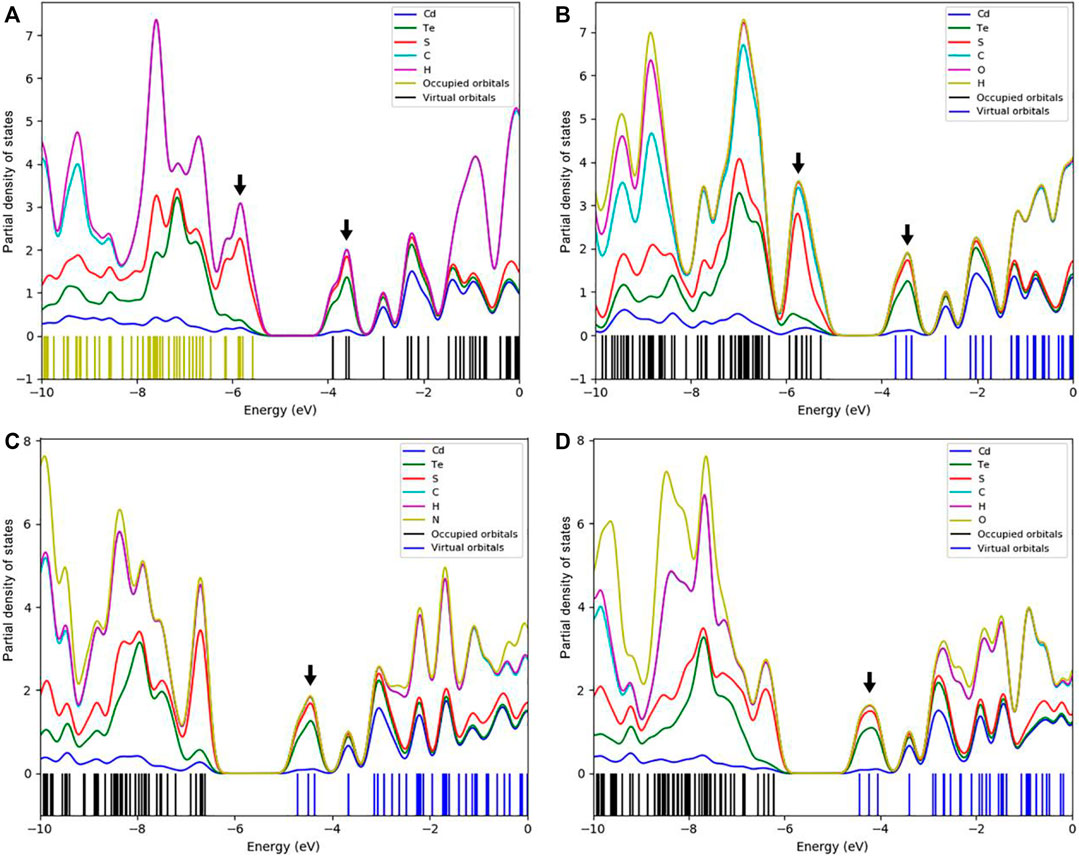
FIGURE 7. The partial density of states (PDOS) plots (stacked) near the HOMO/LUMO gaps for the capped Cd₆Te₆(TP)₆(A), Cd₆Te₆(MBT)₆(B), Cd₆Te₆(MBN)₆(C) and Cd₆Te₆(MBA)₆(D) QDs calculated with B3LYP/Lanl2DZ approach.

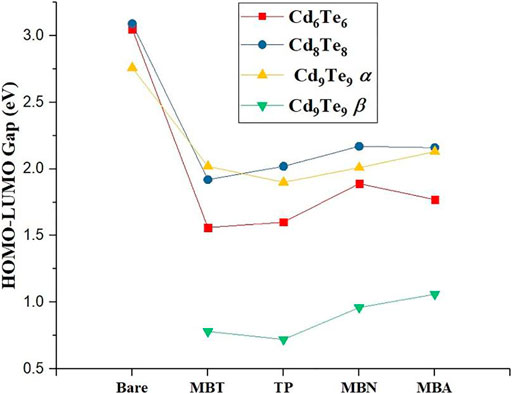
Capping with all four aromatic thiol-radical ligands stabilize the LUMOs of all QDs, while HOMOs are either stabilize or destabilize (see Tables 2 and 5). Both TP and MBT ligands destabilize HOMOs in all capped QDs. The effect is much prominent for HOMOs of MBT capped QDs: MBT destabilizes the HOMO by 8.72 eV for Cd₆Te₆, 8.68 eV for Cd₈Te_8, and 8.44 eV for Cd₉Te₉.

On the other hand, both MBN and MBA ligands tend to stabilize HOMOs of all capped QDs. MBN capped QDs show a more pronounced effect with HOMOs stabilization by 4.52 eV for Cd₆Te₆, 4.19 eV for Cd₈Te₈, and 5.82 eV for Cd₉Te₉. All the aromatic thiol-radical ligands decrease the HOMO-LUMO gap of all the capped QDs (see Tables 2 and 5) due to the interaction of frontier orbitals of ligands with frontier orbitals of QDs, as shown in Figure 8. These observations are due to the stronger stabilization of LUMOs as compared to HOMOs. A drastic decrease in the HOMO-LUMO gap is observed for capped Cd₆Te₆ QDs: 1.45 eV for Cd₆Te₆(TP)₆, 1.49 eV for Cd₆Te₆(MBT)₆, 1.16 eV for Cd₆Te₆(MBN)₆, and 1.28 eV for Cd₆Te₆(MBA)₆. While all the other capped QDs show a less pronounced decrease in the HOMO-LUMO gap. This effect of thiol-radical capping ligands is in line with the previous report, where SCH₂COOH, SCH₂CH₂CO₂H, and SCH₂CH₂NH₂ capped Cd_nSe_n/Cd_nTe_n QDs (n = 3,4,6, and 9) were studied by Lim et al. (2012).

FIGURE 8

FIGURE 8. HOMO-LUMO gap (eV) for bare and capped Cd_nTe_nL_n (n = 6, 8, and 9) QDs.

We further explore the effect of aromatic thiol-radical ligands on vertical and adiabatic IPs and EAs of QDs in the gas phase (see Table 1 and Figure 9). Analysis of IP/EA values for bare, and capped QDs reveals that both IP_v/IP_ad values show a decrease after capping with all aromatic thiol-radical ligands. However, Cd₆Te₆(MBA)₆, Cd₉Te₉(MBN)_9, and Cd₉Te₉(MBA)₉ species exhibited an increase in IP_v/IP_ad values as compared to bare QDs. EA_v/EA_ad values increase after capping with all aromatic thiol-radical ligands as compared to bare QDs. It is worth noticing that the capping of QDs with MBT ligand causes the highest decrease in IPv values. Generally, IP_v and EA_v values are considered to be an index of stability of capped-QDs. It is energetically not favorable for QDs with large IP_v and EA_v values to be activated toward a chemical reaction. Hence QDs with large IP_v and EA_v values can be more stable toward a chemical reaction. It is observed that IP_v and EA_v values of capped-QDs decrease in the order MBA > MBN > TP > MBT, so the large IP_v and EA_v values of MBA capped QDs are associated with their higher stability.

FIGURE 9

FIGURE 9. IP_v(A) and EA_v(B) for bare and capped Cd_nTe_nL_n (n=6, 8, and 9) QDs.

The density of states (DOS) plots of thiol-radical ligands revealed the presence of midgap states which were not present in the parent thiol ligands. The conversion of thiol into thiol-radical by dehydrogenation generates one singly occupied 3p orbital of the sulfur, which appears as midgap states between the HOMO and LUMO states (see Supplementary Figures S5, S6). The PDOS plots of Cd₆Te₆L₆ species are presented in Figure 7 as a representative, while DOS plots of the rest of ligands and QDs (both bare and capped species) are given in the supporting information. As indicated in Figure 7, the Frontier orbitals of the capped Cd₆Te₆ QDs are mainly composed of ligands’ orbitals, which affect the electronic properties of capped QDs, especially the HOMOs and LUMOs energies of the QDs.

To probe the effect of capping on electronic transitions of QDs, we also performed a TD-DFT study. TDB3LYP/Lanl2dz calculations for bare and capped QDs are given in Tables 3 and 6. We computed excitation energies (E_max), and maximum absorption wavelengths (λ_max) for maximum intensity excited states in the gas phase and with implicit solvent (toluene).

TABLE 6

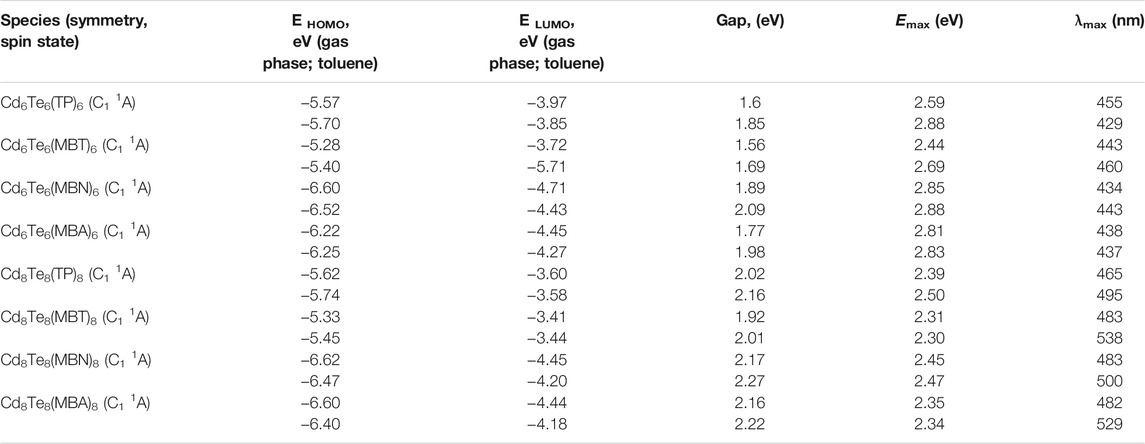
TABLE 6. Calculated E_HOMO energy (eV), E_LUMO energy (eV), HOMO-LUMO gaps (eV), excitation energies (E_max) (eV), and maximum absorption wavelengths (λ_max) (nm), of the excited states with maximum oscillator strength of capped Cd_nTe_nL_n (n = 6 and 8) QDs (where L = TP, MBT, MBN, and MBA) in the gas phase and toluene.

All ligated QDs displayed a decrease in excitation energies compared to the excitation energies of their respective bare QDs. For capped QDs species, all the thiol-radical ligands altered the absorption spectra of bare Cd₆Te₆ and Cd₈Te₈ QDs by shifting the absorption peaks towards lower energy (redshift) because of the midgap states generated by 3p orbitals of sulfur, as shown in Figure 10. Aromatic ligands are known to influence the electronic and optical properties of QDs by stabilizing the LUMOs and reducing the bandgap. The delocalization of the exciton across the ligand shell is attributed to a significant redshift in the absorption spectra of capped CdTe QDs compared to bare QDs. The ligands’ Frontier orbitals coincide with the bandgap of CdTe QDs. Such a resonance situation might generate interfacial QD-ligand states, which would improve the optical properties of the QDs and perhaps open up new relaxation routes for photoexcited charge carriers, hence cause a redshift of the absorption peaks in capped QDs.

FIGURE 10

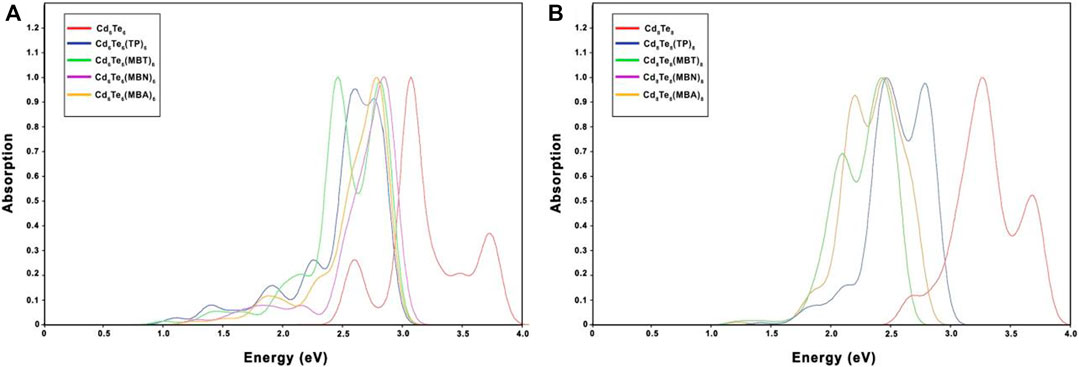
FIGURE 10. Absorption spectra of bare and capped Cd₆Te₆(A) and Cd₈Te₈(B), calculated with TDB3LYP/Lanl2DZ approach.

The addition of the solvent shifted the redshift toward higher wavelengths for all capped QDs except for Cd₆Te₆(TP)₆ and Cd₆Te₆(MBA)₆ QDs. It was observed that the redshift in the gas phase for capped-Cd₆Te₆ QDs decreased in the following order: TP > MBT > MBA > MBN. For capped-Cd₈Te₈ QDs, it decreased in the order: MBT ≈ MBN > MBA > TP. These results align with previous studies of similar QDs, which suggested that aromatic thiol ligands cause a redshift of the spectrum (Tan et al., 2012; Nadler and Sanz, 2015; Plata et al., 2017).

Conclusion

The effects of aromatic thiol-radical ligands on the structural and electronic properties of Cd_nTe_n quantum dots (n = 6,8,9) were investigated by a systematic DFT study using B3LYP/Lanl2dz theory level. We chose thiophenol (TP), 4-methoxybenzene-thiol (MBT), 4-mercaptobenzonitrile (MBN), and 4-mercaptobenzoic acid (MBA) as model capping ligands (see Figure 1). All the four ligands coordinated to the Cd_nTe_n QDs successfully and formed stable ligand-QD species when subjected to geometry optimization. Generally, the ligands slightly opened up the Cd₆Te₆ and Cd₈Te₈ QDs, but the overall structural motif remained intact. While in the case of Cd₉Te_9, QDs capping with ligands caused the complete opening of the closed structure of bare QDs. Each QDs ligands-QD complexes shows a steady increase in ligand binding energies in the order: MBT < TP < MBN < MBA. The capping of aromatic thiol-radical ligands causes a slight increase in Cd atoms’ positive charges due to their electron-withdrawing ability. Adsorption of the ligands decreases the HOMO-LUMO gap due to the stabilization of the LUMOs of QDs. Finally, the TD-DFT study revealed that all the ligands shifted the absorption spectra to redshift in the gas phase and with implicit solvent (toluene).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The research idea belongs to MJS. MI performed major computational work. TF and JI have significantly contributed to the discussion and write-up.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.755332/full#supplementary-material

References

Akamatsu, K., Tsuruoka, T., and Nawafune, H. (2005). Band gap Engineering of CdTe Nanocrystals through Chemical Surface Modification. J. Am. Chem. Soc. 127 (6), 1634–1635. doi:10.1021/ja044150b

CrossRef Full Text | Google Scholar

Allouche, A.-R. (2011). Gabedit-A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 32, 174–182. doi:10.1002/jcc.21600

CrossRef Full Text | Google Scholar

Alnemrat, S., Ho ParkVasiliev, Y. I., and Vasiliev, I. (2014). Ab Initio study of ZnSe and CdTe Semiconductor Quantum Dots. Physica E: Low-dimensional Syst. Nanostructures 57, 96–102. doi:10.1016/j.physe.2013.10.037

CrossRef Full Text | Google Scholar

Amelia, M., Lincheneau, C., Silvi, S., and Credi, A. (2012). Electrochemical Properties of CdSe and CdTe Quantum Dots. Chem. Soc. Rev. 41 (17), 5728–5743. doi:10.1039/c2cs35117j

PubMed Abstract | CrossRef Full Text | Google Scholar

Amin, V. A., Aruda, K. O., Lau, B., Rasmussen, A. M., Edme, K., and Weiss, E. A. (2015). Dependence of the Band Gap of CdSe Quantum Dots on the Surface Coverage and Binding Mode of an Exciton-Delocalizing Ligand, Methylthiophenolate. J. Phys. Chem. C 119 (33), 19423–19429. doi:10.1021/acs.jpcc.5b04306

CrossRef Full Text | Google Scholar

Anikeena, P. O., Halpert, J. E., Bawendi, M. G., and Bulovic, V. (2009). Quantum Dot Light-Emitting Devices with Electroluminescence Tunabe over the Entire Visible Spectrum. Nano Lett. 9, 2532–2536. doi:10.1021/nl9002969

PubMed Abstract | CrossRef Full Text | Google Scholar

Aruda, K. O., Amin, V. A., Thompson, C. M., Lau, B., Nepomnyashchii, A. B., and Weiss, E. A. (2016). Description of the Adsorption and Exciton Delocalizing Properties of P-Substituted Thiophenols on CdSe Quantum Dots. Langmuir 32 (14), 3354–3364. doi:10.1021/acs.langmuir.6b00689

PubMed Abstract | CrossRef Full Text | Google Scholar

Barkhouse, D. A. R., Pattantyus-Abraham, A. G., Levina, L., and Sargent, E. H. (2008). Thiols Passivate Recombination Centers in Colloidal Quantum Dots Leading to Enhanced Photovoltaic Device Efficiency. ACS Nano 2 (11), 2356–2362. doi:10.1021/nn800471c

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (1993). Density‐functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98 (7), 5648–5652. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

Bhattacharya, S. K., and Kshirsagar, A. (2007). Ab Initio calculations of Structural and Electronic Properties of CdTe Clusters. Phys. Rev. B 75 (3), 035402. doi:10.1103/physrevb.75.035402

CrossRef Full Text | Google Scholar

Bhattacharya, S. K., and Kshirsagar, A. (2008). First Principle Study of Free and Surface Terminated CdTe Nanoparticles. Eur. Phys. J. D 48 (3), 355–364. doi:10.1140/epjd/e2008-00114-3

CrossRef Full Text | Google Scholar

Bloom, B. P., Zhao, L.-B., Wang, Y., Waldeck, D. H., Liu, R., Zhang, P., et al. (2013). Ligand-Induced Changes in the Characteristic Size-dependent Electronic Energies of CdSe Nanocrystals. J. Phys. Chem. C 117 (43), 22401–22411. doi:10.1021/jp403164w

CrossRef Full Text | Google Scholar

Bosio, A., Rosa, G., and Romeo, N. (2017). Past, Present and Future of the Thin Film CdTe/CdS Solar Cells. Sol. Energ. 175, 31–43. doi:10.1016/j.solener.2018.01.018

CrossRef Full Text | Google Scholar

Cao, A., Tan, T., Zhang, H., Du, Y., Sun, Y., and Zha, G. (2018). Electronic Structures and Optical Properties of the CdTe/CdS Heterojunction Interface from the First-Principles Calculations. Physica B: Condensed Matter 545, 323–329. doi:10.1016/j.physb.2018.06.035

CrossRef Full Text | Google Scholar

Carey, G. H., Abdelhady, A. L., Ning, Z., Thon, S. M., Bakr, O. M., and Sargent, E. H. (2015). Colloidal Quantum Dot Solar Cells. Chem. Rev. 115 (23), 12732–12763. doi:10.1021/acs.chemrev.5b00063

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, D., Qu, L., Li, Y., and Gu, Y. (2013). Versatile Self-Assembly of Water-Soluble Thiol-Capped Cdte Quantum Dots: External Destabilization and Internal Stability of Colloidal Qds. Langmuir 29, 10907–10914. doi:10.1021/la401999r

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, J., Song, L., and Zhan, J. (2009). One-Pot Synthesis of Highly Luminescent CdTe Quantum Dots by Microwave Irradiation Reduction and Their Hg2+-Sensitive Properties. Nano Res. 2 (1), 61–68. doi:10.1007/s12274-009-9004-0

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2013). Gaussian 09, Revision D.01. Wallingford CT: Gaussian, Inc.

Guo, J., Yang, W., and Wang, C. (2005). Systematic Study of the Photoluminescence Dependence of Thiol-Capped CdTe Nanocrystals on the Reaction Conditions. J. Phys. Chem. B 109 (37), 17467–17473. doi:10.1021/jp044770z

CrossRef Full Text | Google Scholar

Haram, S. K., Kshirsagar, A., Gujarathi, Y. D., Ingole, P. P., Nene, O. A., Markad, G. B., et al. (2011). Quantum Confinement in CdTe Quantum Dots: Investigation through Cyclic Voltammetry Supported by Density Functional Theory (DFT). J. Phys. Chem. C 115 (14), 6243–6249. doi:10.1021/jp111463f

CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg. J. Chem. Phys. 82 (1), 270–283. doi:10.1063/1.448799

CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for K to Au Including the Outermost Core Orbitals. J. Chem. Phys. 82 (1), 299–310. doi:10.1063/1.448975

CrossRef Full Text | Google Scholar

He, X., and Ma, N. (2014). An Overview of Recent Advances in Quantum Dots for Biomedical Applications. Colloids Surf. B: Biointerfaces 124, 118–131. doi:10.1016/j.colsurfb.2014.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, D. A., and Kamat, P. V. (2013). Quantum Dot Surface Chemistry: Ligand Effects and Electron Transfer Reactions. J. Phys. Chem. C 117 (27), 14418–14426. doi:10.1021/jp404031s

CrossRef Full Text | Google Scholar

Hines, D. A., and Kamat, P. V. (2014). Recent Advances in Quantum Dot Surface Chemistry. ACS Appl. Mater. Inter. 6 (5), 3041–3057. doi:10.1021/am405196u

CrossRef Full Text | Google Scholar

Huang, J., Xu, B., Yuan, C., Chen, H., Sun, J., Sun, L., et al. (2014). Improved Performance of Colloidal CdSe Quantum Dot-Sensitized Solar Cells by Hybrid Passivation. ACS Appl. Mater. Inter. 6 (21), 18808–18815. doi:10.1021/am504536a

CrossRef Full Text | Google Scholar

Imran, M., Saif, M. J., Kuznetsov, A. E., Idrees, N., Iqbal, J., and Tahir, A. A. (2019). Computational Investigations into the Structural and Electronic Properties of CdnTen (N = 1-17) Quantum Dots. RSC Adv. 9, 5091–5099. doi:10.1039/c8ra09465a

CrossRef Full Text | Google Scholar

Kanagasubbulakshmi, S., Kathiresan, R., and Kadirvelu, K. (2018). Structure and Physiochemical Properties Based Interaction Patterns of Organophosphorous Pesticides with Quantum Dots: Experimental and Theoretical Studies. Colloids Surf. A: Physicochemical Eng. Aspects 549, 155–163. doi:10.1016/j.colsurfa.2018.04.007

CrossRef Full Text | Google Scholar

Kershaw, S. V., Jing, L., Huang, X., Gao, M., and Rogach, A. L. (2017). Materials Aspects of Semiconductor Nanocrystals for Optoelectronic Applications. Mater. Horiz. 4 (2), 155–205. doi:10.1039/c6mh00469e

CrossRef Full Text | Google Scholar

Kilina, S. V., Tamukong, P. K., and Kilin, D. S. (2016). Surface Chemistry of Semiconducting Quantum Dots: Theoretical Perspectives. Acc. Chem. Res. 49 (10), 2127–2135. doi:10.1021/acs.accounts.6b00196

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, S. G., and Rao, K. S. R. K. (2014). Physics and Chemistry of CdTe/CdS Thin Film Heterojunction Photovoltaic Devices: Fundamental and Critical Aspects. Energy Environ. Sci. 7 (1), 45–102. doi:10.1039/c3ee41981a

CrossRef Full Text | Google Scholar

Kumar, A. P., Huy, B. T., Kumar, B. P., Kim, J. H., Dao, V.-D., Choi, H.-S., et al. (2015). Novel Dithiols as Capping Ligands for CdSe Quantum Dots: Optical Properties and Solar Cell Applications. J. Mater. Chem. C 3 (9), 1957–1964. doi:10.1039/c4tc01863j

CrossRef Full Text | Google Scholar

Kurban, M., Gündüz, B., and Göktaş, F. (2019). Experimental and Theoretical Studies of the Structural, Electronic and Optical Properties of BCzVB Organic Material. Optik 182, 611–617. doi:10.1016/j.ijleo.2019.01.080

CrossRef Full Text | Google Scholar

Kuznetsov, A. E., and Beratan, D. N. (2014). Structural and Electronic Properties of Bare and Capped Cd33Se33 and Cd33Te33 Quantum Dots. J. Phys. Chem. C 118 (13), 7094–7109. doi:10.1021/jp4007747

CrossRef Full Text | Google Scholar

Kuznetsov, A. E., Balamurugan, D., Skourtis, S. S., and Beratan, D. N. (2012). Structural and Electronic Properties of Bare and Capped CdnSen/CdnTen Nanoparticles (N = 6, 9). J. Phys. Chem. C 116 (12), 6817–6830. doi:10.1021/jp2109187

CrossRef Full Text | Google Scholar

Leubner, S., Hatami, S., Esendemir, N., Lorenz, T., Joswig, J.-O., Lesnyak, V., et al. (2013). Experimental and Theoretical Investigations of the Ligand Structure of Water-Soluble CdTe Nanocrystals. Dalton Trans. 42 (35), 12733–12740. doi:10.1039/c3dt50802a

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, H., Song, D., and Gong, J. (2014). Signal-On Electrochemiluminescence of Biofunctional CdTe Quantum Dots for Biosensing of Organophosphate Pesticides. Biosens. Bioelectron. 53, 363–369. doi:10.1016/j.bios.2013.10.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, E., Kuznetsov, A. E., and Beratan, D. N. (2012). Effects of S-Containing Ligands on the Structure and Electronic Properties of CdnSen/CdnTen Nanoparticles (N=3, 4, 6, and 9). Chem. Phys. 407, 97–109. doi:10.1016/j.chemphys.2012.09.005

CrossRef Full Text | Google Scholar

Lin, Y.-C., Chou, W.-C., Susha, A. S., Kershaw, S. V., and Rogach, A. L. (2013). Photoluminescence and Time-Resolved Carrier Dynamics in Thiol-Capped CdTe Nanocrystals under High Pressure. Nanoscale 5 (8), 3400–3405. doi:10.1039/c3nr33928a

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, X., Xu, S., Wang, C., Wang, Z., and Cui, Y. (2014). Synthesis of Thiosalicylic Acid-Capped CdTe Quantum Dots. RSC Adv. 4 (10), 4993–4997. doi:10.1039/c3ra44307h

CrossRef Full Text | Google Scholar

Liu, F., Laurent, S., Elst, L. V., and Muller, R. N. (2015). Synthesis of CdTe QDs by Hydrothermal Method, with Tunable Emission Fluorescence. Mater. Res. Express 2 (9), 95901. doi:10.1088/2053-1591/2/9/095901

CrossRef Full Text | Google Scholar

Ma, L., Wang, J., and Wang, G. (2012). Search for Global Minimum Geometries of Medium Sized CdnTen Clusters (N=15, 16, 20, 24 and 28). Chem. Phys. Lett. 552, 73–77. doi:10.1016/j.cplett.2012.09.036

CrossRef Full Text | Google Scholar

Muz, İ., and Kurban, M. (2020). The Electronic Structure, Transport and Structural Properties of Nitrogen-Decorated Graphdiyne Nanomaterials. J. Alloys Compd. 842, 155983. doi:10.1016/j.jallcom.2020.155983

CrossRef Full Text | Google Scholar

Nadler, R., and Sanz, J. F. (2015). Effect of Capping Ligands and TiO2 Supporting on the Optical Properties of a (CdSe)13 Cluster. J. Phys. Chem. A. 119, 1218–1227. doi:10.1021/acs.jpca.5b00625

CrossRef Full Text | Google Scholar

Plata, J. J., Ma, A. M., Márquez, A. M., and Sanz, J. F. (2017). Surface on the Electron Injection Mechanism of Copper Sulfide Quantum Dot-Sensitized Solar Cells. Phys. Chem. Chem. Phys. 19, 14580–14587. doi:10.1039/C7CP01076A

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajbanshi, B., Sarkar, S., and Sarkar, P. (2014). Band gap Engineering of Graphene-CdTe Quantum Dot Hybrid Nanostructures. J. Mater. Chem. C 2 (42), 8967–8975. doi:10.1039/c4tc01735h

CrossRef Full Text | Google Scholar

Salzner, U., and Aydin, A. (2011). Improved Prediction of Properties of π-Conjugated Oligomers with Range-Separated Hybrid Density Functionals. J. Chem. Theor. Comput. 7 (8), 2568–2583. doi:10.1021/ct2003447

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, S., Saha, S., Pal, S., and Sarkar, P. (2014). Electronic Structure and Bandgap Engineering of CdTe Nanotubes and Designing the CdTe Nanotube-Fullerene Hybrid Nanostructures for Photovoltaic Applications. RSC Adv. 4 (28), 14673–14683. doi:10.1039/c3ra47620k

CrossRef Full Text | Google Scholar

Schaftenaar, G., and Noordik, J. H. (2000). Molden: A Pre- and Post-Processing Program for Molecular and Electronic Structures. J. Comput. Aided Mol. Des. 14, 123–134. doi:10.1023/a:1008193805436

CrossRef Full Text | Google Scholar

Schnitzenbaumer, K. J., and Dukovic, G. (2018). Comparison of Phonon Damping Behavior in Quantum Dots Capped with Organic and Inorganic Ligands. Nano Lett. 18, 3667–3674. doi:10.1021/acs.nanolett.8b00800

PubMed Abstract | CrossRef Full Text | Google Scholar

Seal, P., Sen, S., and Chakrabarti, S. (2010). Ab Initio investigation on the Nonlinear Optical Properties of CdnTen (N = 1–10) Clusters. Chem. Phys. 367 (2-3), 152–159. doi:10.1016/j.chemphys.2009.11.014

CrossRef Full Text | Google Scholar

Shah, E. V., and Roy, D. R. (2014). A Comparative DFT Study on Electronic, Thermodynamic and Optical Properties of telluride Compounds. Comput. Mater. Sci. 88, 156–162. doi:10.1016/j.commatsci.2014.03.013

CrossRef Full Text | Google Scholar

Sriram, S., and Chandiramouli, R. (2013). DFT Studies on the Stability of Linear, Ring, and 3D Structures in CdTe Nanoclusters. Res. Chem. Intermed 41 (4), 2095–2124. doi:10.1007/s11164-013-1334-6

CrossRef Full Text | Google Scholar

Swenson, N. K., Ratner, M. A., and Weiss, E. A. (2016). Computational Study of the Influence of the Binding Geometries of Organic Ligands on the Photoluminescence Quantum Yield of CdSe Clusters. J. Phys. Chem. C 120 (12), 6859–6868. doi:10.1021/acs.jpcc.5b12770

CrossRef Full Text | Google Scholar

Talapin, D. V., Lee, J.-S., Kovalenko, M. V., and Shevchenko, E. V. (2010). Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications. Chem. Rev. 110 (1), 389–458. doi:10.1021/cr900137k

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, Y., Jin, S., and Hamers, R. J. (2012). Influence of Hole-Sequestering Ligands on the Photostability of CdSe Quantum Dots. J. Phys. Chem. C 117, 313–320. doi:10.1021/jp309587k

CrossRef Full Text | Google Scholar

Tu, C. C., and Lin, L. Y. (2008). High Efficiency Photodetectors Fabricated by Electrostatic Layer-By-Layer Self-Assembly of CdTe Quantum Dots. Appl. Phys. Lett. 93 (16), 6–9. doi:10.1063/1.3003883

CrossRef Full Text | Google Scholar

Wadt, W. R., Hay, P. J., Wadt, W. A., and Hay, P. J. (1985). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for Main Group Elements Na to Bi. J. Chem. Phys. 82, 284–298. doi:10.1063/1.448800

CrossRef Full Text | Google Scholar

Wang, J., Ma, L., Zhao, J., and Jackson, K. A. (2009). Structural Growth Behavior and Polarizability of CdnTen (N=1-14) Clusters. J. Chem. Phys. 130 (21), 214307. doi:10.1063/1.3147519

CrossRef Full Text | Google Scholar

Weng, J., Song, X., Li, L., Qian, H., Chen, K., Xu, X., et al. (2006). Highly Luminescent CdTe Quantum Dots Prepared in Aqueous Phase as an Alternative Fluorescent Probe for Cell Imaging. Talanta 70 (2), 397–402. doi:10.1016/j.talanta.2006.02.064

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Z., Zhang, Y., Huang, S., and Zhang, S. (2013). Theoretical Investigation of Assembled (CdTe)12×N (N=1-5) Multi-Cage Nanochains. Comput. Mater. Sci. 68, 238–244. doi:10.1016/j.commatsci.2012.10.040

CrossRef Full Text | Google Scholar

Wuister, S. F., Swart, I., van Driel, F., Hickey, S. G., and de Mello Donegá, C. (2003). Highly Luminescent Water-Soluble CdTe Quantum Dots. Nano Lett. 3 (4), 503–507. doi:10.1021/nl034054t

CrossRef Full Text | Google Scholar

Wuister, S. F., de Mello Donegá, C., and Meijerink, A. (2004). Local-Field Effects on the Spontaneous Emission Rate of CdTe and CdSe Quantum Dots in Dielectric media. J. Chem. Phys. 121, 4310–4315. doi:10.1063/1.1773154

CrossRef Full Text | Google Scholar

Xiao, J.-W., Ma, S., Yu, S., Zhou, C., Liu, P., Chen, Y., et al. (2018). Ligand Engineering on CdTe Quantum Dots in Perovskite Solar Cells for Suppressed Hysteresis. Nano Energy 46, 45–53. doi:10.1016/j.nanoen.2018.01.035

CrossRef Full Text | Google Scholar

Xu, S., Wang, C., and Cui, Y. (2010). Theoretical Simulation of CdTe Nanocrystals in Aqueous Synthesis. Struct. Chem. 21 (3), 519–525. doi:10.1007/s11224-009-9580-3

CrossRef Full Text | Google Scholar

Xu, S., Wang, C., and Cui, Y. (2010). Theoretical Investigation of CdSe Clusters: Influence of Solvent and Ligand on Nanocrystals. J. Mol. Model. 16, 469–473. doi:10.1007/s00894-009-0564-4

CrossRef Full Text | Google Scholar

Yaacobi-Gross, N., Garphunkin, N., Solomeshch, O., Vaneski, A., Susha, A. S., Rogach, A. L., et al. (2012). Combining Ligand-Induced Quantum-Confined Stark Effect with Type II Heterojunction Bilayer Structure in CdTe and CdSe Nanocrystal-Based Solar Cells. ACS Nano 6 (4), 3128–3133. doi:10.1021/nn204910g

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaghini, E., Seifalian, A. M., and MacRobert, A. J. (2009). Quantum Dots and Their Potential Biomedical Applications in Photosensitization for Photodynamic Therapy. Nanomedicine 4 (3), 353–363. doi:10.2217/nnm.09.9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Y., Gao, S., and Ying, J. Y. (2007). Synthesis and Cell-Imaging Applications of Glutathione-Capped CdTe Quantum Dots. Adv. Mater. 19 (3), 376–380. doi:10.1002/adma.200600342

CrossRef Full Text | Google Scholar

Zou, H., Liu, M., Zhou, D., Zhang, X., Liu, Y., Yang, B., et al. (2017). Employing CdSexTe1-X Alloyed Quantum Dots to Avoid the Temperature-Dependent Emission Shift of Light-Emitting Diodes. J. Phys. Chem. C 121 (9), 5313–5323. doi:10.1021/acs.jpcc.6b12129

CrossRef Full Text | Google Scholar