Thermal Conductivity of Sodium Silicate Glasses and Melts: Contribution of Diffusive and Propagative Vibration Modes

The thermal conductivity of silicate melts and glasses is an important physical property for understanding the temperature distribution in high-temperature metallurgical processes; however, the mechanism of heat conduction in these non-crystalline materials remains unclear. Two types of vibration modes must be considered to understand the mechanism of heat conduction, namely, propagative and diffusive vibration modes. In the present study, we carefully derived the thermal conductivity of pure silica and sodium disilicate glasses and melts, and estimated the contribution of the diffusive vibration mode using a recently developed model. The results indicated that the diffusive vibration mode was not dominant in the silicate non-crystalline materials, whereas the propagative vibration mode (i.e., phonons) was dominant in the heat conduction of silicate glasses and melts, which is in contrast with borate glasses.

Introduction

The thermal conductivity of silicate melts and glasses is one of the least understood properties among the physical properties of non-crystalline materials, despite its importance in the design of industrial plants and processes at elevated temperatures (such as glass-making and metallurgical processes) (Glaser and Sichen, 2013; Pilon et al., 2014; Wang and Sohn, 2020; Li et al., 2021). Owing to the limited data on their thermal conductivity, a larger number of reliable measurements and an in-depth interpretation of the thermal conductivities are required to improve the precision of the process control (e.g., slag cooling) and the development of the thermophysics of these disordered materials. Empirically, it is known that the thermal conductivity of silicate melts and glasses is influenced by the overall polymerization degree (Susa et al., 2001; Aune et al., 2002; Eriksson et al., 2003; Eriksson and Seetharaman, 2004; Kang and Morita, 2006; Hasegawa et al., 2012a; Hasegawa et al., 2012b; Kang et al., 2012; Hofmeister et al., 2016; Park and Sohn, 2016; Mills and Däcker, 2017; Wang et al., 2020), type of non-framework (e.g., Na⁺, Ca²⁺) (Hayashi et al., 2001; Hiroshima et al., 2008; Ozawa et al., 2007; Wang et al., 2020), framework cations (Si⁴⁺, B³⁺, Al³⁺) (Kim et al., 2015; Kim and Morita, 2015; Wang et al., 2019; Shirayama et al., 2020), and temperature (Chebykin et al., 2020; Wang et al., 2020); however, the detailed mechanism of the compositional- and temperature-dependences of the thermal conductivity of silicate melts and glasses remains unclear (Varshneya and Mauro, 2019). Kittel (1949) proposed that phonons are carriers of intrinsic heat conduction. The thermal conductivity (κ) is commonly related to the phonon mean free path (MFP, l) as given in Eq. 1:

$\kappa =\frac{1}{3}{C}_V\cdot v\cdot l,(1)$

where C_v (J m⁻³ K⁻¹) denotes the volumetric heat capacity and v (m s⁻¹) denotes the velocity of sound. Recently, it has been found that both propagative (propagons) and diffusive modes (diffusons) contribute to the thermal conductivity of disordered materials (e.g., glasses) (Agne et al., 2018; Sørensen et al., 2020; Sørensen et al., 2021). According to the definition by Allen and Feldman (Allen et al., 1999), “propagons” are similar to propagating phonons with a definable vector, whereas “diffusons” are vibrational modes without a definable vector. Additionally, it has been reported that the thermal conductivity of borate glasses is dominated by the diffusive vibration mode (Sørensen et al., 2020), whereas the contribution of the propagative vibration mode (phonon) is significant in silicate glasses. However, the contribution of the diffusive vibration mode has not been investigated for silicate systems over a wide temperature range from room temperature (∼300 K) to elevated temperatures higher than their liquidus. Although the thermal conductivity of silicate glasses and melts has been associated with the MFP of phonons for a long time, it remains unclear whether this classical concept is applicable to non-crystalline silicate materials at elevated temperatures. In addition, the temperature dependence of the MFP for the silicate melts has not been carefully discussed from the viewpoint of the structure. To carefully consider the contribution of the two types of vibration modes, the physical properties of the target sample (i.e., the density, heat capacity, and velocity of sound) are required. Among the wide variety of silicate systems, unary silica (SiO₂) and binary sodium silicate (Na₂O–SiO₂) are well-studied systems in terms of their thermophysical properties (such as density and heat capacity) and structure, where silica (SiO₂) acts as a network former and sodium oxide (Na₂O) acts as a network modifier. Previous studies (Manako et al., 2018; Nishi et al., 2019) have measured the thermal effusivity of sodium disilicate melts (Na₂O·2SiO₂, NS2) at temperatures higher than their liquidus. In the present study, we carefully derived the thermal conductivity of the NS2 melt from the reported thermal effusivity, density and heat capacity. The obtained thermal conductivity of NS2 melts was compared with that of NS2 glass at room temperature (300 K) as well as that of silica glass and melt. Additionally, the contribution of the diffusive and propagative vibration modes to the thermal conductivity was investigated.

Experimental Methods

Thermal Conductivity of Glasses at Room Temperature

The thermal conductivities of the SiO₂ and Na₂O·2SiO₂ (NS2) glasses were evaluated at room temperature (room temperature was assumed to be 300 K in the present study). High-purity synthetic silica (Suprasil F300) was shaped into a plate (5 $\times$ 5 $\times$ 1 mm), which was used as the SiO₂ glass sample. NS2 glass was fabricated using the conventional melt-quench method. Reagent powders of SiO₂ and Na₂SiO₃ were carefully weighed and mixed in a mullite mortar. The powder mixture was placed in a platinum crucible and melted in an air atmosphere at 1673 K for 30 min. The melt was quenched on a copper plate to obtain a glassy sample. To ensure sample homogeneity, the quenched glass was crushed into a powder and re-melted at 1773 K to remove bubbles from the melt. Finally, the bottom of the platinum crucible was placed in contact with water to quench the sample melt. The obtained bubble-free bulk glass was annealed at 30 K below the glass transition temperature for 4 h. The annealed glass was shaped into a glass plate (5 $\times$ 5 $\times$ 1 mm) and used for thermal diffusivity and density measurements. Specific heat capacity measurements were performed for the NS2 sample with a cylindrical shape (diameter: 3 mm, thickness: 1.5 mm). Wavelength-dispersive X-ray spectroscopy was used to determine the composition of the NS2 glass, (this is listed in Table 1). The analyzed composition was close to the nominal value, indicating that the evaporation amount of the Na₂O component during melting was small and negligible.

TABLE 1

TABLE 1. Composition and properties of the glass samples at room temperature. The analyzed composition of the NS2 glass is indicated in parentheses. Assuming the uncertainty in the C_p is ±1%, the possible error range for the derived κ value is ±2.2%.

The thermal conductivity of these glasses at 300 K was determined using Eq. 2 considering three types of properties of the samples: thermal diffusivity [α (m² s⁻¹)], density [ρ (kg m⁻³)], and specific heat capacity [C_p (J kg⁻¹ K⁻¹)]:

$\kappa =\alpha \cdot \rho \cdot C_{\mathrm{p}},(2)$

where κ denotes the thermal conductivity (W m⁻¹ K⁻¹). The α values of the samples were determined using the laser flash method (Shibata et al., 1996). Since the temperature response of the sample was measured using an infrared ray detector, a laser beam absorber and an infrared ray emitter were required for measurements involving transparent materials, such as oxide glasses. Therefore, the sample glass plate was coated with a thin gold film (≈150 nm) and carbon powder spray. The samples were placed in a vacuum chamber of the apparatus, and the upper side of the sample was heated using a Nd:YAG laser with a wavelength of 1,064 nm under vacuum. The temperature variation at the bottom of the sample was measured using an infrared detector at room temperature. The value of α was derived by analyzing the temperature response curve according to a well-established procedure (Shibata et al., 1996). The measurement of α was repeated at least five times for each sample. The obtained α values are listed in Table 1. The density (ρ) of the glass samples was measured using a conventional Archimedean method with ethanol fluid at 300 K. Density measurements were performed five times for each sample. The average values are presented in Table 1. The specific heat capacity (C_p) of the NS2 glass sample was measured using differential scanning calorimetry (DSC, Netzsch 3,500 Sirius) during the continuous heating process in the temperature range of 278–873 K, whereas the reported C_p value (Richet et al., 1982) for silica glass was used to determine its κ value. The obtained values of ρ and C_p are listed in Table 1.

Thermal Conductivity of Molten Samples at Elevated Temperatures

In previous studies, the thermal effusivity [b (m² s⁻¹)] of the NS2 melts was measured using a front-heating front-detection laser flash method at temperatures above their liquidus (Manako et al., 2018; Nishi et al., 2019). The relationship between b and κ is expressed by Eq. 3:

$\kappa =\frac{b^2}{\rho \cdot C_{\mathrm{p}}},(3)$

The thermal conductivity (κ) of the NS2 melt was derived using the reported density (Shartsis et al., 1952) and the estimated specific heat capacity (C_p) based on the model proposed by Richet and Bottinga (1985). It is well known that their model reproduces the C_p of alkali silicate systems. For the thermal conductivity of pure SiO₂ glass and melt, the values measured by Hofmeister and Whittington (2012) using a laser flash method were employed for comparison.

Structural Characterization of NS2 Glass

The thermal conductivity of silicate materials should be structure-sensitive. The synchrotron X-ray total scattering was measured for the NS2 glass at the BL04B2 beamline in SPring-8 (Japan) to obtain the total correlation function T(r), which provides the correlation length between two atoms. The crushed NS2 glass powder was packed in polyimide capillary tubes (diameter: 3 mm), and the scattering patterns of the samples were collected using a horizontal two-axis diffractometer under vacuum at room temperature with an incident X-ray energy of 61 keV (λ = 0.0202 nm). This high-energy X-ray enables the collection of scattering patterns with wave vectors (q) as high as 260 nm⁻¹, which are sufficiently high to accurately determine the interatomic distance in non-crystalline solids. To obtain a Faber–Ziman structure factor (S(q)), scattering patterns were handled according to a well-established procedure (Ohara et al., 2020). In an X-ray scattering experiment on glasses containing n chemical components, the total structure factor S(q) is represented by Eqs 4–6:

$S\left(q\right)=1+\frac{1}{{\left|\langle w\left(q\right)\rangle \right|}^2}{\displaystyle \sum _{\beta =1}^n{\displaystyle \sum _{\gamma =1}^n{c}_{\beta }{c}_{\gamma }{w}_{\beta }\left(q\right)w_{\gamma }\left(q\right)\left[S_{\beta \gamma }\left(q\right)-1\right]}},(4)$

$\langle w\left(q\right)\rangle ={\displaystyle \sum _i{c}_i{\mathit{w}}_i\left(q\right)},(5)$

$q=\frac{4\pi \sin \theta }{\lambda },(6)$

where q is the wave vector, c_β is the atomic fraction of the chemical component β; w_β(q) is a q-independent atomic form factor with dispersion terms in X-ray scattering, S_βγ(q) is a partial structure factor, λ is the wavelength of the X-ray, and $2\theta$ is the scattering angle. To determine the interatomic distance between the two atoms, the total correlation function T(r) was obtained from the Fourier transform relation Eq. 7 and Eq. 8 (Kohara, 2017):

$T\left(r\right)=4\pi r{\rho }_{0}g\left(r\right),(7)$

$g\left(r\right)=1+\frac{1}{2{\pi }^2{\rho }_{0}r}{\displaystyle {\int }_{q_{\min }}^{q_{\max }}q\left[S\left(q\right)-1\right]}\sin \left(qr\right)\mathit{d}q,(8)$

where ρ₀ (m⁻³) denotes the number of atoms per unit volume and g(r) represents the weighted sum of the partial functions.

Results

Equations 2, 3 indicate that the thermal conductivity of the glasses and melts is the product of the density, heat capacity, and thermal diffusivity of the samples. Understanding these three parameters is essential for interpreting the compositional and temperature dependences of thermal conductivity. Figure 1A illustrates the temperature dependence of the density of silica and the NS2 glasses and melts. The measured density of the pure silica glass at 300 K was 2,200 ± 2 kg m⁻³, which agrees well with the reported value for synthetic silica glass (e.g., 2,202 kg m⁻³ (Mazurin et al., 1983)) at room temperature, validating our methodology for density measurements. The measured density of the NS2 glass at 300 K was 2,490 ± 10 kg m⁻³, which is larger than that of silica glass and lies in the range of reported values for similar compositions (2,488–2,495 kg m⁻³) (Morey and Merwin, 1932; Verweij et al., 1979), confirming the presence of a bubble-free sample. As depicted in Figure 1A, the density of silica exhibited a small temperature dependence because of its small linear thermal expansion coefficient (≈10⁻⁶ K⁻¹ (Kobayashi et al., 2011; Hofmeister and Whittington, 2012). However, the reported densities of the NS2 melts (Shartsis et al., 1952) were considerably smaller than those of the NS2 glass and exhibited a negative temperature dependence, indicating a larger thermal expansion coefficient of the sodium-containing system than that of pure silica.

FIGURE 1

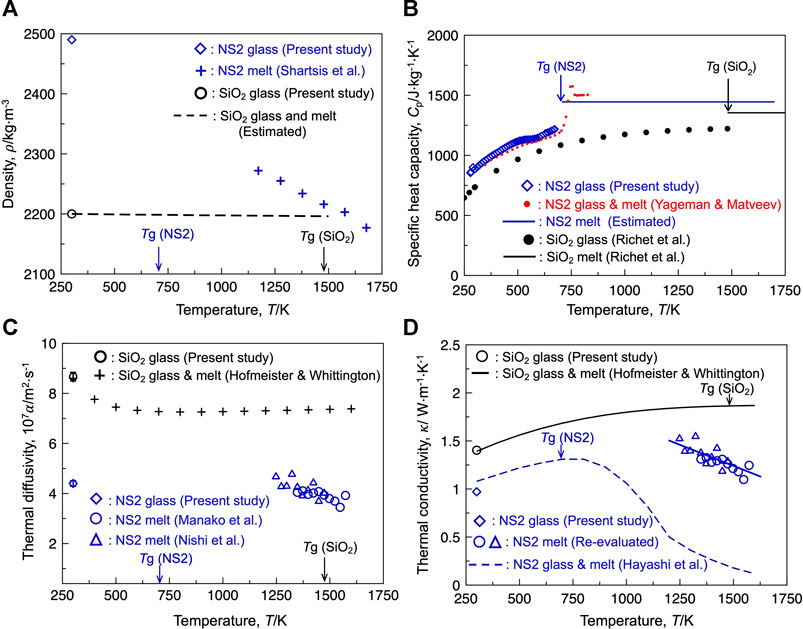
FIGURE 1. (A) Temperature dependence of the density of the silica and sodium disilicate (NS2) compositions. Reported value by Shartsis et al. (1952) was plotted as the density of the NS2 melt. The dashed line indicates the estimated density of silica glass based on the thermal expansivity. (B) Specific heat capacity of the silica and NS2 compositions. (C) Thermal diffusivity of the silica and NS2 compositions. The blue triangle and circle represent the thermal diffusivities of the NS2 melts, which are derived from the thermal effusivity reported by Nishi et al. (2019) and Manako et al. (2018), respectively. (D) Thermal conductivity of the silica and NS2 compositions. The blue dashed line represents the thermal conductivity of NS2 melt and glass obtained using the transient hot-wire method (Hayashi et al., 2001). Applying the uncertainty in the reported thermal effusivity (±5%, Nishi et al., 2019), density (±1%, Mazurin, 2005), and specific heat capacity (±1%, Richet and Bottinga, 1985) for the NS2 melt, the propagation of error in the thermal conductivity of the NS2 melt obtained using the laser flash method should be ±7.2%.

Figure 1B depicts the temperature dependence of the specific heat capacity (C_p) for silica and NS2 glasses and melts. The C_p value reported for silica glass (Richet et al., 1982) and the measured values for the NS2 glass gradually increased with increasing temperature up to its glass transition temperature (T_g). The measured values for the present NS2 glass were close to the values reported by Yageman and Matveev (1982) at temperatures higher than 346 K. This agreement validates the reasonability of the measured C_p of the NS2 glass at temperatures close to room temperature (300 K). In general, the C_p value of silicate glass significantly increases at temperatures close to T_g, and the C_p value of the silicate melts is almost constant at temperatures higher than its T_g unless it does not contain alumina or boron oxide (Sugawara et al., 2013). The C_p values reported for silica melt and the estimated values for NS2 melts based on the well-known Richet and Bottinga model (Richet and Bottinga, 1985) are depicted in Figure 1B. The C_p value of the NS2 glass and melt was higher than that of silica in the temperature range of 300–1750 K.

The thermal diffusivities (α) of the silica and NS2 glasses and melts are shown in Figure 1C. The measured α value of the silica glass was higher than that of the NS2 glass at room temperature. It has been reported that the value of α for silica glass decreases as the temperature is elevated and plateaus at temperatures above 750 K (Hofmeister and Whittington (2012)). The value of α for NS2 glass has not been reported for temperatures close to the glass transition temperature. The α value for the NS2 melt was calculated from the reported thermal effusivity (b) of the melt (Manako et al., 2018; Nishi et al., 2019). The derived α values of the NS2 melt based on the reported value of b in the two different studies (Manako et al., 2018; Nishi et al., 2019) agreed well. It was found that the α values of the NS2 melt at 1250 K (Manako et al., 2018; Nishi et al., 2019) were close to that of the NS2 glass at 300 K; however, the α value of the NS2 melts exhibited a negative temperature dependence at temperatures higher than their liquidus (i.e., 1147 K).

Using Eqs 2, 3, the thermal conductivity (κ) of the NS2 composition obtained by the laser flash method was carefully derived in the present study and is depicted in Figure 1D. For comparison, the reported κ value of silica obtained using the laser flash method (Hofmeister and Whittington, 2012) is also shown in the figure. The κ value of silica gradually increased with increasing temperature from 300 K and plateaued at temperatures above 1250 K. The measured κ value of the NS2 glass in the present study was lower than that of silica glass at 300 K. The derived κ value of the NS2 melt at temperatures above 1250 K was close to that of the NS2 glass; however, it was found that the κ value of the NS2 melt exhibited a negative temperature dependence, which was not observed for pure silica. This contrasting temperature dependence can be attributed to the difference in the thermal expansivities of the two samples. The negative temperature dependence of the NS2 melt is due to its higher thermal expansion coefficient, which should be correlated with the smaller average bond strength of the NS2 melt than that of silica (Mysen and Richet, 2019). A comparison of the derived κ value of the NS2 melt (obtained using the laser flash method) with that obtained using the transient hot-wire method (Hayashi et al., 2001) revealed that the κ values obtained using the two measurement techniques agreed well at temperatures close to 300 K, whereas the κ value obtained using the transient hot-wire method significantly decreased at temperatures higher than 750 K. At 1250 K, the κ value of the NS2 melt obtained using the laser flash method was more than three times higher than that obtained using the transient hot-wire method. This difference, depending on the measurement technique, has long been discussed by researchers, and the following indications have been suggested (Mills, 2016; Mills and Däcker, 2017):

1) The κ value obtained using the laser flash method would contain the contribution of radiation conduction, in comparison with that obtained using the transient hot-wire method.

2) The κ value measured using the transient hot-wire method is expected to be influenced by electrical leakage from the hot wire to the melt.

The former indication was examined by Shibata et al. (2005), who concluded that radiative components do not significantly affect the obtained thermal conductivity. In addition, previous reports (Takeuchi et al., 1983; Kang et al., 2013) have confirmed that the experimental error caused by current leakage during thermal conductivity measurement is insignificant for sodium silicate melts. The reason for the disagreement between the observed values remains unclear; however, both methods typically demonstrate a similar tendency in terms of compositional dependence. The present study considered the κ value obtained using the laser flash method for the discussion.

Discussion

Contribution of Diffusive Vibration Mode

Hiroshima et al. (2008) proposed that the heat conduction of silicate melts and glasses is dominated by propagative vibration modes (i.e., phonons), which have been successfully used to explain the heat conduction in crystalline materials with high rigidity. In contrast, heat conduction in low-rigidity non-crystalline solids tends to be controlled by diffusive vibration modes (i.e., diffusons), which do not have well-defined wave vectors, limiting their contribution to heat conduction (Sørensen et al., 2021). To clarify whether phonons are the main carriers of heat in silicate melts and glasses, the present study estimates the contribution of the diffusive mode (κ_diff) based on a recently developed model (Agne et al., 2018):

${\kappa }_{\text{diff}}\approx \frac{{\rho }_0^{-\left(\frac{2}{3}\right)}{k}_{\mathrm{B}}}{2{\pi }^3{v}^3}{\left(\frac{k_{B}T}{h}\right)}^4{\displaystyle {\int }_0^{0.95{\theta }_{\mathrm{D}}{T}^{-1}}\left(\frac{x^5{e}^x}{{\left(e^x-1\right)}^2}\right)dx,}(9)$

where ρ₀ denotes the atomic number density, k_B denotes the Boltzmann’s constant, ν represents the velocity of sound, T denotes the temperature, $\hslash =h{\left(2\pi \right)}^{-1}$ denotes the reduced Planck’s constant, ${\theta }_{\mathrm{D}}$ refers to the Debye temperature, and $x=\hslash \omega {\left(k_{\mathrm{B}}T\right)}^{-1}$, where ω represents the frequency. Here, ${\theta }_{\mathrm{D}}$ is estimated using Eq. 10 (Sørensen et al., 2021):

${\theta }_{\mathrm{D}}=\hslash {\left(6{\pi }^2{\rho }_0\right)}^{1/3}v{k}_{\mathrm{B}}^{-1}.(10)$

Figure 2A depicts the temperature dependence of the sound velocity (ν) of the silica and NS2 compositions. The value of ν for the silica glass and melt was estimated using the reported Young’s modulus (Carnevale et al., 1964), as shown in Eq. 11 (Inaba et al., 2001):

$v=\sqrt{\frac{E}{2\rho },}(11)$

where E represents the Young’s modulus. For the NS2 composition, the reported ν values of the glass (Hiroshima et al., 2008) and melt (Hayashi et al., 2011) are shown in the figure. The ν for silica gradually increased with increasing temperature, whereas that for NS2 decreased with increasing temperature. The estimated κ_diff values were compared with the experimental thermal conductivities (κ_exp) of the silica and NS2 compositions obtained using the laser flash method (Figure 2B). As shown in the figure, the contribution of κ_diff to κ_exp is less than 30%, indicating that the contribution of the diffusive vibration mode is limited to the thermal conduction of the selected silicate systems, whereas the propagative mode (i.e., phonons) contributes significantly to the heat conduction.

FIGURE 2

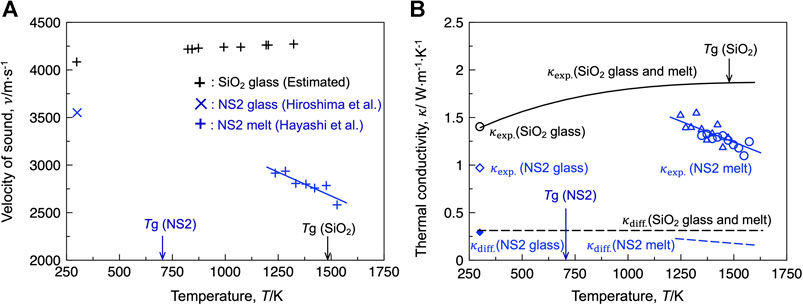
FIGURE 2. (A) Velocity of sound for the silica and NS2 glass and melt. (B) Comparison of the estimated contribution of the diffusive vibration mode $\left({\kappa }_{diff}\right)$ with the experimental thermal conductivity $\left({\kappa }_{\exp }\right)$.

Phonon Mean Free Path

When the phonon is the main carrier of heat in the system, it is meaningful to relate the phonon MFP to the structure. Assuming that the heat conduction in the non-crystalline silica and NS2 composition is completely dominated by the propagative mode (i.e., phonon), the phonon MFP is estimated using Eq. 1. Figure 3A depicts the estimated phonon MFP (l) of the silica and NS2 compositions. The value of l for the silica glass was approximately 0.6 nm at 300 K, whereas that for the NS2 glass was close to 0.4 nm at 300 K. Figures 3B,C depict the total structure factor S(q) and total correlation function (T(r)) derived from S(q). As shown in Figure 3C, T(r) exhibited major peaks at 0.163, 0.233, 0.264, and 0.316 nm, which could be assigned to the Si-O, Na-O, O-O, and Si-Si correlations (Saito et al., 2016), respectively. The l value of the NS2 glass was slightly larger than the length of the Si-Si correlation (Figure 3C). The l value of the silica glass was close to 0.6 nm, which is close to the distance from a silicon atom to its second neighbor silicon atom (Si-Si_2nd) (Waseda and Toguri, 1978). These results indicate that the value of l should be decreased by breaking the silicate network structure with the addition of a modifier cation (i.e., sodium cation). This tendency agrees with the general interpretation of the contribution of network modifiers to the thermal conductivity of non-crystalline silicate materials (Nishi et al., 2018). Based on the temperature dependence of l (Figure 3A), the l value of the silica composition slightly decreased with increasing temperature, whereas the opposite tendency was observed for the NS2 composition. The l values of the silica and NS2 compositions were similar in the temperature range of 1,250–1500 K. Although the detailed mechanism of these contrasting temperature dependences remains unresolved, it has been reported that the number of small ring species (“e.g., 3-membered ring”) increases with increasing temperature for the silica melt, which is mainly composed of larger ring species, such as 4–6 membered rings (McMillan et al., 1994; Zhou et al., 2021). The formation of such a “defect” structure (i.e., 3-membered ring) is expected to decrease the phonon MFP of silica by elevating the temperature. In the case of the NS2 melt, previous in situ Raman experiments (Maehara et al., 2005; Malfait et al., 2008; Mysen and Frantz, 1992) have quantified the Qⁿ species [i.e., SiO₄ unit with (n = 0, 1, 2, 3, or 4) bridging oxygen atoms connected to the silicon atom] in sodium silicate melts. They suggest that NS2 glass is mainly composed of Q³ species and the speciation reaction 2Q³ = Q² + Q⁴ proceeds to the right-hand side with an increase in temperature, resulting in an increase in Q⁴ species. The Q⁴ species is expected to contribute to an increase in the l value of the sodium silicate melts. To prove the reasonability of these speculations, the influence of the ring structure and Qⁿ distribution on the l value of non-crystalline silicate materials should be carefully examined in future work.

FIGURE 3

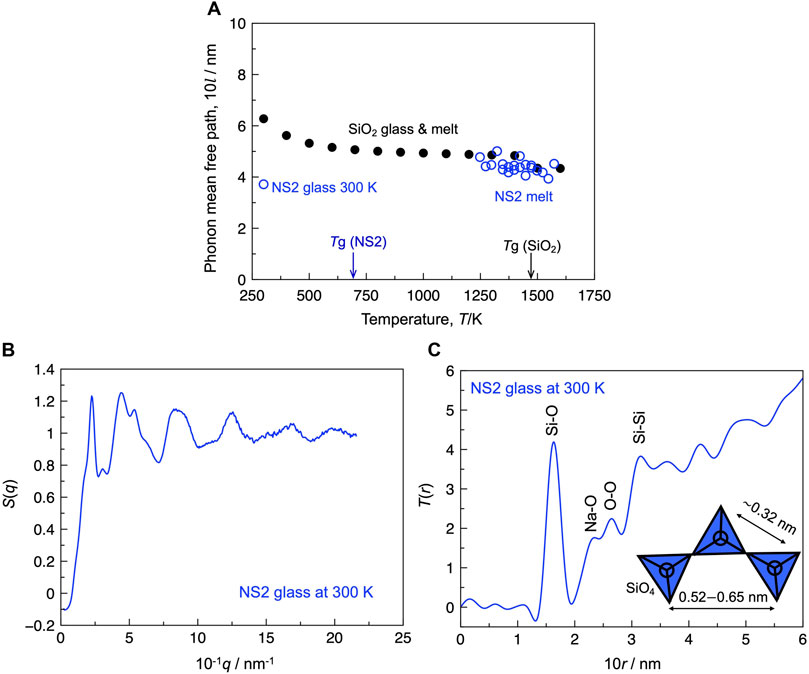
FIGURE 3. (A) Estimated phonon mean free path of the silica and NS2 glass and melt. (B) S(q) of the NS2 glass at 300 K. (C) Total correlation function [T(r)] of the NS2 glass at 300 K. Inset: schematic illustrations of the structure composed of SiO₄ tetrahedra with the typical range of interatomic distance between two silicon atoms (Waseda and Toguri, 1978).

Conclusion

The thermal conductivities of the silica and NS2 glasses and melts were carefully derived based on the data obtained using the laser flash method. The experimental data was compared with the estimated contributions of the diffusive vibration mode. The present study confirms that the contribution of the diffusive vibration mode is insignificant for the present silicate system, indicating that the propagative vibration mode (i.e., phonons) mainly contributes to heat conduction. The decrease in the thermal conductivity of the silica glass with the addition of Na₂O can be attributed to the decrease in the phonon MFP of the glass at 300 K. Although the phonon MFP of silica is similar to that of the NS2 melt at temperatures higher than 1250 K, the thermal conductivity of the silica melt is higher than that of the NS2 melt, which can be attributed to the difference in the velocity of sound. Experimental data on the velocity of sound for the molten oxide are quite limited; however, this data is expected to be essential for understanding the mechanism of heat conduction in silicate melts at elevated temperatures. Thus, more measurements are required for the sound velocity of silicate melts at elevated temperatures.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author Contributions

SS designed and drafted the manuscript. TE, TN, HO, and KI measured the density and thermal conductivity of the glasses. HY, KO, and TW measured and analyzed the synchrotron X-ray total scattering of the glass. SS, SK, and HS discussed the interpretation of the results. All authors contributed to the writing of the manuscript.

Funding

This work was performed under the Cooperative Research Program of “NJRC Mater. and Dev.” This work was also partially supported by JSPS KAKENHI (Grant Number 19K05106).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The synchrotron X-ray total scattering of the glass sample was measured at the BL04B2 beamline at Spring-8 with the approval of JASRI (Proposal No. 2017B1400). We would like to thank Masanori Tashiro (Tohoku University) for his technical support in the wavelength-dispersive X-ray spectroscopy measurements of the NS2 glass.

References

Agne, M. T., Hanus, R., and Snyder, G. J. (2018). Minimum thermal Conductivity in the Context of Diffuson-Mediated thermal Transport. Energy Environ. Sci. 11, 609–616. doi:10.1039/C7EE03256K

CrossRef Full Text | Google Scholar

Allen, P. B., Feldman, J. L., Fabian, J., and Wooten, F. (1999). Diffusons, Locons and Propagons: Character of Atomie Yibrations in Amorphous Si. Philosophical Mag. B 79, 1715–1731. doi:10.1080/13642819908223054

CrossRef Full Text | Google Scholar

Aune, R. E., Hayashi, M., Nakajima, K., and Seetharaman, S. (2002). Thermophysical Properties of Silicate Slags. JOM 54, 62–69. doi:10.1007/BF02709753

CrossRef Full Text | Google Scholar

Carnevale, E. H., Lynnworth, L. C., and Larson, G. S. (1964). Ultrasonic Measurement of Elastic Moduli at Elevated Temperatures, Using Momentary Contact. The J. Acoust. Soc. Am. 36, 1678–1684. doi:10.1121/1.1919264

CrossRef Full Text | Google Scholar

Chebykin, D., Heller, H.-P., Saenko, I., Bartzsch, G., Endo, R., and Volkova, O. (2020). Effect of Glass Transition: Density and thermal Conductivity Measurements of B₂O₃. High Temp. High Press 49, 125–142. doi:10.32908/hthp.v49.801

CrossRef Full Text | Google Scholar

Eriksson, R., Hayashi, M., and Seetharaman, S. (2003). Thermal Diffusivity Measurements of Liquid Silicate Melts. Int. J. Thermophys. 24, 785–797. doi:10.1023/A:1024048518617

CrossRef Full Text | Google Scholar

Eriksson, R., and Seetharaman, S. (2004). Thermal Diffusivity Measurements of Some Synthetic CaO-Al₂O₃-SiO₂ Slags. Metall. Mater. Trans. B 35, 461–469. doi:10.1007/s11663-004-0047-z

CrossRef Full Text | Google Scholar

Glaser, B., and Sichen, D. (2013). Thermal Conductivity Measurements of Ladle Slag Using Transient Hot Wire Method. Metall. Mater. Trans. B 44, 1–4. doi:10.1007/s11663-012-9773-9

CrossRef Full Text | Google Scholar

Hasegawa, H., Hoshino, Y., Kasamoto, T., Akaida, Y., Kowatari, T., Shiroki, Y., et al. (2012a). Thermal Conductivity Measurements of Some Synthetic Al₂O₃-CaO-SiO₂ Slags by Means of a Front-Heating and Front-Detection Laser-Flash Method. Metall. Mater. Trans. B 43, 1405–1412. doi:10.1007/s11663-012-9702-y

CrossRef Full Text | Google Scholar

Hasegawa, H., Kowatari, T., Shiroki, Y., Shibata, H., Ohta, H., and Waseda, Y. (2012b). Thermal Conductivity of Molten Silicate of Al₂O₃-CaO-Na₂O-SiO₂ Measured by Means of a Front Heating-Front Detection Laser Flash Method. Metall. Mater. Trans. B 43, 1413–1419. doi:10.1007/s11663-012-9745-0

CrossRef Full Text | Google Scholar

Hayashi, M., Ishii, H., Susa, M., Fukuyama, H., and Nagata, K. (2001). Effect of Ionicity of Nonbridging Oxygen Ions on thermal Conductivity of Molten Alkali Silicates. Phys. Chem. Glasses 42, 6–11.

Google Scholar

Hayashi, M., Matsuzono, Y., and Nagata, K. (2011). Ultrasonic Velocities of Molten Alkali Silicates. ISIJ Int. 51, 689–695. doi:10.2355/isijinternational.51.689

CrossRef Full Text | Google Scholar

Hiroshima, Y., Hamamoto, Y., Yoshida, S., and Matsuoka, J. (2008). Thermal Conductivity of Mixed Alkali Silicate Glasses at Low Temperature. J. Non-Cryst. Solids 354, 341–344. doi:10.1016/j.jnoncrysol.2007.08.082

CrossRef Full Text | Google Scholar

Hofmeister, A. M., Sehlke, A., Avard, G., Bollasina, A. J., Robert, G., and Whittington, A. G. (2016). Transport Properties of Glassy and Molten Lavas as a Function of Temperature and Composition. J. Volcanol. Geotherm. Res. 327, 330–348. doi:10.1016/j.jvolgeores.2016.08.015

CrossRef Full Text | Google Scholar

Hofmeister, A. M., and Whittington, A. G. (2012). Effects of Hydration, Annealing, and Melting on Heat Transport Properties of Fused Quartz and Fused Silica from Laser-Flash Analysis. J. Non-Cryst. Solids 358, 1072–1082. doi:10.1016/j.jnoncrysol.2012.02.012

CrossRef Full Text | Google Scholar

Inaba, S., Oda, S., and Morinaga, K. (2001). Equation for Estimating the thermal Diffusivity, Specific Heat and thermal Conductivity of Oxide Glasses. J. Jpn. Inst. Met. Mater. 65, 680–687. doi:10.2320/jinstmet1952.65.8_680

CrossRef Full Text | Google Scholar

Kang, Y., Lee, J., and Morita, K. (2013). Comment on "Thermal Conductivity Measurements of Some Synthetic Al₂O₃-CaO-SiO₂ Slags by Means of a Front-Heating and Front-Detection Laser-Flash Method". Metall. Mater. Trans. B 44, 1321–1323. doi:10.1007/s11663-013-9933-6

CrossRef Full Text | Google Scholar

Kang, Y., and Morita, K. (2006). Thermal Conductivity of the CaO-Al₂O₃-SiO₂ System. ISIJ Int. 46, 420–426. doi:10.2355/isijinternational.46.420

CrossRef Full Text | Google Scholar

Kang, Y., Nomura, K., Tokumitsu, K., Tobo, H., and Morita, K. (2012). Thermal Conductivity of the Molten CaO-SiO₂-FeO X System. Metall. Mater. Trans. B 43, 1420–1426. doi:10.1007/s11663-012-9706-7

CrossRef Full Text | Google Scholar

Kim, Y., and Morita, K. (2015). Thermal Conductivity of Molten B₂O₃, B₂O₃–SiO₂, Na₂O–B₂O₃, and Na₂O–SiO₂ Systems. J. Am. Ceram. Soc. 98, 1588–1595. doi:10.1111/jace.13490

CrossRef Full Text | Google Scholar

Kim, Y., Yanaba, Y., and Morita, K. (2015). The Effect of Borate and Silicate Structure on thermal Conductivity in the Molten Na₂O-B₂O₃-SiO₂ System. J. Non-Cryst. Solids 415, 1–8. doi:10.1016/j.jnoncrysol.2015.02.008

CrossRef Full Text | Google Scholar

Kittel, C. (1949). Interpretation of the thermal Conductivity of Glasses. Phys. Rev. 75, 972–974. doi:10.1103/PhysRev.75.972

CrossRef Full Text | Google Scholar

Kobayashi, Y., Shimizu, T., Miyashita, S., Endo, R., and Susa, M. (2011). Determination of Refractive Indices and Linear Coefficients of thermal Expansion of Silicate Glasses Containing Titanium Oxides. ISIJ Int. 51, 186–192. doi:10.2355/isijinternational.51.186

CrossRef Full Text | Google Scholar

Kohara, S. (2017). Atomistic and Electronic Structures of Functional Disordered Materials Revealed by a Combination of Quantum-Beam Measurements and Computer Simulations. J. Ceram. Soc. Jpn. 125, 799–807. doi:10.2109/jcersj2.17101

CrossRef Full Text | Google Scholar

Li, Q., Wang, Q., Zhang, J., Wang, W., and Liu, J. (2021). Transition Temperature and thermal Conduction Behavior of Slag in Gasification Process. Energy 222 (9), 119940. doi:10.1016/j.energy.2021.119940

CrossRef Full Text | Google Scholar

Maehara, T., Yano, T., and Shibata, S. (2005). Structural Rules of Phase Separation in Alkali Silicate Melts Analyzed by High-Temperature Raman Spectroscopy. J. Non-Cryst. Solids 351, 3685–3692. doi:10.1016/j.jnoncrysol.2005.10.003

CrossRef Full Text | Google Scholar

Malfait, W. J., Zakaznova-Herzog, V. P., and Halter, W. E. (2008). Amorphous Materials: Properties, Structure, and Durability: Quantitative Raman Spectroscopy: Speciation of Na-Silicate Glasses and Melts. Am. Mineral. 93, 1505–1518. doi:10.2138/am.2008.2783

CrossRef Full Text | Google Scholar

Manako, T., Nishi, T., Ohta, H., Sukenaga, S., and Shibata, H. (2018). Measurement of the Thermal Effisivities for AlO_1.5-R₂O-SiO₂(R=Li, Na) Melts. J. Jpn. Inst. Met. Mater. 82, 419–422. doi:10.2320/jinstmet.JAW201803

CrossRef Full Text | Google Scholar

Mazurin, O. V. (2005). “Chapter 7 Density of Glass Melt,” in Properties of Glass-Forming Melts. Editors L. D. Pye, A. Montenero, and I. Josef (Milton Park, Oxfordshire: Taylor & Francis), 193–226.

Google Scholar

Mazurin, O. V., Streltsina, M. V., and Shvaiko-Shvaikovskaya, T. P. (1983). “Part A Silica Glass and Binary Silicate Glasses” in Hand Book of Glass Data. Amsterdam, Netherlands: Elsevier, 16–17.

Google Scholar

Mcmillan, P. F., Poe, B. T., Gillet, P. H., and Reynard, B. (1994). A Study of SiO2 Glass and Supercooled Liquid to 1950 K via High-Temperature Raman Spectroscopy. Geochim. Cosmochim. Acta 58, 3653–3664. doi:10.1016/0016-7037(94)90156-2

CrossRef Full Text | Google Scholar

Mills, K. C., and Däcker, C.-A. (2017). Heat Transfer in the Mould and Shell Solidification” in the Casting Powders Book. New York, United States: Cham: Springer International Publishing, 59–108. doi:10.1007/978-3-319-53616-3_3

CrossRef Full Text | Google Scholar

Mills, K. C. (2016). Structure and Properties of Slags Used in the Continuous Casting of Steel: Part 1 Conventional Mould Powders. ISIJ Int. 56, 1–13. doi:10.2355/isijinternational.ISIJINT-2015-231

CrossRef Full Text | Google Scholar

Morey, G. W., and Merwin, H. E. (1932). The Relation between the Composition and the Density and Optical Properties of Glass I the Soda-Lime-Silica Glasses. J. Opt. Soc. Am. 22, 632–662. doi:10.1364/JOSA.22.000632

CrossRef Full Text | Google Scholar

Mysen, B. O., and Frantz, J. D. (1992). Raman Spectroscopy of Silicate Melts at Magmatic Temperatures: Na₂O-SiO₂, K₂O-SiO₂ and Li₂O-SiO₂ Binary Compositions in the Temperature Range 25-1475°C. Chem. Geol. 96, 321–332. doi:10.1016/0009-2541(92)90062-A

CrossRef Full Text | Google Scholar

Mysen, B. O., and Richet, P. (2019). Chapter 6 Properties of Metal Oxide-Silica Systems,” in Silicate Glasses and Melts. 2nd ed. Amsterdam, Netherlands: Elsevier, 203–206.

Google Scholar

Nishi, T., Ohnuma, K., Tanaka, K., Manako, T., Yamato, Y., Ohta, H., et al. (2019). Thermal Conductivities of Alkali-Silicate and Calcium-Alkali-Silicate Melts. J. Non-Cryst. Solids 511, 36–40. doi:10.1016/j.jnoncrysol.2019.01.038

CrossRef Full Text | Google Scholar

Nishi, T., Ohta, H., Sukenaga, S., and Shibata, H. (2018). Estimation of thermal Conductivity of Silicate Melts Using Three-Dimensional thermal Resistor Network Model. J. Non-Cryst. Sol. 482, 9–13. doi:10.1016/j.jnoncrysol.2017.11.014

CrossRef Full Text | Google Scholar

Ohara, K., Onodera, Y., Kohara, S., Koyama, C., Masuno, A., Mizuno, A., et al. (2020). Accurate Synchrotron Hard X-ray Diffraction Measurements on High-Temperature Liquid Oxides. Int. J. Microgravity Sci. Appl. 37, 370202. doi:10.15011/jasma.37.2.370202

CrossRef Full Text | Google Scholar

Ozawa, S., Endo, R., and Susa, M. (2007). Thermal Conductivity Measurements and Prediction for R₂O-CaO-SiO₂ (R=Li, Na, K) Slags. Tetsu-to-Hagan 93, 416–423. doi:10.2355/tetsutohagane.93.416

CrossRef Full Text | Google Scholar

Park, S., and Sohn, I. (2016). Effect of Na₂O on the High-Temperature Thermal Conductivity and Structure of Na₂O-B₂O₃ Melts. J. Am. Ceram. Soc. 99, 612–618. doi:10.1111/jace.14013

CrossRef Full Text | Google Scholar

Pilon, L., Janos, F., and Kitamura, R. (2014). Effective Thermal Conductivity of Soda-Lime Silicate Glassmelts with Different Iron Contents between 1100°C and 1500°C. J. Am. Ceram. Soc. 97, 442–450. doi:10.1111/jace.12768

CrossRef Full Text | Google Scholar

Richet, P., Bottinga, Y., Denielou, L., Petitet, J. P., and Tequi, C. (1982). Thermodynamic Properties of Quartz, Cristobalite and Amorphous SiO₂: Drop Calorimetry Measurements between 1000 and 1800 K and a Review from 0 to 2000 K. Geochim. Cosmochim. Acta 46, 2639–2658. doi:10.1016/0016-7037(82)90383-0

CrossRef Full Text | Google Scholar

Richet, P., and Bottinga, Y. (1985). Heat Capacity of Aluminum-free Liquid Silicates. Geochim. Cosmochim. Acta 49, 471–486. doi:10.1016/0016-7037(85)90039-0

CrossRef Full Text | Google Scholar

Saito, Y., Yonemura, T., Masuno, A., Inoue, H., Ohara, K., and Kohara, S. (2016). Structural Change of Na₂O-Doped SiO₂ Glasses by Melting. J. Ceram. Soc. Jpn. 124, 717–720. doi:10.2109/jcersj2.16028

CrossRef Full Text | Google Scholar

Shartsis, L., Spinner, S., and Capps, W. (1952). Density, Expansivity, and Viscosity of Molten Alkali Silicates. J. Am. Ceram. Soc. 35, 155–160. doi:10.1111/j.1151-2916.1952.tb13090.x

CrossRef Full Text | Google Scholar

Shibata, H., Emi, T., Waseda, Y., Kondo, K., Oiita, H., and Nakajima, K. (1996). Thermal Diffusivities of Continuous Casting Mold Fluxes for Steel in the Glassy and Crystalline States. Tetsu-to-Hagan 82, 504–508. doi:10.2355/tetsutohagane1955.82.6_504

CrossRef Full Text | Google Scholar

Shibata, H., Suzuki, A., and Ohta, H. (2005). Measurement of thermal Transport Properties for Molten Silicate Glasses at High Temperatures by Means of a Novel Laser Flash Technique. Mater. Trans. 46, 1877–1881. doi:10.2320/matertrans.46.1877

CrossRef Full Text | Google Scholar

Shirayama, S., Aoki, H., Yanaba, Y., Kim, Y., and Morita, K. (2020). Relationship Between Thermal Conductivity and Structure of the CaO–BO_1.5–AlO_1.5 System. ISIJ Int. 60, 392–399. doi:10.2355/isijinternational.ISIJINT-2019-251

CrossRef Full Text | Google Scholar

Sørensen, S. S., Bødker, M. S., Johra, H., Youngman, R. E., Logunov, S. L., Bockowski, M., et al. (2021). Thermal Conductivity of Densified Borosilicate Glasses. J. Non-Cryst. Solids 557, 120644. doi:10.1016/j.jnoncrysol.2021.120644

CrossRef Full Text | Google Scholar

Sørensen, S. S., Pedersen, E. J., Paulsen, F. K., Adamsen, I. H., Laursen, J. L., Christensen, S., et al. (2020). Heat Conduction in Oxide Glasses: Balancing Diffusons and Propagons by Network Rigidity. Appl. Phys. Lett. 117, 031901. doi:10.1063/5.0013400

CrossRef Full Text | Google Scholar

Sugawara, T., Hamano, Y., Yoshida, S., and Matsuoka, J. (2013). Heat Capacity Measurements of 75SiO₂-6B₂O₃-10Al₂O₃-9MO (M=Mg, Ca, Sr and Ba) Glasses and Melts. J. Ceram. Soc. Jpn. 121, 972–980. doi:10.2109/jcersj2.121.972

CrossRef Full Text | Google Scholar

Susa, M., Kubota, S., Hayashi, M., and Mills, K. C. (2001). Thermal Conductivity and Structure of Alkali Silicate Melts Containing Fluorides. Ironmaking Steelmaking 28, 390–395. doi:10.1179/irs.2001.28.5.390

CrossRef Full Text | Google Scholar

Takeuchi, M., Suzuki, M., and Nagata, K. (1983). Analytical Discussion on the Transient Hot Wire Method : Applicability to Measurement of an Electrically Conductive Medium. Trans. JSME, Ser.B 49, 1468–1476. doi:10.1299/kikaib.49.1468

CrossRef Full Text | Google Scholar

Varshneya, A. K., and Mauro, J. C. (2019). “Thermal Conductivity and Acoustic Properties of Glass,” in Fundamentals of Inorganic Glasses. Editors A. K. Varshneya, and J. C. Mauro. 3rd ed. (Amsterdam, Netherlands: Elsevier), 283–291. doi:10.1016/b978-0-12-816225-5.00012-2

CrossRef Full Text | Google Scholar

Verweij, H., Buster, J. H. J. M., and Remmers, G. F. (1979). Refractive index and Density of Li-, Na- and K-Germanosilicate Glasses. J. Mater. Sci. 14, 931–940. doi:10.1007/BF00550724

CrossRef Full Text | Google Scholar

Wang, Q., Wang, D., Li, Q., and Zhang, J. (2019). Relationship between Microstructure and thermal Conductivity in Coal Slags with Variable Silica and Alumina. Energy Fuels 33, 6226–6233. doi:10.1021/acs.energyfuels.9b01090

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, J., Liu, J., Wu, W., Qi, X., and Deng, H. (2020). Thermal Conduction Mechanism Based on Microstructural Transformations of Molten Slag: The Role of Calcium Oxide. Int. J. Heat Mass Transfer 160, 120167. doi:10.1016/j.ijheatmasstransfer.2020.120167

CrossRef Full Text | Google Scholar

Wang, Z., Wen, G., Liu, Q., Huang, S., Tang, P., and Yu, L. (2020a). Estimating the thermal Conductivity of CaO-Al₂O₃-SiO₂ Slags by Equilibrium Molecular Dynamics Simulations. J. Non-Cryst. Solids 531, 119851. doi:10.1016/j.jnoncrysol.2019.119851

CrossRef Full Text | Google Scholar

Wang, Z., Huang, S., Wen, G., Jiang, W., Chen, F., and Tang, P. (2020b). Effects of Temperature on the thermal Conductivity of Amorphous CaO-SiO₂-Al₂O₃ Slags: a Computational Insight. Phys. Chem. Chem. Phys. 22, 8808–8816. doi:10.1039/d0cp00382d

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., and Sohn, I. (2020). Review on the High-Temperature Thermophysical Properties of Continuous Casting Mold Fluxes for Highly Alloyed Steels. ISIJ Int. 60, 2705–2716. doi:10.2355/isijinternational.ISIJINT-2019-522

CrossRef Full Text | Google Scholar

Waseda, Y., and Toguri, J. M. (1978). The Structure of the Molten FeO-SiO₂ System. Met. Trans. B 9, 595–601. doi:10.1007/BF03257207

CrossRef Full Text | Google Scholar

Yageman, V. D., and Matveev, G. M. (1982). Thermal Capacity of Glasses in SiO₂-Na₂O·2SiO₂ System. Sov. J. Glass Phys. Chem. 8, 168–175.

Google Scholar

Zhou, Q., Shi, Y., Deng, B., Neuefeind, J., and Bauchy, M. (2021). Experimental Method to Quantify the Ring Size Distribution in Silicate Glasses and Simulation Validation Thereof. Sci. Adv. 7, eabh1761. doi:10.1126/sciadv.abh1761

PubMed Abstract | CrossRef Full Text | Google Scholar