A Systematic Approach for Semiconductor Half-Heusler

The key to designing a half-Heusler begins from the understanding of atomic interactions within the compound. However, this pool of knowledge in half-Heusler compounds is briefly segregated in many papers for specific explanations. The nature of the chemical bonding has been systematically explored for the large transition-metal branch of the half-Heusler family using density-of-states, charge-density, charge transfer, electron-localization-function, and crystal-orbital-Hamilton-population plots. This review aims to simplify the study of a conventional 18-electron configuration half-Heusler by applying rules proposed by renowned scientists to explain concepts such as Zintl-Klemm, hybridization, and valence electron content (VEC). Atomic and molecular orbital diagrams illustrate the electron orbital transitions and provide clarity to the semiconducting behavior (VEC = 18) of half-Heusler. Eighteen-electron half-Heusler usually exhibits good thermoelectric properties owing to favorable electronic structures such as narrow bandgap (<1.1 eV), thermal stability, and robust mechanical properties. The insights derived from this review can be used to design high-performance half-Heusler thermoelectrics.

Introduction

There is an appreciating interest to clean energy solutions on combating climate change. The demand of alternate energy technologies draws attention to thermoelectric (TE) materials that convert waste heat to electricity (Hamid Elsheikh et al., 2014; Ul Haq et al., 2018; Suwardi et al., 2020). TE devices consist of n- and p-type TE materials that are electrically connected in a series circuit while the heat gradients applied are parallel to the device.

TE generators have been used for decades in space and automotive applications (Yang and Caillat 2006; LeBlanc 2014), and recently in wearable electronic devices (Hong et al., 2019; Wang et al., 2020). However, the efficiency of TE generators needs to be improved for commercialization. To date, the highest module efficiency achieved is ∼12% with Bi₂Te₃-based materials (Zhang et al., 2017). A high-performance thermoelectric material should have high electrical conductivity and low thermal conductivity to maintain a robust temperature gradient. To quantify a thermoelectric material’s efficiency, a dimensionless thermoelectric figure of merit, zT, is used. zT comprises of both the electronic and thermal conductivity components expressed as: $zT=(S^2\sigma /k).T$, where the Seebeck coefficient, S, is the voltage response to temperature gradient, $\sigma$ is the electrical conductivity, k is the sum of electronic k_el and lattice k_lat thermal conductivity, and T is the absolute temperature. There are trade-off relations among these properties, e.g., an increase of the Seebeck coefficient obtained by decreasing the carrier concentration is generally accompanied by a reduction in the electrical conductivity. Also, an increase of the electrical conductivity typically coincides with an increase of the electronic part of the thermal conductivity, k_e. These corelations make it challenging to improve and optimize the dimensionless figure of merit, zT. To date, there are only few reliable strategies to enhance the zT such as band convergence, scattering manipulation, and lattice thermal conductivity reduction (Jia et al., 2021; Jia et al., 2021; Yang et al., 2021).

The maximum TE efficiency, N_max, is the increasing function of zT and is expressed as:

${\text{N}}_{\text{max }}=\frac{T_h-T_c}{T_h} \frac{\sqrt[2]{1+z{T}_{eff}} -1}{\sqrt[2]{1+z{T}_{eff}} +T_c/T_h}(1)$

There have been many research studies on possible thermoelectric materials, ranging from metals to polymers. These thermoelectric materials all have one thing in common, that is, they exhibit semiconducting properties that are essential for thermoelectric properties. This characteristic opens vast possibilities for optimizing TE efficiency in designing materials and bandgaps. However, materials (such as Te and Pb) used to make high performance chalcogenides and skutterudites thermoelectrics can be costly and environmentally toxic (Zevalkink et al., 2011; Mulla and Rabinal 2018; Recatala-Gomez et al., 2020; Suwardi et al., 2020; Zheng et al., 2021). Furthermore, thermoelectric materials can be thermally unstable above room temperature and tends to form secondary phases due to interface instability. These factors can undermine thermoelectric performance that would require post-chemical treatment and maintenance costs (Rull-Bravo et al., 2015; Aswathy et al., 2017; Colombara et al., 2020; Qin et al., 2020; Al Malki et al., 2021).

Half-Heusler (HH)-based thermoelectrics are thermally stable with desirable mechanical properties. Another advantage is that their junction with metal electrodes is robust as compared to non-HH semiconductors. Utilizing HH thermoelectrics can be one of the viable means to reduce the unseen costs and use of toxic metals for converting waste heat energy into electricity (Joshi et al., 2019). A recent work developed p-type TaFeSb-based HH, which achieved a record high zT of ∼1.52 at 973K and an ultrahigh average zT of ∼0.93 between 300 and 973K (Zhu et al., 2019). Research works have also developed state-of-the-art HH such as (Ti/Zr/Hf)CoSb (Yan et al., 2013) (Ti/Zr/Hf)NiSn (Sakurada and Shutoh 2005; Chen et al., 2013), ZrNiPb (Mao et al., 2017), ZrCoBi (Zhu et al., 2018), and NbCoSn (He et al., 2016), all of which provides insights into further optimization of zT.

HH compounds have a fundamental composition 1:1:1, with general formula XYZ, where X is the least electronegative element from the left. It is generally understood on the exceptions that are mainly applicable in the case of Y being the most electronegative rare-earth element to derive chemical formula YXZ. Both X and Y elements consist of transition metals, d-block, while Y also includes f-block rare-earth metals. Lastly, Z consists of P-block main group elements. However, this nomenclature may not apply to some HH compounds and caution must be exercised when deriving atomic parameters and lattice positions for theoretical predictions. In general, the formula derived as such is to provide a systematic overview of the metavalent interactions between the X, Y, and Z atoms. There are papers that cover essential topics such as high band degeneracy (Fu et al., 2014), resonant doping (Chen et al., 2017), mass fluctuation (Chen et al., 2017) (Yan et al., 2013), substitution doping (Culp et al., 2008), phase separation (Kirievsky et al., 2013) (Li et al., 2020), nano inclusion (Chen and Ren 2013), and synthesis methods for a broad range of HH compounds. An essential review paper for an overview of the abovementioned was recently published (Poon 2019). However, there are still initial gaps to fill to understand these years of excellent works. Therefore, we take advantage of existing concepts and theories to provide an insightful yet succinct review on two specific HH systems that are widely studied, namely, MCoSb and MNiSn, where M = (Ti,Zr, Hf).

Half-Heusler and the Zintl Model Based on the Zintl-Klemm Concept

The HH structure consists of a covalent and ionic part, which are based on zincblende and rock salt structures, respectively. HH crystal structures consist of three interpenetrating FCC lattices, of which the atoms of the NaCl (Rock salt) structure occupies the octahedral sites while the covalent dominant ZnS structure (Zinc blende) occupies the remaining tetrahedral holes. The rock salt type sublattice is formed by the least and most electropositive element (X and Z), which has the most ionic interaction while the zinc blende type sublattice consists of Y and Z elements, which have the smallest difference in electronegativity. Y atoms occupy the remaining tetrahedral holes. The strongest ionic or covalent interaction of X, Y, and Z atoms determines the crystal lattice structure of the compound (Graf et al., 2011).

For simplicity and understanding of these complex materials, the Zintl-Anion Framework based on the Zintl model is superimposed on the similar ZnS lattice (YZ) of the HH structure and is termed as the YZ framework. This approach was originally proposed by Köhler and co-workers (Köhler et al., 2007). Zintl compounds are solids composed of electropositive cations that donate their valence electrons to form an anionic framework and a closed valence shell configuration, achieved by combining formal charge transfer with covalent bonding (Zeier et al., 2016). According to the Zintl-Klemm concept, HH compounds can be described as the ionic interaction Xⁿ⁺(YZ)ⁿ⁻, which alludes the valence electron interaction between the most electropositive element X and YZ framework (Nesper 2014). Element X donates all its valence electrons to the more electronegative elements Y and Z. As a result, each of the elements reached a closed-shell configuration leading to an 18-electron configuration for XYZ, in which Y is a d¹⁰ transition metal. This closed-shell 18-electron configuration makes HH compounds very stable. The valence balanced rule that generalizes the 18-electron rule for HHs states that most compounds with net valence (NV) of the three components equals zero are stable (Anand et al., 2018).

$\mathrm{N}\mathrm{V}\mathrm{o}\mathrm{f}\mathrm{T}\mathrm{i}\mathrm{N}\mathrm{i}\mathrm{S}\mathrm{n}=4\left(\mathrm{T}{\mathrm{i}}^{+4}{S}^0{d}^0\right)-1(\mathrm{N}\mathrm{i0}d10)-3\left(\mathrm{S}{\mathrm{n}}^{-4}{S}^2{P}^6\right)=0$

The rule proposed by Chemist Irving Langmuir in 1921 states that an 18-valence electron metal complex that contains a transition metal is said to have achieved the same electron configuration as the noble gas (Rasmussen 2015). There are some exceptions to stable HH having other electron configuration besides 18-valence electron count (VEC). With the addition of rare-earth (RE) elements, the total number of valence electrons added up can be expressed as 18+ 4fⁿ, which is stabilized by the strong localization of the RE f-orbital electrons (Graf, Felser and Parkin 2011). HH with VEC >18 have spintronic properties and the magnetic moment can be predicted using the Slater-Pauling equation, which is expressed as M = (Z—18)μB, where M and Z are the magnetic moment and the number of valence electron in the unit cell (Şaşıoğlu et al., 2005; Galanakis et al., 2006). For example, the total number of valence electrons in MCoSb (M = Ti, Zr, Hf) is 18, so we can predict it to be a non-magnetic semiconductor, having magnetic moment 0 μB. HH compounds aside from an 18-electron configuration exhibit magnetic properties and crystallize in a different structure (Joshi et al., 2019). This review will focus mainly on semiconductor HH compounds with VEC = 18.

S- and P- Orbital Hybridization

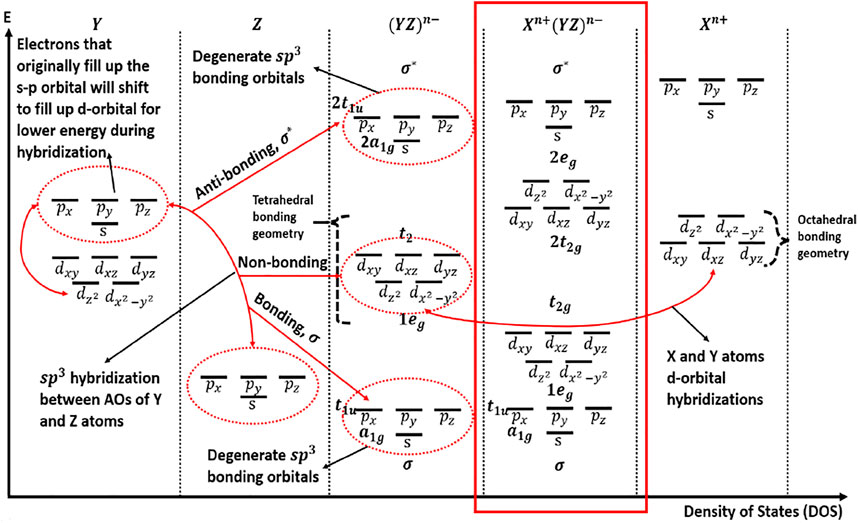
Scientist Pauling first introduced the concept of s- and p- orbital hybridization to form degenerate sp- orbitals up to three levels: sp, sp², sp³, which describes the redistribution of the energy of orbitals of individual atoms to give new orbitals of equivalent energy known as hybrid orbitals (Ingold, 1940). The energy of degenerate sp- orbitals fulfills the VSEPR theory, which states that each atom in a molecule will achieve a geometry that minimizes the repulsion between electrons in the valence shell of that atom (Billo 1985). Usually, sp³ hybridization applies to the solid-state chemistry of HH materials as its components are X^d-blockY^{d-block/lanthanides}Z^{p- block}, all of which have at least three valence orbital shells.

The combination of orbitals with high energy differences may lead to orbitals with non-bonding character. Atomic orbitals that have similar energies will have the strongest interactions and result in stronger bonding and anti-bonding character. On the other hand, atomic orbitals with very unequal energies have weaker interaction because the molecular orbitals are closer in energy to the atomic orbital energies and thus there is less energy benefit to putting electrons in the bonding molecular orbitals. Hence, the greater the energy difference between atomic orbitals and the bonding molecular orbital, the more energetically favorable for bonding to occur. The energy difference of the various atomic and molecular is illustrated in Figure 1.

FIGURE 1

FIGURE 1. MO and AO interactions of XYZ components.

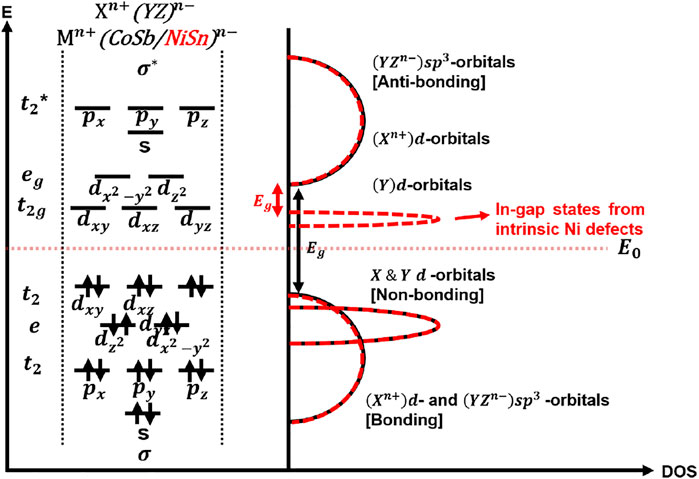
Figure 2 illustrates the systematic interaction of X, Y, and Z components. Do note that this figure may not be applicable to some HH compounds such as Lr compounds where the low-lying antibonding s-state of element Y, Ir hybridizes with the d-states of element X (Lee et al., 2011). Figure 2 can be used as reference for MCoSb and MNiSn compounds (Galanakis et al., 2006). The bonding of XYZ and its semiconductor behavior can be described in terms of X⁺ⁿ (dⁿ), Y⁻ⁿ (dⁿ), and Z^-n (sⁿpⁿ) ions.

FIGURE 2

FIGURE 2. MO diagram illustrating differences between MCoSb and MNiSn.

The 3d orbital contribution of element Y and 5p orbital contribution of Element Z occurs mainly below the 18-electron bandgap, while 3d orbital contribution of Element X occurs primarily above the 18-electron bandgap (Zeier et al., 2016). The size of the bandgap is dependent on the formation of sp³ states in the YZ framework (Bond strength), coupled with the hybridization of Y and X d-orbitals, also known as crystal field splitting in the tetrahedral and octahedral coordinates, which form bonding, sometimes non-bonding and anti-bonding states (Owen and Thornley 1966; Galanakis et al., 2006). The formation of non-bonding states is dependent on the level of energy difference between the molecular orbital of YZ framework and atomic orbital of X. DOS peaks in the conduction region of HH MCoSb are due to the d-states of M atom (M = Ti, Zr, and Hf), and d-states of Co. contribute largely in the valence region (Joshi et al., 2019). A similar trend is found in HH MNiSn, which is neatly summarized by Raia and co-workers (Rai et al., 2015) and in sync with the MO diagram, which also illustrates the differences between MCoSb and MNiSn in terms of the DOS peaks and size of bandgaps (Figure 2).

Doping Trends and Phonon Scattering Mechanisms

Research works carried out for HH compounds have been facing the bottleneck of high lattice thermal conductivity, K_L. Various phonon scattering mechanisms are explored to optimize the compositions with alloying where $\text{µ}\propto T^{-1/2}$, acoustic phonon scattering where $\text{µ}\propto T^{-3/2}$, ionized impurity scattering, nano-structuring, grain boundary scattering, and secondary phase (Ren et al., 2020). XYZ doping compositions can be expressed as but not limited by X′_1-X″X″ Y′_1-Y″ Y″ Z′_1-Z″ Z”. The change in Z atom compositions can result in the shift of the Fermi level of the analogous rigid band model (Azadani et al., 2016) while the change in X and Y compositions can result in the change in bandgap size (Kandpal et al., 2006).

An interesting observation is made from the M-doping trend, where x > 0.5 results in the widening of bandgap, but does not exceed the latter nominal HH compound at X = 1 (Joshi et al., 2019). Figure 3 shows the correlation between band gap and X fraction in Half-Heusler. The lattice constants of MCoSb and MNiSn are of similar values but are to be understood based on parent YZ basis. Generally, a system with a lower lattice constant will have a stronger hybridization between s- orbitals in the YZ system leading to larger energy separation between bonding and antibonding states (Kulkova et al., 2006). As shown in Table 1, with increasing unit cell volume, Eg will be larger because the orbital hybridization will decrease owing to longer distance between the adjacent atoms (Qiu et al., 2009).

FIGURE 3

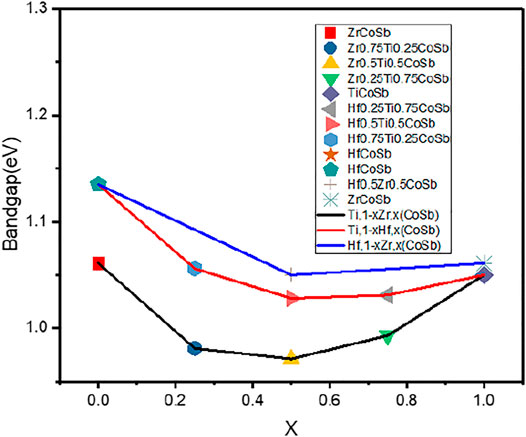
FIGURE 3. Graph plot based on data by Joshi and co-workers (Joshi et al., 2019).

TABLE 1

TABLE 1. Lattice constants and bandgap values.

Electronic Band Structures and zT

The DOS near band edge at Conduction Band Minima (CBM) or Valence Band Maxima (VBM) can reveal the HH performance as potential n- or p-type semiconductors based on the symmetry points from the electronic band structures. HH compounds with 18 valence electrons per unit cell are semiconductors possessing the narrow gap and sharp slope of the density of states (DOS) around the Fermi level. A rapid change in the DOS is a good indicator of large thermopower (Chauhan et al., 2018; Suwardi et al., 2020; Cao et al., 2021).

Electronic Band Structure of MCoSb

MCoSb (where M represents Ti, Zr, and Hf) exhibits small Seebeck coefficient values and can be described as “nearly compensated” semimetals, with the electrons and holes contributing nearly equally to the thermopower (Xia et al., 2000). Based on Parabolic Band Equation (PBE) model calculations, both TiCoSb and HfCoSb have VBMs and CBMs at the Γ and X points, respectively. While for HfCoSb, its VBM is located at the L point and its CBM is at the symmetry point X, although various calculation models such as the GW₀ model may derive all to be the same as the latter. MCoSb compounds have indirect bandgaps. The band degeneracy and the bands along the L-Γ direction in the valence band are responsible for positive values of S (P-type), while that along the Γ-X direction in the conduction band contributes to negative S values (N-type) (Lee, Poudeu and Mahanti 2011). Studies revealed that slight n-doping on MCoSb results in a more p-type as compared to n-type MCoSb HH compounds (Sekimoto et al., 2005; Joshi et al., 2019). This can be explained by the MCoSb band structures that revealed sharp DOS peaks near the VBM around E_F. The DOS near the VBM allows room for improvement in the electronic transport properties such as increase in effective mass carrier, m*, and Seebeck coefficients via M-doping.

Electronic Band Structure of MNiSn

MNiSn (where M represents Ti, Zr, and Hf) exhibits small negative Seebeck coefficient values and have indirect bandgaps with the conduction band extrema located at the X point of the Brillouin zone. MNiSn have VBMs and CBMs at the Γ and X points. Like MCoSb, the band degeneracy and the bands along the L-Γ direction in the valence band are responsible for positive values of S (P-type), while that along the Γ-X direction in the conduction band contributes to negative S values (N-type). The differences between MCoSb and MNiSn are the size of the bandgaps due to the intrinsic in-gap states in MNiSn induced from the Ni defects and its DOS peak near the CBM (Zeier et al., 2016).

Approach to Enhanced zT

For a large-scale application of thermoelectric generation, it is important to achieve high zT in TE materials. There are two approaches adopted to enhance zT. The first approach is to increase the power factor, which is composed of the temperature-dependent Seebeck coefficient, S, and electrical conductivity, $\sigma$, by engineering the electronic structure. The second approach is to reduce k_L by introducing additional phonon scattering without the deterioration of the power factor.

For bulk thermoelectric materials, the dominant elastic scattering mechanisms are mostly acoustic phonon scattering (Zeier et al., 2016), and optimal zT can be calculated based on acoustical scattering mechanisms (Chasmar and Stratton 1959). On the contrary for HH, the combination of large DOS effective mass and low electron–phonon interaction (EPI) from non-bonding states is beneficial for its TE properties. A study on crystal symmetry-protected non-bonding orbital in HH done by Zhou and colleagues suggests that simultaneous coupling of high DOS and high charge mobility is plausible for enhanced TE (Zhou et al., 2018). This contrasts with a large effective mass, m*, which is favorable for high S, which leads to reduction in mobility and electrical conductivity, $\sigma$ (Pei et al., 2012). The relation between mobility and scattering time is as such (Zeier et al., 2016) (Krez et al., 2014):

$\mu =\frac{q}{m^{\ast }} \tau (2)$

where $\mu$, $q$, m*$\tau$, are mobility, elementary charge, effective mass, and average scattering time, respectively.

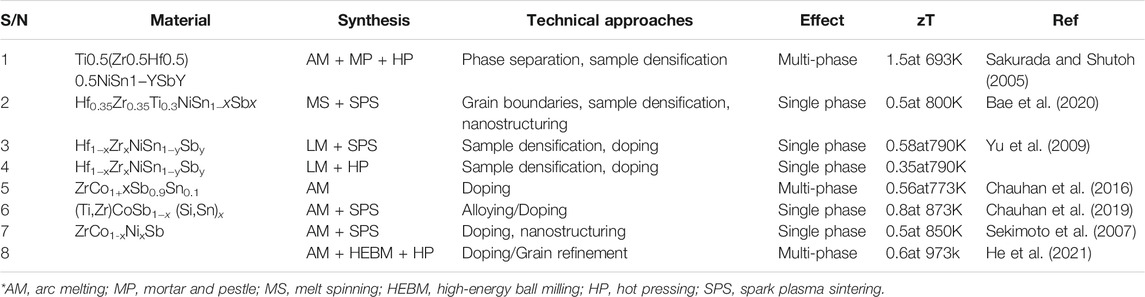
Enhanced Seebeck coefficient in slight n- or p-doping for p-type MCoSb and n-type MNiSn, respectively, is observed relative to optimal charge carrier concentration (Sekimoto et al., 2005; Yousuf and Gupta 2019). In general, the optimal charge carrier concentration for HH compounds ranges from ∼10¹⁹ cm⁻³ to ∼10²¹ cm⁻³ (Xie et al., 2014; Yousuf and Gupta 2019). Optimal alloying of X elements of different atomic weights increases S and lowers the lattice thermal conductivity, k_L, owing to the mass fluctuations (atomic weight difference) and strain field fluctuations (atomic size difference) without charge disorder (Callaway and von Baeyer 1960; Wu et al., 2007; Qiu et al., 2009; Shiomi et al., 2011). A recent study in 2020 demonstrated that the processing methods have a significant influence on the zT (Aversano et al., 2020). Table 2 suggests that the listed methods are not superior from the other and emphasizes the importance in the choice of method for technical approaches and desired outcome.

TABLE 2

TABLE 2. Processing methods make a difference to the outcome.

The traditional way to prepare a HH compound is by arc melting, followed by a long-time annealing of about 1 week for producing homogeneity and improving atomic ordering in the sample. It is observed from the tabulated trend that achieving single-phase Sb-containing HH is a challenge for processing methods without SPS. This is due to the high melting point of Sb. Processing methods can complement doping based on example from S/N 3 and four of Table 2. The work by Yu et al. suggests that SPS samples have higher density than LM samples, which results in a larger power factor. Table 2 further illustrates the importance of processing methods for desired outcome and emphasizes the equality of techniques that is required for designing HHs. For example, see items seven and eight of Table 2; the difference in technique would make a difference to zT due to factors such as density, nano/microstructure, and grain boundaries.

Guiding Principles

There are three guiding principles to follow to apply this approach. The first is to identify the choice of the HH system, mainly two types: with and without spin properties. This would also mean that the total VEC is crucial. If the system is required to have spin properties, then more consideration can be done on VEC >18 systems. As this review covers content limited to only VEC = 18 systems, the reviewed HHs are semiconductor non-spin type.

Second, the choice of X and Y components in the HH should have similar d-orbital energy for hybridization to occur. This is important for the formation of bandgap and the semiconducting properties of HH, which is essential for thermoelectric performance.

Last, besides the systematic approach provided in Electronic Band Structures and zT, the objective of the experiment is just as important for researchers to consider as the use of dopants and processing methods hold a crucial role to enhance power factor and reduce lattice thermal conductivity.

Conclusion

A variety of thermoelectric properties has been reported for the TiCoSb and TiNiSn systems. These two systems are the most widely studied compounds among the HH materials. This review proposed a systematic approach for designing HHs while keeping the guiding principles. The first would be to understand the atomic and molecular orbital interactions and the electronic band structures of the HH system. This could lead to viable combinations of elements of X, Y, and Z. Next would be to explore dopant compositions that would influence the power factor, $S^2\sigma T,$ based on considerable carrier concentration and crystal symmetry. The last would be the optimal thermal conductivity, $\text{k}$_L, by alloy doping and processing methods to exploit phonon scattering mechanisms. Encompassing this approach is the aspect of minimum entropy per carrier, which will prevail and dominate the overall performance for materials with small lattice (and total) thermal conductivity. HH systems have large power factors but also large thermal conductivities that impede zT. That said, these two characteristics still provide a broad space for zT optimization. With the openness to combat climate change and the vast space for enhancing zT in thermoelectric materials, the prospects of HH compounds for thermoelectric applications are indeed promising.

Author Contributions

WL initiate the planning and resource gathering. DZ, SD, XT, CT, and JX help with part of the proofread and writing. AS supervised the work and finalize the writing.

Funding

This work is funded by the A*STAR Career Development Fund C210112022.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al Malki, M. M., Shi, X., Qiu, P., Snyder, G. J., and Dunand, D. C. (2021). Creep Behavior and post-creep Thermoelectric Performance of the N-type Skutterudite alloy Yb0.3Co4Sb12. J. Materiomics 7, 89–97. doi:10.1016/j.jmat.2020.07.012

CrossRef Full Text | Google Scholar

Anand, S., Xia, K., I. Hegde, V., Aydemir, U., Kocevski, V., Zhu, T., et al. (2018). A Valence Balanced Rule for Discovery of 18-electron Half-Heuslers with Defects. Energy Environ. Sci. 11, 1480–1488. doi:10.1039/c8ee00306h

CrossRef Full Text | Google Scholar

Aswathy, V. S., Sankar, C. R., Varma, M. R., Assoud, A., Bieringer, M., and Kleinke, H. (2017). Thermoelectric Properties and thermal Stability of Layered Chalcogenides, TlScQ2, Q = Se, Te. Dalton Trans. 46, 17053–17060. doi:10.1039/c7dt03446f

PubMed Abstract | CrossRef Full Text | Google Scholar

Aversano, F., Palumbo, M., Ferrario, A., Boldrini, S., Fanciulli, C., Baricco, M., et al. (2020). Role of Secondary Phases and thermal Cycling on Thermoelectric Properties of TiNiSn Half-Heusler alloy Prepared by Different Processing Routes. Intermetallics 127, 106988. doi:10.1016/j.intermet.2020.106988

CrossRef Full Text | Google Scholar

Azadani, J. G., Munira, K., Romero, J., Ma, J., Sivakumar, C., Ghosh, A. W., et al. (2016). Anisotropy in Layered Half-Metallic Heusler alloy Superlattices. J. Appl. Phys. 119, 043904. doi:10.1063/1.4940878

CrossRef Full Text | Google Scholar

Bae, K. W., Hwang, J. Y., Kim, S-i., Jeong, H. M., Kim, S., Lim, J-H., et al. (2020). Thermoelectric Transport Properties of N-type Sb-Doped (Hf,Zr,Ti)NiSn Half-Heusler Alloys Prepared by Temperature-Regulated Melt Spinning and Spark Plasma Sintering. Appl. Sci. 10 (14), 4963. doi:10.3390/app10144963

CrossRef Full Text | Google Scholar

Billo, E. J. (1985). Modern Inorganic Chemistry (Jolly, William L.). J. Chem. Educ. 62, A137. doi:10.1021/ed062pa137.1

CrossRef Full Text | Google Scholar

Callaway, J., and von Baeyer, H. C. (1960). Effect of Point Imperfections on Lattice Thermal Conductivity. Phys. Rev. 120, 1149–1154. doi:10.1103/physrev.120.1149

CrossRef Full Text | Google Scholar

Cao, J., Chien, S., Tan, X. Y., Tan, C. K. I., Zhu, Q., Wu, J., et al. (2021). Realizing zT 2 in Cubic GeTe. ChemNanoMat 02/18, 7.

Google Scholar

Chasmar, R. P., and Stratton, R. (1959). The Thermoelectric Figure of Merit and its Relation to Thermoelectric Generators†. J. Electro. Control. 7, 52–72. doi:10.1080/00207215908937186

CrossRef Full Text | Google Scholar

Chauhan, N. S., Bathula, S., Gahtori, B., Kolen’ko, Y. V., and Dhar, A. (2019). Enhanced Thermoelectric Performance in Hf-free P-type (Ti, Zr)CoSb Half-Heusler Alloys. J. Elec Materi 48, 6700–6709. doi:10.1007/s11664-019-07486-y

CrossRef Full Text | Google Scholar

Chauhan, N. S., Bathula, S., Vishwakarma, A., Bhardwaj, R., Gahtori, B., Kumar, A., et al. (2018). Vanadium-Doping-Induced Resonant Energy Levels for the Enhancement of Thermoelectric Performance in Hf-free ZrNiSn Half-Heusler Alloys. ACS Appl. Energ. Mater. 1, 757–764. doi:10.1021/acsaem.7b00203

CrossRef Full Text | Google Scholar

Chauhan, N. S., Bhardwaj, A., Senguttuvan, T. D., Pant, R. P., Mallik, R. C., and Misra, D. K. (2016). A Synergistic Combination of Atomic Scale Structural Engineering and Panoscopic Approach in P-type ZrCoSb-Based Half-Heusler Thermoelectric Materials for Achieving High ZT. J. Mater. Chem. C 4, 5766–5778. doi:10.1039/c6tc01115b

CrossRef Full Text | Google Scholar

Chen, L., Liu, Y., He, J., Tritt, T. M., and Poon, S. J. (2017). High Thermoelectric Figure of merit by Resonant Dopant in Half-Heusler Alloys. AIP Adv. 7, 065208. doi:10.1063/1.4986760

CrossRef Full Text | Google Scholar

Chen, S., Lukas, K. C., Liu, W., Opeil, C. P., Chen, G., and Ren, Z. (2013). Effect of Hf Concentration on Thermoelectric Properties of Nanostructured N-type Half-Heusler Materials HfxZr1-xNiSn0.99Sb0.01. Adv. Energ. Mater. 3, 1210–1214. doi:10.1002/aenm.201300336

CrossRef Full Text | Google Scholar

Chen, S., and Ren, Z. (2013). Recent Progress of Half-Heusler for Moderate Temperature Thermoelectric Applications. Mater. Today 16, 387–395. doi:10.1016/j.mattod.2013.09.015

CrossRef Full Text | Google Scholar

Colombara, D., Elanzeery, H., Nicoara, N., Sharma, D., Claro, M., Schwarz, T., et al. (2020). Chemical Instability at Chalcogenide Surfaces Impacts Chalcopyrite Devices Well beyond the Surface. Nat. Commun. 11, 3634. doi:10.1038/s41467-020-17434-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Culp, S. R., Simonson, J. W., Poon, S. J., Ponnambalam, V., Edwards, J., and Tritt, T. M. (2008). (Zr,Hf)Co(Sb,Sn) Half-Heusler Phases as High-Temperature (>700°C) P-type Thermoelectric Materials. Appl. Phys. Lett. 93, 022105. doi:10.1063/1.2959103

CrossRef Full Text | Google Scholar

Downie, R. A., MacLaren, D. A., Smith, R. I., and Bos, J. W. G. (2013). Enhanced Thermoelectric Performance in TiNiSn-Based Half-Heuslers. Chem. Commun. 49, 4184–4186. doi:10.1039/c2cc37121a

CrossRef Full Text | Google Scholar

Fu, C., Zhu, T., Pei, Y., Xie, H., Wang, H., Snyder, G. J., et al. (2014). High Band Degeneracy Contributes to High Thermoelectric Performance in P-type Half-Heusler Compounds. Adv. Energ. Mater. 4, 1400600. doi:10.1002/aenm.201400600

CrossRef Full Text | Google Scholar

Galanakis, I., Mavropoulos, P., and Dederichs, P. H. (2006). Electronic Structure and Slater-Pauling Behaviour in Half-Metallic Heusler Alloys Calculated from First Principles. J. Phys. D: Appl. Phys. 39, 765–775. doi:10.1088/0022-3727/39/5/s01

CrossRef Full Text | Google Scholar

Graf, T., Felser, C., and Parkin, S. S. P. (2011). Simple Rules for the Understanding of Heusler Compounds. Prog. Solid State. Chem. 39, 1–50. doi:10.1016/j.progsolidstchem.2011.02.001

CrossRef Full Text | Google Scholar

Hamid Elsheikh, M., Shnawah, D. A., Sabri, M. F. M., Said, S. B. M., Haji Hassan, M., Ali Bashir, M. B., et al. (2014). A Review on Thermoelectric Renewable Energy: Principle Parameters that Affect Their Performance. Renew. Sustain. Energ. Rev. 30, 337–355. doi:10.1016/j.rser.2013.10.027

CrossRef Full Text | Google Scholar

He, R., Huang, L., Wang, Y., Samsonidze, G., Kozinsky, B., Zhang, Q., et al. (2016). Enhanced Thermoelectric Properties of N-type NbCoSn Half-Heusler by Improving Phase Purity. APL Mater. 4, 104804. doi:10.1063/1.4952994

CrossRef Full Text | Google Scholar

He, R., Zhu, T., Ying, P., Chen, J., Giebeler, L., Kühn, U., et al. (2021). High‐Pressure‐Sintering‐Induced Microstructural Engineering for an Ultimate Phonon Scattering of Thermoelectric Half‐Heusler Compounds. Small 17, 2102045. doi:10.1002/smll.202102045

CrossRef Full Text | Google Scholar

Hong, S., Gu, Y., Seo, J. K., Wang, J., Liu, P., Meng, Y. S., et al. (2019). Wearable Thermoelectrics for Personalized Thermoregulation. Sci. Adv. 5, eaaw0536. doi:10.1126/sciadv.aaw0536

PubMed Abstract | CrossRef Full Text | Google Scholar

Ingold, C. K. (1940). The Nature of the Chemical Bond and the Structure of Molecules and Crystals, by Linus Pauling. 2nd Edition. J. Am. Pharm. Assoc. 30, 30. xvi + 450 pages.Cornell University Press, Ithaca, N. Y.

Google Scholar

Jia, N., Cao, J., Tan, X. Y., Zheng, J., Chien, S. W., Yang, L., et al. (2021). Suppressing Ge-Vacancies to Achieve High Single-Leg Efficiency in GeTe with an Ultra-high Room Temperature Power Factor. J. Mater. Chem. A 9, 23335–23344. doi:10.1039/d1ta05866e

CrossRef Full Text | Google Scholar

Jia, N., Cao, J., Tan, X. Y., Dong, J., Liu, H., Tan, C. K. I., et al. (2021). Thermoelectric Materials and Transport Physics. Mater. Today Phys. 21, 100519. doi:10.1016/j.mtphys.2021.100519

CrossRef Full Text | Google Scholar

Joshi, H., Rai, D. P., Hnamte, L., Laref, A., and Thapa, R. K. (2019). A Theoretical Analysis of Elastic and Optical Properties of Half Heusler MCoSb (M=Ti, Zr and Hf). Heliyon 5, e01155. doi:10.1016/j.heliyon.2019.e01155

PubMed Abstract | CrossRef Full Text | Google Scholar

Joshi, H., Rai, D. P., Laref, A., and Thapa, R. K. (2019). Electronic, and Thermoelectric Properties of Half-Heusler Compounds MCoSb (M = Ti, Zr, Hf): a First Principles Study. Mater. Res. Express 6, 066307. doi:10.1088/2053-1591/ab0c68

CrossRef Full Text | Google Scholar

Kandpal, H. C., Felser, C., and Seshadri, R. (2006). Covalent Bonding and the Nature of Band Gaps in Some Half-Heusler Compounds. J. Phys. D: Appl. Phys. 39, 776–785. doi:10.1088/0022-3727/39/5/s02

CrossRef Full Text | Google Scholar

Kirievsky, K., Gelbstein, Y., and Fuks, D. (2013). Phase Separation and Antisite Defects in the Thermoelectric TiNiSn Half-Heusler Alloys. J. Solid State. Chem. 203, 247–254. doi:10.1016/j.jssc.2013.04.032

CrossRef Full Text | Google Scholar

Köhler, J., Deng, S., Lee, C., and Whangbo, M.-H. (2007). On the Origin of a Band Gap in Compounds of Diamond-like Structures. Inorg. Chem. 46, 1957–1959. doi:10.1021/ic062256x

PubMed Abstract | CrossRef Full Text | Google Scholar

Krez, J., Schmitt, J., Jeffrey Snyder, G., Felser, C., Hermes, W., and Schwind, M. (2014). Optimization of the Carrier Concentration in Phase-Separated Half-Heusler Compounds. J. Mater. Chem. A. 2, 13513–13518. doi:10.1039/c4ta03000a

CrossRef Full Text | Google Scholar

Kulkova, S. E., Eremeev, S. V., Kakeshita, T., Kulkov, S. S., and Rudenski, G. E. (2006). The Electronic Structure and Magnetic Properties of Full- and Half-Heusler Alloys. Mater. Trans. 47, 599–606. doi:10.2320/matertrans.47.599

CrossRef Full Text | Google Scholar

LeBlanc, S. (2014). Thermoelectric Generators: Linking Material Properties and Systems Engineering for Waste Heat Recovery Applications. Sustain. Mater. Tech. 1-2, 26–35. doi:10.1016/j.susmat.2014.11.002

CrossRef Full Text | Google Scholar

Lee, M-S., Poudeu, F. P., and Mahanti, S. D. (2011). Electronic Structure and Thermoelectric Properties of Sb-Based Semiconducting Half-Heusler Compounds. Phys. Rev. B 83, 085204. doi:10.1103/physrevb.83.159907

CrossRef Full Text | Google Scholar

Li, X., Yang, P., Wang, Y., Zhang, Z., Qin, D., Xue, W., et al. (2020). Phase Boundary Mapping in ZrNiSn Half-Heusler for Enhanced Thermoelectric Performance. Research (Wash D C) 2020, 4630948. doi:10.34133/2020/4630948

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, J., Zhou, J., Zhu, H., Liu, Z., Zhang, H., He, R., et al. (2017). Thermoelectric Properties of N-type ZrNiPb-Based Half-Heuslers. Chem. Mater. 29, 867–872. doi:10.1021/acs.chemmater.6b04898

CrossRef Full Text | Google Scholar

Mulla, R., and Rabinal, M. (2018). Copper Sulfides: Earth‐Abundant and Low‐Cost Thermoelectric Materials (Berlin: Wiley), 10/10.

Google Scholar

Nesper, R. (2014). The Zintl-Klemm Concept - A Historical Survey. Z. Anorg. Allg. Chem. 640, 2639–2648. doi:10.1002/zaac.201400403

CrossRef Full Text | Google Scholar

Owen, J., and Thornley, J. H. M. (1966). Covalent Bonding and Magnetic Properties of Transition Metal Ions. Rep. Prog. Phys. 29, 675–728. doi:10.1088/0034-4885/29/2/306

CrossRef Full Text | Google Scholar

Pei, Y., LaLonde, A. D., Wang, H., and Snyder, G. J. (2012). Low Effective Mass Leading to High Thermoelectric Performance. Energ. Environ. Sci. 5, 7963–7969. doi:10.1039/c2ee21536e

CrossRef Full Text | Google Scholar

Poon, S. J. (2019). Half Heusler Compounds: Promising Materials for Mid-to-high Temperature Thermoelectric Conversion. J. Phys. D: Appl. Phys. 52, 493001. doi:10.1088/1361-6463/ab3d71

CrossRef Full Text | Google Scholar

Qin, F., Nikolaev, S. A., Suwardi, A., Wood, M., Zhu, Y., Tan, X., et al. (2020). Crystal Structure and Atomic Vacancy Optimized Thermoelectric Properties in Gadolinium Selenides. Chem. Mater. 32, 10130–10139. doi:10.1021/acs.chemmater.0c03581

CrossRef Full Text | Google Scholar

Qiu, P., Huang, X., Chen, X., and Chen, L. (2009). Enhanced Thermoelectric Performance by the Combination of Alloying and Doping in TiCoSb-Based Half-Heusler Compounds. J. Appl. Phys. 106, 103703. doi:10.1063/1.3238363

CrossRef Full Text | Google Scholar

Rai, D. P., Sandeep, Shankar. A., Shankar, A., Aly, A. E., Patra, P. K., and Thapa, R. K. (2016). Electronic and Piezoelectric Properties of Half-Heusler Compounds: A First Principles Study. J. Phys. Conf. Ser. 765, 012005. doi:10.1088/1742-6596/765/1/012005

CrossRef Full Text | Google Scholar

Rai, D. P., Shankar, A., Sandeep, S., Ghimire, M. P., Khenata, R., and Thapa, R. K. (2015). Study of the Enhanced Electronic and Thermoelectric (TE) Properties of ZrxHf1−x−yTayNiSn: a First Principles Study. RSC Adv. 5, 95353–95359. doi:10.1039/c5ra12897h

CrossRef Full Text | Google Scholar

Rasmussen, S. C. (2015). The 18-electron Rule and Electron Counting in Transition Metal Compounds: Theory and Application. ChemTexts 1, 10. doi:10.1007/s40828-015-0010-4

CrossRef Full Text | Google Scholar

Recatala-Gomez, J., Kumar, P., Suwardi, A., Abutaha, A., Nandhakumar, I., and Hippalgaonkar, K. (2020). Direct Measurement of the Thermoelectric Properties of Electrochemically Deposited Bi2Te3 Thin Films. Sci. Rep. 10, 17922–18010. doi:10.1038/s41598-020-74887-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, Q., Fu, C., Qiu, Q., Dai, S., Liu, Z., Masuda, T., et al. (2020). Establishing the Carrier Scattering Phase Diagram for ZrNiSn-Based Half-Heusler Thermoelectric Materials. Nat. Commun. 11, 3142. doi:10.1038/s41467-020-16913-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Rull-Bravo, M., Moure, A., Fernández, J. F., and Martín-González, M. (2015). Skutterudites as Thermoelectric Materials: Revisited. RSC Adv. 5, 41653–41667. doi:10.1039/c5ra03942h

CrossRef Full Text | Google Scholar

Sakurada, S., and Shutoh, N. (2005). Effect of Ti Substitution on the Thermoelectric Properties of (Zr,Hf)NiSn Half-Heusler Compounds. Appl. Phys. Lett. 86, 082105. doi:10.1063/1.1868063

CrossRef Full Text | Google Scholar

Şaşıoğlu, E., Sandratskii, L. M., Bruno, P., and Galanakis, I. (2005). Exchange Interactions and Temperature Dependence of Magnetization in Half-Metallic Heusler Alloys. Phys. Rev. B 72, 184415. doi:10.1103/PhysRevB.72.184415

CrossRef Full Text | Google Scholar

Sekimoto, T., Kurosaki, K., Muta, H., and Yamanaka, S. (2007). High-Thermoelectric Figure of Merit Realized in P-type Half-Heusler Compounds: ZrCoSnxSb1-X. Jpn. J. Appl. Phys. 46, L673–L675. doi:10.1143/jjap.46.l673

CrossRef Full Text | Google Scholar

Sekimoto, T., Kurosaki, K., Muta, H., and Yamanaka, S. (2005). Thermoelectric Properties of (Ti,Zr,Hf)CoSb Type Half-Heusler Compounds. Mater. Trans. 46, 1481–1484. doi:10.2320/matertrans.46.1481

CrossRef Full Text | Google Scholar

Shiomi, J., Esfarjani, K., and Chen, G. (2011). Thermal Conductivity of Half-Heusler Compounds from First-Principles Calculations. Phys. Rev. B 84, 104302. doi:10.1103/physrevb.84.104302

CrossRef Full Text | Google Scholar

Suwardi, A., Lim, S. H., Zheng, Y., Wang, X., Chien, S. W., Tan, X. Y., et al. (2020). Effective Enhancement of Thermoelectric and Mechanical Properties of Germanium telluride via Rhenium-Doping. J. Mater. Chem. C 8, 16940–16948. doi:10.1039/d0tc04903d

CrossRef Full Text | Google Scholar

Tillard, M., Berche, A., and Jund, P. (2018). Synthesis of Pure NiTiSn by Mechanical Alloying: An Investigation of the Optimal Experimental Conditions Supported by First Principles Calculations. Metals 8 (10), 835. doi:10.3390/met8100835

CrossRef Full Text | Google Scholar

Ul Haq, B., Ahmed, R., AlFaify, S., Butt, F. K., Shaari, A., and Laref, A. (2018). Exploring Thermoelectric Materials for Renewable Energy Applications: The Case of Highly Mismatched Alloys Based on AlBi1-xSbx and InBi1-xSbx. Intermetallics 93, 235–243. doi:10.1016/j.intermet.2017.09.017

CrossRef Full Text | Google Scholar

Wang, X., Suwardi, A., Lim, S. L., Wei, F., and Xu, J. (2020). Transparent Flexible Thin-Film P-N junction Thermoelectric Module. Npj Flex Electron. 4, 19. doi:10.1038/s41528-020-00082-9

CrossRef Full Text | Google Scholar

Wu, T., Jiang, W., Li, X., Zhou, Y., and Chen, L. (2007). Thermoelectric Properties of P-type Fe-Doped TiCoSb Half-Heusler Compounds. J. Appl. Phys. 102, 103705. doi:10.1063/1.2809377

CrossRef Full Text | Google Scholar

Xia, Y., Bhattacharya, S., Ponnambalam, V., Pope, A. L., Poon, S. J., and Tritt, T. M. (2000). Thermoelectric Properties of Semimetallic (Zr, Hf)CoSb Half-Heusler Phases. J. Appl. Phys. 88, 1952–1955. doi:10.1063/1.1305829

CrossRef Full Text | Google Scholar

Xie, H., Wang, H., Fu, C., Liu, Y., Snyder, G. J., Zhao, X., et al. (2014). The Intrinsic Disorder Related alloy Scattering in ZrNiSn Half-Heusler Thermoelectric Materials. Sci. Rep. 4, 6888. doi:10.1038/srep06888

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, X., Liu, W., Chen, S., Wang, H., Zhang, Q., Chen, G., et al. (2013). Thermoelectric Property Study of Nanostructured P-type Half-Heuslers (Hf, Zr, Ti)CoSb0.8Sn0.2. Adv. Energ. Mater. 3, 1195–1200. doi:10.1002/aenm.201200973

CrossRef Full Text | Google Scholar

Yang, F., Wu, J., Suwardi, A., Zhao, Y., Liang, B., Jiang, J., et al. (2021). Gate‐Tunable Polar Optical Phonon to Piezoelectric Scattering in Few‐Layer Bi 2 O 2 Se for High‐Performance Thermoelectrics. Adv. Mater. 33, 2004786. doi:10.1002/adma.202004786

CrossRef Full Text | Google Scholar

Yang, J., and Caillat, T. (2006). Thermoelectric Materials for Space and Automotive Power Generation. MRS Bull. 31, 224–229. doi:10.1557/mrs2006.49

CrossRef Full Text | Google Scholar

Yousuf, S., and Gupta, D. C. (2019). Thermoelectric Response of ZrNiSn and ZrNiPb Half-Heuslers: Applicability of Semi-classical Boltzmann Transport Theory. Results Phys., 12, 1382–1386. doi:10.1016/j.rinp.2019.01.026

CrossRef Full Text | Google Scholar

Yu, C., Zhu, T.-J., Shi, R.-Z., Zhang, Y., Zhao, X.-B., and He, J. (2009). High-performance Half-Heusler Thermoelectric Materials Hf1−x ZrxNiSn1−ySby Prepared by Levitation Melting and Spark Plasma Sintering. Acta Materialia 57, 2757–2764. doi:10.1016/j.actamat.2009.02.026

CrossRef Full Text | Google Scholar

Zahedifar, M., and Kratzer, P. (2018). Band Structure and Thermoelectric Properties of Half-Heusler Semiconductors from many-body Perturbation Theory. Phys. Rev. B 97, 035204. doi:10.1103/physrevb.97.035204

CrossRef Full Text | Google Scholar

Zeier, W. G., Schmitt, J., Hautier, G., Aydemir, U., Gibbs, Z. M., Felser, C., et al. (2016). Engineering Half-Heusler Thermoelectric Materials Using Zintl Chemistry. Nat. Rev. Mater. 1, 16032. doi:10.1038/natrevmats.2016.32

CrossRef Full Text | Google Scholar

Zevalkink, A., Toberer, E. S., Zeier, W. G., Flage-Larsen, E., and Snyder, G. J. (2011). Ca3AlSb3: an Inexpensive, Non-toxic Thermoelectric Material for Waste Heat Recovery. Energ. Environ. Sci. 4, 510–518. doi:10.1039/c0ee00517g

CrossRef Full Text | Google Scholar

Zhang, Q., Liao, J., Tang, Y., Gu, M., Ming, C., Qiu, P., et al. (2017). Realizing a Thermoelectric Conversion Efficiency of 12% in Bismuth telluride/skutterudite Segmented Modules through Full-Parameter Optimization and Energy-Loss Minimized Integration. Energ. Environ. Sci. 10, 956–963. doi:10.1039/C7EE00447H

CrossRef Full Text | Google Scholar

Zheng, Y., Slade, T. J., Hu, L., Tan, X. Y., Luo, Y., Luo, Z. Z., et al. (2021). Defect Engineering in Thermoelectric Materials: What Have We Learned?. Chem. Soc. Rev. 50, 9022–9054.

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, J., Zhu, H., Liu, T.-H., Song, Q., He, R., Mao, J., et al. (2018). Large Thermoelectric Power Factor from crystal Symmetry-Protected Non-bonding Orbital in Half-Heuslers. Nat. Commun. 9, 1721. doi:10.1038/s41467-018-03866-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, H., He, R., Mao, J., Zhu, Q., Li, C., Sun, J., et al. (2018). Discovery of ZrCoBi Based Half Heuslers with High Thermoelectric Conversion Efficiency. London: Springer Nature.

Google Scholar

Zhu, H., Mao, J., Li, Y., Sun, J., Wang, Y., Zhu, Q., et al. (2019). Discovery of TaFeSb-Based Half-Heuslers with High Thermoelectric Performance. Nat. Commun. 10, 270. doi:10.1038/s41467-018-08223-5

PubMed Abstract | CrossRef Full Text | Google Scholar