Modified Bouc-Wen Model Based on Fractional Derivative and Application in Magnetorheological Elastomer

To accurately characterize the mechanical behavior of magnetorheological elastomer (MRE) under a wide range of strain amplitude, excitation frequency, and magnetic field, the viscoelastic fractional derivative was introduced, and a modified Bouc-Wen model based on fractional derivative for MRE in a nonlinear viscoelastic region was established. The Bouc-Wen model can accurately describe the hysteretic characteristics of the MRE nonlinear viscoelastic region, but it cannot accurately simulate magneto-viscoelasticity and frequency dependence. The fractional derivative can express this characteristic with fewer parameters and higher accuracy. The model’s validity was verified by fitting the experimental data of stress and strain measured in shear mode. By analyzing the coupling relationship between the model parameters and strain amplitude, frequency, and magnetic flux densities, a method of parameter identification under multi-loading conditions was proposed, and the modified model parameters were identified. The results reveal that the modified Bouc-Wen model can accurately characterize the mechanical properties of the nonlinear viscoelastic region of MRE, and the fitting accuracy is significantly improved compared with the Bouc-Wen model. The expression of the model parameters obtained from the method of parameter identification under multi-loading conditions is accurate in a wide range of strain amplitude, frequency, and magnetic flux density. The fitness values of simulation data and experimental data under identified and non-identified conditions exceed 90%, showcasing the effectiveness of the modified Bouc-Wen model and the feasibility of the parameter identification method under multi-loading conditions.

Introduction

Magnetorheological elastomer (MRE) is a new type of magnetosensitive smart material, which is composed of elastomer matrix, magnetic particles, and additives, and displays a good magnetorheological effect (Dong et al., 2012; Sun et al., 2018). Compared with magnetorheological fluid, MRE is characterized by good stability, fast response, no settlement and no leakage, thus showing promising application prospects in the field of tuned damper, nodal bushing and variable stiffness suspension, amongst others (Ahamed et al., 2018). Many academics have long focused on MRE research and carried out systematic research on the preparation, mechanical properties, and performance control of MRE (Xu et al., 2016; Zhang et al., 2020).

Presently, the mechanical properties of MRE are mainly studied from micro and macro aspects. The micro constitutive models are proposed based on the magnetic dipole theory, which mainly delineate the mechanism of magnetorheological effect and the relationship between magnetostrictive modulus and various factors. Micro constitutive models include the magnetic dipole model (Jolly et al., 1996), chain model (Davis, 1999; Xu and Sun, 2021), column model (Chen et al., 2007), grid model (Zhang et al., 2008). The micro model based on magnetic dipole theory explained the causes of the magnetorheological effect. However, they failed to depict the dynamic behavior of MRE comprehensively in magnetic fields.

To apply MRE to engineering practice, a model that can describe the macro mechanical behavior of MRE is also required. The macro mechanical model should comprehensively consider the effects of the external magnetic field, strain amplitude, and loading frequency on the mechanical properties of MRE (Hemmatian et al., 2020; Wang and Kari, 2020). Viscoelastic parameter models are widely employed to predict the mechanical properties of MRE. (Li et al., 2010) proposed a four-parameter linear viscoelastic model to predict the mechanical properties of MRE. The model can portray the influence of excitation frequency on the mechanical properties of MRE. However, the linear viscoelastic model using only springs and damping elements does not effectively trigger the nonlinear hysteretic characteristics of MRE. Some academics believe that the parallelogram characteristic of the MRE hysteretic curve under large strain is caused by friction between the elastomer matrix and magnetic particles. Therefore, the Coulomb friction model was used to describe this phenomenon (Kari and Blom, 2005). Chen proposed a linear viscoelastic model with the Coulomb friction model based on the viscoelastic parameter model (Chen and Jerrams, 2011). Also, Wang proposed a new nonlinear constitutive model of MS rubber by amalgamating the elastic and the boundary interface model (Blom and Kari, 2011). Due to the existence of Coulomb friction elements, the hysteretic curves of the above models possess the characteristics of a parallelogram, but they cannot accurately reflect the gradual change law of tangent modulus during loading.

Compared with the integer derivative viscoelastic model, the advantage of the fractional derivative model is that it can describe the magneto-viscoelasticity and frequency dependence of MRE with fewer parameters and higher accuracy (Xu et al., 2003; Xu et al., 2015). Moreover, the mechanical properties of viscoelastic materials are intricately related to the loading process, and the fractional derivative has the function of time memory, which better describes the physical phenomena with the history-dependent process (Behrooz et al., 2014). (Zhu et al., 2012; Xu et al., 2018) proposed a magneto-viscoelastic parameter model and an improved fractional derivative model based on the Kraus model in the form of fractional derivative according to matrix viscoelasticity and magneto-viscoelasticity. Based on the experimental results of MRE dynamic viscoelasticity, Wang established a fractional nonlinear constitutive model. Research reveals that the fractional derivative element can achieve fewer parameters and higher accuracy to describe frequency dependence (Wang and Kari, 2019). The results reveal that the fractional viscoelastic model can accurately characterize the magneto-viscoelasticity and frequency dependence of MRE.

The Bouc-Wen model has been widely used to delineate field-dependent nonlinear hysteretic systems and other complex dynamic characteristics (Ikhouane et al., 2007). (Dominguez et al., 2004) introduced the excitation current of the MR damper as a variable into the Bouc-Wen model, so that the model can consider the influence of different current intensities on the mechanical properties of the MR damper. (Yang et al., 2013) first used the Bouc-Wen model to simulate the mechanical characteristics of the MRE isolator. The study shows that the Bouc-Wen model can effectively simulate the hysteretic characteristics of the MRE nonlinear viscoelastic region. Still, it cannot accurately reflect the dependence of the hysteretic curve on frequency. Many scholars continue to modify the Bouc-Wen model. (Kwok et al., 2007) expressed the parameters describing deformation in the Bouc-Wen model with absolute values, and proposed the asymmetric Bouc-Wen model. Furthermore, (Xu et al., 2005) proposed a temperature phenomenological model with mass elements based on the Bouc-Wen model and considering the temperature rise effect and inertia effect of magnetorheological fluid. (Wang et al., 2017) considered the nonlinearity and frequency dependence of MRE and proposed a nonlinear constitutive model of MRE based on Bouc-Wen. The above Bouc-Wen model can simulate the nonlinear characteristics of stress and strain. Because the hysteretic curve of the Bouc-Wen hysteretic operator under sinusoidal load is independent of loading frequency, the Bouc-Wen model cannot accurately characterize the magneto-viscoelasticity and frequency dependence of MRE only by the Kelvin model composed of spring and damping element. Therefore, the Bouc-Wen model requires further improvement.

Numerous methods of parameters identification for the Bouc-Wen model have been proposed, which can be divided into two main types. One is the identification of the parameters by studying the forced limit cycle characterization of the Bouc-Wen model. The method has been adopted to identify the parameters of the Bouc-Wen model adopted to reproduce the hysteresis of a vibration isolator (Wang et al., 2015) and magnetorheological fluid damper (Rodriguez et al., 2008). Several individual data points have been used in the method to identify the model parameters, which makes the results prone to data noise and has a high requirement for the experimental sampling frequency (Zhu et al., 2019). The other one is adopting a numerical optimization algorithm with an appropriate fitness function. Different numerical optimization algorithms have been adopted to identify several parameters in the method. Chae used particle swarm optimization to identify the parameters of the Bouc-Wen model (Chae et al., 2013). Giuclea proposed an improved Bouc-Wen model, and the model parameters were obtained by a genetic algorithm (Giuclea et al., 2004). Then, charalampakis used a hybrid evolutionary algorithm to identify Bouc-Wen hysteretic systems (Charalampakis and Koumousis, 2008). Due to applying numerical optimization algorithms, the result can be easily trapped in a locally optimal solution. Moreover, this method overlooks the physical meaning of model parameters.

Despite the proof of the validity of the above mechanical models by the scholars, they still perform unsatisfactorily in engineering applications. The Bouc-Wen model has good universality and can well simulate the nonlinear hysteretic characteristics under a large strain load. Still, it cannot accurately predict the magneto-viscoelasticity and frequency dependence of MRE. The fractional derivative model can describe this characteristic with fewer parameters and higher accuracy. Furthermore, the fractional derivative has a memory function, which describes the historical dependence of viscoelasticity of MRE during loading. To accurately characterize the mechanical behavior of MRE under a wide range of strain amplitude, excitation frequency, and magnetic field, based on the Bouc-Wen model, the viscoelastic fractional derivative element is introduced into the stress-strain relationship of MRE, and a modified Bouc-Wen model based on fractional derivative for MRE in a nonlinear viscoelastic region was established. The model’s validity was verified by fitting the experimental data of stress and strain measured in shear mode. Through analysis of the coupling relationship between the model parameters and strain amplitude, frequency, and magnetic flux density, a method of parameter identification under multi-loading conditions was proposed, and the parameters of the modified Bouc-Wen model were identified.

Experiment and Modeling

Performance Tests of MRE

Isotropic MRE with 80% carbonyl iron particles (CIP) content was prepared by using natural rubber (NR), CIP, and additives as raw materials. CIP was procured from Jiangsu Tianyi Ultrafine Metal Powder Co., Ltd. with an average particle size of 5.5 μm. The main additives used were stearic acid, zinc oxide, accelerator (CZ), antioxidant (RD), antioxidant (4010NA), coumarone resin, and sulfur. NR and additives were provided by Hengshui Railway Construction Engineering Rubber Co., Ltd. The composition ratio of MRE is shown in Supplementary Appendix Table S1. The equipments used include: internal mixer CF-2L (produced by Dongguan Changfeng Machinery Technology Co., Ltd.), open mill RL-6 (produced by Baihong Machinery Co., Ltd.), vulcameter M-2000-AN (produced by Gotech Testing Machines Co., Ltd.), plate vulcanization machine XLB-25 (produced by Xingtai Weist Machinery Co., Ltd.), and the preparation process is shown in Figure 1.

FIGURE 1

FIGURE 1. Preparation process of MRE.

The dynamic performances of MRE under various conditions were measured by a Physica MCR301 rheometer (Anton Paar, Austria) fitted with a magneto-rheological module (MRD180). The rheometer can apply different magnetic flux densities on the parallel plates system (PP20) by altering direct current. The upper rotor applies the rotational shear strain parallel to the specimen according to the set program, and the internal precision sensor measures the feedback stress of the specimen. The required results are calculated by the instrument control software. In the oscillatory shear test mode, the software can record 257 stress-strain data points in each sinusoidal strain loading cycle and draw the stress-strain curve in each sinusoidal strain loading cycle according to these data points. The steady-state response of MRE under different strain amplitudes, frequencies, and magnetic flux densities was tested under sinusoidal shear strain excitation. The test conditions are listed in Supplementary Appendix Table S2; Figure 2 depicts the rotary rheometer, the specimen, and the schematic diagram of the test, in which the specimen is a disc with a diameter of 20 mm of a thickness of 1 mm.

FIGURE 2

FIGURE 2. Rotary rheometer, specimen and schematic of the measuring system.

Modified Bouc-Wen Model

As a classic model to describe the hysteresis loops, the Bouc-Wen model was first proposed by Bouc and Wen, using nonlinear differential equations to describe the hysteresis characteristics. Yang first utilized the Bouc-Wen model to fit the force-displacement relationship of the MRE isolator (Yang et al., 2013) and the governing equation is given by:

$F=\alpha kx+\left(1-\alpha \right)kz+c\dot{x}(1)$

$\dot{z}=A\dot{x}-\gamma \left|\dot{x}\right|z{\left|z\right|}^{n-1}-\beta \dot{x}{\left|z\right|}^n(2)$

where z denotes the evolutionary variable; k represents the coefficient of stiffness; c represents the coefficient of damping; α ranges between 0 and 1, denoting the linearity level of the hysteresis loops, while the non-dimensional parameters, i.e., A, n, β, and γ affect the shape and the size of the hysteresis loops.

According to the MRE performance test, the shape of the hysteresis loop of MRE will fluctuate with the change of strain amplitude. Under the action of a small strain load, the shape of the hysteresis loop is an approximately inclined ellipse. With the increase of strain amplitude, the hysteresis loop gradually evolves from an ellipse to an olive shape with two tips. When the strain amplitude is greater than 20%, the shape of the hysteresis loop presents the characteristics of a parallelogram (Wang et al., 2017). Therefore, MRE has obvious nonlinear hysteretic characteristics. The linear viscoelastic parameter model cannot simulate the parallelogram characteristics of the MRE hysteretic loop. Still, the Bouc-Wen model can well simulate this characteristic, especially under large strain amplitude, which is vital in engineering applications. Taking seismic isolation as an example, it often reaches large strain and enters the nonlinear stage. On the other hand, due to the hysteretic curve of the Bouc-Wen hysteretic operator under sinusoidal load is independent of loading frequency, the Bouc-Wen model cannot accurately characterize the magneto-viscoelasticity and frequency dependence of MRE only by the Kelvin model composed of spring and damping element. Therefore, the Bouc-Wen model warrants further improvements.

Compared with the integer derivative viscoelastic model, the advantage of the fractional derivative model is that it can describe the magneto-viscoelasticity and frequency dependence of MRE with fewer parameters and higher accuracy. Moreover, as opposed to the integer derivative only reflecting the instantaneous state, the fractional derivative is related to the whole process, which is more suitable to describe the physical phenomena of history-dependent processes. The stress-strain relationship of MRE is closely related to the loading process, so the fractional derivative model accurately portrays the mechanical properties of MRE. To accurately characterize the mechanical behavior of MRE under a wide range of strain amplitude, excitation frequency, and magnetic field, based on the Bouc-Wen model, the viscoelastic fractional derivative element was introduced into the stress-strain relationship of MRE, and a modified Bouc-Wen model based on fractional derivative for MRE in a nonlinear viscoelastic region was established, as illustrated in Figure 3. The governing equation is given by:

$F=\alpha kx+\left(1-\alpha \right)kz+c{D}_t^{p}x(3)$

$\dot{z}=A\dot{x}-\gamma \left|\dot{x}\right|z|z{|}^{n-1}-\beta \dot{x}|z{|}^n(4)$

where k denotes the shear modulus of MRE, including the modulus of elastomer matrix and the modulus generated from the magnetorheological effects; c denotes the coefficient of fractional derivative, including the damping of elastomer matrix and magneto-damping characteristics (Zhu et al., 2012); p is the order of fractional derivative, ranging from 0 to 1. ${\text{D}}_t^{p}x$ represents the p derivative of strain x concerning time t. Other parameters are identical to the Bouc-Wen model.

FIGURE 3

FIGURE 3. Modified Bouc-Wen model.

Simplification of the Fractional Derivative Part

The definition of the fractional derivative has many forms. In this paper, a Caputo type definition was used to describe

$D_t^{p}x\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(1-p\right)}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{\dot{x}\left(\tau \right)}{{\left(t-\tau \right)}^p}}d\tau (5)$

where the gamma function $\Gamma \left(z\right)$ is described as:

$\mathrm{\Gamma }\left(z\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z-1}dt}(6)$

The loading shear strain of the MRE performance test is set as follows:

$x\left(t\right)=x_m\sin \left(\omega t+\phi \right)(7)$

where x_m denotes the strain amplitude, and φ is the phase angle. According to reference (Chang et al., 2020), the fractional derivative term is simplified, and we can obtain:

$D_t^{p}x\left(t\right)=x_m{\omega }^p\sin \left(p\pi /2+\omega t+\phi \right)(8)$

\The commonly used algorithms for solving fractional derivatives are approximate analytical, numerical, and filter algorithms. Professor Oustaloup, a French scholar, proposed a fractional-order operator filter called the Oustaloup filter. These kinds of filters allow users to freely choose the fitting frequency band (ω_b, ω_h) and order N of interest, and use the integer-order transfer function model to approximate the fractional calculus operator (Oustaloup et al., 2000; Xu, 2018).

In this paper, the Oustaloup filter algorithm was used for approximate calculation. The basic idea is to do the approximate replacement of fractional operator s^p in the selected frequency range (ω_b, ω_h), in which (ω_b, ω_h) is freely selected according to the frequency range of the research object. According to this idea, the Oustaloup filter is constructed as follows (Xue et al., 2006; You et al., 2018):

$s^p\approx {\omega }_{\text{h}}^p{\displaystyle \prod _i^N\frac{s+{\omega }_i^{\ast }}{s+{\omega }_i}}(9)$

where N represents the order of the filter, and the zeros and poles of the filter can be written as:

${\omega }_i^{\ast }={\omega }_b{\left(\sqrt{{\omega }_h/{\omega }_b}\right)}^{\left(2i-1-p\right)/N}(10)$

${\omega }_i={\omega }_{\text{b}}{\left(\sqrt{{\omega }_h/{\omega }_b}\right)}^{\left(2i-1+p\right)/N}(11)$

Let x(t) be the input signal of the filter; then, the output signal is approximately equal to $D_t^{p}x\left(t\right)$ . For example, when the fractional order operator is $s^{0.5}$, the selected frequency range is (0.001 rad/ s, 1,000 rad/ s), and the order of the Oustaloup filter is 5, 7, and 9, respectively, the frequency response curve is depicted in Figure 4. As inferred from Figure 4, when the filter order is N = 9, the results obtained by the algorithm in the selected frequency range tend closer to the real value.

FIGURE 4

FIGURE 4. Frequency response curve.

Validation of MRE Constitutive Model

Parameter Identification Optimization Algorithm

Particle swarm optimization (PSO) has good optimization ability among many optimization algorithms, especially for complex engineering problems. Suppose that in the D dimensional search space, there are m particles forming a population of X, the current number of iterations is n, the current position of the particle is X_i, the flight speed is V_i, the current optimal position of the particle is p_i, and the current optimal position of the population is g. The position of each particle is a potential solution, which is substituted into the objective function L(x) to calculate the fitness value, and the solution is evaluated according to the fitness value. The optimal position of the i th particle is updated as follows:

$p_i\left(n+1\right)=\{\begin{array}{cc}{p}_i\left(n\right)& ,L\left[X_i\left(n+1\right)\right]\ge L\left[p_i\left(n\right)\right]\\ X_i\left(n+1\right)& ,L\left[X_i\left(n+1\right)\right]<L\left[p_i\left(n\right)\right]\end{array}(12)$

The current optimal position of the population is determined by the following formula:

$L\left[g\left(n\right)\right]=\min \left\{L\left[p_1\left(n\right)\right],\cdots ,L\left[p_m\left(n\right)\right]\right\}(13)$

The velocity update formula of the particles in search space is as follows:

$v_{ij}\left(n+1\right)=\omega v_{ij}\left(n\right)+d_1{r}_1\left[p_{ij}\left(n\right)-x_{ij}\left(n\right)\right]+d_2{r}_2\left[g_j\left(n\right)-x_{ij}\left(n\right)\right](14)$

The update formula of the particle position in search space is as follows:

$x_{ij}\left(n+1\right)=x_{ij}\left(n\right)+v_{ij}\left(n+1\right)(15)$

where i = [1,2, … , m], j = [1,2, … , D]; ω refers to the inertia weight; d₁ and d₂ represent the acceleration constants; and r₁ and r₂ are the random number in (0,1), respectively. Set the velocity range of the particles as (v_min, v_max) and the position range as (x_min, x_max). If the range is exceeded, the boundary value will be taken.

Despite the good optimization ability of PSO, it may easily fall into local optimum. Besides, the poor local-searching performance of PSO could induce a slow-down of the convergence at the later stage and yield an inaccurate result (Banks et al., 2008). As an optimization method based on probability, the Genetic Algorithm (GA) can adaptively adjust the search direction with an outstanding local searching capacity (Kumar et al., 2010). The optimization process is time-consuming and sensitive to population initialization. The combined use of GA and PSO algorithms improves the shortcoming that easily falls into the local extreme value and slow operation speed of the GA algorithm and improves the operation accuracy of the PSO algorithm (Bi and Qiu, 2019; Chen and Li, 2019).

In this paper, the hybrid GA-PSO algorithm was chosen to identify the parameters of the MRE mechanical model (Liu et al., 2020). The genetic operator is embedded in the PSO algorithm to improve the balance between exploration and development capabilities. First, the particle swarm population was initialized, and then the fitness value of the individual particle swarm was calculated. The individual optimal particle and the optimal group particle were updated according to the particle fitness value. After generating a new generation in the PSO iteration, the current population was replaced with a better population through GA operations such as selection, crossover, and mutation; then, a new population was created (Garg, 2016).

In this paper, the fitness values between simulation data and test data were taken as the quantitative standard of the fitting error. Moreover, the fitness values of the simulation data of the MRE model can be obtained by subtracting the error rate from 100%. The error rate calculation formula proposed by Spencer was taken as the objective function for parameter identification (Liu et al., 2011), as shown below:

$J=\frac{\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m{\left({\tau }_i^{test}-{\tau }_i^{sim}\right)}^2}}}{\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m{\left({\tau }_i^{test}-{\overline{\tau }}^{test}\right)}^2}}}(16)$

where ${\tau }_i^{test}$ refers to the shear stress test data of MRE, ${\overline{\tau }}_i^{test}$represents the mean value of test data, ${\tau }_i^{sim}$denotes the simulation data of shear stress, and m is the number of data points.

According to the control equation of the modified Bouc-Wen model, the simulation model was established by using the Simulink software, as illustrated in Figure 5A. The parameter identification based on MRE mechanical model refers to the optimization process of minimizing the objective function. The flow chart is shown in Figure 5B.

FIGURE 5

FIGURE 5. (A) Modified model in simulink software and (B) flowchart of Hybrid GA-PSO algorithm.

Model Validation Under the Single-Loading Condition

A GA-PSO algorithm was used for the identification of all unknown parameters in the MRE mechanical model with the following settings, including inertia weight ω = 1, acceleration constant d₁ = d₂ = 3.5, particle number m = 36, iteration number n = 400, chromosome coding length of 8, crossover probability of 0.7 and mutation probability of 0.3.

Model Validation Under Different Strain Amplitudes

The stress-strain curve of MRE will fluctuate with the strain amplitude of sinusoidal load. This section discusses the ability of the modified Bouc-Wen model to predict the nonlinear hysteretic characteristics of MRE, and whether the modified model can accurately reflect the variation law of viscoelasticity with strain amplitude.

At the magnetic flux density of 0 mT and the strain frequency of 1 Hz, the experimental data under different strain amplitudes (1.36, 2.51, 4.64, 8.57, 15.8, and 29.3%) were selected to identify the parameters of the Bouc-Wen model and the modified Bouc-Wen model. The comparison between the simulation data and experimental data is depicted in Figure 6.

FIGURE 6

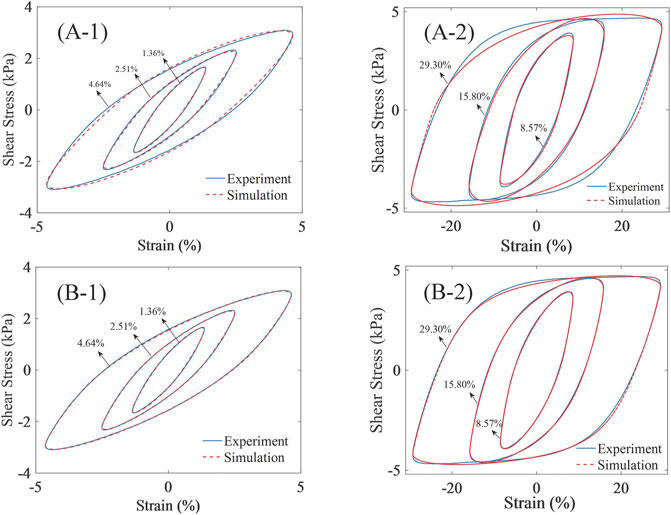
FIGURE 6. Simulation data and experimental data under different amplitudes: (A) Bouc-Wen model and (B) modified Bouc-Wen model.

As per Figure 6, the fitting effect of the Bouc-Wen model performs better at low strain amplitude. However, with the increase of strain amplitude, the error between simulation data of the Bouc-Wen model and experimental data increases gradually. At the strain amplitude of 29.3%, the hysteresis loops of simulation and experiment markedly differ. The fitting effect of the modified Bouc-Wen model under different strain amplitudes is significantly improved compared with that of the Bouc-Wen model. At the strain amplitude of 29.3%, the data fitness degree is high, indicating that the modified model can be effectively used to simulate the mechanical characteristics of MRE.

Model Validation Under Different Frequencies

The mechanical properties of MRE depend on the loading frequency. Because the Bouc-Wen hysteretic operator is independent of the loading frequency, the Bouc-Wen model cannot accurately characterize the frequency dependence of MRE. Whether the modified Bouc-Wen model based on fractional derivative can accurately describe the influence of loading frequency on shear modulus and damping requires further studies.

At the magnetic flux density of 405 mT and the strain amplitude of 0.40%, the experimental data under different strain frequencies (0.5, 1, 3, and 5 Hz) were selected to identify the parameters of the Bouc-Wen model and the modified Bouc-Wen model. The comparison between the simulation data and experimental data is illustrated in Figure 7.

FIGURE 7

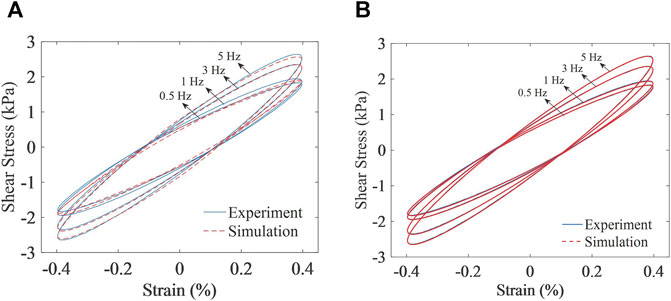
FIGURE 7. Simulation data and experimental data under different frequencies: (A) Bouc-Wen model and (B) modified Bouc-Wen model.

As inferred from Figure 7, the fitness values of the Bouc-Wen model under four loading frequencies are 95.54, 94.19,97.65, and 97.41%, respectively. The fitness values of the modified Bouc-Wen model under four loading frequencies are 99.24, 99.18, 99.55, and 99.57%. The comparison shows that the fitting effect of simulation data of the modified Bouc-Wen model and experimental data at different strain frequencies outperforms that of the Bouc-Wen model. This also reflects that the Bouc-Wen model cannot accurately identify the variation law of the hysteresis curve with frequency. The modified Bouc-Wen model is more accurate in reflecting the frequency variation characteristics of the MRE hysteresis curve.

Model Validation Under Different Magnetic Flux Densities

The storage modulus and loss modulus of MRE increase with the increase of magnetic flux density; that is, the viscoelasticity of MRE is magnetic field dependent. Compared with other viscoelastic materials, the accuracy of magneto-viscoelastic prediction is crucial for MRE. This section discusses whether the modified Bouc-Wen model can accurately reflect the influence of the MRE magnetorheological effect on its mechanical properties.

At the strain amplitude of 2.51% and the strain frequency of 1 Hz, the experimental data under different magnetic flux densities (115 mT, 234 mT, 405 mT, 456 mT, and 545 mT) are selected for the identification of the parameters of the Bouc-Wen model and the modified Bouc-Wen model. The comparison between the simulation data and experimental data is illustrated in Figure 8.

FIGURE 8

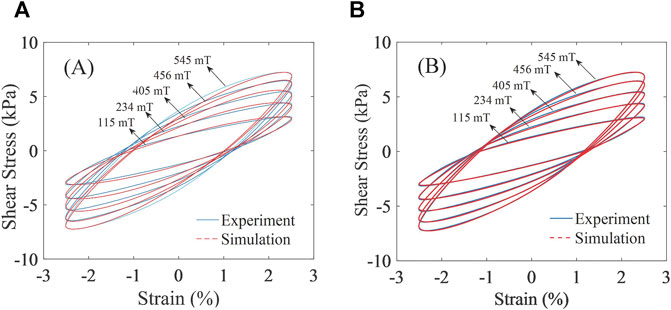
FIGURE 8. Simulation data and experimental data under different magnetic flux density (A). Bouc-Wen model and (B) modified Bouc-Wen model.

According to Figure 8, the simulation data of the modified Bouc-Wen model under different magnetic flux densities is in perfect agreement with the experimental data. The fitting accuracy is significantly higher than that of the Bouc-Wen model, indicating that the modified Bouc-Wen model can accurately reflect the influence of magnetic flux density on the mechanical properties of MRE.

The parameter identification results of the two MRE models under the above conditions are shown in Supplementary Appendix Table S3, S4. The data in the table shows that under the same test conditions, the coincidence rate between the simulation data and the experimental data of the modified Bouc-Wen model is higher than that of the Bouc-Wen model, showing that the modified model has a higher fitting accuracy.

Results and Discussion

As the modified Bouc-Wen model has a total of eight parameters, yielding the optimal results for the eight target parameters in each application of the model will result in greater difficulty in the utilization of the model and the engineering application of the model will also be impacted. Moreover, it is difficult to ensure the consistency of the optimization results. Therefore, this paper proposes a method of parameter identification under multi-loading conditions.

Parameter Coupling Analysis

The modified Bouc-Wen model can accurately reflect the viscoelastic characteristics of MRE under the single-loading condition. To ensure that the identification results of the model parameters are applicable under other loading conditions, it is also necessary to analyze whether the model parameters are coupled with other factors, such as strain frequency, amplitude, and magnetic flux density. By dividing both sides of the equation $\dot{z}=A\dot{x}-\gamma \left|\dot{x}\right|z{\left|z\right|}^{n-1}-\beta \dot{x}{\left|z\right|}^n$ by $\dot{x}$, then we can obtain:

$\frac{dz}{dx}=A-\gamma \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\dot{x}\right)z{\left|z\right|}^{n-1}-\beta {\left|z\right|}^n(17)$

Eq. 17 indicates that no correlation exists between the z-x curve and frequency under sinusoidal strain. There is no coupling relationship between parameter A, γ, β, n, and the frequency. The first derivative of the equation $F=\alpha kx+\left(1-\alpha \right)kz+c{D}_t^{p}x$ with respect to x can be obtained as follows:

$\frac{dF}{dx}=\alpha k+\left(1-\alpha \right)k\frac{dz}{dx}+c{\mathrm{D}}_t^{p-1}x(18)$

The first derivative of Eq. 14 with respect to x can be obtained as follows:

${\mathrm{D}}_t^{p-1}x\left(t\right)=x_m{\omega }^{p+1}\cos \left(p\pi /2+\omega t+\varphi \right)(19)$

Substituting Eqs 17, 19 into Eq. 18, we can obtain:

$\frac{dF}{dx}=\alpha k+\left(1-\alpha \right)k\left(A-\gamma \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\dot{x}\right)z{\left|z\right|}^{n-1}-\beta {\left|z\right|}^n\right)+c{x}_m{\omega }^{p+1}\cos \left(p\pi /2+\omega t+\varphi \right)(20)$

According to Eq. 20, for sinusoidal strains with different frequencies, the difference between the hysteretic loops obtained using the modified Bouc-Wen model is only related to $c{D}_t^{p}x$, coupling relationship between parameters c, p, and frequency.

According to further analysis of the modified model, at the same strain frequency and magnetic flux density, the identification results of the model parameters obtained under the strain amplitude of 1.36% are used for the prediction under the strain amplitude of 2.51, 4.64, 8.57, 15.8 and 29.3%, respectively. It was concluded that there was a large fitting error between the model simulation data and the experimental data, which made it unavailable to accurately simulate the hysteretic loop under different strain amplitudes. Similarly, when the parameters obtained under other amplitude conditions are used to predict under the condition with the amplitude of 1.36%, the agreement between the simulation data and the experimental data is low. A large fitting difference between the curves indicates that coupling exists between the parameters and the loading amplitude when using the modified Bouc-Wen model. Figure 9A shows the hysteresis loops of MRE experimental data under different amplitudes at the magnetic flux density of 0 mT and the strain frequency of 1 Hz. According to Figure 9A, with the increase of strain amplitude, the equivalent stiffness (diagonal slope of the hysteresis loop) of the hysteresis loop decreases (Yang et al., 2013), while the equivalent damping (area of the hysteresis loop) of the hysteresis loop increases (Xia and Yue, 2004). Parameter k represents the elastic force coefficient of the model, and c refers to the viscous force coefficient of the model, also proving that the parameters of k and c are related to the strain amplitude.

FIGURE 9

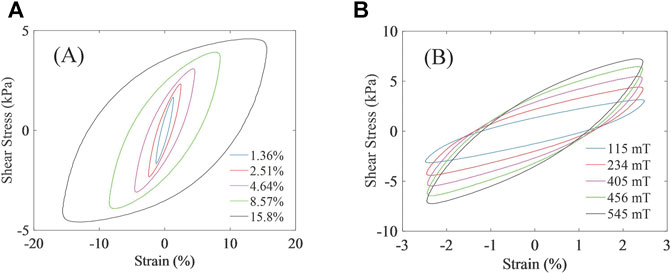
FIGURE 9. Experimental data of MRE (A). different strain amplitudes and (B) different magnetic flux density.

Figure 9B exhibits the hysteresis loops of MRE experimental data under different magnetic flux densities at the frequency of 1 Hz and the amplitude of 2.51%. It can be inferred from Figure 11 that the shape of the hysteresis loop basically remains unchanged with different magnetic flux densities, which denotes that the shape of the hysteresis loop does not change with the magnetic flux density. The shape of the hysteresis loop is jointly controlled by the parameters of α, γ, β, and n. Therefore, the parameters of α, γ, β, and n are less affected by the magnetic flux density, and the coupling relationship between the parameters of α, γ, β, and n the magnetic flux density are no longer considered here. Moreover, with the increase of the magnetic flux density, the equivalent stiffness and equivalent damping of the hysteresis loop increase gradually, indicating that the magnetic flux density is related to the parameters of k and c. Parameter α represents the linearity level of the hysteresis loop, and p refers to the order of fractional derivative, both of them are related to the stiffness and damping of the hysteresis loop. Therefore, they have a certain functional relationship with the magnetic flux density.

In conclusion, strain frequency, strain amplitude, and magnetic flux density are coupled with the parameters of the modified Bouc-Wen model. The parameters related to strain frequency are c and p; while those related to the strain amplitude include k, c, A, γ, β, n, α, and p; besides, the parameters associated with the magnetic flux density include k, c, α, and p.

Model Parameter Identification Method

According to the analysis described in the previous section, the parameters of the modified Bouc-Wen model are coupled with multiple factors simultaneously. Therefore, it is difficult to quantify all the coupling relationships. To lower the difficulty degree of parameter identification and universalize the results, this paper simplified the coupling relationship of parameters. It proposed a method for parameter identification under multi-loading conditions.

The fundamental idea is that the influence of the magnetic field on α and p is ignored in the entire identification. The functional relationship between model parameters and amplitude and magnetic field can be explored at any frequency without consideration for the effect of frequency on k and c. Finally, with the comprehensive consideration of the influence of frequency on k and c, the parameter expressions are modified appropriately to improve the fitting accuracy at different frequencies. The specific steps are as follows:

1) At the frequency of 1 Hz, the experimental data under 25 load conditions (the strain amplitudes are 1.36, 2.51, 4.64, 8.57, and 15.8%, and the magnetic flux density at 0 mT, 115 mT, 234 mT, 456 mT, and 545 mT, respectively) were identified for the first time. The identification results include k_ij, c_ij, A_ij, γ_ij, β_ij, n_ij, α_ij, p_ij, where the subscript i represents the strain amplitude, and the subscript j denotes the magnetic flux density.

2) With the same strain amplitude, the mean value of parameters corresponding to different magnetic flux densities (0m T, 115 m T, 234 mT, 456 mT and 545 mT) is taken, and ${\overline{A}}_i$, ${\overline{r}}_i$, ${\overline{\beta }}_i$, ${\overline{n}}_i$, ${\overline{\alpha }}_i$, ${\overline{p}}_i$ could be obtained.

3) Analysis of the variation trend of ${\overline{A}}_i$, ${\overline{r}}_i$, ${\overline{\beta }}_i$, ${\overline{n}}_i$, ${\overline{\alpha }}_i$, ${\overline{p}}_i$ obtained in Step 2) with strain amplitude, the curve fitting toolbox was used to determine the expression of each parameter as [A, γ, β, n, α, p] = F₁ (x_m) where x_m represents the strain amplitude.

4) A_i, γ_i, β_i, n_i, α_i, p_i under different strain amplitudes (1.36, 2.51, 4.64, 8.57 and 15.8%) were obtained based on the expression of [A, γ, β, n, α, p] = F₁ (x_m). A_i, γ_i, β_i, n_i, α_i, and p_i were substituted as the determined value in the MRE model. Therefore, only the parameters of k and c remain unknown in the MRE model. The parameters of k and c were identified for the second time by using the experimental data of 25 conditions in Step (1), in this case, ${\tilde{k}}_{ij}$ and ${\tilde{c}}_{ij}$ are yielded.

5) Analysis of the variation trend of ${\tilde{k}}_{ij}$ and ${\tilde{c}}_{ij}$ obtained in Step 4) with strain amplitude and magnetic flux density, the curve fitting toolbox was used to determine the expression of each parameter as [k, c] = F₂ (x_m, B) where B refers to the magnetic flux density.

6) Combined with the influence of frequency on the parameters of k and c, the expressions of the parameters of k and c were modified to obtain [k, c] = F₃ (f)·F₂ (x_m, B).

Based on the above identification method, the parameters were identified according to the experimental data of 25 selected load conditions. The values identified first are listed in Supplementary Appendix Table S5, while those identified for the second time are shown in Supplementary Appendix Table S6. The curve fitting was conducted according to the variation trend of the mean value of the parameters of A, γ, β, n, α, and p in Supplementary Appendix Table S5 with the amplitude. The results are illustrated in Figure 10. The parameter expression of the fitting is as follows:

$A\left(x_{\text{m}}\right)=0.9497x_{\text{m}}+26.16(21)$

$\gamma \left(x_m\right)=-2.554\times {10}^{-3}{x}_m^3+0.06056x_m^2-0.431x_m+18.89(22)$

$\beta \left(x_m\right)=2.861\times {10}^{-3}{x}_m^3-9.676\times {10}^{-2}{x}_m^2+0.956x_m+0.5547(23)$

$n\left(x_m\right)=-9.6\times {10}^{-4}{x}_m^3+0.02539x_m^2-0.1291x_m+0.7127(24)$

$\alpha \left(x_m\right)=-0.2798x^{-1.302}+0.6506(25)$

$p\left(x_m\right)=7.647\times {10}^{-4}{x}_m^3+2.167\times {10}^{-2}{x}_m^2-0.1709x_m+0.8195(26)$

where x_m represents the strain amplitude.

FIGURE 10

FIGURE 10. Parameter fitting curve of modified Bouc-Wen model.

The curve fitting was conducted according to the variation trend of the parameters of k and c in Supplementary Appendix Table S6 with the amplitude and magnetic flux density. The results are shown in Figure 11, and the parameter expression of the fitting is as follows:

$\begin{array}{l}k\left(x_{\text{m}},B\right)=8.437-1.106x_{\text{m}}-1\text{.}244\times {10}^{-2}B+7\text{.}365\times {10}^{-2}{x}_{\text{m}}^2-5\text{.}14\times {10}^{-3}{x}_{\text{m}}B+\\ 1\text{.}637\times {10}^{-4}{B}^2-1\text{.}593\times {10}^{-3}{x}_{\text{m}}^3+6\text{.}261\times {10}^{-4}{x}_{\text{m}}^{2}B-\\ 2.852\times {10}^{-6}{x}_{\text{m}}{B}^2-2.179\times {10}^{-7}{B}^3-1.733\times {10}^{-5}{x}_{\text{m}}^{3}B-\\ 1.883\times {10}^{-7}{x}_{\text{m}}^2{B}^2+7.25\times {10}^{-9}{x}_{\text{m}}{B}^3+4.17\times {10}^{-11}{B}^4\end{array}(27)$

$\begin{array}{l}c\left(x_{\text{m}},B\right)=9.485-0.3246x_{\text{m}}-4\text{.}419\times {10}^{-2}B+0.7159x_{\text{m}}^2+\\ 3\text{.}252\times {10}^{-2}{x}_{\text{m}}B+2\text{.}59\times {10}^{-4}{B}^2-0.122x_{\text{m}}^3-3\text{.}774\times {10}^{-3}{x}_{\text{m}}^{2}B-\\ 3.678\times {10}^{-5}{x}_{\text{m}}{B}^2-3.318\times {10}^{-7}{B}^3+4\text{.}877\times {10}^{-3}{x}_{\text{m}}^4+\\ 1\text{.}264\times {10}^{-4}{x}_{\text{m}}^{3}B+9.385\times {10}^{-7}{x}_{\text{m}}^2{B}^2+2.744\times {10}^{-8}{x}_{\text{m}}{B}^3\end{array}(28)$

where x_m denotes the strain amplitude, B represents the applied magnetic flux density.

FIGURE 11

FIGURE 11. Parameter fitting curve of modified Bouc-Wen model.

At the magnetic flux density of 405 mT and the strain amplitude of 0.40%, the experimental data with the frequencies of 0.5, 1, 3, and 5 Hz, respectively, were selected for the analysis of the functional relationship between the parameters of k and c and the frequency. Moreover, Eqs 27, 28 were modified. Based on the improved Bouc-Wen model, the experimental data under the frequency of 1 Hz were identified. The identified values of parameters were substituted into the modified Bouc-Wen model as the determined values. Therefore, the parameters of k and c were left unknown in the model only. The parameters of k and c were subsequently identified with the experimental data at the frequency of 0.5, 3, and 5 Hz, respectively. Supplementary Appendix Table S7 shows the identified values of the parameters of k and c at different frequencies (the results obtained at 1 Hz are regarded as unit 1, and the others are the relative values). Fitting the data in Supplementary Appendix Table S7, the functional relationship between the parameters of k and c and the frequency can be expressed as follows:

$F_k\left(f\right)=-0.2706\times f^3+2.298\times f^2-4.973\times f+3.946(29)$

$F_c\left(f\right)=-0.1933\times f^3+1.69\times f^2-4.197\times f+3.7(30)$

where f denotes the frequency.

In conclusion, the modified expressions of the parameters of k and c are as follows:

$\begin{array}{l}k\left(x_m,B,f\right)=F_k\left(f\right)\times (8.437-1.106x_m-1.244\times {10}^{-2}B+7.365\times {10}^{-2}{x}_m^2-\\ 5.14\times {10}^{-3}{x}_{m}B+1.637\times {10}^{-4}{B}^2-1.593\times {10}^{-3}{x}_m^3+\\ 6.261\times {10}^{-4}{x}_m^{2}B-2.852\times {10}^{-6}{x}_m{B}^2-2.179\times {10}^{-7}{B}^3-\\ 1.733\times {10}^{-5}{x}_m^{3}B-1.883\times {10}^{-7}{x}_m^2{B}^2+7.25\times {10}^{-9}{x}_m{B}^3+4.17\times {10}^{-11}{B}^4)\end{array}(31)$

$\begin{array}{l}c\left(x_m,B,f\right)=F_c\left(f\right)\times (9.485-0.3246x_m-4.419\times {10}^{-2}B+0.7159x_m^2+\\ 3.252\times {10}^{-2}{x}_{m}B+2.59\times {10}^{-4}{B}^2-0.122x_m^3-3.774\times {10}^{-3}{x}_m^{2}B-\\ 3.678\times {10}^{-5}{x}_m{B}^2-3.318\times {10}^{-7}{B}^3+4.877\times {10}^{-3}{x}_m^4+\\ 1.264\times {10}^{-4}{x}_m^{3}B+9.385\times {10}^{-7}{x}_m^2{B}^2+2.744\times {10}^{-8}{x}_m{B}^3)\end{array}(32)$

where x_m represents the strain amplitude, B represents the applied magnetic flux density, f denotes the frequency.

Verification of Identification Results

To verify the correctness of the identification results under the load condition of both identification and non-identification, the fitness values of the simulation data based on the method of multi-loading conditions parameter identification and experimental data were analyzed.

Verification Under Identification Condition

For 25 identification conditions at the frequency of 1 Hz, different amplitudes (1.36, 2.51, 4.64, 8.57, and 15.8%) and magnetic flux densities (0 mT, 115 mT, 234 mT, 456 mT, and 545 mT), the simulation data obtained by using the method of parameter identification under multi-condition is compared with the experimental data, as illustrated in Figure 12. The fitness values are shown in Supplementary Appendix Table S8.

FIGURE 12

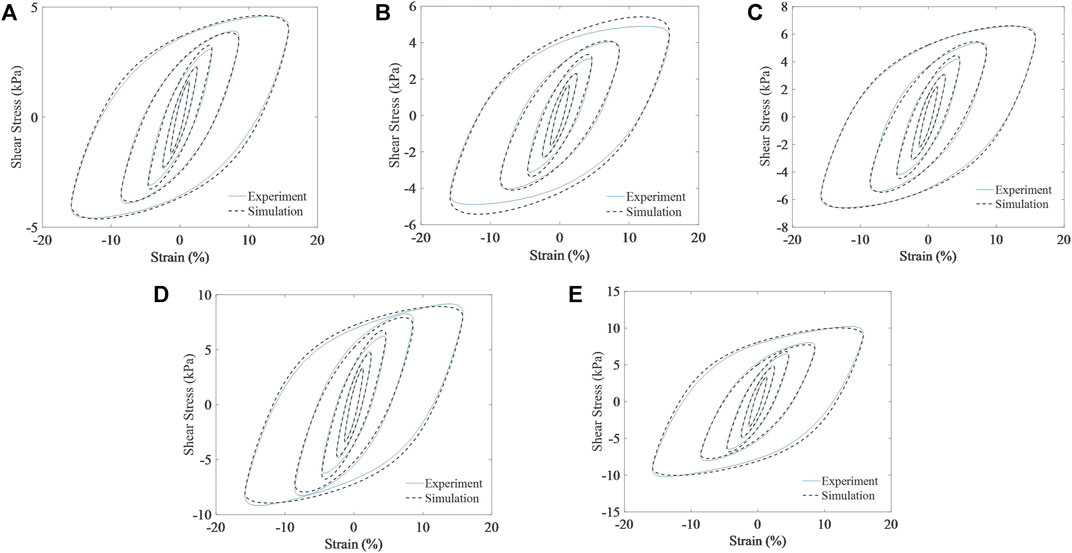
FIGURE 12. Simulation data and experimental data under identification conditions: (A) 0 mT, (B) 115 mT, (C) 234 mT, (D) 456 mT, and (E) 545 mT.

As illustrated in Figure 12, the fitness values of simulation data and experimental data are higher than 90% under different amplitudes or magnetic flux densities conditions. The hysteresis loops of model simulation can accurately track the change law of mechanical properties of MRE, indicating that the parameter identification results are effective for identification conditions with a good fitting effect.

Verification Under Non-identification Conditions

At the magnetic flux density of 115 mT, the amplitudes are 2.51 and 4.64%, and the frequencies are 0.5, 3, and 5 Hz, respectively; in comparison, at the magnetic flux density of 234 mT, the amplitude is 1.36%, and the frequency is 0.5, 3, and 5 Hz, respectively. The simulation data obtained using the method for parameter identification under multi-condition is compared with the experimental data, as illustrated in Figure 13. The fitness values are shown in Supplementary Appendix Table S9.

FIGURE 13

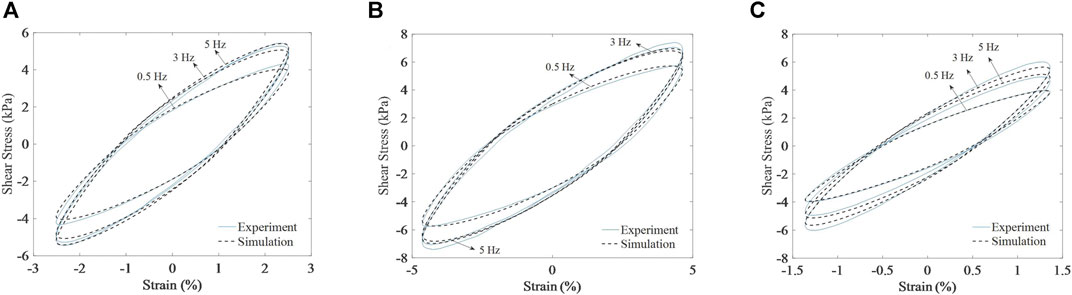
FIGURE 13. Simulation data and experimental data under non identification condition: (A) 115 mT-2.51%; (B) 115 mT-4.64%; and (C) 234 mT-1.36%.

It can be inferred from Figure 13 that at different frequencies, amplitudes, and magnetic flux densities, the hysteretic loops of simulation data and experimental data are in good agreement. The modified Bouc-Wen model is available for a more accurate reflection of the variation of MRE hysteretic characteristics with frequency. The fitting error of individual load conditions is substantial. Still, the fitness values of simulation data and experimental data exceed 90%, showing that the parameter identification results are effective for non-identification conditions with a good fitting effect.

Conclusion

The hysteresis loops of MRE under different strain amplitudes, frequencies, and magnetic flux densities markedly differ. To effectively simulate the mechanical characteristics of MRE, a modified Bouc-Wen model based on fractional derivative viscosity characteristics was proposed. Based on the analysis of the coupling relationship of model parameters, a method for parameter identification under multi-loading conditions was proposed. The parameters were identified and verified according to the MRE experimental data. The results are as follows:

1) A modified Bouc-Wen model of fractional derivative was proposed, and the coupling relationship between parameters and strain amplitude, frequency, and magnetic flux density was obtained. The fitting results under different amplitudes, frequencies, and magnetic flux densities conditions show that the model can accurately describe the mechanical characteristics of MRE, and the fitting accuracy was significantly improved compared with the Bouc-Wen model. The model applies to the loading conditions with the magnetic flux density ranging from 0–545 mT, the strain amplitude ranging from 0.04–29.3%, and the frequency within the range from 0.5 to 5 Hz.

2) A method for parameter identification under multi-loading conditions was proposed. The expression of model parameters was obtained through fitting, and the relationship between parameters and influencing factors was quantified. The identification results were verified under the identified and non-identified loading conditions. The fitness values of each loading condition exceeded 90%, indicating the feasibility of the identification method. The method can also be widely applied in the parameter identification of other models.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SY, PW, YL, XD, YT, and YZ participated in the conception and design of this study. PW prepared MRE samples, proposed the modified constitutive model and the parameter identification method, and carried out simulation and verification. XD and YT were used to test the performance of MRE samples. SY and YL supervised the study. PW drafted the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (Nos. 11790282, 12072208, and 52072249), the Opening Foundation of State Key Laboratory of Shijiazhuang Tiedao University (ZZ2021-13) and the Postgraduate Foundation of Hebei Province (CXZZBS2021112).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the State Key Laboratory of Mechanical Behaviour in Traffic Engineering Structure and System Safety for providing equipments to the experiment.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.743716/full#supplementary-material

References

Ahamed, R., Choi, S.-B., and Ferdaus, M. M. (2018). A State of Art on Magneto-Rheological Materials and Their Potential Applications. J. Intell. Mater. Syst. Structures 29, 2051–2095. doi:10.1177/1045389X18754350

CrossRef Full Text | Google Scholar

Banks, A., Vincent, J., and Anyakoha, C. (2008). A Review of Particle Swarm Optimization. Part Ii: Hybridisation, Combinatorial, Multicriteria and Constrained Optimization, and Indicative Applications. Nat. Comput. 7, 109–124. doi:10.1007/s11047-007-9050-z

CrossRef Full Text | Google Scholar

Behrooz, M., Wang, X., and Gordaninejad, F. (2014). Modeling of a New Semi-active/passive Magnetorheological Elastomer Isolator. Smart Mater. Struct. 23, 045013. doi:10.1088/0964-1726/23/4/045013

CrossRef Full Text | Google Scholar

Bi, K., and Qiu, T. (2019). An Intelligent SVM Modeling Process for Crude Oil Properties Prediction Based on a Hybrid GA-PSO Method. Chin. J. Chem. Eng. 27, 1888–1894. doi:10.1016/j.cjche.2018.12.015

CrossRef Full Text | Google Scholar

Blom, P., and Kari, L. (2011). A Nonlinear Constitutive Audio Frequency Magneto-Sensitive Rubber Model Including Amplitude, Frequency and Magnetic Field Dependence. J. sound vibration 330, 947–954. doi:10.1016/j.jsv.2010.09.010

CrossRef Full Text | Google Scholar

Chae, Y., Ricles, J. M., and Sause, R. (2013). Modeling of a Large-Scale Magneto-Rheological Damper for Seismic hazard Mitigation. Part II: Semi-active Mode. Earthquake Engng Struct. Dyn. 42, 687–703. doi:10.1002/eqe.223710.1002/eqe.2236

CrossRef Full Text | Google Scholar

Chang, Y. J., Tian, W. W., Chen, E. L., Shen, Y. J., and Xing, W. C. (2020). Dynamic Model for the Nonlinear Hysteresis of Metal Rubber Baser on the Fractional-Order Derivative. J. Vibration Shock 39, 233–241.

Google Scholar

Charalampakis, A. E., and Koumousis, V. K. (2008). Identification of Bouc-Wen Hysteretic Systems by a Hybrid Evolutionary Algorithm. J. Sound Vibration 314 (3-5), 571–585. doi:10.1016/j.jsv.2008.01.018

CrossRef Full Text | Google Scholar

Chen, J., and Li, H. (2019). Airfoil Optimization of Land-Yacht Robot Based on Hybrid PSO and GA. Int. J. Patt. Recogn. Artif. Intell. 33, 1959041. doi:10.1142/S0218001419590419

CrossRef Full Text | Google Scholar

Chen, L., Gong, X. L., and Li, W. H. (2007). Microstructures and Viscoelastic Properties of Anisotropic Magnetorheological Elastomers. Smart Mater. Struct. 16, 2645–2650. doi:10.1088/0964-1726/16/6/069

CrossRef Full Text | Google Scholar

Chen, L., and Jerrams, S. (2011). A Rheological Model of the Dynamic Behavior of Magnetorheological Elastomers. J. Appl. Phys. 110, 013513. doi:10.1063/1.3603052

CrossRef Full Text | Google Scholar

Davis, L. C. (1999). Model of Magnetorheological Elastomers. J. Appl. Phys. 85, 3348–3351. doi:10.1063/1.369682

CrossRef Full Text | Google Scholar

Dominguez, A., Sedaghati, R., and Stiharu, I. (2004). Modelling the Hysteresis Phenomenon of Magnetorheological Dampers. Smart Mater. Struct. 13, 1351–1361. doi:10.1088/0964-1726/13/6/008

CrossRef Full Text | Google Scholar

Dong, X., Ma, N., Qi, M., Li, J., Chen, R., and Ou, J. (2012). The Pressure-dependent MR Effect of Magnetorheological Elastomers. Smart Mater. Struct. 21, 416–422. doi:10.1088/0964-1726/21/7/075014

CrossRef Full Text | Google Scholar

Garg, H. (2016). A Hybrid PSO-GA Algorithm for Constrained Optimization Problems. Appl. Maths. Comput. 274, 292–305. doi:10.1016/j.amc.2015.11.001

CrossRef Full Text | Google Scholar

Giuclea, M., Sireteanu, T., Stancioiu, D., and Stammers, C. W. (2004). Model Parameter Identification for Vehicle Vibration Control with Magnetorheological Dampers Using Computational Intelligence Methods. Proc. Inst. Mech. Eng. J. Syst. Control. Eng. 218, 569–581. doi:10.1243/095965104271524010.1177/095965180421800705

CrossRef Full Text | Google Scholar

Hemmatian, M., Sedaghati, R., and Rakheja, S. (2020). Characterization and Modeling of Temperature Effect on the Shear Mode Properties of Magnetorheological Elastomers. Smart Mater. Struct. 29, 115001. doi:10.1088/1361-665X/abb359

CrossRef Full Text | Google Scholar

Ikhouane, F., Mañosa, V., and Rodellar, J. (2007). Dynamic Properties of the Hysteretic Bouc-Wen Model. Syst. Control. Lett. 56 (3), 197–205. doi:10.1016/j.sysconle.2006.09.001

CrossRef Full Text | Google Scholar

Jolly, M. R., Carlson, J. D., and Muñoz, B. C. (1996). A Model of the Behaviour of Magnetorheological Materials. Smart Mater. Struct. 5, 607–614. doi:10.1088/0964-1726/5/5/009

CrossRef Full Text | Google Scholar

Kari, L., and Blom, P. (2005). Magneto-sensitive Rubber in a Noise Reduction Context - Exploring the Potential. Plastics, rubber and composites 34, 365–371. doi:10.1179/174328905X59692

CrossRef Full Text | Google Scholar

Kumar, M., Husain, M., Upreti, N., and Gupta, D. (2010). Genetic Algorithm: Review and Application. J. Inf. Knowledge Manage. 2, 451–454.

Google Scholar

Kwok, N. M., Ha, Q. P., Nguyen, M. T., Li, J., and Samali, B. (2007). Bouc-Wen Model Parameter Identification for a MR Fluid Damper Using Computationally Efficient GA. ISA Trans. 46 (2), 167–179. doi:10.1016/j.isatra.2006.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W. H., Zhou, Y., and Tian, T. F. (2010). Viscoelastic Properties of MR Elastomers under Harmonic Loading. Rheol Acta 49, 733–740. doi:10.1007/s00397-010-0446-9

CrossRef Full Text | Google Scholar

Liu, Y., Dai, J., Zhao, S., Zhang, J., Shang, W., Li, T., et al. (2020). Optimization of Five-Parameter BRDF Model Based on Hybrid GA-PSO Algorithm. Optik 219, 164978. doi:10.1016/j.ijleo.2020.164978

CrossRef Full Text | Google Scholar

Liu, Y., Yang, S., and Liao, Y. (2011). A Quantizing Method for Determination of Controlled Damping Parameters of Magnetorheological Damper Models. J. Intell. Mater. Syst. structures 22, 2127–2136. doi:10.1177/1045389X11425278

CrossRef Full Text | Google Scholar

Oustaloup, A., Levron, F., Mathieu, B., and Nanot, F. M. (2000). Frequency-band Complex Noninteger Differentiator: Characterization and Synthesis. IEEE Trans. Circuits Syst. 47, 25–39. doi:10.1109/81.817385

CrossRef Full Text | Google Scholar

Rodriguez, A., Iwata, N., Ikhouane, F., and Rodellar, J. (2008). Modeling and Identification of a Large-Scale Magnetorheological Fluid Damper. Ast 56, 374–379. doi:10.4028/www.scientific.net/AST.56.374

CrossRef Full Text | Google Scholar

Sun, S., Yang, J., Du, H., and Li, W. (2018). Overcoming the Conflict Requirement between High-Speed Stability and Curving Trafficability of the Train Using an Innovative Magnetorheological Elastomer Rubber Joint. J. Intell. Mater. Syst. Structures 29, 214–222. doi:10.1177/1045389X17698591

CrossRef Full Text | Google Scholar

Wang, B., and Kari, L. (2020). A Visco-Elastic-Plastic Constitutive Model of Isotropic Magneto-Sensitive Rubber with Amplitude, Frequency and Magnetic Dependency. Int. J. plasticity 132, 102756. doi:10.1016/j.ijplas.2020.102775

CrossRef Full Text | Google Scholar

Wang, B., and Kari, L. (2019). Modeling and Vibration Control of a Smart Vibration Isolation System Based on Magneto-Sensitive Rubber. Smart Mater. Struct. 28, 065026. doi:10.1088/1361-665X/ab1ab4

CrossRef Full Text | Google Scholar

Wang, H.-X., Gong, X.-S., Pan, F., and Dang, X.-J. (2015). Experimental Investigations on the Dynamic Behaviour of O-type Wire-cable Vibration Isolators. Shock and Vibration 2015, 1–12. doi:10.1155/2015/869325

CrossRef Full Text | Google Scholar

Wang, Q., Dong, X., Li, L., and Ou, J. (2017). A Nonlinear Model of Magnetorheological Elastomer with Wide Amplitude Range and Variable Frequencies. Smart Mater. Struct. 26, 065010. doi:10.1088/1361-665X/aa66e3

CrossRef Full Text | Google Scholar

Xia, P. Q., and Yue, H. L. (2004). Performance of Magnetorheological Damper with its Application to Vibration Control. J. Aerospace Power 19, 305–309. doi:10.3969/j.issn.1000-8055.2004.03.004

CrossRef Full Text | Google Scholar

Xu, D. Y. (2018). Fractional Calculus and Fractional-Order Control [M]. Beijing: Science Press.

Xu, Z.-D., Shen, Y.-P., and Guo, Y.-Q. (2003). Semi-active Control of Structures Incorporated with Magnetorheological Dampers Using Neural Networks. Smart Mater. Struct. 12, 80–87. doi:10.1088/0964-1726/12/1/309

CrossRef Full Text | Google Scholar

Xu, Z.-D., and Sun, C.-L. (2021). Single-double Chains Micromechanical Model and Experimental Verification of MR Fluids with MWCNTs/GO Composites Coated Ferromagnetic Particles. J. Intell. Mater. Syst. Structures 5. doi:10.1177/1045389X20988779

CrossRef Full Text | Google Scholar

Xu, Z.-D., Suo, S., and Lu, Y. (2016). Vibration Control of Platform Structures with Magnetorheological Elastomer Isolators Based on an Improved Savs Law. Smart Mater. Struct. 25. doi:10.1088/0964-1726/25/6/065002

CrossRef Full Text | Google Scholar

Xu, Z.-D., Suo, S., Zhu, J.-T., and Guo, Y.-Q. (2018). Performance Tests and Modeling on High Damping Magnetorheological Elastomers Based on Bromobutyl Rubber. J. Intell. Mater. Syst. Structures 29, 1025–1037. doi:10.1177/1045389X17730909

CrossRef Full Text | Google Scholar

Xu, Z.-D., Xu, C., and Hu, J. (2015). Equivalent Fractional Kelvin Model and Experimental Study on Viscoelastic Damper. J. Vibration Control. 21, 2536–2552. doi:10.1177/1077546313513604

CrossRef Full Text | Google Scholar

Xu, Z. D., Li, A. Q., Cheng, W. R., and Ye, J. H. (2005). A Temperature Phenomenological Model with Mass Element of Magnetorheological Damper. Eng. Mech. 22, 144–148. doi:10.1080/02726340590910084

CrossRef Full Text | Google Scholar

Xue, D., Zhao, C., and Chen, Y. Q. (2006). A Modified Approximation Method of Fractional Order System. IEEE Int. Conf. Mechatronics Automation. IEEE., 1043–1048. doi:10.1109/icma.2006.257769

CrossRef Full Text | Google Scholar

Yang, J., Du, H., Li, W., Li, Y., Li, J., Sun, S., et al. (2013). Experimental Study and Modeling of a Novel Magnetorheological Elastomer Isolator. Smart Mater. Struct. 22, 117001. doi:10.1088/0964-1726/22/11/117001

CrossRef Full Text | Google Scholar

You, H., Shen, Y., Xing, H., and Yang, S. (2018). Optimal Control and Parameters Design for the Fractional-Order Vehicle Suspension System. J. Low Frequency Noise, Vibration Active Control. 37, 456–467. doi:10.1177/0263092317717166

CrossRef Full Text | Google Scholar

Zhang, J., Pang, H., Wang, Y., and Gong, X. (2020). The Magneto-Mechanical Properties of off-axis Anisotropic Magnetorheological Elastomers. Composites Sci. Technol. 191, 108079. doi:10.1016/j.compscitech.2020.108079

CrossRef Full Text | Google Scholar

Zhang, X., Peng, S., Wen, W., and Li, W. (2008). Analysis and Fabrication of Patterned Magnetorheological Elastomers. Smart Mater. Struct. 17, 45001–45005. doi:10.1088/0964-1726/17/4/045001

CrossRef Full Text | Google Scholar

Zhu, H., Rui, X., Yang, F., Zhu, W., and Wei, M. (2019). An Efficient Parameters Identification Method of Normalized Bouc-Wen Model for MR Damper. J. Sound Vibration 448, 146–158. doi:10.1016/j.jsv.2019.02.019

CrossRef Full Text | Google Scholar

Zhu, J.-T., Xu, Z.-D., and Guo, Y.-Q. (2012). Magnetoviscoelasticity Parametric Model of an MR Elastomer Vibration Mitigation Device. Smart Mater. Struct. 21 (7), 075034. doi:10.1088/0964-1726/21/7/075034

CrossRef Full Text | Google Scholar